-
在半导体制造、空间工程及薄膜沉积等真空应用中(10−8 Pa至常压),气体流量与压力的精准控制是保障纳米级工艺(如原子层沉积)和微推进系统稳定运行的关键因素[1-2]。压电微调阀基于压电陶瓷(如 PZT-5H 材料)的逆压电效应[3],通过亚微米到数十微米的位移控制实现亚毫秒级响应与低功耗运行,相较于传统电磁/气动阀门在响应时间、流量分辨率及功耗方面有明显优势,成为真空精密控制的理想方案,广泛应用于半导体、光学、航天航空、机械制造等领域[4-5]。此外,压电微调阀还具有对磁场不敏感的特性,是少数能用于磁约束核聚变装置进气控制的阀门之一[6]。然而,压电材料电畴翻转的热激活过程与畴壁运动的粘滞特性,使得压电微调阀流导值与激励信号之间的响应关系复杂[7-8],同一激励信号下多次响应一致性不高,严重制约高精度闭环控制的实现。
现有研究多聚焦于压电材料的电−机耦合模型及控制理论方面的探索[9-12],通过建立压电材料的本构方程,对电场与机械应变之间的非线性关系进行分析,并针对压电陶瓷的迟滞效应提出了多种数学描述方法以优化控制精度。然而,以上研究多基于理想化条件,对真空系统压力调控的实际工况中压电微调阀气体流导特性与不同激励信号之间关系的实验研究较少。
针对以上问题,本文设计了一种压电微调阀流导特性测试系统,选择真空装备常用的压电微调阀作为研究对象,对不同激励电压幅值、波形和施加历史作用下压电微调阀流导特性进行了实验研究和分析讨论。
-
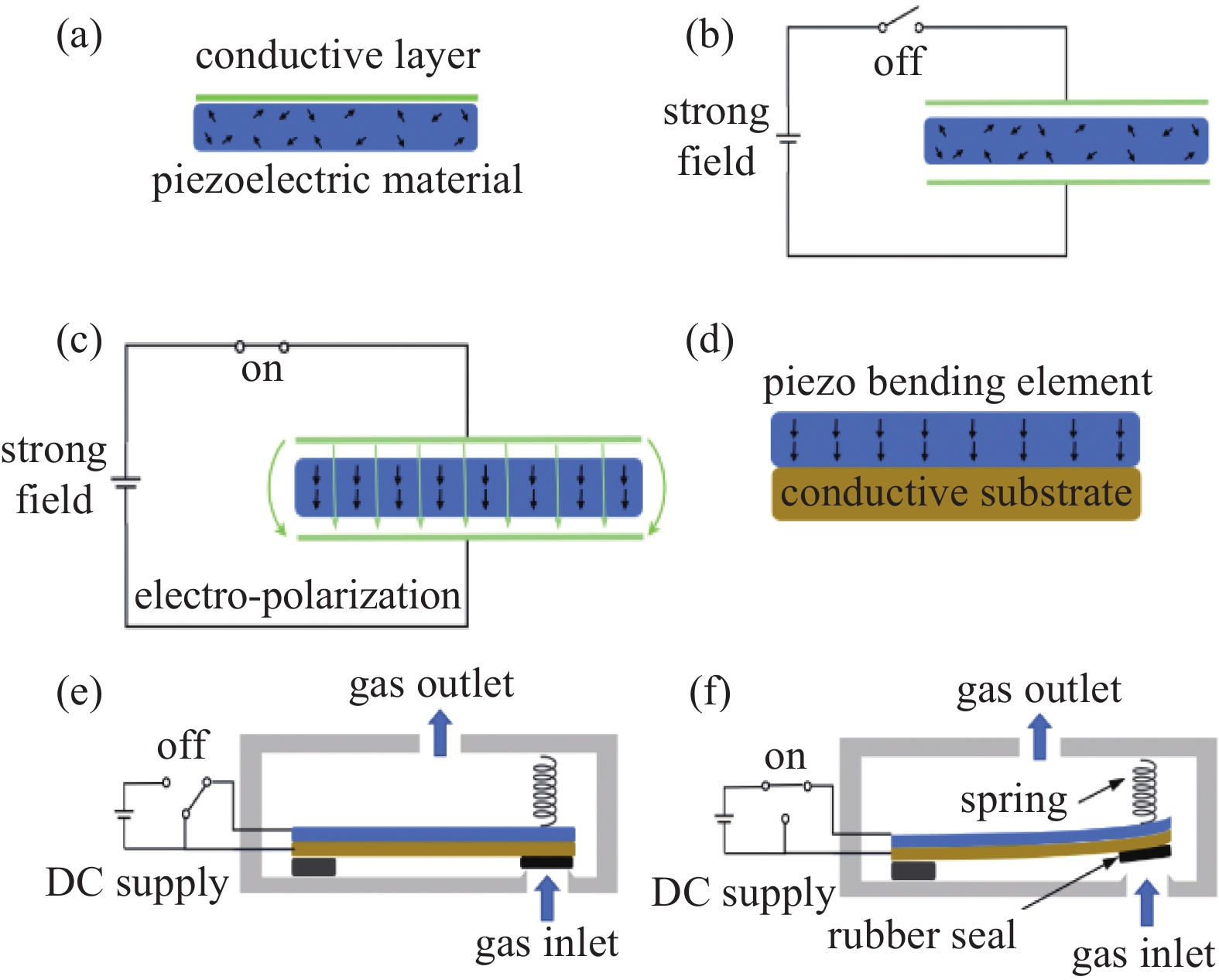
压电微调阀的核心组件是基于压电陶瓷材料的极化特性设计的。压电陶瓷在居里温度以下具有不对称晶格结构[8],在其表面制备上导电层后(如图1(a)),可以通过强电场极化处理形成定向电畴(如图1(b)、图1(c))。极化后的压电材料具有逆压电效应,即施加直流电压时,压电陶瓷沿电场方向伸长(正应变),垂直方向收缩(负应变)。
如图1(d)所示,一般可以将导电层基板与极化的压电陶瓷材料结合制成压电弯曲组件,作为压电微调阀的核心动作组件。图1(e)和图1(f)展示了一种典型的压电微调阀构成示意图:阀门主要由压电弯曲组件、板弹簧及外壳构成,压电弯曲组件上有氟橡胶密封圈。当在极化的压电陶瓷材料两端不施加直流电压时,板弹簧会压住压电弯曲组件,氟橡胶密封圈与外壳刀口形成良好密封,隔绝进气口进气;当在极化的压电陶瓷材料两端施加一定范围的直流电压,压电弯曲组件发生弯曲变形,总的形变量可在亚微米到几十微米范围内,固定在压电陶瓷片上的氟橡胶密封圈轻微地抬起形成一个细小孔隙,阀门进气端的气体便通过该孔隙流到阀门出气端。施加不同直流电压时,压电弯曲组件产生不同程度的弯曲变形,依此,可以在进气端和出气端之间形成不同的气体流导结构,在一定范围内实现对出口流量连续调节的功能。
本文中选取一款常用于真空系统压力控制的压电微调阀作为测试研究的对象,其主要技术参数如表1所示。
-
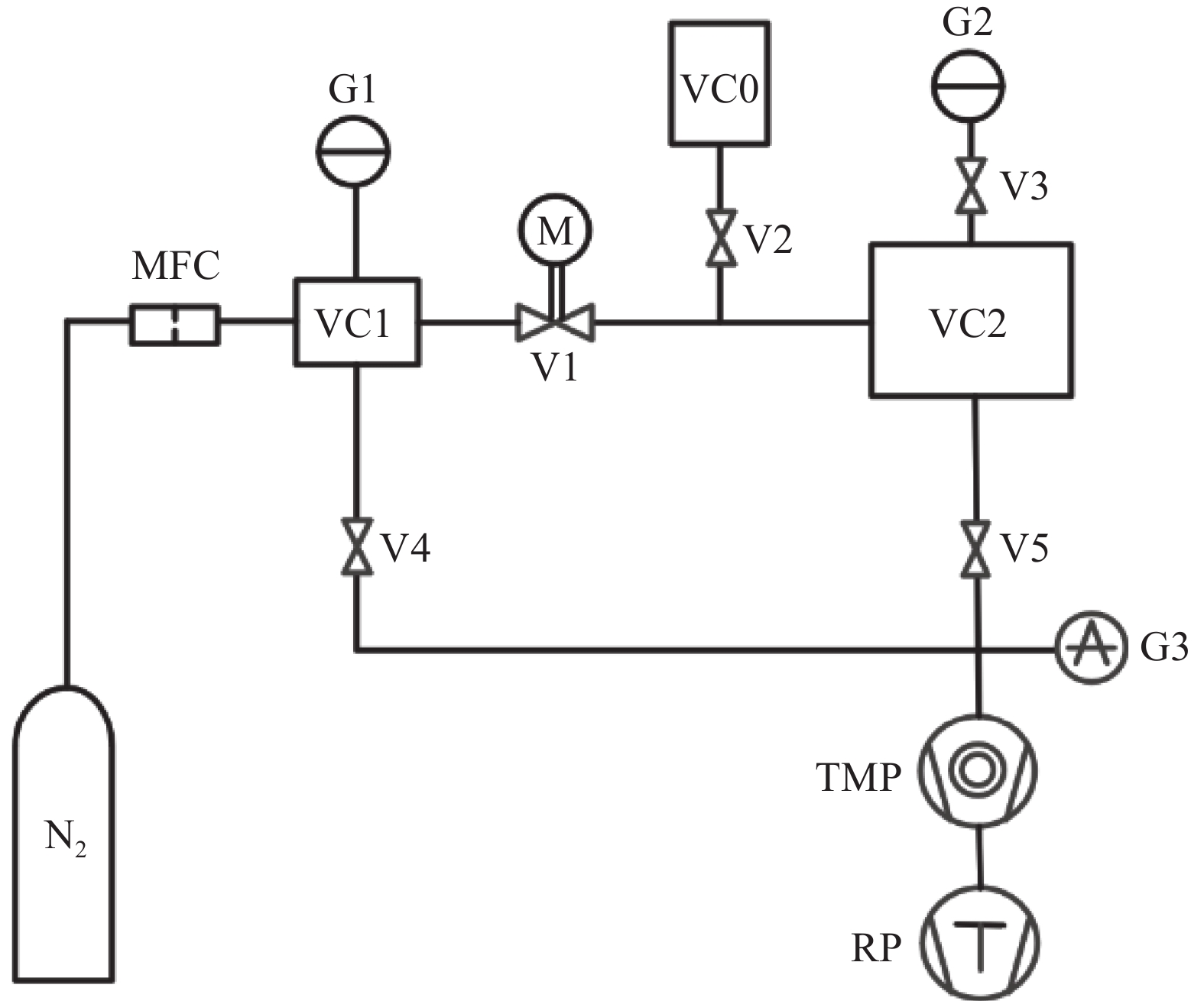
为了能够对压电微调阀在不同激励信号下的流导特性进行精确测试,设计了一种基于定容法的压电微调阀的流导特性测试系统。测试系统主要由被测压电微调阀、稳压室、标准容积室、定容室、供气单元、测量单元、抽气单元和数采与控制单元组成,结构原理如图2所示。
被测压电微调阀门V1安装在稳压室VC1和定容室VC2之间。标准容积室VC0的容积经专业计量机构计量,体积为0.9993 L,用以利用静态膨胀的方法[13]精确测量定容室VC2及附属管道容积。安装好被测压电微调阀V1后,定容室VC2的容积经测定为9.976 L (此时阀门V1、V2、V5为关闭状态,阀门V3为开启状态)。气体流量控制器MFC作用是对稳压室VC1进气流量反馈控制,使测量过程中被测压电微调阀入口压力保持在3×105 Pa附近。测量单元由满量程10000 Torr的高精度电容薄膜压力计G1、满量程1000 Torr的高精度电容薄膜压力计G2和全量程真空计G3组成,G1和G2分别测量稳压室VC1和定容室VC2内的压力,G3用来监测分子泵泵口的压力。控制单元主要作用是对压电微调阀V1、气体流量控制器MFC、真空泵组进行调节和开关控制,对测量单元进行实时数据采集,以及通过闭环PID控制保持测量过程中稳压室VC1的压力稳定。
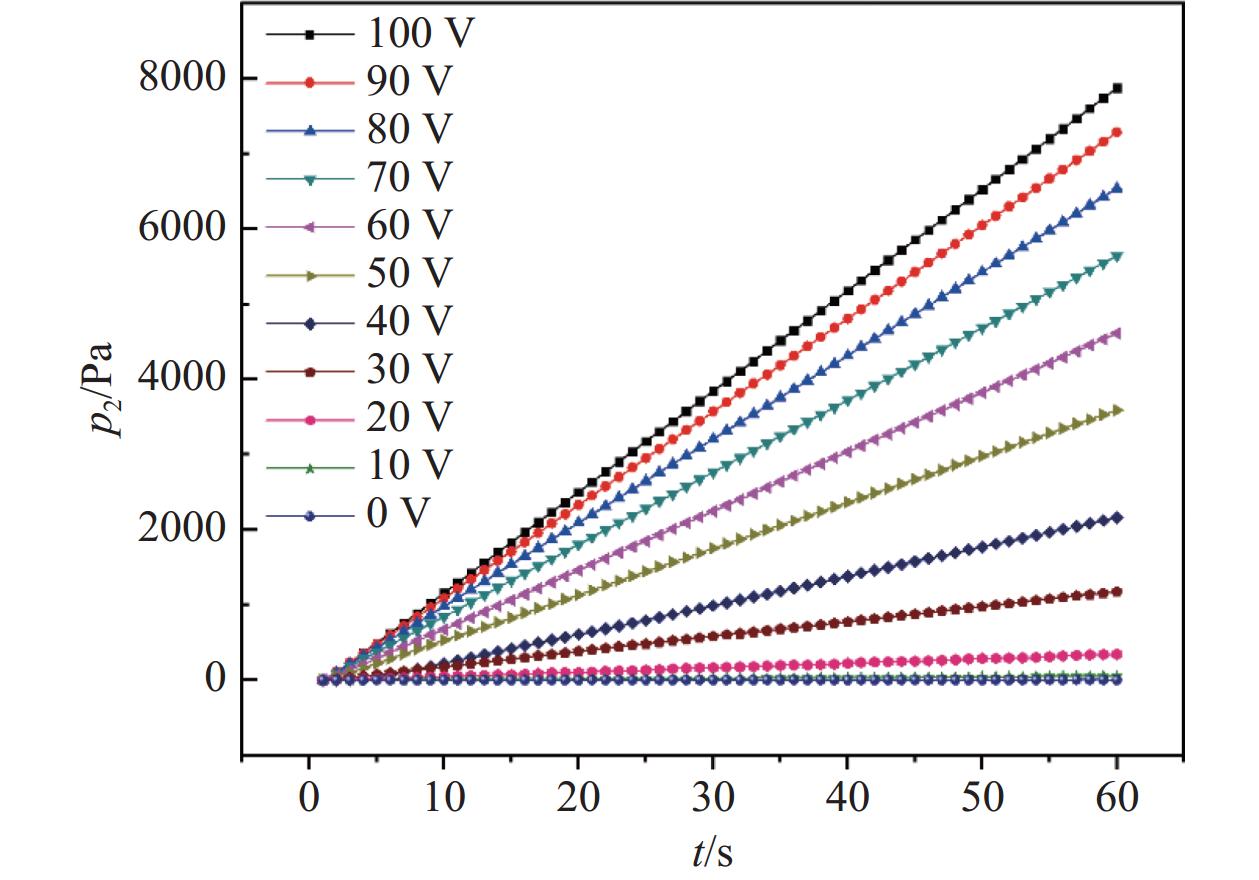
对压电微调阀V1流导特性进行测试时,首先利用质谱检漏仪对测试系统进行检漏,确保各个接口单点漏率<5×10−10 Pa·m3/s,避免外部气体泄漏对测试数据的影响。之后打开真空截止阀V4、V5利用干泵RP、分子泵TMP对稳压室VC1和定容室VC2进行抽气,当真空计G3示数低于1×10−3 Pa后结束抽气,以此排除杂质气体对测试结果的影响;然后打开氮气气源(纯度99.99%),通过气体流量控制器MFC和电容薄膜真空计G1的反馈控制,将稳压室VC1的压力控制在3×105 Pa附近;利用控制单元将设定激励电压施加给压电微调阀V1,此时刻记为t1,一定时间后,将激励电压调至0 V,此时刻记为t2,记录此过程中电容薄膜真空计G1和G2的压力变化。根据试验数据,控制单元可以将稳压室VC1内气体压力
$ {p}_{1} $ 稳定维持在3×105 Pa,压力波动不超过±1.5%。定容室VC2中压力$ {p}_{2} $ 变化如图3所示。由图3可知,定容室VC2内压力随时间呈现良好的线性增长,这说明在入口压力和激励电压恒定的情况下,通过压电微调阀流入低压状态(最大压力低于1×104 Pa)的定容室VC2的气体流量保持持续稳定。流入定容室VC2的气体体积流量可以通过公式(1)和公式(2)进行计算[14-15]:
式中,
${Q_{\mathrm{i}}}$ 为某一激励电压下流过压电微调阀气体的体积流量,单位为Pa·m3/s;$ {C_{\mathrm{i}}} $ 为某一激励电压下压电微调阀流导值,单位为m3/s;$ {p_1} $ 为稳压室VC1内压力、$ {p_2} $ 为定容室VC2内压力,单位为Pa;$V$ 为定容室VC2及附属管道的容积,单位为m3;${t_1}$ 和${t_2}$ 分别为压电微调阀被施加激励电压后开始测量压力$ {p_2} $ 的时刻和终止测量的时刻;$\Delta p$ 为${t_1}$ 和${t_2}$ 时刻之间压力$ {p_2} $ 的变化值。由于稳压室内压力
$ {p_1} $ 约为3×105 Pa,远大于测试过程中定容室压力$ {p_2} $ (最大约为8×103 Pa),联立公式(1)和(2)并简化后,可以将被测压电微调阀流导值用以下公式进行计算: -
本文对不同激励电压作用下压电微调阀的流导特性进行精确实验测试和讨论分析,以系统评价压电微调阀的流导调节性能,并探索提高调节稳定性的方法。
-
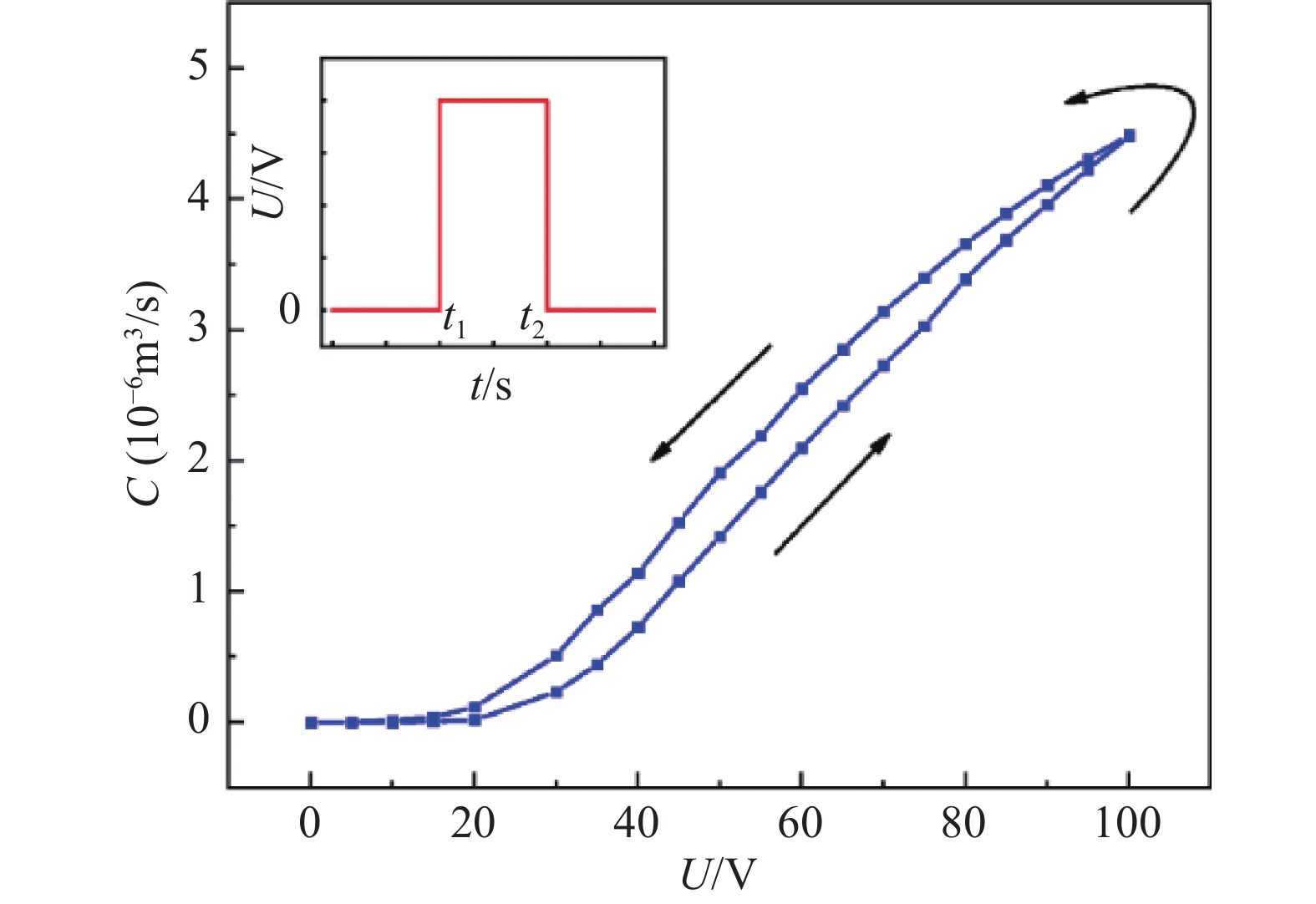
按照前文所述方法,测试了不同激励电压下压电微调阀的流导值。如图4中插图所示,每次施加给压电微调阀的激励电压均从0 V直接升至设定电压Ui,恒定一定时间后降回到0 V。以5 V为步长,依次序对0 V~100 V和100 V~0 V的激励电压下压电微调阀的流导值进行了连续测试。每个激励电压下流导值测量时长为60 s,相邻两次测量间隔约为5 min,以便通过抽气单元抽除定容室内测试气体,进行压力复原。
测试结果如图4所示,在激励电压0 V~100 V升压过程的测试中,在20 V以下,压电微调阀流导值较小,随激励电压升高,流导值的绝对值变化不大;在20 V以上,随着激励电压的升高,压电微调阀的流导值基本呈线性增大趋势,由1.85×10−8 m3/s(激励电压为20 V时)增至4.48×10−6 m3/s(激励电压为100 V时)。在激励电压100 V~0 V降压过程的测试中,流导值变化规律和0 V~100 V过程大致类似,但是在相同激励电压下,降压过程流导值明显高于升压过程,如在激励电压为50 V时,流导值相对差异达到35%((较大值−较小值)/较小值),使得流导值随激励电压变化的循环曲线出现明显回滞现象,说明压电微调阀的流导值与施加激励电压的历史有关。出现这种现象的原因可能是,在经历高电压激励(100 V)后,阀门压电材料内部残留应力的释放或电畴结构重新排列具有弛豫特征,需要较长的时间的才能完全恢复初始状态[7],导致降压过程中同一电压下的形变量较升压过程更大,表现为流导值增大。
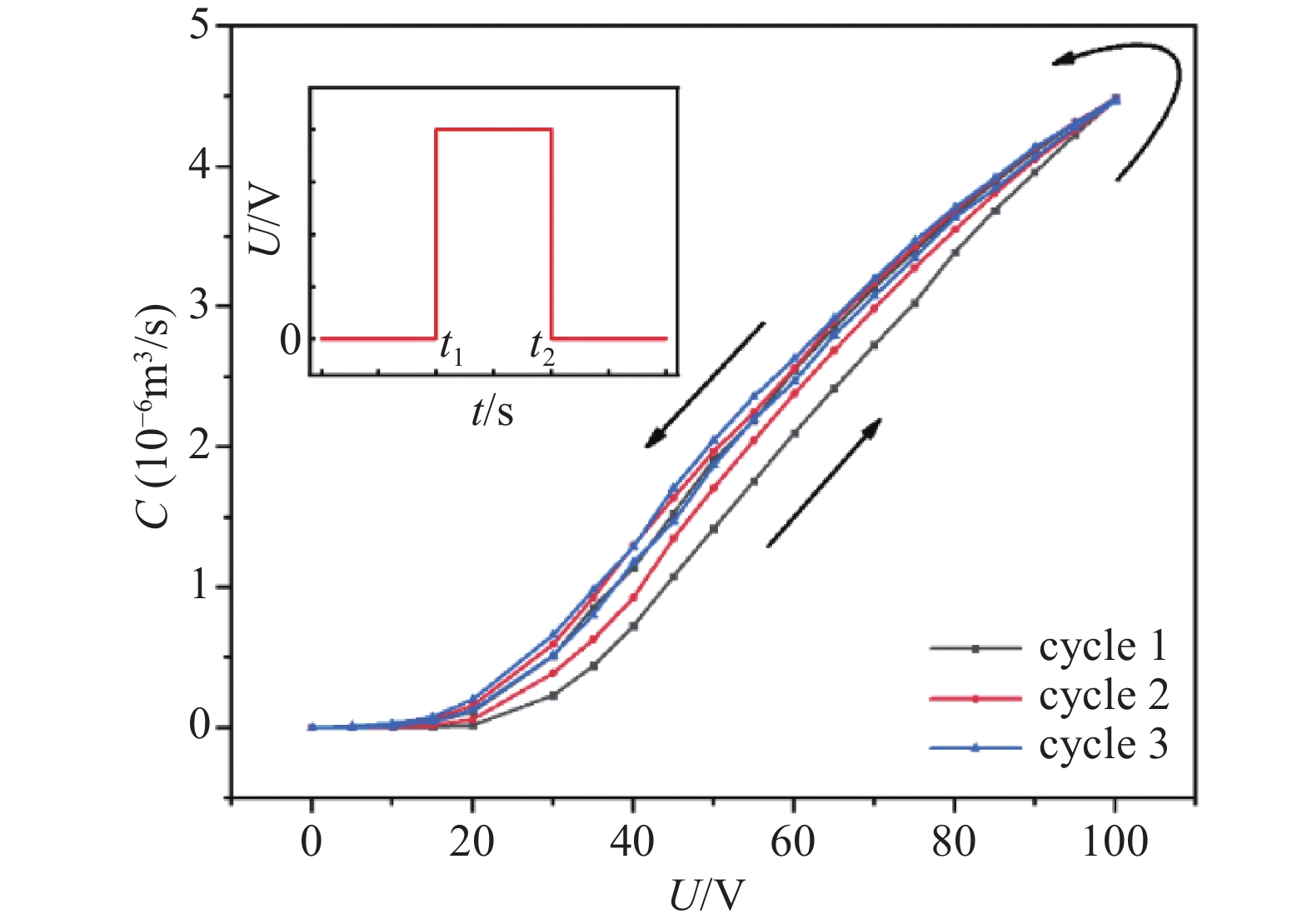
为了进一步研究压电微调阀流导与激励电压施加历史的关系,测试了3个连续循环下的流导值与激励电压的变化关系,结果如图5所示。
由图5可知,在每个循环中,在对压电微调阀施加相同激励电压条件下,均是升压过程的流导值大于降压过程的流导值,但二者的差值随循环次数的增多而明显减小,表现为流导值随激励电压变化循环曲线的回滞性随循环次数增大而明显减小。对于不同的循环,升压过程中相同激励电压下流导值随循环次数增多而出现明显增大,而降压过程中,相同激励电压下流导值随循环次数增多无明显变化。这可能是由于阀门压电材料经历100 V的高电压激励后出现较大的残留应力和电畴结构改变,电畴结构弛豫和残余应力释放具有时间依赖性,与之时间间隔越短影响越大,表现为降压过程具有较大且相对稳定的流导。而且这种高电压激励产生的残余应力和电畴结构的改变具有一定塑性,随着循环次数增多而加强,从而使循环曲线的回滞特性随循环次数增多而减弱[7,16-17]。
-
根据3.1节中压电微调阀流导值与激励电压循环曲线的分析,阀门流导不仅与当前激励电压幅值有关,与其经历的历史激励电压也有关。为进一步厘清阀门流导与激励电压施加历史关系,对不同波形激励电压下的压电微调阀流导值进行了测试。
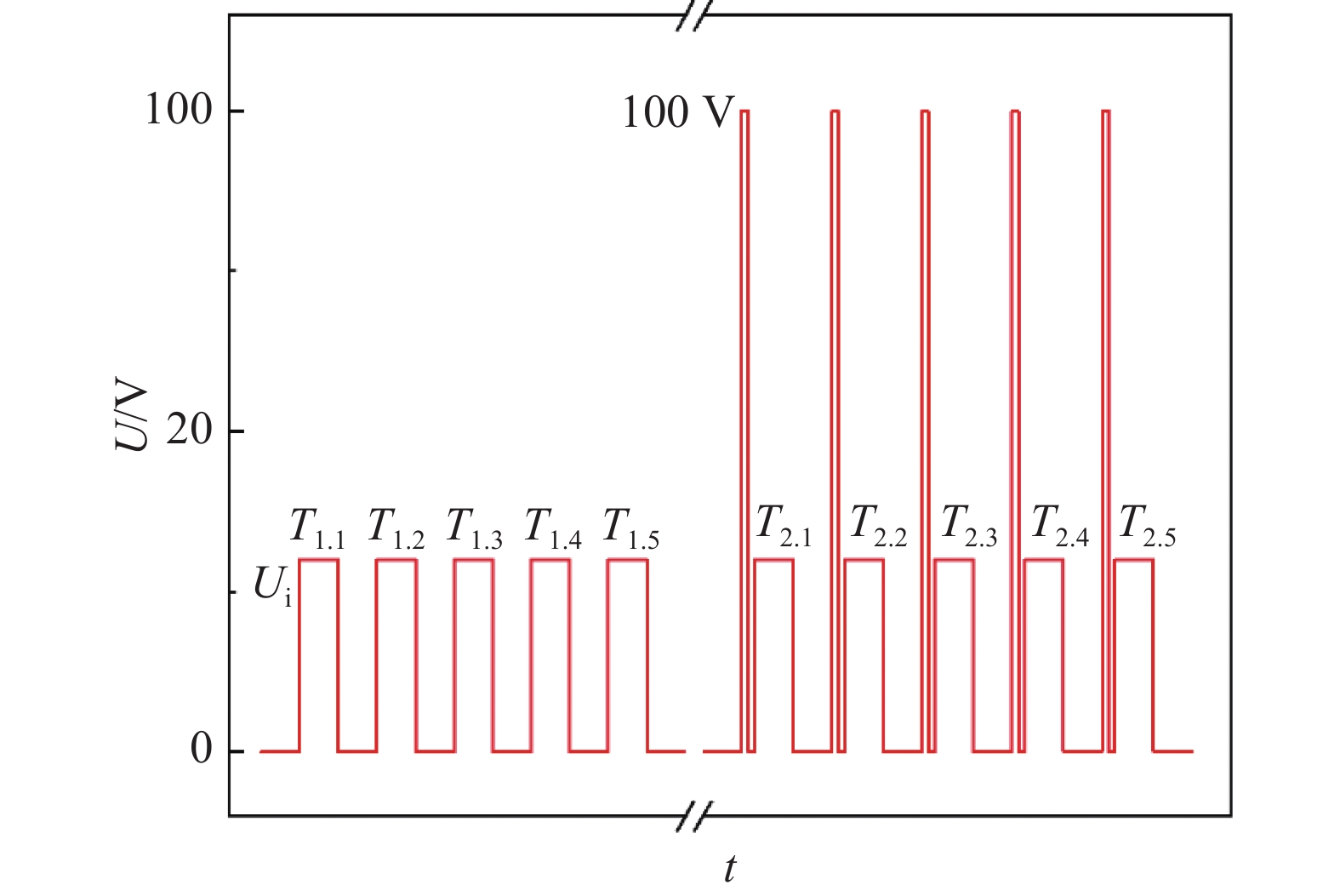
根据压电微调阀流导值随激励电压的变化曲线,选择30 V、50 V和70 V等作为典型目标激励电压进行流导值重复性测试。如图6所示,对于某一目标激励电压Ui,进行两组实验测试:T1组测试直接由0 V增加至Ui,维持恒定60 s,进行流导值测试,然后降至0 V;T2组测试先将激励电压调至100 V,维持恒定10 s后再降至0 V,等待10 s再升高至Ui,维持恒定60 s,进行流导值测试,然后降至0 V。各组测试均重复5次,每次测试之间均对定容室进行真空抽气,所需间隔时间约为5 min。测试结果如表2所示。
重复性用相对标准偏差来表示,计算公式如下:
式中:RSD为相对标准偏差,为无量纲数;s为5次流导测试结果的标准偏差,单位为m3/s;
$ \overline{C} $ 为5次流导测试结果的平均值,m3/s。根据表2的实验数据,不同激励电压施加历史对压电微调阀流导特性的影响显著。对于30 V、50 V和70 V三种目标激励电压,直接升压至目标激励电压(T1组)与施加100 V预处理后再降至目标激励电压(T2组)的流导值及重复性存在明显差异。在30 V激励电压下,T1组的平均流导值为4.36×10−7 m3/s, RSD为6.51%,而T2组的平均流导值提升至5.83×10−7 m3/s,RSD降至2.42%。类似地,在50 V和70 V时,T2组的平均流导值(50 V: 1.93×10−6 m3/s;70 V: 3.16×10−6 m3/s)均高于T1组(50 V: 1.72×10−6 m3/s;70 V: 3.00×10−6 m3/s),且重复性显著改善(50 V RSD从4.45%降至1.49%;70 V RSD从2.34%降至0.73%)。这一现象验证了 3.1 节关于高电压激励可优化压电材料电畴结构的弛豫行为和材料内部应力分布,获得一致性较高的初始状态,从而降低后续低电压下的形变滞后效应的猜想。值得注意的是,不同电压下的改善幅度存在差异,表明预激励对低目标激励电压调控的补偿效果更显著,这可能与压电陶瓷在低场强下的畴壁运动更易受历史电压影响有关。
-
本文针对应用于真空系统的压电微调阀流导调控不稳定的情况,设计了一种基于定容法的流导特性测试系统,通过测试实验,分析研究了激励电压幅值、波形和施加历史等因素对压电微调阀流导的影响。结果表明:压电微调阀的流导−激励电压循环曲线呈现明显回滞效应,降压过程流导值较升压过程平均偏高 15%~35%,说明阀门流导与激励电压施加历史有关,其机制可能源于压电陶瓷电畴结构弛豫和残余应力释放的时间依赖性;通过预加 100 V 高电压激励策略,使 30 V、50 V、70 V 目标激励电压下的流导值相对标准偏差明显下降,说明激励响应重复性明显提高,可能源于高电压预激励可有效提高压电材料内部应力分布与电畴排列的一致性,进而提高了阀门流导对同一激励信号响应的重复性。该研究揭示了激励电压历史对阀门流导特性的关键影响,可以为工程应用中通过预激励策略提升真空系统压力控制精度提供实验依据和新思路。
适用于真空系统的压电微调阀门流导测试和调节特性研究
Flow Conductance and Regulatory Properties of Piezoelectric Microvalves for Vacuum Systems
-
摘要: 针对真空系统中压电微调阀流导调控稳定性不足的问题,文章设计了一种基于定容法的流导特性测试系统,研究了激励电压幅值、波形及施加历史对典型压电微调阀流导特性的影响。实验结果表明,压电微调阀的流导−激励电压循环曲线存在显著回滞效应,降压过程流导值较升压过程均显著偏高,其机制可能与压电陶瓷电畴结构弛豫和残余应力释放的时间依赖性相关。通过预加100 V高电压激励,典型激励电压下的流导值重复性显著提升,说明了预激励可优化电畴结构排列和残余应力分布一致性并降低形变滞后效应。该研究揭示了激励电压施加历史对压电微调阀流导调节性能的关键影响,为提升真空系统压力控制精度提供了实验依据和思路。Abstract: To address the instability in flow conductance regulation of piezoelectric micro-adjustment valves used in vacuum systems, this study designs a flow conductance measurement system based on the constant-volume method, investigating the effects of excitation voltage amplitude, waveform, and application history on the flow characteristics of a typical piezoelectric micro-adjustment. Experimental results reveal significant hysteresis in the flow conductance-excitation voltage cyclic curve, where the flow conductance during voltage reduction was notably higher than during voltage increase, likely due to the time-dependent relaxation of piezoelectric ceramic domain structures and residual stress release. A high voltage pre-excitation with 100 V is applied, leading to remarkable improvements in the repeatability of flow conductance at typical voltages. This indicates that pre-excitation optimizes domain structure alignment and residual stress distribution consistency, reducing deformation hysteresis. The research uncovers the critical influence of excitation voltage application history on flow regulation performance, providing experimental evidence and insights for enhancing pressure control precision in vacuum systems.
-
Key words:
- Piezoelectric micro-adjustment valve /
- Flow conductance /
- Excitation voltage /
- Pressure control .
-

-
图 1 压电微调阀结构示意图。(a)压电材料电极结构,(b)极化前电畴结构,(c)极化后电畴结构,(d)压电弯曲组件结构,(e)未施加直流电压的阀门,(f)施加直流电压后阀门
Figure 1. Schematic diagram of piezoelectric ceramic valve structure. (a) The electrode structure of piezoelectric material, (b) electric domains before polarization, (c) electric domains after polarization, (d) piezoelectric bending component, (e) valve without driving DC voltage, (f) valve with driving DC voltage
表 1 被测压电微调阀标称技术参数
Table 1. Nominal technical parameters of the piezoelectric micro-adjustment valve under test
技术参数 数值 流量范围 0~500 sccm 漏率(激励电压0 V时) 1×10−6 Pa·L/s 最大进气压力 50 PSI 驱动电压 0−100 VDC 驱动电流 <10 μA 工作温度 10℃~60℃ 表 2 施加不同时序激励电压下压电微调阀的流导值
Table 2. Flow conductance of the piezoelectric micro-adjustment valve under different waveforms of excitation voltage
Ui 测试序号 流导值/
(m3/s)重复性RSD 30 V T1.1 4.20×10−7 6.51% T1.2 4.05×10−7 T1.3 4.78×10−7 T1.4 4.37×10−7 T1.5 4.52×10−7 T2.1 5.91×10−7 2.42% T2.2 5.76×10−7 T2.3 5.64×10−7 T2.4 6.01×10−7 T2.5 5.82×10−7 50 V T1.1 1.64×10−6 4.45% T1.2 1.81×10−6 T1.3 1.65×10−6 T1.4 1.73×10−6 T1.5 1.78×10−6 T2.1 1.97×10−6 1.49% T2.2 1.91×10−6 T2.3 1.90×10−6 T2.4 1.93×10−6 T2.5 1.95×10−6 70 V T1.1 2.98×10−6 2.34% T1.2 2.96×10−6 T1.3 3.07×10−6 T1.4 3.08×10−6 T1.5 2.92×10−6 T2.1 3.17×10−6 0.73% T2.2 3.14×10−6 T2.3 3.20×10−6 T2.4 3.16×10−6 T2.5 3.15×10−6 -
[1] Huff M. Review—Important considerations regarding device parameter process variations in semiconductor-based manufacturing[J]. ECS Journal of Solid State Science and Technology, 2021, 10(6): 064002 doi: 10.1149/2162-8777/ac02a4 [2] Zhao C S, Zhang J T, Zhang J H, et al. Development and application prospects of piezoelectric precision driving technology[J]. Frontiers of Mechanical Engineering in China, 2008, 3(2): 119−132 doi: 10.1007/s11465-008-0034-1 [3] 张涛, 孙立宁, 蔡鹤皋. 压电陶瓷基本特性研究[J]. 光学 精密工程, 1998, 6(5): 26−32 (in Chinese) Zhang T, Sun L N, Cai H G. Study on the fundamental characteristics of piezoelectric element[J]. Optics and Precision Engineering, 1998, 6(5): 26−32 [4] Nunn W, Truttmann T K, Jalan B. A review of molecular-beam epitaxy of wide bandgap complex oxide semiconductors[J]. Journal of Materials Research, 2021, 36(23): 4846−4864 doi: 10.1557/s43578-021-00377-1 [5] Deng L S, Ling M X. Design and integrated stroke sensing of a high-response piezoelectric direct-drive valve enhanced by push-pull compliant mechanisms[J]. Review of Scientific Instruments, 2022, 93(3): 035008 doi: 10.1063/5.0067483 [6] Griener M, Schmitz O, Bald K, et al. Fast piezoelectric valve offering controlled gas injection in magnetically confined fusion plasmas for diagnostic and fuelling purposes[J]. Review of Scientific Instruments, 2017, 88(3): 033509 doi: 10.1063/1.4978629 [7] Arlt G. Domain contributions to piezoelectricity in ceramics[C]//Proceedings of the IEEE Symposium on Ultrasonics, Honolulu, USA: IEEE, 1990: 733−742 [8] Kim S, Miyauchi R, Sato Y, et al. Piezoelectric actuation mechanism involving extrinsic nanodomain dynamics in lead-free piezoelectrics[J]. Advanced Materials, 2023, 35(11): 2208717 doi: 10.1002/adma.202208717 [9] 王义冬, 李庆春, 赵慧. 压电陶瓷驱动器迟滞非线性误差的建模与分析[J]. 计算机测量与控制, 2023, 31(2): 196−203 (in Chinese) Wang Y D, Li Q C, Zhao H. Modeling and analysis of hysteresis nonlinear error of piezoelectric ceramic actuator[J]. Computer Measurement & Control, 2023, 31(2): 196−203 [10] 于志亮, 刘杨, 王岩, 等. 基于改进PI模型的压电陶瓷迟滞特性补偿控制[J]. 仪器仪表学报, 2017, 38(1): 129−135 (in Chinese) doi: 10.3969/j.issn.0254-3087.2017.01.017 Yu Z L, Liu Y, Wang Y, et al. Hysteresis compensation and control of piezoelectric actuator based on an improved PI model[J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 129−135 doi: 10.3969/j.issn.0254-3087.2017.01.017 [11] 陈海初, 王宣银, 张蕊华, 等. 压电陶瓷驱动精密流量阀的设计与建模[J]. 浙江大学学报(工学版), 2008, 42(11): 1936−1939, 1945 (in Chinese) Chen H C, Wang X Y, Zhang R H, et al. Design and modeling of precise flux valve driven by piezoelectric ceramics[J]. Journal of Zhejiang University (Engineering Science), 2008, 42(11): 1936−1939, 1945 [12] 胡小玲, 徐科军, 杨庆庆, 等. 压电比例式阀门定位器的控制方法研究[J]. 电子测量与仪器学报, 2011, 25(11): 978−984 (in Chinese) Hu X L, Xu K J, Yang Q Q, et al. Study on control method of proportional piezoelectric valve positioner[J]. Journal of Electronic Measurement and Instrumentation, 2011, 25(11): 978−984 [13] 于红燕, 王池, 赵士燕, 等. 静态膨胀法真空系统[J]. 真空科学与技术学报, 2008, 28(1): 90−93 (in Chinese) Yu H Y, Wang C, Zhao S Y, et al. Development of static expansion vacuum system[J]. Chinese Journal of Vacuum Science and Technology, 2008, 28(1): 90−93 [14] 姚雪琦, 董云宁, 闫睿, 等. 便携式分压力质谱计校准装置的性能测试研究[J]. 真空科学与技术学报, 2024, 44(4): 306−311 (in Chinese) Yao X Q, Dong Y N, Yan R, et al. Performance study on portable calibration apparatus of mass spectrometers for partial pressure[J]. Chinese Journal of Vacuum Science and Technology, 2024, 44(4): 306−311 [15] 卢耀文, 陈旭, 李得天, 等. 便携式真空计校准装置[J]. 真空科学与技术学报, 2013, 33(5): 462−467 (in Chinese) doi: 10.3969/j.issn.1672-7126.2013.05.13 Lu Y W, Chen X, Li D T, et al. Novel type of portable vacuum gauge calibration apparatus[J]. Chinese Journal of Vacuum Science and Technology, 2013, 33(5): 462−467 doi: 10.3969/j.issn.1672-7126.2013.05.13 [16] Yang C S, Shang D S, Chai Y S, et al. Electrochemical-reaction-induced synaptic plasticity in MoOx-based solid state electrochemical cells[J]. Physical Chemistry Chemical Physics, 2017, 19(6): 4190−4198 doi: 10.1039/C6CP06004H [17] Zhai K, Shang D S, Chai Y S, et al. Room-temperature nonvolatile memory based on a single-phase multiferroic hexaferrite[J]. Advanced Functional Materials, 2018, 28(9): 1705771 doi: 10.1002/adfm.201705771 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: