等离激元光电器件是基于金属纳米结构的表面等离激元共振现象^[1,2], 通过急剧增强近场区域的电场强度和对光的捕获能力, 从而大幅度提高光电探测器性能. 与传统光电器件不同, 等离激元光电器件利用表面等离激元非辐射衰减产生的高能、非平衡“热”电子-空穴对(热载流子)实现高效的能量转换, 并调节热载流子的能量分布^[3,4], 这为热载流子光电器件带来全新发展机遇. 作为等离激元光电器件实践应用的基础, 寻找性能优异的等离激元金属材料一直是热载流子光电器件领域关注的重要课题之一. 近年来, 二维材料, 如石墨烯^[5]、石墨烯衍生物和二维层状结构过渡金属碳化物、氮化物(MXenes)等由于元素含量丰富, 且具有大比表面积和高稳定性等优点, 成为一系列富有前景的等离激元金属材料. 特别地, MXenes展现出优异的光学性质、独特的电化学/化学可调的等离激元特性^[6], 其带间跃迁和等离激元共振峰覆盖了整个紫外、可见光和近红外范围^[7], 被认为有望取代石墨烯和其他二维材料, 成为等离激元光电器件领域理想候选材料之一. 例如, 2019年 Jeon 等^[8]构建了基于MXenes 混合结构的表面等离激元光电探测器, 在室温下实现了 10³ A/W 的高灵敏度和10²的高光开关比. 相比MoS₂ 光电探测器^[9], MXenes在光通信波长 1310 nm 处的灵敏度提高了3个数量级.

表面等离激元不可避免地以朗道弛豫(声子协助带内电子跃迁和直接带间电子跃迁)方式发生非辐射衰减, 并且产生大量热载流子(热电子和热空穴)^[10–12]. 紧接着, 热载流子迁移到金属材料表面从而在光电器件中产生电流信号. 该过程是表面等离激元应用于热载流子光电器件的物理基础. 理想的 MXenes 基等离激元光电器件需要具备环境稳定且持久的高效光探测能力, 因此迫切需要了解表面等离激元诱导热载流子的产生和输运特性在能量和空间尺度的信息. 目前为止, 人们对 MXenes 的独特表面等离激元热载流子特性展开了持续深入的实验和理论研究. 例如, Zhang等^[13]采用飞秒瞬态吸收谱捕获了 MXenes 等离激元的能量弛豫过程, 该研究通过监测电子和声子的动力学弛豫过程发现了等离激元的不同能量传输通道. Jermyn 等^[14]提出结合相空间和粒子方法的空间与能量非平衡散射(NESSE)理论计算框架, 将原子尺度的等离激元衰变和热载流子碰撞积分的第一性原理电子结构预测与纳米到中尺度的电磁场模拟联系起来, 从而预测了等离激元诱导热载流子的空间分辨能量分布特征. 此外, Liu等^[15]采用第一性原理和蒙特卡罗模拟方法研究 MXenes 热载流子动力学特征, 研究表明施加合适压缩应变可获得更高的热载流子平均自由程.

MXenes 基等离激元光电器件的探测性能环境稳定性与热载流子对环境温度的依赖关系密切相关. 环境温度对热载流子特性的影响贯穿始终, 包括热载流子的产生、能量空间分布特征和输运过程. 表面等离激元非辐射衰减产生热载流子的效率, 其温度依变性表现为环境温度对电子跃迁概率的影响, 从而反映在与电子结构密切相关的介电函数中. 例如, Han等^[16]采用第一性原理研究电子和声子的温度依变性, 从而获得了CeO₂的温度有关介电函数, 并且理论计算的CeO₂折射率与文献和温度相关椭偏仪实验的测量数据符合较好. Reddy 等^[17]使用原位高温椭偏仪获得 TiN 薄膜的温度依赖性介电函数, 研究表明高温环境下 TiN 的介电函数均偏离了室温下的光学参数, 因此与介电常数实部和虚部有关的等离激元特性也发生退化现象. 此外, Brown等^[18]鉴于超快激光实验中时间分辨光学探针在电子-声子相互作用测量限制, 提出了表面等离激元诱导热电子与温度相关的介电响应的第一性原理计算, 包括带间电子直接跃迁和声子协助的带内电子跃迁贡献. 同时, Brown等^[19]预测带间直接电子跃迁概率受环境温度影响较小, 而声子协助的电子跃迁概率由于低温下声子吸收冻结导致减小程度比较大. 因此, 环境温度不仅影响材料中表面等离激元诱导热载流子的产生效率, 而且导致产生热载流子的主导微观物理机制发生变化. 此外, 环境温度升高将加剧晶体材料的晶格振动, 导致电子-电子和电子-声子相互作用程度增大, 将直接影响热载流子的能量损耗与输运特性. 例如, Zhou 等^[20]基于第一性原理计算 SrTiO₃ 晶体中, 所有依赖温度的声子模式与电子-声子耦合强度参量, 预测热载流子在 150—300 K 之间的温度依变性迁移率. 王善江等^[21]指出表面等离激元诱导热载流子的弛豫及热耗散过程中, 光子、电子及声子的相互作用是高能热载流子逐渐热化的关键所在. 然而, 目前 MXenes 研究更侧重于构建探测性能优异的等离激元光电器件系统与结构^[8], 缺乏微观层面上热载流子特性对环境温度依赖关系的量化研究.

与石墨烯(graphene)、二硫化钼(MoS₂)和硼烯(borophene)等二维材料的固定表面端不同, MXenes 具有丰富表面官能团且极易被高温氧化改性, 从而对等离激元光电器件的寿命和性能稳定性产生极大影响. 鉴于实验研究连续变温条件下 MXenes 中热载流子动力学特性的限制问题, 本文采用基于现代量子力学理论的第一性原理计算方法, 从表面等离激元的非辐射衰减角度出发, 将温度效应引入带间电子直接跃迁和声子协助电子跃迁过程, 以获得表征热载流子产生效率的介电函数虚部值, 研究环境温度对Ti₃C₂T_xMXene中热载流子产生效率和能量空间分布的微观影响机制. 进一步地, 考虑环境温度对电子-电子散射和电子-声子散射效应的影响, 研究热载流子寿命与平均自由程对环境温度的依赖关系, 最终全面表征Ti₃C₂T_x MXene表面等离激元诱导热载流子对环境温度的依赖关系, 为量化评估实践环境中MXenes等离激元光电器件的环境温度稳定性提供理论与数据支持.

采用第一性原理计算开源代码 JDFTx^[22] 软件计算二维材料 Ti₃C₂T_x MXene 的电子结构, 声子谱和电子-声子相互作用矩阵元. 本文使用全相对论范数守恒赝势(SG15), Perdew-Burke-Ernzerh (PBE)广义梯度近似函数描述交换关联能量, 并且对 Ti₃C₂T_x的二维周期性结构设置平板模型以截断库仑相互作用^[23]. 此外, 平面波截止能量取值为 25 Hartrees (1 Hartree = 110.5×10²¹ J), Fermi-Dirac 展宽取值为 0.01 Hartrees, 以近似描述费米面的电子态分布. 针对优化后的 Ti₃C₂T_x晶体结构, 本文在第一布里渊区内使用以 Gamma 点为中心的 12× 12× 1 均匀k点网格计算能带结构, 并采用 3× 3× 1 超晶胞结构计算不同温度的声子谱和电子-声子相互作用矩阵元. 上述所有参数均经过收敛性测试, 可以获得准确可靠的数值计算结果.

紧接着, 将上述计算的电子能量、声子能量和电子-声子相互作用矩阵元, 分别转换为最大局域函数(MLWFs)基^[24,25]表示的形式, 以便在极细网格中获得任意采样点k 处的电子本征能量、声子能量和电声相互作用矩阵元素. 具体来说, 本文使用 35 个 Wannier 基带准确复现了 Ti₃C₂T_x费米能级以上 25 eV 内的电子态分布、声子能量和电子-声子矩阵元素值. 最后, 在第一布里渊区内利用蒙特卡罗采样以获得足够的密集采样点信息, 并通过积分求和实现对不同温度下 Ti₃C₂T_x中热载流子性质的量化计算.

表面等离激元通过朗道弛豫进行非辐射衰减, 其重要产物是高能热电子和热空穴. 当激发能量大于带间阈值时, 能量守恒要求电子跃迁的始末态能量差等于光子能量, 并且由于光子在电子尺度上的动量可以忽略不计, 因此动量守恒意味着始末态在相同的k 点. 基于微扰理论和费米黄金法则计算给定光强度下这一电子跃迁概率, 并由此确定相应的介电函数虚部为^[26]

式中, $\omega $ 是入射光频率; $ {f_{{\boldsymbol{k}}n}} = f\left( {{\varepsilon _{{\boldsymbol{k}}n}}, {{{T}}_{\mathrm{e}}}} \right) $ 是量子态 kn 处与电子温度${T_{\text{e}}}$有关的电子占据数, 采用 Fermi-Dirac 分布函数描述; ${E_{kn}}$ 是量子态kn处的电子态能量, 可通过第一性原理计算 Ti₃C₂T_x的电子结构获得; e是电子常数; ${m_{\text{e}}}$是电子有效质量; ${g_{\text{s}}}$是自旋因子; $ \left\langle {\boldsymbol{P}} \right\rangle _{n'm}^{{\boldsymbol{k}}'} $是相应量子态间的动量矩阵元. $\delta $函数描述带间电子直接跃迁过程所满足的动量和能量守恒.

当激发能量低于带间阈值时, 声子可以提供必要的动量满足电子跃迁规则. 基于二阶微扰理论计算给定光强度下声子协助的电子跃迁概率, 由此确定的相应介电函数虚部值计算公式为^[19]

式中, $ \hbar {\omega _{k, \alpha }} $是量子态$k\alpha $ 处的声子态能量; $ {n_{k' - k, \alpha }} = n\left( {\hbar {\omega _{k' - k, \alpha }}, {T_{\mathrm{l}}}} \right) $ 是量子态$k\alpha $ 处与晶格温度${T_{\mathrm{l}}}$有关的声子占据数, 采用 Bose-Einstein 分布函数描述; $ g_{k'n', kn}^{k' - k, \alpha } $是相应量子态 $k, k', \alpha , n, n'$ 处的电声相互作用矩阵元素值; $ \eta $是数值计算的约束参数; $\delta $函数描述声子协助电子跃迁过程所满足的动量和能量守恒.

基于上述精确计算的 Ti₃C₂T_x能带结构, 本文采用第一性原理计算获得与环境温度有关的电子-电子和电子-声子散射线宽, 进而表征热载流子的寿命和平均自由程与能量的函数关系, 以此讨论 Ti₃C₂T_x中热载流子输运性质的温度依变性.

针对电子-电子散射效应影响, 从随机相近似(random phase approximation, RPA)内准粒子自能虚部值计算的热载流子弛豫率为^[27,28]

式中, $ {{\mathrm{Im}}} \displaystyle\sum\nolimits_{kn}^{{\text{e-e}}} {} $是电子-电子散射产生的载流子线宽, 本文使用开源 JDFTx软件计算 Ti₃C₂T_x的电子-电子散射线宽. 其中, 积分频率的分辨率设置为 0.08 eV, 局域电场的截断能设置为 200 eV. 基于晶体结构的对称性特征, 采用上述参数设置计算 Ti₃C₂T_x在第一布里渊区内 48×48×1采样点k处, 电子-电子散射线宽以获得热载流子在量子态kn的弛豫率, 其计算结果经过了收敛性测试.

根据自由电子的 Fermi-liquid 理论, 电子-电子散射导致的热载流子弛豫率对环境温度的依赖关系可近似表示为^[29,30]

式中, ${D_{\text{e}}}/\hbar $ 是比例常数, 可通过计算室温下(300 K)的(3)式, 并结合(4)式拟合获得. 进一步地, 在(3)式中增大温度系数$\left(D_{\text{e}}/\hbar \right){\left( {{\text{π}}{k_{\text{B}}}} \right)^2}\left( {T_{\text{e}}^{2} - T_0^2} \right)$ 即可获得有限温度下的热载流子弛豫率.

针对电子-声子散射效应影响, 基于费米黄金法则计算不同环境温度下热载流子弛豫率为^[31,32]

式中${{\mathrm{Im}}} \displaystyle \sum\nolimits_{kn}^{{\text{e-ph}}} {} $是电子-声子散射产生的载流子线宽; $\eta $ 是一个非常小的洛伦兹展宽(约25 meV), 其中对环境温度的依赖性分别体现在电子态与声子态的占据数中. 对(5)式进行积分求和计算时, 采用与电子-电子散射计算的相同量子态$kn$, 并通过蒙特卡罗采样在第一布里渊区内获得 2× 10⁵ 采样点k, 以保证计算结果的收敛性. 此外, 本文通过控制声子模式参数 $\alpha $ 分别研究了声学声子和光学声子模式对应的电子-声子散射贡献.

综合考虑电子-电子和电子-声子散射贡献, 计算热载流子的寿命为

最后, 结合量子态$kn$处的热载流子平均群速度${\nu _{kn}}$, 即无质量狄拉克费米子的传输速度, 定义其平均自由程为

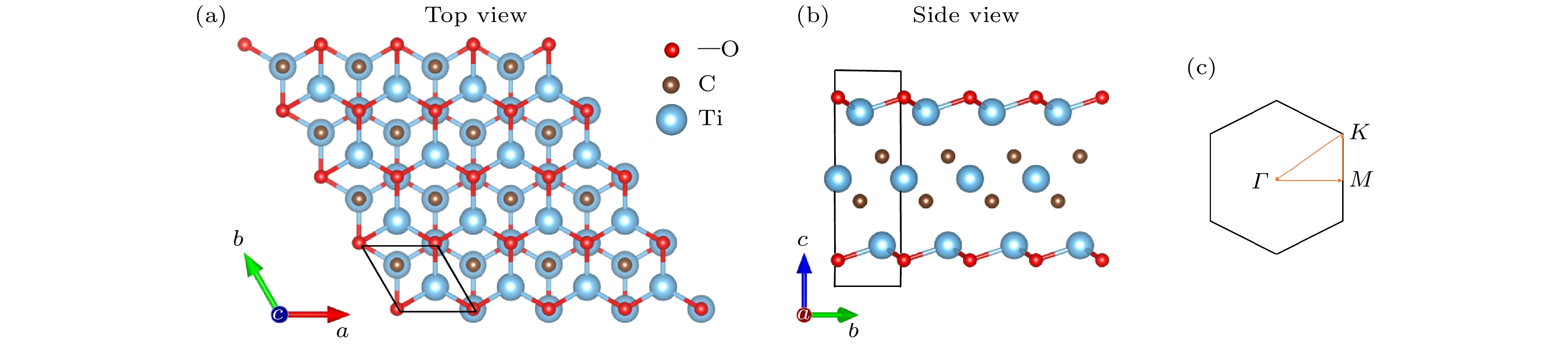
实验室通常是通过选择性蚀刻 Ti₃AlC₂ MAX 相以获得 Ti₃C₂T_x MXene 晶体^[33]. 与实验制备过程类似, 本文基于无机晶体数据库中 Ti₃AlC₂ 晶体结构^[34], 通过移除中间层的 Al 原子构建二维 Ti₃C₂T_x MXene 单层. 由于实验中大多数使用氟化物为主的刻蚀剂, MXenes 的暴露表面总以—F, —O 和—OH 基团封端, 并且高温环境下—OH 型基团非常容易转化为—O 型基团^[35,36], 因此本文主要讨论一定环境温度下 Ti₃C₂O₂ MXene 中热载流子的产生与输运特性. 图1 展示了优化后具有稳定构型的 Ti₃C₂O₂ MXene 单层, 其中表面官能团—O 位于3个相邻 C 原子的空心位置之上, Ti 原子位于两层 C 原子中间. 表1 列出了优化后 Ti₃C₂O₂ 的晶格常数, 显然本文构建的 Ti₃C₂O₂ 晶体结构参数与文献中的数据非常符合. 此外, 与母体 Ti₃AlC₂ 相比, 移除 Al 原子后 Ti₃C₂O₂ MXene 单层晶格常数减小.

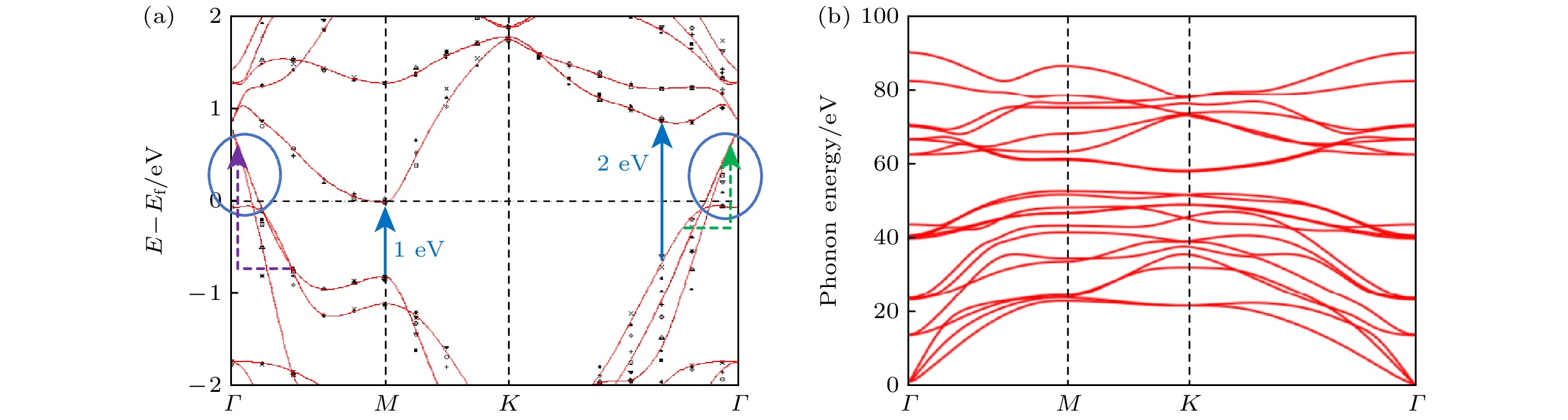
基于晶体结构对称性特征计算 Ti₃C₂O₂ MXene 电子态分布时, 如图2(a) 所示, 能带沿图1(c) 所示的第一布里渊区高对称点路径 $ \varGamma $-M-K-$ \varGamma $ 展开, 其中红色曲线代表 Wannier 能带分布, 黑色点代表 DFT 能带分布, 并且这两种理论计算能带分布趋势完全符合. 在 Ti₃C₂O₂ 能带结构图中, 显然高对称点$ \varGamma $附近的能带穿越了费米能级, 表明 Ti₃C₂O₂ MXene 具有金属特性. 图2(b) 所示的室温下(300 K) Ti₃C₂O₂ MXene 单层声子谱中, 第1阶段声子频率位于 50 meV 以下, 由 3 个声学分支和 Ti 原子的部分光学分支构成; 第2阶段声子频率位于 50—100 meV 之间, 主要对应于 C 原子和 O 原子的面内(低能量分支)和面外(高能量分支)的光学振动. 此外, $ \varGamma $ 点附近存在两条平面内线性色散曲线和一条平面外抛物线色散曲线, 这是二维晶体材料声子谱的典型特征. 特别地, 理论计算不同环境温度下的声子谱中均没有出现虚频, 表明 Ti₃C₂O₂ MXene 单层的晶体结构是动力学稳定的. 此外, 声子谱中光学声子的截止能量大约 90 meV, 表明 Ti₃C₂O₂ MXene 在超过 0.09 eV 光子能量时就会由于强烈的光子-声子散射而导致自由电子的弛豫时间急剧下降, 并且其高弛豫特征的维持能力远小于石墨烯单层(约200 meV)^[38].

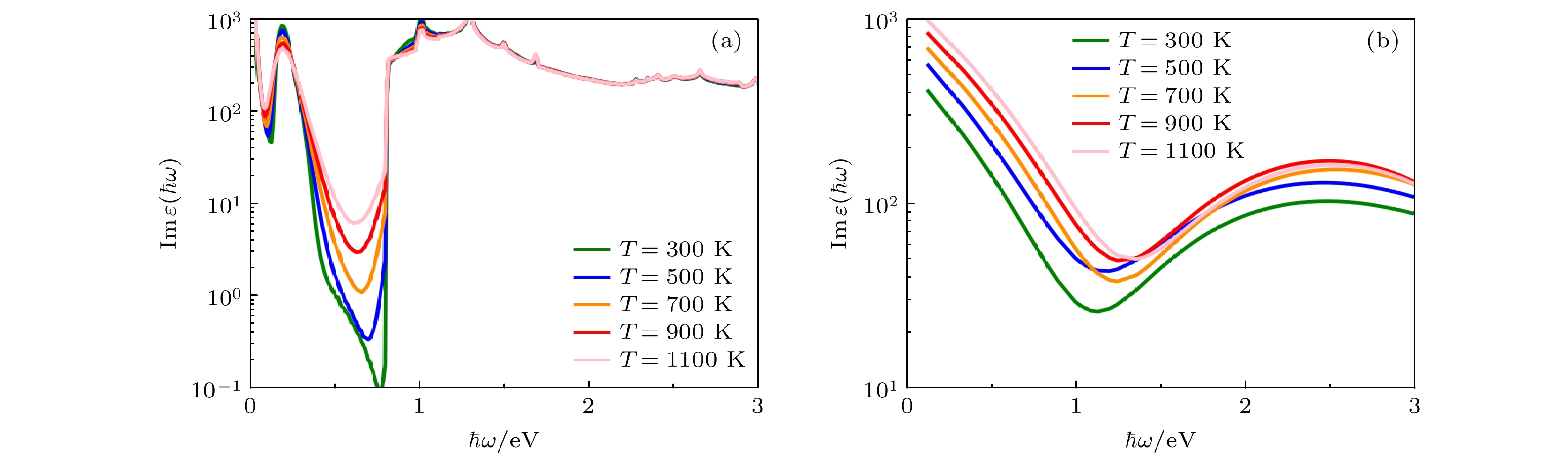
大量的实验与理论研究表明, MXenes 材料表现出独特的表面等离激元现象, 并通过朗道阻尼产生高能热载流子(热电子与热空穴), 在光电和等离子体领域中应用潜力巨大. 金属性 Ti₃C₂O₂ MXene 等离子体材料中, 表面等离激元通过朗道弛豫形式的非辐射衰减产生热载流子物理机制, 主要包括直接带间电子跃迁和声子协助电子跃迁过程. 如图3 所示, 本文利用介电函数的虚部值量化 0—3 eV 能量范围内, 上述两种物理机制在不同环境温度下对热载流子产生效率的贡献. 图3(a)展示了表征带间电子跃迁产生热载流子效率的介电函数虚部值分布. 介电函数虚部值计算与电子跃迁矩阵元有关, 因此图2(a) 能带结构中能级之间的能量差决定了介电函数虚部值的频率分布范围. 从图中可知, 入射光子能量处于 0.2—0.5 eV 范围内时介电函数虚部值高达 10³ eV, 主要是激发了如图2(a) 中蓝色圆圈标记的费米能级附近带间电子跃迁. 随着入射光子能量增加, 0.5—1.0 eV 能量范围内介电函数虚部值急剧下降. 这是由于激发如图2(a) 中蓝色箭头所标记带间电子跃迁的能量阈值为 1 eV, 因此 0.5—1.0 eV 能量范围内入射光子无法激发带间电子跃迁. 当入射光子能量大于带间跃迁阈值时, 介电函数虚部值在 1—3 eV 能量范围内急剧增大后持续稳定高达 10³ eV. 值得注意的是, 环境温度对低能量范围内的带间电子跃迁的热载流子产生效率影响非常显著. 特别地, 在 0.5— 1.0 eV能量范围内, 环境温度升高导致带间电子跃迁产生热载流子效率几乎提高了2个数量级. 然而, 在 1.0—3.0 eV 高能量范围内, 环境温度升高对高能量处的带间电子跃迁产生热载流子效率几乎没有影响.

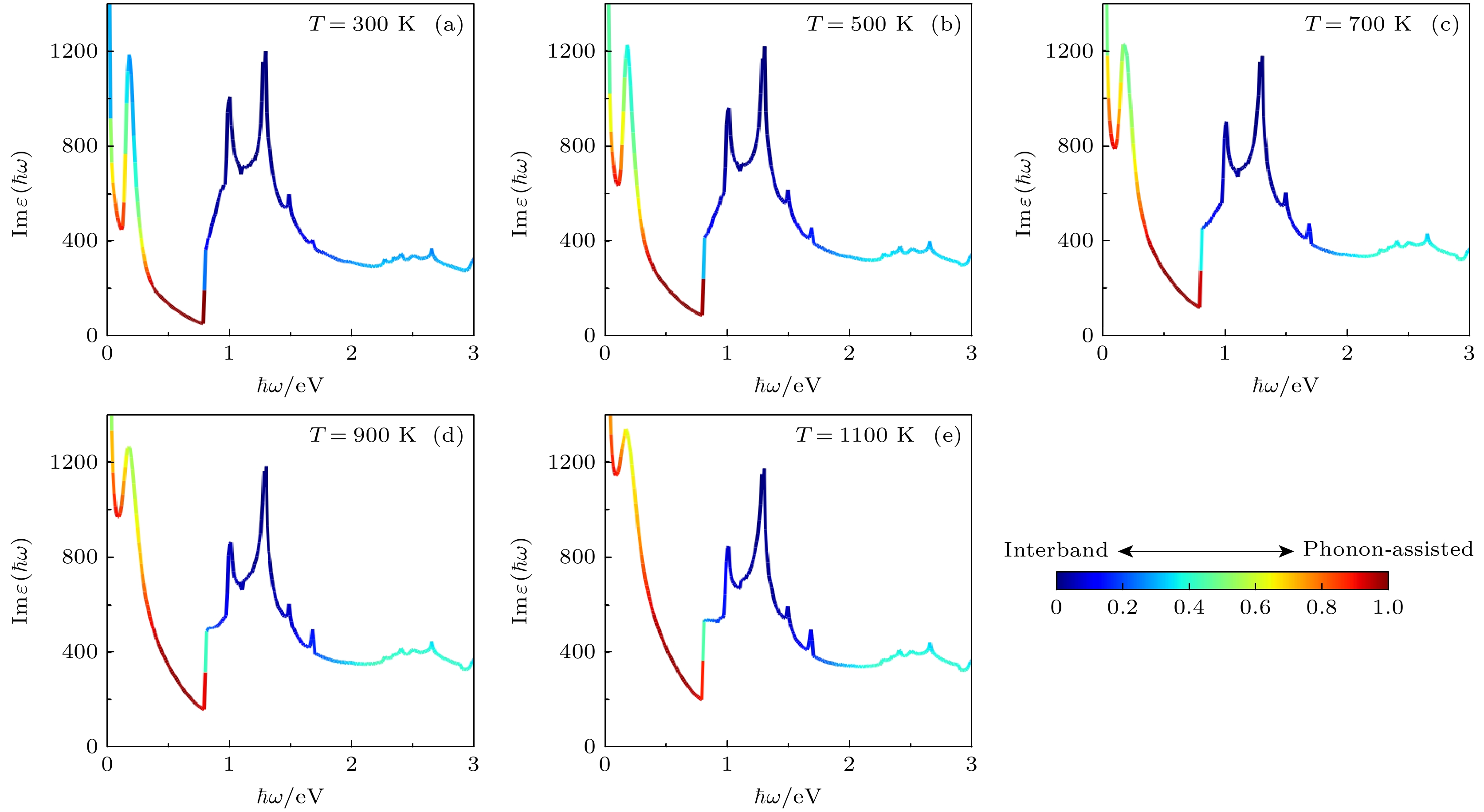
图3(b) 展示了表征声子协助电子跃迁产生热载流子效率的介电函数虚部值分布. 从图中可知, 0—1 eV 低能量范围内介电函数虚部值高达 10³ eV, 甚至与带间电子跃迁量级相当. 如图2(a)中绿色箭头标记所示, 声子可以提供足够的动量协助入射光子激发在高对称点 $ \varGamma $ 附近的带内电子跃迁. 随着入射光子能量增加, 在 1—3 eV 能量范围内介电函数虚部值逐渐下降. 如图2(a) 中紫色箭头标记所示, 在该高能量范围内声子提供的微小动量无法满足带内电子跃迁的动量守恒要求, 因此激发声子协助电子跃迁比较困难同时带间直接电子跃迁开始占据主导. 此外, 计算结果表明随着环境温度升高, 声子协助电子跃迁的热载流子产生效率逐渐增大, 并且低能量范围内的增大程度要显著于高能量范围. 因此, Ti₃C₂O₂ MXene 中带间电子跃迁与声子协助电子跃迁均可以高效地产生热载流子, 并且环境温度升高显著提高了 0—0.8 eV (红外波段) 能量范围内的热载流子产生效率, 但是几乎不影响 0.8—3.0 eV (可见光波段)能量范围内的热载流子产生效率.

为了探究环境温度对热载流子产生物理机制的影响, 图4 展示了不同环境温度下, Ti₃C₂O₂ MXene 的带间电子跃迁和声子协助电子跃迁过程对热载流子产生效率的相对贡献. 其中, 颜色条的色阶表示归一化的相对贡献比例, 颜色越接近蓝色代表带间电子跃迁的贡献越多, 反之则声子协助电子跃迁的贡献越多. 从图4可以看到, 声子协助电子跃迁过程是 0—0.8 eV (红外波段)能量范围内产生热载流子的主导物理机制, 带间电子跃迁则是 0.8—2.0 eV(可见光波段)能量范围的主导物理机制. 此外, 在部分特定能量范围内, 声子协助电子跃迁对热载流子产生的贡献与带间电子跃迁几乎相同, 因此在研究 Ti₃C₂O₂ MXene 中热载流子相关特性时不能忽略声子协助电子跃迁过程影响. 值得注意的是, 随着环境温度逐渐升高, 在 0—0.8 eV(红外波段)能量范围内声子协助电子跃迁贡献在热载流子产生效率中的占比逐渐增大, 但是在 0.8—3.0 eV(可见光波段)能量范围内两种电子跃迁的贡献比例基本保持不变. 综上, 环境温度升高会增大 Ti₃C₂O₂ MXene 在 0—0.8 eV (红外波段)能量范围内声子协助电子跃迁的热载流子产生效率, 但是几乎不影响 0.8—3.0 eV(可见光波段)能量范围内的热载流子产生微观物理机制.

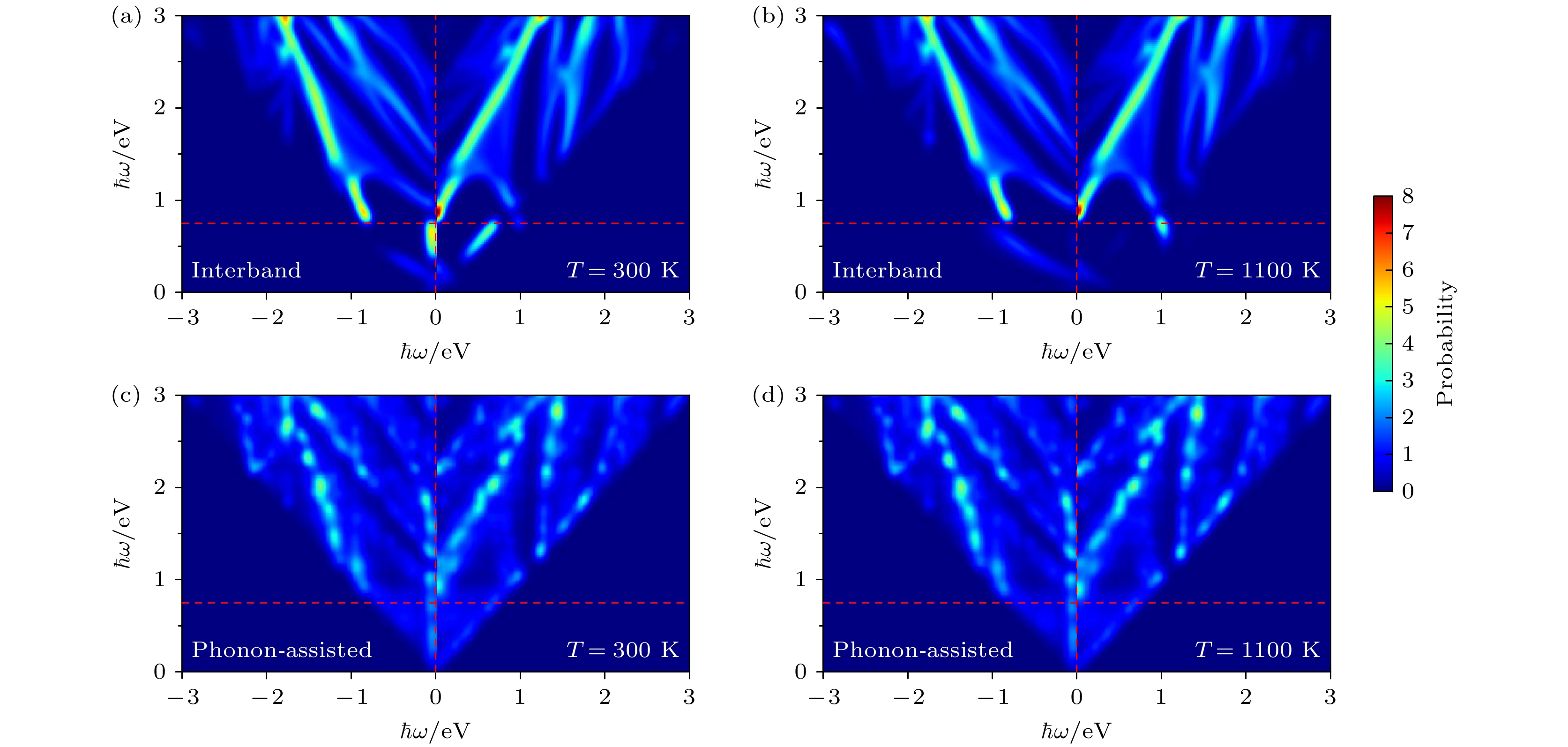
热载流子的能量分布决定了特定能量等离激元/光子, 在 Ti₃C₂O₂ MXene 中激发的热载流子主导类型. 本文采用始态(空穴)和末态(电子)能量对(1)式和(2)式的积分计算进行直方图统计, 从而获得两种物理机制产生的初始热载流子能量分布与等离激元/光子能量之间的关系. 需要指出的是, 遵守能量守恒时热载流子的洛伦兹展宽导致其能量略微超过了等离激元/光子能量. 图5(a) 和 图5(b) 展示了室温(300 K)和高温(1100 K)环境中带间电子跃迁产生的热载流子能量分布. 热载流子在能量空间分布呈现出条状的“陡峰”态势, 并且热电子与热空穴的能量分布不对称, 因此讨论热载流子的主导类型非常有意义. 从图中可知, 0.8—3.0 eV 能量的等离激元/光子激发时, 产生的高能热载流子分布概率非常大, 并且高能热空穴的能量大于高能热电子. 随着环境温度升高, 0—0.8 eV 范围内的热载流子分布概率逐渐减小, 但是 0.8 eV 能量以上的可见光波段几乎不受影响. 此外, 环境温度升高并不能改变热载流子的能量空间位置分布, 其主要取决于精确计算的 Ti₃C₂O₂ MXene 能带结构. 图5(c), (d) 展示了室温(300 K)和高温环境(1100 K)中声子协助电子跃迁产生的热载流子能量分布. 显然, 声子协助电子跃迁产生的热载流子在能量空间分布的连续性比较好. 与带间电子跃迁类似, 0.8—3.0 eV 能量范围内产生的高能热载流子分布概率比较大, 并且高能热空穴能量高于高能热电子. 与带间电子跃迁相比, 0—0.8 eV 能量范围内声子协助电子跃迁产生的热载流子分布概率比较大, 然而 0.8—3.0 eV 能量范围内声子协助电子跃迁产生的热载流子分布概率非常小. 随着环境温度升高, 声子协助电子跃迁产生的热载流子在能量空间的分布概率逐渐增大. 综上所述, Ti₃C₂O₂ MXene 适用于热空穴主导的热载流子光电器件, 并且 0.8—3.0 eV (可见光波段)能量范围内产生的高能热空穴表现出优异的环境温度稳定性, 该现象可通过单分子电荷输运的扫描探针技术, 并结合纳米等离子体实验方案进一步验证^[39].

表面等离激元非辐射衰减产生的热载流子必须存活足够长时间, 或迁移足够远距离才能被收集或探测到. 因此, 非平衡载流子输运的时间和长度尺度一直是 Ti₃C₂O₂ MXene 基光电器件关注的重要参数^[40]. 基于上述精确计算的能带结构, 考虑不同环境温度下的电子-电子与电子-声子散射效应, 本文给出了 Ti₃C₂O₂ MXene 中热载流子寿命与平均自由程的定量计算结果.

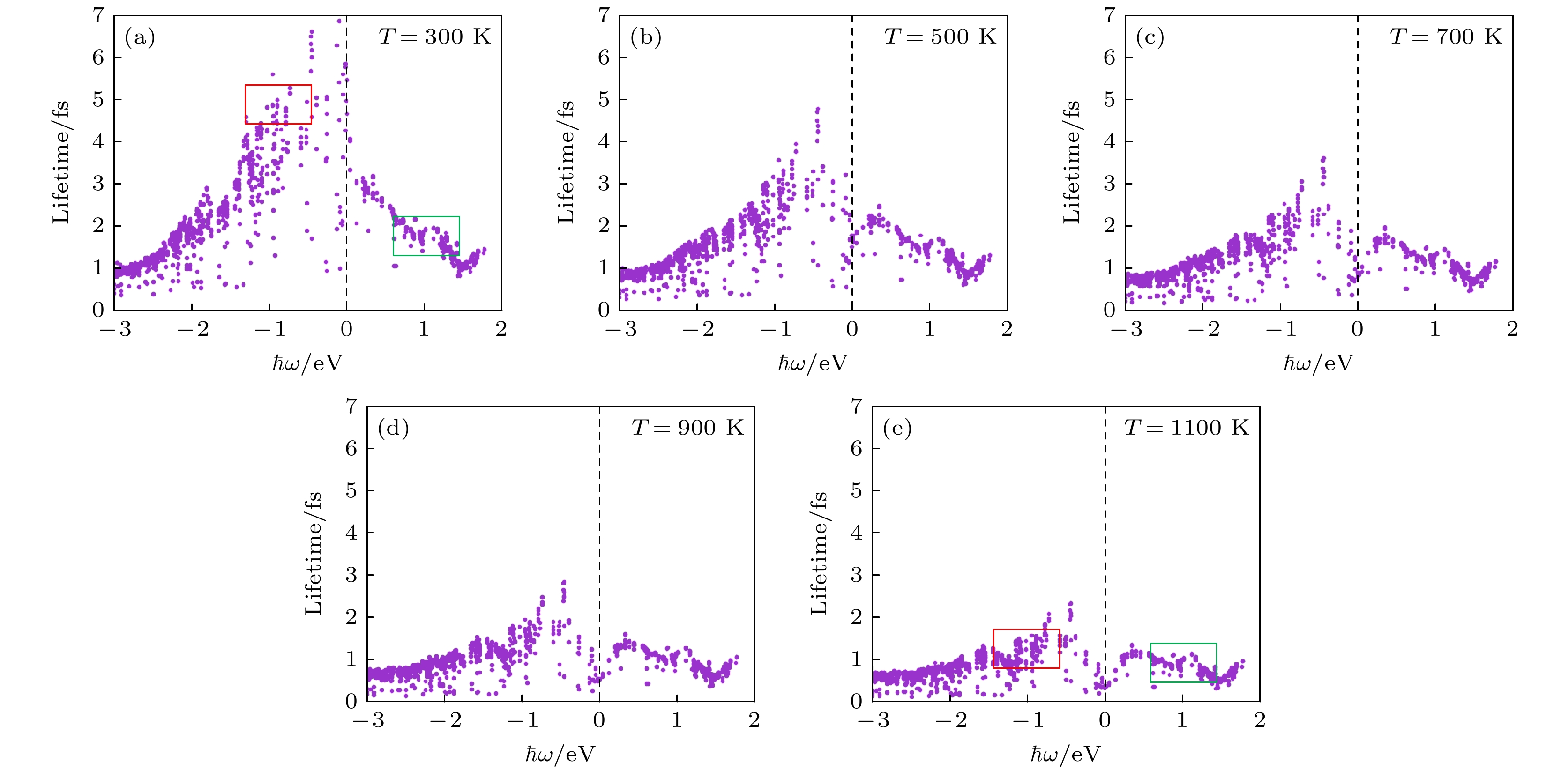
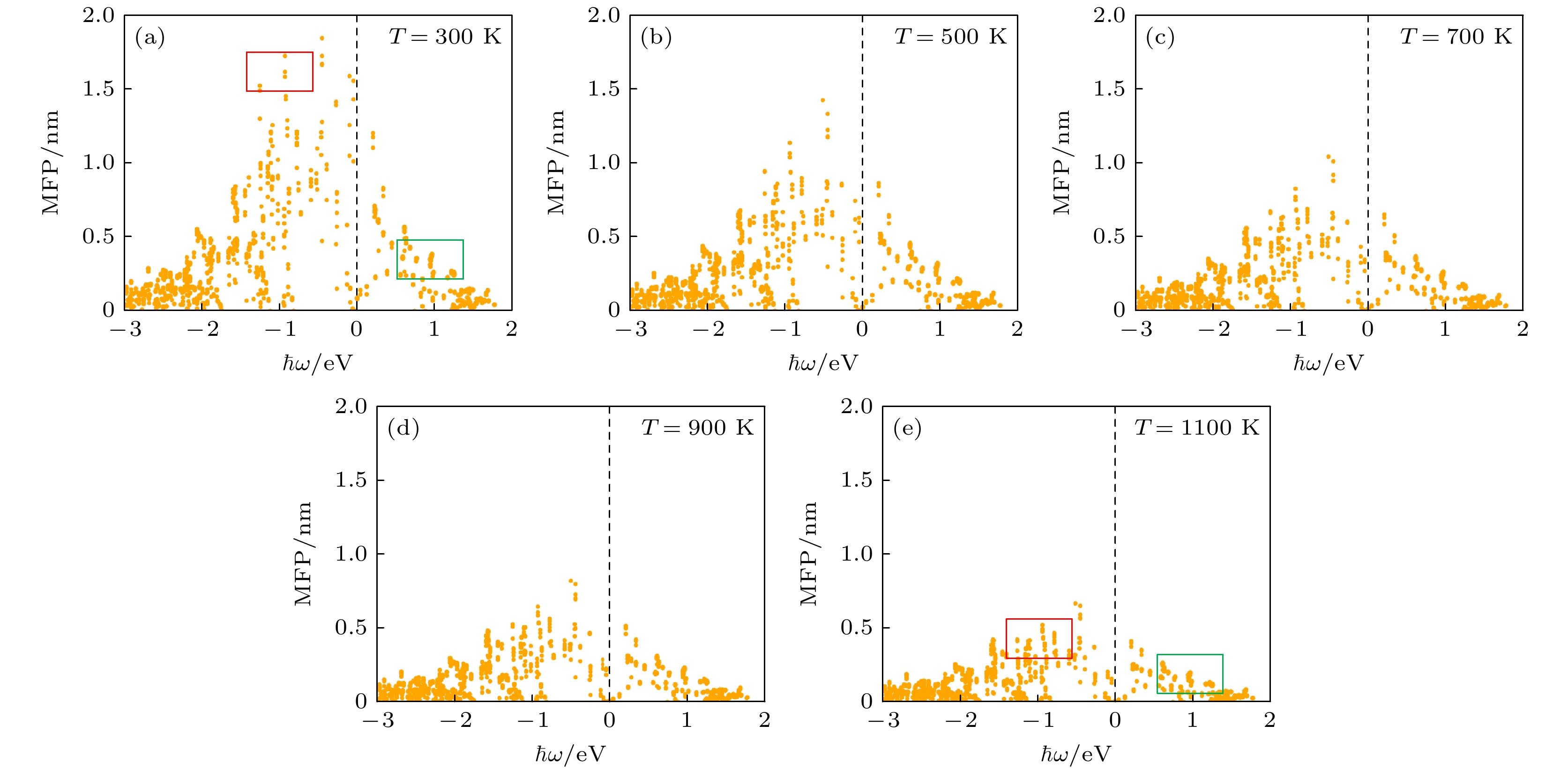
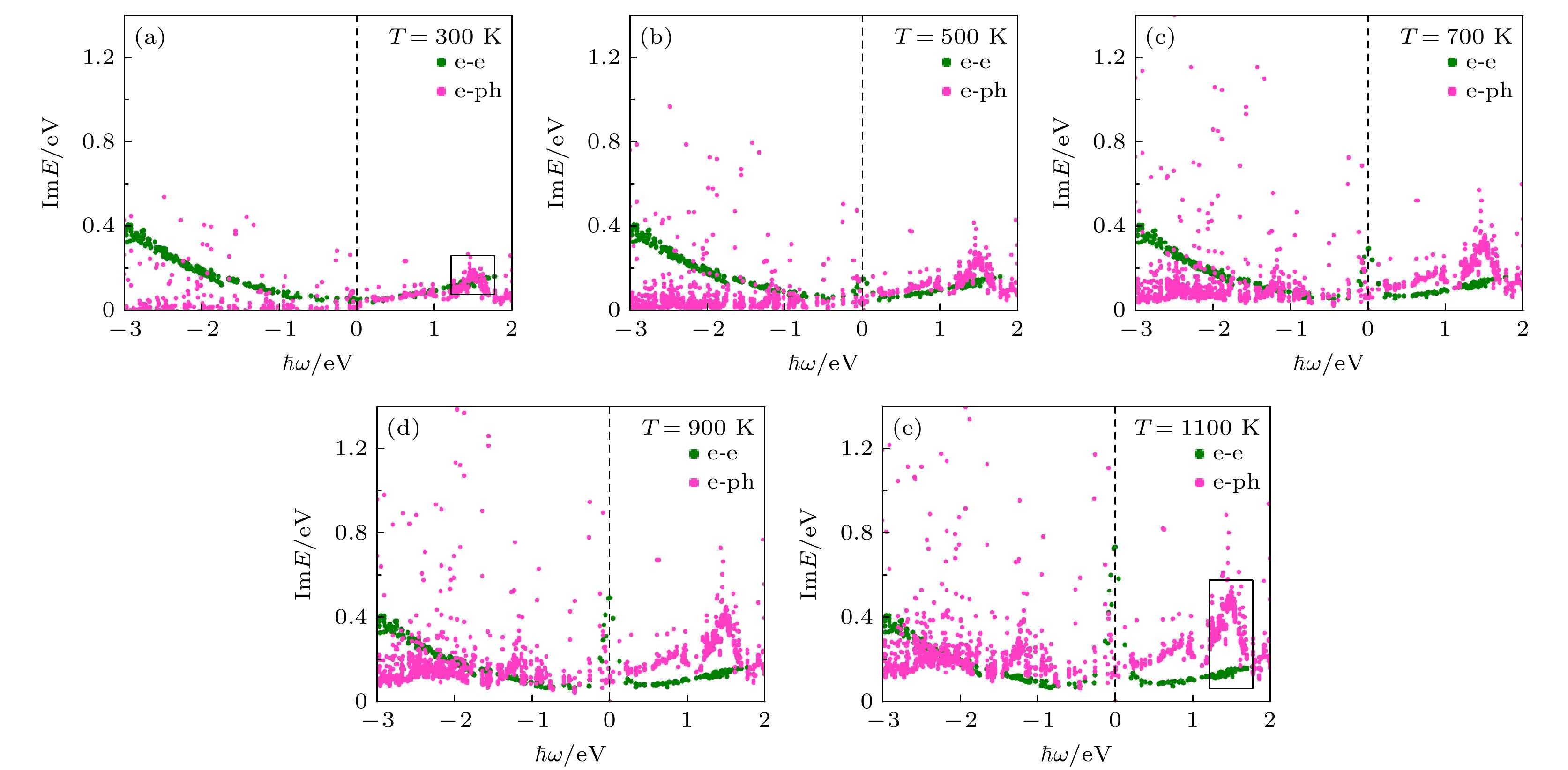
图6 和图7 分别展示了不同环境温度下, Ti₃C₂O₂ MXene 中热载流子寿命与平均自由程的能量空间分布. 由于 Ti₃C₂O₂ 晶体结构在微观层面具有各向异性, 导致相同能量下具有不同波矢量的电子态kn具有不同的相空间和散射矩阵元素, 因此相同能量的热载流子${E_{kn}}$具有不同的寿命和平均自由程. 图5 的热载流子能量分布表明, Ti₃C₂O₂ MXene 中热空穴与热电子的能量分别聚集在 0—3.0 eV 与 0—2.0 eV 范围内, 因此本文主要讨论该范围内的热载流子输运性质. 从图6 和图7 可以看到, 费米能级附近的低能热载流子具有最长的寿命和平均自由程, 并且随着能量增大而逐渐减小. 此外, 具有相同能量的热空穴寿命和平均自由程均显著大于热电子. 在室温(300 K)下, Ti₃C₂O₂ MXene 中热载流子的最大寿命接近 7 fs , 最大平均自由程接近 2 nm , 与单层硼烯^[41]中热载流子的输运特性非常接近. 然而, 与传统等离激元材料贵金属(Au, Ag, Cu)相比^[19], 最大热载流子寿命为约30 fs, 平均自由程为约50 nm, Ti₃C₂O₂ MXene 的最大热载流子寿命和平均自由程均远远小于贵金属. 因此, 非常有必要探索热载流子输运性能优化方法, 以提高 MXenes 基表面等离激元光电探测器件性能. 随着环境温度升高, 热载流子的寿命与平均自由程均逐渐减小, 尤其是费米能级附近低能热载流子的减小程度最显著. 特别地, 环境温度升高对高能热空穴输运性质的影响大于高能热电子. 例如, 如图6 中方框标记所示, 热空穴的寿命从 300 K 时的 5.58 fs 降低到 1100 K 时的 1.58 fs, 同时高能热电子的寿命从300 K 时的 1.94 fs 降低到 1100 K 时的 1.04 fs . 如图7 中方框标记所示, 高能热空穴的平均自由程从 300 K 时的 1.72 nm 减小到 1100 K 时的 0.52 nm , 同时高能热电子的平均自由程从 300 K 时的 0.39 nm 减小到 1100 K 时的 0.20 nm. 此外, 在 0—0.8 eV 能量范围内, 具有长寿命和平均自由程的热空穴表现出强烈的温度依赖性, 然而在 0.8—3.0 eV 能量范围内, 热电子与热空穴受环境温度影响都比较小. 因此, Ti₃C₂O₂ MXene 中产生了寿命长、迁移距离远的高能热空穴, 并且其在可见光波段受环境温度的影响比较小.

热载流子的输运性质与电子-电子和电子-声子散射效应密切相关. 如图8 所示, 本文分别计算电子-电子散射和电子-声子散射导致的载流子线宽, 研究环境温度对 Ti₃C₂O₂ MXene 的散射效应影响. 从结果可以看到, 室温(300 K) Ti₃C₂O₂ MXene 中, 电子-电子散射对热空穴的影响远大于电子-声子散射, 但是对热电子的影响与电子-声子散射相当. 随着远离费米能级的热载流子能量增加, 电子-电子散射急剧增加, 电子-声子散射则几乎保持不变, 最终导致热载流子寿命和平均自由程逐渐减小. 随着环境温度逐渐升高, 电子-电子散射几乎不变, 电子-声子散射则显著增大. 例如, 如图8 中黑色方框标记所示, 环境温度从 300 K 升高到 1100 K 后, 1.5 eV 处的电子-声子散射线宽增加了大约 0.31 eV, 相应的电子-电子散射线宽几乎没有改变. 特别地, 随着环境温度升高, 电子-声子散射甚至成为了影响热载流子寿命与平均自由程的主导因素. 因此, 环境温度主要影响的是电子-声子散射效应, 并且温度越高电子-声子散射越大.

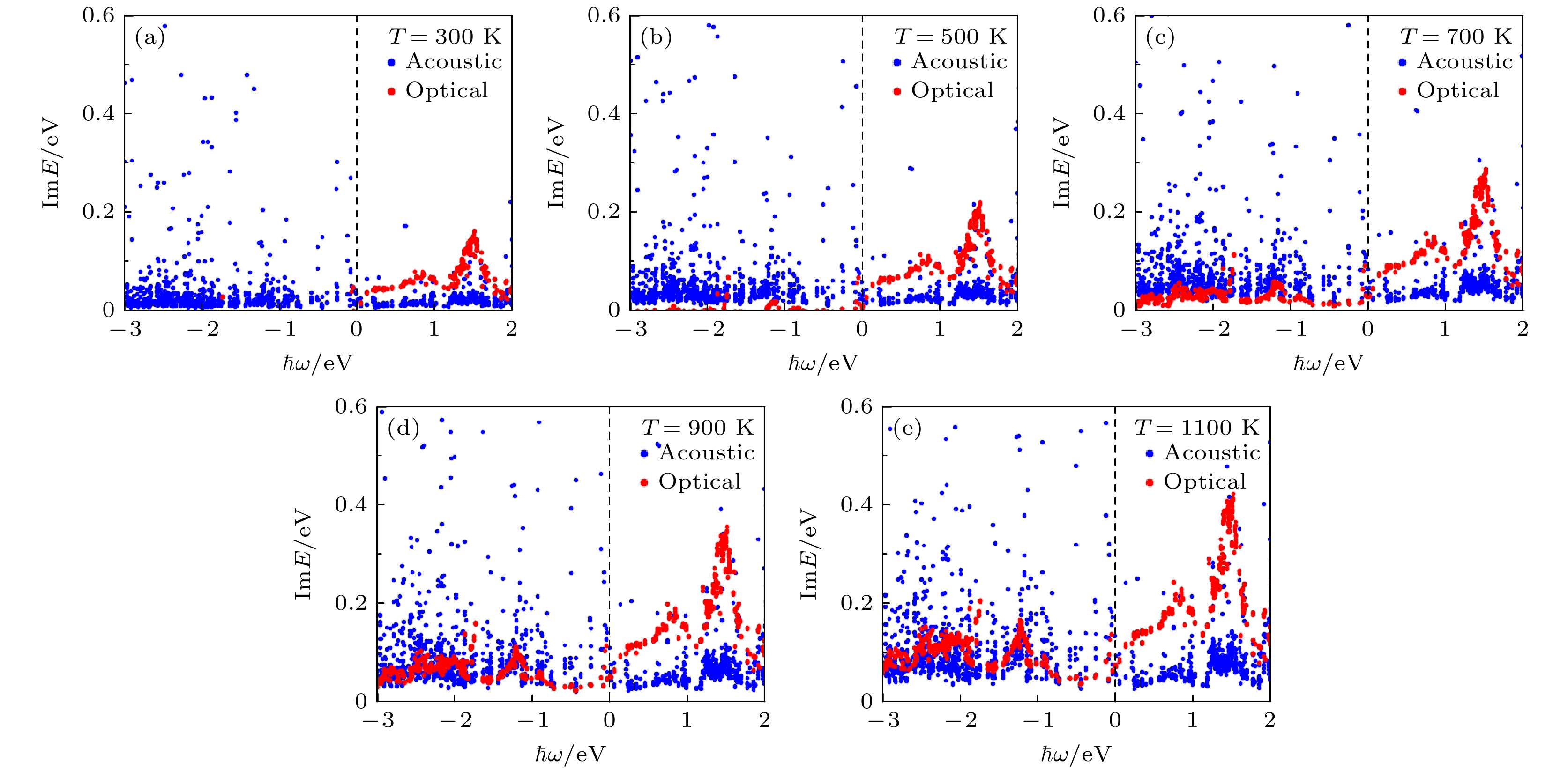
基于上述结论, 本文进一步研究了不同环境温度下 Ti₃C₂O₂ MXene 的声学声子和光学声子分别与电子的相互散射效应. 如图9 所示, 对于热空穴而言, 电子与声学声子的相互作用占据主导, 而热电子主要是电子与光学声子的相互作用. 随着环境温度升高, 电子与声学声子散射稍微增加, 而电子与光学声子散射明显增大. 可以看到, 对于图8 中的热电子而言, 其增强的电子-声子散射主要源于电子与光学声子的相互作用. 该现象可以理解为, 环境温度升高增加了 Ti₃C₂O₂ MXene 的晶格振动能量, 促使更多的原子很大可能进行反向运动, 这种原子振动模式显著加剧了电子与光学声子的碰撞散射概率. 上述研究表明, Ti₃C₂O₂ MXene 中热载流子的输运性质温度依变性主要源于电子与声子光学分支间的碰撞散射效应, 并且对热电子的输运特性影响非常大.

基于多体微扰理论和量子力学理论, 本文采用第一性原理的量化计算方法, 系统研究了 MXene 材料中热载流子对环境温度的依赖特性, 包括热载流子的产生效率、能量空间分布和输运性质. 研究结果表明, Ti₃C₂O₂ MXene 中产生的高效热载流子源于带间电子跃迁与声子协助电子跃迁的共同贡献. 特别地, 环境温度升高后显著提高了 0—0.8 eV(红外波段)能量范围内的热载流子产生效率, 原因是环境温度升高增大了声子协助的电子跃迁概率. 同时, 环境温度几乎不影响 0.8—3.0 eV (可见光波段)能量范围内的优异热载流子产生效率; Ti₃C₂O₂ MXene 中热载流子的能量分布特征显著依赖于激发能量, 并且产生了大量的高能热空穴. 特别是, 0.8—3.0 eV (可见光波段)能量范围的高能热空穴表现出优异的环境温度热稳定性; Ti₃C₂O₂ MXene 中热空穴的寿命与平均自由程均显著大于热电子. 环境温度升高降低了热载流子的寿命与平均自由程, 源于增强的电子与光学声子散射作用. 此外, 在 0.8—3.0 eV(可见光波段)能量范围内, 环境温度升高对热载流子的输运性质影响比较小. 因此, Ti₃C₂O₂ MXene 非常有潜力成为性能稳定的热空穴型光电器件材料. 研究结果将为 Ti₃C₂O₂ MXene 基热载流子光电器件的性能优化提供理论基础与指导, 从而助力于 MXenes 材料的进一步实践应用发展.