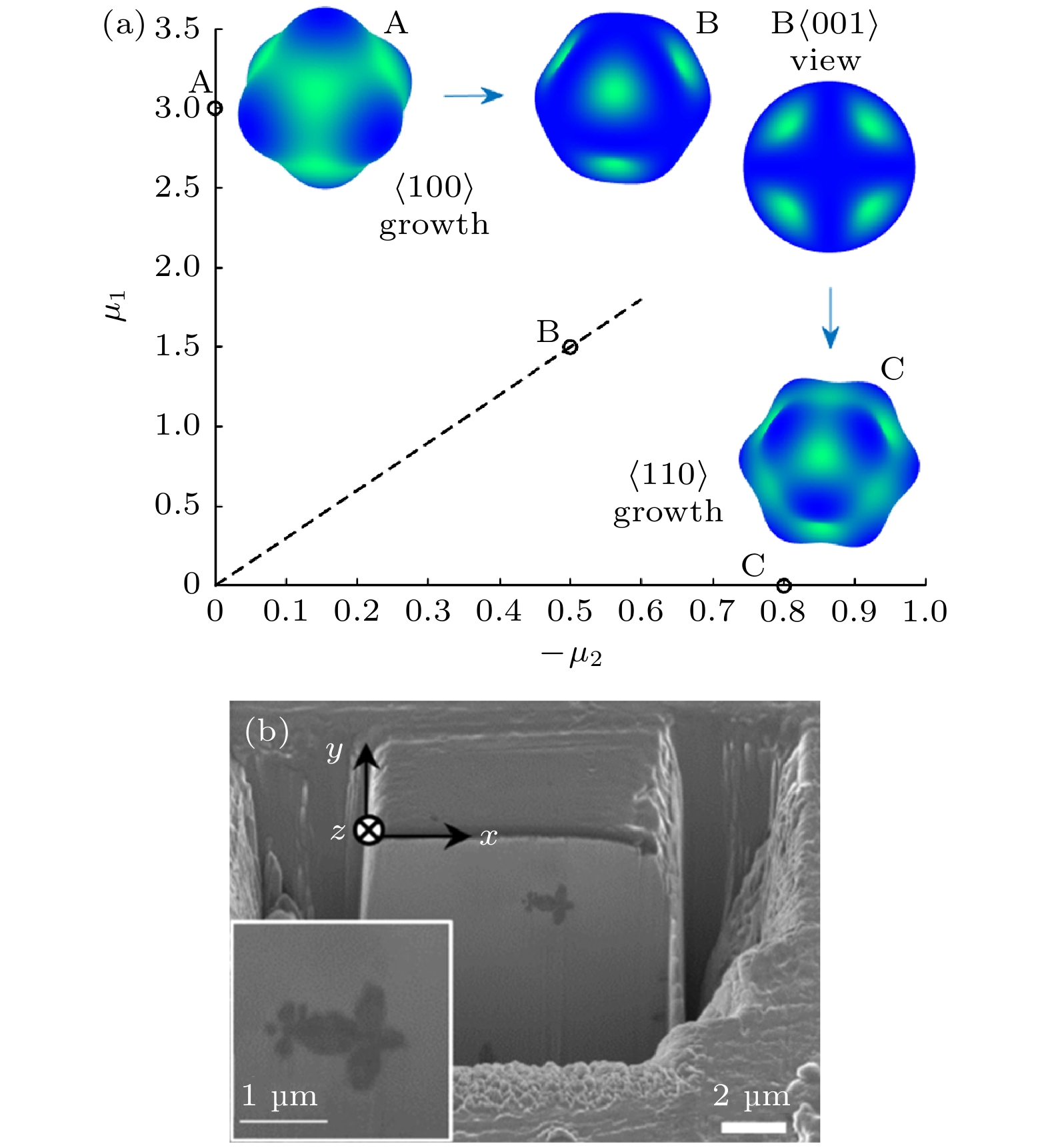
定向凝固过程中晶体形态的不稳定性可能会导致凝固系统的液-固呈现出不同的微观结构, 极大地影响着产品的质量和性能. 典型的固液界面微结构形态是胞晶和枝晶. 在定向凝固过程中, 胞晶和枝晶界面形态在很大程度上取决于拉速$V$^[1]. 图1展示了随着拉速$V$增加, 定向凝固过程中出现的胞晶列和枝晶列结构图^[2], 当拉速$V$足够小时, 可假定固液界面是平直界面, 随着拉速逐渐增大, 界面逐次演化为弯曲的小振幅胞晶界面、振幅较大的深胞晶界面, 在超过某个临界值${V_{\mathrm{C}}}$时, 深胞晶界面继续演化为枝晶界面. 因此, 对凝固系统界面结构及其稳定性的研究是材料科学的重要课题之一, 在过去的几十年里引起了人们的广泛关注. Mullins和Sekerka^[3,4]首先研究了晶体生长的界面稳定性, 并提出了平滑界面线性稳定性理论(M-S理论), 为研究固液界面形态特征提供了重要依据. Langer^[5]讨论了定向凝固中的非线性效应, 发现在这种情况下出现的非平面胞晶界面与流体力学中的对流模式具有相似性. Pelcé与Pumir^[6]和Dombre与Haankim^[7]分别研究了小Péclet数和$ {\lambda _0} \approx 1 $情况下胞晶生长的定常态, 发现定向凝固过程中胞晶生长与Hele-Shaw流中粘指生长具有内在相似性. Pelcé^[8], Karma 和Pelcé^[9], Benamar等^[10]分别在对于定常针晶的研究中, 为了使问题在对根部无穷远渐近条件的情况下有解, 引入了界面条件中的各向异性, 形成了微观可解性条件(MSC)理论, 认为沿固液界面方向的表面张力各向异性在界面形态选择中起着极其重要的作用. Xu^[11–13]提出的界面波(IFW)理论则揭示了枝晶生长属于波动现象中的一种, 晶体界面上的枝状结构是从尖端到根部的两种界面行波${H_1}$和${H_3}$的相互作用与叠加, 该理论采用符合物理学原理的数学模型, 可以系统地研究各种晶体生长.

大量的研究表明, 界面动力学各向异性是影响晶体生长形态演化与微观组织选择的一个非常重要的参数. Trivedi等^[14]研究发现, 界面动力学各向异性会使胞晶界面发生倾斜, 晶体不会总是沿着热流方向生长. Coriell与Sekerka^[15]和Young等^[16]对界面动力学各向异性的研究表明, 扰动波除了沿垂直界面传播, 还存在一个沿平行界面传播的平行波, 而后者造成胞晶生长方向偏离热流方向. 袁训锋^[17]采用耦合流场的Wheeler相场模型, 对界面动力学各向异性作用下的纯镍凝固中的枝晶生长进行模拟, 揭示了其对枝晶形貌及尖端生长行为产生的影响. 王自东等^[18,19]用渐近方法研究了具有各向异性界面原子附着动力学的过冷熔体中粒子的形态模式, 揭示了晶粒生长初期粒子局部向内凹的生长和取向选择的变化. 随着界面原子附着动力学各向异性参数的系统改变, 颗粒的优先生长方向不断地从一个优先生长方向改变到另一个优先生长方向, 产生了具有各种形态的花瓣状图案, 与Chen等^[20]得到的实验结果相一致(见图2). 以上研究均说明了各向异性界面动力学对晶体形貌具有的影响. 本文采用多重变量法和匹配渐近法对考虑了各向异性界面动力学参数的深胞晶生长界面稳定性进行研究.

考虑二维空间下定向凝固的深胞晶生长, 样本材料位于Hele-Shaw生长室的二元合金熔体, 这是一个细长的生长室, 可以看作二维空间O_xy下的定向凝固过程, 原点位于胞晶尖端. 固相中溶质的扩散忽略不计, 其他热力学性质相同, 且系统内无对流. 界面的拉动速度为$V$, 方向指向上液相方向, 温度梯度为${G_T}$, 浓度为$C$, 远场浓度为${C_\infty }$(本文指摩尔百分比), 深胞晶生长满足热传导方程、溶质扩散方程、界面方程, 包括热平衡条件、Gibbs-Thomson条件、熵守恒条件、溶质守恒条件和界面分离条件. 各向异性界面动力学用四重对称函数$ \mu = {\mu _0}\left[ {1 + {\beta _4}{\text{cos}}\left( {4\theta } \right)} \right] $表示, 其中$ {\mu _0} $为各向同性界面动力学系数, $\theta $为界面法向量与O_y轴之间的夹角, $ {\beta _4} $为各向异性界面动力学系数. 胞晶列周期为${l_w}$, 纯熔体温度为${T_{{\mathrm{M}}0}}$, 溶质扩散率为${k_{\mathrm{D}}}$, 假设深胞晶尖端曲率半径${l_{\mathrm{t}}}$远小于溶质扩散长度${l_{\mathrm{D}}} = {k_{\mathrm{D}}}/V$, 单位体积内固相产生的潜热为$ \Delta H $, 毛细长度为${l_{{\mathrm{c}}}} = \gamma {c_{\mathrm{p}}}\rho {T_{{\mathrm{M}}0}}$, 其中$\gamma $为表面张力, $\rho $为熔体密度, ${c_{\mathrm{p}}}$为液相比热容, 定义主间距参数$W = {l_{\mathrm{W}}}/{l_{\mathrm{t}}}$. 为了进行渐近分析, 对系统进行无量纲化, 选取深胞晶尖端${l_{\mathrm{t}}}$为长度尺度, $V$为速度尺度, ${l_{\mathrm{t}}}/V$为时间尺度, $ \Delta H/\left( {{c_{\mathrm{p}}}\rho } \right) $为温度尺度, ${C_\infty }$为浓度尺度. 进一步选小参数$\varepsilon = \sqrt \varGamma = \sqrt {{l_{\mathrm{c}}}/{l_{\mathrm{t}}}} $为界面稳定性参数, $ {\mathrm{Peclet}} $数$Pe = \varepsilon \hat Pe$, 其中$\hat Pe = O(1)$. 无量纲化的温度梯度为$ G = \dfrac{{{l_{\mathrm{D}}}}}{{\Delta M/({c_{\mathrm{p}}}\rho )}}{G_{{T}}} $, 形态学参数为$ M = - \dfrac{{m{C_\infty }}}{{\Delta M/({c_{\mathrm{p}}}\rho )}} $, 其中$ m < 0 $是相图中液相线的斜率. 参数${\lambda _G} = {l_{\mathrm{D}}}/{l_G}$, ${l_G} = - m{C_\infty }/{G_T}$, $ E = \Delta H/\left( {{c_{\mathrm{p}}}\rho {T_{\mathrm{M}}}} \right) $, 深胞晶生长满足的热传导方程、溶质扩散方程以及界面条件转化为无量纲的控制方程. 深胞晶界面形态具有周期性, 只需研究胞晶界面单个周期的界面形态, 每个胞晶宽度为$W$. 基于Saffmen-Taylor解构造曲线坐标系^[21]$(\xi , \eta )$, 它与平面直角坐标系的关系为

其中$ {\lambda _0} $是胞晶相对宽度, 与主间距参数$W$有关.

在曲线坐标系$(\xi , \eta)$下, 生长区内的温度分布可以近似表示为线性方程$T (\xi , \eta, \varepsilon) = \varepsilon G[ WY(\xi , \eta ) - {y_0} ] + O\left( {{\varepsilon ^2}} \right)$. 在进行稳定性分析时, 把深胞晶生长的非稳态解表示为基态解$ \{ {C_{\mathrm{}}B}( \xi , \eta , t, \varepsilon ), {\eta _{\mathrm{B}}}(\xi , t, \varepsilon) \} $和扰动态解$ \{ \tilde C (\xi , \eta , t,\varepsilon ), {{\tilde \eta }_{\mathrm{s}}}( \xi , t, \varepsilon ) \} $的叠加. 假定$ {\lambda _0} $是给定常数, 则胞晶尖端位置${y_{*0}}$和主间距$W$无扰动, 定常基态解表示为^[22]

其中

线性扰动系统满足控制方程:

相应的边界条件: 在界面$\eta = {\eta _{\mathrm{B}}}$处, 有Gibbs-Thomson条件和质量守恒条件:

其中

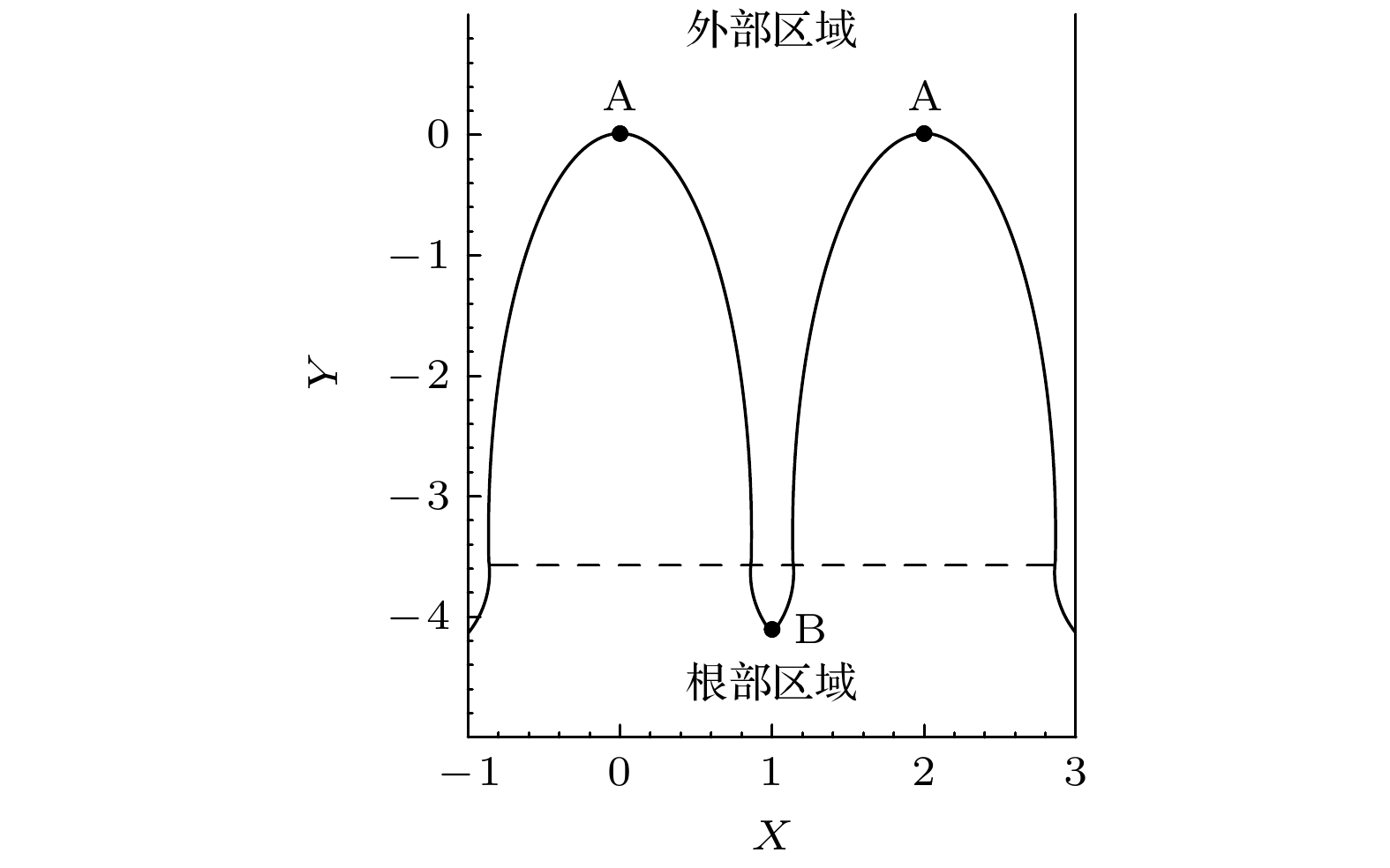
由于系统的一阶近似解存在一个特殊的简单拐点, 在拐点附近, 多变量展开(MVE)方法失效, 为了求全局解, 必须将整个复平面划分为外部区域和拐点附近的根部区域^[11](见图3). 下面将在外部区域和根部区域分别求出渐近解, 然后将它们匹配得到在整个区域的一致有效渐近解.

应用多重变量法求扰动态的渐近解, 定义快变量^[23]:

寻求扰动态解在$\varepsilon \to 0$时的渐近展开式:

将(8)式代入(4)式—(6)式, 得到该系统首级近似的控制方程为

边界条件: 在上流远场处, 当$\eta \to \infty $时, 有${\tilde C_0} \to 0$; 在侧壁区域, 当$\xi = \pm 1$, 有$ {{\partial {{\tilde C}_0}}}/{{\partial \xi }} = 0 $; 在界面$\eta = {\eta _ + } = 0$处, 有Gibbs-Thomson条件和质量守恒条件:

首级近似方程(9)具有一般模式解:

${\tilde D_0}$是任意常复数. 由(10)式—(12)式, 导出色散公式:

其中

解得方程(14)的三个根为

其中

注意到在远场区域, 只有波函数$ {k_{\mathrm{e}}}^{(1)}\left( \rho \right) $的解${H_1}\left( \rho \right)$和波函数$ k_{\text{e}}^{(3)}(\rho) $的解${H_3}\left( \rho \right)$满足${\tilde C_0} \to 0$. 因此, 外部区域的通解可以被表示为两个基本界面行波的组合:

这里$ {D_1} , {D_3} $是在复平面$\rho $上沿$\rho $的实轴的分段常数.

浓度场满足的一级近似控制方程为

根据一般模式解:

得到Gibbs-Thomson条件和质量守恒条件:

其中

这里${\hat A_1}(\xi ) = {\tilde A_1}(\xi , 0)$.

根据${I_1}$, $ {I_2} $, 方程(19)、方程(20)联立的方程组有非平凡解的相容性条件为

其中

一级近似解${k_1}$在$ F(\xi ) $的根处有奇异性, 且根位于$\xi $的扩展复平面$\zeta = \xi + {\mathrm{i}}{\xi _I}$内. 将$F\left( \xi \right)$等函数扩展到复$\xi $平面内, 波函数${k_0}\left( {\zeta , 0} \right)$服从扩展后的色散方程:

用变量$\rho $表示的奇异点${\rho _{\text{c}}}$位于复平面$\rho $内, 且满足方程:

结合(13)式、(24)式和(25)式, 可以得到

该等式有三个复奇异点, 它们皆依赖于${\sigma _0}$, ${\bar \varLambda _0}$和${\bar \varLambda _1}$. 当$ {\sigma _0} \to 0 $时, 奇异点$ {\rho _c} \to - {\mathrm{i}} $. 由于$ {\sigma _0} $是复数, 且$0 \leqslant {Re} \{ {\sigma _0}\} \ll 1$, 则奇异点${\rho _c}$位于复平面内且远离点$\rho = - {\mathrm{i}}$.

给定${\sigma _0}$, 对(24)式求关于$\zeta $的全导数和偏导数, 有

其中

当$\zeta \to {\zeta _{\mathrm{c}}}$时, 有$ F({\zeta _{\mathrm{c}}})F^{\prime} ({\zeta _{\mathrm{c}}}) = O(1) $或$ F(\zeta ) \propto (\zeta - {\zeta _{\text{c}}})^{\frac{1}{2}} $. 则(21)式化为

其中

从(28)式可知, $ {k_1}\left( \zeta \right) $有一个孤立奇点${\zeta _{\text{c}}}$, 当$ \zeta \to {\zeta _c} $时, 有

这里${m_1} = {m_2} = O\left( 1 \right)$.

在复平面上, 函数${k_1}\left( \zeta \right)$是一个解析函数, 它可以在奇异点${\zeta _{\text{c}}}$附近展开为Laurent级数. 由(29)式可知, $ {R_1}\left( {{\zeta _{\text{c}}}} \right) = 0 $, 奇异点${\zeta _{\text{c}}}$是${k_1}\left( \zeta \right)$的单极点, 则有特征值的一级近似${\sigma _1}$的表达式为

引进内变量^[23]:

这里$\alpha $待定. 把内解作渐近展开:

结合(4)式—(6)式和(32)式, 内解满足控制方程:

当${\eta _*} = 0$时, 有Gibbs-Thomson条件和质量守恒条件:

根据解析性$ \dfrac{{\partial {{\tilde C}_{*0}}}}{{\partial {\eta _*}}} = {\mathrm{i}}\dfrac{{\partial {{\tilde C}_{*0}}}}{{\partial {\zeta _*}}} $, 并分别对外部和内部区域的解应用以下变换:

这里内变量$ {\rho _*} = ({{\rho - {\rho _{\text{c}}}}})/{{{\varepsilon ^\alpha }}} $, 参照函数$ {k_{\text{c}}}\left( {{\rho _1}} \right) $待定. 通过令$ {k_{\text{c}}} = \sqrt {\dfrac{{{{\bar \varLambda }_1}{\lambda _0^2} S(\rho )(1 - {\mathrm{i}}\rho )}}{{3{P^2}(\rho )}}} $, 可得到

方程(36)有五个孤立的奇异点和拐点: $\rho = \pm {\mathrm{i}}, \pm {\text{i}}a, {\text{ }}{\rho _{\text{c}}}$. 由于

在拐点${\rho _{\mathrm{c}}}$附近, 需要考虑两种情况: 1) $|{\sigma _0}| = O\left( 1 \right)$, 2) $ |{\sigma _0}|\ll 1$. 以统一的形式得到两种情况下的连接条件:

情况$\left. 1 \right)$导致复特征值的频谱${\sigma _0} = {\sigma _{\text{R}}} - {\text{i}}\omega ( \omega > 0 )$, 外部区域的物理解表示为${{\mathrm{Re}}} \{ {{\tilde h}_0} (\rho, t) \} = {{\mathrm{Re}}} \big\{ {H ( \rho ){{\mathrm{exp}} ({ {{{\sigma _0}t}}/{{\sqrt \varepsilon }}}}} )\big\}$, 其中$H (\rho ) = {D_1}{H_1} + {D_3}{H_3}$, 令

则有

根据尖端光滑性条件, ${d_1}$, ${d_3}$还须满足以下条件:

根据(40)式—(41)式, 得到量子化条件:

这里$ \hat k_0^{(i)} (\rho) = \dfrac{{k_0^{(i)} (\rho)}}{{G (\rho)}} = \dfrac{{\tilde k_0^{ (i)} (\rho)}}{{{\lambda _0}\sqrt {{{\bar \varLambda }_1}} }} $. 且满足:

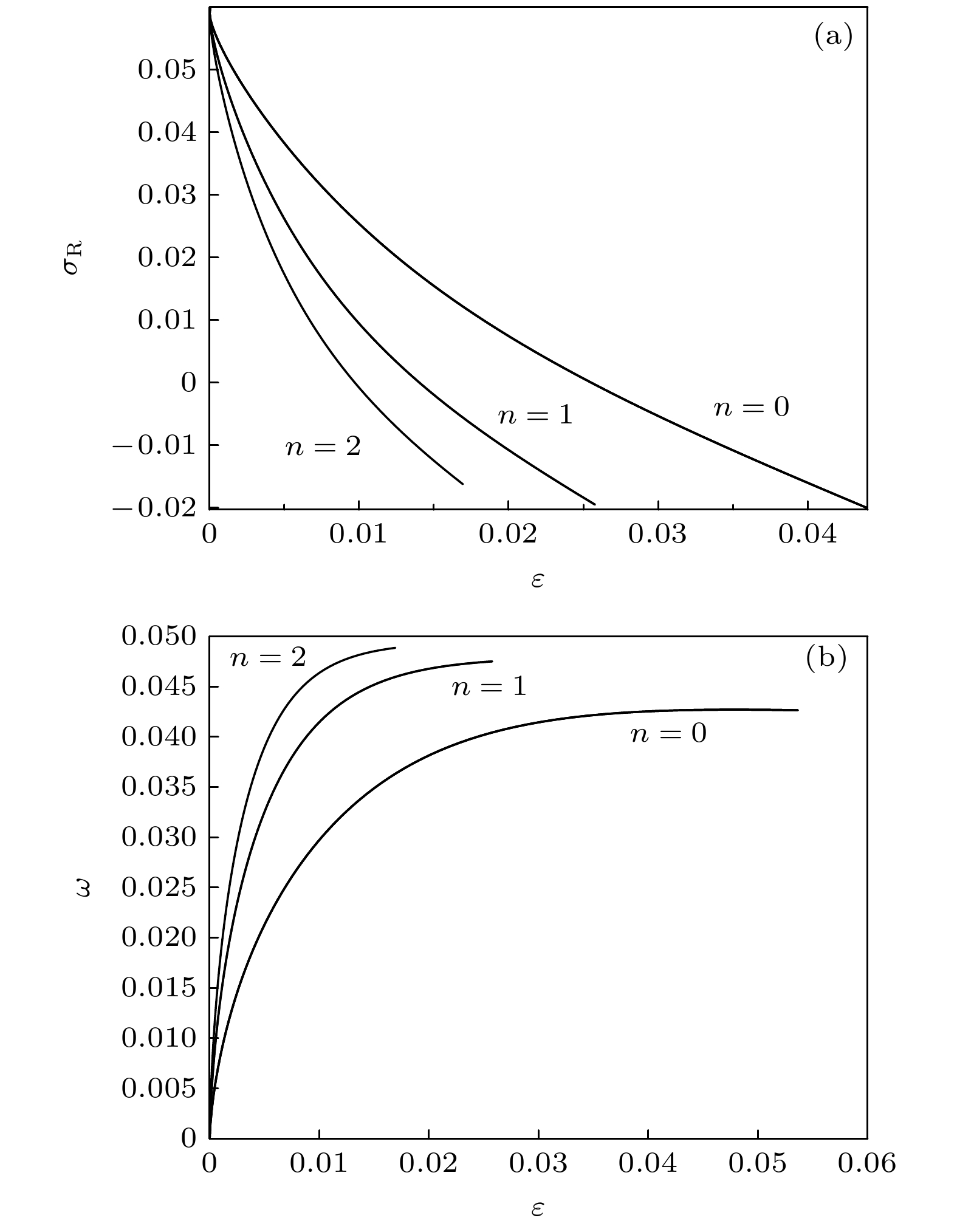
量子化条件(42)式确定了特征值$|{\sigma _0}| = O\left( 1 \right)$的谱: $\left\{ {{\sigma _{0, n}}} \right\}{\text{ }}\left( {n = 0, 1, 2, \cdots } \right)$. 这样的谱产生S-模式和A-模式两个模式的离散本征模式列. 图4给出了量子化条件(42)式下特征值${\sigma _0}$随稳定性参数$\varepsilon $变化曲线图, 可以看到, 给定$ {\lambda _0}, \hat Pe $和其他物理参数, 系统允许一种中性稳定模式${\sigma _{\text{R}}} = 0$, 此时$\varepsilon = {\varepsilon _{*, n}}{\text{ }}\left( {n = 0, 1, 2, \cdots } \right)$且${\varepsilon _*} = {\varepsilon _{*, 0}} > {\varepsilon _{*, 1}} > {\varepsilon _{*, 2}} > \cdots $, 这些模式表现为沿着界面传播的行波, 故也称整体振荡不稳定性机制为整体行波(GTW)机制.

此外, 由于

则参数${\bar \varLambda _1} = M{W^2}\hat Pe\left[ {\left( {1 - k} \right){y_{*0}} - {\lambda _G}} \right]$仍是${\lambda _0}$的函数.

首级近似下, 可以利用${\text{R}}\left\{ {{\sigma _0}} \right\} = 0$(R{ }表示求实部)来计算临界稳定数${\varepsilon _*}$的值, 一级近似下则利用${\text{R}}\left\{ {{\sigma _0} + \varepsilon {\sigma _1}} \right\} = 0$来计算${\varepsilon _*}$的值. 为单独检测每一个操作条件对特征值的影响, 采用新的操作参数:

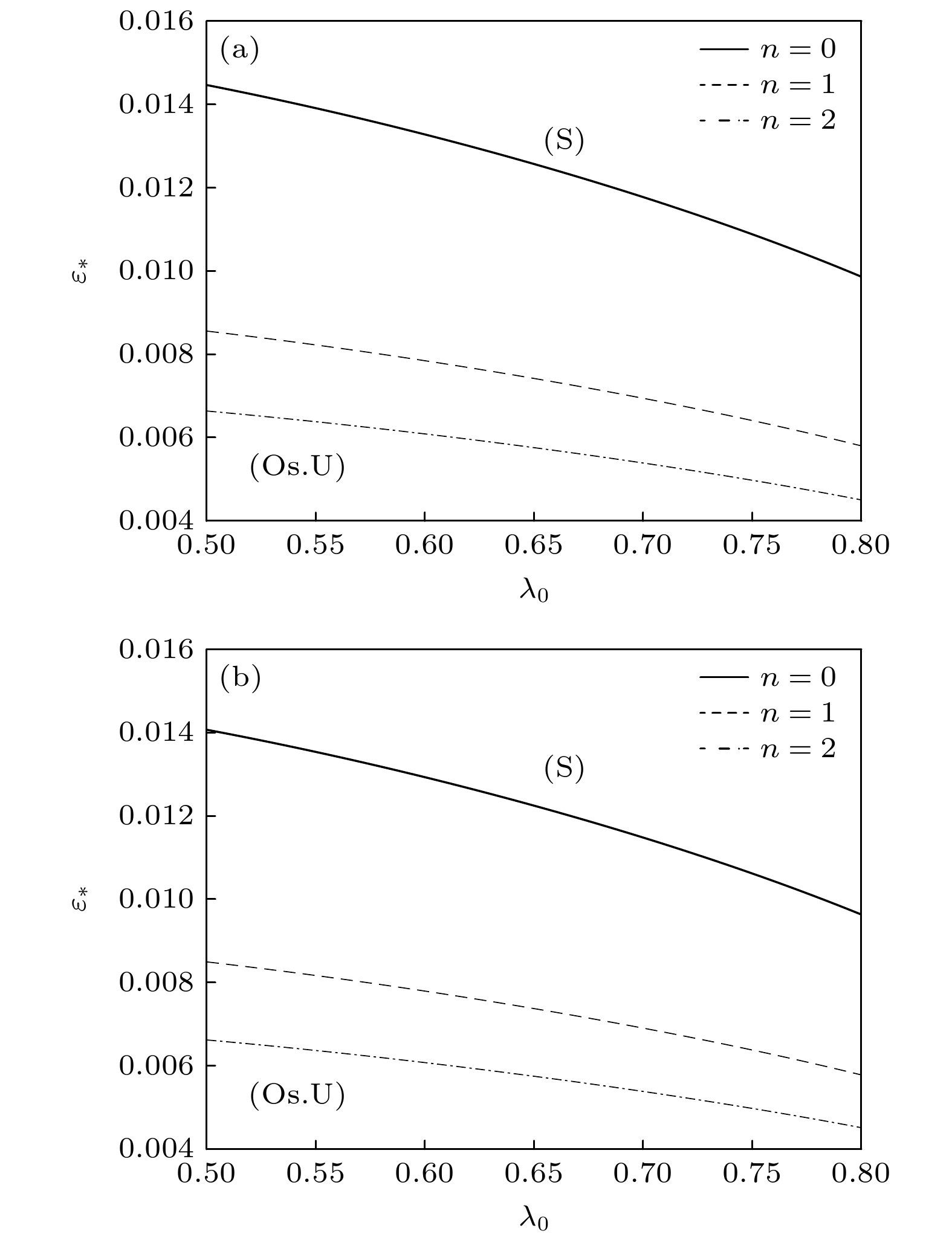
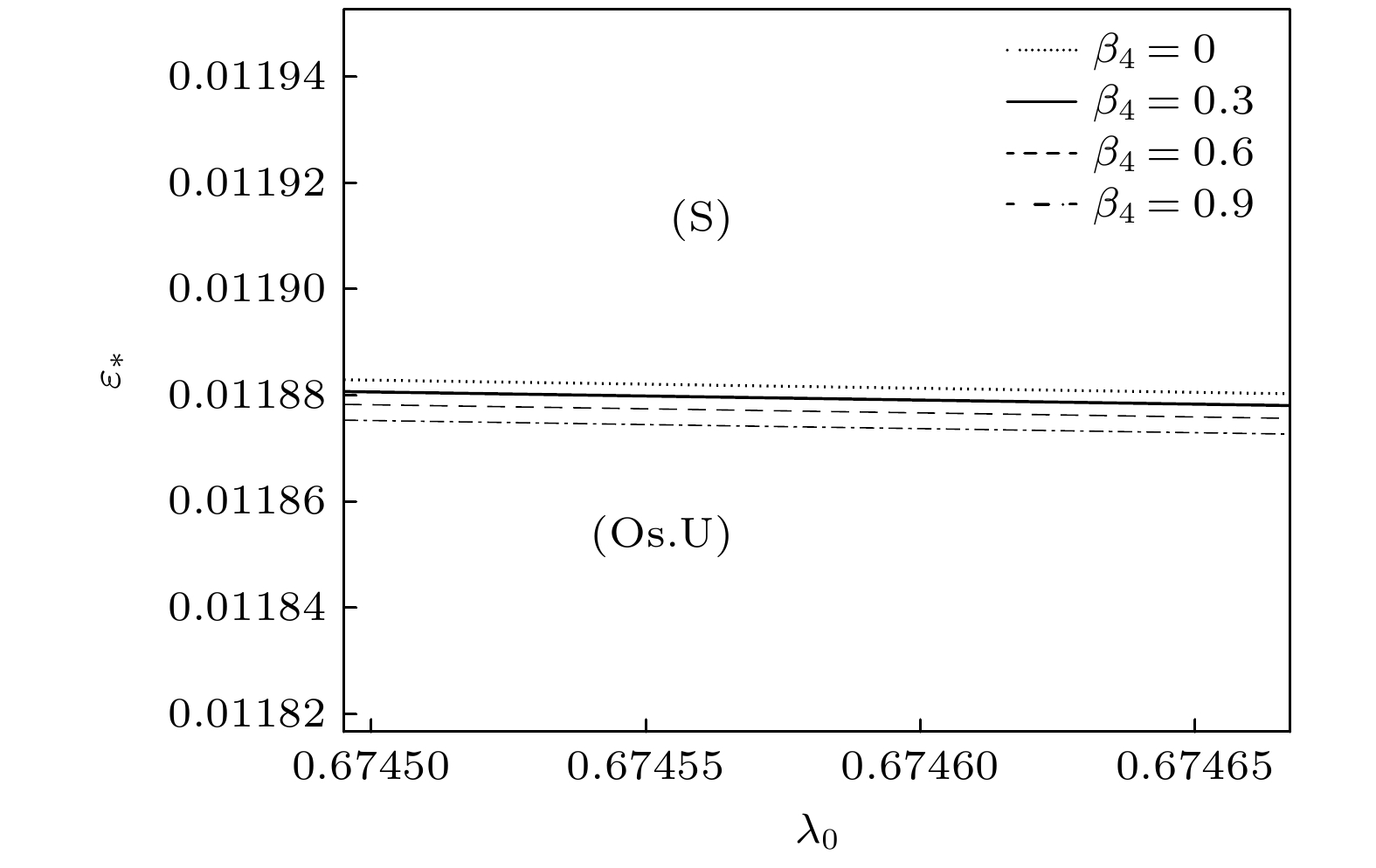
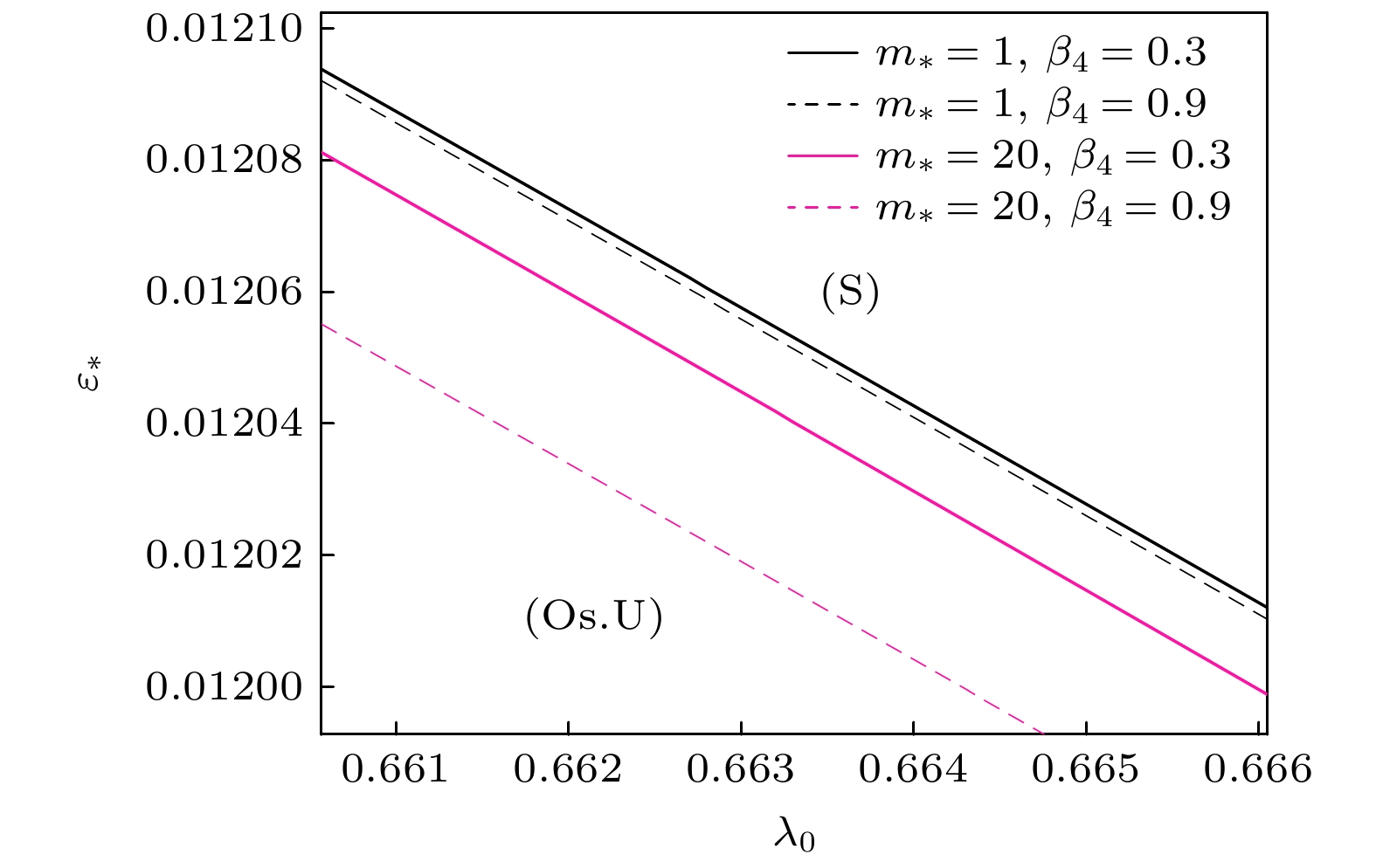
通过计算A-模式和S-模式的量子化条件发现, 对同一个$n$, S-模式比A-模式更危险. 可以得到稳定性判据为, 当$\varepsilon > {\varepsilon _*}$时, 深胞晶的生长是 稳定的, 当$\varepsilon < {\varepsilon _*}$时, 深胞晶的生长是不稳定的. 图5(a)和图5(b)分别展示了首级近似和一级近似下$n = 0, {\text{ }}1, {\text{ }}2$时的GTW-S中性模式曲线图, 首级近似下$\left( {{\lambda _0}, {\varepsilon _*}} \right)$曲线图与Niu和Jiang^[24]的结果相同, 且界面动力学各向异性参数不起作用, 在${\lambda _0}$固定的情况下, $n = 0$是最危险的模式, 即$n = 0$时最不稳定, 其次是$n = 1$, 最后是$n = 2$. 通过对比首级近似和一级近似在$n = 0$时的中性模式曲线, 发现在各向异性的影响下, 一级近似下的${\varepsilon _*}$相比首级近似下的${\varepsilon _*}$较小. 图6给出了各向异性界面动力学参数${\beta _4}$分别为$0, {\text{ }}0.3, {\text{ }}0.6, {\text{ }}0.9$情况下的GTW-S中性模式$\left( {n = 0} \right)$曲线图, 其中${\beta _4} = 0$的情况与文献[24]的结果相同. 取相同的${\lambda _0}$, ${\varepsilon _*}$随着各向异性界面动力学参数的增大而减小, 即界面动力学各向异性越大, 系统越稳定. 图7中展示了在一级近似下, 动力学参数${m_*}$和各向异性动力学参数${\beta _4}$分别取两个不同的值时所对应的GTW-S中性模式$\left( {n = 0} \right)$曲线图, 发现参数${\beta _4}$对系统不稳定性的影响随着${m_*}$的增大而增大, 且在参数${\beta _4}$不为$0$时, 界面动力学参数${m_*}$增大后对系统的影响更加显著.

综上, GTW-S中性模式曲线将平面分为两个区域: 稳定性区域$\left( S \right)$、不稳定性区域$\left( {{\text{Os}}{\text{.U}}} \right)$, 得到系统的振荡稳定性判据:

1) $(\varepsilon ,{\lambda }_{0})\in (S) $, 稳定;

2) $\left(\varepsilon ,{\lambda }_{0}\right)\in \left(\text{Os}\text{.U}\right) $, 不稳定.

情况$\left. 2 \right)$导致实特征值的频谱, 系统允许对称模式和反对称模式两种类型的整体低频模式, 由于在特征值的首级近似中, 界面动力学各向异性参数不影响系统在该模式下的稳定性, 此情况暂不做论述, 后续将继续研究一级近似下各向异性参数对稳定性的影响.

本文基于界面波理论, 建立在定向凝固过程中界面动力学为各向异性时深胞晶生长的数学模型, 再利用多重变量法和匹配渐近法, 研究了各向异性界面动力学对定向凝固过程中深胞晶生长界面形态稳定性的影响. 加入各向异性后系统有两种整体不稳定性机制: 整体波动不稳定性机制、低频不稳定性机制. 深胞晶生长的界面形态稳定性取决于一个重要的临界稳定数${\varepsilon _*}$, 该值与界面动力学各向异性系数的取值密切相关. 低阶时复特征值的频谱导致整体波动不稳定性, 实特征值的频谱则导致低频不稳定性, 稳定性分析表明, 在其他参数固定的情况下, 中性模式下产生强振荡的枝晶结构的整体波动不稳定性中, GTW-S模式下$n = 0$的情况最为危险, 且界面动力学各向异性参数越大, 系统的整体波动不稳定性的不稳定区域越小; 同时界面动力学参数${m_*}$越大, 界面动力学各向异性对系统不稳定性的影响也越大.