首页
登录
注册
-
动物及人类的各种生理功能活动受神经系统调控, 而神经元是神经系统结构与功能的基本单位[1,2]. 神经元的电活动与神经元间突触的化学活动共同参与完成神经信息的编码、传输、处理和整合[3,4]. 因此, 神经系统是由大量神经元通过突触耦合形成的复杂生物动力学网络[5]. 为便于模拟和分析生物神经系统的结构和功能特征, 大量神经元模型及神经网络模型被提出. 神经网络模型以其独特的结构和信息处理方式, 在模式识别、信号处理、人工智能等领域中发挥着重要作用[6–8]. 连续神经元模型, 如Morris-Lecar (ML)[9], FitzHugh-Nagumo (FN)[10], Hindmarsh-Rose(HR)[11], Hopfield neuron (HN)[12], tabu learning neuron[13]等, 主要基于Hodgkin-Huxley (HH)模型[14]构建. 同时, 在连续神经元模型的基础上, 学者们构建了许多离散神经元模型. 比如, Chialvo对HH连续模型进行简化, 建立了Chialvo离散神经元模型[15]. 受此启发, Rulkov和Kinouchi-Tragtenberg进一步建立了Rulkov[16], KT[17]及KTZ[18]等离散神经元模型. 相关研究表明, 离散神经元模型同样能用于模拟真实生物神经元的放电特性及行为特征, 且在计算复杂度、存储容量等方面比连续神经元模型更具优势[19]. 因此, 从某种意义上讲, 离散神经元模型更适合模拟神经网络并进行理论分析[20].
忆阻器被认为是除电阻、电容和电感之外的第四类无源电路元件, 具有纳米尺寸、本征复杂、非易失存储及类神经突触可塑性等独特性质. 因此, 忆阻器是模拟生物神经突触的理想器件[21–24], 为人工神经网络的构建提供了新的思路. 局部有源性被认为是动力系统复杂性的起源[25]. 局部有源忆阻器能放大无限小能量振荡行为, 应用于神经网络系统或神经元电路时易于诱发各类神经形态放电行为[26]. 因此, 利用局部有源忆阻器模拟生物神经突触受到越来越多的关注. 将离散局部有源忆阻器引入人工神经网络或神经元, 可以更准确地模拟生物神经元之间的电活动和信息传递, 有助于揭示神经系统疾病的电生理学机制. Lai和Yang[27]基于无离散忆阻器、离散忆阻器模拟电磁辐射刺激、离散局部有源忆阻器模拟生物突触等方式构建了三种离散神经网络模型; 研究表明, 离散忆阻器可使得神经网络模型产生更为复杂的混沌放电动力学行为. Li等[28]构建了一类离散忆阻Rulkov神经元模型, 研究发现忆阻器可以有效地模拟离散神经元模型的磁感应效应. 此外, Lu等[29]研究了基于离散忆阻器的分数阶神经网络, 发现其具有比整数阶神经网络更丰富的动力学行为. 事实上, 生物神经信息的处理和传递由不同脑区神经元的电磁活动共同完成, 因此, 探索异质离散神经网络的放电动力学和同步行为具有重要实际意义[13].
突触间的串扰由神经递质从一个突触溢出至另一个突触引起. 突触神经递质的溢出将对相邻突触的连接强度产生干扰, 因此, 突触串扰将影响神经信号的放电及传输特性[30,31]. Li和Yi[32]提出一种基于忆阻器突触的联想记忆电路, 并研究了突触串扰对忆阻器功能的影响. Ding等[33]揭示了不同串扰强度下, 忆阻器耦合HR神经网络平衡点的数量和稳定性具有多样性. 另外, 越来越多的证据表明, 突触串扰存在于多个不同大脑区域. 例如, Li等[34]建立了一个异质神经网络, 探讨了串扰强度对神经网络放电活动的影响, 发现随着串扰强度的降低, 异质神经元的放电行为从初始振荡逐渐过渡到完全同步. Ma等[35]则从数值模拟角度探讨了串扰强度对异质离散神经网络放电行为和同步行为的影响. 然而, 目前尚没有关于突触串扰强度对神经网络共存放电行为影响的研究. 事实上, 共存放电意味着神经系统的不同等待状态[36], 即在不同时间或环境下, 神经系统中神经元的放电模式可能有所不同, 从而释放不同的神经信息. 这些不同的放电模式和神经信息对外界环境的刺激和内部状态的改变做出反应, 从而呈现出不同的神经特征. 因此, 神经系统共存放电现象为临床上不同个体或不同阶段的同病异症及同病异诊提供了电生理学理论基础. 同时, 医生还可根据患者的共存放电模式和特征, 预测疾病的发展趋势和预后结果, 从而采取相应的干预措施和监测方案. 因此, 神经系统共存放电研究有助于神经系统疾病的综合治疗.
综上可知, 探索突触串扰对异质离散神经网络放电特性与同步行为的影响具有重要意义, 但有关忆阻突触异质离散神经网络的研究相对较少. 本文首先设计一类局部有源离散忆阻器, 用于模拟生物神经突触并耦合Chialvo神经元和Rulkov神经元, 建立一类具有突触串扰的忆阻耦合异质离散神经网络. 进而, 分析离散神经网络的不动点和稳定性、共存放电行为、变量偏置控制. 此外, 具体研究不同耦合强度及不同系统初始条件和参数情形下, 离散神经网络的同步行为, 及突触串扰强度对神经网络同步行为的影响.
-
根据Chua关于忆阻器的定义[37], 一类磁控型离散忆阻器设计为
其中v(n)和i(n)为忆阻器的输入电压和输出电流;
$\varphi(n) $ 为忆阻器的内部状态变量. 本节中, 忆阻器参数设置为a = 1, b = 0, c = 2, d = –0.5, e = 0.2.为了模拟突触串扰现象, 考虑两个忆阻器之间的相互作用, 描述如下:
式中, W1(
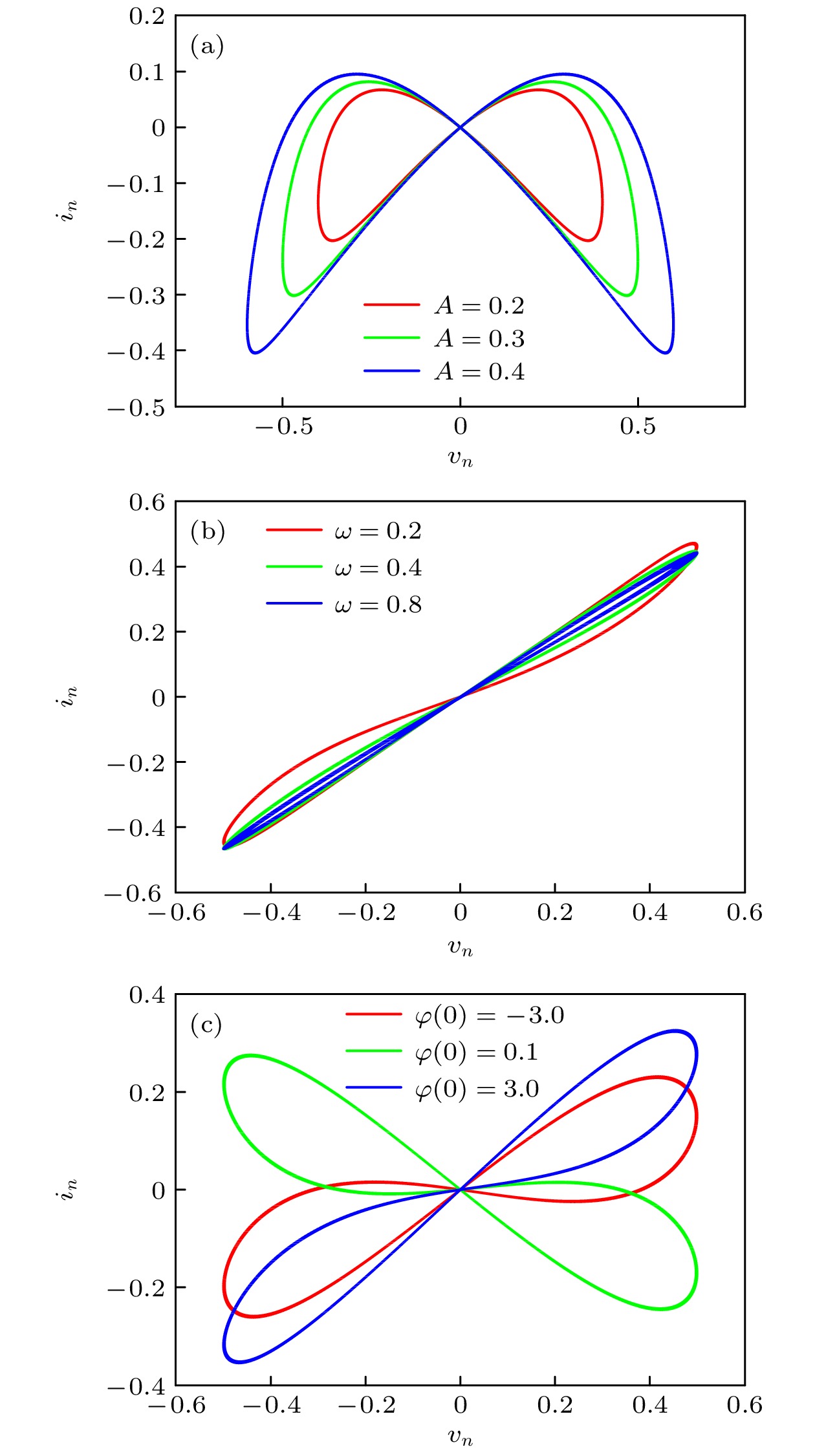
$\varphi $ )和W2($\varphi $ )分别表示考虑串扰时第一个突触和第二个突触的权重; p1和p2为突触之间的串扰强度, 其中p1sin($a\varphi _2+b$ )表示第二个突触对第一个突触的影响, p2sin($a\varphi_1+b $ )表示第一个突触对第二个突触的影响.在输入正弦电压信号v(n) = Asin(ωn)时, 离散忆阻器的电压–电流特性曲线如图1所示. 由图1(a)可知, 电压-电流曲线呈现出穿过原点的“8”字形磁滞回线, 且磁滞回线的面积随着振幅A的增加而逐渐增大. 图1(b)中, “8”字形磁滞回线的面积随着频率ω的增大而减小. 图1(c)则表明, 磁滞回线的形状随着初始值的变化而改变, 表现出多稳态性和记忆特性. 因此, 该离散忆阻器具有广义忆阻器的指纹特征[38], 是一类广义磁控型离散忆阻器.
令(1)式中第二个方程的v(n) = 0, 可得
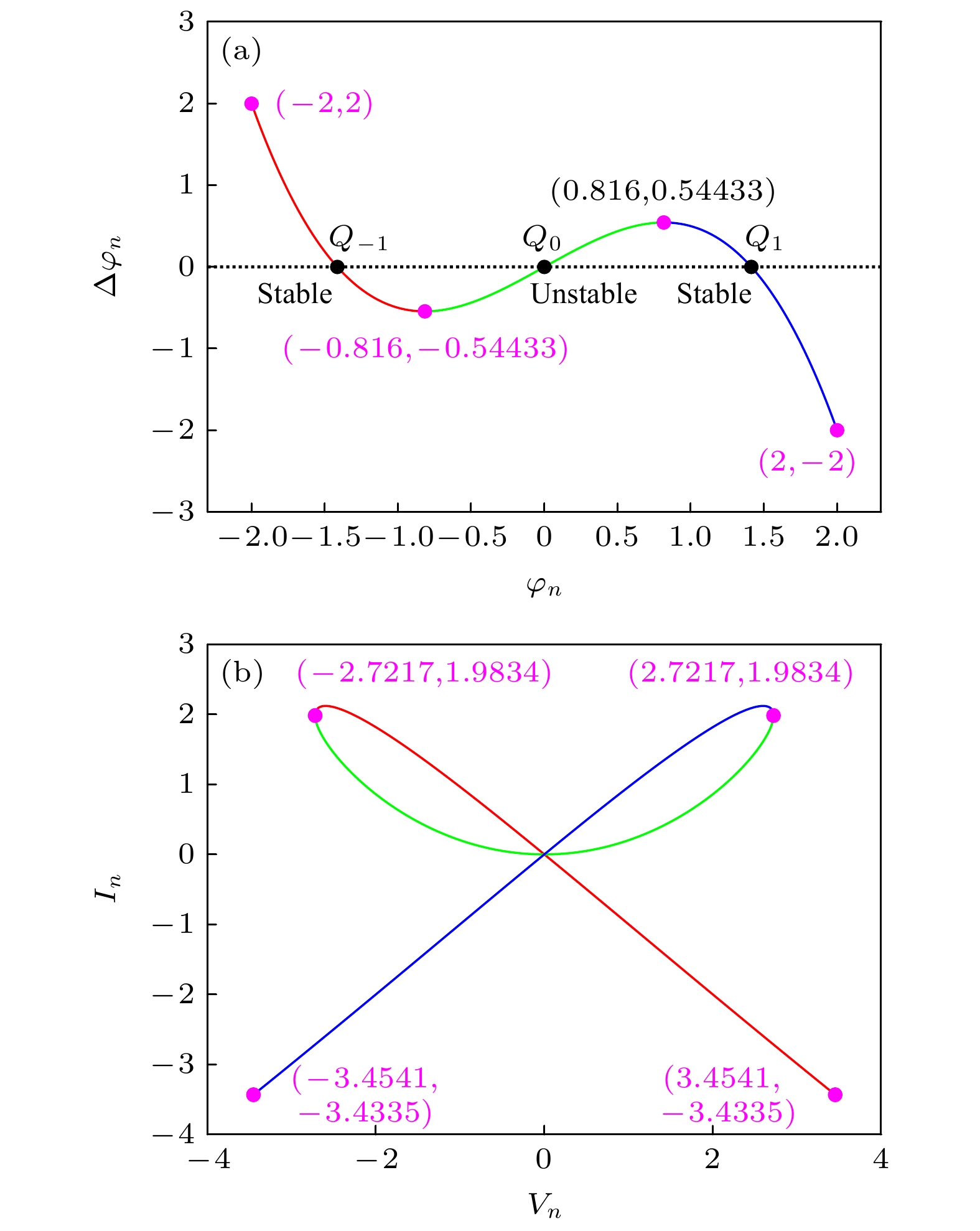
基于(3)式, 忆阻器的断电图绘制于图2(a)所示, 其与
$\Delta \varphi_n = 0$ 轴的交点为Q–1, Q0, Q1. 可知, 交点Q–1和Q1处的斜率为负, 因此, 忆阻器是非易失性的.假设(1)式中
$\varphi $ (n) = Φn, v(n) = Vn, 且$\varphi $ (n+1)–$\varphi $ (n) = 0, 则式中, Vn, In分别表示直流电压和直流电流. 对 应的DC V-I曲线如图2(b)所示. 可知, 在区域 Vn∈[–2.7217, 0]∪In∈[0, 1.9834]及Vn∈[–2.7217, 3.4541]∪In∈[–3.4335, 1.9834]内, DC V-I曲线的斜率为负, 即忆阻器具有负的电阻值. 因此, 忆阻器是局部有源的.
-
二维离散Chialvo神经元的数学模型如下:
其中x(n)表示神经元的膜电位; y(n)表示恢复变量; 参数a表示恢复时间(a < 1); 恢复过程的激活依赖性由b (b < 1)定义; c为偏移值; I可视为外部输入电流.
二维离散Rulkov神经元定义如下:
式中, x(n)为神经元的膜电位, y(n)为神经元的减速变量. 因为变量y(n)的变化速度由b和c 控制, 而b是一个非常小的值(0<b
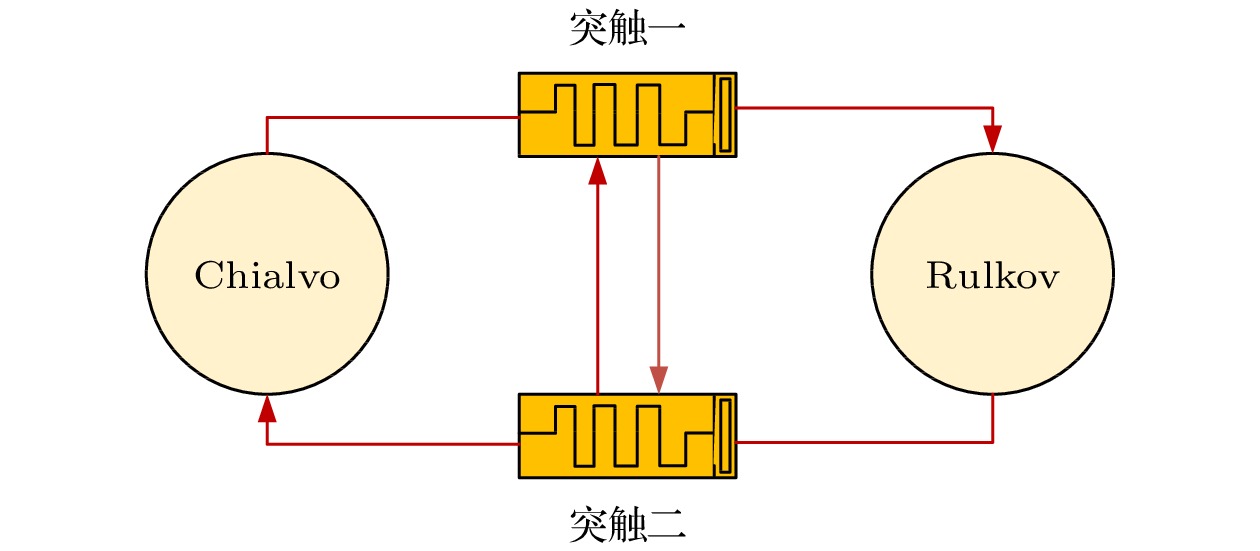
$\ll1 $ ), 因此变量y(n)会随时间缓慢变化. 参数a为非线性映射参数, 参数c是神经元的外部直流电流, b的值为0.001.以上设计的忆阻器模拟生物神经突触, 将Chialvo离散神经元和Rulkov离散神经元耦合起来, 并考虑突触间的串扰行为, 构建一类忆阻突触耦合异质离散神经网络, 如图3所示. 神经网络模型描述如下:
其中x1和x2表示膜电位; y1和y2分别表示恢复变量和减速变量;
$\varphi_1 $ 和$\varphi_2 $ 表示磁通量; k为神经元的耦合强度. 神经网络参数如下: a1 = 0.89, b1 = 0.005, c1 = 0.28, I = 0.03, a2 = 2.8, b2 = 0.001, c2 = 0.1, c = 1, d = –0.5, e = 0.2, k = 0.1和p1 = 0.1. 当p2∈[0, 0.345], 模型表现为超混沌放电行为; 当p2∈[0.345, 1], 模型表现为混沌放电行为. -
设神经网络系统的不动点为P = (X1, Y1, X2, Y2, Z1, Z2), 则P满足以下方程:
根据(8)式, 可以得神经网络系统的不动点:
对应的雅可比矩阵如下:
其中
$ A = 2{X_1}{{\mathrm{e}}^{({Y_1} - {X_1})}} - X_1^2{{\mathrm{e}}^{({Y_1} - {X_1})}} $ ,$ B = X_1^2{{\text{e}}^{({Y_1} - {X_1})}} $ ,$ C = - k[{p_2}\cos (a{Z_1} + b)a]\tanh {X_2} $ ,$ D = - k[\cos (a{Z_2} + b)a]\tanh {X_2} $ ,$ E = k[\cos (a{Z_1} + b)a]\times \tanh {X_1} $ ,$ F = k[{p_1}\cos (a{Z_2} + b)a]\tanh {X_1} $ .雅可比矩阵的特征值可由
$ \det (\lambda I - {\boldsymbol{J}}) = 0 $ 得到. 表1列出了不同串扰强度下离散神经模型的不动点和特征值. 可知, 神经网络不动点的数量及稳定性依赖于突触串扰强度. -
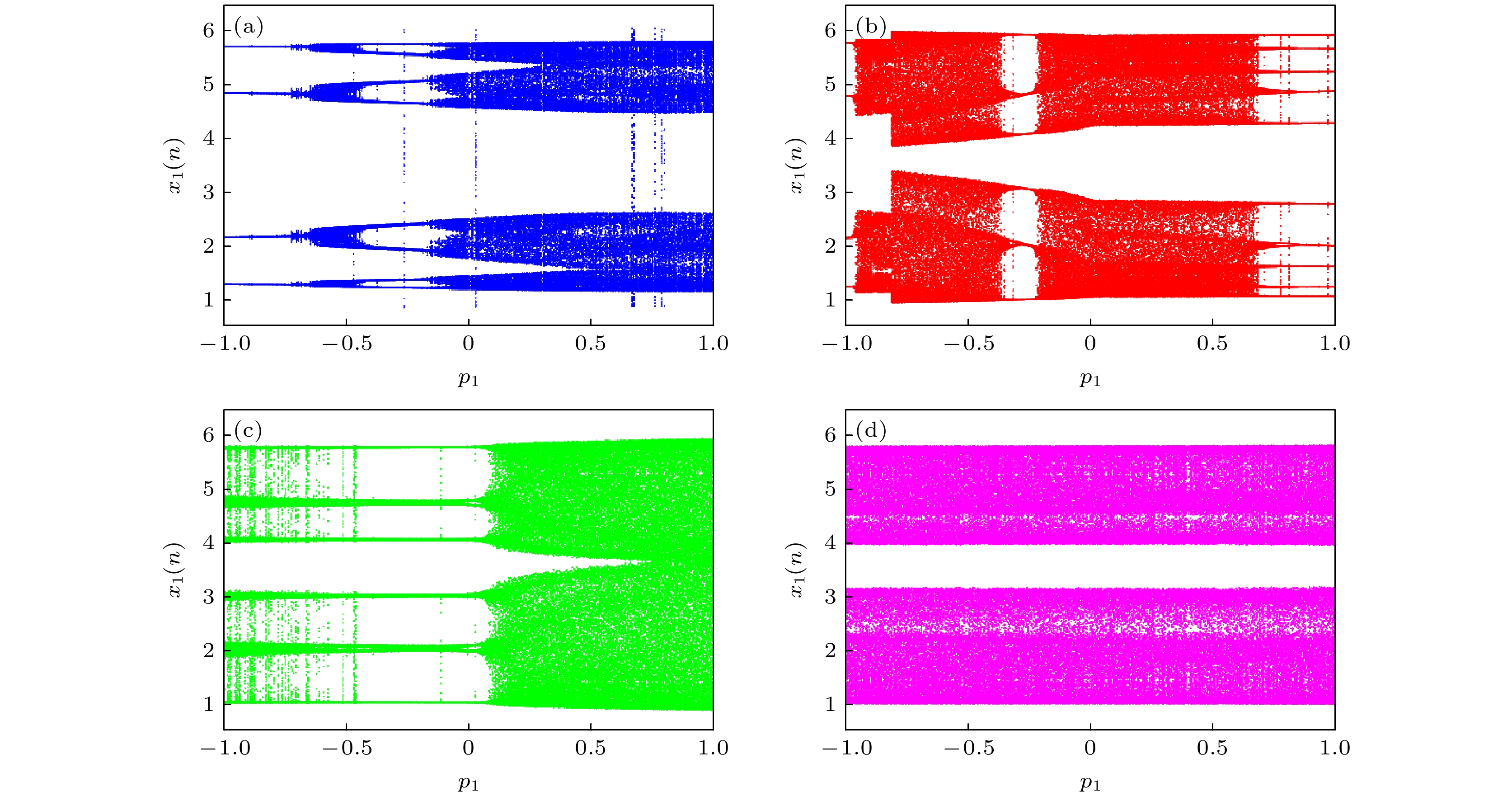
当耦合强度k = 0.1及串扰强度p2 = 0.3时, 发现在不同初始条件下, 神经网络系统关于串扰强度p1的分岔图各不相同, 如图4所示, 蓝色、红色、绿色、洋红色分别对应于初始条件IC1 = (1, 1, 1, –1, 1, 0), IC2 = (1, 1, 1, –2.4, 1, 0), IC3 = (1, 1, 1, 1, 1, 0), IC4 = (1, 1, 1, 2, 1, 0). 对于初始值(1, 1, 1, –1, 1, 0), 随着串扰强度p1的增加, 神经网络历经周期到混沌的倍周期分岔路径, 依次表现出周期4、混沌、周期8、周期16、混沌等不同放电模式, 如图4(a)所示; 对于初始值(1, 1, 1, –2.4, 1, 0), 神经网络历经倍周期分岔及反向倍周期分岔等路径, 依次表现出周期4、周期8、混沌、周期12、周期6、混沌、周期10等不同放电模式, 如图4(b)所示; 对于初始值(1, 1, 1, 1, 1, 0), 神经网络历经倍周期分岔路径, 可表现出周期6、周期12、混沌等放电模式, 如图4(c)所示; 对于初始值(1, 1, 1, 2, 1, 0), 神经网络表现为鲁棒的混沌放电模式, 如图4(d)所示. 显然, 神经网络系统具有多重稳定的共存放电特性.
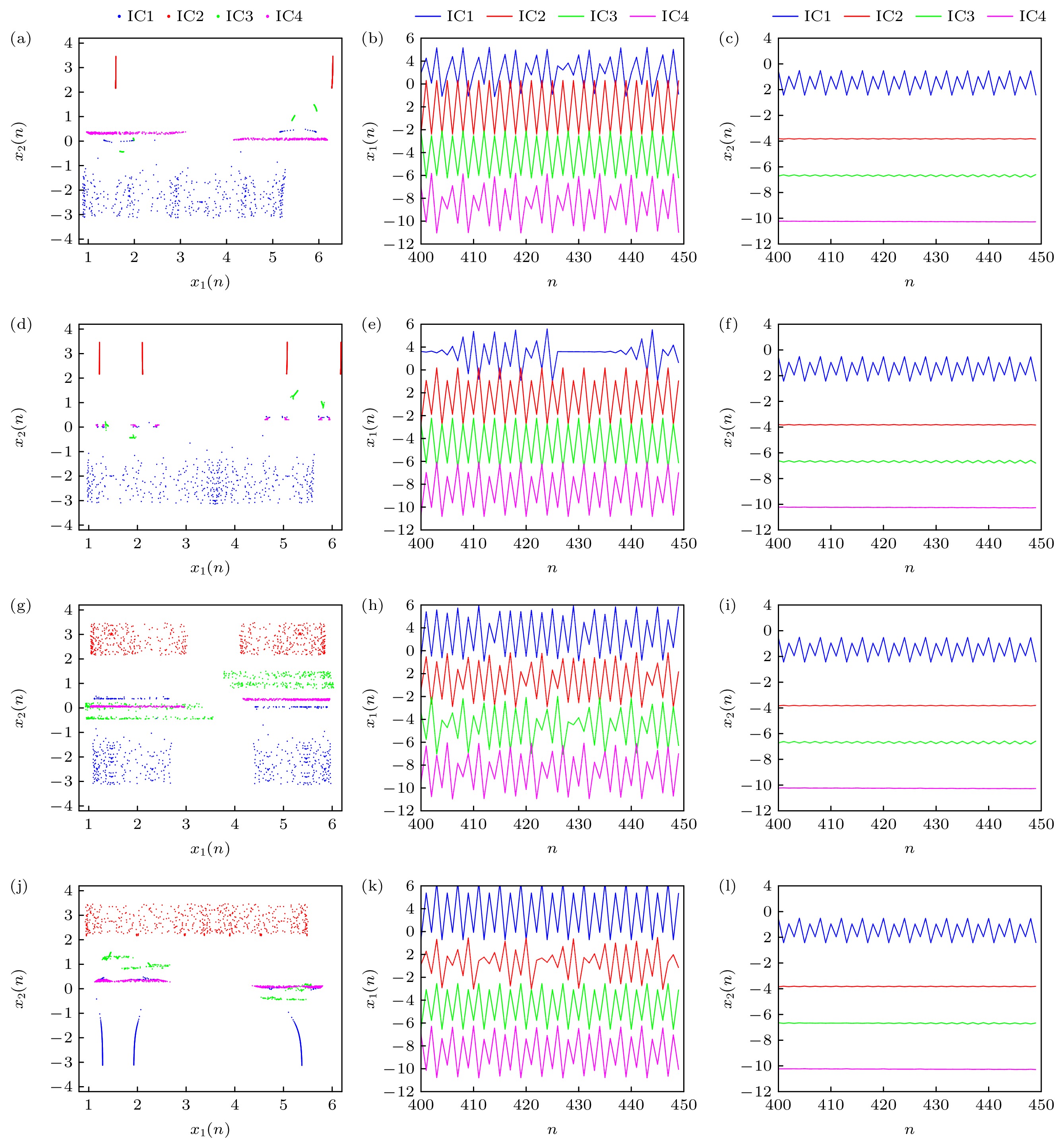
为了更加直观地观测串扰强度对共存放电特性的影响, 考虑初始条件IC1, IC2, IC3, IC4下, 不同串扰强度p1作用时神经网络的共存吸引子及共存放电序列, 如图5所示. 具体地, 当p1 = –0.8, 神经网络表现为周期2(蓝色)、周期3(绿色)、混沌(红色、洋红色)等放电形式, 如图5(a)—(c); 当p1 = –0.4, 神经网络表现为周期4(蓝色)、周期3(红色、绿色)、混沌(洋红色)等放电形式, 如图5(d)—(f); 当p1 = 0.2, 神经网络表现为混沌放电形式, 如图5(g)—(i); 当p1 = 0.8, 神经网络表现为周期5(红色)、混沌(其余)混沌放电形式, 如图5(j)—(l).
-
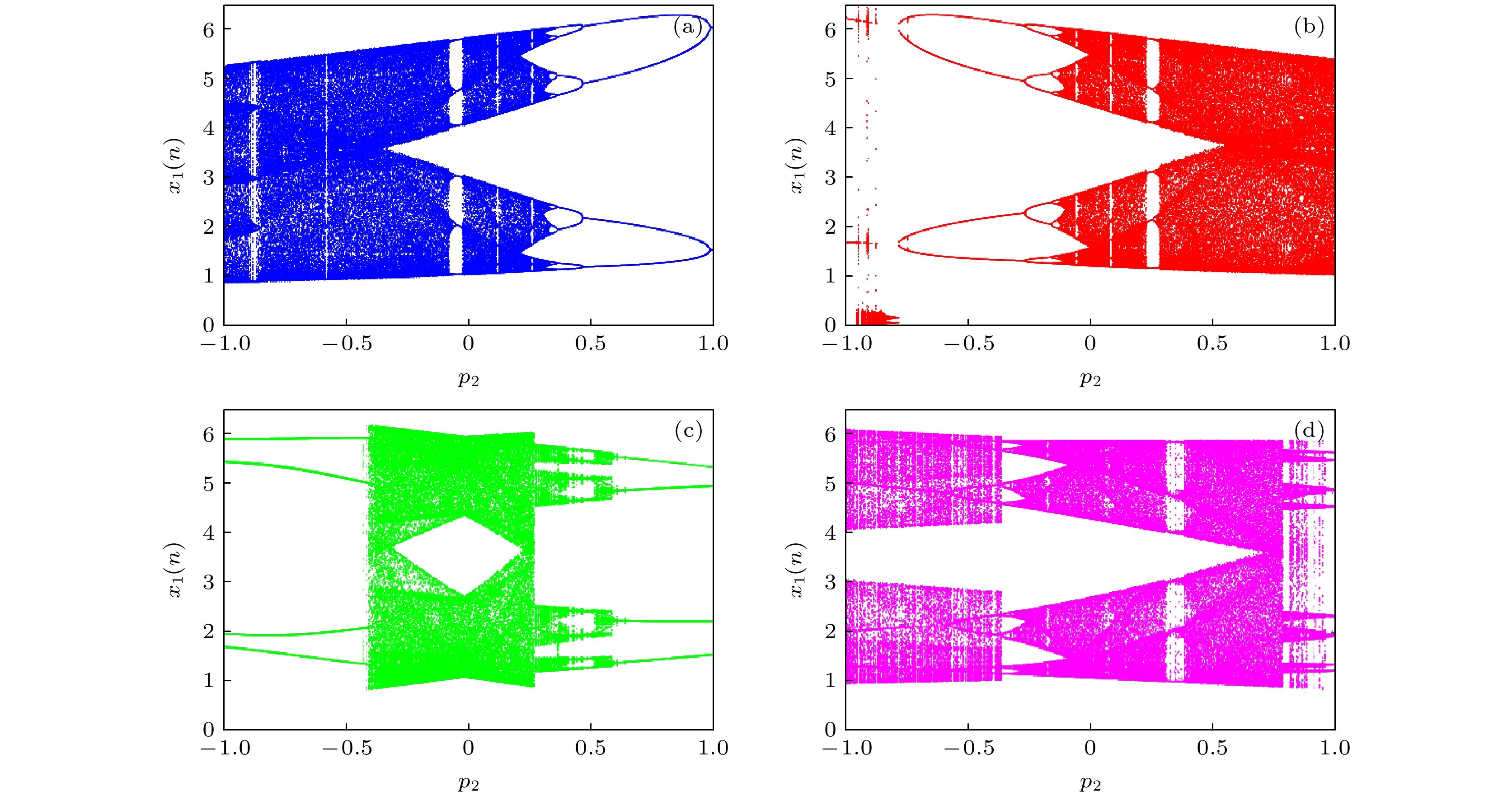
当耦合强度k = 0.1及串扰强度p1 = 0.1时, 不同初始条件下神经网络系统关于串扰强度p2的分岔图如图6所示, 其中蓝色、红色、绿色、洋红色分别对应于初始条件IC1 = (1, 1, 1, –5, 1, 0), IC2 = (1, 1, 1, 5, 1, 0), IC3 = (1, 1, 1, –1, 1, 0), IC4 = (1, 1, 1, –3, 1, 0). 对于初始值(1, 1, 1, –5, 1, 0), 随着串扰强度p2的增加, 神经网络历经混沌到周期的反向倍周期分岔及切分岔等路径, 依次表现为混沌、周期12、周期6、周期16、周期8、周期4、周期2等不同放电模式, 如图6(a)所示; 对于初始值(1, 1, 1, 5, 1, 0), 神经网络历经周期到混沌的倍周期分岔及切分岔等路径, 依次表现为周期2、周期4、周期8、周期16、混沌、周期6、周期12等不同放电模式, 如图6(b)所示; 对于初始值(1, 1, 1, –1, 1, 0), 神经网络历经切分岔等路径, 可表现出周期4、不同幅度混沌、周期8等放电模式, 如图6(c)所示; 对于初始值(1, 1, 1, –3, 1, 0), 神经网络历经倍周期分岔、切分岔等路径, 可表现出周期8、周期16、周期3、周期6、混沌等放电模式, 如图6(d)所示. 因此, 神经网络系统同样具有多重稳定的共存放电行为.
类似地, 考虑初始条件IC1, IC2, IC3, IC4下, 不同串扰强度p2作用时神经网络的共存吸引子及共存放电序列, 以更直观地观测串扰强度对共存放电特性的影响, 如图7所示. 具体地, 当p2 = –1.1, 神经网络表现为混沌(蓝色、洋红色)、周期(红色、绿色)放电形式, 如图7(a)—(c); 当p2 = –0.4, 神经网络表现为混沌(蓝色)、周期(其余)放电形式, 如图7(d)—(f); 当p2 = 0.2, 神经网络表现为混沌放电形式, 如图7(g)—(i); 当p2 = 0.8, 神经网络表现为混沌(红色)、周期(其余)放电形式, 如图7(j)—(l).
-
偏置控制是指在不改变动力系统解的情况下, 在其解空间中移动吸引子位置及吸引盆的一种方法[39,40]. 由(7)式所示异质离散神经网络可知, 状态变量y2仅以线性项形式出现, 因此可用于偏置控制. 据此, 在(7)式的状态变量y2中引入控制参数m, 得到偏置可控神经网络系统:
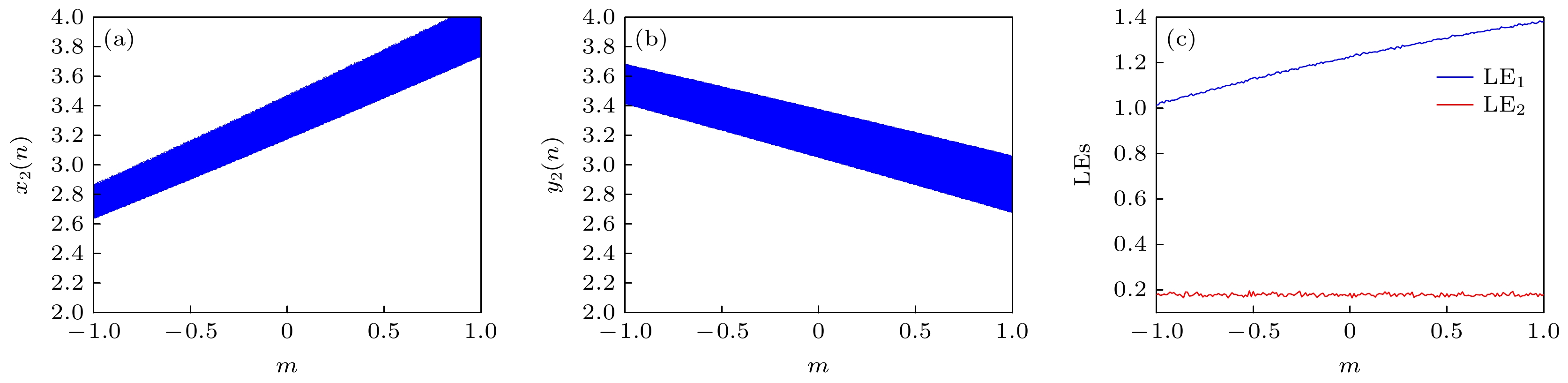
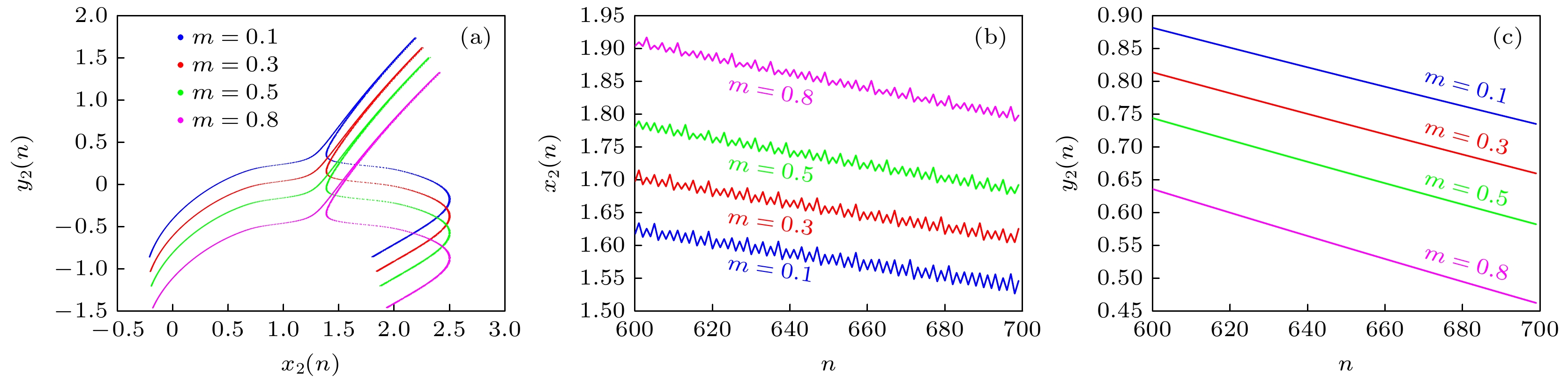
设置k = 0.1, p1 = 0.1, p2 = 0.1, 初始值(1, 1, 1, 5, 1, 0), 其他系统参数保持不变, 绘制状态变量x2, y2关于参数m的分岔图, 如图8(a), (b)所示. 可知, 随着m的增加, 状态变量x2, y2的偏置随m线性变化. 图8(c)绘制了系统前两个李雅普诺夫指数随参数m的演化过程, 可知, 最大李雅普诺夫指数随参数m逐渐增加, 而第二个李雅普诺夫指数保持恒定. 根据偏置控制对多稳态性的辨识原理[41]可判定, 随参数m的增加, 系统表现为无穷稳定状态. 图9为m = 0.1, 0.3, 0.5, 0.8时神经网络的x2-y2平面相图及时序图, 进一步证实了参数m对状态变量x2, y2的偏置调控特性及系统的无穷稳定状态特性. 变量偏置控制意味着引入偏置控制参数后, 神经放电序列的强度可得到灵活的控制[42].
-
同步是神经网络的基本现象, 也是大脑信息处理的关键. 如前所述, 耦合强度、串扰强度、系统参数及初始值对异质神经网络的放电动力学有着较大的影响, 从而可能产生同步跃迁. 本节拟基于神经元放电序列的相位差及同步因子, 研究异质神经网络系统的同步放电行为. 神经元膜电位序列x1(t)和x2(t)的相位差由下式求得:
其中
$ {\hat x_1}(t) $ 和$ {\hat x_2}(t) $ 是采样序列x1(t)和x2(t)的希尔伯特变换,式中, PV是柯西意义上的积分. 当神经元膜电位序列x1(t)和x2(t)的相位差∆
$ \phi $ 的绝对值小于2π 时, 可以检测到相位同步行为.基于平均场理论, 同步因子R定义如下:
其中
$ \bar x $ 为神经元序列x的平均值;$ \left\langle x \right\rangle = \dfrac 1 {\Delta t}\displaystyle\sum\limits_{t = {t_{\text{i}}}}^{{t_{\text{f}}}} x $ 为序列x在时间上的平均值, ∆t = tf – ti, ti和tf分别为计算开始和结束时间. 因此, R(x)∈[0, 1], 且R(x)→1表示时间序列x1(t)和x2(t)达到完全同步状态. -
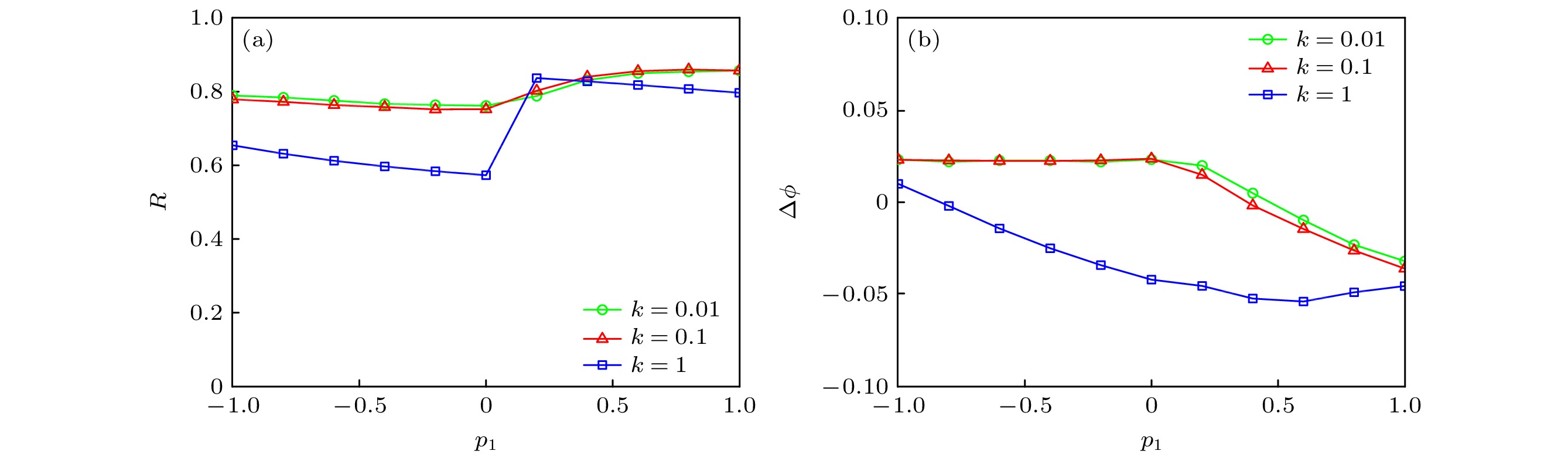
固定串扰强度p2 = 0.1及初始值(1, 1, 1, 1, 1, 0), 考虑不同耦合强度、系统初始值和系统参数下, 串扰强度p1对网络同步行为的影响. 如图10(a)所示, 当p1∈[–1, 1], 神经网络具有较大的同步因子; 以p1 = 0为分界点, 同步因子R先减小后增大; 且耦合强度k越低, 同步因子R越大, 同步性能越好. 同时, 从图10(b)可以观察到, 神经元膜电位序列的相位差满足 |∆
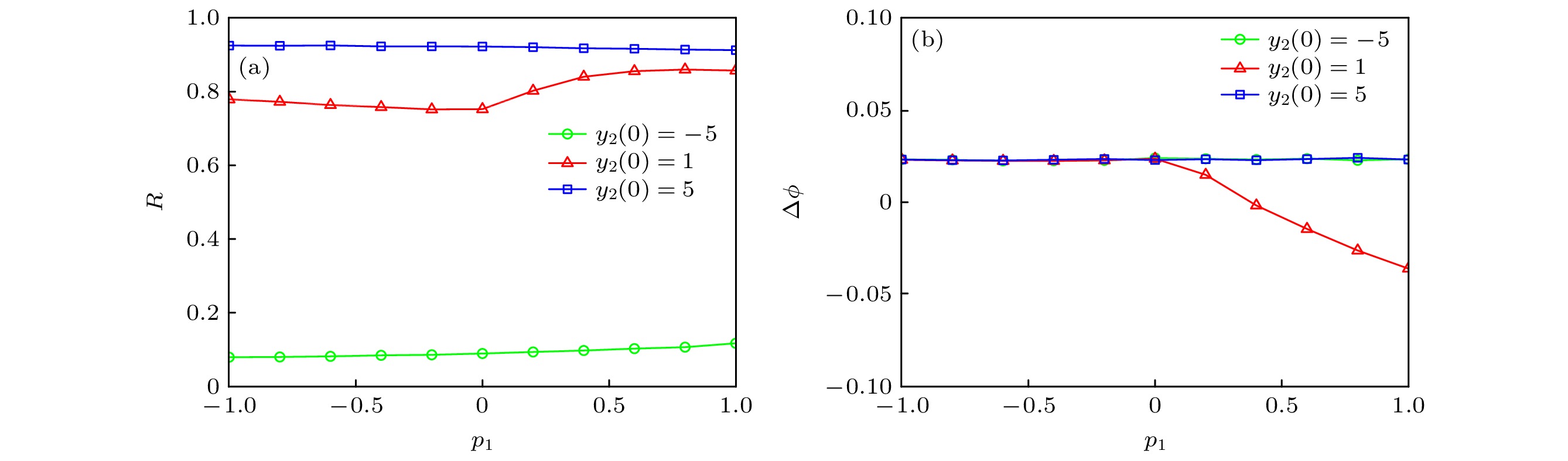
$\phi $ | < 2π, 说明Chialvo神经元和Rulkov神经元处于相位同步状态.根据前文的探讨, 发现初始值y2(0)对神经网络放电行为有一定影响. 因此, 进一步研究不同初始值y2(0)下, 串扰强度p1对神经网络同步行为的影响. 如图11(a)所示, 在不同初值下, 串扰强度p1对神经网络的同步行为影响较小; 但y2(0)的取值过小时(如y2(0) = –5), 同步因子R的值较小. 而当y2(0) = 1时, 从p1 = 0开始同步因子R的值随着串扰强度p1增加而不断增大; 此时, 相位差随着p1增加逐渐减小, 且始终满足 |∆
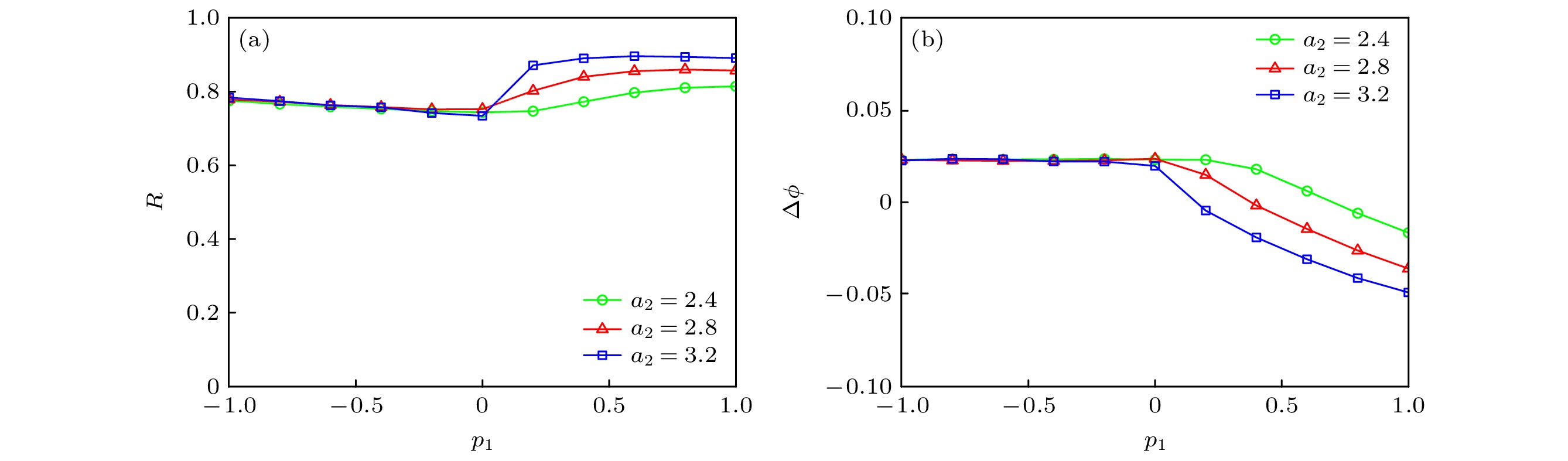
$\phi $ | < 2π, 如图11(b)所示.图12描述了取不同系统参数a2时, 串扰强度p1对神经网络同步行为的影响. 可知, 当p1∈[–1, 0]时, 相位差∆
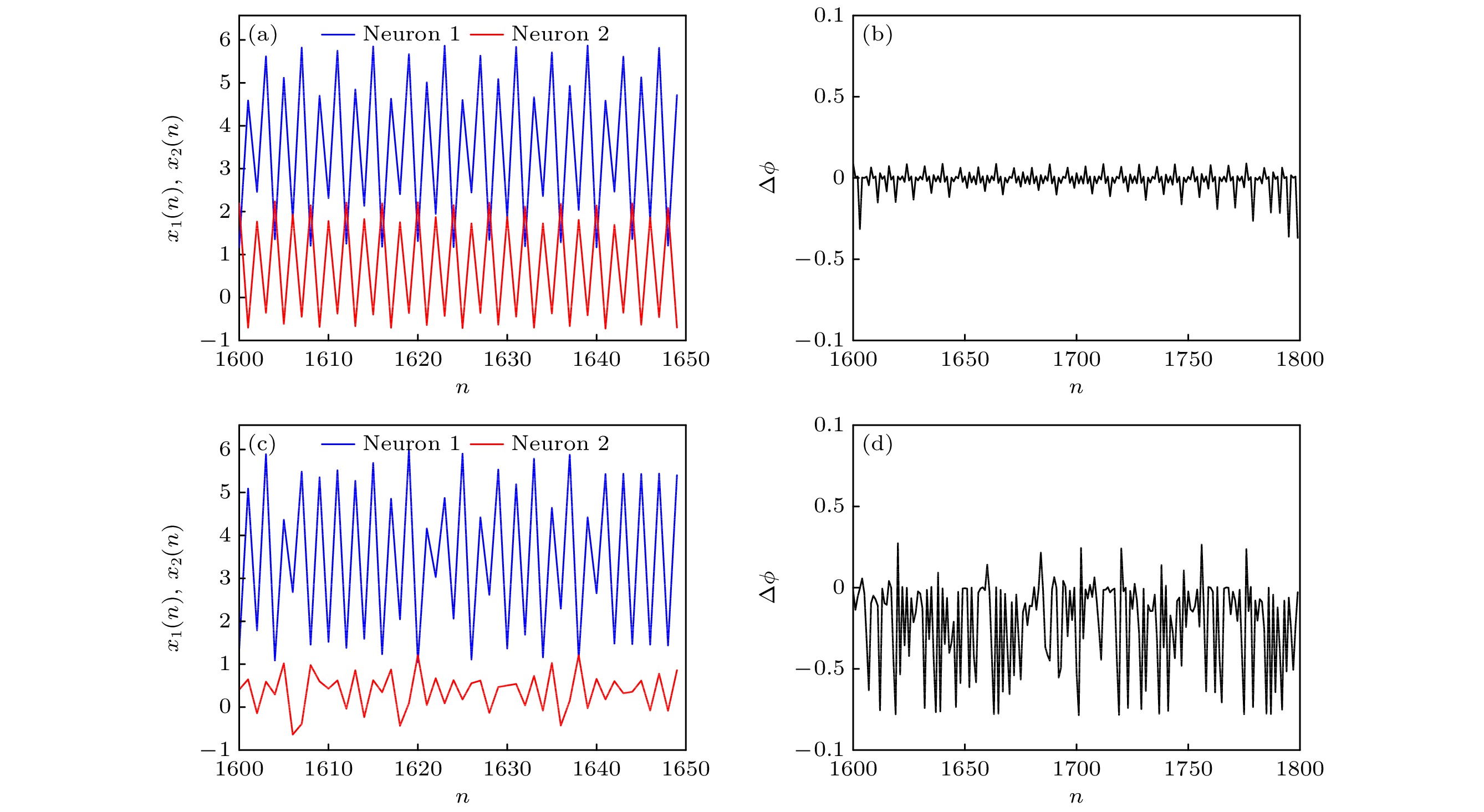
$\phi $ 和同步因子R受参数a2的影响较小, 即神经网络同步行为对a2的依赖性较低; 而当p1∈(0, 1]时, R的值逐渐增大, 而相位差∆$\phi $ 逐渐减小, 并且参数a2的值越大, 神经网络的同步性越高.为更直观地观察神经网络的同步放电行为, 固定参数a1 = 0.89, b1 = 0.005, c1 = 0.28, I = 0.03, a2 = 2.8, b2 = 0.001, c2 = 0.1, c = 1.0, d = –0.5, e = 0.2, k = 0.1, p2 = 0.1, 考虑不同串扰强度p1下膜电位和相位差随时间的演化, 如图13. 可知, 串扰强度p1取不同值时, 两个异质神经元一直处于相位同步状态.
-
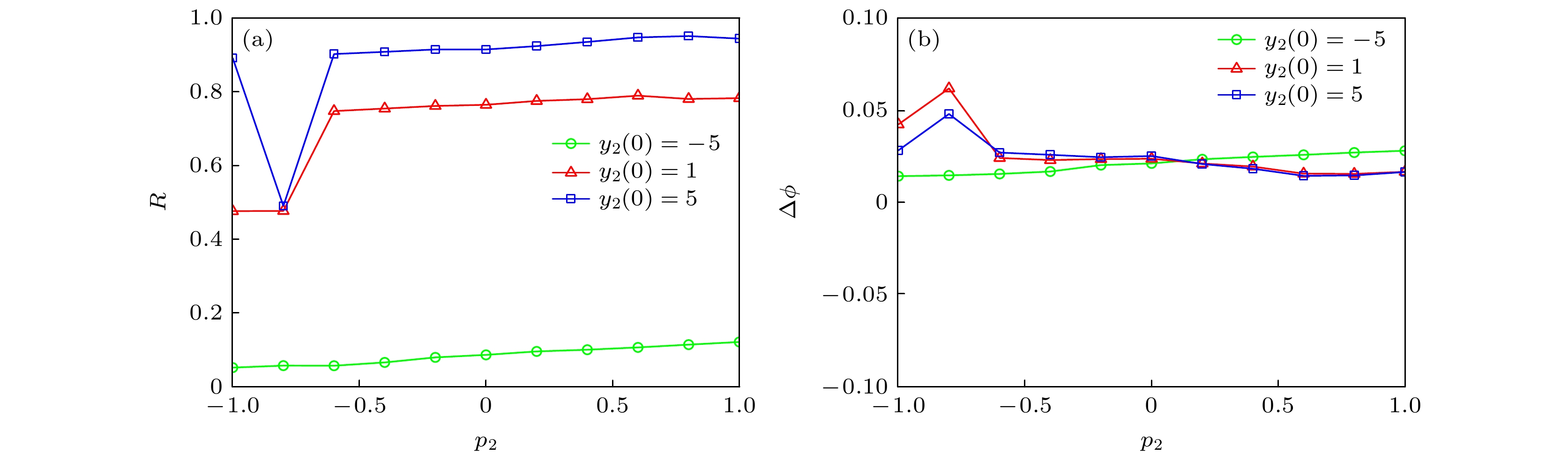
固定串扰强度p1 = 0.1及初始值(1, 1, 1, 1, 1, 0), 考虑不同耦合强度、初始值及系统参数下, 串扰强度p2对神经网络同步行为的影响. 从图14(a)中可以看出, 耦合强度k较大或者较小时(如k = 0.01, 1), 神经网络同步因子R的值基本保持不变; 而当k = 0.1时, 同步因子R值在p2 = –0.8处有一个大幅度的提升, 继而在p2 > –0.6时基本保持不变. 与之对应, k = 0.1时, 相位差在p2 = –0.8处减小并在p2 > –0.6时基本保持不变, 且满足 |∆
$\phi $ | < 2π, 如图14(b)所示.从图15中可以看出, 初始值y2(0)过小时(如y2(0) = –5), 随着p2的变化, 神经网络的同步因子及相位差基本不变, 但同步因子的值较小. 初始值y2(0)较大时(如y2(0) = 1, 5), 串扰强度p2对神经网络同步行为的影响较大. 具体地, p2∈[–1, –0.62]时, 同步因子先变小后增大, 相位差先增加后减小; p2 > –0.62时, 同步因子和相位差变化较为平缓. 但当p2∈[–1, 1], 始终满足 |∆
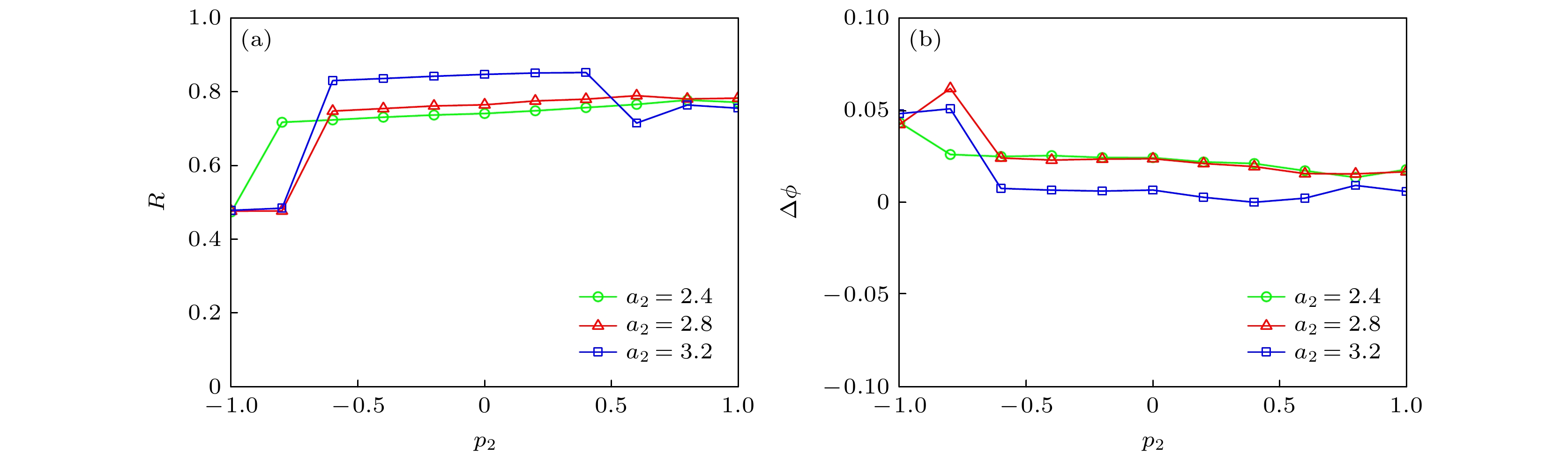
$\phi $ | < 2π, 表明神经网络处于相位同步状态.取不同的神经网络参数a2时, 串扰强度p2对神经网络同步行为的影响如图16所示. 可知, 串扰强度p2对神经网络同步行为的影响较大. 随着a2的增加, 同步因子先减小后增加, 随后基本稳定, 如图16(a)所示. 而随着a2的增加, 相位差基本呈减小趋势, 如图16(b)所示.
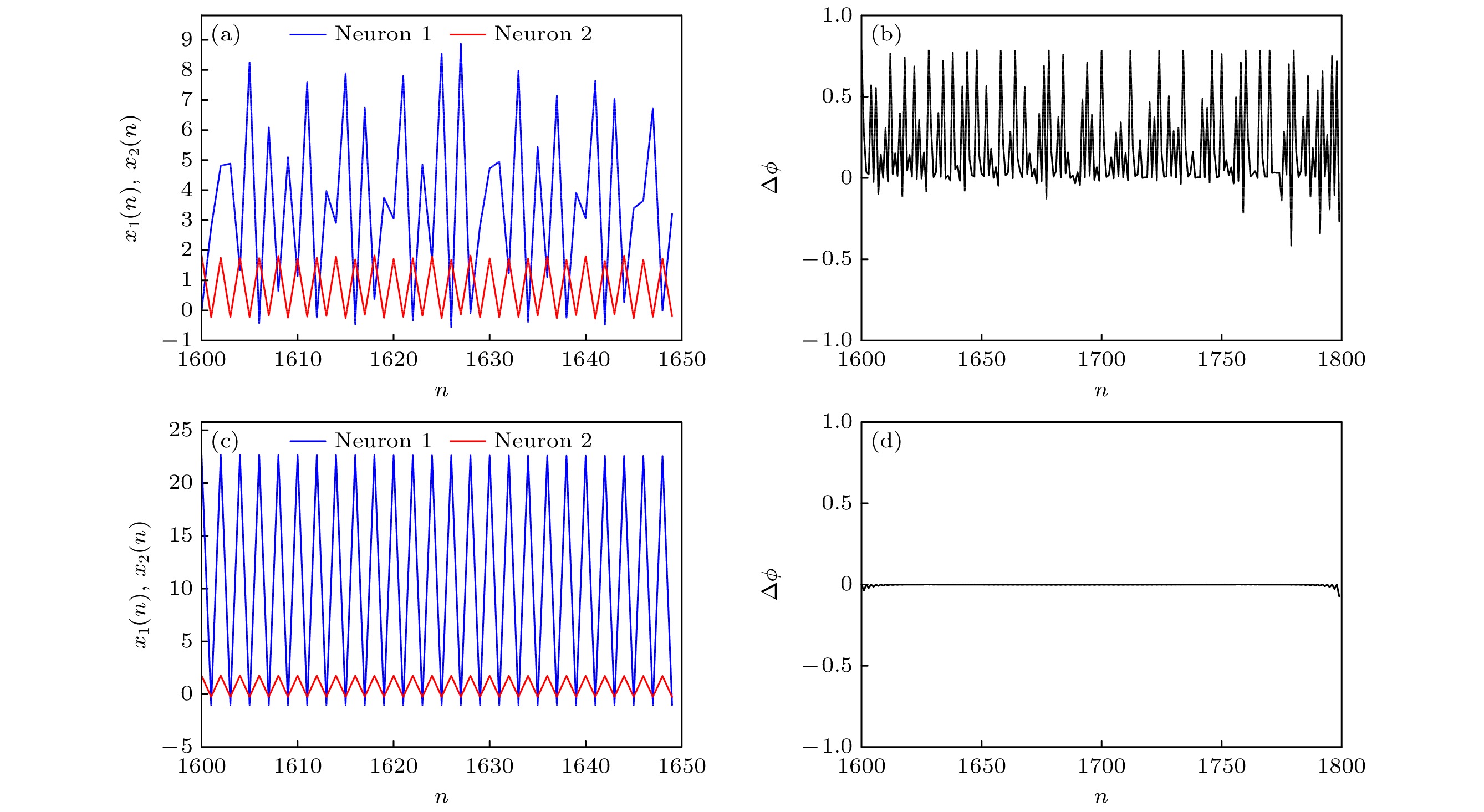
同样, 为了更直观地观察神经网络系统的同步放电行为, 选取参数a1 = 0.89, b1 = 0.005, c1 = 0.28, I = 0.03, a2 = 2.8, b2 = 0.001, c2 = 0.1, c = 1.0, d = –0.5, e = 0.2, k = 0.1, p1 = 0.1, 考虑串扰强度p2 = –5和p2 = 5时膜电位序列及其相位差随时间的演化, 如图17. 可知, 随着时间的演化, 膜电位序列相位差满足 |∆
$\phi $ | < 2π, 从而Chialvo和Rulkov两个异质神经元处于相位同步状态.对比发现, 串扰强度p1对耦合强度k的依赖性更强, 而串扰强度p2则对系统参数a2的依赖性更强. 但它们都对初始值y2(0)的依赖性不高, 且都在初始值y2(0)的取值过小时(如y2(0) = –5), 该系统的同步因子R的值会较小. 不过, 不管两个串扰强度取何值, 该系统都处于相位同步状态.
-
异质神经元的共存放电行为反映了神经系统的不同等待状态, 对临床上病理的诊断具有重要理论意义. 本文设计一类具有正弦记忆状态的局部有源离散忆阻器, 并用于耦合Chialvo离散神经元和Rulkov离散神经元, 从而建立一类突触串扰型忆阻异质离散神经网络. 采用相图、分岔图、时序图等数值模拟方法, 研究了突触串扰对神经网络共存放电行为的影响. 同时, 还研究了神经网络的偏移增强特性. 此外, 基于神经元放电序列的相位差及同步因子, 研究了不同耦合强度、系统初始值和系统参数情形下, 串扰强度对神经网络同步行为的影响. 本研究将有助于揭示生物神经信息处理和传递的电生理学机制, 也可为临床上同病异症的诊断及治疗提供电生理学理论支持. 同时, 还可以用于神经系统疾病的预后评估, 即医生可以根据患者的放电模式和特征, 预测疾病的发展趋势和预后结果, 从而采取相应的干预措施和监测方案.
串扰忆阻突触异质离散神经网络的共存放电与同步行为
Coexisting discharge and synchronization of heterogeneous discrete neural network with crosstalk memristor synapses
-
摘要: 突触串扰由相邻突触间神经递质的溢出引起, 对神经系统的放电特性及信号传输有着深远影响. 利用两个忆阻器模拟生物神经突触, 双向耦合Chialvo离散神经元和Rulkov离散神经元, 并考虑耦合状态下突触间的串扰行为, 构建一类忆阻突触耦合异质离散神经网络. 研究分析表明, 神经网络不动点的数量及稳定性依赖于突触串扰强度. 同时, 通过分析分岔图、相图、李雅普诺夫指数谱和时序图等发现, 随着突触串扰强度的变化, 神经网络表现出不同的共存放电行为. 此外, 基于神经元放电序列的相位差及同步因子, 研究了不同耦合强度及不同系统初始条件和参数情形下, 突触串扰强度对神经网络同步行为的影响.Abstract: Synaptic crosstalk, which occurs due to the overflow of neurotransmitters between neighboring synapses, holds a crucial position in shaping the discharge characteristics and signal transmission within nervous systems. In this work, two memristors are employed to simulate biological neural synapses and bidirectionally coupled Chialvo discrete neuron and Rulkov discrete neuron. Thus, a heterogeneous discrete neural network with memristor-synapse coupling is constructed, with the crosstalk behavior between memristor synapses in the coupled state taken into account. The analysis demonstrates that the quantity and stability of fixed points within this neural network greatly depend on the strength of synaptic crosstalk. Additionally, through a thorough investigation of bifurcation diagrams, phase diagrams, Lyapunov exponents, and time sequences, we uncover the multi-stable state property exhibited by the neural network. This characteristic manifests as the coexistence of diverse discharge behaviors, which significantly change with the intensity of synaptic crosstalk. Interestingly, the introduction of control parameter into state variables can lead the bias to increase, and also the infinite stable states to occur in the neural network. Furthermore, we comprehensively study the influence of synaptic crosstalk strength on the synchronization behavior of the neural network, with consideration of various coupling strengths, initial conditions, and parameters. Our analysis, which is based on the phase difference and synchronization factor of neuronal discharge sequences, reveales that the neural network maintains phase synchronization despite the variations of the two crosstalk strengths. The insights gained from this work provide important support for elucidating the electrophysiological mechanisms behind the processing and transmission of biological neural information. Especially, the coexisting discharge phenomenon in the neural network provides an electrophysiological theoretical foundation for the clinical symptoms and diagnosis of the same neurological disease among different individuals or at different stages. And the doctors can predict the progression and prognosis of neurological disease based on the patterns and characteristics of coexisting discharge in patients, enabling them to adopt appropriate intervention measures and monitoring plans. Therefore, the research on coexisting discharge in the neural system contributes to the comprehensive treatment of nervous system disease.
-
-
图 1 忆阻器的电压-电流特性曲线 (a)
$\varphi $ (0) = 0.1, ω = 0.1, A = 0.2, 0.3, 0.4; (b)$\varphi $ (0) = 0.1, A = 0.5, ω = 0.2, 0.4, 0.8; (c) A = 0.5, ω = 0.2,$\varphi $ (0) = –3.0, 0.1, 3.0Figure 1. Hysteresis loop for discrete memristor: (a)
$\varphi $ (0) = 0.1, ω = 0.1 and A = 0.2, 0.3, 0.4; (b)$\varphi $ (0) = 0.1, A = 0.5 and ω = 0.2, 0.4, 0.8; (c) A = 0.5, ω = 0.2 and$\varphi $ (0) = –3.0, 0.1, 3.0.
图 4 不同初始条件时, 状态变量x1(n)关于p1的分岔图 (a) (1, 1, 1, –1, 1, 0); (b) (1, 1, 1, –2.4, 1, 0); (c) (1, 1, 1, 1, 1, 0); (d) (1, 1, 1, 2, 1, 0)
Figure 4. Bifurcation diagrams of state variable x1(n) versus p1 under different initial conditions: (a) (1, 1, 1, –1, 1, 0); (b) (1, 1, 1, –2.4, 1, 0); (c) (1, 1, 1, 1, 1, 0); (d) (1, 1, 1, 2, 1, 0).
图 5 p1取不同值时, 神经网络的共存吸引子及共存放电序列 (a)—(c) p1 = –0.8; (d)—(f) p1 = –0.4; (g)—(i) p1 = 0.2; (j)—(l) p1 = 0.8
Figure 5. Coexisting attractors and coexisting discharge sequences under different p1 value: (a)–(c) p1 = –0.8; (d)–(f) p1 = –0.4; (g)–(i) p1 = 0.2; (j)–(l) p1 = 0.8.
图 6 不同初始条件时状态变量x1(n)关于p2的分岔图 (a) (1, 1, 1, –5, 1, 0); (b) (1, 1, 1, 5, 1, 0); (c) (1, 1, 1, –1, 1, 0); (d) (1, 1, 1, –3, 1, 0)
Figure 6. Bifurcation diagrams of state variable x1(n) versus p2 under different initial conditions: (a) (1, 1, 1, –5, 1, 0); (b) (1, 1, 1, 5, 1, 0); (c) (1, 1, 1, –1, 1, 0); (d) (1, 1, 1, –3, 1, 0).
图 7 不同p2值时神经网络的共存吸引子及共存放电序列 (a)—(c) p2 = –1.1; (d)—(f) p2 = –0.4; (g)—(i) p2 = 0.2; (j)—(l) p2 = 0.8
Figure 7. Coexisting attractors and coexisting discharge sequences under different p2 value: (a)–(c) p2 = –0.7; (d)–(f) p2 = –0.4; (g)–(i) p2 = 0.2; (j)–(l) p2 = 0.8.
图 8 (a), (b) 状态变量x2, y2关于参数m的分岔图; (c)关于参数m的李雅普诺夫指数图
Figure 8. (a), (b) Bifurcation diagram and (c) Lyapunov exponent versus m.
图 9 不同m取值时 (a) x2-y2的相图; (b), (c)状态变量x2, y2的放电序列
Figure 9. For different values of m: (a) x2-y2 phase diagrams; (b), (c) discharge sequences for state variables x2, y2.
图 10 不同耦合强度k (a) p1对同步因子的影响; (b) p1对相位差的影响
Figure 10. For different k: (a) Dependence of synchronization factor on p1; (b) dependence of phase difference on p1.
图 11 不同初始值y2(0) (a) p1对同步因子的影响; (b) p1对相位差的影响
Figure 11. For different y2(0): (a) Dependence of synchronization factor on p1; (b) dependence of phase difference on p1.
图 12 不同系统参数a2 (a) p1对同步因子的影响; (b) p1对相位差的影响
Figure 12. For different a2: (a) Dependence of synchronization factor on p1; (b) dependence of phase difference on p1.
图 13 (a) p1 = –5时的时间序列; (b) p1 = –5时的相位差; (c) p1 = 5时的时间序列; (d) p1 = 5时的相位差
Figure 13. (a) Time series when p1 = –5; (b) phase difference when p1 = –5; (d) time series when p1 = 5; (d) phase difference when p1 = 5.
图 14 不同耦合强度k (a) p2对同步因子的影响; (b) p2对相位差的影响
Figure 14. For different k: (a) Dependence of synchronization factor on p2; (b) dependence of phase difference on p2.
图 15 不同初始值y2(0) (a) p2对同步因子的影响; (b) p2对相位差的影响
Figure 15. For different y2(0): (a) Dependence of synchronization factor on p2; (b) dependence of phase difference on p2.
图 16 不同参数a2 (a) p2对同步因子的影响; (b) p2对相位差的影响
Figure 16. For different a2: (a) Dependence of synchronization factor on p2; (b) dependence of phase difference on p2.
图 17 (a) p2 = –5时的时间序列; (b) p2 = –5时的相位差; (c) p2 = 5时的时间序列; (d) p2 = 5时的相位差.
Figure 17. (a) Time series when p2 = –5; (b) phase difference when p2 = –5; (d) time series when p2 = 5; (d) phase difference when p2 = 5.
表 1 神经网络的平衡点、特征值和稳定性
Table 1. Equilibrium points, eigenvalues, and stability of neural network.
(p1, p2) (x1(n), y2(n), $\varphi $ 1(n),
$\varphi $ 2(n))
特征值 稳定性 (0.1, 0.1) (0.0342, 0.001, 0.0323, 0.0086) –0.5593, 0.8269, 0.8889, 0.9994±0.0022i, 1 不稳定鞍焦点 (0.0352, 0.001, 0.036, –0.3372) –0.5593, 0.8509, 0.8291, 0.8881, 0.9990, 0.9996 不稳定鞍结点 (0.0392, 0.0021, –0.2489, –0.3372) –0.5587, 0.8296, 0.9425, 0.9017, 0.8926, 0.9994 不稳定鞍结点 (168.8416, 0.0715, –0.7368, –0.3416) 0, 0.8900, –0.5580, 0.1857, 0.8236, 0.9994 不稳定鞍结点 (1, 1) (0.0339, 0.0009, 0.0973, –0.0618) –0.5589, 0.8097, 0.8892, 0.9953±0.0015i, 0.9995 不稳定鞍焦点 (0.0347, 0.0018, 0.1062, –0.3375) –0.5586, 0.8277±0.0047i, 0.8890, 0.9955, 0.9994 不稳定鞍焦点 (0.0383, 0.0031–0.224, –0.3365) –0.5569, 0.8305, 0.8838±0.0020i, 0.9645, 0.9994 不稳定鞍焦点 (168.8425, 0.1017, –0.7368, –0.3416) 0, 0.89, –0.5457, 0.1857, 0.8113, 0.9994 不稳定鞍结点 
下载: 导出CSV
-
[1] 白婧, 关富荣, 唐国宁 2021 物理学报 70 170502 doi: 10.7498/aps.70.20210142 Bai J, Guan F R, Tang G N 2021 Acta Phys. Sin. 70 170502 doi: 10.7498/aps.70.20210142 [2] Stein R B, Gossen E R, Jones K E 2005 Nat. Rev. Neurosci. 6 389 [3] 安新磊, 乔帅, 张莉 2021 物理学报 70 050501 doi: 10.7498/aps.70.20201347 An X L, Qiao S, Zhang L 2021 Acta Phys. Sin. 70 050501 doi: 10.7498/aps.70.20201347 [4] Tan F, Zhou L L, Lu J W, Quan, H Z, Liu K Y 2022 Eur. J. Control 70 100764 [5] 徐泠风, 李传东, 陈玲 2016 物理学报 65 240701 doi: 10.7498/aps.65.240701 Xu L F, Li C D, Chen L 2016 Acta Phys. Sin. 65 240701 doi: 10.7498/aps.65.240701 [6] Liu B, Peng X N, Li C L 2024 Int. J. Electron. Commun. 178 155283 [7] Guo M, Zhu Y L, Liu R Y, Zhao K X, Dou G 2021 Neurocomputing 472 12 [8] 徐聪, 王春华, 孙晶茹 2023 中国科学: 信息科学 53 164 doi: 10.1360/SSI-2022-0027 Xu C, Wang C H, Sun J R 2023 Sci. Sin. Inf. 53 164 doi: 10.1360/SSI-2022-0027 [9] 张美娇, 张建刚, 魏立祥, 南梦冉 2021 中国医学物理学杂志 38 1273 Zhang M J, Zhang J G, Wei L X, Nan M R 2021 Chin. J. Med. Phys. 38 1273 [10] Xu Q, Zhu D 2020 IETE Tech. Rev. 38 563 [11] Lu Y C, Li H M, Li C L 2023 Neurocomputing 544 126246 doi: 10.1016/j.neucom.2023.126246 [12] Li C L, Yang Y Y, Yang X B, Zi X Y, Xiao F L 2022 Nonlinear Dyn. 108 1697 doi: 10.1007/s11071-022-07268-y [13] Li C L, Wang X, Du J R, Li Z J 2023 Nonlinear Dyn. 111 21333 doi: 10.1007/s11071-023-08998-3 [14] Tian Z K, Zhou D 2019 Front. Comput. Neurosci. 14 40 [15] Ma M L, Xiong K L, Li Z J Sun Y C 2023 Mathematics 11 375 doi: 10.3390/math11020375 [16] Bashkirtseva I A, Nasyrova V, Ryashko L B 2018 Chaos, Solitons Fractals 110 76 doi: 10.1016/j.chaos.2018.03.011 [17] Kinouchi O, Tragtenberg M H R 1996 Int. J. Bifurcation Chaos 6 2343 doi: 10.1142/S0218127496001508 [18] Girardi-Schappo M, Tragtenberg M H, Kinouchi O 2013 J. Neurosci. Methods 220 116 doi: 10.1016/j.jneumeth.2013.07.014 [19] Rosenblatt F 1963 Am. J. Psychol. 76 705 doi: 10.2307/1419730 [20] Li H D, Li C L, He S B 2023 Int. J. Bifurcation Chaos 33 2350032 doi: 10.1142/S0218127423500323 [21] 郭慧朦, 梁燕, 董玉姣, 王光义 2023 物理学报 72 070501 doi: 10.7498/aps.72.20222013 Guo H M, Liang Y, Dong Y J, Wang G Y 2023 Acta Phys. Sin. 72 070501 doi: 10.7498/aps.72.20222013 [22] Zhou L L, Lin H C, Tan F 2023 Chaos, Solitons Fractals 173 113643 doi: 10.1016/j.chaos.2023.113643 [23] 秦铭宏, 赖强, 吴永红 2022 物理学报 71 160502 doi: 10.7498/aps.71.20220593 Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502 doi: 10.7498/aps.71.20220593 [24] 吴朝俊, 方礼熠, 杨宁宁 2024 物理学报 73 010501 doi: 10.7498/aps.73.20231211 Wu C J, Fang L Y, Yang N N 2024 Acta Phys. Sin. 73 010501 doi: 10.7498/aps.73.20231211 [25] Chua L O 2005 Int. J. Bifurcation Chaos 15 3435 doi: 10.1142/S0218127405014337 [26] Jin P P, Wang G Y, Liang Y, Iu H H, Chua L O 2021 IEEE Trans. Circuits Syst. Regul. Pap. 68 4419 doi: 10.1109/TCSI.2021.3121676 [27] Lai Q, Yang L 2022 Chaos, Solitons Fractals 165 112781 doi: 10.1016/j.chaos.2022.112781 [28] Li K X, Bao H, Li H Z, Ma J, Hua Z Y, Bao B C 2021 IEEE Trans. Ind. Inf. 18 1726 [29] Lu Y M, Wang C H, Deng Q L, Xu C 2022 Chin. Phys. B 31 060502 doi: 10.1088/1674-1056/ac539a [30] Kawahara M, Kato‐Negishi M, Tanaka K 2017 Metallomics 9 619 doi: 10.1039/C7MT00046D [31] A N Shrivastava, A Triller, W Sieghart 2011 Front. Cell. Neurosci. 5 7 [32] Li Z J, Yi Z 2022 Electron. Lett. 58 539 doi: 10.1049/ell2.12533 [33] Ding D W, Chen X Y, Yang Z L, Hu Y B, Wang M Y, Zhang H W, Zhang X 2022 Chaos, Solitons Fractals 158 112014 doi: 10.1016/j.chaos.2022.112014 [34] Li Z J, Peng C, Wang M J, Ma M L 2024 Indian J. Phys. 98 1043 doi: 10.1007/s12648-023-02845-2 [35] Ma M L, Xiong K L, Li Z J, He S B 2024 Chin. Phys. B 33 028706 doi: 10.1088/1674-1056/aceee9 [36] Pool R 1989 Science 243 604 doi: 10.1126/science.2916117 [37] Adhikari S P, Sah M P, Kim H, Chua L O 2013 IEEE Trans. Circuits Syst. Regul. Pap. 60 3008 doi: 10.1109/TCSI.2013.2256171 [38] Ren L J, Mou J, Banerjee S, Zhang Y S 2023 Chaos, Solitons Fractals 167 113024 doi: 10.1016/j.chaos.2022.113024 [39] Li C, Yi C, Li Y, Mitro S, Wang Z 2024 Chaos 34 031102 doi: 10.1063/5.0199236 [40] Ma C G, Mou J, Xiong L, Banerjee S, Liu T M, Han X T 2021 Nonlinear Dyn. 103 2867 doi: 10.1007/s11071-021-06276-8 [41] Li C, Wang X, Chen G 2017 Nonlinear Dyn. 90 1335 doi: 10.1007/s11071-017-3729-1 [42] Li C, Gao Y, Lei T, Li RY, Xu Y 2024 Int. J. Bifurcation Chaos 34 2450008 doi: 10.1142/S0218127424500081 -
计量
- 文章访问数: 186
- HTML全文浏览数: 186
- PDF下载数: 3
- 施引文献: 0