随着计算机科学的快速发展, 数值模拟在各类流体系统的研究中发挥着越来越重要的作用. 事实上, 这种发展趋势在计算流体动力学(computational fluid dynamics, CFD) 的早期阶段就已经初现端倪, 当时CFD的发展正是始于计算机的出现, 并围绕如Euler方程等宏观方程的数值计算方法而不断发展^[1]. 传统的宏观方法基于连续介质假设, 将流体近似为空间上连续分布且宏观充分小的流体微团, 并且侧重于系统宏观演化过程的模拟研究. 实际上, 流体系统在演化过程中, 除了在宏观层次上表现出丰富多变的流体力学非平衡行为之外, 还在微介观层次具有与之时时伴随的诸多热力学非平衡行为. 随着非平衡程度的增加, 仅关注近平衡模型中描述的宏观物理信息往往会表现出一定的局限性, 例如在描述非平衡流动方面的能力不足等^[2]. 与之相对, 微观层次可以准确描述系统的演化过程, 并且有效捕捉系统的演化细节. 比如, 分子动力学模拟可以实时追踪每个分子的运动轨迹并进行统计学处理, 给出宏观物理量的演化结果, 而且摆脱了局部平衡的假设, 可以弥补宏观模型在物理精度方面的不足, 但是其计算量通常会局限于纳米尺度的空间范围^[3].

作为联系宏观和微观的桥梁, 介观方法能够有效解决物理精度描述不足和数值计算效率不高之间的矛盾^[4]. 一种常用的介观方法是基于非平衡统计物理的基本方程, 即Boltzmann方程, 其中, 格子Boltzmann方法(lattice Boltzmann method, LBM)被当作是这样一种方法^[4,5]. 实际上, 根据具体应用的功能目标, LBM可以分为两大类: 一类是在数学上用于有效求解各种偏微分方程(组); 另一类是在物理上用于复杂系统的高精度或者高效率的动理学建模. 另外, 从离散格式的角度来看, LBM可以分为标准的LBM和非标准的LBM. 在标准的LBM中, 时间步长、空间步长和离散速度大小绑定在一起, 即虚拟粒子在一个时间步长内只能从一个格点迁移到另外一个格点. 在非标准的LBM中, 时间步长、空间步长和离散速度大小解耦, 因此可以更加灵活地选取合适的离散格式, 如有限差分^[6]、有限体积^[7]、有限元^[8]等方法.

近十年发展的离散Boltzmann方法(discrete Boltzmann method, DBM)可以看作是一种非标准LBM的进一步发展, 其在早期又被称作LBM动理学模型^[9]. 在物理功能方面, DBM不仅具有传统方法描述流体力学行为的能力, 同时继承了Boltzmann方程描述热力学行为的重要功能^[10-15]. 换言之, DBM不仅在连续性极限条件下可以恢复宏观流体控制方程组, 而且还等价于描述热力学非平衡效应的粗粒化模型. 2014年, Lin等^[10]提出了可压缩流的极坐标DBM, 该模型中对流项的空间离散采用修正的Warming-Beam格式. 2019年, Zhang等^[11]提出了一种基于Shakhov模型的DBM一般框架, 并采用一阶和二阶混合迎风格式处理空间偏导数. 2021年, Ji等^[12]针对非平衡可压缩反应流问题, 提出了一个三维多松弛时间离散Boltzmann方法, 并采用WENO格式处理空间偏导数. 2022年, 林传栋^[13]提出了适用于超声速可压缩化学反应流的二维简化DBM, 并使用无波动、无自由参数的耗散差分格式来处理空间偏导数. 2023年, Lin等^[14]针对外力场中比热比可调的可压缩系统, 建立了离散速度对称的离散Boltzmann方法, 并证明该模型具有更好的空间对称性和数值精度. 同年, Sun等^[15]用16阶快速傅里叶变换方案来离散DBM中的空间偏导数, 并研究了两初始静止液滴聚并过程中的热力学非平衡效应, 详细分析了非平衡效应、总熵产生率与各种运动学和动力学物理量之间的关系.

需要说明的是, DBM的演化方程涉及时间离散、空间离散和速度离散. 现有的DBM文献基本上都采用有限差分法处理空间离散. 不同于以往工作, 本文将有限体积法引入到DBM. 对于有限体积法, 每个控制体上的数值都对应着特定的物理量, 物理内涵清晰, 推导过程直观. 此外, 采用合适的数值格式, 有限体积法能够有效减少数值振荡和虚假振荡, 具有良好的数值稳定性, 从而确保计算结果的可靠性, 尤其是在处理具有强间断特性的流动问题时, 如激波、爆轰波等. 相较于基于有限差分法, 有限体积在处理不同几何结构的边界条件时也较为方便和灵活, 适应于各种复杂边界条件的系统. 因此, 有限体积法能够进一步拓宽DBM在实际应用中的适用范围. 后文的结构如下: 第2节简要介绍了DBM的基本理论; 第3节介绍了基于有限体积法的离散Boltzmann演化方程, 并引入了MUSCL通量限制器; 第4节对一些经典的可压缩流体问题进行了数值模拟, 以验证基于有限体积法的DBM模型的准确性; 第5节是结论.

DBM的演化方程如下:

其中, t表示时间, $ {{f}_{i}} $是离散分布函数, $ {{\boldsymbol{v}}_{i}} $是离散速度, i = 0, 1, 2, ···, N用于标记离散速度, N为离散速度总数, $ {{{\varOmega} }_{i}} $是碰撞项. 本文所使用的碰撞项是由Bhatnagar, Gross和Krook于1954年提出的BGK近似^[16]:

式中的$ f_{i}^\text{eq} $代表离散化的局部平衡态分布函数, 其数学表达式采用矩阵求逆的方式计算^[17].

宏观物理量如密度ρ, 流体的速度u, 以及能量E, 可以根据离散分布函数$ {{f}_{i}} $获得:

其中$ {{v}_{i}} = \left| {{\boldsymbol{v}}_{i}} \right| $表示离散速度的大小; γ 表示比热比, 其表达式如下:

由γ的表达式可以看出, 该DBM具有灵活可调的比热比.

在本文中, 离散化的局部平衡态分布函数$ f_{i}^\text{eq} $满足下面7个矩关系:

其中D = 2表示空间维度, I是分子振动和(或)旋转所对应的额外自由度, 并且$ {{\eta }_{i}} $用于描述振动和(或)旋转能量. 前三个矩关系代表质量、动量、能量守恒定律对应的守恒矩, 后四个矩关系代表高阶矩.

通过Chapman-Enskog多尺度分析可以证明, 在连续极限条件下, 该DBM能够恢复Navier-Stokes方程组. 除此之外, DBM还具有描述热力学非平衡行为的功能. 具体来说, 可以使用($ f_{i}^{{}}- f_{i}^\text{eq} $)非守恒动理学矩的独立分量为基来构建相空间, 并使用该相空间来描述系统的非平衡行为特征. 为此, 引入中心速度$ {{\boldsymbol{v}}_{i}}^{*} = {{\boldsymbol{v}}_{i}}-{{\boldsymbol{u}}} $, 并引入符号$ \varDelta _{{}}^{*} $表示中心矩, 那么非平衡量的表达式为

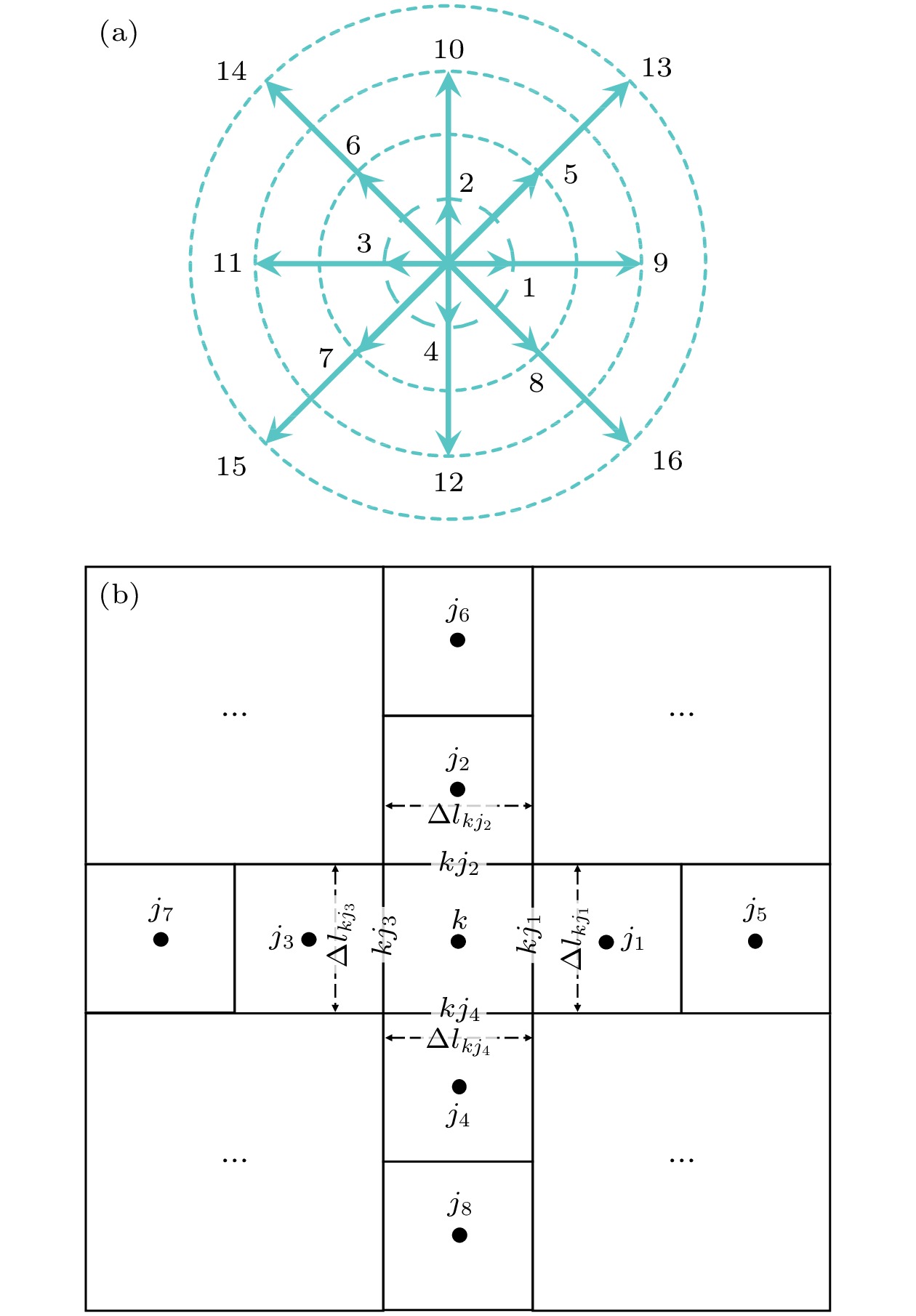
其中下标“2”表示二阶张量, 下标“3”用于标记三阶张量, 下标“3, 1”表示三阶张量缩并为一阶张量, 下标“4, 2”表示四阶张量缩并为二阶张量. 这些表达式分别对应不同的物理意义, 其中$ \varDelta _{2}^{*} $对应黏性剪切和非组织动量通量, $ \varDelta _{3, 1}^{*} $对应非组织能量和热通量, $ \varDelta _{3}^{*} $对应非组织能量通量, $ \varDelta _{4, 2}^{*} $对应非组织能量通量的通量.

另外, 本文使用的离散速度模型是D2V16, 即二维十六速度模型. 图1描绘了离散速度与空间离散单元的示意图. 离散速度分为4组, 每组速度大小相同且可以调节, 但方向不同, 具体配置如下:

同时, 可调节参数$ {{\eta }_{i}} $的配置如下:

在(18)式和(19)式中, $ {{v}_\text{a}}, {{v}_\text{b}}, {{v}_\text{c}}, {{v}_\text{d}}, {{\eta }_\text{a}}, {{\eta }_\text{b}}, {{\eta }_\text{c}}, {{\eta }_\text{d}} $为可调参数, 即通过调整这些参数的值优化模型, 确保模型具有较好的数值稳定性和精确度.

本节介绍有限体积法在DBM中的具体应用. 对于有限体积法, 首先需要确定物理空间单元的编号以及它们之间的相邻关系. 由于计算区域是二维区域, 所以本文提到的控制体或控制单元的形状都是二维平面. 如图1所示, 整个流域被离散成相互不重叠的矩形单元, 其中单元k被认为是主单元, 而与单元k相邻的$ j_{1}^{{}} $, $ j_{2}^{{}} $, $ j_{3}^{{}} $, $ j_{4}^{{}} $四个单元被认为是邻单元. 物理量被存储在单元的几何中心处, 连接单元k与j的边界面被称为$ kj $面.

确定好计算网格后, 下一步是在每个单元上对离散Boltzmann方程进行积分运算, 以实现方程的离散化和数值求解. 在积分的过程中, 由$ {{S}_{k}} $表示第k个二维控制单元, 所以离散Boltzmann方程在控制单元$ {{S}_{k}} $上进行积分可得:

其中$ {{f}_{i, k}} $表示第k个控制单元的第i个离散速度分布函数, 碰撞项$ {{{\varOmega} }_{i, k}} $同理. 由此可以看到(20)式包含三部分, 第一部分为时间项对空间的积分, 第二部分为对流项对空间的积分, 第三部分为碰撞项对空间的积分. 下文将讨论这三部分的处理方式.

对计算区域进行空间离散化的时候, 为了获得精确的数值结果, 需要让控制体单元足够小. 物理量在控制体单元内的空间变化非常小, 那么可以被认为在控制体上基本上是均匀分布的. 因此, 碰撞项的积分表达式可进行如下的推导:

其中$ {{A}_{k}} = \displaystyle\iint_{{{S}_{k}}}{\text{d}S} $表示控制单元的面积. $ {{f}_{i, k}} $与$ f_{i, k}^\text{eq} $分别代表k控制体中离散速度分布函数和平衡态离散速度分布函数的平均值(本文控制单元中的物理量及其平均量采用相同的符号表示).

现在考虑对流项在控制体上的积分. 因为该部分在数学上为二重积分, 所以利用高斯定理可以将对平面控制单元$ {{S}_{k}} $的面积分转化为对闭合边界$ \partial {{S}_{k}} $的环路积分:

其中, $ {{\hat{F}}_{i, kj}} $是$ {{f}_{i, k}} $穿过边界的微观通量, 其表达式为

其中, n表示向外垂直于单元边界的单位法向量.

针对本文所使用的计算网格, 可以将闭合边界$ \partial {{S}_{k}} $的环路积分进一步处理为4条边界上的通量之和:

其中$ \Delta {{l}_{k{{j}_{n}}}} $表示控制单元边界的长度.

下面阐述界面微观通量的重构方法. 以x方向的通量$ {{\hat{F}}_{i, k{{j}_{1}}}} $和$ {{\hat{F}}_{i, k{{j}_{3}}}} $为例, 根据离散速度$ {{\boldsymbol{v}}_{i}} $的大小, 可以将$ {{\hat{F}}_{i, k{{j}_{1}}}} $和$ {{\hat{F}}_{i, k{{j}_{3}}}} $写成下列形式:

在满足二阶精度要求的前提下, 用边界面$ k{{j}_{1}} $和$ k{{j}_{3}} $中心点处的值来代替$ k{{j}_{1}} $和$ k{{j}_{3}} $面上的均值. 考虑到在计算单元交界处通量时, 可压缩流体可能存在不连续性, 需要利用交界面附近的控制单元来重构出不同的值$ f_{i, k{{j}_{1}}}^\text{L} $, $ f_{i, k{{j}_{1}}}^\text{R} $以及$ f_{i, k{{j}_{3}}}^\text{L} $, $ f_{i, k{{j}_{3}}}^\text{R} $.

本文采用二阶精度的单调迎风中心守恒律(monotonic upwind scheme for conservation laws, MUSCL)格式^[18]来进行重构. MUSCL格式在处理间断和激波等相关问题时表现出明显的优势. 具体来说, $ f_{i, k{{j}_{1}}}^\text{L} $, $ f_{i, k{{j}_{1}}}^\text{R} $以及$ f_{i, k{{j}_{3}}}^\text{L} $, $ f_{i, k{{j}_{3}}}^\text{R} $分别被确定为以下形式:

其中参数取值为$ b = \dfrac{1}{3} $; 函数$ \min \text{mod} ({{\varDelta }^{-}}, {{\varDelta }^{+}}) $为限制器, 其定义如下:

式中, $ {{({{\varDelta }^{-}})}_{k_{x}}} = {{f}_{i, k}}-{{f}_{i, {{j}_{3}}}} $, $ {{({{\varDelta }^{+}})}_{k_{x}}} = {{f}_{i, {{j}_{1}}}}- {{f}_{i, k}} $; $ {{({{\varDelta }^{-}})}_{j_{1}}} = {{f}_{i, j_{1}}} - {{f}_{i, {k}}} $, $ {{({{\varDelta }^{+}})}_{j_{1}}} = {{f}_{i, j_{5}}} - {{f}_{i, j_{1}}} $; $ {{({{\varDelta }^{-}})}_{j_{3}}} = {{f}_{i, j_{3}}}-{{f}_{i, j_{7}}} $, $ {{({{\varDelta }^{+}})}_{j_{3}}} = {{f}_{i, k}}-{{f}_{i, j_{3}}} $. 需要说明的是, 限制器的作用是为了限制数值解的变化率, 即当发现数值解的变化率超过一定阈值时, 就会对其进行调整以抑制数值振荡.

如前所述, 有限体积法考虑的是在微小控制体内的平均物理量. 因此, 类似于(21)式的推导过程, 离散速度分布函数的时间偏微分具有以下关系:

将(21)式、(24)式与(32)式代入到(20)式, 整理后可得到半离散形式的离散Boltzmann-BGK方程, 即仅时间项为偏导数的形式:

其中, 引入符号$ L({f}_{i, k}) $来表示离散后的对流项与碰撞项之和. 最后, 使用二阶精度的龙格-库塔格式^[19]处理上述方程的时间偏微分:

在(34)—(37)式中, 上角标t和$ t+\Delta t $代表时刻, $ \Delta t $代表时间步长, 上角标(0), (1), (2)代表二阶龙格-库塔格式中的中间变量.

本节将对基于有限体积法离散的DBM进行数值验证. 为此考虑3个典型算例: 冲击波、Lax激波管和声波.

现在考虑沿x方向向前传播的一维稳定冲击波, 其马赫数$ {{Ma}} = 2.0 $, 比热比γ = 2.0, 初始物理场设置为

其中下标$ \text{L} $表示左侧$ 0\leqslant x\leqslant 0.01 $的区域, $ \text{R} $表示右侧$ 0.01\leqslant x\leqslant 1.0 $的区域. 时间步长设置为$ \Delta t = 5.0\times {{10}^{-6}} $, 松弛时间$ \tau = 5.0\times {{10}^{-4}} $, 离散参数为$ ({{v}_\text{a}}, {{v}_\text{b}}, {{v}_\text{c}}, {{v}_\text{d}}) = (3.3, 3.0, 2.5, 1.0) $和$ ({{\eta }_\text{a}}, {{\eta }_\text{b}}, {{\eta }_\text{c}}, {{\eta }_\text{d}}) = (3.0, 0, 0, 0) $. 另外, 在x方向上采用流入/流出边界条件, 在y方向上采用周期性边界条件.

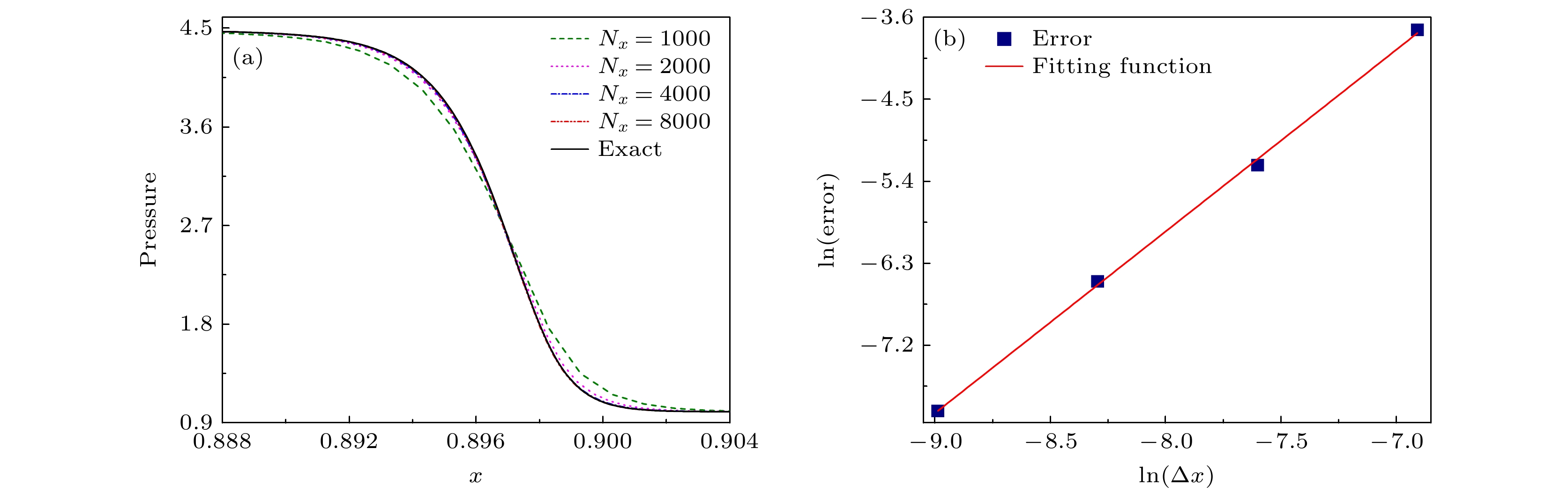
首先来验证程序的网格无关性, 为此建立了4套网格进行分析, 在x方向选择的网格数$ N_x $分别为1000, 2000, 4000, 8000, 在y方向选择的网格数$ N_y $均为1, 图2(a)对比了4套网格下波阵面附近压强的计算结果, 其中黑色实线代表精确解, 其他颜色和线型代表不同网格数下的数值解. 可以看出随着网格数的增加, 计算结果逐渐收敛于精确解, 值得注意的是当$ N_x = 8000 $时, 在数值结果与精确解偏离最大的位置处, 两者的相对误差仅为0.26082%, 因此该DBM的网格无关性得到了有效验证.

为了定量分析当前模型在空间上精度, 图2(b)给出了相对误差与空间步长的关系, 其中相对误差的计算公式为

式中$ {\varphi }_\text{e} $和$ {\varphi }_\text{n} $分别表示变量$ {\varphi} $的精确解和数值解. 图2(b)中正方形代表DBM的计算结果, 直线代表拟合函数$ {\rm{ln}}(\text{Error}) = 1.99342{\rm{ln}}(\Delta x)+ 9.99681 $. 显然, 拟合函数的斜率近似等于2.0, 这表明当前模型在空间上具有二阶收敛速率.

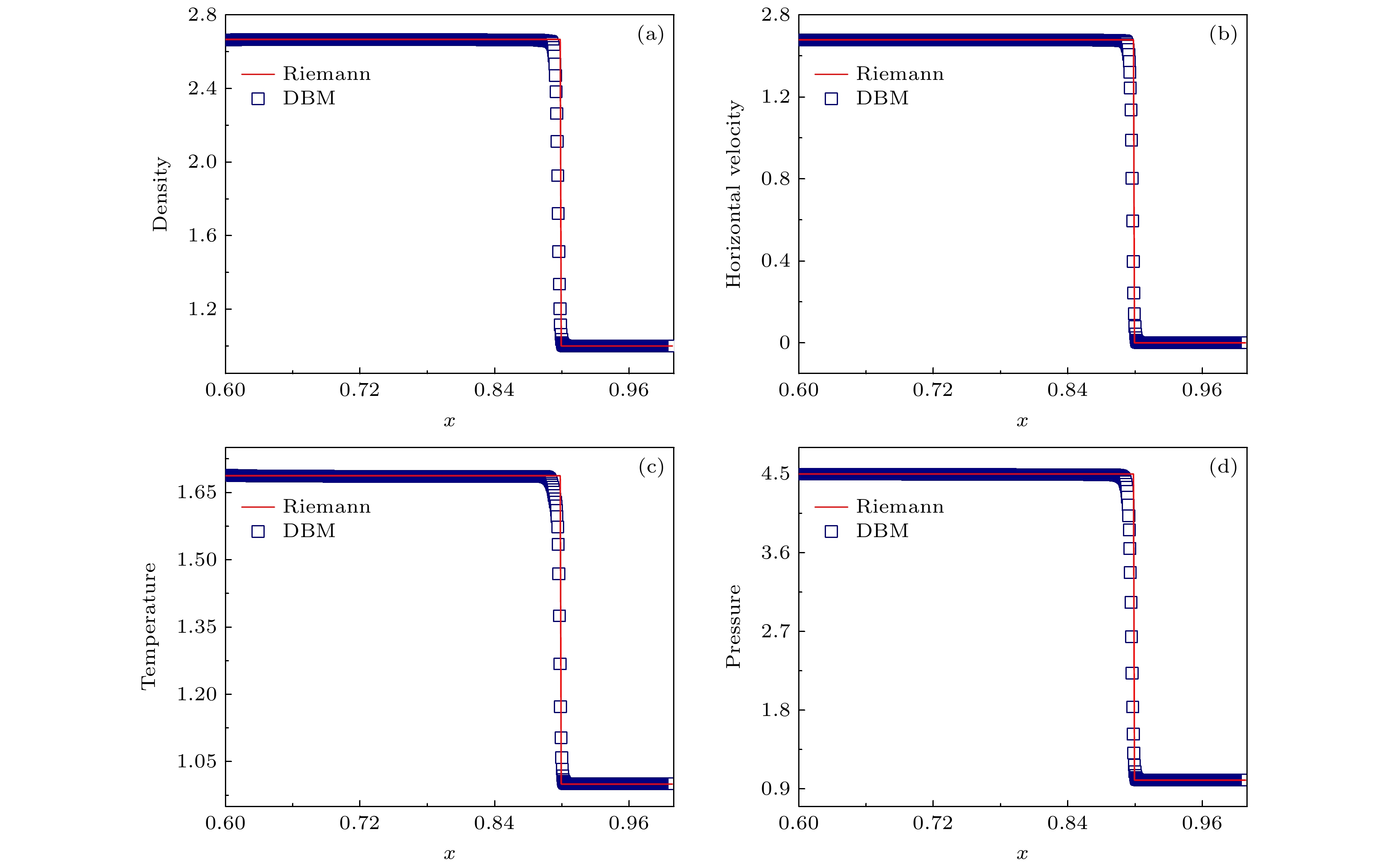
图3显示了在$ t = 0.375 $时刻冲击波附近的物理量. 在冲击波波后稳定区域处, 密度、水平速度、温度和压强的DBM模拟结果分别为$ \rho = 2.66704 $, $ {u_x} = 1.47840 $, $ T = 1.68778 $和$ p = 4.50137 $, 与Riemann解的相对误差分别为$ 0.01387{\text{%}} $, $ 0.04192{\text{%}} $, $ 0.01659{\text{%}} $和$ 0.03044{\text{%}} $. 另外, DBM模拟的波速为$ {u_{\mathrm{s}}} = 2.36286 $, 而理论波速为$ 2.36643 $, 相对误差为$ 0.15086{\text{%}} $. 可以看出本模型的结果与Riemann解符合良好, 说明其可以有效地捕捉冲击波.

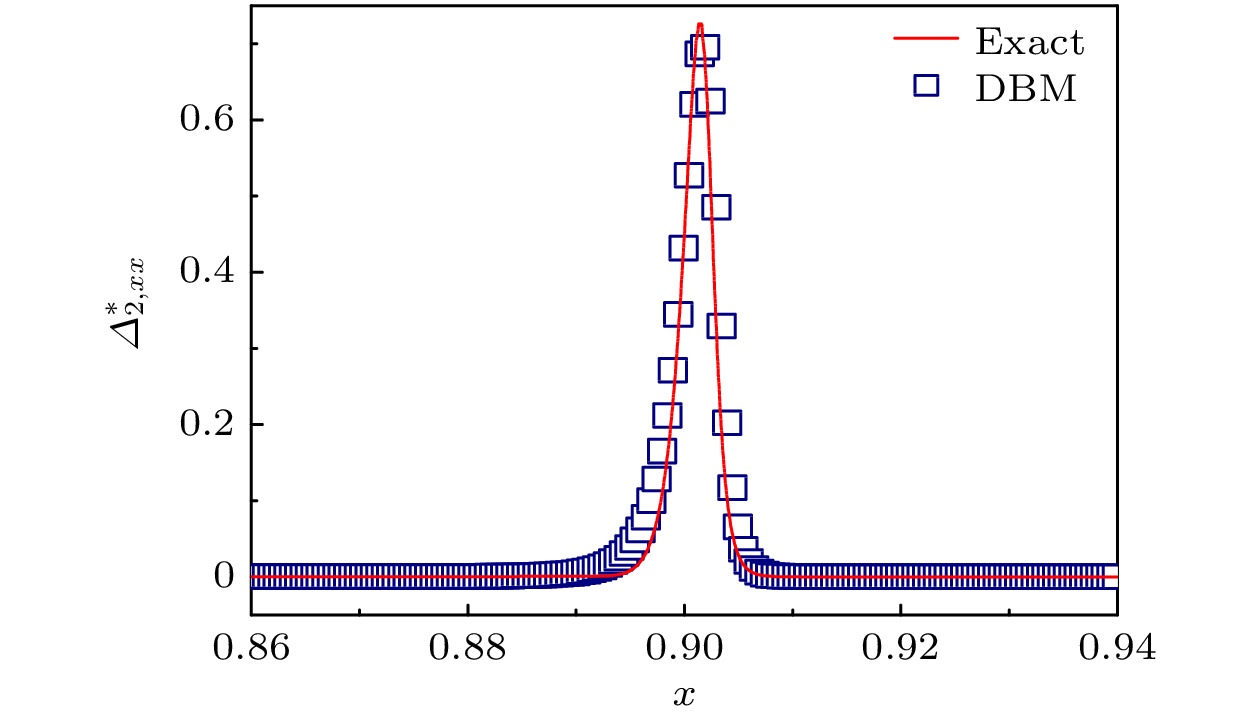
需要说明的是, 能够描述系统的非平衡状态并且提取非平衡信息, 这是DBM的核心功能, 同时也是DBM超越传统流体模型的一个优点. 图4展示的是在冲击波演化过程中, 在$ t = 0.375 $时刻非平衡量$ \varDelta _{2, xx}^{*} $的精确解^[20]与数值解的对比, 其中正方形代表计算的结果, 实线代表精确解. 可以看出, 在$ x = 0.9 $附近系统明显偏离平衡态, 呈现出先上升再下降的趋势. 偏离平衡态最大位置处的DBM模拟结果为$ 0.70084 $, 而精确解为$ 0.70773 $, 相对误差达到$ 0.97354{\text{%}} $, 本文模拟的结果与精确解高度一致, 这说明该模型可以准确地描述系统的非平衡行为.

接下来使用Lax激波管来进一步验证本模型能够描述可压缩流体系统的能力. Lax激波管的初始参数设置为

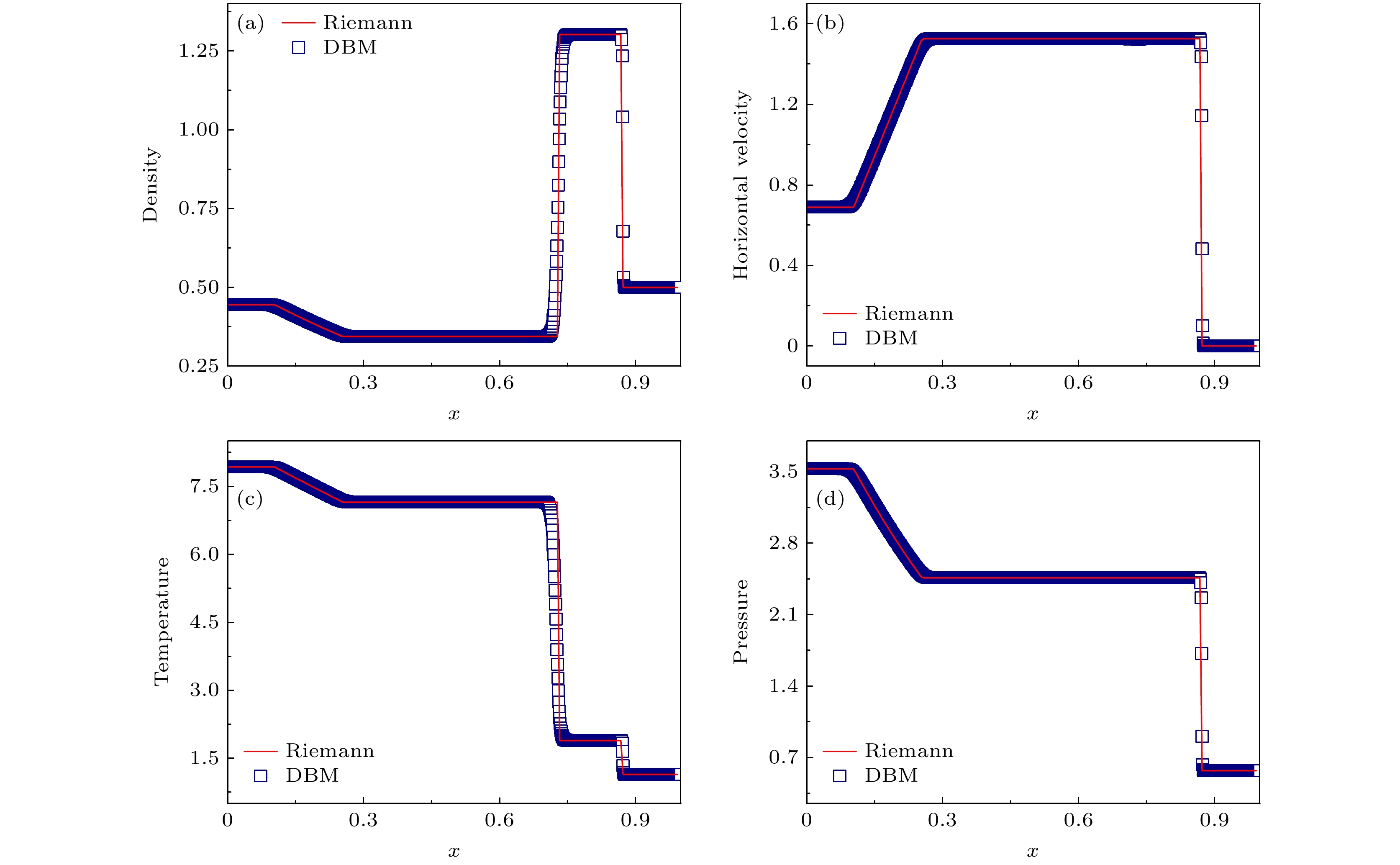
其中, 下标$ \text{L} $和$ \text{R} $分别表示$ 0\leqslant x\leqslant 0.5 $和$ 0.5\leqslant x\leqslant 1.0 $的计算区域. 本算例选择的计算网格为$ N_x \times N_y = 1000 \times 1 $, 空间步长为$ \Delta x = \Delta y = {{10}^{-3}} $, 时间步长为$ \Delta t = 2\times {{10}^{-6}} $, 比热比$ \gamma = 1.4 $, 离散参数为$ ({{v}_\text{a}}, {{v}_\text{b}}, {{v}_\text{c}}, {{v}_\text{d}}) = (5.5, 5.0, 1.5, 1.5) $, $ ({{\eta }_\text{a}}, {{\eta }_\text{b}}, {{\eta }_\text{c}}, {{\eta }_\text{d}}) = (0, 0, 0, 5.3) $. 在x方向上采用流入/流出边界条件, 在y方向上采用周期性边界条件.

图5显示的是Lax激波管在$ t = 0.15 $时的数值解与Riemann解的对比. 从图5的子图中可以看出: 在左侧区域存在稀疏波, 该区域的波速较低, 并且随着时间的演化各物理量的梯度逐渐减小; 在中间区域存在接触间断, 在接触间断两侧, 密度和温度具有明显差异, 而压强和速度呈现均匀分布; 在右侧区域, 冲击波向右传播, 物理量(包括密度、水平速度、温度和压强)的梯度剧烈变化, 并且在波后的流速和密度较大. 在上述演化过程中, DBM与Riemann解具有相当高的匹配度, 说明DBM能够精确地捕捉稀疏波、物质界面和冲击波的空间分布.

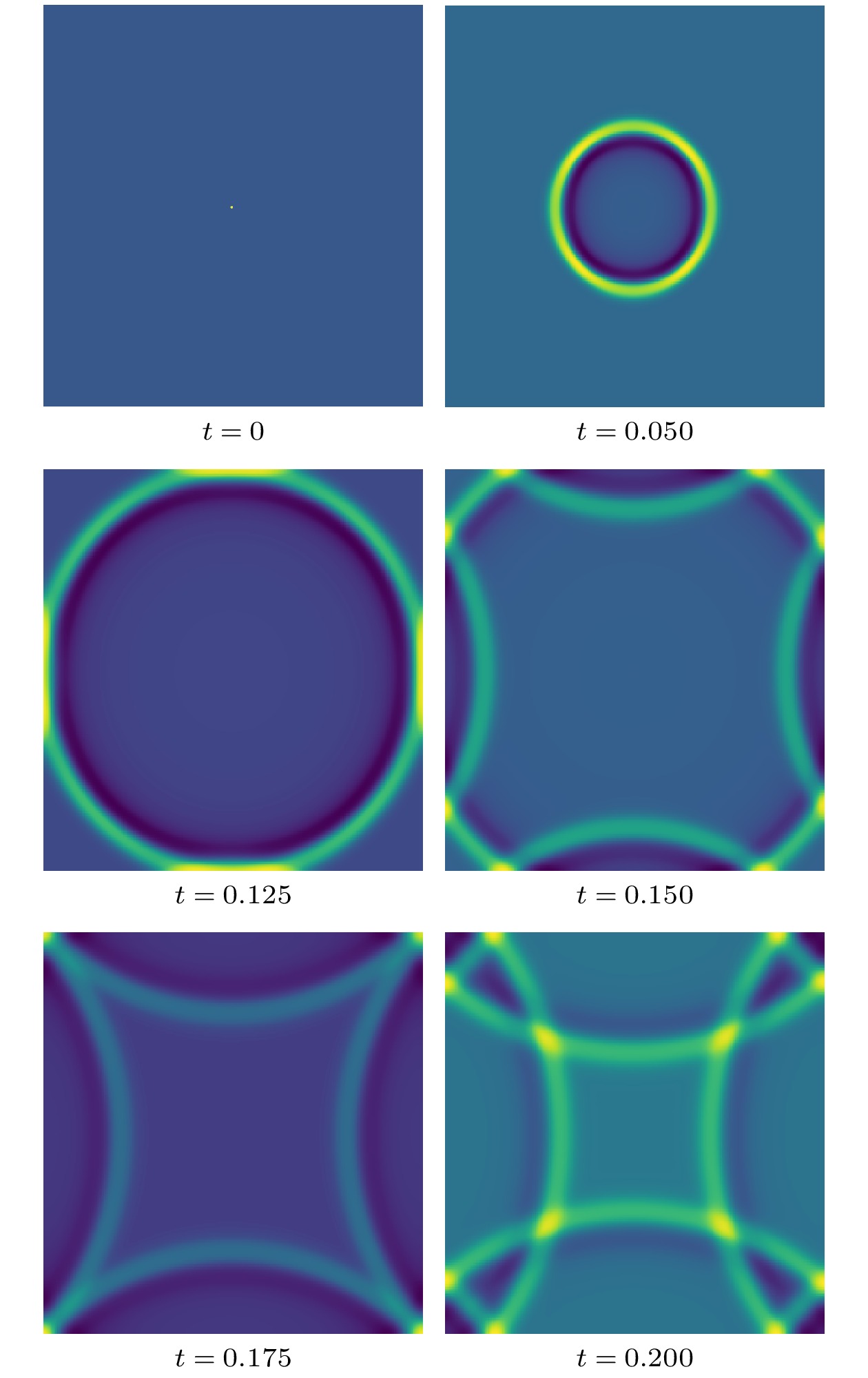
本节讨论该模型的声波捕获能力. 设置一块正方形计算区域, 初始物理场设置为$ (\rho, {{u}_{x}}, {{u}_{y}}, P) = (1.0, 0, 0, 1.0) $. 在计算域中心处施加一个微弱的扰动$ (\rho, P) = (1.01, 1.01) $后, 声波会向四周进行传播, 传播速度为声速. 声速是比热比和温度的函数, 其计算公式为$ {{v}_{{\mathrm{s}}}} = ({\gamma T})^{1/2} $. 本算例中, 计算网格数为$ {N_x} \times {N_y} = 301 \times 301 $, 网格精度设为$ \Delta x = \Delta y = {{10}^{-3}} $, 时间步长为$ \Delta t = {{10}^{-4}} $, 计算区域的边界施加镜面反射边界条件, 选择的离散参数为$ ({{v}_\text{a}}, {{v}_\text{b}}, {{v}_\text{c}}, {{v}_\text{d}}) = (1.4, 1.1, 1.1, 1.0) $, $ ({{\eta }_\text{a}}, {{\eta }_\text{b}}, {{\eta }_\text{c}}, {{\eta }_\text{d}}) $ =$ ( 3.0 , 0 , 0 , 0 ) $.

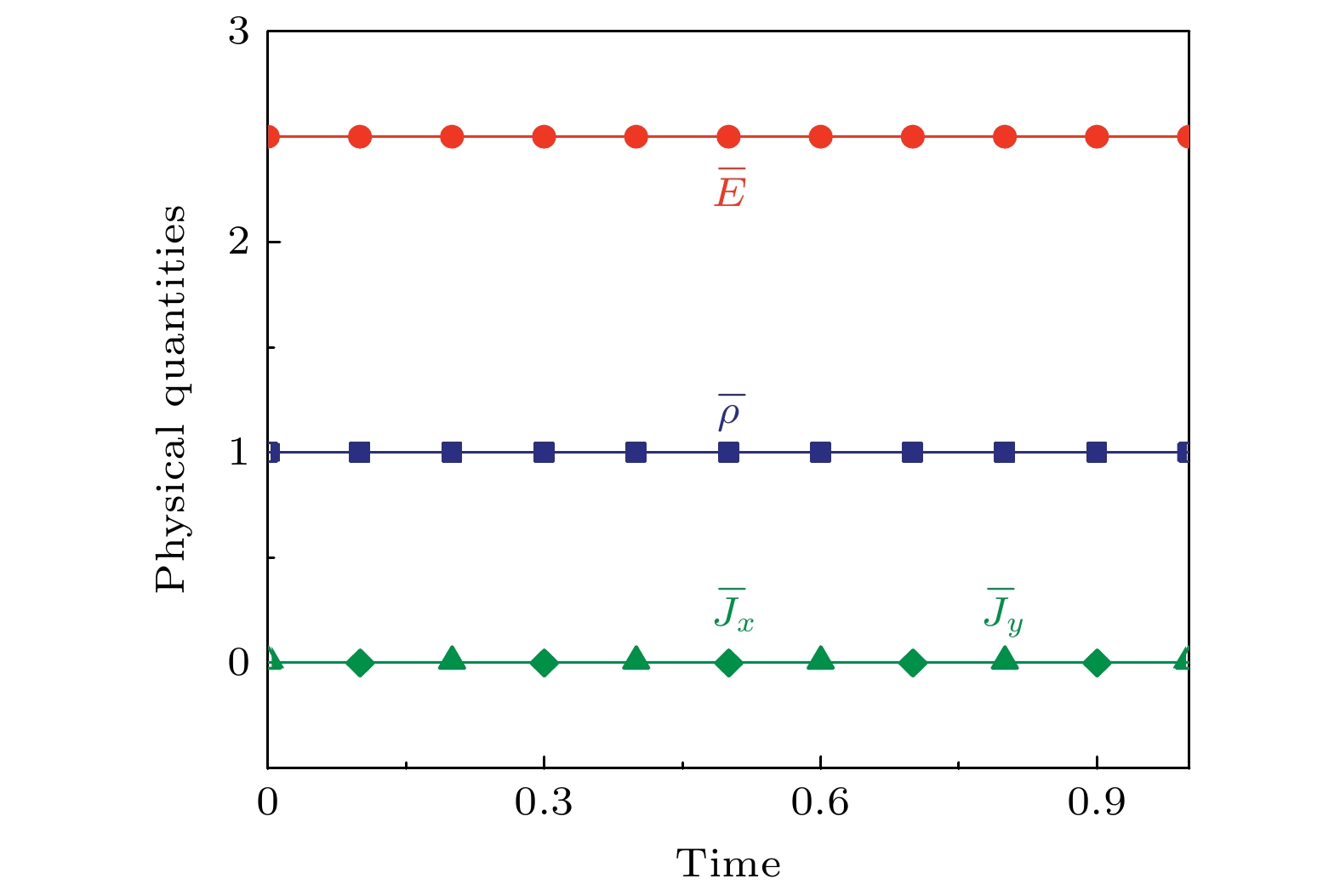
图6展示了$ t = 0 $, $ 0.05 $, $ 0.125 $, $ 0.15 $, $ 0.175 $, $ 0.2 $时刻, 比热比$ \gamma = 1.4 $以及温度$ T = 1.0 $的压强演化过程. 如图所示, 该区域为一个温度均匀分布的计算区域, 并在其正中央设置了一个初始扰动. 随后, 该扰动引发了一个圆形声波并以声速向外扩散. 声波在传播过程中, 其形态保持圆形, 呈现良好的对称性. 在$ t = 0.125 $时刻, 声波到达了计算区域的边界并被反射. 在后续的时刻, 反射后的声波与反射前的声波发生了叠加. 可以看出, DBM能够有效描述声波的传播过程.

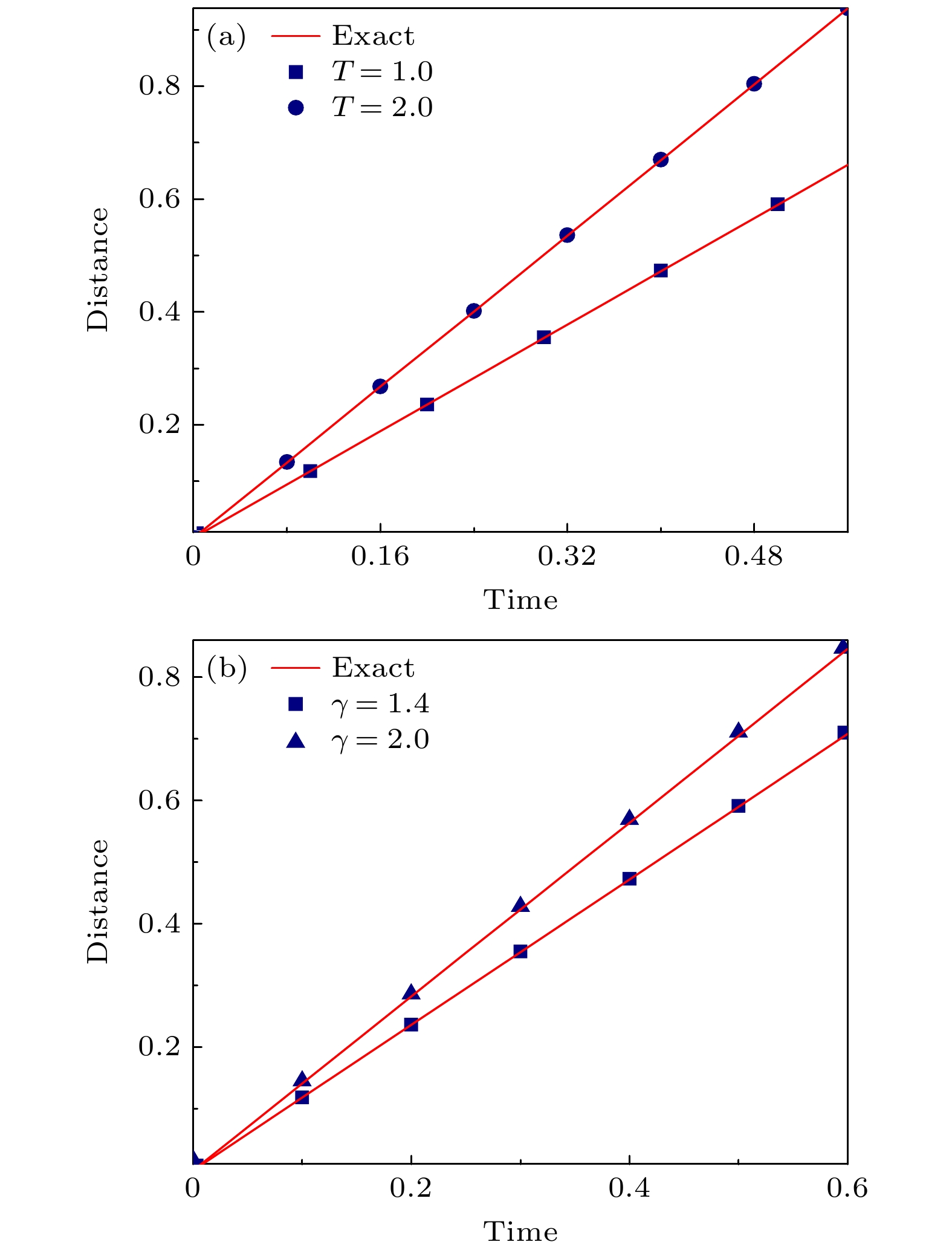
另外, 为了验证有限体积DBM的守恒性, 图7展示了在声波演化过程中平均密度$ \bar{\rho } $, x方向平均动量$ {{\bar{J}}_{x}} $, y方向平均动量$ {{\bar{J}}_{y}} $和平均能量$ \bar{E } $随时间的变化情况. 不同符号代表DBM对不同物理量的模拟结果, 实线代表对应的精确解: 平均密度$ \bar{\rho } = 1 $, 平均动量$ ({{\bar{J}}_{x}}, {{\bar{J}}_{y}}) = (0, 0) $, 平均能量$ \bar{E } = 2.5 $. 从图7可以清晰地观察到, 数值结果与精确解始终保持一致. 这充分说明有限体积DBM具有良好的守恒性特征.

下面进一步验证在不同的比热比以及温度下, 该模型对声波的捕捉能力. 图8(a)展示了当比热比$ \gamma = 1.4 $时, 在不同温度下声波传播的距离与时间的关系. 图8(b)是当温度$ T = 1.0 $时, 在两个不同的比热比下的结果. 从图8可以明显看出, 随着时间的演进, 声波的传播距离呈线性增长, 拟合直线的斜率与理论值$ {v}_{{\mathrm{s}}} = ({\gamma T})^{1/2} $的相对误差均小于$ 0.01{\text{%}} $, 模拟的结果与理论值$ x = {v}_{{\mathrm{s}}}t $符合得比较好, 从而证实了本文提到的模型在不同温度和比热比下都具有捕获声波的能力.

本文采用有限体积法对离散Boltzmann-BGK方程进行数值求解, 该方法具有守恒性强和精度高等优点. 具体来说, 首先在控制体上分别对该方程的碰撞项、对流项以及时间项进行积分, 得到半离散形式的离散Boltzmann-BGK方程. 其中, 利用高斯定理, 对流项可以转换为微观通量的形式. 为了有效处理对流项, 本文采用二阶精度的MUSCL格式进行重构, 并引入了通量限制器以提高数值计算的稳定性. 然后, 使用二阶精度的龙格-库塔格式处理时间偏微分, 最终得到用于程序迭代运算的DBM演化方程.

为了对有限体积DBM进行数值验证, 本文使用了3个经典算例: 稳定冲击波、Lax激波管和声波的传播. 首先, 通过冲击波算例对程序的网格无关性进行了验证, 验证了该方法能够准确测量可压缩流体系统的流体力学和热力学非平衡效应; 然后, 通过Lax激波管算例, 验证了该方法能够准确描述冲击波、稀疏波以及物质界面的演化过程; 最后, 通过二维声波的传播算例, 验证了该方法能够在不同比热比和温度下对声波进行有效捕捉, 并且具有良好的守恒性特征.