高级搜索

单轴应变对Sb2Se3空穴迁移率的影响

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张冷, 沈宇皓, 汤朝阳, 吴孔平, 张鹏展, 刘飞, 侯纪伟. 单轴应变对Sb2Se3空穴迁移率的影响[J]. 物理学报, 2024, 73(11): 117101-1. doi: 10.7498/aps.73.20240175
引用本文: 张冷, 沈宇皓, 汤朝阳, 吴孔平, 张鹏展, 刘飞, 侯纪伟. 单轴应变对Sb2Se3空穴迁移率的影响[J]. 物理学报, 2024, 73(11): 117101-1. doi: 10.7498/aps.73.20240175
shu
Leng Zhang, Yu-Hao Shen, Chao-Yang Tang, Kong-Ping Wu, Peng-Zhan Zhang, Fei Liu, Ji-Wei Hou. Effect of uniaxial strain on Hole mobility of Sb2Se3[J]. Acta Physica Sinica, 2024, 73(11): 117101-1. doi: 10.7498/aps.73.20240175
Citation: Leng Zhang, Yu-Hao Shen, Chao-Yang Tang, Kong-Ping Wu, Peng-Zhan Zhang, Fei Liu, Ji-Wei Hou. Effect of uniaxial strain on Hole mobility of Sb2Se3[J]. Acta Physica Sinica, 2024, 73(11): 117101-1. doi: 10.7498/aps.73.20240175
shu

单轴应变对Sb2Se3空穴迁移率的影响

  • 1.

    金陵科技学院电子信息工程学院, 南京　211169

  • 2.

    南京大学物理学院, 固体微结构国家实验室, 南京　210093

  • 3.

    南京工业大学数理科学学院, 南京　211816

    • 作者简介: 张冷: zhangleng2018@jit.edu.cn .
    通讯作者: E-mail:jwhou@njtech.edu.cn

  • 中图分类号: 71.15.Mb, 51.50.+v, 71.70.Fk

Effect of uniaxial strain on Hole mobility of Sb2Se3

  • 1.

    School of Electronics and Information Engineering, Jinling Institute of Technology, Nanjing 211169, China

  • 2.

    National Laboratory of Solid State Microstructures, School of Physics, Nanjing University, Nanjing 210093, China

  • 3.

    Department of Physics, School of Physical and Mathematical Sciences, Nanjing Tech University, Nanjing 211816, China

    • Corresponding author: E-mail:jwhou@njtech.edu.cn

  • MSC: 71.15.Mb, 51.50.+v, 71.70.Fk

  • 摘要: 硒化锑(Sb2Se3)是一种物相简单、元素丰富、经济友好的太阳电池吸收层材料, 具有广阔的应用前景. 然而, Sb2Se3较弱的导电性成为了限制电池器件性能的重要因素. 迁移率是材料与器件的重要电学参数, 应变可以改变载流子迁移率, 因此, 研究应变对Sb2Se3的载流子迁移率特性影响具有实际意义. 本文通过密度泛函理论和形变势理论, 系统研究了单轴应变对Sb2Se3能带结构、禁带宽度、等能面、有效质量的影响, 分析了沿着x, y, z方向的三种单轴应变对载流子沿着x, y, z方向的迁移率μx, μy, μz的影响. 研究发现, 对于无应变的Sb2Se3, μx远大于μy和μz, 实验上应该将x方向作为Sb2Se3的特定生长方向(即内建电场方向). 综合应变对带隙、等能面、分态密度及迁移率的影响, 本研究认为当应变沿着y轴方向, 且压应变为3%的时候, 能获得最佳性能的Sb2Se3太阳电池吸收层材料.
    Abstract: Antimony selenide (Sb2Se3) is a simple-phase, element-rich, and economically friendly material for solar cell absorption layers, with broad application prospects. However, the weak conductivity of Sb2Se3 has become a significant factor limiting the performance of solar cell devices. Carrier mobility is an important electrical parameter for both materials and devices, and strain can change carrier mobility. Therefore, studying the effect of strain on the carrier mobility of Sb2Se3 is of practical significance. In this work, using density functional theory and deformation potential theory, we systematically investigate the influence of uniaxial strain on the band structure, bandgap width, iso-surface, and effective mass of Sb2Se3. We analyze the effects of three types of uniaxial strains along the x-, y-, and z-direction on the carrier mobilities along the x-, y-, and z-direction, which are denoted by μx, μy, and μz, respectively. It is found that under these strains, the valence band maximum (VBM) position of Sb2Se3 remains unchanged, and the bandgap decreases with the increase of strain along the y- and z-direction, while it increases along the x-direction. The variation in bandgap may be related to the coupling strength between the Sb-5p orbital and Se-4p orbital of the conduction band minimum (CBM). For fully relaxed Sb2Se3, its iso-surface exhibits a distorted cylindrical shape, with low dispersion along the z-axis and high dispersion along the x- and y-axis, where μx is greater than μy and μz, suggesting that the x-direction should be considered as the specific growth direction for Sb2Se3 experimentally. When the strain is applied along the x- and z-direction, μx gradually increases with strain increasing, while it decreases when the strain is applied along the y-direction. Taking into account the combined effects of strain on bandgap, iso-surface, density of states, and mobility, this study suggests that the optimal performance of Sb2Se3 solar cell absorber layer material can be realized when the strain is applied along the y-axis, with a compressive strain of 3%.
  • 加载中

  • 图 1  Sb2Se3的晶胞, 棕色球体代表阳离子锑, 绿色球体代表阴离子硒

    Figure 1.  Crystal structure of Sb2Se3 computational model, brown spheres represent cation antimony, and green spheres represent anion selenium.

    下载: 全尺寸图片 幻灯片

    图 2  不同能带结构随εx的变化, 正号表示拉应变, 负号表示压应变, VBM与CBM均用红圈标注

    Figure 2.  The variation of energy band structure under different εx strains. Positive sign indicates tensile strain, and negative sign indicates compressive strain. The VBM and the CBM are marked with red circles.

    下载: 全尺寸图片 幻灯片

    图 3  费米能级、VBM、CBM及带隙随应变的变化　(a)应变沿x方向; (b)应变沿y方向; (c)应变沿z方向

    Figure 3.  Variation of Fermi level, VBM, CBM and band gap with strain: (a) Strain along x direction; (b) strain along y direction; (c) strain along z direction.

    下载: 全尺寸图片 幻灯片

    图 4  Sb2Se3价带顶下100 meV处的等能面的变化. 应变沿着x方向上　(a) εx = 0, (b) εx = –4.5%, (c) εx = +4.5%; 应变沿y方向上　(d) εy = –4.5%, (e) εy = +4.5%; 应变沿z方向上　(f) εz = –4.5%, (g) εz = +4.5%

    Figure 4.  Variation of the isosurface at 100 meV below VBM. The strain is applied along x direction: (a) εx = 0, (b) εx = –4.5%, and (c) εx = +4.5%. The strain is applied along y direction: (d) εy = –4.5% and (e) εy = +4.5%. The strain is applied along z direction: (f) εz = –4.5% and (g) εz = +4.5%.

    下载: 全尺寸图片 幻灯片

    图 5  Sb2Se3分态密度图. 应变沿着x方向上　(a) εx = 0, (b) εx = –4.5%, (c) εx = +4.5%; 应变沿y方向上　(d) εy = –4.5%, (e) εy = +4.5%; 应变沿z方向上　(f) εz = –4.5%, (g) εz = +4.5%

    Figure 5.  Partial density of states of Sb2Se3. The strain is applied along x direction: (a) εx = 0, (b) εx = –4.5%, and (c) εx = +4.5%. The strain is applied along y direction: (d) εy = –4.5% and (e) εy = +4.5%. The strain is applied along z direction: (f) εz = –4.5% and (g) εz = +4.5%.

    下载: 全尺寸图片 幻灯片

    图 6  迁移率随应变的变化　(a)应变沿x方向; (b)应变沿y方向; (c)应变沿z方向

    Figure 6.  Mobility variation with strain: (a) Strain along the x direction; (b) strain along the y direction; (c) strain along the z direction.

    下载: 全尺寸图片 幻灯片

    表 1  不同应变方向及应变量下, 沿x, y, z方向的有效质量

    Table 1.  Effective mass along x, y, z directions under different strain directions and strain amounts.

    应变方向ε/%$ {m}_{x}^{{\mathrm{*}}} $/m0$ {m}_{y}^{{\mathrm{*}}} $/m0$ {m}_{z}^{{\mathrm{*}}} $/m0



    x方向    		–4.50.580.730.77
    –3.00.510.780.86
    –1.50.460.850.96
    00.440.941.12
    1.50.421.081.32
    3.00.411.321.59
    4.50.401.821.97



    y方向    		–4.50.355.281.37
    –3.00.374.241.29
    –1.50.401.511.20
    00.440.941.12
    1.50.480.701.03
    3.00.530.590.95
    4.50.600.530.88



    z方向    		–4.50.550.941.62
    –3.00.500.941.27
    –1.50.460.931.15
    00.440.941.12
    1.50.421.021.11
    3.00.401.351.12
    4.50.403.831.13
    下载: 导出CSV
  • [1] Green M A, Dunlop E D, Yoshita M 2023 Prog. Photovolt. Res. Appl. 31 651 doi: 10.1002/pip.3726
    [2] Chen C, Li K H, Tang J 2022 Sol. RRL 6 2200094 doi: 10.1002/solr.202200094
    [3] Zhang X, Li C, Sun K, Zhou J, Zhang Z 2021 Adv. Energy Mater. 11 2002614 doi: 10.1002/aenm.202002614
    [4] 薛丁江, 石杭杰, 唐江 2015 物理学报 64 038406 doi: 10.7498/aps.64.038406 Xue D J, Shi H J, Tang J 2015 Acta Phys. Sin. 64 038406 doi: 10.7498/aps.64.038406
    [5] Zhao Y Q, Wang S Y, Li C, Che B, Chen X L, Chen H Y, Tang R F, Wang X M, Chen G L, Wang T, Gong J B, Chen T, Xiao X D, Li J M 2022 Energy Environ. Sci. 15 5118 doi: 10.1039/D2EE02261C
    [6] Li Z Q, Liang X Y, Li G, Liu H X, Zhang H Y, Guo J X, Chen J W, Shen K, San X Y, Yu W Y, Schropp R, Mai Y H 2019 Nat. Commun. 10 125 doi: 10.1038/s41467-018-07903-6
    [7] Takagi S, Hoyt J L, Welser J J, Gibbons J F 1996 J. Appl. Phys. 80 1567 doi: 10.1063/1.362953
    [8] Welser J, Hoyt J L, Gibbons J F 1992 International Technical Digest on Electron Devices Meeting, San Francisco, CA, USA 1992, December 13–16, 1992 p1000
    [9] 宋建军, 张鹤鸣, 胡辉勇, 宣荣喜, 戴显英 2010 物理学报 59 579 doi: 10.7498/aps.59.579 Song J J, Zhang H M, Hu H Y, Xuan R X, Dai X Y 2010 Acta Phys. Sin. 59 579 doi: 10.7498/aps.59.579
    [10] Jia W L, He Y, Cao Y L, Wang X M, Lin Z, Li W T, Xu M, Li E L 2022 Micro Nanostructures 168 207300 doi: 10.1016/j.micrna.2022.207300
    [11] Datye I M, Daus A, Grady R W, Brenner K, Vaziri S, Pop E 2022 Nano Lett. 22 8052 doi: 10.1021/acs.nanolett.2c01707
    [12] Ge G X, Zhang Y W, Yan H X, Yang J M, Zhou L, Sui X J 2021 Appl. Surf. Sci. 538 148009 doi: 10.1016/j.apsusc.2020.148009
    [13] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [14] Vadapoo R, Krishnan S, Yilmaz H, Marin C 2011 Phys. Status Solidi B 248 700 doi: 10.1002/pssb.201046225
    [15] Bardekn J, Shockley W 1950 Phys. Rev. 80 72 doi: 10.1103/PhysRev.80.72
    [16] Xi J Y, Long M Q, Tang L, Wang D, Shuai Z G 2012 Nanoscale 4 4348 doi: 10.1039/c2nr30585b
    [17] El-Sayad E A, Moustafa A M, Marzouk S Y 2009 Physica B 404 1119 doi: 10.1016/j.physb.2008.11.086
    [18] Kumar A, Ahluwalia P K 2013 Physica B 419 66 doi: 10.1016/j.physb.2013.03.029
    [19] Peng X H, Ganti S, Alizadeh A, Sharma P, Kumar S K, and Nayak S K 2006 Phys. Rev. B 74 035339 doi: 10.1103/PhysRevB.74.035339
    [20] Wang V, Xu N, Liu J C, Tang G, Geng W T 2021 Comput. Phys. Commun. 267 108033 doi: 10.1016/j.cpc.2021.108033
    [21] Kawamura M 2019 Comput. Phys. Commun. 239 197 doi: 10.1016/j.cpc.2019.01.017
    [22] Wang X W, Li Z Z, Kavanagh S R, Ganose A M, Walsh A 2022 Phys. Chem. Chem. Phys. 24 7195 doi: 10.1039/D1CP05373F
    [23] Effective Mass Calculator for Semiconductors, Fonari A, Sutton Chttps://github.com/afonari/emc [2013-3-18]
    [24] Zhang B Y, Qian X F 2022 ACS Appl. Energy Mater. 5 492 doi: 10.1021/acsaem.1c03023
    [25] Zhou Y, Wang L, Chen S Y, Qin S K, Liu X S, Chen Jie, Xue D J, Luo M, Cao Y Z, Cheng Y B, Sargent E H, Tang J 2015 Nat. Photonics 9 409 doi: 10.1038/nphoton.2015.78
    [26] Chen C, Bobela D C, Yang Ye, Lu S C, Zeng K, Ge C, Yang B, Gao L, Zhao Y, Beard M C, Tang J 2017 Front. Optoelectron. 10 18 doi: 10.1007/s12200-017-0702-z
  • 加载中
图( 6) 表( 1)
计量
  • 文章访问数:  323
  • HTML全文浏览数:  323
  • PDF下载数:  6
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-01-26
  • 刊出日期:  2024-06-05

单轴应变对Sb2Se3空穴迁移率的影响

    通讯作者: E-mail:jwhou@njtech.edu.cn
    作者简介: 张冷: zhangleng2018@jit.edu.cn
  • 1. 金陵科技学院电子信息工程学院, 南京　211169
  • 2. 南京大学物理学院, 固体微结构国家实验室, 南京　210093
  • 3. 南京工业大学数理科学学院, 南京　211816
  • 收稿日期:  2024-01-26

摘要: 硒化锑(Sb2Se3)是一种物相简单、元素丰富、经济友好的太阳电池吸收层材料, 具有广阔的应用前景. 然而, Sb2Se3较弱的导电性成为了限制电池器件性能的重要因素. 迁移率是材料与器件的重要电学参数, 应变可以改变载流子迁移率, 因此, 研究应变对Sb2Se3的载流子迁移率特性影响具有实际意义. 本文通过密度泛函理论和形变势理论, 系统研究了单轴应变对Sb2Se3能带结构、禁带宽度、等能面、有效质量的影响, 分析了沿着x, y, z方向的三种单轴应变对载流子沿着x, y, z方向的迁移率μx, μy, μz的影响. 研究发现, 对于无应变的Sb2Se3, μx远大于μy和μz, 实验上应该将x方向作为Sb2Se3的特定生长方向(即内建电场方向). 综合应变对带隙、等能面、分态密度及迁移率的影响, 本研究认为当应变沿着y轴方向, 且压应变为3%的时候, 能获得最佳性能的Sb2Se3太阳电池吸收层材料.

English Abstract

    全文HTML

    1.   引　言

    • 薄膜太阳电池吸收层厚度仅1—2 μm, 可应用于柔性电池移动能源、光伏建筑一体化及可穿戴电子设备等, 具有广阔的应用空间. 目前产业化应用的薄膜电池有碲化镉(CdTe)、铜铟镓硒(CIGS)和钙钛矿[1]太阳电池, 但是镉元素有毒, 碲资源丰度很小, 铟和镓是稀有元素, 钙钛矿有性能不稳定的问题, 使得薄膜电池成本居高不下, 故而在规模化生产和应用上受到很大限制. 硒化锑(Sb2Se3)材料具有吸收系数大、禁带宽度合适、物相简单、原材料丰度高、便宜无毒的优势, 非常有潜力拓宽目前的薄膜太阳电池应用市场[2–4]. 近十年来, Sb2Se3太阳能电池的最高转换效率逐年攀升, 目前世界纪录效率达到了10.57%[5,6]. 然而, 这距离产业化所要求的转换效率仍有较大距离. 限制Sb2Se3电池性能的关键因素之一是其弱导电性. 导电性主要与载流子浓度和迁移率相关. 迁移率反映了载流子在电场下移动的速率, 是衡量半导体导电能力的重要物理指标, 也决定了太阳电池等电子器件的工作效率. Sb2Se3材料的结构呈带状, 由许多一维的(Sb4Se6)n纳米带通过范德瓦耳斯力堆叠而成. 因为这样的结构, Sb2Se3的载流子迁移率呈现显著的各向异性. 通过调节工艺条件, 将pn结的内建电场方向与载流子传输能力强的方向保持一致, 有望提高载流子的输运效率. 因此, 对Sb2Se3的迁移率进行系统研究与调控具有重要意义.

      应变工程是调控半导体电学性质的重要方法, 其在提高硅基晶体管的迁移率方面的应用已有数十年[7–9], 在其他材料的调控上亦有报道. Jia等[10]对氮化镓施加1.5%的张应变, 发现其电子迁移率增加约10%. Datye等[11]对单层MoS2晶体管施加0.7%的张应变, 使得通态电流与迁移率翻倍. Ge等[12]对单层GeTe施加单轴应变, 可使电子迁移率提高至弛豫态下的上百倍.

      当前对于Sb2Se3载流子输运的调控研究还很少, 基于此, 本文系统研究了单轴应变对能带结构、禁带宽度、等能面、有效质量的影响, 分析了沿着x, y, z方向的三种单轴应变对载流子沿着x, y, z方向的迁移率影响, 相关结论可以为设计高性能的太阳电池器件提供参考.

    2.   计算方法与模型

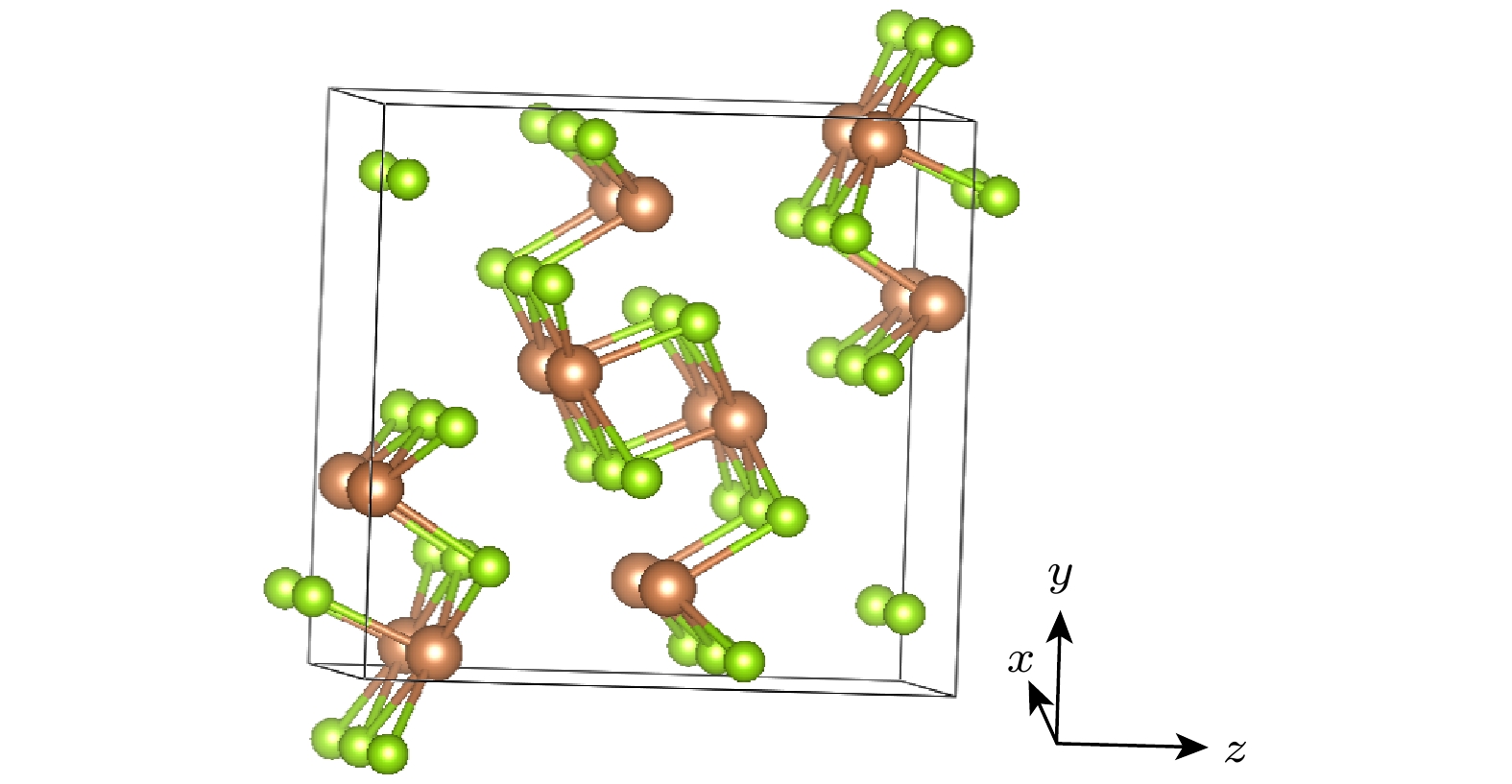
    • 本研究采用VASP (Vienna ab initio simulation package)中的第一性原理计算方法进行探究, 通过平面波基组展开电子波函数, 使用广义梯度近似(GGA)下的PBE交换泛函来描述电子与电子之间的交换关联作用[13]. 为确保计算的准确性, 进行了收敛性测试. 选择平面波截断能量400 eV, 使用4×3×3的k空间取样密度, 能保证总能量的收敛性. 迭代过程中, 收敛精度选择1×10–6 eV/atom. 在布里渊区中, 选取了如下特殊K点[14], 分别是G(0, 0, 0), X(0.5, 0, 0), Z(0, 0, 0.5), U(0.5, 0, 0.5), Y(0, 0.5, 0), S(0.5, 0.5, 0), T(0, 0.5, 0.5), R(0.5, 0.5, 0.5), 能带结构中的布里渊区路径为G-X-Z-U-Y-S-T-R. 研究的超胞模型结构如图1所示, 共40个原子, 其中包括24个硒原子和16个锑原子.

      根据形变势理论, 结合玻尔兹曼输运理论下的弛豫时间近似和DFT能带结构理论的有效质量近似[15,16], 可得三维材料体系的迁移率为

      其中, e代表单电荷电量, $\hbar $代表约化普朗克常数, $ {C}_{\alpha }^{3{\mathrm{D}}} $表示沿载流子输运方向α的弹性常数, kB代表玻尔兹曼常数, T代表温度, Eɑ是α方向的形变势能, $ {m}_{\alpha }^{{\mathrm{*}}} $是α方向的载流子有效质量. 为了直观表示, 本文只计算x, y, z三个方向上的载流子迁移率.

      $m^*$的计算方法为

      其中, i和j分别表示在倒空间的分量, $ E\left(\boldsymbol{k}\right) $是导带底或价带顶附近的能量-波矢关系.

    3.   结果与讨论

      3.1.   晶体结构

    • 在进行能量和性质计算之前, 先对晶体结构进行了优化, 优化过程考虑了范德瓦耳斯修正. 所计算出的晶格常数为3.99, 11.34, 11.64 Å, 与实验测量值3.98, 11.65, 11.80 Å[17]接近, 确保了晶体结构计算上的可靠性.

      • 3.2.   应变对价带结构的影响

    • 采用密度泛函理论(DFT) PBE交换关联泛函算出的无应变Sb2Se3带隙为0.83 eV, 低于实验值1.20 eV, 因为PBE会低估半导体的带隙. 本文重点关注应变对价带顶(VBM)和导带底(CBM)的位置及能带形状的影响. 此前的研究表明, PBE也可以正确预测不同应变下能带的变化趋势[18,19]. 为保证计算效率, 本文采用PBE泛函来计算应变对Sb2Se3能带结构的影响.

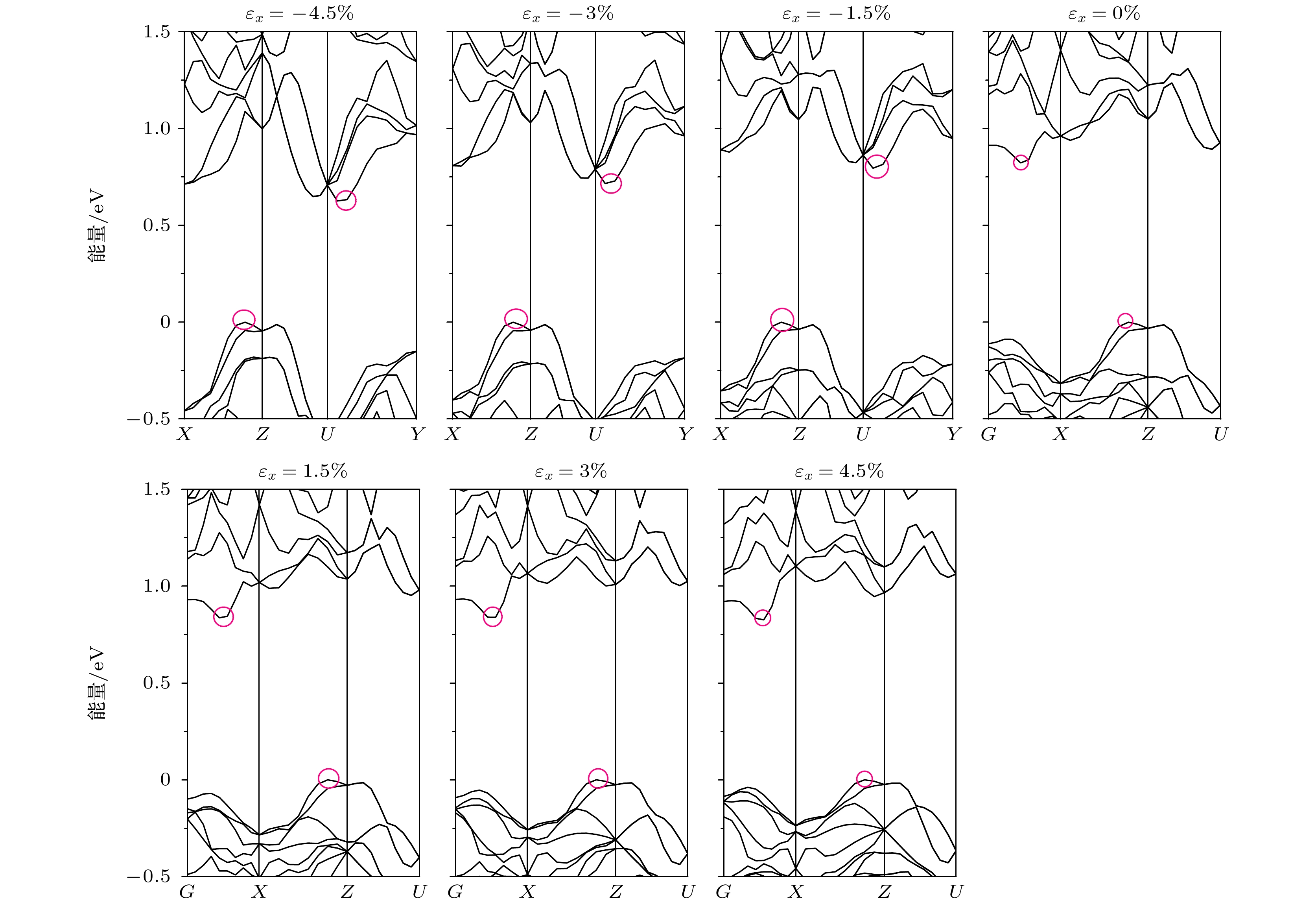
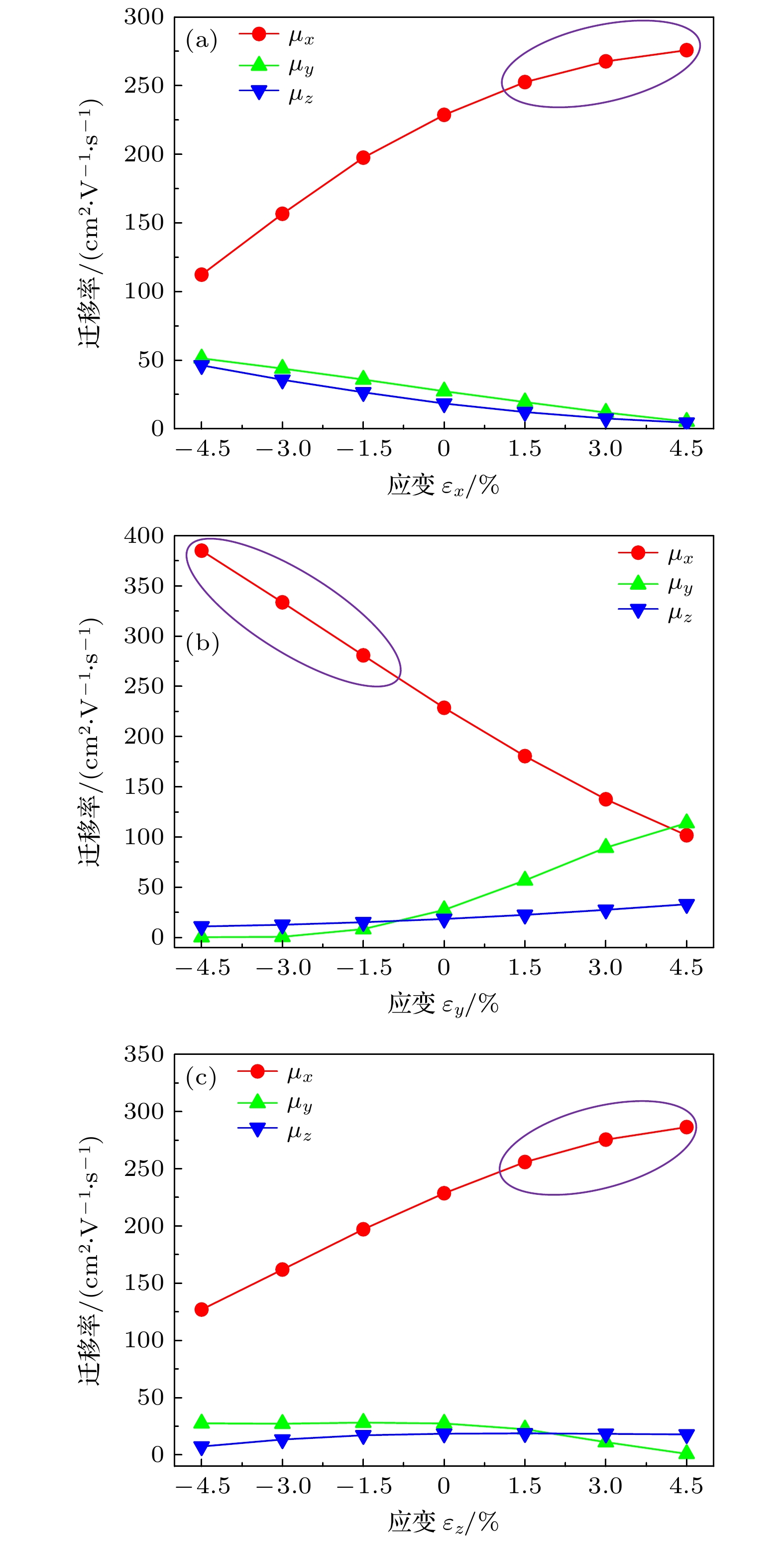
      图2展示了施加在x方向上的不同应变(εx)下能带结构的变化, 其中, 费米能级设置在了0 eV. 可以发现, 无应变的Sb2Se3是间接带隙半导体, 以波矢(kx, ky, kz)标记, 其VBM和CBM分别位于(0.111, 0, 0.389)和(0.278, 0, 0). 对于施加了张应变的结构, 其VBM和CBM位置保持不变; 对于施加了压应变下的结构, CBM位置到了 (0.444, 0.056, 0.444), VBM位置依然保持不变. 因为Sb2Se3应用在光伏领域, 主要是p型导电为主, 因此本文重点研究VBM附近的空穴特性. 对于施加在y, z方向上的不同应变(εy, εz)下, 其VBM位置也稳定在(0.111, 0, 0.389), 其图片不再列出.

      • 3.3.   应变对带隙的影响

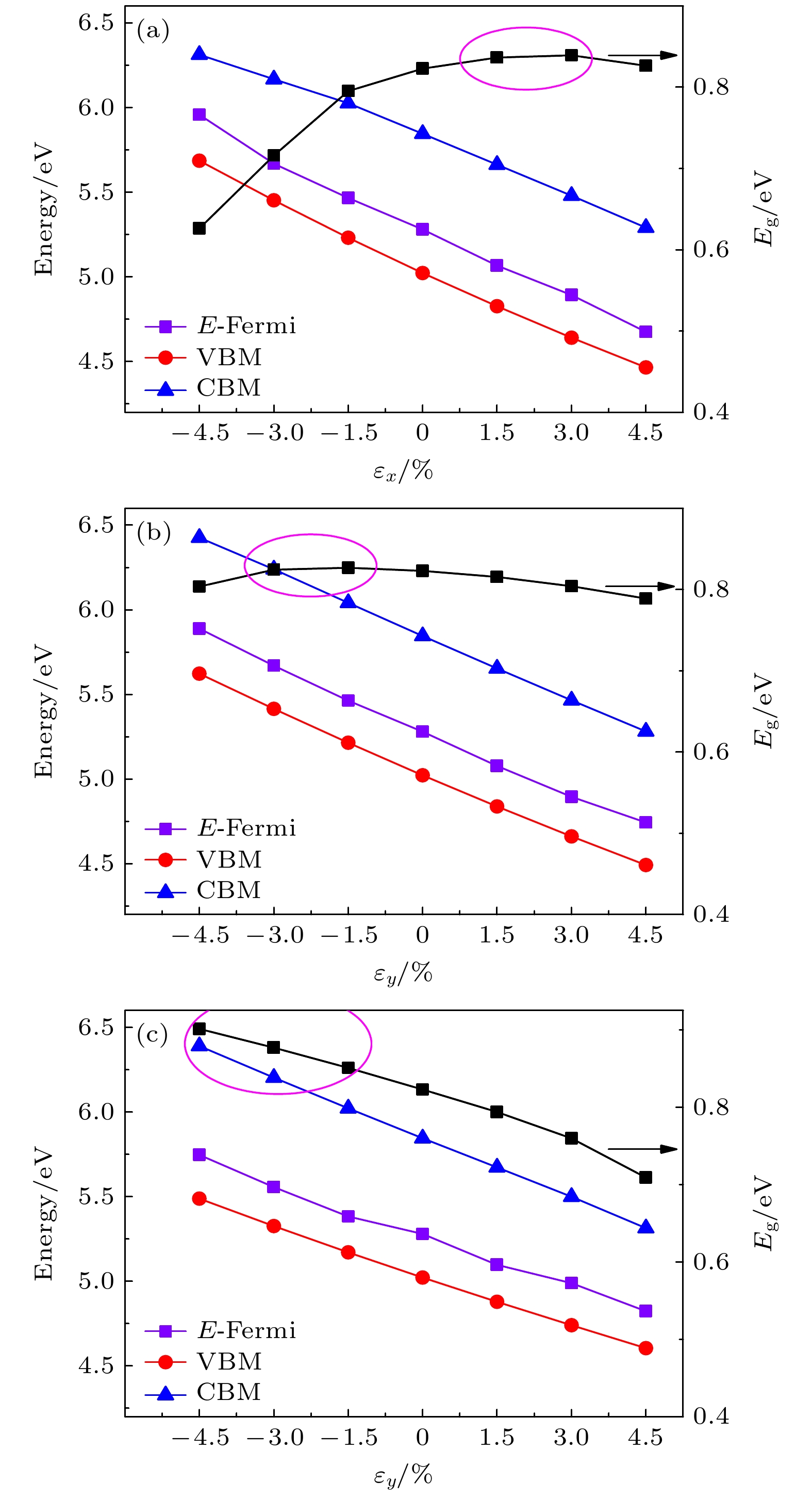
    • 带隙是CBM与VBM之间的能量差, 从图2可以看出, 应变对带隙有一定的影响. 图3绘制了费米能级、VBM、CBM与带隙随应变εx, εy和εz的变化曲线. 对于沿着x方向施加的应变, 随着应变量增大, 带隙从0.63 eV(–4.5%)增至0.84 eV(+3.0%), 随后下降至0.83 eV(+4.5%); 对于沿着y方向施加的应变, 随着应变量增大, 带隙从0.80 eV(–4.5%)增至0.83 eV(–1.5%), 随后下降至0.79 eV(+4.5%); 对于沿着z方向施加的应变, 随着应变量增大, 带隙从0.90 eV(–4.5%)下降至0.71 eV (+4.5%). 实验测到的Sb2Se3带隙为 1.20 eV左右, 低于理想的太阳电池带隙为1.4 eV[1]. 可以看出, 沿着x方向的张应变、y方向的部分压应变、z方向的压应变(如紫框所示)应该对提高带隙有利. 施加在y方向的应变对禁带宽度影响较小, 施加在x, z方向的应变对禁带宽度影响较大. 对x方向施加张应变, 对应地, y, z方向的晶格常数会减小, 相当于这两方向施加了压应变; 同理, 对z方向施加张应变, 对应地, x, y方向的晶格常数会减小, 相当于这两方向施加了压应变. 因此, Eg-εx的变化趋势与Eg-εz的变化趋势相反. 此外, 施加应变会使得体系变得更加稳定或不稳定, 因此费米能级发生改变, 相应地, VBM和CBM的能量也发生改变. 从图3可以看出, VBM的改变幅度与费米能级的改变幅度接近, 因此Eg的变 化基本是由CBM的变化所致. 结合后面的态密度图, CBM主要由Sb-5p与Se-4p轨道所贡献, 应变导致的键长、键角变化, 可能影响了Sb-5p与Se-4p轨道的耦合强度, 进而影响了CBM能量与带隙.

      • 3.4.   应变对等能面的影响

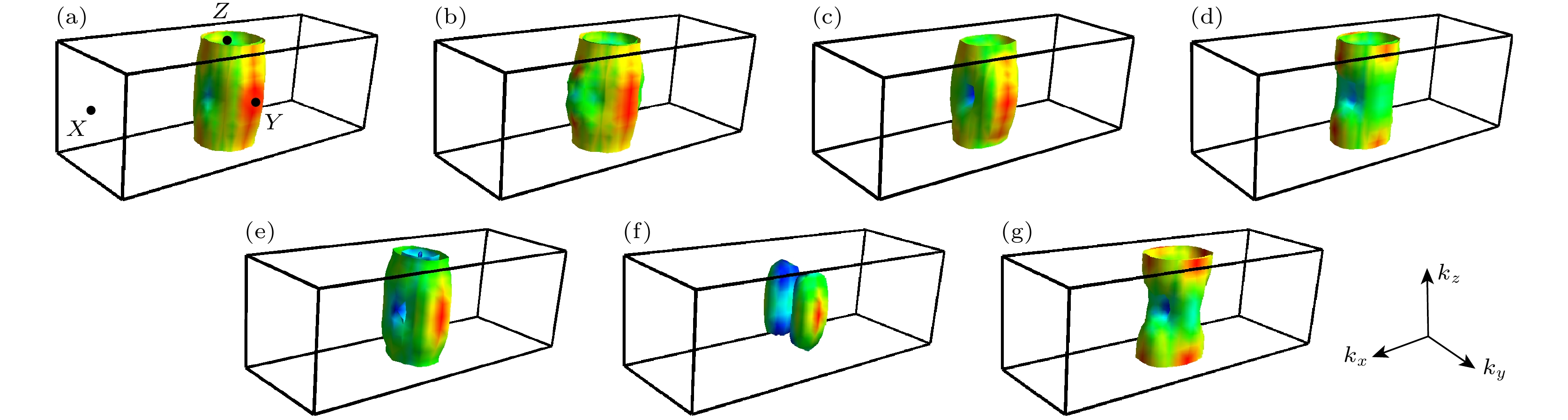
    • 为了直观展示空穴传输的方向性, 本研究采用vaspkit计算等能面数据[20], 结合Fermisurfer软件进行等能面的可视化[21]. 图4分别为无应变以及当应变沿x, y, z方向上时, Sb2Se3价带带边100 meV的三维等能图. 根据费米-狄拉克分布函数, 室温下载流子会占据此能量范围, 因此, 等能面可以反映载流子传输的各向异性. 图中黑线围成的区域是第一布里渊区, 六面体的正中心是VBM, kx波矢和ky波矢分别向左前和右前, kz波矢向上. 无应变的Sb2Se3等能面图(图4(a))呈现翘曲圆柱体形状, 其在z轴方向具有较小的色散, 在x, y轴方向具有较大的色散, 与Wang等[22]计算的Sb2Se3等能面相似, 这种特性比较像准二维材料. 相较于图4(a), 图4(c), (d), (g)在x方向上更向内凹, 色散更大; 同时, 图4(b), (e), (f)在x方向更向外凸, 色散减小. 这些是对Sb2Se3输运性质的定性探讨, 下面对输运性质进行定量探讨.

      • 3.5.   应变对分态密度的影响

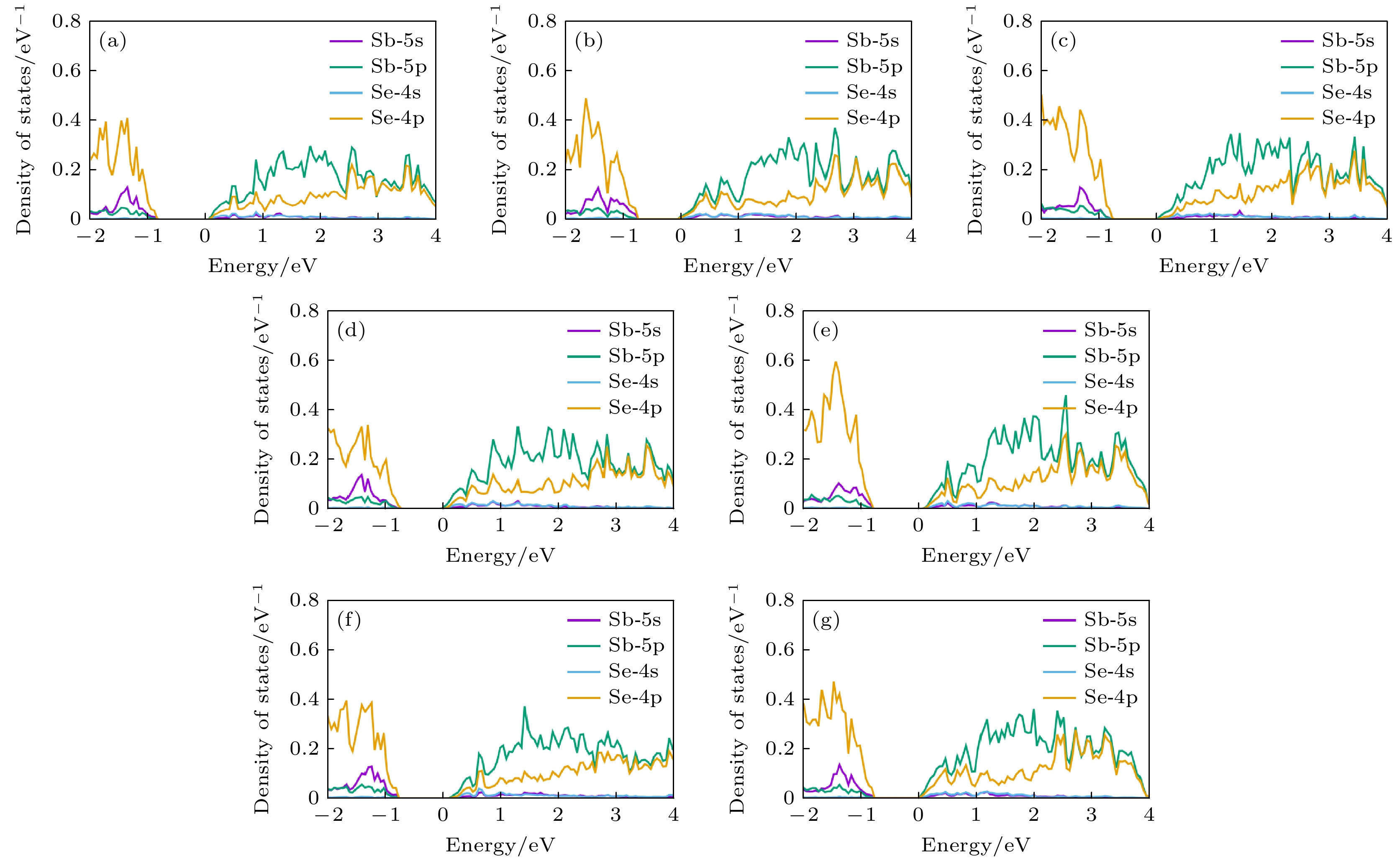
    • 为了深入探讨Sb2Se3的电子结构与有效质量的关系, 对Sb2Se3进行分态密度计算, 计算结果如图5所示. 由无应变的Sb2Se3可以看出, VBM主要是由Se 4p态和Sb 5s态所贡献, 且Se 4p, Sb 5s态在VBM附近出现局域化. 当应变沿x方向, εx为–4.5%时(图5(b))局域化最大, 价带最平坦, 色散最小, 有效质量最大; 其次是εx为0(图5(a)), 局域化最小的是εx为+4.5%时(图5(c)), 色散最大, 有效质量较小. 当应变沿着y方向, 如图5(d), (e)所示, Se 4p, Sb 5s态在εy为+4.5%时候的局域程度远大于εy为–4.5%时, 所以, εy为–4.5%时色散较大, 有效质量较小. 同理, 当应变沿着z方向, 如图5(f), (g)所示, εz为–4.5%时局域化程度大于εz为4.5%时, 因此, 后者有效质量更小.

      • 3.6.   应变对空穴迁移率的影响

    • 结合有效质量计算器(EMC)[23], 采用有限差分法(而不是能带抛物线拟合法), 我们计算了价带顶处的有效质量, 表1展示了不同应变方向及应变量下沿着x, y, z方向的有效质量. 可以看出, 无应变条件下, 空穴沿着x, y, z方向的有效质量分别为0.44m0, 0.94m0, 1.12m0, 与Zhang等[24]所计算的0.53m0, 0.42m0, 0.83m0及Wang等[22]所计算的0.85m0, 0.55m0, 3m0对比可以看出, 3组数据均在z方向上有效质量较大, 传输性能最弱; 此外, 本文计算的$ {m}_{x}^{*} $最小, 而这两篇文献所计算的$ {m}_{y}^{*} $最小, 这可能与采用的计算方法不同有关. 从图6迁移率的数据可得, 无应变下, μx为228.7 cm2/(V·s), μy为27.4 cm2/(V·s), μz为18.4 cm2/(V·s). 这印证了文献中[122] 择优取向(以共价键结合的(Sb4Se6)n带为主)的电池, 性能好于[012]择优取向(以范德瓦耳斯力结合为主)的电池[25], 也与实验测量值[26]的μx为2.59 cm2/(V·s), μy为1.17 cm2/(V·s), μz为0.6 cm2/(V·s)趋势相似. 本研究的计算结果大于实验值, 可能因为测试样品中存在杂质和缺陷, 测试值低估了 Sb2Se3 的迁移率; 还可能因为, 形变势理论只考虑了声学形变势散射, 没有考虑电离杂质散射、极性光学声子散射、压电散射等因素. 基于μx最大, 要高效分离pn结的光生载流子及提高载流子的传输, 实验上应该将x方向作为Sb2Se3的特定生长方向, 且此方向沿着内建电场的方向.

      结合表1及图6, 可以发现当应变方向沿x方向, 随着应变量的增大, $ {m}_{x}^{*} $逐渐减小, μx逐渐增大; $ {m}_{y}^{*} $和$ {m}_{z}^{*} $逐渐增大, μy和μz逐渐减小; 当应变方向沿y方向, 随着应变量的增大, $ {m}_{x}^{*} $逐渐增大, μx逐渐减小; $ {m}_{y}^{*} $和$ {m}_{z}^{*} $逐渐减小, 而μy和μz逐渐增大; 当应变方向沿z方向, 随着应变量的增大, $ {m}_{x}^{*} $逐渐减小, μx逐渐增大; $ {m}_{y}^{*} $先基本维持不变, 再逐渐增大, $ {m}_{z}^{*} $先逐渐减小, 再基本维持不变. 这部分应变对m*的影响与上部分等能面提供的信息基本一致, 表明本计算方法基本可靠.

      从图6还可以看出, 当应变沿着x, z方向的时候, 拉应变可以获得更高的μx (如紫框所示). 当应变方向沿着y方向的时候, 压应变可以获得更高的μx. 结合应变对带隙的影响, z方向的拉应力会使带隙变小, 不利于最大限度地吸收光子, 不宜于提升太阳电池的光电转化性能. 对比应变沿着x, y方向上迁移率的具体数值, 考虑应变对带隙的影响, 发现当应变为εy = –3.0%时, μx达到本计算的最大值333.6 cm2/(V·s).

    4.   结　论

    • 通过密度泛函理论和形变势理论, 本文系统研究了沿着x, y, z方向的3种单轴应变对Sb2Se3的能带结构、禁带宽度、等能面、有效质量影响. 研究发现在这些应变下, Sb2Se3的VBM位置维持不变, 沿着y, z方向应变时, 随着应变量增大, 其带隙整体降低; 沿着x方向应变时, 随着应变量增大, 其带隙增大. 带隙的变化可能由CBM的Sb-5p与Se-4p轨道的耦合强度变化有关. 对于充分弛豫的Sb2Se3, 其等能面呈现翘曲圆柱体形状, 在z轴方向色散小, x, y轴方向色散大, μx大于μy和μz, 实验上应该将x方向作为Sb2Se3的特定生长方向. 当应变沿着x, z方向, 随着应变量的增大, $ {m}_{x}^{*} $逐渐变小, μx逐渐增大; 当应变沿着y方向, 随着应变量的增大, $ {m}_{x}^{*} $逐渐变大, μx减小. 综合应变对带隙和迁移率的影响, 我们认为当应变沿着y方向, 且压应变为3%的时候, 能获得最佳的Sb2Se3太阳电池吸收层材料.

    参考文献 (26)

目录

/

返回文章
返回