首页
登录
注册
-
传统摩擦学理论认为, 降低摩擦副表面的粗糙程度有利于提高其摩擦学性能. 然而, 大量研究表明, 在摩擦副表面设计和制备适当的拓扑形貌能提高润滑表面之间的摩擦学性能. 早在1966年, Hamilton等[1]就发现旋转轴密封件表面微凸体能产生流体动压效应并能提高轴承的承载能力. 自此, 大量关于表面微观结构对流体动压润滑影响的实验和理论研究相继展开. Zhong等[2]利用激光造型技术在AISI1045钢表面加工沟槽并形成类似于蛇皮六角鳞片的结构, 通过摩擦磨损实验发现表面六角形结构的覆盖率达到25%即可使摩擦系数降低41%. Mourier等[3]发现当凹坑或沟槽较浅时(1—50 μm), 润滑过程中该区域内润滑油的黏度明显增大, 引起润滑膜厚度增大且能增强弹流润滑效应. 与此同时, 有关织构化表面影响摩擦学性能的机理也得到广泛而深入的研究. 一方面, 织构化表面的凹坑或沟槽可容纳更多的润滑剂, 从而改善润滑性能; 另一方面, 当润滑剂流经微结构区域时, 在发散区产生的空化现象可以提升沿凹坑壁面产生的流体动升力, 增强动压润滑效应[4,5].
基于表面微观形貌对摩擦学性能影响规律的分析, 如何合理设计和制造摩擦副表面微观拓扑结构并优化其摩擦学性能, 成为国内外学者普遍关注的焦点问题. Braun等[6]采用激光造型技术在C85钢制备了尺寸为15—800 μm的圆形凹坑结构, 其摩擦实验结果显示凹坑尺寸在40 μm时摩擦系数最小, 且当相对滑动速度为500 mm/s时, 摩擦系数降幅甚至可达80%. Hsu等[7]利用光刻技术在304不锈钢表面制备深度和覆盖率均一致(分别为8 μm和7%)的圆形、椭圆形和三角形凹坑结构, 分析摩擦磨损实验结果发现圆形和椭圆形凹坑能有效降低摩擦系数, 在边界润滑和混合润滑条件下摩擦系数降幅可达64%和80%. 安书董等[8]利用离子束表面改性技术在硅基底上形成不同形貌的纳米结构, 进行摩擦磨损实验后发现其磨损时间从10 min提高到70 min, 耐磨性得到明显提升.
此外, 研究还发现, 当摩擦方向与表面微织构的排列方向密切相关, 并且在较低的滑动速度条件下也能使边界润滑转变为混合润滑. Rosenkranz等[9]利用热压印技术在AISI304不锈钢表面制备半球状凹坑结构, 研究发现表面凹坑深度和覆盖率分别为25 μm和5%时摩擦系数最低. 不仅如此, 与尺度在几十到几百微米的表面织构相比, 轮廓的算术平均偏差(Ra < 1 m)也是影响摩擦学性能的关键因素. 纪敬虎等[10]研究了45号钢表面微凹坑和粗糙度共存时对摩擦学性能的影响规律, 其结果表明, 在混合润滑条件下表面粗糙度可显著影响摩擦学性能且存在一个最佳的粗糙度值(Ra= 0.15 μm)使摩擦系数达到最小, 并认为表面存在的凹凸体也能产生流体动压效应, 从而提高减摩润滑性能. Qiu等[11]采用计算流体动力学方法分析了止推轴承表面微凹坑及其表面粗糙度对动压润滑效应的影响, 分析适宜的表面粗糙度能显著提升微凹坑织构表面的承载能力.
实际生产加工中水润滑轴承的轴套或轴瓦经磨削或珩磨等机械加工后, 其表面会残留有粗糙不平的平行沟槽结构. 因此, 在评价摩擦副表面微观形貌的摩擦学性能时, 除考虑表面微织构外, 还应考虑表面粗糙度对摩擦学性能产生的影响. Lahayne等[12]发现表面粗糙度中轮廓的均方根偏差(Rq) 值能用于有效预测橡胶在粗糙冰面上的摩擦系数. Feng等[13]认为综合对偶件表面粗糙度参数中的Ra, Rq和二维轮廓最大高度(Rz)值可以预测丁腈橡胶(NBR)材料的润滑性能. Sedlaček等[14]提出表面粗糙度评定参数中的轮廓峰度(Rku)、偏度(Rsk)、简约峰高(Rpk)和简约谷深(Rvk)值能够有效表征摩擦系数的变化规律. Menezes等[15]认为平均峰间距(Sm)、表面均方根偏差(Sq)、峰密度(Sds)等表面粗糙度评定参数组能够有效评估镁铝合金表面粗糙程度对摩擦学性能的影响. 然而, 由于粗糙表面的评价参数较多且各指标参数间互相影响、并非独立, 因此用于评估粗糙表面摩擦学性能的参数或指标不统一, 甚至有可能出现相悖的结论[16]. 因此, 有必要分析材料表面微结构和表面粗糙度等评价参数对水润滑轴承摩擦副摩擦学性能的影响规律.
-
当有稳定润滑膜将摩擦界面完全分离, 不再有接触部分, 这种状态就称为流体动压润滑[17,18]. 此时, 可使用Navier-Stokes方程(N-S方程)求解流体运动问题[19,20]. 本研究中, 采用计算流体动力学(CFD)方法分析微纳结构表面的水润滑特性时, 提出如下假设: 1)润滑介质为牛顿流体且不可压缩, 黏度恒定, 并忽略体积力的影响; 2)流场内的流体流动为定常流动, 且壁面流体流速与壁面运动速度相同; 3)摩擦副表面无形变, 为绝对刚体理想模型.
在流体润滑状态下, 若仅考虑稳态情况下二维织构化表面流体润滑模型, 其沿x, y方向的 N-S方程展开式如下[21]:
且满足连续方程
上述式中, ρ为润滑介质密度, 本研究中润滑介质为水, 其密度为0.9982 g/cm3. η为水黏度, 其值为0.001
$ \rm kg/(m{\cdot}s)$ , u和v分别为x和y向的流速, p为润滑膜压力.研究表明, 空泡溃灭瞬时将产生局部压力变化, 将导致流场内部阻力与能量等变化[22]. 首先, 空化效应的产生与织构内流体压力变化密切相关. 禄晓敏等[23]通过计算流体动力学方法模拟织构化表面的润滑性能, 发现表面微观结构引起的空化效应使微结构出口处的流场压力大幅增大. 其次, 空化效应的出现在一定程度上改善了流体润滑特性. Mao等[24]建立了变密度的织构表面流体润滑空化模型, 解析了织构内部的润滑特性. 其结果表明, 合理的表面织构引起的空化效应, 会相应的引起流体压力变化, 从而提高润滑膜支撑力, 最终改善流体动力润滑性能. 最后, 在流体动压润滑中, 气相体积变化会对影响流场中流体物理性质. Ma等[25]研究了流体空化等对平行织构表面流体压力的影响, 发现空化效应引起的压力变化会引起空化区域流体密度降低. 因此在流体仿真中空化效应产生压力变化的影响不容忽视. 另一方面, 空化现象导致织构内区域温度变化不明显[26–28].
本研究采用Singhal等[28,29]提出的全空化模型, 该模型考虑到空化过程中的诸多因素, 如气体压缩性、黏性、相变过程、流场压力等. 该空化模型中蒸汽质量分数为传输方程中的独立变量, 其控制方程为
其中, fv为气相质量分数, Γ为扩散系数.
此外, 流体润滑模型中的承载力可以通过对润滑模型的上表面压力进行积分获得, 其公式为
其中, p(x, y)是润滑膜某一截面的压力分布.
润滑膜与上表面之间的摩擦力, 可通过对上表面区域的切应力积分获得, 其计算公式为
其中, Ft是润滑膜与上表面之间摩擦力, 其方向与壁面运动方向相反; τ(x, y)为切应力分布函数.
摩擦系数(μ)为摩擦力与润滑膜承载力之间的比值,
用以评价表面微纳结构的润滑性能.
-
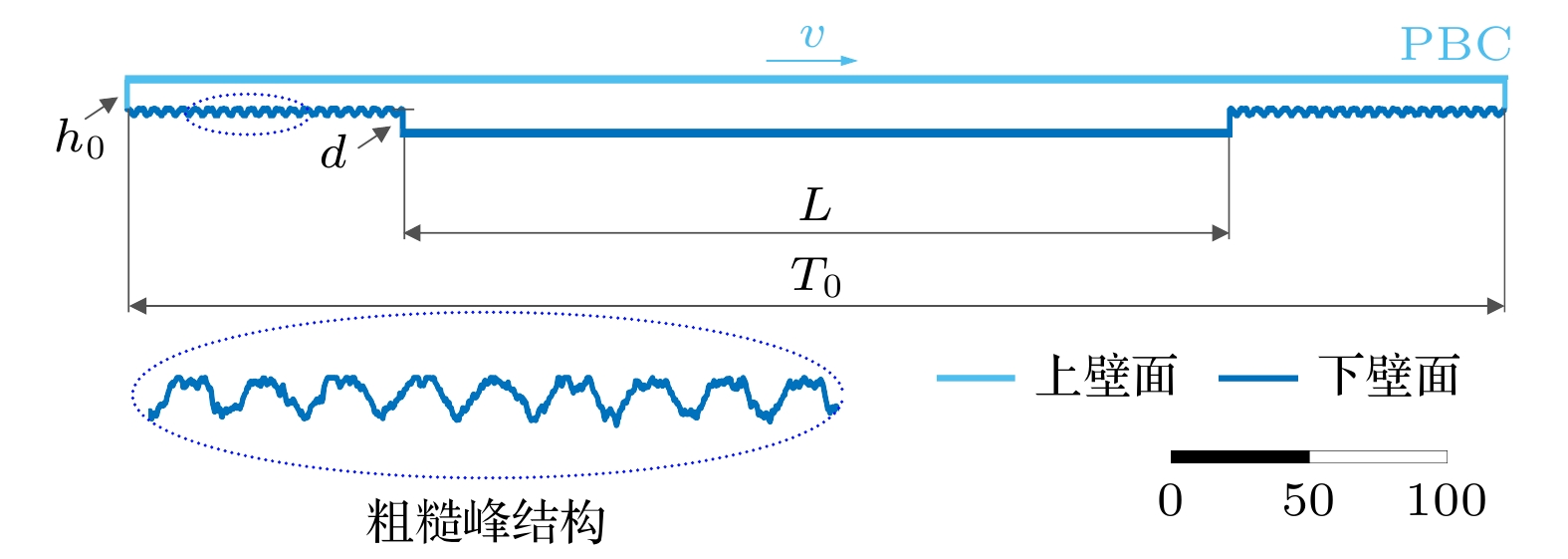
本研究中, 将在矩形微织构表面引入粗糙峰模型, 分析计入粗糙峰的复合结构表面的水润滑特性. 计入粗糙峰的矩形织构润滑模型如图1所示, 下壁面具有微观复合结构. 在有关表面微织构动压润滑特性分析的理论和实验研究中, 润滑模型中的上表面移动速度可达1—12 m/s[30–33]. 模拟过程中, 润滑模型下壁面处于静止, 上表面沿x方向作匀速移动(v = 10 m/s). 润滑模型上表面和下壁面之间为流体润滑膜, 分别在润滑膜的左右边界设置周期性边界条件(PBC), 保证目标边界的场值与物质通量为周期性变化.
如图1模型所示, 其中矩形织构模型单元长度为T0, 织构凹坑长度为L, 织构凹坑深度为d, 油膜厚度为h0. 表面织构润滑理论中几何参数是影响织构动压润滑性能的主要因素, 合理的微织构几何参数可以有效改善摩擦副摩擦学特性, 同时提高织构动压承载能力. 为消除物理量单位对仿真结果影响, 简化变量描述便于理解说明, 将定义构型参数如下:
其中, H为织构深度比, W为织构宽度比.
本研究分别以微织构深度、宽度为变量参数进行模拟仿真, 探究微织构几何参数对润滑特性影响. 因此, 本文将水润滑仿真模型分为模型Ⅰ和Ⅱ, 模型参数如表1所示. 其中, 模型Ⅰ将探讨W值恒定为0.6时, H数值变化对润滑性能的影响; 模型Ⅱ将分析H值恒定为1的情况下, W数值变化对润滑性能的影响.
本研究还将选定织构参数T0 = 500 μm, H = 1.0, W = 0.6的矩形微织构单元为基础, 在其表面引入粗糙峰结构. 通过改变控制函数, 构造三类不同粗糙峰结构模型, 分别为高斯型随机粗糙峰模型(Gauss型)、半正弦函数型峰模型(Sin型), 以及高斯序列和半正弦函数共同控制复合粗糙峰模型(Sin+Gauss型), 其形貌与控制参数如表2所示.
Gauss型表面的生成将采取数字滤波法, 将高斯表面视为一个随机信号, 对其进行滤波即可得到所需表面形貌. 本研究以Matlab中的标准正态函数生成一维高斯白噪声随机序列rδ (如(10)式)为输入序列, 其均值为0, 表面粗糙度高度离散点的标准差为δ. 可以通过(11)式将输入序列转化为最终我们想得到的输出序列(zδ), zδ对应的则是所需的表面起伏轮廓.
其中, r(1, N)为随机生成的一维矩阵; N为总采样数; l(x)为滤波器冲激响应函数.
傅里叶变换是信号处理常用的分析手段, 可将信号或序列从时域转换到频域, 公式为
其中, ω为角频率; F(ω)为f(t)傅里叶变换结果; f(t)代表输入序列; j代表虚数单位; e–jωt为一个指数函数, 表示一个正弦波或余弦波.
对(11)式两侧同时进行傅里叶变换得到
冲激响应函数进行傅里叶变换得到传递函数
$\mathcal{F}[l(x)]$ , 其表达式可由输入、输出信号的功率谱密度函数得出. 功率谱密度是表达信号在不同频率上的能量分布, 其函数表达式为其中, P(ω)是f(t)的功率谱密度, T为信号长度.
输入、输出功率谱密度与传递函数
$\mathcal{F}[l(x)]$ 关系如下:其中,
${P_{{z_\delta }}}(x)$ ,${P_{{r_\delta }}}(x)$ 分别为输出、输入序列的功率谱密度, 计算得到的输入序列的功率谱密度为常数C.由维纳-辛钦定理(Winner-Khitchine)可知, 如果信号可以看作平稳随机过程, 功率谱密度函数就是相关函数的傅里叶变换, 本文选定的自相关函数为
因此可以得到
$\mathcal{F}[l(x)]$ , 表达式为将
$\mathcal{F}[l(x)]$ 代回(13)式就可以得到输出信号的傅里叶变换$ \mathcal{F}[{z_\delta }] $ :对
$ \mathcal{F}[{z_\delta }] $ 进行傅里叶逆变换就可以获得最终的高斯随机粗糙表面高度分布, 表达式为式中, z(x)为高斯随机粗糙表面高度分布序列.
Sin型表面轮廓是由S(x)函数控制, 其表达式为
其中, hs为半正弦深度; i是半正弦单位凹坑间距, 其值恒定为1; l为半正弦凹坑宽度, 其值为3; Til为半正弦结构周期, 且Til = l + 2i; k为半正弦结构周期数, 且其值为整数.
-
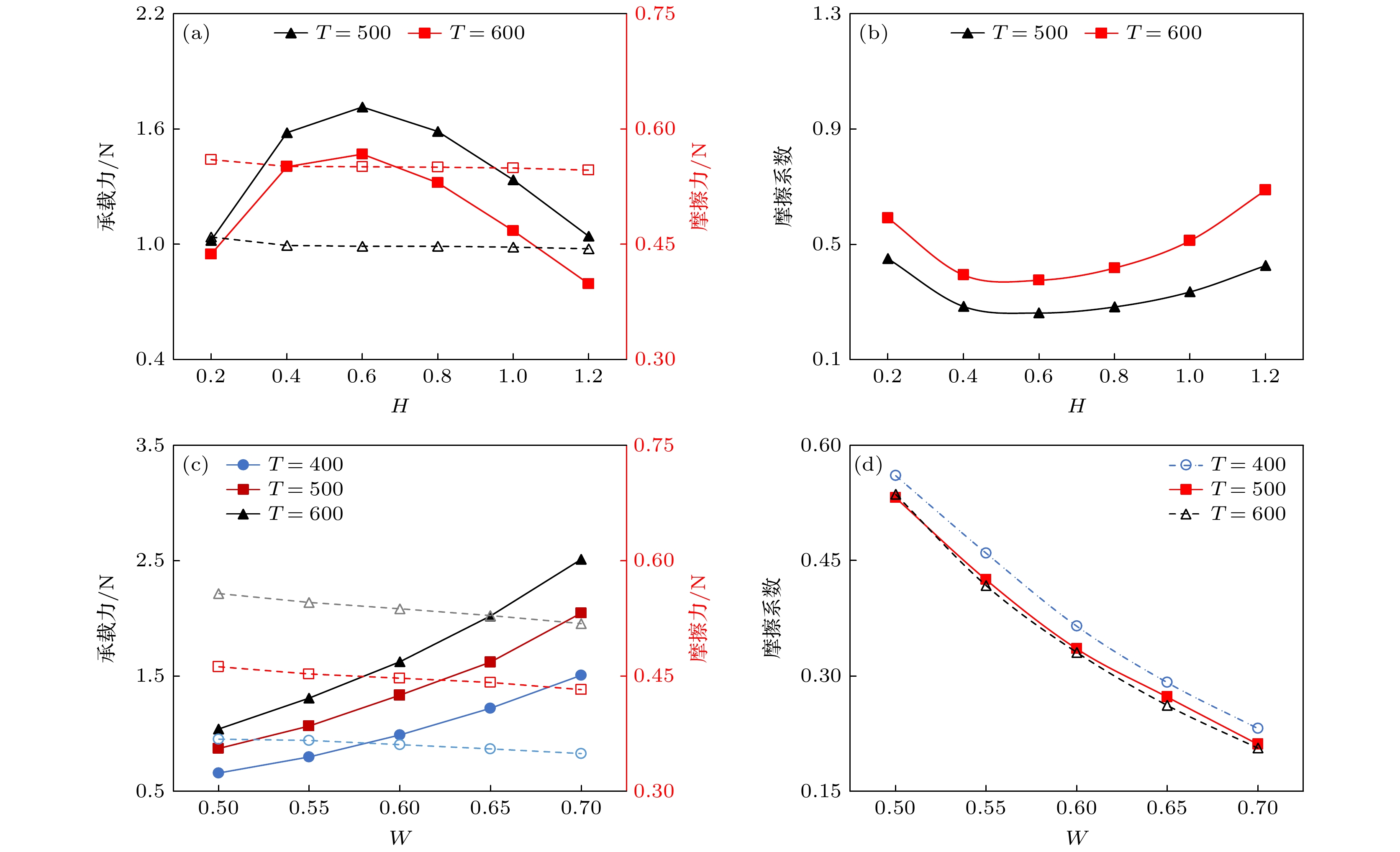
图2为微织构模型Ⅰ和Ⅱ中承载力、摩擦力和摩擦系数的变化曲线. 从微织构模型Ⅰ的仿真结果曲线(图2(a))可以看出, 随矩形微织构深度比H值增大, 承载力先增大后减小, 当H值达到0.6时水膜所提供承载力最大; 然而, H数值变化对摩擦力影响并不明显. 在图2(b)中, 摩擦系数随H值增大呈现先下降后上升, 且在H = 0.6处摩擦系数最小. 在微织构模型Ⅱ中, 当深度比H恒定时, 如图2(c), (d)所示, 随宽度比W增大, 水膜承载力不断上升, 而摩擦力与摩擦系数均呈现下降趋势. 因此, 宽度比W增大, 动压润滑效果越好.
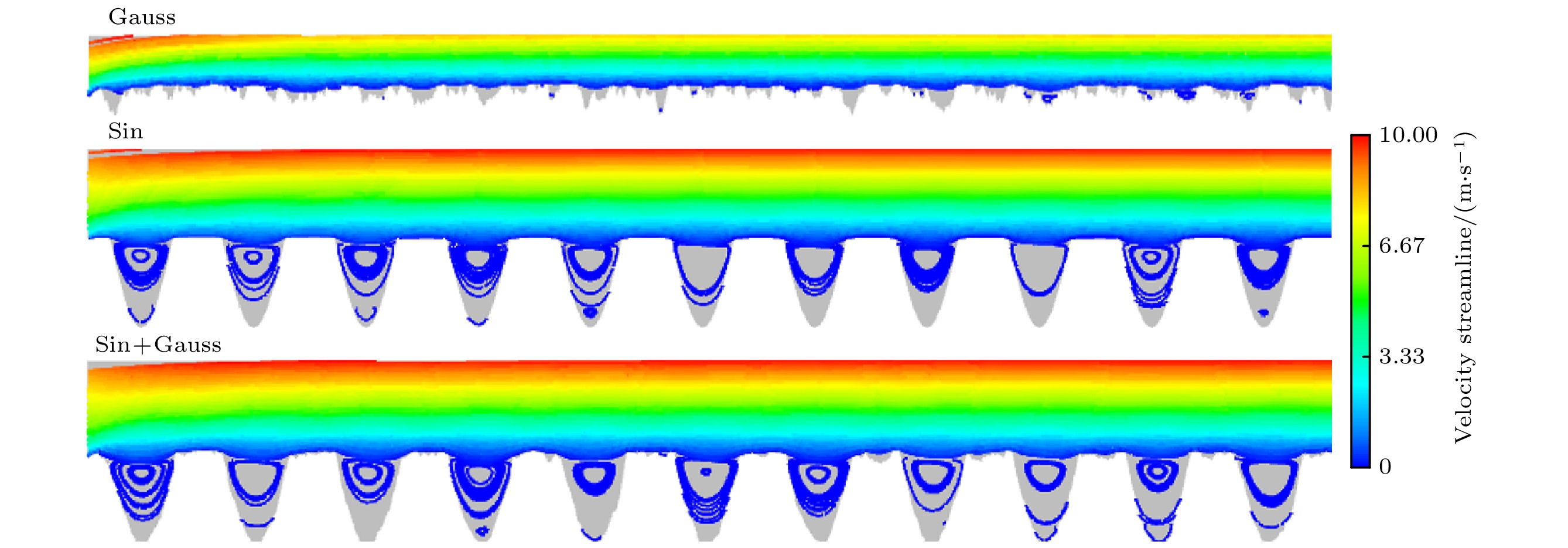
当润滑介质流过发散区时, 润滑介质因流动截面面积变化发生扰动形成涡流, 引起润滑膜能量耗散. 在流体润滑仿真中可通过绘制流场流线分布图, 进而观察流场内涡流情况, 图3(a), (b)为不同微织构模型的流场流线分布图. 由图可知, 在模型Ⅰ中, 当H = 0.2时, 由于微织构凹坑深度较浅, 流场呈现层状分布, 未产生明显的动压润滑效果. 当H值逐渐增大, 发散区流场中形成涡流尺寸也随之增大. 当H达到最大值1.2时, 涡流区域达到最大. 相比而言, 在模型Ⅱ中, 发散区的涡流区域随W值增大而不断减小, 并且涡流在织构空间内占比也逐渐减小. 当W值较小时, 涡流填充织构大部分空间; W值较大时, 涡流仅集中在发散区. 微织构内涡流形成会改变流体流动特性, 也是织构内剪切力变化的原因之一[34]. Shankar和Deshpande[35]研究表明, 这种涡流形成会导致较低的压力梯度和压力, 从而将引起织构内压力分布差异. 流场内压力骤降到压力临界值, 即达到润滑介质在当前温度开始汽化的压力以下时, 会使润滑介质中气体析出生成气泡, 产生空化现象[36–38]. 随着润滑介质流向压力较高区域, 析出的气体将溶解, 导致润滑膜承载力得到提升. 涡流产生也会使流场内能量发生耗散, 耗散量与涡流尺寸成正比. 场内能量耗散较大时, 织构模型承载力提升效果将被削弱. 在模型Ⅰ中, 当H值达到1.2时, 织构模型内充满涡流, 大面积涡流导致织构模型流场能量耗散, 导致动压润滑效果不明显. 对比之下, 在模型Ⅱ中, 涡流尺寸逐渐缩小, 能量耗散量减少, 气体溶解或气泡溃灭所产生承载力得到提升, 最终使承载力明显提升, 动压润滑效果明显增大.
流场内涡量变化将影响织构内流体剪切力, 对上表面剪切力积分后可得到润滑模型上表面的摩擦力. 因此, 上表面涡量变化也将反映出摩擦力变化. 图4(a), (b)为微织构润滑模型Ⅰ和Ⅱ中上表面涡量分布云图, 可以看出, 随H和W逐渐增大, 两组模型上表面涡量均出现减少现象, 相应地, 上表面摩擦力也随之减小.
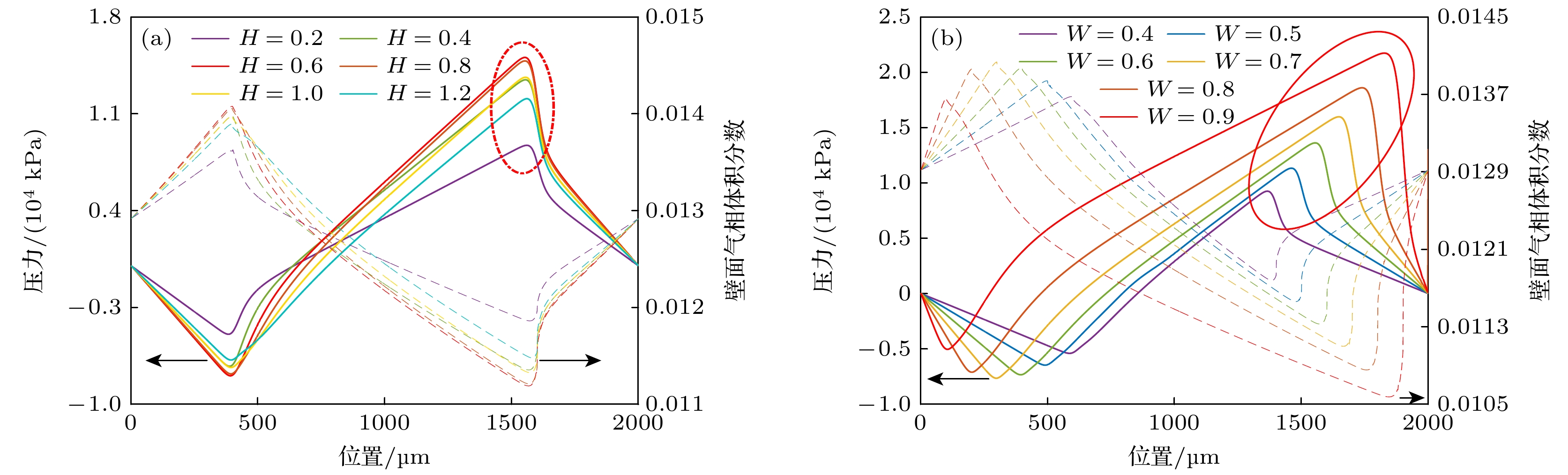
润滑介质中气体析出与溶解将导致流场内部气相体积分数变化, 为进一步验证微织构润滑模型上表面压力提升与织构内气体析出之间关系, 将上述润滑模型中的上表面压力曲线与织构气相体积分数曲线联合分析, 其结果如图5所示. 由图可知, 流场中气相体积分数曲线的峰值恰好对应润滑模型的上表面压力曲线最低点, 而气相体积分数曲线的最小值对应上表面正压力峰值, 即流体流经织构发散区域时, 压力下降导致润滑介质中气体析出, 气体析出最多时上表面压力会迅速减小至负压. 随着润滑介质流向收敛区域, 模型内的压力上升使得流场内气体受压溶解, 气相体积分数降低, 最终上表面压力逐渐上升为正值并达到峰值. 不仅如此, 如图5(a)中红色虚线所示, 随H值增大, 润滑模型的上表面压力峰值呈现先增大后减小的趋势, 并在H = 0.6时呈现最大压力峰值. 在图5(b)中, 随W值增大, 上表面压力峰值也随之增大. 这与润滑模型中上表面的承载力变化规律(图2(a), (c))相同.
采用表面微织构加工技术制备图案化表面时, 合理的织构几何参数可有效提升动压润滑效果. 刘天霞等[39]在对微织构形貌进行优化改进时发现, 深度参数对平均摩擦系数影响显著. 此外, Babu等[40]与Wos等[41]均发现, 随织构化表面微织构深度增大, 摩擦系数呈现先下降后上升的变化趋势, 且存在一个最优值使其润滑性能达到最优. Wang等[42]通过摩擦实验研究了摩擦副表面织构引起的空化效应对摩擦副润滑特性的影响, 其实验结果也表明, 当凹坑深度较小时, 流过凹坑的润滑介质界面较小, 动压效果不明显; 而深度过深时, 动压效应则同样较弱. 此外, Venkateswara等[43]则对不同高度的方形织构进行摩擦实验, 其结果表明, 当织构深度为25 μm时, 摩擦系数最低. 本文即通过分析不同深度比与宽度比的矩形织构模型在动压润滑模拟中的模拟结果, 发现织构深度比与宽度比均影响动压润滑效果. 当深度比为0.6时, 摩擦系数达到最低; 此外, 本研究还发现, 随宽度比增大, 动压效果越明显.
-
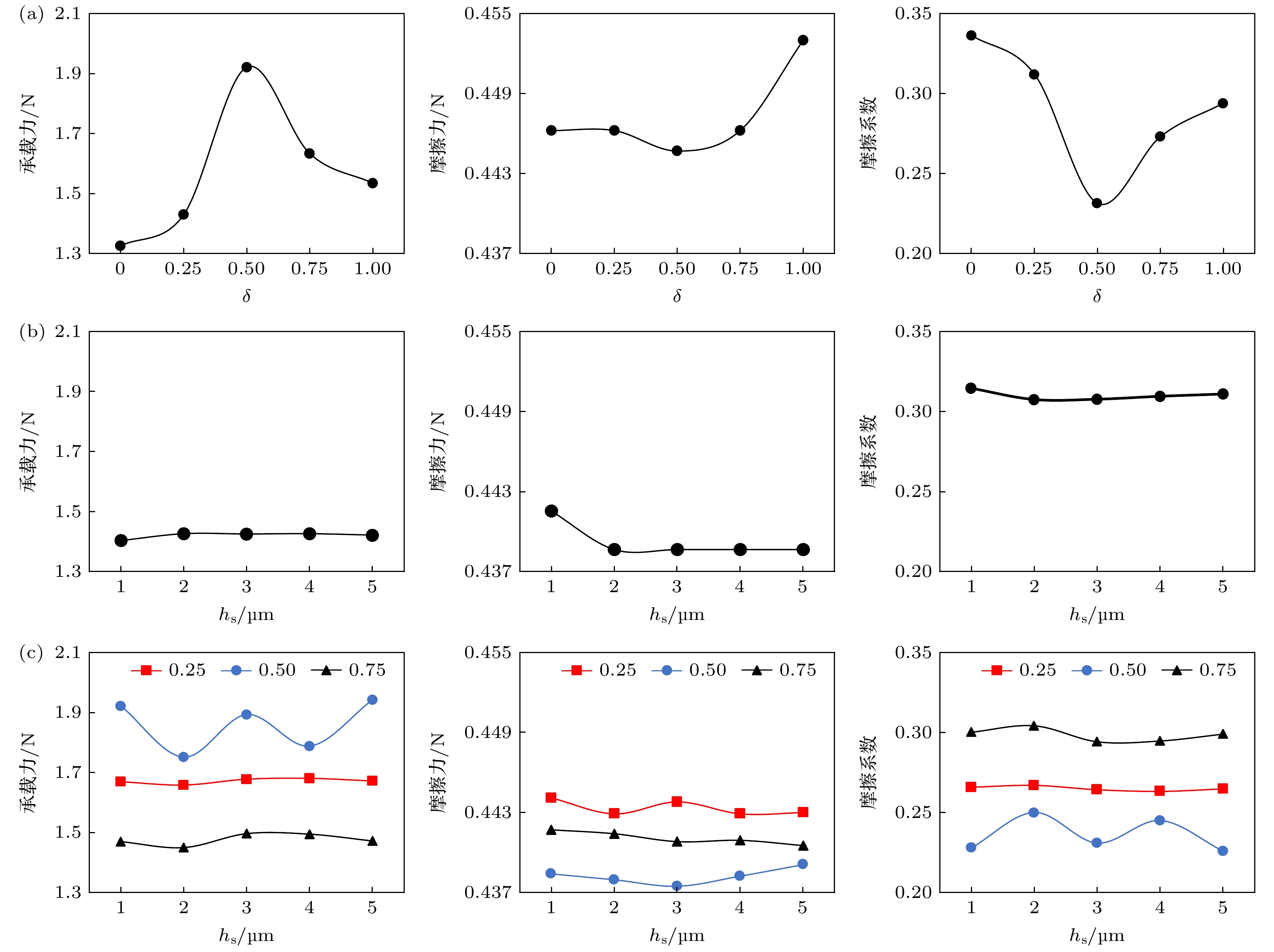
本文将对Gauss, Sin, Sin+Gauss三组不同粗糙峰结构织构润滑模型仿真结果进行对比分析, 为了更好地模拟探究实际表面应用中粗糙峰对动压润滑效果影响. 图6(a)为Gauss模型组润滑特性仿真结果曲线, 如图所示, 当δ<0.5时, 润滑模型的承载力随δ数值增大呈现大幅上升趋势, 并在δ = 0.5处承载力数值达到峰值; 之后, 随δ值再增大, 承载力则逐渐下降. 在摩擦力曲线中, 随δ增大, 摩擦力呈先小幅减小后小幅增大的趋势. 从润滑特性角度考虑, Gauss模型中, 当δ = 0.5时, 润滑模型的摩擦力最小, 承载力最大, 故摩擦系数最小. Sin模型的仿真结果如图6(b)所示, 从图中可以明显地看出, hs数值变化对承载力和摩擦系数影响均不明显. 在摩擦力曲线中, hs值从1增大到2时, 摩擦力呈小幅下降; hs值进一步增大, 摩擦力则基本不变. 因此, Sin模型的润滑特性随粗糙峰参数变化较小. 不仅如此, 此处还对Gauss型粗糙峰和Sin型粗糙峰进行叠加, 得到Sin+Gauss复合表面的润滑模型, 探究多种粗糙峰耦合现象对织构模型润滑特性影响规律. 图6(c)为润滑模型中Gauss型粗糙峰结构参数(δ = 0.25, 0.5, 0.75)和Sin型粗糙峰结构参数(hs)同时变化时的润滑特性结果. 当hs值相同时, 润滑模型所产生的承载力在δ = 0.5时最大, 且此时相应的摩擦力和摩擦系数最小. 若δ值不变, 改变hs值对润滑特性的影响不明显; 但在δ=0.5时, 随hs值增大, 润滑特性则呈现小幅波动现象. 从承载力数值也可以得出, 引入Gauss型粗糙峰后, 承载力最大可提升44%; 引入Sin+Gauss复合型粗糙峰后, 承载力最大可提升42%; 然而, 仅在下壁面引入Sin型粗糙峰时, 承载力变动范围均小于10%, 远低于其他两组模型.
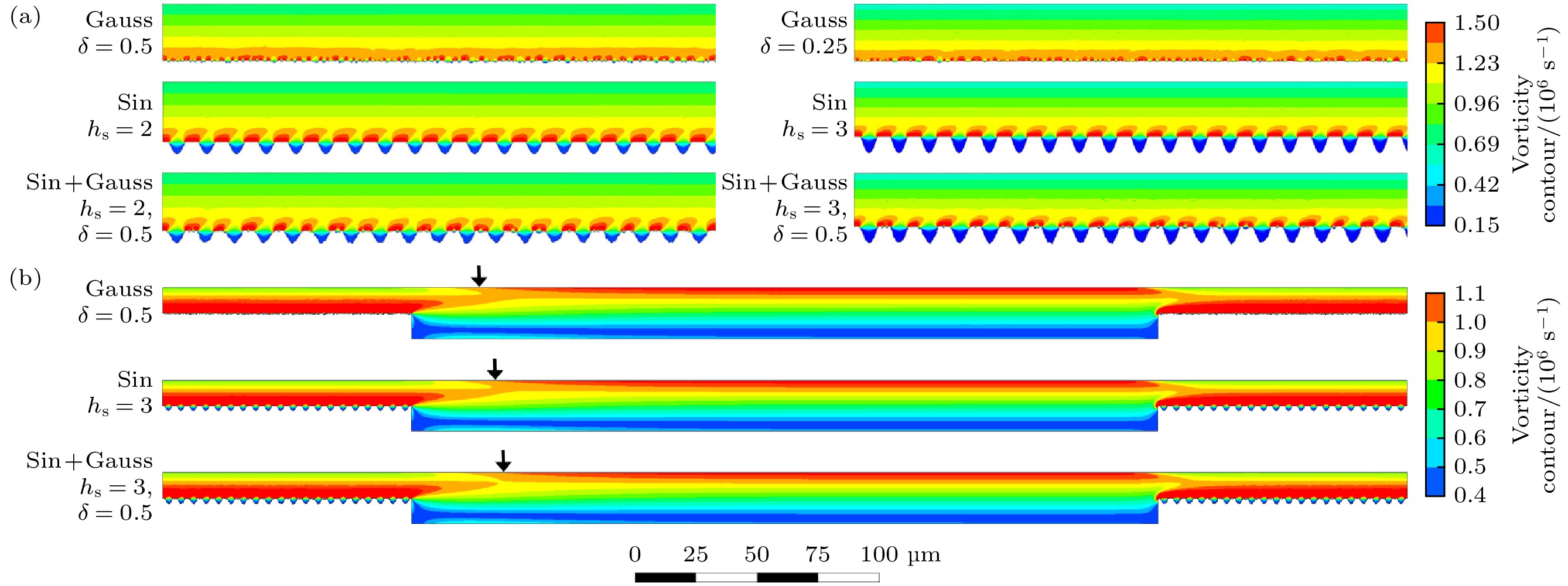
与光滑表面相比(图6(a)中δ = 0), 引入粗糙峰结构后, 上述所有复合微纳织构润滑模型的承载力和摩擦系数均得到改善, 但不同模型组提升效果存在明显差异. 为分析不同粗糙峰下的润滑特性的差异, 图7给出了引入不同粗糙峰结构时的流场流线分布图. 当润滑介质流过不同粗糙峰结构表面纹理时, 润滑介质会在表面微凹坑中产生一定程度扰动生成不同尺寸涡流. 如图7所示, 可明显观察到Sin模型组产生的涡流总尺寸最大, 即能量耗散最高, 承载力提升效果被削弱. 此外这些涡流的存在会对织构内气相体积与压力产生影响.
图8为计入不同粗糙峰的润滑模型中的涡量云图. 在图8(a)中, 引入Gauss型粗糙峰后, 润滑模型下壁面的微凹坑内产生不均匀的涡量分布, 数量较多且连续成片, 总涡量值较大; 而改变δ值时, 模型涡量变化较小. 在Sin模型中, 下壁面涡量的分布与半正弦结构有关, 且呈规律性分布; 单个凹坑产生涡量值较大, 但呈间隔分布. 在Sin+Gauss模型中, 尽管涡量分布与Sin模型组结果类似, 但引入Gauss型粗糙峰结构后, 削减了单个凹坑产生涡量值大小, 从而改变了涡量规律性分布的现象, 使总涡量值减少. 此外, 由于润滑模型中, 下壁面涡量差异会逐步影响到模型上表面涡量分布, 造成能量耗散. 因此, 对比各模型的上表面涡量变化, 其结果如图8(b)所示. 结合图8(a), 由于Gauss模型中下壁面涡量分布连续, 且总涡量较大, 因而导致上表面涡量大量堆积. 在Sin模型中, 尽管下壁面单个半正弦凹坑周围的涡量较大, 但由于其分布不连续, 因而上表面总涡量的分布强度略小于Gauss模型, 如图8(b)图中箭头位置差异所示. 最后, 在Sin+Gauss模型中, 由于随机Gauss粗糙峰扰乱了原Sin模型中的下壁面规律性分布的涡量, 因而进一步削弱了下壁面涡量对上表面涡量的影响, 使其上表面总涡量分布强度减小. 这也导致Sin+Gauss模型模型中, 摩擦力较小, 这与图6(c)中摩擦力变化规律相同.
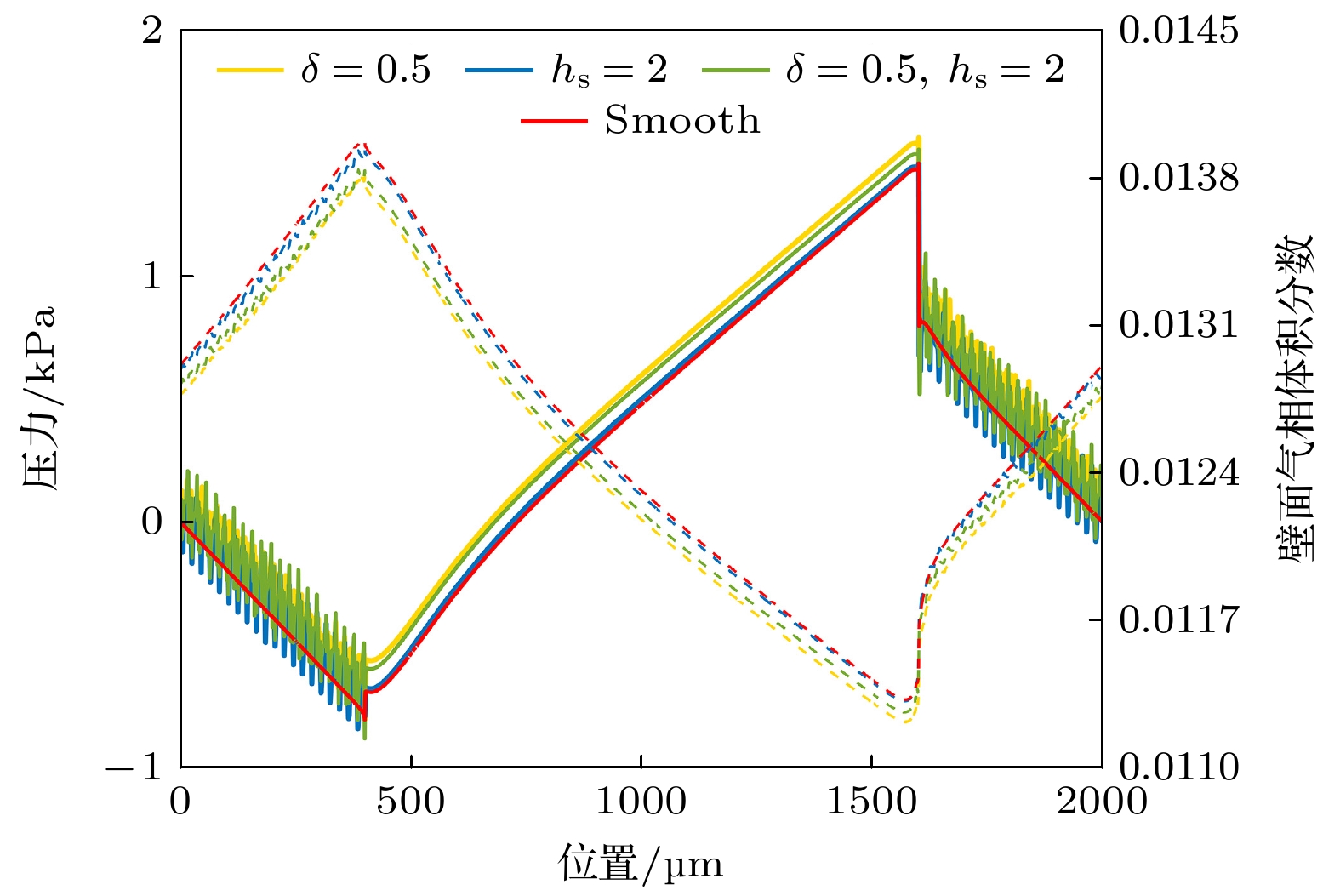
图9给出了计入粗糙峰后润滑模型中的上表面压力和气相体积分数图. 由图可知, 相较于Smooth模型, Gauss模型和Sin+Gauss模型中的上表面气相体积分数曲线分布整体下移, 而两种模型中上表面压力均有明显抬升, 而Sin模型则无此变化. 由此可知, 在润滑模型中引入适当的Gauss型粗糙峰后, 可使上表面压力得到提升, 即承载力增大, 动压润滑效果增强.
研究表明, 在润滑界面引入粗糙度, 对润滑膜压力分布与剪切力有着显著影响[44,45], 且与空化效应和涡流现象有直接关系. Jiang等[46]认为空化气穴的出现是微织构润滑中润滑膜承载能力提升的主要原因. 另一方面, 流场中涡流的存在会导致能量耗散, 最终降低动压轴承承载力, 且耗散程度与涡区大小相关[22]. Wang等[47]采用CFD模拟从微流动角度分析径向轴承织构纹理中的局部润滑机制, 结果表明, 织构的微流体动力压力产生的原因之一是压力降(空化气蚀)引起; 并且在摩擦方面, 织构中漩涡产生的最大剪切力影响摩擦力. 此外, 对于引入粗糙度改善润滑特性的实验表明, 粗糙度会对摩擦系数、等参数产生影响. Huang等 [48]制备了不同表面粗糙度的铅黄铜并研究其在干摩擦条件下的摩擦学行为, 实验结果表明, 摩擦系数最大降低率可达13.28%. 在织构中引入不同粗糙峰后, 在粗糙坑中发生空化效应, 从而提升润滑膜承载力; 与此同时, 粗糙坑中涡流的改变流体流动特性, 影响织构内流体剪切力, 进一步影响了摩擦力的变化.
本研究中, 通过分析在织构表面引入不同结构的粗糙峰结构, 在流体动压润滑模拟中发现织构表面粗糙峰的存在将提升承载力, 降低摩擦系数, 改善润滑特性. 但相比较而言, 不同粗糙峰结构改善润滑特性能力不同, 其中, 当引入高斯随机粗糙峰(Gauss模型)或高斯随机与半正弦的叠加粗糙峰(Sin+Gauss模型)时, 可改善动压润滑特性; 而引入半正弦粗糙峰时(Sin模型), 动压润滑效果变化不明显.
-
借助流体动力学仿真模拟方法, 本文研究了水润滑条件下微织构表面的动压润滑形成机理以及织构参数变化对润滑特性影响规律, 并探讨了计入不同粗糙峰结构的润滑模型对其润滑特性影响规律.
1) 水润滑条件下润滑模型的润滑特性受到微织构几何参数影响, 对矩形织构模型, 适当的深度比(H = 0.6)可使其表面动压润滑效应达到最优; 而增大织构宽度比(W ), 动压润滑效应增强.
2) 在微织构表面引入高斯随机粗糙峰后(Gauss模型), 当随机粗糙峰高度变化标准差δ为0.5时, 承载力可提升44%, 摩擦系数降低30.9%. 当微织构表面引入半正弦粗糙峰时(Sin模型), 随粗糙峰结构参数变化, 承载力和摩擦系数的变化幅度在10%以内, 对润滑效果的影响不明显. 若同时引入高斯随机粗糙峰和半正弦粗糙峰(Sin+Gauss模型), 承载力可提升42%, 摩擦系数下降31.1%, 即表面动压润滑效果提升也较为显著.
3) 微纳复合织构表面的润滑特性与润滑模型中上表面气相体积分数和涡量的分布密切相关. 在微织构表面或同时引入粗糙峰的情况下, 微凹坑内会产生涡流将影响涡量分布, 造成能量耗散并最终改变摩擦力. 在润滑模型中引入适当的Gauss型粗糙峰后, 可使上表面压力得到提升, 即承载力增大, 动压润滑效果增强.
计入粗糙峰的微纳结构表面水润滑流体动力学仿真
Fluid dynamics simulation on water lubricating performance of micro-/nano-textured surfaces considering roughness structures
-
摘要: 随着表面精密加工技术与润滑减摩研究的发展, 利用表面织构化技术提升其表面减摩效果的研究已引起广泛关注, 但少有研究考虑摩擦副表面粗糙形貌对润滑特性带来影响. 本研究采用计算流体动力学(CFD)模拟方法, 建立了矩形织构模型, 并在其表面计入粗糙峰结构, 讨论水润滑条件下不同粗糙峰结构模型润滑特性变化规律. 结果表明: 调节微纳复合表面结构参数, 将改变润滑水膜承载力, 进而影响微纳复合结构表面的动压润滑效果. 此外, 织构内涡流生成导致涡量变化, 引起能量耗散并影响摩擦力. 对矩形织构模型, 适当的深度比(H = 0.6)可使其表面动压润滑效应达到最优; 而增大织构宽度比(W), 动压润滑效应增强. 在微织构表面引入高斯随机粗糙峰后, 当随机粗糙峰高度变化标准差δ为0.5时, 承载力可提升44%, 摩擦系数降低30.9%. 若引入半正弦粗糙峰, 承载力和摩擦系数的变化范围均小于10%, 对润滑效果的影响不明显. 若同时引入高斯随机粗糙峰和半正弦粗糙峰, 承载力可提升42%, 摩擦系数下降31.1%, 即表面动压润滑效果提升也较为显著.Abstract: With the development of surface precision machining technology and extensive studies on lubrication and friction reduction, the use of surface texture to reduce friction has attracted widespread attention, but few studies have considered the influence of surface roughness on lubrication characteristics. By employing the computational fluid dynamics (CFD) simulation method, the lubrication models with rectangular textures and the introduction of rough asperity structures at the same time are established. The effects of the corresponding structure parameters on the lubrication performance of textured and roughed surfaces are studied under water lubrication conditions. Our results suggest that the adjustment of geometric parameters on the micro-/nano-structured surfaces can influence the load-bearing capacity of the water lubrication film, thus affecting the hydrodynamic lubrication performance on the surface. In addition, the generation of vortex in the micro-textures can bring changes in vorticity, which causes energy dissipation and affects frictional forces. In the lubrication model with rectangular textures, optimal hydrodynamic lubrication performance is obtained under the appropriate depth ratio H = 0.6. Meanwhile, the corresponding lubrication performance can be enhanced by increasing the width ratio (W) of surface texture. After introducing random asperity structures on the micro-textured surface with a standard deviation δ = 0.5, the bearing capacity is increased by 44%, and the friction coefficient is reduced by 30.9%. Moreover, the introduction of half-sine rough asperity structures can only result in relatively minor differences in the lubrication performance, i.e. the changes of bearing capacity and friction coefficient are less than 10%. However, the introduction of compound hierarchical structure consisting of random asperity structures and half-sine rough asperity structures can result in an increase in the corresponding bearing capacity by 42% and a reduction in the friction coefficient by 31.1%, which implies a significant enhancement in the hydrodynamic lubrication performance.
-
Key words:
- micro-texture /
- roughness /
- hydrodynamic lubrication /
- computational fluid dynamics simulation .
-
-
图 1 计入粗糙峰的矩形微观复合织构的润滑模型
Figure 1. The lubrication model of textured surfaces consisting of rectangular grooves and rough peaks.
图 2 润滑模型Ⅰ和Ⅱ的润滑特性 (a) 模型Ⅰ的承载力与摩擦力; (b) 模型Ⅰ的摩擦系数; (c) 模型Ⅱ的承载力与摩擦力; (d) 模型Ⅱ的摩擦系数
Figure 2. The lubrication performance in models I and II: (a) Bearing capacity and friction force in model I; (b) frictional coefficient in model I; (c) bearing capacity and friction force in model II; (d) frictional coefficient in model II.
图 3 润滑模型Ⅰ和Ⅱ中流场流线分布图 (a) 模型Ⅰ; (b) 模型Ⅱ
Figure 3. Distribution of streamlines in models I and II: (a) Model I; (b) Model II.
图 4 润滑模型Ⅰ和Ⅱ中的上表面涡量云图 (a) 模型Ⅰ; (b) 模型Ⅱ
Figure 4. Distribution of vorticity in models I and II: (a) Model I; (b) Model II.
图 5 润滑模型Ⅰ和Ⅱ中的上表面压力和空化气相分布图 (a) 模型Ⅰ; (b) 模型Ⅱ
Figure 5. Distribution of pressure and gas volume fraction on the upper surfaces of models I and II: (a) Model I; (b) Model II.
图 6 计入不同粗糙峰结构的润滑模型的润滑特性 (a) Gauss模型中承载力、摩擦力与摩擦系数; (b) Sin模型中承载力、摩擦力与摩擦系数; (c) Sin+Gauss模型中承载力、摩擦力与摩擦系数
Figure 6. The lubrication performance on the textured models with rough peaks: (a) The bearing capacity, frictional force and frictional coefficient in the Gauss model; (b) the bearing capacity, frictional force and frictional coefficient in the Sin model; (c) the bearing capacity, frictional force and frictional coefficient in the Sin+Gauss model.
图 7 不同粗糙峰结构模型组流场流线分布图
Figure 7. Distribution of streamlines in the lubrication models with rough peaks.
图 8 不同粗糙峰结构模型组上、下壁面涡量云图 (a)下壁面涡量云图; (b)上表面涡量云图
Figure 8. Distribution of vorticity on the surfaces of lubrication models with rough peaks: (a) Distribution of vorticity on the lower wall surfaces; (b) distribution of vorticity on the upper wall surfaces.
图 9 不同粗糙峰结构模型组上表面压力和气相体积分数图
Figure 9. Distribution of pressure and gas volume fraction on the upper wall surface of lubrication models with rough peaks.
表 1 水润滑微织构模型参数变化
Table 1. The geometrical parameters for textured models.
模型 T0 W H 模型Ⅰ (恒定宽度比W ) 500/600 0.60 0.2/ 0.4/ 0.6/ 0.8 /1.0/ 1.2 模型Ⅱ (恒定深度比H ) 400/500/600 0.50/ 0.55/ 0.60 /0.65/ 0.70 1.0 
下载: 导出CSV
表 2 润滑模型中的下壁面微观形貌示意图
Table 2. Sketch maps of textures on the lower wall surfaces of the lubrication models.
模型名称 微织构表面粗糙峰轮廓 函数变化参数 光滑表面
(Smooth)
δ = 0
hs = 0Gauss 
δ = 0.25/0.5/0.75/1
hs = 0Sin 
δ = 0
hs = 1/2/3/4/5
l = 3
i = 1Sin+Gauss 
δ = 0.25/0.5/0.75/1
hs = 1/2/3/4/5
l = 3
i = 3
下载: 导出CSV
-
[1] Hamilton D B, Walowit J A, Allen C M 1966 J. Fluids Eng. 88 177 [2] Zhong Y H, Zheng L, Gao Y H, Liu Z N 2019 Tribol. Int. 129 151 doi: 10.1016/j.triboint.2018.08.010 [3] Mourier L, Mazuyer D, Ninove F P, Lubrecht A A 2010 Proc. Inst. Mech. Eng. , Part J: J. Eng. Tribol. 224 697. doi: 10.1243/13506501JET771 [4] Zhang J Y, Meng Y G 2012 Tribol. Lett. 46 147 doi: 10.1007/s11249-012-9935-6 [5] Gropper D, Wang L, Harvey T J 2016 Tribol. Int. 94 509 doi: 10.1016/j.triboint.2015.10.009 [6] Braun D, Greiner C, Schneider J, Gumbsch P 2014 Tribol. Int. 77 142 doi: 10.1016/j.triboint.2014.04.012 [7] Hsu S M, Jing Y, Hua D, Zhang H 2014 J. Phys. D: Appl. Phys. 47 335307 doi: 10.1088/0022-3727/47/33/335307 [8] 安书董, 王晓燕, 陈仙, 王炎武, 王晓波, 赵玉清 2015 物理学报 64 036801 doi: 10.7498/aps.64.036801 An S D, Wang X Y, Chen X, Wang Y W, Wang X B, Zhao Y Q 2015 Acta Phys. Sin. 64 036801 doi: 10.7498/aps.64.036801 [9] Rosenkranz A, Szurdak A, Gachot C, Hirt G, Mücklich F 2016 Tribol. Int. 95 290. doi: 10.1016/j.triboint.2015.11.035 [10] 纪敬虎, 管采薇, 符昊, 华希俊, 符永宏 2018 润滑与密封 43 20 doi: 10.3969/j.issn.0254-0150.2018.01.005 Ji J H, Guan C W, Fu H, Hua X J, Fu Y H 2018 Lubr. Eng. 43 20 doi: 10.3969/j.issn.0254-0150.2018.01.005 [11] Qiu Y, Khonsari M M 2011 J. Tribol. 133 021704 doi: 10.1115/1.4003303 [12] Lahayne O, Pichler B, Reihsner R, Eberhardsteiner J, Suh J, Kim D, Nam S, Paek H, Lorenz B, Persson B N J 2016 Tribol. Lett. 62 17 doi: 10.1007/s11249-016-0665-z [13] Feng D, Shen M X, Peng X D, Meng X K 2017 Tribol. Lett. 65 1 doi: 10.1007/s11249-016-0787-3 [14] Sedlaček M, Podgornik B, Vižintin J 2009 Wear 266 482 doi: 10.1016/j.wear.2008.04.017 [15] Menezes P L, Kishore, Kailas S V, Lovell M R 2011 Tribol. Lett. 41 1 doi: 10.1007/s11249-010-9676-3 [16] Rasp W, Wichern C M 2002 J. Mater. Process. Technol. 125 379 [17] 王悦昶, 刘莹, 黄伟峰, 郭飞, 王玉明 2016 摩擦学学报 36 520 Wang Y C, Liu Y, Huang W F, Guo F, Wang Y M 2016 Tribology 36 520 [18] Rosenkranz A, Costa H L, Profito F, Gachot C, Medina S, Dini D 2019 Tribol. Int. 134 190 doi: 10.1016/j.triboint.2019.01.042 [19] Brajdic-Mitidieri P, Gosman A D, Ioannides E, Spikes H A 2005 J. Tribol. 127 803 doi: 10.1115/1.2032990 [20] Sahlin F, Glavatskih S B, Almqvist T, Larsson R 2005 J. Tribol. 127 96 doi: 10.1115/1.1828067 [21] Vilhena L, Sedlaček M, Podgornik B, Rek Z, Žun I 2018 Lubricants 6 15 doi: 10.3390/lubricants6010015 [22] Zhang L, Luo J, Yuan R B, He M 2012 Procedia Eng. 31 220 doi: 10.1016/j.proeng.2012.01.1015 [23] 禄晓敏, 王权岱, 肖继明, 杨振朝 2016 润滑与密封 41 70 doi: 10.3969/j.issn.0254-0150.2016.01.013 Lu X M, Wang Q D, Xiao J M, Yang Z C 2016 Lubr. Eng. 41 70 doi: 10.3969/j.issn.0254-0150.2016.01.013 [24] Mao Y, Zeng L C, Lu Y 2016 Tribol. Int. 104 212 doi: 10.1016/j.triboint.2016.09.002 [25] Ma X 2023 Lubricants 11 270 doi: 10.3390/lubricants11070270 [26] Li Q, Zhang S, Wang Y J, Xu W W, Wang Z B 2019 Ind. Lubr. Tribol. 71 109 doi: 10.1108/ILT-03-2018-0113 [27] He T, Li J M, Deng H S, Wang C L, Shi R, Chen G Y, Li Z P 2021 AIP Adv. 11 015222 doi: 10.1063/5.0025507 [28] Singhal A K, Athavale M M, Li H, Jiang Y 2002 ASME J. Fluids Eng. 124 617 doi: 10.1115/1.1486223 [29] Pellone C, Franc J P, Perrin M 2004 C. R. Math. 332 827 [30] Buscaglia G C, El Alaoui Talibi M, Jai M 2015 Math. Comput. Simul 118 130 doi: 10.1016/j.matcom.2014.11.026 [31] Wei Y, Tomkowski R, Archenti A 2020 Metals 10 361 doi: 10.3390/met10030361 [32] Wang W, He Y Y, Li Y, Wei B, Hu Y T, Luo J B 2018 Ind. Lubr. Tribol. 70 754 doi: 10.1108/ILT-08-2017-0224 [33] Gao G Y, Yin Z W, Jiang D, Zhang X L 2014 Tribol. Int. 75 31 doi: 10.1016/j.triboint.2014.03.009 [34] Podgornik B, Vilhena L M, Sedlaček M, Rek Z, Žun I 2012 Meccanica 47 1613 doi: 10.1007/s11012-012-9540-7 [35] Shankar P N, Deshpande M D 2000 Annu. Rev. Fluid Mech. 32 93 doi: 10.1146/annurev.fluid.32.1.93 [36] Sahlin F, Almqvist A, Larsson R, Glavatskih S 2007 Tribol. Int. 40 1294 doi: 10.1016/j.triboint.2007.02.009 [37] Ausas R, Ragot P, Leiva J, Jai M, Bayada G, Buscaglia G C 2007 J. Tribol. 129 868 doi: 10.1115/1.2768088 [38] Wahl R, Schneider J, Gumbsch P 2012 Tribol. Int. 55 81. doi: 10.1016/j.triboint.2012.05.014 [39] 刘天霞, 李靖, 卢星, 江志波 2023 润滑与密封 48 74 doi: 10.3969/j.issn.0254-0150.2023.05.011 Liu T X, Li J, Lu X, Jiang Z B 2023 Lubr. Eng. 48 74 doi: 10.3969/j.issn.0254-0150.2023.05.011 [40] Babu P V, Ismail S, Ben B S 2021 Proc. Inst. Mech. Eng. , Part J: J. Eng. Tribol. 235 360 doi: 10.1177/1350650120930911 [41] Wos S, Koszela W, Pawlus P 2020 Tribol. Int. 146 106205. doi: 10.1016/j.triboint.2020.106205 [42] Wang J H, Yan Z J, Fang X, Shen Z Y, Pan X X 2020 Lubr. Sci. 32 404 doi: 10.1002/ls.1520 [43] Venkateswara Babu P, Syed I, Benbeera S 2020 Mater. Today Proc. 24 1112 doi: 10.1016/j.matpr.2020.04.424 [44] 樊智敏, 马瑞磷, 江峰 2021 润滑与密封 46 44 doi: 10.3969/j.issn.0254-0150.2021.02.007 Fan Z M, Ma R L, Jiang F 2021 Lubr. Eng. 46 44 doi: 10.3969/j.issn.0254-0150.2021.02.007 [45] 纪敬虎, 周加鹏, 王沫阳, 王伟, 符永宏 2019 表面技术 48 139 Ji J H, Zhou J P, Wang M Y, Wang W, Fu Y H 2019 Surf. Technol. 48 139 [46] Jiang Y Y, Yan Z J, Zhang S W, Shen Z Y, Sun H C 2022 Sci. Rep. 12 13455 doi: 10.1038/s41598-022-17258-0 [47] Wang Y, Jacobs G, König F, Zhang S, von Goeldel S 2023 Lubricants 11 20 doi: 10.3390/lubricants11010020 [48] Huang J Y, Guan Y C, Ramakrishna S 2021 Tribol. Int. 162 107115 doi: 10.1016/j.triboint.2021.107115 -
计量
- 文章访问数: 90
- HTML全文浏览数: 90
- PDF下载数: 1
- 施引文献: 0