首页
登录
注册
-
随着量子计算机及量子算法的迅速发展, 经典密码体制的安全性将面临巨大挑战[1,2]. 量子密钥分发(quantum key distribution, QKD)[3,4]不依赖于任何计算复杂性的假设, 可以为用户提供无条件安全的密钥, 确保机密信息的安全传输, 并能有效抵御量子计算机的攻击. 然而, 目前QKD物理层和网络层相关技术均处在发展阶段, 其广泛部署和应用仍然面临挑战.
自1984年第一个QKD协议, 即BB84 (Bennett-Brassard-1984)协议[5]提出以来, 各种具有不同特性的QKD协议被相继提出. 不同的QKD协议会表现出不同的性能. 例如, 测量设备无关(measurement-device-independent, MDI)协议消除了探测端漏洞, 具有更高的现实安全性[6]; BB84协议成熟度较高, 可以实现较高的密钥生成率[7]. 随着QKD系统的不断发展, 新型量子网络不断涌现[8], 越来越多的量子网络开始在城域范围内部署应用[9], 如基于MDI协议的合肥城域量子网络(2016年)[10]; 基于BB84协议的布里斯托尔量子网络(2020年)[11]; 基于BB84协议的帕多瓦量子网络(2023年)[12]. 上述工作验证了基于不同QKD协议构建城域量子网络的可行性. 由于不同的QKD协议具有不同的特征与适用场景, 大规模量子网络可能由依赖不同QKD协议实现的多个城域组成, 这样的量子网络也被称为多域量子网络.
近年来, 基于不同QKD协议的大规模量子网络研究已经取得了初步的进展. 2022年, Cao等[13]提出了多协议转译框架, 可以支持量子网络从单协议到多协议演进. 文献[14]提出了一种软件定义的异构QKD链组网架构, 提供了考虑多协议特征的网络层解决方案. 这些工作为多协议量子网络的实际应用提供了支撑. 此外, 文献[15]提出了一种异步MDI-QKD方案, 在无需全局相位跟踪的条件下突破了安全码率界限. 文献[16]验证了BB84协议与MDI协议的设备兼容性和互操作性, 为BB84城域量子网络与MDI城域量子网络的域间互联互通奠定了基础. 虽然多协议量子网络的研究已经取得了初步进展, 但针对多域跨协议量子网络的研究仍然有待进一步探索, 尤其是该网络场景下域间密钥业务还存在成功率低、密钥供需不适配等问题, 如何在多域跨协议量子网络中实现域间密钥业务的按需提供是亟待解决的关键问题.
针对以上问题, 本文提出了多域跨协议量子网络的域间密钥业务按需提供策略, 包括MDI旁路优先策略和BB84旁路优先策略. 同时, 构建了多域跨协议量子网络的业务提供模型, 设计了内嵌两种策略的域间密钥业务按需提供算法. 并且, 结合双域和三域两类量子网络扑结构, 在高密钥率需求和低密钥率需求两种场景下进行了数值仿真与性能分析, 验证了所提出的策略可以有效提高域间密钥业务请求的成功率, 提高全网的密钥供需均衡度.
-
在多域量子网络中, 每个城域使用单一的QKD协议(本文考虑使用BB84或MDI协议), 多个城域通过域间链路相连, 域间QKD业务的源宿节点分别位于不同的城域. 由于不同的城域可能使用不同的QKD协议, 因此域间QKD业务可能横跨多个基于不同QKD协议实现的城域量子网络. 量子网络由多个QKD节点和多条光纤QKD链路组成[17]. 其中, 每个QKD节点都部署一定数量的QKD设备, 具体包括QKD发送机(QKD transmitter, QTx)和QKD接收机(QKD receiver, QRx); 每条光纤QKD链路由量子信道和经典信道组成, 量子信道用来传输量子信号, 经典信道用来实现同步和协商功能.
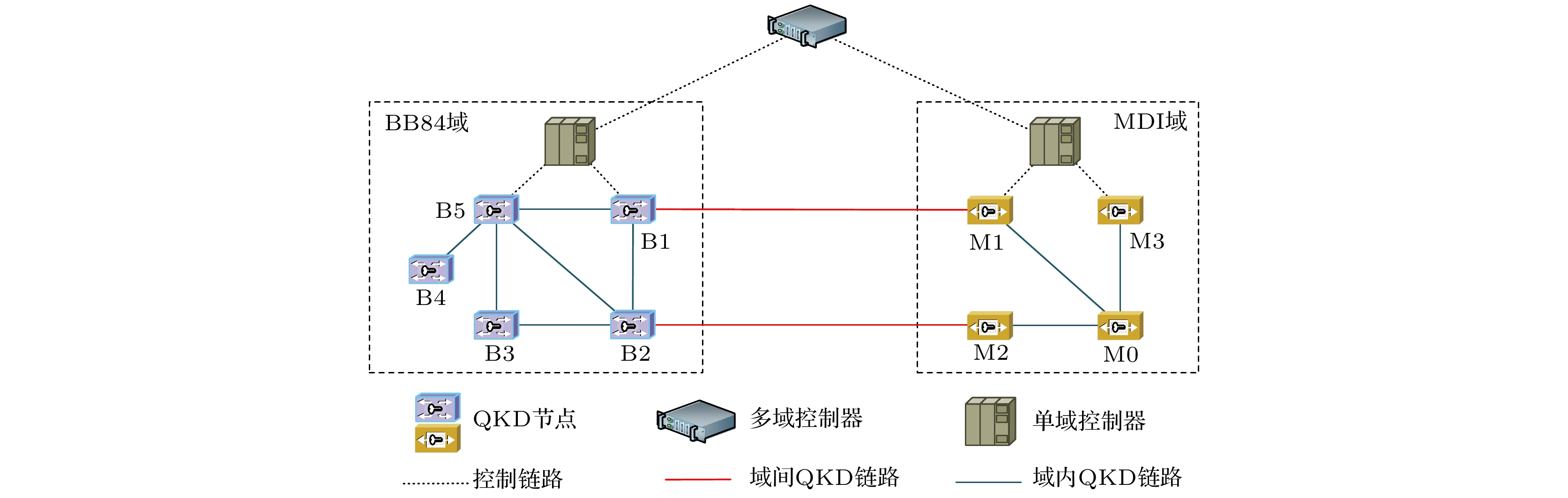
如图1所示, 域间密钥业务的源节点与宿节点处于不同的QKD协议域, 业务请求发出后, 多域控制器根据QKD节点的连接方式和QKD设备的占用情况, 合理选择域间密钥业务提供策略. 为了实现密钥供需均衡, 本文提出了两种域间密钥业务按需提供策略, 分别是: MDI旁路优先(MDI bypass first, MDI-BF)策略, 即优先旁路MDI协议域的域间节点; BB84旁路优先(BB84 bypass first, BB84-BF)策略, 即优先旁路BB84协议域的域间节点. 域间节点是可以建立域间链路, 连接不同城域量子网络的QKD节点; 域内节点是位于某个城域量子网络中, 未与其他域直接相连的QKD节点. 域间节点不仅具备其所在量子网络域的设备资源, 还具备连接其他量子网络域的设备资源, 而域内节点仅具备其所在域的设备资源. 多域控制器选择策略后并执行相应的算法获得密钥中继路径, 然后通过单域控制器向QKD节点下发控制信息, 完成域间密钥业务的提供. 密钥中继路径是指密钥业务源宿节点间经过的路径, 该路径上所有节点均为可信节点, 每个可信节点可以执行密钥中继操作. 相邻可信节点之间可能存在一到多个旁路节点, 旁路节点是进行光旁路的QKD节点, 量子信号经过该节点时不会被处理, 将透明通过.
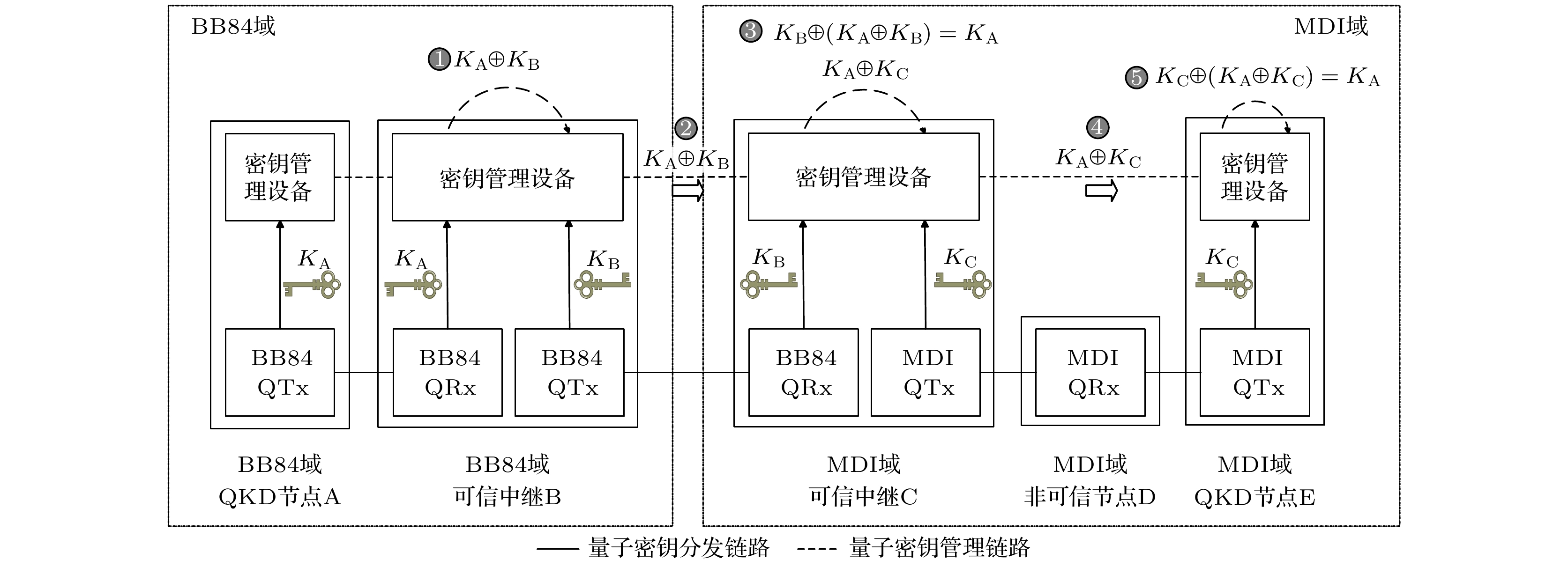
多域跨协议量子网络的密钥中继结构示例如图2所示. BB84域节点A和MDI域节点E分别是源节点和宿节点. QTx通过QKD链路与QRx相连. 通过执行BB84-QKD, 节点A与B、节点B与C之间分别共享密钥KA, KB. 通过执行MDI-QKD, 使得节点C与节点E之间共享密钥KC, 其中, 非可信节点D虽然参与MDI-QKD的过程, 但不会掌握密钥KC. 通过QKD生成的密钥均存储在相应的密钥管理设备中. 为了实现源宿节点A与E之间的域间密钥业务, 在网络层需执行以下步骤(其中KA, KB, KC密钥长度相同):
1) 节点B利用KB对KA进行加密: KA⊕KB;
2) 节点B将KA⊕KB发送给节点C;
3) 节点C利用KB对KA⊕KB进行解密, 得到密钥KA, 然后节点C利用KC对KA进行加密: KA⊕KC;
4) 节点C将KA⊕KC发送给节点E;
5) 节点E利用KC对KA⊕KC进行解密, 得到密钥KA, 至此源宿节点A与E之间成功共享密钥KA.
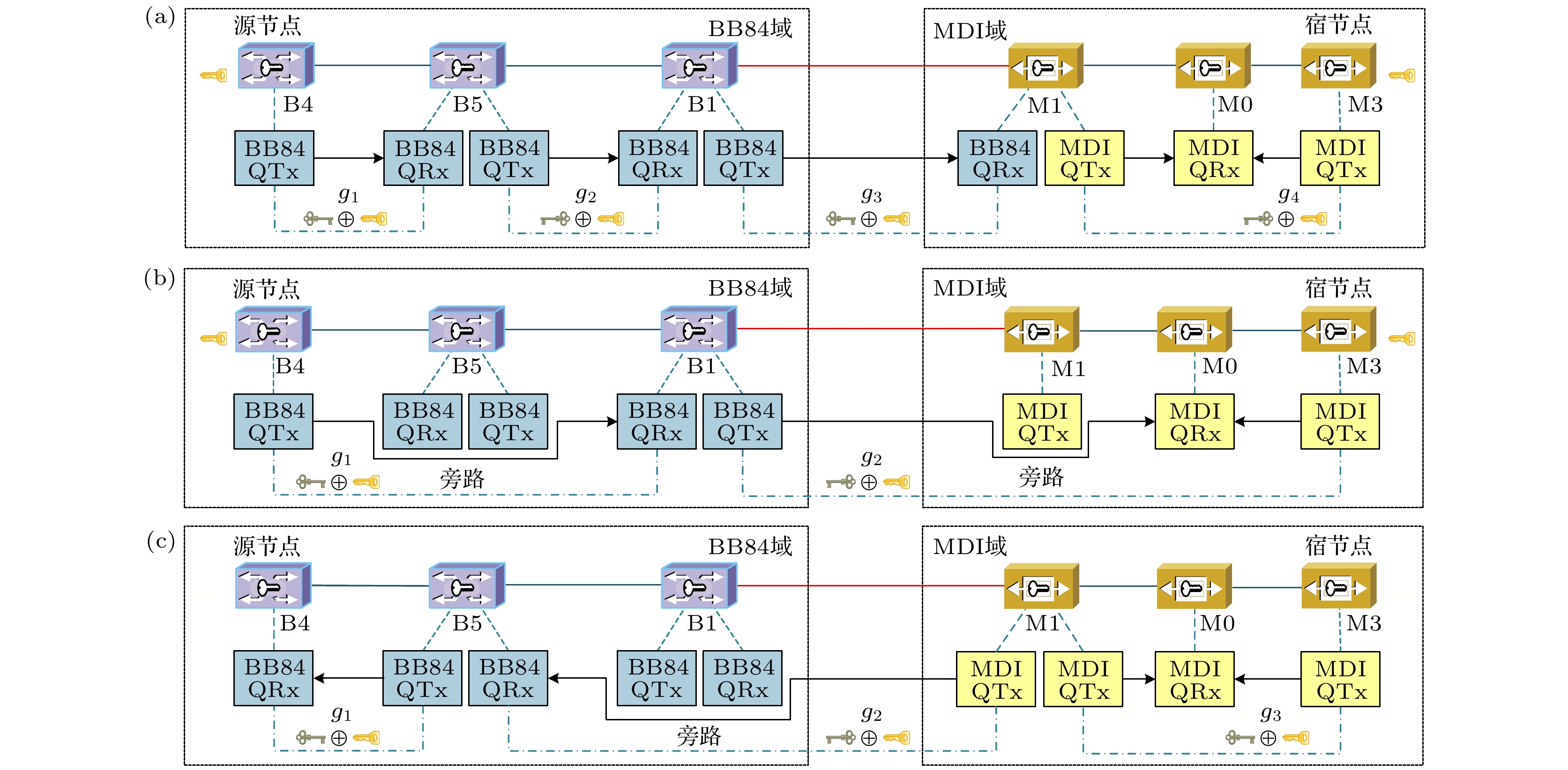
结合图3, 具体描述传统域间密钥业务提供策略和本文提出的两种按需提供策略. 图3(a)示意了传统策略下域间密钥业务的提供方式[18], 其中每个节点均不会被旁路. 以源宿节点分别为B4与M3的密钥业务为例, 首先通过路由算法获得源宿节点间的密钥中继路径“B4-B5-B1-M1-M3”(M0为非可信节点), 然后在节点M1处部署BB84-QRx来实现域间密钥业务的提供. 传统策略下密钥中继路径上每个节点都用作可信中继, 因此会占用较多的QKD设备. 并且, 考虑到MDI协议自身连接模式“发送机-接收机-发送机”的特点, 需要在MDI域间节点处部署更多的QKD设备来满足域间密钥业务提供的需求, 进而增加了设备成本.
图3(b)示意了MDI-BF策略下域间密钥业务的提供方式. MDI-BF策略优先旁路了MDI域间节点(M1). 在选择BB84域的密钥中继路径时, 考虑到该路径的密钥供应速率为各链路密钥生成率中的最小值, 高于此最小值的链路会造成资源的浪费, 所以B5节点被旁路, 减少了对QKD设备的占用. 由于B5节点与M1节点进行了旁路, 密钥中继路径为“B4-B1-M3”(M0为非可信节点). 本策略减少了对QKD设备的占用, 可以使量子网络容纳更多的域间密钥业务, 从而降低了多域量子网络的阻塞率, 更高效地完成了域间密钥业务的按需提供.
图3(c)示意了BB84-BF策略下域间密钥业务的提供方式. 该策略在MDI域间节点(M1)处占用两个QTx, 两个QTx分别与BB84-QRx和MDI-QTx共享密钥. 同时, 本策略优先旁路了BB84域的节点, 通过旁路B1节点, 减少了对QKD设备的占用. 最终, 密钥中继路径为“B4-B5-M1-M3”(M0为非可信节点). 密钥中继路径的密钥供应速率是否能够满足域间密钥业务请求的密钥率需求, 是能否实现域间密钥业务提供的关键. 该策略中MDI域内链路较短, 相应密钥中继路径的密钥供应速率较高.
经典密码网络中通常基于特定的密码学算法生成密钥, 占用公网资源, 但业务提供通常无需考虑物理层的资源状态, 本文场景下域间密钥业务的实现还需具体考虑物理层的设备和光纤链路资源状态. 此外, 由于不同QKD协议的连接模式不同, 本文方案还需具体考虑并解决不同协议的光路连接模式不同而造成的冲突问题, 该问题在经典密码网络中通常无需考虑. 不同QKD协议的密钥生成率、域间密钥业务的密钥率需求以及密钥中继路径的密钥供应速率将在第3节具体讨论.
-
本节构建了多域跨协议量子网络的业务提供模型, 主要包括网络模型和密钥供应模型.
-
将多域跨协议量子网络的拓扑结构定义为
$ G(V, E) $ , 其中$V$ 表示QKD节点集合,$ E $ 表示光纤QKD链路集合. 本文研究的多域跨协议量子网络包括BB84协议域和MDI协议域, 因此全网QKD节点集合$V$ 由BB84域QKD节点集合${V_{\text{B}}}$ 和MDI域QKD节点集合${V_{\text{M}}}$ 组成. 每个协议域的QKD节点又分为域内节点和域间节点, 分别将BB84域和MDI域的域间节点集合定义为${V_{\text{B}}}_{\text{J}}$ 和${V_{\text{M}}}_{\text{J}}$ . 对于QKD节点集合$V$ 中任意的QKD节点${v_i} \in V$ , 其中可以使用的QTx数量与QRx数量分别定义为${\lambda _{{v_i}}}$ 与$ {\varepsilon _{{v_i}}} $ . 根据不同QKD协议密钥生成率与传输距离的关系, 可以得到每条QKD链路对应的密钥生成率, 具体模型和公式将在下一节中阐述.将域间密钥业务请求集合定义为
$R$ , 一个域间密钥业务请求可以表示为$r({s_r}, {d_r}, {k_r}, {t_r})$ , 其中,${s_r}$ 和${d_r}$ 分别表示该域间密钥业务请求的源节点和宿节点, 且${s_r}$ 和${d_r}$ 分别位于两个不同的城域量子网络,${k_r}$ 表示该域间密钥业务请求的密钥率需求,${t_r}$ 表示该业务请求的持续时间. 本文将域间密钥业务请求的成功率定义为: 成功提供的域间密钥业务请求数量与全网域间密钥业务请求总数之比, 成功提供的域间密钥业务请求集合表示为${R_{\text{S}}}$ . 将域间密钥业务请求$r$ 选择的密钥中继路径表示为${p_r}( {N_{{p_r}}}, {L_{{p_r}}}, {B_{{p_r}}}, {m_{{p_r}}} ) \in {P_r}$ , 其中,${N_{{p_r}}}$ 和${L_{{p_r}}}$ 分别表示该路径上的QKD节点集合和QKD链路集合,${B_{{p_r}}}$ 表示该路径上的旁路节点集合,${m_{{p_r}}}$ 表示该路径的密钥供应速率,${P_r}$ 为域间密钥业务请求$r$ 的备选密钥中继路径集合. 在密钥中继路径上, 旁路节点不获取密钥信息(量子信号透明传输), MDI域中心节点为非可信节点, 其余节点均为可信节点. 可信节点会掌握全局密钥信息, 且需要占用QKD设备以完成对量子信号的收发操作, 因此, 可信节点数量一定程度上可以反映提供域间密钥业务的成本和现实安全水平.本文探讨了两类网络场景, 分别是双域和三域量子网络: 双域量子网络包括一个BB84域和一个MDI域, 三域量子网络包括两个BB84域和一个MDI域, 且任意两个城域量子网络之间均可以提供域间密钥业务.
针对每个成功的BB84域与MDI域之间的密钥业务请求
$ r \in {R_{\text{S}}} \cap {R_{{\text{BM}}}} $ (RBM表示BB84域与MDI域之间的密钥业务请求集合), 其密钥中继路径经过的QKD节点总数为$\alpha _{\text{N}}^r$ , 其中旁路的节点数量为$\alpha _{\text{B}}^r$ , 则可信节点数量可以表示为其中, 减去1的原因是MDI域中心节点为非可信节点.
因此, BB84域与MDI域之间密钥业务的平均可信节点数量可以表示为
针对每个成功的两个BB84域之间的密钥业务请求r∈RS∩RBB(RBB表示两个BB84域之间的密钥业务请求集合), 其密钥中继路径经过的QKD节点总数为
$\alpha _{\text{N}}^r$ , 其中旁路的节点数量为$\alpha _{\text{B}}^r$ , 则可信节点数量可以表示为其中, 在两个BB84域之间密钥业务的密钥中继路径上, 除旁路节点外, 其余节点均为可信节点.
因此, 两个BB84域之间密钥业务的平均可信节点数量可以表示为
综上, 双域量子网络中域间密钥业务的平均可信节点数量可以通过(2)式计算, 而三域量子网络中域间密钥业务的平均可信节点数量可以表示为
-
下文将给出BB84和MDI协议的密钥生成率计算公式, 并分析密钥中继路径的密钥供应速率.
其中,
$q$ 为对基效率,$ {f}_{\text{e}}(\cdot) $ 为纠错效率函数,$ {Q_{\mu}} $ 为总增益,$ {E_{\mu}} $ 为平均量子比特误码率,$Q_1^{}$ 和$e_1^{}$ 分别为单光子脉冲的增益和误码率,${H_2}\left( x \right)$ 是二元香农熵函数, 表达式为其中,
$P_{11}^{\text{Z}}$ 表示Z基下发送单光子的概率;$Q_{\mu \mu }^{\text{Z}}$ 和$E_{\mu \mu }^{\text{Z}}$ 分别为Z基下制备信号态的增益和量子比特误码率,$Q_{\mu \mu }^{\text{Z}}$ 和$E_{\mu \mu }^{\text{Z}}$ 可以通过实测获取; µ为信号态强度;$Y_{11}^{\text{Z}}$ 和$e_{11}^{\text{X}}$ 分别为Z基下单光子响应率和X基下单光子量子比特误码率,$Y_{11}^{\text{Z}}$ 和$e_{11}^{\text{X}}$ 可以用诱骗态方法估计[22–26], 本文选取三强度诱骗态方法.结合以上BB84协议和MDI协议的密钥生成率计算公式, 可以得到密钥中继路径上所有相邻可信节点间的密钥生成率, 其中最小的密钥生成率即为整条密钥中继路径的密钥供应速率. 以第2节图3(b)示意的MDI-BF策略为例, 由于B5节点与M1节点的旁路, 相邻可信节点变为B4-B1, B1-M3, 对应的密钥生成率分别为
${g_1}, {g_2}$ , 则该密钥中继路径的密钥供应速率可以表示为$\min ({g_1}, {g_2})$ . 根据此原则, 密钥中继路径${p_r}$ 的密钥供应速率${m_{{p_r}}}$ 可以表示为其中,
$ g_1^r, g_2^r,\cdots, g_{{\text{end}}}^r $ 分别表示密钥中继路径${p_r}$ 上第一对至最后一对相邻可信节点间的密钥生成率.将域间密钥业务请求r的密钥率需求表示为
${k_r}$ , 该业务密钥中继路径的密钥供应速率表示为${m_r}$ , 当${m_r} \geqslant {k_r}$ 时, 可以认为该路径能够完成域间密钥业务的提供. 然而, 这并不意味着密钥中继路径的密钥供应速率${m_r}$ 越大越好, 当${m_r}$ 过大时, 密钥的供应远大于需求, 反而容易造成密钥资源的浪费, 导致过多的设备被占用. 因此, 本节定义了一个性能评估指标: 密钥供需均衡度, 以衡量密钥供应与需求之间的均衡关系. 密钥供需均衡度定义为域间密钥业务请求的密钥率需求与密钥中继路径的密钥供应速率之比, 可以表示为其中, 密钥供需均衡度的数值大小介于0到1之间, 且越接近1代表均衡度越高, 对密钥资源的利用越充分; 反之代表均衡度越低, 密钥资源的浪费越多.
因此, 整个多域跨协议量子网络的密钥供需均衡度可以表示为
-
本节提出了内嵌MDI-BF和BB84-BF策略的域间密钥业务按需提供算法, 该算法具有可扩展性, 能够容纳更多的域间密钥业务提供策略.
表1给出了域间密钥业务按需提供算法的详细流程(伪代码), 其中, MDI-BF策略优先旁路MDI域间节点, 而BB84-BF策略优先旁路BB84域间节点. 步骤1完成了变量的初始化. 对于每个域间密钥业务请求, 步骤3更新了量子网络中各QKD节点的设备占用状态. 步骤4将源宿节点中没有可用QKD设备的域间密钥业务判断为失败. 若采用BB84-BF策略, 则执行步骤5—11, 将可用QTx数量小于2的MDI域间节点从量子网络拓扑中删除. 步骤12—15通过K短路径算法计算出从源节点到宿节点的K条备选密钥中继路径, 如果无法找到任何密钥中继路径, 则认为当前域间密钥业务请求r失败, 开始处理下一个域间密钥业务请求.
接下来, 需要从K条备选密钥中继路径中选出最佳的路径, 并确定密钥中继路径上各个节点的旁路情况. 步骤19—21首先判断是否使用MDI-BF策略, 若是则将MDI域间节点进行旁路. 步骤22—24将BB84域中缺少一对可用QTx和QRx的节点进行旁路. 步骤26—28重新计算密钥中继路径的密钥供应速率, 并判断其是否高于业务请求的密钥率需求, 若小于则当前路径无法满足需求, 继续处理下一条密钥中继路径; 反之则执行步骤30—36. 步骤30—34为确定BB84域中可以被旁路的节点, 如果BB84域中的节点(除源宿节点)旁路后不会导致密钥中继路径的密钥供应速率低于业务请求的密钥率需求, 则旁路该节点, 并更新密钥中继路径的密钥供应速率. 步骤35—36将当前密钥中继路径输出作为当前域间密钥业务请求r的密钥中继路径, 并将相应密钥业务加入成功业务集合中, 然后继续处理下一个域间密钥业务请求. 步骤39将备选路径集合中没有满足密钥率需求的密钥中继路径的域间密钥业务判断为失败.
域间密钥业务按需提供算法的时间复杂度分析如下. 在最坏情况下, 步骤3—11与步骤12—15的时间复杂度分别为
$O\left( {\left| {{V_{{\text{MJ}}}}} \right|} \right)$ 和$O( K\left| V \right|( \left| E \right| + \left| V \right|{\text{log}}\left| V \right| ) )$ , 步骤16—39时间复杂度为$O\left( {2 K\left| V \right|} \right)$ . 因此, 该算法处理域间密钥业务请求的整体时间复杂度为$ O\left( {\left| R \right|\left( {K\left| V \right|\left( {\left| E \right| + \left| V \right|{\text{log}}\left| V \right| + 2} \right) + \left| {{V_{{\text{MJ}}}}} \right|} \right)} \right) $ . 此外, 该算法对于不同拓扑结构、不同规模的量子网络具有适用性. 如果每个域有比较复杂的结构, 包括若干主、次和分支节点, 仍可以通过执行该算法获取密钥中继路径, 进而完成域间密钥业务的按需提供. -
本节通过数值仿真来实现设计的域间密钥业务按需提供算法, 进而评估MDI-BF和BB84-BF策略在不同场景下的适用性与有效性. 以第2节中介绍的传统策略作为基准, 与所提出的两种按需提供策略进行对比分析.
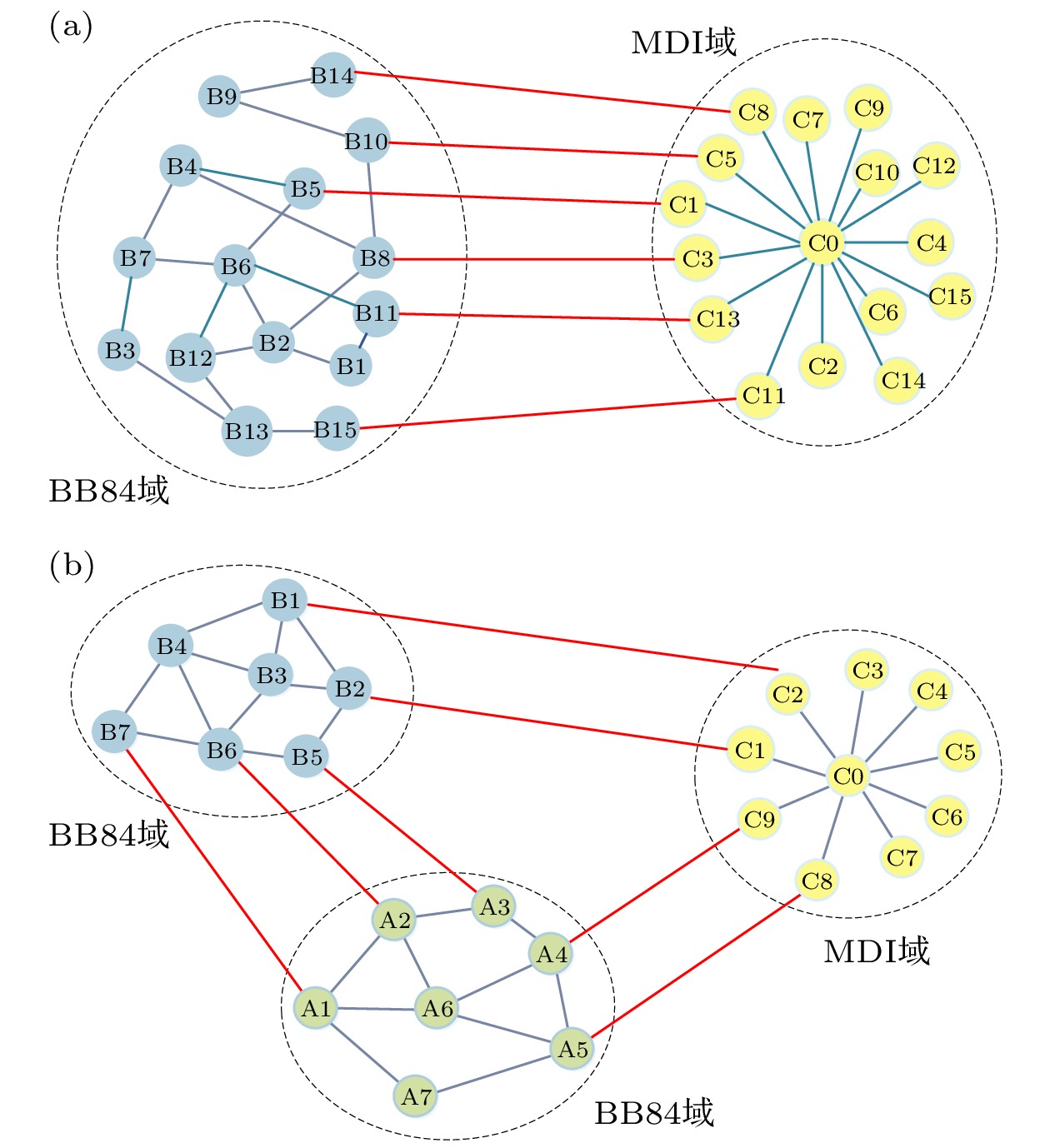
结合现实中已部署量子网络的规模和特点, 仿真使用的两个多域量子网络拓扑结构如图4所示. 图4(a)中双域量子网络拓扑包含一个BB84域和一个MDI域. 图4(b)中三域量子网络拓扑由两个BB84域和一个MDI域组成. 考虑到BB84和MDI协议的连接模式及特点, BB84城域量子网络拓扑采用网状结构, 而MDI城域量子网络拓扑采用星形结构. 结合实际应用情况, MDI域内QKD链路物理长度设为10—20 km, BB84域内QKD链路物理长度设为30—50 km, 域间链路长度设为50—70 km, 并且假设每条QKD链路上的可用信道数量充足. 鉴于域间业务流量通常较大, 设置域内节点处部署的QKD设备数量为15, 且域间节点处部署的QKD设备数量为30. 此外, 每个域间密钥业务请求在任意两个域之间随机生成, K短路径算法的K设置为3.
针对域间密钥业务请求的密钥率需求, 结合不同城域数量及协议类型的影响, 本文考虑了两种情况.
1) 低密钥率需求情况. 双域量子网络中低密钥率需求设为600—1000 b/s, 三域量子网络中低密钥率需求设为400—800 b/s.
2) 高密钥率需求情况. 双域量子网络中高密钥率需求设为3—5 kb/s, 三域量子网络中高密钥率需求设为2—4 kb/s.
每个域间密钥业务请求的密钥率需求在上述区间中服从均匀分布随机生成. 通过对不同密钥率需求场景进行仿真, 可以更全面地评估每个密钥业务提供策略的有效性, 明确各策略的适用场景. 此外, 仿真中域间密钥业务请求的总量为
$1.5 \times {10^5}$ , 域间密钥业务请求服从泊松分布动态到达. 表2给出了BB84协议和MDI协议的密钥生成率仿真参数[27]. 鉴于本研究侧重在网络层, 为了简化分析, 本文未对有限长效应进行具体考虑. -
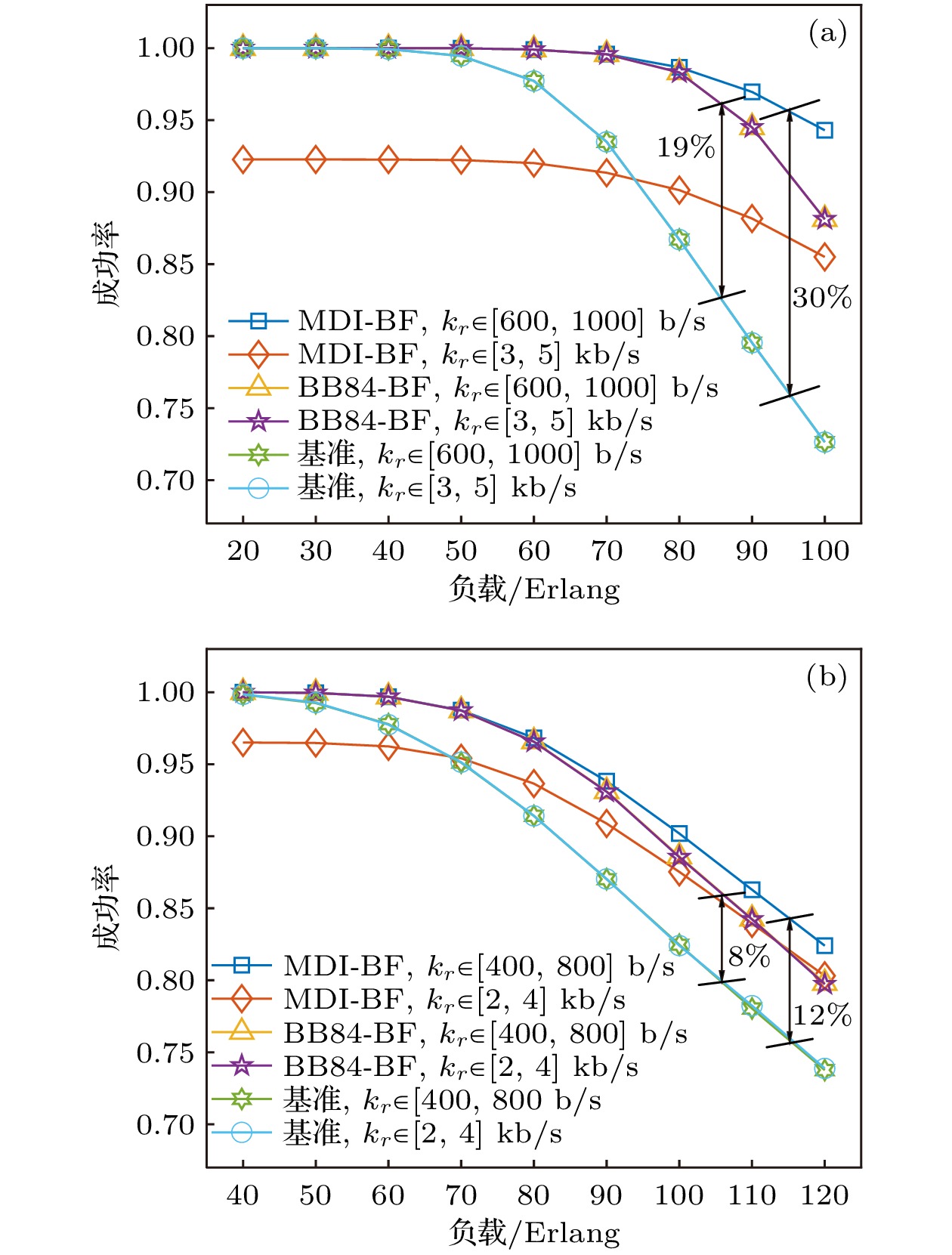
图5给出了双域和三域两种不同量子网络中域间密钥业务请求成功率随负载的变化关系. 可以看出, 随着负载的增大, 不同策略下域间密钥业务请求的成功率均逐步下降, 其原因在于负载增大导致了域间密钥业务请求的平均持续时间变长, 从而增加了实时占用的QKD设备数量, 导致密钥业务请求成功率降低.
如图5(a), (b)所示, 当负载较大时, MDI-BF策略与BB84-BF策略下域间密钥业务请求的成功率均高于基准. 这是由于两种按需提供策略均可以通过动态旁路来差异化适配密钥率需求, 从而减少了对QKD设备的占用. 通过对比两种按需提供策略在不同密钥率需求下的仿真结果, 可以发现: 当负载较高时, 在低密钥率需求下, MDI-BF策略的密钥业务请求成功率更高, 在双域量子网络中相比基准提高了30%, 而在三域量子网络中相比基准提高了12%; 在高密钥率需求下, BB84-BF策略则取得了更好的效果, 密钥业务请求成功率在双域和三域量子网络中相比基准分别提高了19%和8%. 其原因在于, MDI-BF策略通过旁路MDI域间节点, 以降低密钥中继路径的密钥供应速率为代价减少了QKD设备的占用, 从而使其在低密钥率需求场景下拥有更高的密钥业务请求成功率; 而BB84-BF策略通过在MDI域间节点处占用两个QTx, 通过多占用部分QKD设备来获取更高的密钥供应速率, 从而在高密钥率需求下体现出了更大的优势.
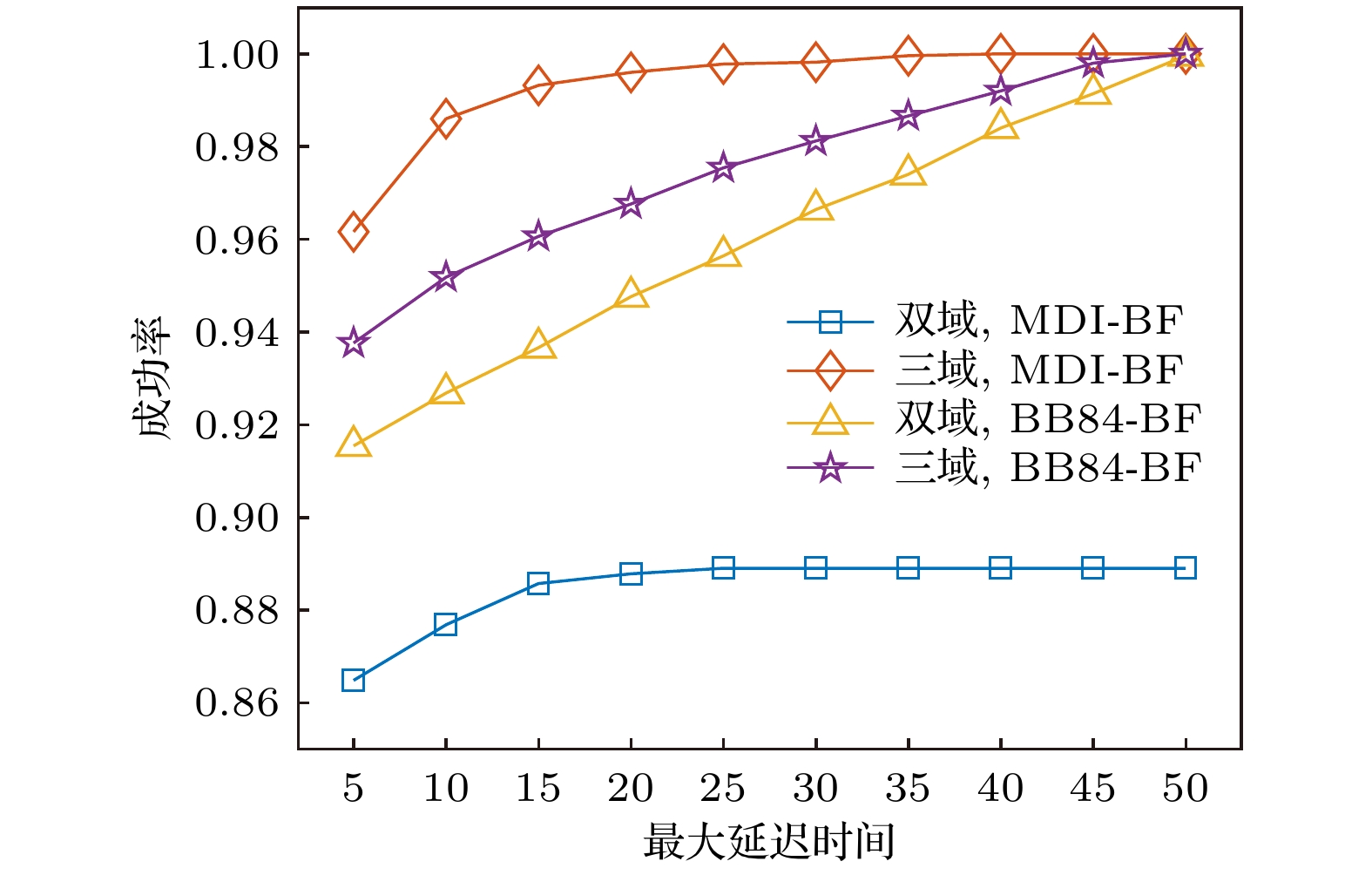
此前的仿真中并未设置最大延迟时间, 业务请求到达后如果无法获取足够的资源则会失败. 实际场景下, 还可以允许一定量时间的延迟, 超过最大延迟时间后判定当前业务提供失败, 并进行下一组业务提供. 因此, 下面将设置最大延迟时间, 以探究其在高负载(100 Erlang)和高密钥率需求(4 kb/s)下, 对网络性能的影响, 最大延迟时间的单位为归一化的时间单元(单位时间).
图6给出了不同策略下域间密钥业务请求成功率随最大延迟时间的变化关系. 从图6可以看出, 随着最大延迟时间的增大, 域间密钥业务请求成功率先逐步上升, 然后趋于稳定, 这说明允许一定量时间的延迟能够在一定程度上增加完成的业务数量. 其原因在于, 在一定时间范围内, 当最大延迟时间增加时, 业务有相对更大的机率等待网络中资源释放, 并利用释放后空闲的资源完成业务提供.
综上, MDI-BF策略和BB84-BF策略在不同的多域量子网络场景下均优于传统策略, 验证了其在不同多域量子网络拓扑下的适用性. 其中, MDI-BF策略在低密钥率需求场景下域间密钥业务请求成功率更高, 而BB84-BF策略则更适用于高密钥率需求场景.
-
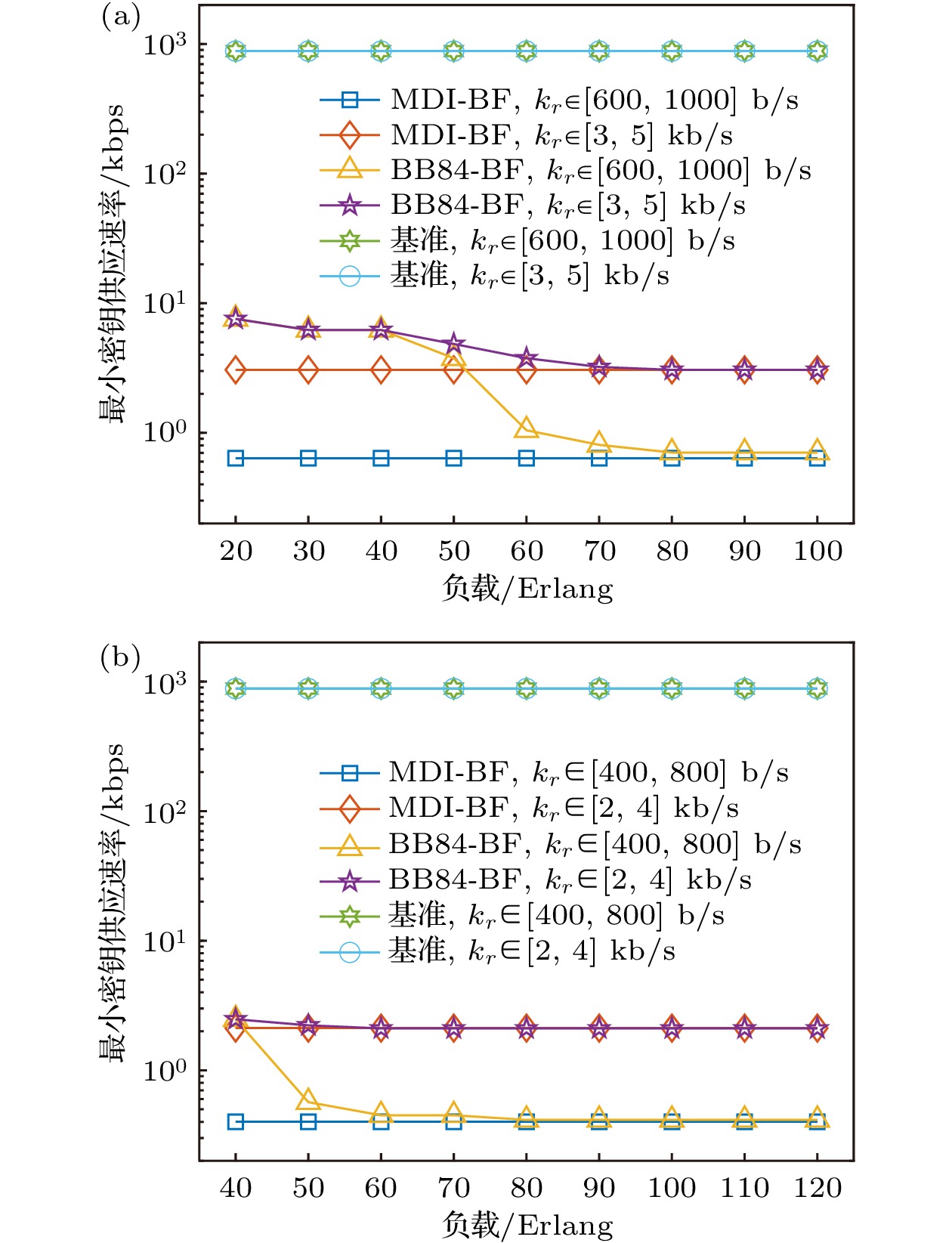
为了更好地评估不同密钥率需求下的密钥供应性能, 对全网最小密钥供应速率进行了仿真分析, 图7给出了不同策略下全网最小密钥供应速率随负载的变化关系. 在双域和三域量子网络中, 全网最小密钥供应速率呈现出相似的结果, 显示了所提出的策略在不同多域量子网络场景中具有适用性. 在相同密钥率需求下, 基准的全网最小密钥供应速率最大, BB84-BF策略次之, MDI-BF策略最低, 符合BB84协议和MDI协议的特点. 通过对比不同密钥率需求下的全网最小密钥供应速率, 可以发现: 基准几乎不受密钥率需求变化所影响, 而MDI-BF策略与BB84-BF策略则对密钥率需求较为敏感, 随密钥率需求的变化也更加明显. 这是因为所提出的两种按需提供策略可以进行密钥的按需供应, 其密钥供应速率与业务请求的密钥率需求直接相关, 而基准的密钥供应速率忽略了密钥率需求的变化, 虽然实现了较高的密钥供应速率, 但其无法充分利用密钥资源.
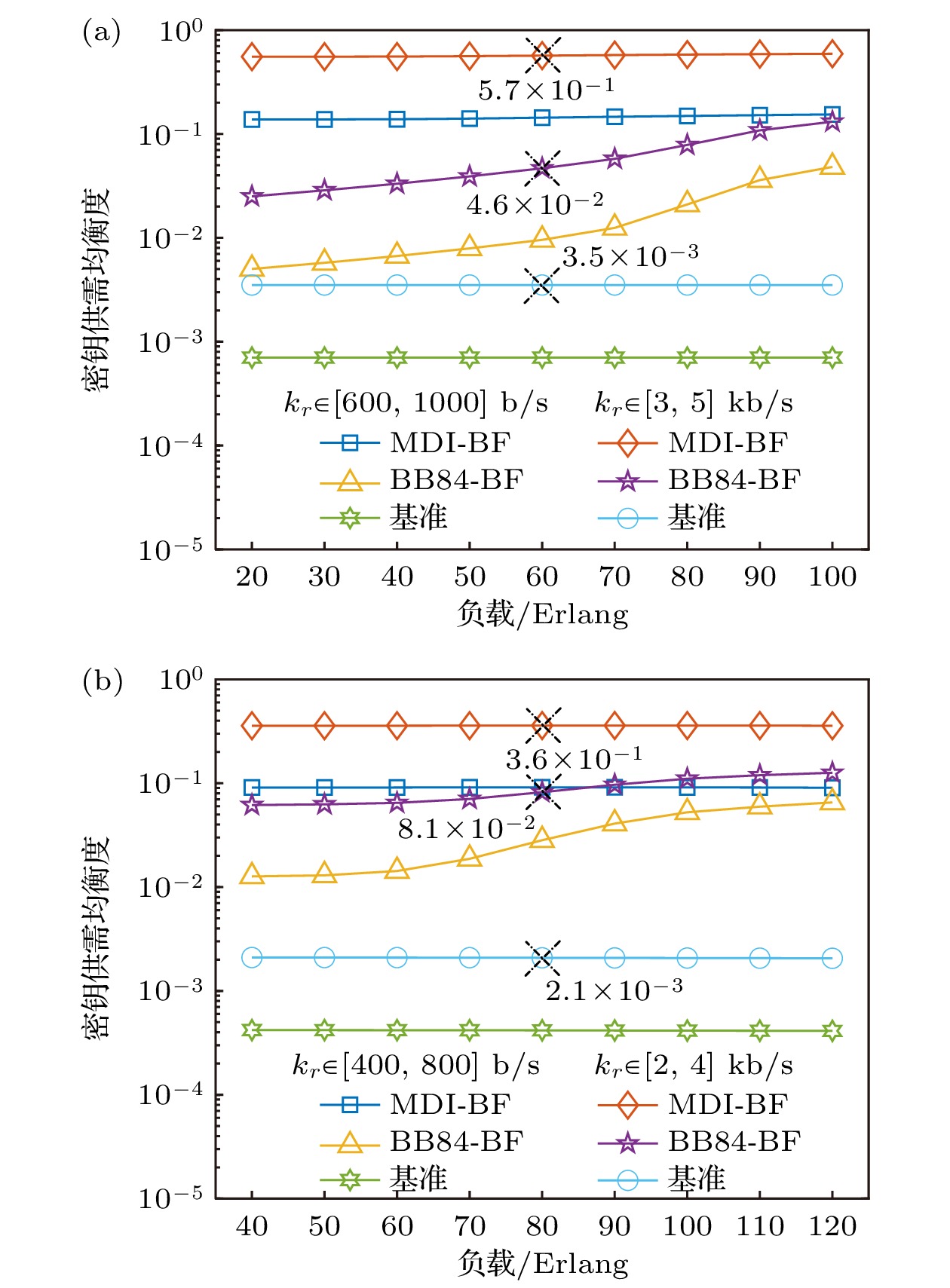
为了衡量密钥供应速率与密钥率需求之间的适配效果, 对密钥供需均衡度进行了仿真分析, 图8给出了不同策略下密钥供需均衡度随负载的变化关系. 可以看出, 随着负载的增大, MDI-BF策略和基准对应的密钥供需均衡度基本保持稳定, 而BB84-BF策略的密钥供需均衡度则逐步提升. 这反映了MDI-BF策略和基准实现的密钥供应速率几乎与负载大小无关, 而BB84-BF策略的密钥供应速率容易受负载影响. 如图8所示, 在相同密钥率需求下, MDI-BF策略的密钥供需均衡度最高, BB84-BF策略次之, 基准最低. 通过对比可以发现, 在双域量子网络(负载为60 Erlang)和三域量子网络(负载为80 Erlang)中, 高密钥率需求下, MDI-BF策略的密钥供需均衡度相比基准提高了约两个数量级, 而BB84-BF策略相比基准提高了约一个数量级. 所提出的两种策略均可以根据业务的密钥率需求有效调控密钥供应速率, 实现密钥的按需供应, 而受MDI协议的影响, MDI-BF策略的密钥供应速率随密钥率需求的变化更加明显, 因此相较于基准获得了更高的密钥供需均衡度. 这反映出MDI-BF策略和BB84-BF策略实现的密钥供应速率可以更有效地适配密钥率需求, 一定程度上避免因提供冗余密钥而导致的密钥资源浪费.
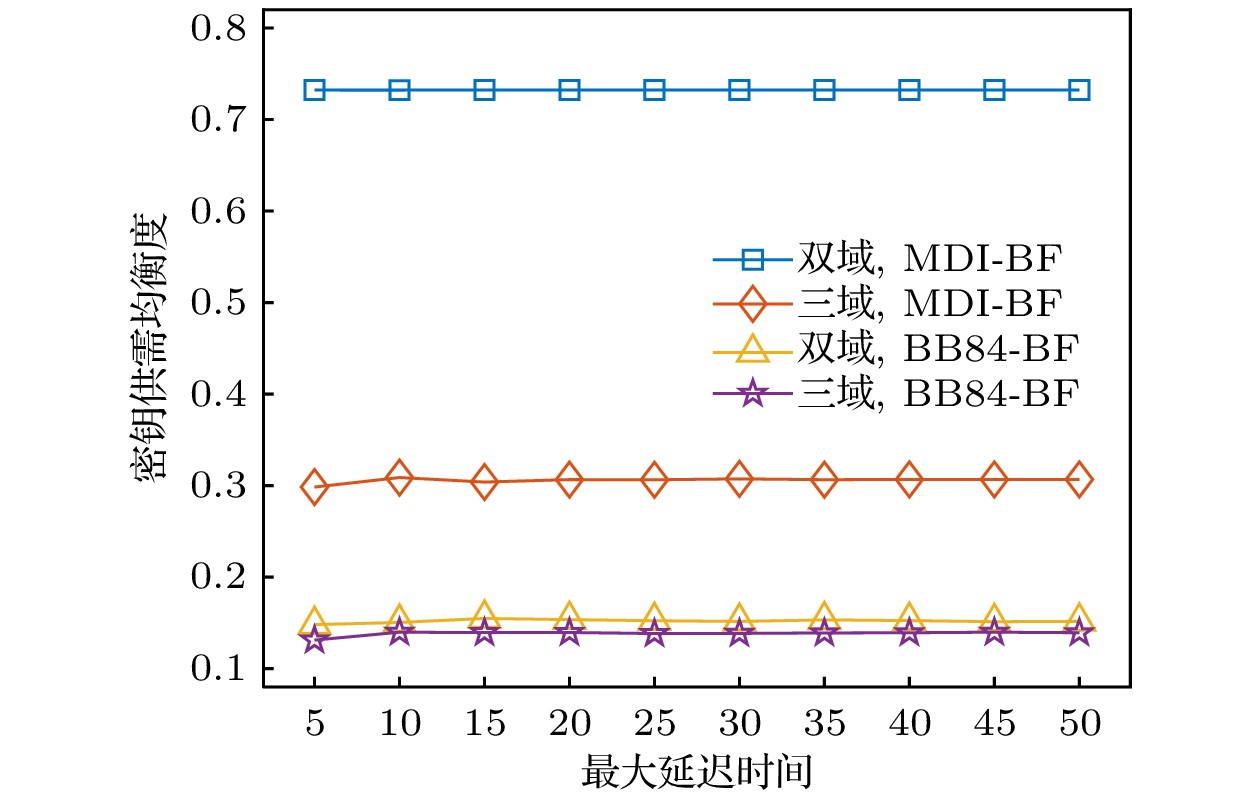
图9给出了不同策略下密钥供需均衡度随最大延迟时间的变化关系. 可以看出, 随着最大延迟时间的延长, 密钥供需均衡度基本保持稳定. 其原因在于, 密钥供需均衡度的大小主要取决于密钥中继路径的密钥供应速率, 而最大延迟时间的设置不会影响密钥中继路径的选择, 因此对密钥供需均衡度的影响较小.
综上, MDI-BF和BB84-BF策略在不同网络场景和不同密钥率需求下均具有较好的适用性. 相较于传统策略, MDI-BF和BB84-BF策略可以实现更高效的域间密钥业务按需提供, 通过充分调控密钥供应速率来适配密钥率需求, 可以有效减少冗余密钥的产生, 从而实现更高的密钥供需均衡度.
-
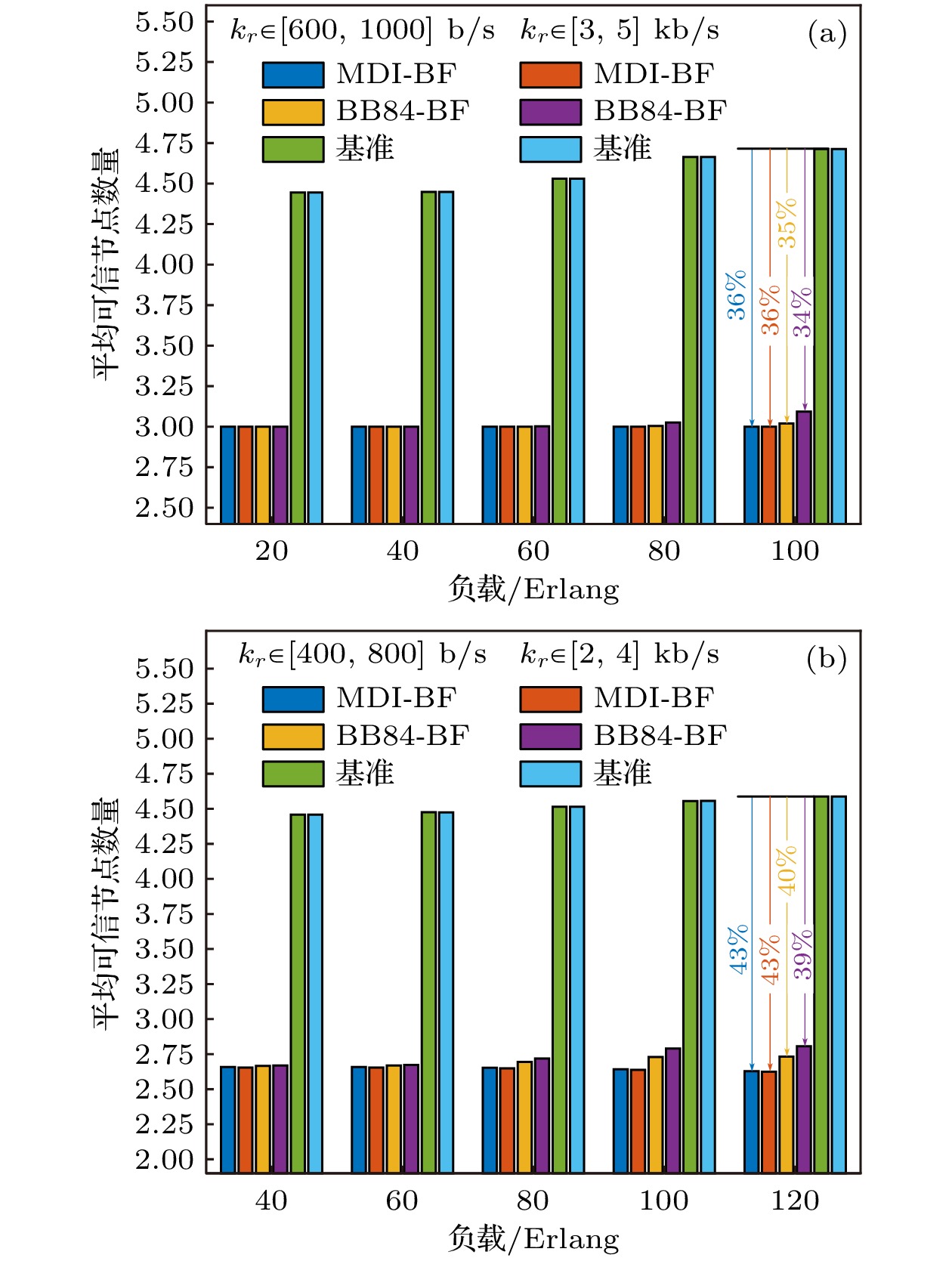
可信节点的数量可以在一定程度上反映域间密钥业务提供的成本和现实安全水平, 可信节点数量越多, 成本越高, 现实安全水平越低. 图10给出了不同策略下域间密钥业务的平均可信节点数量随负载的变化关系. 此处的可信节点包括源宿节点和中继节点(可信中继). 从图10可以看出, 随着负载的增大, 不同策略下域间密钥业务的平均可信节点数量先是保持相对稳定, 然后在高负载下逐步增加, 这是因为密钥中继路径的跳数会随着负载的增大而增加, 导致提供域间密钥业务所需的可信节点数量增多.
如图10所示, 通过对比不同密钥率需求下域间密钥业务的平均可信节点数量, 可发现两种按需提供策略的平均可信节点数量均低于基准, 且高负载下MDI-BF策略的平均可信节点数量小于BB84-BF策略. 例如, 双域量子网络(负载为100 Erlang)中, 在高密钥率需求和低密钥率需求下, MDI-BF和BB84-BF策略相比基准均可以将平均可信节点数量减少30%以上; 三域量子网络(负载为120 Erlang)中, 相较于基准, MDI-BF和BB84-BF策略的平均可信节点减少量可达约40%. 其原因在于, MDI-BF和BB84-BF策略通过优先旁路不同域的节点, 有效减少了密钥中继路径的跳数, 从而降低了可信节点数量, 一定程度上减少了域间密钥业务提供的成本, 提高了现实安全水平. 并且, 在高密钥率需求下, 为了实现更高的密钥供应速率, 密钥中继路径的旁路节点数量相较于低密钥率需求下更少, 导致其所需的可信节点数量更多.
综上, 相比传统策略, MDI-BF和BB84-BF策略均可以采用更少的可信节点来实现域间密钥业务的按需提供, 进而有助于降低域间密钥业务的开通成本和风险概率.
当域间密钥业务需跨越两个或三个甚至更多域时, 本文所提策略的适用性取决于跨越城域量子网络的协议类型和连接模式, 如果跨越的域不存在相邻MDI协议域, 则本文策略具有适用性, 反之需要对策略进行优化与改进, 如可以使MDI-BF策略不再旁路所有MDI域间节点等. 此外, 当跨越的城域量子网络采用其他更多类型的QKD协议时, 需要重点考虑不同协议的特点进一步设计与研究.
-
本文面向两类QKD协议(BB84和MDI)组成的多域量子网络, 提出了MDI-BF和BB84-BF的域间密钥业务按需提供策略. 构建了多域跨协议量子网络的业务提供模型, 并且定义了密钥供需均衡度来衡量密钥供应与需求之间的均衡关系. 同时, 设计了内嵌MDI-BF和BB84-BF策略的域间密钥业务按需提供算法. 通过数值仿真, 在两类多域量子网络拓扑下以及高/低密钥率需求场景下, 开展了域间密钥业务请求成功率、密钥供需均衡度、可信节点数量等性能分析.
仿真结果表明, MDI-BF和BB84-BF策略在双域和三域量子网络中呈现出相似的性能优势, 验证了所提出的按需提供策略对于不同的多域量子网络具有较好的适用性. 此外, 针对不同的密钥率需求, BB84-BF与MDI-BF策略在不同性能指标下具有不同的性能优势, 例如, 在域间密钥业务请求成功率方面, MDI-BF策略更加适用于低密钥率需求(双域下相比传统策略提高30%), BB84-BF策略则更适合高密钥率需求(双域下相比传统策略提高19%). 同时, 两种按需提供策略相比传统策略可将密钥供需均衡度提高1个数量级以上. 综合来看, 所提出的两种按需提供策略均可以根据域间密钥业务的密钥率需求来进行密钥供应速率的动态调节, 有利于减少冗余密钥资源的产生, 从而实现更好的密钥供需适配.
由于QKD协议种类复杂多样, 本文未对双场类、纠缠类、连续变量类等协议进行分析, 未来可以针对更多不同类型QKD协议构建而成的多域量子网络开展研究. 此外, 不同的QKD系统可能具有不同的物理参数, 如光子自由度、维度、链路媒介等, 未来针对实际场景下不同的QKD系统还可以进一步探索, 进而提出多场景多约束下的域间密钥业务按需提供策略.
多域跨协议量子网络的域间密钥业务按需提供策略
On-demand provisioning strategy for inter-domain key services in multi-domain cross-protocol quantum networks
-
摘要: 现有的城域量子网络大多基于单一的量子密钥分发协议实现, 将不同协议实现的城域量子网络进行互联是大规模量子网络的发展趋势, 但其域间密钥业务提供仍存在成功率低、密钥供需不适配等问题. 针对以上问题, 本文面向多域跨协议量子网络提出了两种域间密钥业务按需提供策略, 分别是基于BB84(Bennett-Brassard-1984)旁路优先的按需提供策略和基于测量设备无关(measurement-device-independent, MDI)旁路优先的按需提供策略. 同时, 设计了内嵌两种策略的域间密钥业务按需提供算法. 仿真结果表明, 所提策略能够在双域和三域量子网络中高效完成域间密钥业务的按需提供. 相比传统策略, 两种按需提供策略可将多域量子网络的密钥供需均衡度提高1个数量级以上, MDI旁路优先策略在低密钥率需求下可将域间密钥业务请求成功率提升30%. 此外, 所提策略可在一定程度上降低域间密钥业务提供的成本, 提高现实安全水平.Abstract: Most of the existing metropolitan quantum networks are implemented based on a single quantum key distribution protocol, and interconnecting metropolitan quantum networks implemented by different protocols are the development trend of large-scale quantum networks, but there are still some problems in the provision of inter-domain key services, such as low possibility of success and mismatch between key supply and demand. To solve the above problems, this paper proposes two on-demand inter-domain key service provisioning strategies for multi-domain cross-protocol quantum networks, namely, on-demand provisioning strategy based on BB84 bypass first (BB84-BF) and on-demand provisioning strategy based on MDI bypass first (MDI-BF). Meanwhile, a service provisioning model for multi-domain cross-protocol quantum networks is constructed, and an on-demand inter-domain key service provisioning algorithm is designed. Moreover, numerical simulations and performance evaluation are carried out under two scenarios: high key rate demand and low key rate demand for two-domain and three-domain quantum network topologies. Simulation results verify that the proposed on-demand provisioning strategies have better applicability to different multi-domain quantum networks. In addition, for different key rate requirements, the MDI-BF strategy and BB84-BF strategys have different performance advantages under different performance indicators. For example, in terms of the success possibility of inter-domain key service requests, the MDI-BF strategy is more suitable for the low key rate requirements (~30% higher than the traditional strategies in two domain topologies), while the BB84-BF strategy is more suitable for the high key rate requirements (~19% higher than the traditional strategies under two domain topologies). In addition, compared with the traditional strategies, the proposed on-demand provisioning strategies can increase the balance degree between key supply and demand by more than one order of magnitude. Hence, the proposed strategies can reduce the cost of inter-domain key service provisioning and improve the realistic security level.
-
-
图 2 多域跨协议量子网络的密钥中继结构示例
Figure 2. Example of the key relay structure in a multi-domain cross-protocol quantum network.
图 3 密钥中继路径示例 (a) 传统策略; (b) MDI-BF策略; (c) BB84-BF策略
Figure 3. Examples of QKD relay paths: (a) Traditional strategy; (b) MDI-BF strategy; (c) BB84-BF strategy.
图 4 仿真使用的多域量子网络拓扑 (a) 双域拓扑; (b) 三域拓扑
Figure 4. Multi-domain quantum network topologies used for simulations: (a) Two-domain topology; (b) three-domain topology.
图 5 不同策略下域间密钥业务请求成功率随负载的变化关系 (a) 双域量子网络; (b) 三域量子网络
Figure 5. Success possibility of inter-domain key service requests versus traffic load for different strategies: (a) Two-domain quantum network; (b) three-domain quantum network.
图 6 不同策略下域间密钥业务请求成功率随最大延迟时间的变化关系
Figure 6. Success possibility of inter-domain key service requests versus maximum delay time for different strategies.
图 7 不同策略下全网最小密钥供应速率随负载的变化关系 (a) 双域量子网络; (b) 三域量子网络
Figure 7. Minimum key supply rate versus traffic load for different strategies: (a) Two-domain quantum network; (b) three-domain quantum network.
图 8 不同策略下密钥供需均衡度随负载的变化关系 (a) 双域量子网络; (b) 三域量子网络
Figure 8. Balance degree between key supply and demand versus traffic load for different strategies: (a) Two-domain quantum network; (b) three-domain quantum network.
图 9 不同策略下密钥供需均衡度随最大延迟时间的变化关系
Figure 9. Balance degree between key supply and demand versus maximum delay time for different strategies.
图 10 不同策略下平均可信节点数量随负载的变化关系 (a) 双域量子网络; (b) 三域量子网络
Figure 10. Average number of trusted nodes versus traffic load for different strategies: (a) Two-domain quantum network; (b) three-domain quantum network.
表 1 域间密钥业务按需提供算法
Table 1. Algorithm for on-demand provisioning of inter-domain key services.
输入: $G\left( {V, E} \right)$ ,
${V_{\text{B}}}$ ,
${V_{\text{M}}}$ ,
${V_{{\text{BJ}}}}$ ,
${V_{{\text{MJ}}}}$ ,
$R$ 
输出: 每个成功的域间密钥业务的密钥中继路径 ${p_r}\left( {{N_{{p_r}}}, {L_{{p_r}}}, {B_{{p_r}}}, {m_{{p_r}}}} \right)$ ,
${R_{\text{S}}}$ 
1 初始化变量 ${R_{\text{S}}} \leftarrow \emptyset $ ;
2 for 每个域间密钥业务请求 $r\left( {{s_r}, {d_r}, {k_r}, {t_r}} \right) \in R$ do
3 更新全网各节点设备占用状态; 4 如果源宿节点没有可用的QKD设备, 则该业务失败; 5 if 执行BB84-BF策略 then 6 for ${v_i} \in {V_{{\text{MJ}}}}$ do
7 if ${\lambda _{{v_i}}} < 2$ then
8 将 ${v_i}$ 从
$V$ 中移除并更新
$E$ ;
9 end if 10 end for 11 end if 12 基于K短路径算法计算源宿节点间的K条备选密钥中继路径, 路径集合为 ${P_r}$ ;
13 if ${P_r} = \emptyset $ then
14 域间密钥业务请求r失败; 15 end if 16 for 每条密钥中继路径 ${p_r}\left( {{N_{{p_r}}}, {L_{{p_r}}}, {B_{{p_r}}}, {m_{{p_r}}}} \right) \in {P_r}$ do
17 ${N_{{p_r}}} \leftarrow $ 
${p_r}$ 经过的QKD节点集合,
${L_{{p_r}}} \leftarrow $ 
${p_r}$ 经过的QKD链路集合,
${B_{{p_r}}} \leftarrow \emptyset $ ,
${m_{{p_r}}} \leftarrow {p_r}$ 的密钥供应
速率;18 for $n_{{p_r}}^i \in {N_{{p_r}}}$ do
19 if 执行MDI-BF策略 && $n_{{p_r}}^i \in {V_{{\text{MJ}}}}$ then
20 ${B_{{p_r}}} \leftarrow \{ {B_{{p_r}}}, n_{{p_r}}^i\} $ ;
21 end if 22 if $n_{{p_r}}^i \in {V_{\text{B}}}$ &&
$n_{{p_r}}^i \ne {d_r}$ &&
$n_{{p_r}}^i \ne {s_r}$ && (
${\lambda _{n_{{p_r}}^i}} = 0~||~{\varepsilon _{n_{{p_r}}^i}} = 0 $ ) then
23 ${B_{{p_r}}} \leftarrow \{ {B_{{p_r}}}, n_{{p_r}}^i\} $ ;
24 end if 25 end for 26 ${m_{{p_r}}} \leftarrow $ 根据更新后的密钥中继路径重新计算
${m_{{p_r}}}$ ;
27 if ${m_{{p_r}}} < {k_r}$ then
28 continue; 29 else 30 for $n_{{p_r}}^i \in {N_{{p_r}}}$ do
31 if 旁路 $n_{{p_r}}^i$ 后密钥中继路径密钥供应速率
$ \geqslant {k_r}$ then
32 ${B_{{p_r}}} \leftarrow \{ {B_{{p_r}}}, n_{{p_r}}^i\} $ , 更新
${m_{{p_r}}}$ ;
33 end if 34 end for 35 将 ${p_r}$ 作为域间密钥业务r的最终密钥中继路径,
${R_{\text{S}}} \leftarrow \left\{ {{R_{\text{S}}}, r} \right\}$ ;
36 break; 37 end if 38 end for 39 如果 ${P_r}$ 中没有满足密钥率需求的密钥中继路径, 则该业务失败;
40 end for 41 return 每个成功的域间密钥业务的密钥中继路径 ${p_r}\left( {{N_{{p_r}}}, {L_{{p_r}}}, {B_{{p_r}}}, {m_{{p_r}}}} \right)$ ,
${R_{\text{S}}}$ 
下载: 导出CSV
表 2 密钥生成率仿真参数
Table 2. Simulation parameters for key rates.
参数 取值 真空态误码率 ${e_0}$ 
0.5 本底误码 ${e_{\text{d}}}$ /%
1 暗计数率 ${p_{\text{d}}}$ 
${10^{ - 7}}$ 
探测效率 ${\eta _{\text{d}}}$ /%
40 纠错效率 ${f_{\text{e}}}$ 
1.16 光纤衰减常数 $\alpha $ /(dB·km–1)
0.2 重复频率/GHz 1
下载: 导出CSV
-
[1] Yang Z, Zolanvari M, Jain R 2023 IEEE Commun. Surveys Tuts. 25 1059 doi: 10.1109/COMST.2023.3254481 [2] Gill S S, Kumar A, Singh H, Singh M, Kaur K, Usman M, Buyya R 2022 Softw. Pract. Exp. 52 66 doi: 10.1002/spe.3039 [3] Lo H K, Curty M, Tamaki K 2014 Nat. Photon. 8 595 doi: 10.1038/nphoton.2014.149 [4] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shamsul S J, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photon. 12 1012 doi: 10.1364/AOP.361502 [5] Bennett C H, Brassard G 1984 IEEE Int. Conf. Comput. Syst. Signal Process. Bangalore, India, January, 1984 p175 [6] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503 doi: 10.1103/PhysRevLett.108.130503 [7] Li W, Zhang L K, Tan H, Lu Y C, Liao S K, Huang J, Li H, Wang Z, Mao H K, Yan B Z, Li Q, Liu Y, Zhang Q, Peng C Z, You L X, Xu F H, Pan J W 2023 Nat. Photon. 17 416 doi: 10.1038/s41566-023-01166-4 [8] Yin H L, Fu Y, Li C L, Weng C X, Li B H, Gu J, Lu Y S, Huang S, Chen Z B 2023 Nat. Sci. Rev. 10 nwac228 doi: 10.1093/nsr/nwac228 [9] Cao Y, Zhao Y, Wang Q, Zhang J, Ng S X, Hanzo L 2022 IEEE Commun. Surveys Tuts. 24 839 doi: 10.1109/COMST.2022.3144219 [10] Tang Y L, Yin H L, Zhao Q, Liu H, Sun X X, Huang M Q, Zhang W J, Chen S J, Zhang L, You L X, Wang Z, Liu Yang, Lu C Y, Jiang X, Ma X F, Zhang Q, Chen T Y, Pan J W 2016 Phys. Rev. X 6 011024 doi: 10.1103/PhysRevX.6.011024 [11] Joshi S K, Aktas D, Wengerowsky S, Lončarić M, Neumann S P, Liu B, Scheidl T, Lorenzo G C, Samec Ž, Kling L, Qiu A, Razavi M, Stipčević M, Rarity J G, Ursin R 2020 Sci. Adv. 6 eaba0959 doi: 10.1126/sciadv.aba0959 [12] Avesani M, Foletto G, Padovan M, Calderaro L, Agnesi C, Bazzani E, Berra F, Bertapelle T, Picciariello F, Santagiustina F, Scalcon D, Scriminich A, Stanco A, Vedovato F, Vallone G, Villoresi P 2023 Quantum Computing, Communication, and Simulation III San Francisco, United States, 2023 p112 [13] Cao Y, Zhao Y L, Zhang J, Wang Q, Niyato D, Hanzo L 2022 IEEE Netw. 36 14 doi: 10.1109/MNET.001.2200144 [14] Cao Y, Zhao Y L, Zhang J, Wang Q 2022 IEEE Commun. Mag. 60 38 doi: 10.1109/MCOM.001.2101006 [15] Zhou L, Lin J P, Xie Y M, Lu Y S, Jing Y M, Yin H L, Yuan Z L 2023 Phys. Rev. Lett. 130 250801 doi: 10.1103/PhysRevLett.130.250801 [16] Fan-Yuan G J, Lu F Y, Wang S, Yin Z Q, He D Y, Zhou Z, Teng J, Chen W, Guo G C, Han Z F 2021 Photonics Res. 9 1881 doi: 10.1364/PRJ.428309 [17] Tysowski P K, Ling X, Lütkenhaus N, Mosca M 2018 Quantum Sci. Technol. 3 024001 doi: 10.1088/2058-9565/aa9a5d [18] Li P, Yu X, Zhao Y, Zhang J 2023 Opto-Electronic and Communications Conference Shanghai, China, July 2–6, 2023 p1 [19] Gottesman D, Lo H K, Lutkenhaus N, Preskill J 2004 Quantum Inf. Comput. 4 325 doi: 10.26421/qic4.5-1 [20] Ma X F, Qi B, Zhao Y, Lo H K 2005 Phys. Rev. A 72 012326 doi: 10.1103/PhysRevA.72.012326 [21] Xu F H, Xu H, Lo H K 2014 Phys. Rev. A 89 052333 doi: 10.1103/PhysRevA.89.052333 [22] Ma X F, Fung C H F, Razavi M 2012 Phys. Rev. A 86 052305 doi: 10.1103/PhysRevA.86.052305 [23] Wang X B 2013 Phys. Rev. A 87 012320 doi: 10.1103/PhysRevA.87.012320 [24] Yu Z W, Zhou Y H, Wang X B 2013 Phys. Rev. A 88 062339 doi: 10.1103/PhysRevA.88.062339 [25] Curty M, Xu F, Cui W, Lim C C W, Tamaki K, Lo H K 2014 Nat. Commun. 5 3732 doi: 10.1038/ncomms4732 [26] Wang Q, Wang X B 2014 Sci. Rep. 4 4612 doi: 10.1038/srep04612 [27] Zhou Y H, Yu Z W, Wang X B 2016 Phys. Rev. A 93 042324 doi: 10.1103/PhysRevA.93.042324 -
计量
- 文章访问数: 234
- HTML全文浏览数: 234
- PDF下载数: 7
- 施引文献: 0