量子密钥分发(quantum key distribution, QKD)基于量子力学基本原理在理论上为远程通信双方之间共享信息安全的密钥提供了一种前景广阔的解决方案^[1,2], 已成为一种可行的网络安全技术, 是最有希望实现商业化的量子通信协议之一^[3,4]. 连续变量量子密钥分发(continuous variable quantum key distribution, CVQKD)得益于承载密钥信息的相干态易于制备、可利用相干光电信系统中的组件来构建系统、便于芯片的集成等优势, 近年来受到广泛关注^[5–8], 在安全性证明^[9,10]、实验实现^[11–15], 以及方案改进与性能提升^[16–19]等方面已经取得了较大的进展.

在CVQKD的实验实现中, 正交分量的高斯调制通常通过独立调制相干态的幅度和相位实现^[20]. 然而, 光电调制器电压的有限分辨率特性将导致调制离散化效应的出现, 即原本服从瑞利分布的连续幅度和服从均匀分布的连续相位均退化为离散输出^[21–23], 两者的耦合导致理想的高斯调制退化为离散极化调制(discretized polar modulation, DPM)^[24,25]. 调制离散化效应会造成调制后的正交分量取值偏离真实值, 其影响在制备-测量模型中可以通过正交分量取值的波动表示, 在纠缠等效模型中可以建模为光源端的可信过量噪声^[24].

虽然DPM-CVQKD依然能够实现密钥分发, 但其安全密钥率和传输距离相较于理想高斯调制的CVQKD都会有所下降. 为补偿实际物理场景下的调制离散化效应, 本文使用线性光学克隆机(linear optics cloning machine, LOCM)对DPM-CVQKD进行改进, 在考虑实际探测器的情况下, 提出了LOCM改进的DPM-CVQKD方案(LOCM DPM-CVQKD), 应用LOCM实现可控的放大增益, 进而弥补DPM带来的性能下降. LOCM由线性光学、外差探测, 以及可控位移构成, 被置于接收方一侧^[26,27]. 它借助本征相关性可以生成量子态的近似克隆, 从而代替了传统方案中利用高强度光源泵浦的非线性介质^[28]. 这不仅实现了可控的放大增益, 而且还降低了对高强度光源的依赖, 但其代价则是引入更多的过量噪声. 引入的噪声可以通过在适当的范围内动态调节LOCM的相关参数加以补偿, 其调节过程等效于调节信道附加噪声和外差探测器的信噪比, 从而实现对可容忍过量噪声的动态平衡. 可调谐的LOCM噪声允许信息协调的参考方对估计的散粒噪声进行偏置^[29], 这增加了Alice和Bob之间的互信息, 提高了系统的探测效率和对过量噪声的抗性^[30], 将其应用在DPM-CVQKD中有助于克服调制离散化效应带来的性能退化, 并提升安全密钥率和传输距离.

本文内容安排如下: 第2部分详细介绍了LOCM DPM-CVQKD的PM方案及其EB方案, 并进行安全性分析; 第3部分对本文所提方案进行了数值仿真, 验证了幅值和相位离散化的综合效应, 以及LOCM相关参数对系统的影响, 评估了可组合安全分析下有效码长对传输距离和安全密钥率的影响; 第4部分是对全文的总结.

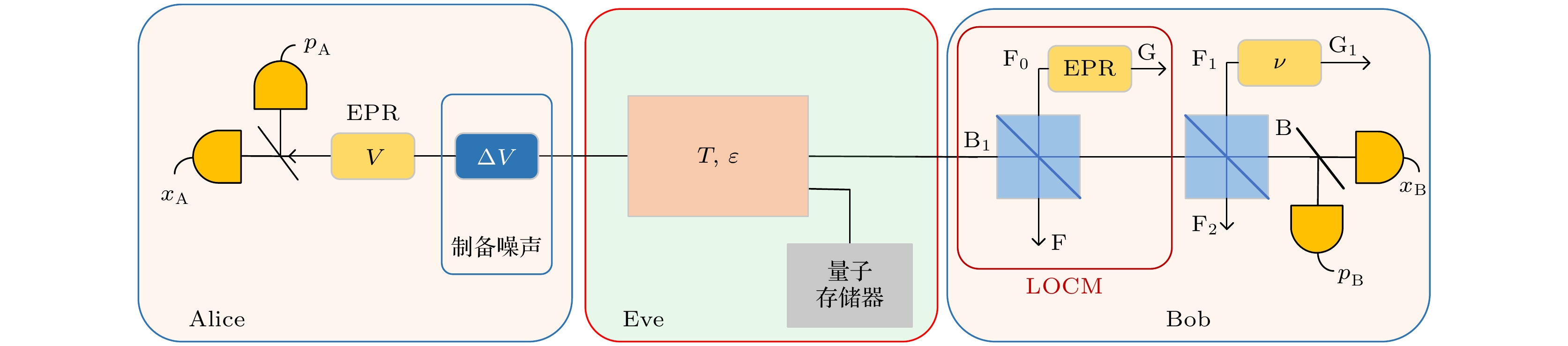
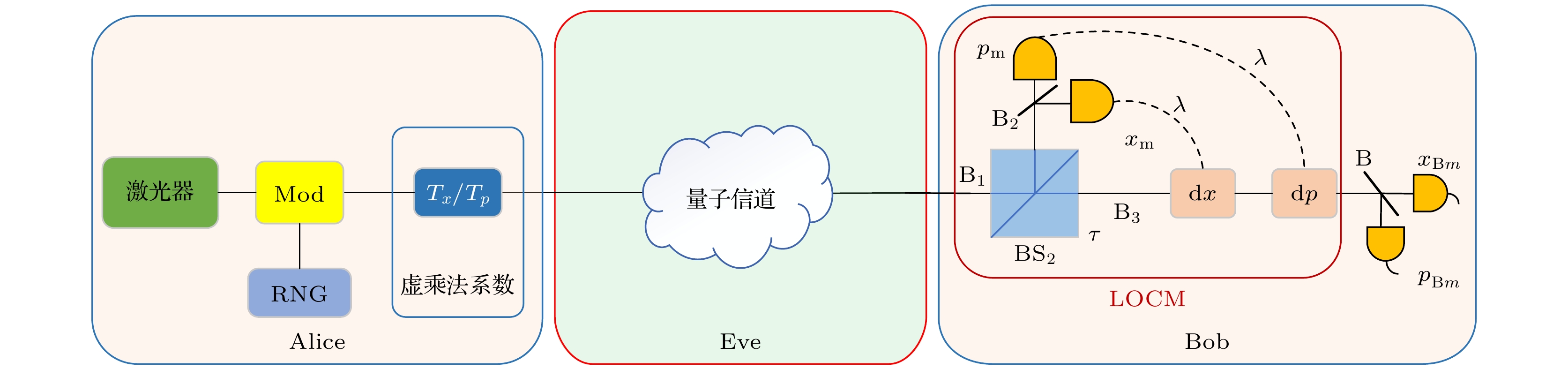
LOCM DPM-CVQKD的PM方案如图1所示. 在发送端, Alice通过激光器、随机数生成器以及调制器将经典的随机变量$\alpha $编码在相干态上以完成量子态的制备过程, 最终生成了服从高斯分布$ \mathcal{N}\left( {0, {V_{\text{A}}}} \right) $的随机数$\left( {{x_{\text{A}}}, {p_{\text{A}}}} \right)$, 其幅度$A = \sqrt {x_{\text{A}}^{2} + p_{\text{A}}^{2}} $, 相位$\theta = \arctan ({{{p_{\text{A}}}}}/{{{x_{\text{A}}}}})$分别服从瑞利分布和均匀分布. 幅度和相位将被采样和离散化后分别独立地通过高斯调制器调制到相干态$\left| \alpha \right\rangle = \left| {{x_{\text{A}}} + {\text{i}}{p_{\text{A}}}} \right\rangle $上, 其离散化的联合效应在PM方案中由虚乘法系数$ {{{T_x}} {/ } {{T_p}}} $进行建模.

在调制器引起的离散化中, 相干态的幅度和相位等价于通过了均匀量化器进行离散化. 假设幅度和相位的分辨率分别为${\delta _{\text{a}}}$和${\delta _{\text{p}}}$, 经过离散化后, 幅度A被分割成大小为${\delta _{\text{a}}}$的N个等间隔区间的集合, 相位$\theta $被分割成大小为${\delta _{\text{p}}}$的M个等间隔区间的集合, 从数值上可分别表示为^[24]

其中$M = 2{\text{π}}/{\delta _{\text{p}}}$. 此时, 任何位于区间j内的幅度A将被投影输出为$ {A^ * } = (j + 0.5){\delta _{\text{a}}} $, 而任何位于区间k内的相位$\theta $则将被投影输出为$ {\theta ^ * } = (k + 0.5){\delta _{\text{p}}} $.

当相干态的幅度和相位被离散化后, 调制后的正交分量将会出现相应的波动^[25], 这种波动状态可以被定量表达为

其中, $ \Delta A = A - {A^ * } \in \left[ { - {\delta _{\text{a}}}/2, {\delta _{\text{a}}}/2} \right) $, $ \Delta \theta = \theta - {\theta ^ * } \in \left[ { - {\delta _{\text{p}}}/2, {\delta _{\text{p}}}/2} \right) $分别代表幅值和相位的波动程度, 当$ \Delta A $和$ \Delta \theta $趋近于0时, $ x_{{\text{A}}}^{{*}}/p_{{\text{A}}}^{{*}} $将逐渐逼近并收敛于理想高斯分布比值$ {x_{\text{A}}}/{p_{\text{A}}} $. 为了更精确地描述高斯调制的离散化效应, 引入虚拟乘法系数${T_x}/{T_p}$来建模正交分量的波动程度^[24], 可以表示为

此时, (2)式可以重写为以下形式:

因为低幅度值比低相位值更容易受到离散化影响, 会直接导致DPM的估计特性严重偏离于真实统计数据. 因此, 这需要通过预选择过程来剔除最容易被离散化的原始数据样本, 以减小偏离程度, 确保调制估计的准确性^[24,25]. 在本文的预选择过程中, 阈值设定为${\eta _{{\text{th}}}} = {\delta _{\text{a}}}$, 会使得虚乘法系数${T_x}/{T_p}$的分布更为集中, 趋近于理想值1, 这也意味着DPM方案正在向理想高斯调制靠近.

在接收端, Bob利用LOCM来放大Alice发送的量子态, 通过3 dB分束器将输入的量子态分为两个部分, 其中一部分与真空态在分束器中进行干涉后利用外差探测器分别测量x和p正交分量. 根据测量结果${x_m}$以及增益$\lambda $对另一部分进行修正后将作为另一模式的位移量, 通过正确选择, Bob可以得到线性放大器对信号模态的变换, 并应用外差探测完成量子态的传输过程. 最后经过参数估计、误码纠错、保密增强和信息协调这一系列后处理过程完成密钥分发过程.

在LOCM中, 受调制离散化效应影响的相干态会经过分束器被分割为两个模式, 其中一个模式被送入一个外差探测器进行探测, 探测后的结果输出会乘以调谐增益$\lambda $进行修正后作为另一模式的位移量^[27]. 最终的输出模式可以表达为

其中$ \tau $是分束器的透射率, $ {x_{{\text{vac}}}} $是具有单位方差的真空噪声. LOCM可视为对输入态的具有等效增益$ G = {1}/({{1 - \tau }}) $的线性放大器, 其输出方差为

LOCM DPM-CVQKD经过PM方案转换的EB (equivalent entanglement-based)方案如图2所示. 在发送端, Alice会制备一个方差为V的EPR态, 对其中一个模式进行外差探测, 得到$\left( {{x_{\text{A}}}, {p_{\text{A}}}} \right)$的值, 并将另一模式投影至以$\left( {{x_{\text{A}}}, {p_{\text{A}}}} \right)$为中心的相干态上. 相干态的幅度和相位离散化的联合效应造成的调制正交分量的波动可建模为在发送端引入的制备噪声. 经过预选择后, Alice制备的离散化相干态$\left( {x_{\text{A}}^{{*}}, p_{\text{A}}^{{*}}} \right)$将通过不可信的量子信道传输给接收端, 此量子信道特征由透射率T和过量噪声$\varepsilon $进行描述. 在接收端, Bob会应用LOCM对传输的量子态进行放大, EPR态的其中一个模式会与传输的离散化相干态在分束器中进行干涉, 利用外差探测器来测量分束器输出的一个模式以得到最终的输出结果. 一方面, 用方差为${N_{{\text{LOCM}}}}$的EPR态对LOCM引入的热噪声进行建模, 另一方面, 可以直接用虚拟分束器的透射率${T_{{\text{LOCM}}}}$来等效地描述LOCM的探测效率, 在数学上可表达为^[28]

因此, 由LOCM引入的噪声可以由下式给出:

传输的量子态经LOCM放大后, 利用实际外差探测器进行测量, 用方差为$\upsilon $的EPR态和传输效率为$\eta $的分束器分别对探测器的电子噪声${\upsilon _{{\text{el}}}}$和探测效率进行建模. 此时, 系统经过正交分量的波动以及插入LOCM之后, 其协方差矩阵可表示为

其中, $V = {V_{\text{A}}} + 1$, I₂为单位矩阵$\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)$, $\boldsymbol\sigma_z$为泡利矩阵$\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)$, $T = {10^{ - \tfrac{{0.2 L}}{{10}}}}$, L代表着通信双方之间的传输距离, $\left\langle \cdot \right\rangle $表示均值操作, DPM引起的离散化效应可被建模为方差为$ E = \left( {\left\langle {T_x^2} \right\rangle - 1} \right){V_{\text{A}}} $的制备噪声. ${\chi _{{\text{tot}}}}$代表归因于信道输入的总噪声, 可以表达为^[31]

其中, ${\chi _{{\text{line}}}} = {1}/{T} - 1 + \varepsilon $为信道传输过程中引入的总噪声, ${\chi _{{\text{LOCM}}}}$为LOCM引入的噪声, ${\chi _{{\text{het}}}} = ( 2 - \eta + 2{\upsilon _{{\text{el}}}} ) {/ } \eta $为外差探测器引入的噪声, 其中$\eta $和${\upsilon _{{\text{el}}}}$分别表示Bob探测器的量子效率和电子噪声.

LOCM DPM-CVQKD方案在反向协调和集体攻击下的安全密钥率可表示为^[32]

其中, $ {p_{{\text{ps}}}} $是经过预选择和用于密钥分发的信号态的百分比, $ {I_{{\text{AB}}}} $是Alice和Bob之间的香农互信息, $ {S_{{\text{BE}}}} $是Bob和Eve之间的互信息的Holevo界, 代表集体攻击下Eve的最大窃取信息, $ \beta $是反向协调的协调效率. 一方面, 根据协方差矩阵$ {\gamma _{{\text{AB}}}} $可以计算$ {I_{{\text{AB}}}} $, 由下式给出:

另一方面, $ {S_{{\text{BE}}}} $可以表达为

其中, $ S(E) $为量子态$E$的冯诺依曼熵, $ S(E|B) $为条件冯诺依曼熵, 取决于协方差矩阵的辛特征值. 在Bob进行外差探测后, Eve可以纯化整个系统, 有$ S(E) = S(AB) $以及$ S(E\left| B \right.) = S(A\left| B \right.) $. 因此, (13)式又可重写为

其中, $G\left( x \right) = \left( {x + 1} \right){\log _2}\left( {x + 1} \right) - x{\log _2}\left( x \right)$, $ {\lambda _i}, i = 1, 2, 3, 4, 5 $为辛特征值, 且${\lambda _5} = 1$. ${\lambda _1}$和${\lambda _2}$可由协方差矩阵${\gamma _{{\text{AB}}}}$确定, 表示为

其中$ A = \det {\gamma _{\text{A}}} + \det {\gamma _{\text{B}}} + \det {\sigma _{{\text{AB}}}} $和$ B = \det {\gamma _{{\text{AB}}}} $. ${\lambda _3}$和${\lambda _4}$可由矩阵${\gamma _{{\text{A}}{{\text{F}}_{0}}{\text{G}}{{\text{F}}_{2}}{{\text{G}}_{1}}}}$确定, 表示为

此时, ${\lambda _3}$和${\lambda _4}$可通过下式进行计算:

其中,

基于上述详尽的推导与分析, 将(12)式和(14)式代入(11)式, 我们可以得到渐进情况下安全密钥率的表达式, 进而可以对LOCM DPM-CVQKD方案的安全性进行评估. 然而, 考虑到实际应用中安全密钥长度的固有局限性, 直接实现这一理论安全性是十分困难的. 因此, 本文采用可组合安全性分析框架进一步对所提方案进行评估, 可使得DPM-CVQKD与LOCM结合使用时, 即使是在有限码长的情形下, 整体协议的安全性仍然能够得到保证^[33–35].

可组合安全性分析允许密钥具有较小的失效概率$ \varepsilon $, 这是因为在密钥生成过程中, 受限于样本量的规模, 统计结果往往难以完全符合理论预期, 存在一定程度的偏差或波动. 通过设置一个较小的失效概率阈值$ \varepsilon $, 在统计波动的允许范围内, 可以确保生成的密钥仍然具有足够高的安全性^[33]. 这一设置有效地平衡了安全性的保障与实际操作中的限制, 使得整个量子密钥分发协议在复杂多变的现实环境中依然能够稳健运行. 如果LOCM DPM-CVQKD是${\varepsilon _{{\text{cor}}}}$正确, ${\varepsilon _{{\text{sec}}}}$保密, 满足$\varepsilon \geqslant {\varepsilon _{{\text{cor}}}} + {\varepsilon _{{\text{sec}}}}$, 那么此方案是$\varepsilon {\text{-secure}}$安全的^[34]. 具体而言, ${\varepsilon _{{\text{cor}}}}$代表通过纠错后不同字符串的残差概率的界限量, ${\varepsilon _{{\text{sec}}}}$代表最终密钥与窃听者完全解耦的理想输出经典量子态之间距离的界限量, 满足

其中${\varepsilon _{\text{s}}}$是平滑参数, ${\varepsilon _{\text{h}}}$是哈希参数. 在本文提出的方案中, 使用下式作为安全参数可保证LOCM DPM-CVQKD是$\varepsilon {\text{ - secure}}$安全的:

其中${p_{{\text{ec}}}}$是误码纠错步骤中的成功概率, ${\varepsilon _{{\text{PE}}}}$是参数估计的失败概率. 与此同时, (11)式中$\beta {I_{{\text{AB}}}}$和$ {S_{{\text{BE}}}} $又可重写为

其中, $ H{\left( {l\left| E \right.} \right)_\rho } $是在单克隆态$\rho $下进行计算的条件冯诺依曼熵, $ S{\left( {l:E} \right)_\rho } $是Eve对代表d比特字符的离散变量l的Holeve界, $H\left( l \right)$是l的香农熵, $ {\text{lea}}{{\text{k}}_{{\text{ec}}}} $是误码纠错期间Bob发送给Alice的侧信息大小. 因此, LOCM DPM-CVQKD方案的可组合性安全密钥率的最低界可表示为^[33]

其中, d是每个测量结果的编码位数, n是用于密钥分发的码长数量. $ {\varDelta _{{\text{aep}}}}\left( {{\varepsilon _{\text{s}}}, d} \right) $和$ \varTheta $可表示为

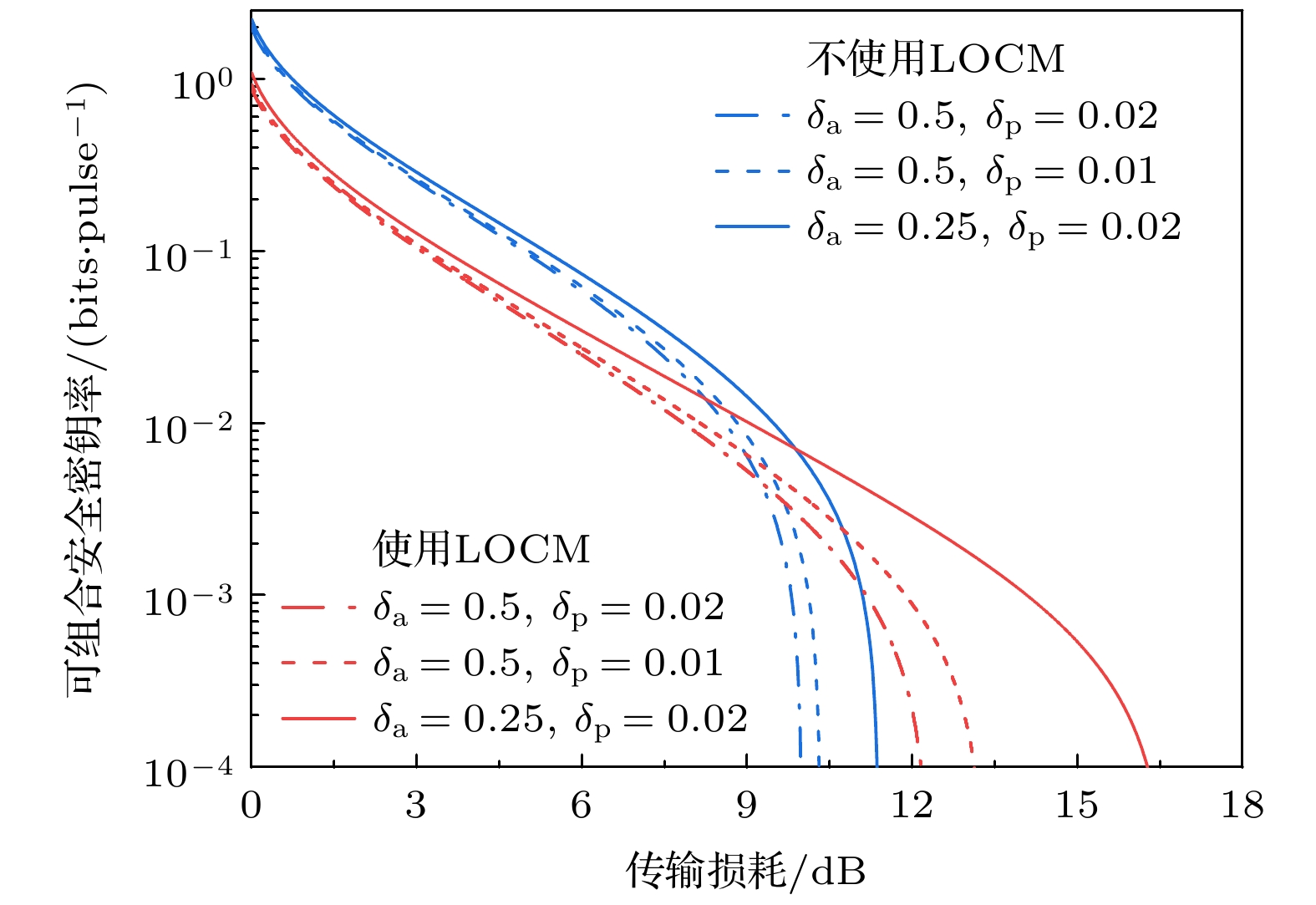
基于上述分析, 我们推导出了LOCM DPM-CVQKD的可组合安全密钥率, 现对此方案的系统性能进行评估. 本文设置的参数如下: $ {V_{\text{A}}} = 25 $, ${p_{{\text{ps}}}} = 1$, $\beta = 0.96$, $\varepsilon = 0.02$, $\eta = 0.6$, ${\upsilon _{{\text{el}}}} = 0.01$, ${p_{{\text{ec}}}}$ = 0.9, d = ${2^5}$, $n = {10^{10}}$, $ {\varepsilon _{\text{h}}} = {\varepsilon _{\text{s}}} = {10^{ - 10}} $, LOCM参数取值为: $\lambda = 0.47$, $\tau = 0.20$.

为了对所提方案的性能进行评估, 我们将DPM-CVQKD方案与LOCM DPM-CVQKD方案在不同幅度分辨率和相位分辨率下进行了详细的对比研究, 结果如图3所示. 在传输损耗较小的场景中, LOCM DPM-CVQKD的安全密钥率低于DPM-CVQKD方案. 其原因在于LOCM以引入过量噪声为代价来提高系统性能, 在传输损耗较小时, 传输的信号衰减相对较小, 此时LOCM引入的过量噪声会导致信噪比下降, 即使通过设置LOCM的相关参数对其进行调节, 也无法在损耗较小时完全对幅度和相位的离散化效应进行补偿, 此时LOCM对系统性能具有负面影响.

然而随着传输损耗的不断增大, LOCM的应用展现出了显著的优势, 在${\delta _{\text{a}}} = 0.25$, ${\delta _{\text{p}}} = 0.02$的情形下, 其最大传输损耗达到了16.67 dB, 比未使用LOCM时高出了5.29 dB. 这是因为在传输一定距离之后, 信号衰减明显增加, LOCM能够有效补偿这种衰减, 通过放大接收信号提升系统性能. 而DPM CVQKD方案在传输损耗稍大时, 信号衰减无法得到补偿, 离散化带来的综合效应对系统的影响也变得显著. 这证明了本文所提方案不仅能够优化安全密钥率, 还能够提升最大传输损耗, 且在传输损耗增大时表现出了更为明显的优势.

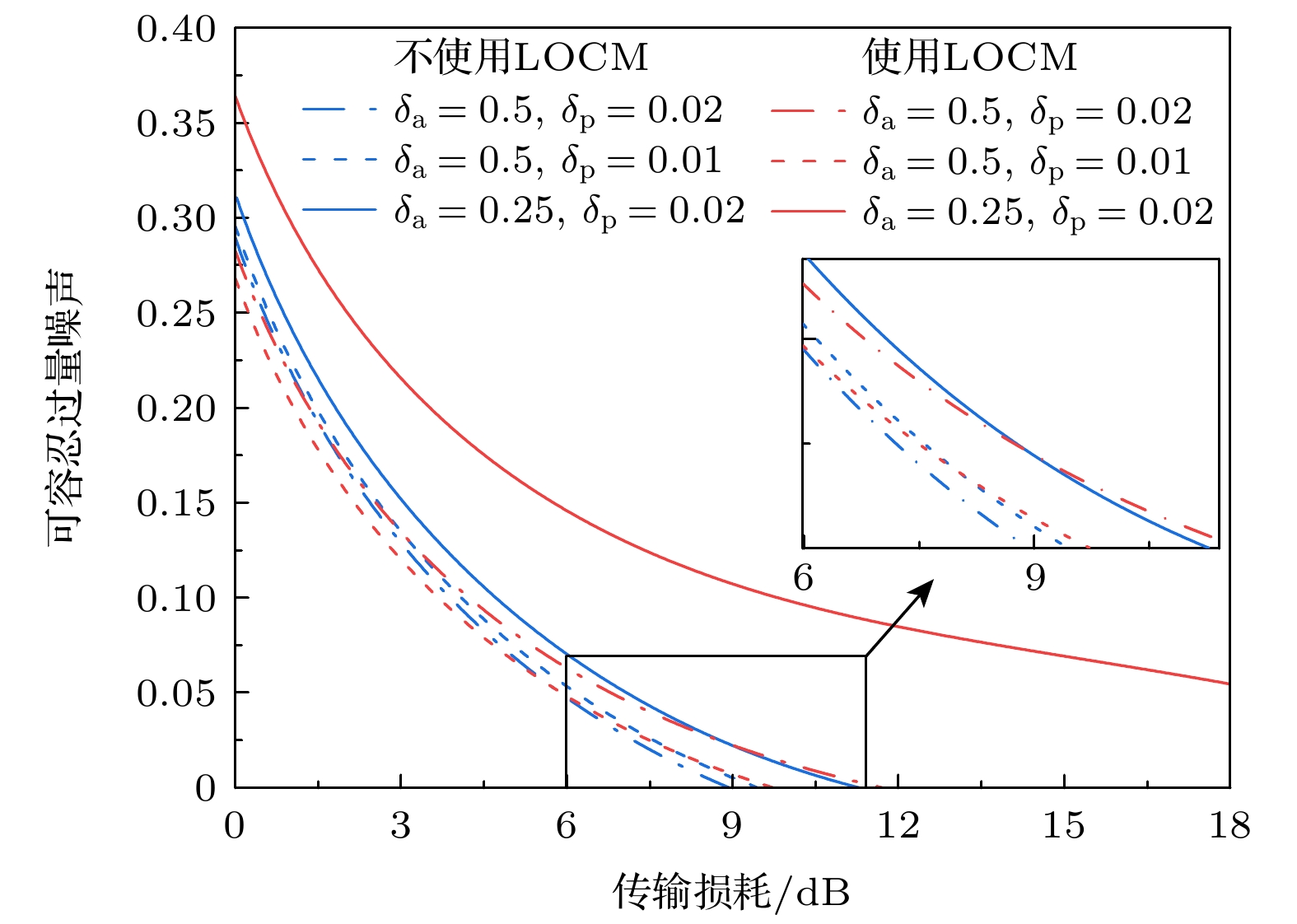
此外, 从图3中可以清晰地看出LOCM调制离散化效应起到了补偿作用. 随着δ_a和δ_p的变化, LOCM DPM-CVQKD的可组合安全密钥率和传输损耗均有所改进, 尤其是对幅度离散化的补偿作用更为显著. 在添加LOCM后, 在${\delta _{\text{a}}} = 0.5$, ${\delta _{\text{p}}} = 0.02$的配置下, 最大安全传输损耗改进了1.5 dB, 而${\delta _{\text{a}}} = 0.25$, ${\delta _{\text{p}}} = 0.02$的配置要比前一种情况多改进了3.79 dB. 这凸显了LOCM能够有效地补偿正交分量的波动, 抑制幅度和相位的离散化过程对系统性能的负面影响, 这是因为通过调节相关参数提供的可调谐放大增益, LOCM对传输过程中的离散化的量子态进行了等效放大, 增强了传输量子态的强度, 提高了传输信号的信噪比, 使得幅度波动和相位波动相对于整体信号功率的占比下降, 从而提升了系统性能. 相比之下, 幅度离散化导致的正交分量波动要强于相位离散化导致的正交分量波动, 因而LOCM对幅度离散化的补偿效果体现得更加明显. 以上结果表明LOCM不仅有效地弥补了离散化过程带来的信息损失造成的性能下降, 还补偿了传输过程中的信号衰减, 也表明了即使量子态经历了离散化过程, 系统仍然能够维持较高的安全密钥生成率和较大的可容忍传输损耗, 提升了系统的稳定性和效率.

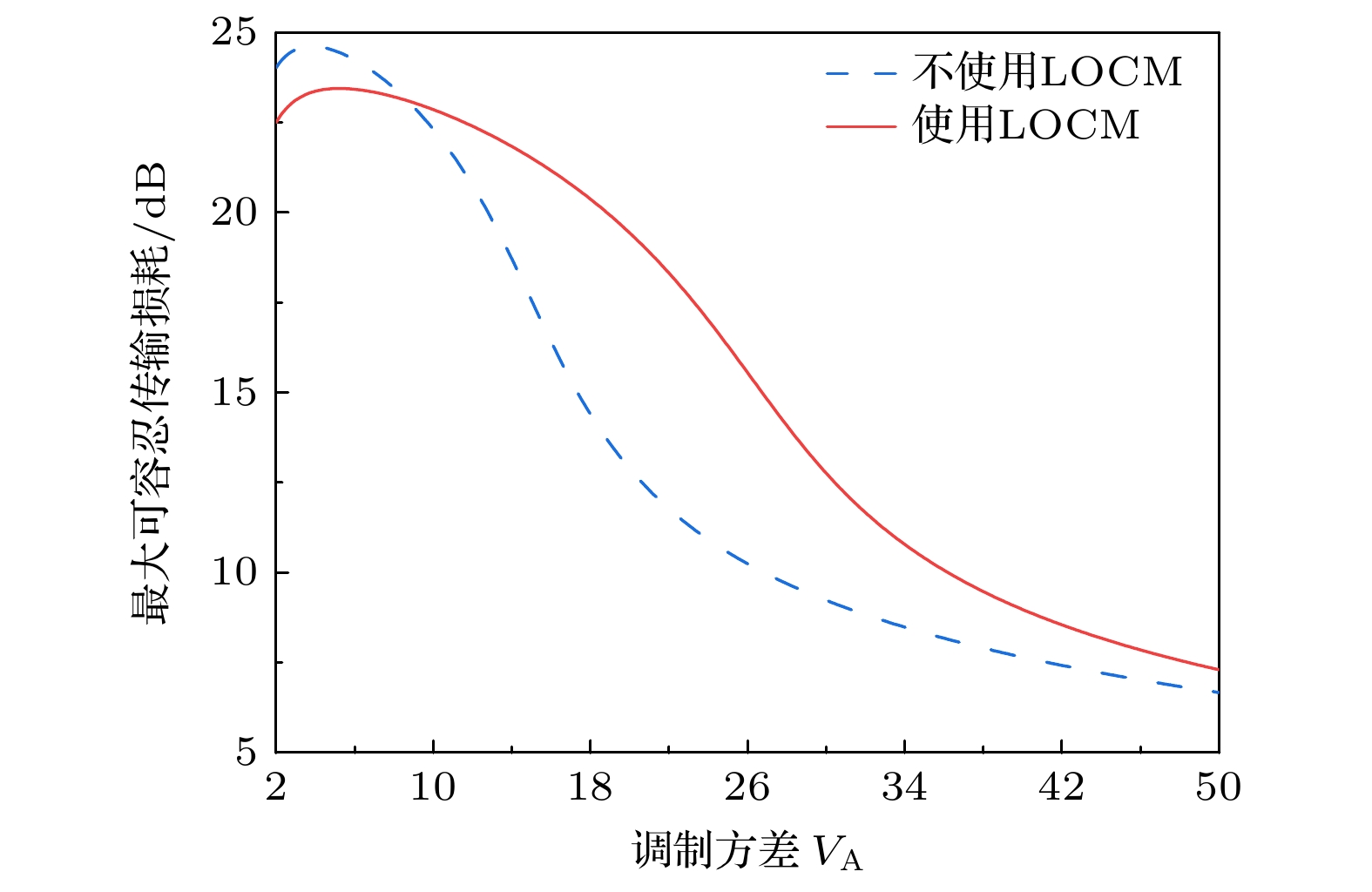
LOCM DPM-CVQKD方案通过引入一定程度的噪声来实现系统性能的提升, 系统的可容忍过量噪声也因此发生改变, 其与传输损耗之间的关系如图4所示. DPM-CVQKD方案和LOCM DPM-CVQKD方案均呈现逐渐下降的趋势, 但是因为LOCM能够弥补幅度和相位离散化过程造成的影响, 所以添加了LOCM的可容忍噪声要比未添加LOCM的略高. 值得注意的是, 添加LOCM后方案相位分辨率对可容忍过量噪声基本上可以忽略不计, 而幅值分辨率的降低则会显著提高系统的可容忍过噪声水平. 具体来说, LOCM DPM-CVQKD方案在${\delta _{\text{a}}} = 0.5$, ${\delta _{\text{p}}} = 0.02$的情形下, 可容忍过量噪声达到最大值0.2827; 而在${\delta _{\text{a}}} = 0.25$, ${\delta _{\text{p}}} = 0.02$的情形下, 可容忍过量噪声达到最大值0.3641, 相比前一种情况提高了0.0814. 这种改善是源于LOCM通过可调谐的参数将引入的噪声转变成了有利于系统的噪声范围之内, 等价于调节了探测器的信噪比, 从而增加了Alice和Bob之间的互信息, Bob和Eve之间的互信息则保持不变. 因此, 利用LOCM改进, 可以提高CVQKD系统对过量噪声的可容忍能力.

方差的选择会影响系统的最大可容忍传输损耗, 如图5所示. 当方差低于阈值8.4时, 未添加LOCM的DPM-CVQKD的可容忍传输损耗明显要优于加入LOCM后的DPM-CVQKD, 但是当方差大于阈值8.4时, LOCM DPM-CVQKD方案反而优于未加入LOCM的DPM-CVQKD方案. 这种变化的原因在于, 当方差较小时, LOCM引入的可调谐噪声无法被有效地控制在有利范围内, 甚至会对系统性能造成衰退, 严重限制了对幅值离散化和相位离散化所产生的综合效应的补偿效果, 其优化作用未能得到充分发挥. 在本文的研究中, 所提出方案的最大可容忍传输损耗能够达到16.67 dB, 而DPM-CVQKD只能达到11.38 dB, 体现出了对系统参数优化的必要性, 也充分证明了LOCM在特定条件下对系统性能提升的重要作用.

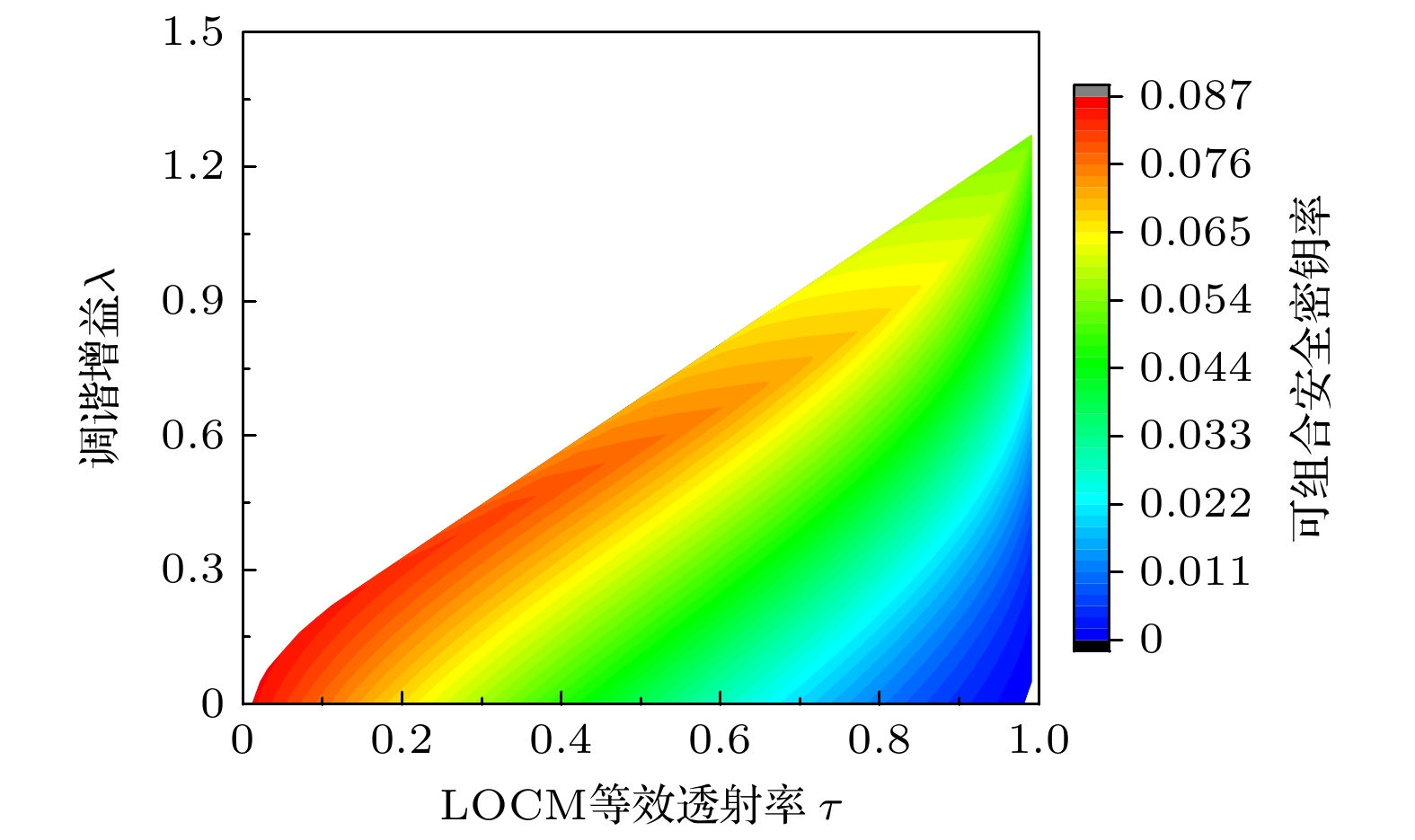
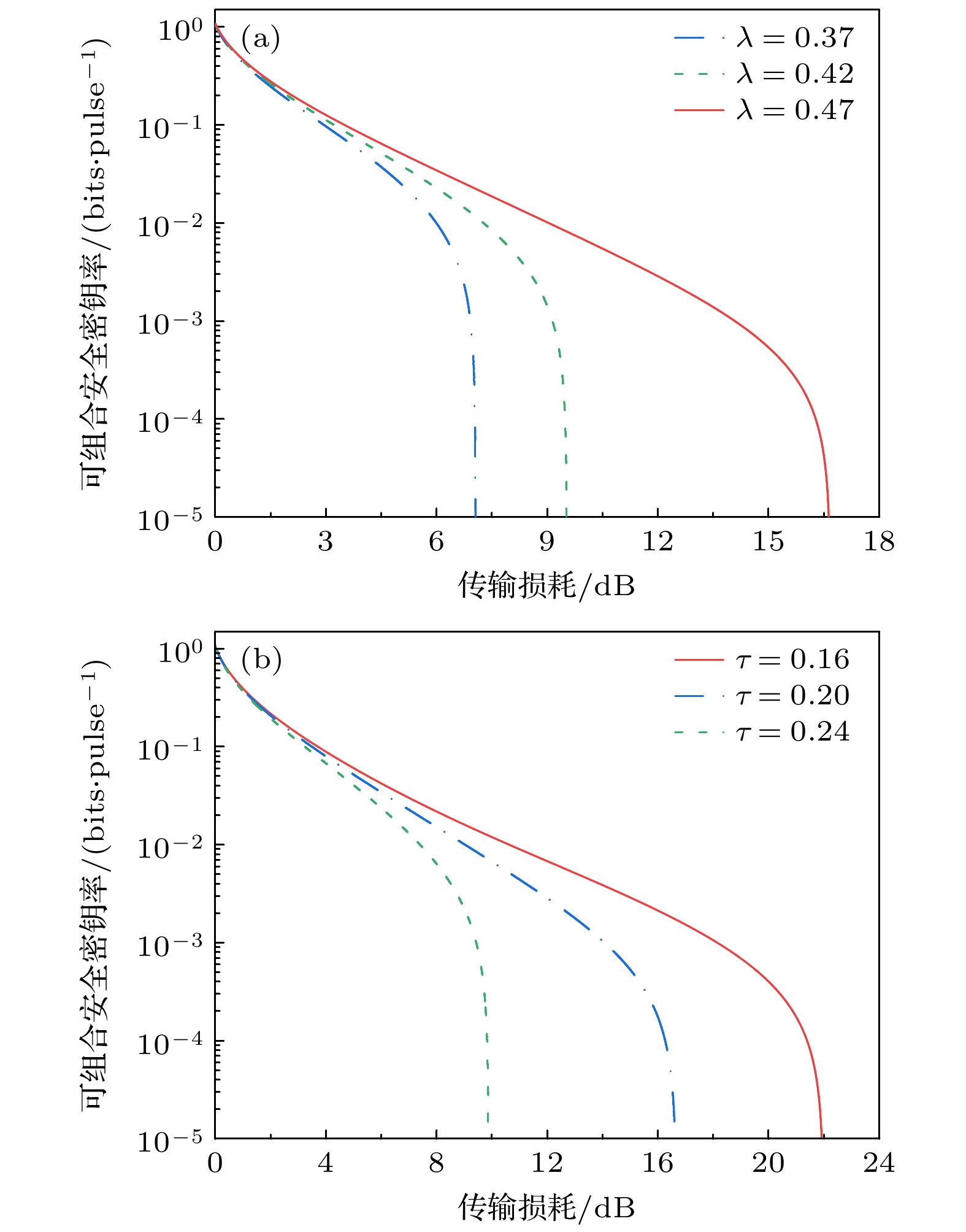
基于上述分析可知, 通过调节LOCM的调谐增益$\lambda $以及透射率$\tau $可实现对LOCM噪声的灵活控制, 这两个参数对可组合安全密钥率的影响如图6所示. 从图6可以观察到, 随着$\tau $的不断增大, 可组合性安全密钥率呈现单调减小的趋势. 但是, 随着$\lambda $的不断增大, 可组合性安全密钥率呈现先增大后减小的趋势. 这种结果表明, 对于固定的$\tau $值, 总能在可控制的范围内找到一个与之匹配的$\lambda $值, 从而使得可组合安全密钥率达到最优值. 这也是因为LOCM引入的可调谐噪声必须控制在有利的范围内才能使其转变成有益于系统的噪声. 通过这种调控, 我们能灵活地优化系统性能, 有效弥补幅值和相位离散化带来的影响.

LOCM参数的选择对于系统的性能也具有至关重要的影响, 不仅体现在对可组合安全密钥率的作用上, 还体现在对传输损耗的作用上, 如图7所示. 从图7(a)可以看出, 随着$\lambda $的逐渐增大, 传输损耗会呈现单调增大的趋势, 而图7(b)表明随着$\tau $的不断增大, 传输损耗则会呈现单调减小的趋势. 在所选择的参数配置中, 当$\lambda = 0.47$, $\tau = 0.2$时, 传输损耗达到了16.67 dB, 这一配置即可满足系统性能提升的需求. 基于前述分析可知, LOCM可视作一个具有线性放大特性的放大器, 其等效放大增益主要受到$\tau $的直接影响. 当$\tau $保持不变的情况下, 其放大增益就是固定的, 那么此时LOCM引入的噪声也只与$\tau $相关. 因此, 在保证LOCM引入的噪声仍然处于对系统有利的范围内的前提下, 只要调节参数$\lambda $至使传输损耗达到最大值, 就可以实现系统性能的最优化.

由图6和图7可以看出, 本方案对系统性能的提升效果依赖于对LOCM参数的精准优化. 由于在实际场景下, LOCM的最优参数组合会受到发送端的调制方差、量子信道的过量噪声和接收端的接收效率等多重因素的影响, 难以求出精确的解析解, 因而可以通过应用机器学习算法估计. 机器学习已被广泛应用于QKD参数的实时预测与动态补偿中, 并取得了良好的效果^[36–40]. 针对本文所提方案, 在参数估计阶段可使用启发式优化算法基于估计结果对LOCM的参数进行寻优; 在系统运行过程中则可构建面向时间序列的机器学习模型, 预测信道过量噪声的潜在变化并主动搜寻LOCM的最优参数配置, 以充分发挥LOCM的改进作用.

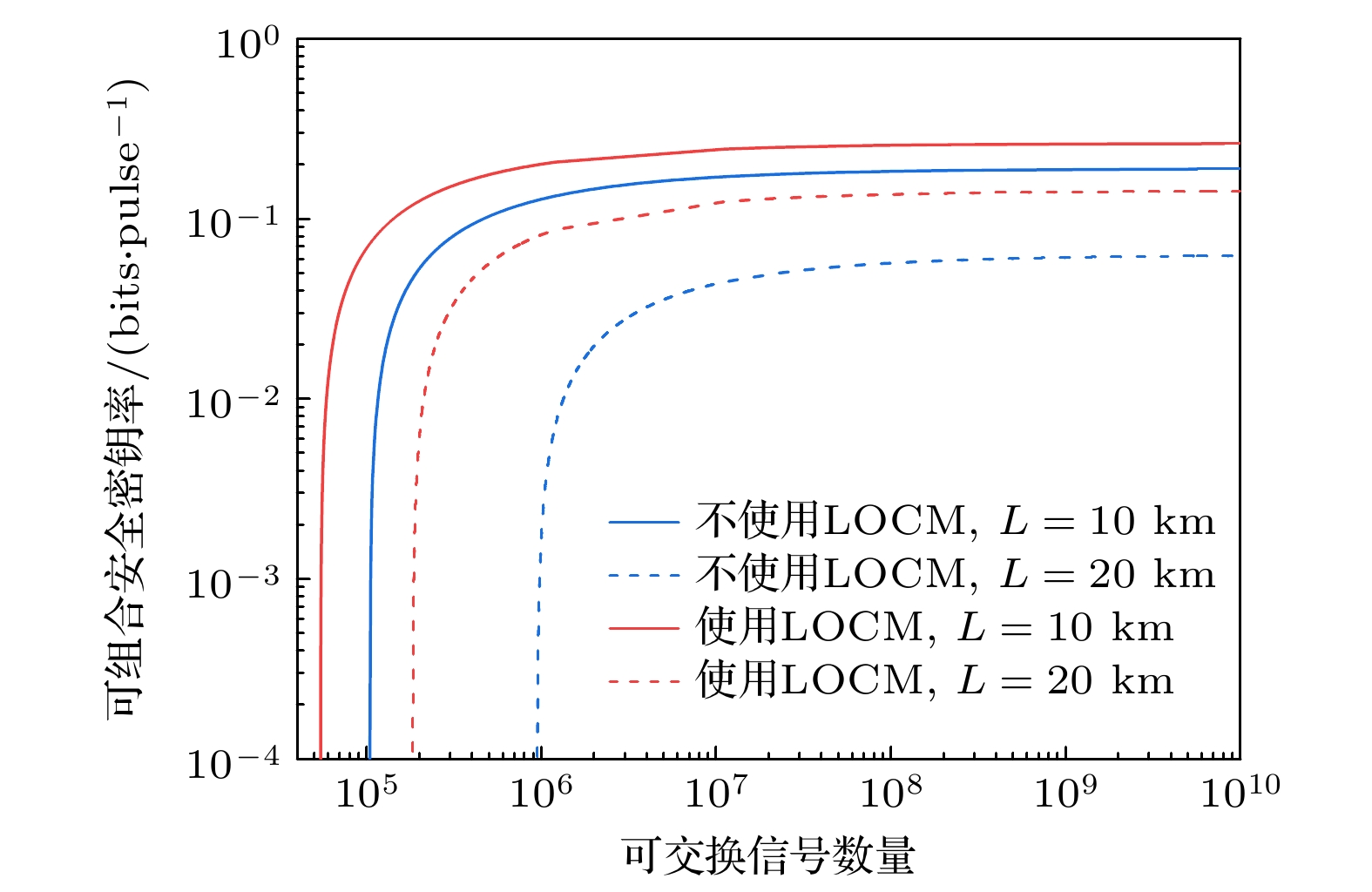
为探究可组合安全性分析中码长对安全密钥率的影响, 我们展示了在不同传输距离下, DPM-CVQKD以及LOCM DPM-CVQKD方案的可交换信号数量与可组合安全密钥率的关系, 如图8所示. 随着码长的逐渐增大, 可组合安全密钥率会经历一个显著的急速上升阶段, 而后在码长为${10^8}$附近趋于平稳. 值得注意的是, LOCM DPM-CVQKD在可组合安全密钥率方面展现出了显著的优势, 明显优于原来的DPM-CVQKD方案. 当传输距离为20 km, 且需要实现0.0611 bit/pulse的安全密钥率时, DPM-CVQKD所需码长为$1.2 \times {10^9}$, 而LOCM DPM-CVQKD仅需要$5.6 \times {10^5}$的码长, 两者之间存在近4个数量级的差异. 这意味着LOCM DPM-CVQKD减小了系统对码长的需求度和复杂度, 同时也减少了实际应用中的成本. 此外, 在传输距离分别为10 km和20 km的情形时, DPM-CVQKD的可组合安全密钥率存在近1个数量级的差异, 而本文提出的方案则仅存在远不到1个数量级的差异, 进一步证明了LOCM DPM-CVQKD在减小因传输距离增大而导致的码长增大需求方面的有效性, 从而提高了系统的灵活性和实用性.

在CVQKD的实验装置中, 调制器驱动电压的有限分辨率会使理想的高斯调制退化成DPM, 导致系统性能下降. 本文提出了LOCM DPM-CVQKD方案, 考虑了接收端探测器噪声的影响, 通过在接收端添加LOCM以补偿调制离散化效应, 实现系统性能的提升. 由于LOCM会引入额外的过量噪声, 因此需要对LOCM的相关参数进行优化, 以利用引入的过量噪声优化安全密钥率及传输距离. 仿真结果表明了LOCM不仅能够补偿调制离散化带来的性能损失, 还能在可组合安全性分析框架下显著降低对码长的需求, 从而为连续变量量子密钥分发的实际应用提供了一种高效的理论方案.

LOCM DPM-CVQKD的实验实现需要高信噪比的外差探测器等光电模块, 并对发送端和接收端的光学结构集成化封装, 这些器件与技术能够与当前相干光通信系统高度兼容, 具备一定的实验可行性. 然而当LOCM DPM-CVQKD的传输距离超过一定范围后, 需要更强的本振光, 可能会导致引入较大的过量噪声, 降低安全传输距离. 未来对LOCM的更深入研究需要聚焦LOCM的实验实现, 构建与实验系统相匹配的安全性分析精确模型, 在此基础上利用机器学习模型实现对LOCM最优参数组合的高效搜寻与动态调整, 以便进一步提升所提方案的实用价值.