谐振子模型在物理学很多领域都具有广泛的应用, 例如: 量子光学中光场的制备^[1]、量子信息中量子态的隐形传输^[2]、固体物理中晶格振动和原子光谱等^[3,4].1926年, 薛定谔在薛定谔方程的基础上, 提出了量子谐振子概念^[5]. 在此基础上构造的谐振子模型是为数不多的能够精确求解的量子力学系统之一^[6,7]. 单模线性量子谐振子的哈密顿量对应的本征态是粒子数态$\left| n \right\rangle $, 本征值是$(n + {1}/{2})\hbar \omega $. 后来, 海森伯提出量子力学上著名的“不确定原理”. 为了寻求满足最小不确定关系的量子态, 薛定谔进一步在谐振子模型基础上提出了相干态的概念. 1963年, 格劳伯^[8]在利用量子谐振子理论研究电磁场时, 发现激光光场对应的状态就是相干态, 从而引起人们的广泛关注.

在单模谐振子模型的基础上, 多模耦合谐振子问题也得到广泛的研究^[9,10]. 一般多模谐振子哈密顿量中都包含耦合项, 因为没有合适的量子表象, 使其本征函数的求解变得异常复杂^[11]. 目前求解此类问题, 主要求解方法是利用量子变换的方法来消除耦合项^[12]. 本文提出一个看似平淡, 却又令人深思的问题, 即有没有一类双模耦合谐振子可以不用消除耦合项而直接求解? 答案是肯定的. 后面将在纠缠态表象的基础上, 提出一种具有新耦合系数特征的双模耦合谐振子理论模型, 并进一步讨论双模真空态在此谐振子作用下随时间演化的情况.

本文第2部分首先简要分析了单模谐振子模型和双模纠缠态表象, 然后构造出新的双模耦合谐振子对应的哈密顿量. 同时分析了此谐振子的能量本征值、Fock空间波函数, 以及时间演化算符对应的量子变换. 最后推导出双模真空态在双模谐振子作用下输出量子态的具体形式. 第3部分利用非经典量子态的理论, 研究了输出量子态在压缩、粒子数分布和量子纠缠方面的性质. 最后总结了本文的主要研究结果, 并对此类谐振子的实际应用进行展望.

单模线性谐振子的哈密量为

式中$P$和$Q$分别是动量算符和坐标算符, $m$和$\omega $分别是谐振子的质量和圆频率.

早在1935年, 爱因斯坦、‌波多尔斯基和‌罗森构造了一对孪生光子, 用以挑战量子力学中哥本哈根学派对波函数的解释^[13]. 在他们的理论中, 若对其中任意一个光子进行量子测量, 便可精准确定另一个光子所处的量子态. 这一结果看似悖逆了“海森伯不确定性原理”, 因此常被人们称为EPR佯谬. 后来, Fan^[14]根据两个光子的相对坐标算符${Q_a} - {Q_b}$和总动量算符${P_a} + {P_b}$满足对易关系$[{Q_a} - {Q_b}, {P_a} + {P_b}] = 0$, 给出了它们的共同本征态:

式中$\eta $是复数, $\eta \equiv {\eta _1} + {\text{i}}{\eta _2}$, ${a^\dagger }$和${b^\dagger }$分别是对应光场的产生算符.

根据有序算符内积分技术, 可以证明$\left| \eta \right\rangle $满足正交归一关系, 即

式中${{\text{d}}^2}\eta \equiv {\text{d}}{\eta _1}{\text{d}}{\eta _2}$.

根据动量算符和坐标算符与产生算符和湮灭算符的关系:

可知

式中$\sqrt 2 {\eta _1}$和$\sqrt 2 {\eta _2}$分别是测量系统中两粒子之间相对位置和总动量的期望值. 实际上, 量子态$\left| \eta \right\rangle $就是一类典型的连续纠缠态表象, 其在压缩态、超导约瑟夫森结和量子霍尔效应等领域已经得到广泛应用^[15]. 在纠缠态表象的启发下, 构造如下双模耦合谐振子的哈密顿量:

为了便于后面理论分析, 取$\hbar = m = 1$.

将(6)式展开得到:

(7)式前两项是系统谐振子的哈密顿量, 第3项与第4项是环境热库的哈密顿量, 最后两项描述的是系统与热库之间相互作用的哈密顿量. 由(6)式可以发现, 对比于经典的谐振子耦合的Caldeira-Leggett 模型, (7)式中哈密顿量耦合项具有特殊耦合系数^[16]. 因此, 在实验方面, 通过改变相关量子调控参数, 便可实现此量子系统的制备.

根据能量本征方程$ H\left| \psi \right\rangle = E\left| \psi \right\rangle $, 对于单模谐振子, $\left| \psi \right\rangle = \left| n \right\rangle $, 则${H_1}\left| n \right\rangle = \omega \left( {{a^\dagger }a + {1}/{2}} \right)\left| n \right\rangle $, 最低能量${1}/{2}\omega $对应的状态是$\left| 0 \right\rangle $, 即真空态. 对于(7)式中的双模谐振子, 借助于传统的量子变换消除耦合项方法很难得到精确的解析解. 本文将${H_2}$直接作用于双模纠缠态$\left| \eta \right\rangle $, 不难得到

系统的相对位置和总动量是连续的, 所以此类谐振子具有宏观量子态的性质, 即能量本征值和本征函数都是连续的, 这与单模谐振子有明显不同. 此外, 为进一步分析双模粒子数态$\left| {m, n} \right\rangle $与纠缠态$\left| \eta \right\rangle $的关系, 引入双变量厄密多项式的母函数:

因此, (2)式中的纠缠态$\left| \eta \right\rangle $可改写为

将(10)式代入(8)式, 得到:

因此, 在纠缠态表象$\left| \eta \right\rangle $内, 双模耦合谐振子在Fock空间的波函数不需要量子变换也可以得到明显的表达式.

因为本文双模耦合谐振子中不含有时间参数, 所以时间演化算符可以很容易由薛定谔方程得出:

为进一步推导$U\left( t \right)$对应的量子变换, 将(12)式改写为

式中$\widetilde{\boldsymbol{ \varLambda}} $是${\boldsymbol{\varLambda }}$的转置, $\boldsymbol{\varLambda}= \left( {\begin{array}{*{20}{c}} {{a^\dagger }}&{{b^\dagger }}&a&b \end{array}} \right) $,

根据文献[17]中算符矩阵理论, $U\left( t \right)$对应的量子变换为

其对应的逆变换是:

单模真空态在一维谐振子作用下, 可以得到相干态. 那么, 双模真空态在此双模耦合谐振子作用下, 会演化成什么样的量子态呢? 为了解决这个问题, 首先利用(3)式中纠缠态表象完备性, 得到

根据(2)式中纠缠态的表达式和(5)式中纠缠态的本征方程, 可以导出

首先对$\eta = {\eta _1} + {\text{i}}{\eta _2}$的虚部${\eta _2}$进行积分:

这里用到了积分公式:

同理, 对$\eta $的实部${\eta _1}$积分, 则

将(19)式和(21)式的积分结果代入(18)式, 化简得到:

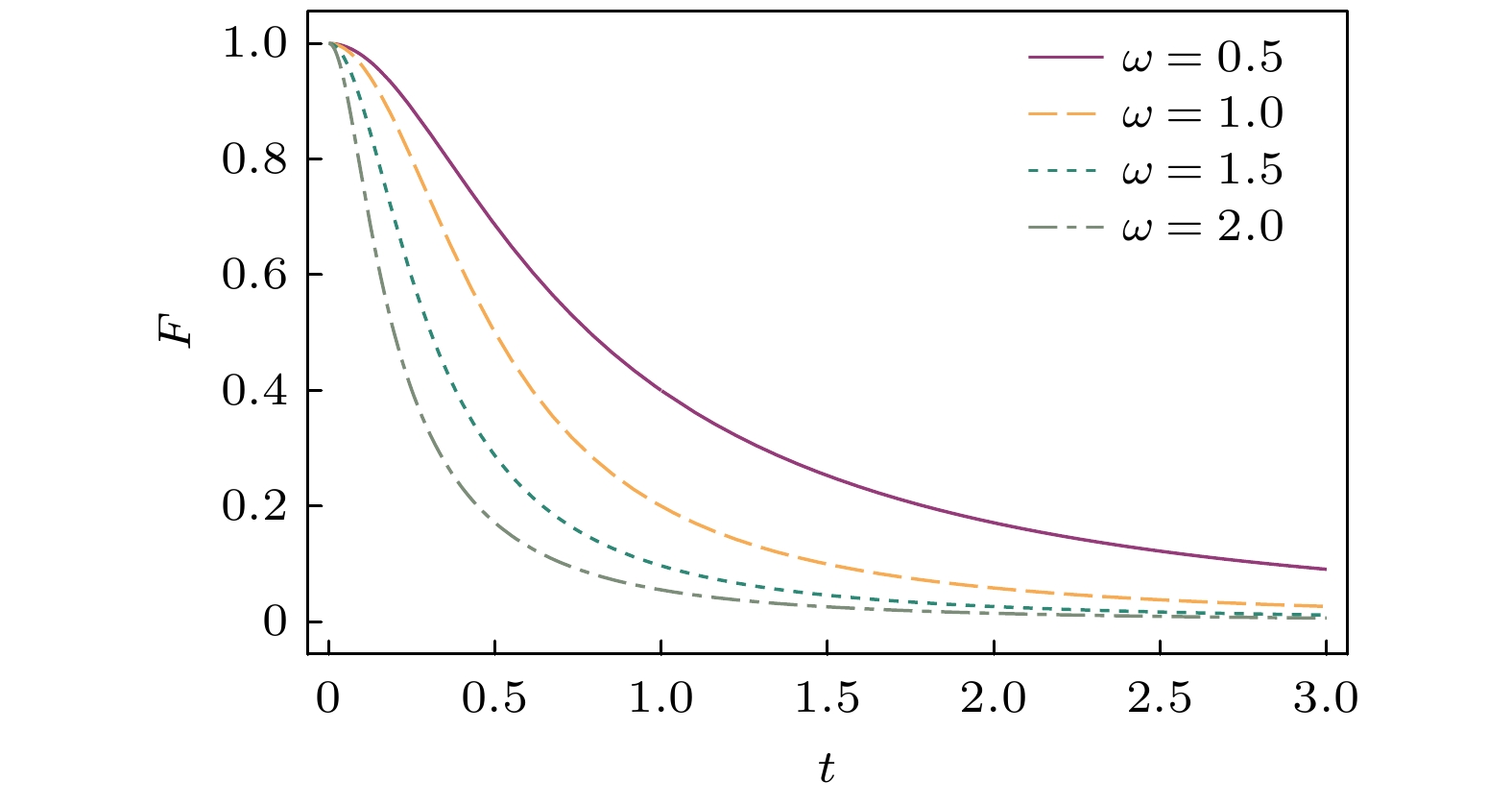
其中$k = \left( {1 + 2{\text{i}}t} \right)\left( {1 + 2{\text{i}}t{\omega ^2}} \right)$.

输出量子态的保真度是量子通信和量子计算关注的重点问题之一, 它的数值大小可以直观反映量子系统的稳定性和可调控性^[18,19]. 一般保真度可以通过两个量子态内积对应模值的平方来计算, 即$F \equiv {\left| {\left\langle {{\psi _{{\text{in}}}}} \right|\left. {{\psi _{{\text{out}}}}} \right\rangle } \right|^2}$. 对于量子态$\left| \tau \right\rangle $, 可得

显然, 在$t = 0$时, 由(23)式可得$F = 1$. 为了更加直观地分析任意时刻不同频率下双模谐振子输出量子态$\left| \tau \right\rangle $的保真度, 在图1绘制了对应的保真度随时间变化曲线. 可以看出, 双模真空态在耦合谐振子中的保真度随时间增长而迅速衰减, 最终趋向于零. 此外, 保真度衰减速度随谐振子频率增大而加快. 因此, 在相同的时间内, 双模真空态在低频振荡的双模谐振腔中更容易保持较高保真度.

根据海森伯不确定原理, 在量子光场两个正交方向量子测量的涨落乘积总是大于或等于$1/4$. 因此, 如果某个方向的量子涨落低于$1/2$, 那么对应的量子态就具有正交压缩效应^[20,21]. 对于双模压缩情形, 引入两个正交算符:

满足对易关系$[{X_{ab}}, {Y_{ab}}] = {\text{i}}$.

如果某量子态具有正交压缩效应, 则至少满足如下不等式中的一个:

将(24)式代入(25)式, 得到:

为求解量子态$\left| \tau \right\rangle $的对应正交压缩量, 首先要得到(26)式中各项算符的平均值. 对于算符${a^\dagger }{b^\dagger }$在量子态$\left| \tau \right\rangle $下的期望值, 可写为

据(16)式的量子变换关系, 进一步得到:

其中,

在双模真空态下, 除常数项平均值不为零, 其余算符平均值均为零. 因此, 将算符排成正规乘积形式后, 得到

同理, 可得

将(31)式各项算符平均值代入(26)式, 化简后得到

从(32)式可知, 双模谐振子在Y方向不具备压缩效应, 而在X方向发生了明显的量子耗散.

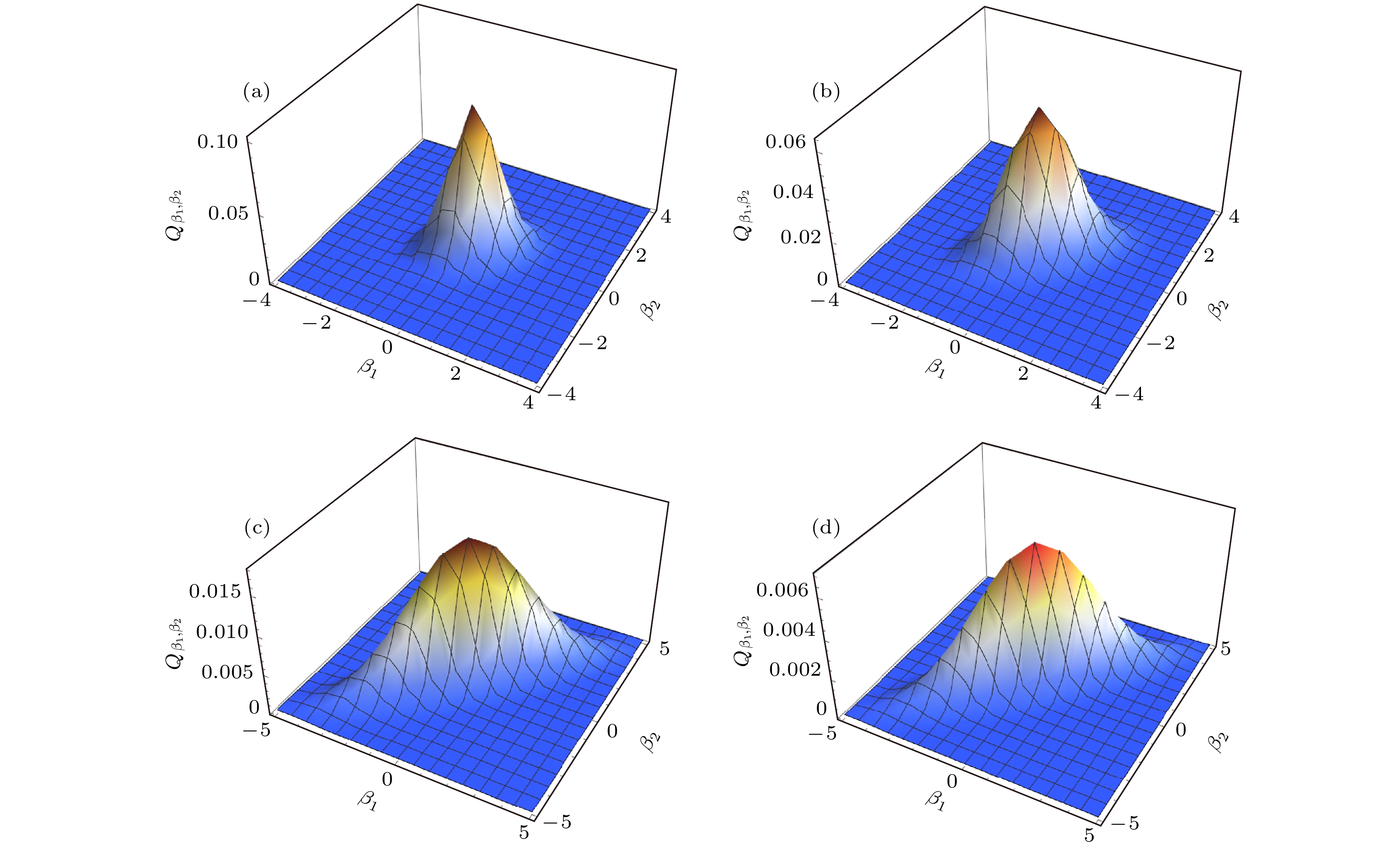
下面用二维相空间Q分布函数来进一步分析输出量子态$\left| \tau \right\rangle $的耗散现象. 在量子光学中, Q函数是一个恒非负的函数, 具有准概率分布的性质. 它在研究量子光场的非经典性质和随时间演化方面有着十分重要的作用. 对于双模量子态, Q函数定义为

其中 $\left| {{\beta _1}, {\beta _2}} \right\rangle \equiv \exp [ - {1}/{2}{{\left| {{\beta _1}} \right|}^2} - {1}/{2}{{\left| {{\beta _2}} \right|}^2} + {\beta _1}{a^\dagger } + {\beta _2}{b^\dagger } ]\left| {00} \right\rangle $是双模相干态.

将(22)式代入(33)式, 得

对比图2(a)—(c), 可以发现在谐振子频率不变的情况下, 输出量子态的Q函数在相空间的分布范围随着时间的延长而逐步变宽, 其峰值对应 概率却迅速减小. 比较图2(c), (d)可知, 谐振子频率对Q函数的分布范围虽然影响较小, 但峰值对应数值却随$\omega $的增大而很快减小. 因此, 整体来看双模谐振子对输入量子态起到了耗散作用. 目前, 人们对一维量子耗散系统已经进行了大量理论和实验方面的研究, 而二维量子耗散系统研究相对较少^[22,23]. 量子耗散在量子态调控、量子退相干和量子传输等诸多量子信息领域具有广泛应用^[24,25]. 一般耗散系统与量子纠缠有密不可分的关系, 它可以在宏观尺度实现较为稳定的量子纠缠^[26]. 因此, 本文双模耦合谐振子模型可以为量子理论计算和实验研究提供有益的参考.

为了描述量子光场的粒子数分布, Mandel^[27]引入了Q参数, 其定义为

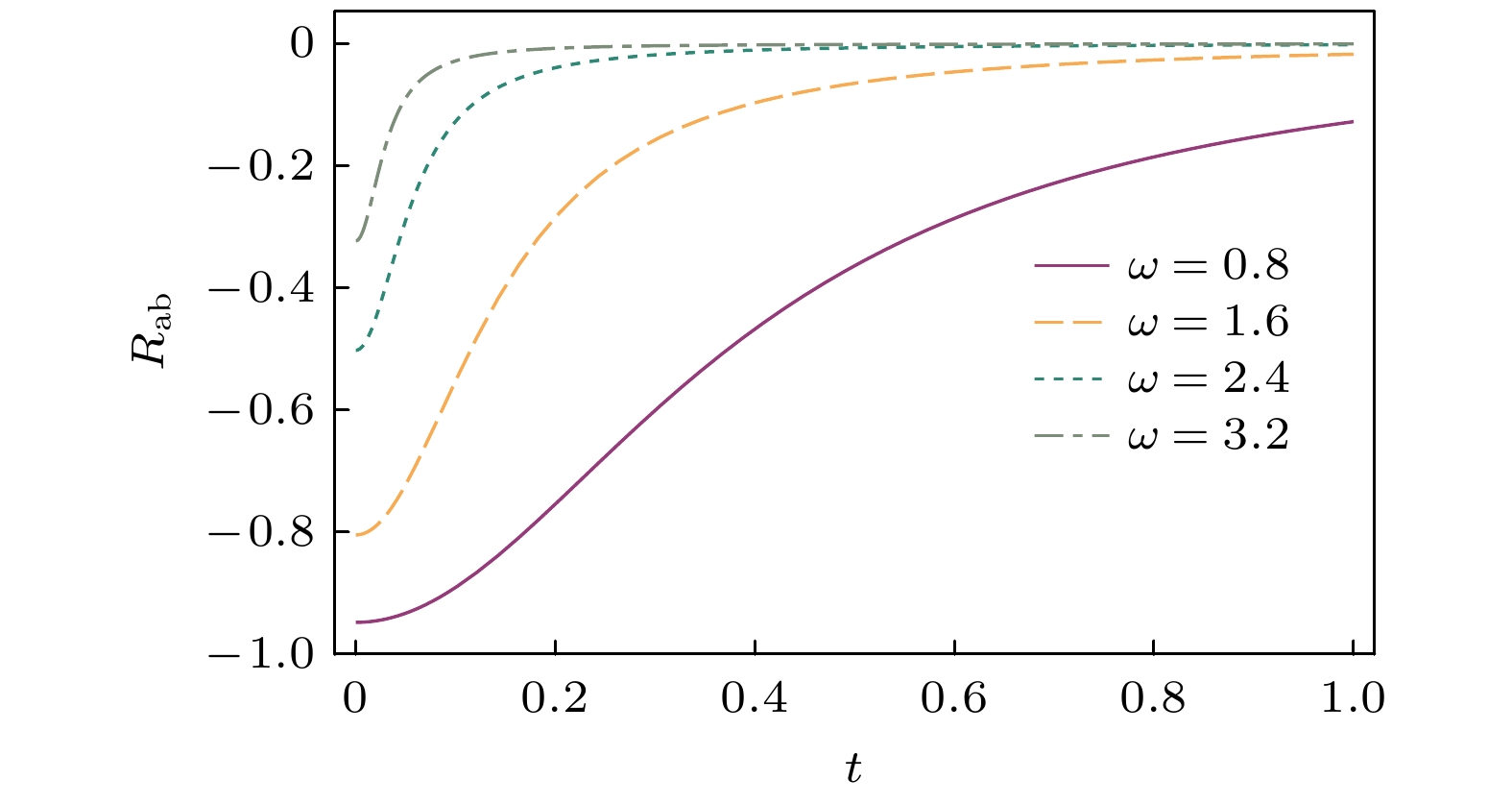
另外, 量子态中的两个光子之间反聚束效应可以通过如下参数来确定^[28]:

一般来讲, 如果$Q \gt 0$, 则光场中光子呈现超泊松分布, 而${R_{ab}} \lt 0$说明光场两个光子存在强关联.

对于量子态$\left| \tau \right\rangle $, 用前面类似的方法可以得到如下算符的平均值:

将(31)式和(37)式分别代入(35)式和(36)式, 得到:

从上面计算结果可以看出, 量子态$\left| \tau \right\rangle $中光子具有超泊松分布, 光子之间具有很强的反聚束效应. 为了更直观地看到Q和${R_{ab}}$函数在不同谐振频率下随时间的演变, 分别绘制了图3和图4. 对比两图, 不难发现在谐振子低频情况下, 输出量子光场中光子分布接近泊松分布, 而且量子反聚束效应也较强. 随着谐振子频率的增大, 输出量子光场中光子超泊松分布愈加明显, 而光子之间的关联也逐步减弱.

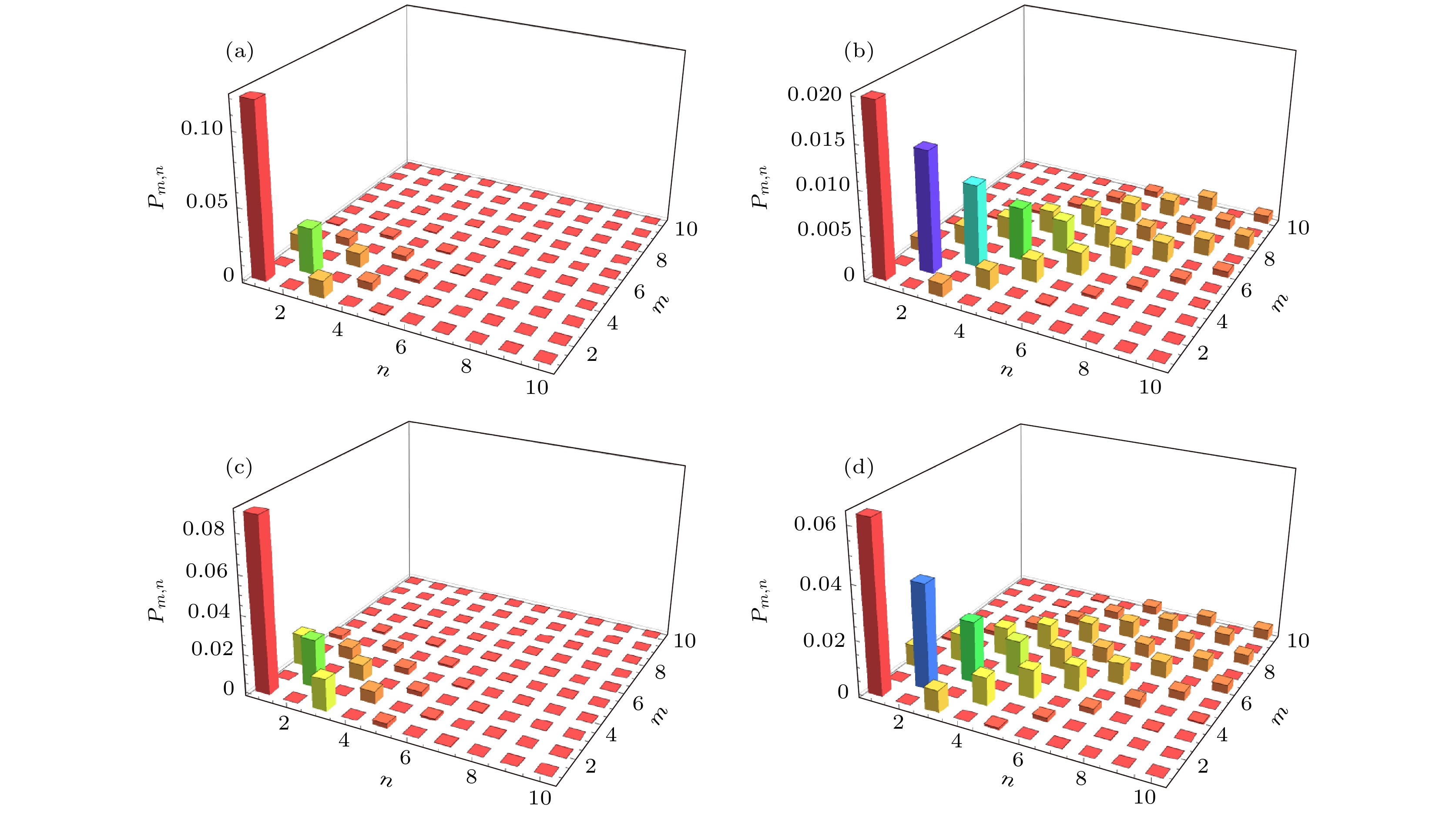
一个有趣的结论是输出光场的超泊松分布与双模压缩真空光场的光子分布类似. 为了更清晰地观测到量子态$\left| \tau \right\rangle $中光子的超泊松分布现象, 下面讨论光子分布函数. 对于双模量子光场, 光子分布概率可定义为^[29]

其中$\left| {m, n} \right\rangle $为粒子数态, $m, n$分别是对应模的光子数.

粒子数态可由未归一化的相干态表示, 即

其中$ \left\langle {\left. {s, t} \right\|} \right. $=$\left\langle {00} \right|\exp \left( {sa + tb} \right)$. 因此, 对于量子态$\left| \tau \right\rangle $光子数分布为

其中${F_{s, t}}$是一类特殊函数, 其定义是:

特别当$m = n$时, ${F_{s, t}}$退化为勒让德多项式:

从图5可以看到, 量子态$\left| \tau \right\rangle $中粒子数分布始终呈现超泊松分布, 这与前面由Q参数得到结论是一致的. 此外, 对比图5(a), (b)发现, 随着时间的延长, 量子场呈现耗散趋势, 而且逐步可以检测到多光子数. 但是, 光子数探测概率从$t = 0.5$时刻的$0.10$下降到了$t = 2.5$时刻的0.020. 进一步由图5(a), (c), (d)可以得出结论, 随着谐振子频率的增大, 虽然多光子不断出现, 但是光子探测概率下降剧烈. 整体来看, 当$n = m$时, 粒子数分布概率较大. $n \ne m$的粒子数对称分布在中心位置两侧.

前面通过${R_{ab}}$的分析, 可以看到输出量子态的光子具有很强的反聚束效应. 最早量子纠缠的概念是与EPR佯谬有密切的关系^[30], 那么在双光子纠缠的基础上构造双模耦合谐振子输出的量子态$\left| \tau \right\rangle $的纠缠度如何呢? Shchukin 和Vogel^[31]提出了一个双模纠缠态的充分判据:

如果量子光场使SV的取值为负, 那么偏离零点程度越高, 对应量子纠缠度就越强. 对于量子态$\left| \tau \right\rangle $, 利用(31)式和(37)式中的算符平均值, 可得

(46)式分析结果表明, 输出量子态纠缠度随着谐振子频率和时间的增加而不断增大, 而且频率变化对纠缠度的影响更大.

本文在单模谐振子的基础上, 结合双模纠缠态表象, 构造了一类新的双模耦合谐振子. 从哈密顿量的形式分析, 该谐振子的哈密顿量包含双粒子坐标与坐标、动量与动量的两个耦合项. 同以往文献采用的量子变换消除耦合项的方法不同, 本文直接利用双光子纠缠态表象得出了谐振子的能量, 并证明了此谐振子的能量是连续的. 在纠缠态表象中, 能量本征值和Fock空间的波函数都可以得到自然表示.

通过算符矩阵理论, 推导得出此双模谐振子时间演化算符对应的量子变换和逆变换. 将时间演化算符作用于双模真空态, 得到一个新的双模连续纠缠态$\left| \tau \right\rangle $. 从量子压缩、粒子数分布和量子纠缠的理论分析和数值模拟来看, 我们提出的双模谐振子模型对输入量子态具有纯耗散作用. 因此, 此类双模耦合谐振子为实验实现双通道的量子耗散, 制备高纠缠度的量子态提供了良好的理论模型.

感谢中国科学技术大学材料科学与科学工程系范洪义教授的指导.