量子密钥分发(quantum key distribution, QKD)技术基于量子不可克隆定理^[1], 为安全通信带来了革命性突破, 提供了传统加密技术无法匹敌的安全性. 在量子通信网络中, 由于大量通信业务的加密需求, 量子密钥的需求量巨大. 然而, 传统依赖可信中继^[2–4]的QKD的网络面临较高的可信管理成本, 因此, 越来越多的研究聚焦于纠缠网络^[5–9]的探索与发展.

当前量子纠缠网络面临三大挑战^[10]: 1)纠缠对稀缺; 2)量子态失真; 3)量子态存储. 本文主要关注其中的纠缠对稀缺问题. 一般而言, 导致稀缺的主要原因有三点: 首先, 远距离纠缠对的建立需要消耗大量链路资源, 链路条件、纠缠成功率和纠缠交换成功率都将影响纠缠对的建立; 其次, 基于纠缠的QKD方案^[11,12]资源利用率较低, 如Ekert91协议中, 只有2/9的纠缠对用于生成原始密钥, 生成安全密钥的比例更低; 最后, 用户的加密需求繁多, 且密钥需求与纠缠资源呈正相关, 随着需求增加, 资源消耗迅速上升, 进一步加剧了资源稀缺问题. 对此, 研究人员提出了不同的方案来缓解这个问题. 在文献[8,13]中, 作者通过优化纠缠路由算法提升网络吞吐量, 增加可用的纠缠对数量, 从而更有效地利用纠缠网络资源. 赖红^[14]提出了一种广义等距张量压缩多光子纠缠态的QKD协议, 该协议通过将多光子纠缠态压缩为单光子态或Bell态^[15], 显著提高了编码效率, 并减少了纠缠对的使用. 这些工作在提升纠缠对数量和降低纠缠对消耗方面取得了进展, 但考虑到量子网络中对纠缠对资源的巨大需求, 纠缠对稀缺问题值得进一步研究.

针对上述问题, 本文进一步提出将多尺度纠缠重整化假设(multiscale entanglement renormalization ansatz, MERA)^[16]应用于QKD网络. 通过利用MERA的独特酉矩阵结构进行无损压缩^[17], 旨在减少存储成本和纠缠资源的消耗, 同时提高密钥分发效率. 本文的主要贡献包括: 1)提出了一种基于MERA架构的QKD方案, 显著降低了纠缠资源的消耗; 2)通过引入安全参数, 在保障QKD安全性的前提下, 提升了密钥分发效率, 以满足高需求量子网络的要求. 通过这些优化, 本文为QKD技术在实际中的应用提供了新的解决方案. 该方案在现有QKD网络基础上显著提高了资源利用率和整体网络性能, 展示了广泛的应用潜力.

在远程通信对之间建立纠缠对以进行密钥分发的方法, 虽然能够提供高安全性的通信, 但资源消耗大、成本高. Shi等^[8]提出的Q-CAST算法有效提升了纠缠网络的吞吐量, 然而, 由于物理限制^[18–20], 随着通信距离的增加, 成功建立远距离纠缠对的概率仍然很低, 因此无法满足大规模加密的需求. 此外, 量子态在节点中的存储^[21–23]也是一个挑战. 尽管当前量子存储器技术^[24–26]已取得显著进展, 存储时长和量子比特数得到显著提升, 但仍无法满足现有的通信需求.

为应对这些挑战, 研究人员提出了多种方法, 包括量子压缩和密钥扩展, 以提升QKD的效率和安全性. 首先, Zhang等^[27]提出了量子密钥扩展(quantum key expansion, QKE)协议, 不仅能扩展密码密钥, 提升密钥产生速率, 还能生成更长的密钥, 并抵御多种攻击, 从而增强QKD协议的安全性. 其次, MERA作为一种层次化的张量网络, 被Lai等^[17]用于构建层次量子秘密共享(hierarchical quantum secret sharing, HQSS)方案. 该方案利用MERA的层次结构, 将参与者的信任和权限层次与MERA结构相关联, 并通过二元和三元MERA生成秘密份额. 这一动态结构允许对参与者进行晋升或降级, 以及新参与者的加入和旧参与者的退出, 确保了HQSS方案的灵活性和安全性. 尽管Lai等设计了等距映射W和解纠缠操作U来压缩原始态, 并通过逆映射无损地解压缩为原始态, 但尚未扩展其设计的等距张量在QKD协议中的应用. 最后, 纠缠态源的压缩也成为QKD协议中的一个重要研究方向. 由于当前量子处理器的原始性和多光子纠缠制备的难度, 对传输的量子数据进行压缩具有重要的实际意义. Lai等^[28]通过构建等距张量实现了纠缠压缩, 这种压缩不仅提高了QKD协议的效率, 还能更好地抵御窃听, 提升了系统的安全性.

MERA展示了一种分层结构, 每一层对应于特定的长度或能量尺度. Lai等^[17]设计了等距映射算符W和解纠缠算符U, 这些操作能够有效地将原始态压缩, 并通过逆映射无损地解压缩回原始态. MERA的分层特性特别适合应用于QKD, 尤其在资源有限和量子存储技术受限的情况下, 因此本文提出了基于MERA的QKD方案. 本文的方案利用纠缠网络在通信双方之间进行纠缠分发, 双方使用这些纠缠对构建一个共享的矩阵乘积态并将该态压缩后存储. 压缩后的光子数量显著少于原始多体态中的光子数量, 从而降低了存储成本. 此外, 当前量子存储器能够长时间保存压缩态, 因此可以利用这段时间, 通过多次解压缩生成所需的密钥.

本节主要介绍本文提出的协议所依赖的背景知识. 首先, 介绍MERA的基本概念和结构特点. 接着, 重点讲述Lai等^[17]构建的等距张量如何用于MERA的压缩与还原过程, 为协议的设计提供理论基础和技术支持.

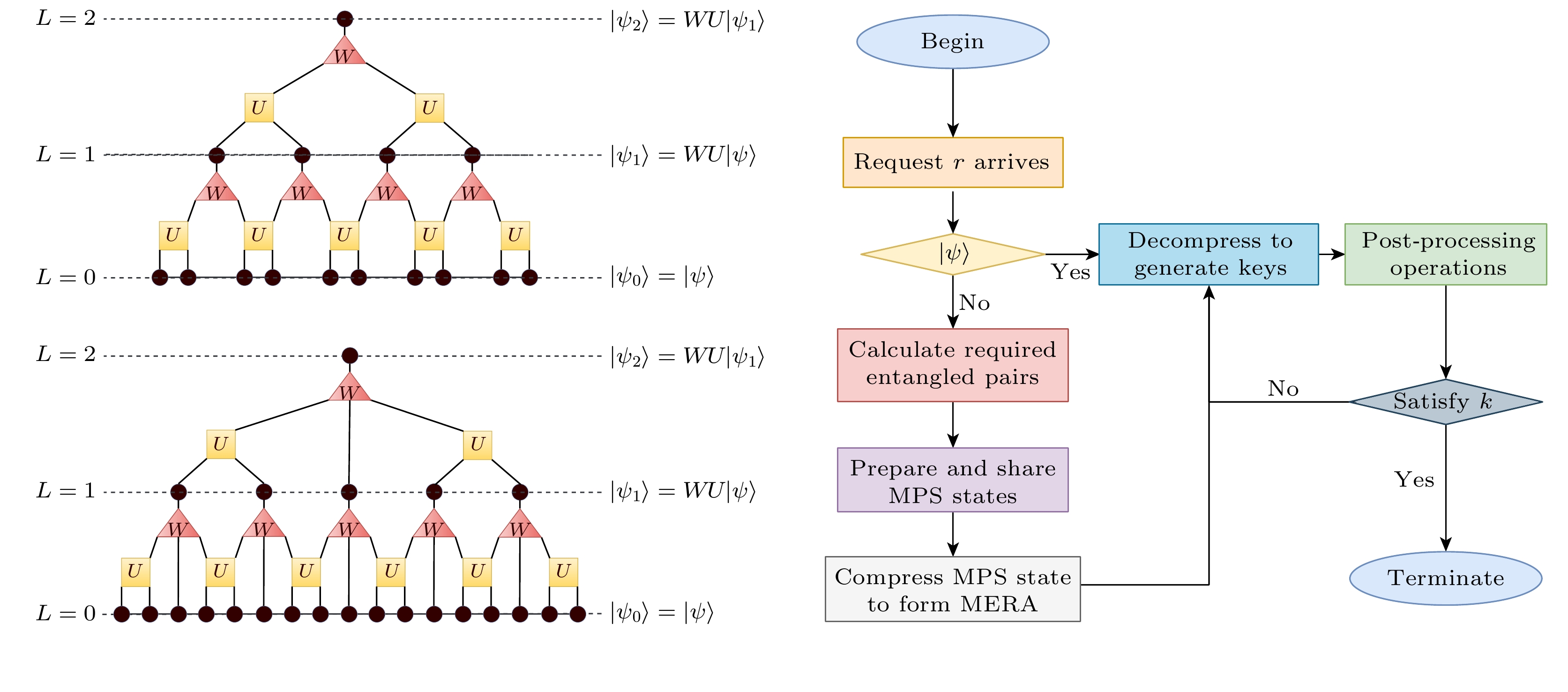
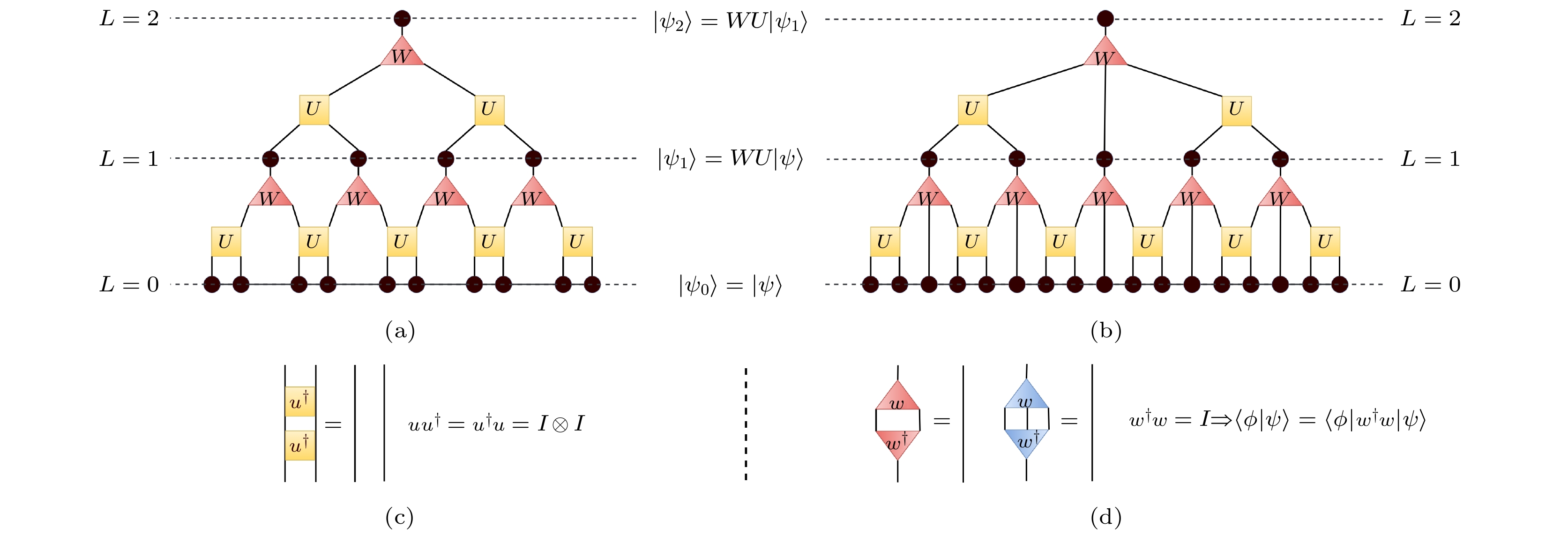
MERA是一种层次化的张量网络结构(如图1所示), 由一系列的等距映射算符W和解纠缠算符U组成. W用于降低系统的自由度, 而U则用于消除局部纠缠. 这种结构使得在计算物理量时能够减少计算复杂度, 同时保留系统的关键纠缠信息.

MERA通过多次纠缠重整化(entanglement renormalization group, ERG)形成, 一次ERG包括以下两步: 1)边界变形: $ \left | \psi \right \rangle \rightarrow U \left | \psi \right \rangle $; 2)粗粒化: $ U \left | \psi \right \rangle \rightarrow WU \left | \psi \right \rangle $. 随着ERG的迭代深入, 量子态中的短程纠缠被逐步规范化并排除, 而长程纠缠的特性则被逐渐揭示. 这表明, 每个ERG层次都记录了原量子态在特定长度尺度上的纠缠特征.

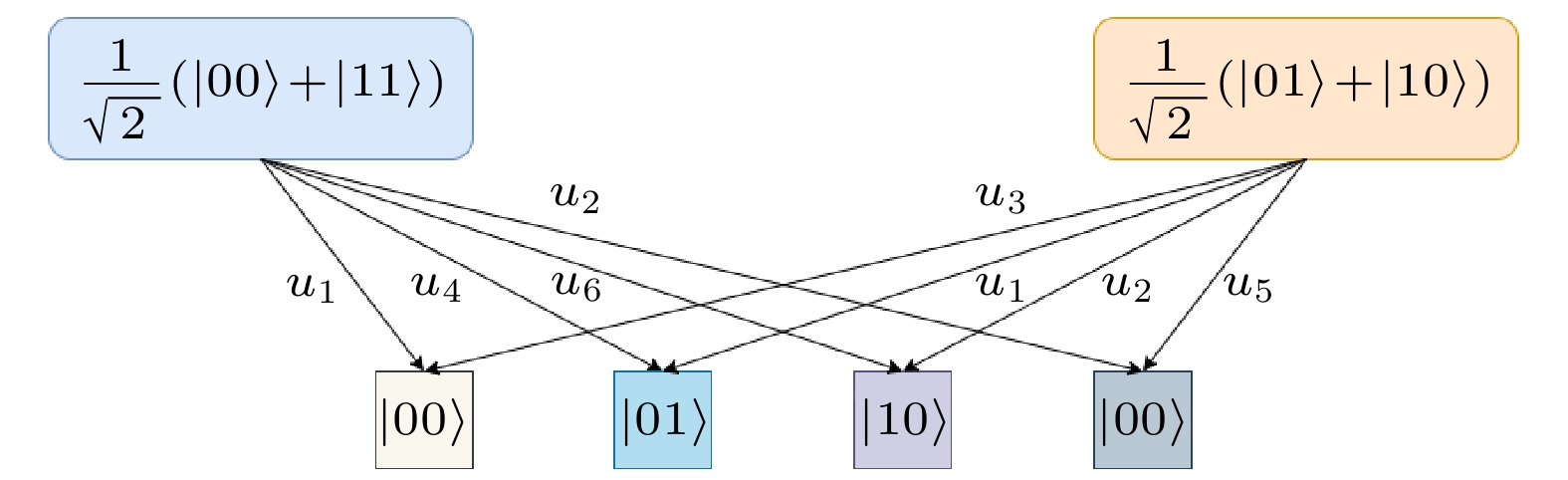
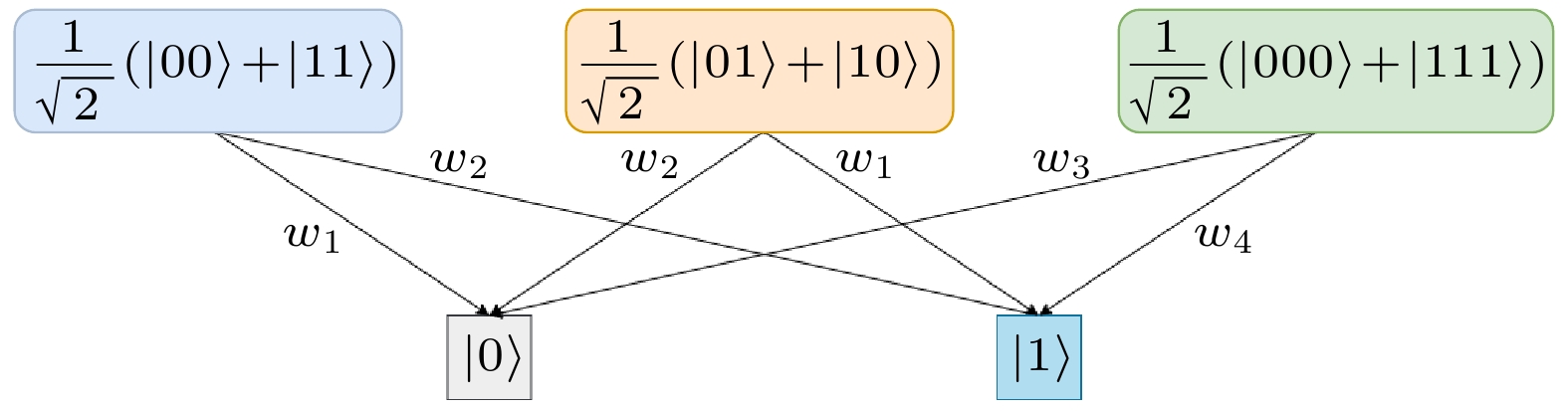
Lai等^[17]注意到MERA的分层结构, 这种层级结构可以与分层秘密共享结合起来, 为了能够完成秘密共享, 他们设计了合适的W和U. 所设计的U有6种, $ U = \left \{{\boldsymbol{u}}_{1}, {\boldsymbol{u}}_{2}, {\boldsymbol{u}}_{3}, {\boldsymbol{u}}_{4}, {\boldsymbol{u}}_{5}, {\boldsymbol{u}}_{6} \right \} $, W有4种, $ W = \left \{{\boldsymbol{w}}_{1}, {\boldsymbol{w}}_{2}, {\boldsymbol{w}}_{3}, {\boldsymbol{w}}_{4} \right \} $.

U可以将纠缠态转换为直积态, 即解纠缠. 假设两点之间的纠缠如(1)式, 下面用$ {\boldsymbol{u}}_{1} $举例进行验证.

解纠缠:

因为u是酉矩阵($ {\boldsymbol{u}}^{\dagger} ={\boldsymbol{ u}}^{-1} $), 所以通过它的逆操作, 可以将解纠缠后的态还原为纠缠态.

不同的U作用在不同的纠缠态上, 可以得到相同或不同的直积态, 其映射关系如图2所示. 所设计的W可以将纠缠态压缩为单光子态, 其映射关系如图3所示.

在Lai等^[17]的工作中, 通过这些操作可以完成MERA态的制备, 形成不同层次的秘密, 同时参与者也可以通过这些操作的逆操作恢复出所共享的秘密. 本文发现, MERA的分层结构能够与加密请求的不同等级相对应, 从而实现差异化处理. 更为关键的是, Lai等^[17]设计的等距映射矩阵W和解纠缠算符U可以无损地对MERA态进行压缩和还原. 压缩后的光子数显著少于压缩前的光子数, 这在现有的物理硬件条件下有助于大幅降低存储成本. 基于这些发现, 本文提出了一种基于MERA的QKD方案.

在量子通信网络中, 随着大量通信业务的加密需求, 量子密钥的需求也急剧增长. 安全通信通常采用一次一密(one time pad, OTP)^[29]方案, 进一步增加了资源消耗. 尽管现有方法通过优化纠缠路由提升了网络吞吐量, 但仍难以满足大规模的加密需求. 本文提出将MERA应用于QKD网络, 这一方案能够在现有技术条件下有效减少资源消耗, 同时满足通信加密的需求. 本节将详细介绍该方案的实现过程, 并构建数学模型, 以进一步验证方案的有效性.

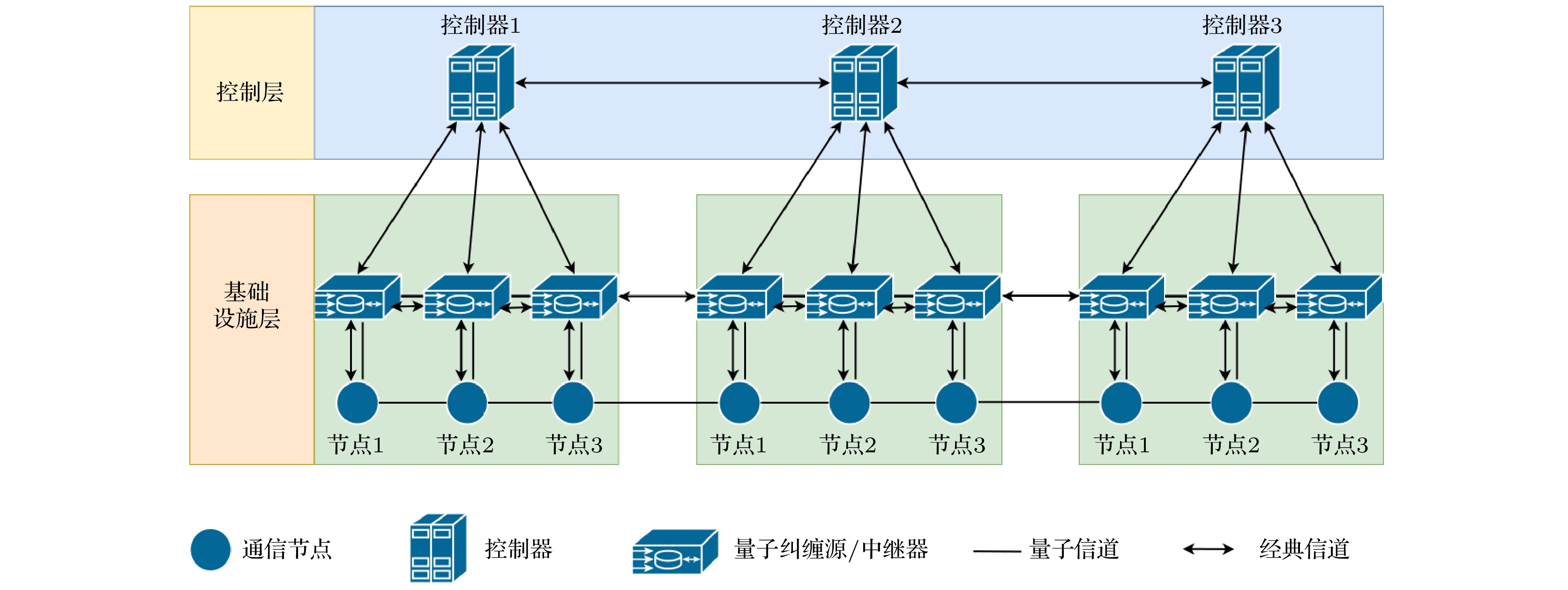
本文根据量子网络的特点, 将网络结构简化为两层——控制层和基础设施层, 如图4所示.

1)控制层: 本层由控制器组成. 控制器负责在网络中管理通信对($ S\text{-}D $)之间的密钥生成, 并执行态的压缩和解压缩操作. 在压缩过程中, 控制器向$ S\text{-}D $下发命令, 该命令包括压缩层数以及使用的U和W操作的序列编号. 但所有的U和W均为公开信息, 窃听者也能获取. 为了降低传输成本, 控制器在下发压缩命令时仅传输操作的序列号, 而非操作本身. 解压缩时, 控制器向通信双方发送命令, 仅包含层数信息, 通信双方据此命令将光子解压缩到相应层.

2)基础设施层: 本层包含了经典网络设备以及与量子相关的设备——纠缠源、量子节点、量子中继器、量子信道. 本层与大多数随机拓扑的量子网络一致, 主要功能是在控制器的控制下建立通信对之间的远距离纠缠.

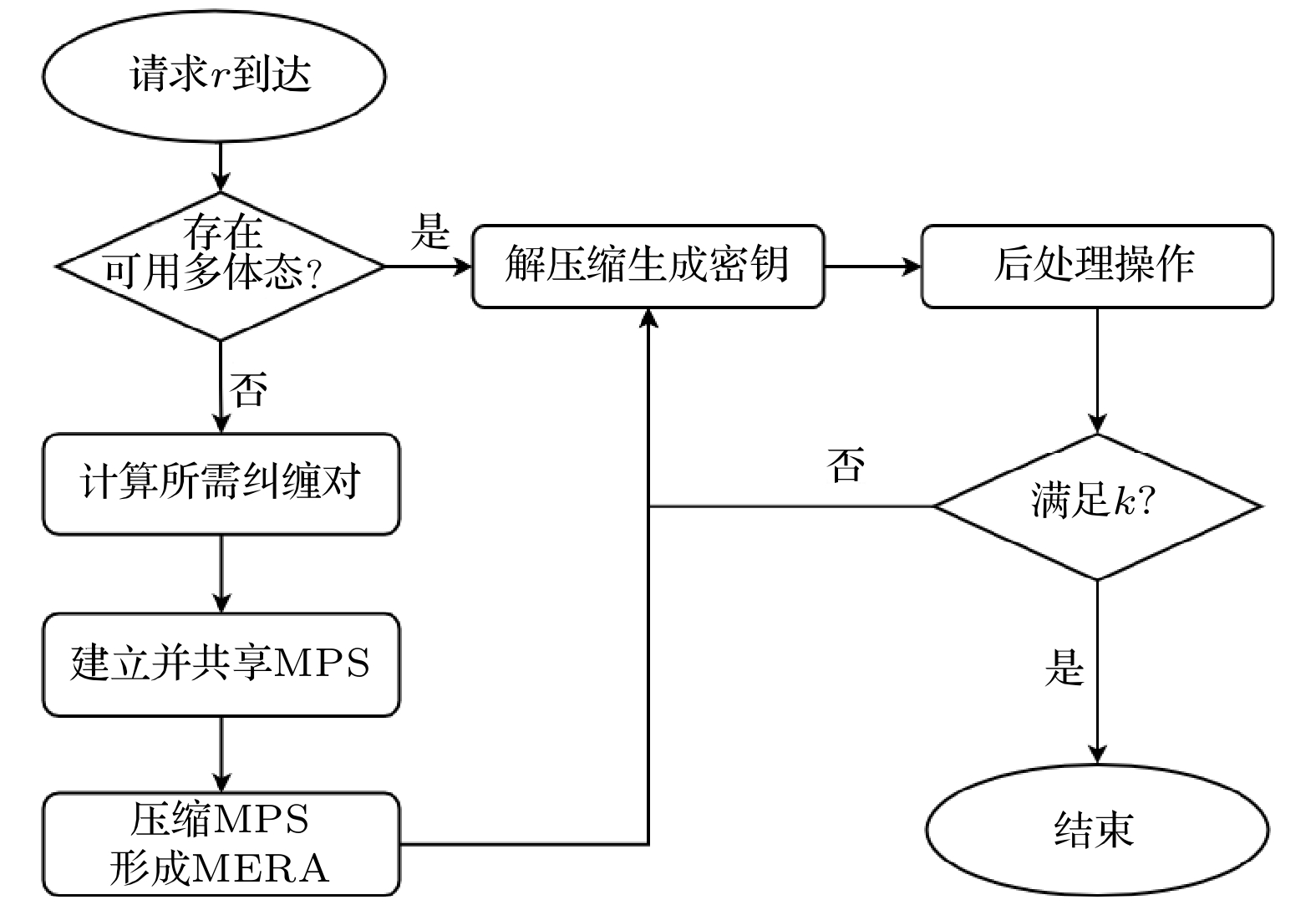
本方案的密钥分发流程如图5所示, 详细过程分为以下8个步骤. 1)计算纠缠对数量: 当通信双方有加密请求时, 控制器根据请求的特性计算所需的纠缠对数量. 2)生成纠缠对: 通信双方通过纠缠网络生成所需数量的纠缠对. 3)生成和共享矩阵乘积态(matrix product state, MPS)^[30]: 利用成功建立的纠缠对生成MPS态, 并在通信双方之间共享该态(注: 即使在没有当前密钥需求时, 用户之间也可以提前制备纠缠, 并通过步骤3)和4)进行压缩后存储在量子存储器中, 以备未来需要时直接使用). 4)压缩存储: 通信双方根据控制器的指令压缩手中的多体态, 并将压缩后的量子态存储. 5)解压缩: 控制器根据请求的特性向通信双方下达解压缩命令, 双方根据命令将手中的态解压缩到指定层. 6)安全性验证: 双方使用Hash函数验证是否接收到相同的解压缩命令, 若一致则将生成的密钥作为完整密钥的一部分, 若不一致则丢弃. 7)后处理阶段: 进行误码纠错和隐私放大, 确保双方获得一致的安全密钥. 8)密钥长度检查: 检查密钥长度是否满足需求, 若不足, 则重复步骤5)—8), 直至密钥长度满足要求.

在QKD网络中, 通信请求可用元组$ r = (S, D, k, P, \Delta t) $进行描述, 具体如表1所列. 某一时刻, 网络中的所有请求组成集合$ R = \{r_{1}, r_{2}, \cdots, r_{n}\} $.

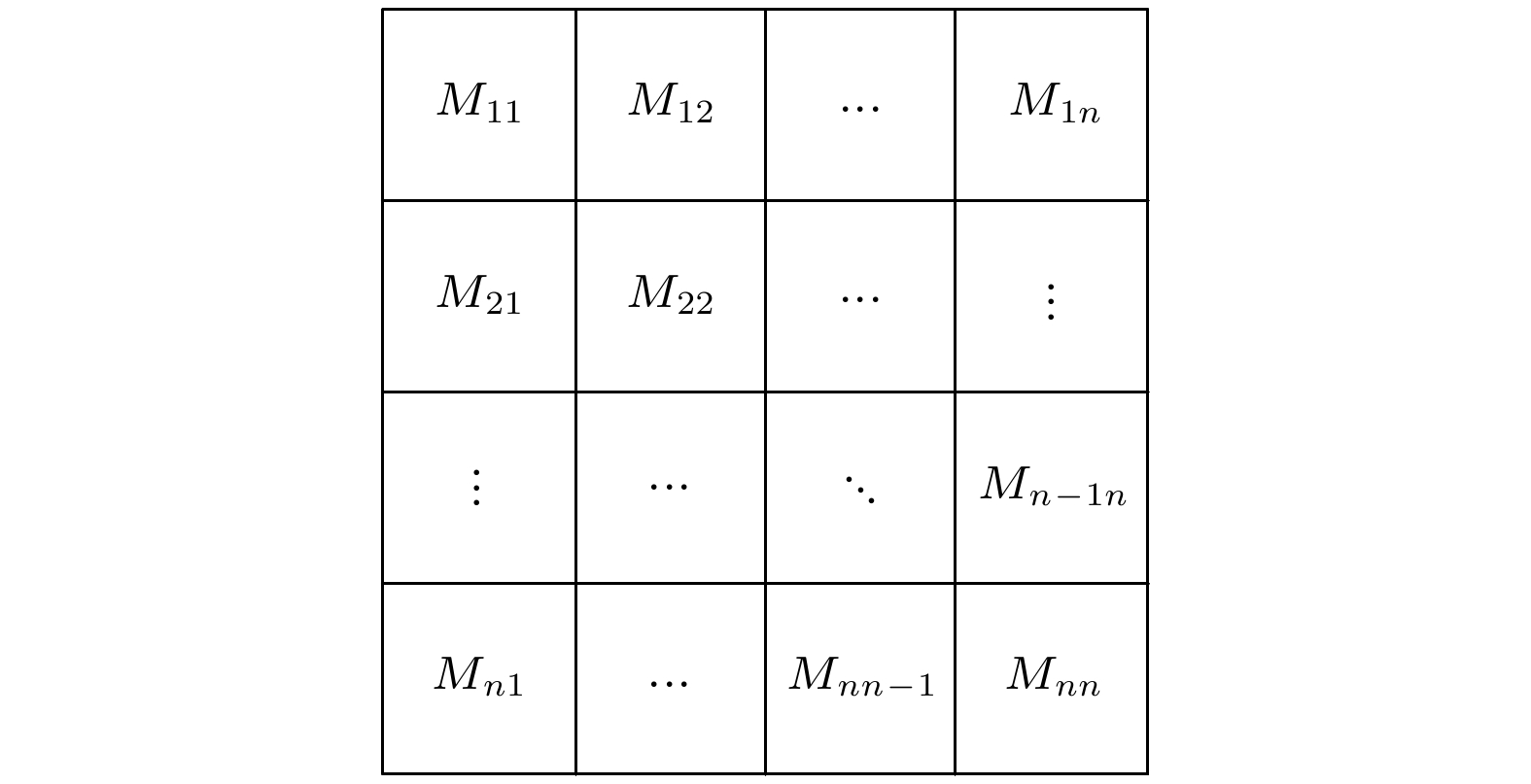
控制器维护一个二维状态表(见图6), 用于判断请求到达时是否存在可用的多体态. 该状态表以对称矩阵的形式表示, 其中每个矩阵元素表示通信对之间的状态信息. 矩阵中元素$ M_{ij} = M_{ji} = 0 $表示第i个节点与第j个节点之间没有可用的多体态, 而$ M_{ij} = M_{ji} = 1 $表示存在可用的多体态. 如果存在可用的多体态, 则直接跳过该步骤; 如果不存在, 则需要生成纠缠对以创建MPS态. 控制器会根据请求的特性来估算生成MPS态所需的纠缠对数量. 由于MPS态中包含的光子数越多, 解压缩时底层光子数越多, 因此每次解压缩生成的密钥长度会更长, 从而减少解压缩次数, 提升密钥生成速率. 为了优化这一过程, 本文在文献[31]的基础上, 综合考虑请求的需求量、优先级和可接受时延, 设计了(5)式来计算所需的纠缠对数量, 从而优化密钥生成效率, 满足方案的需求.

其中, $ \alpha, \beta, \gamma, \delta $分别代表需求量k的权重系数、优先级P的权重系数、可接受时延$ \Delta t $的权重系数、基础纠缠对数量. 假设本文选择以下权重系数: $ \alpha = 10, \quad\beta = 5, \quad\gamma = 5, \quad\delta = 80 $, 存在两个请求$ r_{1}(A, B, 2048, 3, 10) $, $ r_{2}(C, D, 1024, 1, 30) $, 代入(5)式得到结果为: $ Q_{{\text{MPS-AB}}} = 97 $, $ Q_{{\text{MPS-CD}}} = 88 $. 可以观察到$ r_{1} $是一个优先级高、密钥需求大的紧急请求, 因此需要较多的纠缠对; $ r_{2} $优先级、需求量相对较低, 可接受时延较长. 显然, 通过这种计算方式可以清晰地反映不同请求之间的差异.

1) MPS态的生成: 在纠缠网络完成纠缠对的分发后, 通信双方利用这些纠缠对建立原始的MPS态, 并共同共享这个多体态.

其中, $ {\boldsymbol{A}}^{s_i} $是第i个量子比特上的张量, $ s_{i} $是量子比特的状态, n是MPS的长度. 例如: 三光子态$ \left|\varPsi\right\rangle = \dfrac{1}{\sqrt{3}}(\left|001\right\rangle+\left|011\right\rangle+\left|110\right\rangle) $的MPS形式可以表示为

2) MPS态的压缩: 在共享MPS态之后, 控制器向双方下发压缩命令, 包括矩阵U和W的序列及压缩层数L. MERA的总层数L表示如下:

其中N代表MPS态所含光子数. 对于128光子的MPS态, $ 128 = 2^{7} $, 则最大层数为7, 且能够将MPS态压缩为单光子$ \left|{{0}}\right\rangle $或$ \left|{{1}}\right\rangle $; 也可以压缩到第6层, 双光子态$ |00\rangle, |01\rangle, |10\rangle, |11\rangle $; 以此类推. 为了减少存储成本, 本文一般将其压缩到三光子或者更少. 并且由于每层选取的W和U操作的不同, 所形成的MERA态也不同.

3)双方根据命令进行压缩, 完成后向控制器返回确认信息. 为了后续的解压缩过程, 双方需保存U和W操作的序列. 这些操作的共轭转置是解压缩的关键, 因为它们能够将压缩后的量子态恢复到原始态.

1)解压缩: 在密钥分发过程中, 本文实际执行一系列解压缩操作, 直到生成的密钥满足通信需求. 解压缩阶段优先选择解压缩到接近原始态的底层态, 以便生成更长的密钥. 这意味着, 不同的解压缩层级会影响密钥生成速率, 使本文能够根据不同的紧急程度和需求处理通信请求. 在本文的方案中, 控制器在解压缩时会随机选择第1—3层态进行操作. 这些层级的选择确保了生成的密钥长度既不过短, 又能保持所需的安全性. 基于这一策略, 本文可以估算解压缩操作的最大和最小次数.

其中, k表示请求的密钥需求量, t表示解压缩次数, N表示MPS态所含光子数. 例如, 一个长度为2048的密钥请求, 在MPS态为256个光子, MERA态最高层为8时该请求需要$ [16, 64] $次解纠缠才能满足要求.

2) Hash验证: 在每一轮生成密钥后, 双方根据提前共享的安全的哈希函数$ H(x) $将自己手中的密钥$ K_{s} $进行计算, 即$ H(K_{sA}),\; H(K_{sB}) $. 并且以广播的方式进行哈希值的对比, 若$ H(K_{sA}) = H(K_{sB}) $, 则双方的密钥$ K_{_{sA}},\; K_{_{sB}} $一致, 则保留该密钥$ K_{s} $; 否则, 不一致, 废弃该密钥, 因为控制器在下发层数命令时, 可能受到信道噪声影响而导致通信双方接收到的命令不一致; 当废弃的次数过多时, 则表明密钥分发过程受阻, 中断本次通信.

3)对保留的$ K_{s} $进行后处理操作得到$ K_{E} $, 保证双方得到的是正确的、一致的安全密钥.

4)判断当前密钥量是否满足通信需求, 若满足, 则结束密钥分发; 若不满足则继续进行分发过程, 直至满足需求.

本方案旨在最大化现有资源的利用效率, 有效降低资源消耗及成本. 本节将从资源消耗、成本效益和安全性三个关键维度, 对本文的方法进行全面的性能评估.

本节将深入探讨量子密钥分发过程中的资源消耗问题, 重点关注量子资源与经典资源的利用效率. 并详细分析传统Ekert91协议的资源消耗, 与本文提出方案进行比较.

在传统方法中, 依赖于纠缠网络在通信双方之间建立远距离的量子纠缠. 这一过程是密钥分发的基础, 为Ekert91协议提供了必要的纠缠对. 随后, 利用这些纠缠对, 通过Ekert91协议的步骤进行密钥分发.

1)纠缠分发: 纠缠分发通过中继节点利用纠缠交换, 在S和D之间建立远距离纠缠, 纠缠交换的核心操作是贝尔态测量(Bell state measurement BSM). BSM可以产生以下四种测量结果:　$ |\varPhi^{+}\rangle = \dfrac{1}{\sqrt{2}}(|00\rangle + |11\rangle) $,　$ |\varPhi^{-}\rangle = \dfrac{1}{\sqrt{2}}(|00\rangle - |11\rangle) $, $ |\varPsi^{+}\rangle = \dfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle) $,　$ |\varPsi^{-}\rangle = \dfrac{1}{\sqrt{2}}(|01\rangle - |10\rangle) $, 分别用00, 01, 10, 11表示. 测量结果通过经典信道传递给S (或D), 然后根据结果执行相应的操作(如比特翻转或相位翻转), 以实现S和D之间的纠缠. 1跳纠缠分发, 需要消耗2比特经典信息和2个纠缠对; 若推广至K跳路径, 则需消耗$ 2 K $比特经典信息和$ K + 1 $个纠缠对. 同时, 在纠缠网络中, 建立远距离纠缠需要多次短距离纠缠生成和纠缠交换, 这受到物理因素的限制. 关键影响因素包括链路纠缠成功率(p)和纠缠交换成功率(q). 对于1跳纠缠路径, 纠缠分发成功率为$ P_{1} = p^2 q $. 推广至K跳路径, 成功率如(13)式所示. 因此, 所需的纠缠分发次数M可以通过(14)式计算: 大约要$ \dfrac{N}{p^{K+1} q^K} $次纠缠分发才能成功建立N个纠缠对.

2) Ekert91协议: Alice和Bob测量基为Alice,$ \{X, Z, T\} $; Bob, $ \{X, S, T\} $. 对于每一个纠缠对, 双方随机选择一个测量基进行测量. 在一段时间后, 双方通过经典信道交换基的信息(三种选择, 每种用2比特表示). 假设进行N次测量, 则需要消耗$ 2 \cdot N \cdot 2 = 4 N $比特的经典信息. 为了生成密钥, 双方保留了同时选择X和T基的测量结果. 在理想情况下, 大约$ {2}/{9} $的纠缠对测量结果可以用于生成原始密钥.

3)后处理: 由于系统中的缺陷, 如退相干和量子信道噪声, 原始密钥中可能会出现错误, 从而导致一定的误码率. 例如, 对于贝尔态$ \left|\psi^{+}\right\rangle = \dfrac{1}{\sqrt{2}}(\left|01\right\rangle + \left|10\right\rangle) $, Alice与Bob的测量结果应当是反相关的(01或10). 若得到相同的结果(11或00), 则表示出现了错误. 为确保双方获得一致且正确的密钥, 必须进行后处理, 包括误码纠错和保密增强. 本文选择低密度奇偶校验码(low-density parity-check code, LDPC)讨论误码纠错过程. 文献[32]给出了该方式码率$ R_{1} $的计算公式:

其中, e代表误码率, QKD协议中提取绝对密钥的最大错误阈值为11%^[33]; $ f(e) $代表纠错效率, 该值越接近1就说明需要额外传输的信息越少, 效率越高; $ H_{2}(e) $是二进制熵函数, 反映了信息的不确定性.

本文选择Toeplitz矩阵方法^[34]讨论保密增强过程. 假设$ {\boldsymbol{K}}_{A} $的长度为n, 最终密钥长度为$ G{\boldsymbol{K}}_{A} $的目标长度为m, 则得到K的方法是构造一个$ m\times n $的Toeplitz矩阵$ {\boldsymbol{T}}_{m\times n} $, 并使之与$ {\boldsymbol{K}}_{A} $组成的列向量相乘. M可以称为安全密钥长度, 其与根据系统参数所计算出的安全码率$ R_{2} $关系如(20)式, 文献[35]给出$ R_{2} $的计算方式如(21)式.

通过误码纠错和保密增强, 通信双方可以建立安全的密钥. 由上述过程可以得到安全密钥长度k与原始码长度n之间的关系如(22)式, 又因为$ n = ({2}/{9})\cdot N $, 所以可以进一步计算所需纠缠对数量N.

至此, 可以得出如下的资源消耗的计算方式:

其中, $ C_{{\mathrm{E}}} $表示Ekert91协议所消耗的经典资源, $ Q_{{\mathrm{E}}} $表示所消耗的量子资源, $ S_{{\mathrm{E}}} $表示所消耗的总资源.

本文提出的基于MERA的量子密钥分发方案依然依赖纠缠网络来提供远距离纠缠对, 但这些纠缠对并不直接用于生成密钥, 而是用于制备MPS态. 随后, 通过压缩生成MERA态, 再通过解压缩生成密钥. 该方案主要包括以下步骤: 纠缠分发、MPS态建立、MERA态压缩、密钥生成.

1)纠缠分发: 与传统方式类似, K跳纠缠建立过程中资源的消耗可以表示为:

经典资源消耗

量子资源消耗

其中, 所需纠缠对数量N的计算方式为

2) MPS态建立: MPS态的生成方式有多种^[36–38], 本文选择了通过AKLT态^[38,39]进行构建. 实际上, AKLT态的生成涉及到贝尔态, 这与本文的方案紧密契合. 这里本文主要关注所需传输的经典信息量. 在一次投影测量中, 需传输2比特的经典信息. 对于N对贝尔态, 需传输$ 2 N $比特的经典信息.

3) MERA压缩: 为了减少存储成本, 本文把原始的MPS态进行压缩. 压缩时, 由控制器下发命令, 本文所使用的U一共有6种, 用3比特表示; W一共有4种, 用2比特表示, 产生的经典信息为

其中, $ D_{l-1\rightarrow l} $表示从第$ l-1 $层到第l层的解纠缠的次数; $ \displaystyle\sum\nolimits_{l = 1}^{L}I_{l-1\to l} $表示从第$ l-1 $层到第l层的等距映射的次数.

4)密钥生成: 在密钥分发过程中, 控制器需要向双方发送层数命令. 双方根据接收到的层数, 使用相应的矩阵操作序列和逆操作进行解压缩. 因此, 主要传输的经典信息为层数. 由于本文的方案中层数的范围在$ {[1, 10]} $, 因此使用4比特的经典信息来表示层数. 最终传输的经典信息量为

其中, $ D_{e} $表示所需解压缩次数. 同时每次解压缩完成时, 需要验证命令的可信性, 通过SHA-256验证. 一次需要256比特的经典信息传输. 产生的经典信息为

综上所述, MERA方式的资源消耗可以表示为

其中, $ C_{{\mathrm{M}}} $表示MERA方案所消耗的经典资源, $ Q_{{\mathrm{M}}} $表示所消耗的量子资源, $ S_{{\mathrm{M}}} $表示所消耗的总资源.

本节基于前述分析进行了实验设计, 并展开了详细分析. 本文观察到, 误码率、平均路径跳数、链路纠缠成功率以及纠缠交换成功率对资源消耗具有关键影响. 由于这些参数是实际QKD网络中的重要物理因素, 对它们进行深入讨论是必要的.

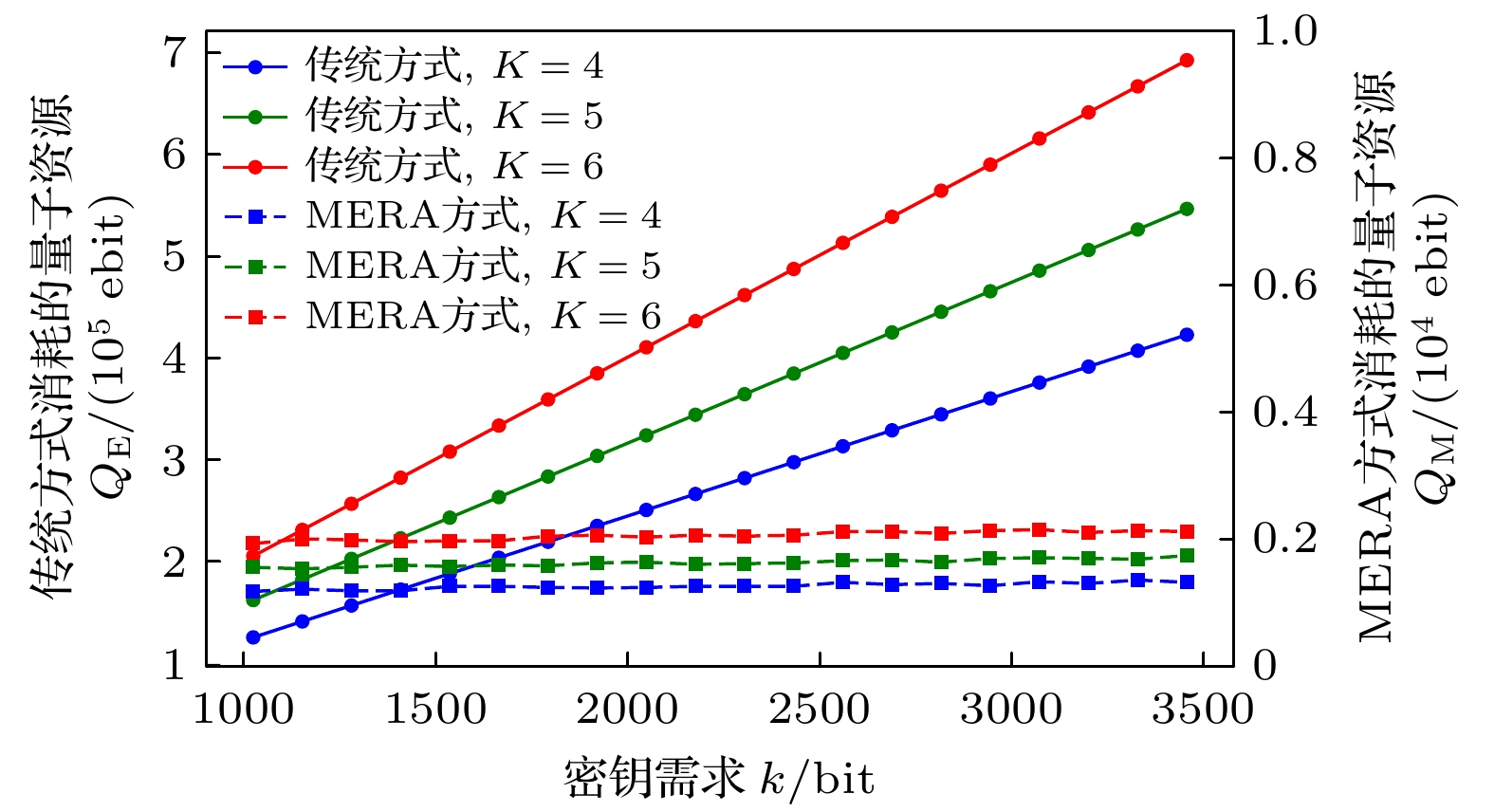
1)需求量k对资源消耗的影响

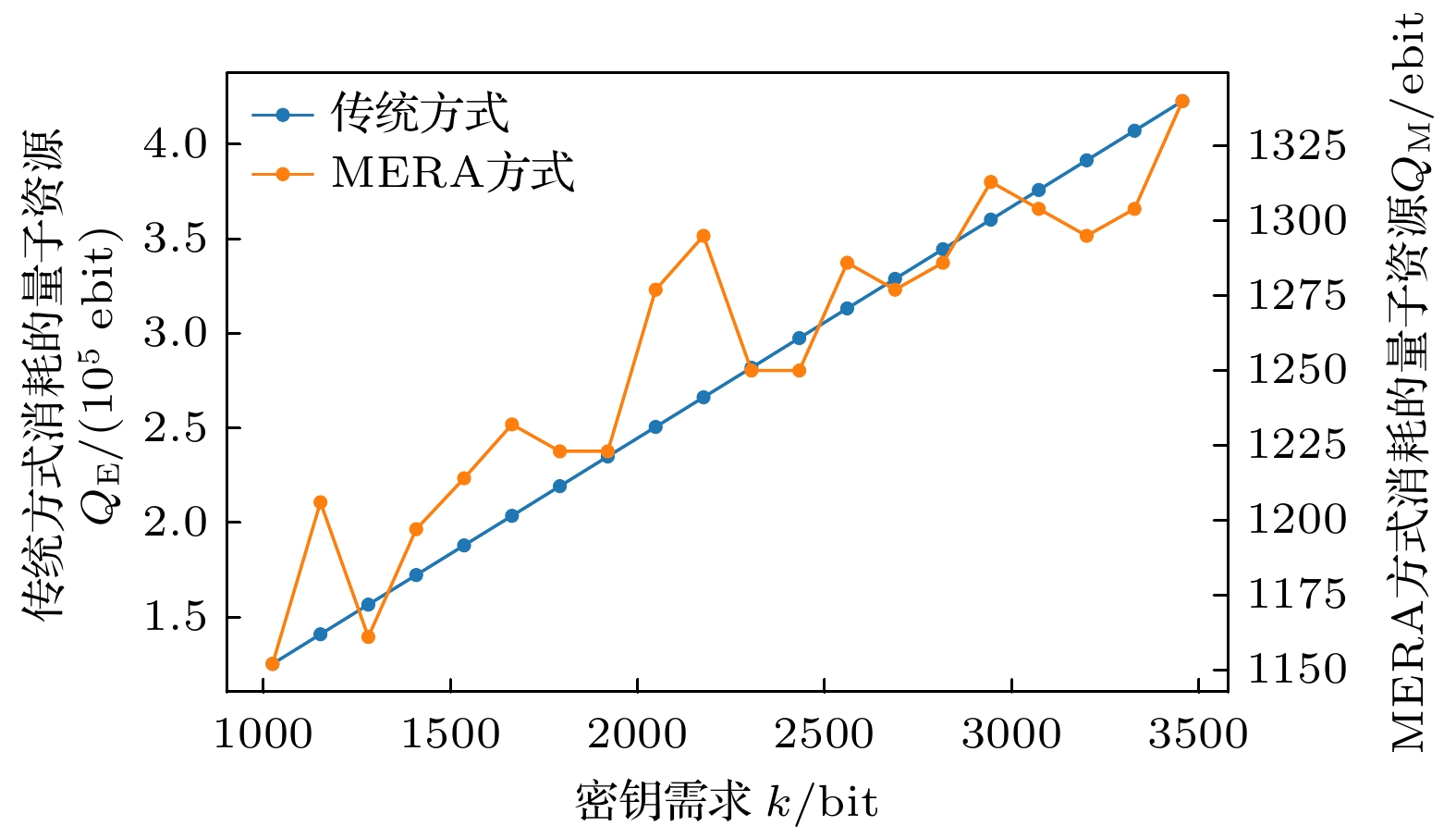
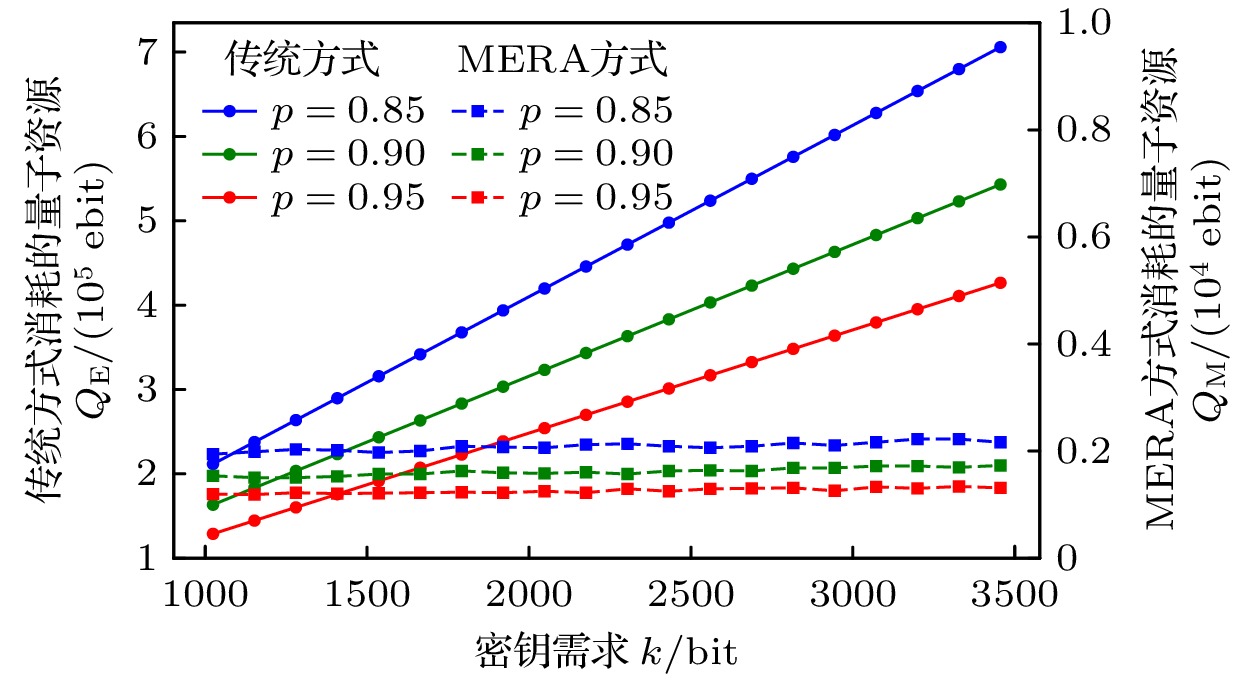
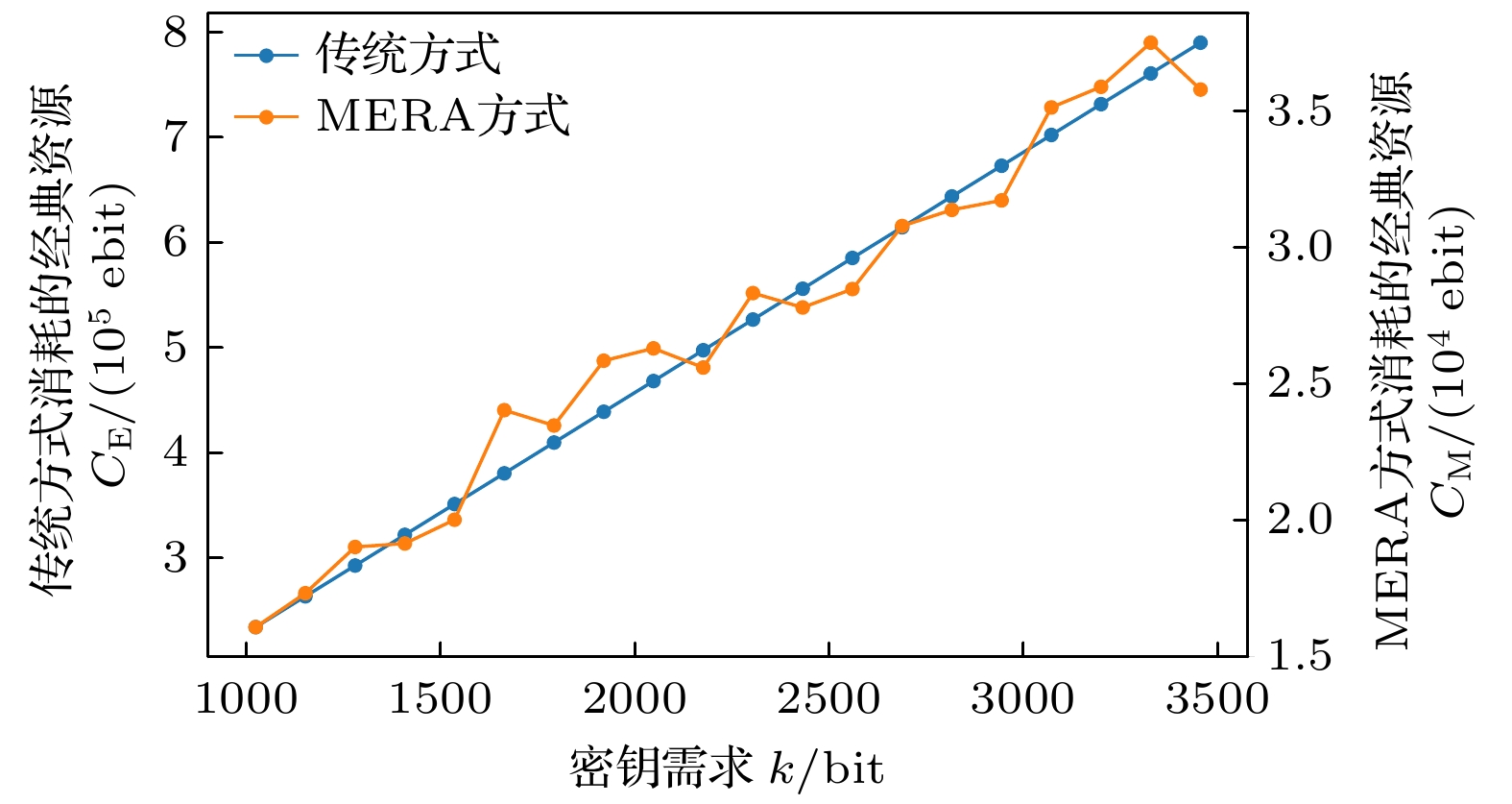
图7展示了在不同需求下, 传统方式与MERA方式的量子资源消耗情况. 实验参数设置为$ K = 4, \;e = 0.08, \;p = 0.95, \;q = 0.95 $. 传统方式的消耗量用左侧纵轴表示, 范围为150000—400000; 而MERA方式的消耗量用右侧纵轴表示, 范围为1150—1325. 从图7可以看出, 随着需求的增加, 传统方式下的量子资源消耗显著上升, 表明需求增长会导致资源快速消耗; 相较之下, MERA方式的资源消耗较少, 且增长速度较为平缓. 相比传统方式, MERA方式在相同需求下显著降低了量子资源的消耗, 展现出其在高需求情况下的资源利用效率优势. 例如, 当需求量为1024比特时, MERA方式节省了124151对纠缠资源. 这表明, 在量子密钥分发网络中, MERA方式通过优化资源使用, 能够更有效地应对不断增长的需求.

根据图8, 虽然经典资源的消耗也呈上升趋势, 但总体上远高于量子资源的消耗. 根据(24)式, (25)式, (33)式和(34)式, 经典资源的消耗与量子资源消耗密切相关. 主要的资源消耗集中在建立远距离纠缠的过程中, 这不仅需要大量链路纠缠, 还涉及多次贝尔态测量, 因此会消耗大量经典资源. 由此可见, 经典资源的消耗趋势与量子资源的消耗趋势相似. 鉴于这一关系, 后续讨论将重点关注量子资源的消耗.

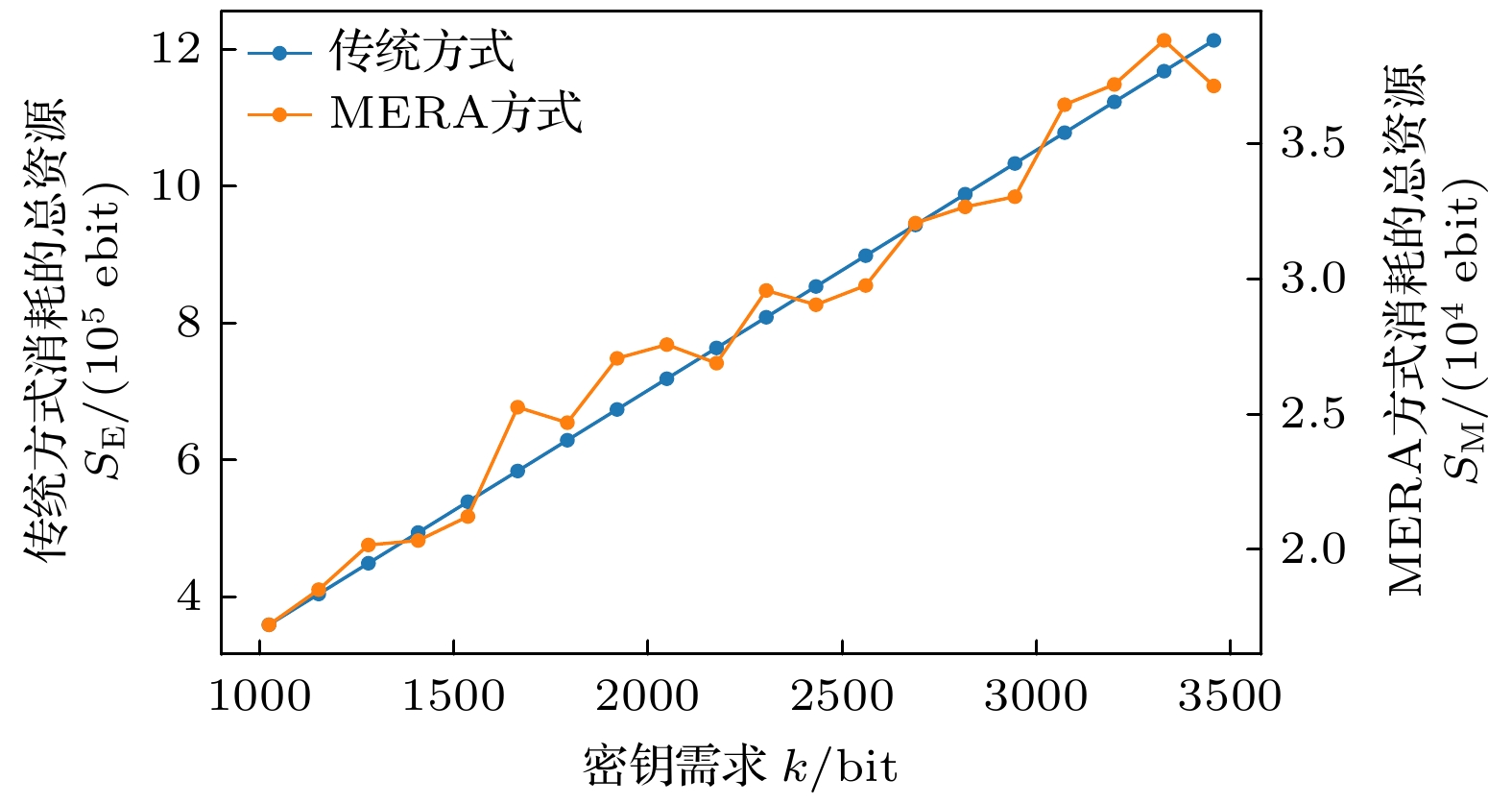
图9展示了量子资源和经典资源总和的变化趋势, 随着需求量的增加, 总资源消耗逐渐上升. 然而, 传统方式的资源消耗增长速度远高于MERA方式. 这主要是因为传统方式的密钥生成直接依赖于大量纠缠资源, 而MERA方式对纠缠资源的需求较弱, 因此其资源消耗增长较为缓慢. 由此可见, MERA方式在资源消耗方面具有显著优势.

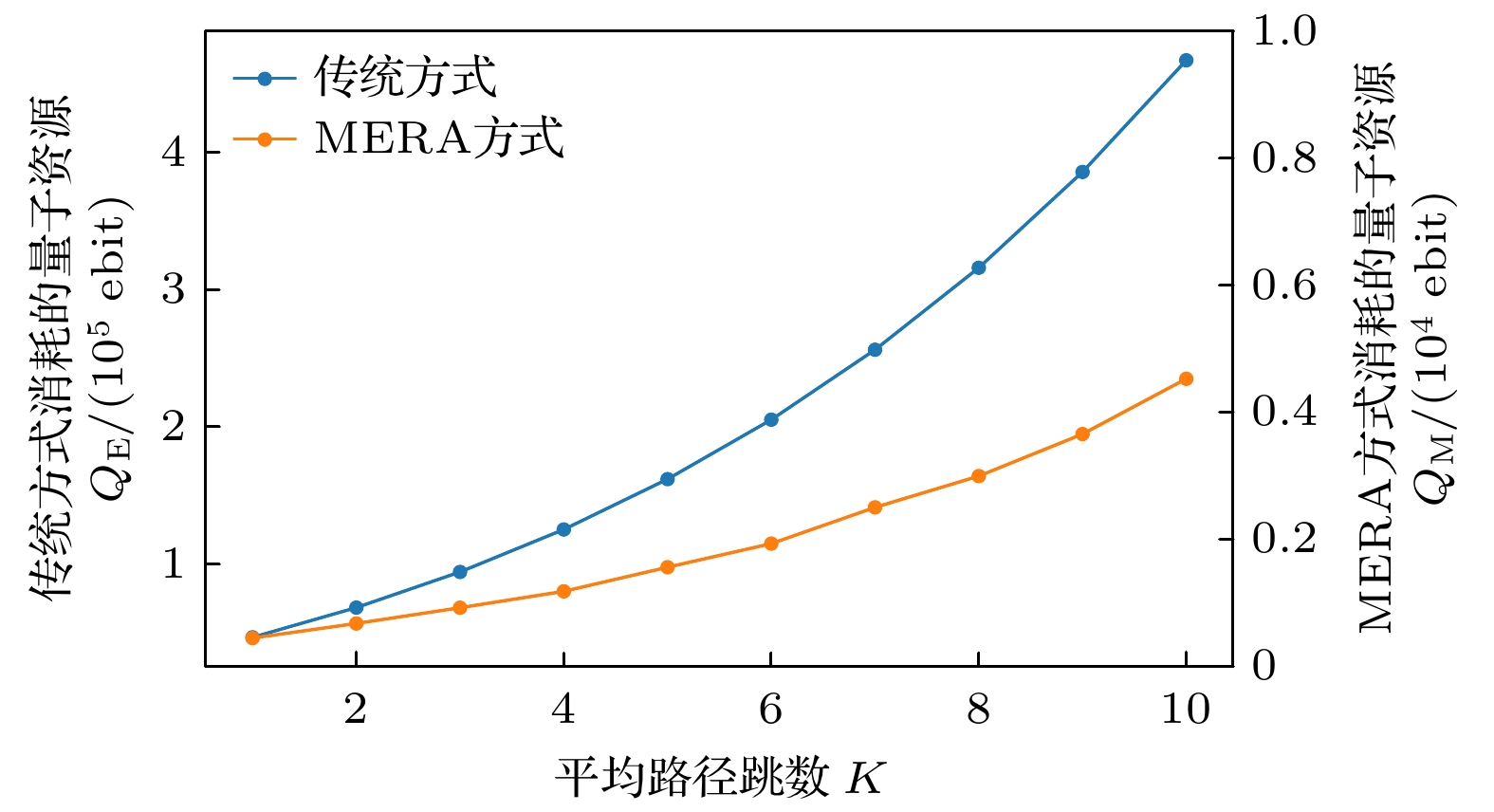
2)平均路径跳数对资源消耗的影响

实验参数设置为$ e = 0.08,\; p = 0.95,\; q = 0.95, k = 1024 $. 从图10可以看出, 随着路径跳数的增加, 两种方法的纠缠资源消耗均呈指数增长. 这是因为随着路径跳数的增加, 成功建立远距离纠缠的概率呈指数下降. 然而, 如图11所示, 无论路径 长度如何, 本文的方法所需的资源明显少于传统 方法. 根据(25)式和(34)式, 它们之间的资源消耗比为$ {Q_{{\mathrm{E}}}}/{Q_{{\mathrm{M}}}} = {N_{1}}/{N_{2}} $, 表明所需纠缠对的数量比与成功建立远距离纠缠对的数量呈正相关. 当$ K = 4 $时, 传统方法消耗的纠缠对数量是MERA方法的106倍.

3) 误码率对资源消耗的影响

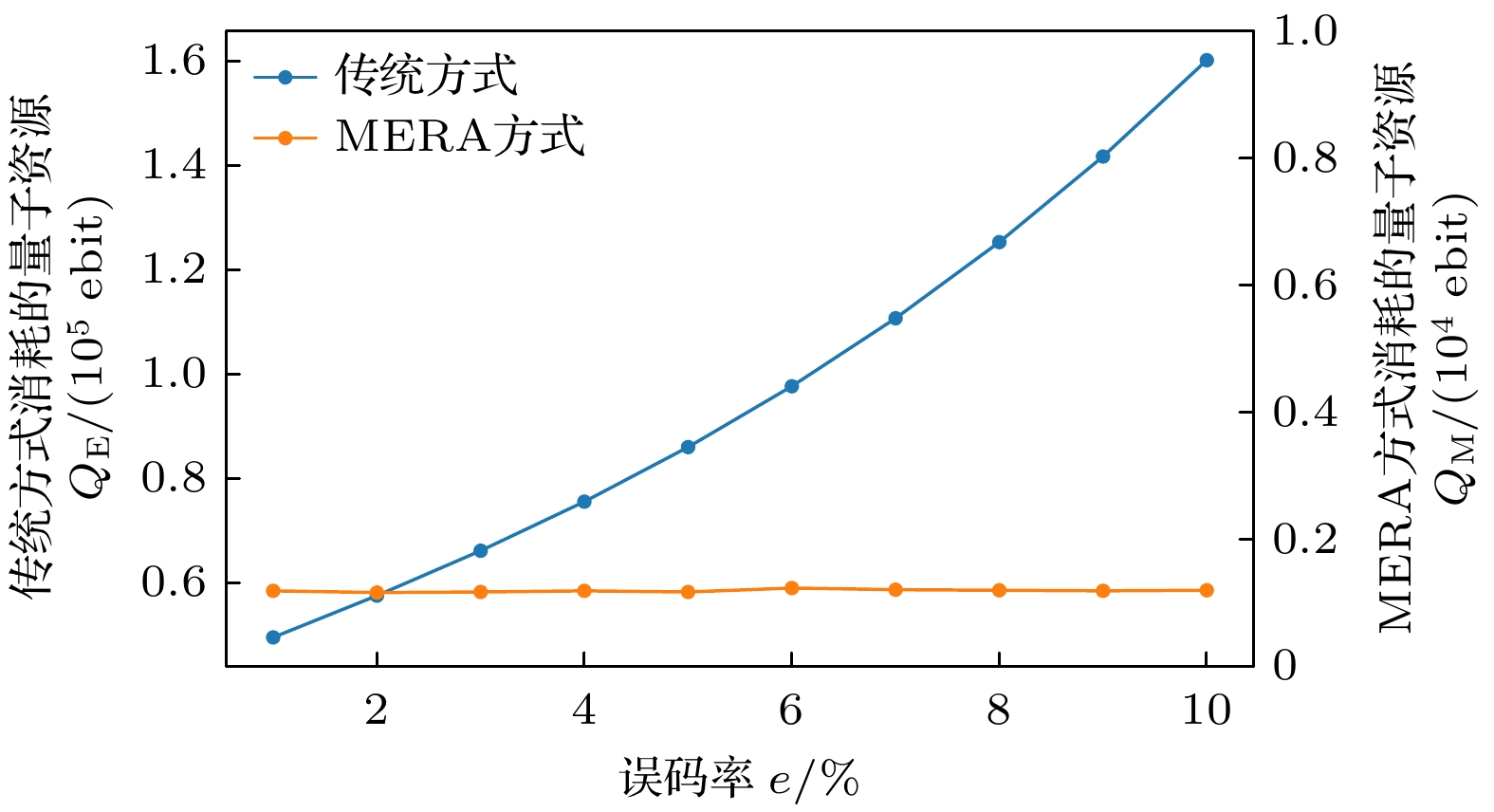
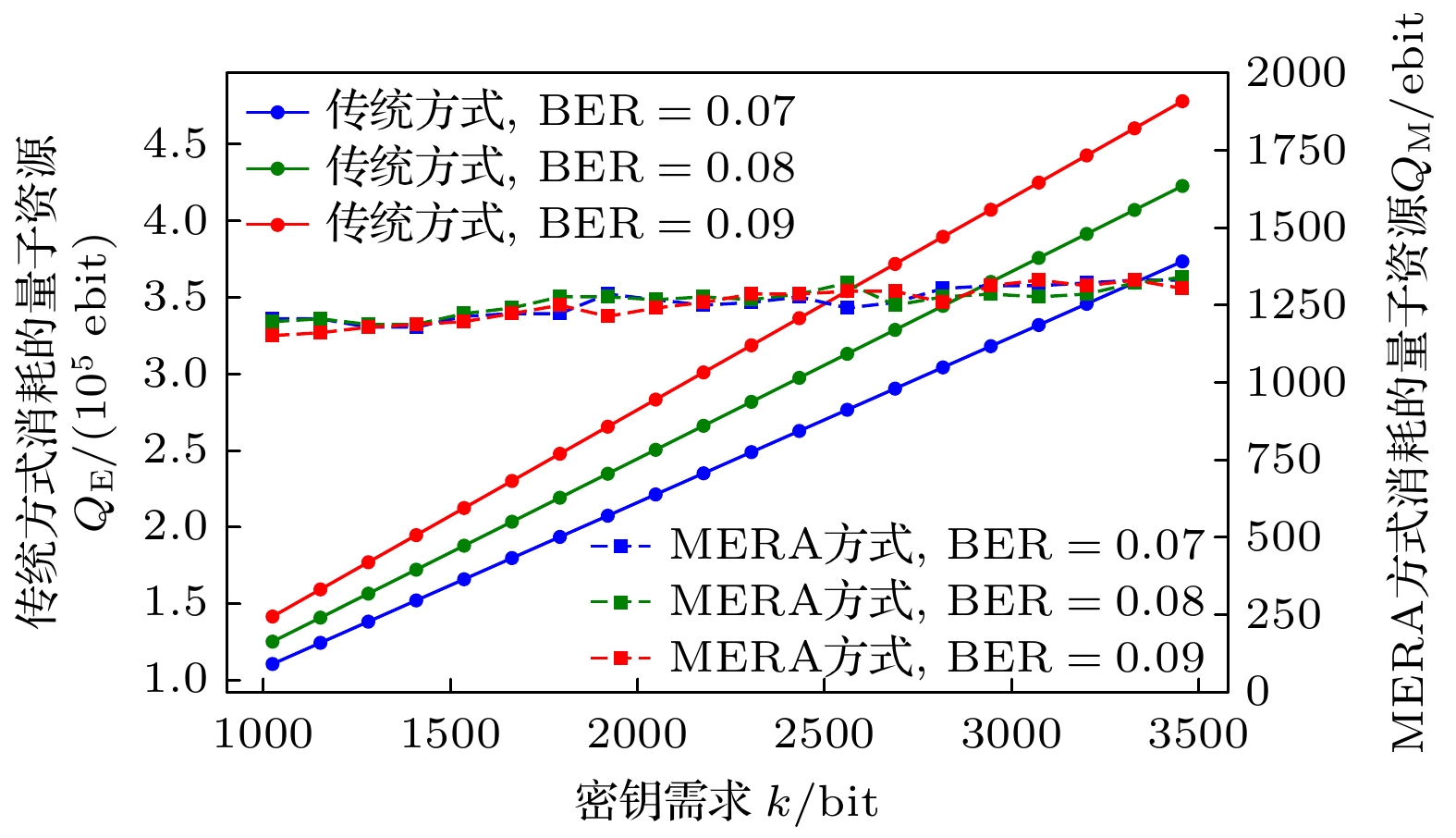
实验参数设置为$ K = 4,\; p = 0.95, \;q = 0.95, k = 1024 $. 根据图12, 误码率对MERA方法几乎没有影响. 根据前面的分析, 误码率主要在后处理阶段影响安全密钥长度, 从而影响原始密钥长度. 传统方法生成一位原始密钥至少需要消耗一个纠缠对, 而MERA方式只消耗一次解压缩后中的一位, 不直接消耗纠缠对. 因此, 在较高的误码率下, 本文的方法表现出明显的优势. 例如, 在误码率为10%时, 本文的方法节省了158960对纠缠. 此外, 图13展示了在误码率分别为7%, 8%和9%时, 两种方法在不同请求量下消耗的量子资源变化情况.

4)链路纠缠成功率对资源消耗的影响

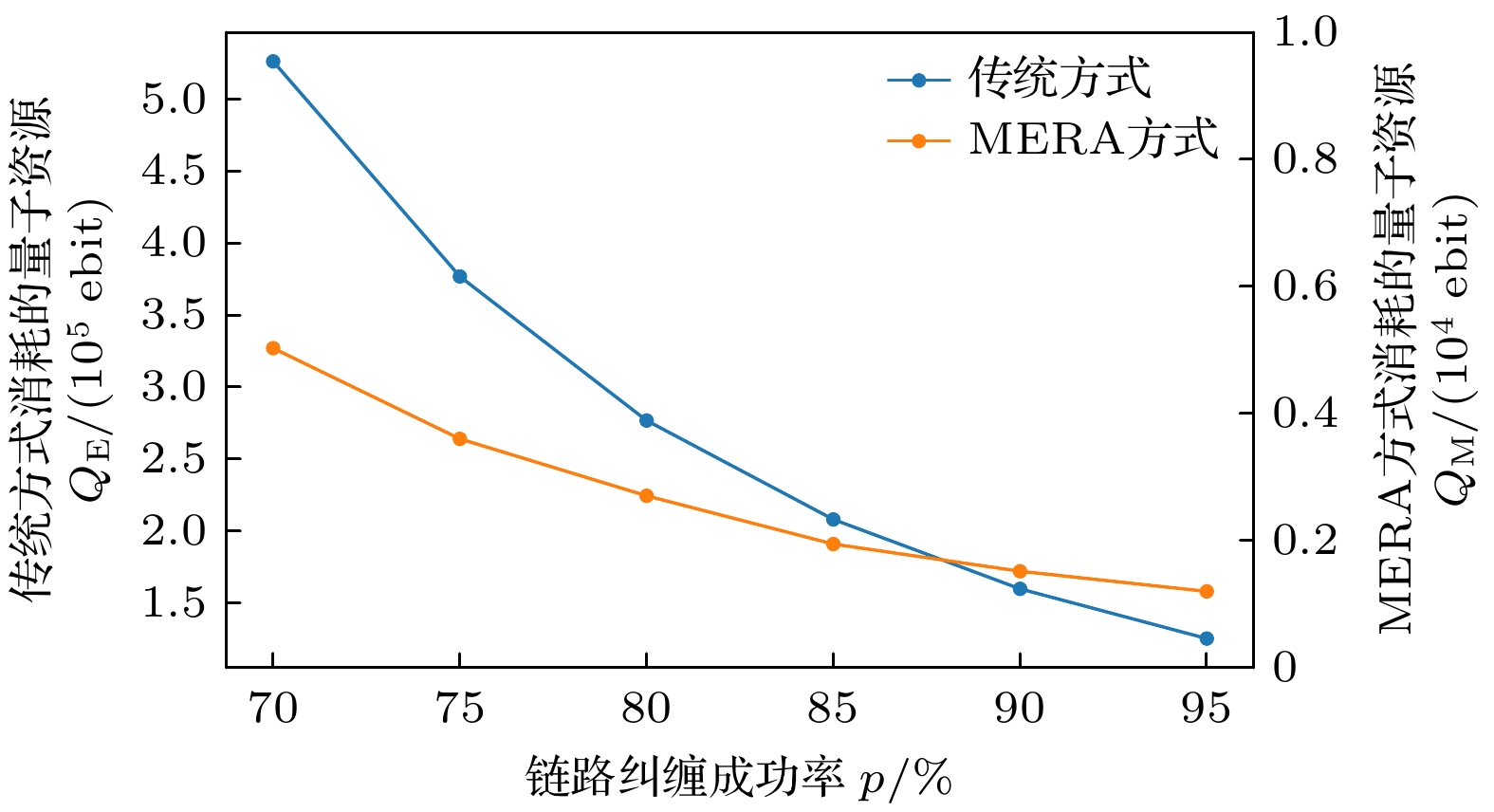
实验参数设置为$ K = 4,\; e = 0.08, \;q = 0.95, k = 1024 $. 根据图14, 链路纠缠成功率是量子网络中的关键物理参数, 受到具体物理器件性能的影响. 该参数直接决定远距离纠缠分发的成功率: 链路纠缠成功率越高, 远距离纠缠成功率也相应提高. 链路纠缠成功率提升时, 两种方式所需纠缠对的数量均呈指数级下降. 此外, 如图15所示, 在相同成功率下, MERA方法的资源消耗显著低于传统方法.

5)纠缠交换成功率对资源消耗的影响

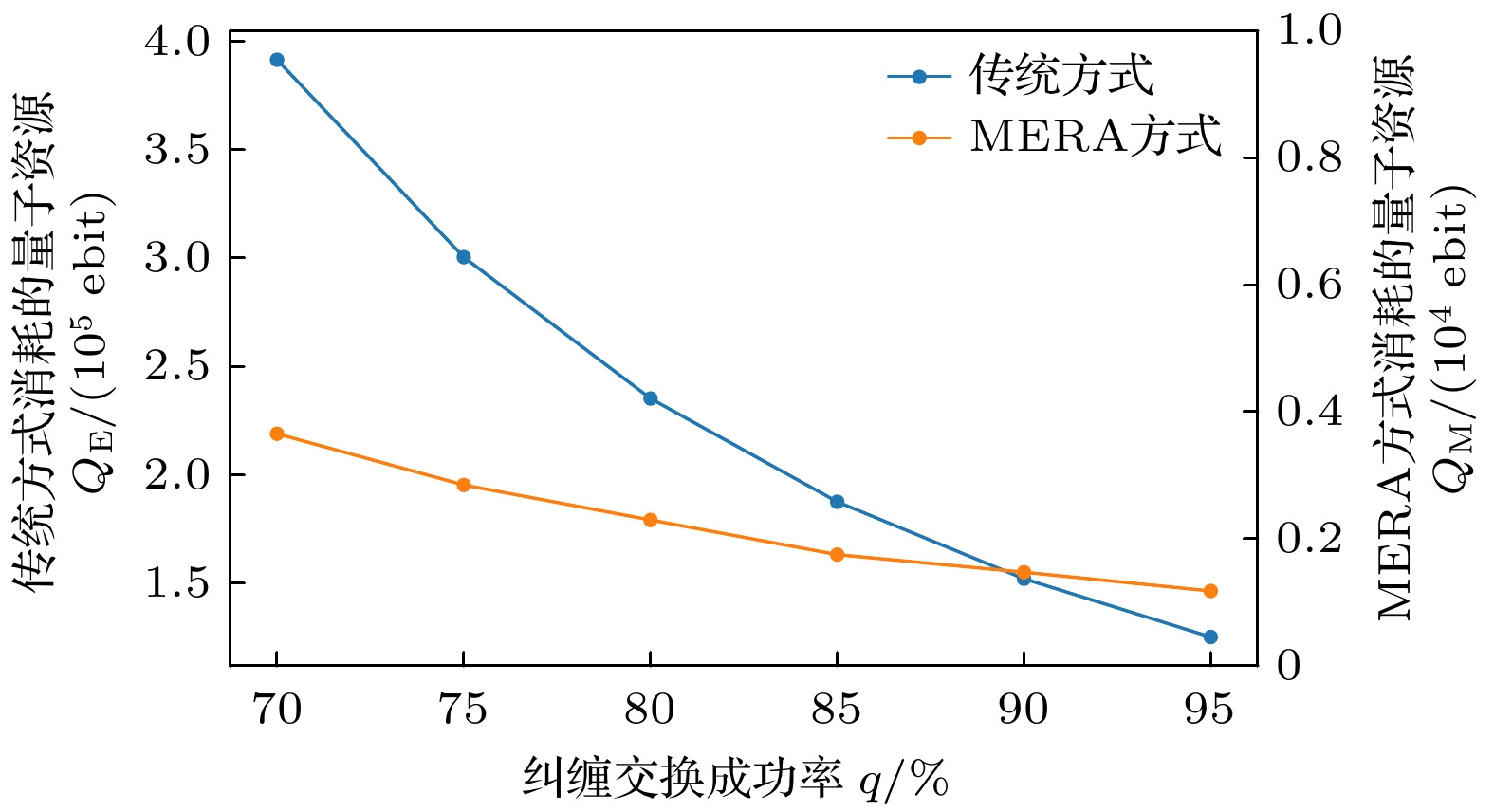
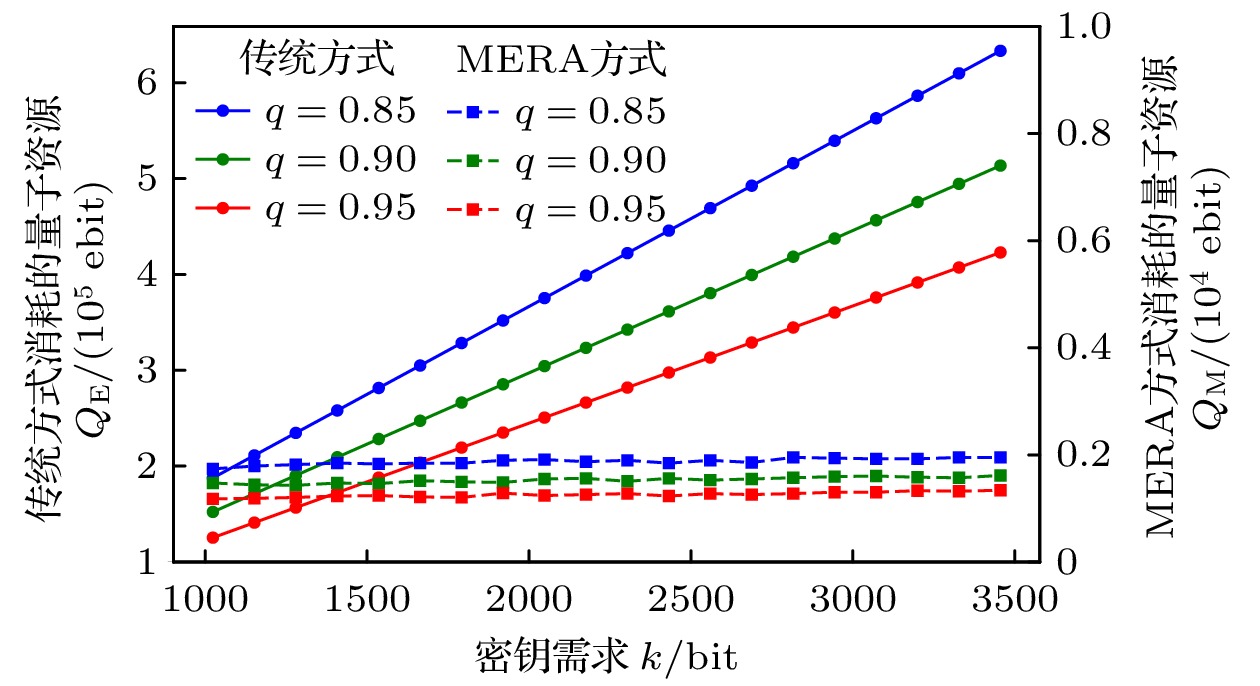
实验参数设置为$ K = 4, \;e = 0.08, \;p = 0.95, k = 1024 $. 纠缠交换成功率与链路纠缠成功率同样影响远距离纠缠的成功率, 所需量子资源数量的变化趋势如图16所示, 但相比之下, 链路纠缠成功率对远距离纠缠成功率的影响更为显著. 纠缠交换成功率越高, 远距离纠缠的成功率提升幅度也越大. 图17展示了在纠缠交换成功率为85%, 90%和95%时, 两种方法在不同请求量下消耗的量子资源变化情况.

通过对比实验可以发现, 平均路径跳数、链路纠缠成功率、纠缠交换成功率和误码率对资源消耗有显著影响. 具体来说, 平均路径跳数越大、链路纠缠成功率越低、纠缠交换成功率越低、误码率越高, 所需资源量也随之增加. 同时, 在相同的物理条件下, 本文的方法资源消耗明显低于传统方法, 且随着需求量的增加, 本文的方法对量子资源的需求增长更为平缓. 在量子资源有限的情况下, 本文的方法展现出了更大的优势.

在$ S\text{-}D $之间生成的原始MPS态量子比特数量较多, 现有的存储技术难以满足需求. 为了解决这一问题, 本文通过应用无损压缩技术, 将原始MPS态压缩为单光子或少量光子的压缩态. 这种处理方式使得在现有技术条件下, 可以实现更长时间的量子态存储. 此外, 存储成本与所需的资源数量密切相关. 因此, 相较于传统方法, 本文的方法在存储成本上具有显著优势.

本文方法的传输成本主要包括三个部分: 首先是$ S\text{-}D $对之间共享的MPS态, 其资源消耗与MPS态的长度相关; 其次是控制器向$ S\text{-}D $对下发的命令, 这些命令通过专用信道传输, 成本较高. 不过, 最频繁传输的是层数, 因此资源需求较少. 此外, 本文对W和U操作采用编号形式传输操作序列, 而非直接传输矩阵本身, 这大大降低了传输成本. 总体而言, 传统方法的资源消耗显著高于MERA方法, 因此其传输成本也远高于MERA方法.

本文提出的方案在安全性上与传统QKD方法保持一致, 并未影响已有的安全性分析模型, 且优化了纠缠资源的使用. 与传统QKD协议相同, 本文方案依赖于不可克隆定理来确保纠缠对的安全分发. 然而, 由于本方案增加了步骤, 在安全性方面需应对新的挑战. 这里重点分析两方面的增强: 一是控制信息的安全传输, 二是共享矩阵积态(MPS)的保密性. 通过详细分析证明了这些增强不影响传统的安全性理论, 并保持了方案的整体安全性.

首先, 协议要求传输经典控制信息(包括MPS态长度、压缩所用的酉变换及解压缩层数), 这一需求在传统QKD协议中并不存在. 尽管如此, 这些信息通过安全专用信道传输, 确保不受窃听威胁. 其次, 解压缩层数采用随机选择, 使窃听者难以推测正确的解压缩过程. 例如, 对于长度为2048的密钥请求, 若MPS态包含256个光子, MERA态最高层数为8, 需进行$ [16, 64] $次解纠缠. 假设解压缩次数为32次, 即便窃听者已获得共享的MPS态, 由于解压缩层数的随机性, 其每次猜对的概率为$ {1}/{8} $, 完全猜对32次的概率为$ {1}/{2^{32}} $, 几乎不可能破解密钥.

此外, 协议要求通信双方共享MPS态. 为防止窃听者获取, 设置安全参数δ, 保证密钥分发的安全性. 若窃听者试图自行制备, 猜测单个量子比特的正确概率为$ {1}/{2} $, 对于长度为128的MPS态, 其成功猜测的概率为${1}/{2^{128}} $. 本协议设置$ \delta = 128 $, 即MPS态长度$ n \geqslant 128 $, 使窃听者的成功概率极低. 即便窃听者截获MPS态, 本协议不直接使用原始态, 而是通过压缩后的MERA态生成密钥, 进一步提升了安全性.

本文针对基于纠缠的QKD协议中的资源消耗问题, 提出了一种优化方案, 该方案充分利用了MERA的层次结构. 研究发现, 通过应用MERA, 可以将MPS压缩为单光子或双光子态, 有效降低了量子存储的成本和复杂性. 在密钥分发过程中, 本文引入了安全参数以防止潜在的攻击, 并通过随机解压缩策略增强了安全性. 为了适应不同的通信需求, 本文方案采取了差异化处理: 在确保安全性的前提下, 仅使用一个共享的MERA态, 并允许对其底三层进行重复使用, 直到生成足够的密钥. 除非必要, 否则避免重新生成MERA态, 从而减少了额外的量子资源消耗. 这一策略在纠缠网络中尤为有效, 因为它减少了对链路纠缠的依赖, 而这些链路纠缠的建立通常受到距离、路径跳数和链路成功率等物理因素的限制.

通过理论分析和实验验证, 本文证明了所提方案在减少经典与量子资源使用方面的显著优势. 在现有技术条件下, 该方案满足了大规模量子密钥分发的需求, 为量子通信网络的资源优化提供了一种切实可行的策略.