-
在现代电子、光子和能源系统中, 特别是在微纳尺度上, 材料的热特性表征对于理解和改善性能至关重要[1–3]. 在众多技术中, 时域热反射(TDTR)[4–6]和频域热反射(FDTR)[7–9]等方法已成为测量薄膜和块体材料热物性的重要工具. 基于温度依赖的反射率变化, 这些技术能够高精度地测量材料的热导率、比热容及界面热阻.
然而, 热反射实验中的数据解释面临诸多挑战, 主要因为实验变量之间的复杂耦合关系. 单一变量分析难以全面捕捉层内和层间特性的相互作用, 进而影响热物性参数的准确提取. 因此, 迫切需要先进的数据分析方法, 以解开变量间的复杂关系, 并提升热反射测量的可靠性.
奇异值分解(SVD)提供了一种有效的方法来计算矩阵的伪逆, 这使其在处理复杂数据时能有效地分离和识别数据中的主要成分[10,11]. 此外, 其稳定性和高效性也使其成为分析大规模数据矩阵的理想选择[12,13]. 本研究应用SVD技术, 对实验变量的相互关系进行系统分析, 既揭示了变量间的潜在关系, 也确定了最大可提取的关键组合参数. 该方法为热反射数据的解析提供了可靠的框架, 从而提高了热物性测量的精度和全面性. 作为实际应用, 本文对铝/蓝宝石样品的FDTR信号进行了分析, 通过敏感性分析确定了可提取的最大变量数量. 该研究深化了对热反射现象的理解, 并为未来热表征技术和材料研究的发展提供了重要支持.
-
热反射技术, 如TDTR和FDTR, 广泛用于测量块体和薄膜材料的热特性, 每种方法根据实验设置和测量目标具有独特优势. TDTR使用飞秒激光脉冲通过时域信号获取皮秒级的时间分辨率; FDTR则通过调节激光调制频率进行频域分析, 不需要机械延迟台, 实验更简便且成本较低. FDTR可在广泛的频率范围内操作, 适用于不同热导率的材料, 但相位测量需要精确的相位校正, 低频时信噪比也较差. 方脉冲热源法(SPS)[14]是一种相对较新的技术, 它结合了TDTR和FDTR的优势, 使用方波调制的泵浦加热源, 既实现了时间分辨的信号观察, 又允许大范围频率调制.
所有热反射方法均依赖于通过多层热扩散模型对测量信号进行拟合, 以提取材料的热物性参数. 这一过程实质上属于反问题求解, 其中敏感性分析发挥着关键的作用. 敏感性分析能够迅速确定目标参数的拟合方向, 并对测量误差进行估计. 在FDTR实验中, 频率
${f_i}$ 处归一化幅值信号${A_{{\text{norm}}}}$ 和相位信号$\phi $ 对某参数${\xi _j}$ 的敏感性系数定义分别为其中当参数
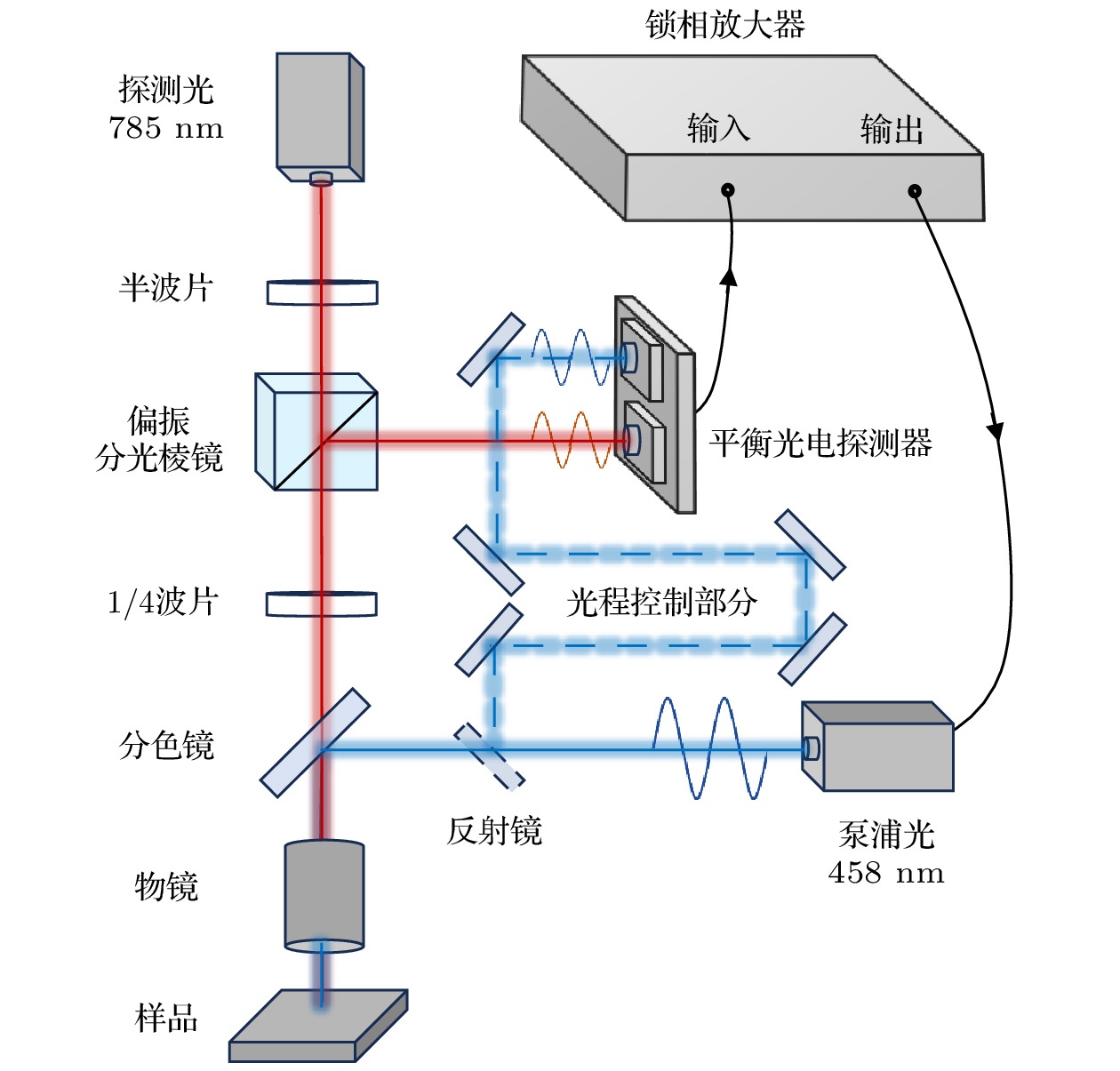
${\xi _j}$ 变化1%时, 归一化幅值信号${A_{{\text{norm}}}}$ 变化${( {S_{{\xi _j}}^{{A_{{\text{norm}}}}}} )_{{f_i}}}\%$ , 相位信号$\phi $ 变化为${( {{S_{{\xi _j}}}} )_{{f_i}}} \times 0.01^\circ $ .本研究以FDTR测量为例, 探索热反射实验中各个热物性参数间的相互关系. 图1为本文搭建的FDTR实验系统示意图. 该系统利用458 nm波长的泵浦光(pump)来加热样品, 并使用785 nm波长的探测光(probe)来监测样品温度响应随加热频率的变化. 实验首先通过反射镜引导泵浦光进入光电探测器, 测量不同加热频率下的泵浦光相位
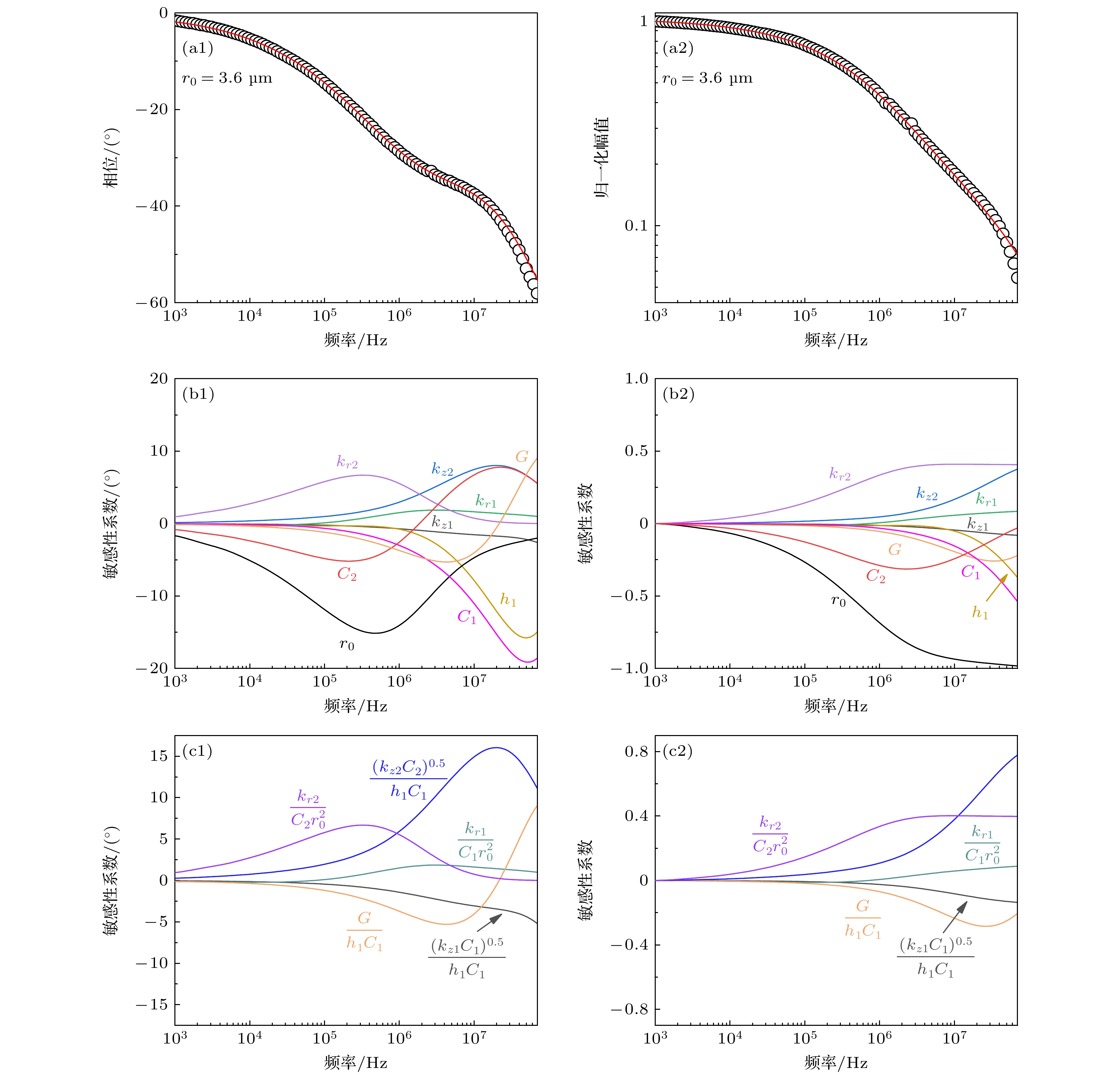
${\phi _{{\text{pump}}}}$ . 随后, 移除反射镜, 使探测光进入探测器以测量不同加热频率下的相位${\phi _{{\text{probe}}}}$ 和幅值, 并对幅值进行归一化处理, 得到FDTR的归一化幅值信号${A_{{\text{norm}}}}$ . 实验系统的设置可能导致泵浦光和探测光之间产生相位偏移${\phi _{{\text{system}}}}$ . 为保证精确测量, 实验要求泵浦光到探测器的光程应等于探测光经样品到探测器的光程和. 若光程不匹配,${\phi _{{\text{system}}}}$ 会随调制频率而变化. FDTR的相位信号表示为$\phi = {\phi _{{\text{probe}}}} - {\phi _{{\text{pump}}}} - {\phi _{{\text{system}}}}$ . 通过使用铝/二氧化硅的标准样品进行光程矫正, 直至${\phi _{{\text{system}}}}$ 为恒定值, 从而完成实验系统的调试. 最后对测得的探测光相位应用矫正公式计算, 得到FDTR的相位信号$\phi $ .图2(a1)和图2(a2)分别展示了采用FDTR对100 nm铝/蓝宝石样品测量的相位信号和归一化幅值信号, 测量频率范围为1 kHz—70 MHz, 光斑半径为
$3.6{\text{ }} {\text{μm}}$ . 该热系统涉及9个主要参数:${k_{r1}}$ ,${k_{z1}}$ ,${C_1}$ ,${h_1}$ ,${k_{r2}}$ ,${k_{z2}}$ ,${C_2}$ ,$G$ 和${r_0}$ , 其中${k_r}$ 和${k_z}$ 分别代表面内及面外热导率,$C$ 为体积热容,$h$ 为厚度,$G$ 是界面热导,${r_0}$ 为光斑半径. 下标“1”和“2”分别表示金属传感层和衬底的属性.图2(b1)和图2(b2)分别展示了相位信号和归一化幅值信号对热系统中所有参数的敏感性系数随调制频率的变化. 敏感性分析结果表明, 在低频(
${f_0} < 100{\text{ kHz}}$ )时, 相位和归一化幅值信号均对组合参数${k_{r2}}/({{C_2}r_0^2})$ 的敏感性较强, 这是由于三者的敏感性系数存在以下关系:${S_{{k_{r2}}}} = - {S_{{C_2}}} = - 0.5{S_{{r_0}}}$ . 然而, 在高频范围内, 随着信号对${k_{z2}}$ ,${h_1}$ 和$G$ 等参数敏感性的增加, 低频下的敏感性关系不再适用. 当频率超过10 MHz时, 相位信号对${k_{r2}}$ 的敏感性逐渐降低至零, 而${k_{z2}}$ 与${C_2}$ 之间呈现显著的耦合关系, 敏感性关系为${S_{{k_{z2}}}} = {S_{{C_2}}}$ . 在高频下, 归一化幅值信号仍对${k_{r2}}$ 保持较高敏感性,${k_{z2}}$ 与${C_2}$ 的耦合关系为${S_{{k_{z2}}}} - {S_{{C_2}}} = {S_{{k_{r2}}}}$ .在FDTR实验中, 不同参数的敏感性系数之间的明确关系较难辨识. 本文通过深入探索, 发现热扩散模型中参数间存在特定的关系, 而且信号本质上是由图2(c1)和图2(c2)所示的几个组合参数来决定的. 理解这些复杂的参数关联对于优化热反射实验中的参数拟合至关重要. 以下将详细讨论如何通过深入数据分析来揭示热反射实验中复杂的参数关联.
-
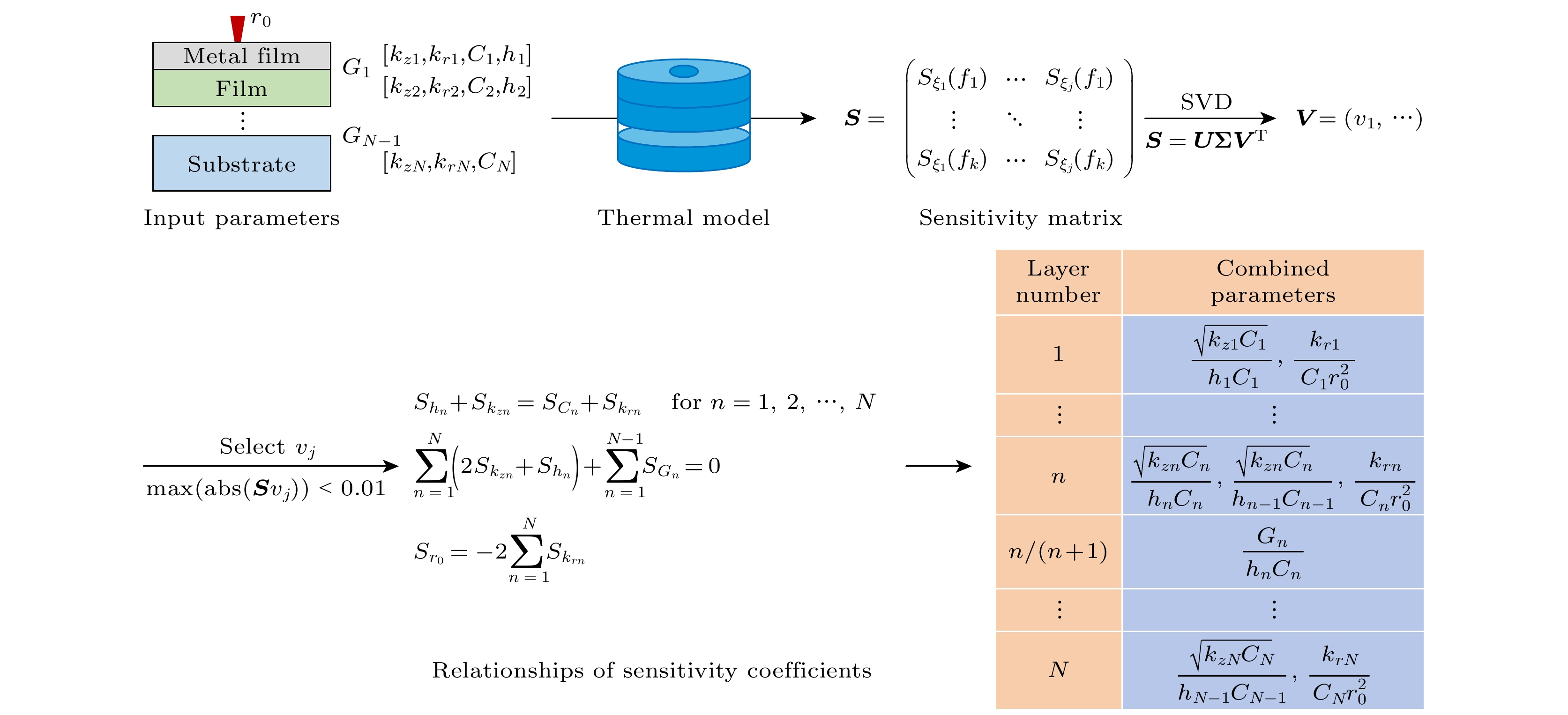
采用SVD技术来揭示热反射实验中不同参 数的敏感性系数之间的关系. 以一个假设的三层 系统为例, 每层包含四个参数
$\left( {{k_z}, {k_r}, C, h} \right)$ , 其他 参数包括两个界面的界面热导率(${G_1}$ 和${G_2}$ ), 以及光斑尺寸${r_0}$ . 表1列出了光斑尺寸及样品的物 性参数.以FDTR方法为例, 我们在对数尺度上选择1 Hz到200 MHz范围内等间隔的1000个调制频率, 生成FDTR信号并计算信号对各参数的敏感性系数. 首先分析第1层材料的四个参数(
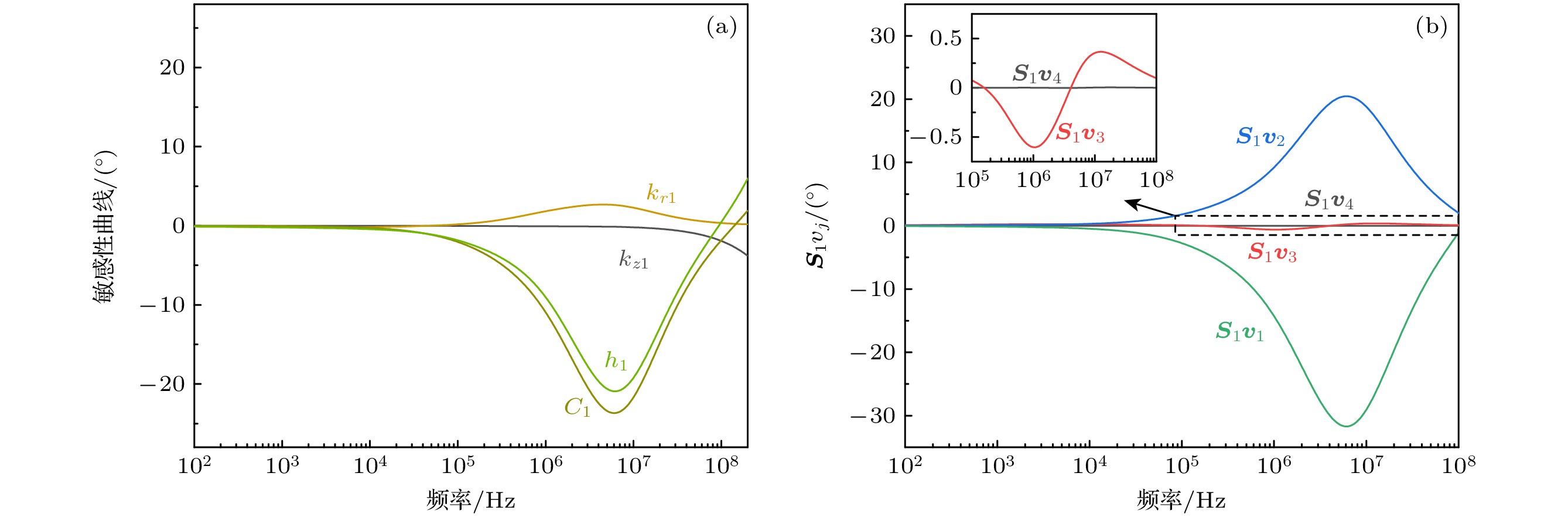
${k_{z1}}, {k_{r1}},\; {C_1}$ ,${h_1}$ )的敏感性系数. 相位信号对这四个参数的敏感性系数随频率的变化如图3(a)所示. 将这四个参数的敏感性系数组成矩阵${{\boldsymbol{S}}_1} = ( {S_{{k_{z1}}}}, {S_{{k_{r1}}}}, {S_{{C_1}}}, {S_{{h_1}}} )$ . 这里, 矩阵S表示为其中
${S_{{\xi _j}}}\left( {{f_k}} \right)$ 表示在调制频率${f_k}$ 下, 相位或幅值信号对参数${\xi _j}$ 的敏感性系数.通过SVD对敏感性系数矩阵
${{\boldsymbol{S}}_1}$ 进行分解, 得到${{\boldsymbol{S}}_1} ={\boldsymbol{ U\varSigma}} {{\boldsymbol{V}}^{\text{T}}}$ , 或者也可以写成[15]:其中
${{\boldsymbol{v}}_j}$ 是矩阵${\boldsymbol{V}}$ 的第$j$ 列;${{\boldsymbol{u}}_j}$ 是矩阵U的第$j$ 列;${\sigma _j}$ 是矩阵${{\boldsymbol{S}}_1}$ 的第$j$ 个奇异值.SVD分解
${{\boldsymbol{S}}_1}$ 的目的是找到满足${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_j} = 0$ 的解${{\boldsymbol{v}}_j}$ . 由于U是正交矩阵, 2-范数$||{{\boldsymbol{u}}_j}|{|_2} \equiv 1$ , 这意味着较小的${\sigma _j}$ 表明${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_j}$ 更接近零向量. 当$\max \left( {{\text{abs}}\left( {{{\boldsymbol{S}}_1}{{\boldsymbol{v}}_j}} \right)} \right) < 0.01^\circ $ 时, 可认为${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_j}$ 足够接近零向量.对
${{\boldsymbol{S}}_1}$ 进行SVD分解得到的奇异值矩阵为${\boldsymbol{\varSigma}} = {\text{diag}}\left( {351, 26, 7, 0.04} \right)$ . 由于${\sigma _4}$ 足够小, 可认为${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_4}$ 接近零. 图3(b)更直观地展示了${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_j}$ 的大小. 显然,${{\boldsymbol{v}}_3}$ 不能满足${{\boldsymbol{S}}_1}{{\boldsymbol{v}}_3} \approx 0$ , 而${{\boldsymbol{v}}_4}$ 满足该条件, 其对应的${{\boldsymbol{v}}_4} = {\left( { - 0.5, 0.5, 0.5, - 0.5} \right)^{\text{T}}}$ .基于
${{\boldsymbol{v}}_4}$ , 我们得出以下关系:或
我们对第2层和第3层的参数进行了相同的分析, 发现方程(5)对所有层均成立.
进一步地, 根据附录A, 若信号
$R$ 是参数A, B和C的函数, 即$R = f\left( {A, B, C} \right)$ , 则敏感性关系${S_A} = b{S_B} + c{S_C}$ 是$R = f\left( {{A^b}B, {A^c}C} \right)$ 的充分必要条件. 基于该分析, 方程(5)说明FDTR的相位和归一化幅值信号主要对每一层的组合参数${k_z}C$ ,${k_r}/C$ 和$hC$ 敏感.根据附录B, 若信号
$R$ 由两个组合参数$\alpha $ 和$\beta $ 决定, 且$\alpha = {A^a}{B^b}$ ,$\beta = {A^c}{B^d}$ , 则独立参数与组合参数的敏感性系数遵循以下关系:${S_A} = a{S_\alpha } + c{S_\beta }$ ,${S_B} = b{S_\alpha } + d{S_\beta }$ . 应用此链式法则, 并考虑信号主要对组合参数${k_z}C$ ,${k_r}/C$ 和$hC$ 敏感, 得出这三个组合参数的敏感性系数与单个参数敏感性系数之间的关系为接下来, 分析包含热扩散系统中所有参数的敏感性系数矩阵
${{\boldsymbol{S}}_2}$ :对
${{\boldsymbol{S}}_2}$ 进行奇异值分解, 得到的奇异值矩阵为$ {\boldsymbol{\varSigma}} = \text{ diag}\left(285, 173, 57, 34, 25, 15, 7.5, 2, 0.3, 0.04, 0.02\right) $ . 其中,${\sigma _{10}}$ 和${\sigma _{11}}$ 足够小, 可认为${{\boldsymbol{S}}_2}{v_{10}}$ 和${{\boldsymbol{S}}_2}{v_{11}}$ 接近零.${v_{10}}$ 和${v_{11}}$ 分别是将
$\left[ {{v_{10}}, {v_{11}}} \right]$ 转换为列阶梯型, 得到${{\boldsymbol{S}}_2}$ 零空间的两个基向量:根据这两个基向量, 得出以下组合参数之间的敏感性系数关系为:
可以进一步写为
方程(5)、方程(7)和方程(8)描述了三层系统的敏感性系数间的关系. 这些关系经过传热模型的验证, 可以推广到具有N层的多层传热系统. 设第n层具有面内热导率
${k_{rn}}$ , 面外热导率${k_{zn}}$ , 比热容${C_n}$ 和厚度${h_n}$ .${G_n}$ 表示第n层和第(n+1)层之间的界面热导,${r_0}$ 是泵浦和探测激光光斑尺寸的均方根(RMS)平均值. 以下通用关系成立:经验证, 以上敏感性关系适用于包括TDTR, FDTR, SPS在内的所有热反射方法.
-
根据附录A, 方程(12)中的灵敏度系数关系表明信号是以下组合参数的函数:
为了以更合理的格式呈现参数, 方程(13)可以改写为
其中参数
$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}$ 来自面外热穿透深度与厚度之比,$\dfrac{{{d_{p, zn}}}}{{{h_n}}} = \dfrac{1}{{\sqrt {\pi {f_0}} }}\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}$ , 它的平方的倒数, 即$\dfrac{{h_n^2{C_n}}}{{{k_{zn}}}}$ , 表示第n层材料所吸收的热量纵向传递穿透该层薄膜所需的时间; 参数$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_{n - 1}}{C_{n - 1}}}}$ 的平方的倒数, 即$\dfrac{{h_{n - 1}^2 C_{n - 1}^2}}{{{k_{zn}}{C_n}}}$ , 表示第(n–1)层材料所吸收的热量扩散穿透第n层材料所需的时间; 参数$\dfrac{{{G_n}}}{{{h_n}{C_n}}}$ 的倒数则表示第n层材料所吸收的热量穿过第n个界面所需的时间[16,17].根据附录A, 方程(15)中的敏感性系数关系表明信号是以下组合参数的函数:
其中参数
$\dfrac{{{k_{rn}}}}{{{C_n}r_0^2}}$ 来自面内热穿透深度与光斑半径之比$\dfrac{{{d_{p, rn}}}}{{{r_0}}} = \dfrac{1}{{\sqrt {\pi {f_0}} }}\sqrt {\dfrac{{{k_{rn}}}}{{{C_n}r_0^2}}} $ , 它的倒数表示第n层材料所吸收的热量在面内方向上扩散到${\text{π}}r_0^2$ 的面积处所需的时间.结合方程(14)和方程(16), N层结构的所有组合参数列在表2中, 它们是由传热模型决定的, 在无噪音情况下最多可提取的参数. 该表适用于任意多层结构的样品以及任意热反射法. 然而, 有两种特殊情况需要注意: 第一, 如果信号对某一层的比热容不敏感, 则应将该层视为界面; 第二, 如果信号对某一层的面外热导率不敏感, 那么应将组合参数
$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}$ 和$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_{n - 1}}{C_{n - 1}}}}$ 进一步合并为$\dfrac{{{h_{n - 1}}{C_{n - 1}}}}{{{h_n}{C_n}}}$ . -
表2总结了对于N层多层结构的热扩散系统中每层结构的主要组合参数, 包括
$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}, \dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_{n - 1}}{C_{n - 1}}}}, {\text{ }}\dfrac{{{k_{rn}}}}{{{C_n}r_0^2}}$ 和$\dfrac{{{G_n}}}{{{h_n}{C_n}}}$ . 这里进一步推导如何根据独立参数的敏感性系数计算这些组合参数的敏感性系数.根据附录A, 得到以下关系:
结合方程(20)和方程(23), 可以得到
${S_{\tfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}}}$ 的递推公式:(25)式和(26)式分别为
$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}$ 和$\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_{n - 1}}{C_{n - 1}}}}$ 的敏感性计算公式, (21)式和(22)式分别为$\dfrac{{{G_n}}}{{{h_n}{C_n}}}$ 和$\dfrac{{{k_{rn}}}}{{{C_n}r_0^2}}$ 的敏感性计算公式. -
将上述结论应用于图2中的100 nm 铝/蓝宝石测量. 根据表2, 该热系统包含5个组合参数: ①
$\dfrac{{\sqrt {{k_{z1}}{C_1}} }}{{{h_1}{C_1}}}$ , ②$\dfrac{{{k_{r1}}}}{{{C_1}r_0^2}}$ , ③$ \dfrac{G}{{h}_{1}{C}_{1}} $ , ④$\dfrac{{\sqrt {{k_{z2}}{C_2}} }}{{{h_1}{C_1}}}$ , ⑤$\dfrac{{{k_{r2}}}}{{{C_2}r_0^2}}$ . 图2(c1)和图2(c2)显示了这些组合参数的敏感性曲线, 每个参数在不同频率下出现峰值或零点, 表明它们彼此解耦, 理论上最多可同时确定5个参数. 但实验信号通常伴有噪声, 因此最大可提取的参数数量还取决于实验系统的噪声水平, 我们只能拟合出对信号敏感性较强的参数. “高”和“低”敏感性的阈值是相对于噪声波动来定义的. 如果某个参数变化5%会引起超出环境噪声的信号变化, 则认为它具有高敏感性; 如果一个参数变化20%才会产生可检测的信号变化, 则认为它具有低敏感性[8]. 通过分析图2(c1)和图2(c2), 发现信号对以下组合参数较为敏感: ①$\dfrac{{\sqrt {{k_{z1}}{C_1}} }}{{{h_1}{C_1}}}$ , ③$ \dfrac{G}{{h}_{1}{C}_{1}} $ , ④$\dfrac{{\sqrt {{k_{z2}}{C_2}} }}{{{h_1}{C_1}}}$ , ⑤$\dfrac{{{k_{r2}}}}{{{C_2}r_0^2}}$ . 而对参数②$\dfrac{{{k_{r1}}}}{{{C_1}r_0^2}}$ 的敏感性较低. 因此, 在已知${h_1}$ ,${C_1}$ 和${r_0}$ 的情况下, 可以准确确定${k_{z1}}$ ,$G$ ,${k_{z2}}{C_2}$ 和${k_{r2}}/{C_2}$ 这4个参数. 当衬底材料是各向同性时,${k_2} = {k_{z2}} = {k_{r2}}$ , 可据此确定${k_2}$ 和${C_2}$ .在输入参数中,
${h_1}$ 由台阶仪测量,${C_1}$ 可查文献数据库[18],${r_0}$ 由刀口法测定. 由于信号对${k_{r1}}$ 敏感性较低, 且金属膜为各向同性, 可简化为${k_1} = {k_{r1}} = {k_{z1}}$ .使用自动拟合(MATLAB函数“lsqnonlin”)对
${k_1}$ ,$G$ ,${k_2}$ 和${C_2}$ 进行拟合, 结果为${k_1} = (105 \pm 9){\text{ W}}/\left( {{\text{m}}{\cdot}{\mathrm{K}}} \right)$ ,$G = (145 \pm 9){\text{ MW}}/( {{{\text{m}}^2}{{\cdot{\mathrm{K}}}}} )$ ,${k_2} = (37 \pm 2){\text{ W}}/\left( {{\text{m}}{\cdot}{\mathrm{K}}} \right)$ ,${C_2} = (3.08 \pm 0.16){\text{ MJ}}/\left( {{{\text{m}}^3}{{\cdot{\mathrm{K}}}}} \right)$ . 这里的不确定度估计是基于最小二乘法的最优拟合来计算的, 既包括了已知参数传递的误差, 也包括了实验噪声引入的误差, 具体的计算细节可以参考相关文献[19,20]. 测量结果中, 铝膜热导率${k_1}$ 与范德堡法和魏德曼-弗朗兹定律计算结果符合; 铝/氧化铝的界面热导${G_1}$ 受到镀膜过程影响, 不宜直接与文献值比较, 因此我们另外采用了TDTR方法测量该样品, 测得$G = (160 \pm 10){\text{ MW}}/\left( {{{\text{m}}^2}{{\cdot{\mathrm{K}}}}} \right)$ , 与FDTR测量结果吻合; 蓝宝石的热导率${k_2}$ 与比热容${C_2}$ 也与Chen等[14]报道的数据高度吻合. 结果验证了该方法的有效性. -
本研究通过奇异值分解方法系统地分析了热反射实验中复杂的参数相互作用, 为多层结构热特性表征提供了新的见解. 对FDTR信号的深入分析, 揭示了面内热导率、纵向热导率、比热容、界面热导及光斑尺寸等关键参数间的相互关系. 厘清了各基本参数的依赖性, 确定了关键组合参数, 为多层系统的热特性表征提供了有效工具. 实测结果验证了组合参数的应用, 确定了可同时提取的最大参数数量, 并明确了实验中需要预先已知的输入参数. 这些成果为未来的热物性测量提供了有力指导, 并有助于进一步提升多层系统的热特性表征技术.
-
设
$R = F\left( {A, B, C} \right)$ , 则${S_A} = b{S_B} + c{S_C}$ 是$R = F( {A^b}B, {A^c}C )$ 的充分必要条件.首先证明必要性. 假设
$R = F\left( {{A^b}B, {A^c}C} \right)$ , 则参数A, B和C的敏感性系数分别为将方程(A2)和方程(A3)代入
$ {S_A} = b{S_B} + c{S_C}$ , 得到然后证明充分性. 假设
${S_A} = b{S_B} + c{S_C}$ , 并假设$R$ 不能仅由两个参数表示, 考虑第三个参数$D$ , 不妨设$D = A$ . 则$R = F\left( {{A^b}B, {A^c}C, D} \right)$ , 此时A, B和C的敏感性系数为将方程 (A5)—方程(A7) 代入
${S_A} = b{S_B} + c{S_C}$ , 得到由于
$A$ ,$B$ 和$C$ 是任意的, 这表明$R$ 不依赖于第三个参数$D$ , 与假设矛盾. 因此, R仅是${A^b}B$ 和${A^c}C$ 的函数, 即$R = F\left( {{A^b}B, {A^c}C} \right)$ . -
假设信号
$R$ 由$R = F\left( {\alpha , \beta } \right)$ 给出, 其中$\alpha $ 和$\beta $ 是决定$R$ 的两个组合参数. 设$\alpha = {A^a}{B^b}$ 和$\beta = {A^c}{B^d}$ , 其中$A$ 和$B$ 是单个参数. 根据链式法则有:根据敏感性定义, 有
方程(B2)表示了敏感性系数的链式法则. 要计算单个参数的敏感性, 只需将该参数在每个组合参数中的幂指数作为组合参数的敏感性系数的系数相加.
揭示热反射实验中热物性参数的本征关系
Unraveling intrinsic relationship of thermal properties in thermoreflectance experiments
-
摘要:
热反射技术是测量块体和薄膜材料热物性的重要工具, 但参数间复杂的相互关系为数据解析带来挑战. 本文以频域热反射法(FDTR)为例, 利用奇异值分解(SVD)对热反射信号进行了深入分析, 系统地揭示了不同变量之间的关联, 并提出了热反射实验中的关键组合参数. 这种方法不仅厘清了变量间的关系, 还明确了实验中可提取的最大参数数量. 作为应用实例, 本文对铝/蓝宝石样品进行了测量和信号分析, 发现相较于常规仅拟合衬底热导率和界面热导两个参数的做法, 最佳拟合FDTR信号能够同时确定金属膜热导率、衬底热导率、衬底比热容和界面热导四个参数. 拟合结果与文献参考值和其他方法测量结果进行了对比, 验证了该方法的有效性. 本研究深化了对热反射现象的理解, 为热表征技术和材料研究的进一步发展提供了有力支持.
Abstract:Thermoreflectance techniques, particularly frequency-domain thermoreflectance (FDTR), play a crucial role in measuring the thermal properties of bulk and thin-film materials. These methods precisely measure thermal conductivity, specific heat capacity, and interfacial thermal conductance by analyzing the surface temperature response signals through thermoreflectance. However, the complex interplay among parameters presents challenges in data analysis, where single-variable analysis often fails to accurately capture intra-layer and inter-layer interactions. In this work, FDTR is used as a case study and the relationships between sensitivity coefficients of various parameters are systematically explored through singular value decomposition (SVD). Specifically, the SVD of sensitivity matrix S of the system's parameters is performed to identify smaller singular values and their corresponding right singular vectors, which are the basis vectors of the null space of matrix S. These vectors reveal the relationships among parameter sensitivities, thereby uncovering the most fundamental combination parameters that determine the thermoreflectance signal. This method not only clarifies the dependency relationships between variables but also determines the maximum number of parameters that can be experimentally extracted, and the parameters that must be known beforehand. To demonstrate the practical value of these combination parameters, this work conducts a detailed analysis of FDTR signals from an aluminum/sapphire sample. Unlike traditional FDTR experiments, which typically fit only the thermal conductivity and interfacial thermal conductance of the substrate, our sensitivity analysis reveals that it is possible to simultaneously determine the thermal conductivity of the metal film, substrate’s thermal conductivity, substrate’s specific heat capacity, and interfacial thermal conductance. The fitting results are consistent with reference values from the literature and measurements from other thermoreflectance techniques, thus validating the effectiveness and reliability of our method. This comprehensive analysis not only deepens the understanding of thermoreflectance phenomena but also provides strong support for the future development of thermal characterization technology and material research, showing the significant potential application of SVD in complex multi-parameter systems.
-

-
图 2 铝/蓝宝石样品的频域热反射分析 (a1), (a2) 1 kHz—70 MHz频率范围内的相位信号和归一化幅值信号; (b1), (b2) 单个参数敏感性随频率的变化; (c1), (c2)组合参数敏感性随频率的变化
Figure 2. FDTR analysis of aluminum/sapphire samples: (a1), (a2) Phase and normalized amplitude signals across frequencies from 1 kHz to 70 MHz; (b1), (b2) how the sensitivity of individual parameters varies with frequency; (c1), (c2) changes in the sensitivity of combined parameters across the frequency spectrum.
图 3 (a)
${k_{z1}}$ ,${k_{r1}}$ ,${C_1}$ ,${h_1}$ 的敏感性曲线, 横坐标为频率; (b) 各个${{\boldsymbol{v}}_j}$ 与敏感性矩阵${{\boldsymbol{S}}_1}$ 相乘得到的结果Figure 3. (a) Sensitivity curves for
${k_{z1}}$ ,${k_{r1}}$ ,${C_1}$ , and${h_1}$ , with frequency as the horizontal axis; (b) the results of multiplying each${{\boldsymbol{v}}_j}$ by the sensitivity matrix${{\boldsymbol{S}}_1}$ .表 1 三明治结构模拟样品的系统参数
Table 1. System parameters of a sandwich structure simulated sample.
${k_z}$ /${\text{(W}} {\cdot }{{\text{m}}^{{{ - 1}}}} \cdot {{\text{K}}^{{{ - 1}}}})$ ${k_r}$ /${\text{(W}}{ \cdot }{{\text{m}}^{{{ - 1}}}} \cdot {{\text{K}}^{{{ - 1}}}})$ $C$ /${\text{(MJ}} {\cdot} {{\text{m}}^{ - 3}}{{\cdot}}{{\text{K}}^{{{ - 1}}}}{)}$ $h$ /${\text{nm}}$ ${r_0}$ /$ {\text{μm}}$ G1/ ${\text{(MW}}{ \cdot} {{\text{m}}^{ - 2}}{{\cdot}}{{\text{K}}^{ - 1}})$ G2/ ${\text{(MW}} {\cdot }{{\text{m}}^{ - 2}}{{\cdot}}{{\text{K}}^{ - 1}})$ 1(Al) $150$ $150$ $2.44$ $100$ $8$ 10 10 2 $10$ $100$ $2$ $2000$ 3(Sub) $100$ $10$ $1.5$ $\infty $ 表 2 面内各向同性多层结构中的组合参数
Table 2. Combined parameters in isotropic multilayer structures in-plane.
层序号 组合参数 1 $\dfrac{{\sqrt {{k_{z1}}{C_1}} }}{{{h_1}{C_1}}}, \;\dfrac{{{k_{r1}}}}{{{C_1}r_0^2}}$ 1/2 $\dfrac{{{G_1}}}{{{h_1}{C_1}}}$ $\vdots $ $\vdots $ n $\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_n}{C_n}}}, \;\dfrac{{\sqrt {{k_{zn}}{C_n}} }}{{{h_{n - 1}}{C_{n - 1}}}}, \;\dfrac{{{k_{rn}}}}{{{C_n}r_0^2}}$ n/(n + 1) $\dfrac{{{G_n}}}{{{h_n}{C_n}}}$ $\vdots $ $\vdots $ N $\dfrac{{\sqrt {{k_{zN}}{C_N}} }}{{{h_{N - 1}}{C_{N - 1}}}},\; \dfrac{{{k_{rN}}}}{{{C_N}r_0^2}}$ -
[1] Goodson K E, Ju Y S 1999 Annu. Rev. Mater. Sci. 29 261 doi: doi.org/10.1146/annurev.matsci.29.1.261 [2] El Sachat A, Alzina F, Sotomayor Torres C M, Chavez Angel E 2021 Nanomaterials 11 175 doi: 10.3390/nano11010175 [3] Tan J, Zhang Y 2024 Molecules 29 3572 doi: 10.3390/molecules29153572 [4] Jiang P, Qian X, Yang R 2017 Rev. Sci. Instrum. 88 074901 doi: 10.1063/1.4991715 [5] Jiang P, Qian X, Yang R 2018 Rev. Sci. Instrum. 89 094902 doi: doi.org/10.1063/1.5029971 [6] Cahill D G 2004 Rev. Sci. Instrum. 75 5119 doi: 10.1063/1.1819431 [7] Schmidt A J, Cheaito R, Chiesa M 2009 Rev. Sci. Instrum. 80 094901 doi: 10.1063/1.3212673 [8] Rodin D, Yee S K 2017 Rev. Sci. Instrum. 88 014902 doi: 10.1063/1.4973297 [9] Tang L, Dames C 2021 Int. J. Heat Mass Transfer 164 120600 doi: doi.org/10.1016/j.ijheatmasstransfer.2020.120600 [10] Zhang C, Wang J, Mou J, Li X, Wang R 2019 IEEE 2nd International Conference on Information Systems and Computer Aided Education (ICISCAE) Dalian, PR China September 28-30, 2019 p10-13 [11] 王芙蓉, 杨帆, 张亚, 李世中, 王鹤峰 2021 物理学报 70 150201 doi: doi.org/10.7498/aps.70.20210411 Wang F R, Yang F, Zhang Y, Li S Z, Wang H F 2021 Acta Phys. Sin. 70 150201 doi: doi.org/10.7498/aps.70.20210411 [12] Han T, Jiang D, Zhang X, Sun Y 2017 Sensors 17 689 doi: 10.3390/s17040689 [13] Yin X, Xu Y, Sheng X, Shen Y 2019 Sensors 19 5032 doi: 10.3390/s19225032 [14] Chen T, Song S, Shen Y, Zhang K, Jiang P 2024 Int. Commun. Heat Mass Transfer 158 107849 doi: 10.1016/j.icheatmasstransfer.2024.107849 [15] Golub G H, van Loan C F 2013 Matrix computations (Bapat R B: Johns Hopkins Uinversity press [16] Wilson O M, Hu X, Cahill D G, Braun P V 2002 Phys. Rev. B 66 224301 doi: 10.1103/PhysRevB.66.224301 [17] Wilson R B, Feser J P, Hohensee G T, Cahill D G 2013 Phys. Rev. B 88 144305 doi: 10.1103/PhysRevB.88.144305 [18] Touloukian Y, Buyco E 1971 Thermophysical properties of matter-the TPRC data series. Volume 4. Specific heat-metallic elements and alloys (Reannouncement) Data book Report [19] Chen T, Song S, Hu R, Jiang P 2025 Int. J. Therm. Sci. 207 109347 doi: 10.1016/j.ijthermalsci.2024.109347 [20] Yang J, Ziade E, Schmidt A J 2016 Rev. Sci. Instrum. 87 014901 doi: doi.org/10.1063/1.4939671 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: