高级搜索

基于改进MRT-LBM的近壁空泡溃灭模拟及诱发壁面损伤的作用力机制

,  ,  , 

downloadPDF

上一篇

下一篇

柴廉洁, 周国龙, 武伟, 张家忠. 基于改进MRT-LBM的近壁空泡溃灭模拟及诱发壁面损伤的作用力机制[J]. 物理学报, 2025, 74(10): 104702-1. doi: 10.7498/aps.74.20241114
引用本文: 柴廉洁, 周国龙, 武伟, 张家忠. 基于改进MRT-LBM的近壁空泡溃灭模拟及诱发壁面损伤的作用力机制[J]. 物理学报, 2025, 74(10): 104702-1. doi: 10.7498/aps.74.20241114
shu
Lianjie CHAI, Guolong ZHOU, Wei WU, Jiazhong ZHANG. Simulation of near-wall bubble collapse and research on load mechanism of wall damage based on improved multi-relaxation-time lattice Boltzmann method[J]. Acta Physica Sinica, 2025, 74(10): 104702-1. doi: 10.7498/aps.74.20241114
Citation: Lianjie CHAI, Guolong ZHOU, Wei WU, Jiazhong ZHANG. Simulation of near-wall bubble collapse and research on load mechanism of wall damage based on improved multi-relaxation-time lattice Boltzmann method[J]. Acta Physica Sinica, 2025, 74(10): 104702-1. doi: 10.7498/aps.74.20241114
shu

基于改进MRT-LBM的近壁空泡溃灭模拟及诱发壁面损伤的作用力机制

  • 西安交通大学能源与动力工程学院, 西安　710049

    • 作者简介: 柴廉洁. E-mail: 445264852@qq.com .
    通讯作者: E-mail: jzzhang@mail.xjtu.edu.cn.

  • 中图分类号: 47.55.dp, 47.61.Jd, 64.70.fh, 47.55.D-

Simulation of near-wall bubble collapse and research on load mechanism of wall damage based on improved multi-relaxation-time lattice Boltzmann method

  • School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China

    • Corresponding author: E-mail: jzzhang@mail.xjtu.edu.cn.

  • MSC: 47.55.dp, 47.61.Jd, 64.70.fh, 47.55.D-

  • 摘要: 使用改进的‌多松弛时间格子玻尔兹曼方法(MRT-LBM)‌对近壁空泡溃灭演化过程开展了数值模拟, 并对空泡溃灭诱发壁面损伤的作用力机制进行研究. 首先, 对改进外力格式的多松弛伪势模型开展Laplace定律验证和热力学一致性验证; 然后, 结合改进外力格式的多松弛伪势模型对近壁空泡溃灭演化进行数值模拟, 获得了近壁空泡溃灭过程的流场细节, 着重研究了溃灭过程中空泡的动力学行为. 研究发现, 近壁空泡溃灭过程中释放的微射流主要来源于第1次溃灭, 而冲击波的产生来源于第1次溃灭和第2次溃灭, 且第2次溃灭产生的冲击波强度显著高于第1次溃灭产生的冲击波; 进一步, 对近壁空泡溃灭过程中壁面处压力与速度的分布特性进行分析, 研究空泡溃灭作用于壁面的载荷机制. 研究发现, 壁面受到冲击波和微射流的共同作用, 冲击波作用范围大, 造成面损伤, 而微射流作用在局部区域, 造成点状破坏. 研究结果揭示近壁空泡溃灭演化过程以及空泡溃灭诱发壁面损伤的作用力机制, 为进一步利用空化效应及减少空蚀带来的破坏提供理论支撑.
    Abstract: To reveal the load mechanism of wall damage induced by bubble collapse, the near-wall cavitation bubble collapse evolution is numerically simulated using an improved multi-relaxation-time lattice Boltzmann method (MRT-LBM), and the dynamic behavior of near-wall cavitation bubble is systematically analyzed. First, the improved multi-relaxation pseudopotential model with a modified force scheme is introduced and validated through the Laplace law and thermodynamic consistency. Subsequently, the near-wall bubble collapse evolution is simulated using the improved model, and the process of the bubble collapse evolution is obtained. The accuracy of the numerical simulation results is confirmed by comparing with previous experimental results. Based on the obtained flow field information, including velocity and pressure distributions, the dynamic behaviors during the bubble collapse are thoroughly analyzed. The results show that the micro-jets released during the near-wall bubble collapse primarily originate from the first collapse, while the shock waves are generated during both the first and the second collapse. Notably, the intensity of the shock waves produced during the second collapse is significantly higher than that during the first collapse. Furthermore, the distribution characteristics of pressure and velocity on the wall during the near-wall bubble collapse are analyzed, revealing the load mechanism of wall damage caused by bubble collapse. The results show that the wall is subjected to the combined effects of shock waves and micro-jets: shock waves cause large-area surface damage due to their extensive propagation range, whereas micro-jets lead to concentrated point damage with their localized high-velocity impact. In summary, this study elucidates the evolution of near-wall bubble collapse and the load mechanism of wall damage induced by bubble collapse, which provides theoretical support for further utilizing the cavitation effects and mitigation of cavitation-induced damage.
  • 加载中

  • 图 1  Laplace定律验证

    Figure 1.  Verification of Laplace’s law

    下载: 全尺寸图片 幻灯片

    图 2  共存密度数值解与解析解

    Figure 2.  Numerical and analytical solutions for coexistence density.

    下载: 全尺寸图片 幻灯片

    图 3  模拟结果与R-P方程对比

    Figure 3.  Simulation results and R-P equation results.

    下载: 全尺寸图片 幻灯片

    图 4  近壁空泡溃灭模型

    Figure 4.  Near-wall bubble collapse model.

    下载: 全尺寸图片 幻灯片

    图 5  近壁空泡溃灭外形的演化数值模拟结果与实验结果对比　(a)数值模拟结果, $\lambda = 1.6, {\text{ }}{r_0} = 80$; (b)实验结果, $\lambda = 1.6,{r_0} = $$ 1.45 \times {10^{ - 3}}$ m

    Figure 5.  Comparison of numerical simulation results and experimental results on the evolution of near-wall bubble collapse shape: (a) Numerical simulation results, $\lambda = 1.6, {\text{ }}{r_0} = 80$; (b) experimental results, $\lambda = 1.6, {\text{ }}{r_0} = 1.45 \times {10^{ - 3}}$ m.

    下载: 全尺寸图片 幻灯片

    图 6  近壁空泡溃灭密度场演化过程　(a) t = 1 ts; (b) t = 300 ts; (c) t = 500 ts; (d) t = 600 ts; (e) t = 700 ts; (f) t = 850 ts; (g) t = 931 ts; (h) t = 950 ts; (i) t = 1050 ts; (j) t = 1150 ts; (k) t = 1175 ts; (l) t = 1180 ts

    Figure 6.  Density evolution of near-wall bubble: (a) t = 1 ts; (b) t = 300 ts; (c) t = 500 ts; (d) t = 600 ts; (e) t = 700 ts; (f) t = 850 ts; (g) t = 931 ts; (h) t = 950 ts; (i) t = 1050 ts; (j) t = 1150 ts; (k) t = 1175 ts; (l) t = 1180 ts.

    下载: 全尺寸图片 幻灯片

    图 7  近壁空泡溃灭压力场演化过程　(a) t = 600 ts; (b) t = 700 ts; (c) t = 850 ts; (d) t = 931 ts; (e) t = 950 ts; (f) t = 1050 ts; (g) t = 1150 ts; (h) t = 1175 ts; (i) t = 1180 ts

    Figure 7.  Pressure evolution of near-wall bubble: (a) t = 600 ts; (b) t = 700 ts; (c) t = 850 ts; (d) t = 931 ts; (e) t = 950 ts; (f) t = 1050 ts; (g) t = 1150 ts; (h) t = 1175 ts; (i) t = 1180 ts.

    下载: 全尺寸图片 幻灯片

    图 8  近壁空泡溃灭速度场演化过程　(a) t = 600 ts; (b) t = 850 ts; (c) t = 950 ts; (d) t = 1050 ts; (e) t = 1150 ts; (f) t = 1180 ts

    Figure 8.  Velocity evolution of near-wall bubble: (a) t = 600 ts; (b) t = 850 ts; (c) t = 950 ts; (d) t = 1050 ts; (e) t = 1150 ts; (f) t = 1180 ts.

    下载: 全尺寸图片 幻灯片

    图 9  各时间步壁面处压力分布

    Figure 9.  Pressure distribution on the wall at each time step.

    下载: 全尺寸图片 幻灯片

    图 10  各时间步壁面处速度分布

    Figure 10.  Velocity distribution on the wall at each time step.

    下载: 全尺寸图片 幻灯片
  • [1] 任嘉乐 2023 硕士学位论文(兰州: 兰州理工大学) Ren J L 2023 M. S. Thesis (Lanzhou: Lanzhou University of Technology
    [2] 米建东 2022 硕士学位论文(兰州: 兰州理工大学) Mi J D 2022 M. S. Thesis (Lanzhou: Lanzhou University of Technology
    [3] Kling C L, Hammitt F G 1972 J. Basic Eng. 94 825 doi: 10.1115/1.3425571
    [4] Plesset M S, Chapman R B 1971 J. Fluid Mech. 47 283 doi: 10.1017/S0022112071001058
    [5] Li B B, Jia W, Zhang H C, Lu J 2014 Shock Waves 24 317 doi: 10.1007/s00193-013-0482-3
    [6] Aganin A A, Ilgamov M A, Kosolapova L A, Malakhov V G 2016 Thermophys. Aeromech. 23 211 doi: 10.1134/S0869864316020074
    [7] 任晟, 张家忠, 张亚苗, 卫丁 2014 物理学报 63 024702 doi: 10.7498/aps.63.024702 Ren S, Zhang J Z, Zhang Y M, Wei D 2014 Acta Phys. Sin. 63 024702 doi: 10.7498/aps.63.024702
    [8] 李旭晖, 单肖文, 段文洋 2022 空气动力学学报 40 46 doi: 10.7638/kqdlxxb-2020.0426 Li X H, Shan X W, Duan W Y 2022 Acta Aerodyn. Sin. 40 46 doi: 10.7638/kqdlxxb-2020.0426
    [9] Li X H, Shi Y Y, Shan X W 2019 Phys. Rev. E 100 013301 doi: 10.1103/PhysRevE.100.013301
    [10] Shan X W, Chen H D 1993 Phys. Rev. E 47 1815 doi: 10.1103/PhysRevE.47.1815
    [11] Shan X W, Chen H D 1994 Phys. Rev. E 49 2941 doi: 10.1103/PhysRevE.49.2941
    [12] Sukop M C, Or D 2005 Phys. Rev. E 71 046703 doi: 10.1103/PhysRevE.71.046703
    [13] Shan M L, Zhu C P, Zhou X, Yin C, Han Q B 2016 J. Hydrodyn. 28 442 doi: 10.1016/S1001-6058(16)60647-9
    [14] Shan M L, Zhu Y, Yao C, Han Q B, Zhu C P 2017 J. Appl. Math. Phys. 5 1243 doi: 10.4236/jamp.2017.56106
    [15] He X L, Zhang J M, Yang Q, Peng H N, Xu W L 2020 Phys. Rev. E 102 063306 doi: 10.1103/PhysRevE.102.063306
    [16] Li Q, Luo K H, Li X J 2013 Phys. Rev. E 87 053301 doi: 10.1103/PhysRevE.87.053301
    [17] Li Q, Luo K H, Li X J 2012 Phys. Rev. E 86 016709 doi: 10.1103/PhysRevE.86.016709
    [18] Peng H N, Zhang J M, He X L, Wang Y R 2021 Comput. Fluids 217 104817 doi: 10.1016/j.compfluid.2020.104817
    [19] Liu Y, Peng Y 2021 J. Mar. Sci. Eng. 9 219 doi: 10.3390/jmse9020219
    [20] Yang Y, Shan M L, Kan X F, Shangguan Y Q, Han Q B 2020 Ultrason. Sonochem. 62 104873 doi: 10.1016/j.ultsonch.2019.104873
    [21] Yang Y, Shan M L, Su N N, Kan X F, Shangguan Y Q, Han Q B 2022 Int. Commun. Heat Mass 134 105988 doi: 10.1016/j.icheatmasstransfer.2022.105988
    [22] 何雅玲, 李庆, 王勇, 童自翔 2023 格子Boltzmann方法的理论及应用 (北京: 高等教育出版社) 第52页 He Y L, Li Q, Wang Y, Tong Z X 2023 Lattice Boltzmann Method: Theory and Applications (Beijing: Higher Education Press) p52
    [23] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第46页 Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) p46
    [24] 任晟 2014 博士学位论文(西安: 西安交通大学) Ren S 2014 Ph. D. Dissertation (Xi’an: Xi’an Jiaotong University
    [25] Li Q, Luo K H, Kang Q J, Chen Q 2014 Phys. Rev. E 90 053301 doi: 10.1103/PhysRevE.90.053301
    [26] Huang H, Sukop M C, Lu X 2015 Multiphase lattice Boltzmann methods: Theory and Application (New Jersey: Wiley Blackwell) p20
    [27] Yuan P, Schaefer L 2006 Phys. Fluids 18 042101 doi: 10.1063/1.2187070
    [28] 张新明, 周超英, Islam Shams, 刘家琦 2009 物理学报 58 8406 doi: 10.7498/aps.58.8406 Zhang X M, Zhou C Y, Islam S, Liu J Q 2009 Acta Phys. Sin. 58 8406 doi: 10.7498/aps.58.8406
    [29] Sofonea V, Biciuşcă T, Busuioc S, Ambruş V E, Gonnella G, Lamura A 2018 Phys. Rev. E 97 023309 doi: 10.1103/PhysRevE.97.023309
    [30] Philipp A, Lauterborn W 1998 J. Fluid Mech. 361 75 doi: 10.1017/S0022112098008738
  • 加载中
图( 10)
计量
  • 文章访问数:  21
  • HTML全文浏览数:  21
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-09
  • 刊出日期:  2025-05-20

基于改进MRT-LBM的近壁空泡溃灭模拟及诱发壁面损伤的作用力机制

    通讯作者: E-mail: jzzhang@mail.xjtu.edu.cn.
    作者简介: 柴廉洁. E-mail: 445264852@qq.com
  • 西安交通大学能源与动力工程学院, 西安　710049
  • 收稿日期:  2024-08-09

摘要: 使用改进的‌多松弛时间格子玻尔兹曼方法(MRT-LBM)‌对近壁空泡溃灭演化过程开展了数值模拟, 并对空泡溃灭诱发壁面损伤的作用力机制进行研究. 首先, 对改进外力格式的多松弛伪势模型开展Laplace定律验证和热力学一致性验证; 然后, 结合改进外力格式的多松弛伪势模型对近壁空泡溃灭演化进行数值模拟, 获得了近壁空泡溃灭过程的流场细节, 着重研究了溃灭过程中空泡的动力学行为. 研究发现, 近壁空泡溃灭过程中释放的微射流主要来源于第1次溃灭, 而冲击波的产生来源于第1次溃灭和第2次溃灭, 且第2次溃灭产生的冲击波强度显著高于第1次溃灭产生的冲击波; 进一步, 对近壁空泡溃灭过程中壁面处压力与速度的分布特性进行分析, 研究空泡溃灭作用于壁面的载荷机制. 研究发现, 壁面受到冲击波和微射流的共同作用, 冲击波作用范围大, 造成面损伤, 而微射流作用在局部区域, 造成点状破坏. 研究结果揭示近壁空泡溃灭演化过程以及空泡溃灭诱发壁面损伤的作用力机制, 为进一步利用空化效应及减少空蚀带来的破坏提供理论支撑.

English Abstract

    全文HTML

    1.   引　言

    • 空化是指液体介质中局部压力下降时, 空泡形成、发展和溃灭的过程, 空泡在低压区形成, 随周围流体进入高压区, 在压差的作用下收缩直至溃灭, 这一过程中往往伴随着一系列空化效应, 包括闪光、放热, 释放高强度的冲击波和微射流, 使得在极短时间内局部压力和温度升高[1,2]. 而空化泡在壁面附近溃灭的过程由于受到固体边界的影响存在着更加复杂的动力学行为, 如: 空泡与壁面的距离影响着溃灭过程中空泡的坍缩次数. Kling和Hammitt[3]计算出靠近壁面的空泡溃灭时释放的射流速度最高达180 m/s, 而在壁面产生的冲击压力最高至170 MPa. 针对空泡溃灭如何释放如此多的能量这一问题, 学术界主要有微射流理论和冲击波理论两种观点, 目前空泡溃灭释放能量的过程具体是微射流占主导作用, 还是冲击波占主导作用, 学术界尚无定论.

      在对空化模拟的研究中, Plesset和Chapman[4]使用宏观层面的有限差分法(FDM)模拟了球形气泡在平壁附近坍缩溃灭继而产生微射流的过程; Li等[5]采用有限体积法(FVM)和流体体积法(VOF)研究了锥形刚性边界附近空泡的溃灭过程; Aganin等[6]应用边界元法(BEM)对空化过程展开模拟研究. 这些研究均为基于求解偏微分方程的宏观数值模拟方法, 其对于分析多相态多组分问题较为复杂, 而格子Boltzmann方法是一种用统计概率粒子分布函数的碰撞和迁移来描述流体系统的介观数值方法, 其具有物理过程清晰、并行性好、边界条件易处理等诸多优点[7], 在研究空化这类复杂问题上具有显著优势[8,9]. 通过引入粒子间相互作用力, LBM体系中的伪势模型[10,11](Shan-Chen模型)能够实现自动追踪相界面运动, 被广泛应用于多相流动的研究. 2005年, Sukop等[12]用单组分多相伪势模型模拟了无限大流场中的均匀和非均匀空化现象, 但未能完整模拟出空泡溃灭的过程; Shan等[13,14]进行了一系列基于LBM模拟单空泡空化过程的研究, 验证了使用LBM描述空化的可行性, 并逐步提高了空化LBM模型的密度比; He等[15]提出了一种大密度比和可调黏度比的多组分多相伪势模型, 并模拟了气泡的溶解过程. 对于空泡溃灭的数值模拟而言, 模拟过程中界面变形程度大, 能否保持溃灭过程中的数值稳定性是关键难点. Li等[16,17]对伪势模型的外力格式进行了改进, 提出了一种热力学一致性可调的外力格式来提升两相流动模拟过程中的数值稳定性. Peng等[18]使用改进的伪势模型对双空泡溃灭及空泡之间的相互作用进行了研究; Liu等[19]和Yang等[20,21]使用耦合温度分布函数的伪势模型对空泡溃灭流动及传热过程进行了分析.

      在已有的利用LBM模拟近壁空泡溃灭过程研究中, 大部分主要关注空泡本身的行为特征, 而对诱发壁面损伤的作用力机制研究较少. 因此, 本文针对近壁空泡溃灭问题, 采用改进外力格式并补充C-S状态方程的多松弛时间格子玻尔兹曼方法(MRT-LBM)模型进行建模, 通过多种验证方法证明该模型的可靠性与准确性, 并对近壁空泡溃灭过程进行数值模拟; 然后, 进一步分析溃灭过程中空泡的动力学行为和诱发壁面损伤的作用力机制, 为进一步利用空化效应及减少空蚀带来的破坏提供了理论支撑.

    2.   MRT-LBM模型的改进

    • 格子Boltzmann方法是通过描述具有离散速度流体粒子分布函数的变化过程来反映流体粒子的运动过程, 最早出现的MRT-LBM分布函数演化方程为[22,23]

      式中, $ {{\boldsymbol{ \varLambda}} _{ij}} $为碰撞矩阵. 该方程描述的分布函数在分布函数空间$ \boldsymbol{V} = {R^b} $演化, 分布函数空间也可称为速度空间. 同时, 定义数量为分布函数空间维度$ b $的矩:

      式中, ${\phi _k}$为基向量, 是粒子速度${c_i}$的函数, 满足线性无关条件. 根据基向量${\phi _k}$, 可得分布函数空间V和矩空间M的关系式:

      矩空间M与基向量${\phi _k}$的关系为: M的第k个行向量为${\phi _k}$的转置矩阵, 因此M为正交变换矩阵, 矩空间M与基向量${\phi _k}$的选择是决定MRT-LBM模型计算稳定性和准确性的关键.

      在伪势MRT-LBM模型中将外力项独立出来后, 分布函数的演化方程可以表示为

      式中, ${\boldsymbol{S}} $为分布函数空间的外力项, 表示为$ \boldsymbol{S} = {\left( {{S_0}, {S_1}, \cdots , {S_8}} \right)^{\text{T}}} $; $ {\bar {\boldsymbol{ \varLambda}} _{ij}} $满足$ {\bar {\boldsymbol{ \varLambda}} _{ij}} = \boldsymbol{M}_{}^{ - 1}{{\boldsymbol{ \varLambda}} _{ij}}\boldsymbol{M} $.

      对于本文使用的D2Q9模型, 平衡态分布函数表达式为

      式中, $ \rho $为宏观密度; $ \boldsymbol{u} $为宏观速度; $ {c_{\text{s}}} $为格子声速, 满足$ {c_{\text{s}}} = c/\sqrt 3 $; 粒子迁移速度$ c = \Delta x/\Delta t $, $ \Delta x $和$ \Delta t $分别为网格步长和时间步长, 取$ \Delta x = \Delta t = 1 $, 因此$ c = 1 $. 离散速度$ \boldsymbol{e} $和权系数$ {\omega _i} $为[24]

      碰撞矩阵$ {\boldsymbol{ \varLambda}} $为对角矩阵, 在D2Q9模型中, $ {\boldsymbol{ \varLambda}} $表示为

      本研究中, $ {\boldsymbol{ \varLambda}} $取值为

      矩空间$ \boldsymbol{M} $表示为

      平衡分布函数${f^\mathrm{eq}}$对应转换矩阵${{\boldsymbol{m}}^\mathrm{eq}}$的关系也符合与(3)式相同的关系, 如(10)式所描述, ${{\boldsymbol{m}}^\mathrm{eq}}$可由(11)式定义:

      在引入正交变换矩阵后, (4)式右侧的碰撞过程可改写为

      式中, I为单位向量; $ \bar{\boldsymbol{S}} $代表矩空间中的外力项, $ \bar{\boldsymbol{S}} = \boldsymbol{MS} $.

      (4)式迁移过程可表示为

      式中, $ {f^*} = {\boldsymbol{M}^{ - 1}}{m^*} $.

      (11)式中的宏观密度和宏观速度的计算式为

      式中, $ \boldsymbol{F} $为系统所受合外力, $ \boldsymbol{F} = \left( {{F_x}, {F_y}} \right) $, 对于伪势模型, $ \boldsymbol{F} $是流体粒子间相互作用力, 计算式如下[25,26]:

      将(16)式进行泰勒展开, 得

      式中, $ G $为流体粒子间相互作用强度; $ \psi $为相互作用势, 即伪势, 基于非理想状态方程的伪势取值如下[27]:

      式中, 设置$ G = - 1 $保证根号内为正值, 其取值不再影响粒子间相互作用强度.

      本文在模型状态方程的选择方面, 补充了C-S状态方程:

      式中, $ R $为气体常数, $ T $为温度. 参数$ a $, $ b $满足$ a = 0.4963{(R{T_{\mathrm{c}}})^2}/{p_{\mathrm{c}}} $, $ b = 0.1873 R{T_{\mathrm{c}}}/{p_{\mathrm{c}}} $. $ {T_{\mathrm{c}}} $为临界温度, $ {p_{\mathrm{c}}} $为临界压力. 本文对参数$ a $, $ b $和$ R $取常用值$ a = 0.5 $, $ b = 4 $, $ R = 1 $, 因此联立(19)式可求出临界密度$ {\rho _{\mathrm{c}}} \approx 0.13045 $, $ {p_{\mathrm{c}}} \approx 0.0022 $, $ {T_{\mathrm{c}}} \approx 0.047 $.

      外力通过$ \bar{\boldsymbol{S}} $项纳入演化方程的计算, 改进外力格式的$\bar{\boldsymbol{S}} $表达式为

      式中, $ \sigma $为热力学稳定性参量, 本文取值$ \sigma = 0.11 $. 原始伪势模型由于热力学不一致性使得模拟过程数值稳定性较差, 求解气液密度比十分有限, 而本文采用改进外力格式的MRT-LBM来调节模型的热力学一致性, 从而提升流动模拟过程中的数值稳定性, 增大气液两相流动的密度比. 本文数值模拟中的单位均为格子单位, 即长度单位为lu (lattice unit), 时间单位为ts (time step), 质量单位为mu(mass unit), 运动黏度单位为lu2/ts, 密度单位为mu/lu3, 压力单位为mu/(lu·ts2).

    3.   改进模型的验证

      3.1.   Laplace定律验证

    • Laplace定律是描述流体表面张力和曲面两侧压力关系的定律, 具体指存在于液体中的气泡由于表面张力的作用, 气液两相在达到稳定状态时, 气泡内外的压力${p_{{\text{in}}}}$和${p_{{\text{out}}}}$满足${p_{\rm in}} > {p_{\rm out}}$, 而且压差$\Delta p$与表面张力的关系式为[28]

      式中, $\sigma $为表面张力, $R$为气泡半径.

      初始平均密度的不同取值对两相的分布形态以及空泡内外的压力值具有显著影响. 为验证Laplace定律, 多次改变此参数, 不考虑重力等外力作用, 在201 lu×201 lu的流动区域内对无限域内静态空泡的演化进行数值计算. 密度场初始化为

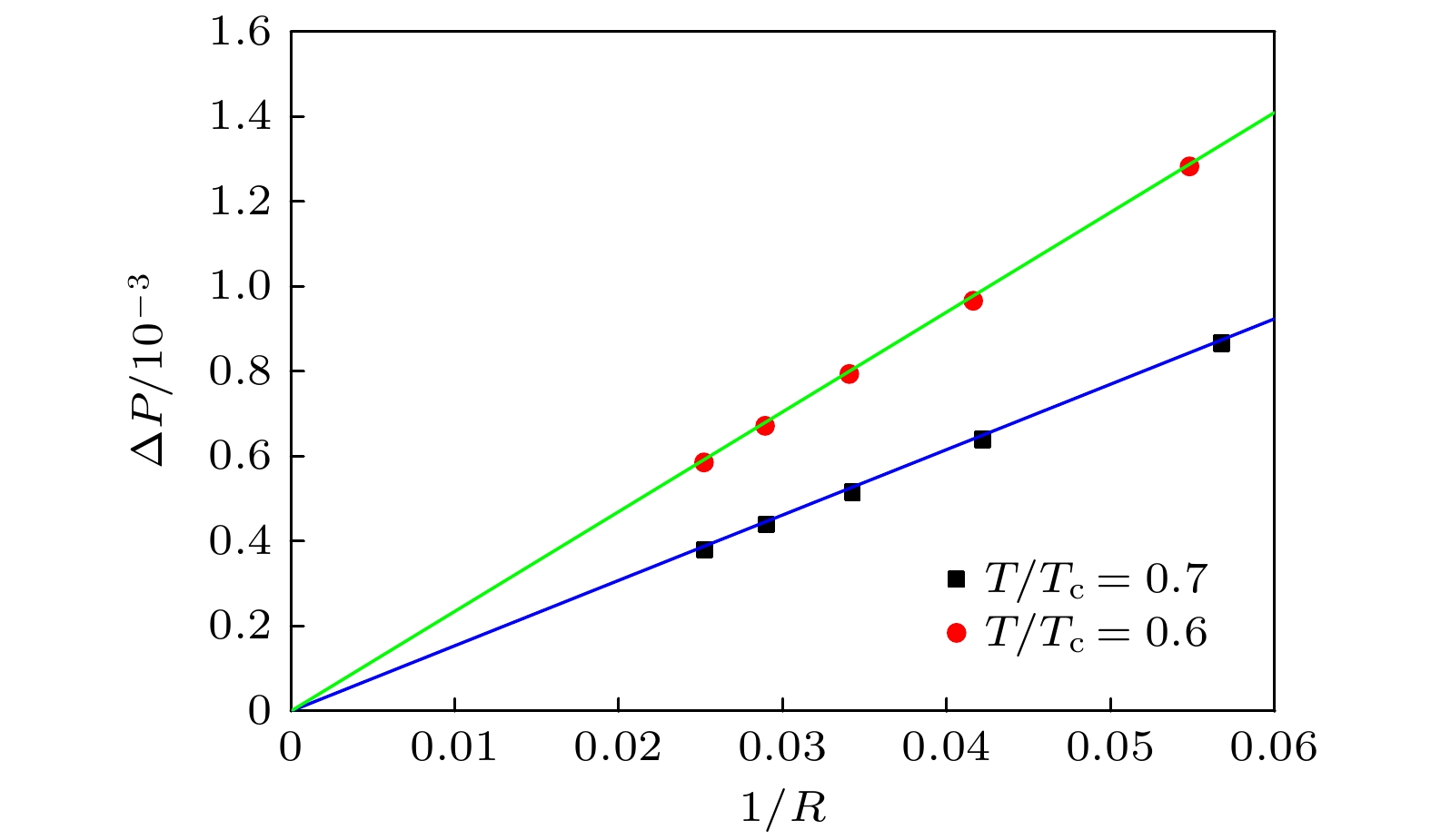
      式中, ${\rho _{\text{l}}}$为液相密度, ${\rho _{\text{g}}}$为气相密度, $ ({x_0}, {y_0}) $为初始时刻圆心坐标, $ {r_0} $为初始半径, $ W $为相界面宽度. 无量纲温度$T/{T_{\text{c}}}$分别取0.6和0.7, 初始时刻的气、液相密度${\rho _{\text{g}}}$和${\rho _{\text{l}}}$均设为根据C-S状态方程计算出的无量纲温度$T/{T_{\text{c}}}$对应的共存密度理论值; 初始时刻圆心坐标$ ({x_0}, {\text{ }}{y_0}) $为(101, 101); 初始半径$ {r_0} $分别取$ {r_0} $= 20, 25, 30, 35, 40; 相界面宽度$W = 5$; 流域的4个边界为周期边界. 当气液两相稳定时, 取流体密度$ \rho = ({\rho _{\text{l}}} + {\rho _{\text{g}}})/2 $的位置作为两相界面, 记录泡内外压力差$\Delta p$与半径倒数$1/R$并作图, 得图1.

      图1两条直线分别是$T/{T_{\mathrm{c}}} = 0.6$和$T/{T_{\mathrm{c}}} = 0.7$对应组离散点的线性拟合, 其斜率分别为0.0235和0.0154, 拟合直线的斜率值即表面张力大小. 随着无量纲温度的升高, 表面张力逐渐减小, 空泡内外压强差与空泡半径的倒数呈线性关系, 模拟结果符合Laplace定律, 验证了改进模型的正确性.

      • 3.2.   热力学一致性验证

    • 伪势模型的热力学一致性是指力学稳定性条件满足Maxwell等面积法则, 且状态方程与热力学中的状态方程保持一致, 保证伪势模型的热力学一致性, 有利于提升气液两相流模拟过程的稳定性.

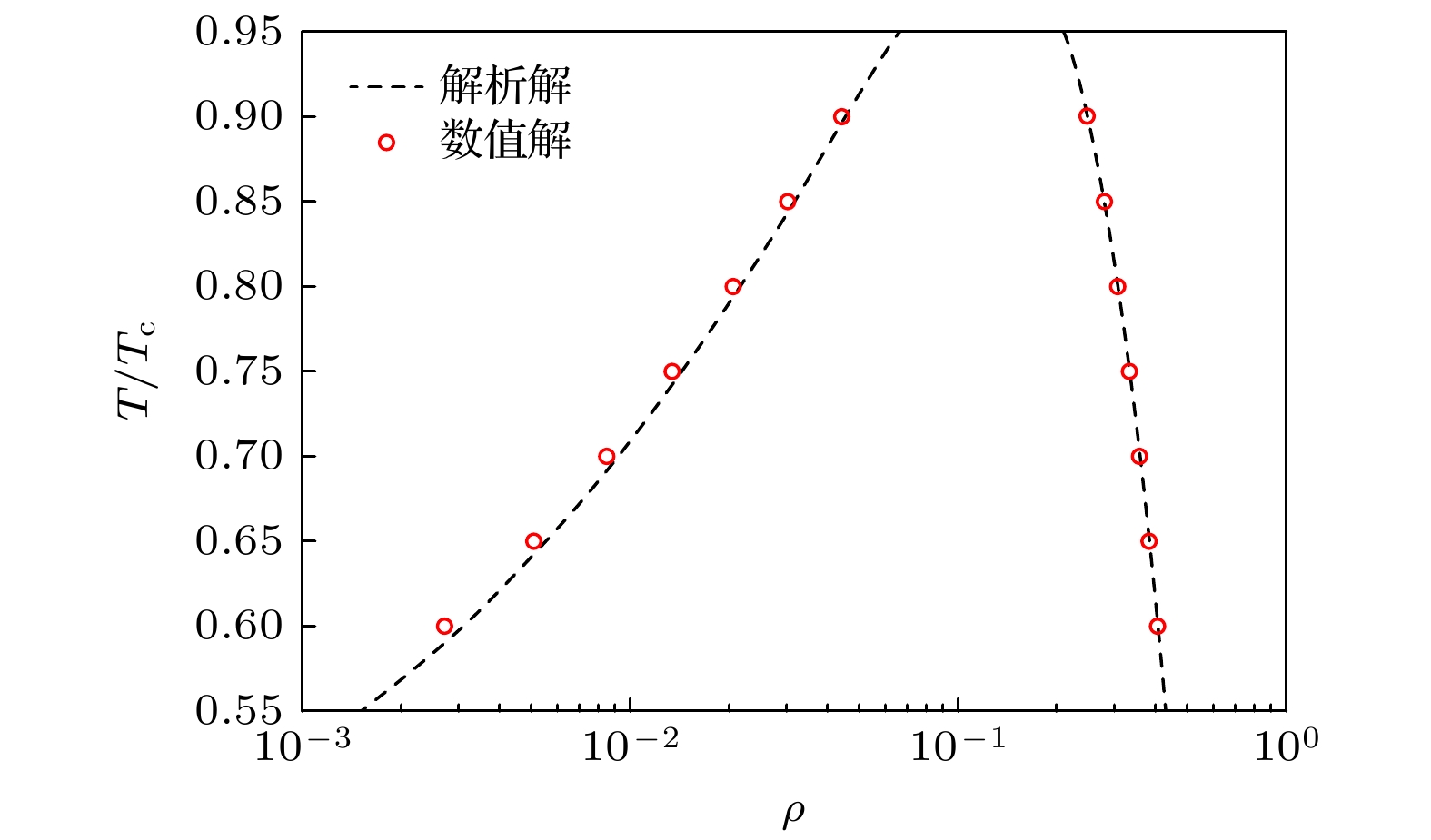
      为了验证本文所使用的模型是否满足热力学一致性需求, 本节对模型进行热力学一致性验证. 首先调整无量纲温度$ T/{T_{\mathrm{c}}} $的取值, 求解气液两相的共存密度, 将数值解与满足热力学一致性需求的共存密度解析解进行对比. 不考虑重力等外力作用, 计算域为201 lu×201 lu, 初始时刻在流场域中心设置一个静态圆形空泡, 密度场仍按照(22)式初始化, 圆心坐标$ ({x_0}, {y_0}) $为(101, 101); 无量纲温度$ T/{T_{\mathrm{c}}} $从0.6—0.9等间隔取7组, 初始时刻的气、液相密度${\rho _{\text{g}}}$和${\rho _{\text{l}}}$设为对应温度$ T/{T_{\mathrm{c}}} $下的共存密度解析值; 设初始半径$ r_0^{} = 30 $; 相界面宽度$W = 5$; 流域4个边界均用周期边界以模拟无限大流场. 在气液两相稳定后, 记录各个无量纲温度对应的气相和液相的密度值并作图, 如图2所示.

      从图2可以看出, 随着无量纲温度$ T/{T_{\mathrm{c}}} $的降低, 气液两相的密度比${\rho _{\text{l}}}/{\rho _{\text{g}}}$逐渐增大. 无量纲温度$ T/{T_{\mathrm{c}}} $较高时, 数值解与解析解的气相密度与液相密度值均基本一致; 而当无量纲温度$ T/{T_{\mathrm{c}}} $降低时, 气相一侧的数值解与解析解的偏差增大, 液相一侧仍保持良好的重合度. 根据模拟结果, 当$T/{T_{\mathrm{c}}} = 0.6$时, 可实现的气液两相密度比${\rho _{\text{l}}}/{\rho _{\text{g}}}$达到140以上. 总之, 可认为通过数值计算得到的数值密度曲线在$T/{T_{\mathrm{c}}} \geqslant 0.6$时与理论分析解具有良好的契合度, 即本文所使用的改进MRT-LBM模型可以在满足热力学一致性需求的同时, 实现较大的密度比和计算的稳定性.

      • 3.3.   Rayleigh-Plesset方程验证

    • 验证Rayleigh-Plesset方程是研究空泡动力学的重要步骤. 该方程描述了球形空泡在液体环境中的动态行为, 二维修正Rayleigh-Plesset (R-P)方程如下[29]:

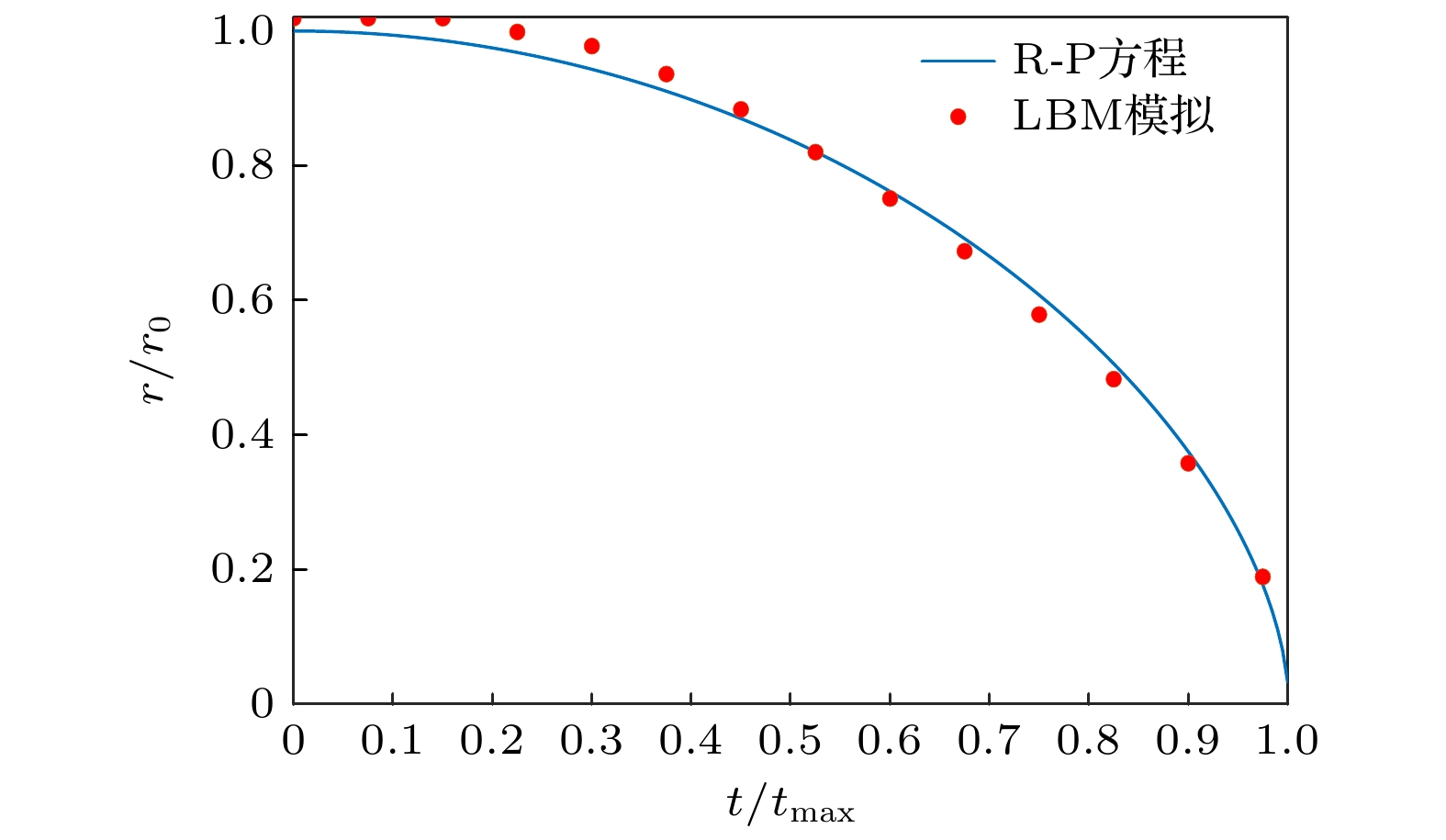
      式中, $ R $为空泡半径, $ {R_{{\text{bound}}}} $为计算域尺寸, $ {P_{{\text{vapor}}}} $是空泡内压力, $ {P_{{\text{bound}}}} $为边界压力, $ \sigma $为表面张力. 设置计算域为201 lu×201 lu, 初始时刻在流场域中心设置一个静态圆形空泡, 密度场仍按照(22)式初始化, 圆心坐标$ ({x_0}, {y_0}) $为(101, 101), 空泡初始半径$ {r_0} = 20 $, 4个边界均采用压力边界. 得出R-P方程预测结果与改进MRT-LBM的模拟结果如图3所示, 其中R-P方程采用龙格-库塔法进行求解.

      根据对比结果可以看出, Rayleigh-Plesset方程的解析解和改进MRT-LBM数值解的空泡半径演化规律基本保持一致. 结果表明, 改进MRT-LBM模型能够合理地预测空泡的溃灭演化过程.

    4.   近壁空泡溃灭的数值建模

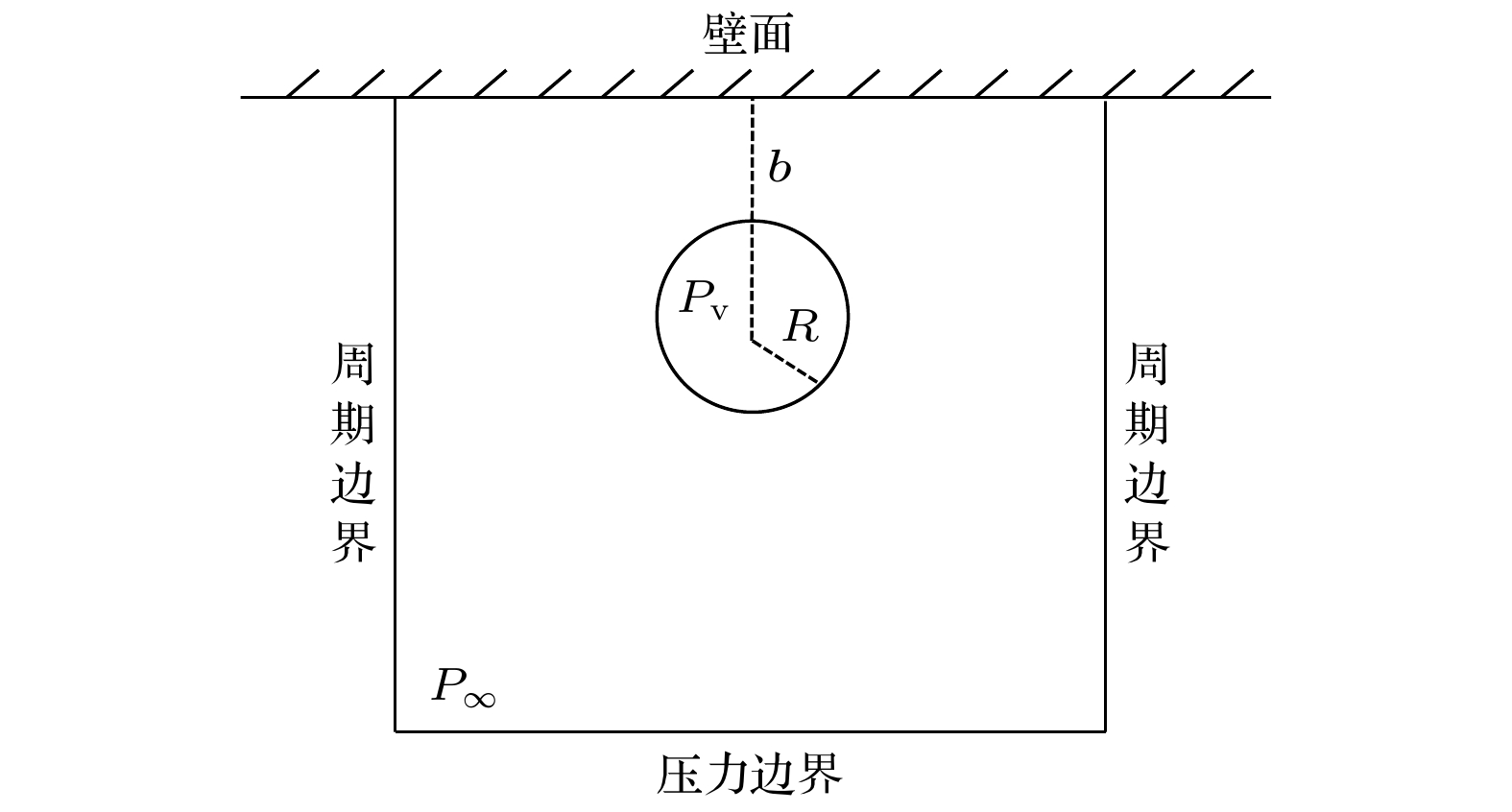
    • 计算模型如图4所示. 计算域设置为401 lu×401 lu. 数值计算区域左右边界采用周期边界格式, 底部采用Zou/He格式的压力边界, 顶部采用标准反弹格式模拟壁面.

      $ {r_0} $为空泡初始半径, b为空泡圆心到顶部壁面的距离, 定义$\lambda = b/{R_0}$表示空泡到壁面的无量纲距离. 初始密度根据(22)式设置, 初始时刻圆心坐标$ \left( {{x_0}, {y_0}} \right) $为$ \left(201, 401-b\right) $, 相界面宽度$W = 5$, ${P_{\text{v}}}$与${P_\infty }$分别表示空泡内压力和环境压力, 压差$\Delta P = {P_\infty } - {P_{\text{v}}}$.

    5.   结果与讨论

      5.1.   与实验对比结果

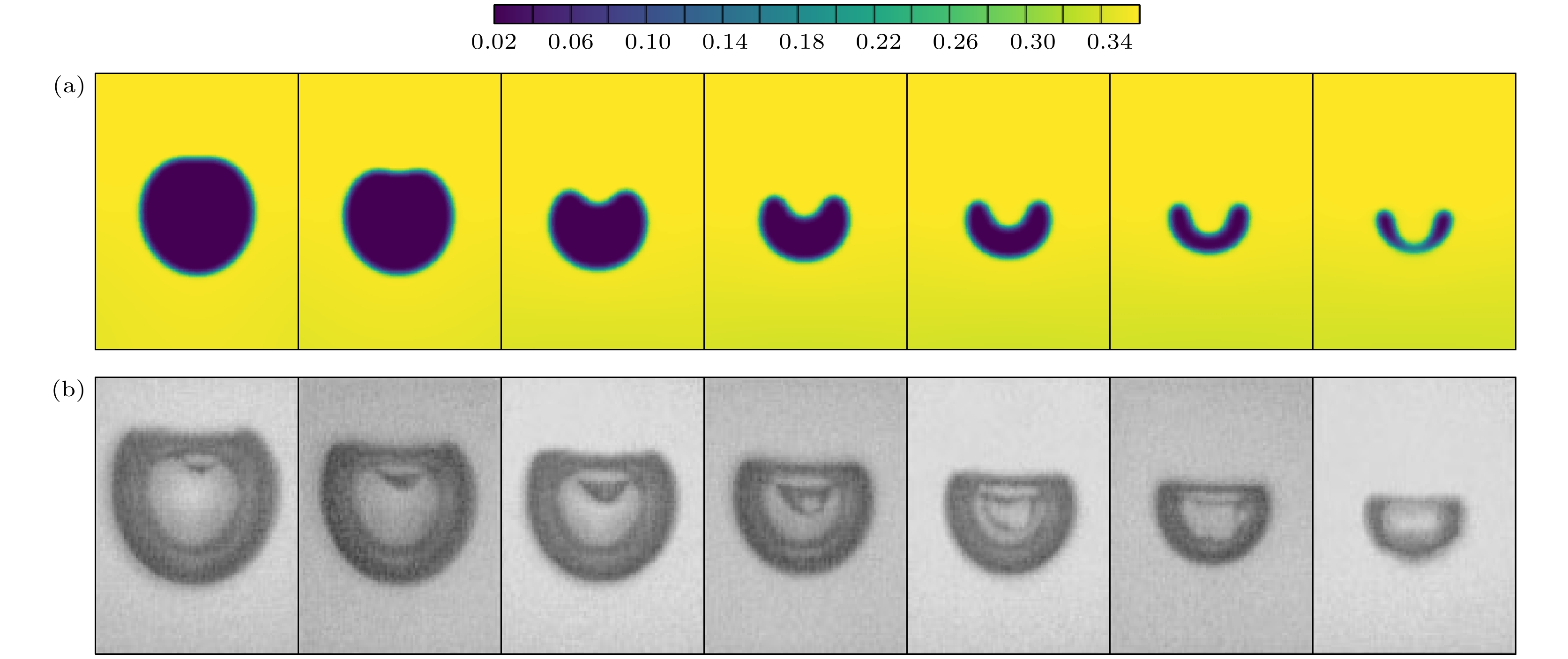
    • 取无量纲温度$ T/{T_{\mathrm{c}}} = 0.7 $, 无量纲距离参数$ \lambda = 1.6 $, 将计算得到的近壁空泡溃灭过程中空泡外形的演化过程同实验结果进行对比, 验证所使用空泡溃灭模型的有效性. 图5(a)为通过模拟计算得到的空泡溃灭过程中不同时刻对应的密度场分布图. 由于实验中壁面条件设在底部, 与本次模拟计算的设置相反, 为了更清楚地对比实验结果[30]和模拟结果, 将LBM模拟计算结果旋转180°后再与实验结果(图5(b))进行比较.

      观察演化图像可知, 溃灭过程中, 圆形空泡在远离壁面的位置先发生向内凹陷, 之后随着时间发展, 空泡凹陷形态基本一致, 但变形程度越来越大, 直至在靠近壁面的底部中心溃灭. 通过对比模拟结果和实验结果, 本文所用改进伪势MRT-LBM模拟的近壁空泡溃灭过程中空泡外形的演化过程同实验结果基本一致, 验证了模型的有效性.

      考虑到本研究物理量均采用格子单位, 因此涉及到实际物理单位与格子单位的转换关系, 为了实现格子单位与实际物理单位之间的转换, 需要确定出对应物理量的参考量, 参考量定义为实际物理单位与格子单位的比值. 以空泡半径为特征长度, 则长度的参考量确定为$L_{\text{r}}^{} = r{'}/r = 1.8125 \times {10^{ - 5}}\;{\text{m}}$, 运动黏度的参考量为$\upsilon _{\text{r}}= \upsilon{'}/\upsilon = 1 \times {10^{ - 5}}\;{\text{m}}_{}^2{\text{/s}}$. 压力参考量$p_{\text{r}} = p{'}_{ \text{c}}/p_{\text{c}}^{} = 1 \times 10_{}^{10} \;{\text{Pa}}$, 通过参考长度$L_{\text{r}}^{}$和参考运动黏度$\upsilon _{\text{r}}^{}$可计算出速度参考量$u_{\text{r}}^{} = \upsilon _{\text{r}}^{}/L_{\text{r}}^{} = 0.5517 \;{\text{m}}/{\text{s}}$.

      • 5.2.   密度场分布

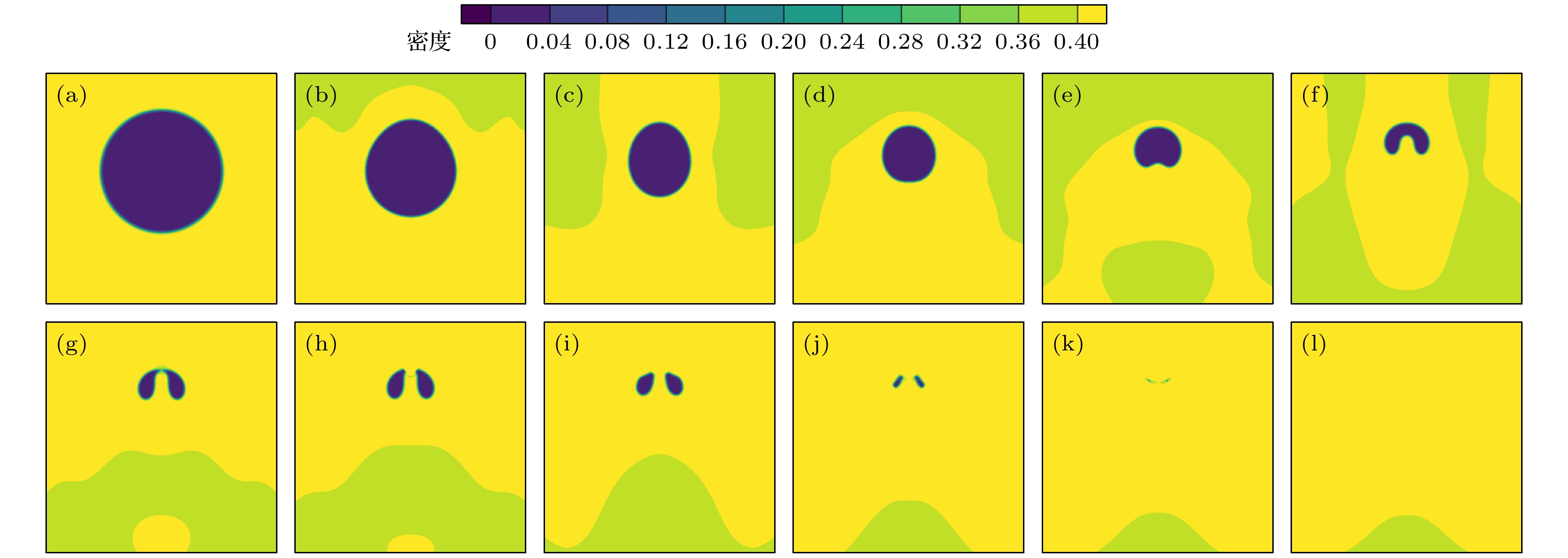
    • 图6为基于改进MRT-LBM模拟得到在空泡初始半径$ {R_0} = 80 $, 初始压差$ \Delta p = 0.0116 $, 无量纲温度$ T/{T_{\mathrm{c}}} = 0.6 $, 无量纲距离$ \lambda = 1.6 $下近壁空泡溃灭密度场的演化过程, 为了对主要变化区域做详细分析, 此处只显示了空泡附近的部分流场区域, 横坐标范围为50—350 lu, 纵坐标范围为100—400 lu.

      初始时刻, 设置在流场内的空泡呈圆形, 由于空泡内外压差大于表面张力的作用, 空泡受压差作用开始向内收缩. 收缩过程中由于壁面的影响, 空泡左右两侧的收缩速度大于上下两侧收缩速度, 且靠近壁面的一端空泡曲率更大, 空泡呈顶部略尖的鸡蛋形. 经过200 ts后, 空泡进一步收缩, 形态上接近椭圆形. 之后, 空泡底部由于旁边液体区域的补充形成高密度区, 即高压区, 空泡受高压区压迫收缩的过程中底部轮廓逐渐变平; 紧接着, 空泡底部在压差作用下开始向内凹陷. 随着时间步增大, 气相区域逐渐减小, 空泡在持续高压差的作用下底部向内凹陷程度越来越大, 空泡呈倒U形.

      在第931 ts时, 凹陷程度达到最大, 空泡底部的泡壁与顶部的泡壁在压差作用下接触, 空泡上下流体开始掺混、形成第1次溃灭. 原本的圆形空泡经过第1次溃灭后变为环形空泡, 在二维流场中体现为对称的两个尖端指向溃灭位置的弯曲水滴型区域, 并在第1次溃灭的位置处形成一个不明显的高密度区. 此时, 环形泡的顶部为高密度区, 底部为低密度区, 顶部压力高于底部, 与第1次溃灭的初始阶段相反, 环形泡在收缩的过程中顶部收缩速率更快, 轮廓逐渐变平.

      在第1150 ts时, 环形空泡界面缩小至细扁状态, 并继续收缩直至第2次溃灭. 最终空泡完全溃灭, 流场完成了气相到液相的相变, 整个空泡的溃灭流程为凹陷、变形、第1次溃灭和第2次溃灭.

      • 5.3.   压力场、速度场分布

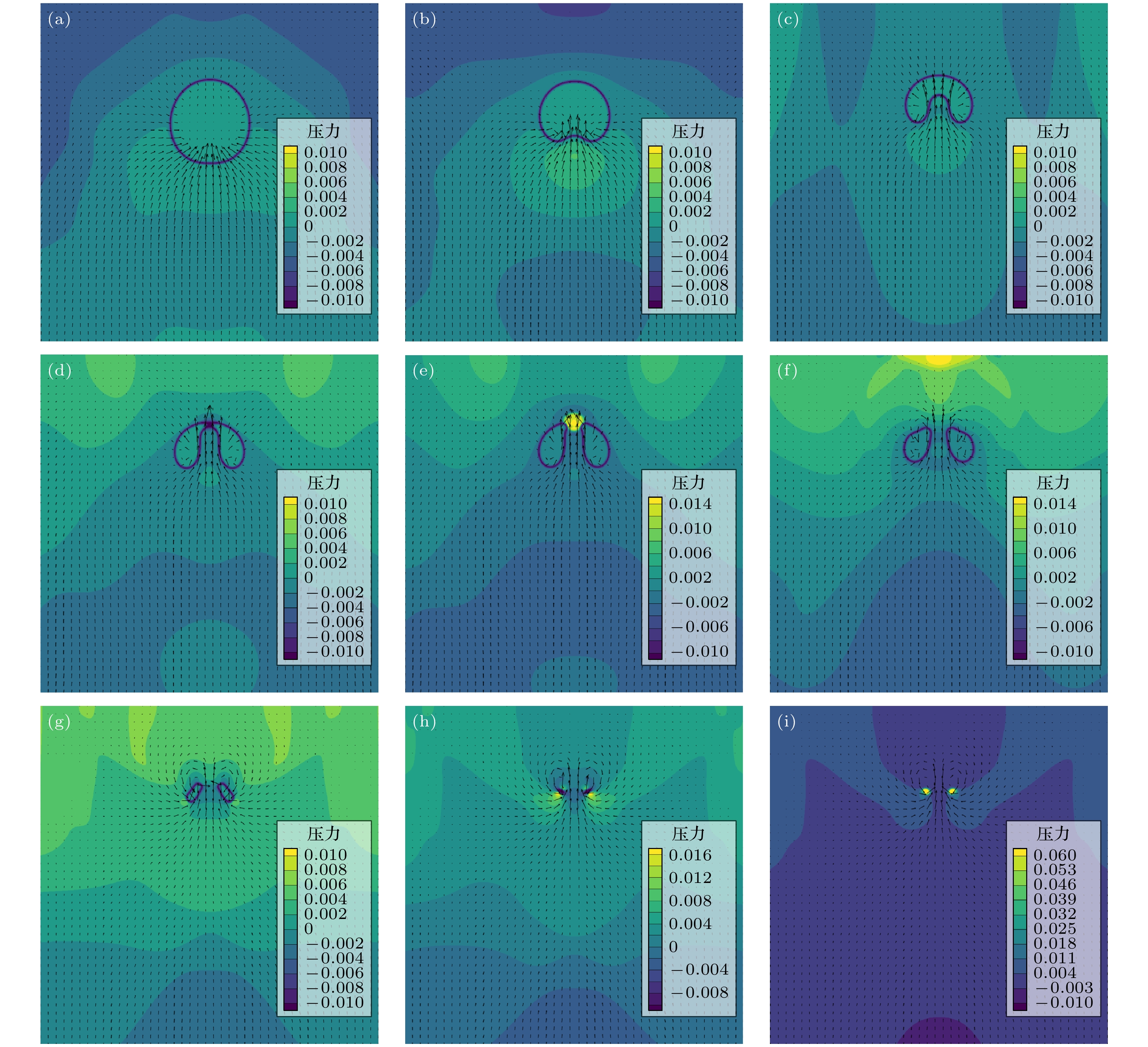
    • 图7为近壁空泡溃灭演化过程中各时间步的压力分布云图, 图中叠加了对应时刻的速度矢量分布图. 根据演化过程可以看出, 空泡在压差作用下缩小时, 空泡远离壁面的一侧形成一个高压区, 将空泡底部泡壁向内压, 空泡底部的流速明显增强, 速度方向指向空泡内部. 在空泡底部高压区的持续作用下, 空泡凹陷程度不断增大, 空泡底部泡壁越来越靠近顶部泡壁, 凹陷处充满了高速度流体, 而空泡靠近壁面一侧液体流速很低, 速度变化不明显.

      在两侧流体的挤压下, 底部泡壁在第931 ts与顶部泡壁接触, 之后在接触位置破裂, 发生第1次溃灭, 形成一个明显的高压区. 同时, 空泡底部的流体终于穿过空泡, 击穿上下两层泡壁, 形成指向壁面的微射流, 空泡形态变为环形, 在二维流场中体现为对称的两个尖端指向溃灭位置的弯曲水滴型区域; 紧接着, 第1次溃灭形成的高压区向外扩散, 由于残余空泡环的阻碍作用产生半圆形冲击波向壁面方向移动, 环形空泡截面的尖端在扩散的高压区的作用下向内凹陷, 底部流体持续以微射流的形式穿过空泡向壁面方向靠近. 随着时间步的增大, 第1次溃灭产生的冲击波继续向外扩散, 但冲击波强度随时间发展逐渐减小. 空泡溃灭形成的微射流速度也是在溃灭中心流速最大, 随着时间发展, 形成的微射流逐渐靠近壁面但是流速降低. 环形空泡在压差作用下截面不断收缩, 在其周围可以观察到涡旋结构. 发展到第1175 ts时, 环形空泡截面已收缩至极小, 即将第2次破裂, 在环形空泡周围再次开始形成高压区域, 且压力最大值显著高于第1次溃灭过程中产生的压力最大值.

      随后, 第1次溃灭后形成的环状空泡也在内外压差作用下溃灭, 在溃灭处形成明显的高压区, 此时溃灭处压力最高值是第1次溃灭时压力最高值的4倍以上, 并产生圆形冲击波向外扩散, 冲击波的碰撞、叠加又在流场中形成高压区, 增加了溃灭演化流场的复杂性.

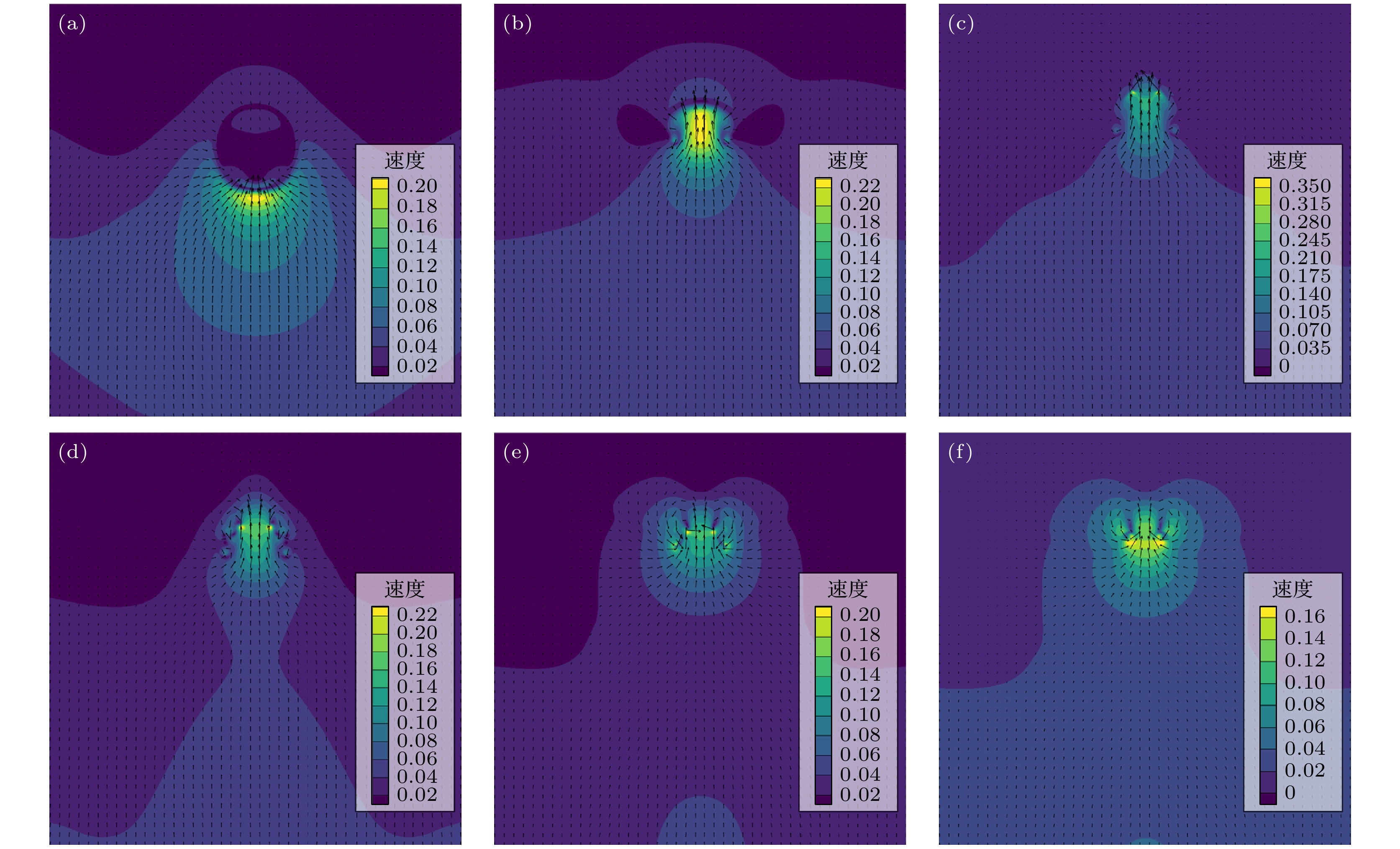
      图8为溃灭过程中的速度分布云图, 可看出在溃灭过程中流场中最大速度始终在空泡处, 是流体受挤压形成微射流的最大速度, 且第1次溃灭过程中流场中速度最大值高于第2次溃灭过程中流场中的速度最大值. 特别是, 产生的微射流速度方向指向壁面.

      • 5.4.   溃灭诱发壁面损伤的作用力机制

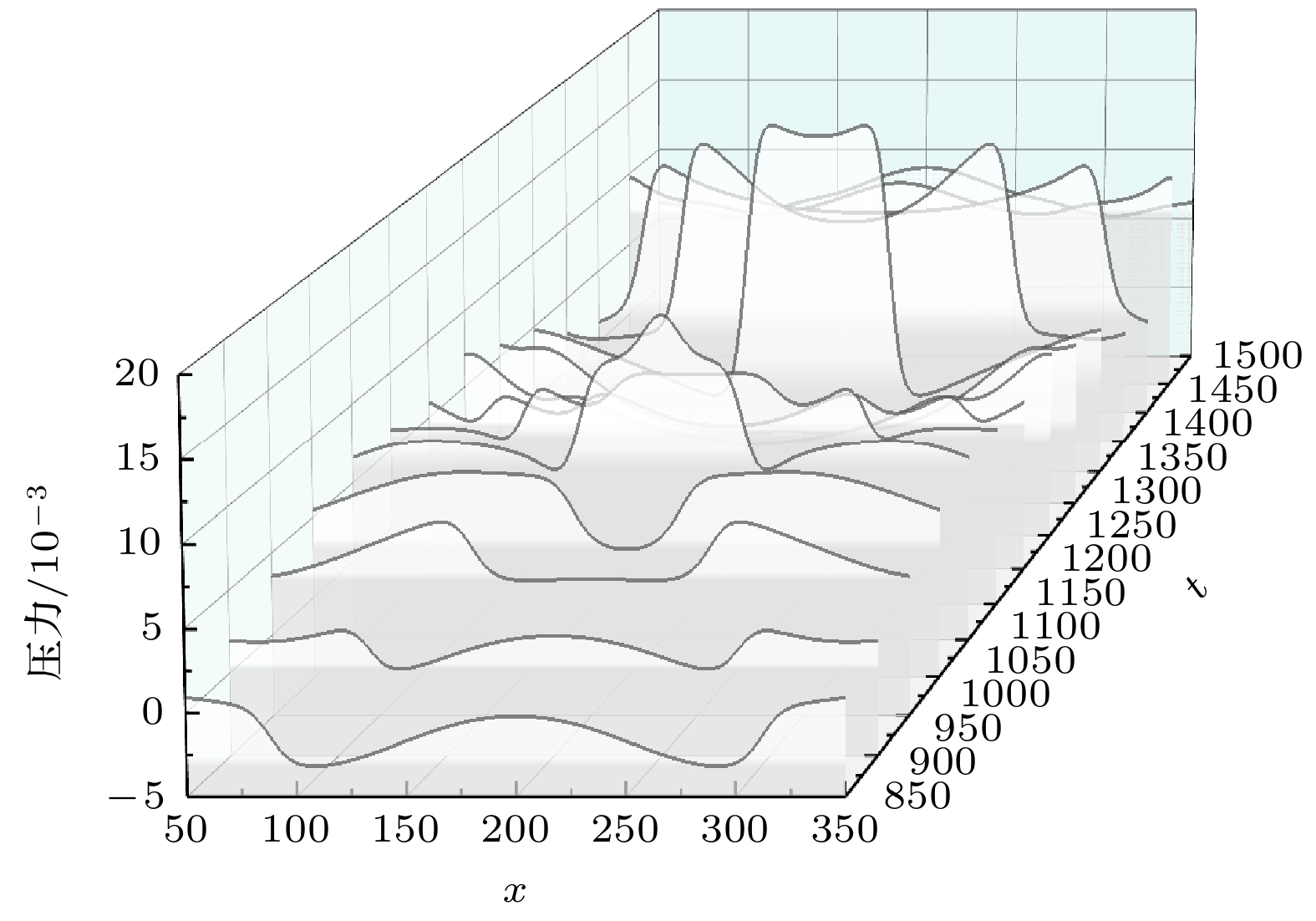
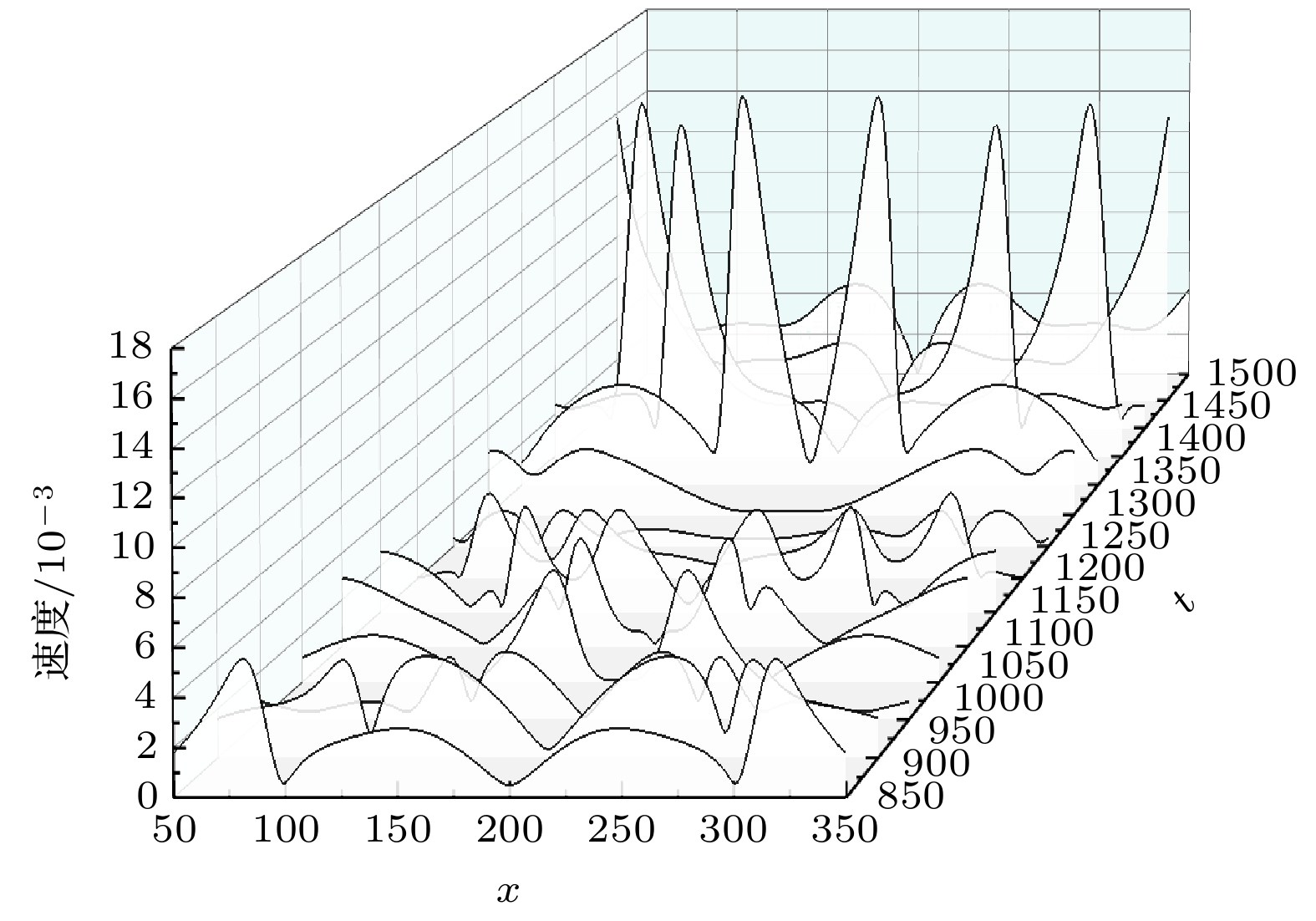
    • 空泡溃灭诱发壁面损伤的作用力机制一直是空化研究的重点课题, 本节从壁面压力和速度角度进行分析, 着重研究近壁空泡溃灭流场中壁面受到的作用. 为更直观地观察壁面处压力和速度值, 监测壁面处850—1500 ts之间的速度和压力的分布, 监测区域选择壁面坐标50—350 lu, 结果如图9和图10所示.

      从图9可以看出, 空泡溃灭的过程中, 第1次溃灭产生的冲击波首先作用于与空泡距离最近的壁面中心点再从中心向两侧扩展. 第2次溃灭后产生的冲击波对壁面的冲击压力最高, 对壁面的作用形式也是先接触与空泡垂直距离最短处, 再从该处向外扩展, 对壁面反复扫掠, 壁面上压力的复杂波动与空泡溃灭过程中产生的冲击波及它们之间的互相作用密切相关, 冲击波的扫掠范围为整个壁面, 使壁面处产生较高的压力梯度, 而较高的压力梯度易引发壁面出现较大的应变. 且由于在冲击波向外膨胀的过程中, 波正面到达区域压力突增, 冲击波扫掠区域压力骤减, 壁面处于交变应力状态. 其中, 距离破裂的空泡最近的位置会反复受到多重冲击波的作用, 最终导致材料的疲劳破坏.

      从图10得出, 演化过程中, 壁面一直受到作用范围较小的射流速度作用. 溃灭过程释放的强烈微射流在第1250 ts后作用于壁面, 不是对整个壁面作用而是局部冲击壁面, 作用区域随时间步增加从壁面中心往两侧移动. 由于微射流作用范围较小, 一个空泡溃灭产生的微射流作用范围为20 lu左右, 直接作用于壁面, 对壁面材料造成点状破坏.

      尽管空泡溃灭时产生的最大射流速度为0.42551, 但由于衰减迅速, 到达壁面时的射流冲击速度仅为0.01851, 壁面受到微射流的冲击速度减小了一个数量级. 而空泡溃灭时产生的最大压力超过0.07, 对壁面的最大压力可达到0.025以上. 因此, 当无量纲距离$\lambda = 1.6$时, 壁面受到的溃灭作用是由溃灭产生的微射流和冲击波共同产生的, 二者的作用范围不同, 形成的破坏方式也不同.

    6.   结　论

    • 本研究基于改进的MRT-LBM模型对近壁空泡溃灭过程进行数值模拟, 研究近壁空泡溃灭动力学演化过程, 并分析空泡溃灭作用于壁面的载荷机制. 研究发现, 近壁空泡溃灭过程的形态演变包括凹陷、变形、第1次溃灭和第2次溃灭, 且溃灭过程中产生了微射流和冲击波. 其中, 空泡溃灭过程中释放的微射流主要来源于第1次溃灭, 冲击波的产生分别来自于第1次溃灭和第2次溃灭, 第2次溃灭产生的冲击波强度明显高于第1次溃灭产生的冲击波. 通过监测壁面处压力与速度分布分析了壁面发生空蚀损伤的载荷机制, 结果表明, 壁面损伤主要来自冲击波和微射流的共同作用, 冲击波在壁面上的扫掠范围较大, 且反复作用于壁面, 易使壁面出现较大的应变. 造成壁面中心附近材料的疲劳破坏. 而微射流的作用范围较小, 易对壁面造成点状破坏.

    参考文献 (30)

目录

/

返回文章
返回