首页
登录
注册
-
铅作为一种常见的材料核, 对其核数据的研究和计算具有重要的理论价值和应用前景. 铅铋共晶合金也是重要的冷却剂, 被应用于欧洲铅冷却系统(ELSY)以及中国铅基研究反应堆(CLEAR-I)[1]等铅冷快堆的建设和第四代反应堆的相关研究中. 此外, 铅的核反应数据对包括加速器驱动的亚临界系统ADS、核废料的嬗变、放射性同位素生产、放射治疗以及反应堆设计[2-5]在内的诸多应用都是非常重要的. 而根据现有的积分基准检验结果以及Lawrence Livermore国家实验室(LLNL)的铅脉冲球实验得到的数据来看, 为了减少相关评估数据的不确定性, 仍需对铅核的核反应数据理论计算进行研究, 进而改进对铅核的核数据评价[6,7].
Koning和Delaroche (K-D)提出了一套球形光学势[8], 采用该光学势可以实现对核子入射能量高达200 MeV时的核子诱发核反应数据的理论计算, 该光学势得到了广泛的应用. 然而, 包括K-D光学势在内的诸多光学势通常将势深表示为多项式形式, 需要额外地添加色散修正项来考虑色散效应, 并且在描述中子和质子入射时需要使用两套不同的势参数, 参数的得出受到单一核子实验数据数量和质量的影响. 近期, 色散光学模型(DOM)被广泛应用于分析和计算核子在大能量区间以及大质量范围内的弹性散射数据[9-12]. 根据因果关系的要求, 色散光学模型在光学势中利用色散关系自洽地引入了色散修正项[13]. 色散光学势的虚部与实部通过色散关系相互联系, 从而在一定程度上减少了光学势参数的数量以及不确定性, 并且消除了几何参数中的能量依赖关系. 同时, 通过对色散光学势的体虚部势进行高能修正, 可以更好地描述核子入射能量远离费米能时的散射数据, 使得光学势适用的核子入射能量可达到200 MeV[14]. 此外, 采用色散光学模型还使得光学势有可能在形式上与Lane方程自洽, 即可以将质子和中子入射看作是两种处于不同状态的同种粒子入射, 通过引入同位旋矢量项来区分核子的这两种状态. 基于此, 描述中子入射和质子入射的光学势的差异可以完全由同位旋矢量项来确定, 由此实现使用同一套势参数的光学势计算两种核子诱发的核反应数据, 并且在拟合势参数时, 可以同时使用中子和质子实验数据. 通过同位旋矢量项确定的差异势还可以实现对(p, n)准弹性散射角分布数据的理论计算[15].
$ ^{208} {\rm{Pb}}$ 是铅核同位素中最稳定且丰度最高的同位素, 对$ ^{208} {\rm{Pb}}$ 核子散射数据的高精度描述是实现对铅核的核反应数据理论计算的关键. 本工作采用色散光学模型, 通过在色散光学势中定义合适的同位旋矢量项构建一套Lane自洽的色散光学势, 实现用同一套参数同时描述中子和质子散射数据, 进而实现对$ ^{208} {\rm{Pb}}$ 中子总截面、核子弹性散射角分布、分析本领以及(p, n)准弹性散射角分布等核子散射数据的高精度描述. -
基于色散光学模型, 本文描述
$ ^{208} {\rm{Pb}}$ 核子弹性散射数据的色散光学势的具体形式如下:其中
$ f_{\rm{ws}} $ 和$ g_{\rm{ws}} $ 为Woods-Saxon形式的势形状因子. (1)式中包含实部Hartree-Fock (HF)势, 体(v)虚部势、表面(s)虚部势、自旋-轨道耦合(so)实部和虚部势[16-19], 各个势的具体表达形式如下:色散修正项由相应的虚部势通过色散关系计算得到[20].
为实现对质子入射情况的计算, 光学势中需要考虑库仑势
$ V_{\rm{Coul}} $ , 并引入有效能量“$ E^\ast $ ”来考虑由于原子核的排斥而引起的库仑修正[21]. 在计算中子入射时, 有效能量$ E^\ast $ 等价于中子的入射能量, 而在质子入射时,$ E^\ast $ 定义为质子的入射能量与$ E_{{\mathrm{Coul}}} $ 的差值, 其中$ E_{{\mathrm{Coul}}} = C_{{\mathrm{Coul}}}({ZZ'}/{A^{1/3}}) $ (Z和$ Z' $ 分别代表入射核子和靶核的电荷数, A为靶核的质量数,$ C_{{\mathrm{Coul}}} $ 为可调参数).本文通过在实部势
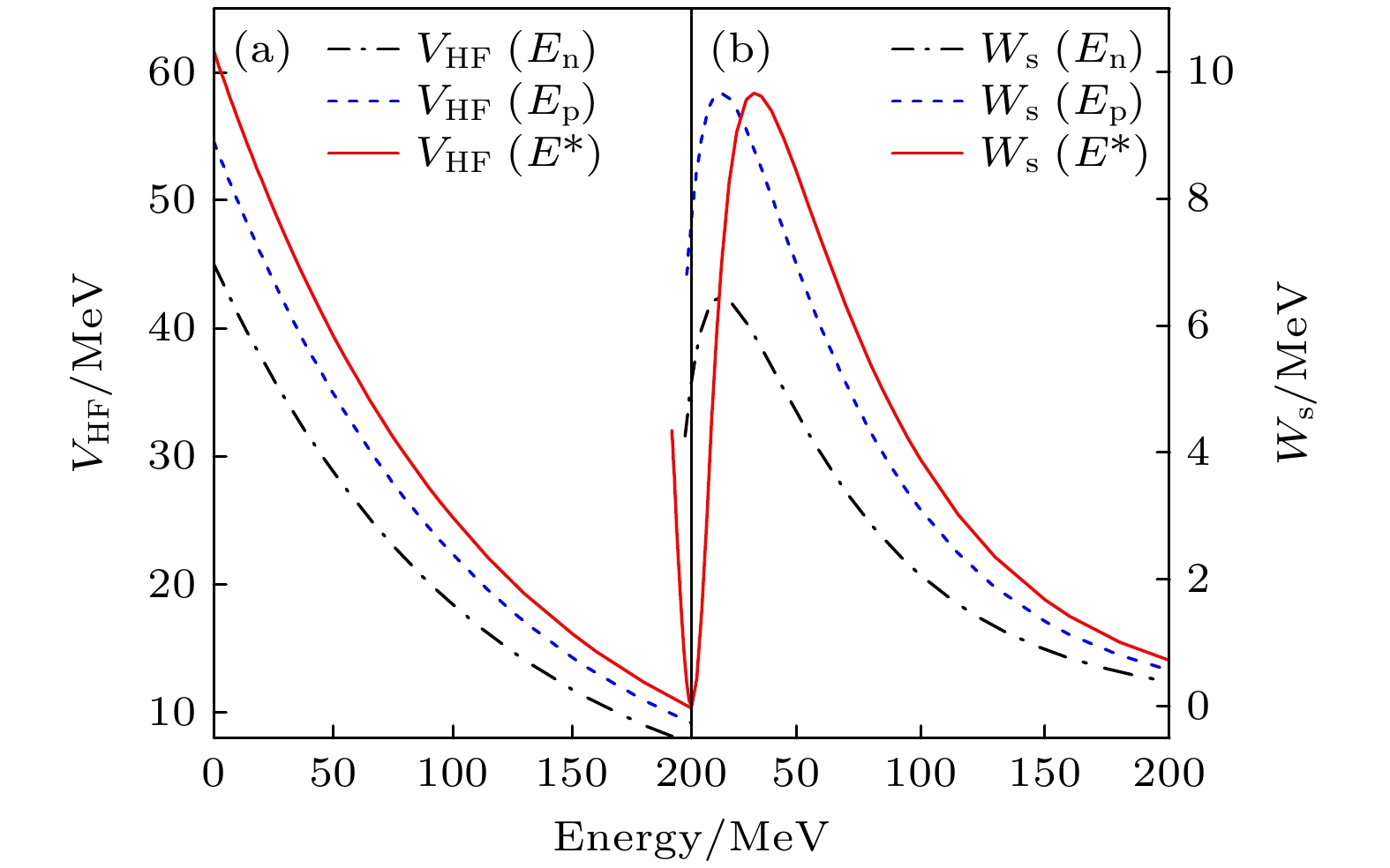
$ V_{\rm{HF}} $ 和表面虚部势$ W_{\rm{s}} $ 的势深常数中引入同位旋矢量项(即Lane项[22,23])合理地考虑了同位旋依赖性, 具体形式如下:中子和质子入射时的实部势
$ V_{\rm{HF}} $ 和表面虚部势$ W_{\rm{s}} $ 深度随能量的变化情况如图1所示. 描述两种核子入射时的光学势之间的差异由同位旋矢量项、库仑修正项决定. 借此, 区别于包括K-D势在内的诸多光学势, 该光学势可以采用一套相同的势参数同时描述中子和质子诱发的核反应数据. 表1列出了本文所采用的色散光学势的参数. -
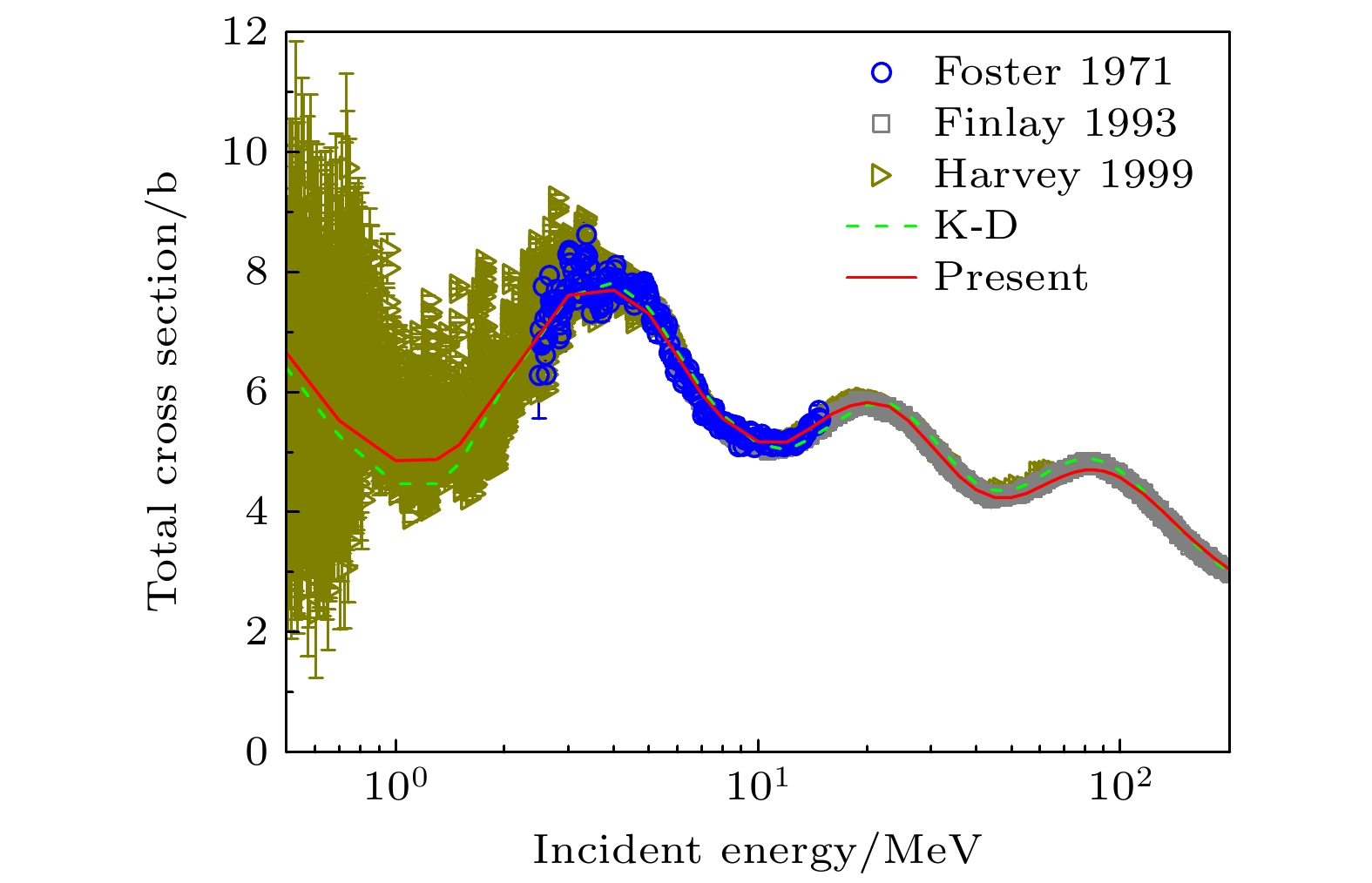
本文对中子总截面的计算结果与实验数据以及由K-D光学势给出的计算结果的比较情况如图2所示. 本文给出的理论计算结果很好地重现 了实验数据, 并且描述情况明显优于K-D光学势, 特别是在中子入射能量为10 MeV左右的能量区域以及对振荡区实验数据平均趋势的描述. 本文所使用的所有实验数据及其文献均可在EXFOR实验数据库[24]中找到, 用于比较的K-D势为RIPL库[25]中分别针对
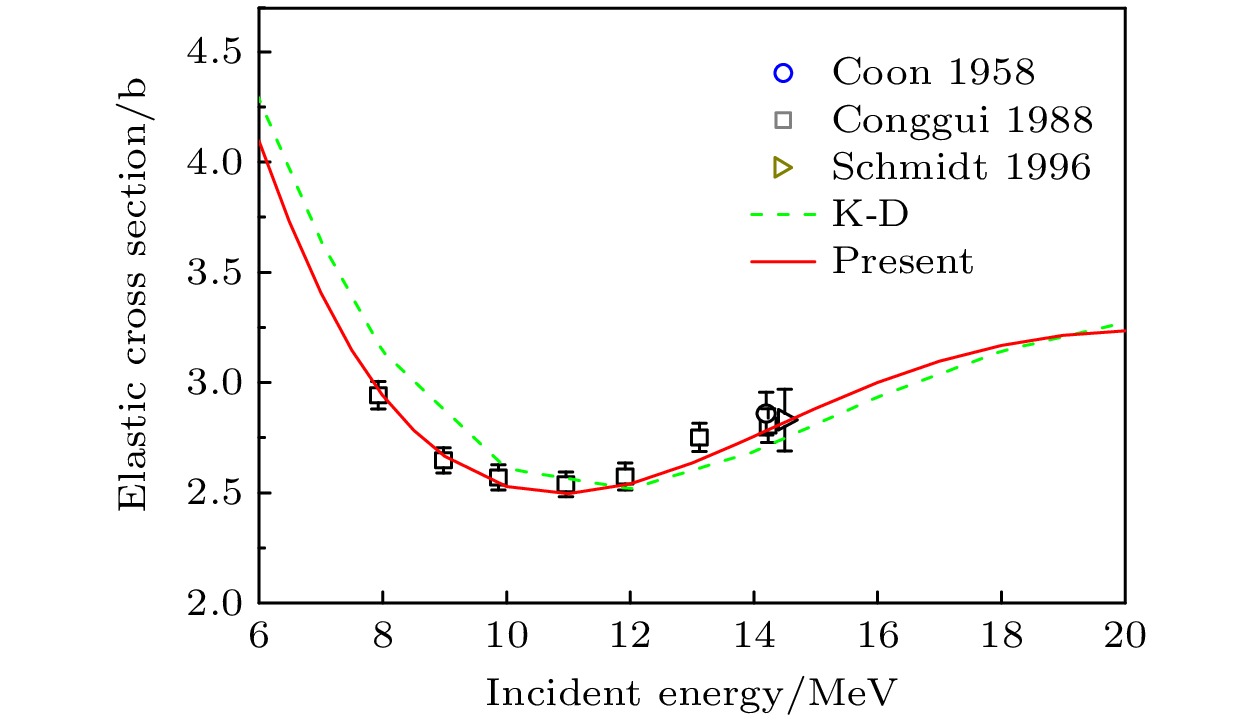
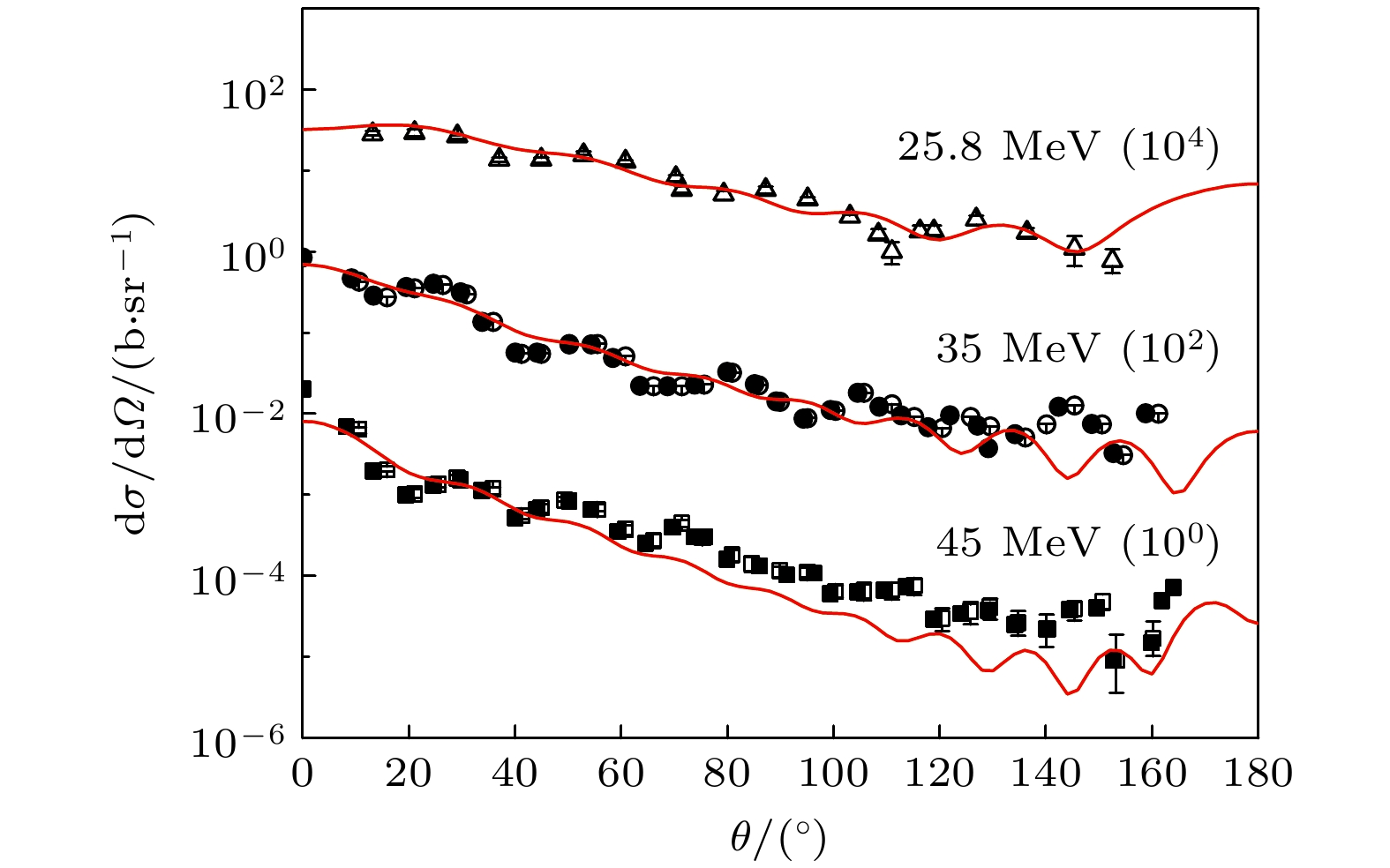
$ ^{208} {\rm{Pb}}$ 的中子和质子散射实验数据进行单独调参得到的中子光学势和质子光学势.本文对中子弹性散射截面的计算结果与天然铅的实验数据的比较情况如图3所示, 我们的计算结果与实验数据表现出非常好的一致性, 明显优于K-D光学势给出的计算结果.
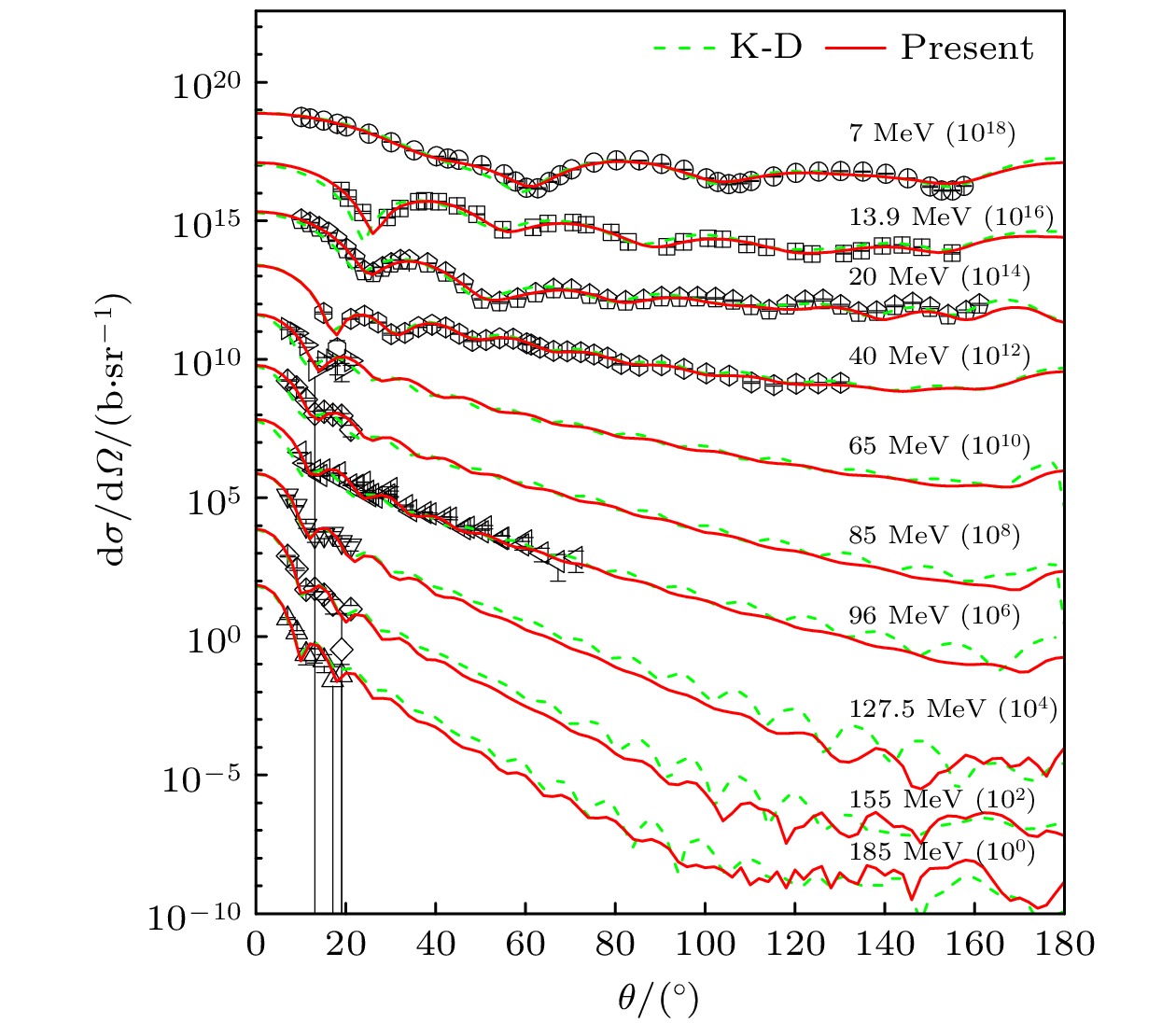
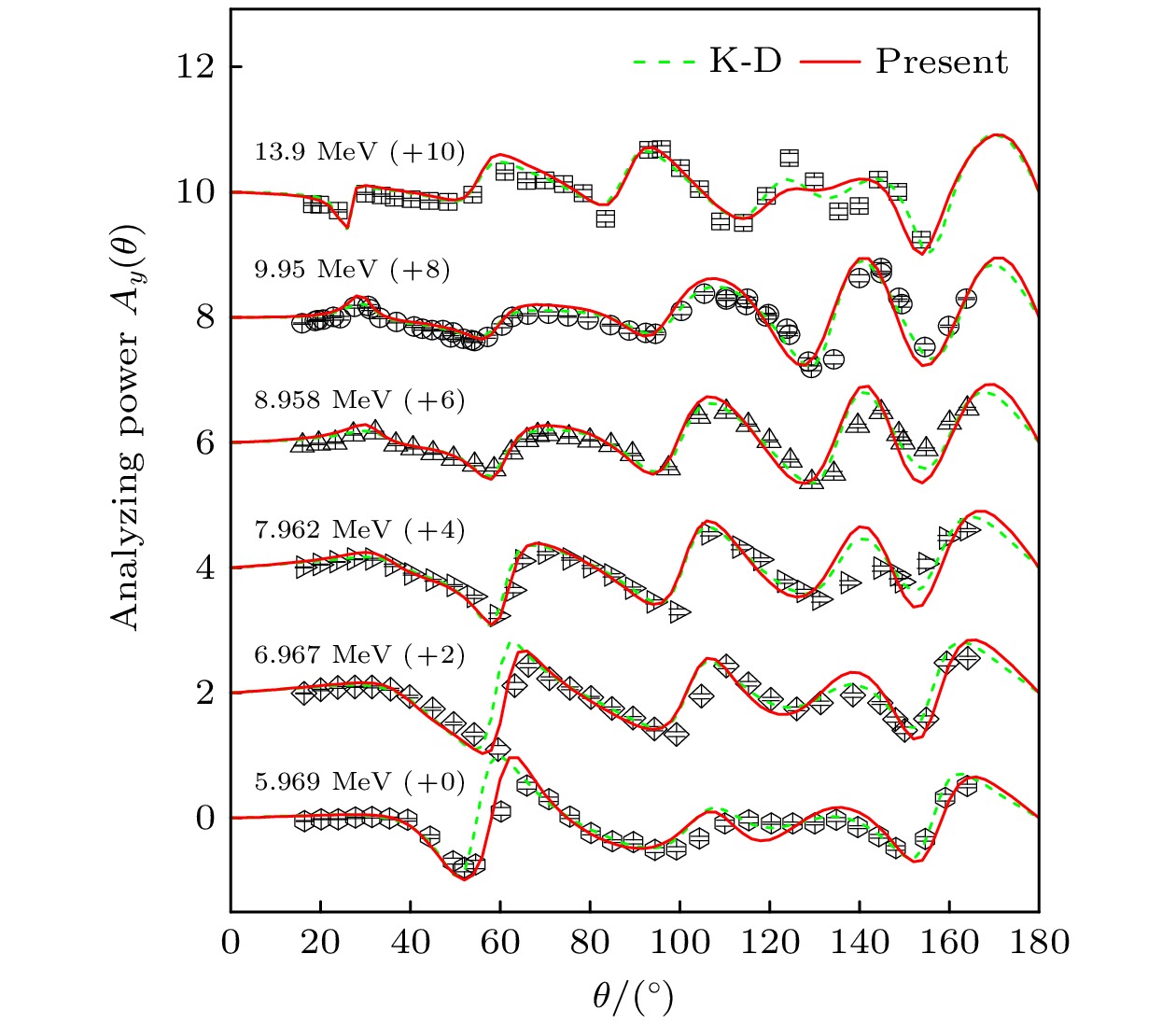
本文对
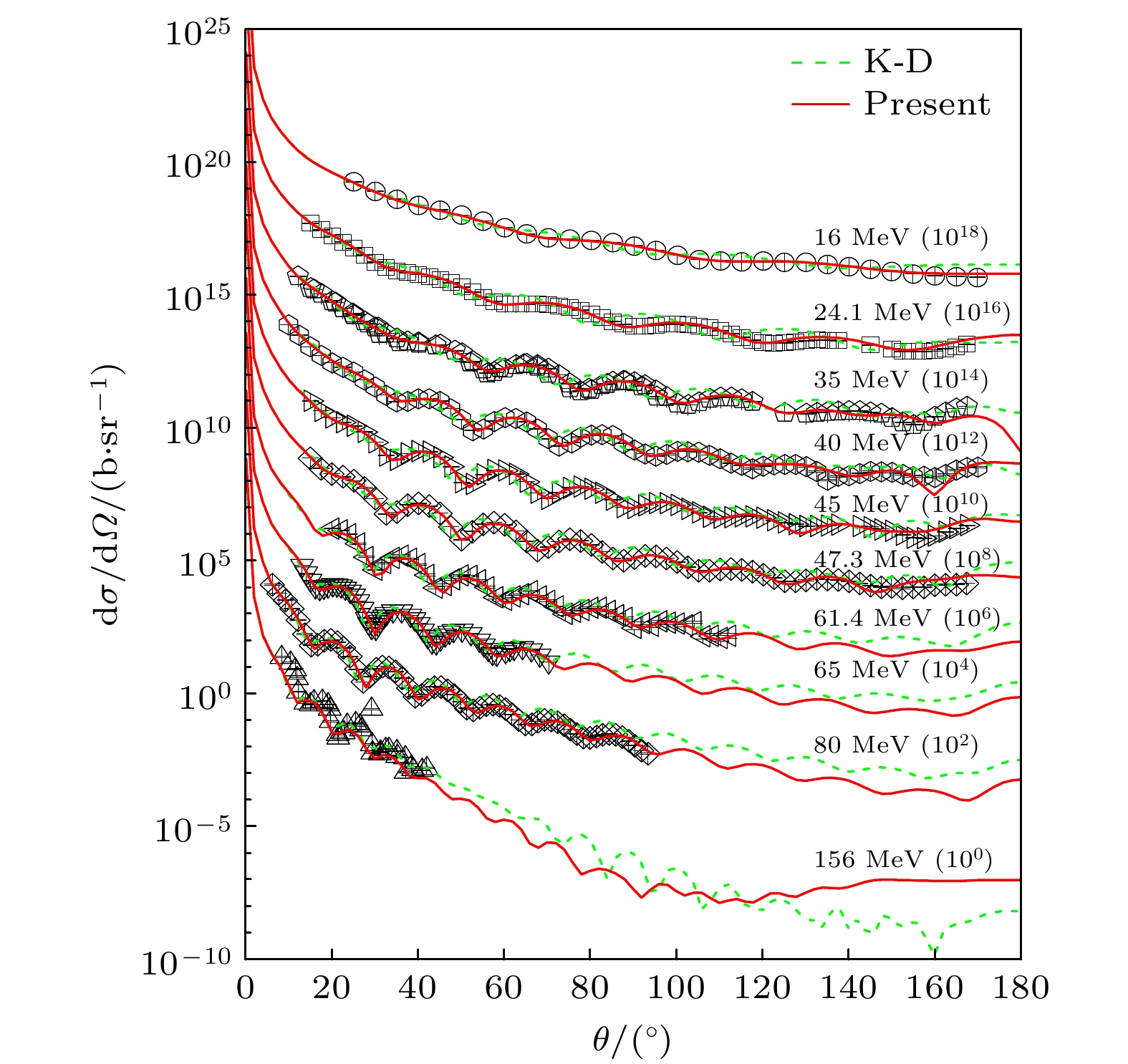
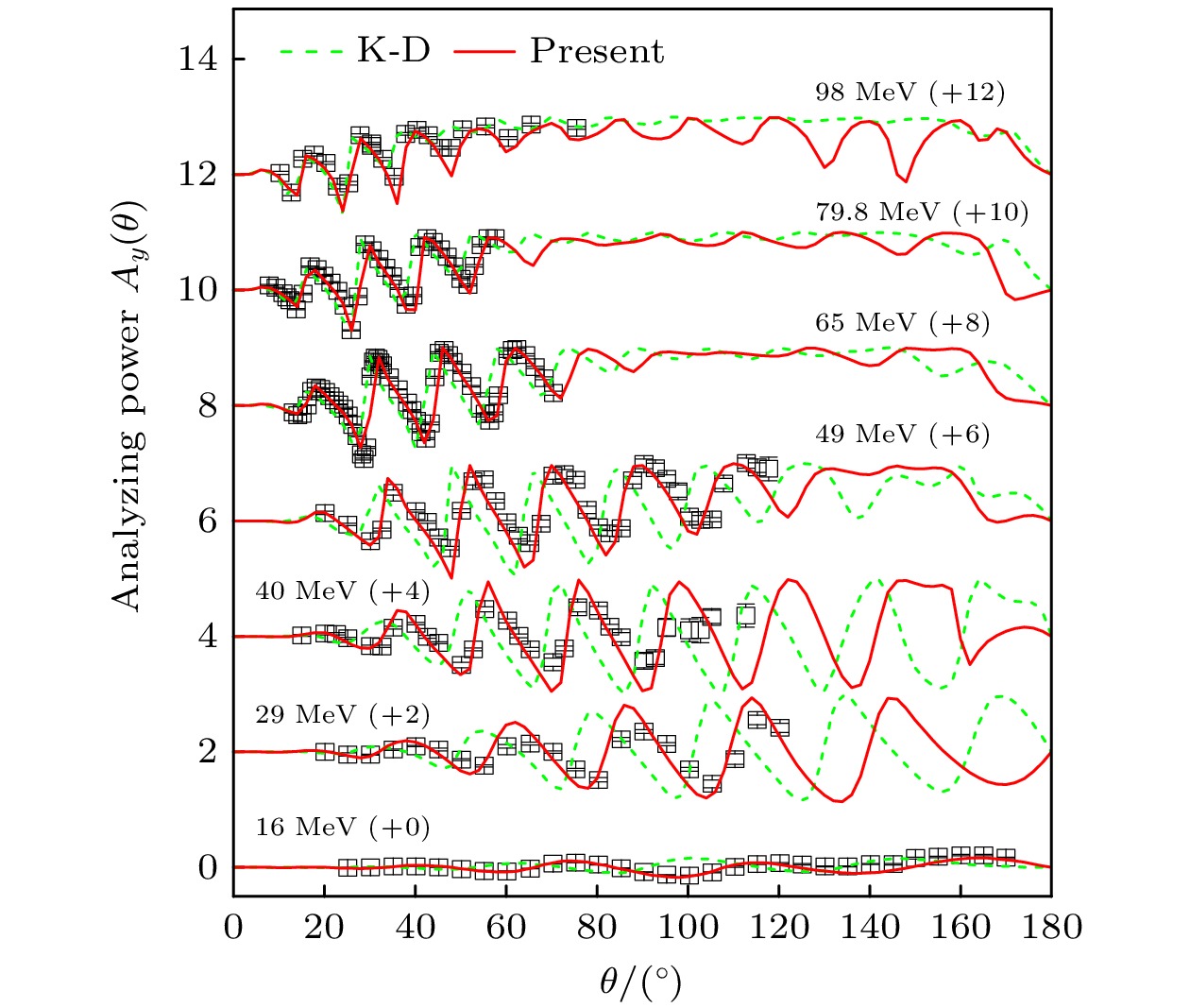
$ ^{208} {\rm{Pb}}$ 的中子弹性散射角分布和分析本领的计算情况如图4和图5所示. 我们的计算结果较好地描述了实验数据, 对实验数据的描述质量优于K-D光学势.本文对
$ ^{208} {\rm{Pb}}$ 的质子弹性散射分析本领的计算情况如图6和图7所示. 我们的计算结果与实验数据符合得很好, 对实验数据的描述质量明显优于K-D光学势给出的结果.如图8所示, 由于描述中子和质子两种核子同位旋态的光学势之间的差异可以由同位旋矢量项来确定, 因此本文实现了对(p, n)准弹性散射角分布数据的合理描述.
-
本文通过引入同位旋矢量项合理地考虑了同位旋依赖性, 使得光学势在形式上与Lane方程自洽, 区别于K-D光学势在计算中子和质子诱发核反应数据时需要采用两套参数, 本文的光学势实现了采用同一套参数计算两种核子入射时的核反应数据. 利用所得到的Lane自洽的色散光学模型及其光学势, 高质量地实现了对
$ ^{208} {\rm{Pb}}$ 包括中子总截面、弹性散射角分布、分析本领以及(p, n)准弹性散射角分布在内的散射数据的描述.
208Pb的Lane自洽色散光学势
Research on Lane-consistent dispersive optical-model potential for 208Pb
-
摘要:
采用色散光学模型成功构建了球形核208Pb的Lane自洽色散光学势, 采用同一套势参数同时对208Pb的两种核子(中子和质子)弹性散射数据进行了良好的描述, 高质量地计算了包括中子总截面、核子弹性散射角分布、分析本领以及(p, n)准弹性散射角分布在内的相关核子散射数据, 理论计算结果与实验数据具有很好的一致性.
Abstract:Lead is an important alloy material and nuclear fuel component. Lead-based eutectic alloys serve as important coolants and have been extensively utilized in the construction of lead-cooled fast reactor, such as the European lead-cooled System (ELSY) and the China lead-based Research reactor (CLEAR-I). These materials also play a significant role in research related to Generation-IV reactors. The study and calculation of lead nuclear data have important theoretical value and application prospects. 208Pb is the most stable and abundant isotope in lead nuclei, and high-quality description of 208Pb nuclear scattering data is important in achieving accurate theoretical calculations of nuclear reaction cross-sections in lead-based nuclear systems Based on the dispersive optical model, the nucleon scattering on 208Pb is described through the implementation of a dispersive optical potential in this work. The dispersive optical model potential is defined as energy-dependent real potential and imaginary potential. The dispersive contribution corresponding to the real potential is calculated analytically from the corresponding imaginary potential by using a dispersion relation, and the isospin dependence is reasonably considered by introducing an isovector component (i.e. Lane term) into the real part and the imaginary part of potential: the depth constant of the real Hartree-Fock potential $ V_{\rm{HF}}$ and the depth constant of surface imaginary potential $ W_{\rm{s}}$. Unlike K-D potential, which requires two different sets of parameters to describe neutron and proton induced scattering data. This optical potential uses the same set of parameters to simultaneously describe nucleon-nucleus scattering data. The derived potential in this work shows a very good description of nucleon-nucleus scattering data on 208Pb with energies up to 200 MeV. The calculated neutron total cross sections, neutron and proton elastic scattering angular distributions, and neutron and proton elastic analyzing powers are shown to be in good agreement with experimental data. Additionally, the difference in potential between neutrons and protons induced is described by an isovector term, achieving the reasonable and good prediction of quasielastic (p, n) scattering data.
-
Key words:
- optical model /
- dispersive optical model potential /
- nucleon elastic scattering .
-
-
图 1 中子和质子入射208Pb时的实部势
$V_{\rm{HF}}$ 和表面虚部势$W_{\rm{s}}$ 深度随能量的变化情况Figure 1. Energy dependence of the real potential
$V_{\rm{HF}}$ and the surface imaginary potential$W_{\rm{s}}$ depths for neutron and proton induced reactions on$^{208}{\rm{Pb}}$ .
图 2
$^{208}{\rm{Pb}}$ 的中子总截面计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较Figure 2. Comparison of the calculated neutron total cross section for
$^{208}{\rm{Pb}}$ with experimental data and those by K-D potential.
图 3
$^{208}{\rm{Pb}}$ 的中子弹性散射截面计算结果与K-D中子光学势给出的计算结果以及天然铅的相关实验数据的比较Figure 3. Comparison of the calculated neutron elastic cross section for
$^{208}{\rm{Pb}}$ with experimental data and those by K-D potential.
图 4
$^{208}{\rm{Pb}}$ 的中子弹性散射角分布计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较Figure 4. Calculated neutron elastic scattering angular distributions for
$^{208}{\rm{Pb}}$ , compared with experimental data and those by K-D potential.
图 5
$^{208}{\rm{Pb}}$ 的中子弹性散射分析本领计算结果与K-D中子光学势给出的计算结果以及相关实验数据的比较Figure 5. Calculated neutron elastic scattering analyzing powers for
$^{208}{\rm{Pb}}$ , compared with experimental data and those by K-D potential.
图 6
$^{208}{\rm{Pb}}$ 的质子弹性散射角分布计算结果与K-D质子光学势给出的计算结果以及相关实验数据的比较Figure 6. Calculated proton elastic scattering angular distributions for
$^{208}{\rm{Pb}}$ , compared with experimental data and those by K-D potential.
图 7
$^{208}{\rm{Pb}}$ 的质子弹性散射分析本领计算结果与K-D质子光学势给出的计算结果以及相关实验数据的比较Figure 7. Calculated proton elastic scattering analyzing powers for
$^{208}{\rm{Pb}}$ , compared with experimental data and those by K-D potential.
图 8
$^{208}{\rm{Pb}}$ 的(p, n)准弹性散射角分布计算结果与相关实验数据的比较Figure 8. Comparison of (p, n) angular distributions of the quasielastic (p, n) scattering on
$^{208}{\rm{Pb}}$ with experimental data.表 1
$^{208}{\rm{Pb}}$ 的色散光学模型势参数Table 1. Dispersive optical-model potential parameters for nucleon induced reactions on
$^{208}{\rm{Pb}}$ .$V_{{\mathrm{HF}}}$ Volume Surface Spin-orbit Coulomb Potential $V_{0}$ = 52.4 MeV$A_{\rm{v}}$ = 12.47 MeV$W_{0}$ = 15.82 MeV$ V_{\rm{SO}} $ = 8.1 MeV$C_{\rm{Coul}}$ = 1.0 MeV$\lambda_{\rm{HF}}$ = 0.009 MeV–1$B_{\rm{v}}$ = 81.67 MeV$B_{\rm{s}}$ = 13.31 MeV$\lambda_{\rm{so}}$ = 0.005 MeV–1$C_{\rm{viso}}$ = 23.85 MeV$E_{\rm{a}}$ = 56 MeV$C_{\rm{s}}$ = 0.02 MeV–1$W_{\rm{SO}}$ = –3.1 MeV$C_{\rm{wiso}}$ = 14.98 MeV$B_{\rm{so}}$ = 160 MeVGeometry $r_{\rm{HF}}$ = 1.24 fm$r_{\rm{v}}$ = 1.25 fm$r_{\rm{s}}$ = 1.18 fm$r_{\rm{so}}$ = 1.08 fm$r_{\rm{c}}$ = 1.03 fm$a_{\rm{HF}}$ = 0.63 fm$a_{\rm{v}}$ = 0.69 fm$a_{\rm{s}}$ = 0.63 fm$a_{\rm{so}}$ = 0.59 fm$a_{\rm{c}}$ = 0.61 fm
下载: 导出CSV
-
[1] 吴宜灿, 柏云清, 宋勇, 黄群英, 刘超, 王明煌, 周涛, 金鸣, 吴庆生, 汪建业, 蒋洁琼, 胡丽琴, 李春京, 高胜, 李亚洲, 龙鹏程, 赵柱民, 郁杰, FDS团队 2014 核科学与工程 34 201 Wu Y C, Bai Y Q, Song Y, Huang Q Y, Liu C, Wang M H, Zhou T, Jin M, Wu Q S, Wang J Y, Jang J Q, Hu L Q, Li C J, Gao S, Li Y Z, Long P C, Zhao Z M, Yu J, FDS Team 2014 Nucl. Sci. and Eng. 34 201 [2] Nifenecker H, David S, Loiseaux J M, Meplan O 2001 Nucl. Instrum. Methods A 463 505 doi: 10.1016/S0168-9002(01)00167-X [3] Gudowski W 2000 Nucl. Phys. A 663-664 169c doi: 10.1016/S0375-9474(99)00585-0 [4] Qaim S M 2001 Radiochim. Acta 89 189 doi: 10.1524/ract.2001.89.4-5.189 [5] Stankovskiy A, Malambu E, Eynde G V D, Diez C J 2014 Nucl. Data Sheets 118 513 doi: 10.1016/j.nds.2014.04.121 [6] Yang W S, Khalil H S 1999 Trans. Am. Nucl. Soc. 81 273 [7] Martin M J 2007 Nucl. Data Sheets 108 1583 doi: 10.1016/j.nds.2007.07.001 [8] Koning A J, Delaroche J P 2003 Nucl. Phys. A 713 231 doi: 10.1016/S0375-9474(02)01321-0 [9] Soukhovitskiĩ E Sh, Capote R, Quesada J M, Chiba S 2005 Phys. Rev. C 72 024604 doi: 10.1103/PhysRevC.72.024604 [10] Capote R, Chiba S, Soukhovitskiĩ E Sh, Quesada J M, Bauge E 2008 J. Nucl. Sci. Tech. 45 333 [11] Zhao X N, Sun W L, Soukhovitskiĩ E Sh, Martyanov D S, Quesada J M, Capote R 2021 J. Phys. G: Nucl. Part. Phys. 48 075101 doi: 10.1088/1361-6471/abe280 [12] Zhao X N, Du W Q, Capote R, Soukhovitskiĩ E Sh 2023 Phys. Rev. C 107 064606 doi: 10.1103/PhysRevC.107.064606 [13] Mahaux C, Sartor R 1986 Phys. Rev. Lett. 57 3015 doi: 10.1103/PhysRevLett.57.3015 [14] 赵岫鸟, 杜文青 2023 物理学报 72 222401 doi: 10.7498/aps.72.20231054 Zhao X N, Du W Q 2023 Acta Phys. Sin. 72 222401 doi: 10.7498/aps.72.20231054 [15] Quesada J M, Capote R, Soukhovitskiĩ E Sh, Chiba S 2007 Phys. Rev. C 76 057602 doi: 10.1103/PhysRevC.76.057602 [16] Lipperheide R 1967 Z. Phys. 202 58 doi: 10.1007/BF01331198 [17] Mahaux C, Sartor R 1991 Nucl. Phys. A 528 253 doi: 10.1016/0375-9474(91)90090-S [18] Brown G E, Rho M 1981 Nucl. Phys. A 372 397 doi: 10.1016/0375-9474(81)90043-9 [19] Delaroche J P, Wang Y, Rapaport J 1989 Phys. Rev. C 39 391 [20] Quesada J M, Capote R, Molina A, Lozano M, Raynal J 2003 Phys. Rev. C 67 067601 doi: 10.1103/PhysRevC.67.067601 [21] Chiba S, Iwamoto O, Yamanouti Y, Sugimoto M, Mizumoto M, Hasegawa K, Soukhovitskiĩ E Sh, Porodzinskiĩ Y V, Watanabe Y 1997 Nucl. Phys. A 624 305 doi: 10.1016/S0375-9474(97)00474-0 [22] Lane A M 1962 Phys. Rev. Lett. 8 171 doi: 10.1103/PhysRevLett.8.171 [23] Lane A M 1962 Nucl. Phys. 35 676 doi: 10.1016/0029-5582(62)90153-0 [24] EXchange FORmat database (EXFOR) is maintained by the Network of Nuclear Reaction Data Centers (see www-nds.iaea.org/nrdc/). Data available online (e.g., at www-nds.iaea.org/exfor/ [25] Capote R, Herman M, Obložinský P, Young P G, Goriely S, Belgya T, Ignatyuk A V, Koning A J, Hilaire S, Plujko V A, Avrigeanu M, Bersillon O, Chadwick M B, Fukahori T, Ge Z G, Han Y L, Kailas S, Kopecky J, Maslov V M, Reffo G, Sin M, Soukhovitskiĩ E Sh, Talou P 2009 Nucl. Data Sheets 110 3107 -
计量
- 文章访问数: 92
- HTML全文浏览数: 92
- PDF下载数: 0
- 施引文献: 0