-
量子色动力学(quantum chromodynamics, QCD)认为在高温高密的条件下, 夸克和胶子解禁闭可形成夸克胶子等离子体(quark-gluon plasma, QGP)[1-3]. 近年来, 在高能重离子碰撞实验中已发现QGP的产生信号[4-6]. 在对QGP物质特性的各项研究中, QCD相结构和临界点的探索是研究的重要热点之一[7-9]. QCD相图是研究相结构的重要工具. 以往的研究主要聚焦于低化学势区域[9,10], 但是最近的BES-II实验结果表明在低化学势范围
$ \mu_{\text{B}} < 450 \text{ MeV} $ 中不存在相变的临界点[11]. 因此, 研究中高化学势区域中的QCD相结构具有重要意义.在之前的工作中[12], 我们在中高化学势区域分别研究了包含
$ {\mathrm{u, d}} $ 夸克的小尺度QGP热滴的边界效应和强子相中π介子受到的两体自相似结构的影响, 以及在两种影响下的相变过程. 在中低能碰撞中, 重子数密度不高, 当转移的横动量大小涨落到低于QCD的Λ尺度时, 碰撞中不足以产生QGP, 只能产生强子物质. 但是当碰撞中存在转移横动量涨落至大于QCD的Λ尺度的区域[13], 则可以产生小尺度的QGP热滴(droplet)[14-16]. 在这些小尺度的QGP热滴的边界处, 一边是QGP, 一边是强子物质, 两边物质的密度不一样大, 由此产生了QGP热滴边界处的表面张力[17,18]. 因此, 需考虑边界的弯曲和表面张力的影响. 计算结果表明边界效应影响了小尺度QGP热滴的热力学性质, 使得QGP的能量和压强减小. 而强子相中, 集体流[19,20]导致强子和相邻的π介子产生共同运动, 继而形成了共振[21,22]. 我们提出了两体分形模型(two-body fractal model, TBFM)来研究由集体流、强相互作用和量子关联引起的π介子的自相似结构. 通过计算发现π介子在自相似结构影响下能量密度和压强增大. 在边界效应和自相似结构的共同影响下, QGP-强子相的相变温度相对于无影响时升高, 说明了边界效应与自相似结构影响是不可忽略的. 在前期的工作中, 我们忽略了$ \text{s} $ 夸克物质对相变的影响. 但是$ \text{s} $ 夸克物质是QGP产生的重要信号[23-25], 是高能碰撞过程中的特殊产物, 研究其特性对QGP和强子相之间的相变过程的影响是很重要的.之前的研究认为在高重子数密度区域, QGP可以产生小尺度的
$ \text{s} $ 夸克(strange quark, 也称奇异夸克)物质, 叫作奇异滴[25-27]. 小尺度的奇异滴可以看成是包含$ \text{s} $ 夸克的QGP热滴, 由于$ \text{s} $ 夸克的质量远比$ \text{u, d} $ 夸克大, 导致热滴的边界效应更加明显, 因此考虑包含$ \text{s} $ 夸克的小尺度QGP热滴的边界效应对相变的影响是很重要的. 经过QGP-强子相相变后, 冷却后形成的强子物质中含有包含$ \text{s} $ 夸克的强子(以$ \text{K} $ 介子为主), 且与轻介子相比, 奇异强子质量更大, 这会导致强子相不同的物理性质. 由于集体流的影响, 奇异强子与相邻π介子产生共同运动, 可能形成共振, 结合强相互作用、量子效应的共同影响, 可能形成$ \text{K} $ -π, π-π等两体自相似结构. 本文将研究这些自相似结构对强子相性质的影响, 继而分析自相似结构对相变的影响.本文将考虑两种效应对中高化学势区域的QGP-强子相变的影响: 其一为QGP热滴的表面张力和弯曲效应; 其二为强子气体中介子的自相似结构. 使用MIT袋模型, 结合多级反射展开(multiple reflection expansion, MRE)的方法来描述包含
$ \text{s, u, d} $ 夸克及其反夸克的小尺度的QGP热滴边界的表面张力和弯曲[28]. 还将考虑$ \text{u, d} $ 夸克的QGP热滴在边界效应影响下的热力学性质, 并与本文的计算结果进行比较. 对于强子气体, 将利用两体分形模型来描述临界温度附近$ \text{K} $ 介子受到的两体自相似结构影响. 最后, 计算两种效应影响下的QGP-强子相变. -
高温或高重子数密度条件下会产生大量解禁闭的夸克和胶子, 形成大尺度的QGP[29]. 在中能碰撞中, 温度不足够高, 重子数密度不足够大[30-32]. 当横动量处在低于QCD的Λ尺度时, 不能产生自由夸克和胶子, 系统中只有强子物质[33,34]. 只有在横动量涨落到高于QCD的Λ尺度区域中时可以产生小尺度的QGP-QGP热滴[14,15]. 而QGP中可以产生
$ \text{s} $ 夸克, 所以小尺度的QGP物质可以看成是一种包含$ \text{s, u, d} $ 夸克及其反夸克的小尺度QGP热滴. 且小尺度QGP热滴存在弯曲, 弯曲的边缘对QGP性质可能造成影响. 而且在热滴边界处, 一边是强子物质, 另一边是QGP. 不一样的物质 密度导致了边界的表面张力. 因此, 本文将详细 分析小尺度的边界效应对QGP特性的影响. MIT袋模型[35]是一种描述袋中夸克和胶子的热力学性质的模型. MRE方法[17,28,36]是一种描述有弯曲边界的系统的方法, 用来研究弯曲边界的影响. 在Madsen的工作中[37,38], MRE方法研究了由$ \text{s} $ 夸克引起奇异滴的有限尺度效应, 同时忽略了$ \text{ u, d} $ 轻夸克的质量. 本文也使用MRE方法来研究包含$ \text{s, u, d} $ 夸克及其反夸克的小尺度QGP热滴的边界弯曲和表面张力效应, 并且将三种夸克的质量考虑其中.QGP热滴中包含了夸克和胶子, 我们将这个热滴当作一个有源场
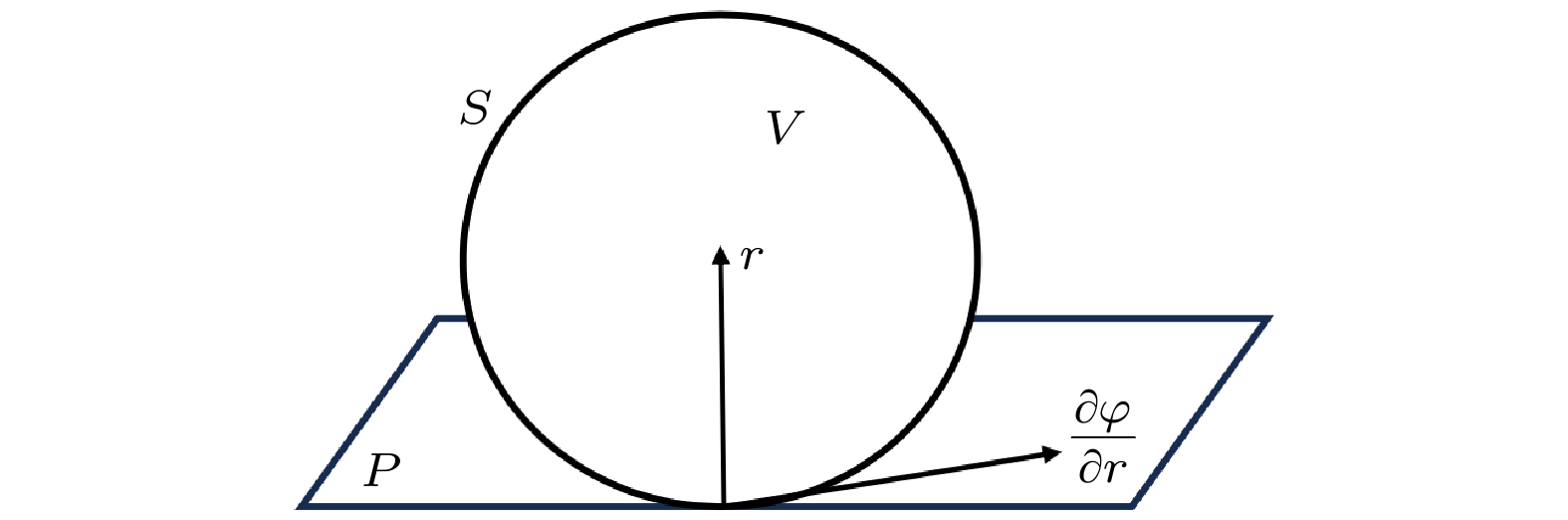
$ {\varphi} $ , QGP热滴的半径指向球心. 势场分布满足方程$ \Delta \varphi+E \varphi = 0 $ [39]. 如图1所示,$ {\partial \varphi }/{\partial r} $ 是表面张力, 方向沿着表面一点的切面P.热力学极限下, 在动量k—
$ k + \text{d}k $ 范围内的微观态数目为当考虑小尺度QGP热滴的边界效应时, 对微观状态数目的修正可以通过对格林函数进行多级反射展开得到. 不含时格林函数的多级反射展开形式为
其中,
$ \text{G}^{(0)} $ 表示自由场, 满足$ \left(\text{i} \gamma^{\mu} \partial_{\mu}-m\right) \text{G}^{(0)}\left(x- x^{\prime}\right)= \delta\left(x-x^{\prime}\right) $ ;$ \mit{\Omega} $ 表示QGP热滴内部的空间;$ K(\alpha) $ 是沿着表面$ \partial \mit{\Omega} $ 进行积分的反射核(reflection kernel), 用来计算不同半径对应边界的弯曲效应的修正, 形式为$ ({1}/{R_1} + {1}/{R_2})^{n}, \, n = 0, 1, \cdots $ , 其中$ R_1 $ 和$ R_2 $ 是弯曲表面对应的主要半径(principal radii),$ R_{1} = R_{2} =R $ ;$ {\boldsymbol{r}} $ 和$ {\boldsymbol{r}}^{\prime} $ 表示在$ \mit{\Omega} $ 中的空间矢量;$ {\boldsymbol{\alpha}} $ 和$ {\boldsymbol{\beta}} $ 是$ \partial \mit{\Omega} $ 表面上的空间矢量.根据态密度
$ \rho(\omega) $ 和格林函数之间的关系[28]可以得到态密度关于
$ {1}/{(kR)} $ 的多级反射展开形式:(4)式中的第二项对应了
$ n = 0 $ 阶中边界弯曲效应的修正, 其中QGP热滴的表面积$ A = 4\pi R^{2} $ 可通过对(2)式中第二项反射核$ K(\alpha) $ 的积分得到, 其中R是QGP热滴的半径; (4)式中的第三项来自$ n = 1 $ 阶下的边界弯曲, C表示通过表面积分$ C = \displaystyle\oint_{\partial \mit{\Omega}} \text{d}^{2} \sigma ({1}/{R_1(\sigma)} + {1}/{R_2(\sigma)}) = 8\pi R $ 得到的弯曲曲率. 考虑格林函数(2)式中第二项的$ n = 0, 1 $ 阶中的边界弯曲效应, 可以得到$ \text{u, d} $ 夸克的$ f_{{\mathrm{S}}, \text{q}}, \, f_{{\mathrm{C}}, \text{q}} $ 和$ \text{s} $ 夸克的$ f_{{\mathrm{S}}, \text{s}}, \, f_{{\mathrm{C}}, \text{s}} $ :其中,
$ m_{\text{q}} $ 和$ p_{\text{q}} $ 是$ \text{u, d} $ 夸克及其反夸克的质量和动量;$ m_{\text{s}} $ 和$ p_{\text{s}} $ 是$ \text{s} $ 夸克及其反夸克的质量和动量. 考虑QGP热滴的表面张力和弯曲效应, 将(5)—(8)式代入到态密度(4)式可得$ \text{u, d}\;(q={\mathrm{u, d}}) $ 夸克及其反夸克$ \bar{\text{u}}, \, \bar{\text{d}} \;(\bar{{{{q}}}}=\bar{\text{u}}, \, \bar{\text{d}}) $ , 以及$ \text{s}, \, \bar{\text{s}} $ 夸克的态密度分别为式中,
$ p_{\text{q}} $ 是$ \text{u, d} $ 夸克、反夸克的动量;$ g_{\text{q}}, \, g_{\text{s}} $ 分别为$ \text{u}, \, \text{d}, \,\bar{\text{u}}, \, \bar{\text{d}} $ 夸克和$ \text{s}, \, \bar{\text{s}} $ 夸克的简并度. 由于胶子质量为零, 考虑胶子边界效应时, 有$ f_{{\mathrm{S}}} = 0 $ ,$ f_{{\mathrm{C}}} = -{1}/{(6\pi^{2})} $ , 则胶子的态密度为其中
$ p_{\text{g}} $ 为胶子动量,$ g_{\text{g}} $ 为胶子的简并度.利用边界效应修正的态密度, QGP热滴的压强可以写成
其中,
$ \varepsilon_{\text{q}(\bar{\text{q}})}, \, \varepsilon_{\text{s}(\bar{\text{s}})}, \, \varepsilon_{\text{g}} $ 分别为$ \text{q}, \, \bar{\text{q}} $ 夸克、$ \text{s}, \, \bar{\text{s}} $ 夸克和胶子的能量,$ \varepsilon_{\text{q}} = \varepsilon_{\bar{\text{q}}} = \sqrt{m_{\text{q}}^{2} + p_{\text{q}}^{2}} $ ,$ \varepsilon_{\text{s}} = \varepsilon_{\bar{\text{s}}} = \sqrt{m_{\text{s}}^{2} + p_{\text{s}}^{2}} $ ,$ \varepsilon_{\text{g}} = p_{\text{g}} $ ;$ f_{\text{q}}, \, f_{\bar{\text{q}}}, \, f_{\text{s}}, \, f_{\bar{\text{s}}} $ 表示$ \text{q}, \, \bar{\text{q}}, \, \text{s}, \, \bar{\text{s}} $ 夸克对应的费米分布,$ f_{\text{q}} = f_{\bar{\text{q}}} $ ,$ f_{\text{s}} = f_{\bar{\text{s}}} $ ;$ f_{\text{g}} $ 为胶子对应的玻色分布. (12)式中的前五项分别对应$ \text{q}, \, \bar{\text{q}}, \, \text{s}, \, \bar{\text{s}} $ 四种夸克和胶子的压强,$ B(T, \mu) $ 表示与温度T, 化学势μ相关的袋压函数[40,41]. 为了与最近格点QCD的结果相对应[42,43], 将袋压函数写为其中
$ B_{0}^{1/4} = 224\; \text{MeV} $ .同时计算了在表面张力和边界弯曲影响下QGP热滴的能量密度和熵密度:
QGP热滴中考虑存在
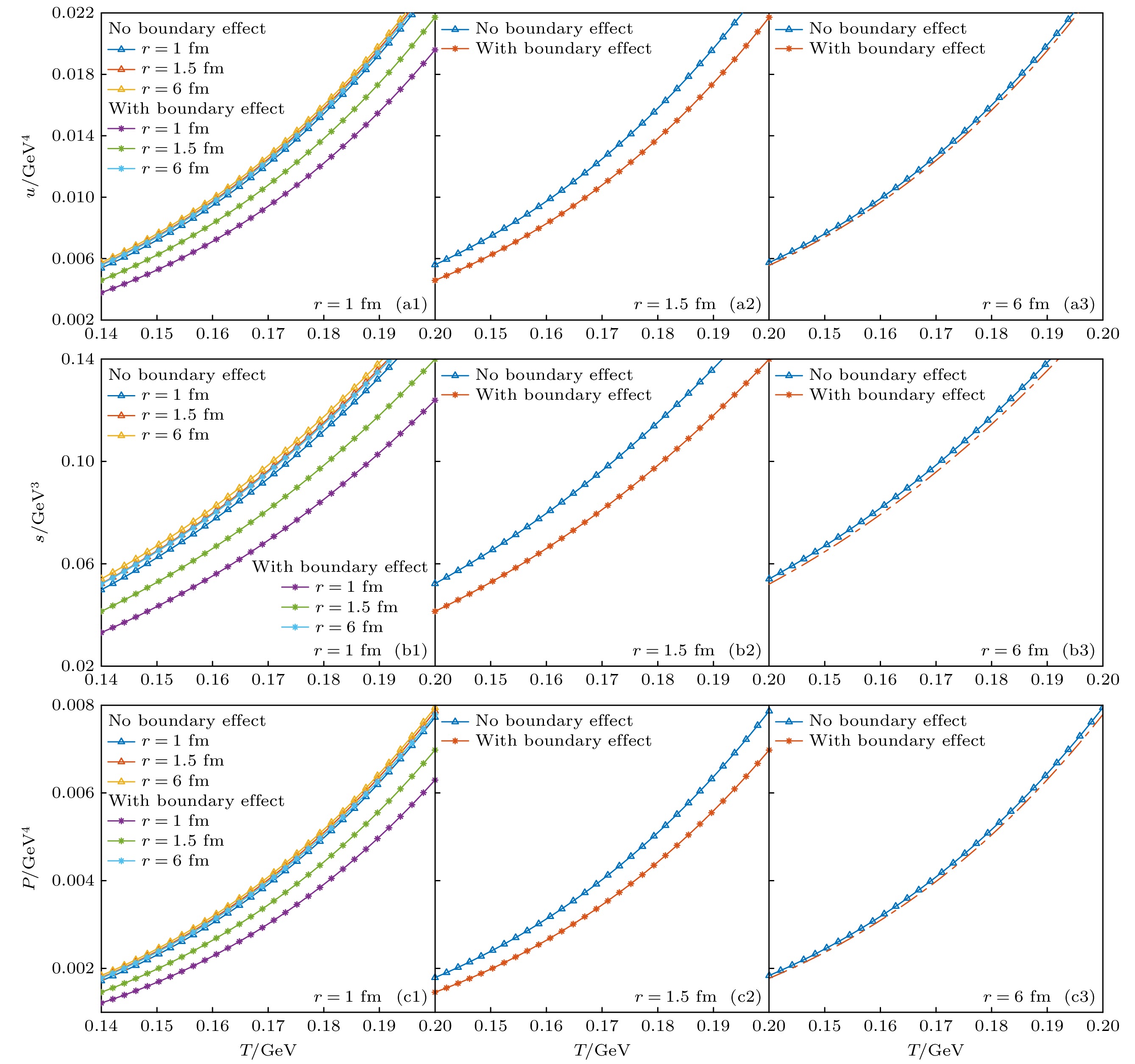
$ \text{s} $ ,$ \text{u} $ ,$ \text{d} $ 三种夸克与对应的反夸克以及胶子. 图2所示为考虑边界效应和不考虑边界效应两种情况下, QGP热滴半径分别为$ r = 1, \, 1.5, \, 6\text{ fm} $ 的能量密度、熵密度、压强与温度之间的变化关系. 从图2(a1), (b1), (c1)可以看出, 能量密度、熵密度和压强都随着温度增大而增大. 为了便于分析, 比较了考虑边界效应与不考虑边界效应两种情况下,$ r = 1.5 \text{ fm} $ 的QGP热滴对应的能量密度、熵密度和压强. 如图2(a2), (b2), (c2)所示, 可以发现, 在$ r = 1.5 \text{ fm} $ 情况下, 考虑边界效应的三种热力学量数值都比不考虑边界效应的结果要小, 说明了边界效应使得$ r = 1.5 \text{ fm} $ 的QGP热滴能量、熵和压强变小. 另外也比较了$ r = 6 \text{ fm} $ 的QGP热滴对应的能量密度、熵密度和压强, 如图2(a3), (b3), (c3)所示, 无论是否考虑边界效应, 三个物理量都近似相等, 说明边界效应的强弱和QGP热滴的大小有关, 即热滴越大, 边界效应越弱.如图3所示, 以QGP热滴
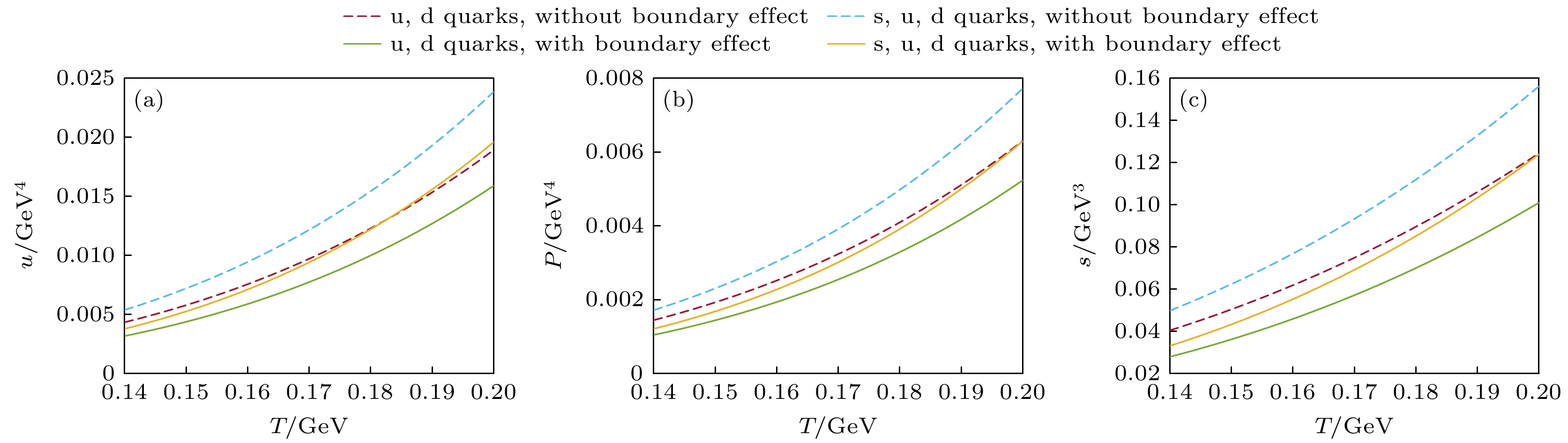
$ r = 1 \text{ fm} $ 为例, 将其热力学量与考虑$ \text{u} $ ,$ \text{d} $ 两种夸克及其反夸克的QGP热滴的热力学量进行比较. 通过分析发现, 不管QGP热滴有没有考虑$ \text{s} $ 夸克, 能量密度、熵密度和压强都随温度的升高而增大. 在比较包含$ \text{s} $ 夸克与不包含$ \text{s} $ 夸克的热力学量时, 从图3可以看出, 在不考虑边界效应时, 相同大小的QGP热滴情况下, 与不包含$ \text{s} $ 夸克的热滴相比, 包含$ \text{s} $ 夸克的热滴具有更大的能量密度、熵密度和压强. 这是因为热滴中多了$ \text{s} $ 夸克之后,$ \text{s} $ 夸克的质量比$ \text{u}, \, \text{d} $ 夸克的质量要大, 三种夸克和反夸克之间的相互作用更加紧密, 能量密度则随之增大, 这个变化趋势和奇异滴的特性是一致的. 当考虑边界效应对热滴的影响时, 发现包含$ \text{s} $ 夸克的热滴的热力学量降低的幅度比没有$ \text{s} $ 夸克的情况要大, 说明边界效应对包含$ \text{s} $ 夸克的热滴的影响更明显. 三种热力学量的降低幅度变大是由于热滴中考虑$ \text{s} $ 夸克之后, 热滴的边界效应比加入$ \text{s} $ 夸克之前内部作用力的影响更大. 虽然热滴中有$ \text{s, u, d} $ 夸克及其反夸克, 使得内部粒子之间的束缚更紧密. 但是$ \text{s} $ 夸克在热滴中时, 内部的夸克数量增多, 边界效应能对更多的粒子产生影响, 对热滴的束缚也更大, 所以边界效应的影响也更加明显. 内部相互作用和边界效应之间是相互抵消的两种效应, 通过计算可以得出, 包含$ \text{s} $ ,$ \text{u} $ ,$ \text{d} $ 三种夸克的QGP热滴的热力学量的降低幅度更大, 说明受边界效应的影响更大. 这种影响在中低能碰撞实验中研究小尺度QGP热滴时不可忽略. -
集体流在碰撞实验中被发现, 是一种重要的现象. 它描述的是碰撞中的粒子与周围粒子产生集体运动, 比如
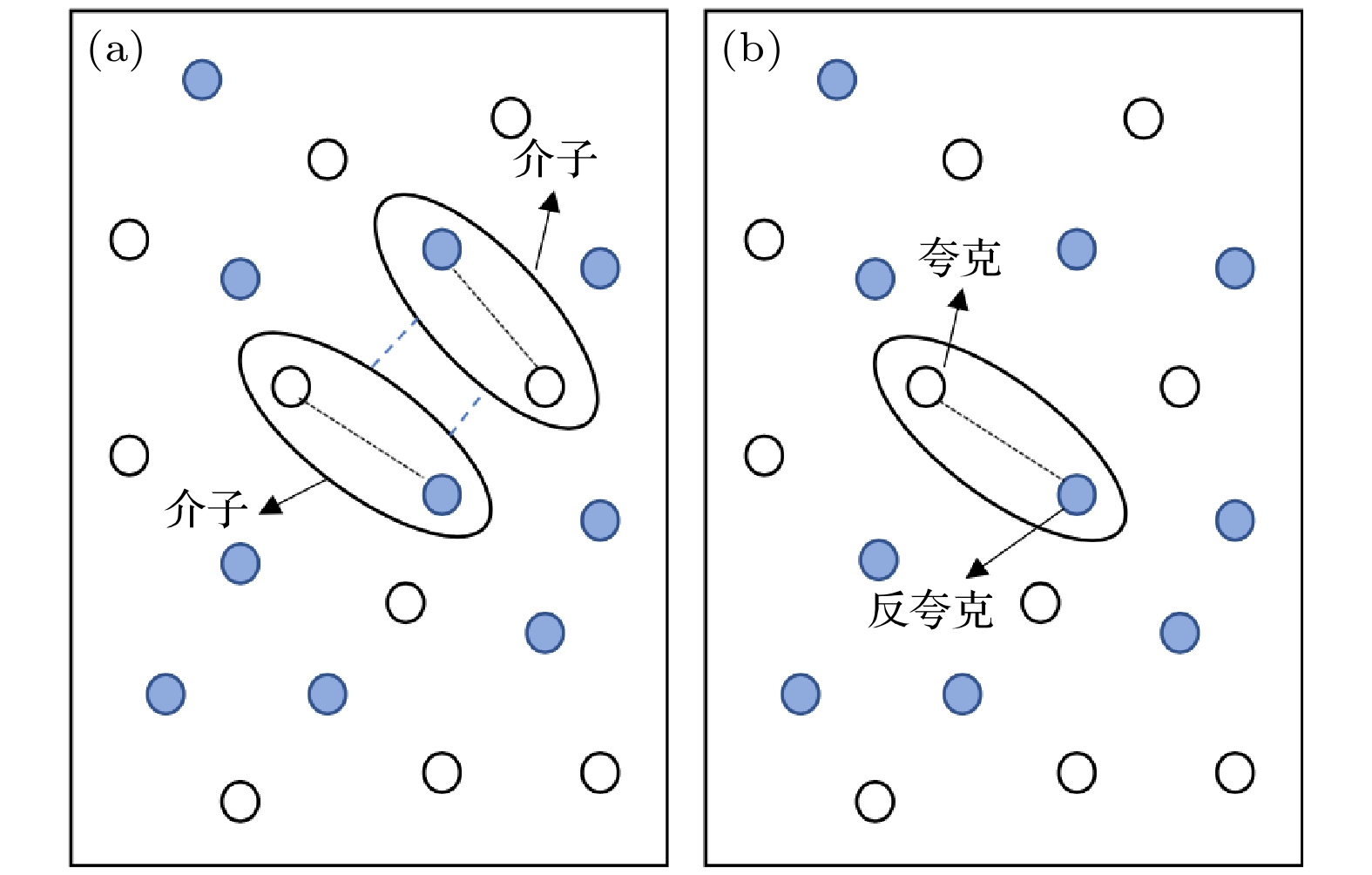
$ \text{K} $ 介子和周围的π介子的共同运动. 如果相邻介子具有相同的动量和频率,$ \text{K} $ 介子与相邻的π介子之间可以形成共振[44]. 其次, 在高能碰撞零化学势附近, 临界温度区域中π介子的粒子数密度为$ {N}/{V} = 0.5 \, \text{fm}^{-3} $ [45], 两个相邻的π介子的平均间距大概是$ ({V}/{N})^{1/3} \approx 1.3\, \text{fm} $ . 这种平均间距小于$ \text{K} $ 介子的热波长$ \lambda_{{\mathrm{T}}}={h}/{\sqrt{2 \pi m k T}} = 1.7031 \, \text{fm} $ [46]. 这说明相邻的π介子和$ \text{K} $ 介子间存在量子关联. 在中低能碰撞中更高的化学势和更大的重子数密度区域, 相邻的介子间的间距要小于零化学势区域的情况. 所以量子关联的效应会比在零化学势区域的情况要更强. 第三, 我们知道当夸克间距l小于$ 1 \, \text{fm} $ 时, 夸克之间存在强相互作用[47]. 因此, 当π介子的平均间距满足$ ({V}/{N})^{1/3} < 2 l $ , 说明$ \text{K} $ 介子和最近邻的π介子存在强相互作用. 综上所述,$ \text{K} $ 介子受到了共振、量子关联和相互作用的影响, 可以形成两体$ \text{K} $ -π的系统, 如图4(a)所示.和
$ \text{K} $ -π的两体系统类似, 单个$ \text{K} $ 介子也是一个两体的夸克-反夸克系统, 如图4(b)所示. 基于这种两体结构, 我们认为两夸克系统和两介子系统有自相似性(self-similarity), 可以使用分形理论来描述. 分形的概念由Mandelbort提出[48,49], 用来描述同一个系统中部分结构和整体之间的相似性. Tsallis统计在分形理论的影响下产生[50,51], 用来研究不同尺度下具有自相似分形结构的各类系统. 在之前的工作中, 我们使用在分形理论和Tsallis统计方法基础上提出的两体分形模型(TBFM), 很好地描述了重夸克偶素[52,53]以及π介子的两体自相似结构. 因此, 本文也将使用TBFM方法来描述$ \text{K} $ 介子和$ \text{K} $ -π束缚态, 将二者作为强子气体中的自相似性结构. -
首先从介子层次出发, 将
$ \text{K} $ 介子看成是由两个夸克组成的束缚态, 受到共振、量子关联和强相互作用的影响. 在这三种效应的影响下,$ \text{K} $ 介子与周围的π介子形成了自相似结构, 并受其影响. 由此, 引入修正因子$ q_{1} $ 来表示自相似结构对$ \text{K} $ 介子的影响. 静止参考系中,$ \text{K} $ 介子的概率是其中,
$ \beta = 1/T $ 为温度的倒数,$ \psi_{0} $ 是$ \text{K} $ 介子($ \text{s}\bar{\text{u}} $ 或者$ \text{s}\bar{\text{d}} $ 基态)的波函数(后面介绍以$ \text{s}\bar{\text{u}} $ 为例),$ \psi_{i} $ 表示$ \text{s}\bar{\text{u}} $ 束缚系统处在不同本征态的波函数.$ \hat{H} $ 为$ \text{s}\bar{\text{u}} $ 束缚态的哈密顿量,$ \sqrt{m_{\text{s} (\bar{\text{u}})}^2 + {\boldsymbol{p}}_{{\boldsymbol{1}}({\boldsymbol{2}})}^{2}} $ 是$ \text{s}, \, \bar{\text{u}} $ 夸克的动能,$ m_{\text{s}} = 250\text{ MeV}, m_{\bar{\text{u}}} = 55\text{ MeV} $ 分别是$ \text{s}, \, \bar{\text{u}} $ 夸克的质量.$ \hat{V}(r) $ 为夸克之间的相互作用势. 本文使用的作用势形式来自于求解两体狄拉克方程(two body Dirac equation, TBDE)的工作[54], 形式为其中, 参数
$ \varLambda_{1} = 0.4218 \text{ GeV} $ ,$ K_{1} = 4.198 $ ,$ B_{1} = 0.05081 $ ,$ \text{e} $ 是自然常数.(15)式的分母为配分函数, 表示
$ \text{s}\bar{\text{u}} $ 系统处于所有微观状态的概率之和. 考虑到$ \text{s}\bar{\text{u}} $ 系统的束缚态能级间隔小, 能量近乎连续, 为了计算方便, 便将其进行积分, 则配分函数可写为(18)式中, V是
$ \text{K} $ 介子的运动空间, 在静止系中由于$ \text{K} $ 介子是静止的, 其运动空间可看成在$ \text{K} $ 介子附近有相对运动的π介子的空间大小,$ V = ({4}/{3})\pi r_{0}^{3} $ ,$ r_{0} $ 为强子气体的半径. 取$ r_{\text{min}} $ 为夸克间距的下限,$ r_{\text{max}} $ 表示为夸克间距的上限, 取为强子气体的半径$ r_{\text{max}} = r_{0} $ .前面根据分形理论分析了考虑自相似性结构的影响下
$ \text{K} $ 介子的伴随概率, 而熵也是研究各类系统物理性质的重要物理量. 由于Tsallis熵通常和伴随概率分布相关, 且满足熵极值原理[55-57], 所以在两体分形模型中, 本文计算$ \text{s}\bar{\text{u}} $ 束缚系统的Tsallis熵为以上考虑了介子层次中
$ \text{s}\bar{\text{u}} $ 束缚系统的伴随概率和熵, 下面在夸克层次中考虑受两体自相似性结构影响下的$ \text{s}\bar{\text{u}} $ 系统. 这里引入参数$ q_{{\mathrm{s}}} $ ,$ q_0 $ 用来描述来自内部夸克之间的强相互作用以及与外部周围的π介子形成的自相似结构对$ \text{s}\bar{\text{u}} $ 系统介子内部$ \text{s}, \, \bar{\text{u}} $ 两个夸克的影响.$ \text{s}\bar{\text{u}} $ 系统内部的$ \text{s}, \, \bar{\text{u}} $ 夸克的概率分布满足幂次(power-law)形式, 可以写成其中,
$ \hat{H}_{\text{s}, \bar{\text{u}}} $ 是$ \text{s}, \, \bar{\text{u}} $ 夸克的哈密顿量,$ \hat{H}_{\text{s}} = \sqrt{m_{\text{s}}^{2} + {\boldsymbol{p}}_{{\boldsymbol{1}}}^{2}}, \, \hat{H}_{\bar{\text{u}}}=\sqrt{m_{\bar{\text{u}}}^{2} + {\boldsymbol{p}}_{{\boldsymbol{2}}}^{2}} $ ;$ \phi_{\text{s}0} $ 和$ \phi_{\text{q}0} $ 为处在$ \text{K} $ 态时$ \text{s}, \, \bar{\text{u}} $ 夸克的波函数;$ \phi_{\text{s}j} $ 与$ \phi_{\text{q}j} $ 是$ \text{s}, \, \bar{\text{u}} $ 夸克处于不同$ \text{s}\bar{\text{u}} $ 束缚态下的波函数.夸克层次下,
$ \text{K} $ 介子的伴随概率可以看成内部两个夸克的伴随概率的乘积$ P_{2} = P_{{\mathrm{s}}} \cdot P_{\bar{{\mathrm{u}}}} $ . 根据非广延统计学中的赝相加性(pseudoadditivity)[50], 定义$ q_{2} $ , 满足其中, 两夸克的总动能为
$ \hat{H}_{{\mathrm{t}}} = \sqrt{m_{\text{s}}^{2} + {\boldsymbol{p}}_{{\boldsymbol{1}}}^{2} }+ \sqrt{m_{\bar{\text{u}}}^{2} + {\boldsymbol{p}}_{{\boldsymbol{2}}}^{2}} $ ,$ \phi_{j} $ 为$ \text{u}\bar{\text{d}} $ 两夸克束缚系统的波函数.所以,
$ \text{K} $ 介子的伴随概率可以写成其中,
$ \phi_{0} $ 为处在$ \text{K} $ 态能级的两夸克系统动能的波函数. (22)式中的分母为$ \text{s}\bar{\text{u}} $ 两个自由夸克的配分函数, 将$ \text{s}\bar{\text{u}} $ 两夸克系统所有可能的微观状态概率进行求和,$ V_{q} $ 为$ \text{s} $ ,$ \bar{\text{u}} $ 夸克的运动空间, 这里可以近似和$ \text{K} $ 介子的运动空间相等, 即$ V_q = V $ . 同时, 对应的Tsallis熵为在以上的分析中, 本文从介子、夸克两个层次出发分别分析了
$ \text{K} $ 介子受两体分形结构影响的概率和$ \text{s}\bar{\text{u}} $ 系统的熵. 在介子层次中,$ \text{K} $ 介子满足自相似性结构, 可通过自相似结构影响下的$ q_{1} $ 得到$ \text{K} $ 介子的概率(15)式和$ \text{s}\bar{\text{u}} $ 系统的熵(19)式. 在夸克层次中,$ \text{K} $ 介子内部的$ \text{s}, \, \bar{\text{u}} $ 夸克也满足自相似性, 其夸克的概率满足幂次形式, 所以$ \text{K} $ 介子的概率为两夸克的概率之积. 在夸克层次中, 本文通过引入伴随参数$ q_{2} $ 来计算$ \text{K} $ 介子的概率(22)式和$ \text{s}\bar{\text{u}} $ 系统的熵(24)式. 分形理论中, 在两个层次下推导出的$ \text{K} $ 介子的概率,$ \text{s}\bar{\text{u}} $ 系统的Tsallis熵相等, 即在不同碰撞能量下求解方程组(25)式可以得到 不同碰撞能量下
$ \text{K} $ 介子受到的两体自相似结构 的影响. 参数$ q_{1} $ 描述了在介子层次中自相似结构对$ \text{K} $ 介子的影响, 伴随参数$ q_{2} $ 则描述了内部夸克之 间的相互作用以及内部夸克受到的自相似性结构影响.为了分析修正参数
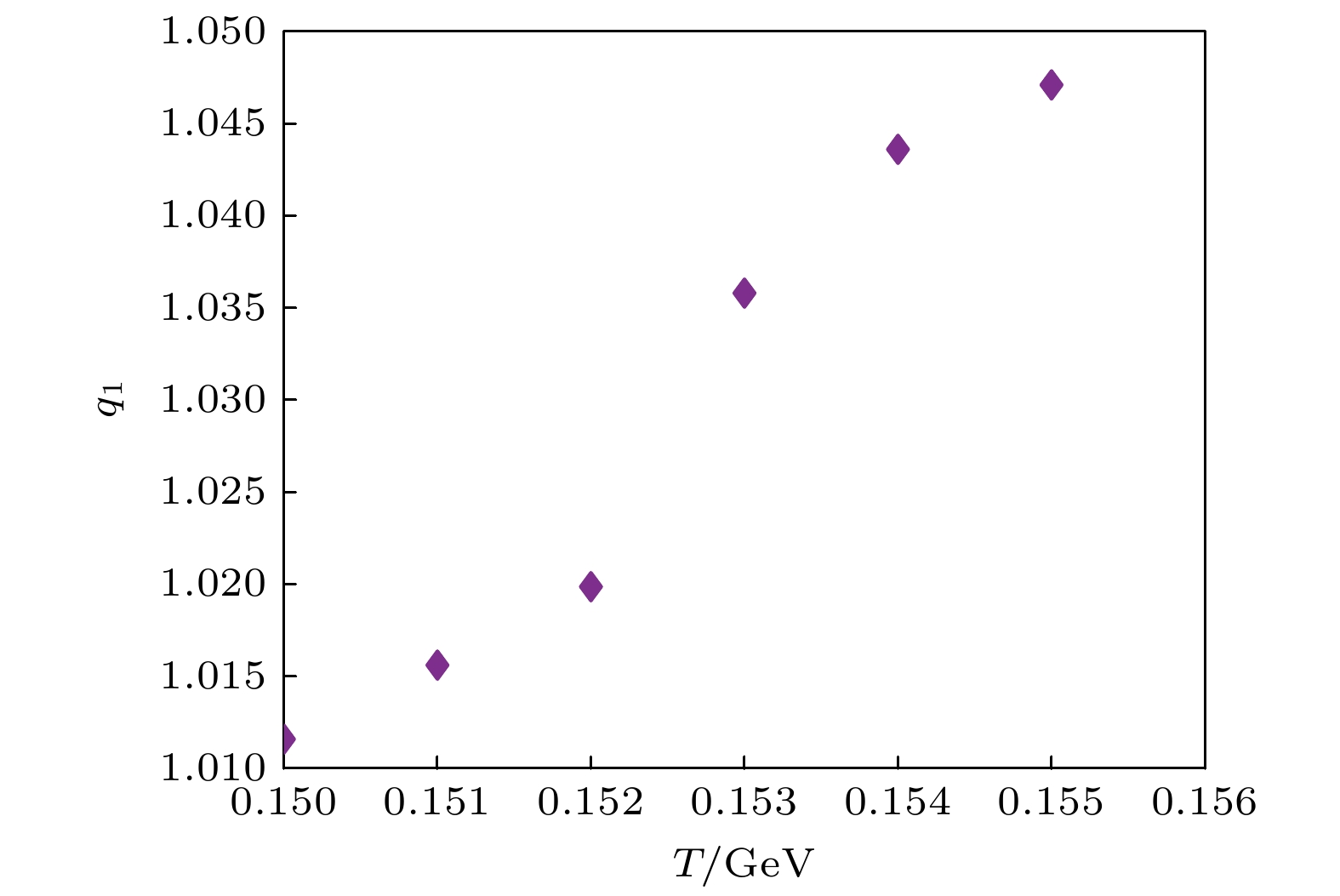
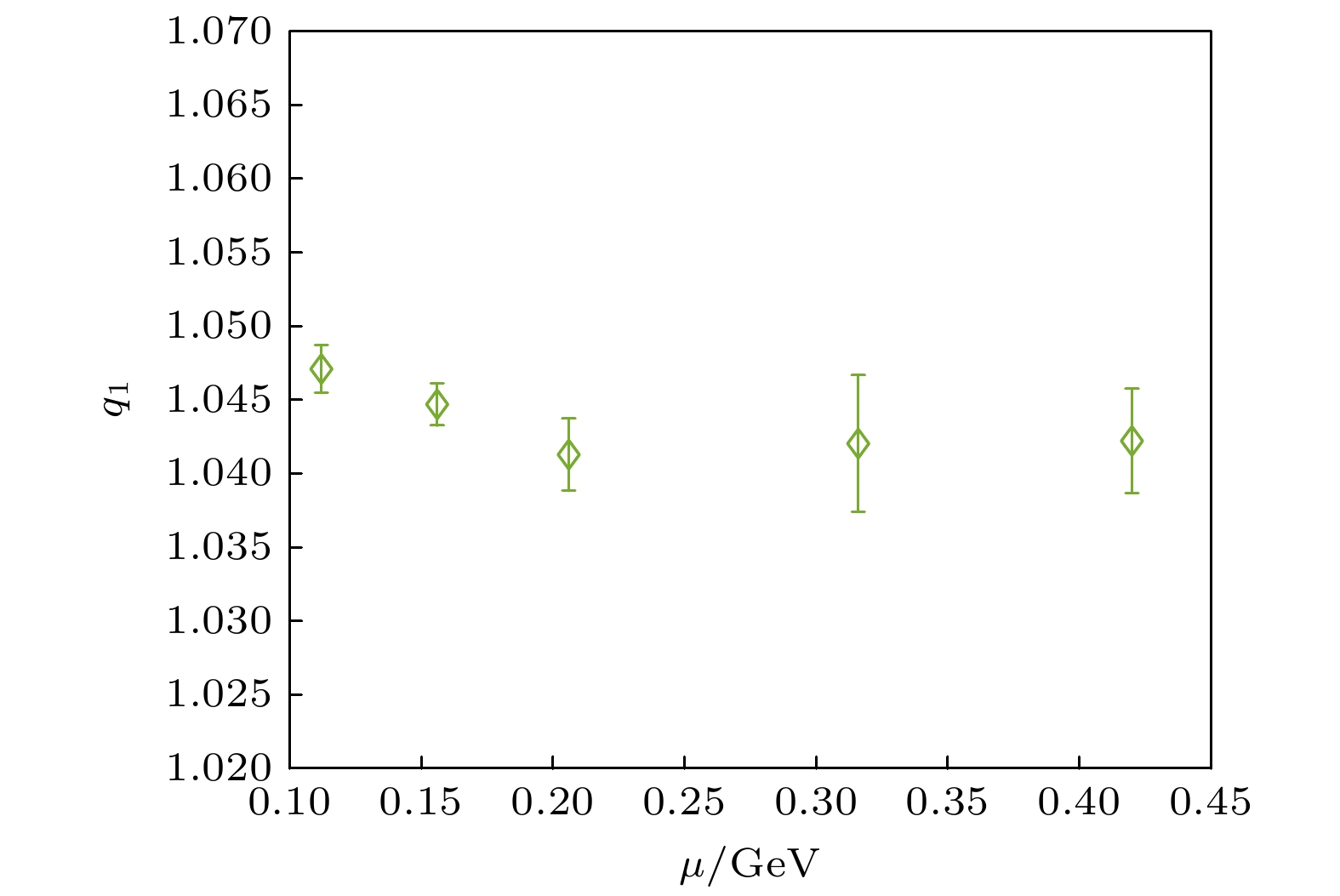
$ q_{1} $ 随温度的变化关系, 求解了Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 下的方程组(25)式, 并分析了临界温度附近$ q_{1} $ 的数值变化. 经计算可得$ q_{1} > 1 $ , 在非广延统计学中, 如果$ q_{1} > 1 $ , 那么$ S_{q_{1}} < S_{\text{B-G}} $ . 因此在自相似结构的影响下, 微观状态数目减少. 在不同的固定温度下,$ q_{1} $ 计算所得的数值如图5所示. 由图5可知$ q_{1} $ 随着温度降低而降低, 所以在强子相中,$ \text{K} $ 介子所受的自相似结构的影响在相变温度附近最大, 我们应该在相变温度附近去分析$ \text{K} $ 介子受到的自相似结构影响.如表1所列, 经计算得到了Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39\text{ GeV} $ 中, 0—5%对心度下的$ q_{1}, \, q_{2} $ . 其中, 相变温度和化学势取自格点QCD的计算结果[9]. 根据不同碰撞情况设定了相应的$ r_{\text{min}} $ 和$ r_{0} $ . 其中,$ r_{\text{min}} $ 参考了格点QCD理论中[58,59]计算轻夸克相关物理量时使用的格点间距(lattice spacing)范围. 由表1可知不同碰撞能量下,$ q_{1} > 1 $ , 说明了自相似结构对$ \text{K} $ 介子存在影响. 随着碰撞能量增加, 相变温度变高,$ \text{K} $ 介子的运动空间变大,$ q_{1} $ 也变得更大. 该趋势说明了自相似结构的影响会随着碰撞能量增大而增大. 这是由于碰撞能量越大, 集体流效应更强, 会导致更强的集体运动从而产生共振, 因此自相似结构的影响也变得明显.根据表1中
$ q_{1} $ 随化学势μ的数值变化可知,$ q_{1} $ 的数值随着碰撞能量$ \sqrt{s_{\text{NN}}} $ 从$ 39\text{ GeV} $ 降低到$ 19.6\text{ GeV} $ 而减小(如图6所示), 待减小到碰撞能量$ \sqrt{s_{\text{NN}}} = 11.5, \, 7.7\text{ GeV} $ 时,$ q_{1} $ 的数值基本变化不大. 因此, 我们预测在HIAF的能区$ \sqrt{s_{\text{NN}}} = 2.2— 4.5 \text{ GeV} $ 范围内,$ q_{1} $ 的数值近似是$ 1.042 $ . -
3.1.1节通过两体分形模型计算出了不同碰撞能量下
$ \text{K} $ 介子的自相似结构影响因子$ q_{1} $ . 通过$ q_{1} $ , 可以推导出强子相中$ \text{K} $ 介子的粒子数分布.将
$ \text{s}\bar{\text{u}} $ 束缚系统看成一个巨正则系统, 根据$ \text{K} $ 介子伴随概率(15)式写出$ \text{s}\bar{\text{u}} $ 束缚系统的归一化密度算符[60]其中, μ是化学势,
$ \hat{H}_{\text{s}\bar{\text{u}}} $ 为$ \text{s}\bar{\text{u}} $ 系统的哈密顿算符,$ \hat{N} $ 为巨正则系综的粒子数算符. 根据参考文献[61,62], 由密度算符可得$ \text{K} $ 介子态的平均粒子数分布为其中,
$ \varepsilon_{\text{K}}=\sqrt{p_{\text{K}}^{2} + m_{\text{K}}^{2}} $ 为$ \text{K} $ 介子的能量;$ p_{\text{K}}, m_{\text{K}} $ 是$ \text{K} $ 介子的动量和质量. 当$ q_{1} \rightarrow 1 $ 时, 该分布则变成玻色-爱因斯坦分布.根据
$ \text{K} $ 介子的粒子数分布(27)式, 可以计算出$ \text{K} $ 介子的能量密度、压强和熵密度分别为其中
$ p_{\text{K}} $ 为$ \text{K} $ 介子的动量,$ g_{\text{K}} = 2 $ 为$ \text{K} $ 介子自旋-同位旋的简并度因子(spin-isospin degeneracy factor). 这里将气体向外膨胀的压强方向定义为正.根据
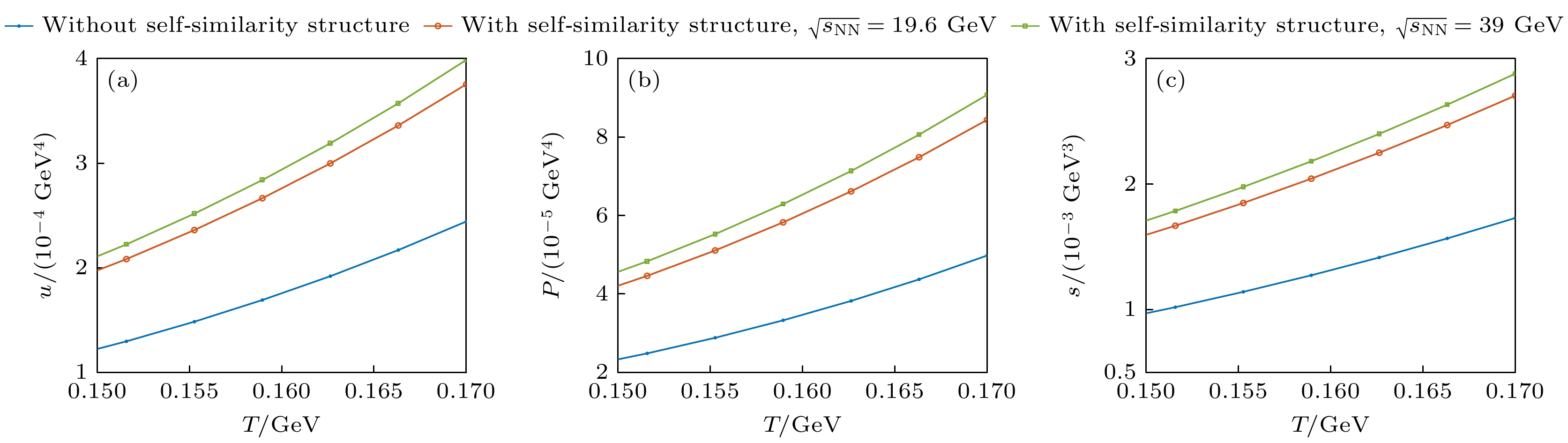
$ \text{K} $ 介子的能量密度、压强和熵密度(28)式可知, 基于粒子数分布(27)式的能量密度、压强和熵密度与温度和自相似结构影响因子$ q_{1} $ 相关. 如图7所示, 以Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 19.6, \, 39\text{ GeV} $ 为例, 将表1中该碰撞能量下$ q_{1} $ 的值代入, 计算并分析了自相似结构影响下的$ \text{K} $ 介子能量密度、压强和熵密度, 并与不存在自相似结构影响的情形进行了比较. 如图7(a)所示, 在相同碰撞能量下, 能量密度随着温度升高而增大. 温度固定时, 碰撞能量越大, 受自相似结构影响的能量密度越大. 这说明撞能量越大, 在集体流、共振效应和强相互作用影响下的自相似结构对$ \text{K} $ 介子的影响越大. 图7(b)为$ \sqrt{s_{\text{NN}}} = 19.6, \, 39\text{ GeV} $ 碰撞中$ \text{K} $ 介子受自相似结构影响下的压强, 并将其与没有该影响的结果进行比较. 通过分析得出, 压强和能量密度的趋势一致, 即在同一碰撞能量下, 压强随着温度升高而增大, 这是由于能量密度的增大导致了压强的增大. 而在固定温度时, 碰撞能量越大, 自相似结构影响下的压强越大. 图7(c)是$ \sqrt{s_{\text{NN}}} = 19.6, 39\text{ GeV} $ 碰撞中, 受自相似结构影响下$ \text{K} $ 介子的熵密度. 从图中可以看出, 相同碰撞能量下, 熵密度随着温度增高而增大. 在温度固定的情况下, 碰撞能量越大, 受自相似结构影响的熵密度越大. 这是由于碰撞能量越大, 集体流、共振效应和强相互作用三种效应使得$ \text{K} $ 介子和附近π介子之间形成的自相似结构越多, 微观状态数目越多, 熵密度也随之增加.除了可以计算
$ \text{K} $ 介子受自相似结构影响下的热力学量, 利用$ \text{K} $ 介子的粒子数分布函数, 考虑能量与横动量$ p_{{\mathrm{T}}} $ 和快度y的关系, 还可以推导出$ \text{K} $ 介子的横动量分布函数:其中,
$ p_{\text{T}} $ 是实验参考系中的横动量;$ m_{\text{T}} = \sqrt{m_{\text{K}}^{2} + p_{\text{T}}^{2}} $ 为$ \text{K} $ 介子的横向质量;$ V_{\text{lab}} = \gamma V $ 为$ \text{K} $ 介子在实验参考系中的运动空间, 通过与质心系的运动空间进行Lorentz变换得到, γ为Lorentz系数. 将TBFM求解得到的$ q_{1} $ 代入到(29)式, 可以得出$ \text{K} $ 介子的横动量谱分布.将Au+Au碰撞能量
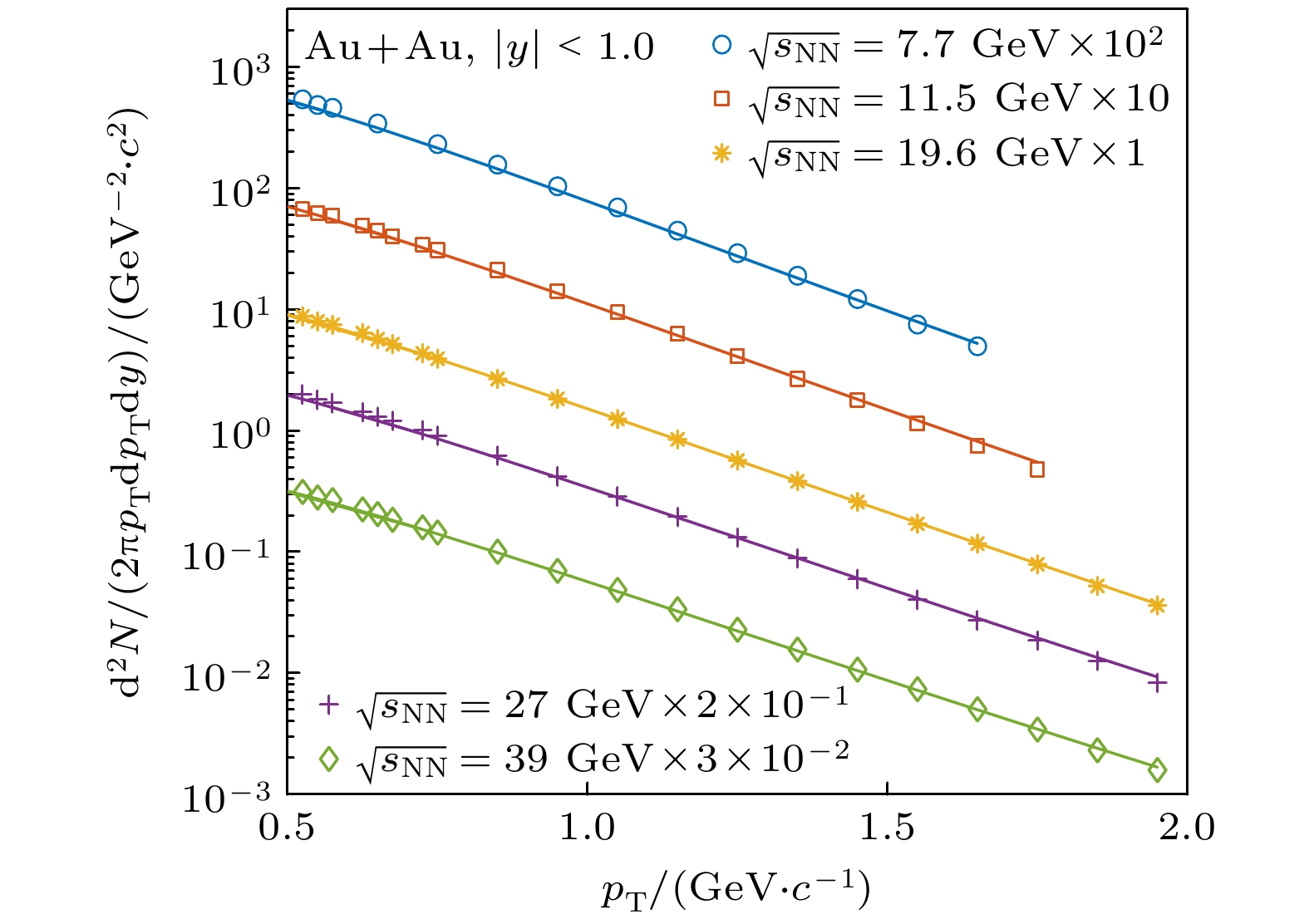
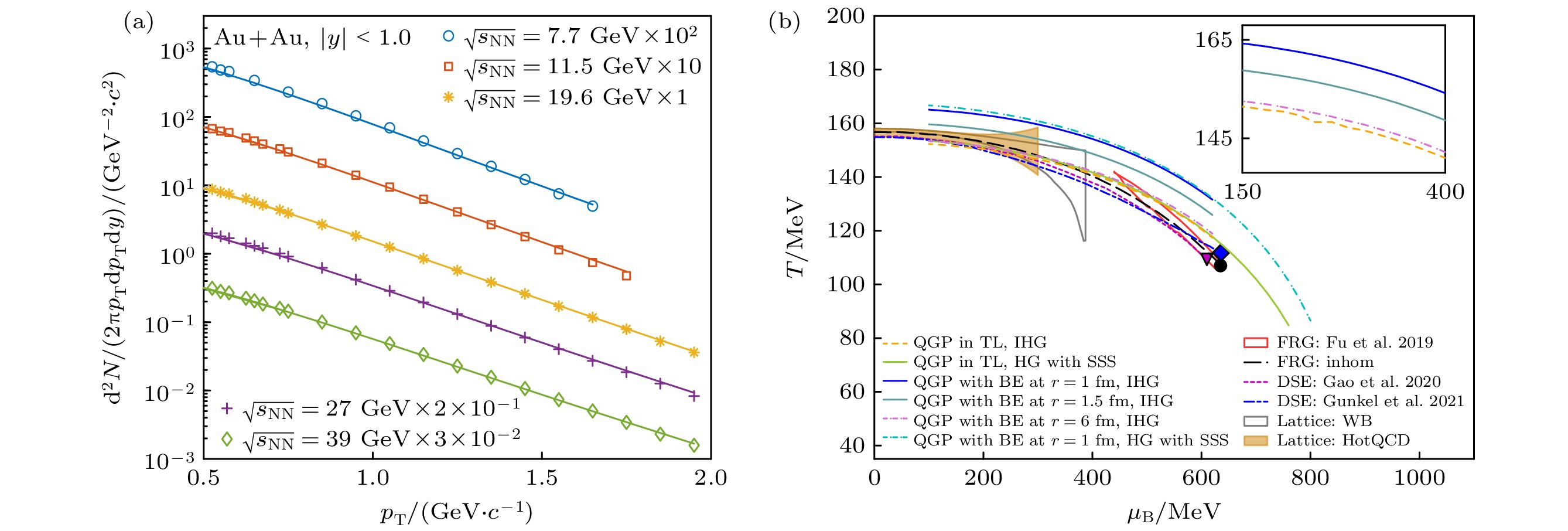
$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, 27, \,39\;\text{ GeV} $ , 0—5%对心度下, TBFM求解得到的$ q_{1} $ 代入到横动量分布公式, 并与实验数据$ (\text{K}^{+}+ \text{K}^{-})/2 $ 的分布结果比对, 如图8所示. 可以看出, 在两体自相似结构影响下的横动量谱分布与实验结果符合较好. 这说明自相似结构存在于这些高能碰撞之中, 影响了$ \text{K} $ 介子的分布. -
高能碰撞中, QGP经过相变形成强子相. 前两小节分别研究了QGP相中QGP受到的边界效应影响以及强子相中
$ \text{K} $ 介子受到的自相似结构影响. 在QGP相中, QGP的压强公式为(12)式. 在强子相中, 强子气体的压强$ P_{\text{H}} $ 考虑包含$ \text{s, u, d} $ 夸克形成的强子的压强之和. 末态强子谱中, π介子产额最多, 约占$ 90\% $ , 奇异强子中$ \text{K} $ 介子其次[63], 由于包含$ \text{s} $ 夸克的其他介子以及超子的产额很少[5], 对压强的贡献可以忽略不计. 所以我们考虑强子气体由$ \text{K} $ 介子和π介子组成, 在自相似结构的影响下, 两种介子的压强分别为其中,
$ q_{1} $ 和$ q_{\pi} $ 分别为$ \text{K} $ 介子与π介子自相似结构影响修正因子,$ q_{\pi} $ 的计算结果来自之前关于π自相似结构影响的工作[12].$ \varepsilon_{\pi(\text{K})}=\sqrt{p_{\pi(\text{K})}^{2} + m_{\pi(\text{K})}^{2}} $ 为$ \pi(\text{K}) $ 介子的能量,$ m_{\pi(\text{K})} $ 是$ \pi(\text{K}) $ 介子的质量. 当忽略自相似结构影响时,$ q_{1(\pi)} \rightarrow 1 $ , (30)式中的粒子数分布则变成玻色分布,$ \pi(\text{K}) $ 介子的压强变为理想玻色气体压强. π介子与$ \text{K} $ 介子达到热平衡, 由于其余种类的奇异介子和超子很少, 我们将强子气体的压强看作π和$ \text{K} $ 介子的压强之和,将QGP相压强(12)式与强子相压强(31)式代入到相变平衡条件
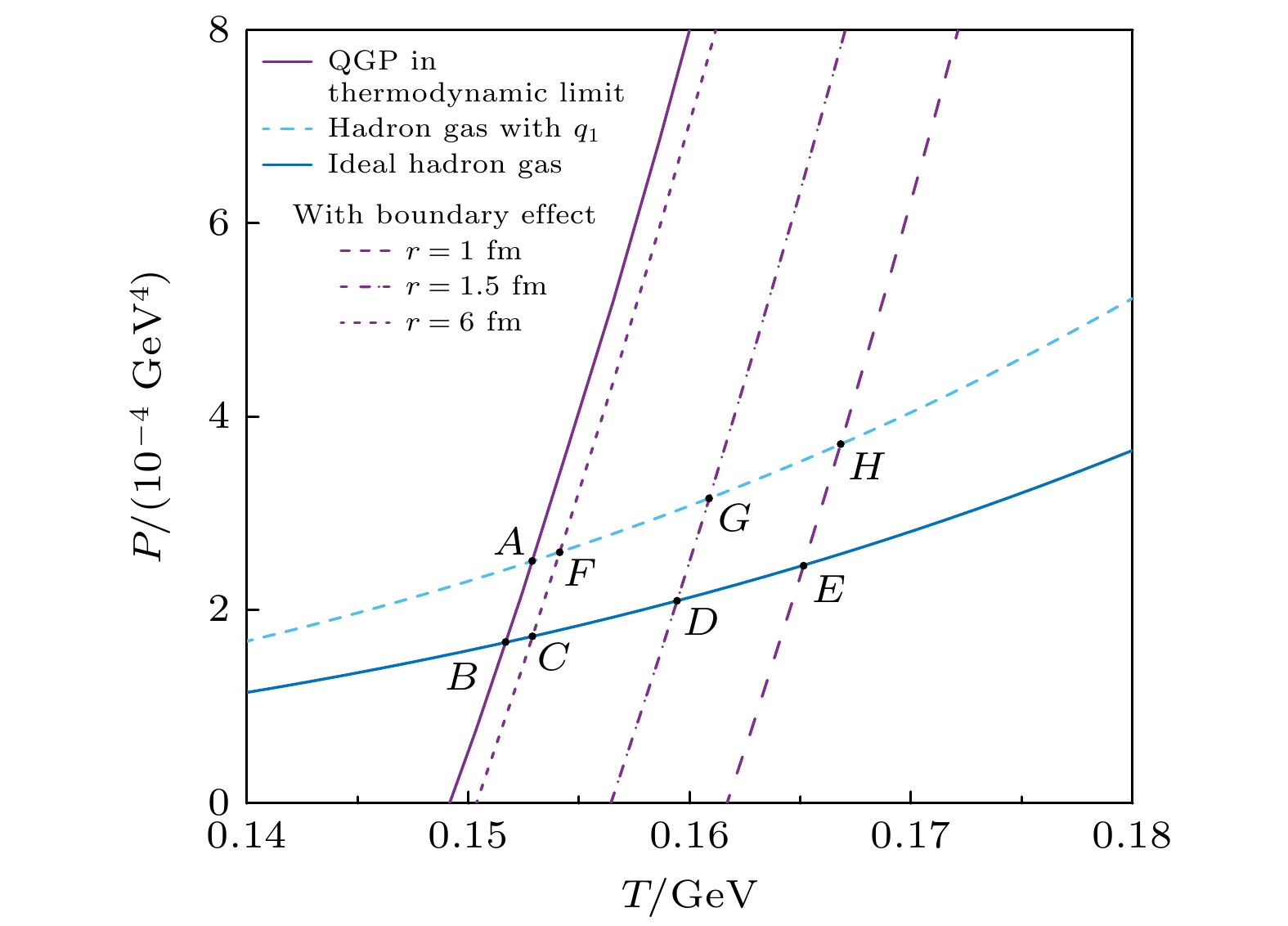
$ T_{\text{QGP}} = T_{\text{H}}, \, P_{\text{QGP}} = P_{\text{H}}, \; \mu_{\text{QGP}} = \mu_{\text{H}} $ 中, 可计算出相变温度. QGP边界效应以及强子相自相似结构影响了两相的热力学性质, 则必会影响相变温度, 具体分析如下. 以Au+Au碰撞$ \sqrt{s_{\text{NN}}} = 39 \text{ GeV} $ 为例, 分析QGP相和强子相的压强与温度的关系, 如图9所示. 图中, 蓝色的实线和虚线分别表示未受到两体自相似结构影响和受到其影响的强子气体的压强, 紫色的实线、点线、点划线、虚线分别代表QGP相热力学极限下和QGP半径为$ r = 6, \, 1.5, \, 1\text{ fm} $ 下的压强.为了单独分析QGP边界效应和
$ \text{K}, \, \pi $ 介子的两体自相似结构对相变的影响, 下面分不同情况进行分析.1) 热力学极限条件下的
$ \text{s} $ 夸克物质相与理想强子气体相相变.两相相交于B点.
2) 边界效应影响下的
$ \text{s} $ 夸克物质相与理想强子气体相相变.如图9所示, 半径分别为
$ r = 6, \, 1.5, \, 1\text{ fm} $ 的$ \text{s} $ 夸克物质相与理想强子气体相相交于$ {C, D, E} $ 三点. 由图可知, 相变温度在边界效应的影响下逐渐升高, 满足$ T_{{B}} < T_{{C}} < T_{{D}} < T_{{E}} $ . 这是由于边界效应减小了$ \text{s} $ 夸克物质的压强, 为满足两相压强相等的相变平衡条件, 相变温度对应必须升高. 且QGP热滴的半径越小, 边界效应越强, 相变温度则升得越多.将碰撞能量
$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 的相变计算结果进一步推广到不同碰撞能量与化学势条件下. 如图10所示, QGP热滴半径分别为$ r = 6, 1.5, \; 1\text{ fm} $ 的相变温度高于热力学极限条件下的结果. 且热滴半径越小, 边界效应越强, 相变温度则升高越多. 这与$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 碰撞能量下的结果是一致的.3) 热力学极限条件下的
$ \text{s} $ 夸克物质相与自相似结构影响下的强子气体相相变.在
$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 碰撞条件下, 如图9所示, 两相相交于A点. 由图可知, 相变温度满足$ T_{{A}} > T_{{B}} $ . 这说明相变温度在强子相中自相似结构的影响下有所升高. 这是由于自相似结构使得强子相的压强增大, 为满足相变平衡, 相变温度随之升高.将
$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 碰撞条件下的计算结果进一步推广, 推广到不同碰撞能量与化学势条件下. 如图10所示, 相较于理想强子气体的情况, 相变温度略有升高, 这与图9计算结构一致. 但与QGP半径较小的边界效应的影响对比, 可看出自相似结构使得相变温度升高的幅度并不大. 这是由于如图9所示, 自相似结构对强子气体压强的影响程度, 相较于QGP半径较小的边界效应对$ \text{s} $ 夸克物质压强的影响程度而言较小, 使得相变温度增大幅度较小.4) 边界效应影响下的
$ \text{s} $ 夸克物质相与自相似结构影响下的强子相相变.由第2)点和第3)点可知,
$ \text{s} $ 夸克物质的边界效应与强子中的自相似结构均会导致相变温度升高. 因此, 两种效应的共同作用使得相变温度进一步升高. 先考虑$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 条件下, 如图9所示, QGP半径$ r = 6 \text{ fm} $ 时, 两种效应共同影响下,$ T_{\text{F}} > T_{\text{A}} $ ,$ T_{\text{F}} > T_{\text{C}} $ ;$ r = 1.5 \text{ fm} $ 时,$ T_{\text{G}} > T_{\text{A}} $ ,$ T_{\text{G}} > T_{\text{D}} $ ;$ r = 1\text{ fm} $ 时,$ T_{\text{H}} > T_{\text{A}} $ ,$ T_{\text{H}} > T_{\text{E}} $ .推广到不同碰撞能量与化学势条件下, 如图10所示, QGP半径
$ r = 1 \text{ fm} $ 时, 两种效应共同影响下的相变温度曲线(蓝色点划线), 略高于只考虑QGP边界效应的相变温度线(蓝色实线), 并高于只考虑自相似结构影响下的温度线(绿色实线). 从上一点可知, 这是由于当QGP半径较小时, QGP边界效应的影响大于强子相的自相似结构对相变温度的影响. 从而导致相较于强子相自相似结构影响下的相变温度, QGP边界效应导致的相变温度升高更多. -
本文分别研究了中低能碰撞中考虑
$ \text{s} $ 夸克在内的QGP热滴的边界效应, 以及强子气体中$ \text{K} $ 介子, π介子的自相似结构. 在包含$ \text{s} $ 夸克物质的QGP相中, 采用MRE方法修正的MIT袋模型用来研究QGP热滴的边界效应. 通过计算不同半径QGP热滴的热力学量, 发现同一个QGP热滴在相同温度下, 相较于不受边界影响的情况, 边界效应导致更低的能量密度、熵密度和压强. 当QGP热滴半径越小时, 边界越弯曲, 能量密度、熵密度和压强则减小得越多. 和没有考虑$ \text{s} $ 夸克、半径大小一样的QGP热滴相比, 在相同温度下, 包含$ \text{s} $ 夸克的QGP热滴在边界效应的影响下, 热力学量减小的幅度更大. 这说明包含$ \text{s} $ 夸克的QGP热滴受边界效应比没有$ \text{s} $ 夸克的热滴影响更大.强子相中, 考虑在共振效应, 强相互作用以及量子关联的共同影响下, 存在
$ \text{K} $ -π和π-π的两介子结构. 对于$ \text{K} $ -π结构, 该两体结构与$ \text{K} $ 介子内部的正反夸克两体结构具有自相似性. 因此, 在前期工作考虑π-π自相似结构的基础上, 我们使用两体分形模型来研究自相似结构对$ \text{K} $ 介子的影响. 引入了修正因子$ q_{1} $ 来描述介子层次中自相似结构与$ \text{K} $ 介子的影响, 引入伴随因子$ q_{2} $ 来描述夸克层次中自相似结构对内部夸克的影响. 考虑介子层次和夸克层次中$ \text{K} $ 介子的概率和Tsallis熵的等价性, 构建概率与熵的方程组, 求解描述自相似结构影响的$ q_{1}, q_{2} $ . 计算结果中$ q_{1} > 1 $ , 说明$ \text{K} $ 介子受到两体自相似结构的影响. 计算结果表明$ q_{1} $ 随着温度降低而降低, 这说明在相变温度附近的自相似结构影响更显著. 分析$ q_{1} $ 和μ的关系时发现, 随着化学势增高,$ q_{1} $ 的数值趋近于$ 1.042 $ , 表明随着碰撞能量降低, 化学势逐渐升高, 集体流速度减小会导致两体结构减少, 减少至$ 1.042 $ 时趋于稳定. 因此, 我们预测在未来HIAF能区$ \sqrt{s_{\text{NN}}} = 2.2 —4.5 \text{ GeV} $ ,$ q_{1} $ 的数值在$ 1.042 $ 左右. 另外还计算了$ \text{K} $ 介子在自相似结构影响下的能量密度、压强和熵. 相同温度下, 发现在自相似结构影响下,$ \text{K} $ 介子的热力学量比热力学极限影响下的结果有所增大. 在Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, 39\text{ GeV} $ , 0—5%对心度下, TBFM求解得到的$ q_{1} $ 代入到$ \text{K} $ 介子的横动量分布公式, 发现与实验结果比对效果较好.最后, 研究分析了QGP热滴的边界效应和强子气体中
$ \text{K} $ 介子与π介子的自相似结构对相变的影响. 当考虑$ \text{s} $ 夸克物质相与理想强子气体相时, 相变温度在边界效应影响下逐渐升高. QGP热滴越小, 边界效应越强, 相变温度升高越多. 当考虑热力学极限条件下的$ \text{s} $ 夸克物质相与自相似结构影响下的强子气体相时, 相变温度在自相似结构的影响下有所升高. 但与QGP半径较小的边界效应的影响相比, 自相似结构使得相变温度升高的幅度并不大. 当考虑边界效应影响下的$ \text{s} $ 夸克物质相与自相似结构影响下的强子相时, 两种效应的共同作用使得相变温度进一步升高. 相较于强子相自相似结构影响下的相变温度, QGP边界效应导致的相变温度升高更多. 这说明了QGP热滴的边界效应在中低能碰撞中是不可忽略的.$ \text{s} $ 夸克物质在中高化学势区域易受到边界效应的影响, 强子相中的奇异强子在自相似结构的影响下热力学特性也发生了改变, 这个结论对可产生QGP热滴的中低能实验具有启发意义. 强子气体中存在的除$ \text{K} $ 介子, π介子以外的少量强子, 这些粒子的自相似结构影响, 以及如何影响相变将在未来工作中进一步研究.
s夸克物质的边界效应和K介子自相似结构对夸克胶子等离子体-强子相变的影响
The boundary effect of s quark matter and self-similarity structure influence of K meson on quark-gluon plasma-hadron phase transition
-
摘要: 聚焦于小尺度$ \text{s} $夸克物质的边界效应和强子气体中强子的自相似结构对夸克胶子等离子体 (QGP)-强子相变的影响, 采用多级反射展开方法研究了包含$ \text{s} $夸克的QGP热滴的边界效应. 通过计算发现在边界效应的影响下, 小尺度$ \text{s} $夸克物质相较于热力学极限条件下具有更低的能量密度、熵密度和压强. 在强子相中, $ \text{K} $介子在集体流、量子关联和强相互作用的影响下, 与相邻π介子形成两体自相似结构. 通过两体分形模型对$ \text{K} $介子的自相似结构影响计算得出, $ \text{K} $介子的自相似结构存在于碰撞系统中, 导致$ \text{K} $介子的能量密度、熵密度和压强增大. 本研究预测在低能碰撞HIAF能区, $ \text{K} $介子的自相似结构影响因子 $ q_{1} = 1.042 $. 考虑边界效应和$ \text{K} $, π介子的自相似结构对相变的影响, 计算发现$ \text{s} $夸克物质在边界效应与自相似结构的影响下相变温度均有所升高. 若$ \text{s} $夸克物质的边界弯曲程度较大, 则相变温度的升幅相较于自相似结构的影响更明显.Abstract: We investigate the boundary effect of small-scale s quark matter and the self-similarity structure influence of strange hadrons in the hadron gas on quark-gluon plasma (QGP)-hadron phase transition. In this study, the multiple reflection expansion method is used to investigate the boundary effect of QGP droplets containing s quarks. The calculation reveals that under the influence of boundary effect, small-scale s quark matter exhibits that energy density, entropy density, and pressure are all lower. In the hadron phase, there exists a two-body self-similarity structure between K mesons and neighboring π mesons, subjected to collective flow, quantum correlations, and strong interactions. By using two-body fractal model to study the self-similarity structure of the K meson in meson and quark aspects, it is found that the self-similarity structure of the K meson exists in hadron phase, resluting in an increase in the energy density, entropy density, and pressure of the K meson. Furthermore, under the influence of self-similarity structure, the derived transverse momentum spectrum of K meson shows excellent agreement with experimental data (Fig. (a)). This study predicts that in the HIAF energy region, the self-similarity structure factor of K meson $ q_{1} $ approaches 1.042. Additionaly, under the combined influence of boundary effects and self-similarity structure of K and π mesons, the phase transition temperature of s quark matter increases (Fig. (b)). Morover, if the boundary of s quark matter is more curved, the increase of phase transition temperature becomes more pronounced compared to the effect of self-similarity structure alone.
-
Key words:
- s quark /
- boundary effect /
- self-similarity structure /
- quantum chromodynamics phase transition .
-

-
图 3 半径为
$ r = 1\text{ fm} $ 的QGP热滴, 包含$ \text{s} $ ,$ \text{u} $ ,$ \text{d} $ 三种夸克, 和包含$ \text{u} $ ,$ \text{d} $ 两种夸克的热力学量 (a)能量密度; (b)压强; (c)熵密度Figure 3. Thermodynamic quantities of QGP droplet
$ r = 1\text{ fm} $ considering$ \text{s} $ ,$ \text{u} $ ,$ \text{d} $ quarks and$ \text{u} $ ,$ \text{d} $ quarks in it, respectively: (a) Energy density; (b) pressure; (c) entropy density.图 6 Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, 39\text{ GeV} $ , 0−5%对心度下,$ \text{K} $ 介子的自相似结构影响的修正因子$ q_{1} $ 和化学势的变化关系图Figure 6. The relationship between the factor
$ q_{1} $ for$ \text{K} $ meson and chemical potential μ in Au+Au collisions at$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39\text{ GeV} $ for 0−5% centrality.图 7 Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 19.6, \, 39\text{ GeV} $ 中, 受自相似结构影响的$ \text{K} $ 介子的热力学量在临界相变温度时的变化 (a)能量密度; (b)压强; (c)熵密度Figure 7. Thermodynamic quantities of kaon with and without the self-similarity structure influence in Au+Au collisions at
$ \sqrt{s_{\text{NN}}} = 39, \, 19.6 \, \text{GeV} $ near the phase transition temperature: (a) Energy density; (b) pressure; (c) entropy density.图 8 Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \; 27, 39\text{ GeV} $ , 0—5%对心度,$ |y| < 0.1 $ 下,$ \text{K} $ 介子受自相似结构影响下$ (\text{K}^{+}+\text{K}^{-})/2 $ 的横动量谱分布. 与之比对的实验数据来自STAR实验组[63]Figure 8. Transverse momentum spectrum of
$ (\text{K}^{+}+\text{K}^{-})/2 $ mesons in Au+Au collisions at$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6,\; 27, $ $ 39\text{ GeV} $ for 0–5% centrality, in mid-rapidity$ |y| < 0.1 $ . The experimental data are from STAR[63].图 9 Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $ 中, QGP热滴半径分别为$ r = 1, \, 1.5, \, 6\text{ fm} $ 的压强随温度的变化, 以及分别考虑强子气体为理想气体和受$ \text{K}, \pi $ 介子自相似结构影响的压强随温度的变化Figure 9. The pressure in hadron phase with and without the influence of self-similarity structure on
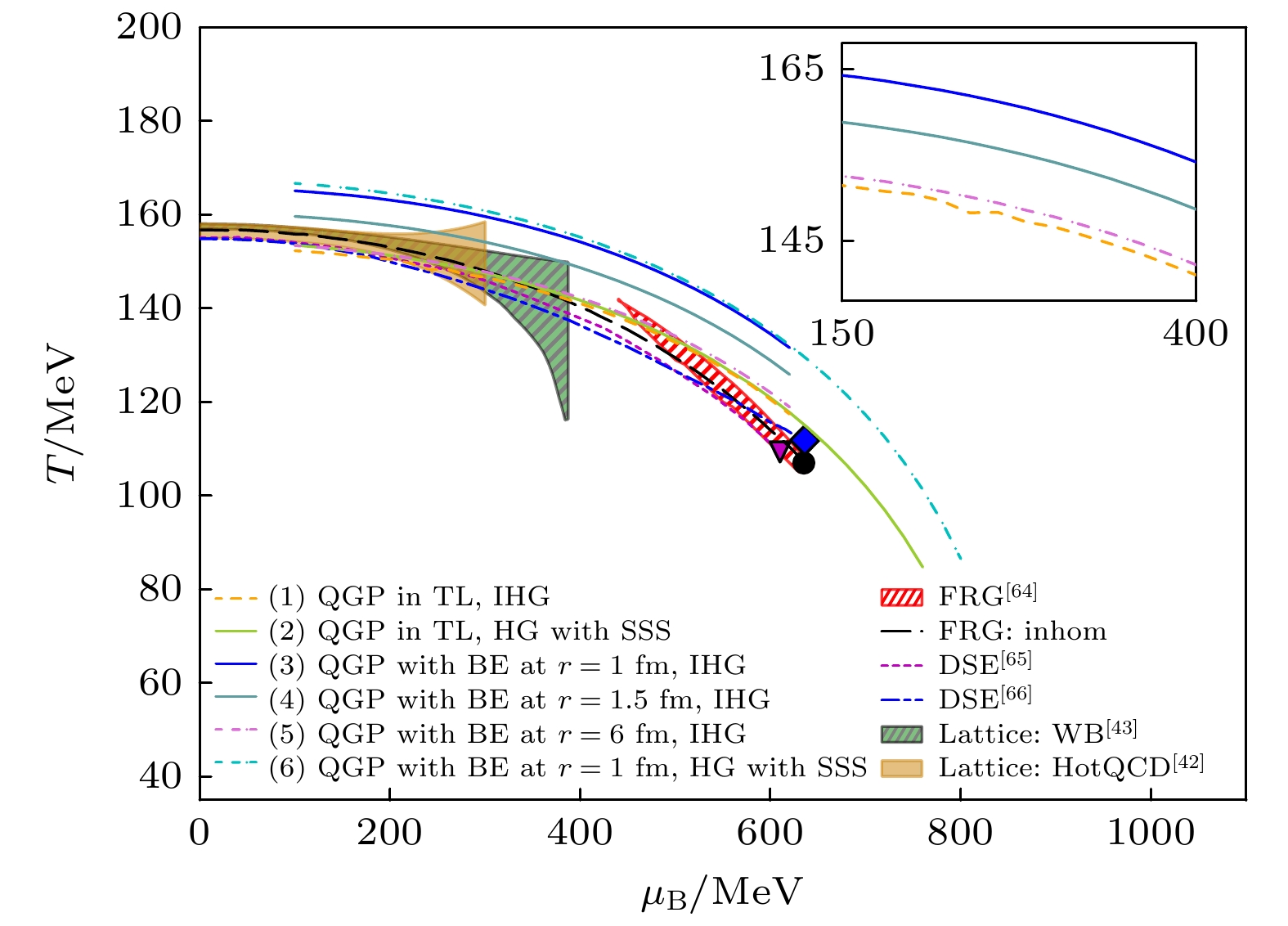
$ \text{K} $ and πmesons in Au+Au collisions at$ \sqrt{s_{\text{NN}}} = 39 \text{ GeV} $ , and the pressure of QGP droplets at radius$ r = 1, \, 1.5, \, 6\text{ fm} $ as a function of temperature T.图 10 不同情况下的相图结果: (1) QGP相处于热力学极限(TL), 强子气体(HG)为理想气体(IHG); (2)QGP相处于热力学极限(TL), 强子气体受自相似结构影响; (3)—(5) QGP热滴半径分别为
$ r = 1, 1.5, 6\text{ fm} $ , 受边界效应(BE)影响, 强子气体为理想气体; (6) QGP热滴半径为$ r = 1 \text{ fm} $ 受边界效应影响, 强子气体受自相似结构影响. 同时也列出了泛函重整化群(fRG)方法[64], Dyson-Schwinger方程模型[65,66]和格点QCD[42,43]在有限化学势区域的相图结果, 以便比较Figure 10. The phase diagram with considering (1) QGP in thermodynamic limit (TL) and ideal hadron gas (IHG), (2) QGP in thermodynamic limit and hadron gas (HG) with the influence of self-similarity structure (SSS), (3)–(5) QGP droplet with the boundary effect (BE) at radius
$ r = 1, 1.5, 6\text{ fm} $ and ideal hadron gas (IHG), respectively, (6) QGP droplet with the boundary effect (BE) at radius$ r = 1 \text{ fm} $ and hadron gas with the influence of self-similarity structure (SSS). We also list the results from fRG model[64], DSE[65,66] and lattice QCD[42,43] for comparison.表 1 Au+Au碰撞能量
$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39\text{ GeV} $ , 0−5%对心度下, 通过TBFM方法求解出$ \text{K} $ 介子的自相似结构影响修正因子$ q_{1} $ 和$ q_{2} $ Table 1. The factors
$ q_{1} $ and$ q_{2} $ for$ \text{K} $ meson in Au+Au collisions at$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39 \text{ GeV} $ for 0−5% centrality solved by TBFM.$ \sqrt{s_{\text{NN}}}/\text{GeV} $ $ T / \text{GeV} $ $ \mu_{\text{B}} / \text{GeV} $ $ r_{\text{min}}/\text{fm} $ $ r_{0}/\text{fm} $ $ q_{1} $ $ q_{2} $ 7.7 0.1424 $ \pm $ 0.001370.42 0.11 6.3 1.04222 $ \pm $ 0.0035251.13941 $ \pm $ 0.01041511.5 0.1483 $ \pm $ 0.001420.316 0.11 6.5 1.04204 $ \pm $ 0.0046351.12682 $ \pm $ 0.0106319.6 0.1527 $ \pm $ 0.001470.206 0.09 6.75 1.04129 $ \pm $ 0.0024451.14432 $ \pm $ 0.00510527 0.1541 $ \pm $ 0.001480.156 0.1 6.8 1.04470 $ \pm $ 0.0014351.12251 $ \pm $ 0.0003939 0.155 $ \pm $ 0.001490.112 0.1 6.85 1.04710 $ \pm $ 0.0016151.11388 $ \pm $ 0.00012 -
[1] Srivastava P K, Tiwari S K, Singh C P 2010 Phys. Rev. D 82 014023 doi: 10.1103/PhysRevD.82.014023 [2] Singh C 1993 Phys. Rep. 236 147 doi: 10.1016/0370-1573(93)90172-A [3] Satz H 2000 Rep. Prog. Phys. 63 1511 doi: 10.1088/0034-4885/63/9/203 [4] Back B, Baker M, Ballintijn M, et al 2005 Nucl. Phys. A 757 28 doi: 10.1016/j.nuclphysa.2005.03.084 [5] STAR Collaboration 2005 Nucl. Phys. A 757 102 doi: 10.1016/j.nuclphysa.2005.03.085 [6] Arsene I, Bearden I, Beavis D, et al 2005 Nucl. Phys. A 757 1 doi: 10.1016/j.nuclphysa.2005.02.130 [7] Karthein J M, Mroczek D, Acuna A R N, et al 2021 Eur. Phys. J. Plus 136 621 doi: 10.1140/epjp/s13360-021-01615-5 [8] Mohanty B 2009 Nucl. Phys. A 830 899c doi: 10.1016/j.nuclphysa.2009.10.132 [9] An X, Bluhm M, Du L, et al 2022 Nucl. Phys. A 1017 122343 doi: 10.1016/j.nuclphysa.2021.122343 [10] Odyniec G 2019 PoS CORFU2018 201 151 [11] Bzdak A, Esumi S, Koch V, otehrs 2020 Phys. Rep. 853 1 doi: 10.1016/j.physrep.2020.01.005 [12] Dai T, Ding H, Cheng L, Zhang W, Wang E 2024 arXiv: 2411.068219 [hep-ph] [13] Deur A, Brodsky S J, de Téramond G F 2016 Prog. Part. Nucl. Phys. 90 1 doi: 10.1016/j.ppnp.2016.04.003 [14] Niida T, Miake Y 2021 AAPPS Bull. 31 12 doi: 10.1007/s43673-021-00014-3 [15] Raghunath S 2019 AAPPS Bull. 29 16 doi: 10.22661/AAPPSBL.2019.29.4.16 [16] Loizides C 2016 Nucl. Phys. A 956 200 doi: 10.1016/j.nuclphysa.2016.04.022 [17] Shneider M N, Pekker M 2019 arXiv: 1901.04329 [physics.flu-dyn] [18] Wong C Y, Zhang W N 2007 Int. J. Mod. Phys. E 16 3271 doi: 10.1142/S0218301307009245 [19] Gustafsson H A, Gutbrod H H, Kolb B, et al 1984 Phys. Rev. Lett. 52 1590 doi: 10.1103/PhysRevLett.52.1590 [20] Danielewicz P, Odyniec G 1985 Phys. Lett. B 157 146 doi: 10.1016/0370-2693(85)91535-7 [21] Wiranata A, Koch V, Prakash M, Wang X N 2014 J. Phys.: Conf. Ser. 509 012049 doi: 10.1088/1742-6596/509/1/012049 [22] Zachariasen F, Zemach C 1962 Phys. Rev. 128 849 doi: 10.1103/PhysRev.128.849 [23] Rafelski J 1982 Phys. Rep. 88 331 [24] Koch P, Müller B, Rafelski J 1986 Phys. Rep. 142 167 doi: 10.1016/0370-1573(86)90096-7 [25] Greiner C, Koch P, Stöcker H 1987 Phys. Rev. Lett. 58 1825 doi: 10.1103/PhysRevLett.58.1825 [26] Greiner C, Rischke D H, Stöcker H, Koch P 1988 Phys. Rev. D 38 2797 doi: 10.1103/PhysRevD.38.2797 [27] Greiner C, Stöcker H 1991 Phys. Rev. D 44 3517 doi: 10.1103/PhysRevD.44.3517 [28] Mønster D 1996 Ph.D. Dissertation (Aarhus: Aarhus University [29] Nordin F 2011 Bachelor Thesis (Lund: Lund University [30] STAR Collaboration 2020 Phys. Rev. C 102 034909 doi: 10.1103/PhysRevC.102.034909 [31] Moreau P, Soloveva O, Oliva L, Song T, Cassing W, Bratkovskaya E 2019 Phys. Rev. C 100 014911 doi: 10.1103/PhysRevC.100.014911 [32] Shen C, Alzhrani S 2020 Phys. Rev. C 102 014909 doi: 10.1103/PhysRevC.102.014909 [33] Albacete J L, Guerrero-Rodríguez P, Marquet C 2019 J. High Energy Phys. 2019 73 doi: 10.1007/JHEP01(2019)073 [34] Grönqvist H 2016 Fluctuations in High-Energy Particle Collisions. Theses, Université Paris Saclay (COmUE [35] Chodos A, Jaffe R L, Johnson K, Thorn C B, Weisskopf V F 1974 Phys. Rev. D 9 3471 doi: 10.1103/PhysRevD.9.3471 [36] Ramanathan R, Gupta K K, Jha A K, Singh S S 2007 Pramana 68 757 doi: 10.1007/s12043-007-0075-8 [37] Madsen J 1993 Phys. Rev. Lett. 70 391 doi: 10.1103/PhysRevLett.70.391 [38] Madsen J 1994 Phys. Rev. D 50 3328 doi: 10.1103/PhysRevD.50.3328 [39] Balian R, Bloch C 1970 Annals of Physics 60 401 doi: 10.1016/0003-4916(70)90497-5 [40] Patra B K, Singh C P 1996 Phys. Rev. D 54 3551 doi: 10.1103/PhysRevD.54.3551 [41] Song G, Enke W, Jiarong L 1992 Phys. Rev. D 46 3211 doi: 10.1103/PhysRevD.46.3211 [42] Bazavov A, Ding H T, Hegde P, et al. 2019 Phys. Lett. B 795 15 doi: 10.1016/j.physletb.2019.05.013 [43] Bellwied R, Borsányi S, Fodor Z, Günther J, Katz S, Ratti C, Szabo K 2015 Phys. Lett. B 751 559 doi: 10.1016/j.physletb.2015.11.011 [44] Hagedorn R 1971 Thermodynamics of strong interactions. Tech. rep., CERN [45] Wong C Y 2002 Phys. Rev. C 65 034902 doi: 10.1103/PhysRevC.65.034902 [46] Pathria R, Beale P D 2022 Formulation of Quantum Statistics (Fourth Edn.) (Lodon: Elseviser) pp117–154 [47] Musakhanov M 2017 EPJ Web Conf. 137 03013 doi: 10.1051/epjconf/201713703013 [48] Mandelbrot B B 1967 Science 156 636 doi: 10.1126/science.156.3775.636 [49] Mandelbrot B B 1986 Self-affne Fractal Sets, I: The Basic Fractal Dimensions (Amsterdam: Elsevier) pp3–15 [50] Tsallis C 1988 J. Stat. Phys 52 479 doi: 10.1007/BF01016429 [51] Abe S, Okamoto Y 2001 Nonextensive Statistical Mechanics and Its Applications (Vol. 560) (Berlin: Springer Science & Business Media) pp5–6 [52] Ding H Q, Dai T T, Cheng L, Zhang W N, Wang E K 2023 Acta Phys. Sin. 72 192501 doi: 10.7498/aps.72.20230990 [53] Ding H, Cheng L, Dai T, Wang E, Zhang W N 2023 Entropy 25 1655 doi: 10.3390/e25121655 [54] Crater H W, Yoon J H, Wong C Y 2009 Phys. Rev. D 79 264 doi: 10.1103/PhysRevD.79.034011 [55] Tsallis C 2009 Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World (Vol. 1) (New York: Springer) pp47–129 [56] Ubriaco M R 1999 Phys. Rev. E 60 165 doi: 10.1103/PhysRevE.60.165 [57] Büyükkiliç F, Demirham D 1993 Phys. Lett. A 181 24 doi: 10.1016/0375-9601(93)91118-O [58] Feng X, Jin L, Riberdy M J 2022 Phys. Rev. Lett. 128 052003 doi: 10.1103/PhysRevLett.128.052003 [59] Wang G, Liang J, Draper T, Liu K F, Yang Y B 2021 Phys. Rev. D 104 074502 doi: 10.1103/PhysRevD.104.074502 [60] Rajagopal A, Mendes R, Lenzi E 1998 Phys. Rev. Lett. 80 3907 doi: 10.1103/PhysRevLett.80.3907 [61] Wang Q A 2002 Chaos, Solitons Fractals 14 765 doi: 10.1016/S0960-0779(02)00035-8 [62] Abe S 2001 Phys. Rev. E 63 061105 doi: 10.1103/PhysRevE.63.061105 [63] STAR Collaboration 2017 Phys. Rev. C 96 044904 doi: 10.1103/PhysRevC.96.044904 [64] Fu W J, Pawlowski J M, Rennecke F 2020 Phys. Rev. D 101 054032 doi: 10.1103/PhysRevD.101.054032 [65] Gao F, Pawlowski J M 2021 Phys. Lett. B 820 136584 doi: 10.1016/j.physletb.2021.136584 [66] Gunkel P J, Fischer C S 2021 Phys. Rev. D 104 054022 doi: 10.1103/PhysRevD.104.054022 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: