首页
登录
注册
-
1999年, 美国航天局(NASA)[1–3]提出了宏观压电纤维复合材料(macro fiber composite, MFC), 将压电陶瓷纤维、聚合物基体以及叉指电极复合成具有三明治多层结构的智能材料, 如图1(a)所示, 这种结构充分发挥了压电陶瓷纤维长度方向的压电效应, 解决了对正交各向异性传感和驱动能力的需求, 具有高压电性、高柔韧性、高机电耦合系数和低损耗等优点[4–8].
随着MFC研究技术的深入发展, 学者们利用MFC内部复杂的结构, 研发出了不同的工作响 应模式: 包括d33型、d31型和d15型[9–13]等. 其中, d33型MFC的极化方向和施加的电场方向一致且均沿着纤维长度方向, 利用了纤维长度方向的压电效应, 因此可以在长度方向累积压电效应, 具有优异的驱动和传感性能, 如图1(b)所示. d33型工作模式是目前MFC应用最广泛的一种工作模式, d33型MFC作为传感智能元件在航空、航天、民用和军事等领域发挥着至关重要的作用. Discalea等[14]基于MFC研究了无人机机翼蒙皮翼梁连接处复合材料粘接状态的监测, 基于有限元分析对频散波传播问题进行了数值研究, 研究了复合材料蒙皮的铺层方式、粘结缺陷和界面脱粘下的超声导波监测, 研究证明了MFC具有良好的灵敏度, 可用于机载监测系统. Konka等[15]对MFC的传感器性能进行了系统性研究, 确定了MFC作为嵌入式传感器的功能优点, 包括可以检测到复合材料的加载条件、服役损伤和疲劳失效等. 测试了嵌入式MFC传感器玻璃纤维-环氧复合材料层压板样品中的应力应变变化规律. 研究验证了MFC能够有效传感机械应力应变的变化, 输入机械应力和输出电压之间存在线性关系. Pearson等[16]提出了MFC传感器的新型应用方式, 将两个MFC粘贴在航空航天用复合材料面板上, 在100, 300和500 kHz频率范围内不仅可以检测复合材料遭遇冲击破坏时释放的声发射(AE), 还可以作为脉冲接收器进一步量化损伤. 此外, MFC的传感性能还被创新地应用于无线传输、导波传递等各领域[17–19].
然而, 目前MFC传感器的研究主要聚焦于材料的应用, 对于MFC传感器建模的研究一般是基于等效体积元模型和对称边界条件对应力、应变和电场等单元模块的变化情况进行分析. 但是, 由于受模型复杂性限制, 对于MFC传感器的整体建模模型缺乏系统性研究, 对于MFC的传感性能预测还缺乏有效的建模. 特别是航空航天领域用MFC传感器, 由于航空航天材料一般使用轻质的铝合金材料等, 结构受激后的高灵敏传感一直是制约传感特性进一步发展的主要因素. 本工作基于有限元分析方法对MFC传感器进行建模, 一方面通过代表性体积元(representative volume element, RVE)模型, 掌握MFC传感器内部的电场分布, 为力-电耦合提供理论依据; 另一方面通过使用直接模型和混合模型对MFC不同传感形式进行分析, 对于MFC智能元件传感器的传感性能做出预测, 实验结果表明, MFC的有限元建模可以有效预测MFC传感器的传感性能, 为MFC传感器的性能预测提供了保障.
-
代表性体积元模型通常用于多尺度计算, 特别是在模拟材料微观性能对宏观行为的影响时, 它通过选取一个具有代表性的微小体积单元来模拟整个材料的性能, 这个单元应足够大以包含材料的所有关键微观特征, 同时又要足够小以在宏观尺度上可被视为均匀介质. MFC的代表性体积元模型理论研究基础是基于复合材料的等效原则、混合定则和压电本构方程对MFC的应力、应变、电位移和电场之间的关系进行分析, 基于平面应力假设将MFC看成多层复合材料, 忽略对应力或电场贡献较小的矢量分量[20–22]. 采用的等效压电本构方程如(1)式所示进行理论分析:
其中,
$ {S_i} $ 和$ {D_k} $ 分别代表应变分量和电位移分量,$ {T_j} $ 和$ {E_l} $ 分别表示应力分量和电场分量,$ s_{ij}^{\text{E}} $ 表示恒电场下的柔性常数分量(单位为m2/N),$ {d_{kj}} $ 是压电常数分量(单位为C/N),$ \varepsilon _{kl}^{\text{T}} $ 代表恒应力下的介电常数分量(单位为F/m). 当下标$i, j = 1, 2, 3$ 时,$ {S_i} $ 和$ {T_j} $ 分别代表在三维坐标系的正方向的分量; 当下标$i, j = 4, 5, 6$ 时,$ {S_i} $ 和$ {T_j} $ 分别代表在三维 坐标系的剪切方向的分量. 基于平面应力假设和均匀场理论可知: d33型工作模式的MFC厚度方向的应力很小, 可以忽略不计, 因此假设应力T1=0; 电场主要加载在纤维的长度方向(即“3”方向), 其他方向的微弱电场可以忽略不计, 因此E1 = E2 = 0.将MFC看成压电等效体, 由于功能相PZT-5H为四方相晶体结构P4mm点群, 存在
$ {d_{32}} = {d_{31}}, {d_{24}} = {d_{15}}, {\varepsilon _{11}} = {\varepsilon _{22}}, {s_{11}} = {s_{22}}, {s_{44}} = {s_{55}}, {s_{13}} = {s_{23}} $ =${s_{32}} $ , 则(1)式可以简化成(2)式:其中, 顶标“~”代表MFC的复合材料层的等效参数, 由此可以看出MFC的应力、应变、电位移和电场之间的关系. 基于梅得林(Mindlin)经典层合板的变形理论[23,24], 可以发现, MFC的压电相和聚合物相在某些方向存在应力或应变相等的情况, 如(3)式所示:
其中, 上标“P”代表压电陶瓷, 上标“E”代表环氧树脂. 对于其他参数, 可以通过引入陶瓷百分比v应用平均值来表示, 如(4)式所示:
进一步推导可以获得MFC的压电等效参数, 如(5)式和(6)式所示:
其中,
$d_{33}^{\rm{p}}$ 代表压电陶瓷矩阵的压电常数${d_{33}}$ ,$d_{31}^ {\mathrm{p}}$ 代表压电陶瓷矩阵的压电常数${d_{31}}$ ,$Y_{\mathrm{L}}^{\mathrm{P}}$ 代表压电陶瓷在纤维长度方向的杨氏模量,$Y_{\mathrm{L}}^{\mathrm{E}}$ 代表环氧树脂在纤维长度方向的杨氏模量,${\mu ^{\text{P}}}$ 代表压电陶瓷的泊松比,${\mu ^{\text{E}}}$ 代表环氧树脂的泊松比.代表性体积元模型虽然可以对MFC的应力、应变或电学性能做出高效的计算, 但是, 其计算结果多为预估结果且边界条件受小应变梯度或周期性条件限制而定义困难, 因此, 基于模型的实际精度需求, 本工作进一步采取了直接模型和混合模型进行建模和分析. 为了进一步厘清MFC的电输出性能, 对MFC的力电耦合进行了分析和推导, 构建悬臂梁模型如图2所示.
根据Euler-Bernoulli理论, 层合梁轴向应变和曲率半径的关系为
式中,
$ {w}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{l}}}\left(x, t\right) $ 为梁中性轴相对于固定参考系的横向位移,$ {S}_{3}\left(x, z, t\right) $ 为X方向的应变. 振动控制方程为其中,
$ M(x, t) $ 为梁内弯矩,$ {c}_{{\mathrm{s}}}I $ 为结构弹性等效阻尼,$ {c}_{{\mathrm{a}}} $ 为空气阻尼系数, m为梁的质量,$ {M}_{{\mathrm{t}}} $ 为悬臂梁端部用于调节谐振频率的质量块重量, L为悬臂梁长度. 进一步推导, MFC传感的耦合力学方程为其中,
$ {\mathrm{Y}}{\mathrm{I}} $ 为MFC悬臂梁的等效刚度,$ K $ 为MFC的机电耦合系数,$ V\left(t\right) $ 为MFC的输出电压. 根据结构力学, 悬臂梁无阻尼自由振动的控制方程为根据模态叠加法, 压电悬臂梁的横向位移为
代入边界条件可以求出R阶模态固有频率:
可以求出模态力系数
其中
$ {\varphi }_{r}\left(x\right) $ 为r阶模态函数.则输出电压峰值为
可以推导出MFC传感电压表达式:
可见, 基于直接模型法和混合模型法进行建模后, 结合模态控制方程对MFC整体结构和MFC悬臂梁结构进行分析, 可以避免代表性体积元预估参数的误差, 更精确地推导出MFC的电输出性能.
-
本工作分别建立了代表性体积元模型、直接模型和混合模型, 分别从细节到整体, 从微观到宏观对MFC的有限元模型进行了建模和分析. 等效体积元模型虽然计算的精确度不高, 但是可以通过对细节的分析, 看出电场和应力的分布趋势. 直接模型建模的MFC和混合模型建模的MFC悬臂梁可以从整体角度分析, 获得MFC的电学输出结果.
建立MFC的代表性体积元模型, 选取一个包含“正-负”叉指电极、压电纤维条和环氧树脂条的单元进行建模, MFC的有限元建模如图3(a)所示. 在建立MFC有限元几何模型时, 涉及的几个重要尺寸参数及其初始值如表1所示.
仿真计算中还涉及压电陶瓷、环氧树脂和叉指铜电极等材料参数, 需要设置压电陶瓷的压电常数矩阵、柔度矩阵、相对介电常数矩阵和密度, 设置环氧树脂和铜电极材料的密度、泊松比、杨氏模量及相对介电常数. 本工作使用压电陶瓷PZT-5H作为功能相材料, 选取的压电陶瓷PZT-5H为课题组制备的压电陶瓷材料, 通过制备符合国标的压电片后, 测试出PZT-5H的材料参数如表2所示. 环氧树脂和铜电极为各向同性材料, 根据制造商提供的数据, 其材料参数如表3所示.
使用有限元分析软件COMSOL Multiphysics进行RVE建模算分析, 图4为计算后生成的电场分布图, 可以看出MFC内部的电场分布是非均匀的. 在叉指电极下端存在电场极小的“电场死区”; 靠近叉指电极区域的非均匀称之为“过渡区”; 在两个叉指电极的中间间距处存在“电场活化区”, 此处的电场分布均匀, 是对压电纤维产生电致伸缩贡 献最大的电场区域. 根据建模也可以推断出MFC内部的电场是均匀分布和非均匀分布共存的, 对MFC使役动作影响最大的是电场活化区的压电陶瓷纤维.
RVE建模可以灵活变换代表性体积元的尺寸参数和材料参数, 较好地表征MFC的电场分布和应力分布的细节变化, 但是对于MFC整体的电场、应力和应变无法精确仿真. 根据MFC的实体结构对MFC的直接模型和混合模型进行建模, 如图5所示.
图5(a)所示的直接模型是对MFC的所有实体结构进行建模, 图5(b)所示的混合模型是在直接模型的基础上加入了悬臂梁基底, 对MFC悬臂梁传感器件进行建模. 在研究传感特性时, 一方面对MFC悬臂梁混合模型沿纵向一端固定, 另一端施加加速度体载荷, 分析其叉指电极两端的电压特性及其谐振特性, 分析MFC的输出电压与尺寸参数之间的关系, 即研究MFC共振式传感器; 另一方面对MFC的悬臂梁整体底面进行固定约束, 并在垂直于材料平面方向施加振动载荷信号, 即研究MFC贴片式传感器.
-
MFC传感器是MFC与板或梁等薄壁结构组成的复合材料器件. MFC与不同尺寸参数和材料参数的基板复合后, 其谐振频率和输出特性差异很大, 为了深入研究MFC复合材料的性能, 将MFC与铝基板复合成悬臂梁器件, 使用有限元分析探讨了MFC传感器的性能. MFC在压电传感时有贴片式传感和共振式传感两种传感模式, 如图6所示, 两种传感器的激振受力方式不同, MFC贴片式传感器的上表面呈自由状态, 下表面受垂直作用力, 传感出的下表面受激振动信号. MFC共振式传感器, 是激振力从基板一端传出, MFC通过与基板同频共振的方式, 传感激振力信号. 对于MFC的两种传感器利用有限元仿真分析并预测了传感性能. 当MFC作为贴片式传感器件时, MFC下方固定于需要传感的材料上, 通过感知材料的下表面载荷实现力电耦合, 进而将下表面载荷信号转换成电信号进行传感. MFC共振式传感器件适用于薄壁材料, MFC传感器设计粘贴于悬臂梁上, 悬臂梁的前端作为固定端、末端作为自由端, 通过与薄壁材料上的载荷信号发生共振而实现振动信号的传感. 因此, 下文将分别从贴片式传感器和共振式传感器两个方面来做预测MFC传感器件的性能.
-
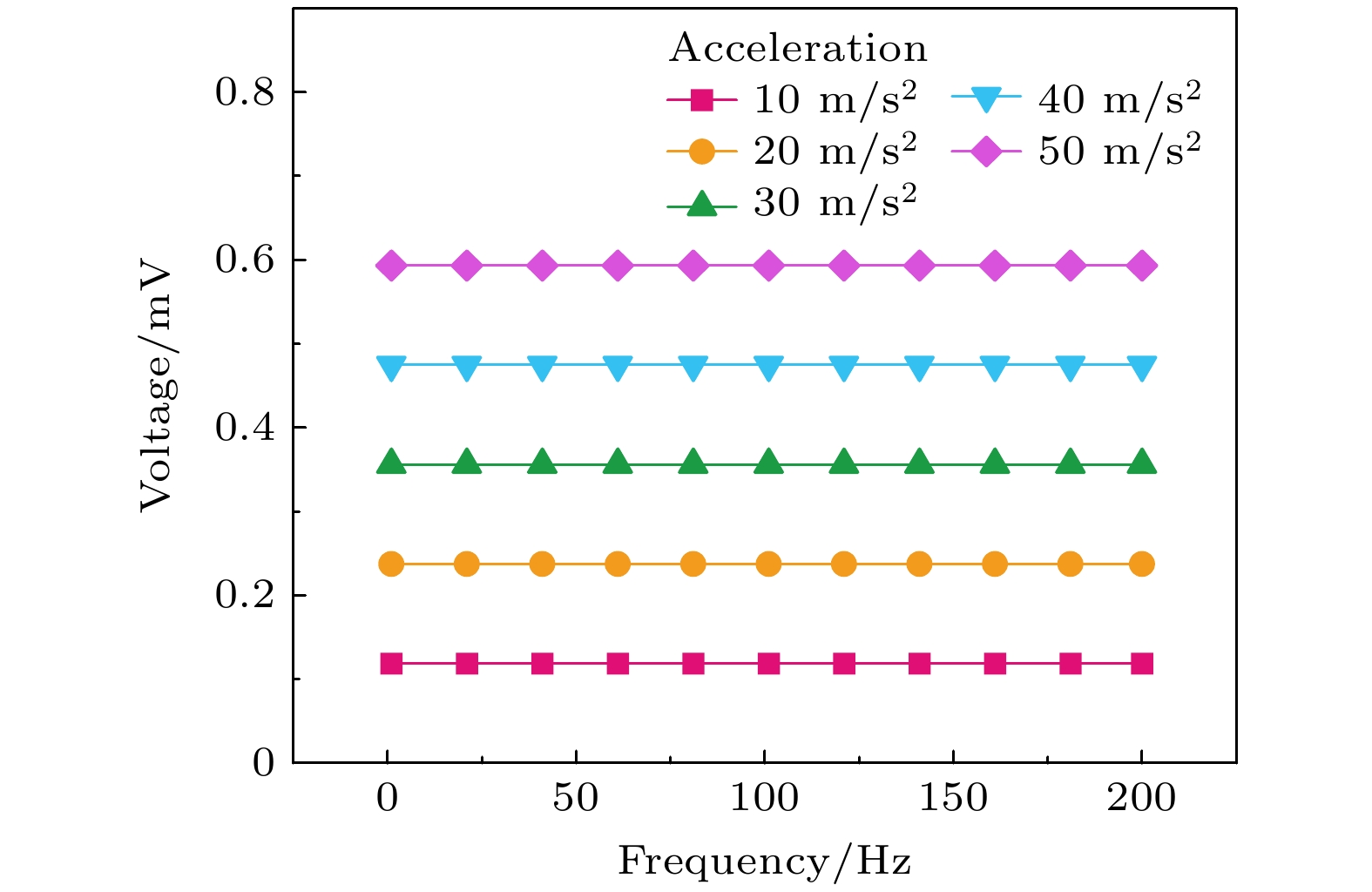
选用相同尺寸的MFC模型粘贴在铝制基板上进行仿真建模. 此时MFC作为贴片式传感器件, 其主要作用是将振动所产生的应力载荷信号转换成电信号. MFC贴片式传感器的边界条件设置时, 在悬臂梁下表面设置固定边界条件, 对MFC悬臂梁输入不同加速度的信号MFC贴片式传感器的性能预测分析结果如图7所示. 可见, MFC传感器件以贴片方式固定后, 输入的加速度载荷越大, MFC的响应电信号越大, MFC的传感输出电信号与输入的加速度载荷信号正相关. 根据不同加速度的电响应信号可以看出, 在加速度固定时, 在200 Hz频率范围内随着频率的增大, 输出的电信号稳定不变. 可见, 这种传感器件输出电压与表面载荷存在线性对应关系. 但是, 由仿真结果也可以看出, 这种测试方式也存在一定的弊端, 即输出的终端电压较小. 在输入的加速度载荷小于10 m/s2时, 输出的电压信号小于1 mV, 这主要是因为贴片式传感器只有下表面接触振动材料, 无法有效传递应力或共振信号. 器件对MFC元件的灵敏度要求较高, 对测试仪器精度要求也较高, 实现起来较困难, 因此, 我们又进一步分析了共振式MFC传感器.
-
共振式MFC传感器采用悬臂梁的方式组装MFC和悬臂梁基板, 将MFC悬臂梁器件一端固定于振动源上, 另一端呈现自由端状态, 当模块振动时带动悬臂梁引起共振, 此时载荷信号通过共振的方式传递到悬臂梁基板上, 悬臂梁上的MFC感知共振信号, 并将其转换成电信号输出.
在研究中发现, 基板的宽度对MFC共振式传感器的谐振频率和输出电压影响不大. 由于工程应用中铝基板材料大多使用0.5 mm厚度. 因此, 在探究共振式传感器的性能时, 使用铝基板厚度为0.5 mm、宽度为15 mm. 将MFC与铝板用布尔运算粘贴装配后构成悬臂梁振子, 一端施加固定约束边界条件, 另一端为自由端, 整体施加10—50 m/s2的体载荷加速度, 分别计算了铝基板长度对MFC传感器的性能影响, 如图8所示.
图8(a)为不同长度铝基板的MFC稳态仿真电压特性曲线, 可以看出, 随着输入体载荷加速度的增大, 共振式MFC的输出电压逐渐增大, 铝基板长度对MFC的输出电压影响很小, 不同长度下的MFC其电压响应基本相同. 图8(b)为输入不同体载荷加速度时的MFC稳态仿真电压特性曲线, 可以看出, 随着激振加速度从10 m/s2逐渐增至50 m/s2, 共振式MFC传感器的输出电压响应从8.52 V增至42.40 V.
图9为铝基板长度对MFC共振式传感器的频率和电压的影响. 可以看出, 在加载5 m/s2的加速度时, 随着基板长度的增大, MFC传感器的谐振频率非线性下降. 当基板长度为60 mm时, MFC共振式传感器的谐振频率为104 Hz, 传感电压为4.18 V; 当基板长度为80 mm时, MFC共振式传感器的谐振频率为67 Hz, 传感电压为4.17 V. 可见, 加载的激振加速度大小对谐振频率没有影响, 但是会影响输出电压线性变化.
仿真计算的结果预测了MFC传感器性能, 为MFC的结构调控和参数设计提供了参考. 与贴片式MFC传感器件相比, 共振式MFC传感器的输出电压更高, 传感信号更灵敏, 且信号识别率比贴片式MFC传感器件更高, 因此本文中后续实验使用的传感器采用共振式MFC传感器.
-
使用激振台(苏州苏试有限公司, 型号DC-1000-15)加载不同的加速度驱动条件, 模拟薄壁 材料的低频噪声振动环境, 搭建MFC传感器进行传感性能的测试. 基于前期的有限元分析结果, 铝悬臂梁基板尺寸为80 mm×15 mm×0.5 mm. 图10(a)所示为PZT-5H基MFC传感器的频率 响应特性曲线, 可以看出, 当施加频率为1 Hz、加速度为2 m/s2的噪声信号时, MFC传感器可以有效感知到振动信号的频率, 并且振幅信号明显, 传 感器输出的电信号与驱动激励振动同频同振幅. 图10(b)所示为不同频率振动激励下, MFC传感器对加速度信号的响应. 可以看出, 在1—200 Hz频率范围振动时, MFC均具有明显的电压输出, 说明此MFC传感器对于1—200 Hz频率范围的振动都可以实现较好的传感检测. 不同频率对应的MFC输出电压不同, 在50—74 Hz频率范围振动时MFC传感器输出电压最大, 说明MFC在这个频率范围的振动可以与悬臂梁基板产生共振. 可见, MFC传感器不仅可以传感频率变化, 也可以传感电压幅值变化, 随着振动信号激励加速度的增大, MFC传感器的输出电压线性增大, 可以根据MFC的输出电压判断器件的振动强度.
图11为 MFC传感器的仿真与实验结果对比, 在铝基板上进行振动激励时, 在谐振频率处传感电压最大, MFC传感器测试的谐振频率为74 Hz, 输出电压为3.59 V; 仿真计算的谐振频率为67 Hz, 输出电压为4.17 V. 仿真计算结果可以有效预测MFC传感器的谐振频率和输出电压, 最大误差不超过13.9%. 可见, MFC传感的结构调控和仿真分析可以有效预测MFC传感器的传感性能.
将MFC传感器的性能参数总结, 如表4所示. 可以看出, MFC作为一种智能传感器件, 具有优异的传感特性, 最高灵敏度为7.35 V/g, 其工作频段低、灵敏度高、输出电压大, 可以有效检测低频振动信号.
本文提出的MFC传感器结构具有普适性, 在进一步的有限元仿真和实验测试中发现, 这些模型可以应用于不同尺寸、不同压电相材料和不同聚合物相材料组成的MFC传感器, 且悬臂梁基板不仅限于铝结构, 还可以适用于钢板、铜板、碳纤维板等各种结构的传感, 为MFC传感器的性能预测提供了新方法.
-
本文基于有限元分析方法和压电本构方程, 针对MFC传感器的应用需求分别构建了有限元模型, 对MFC传感器性能做出预测, 实验结果与预测结果吻合, 得到了以下研究结论.
1) 用有限元分析软件COMSOL Multiphysics分别构建了代表性体积元模型、直接模型和混合模型. 代表性体积元模型可以有效模拟MFC的细节变化, 可以清晰地表征MFC内部电场的复杂分布情况. 而混合模型为MFC传感器有效预测提供了保障. 本文针对不同的分析需求选择了不同的模型.
2) MFC可以组装成悬臂梁制备成MFC传感器, MFC传感器可分为贴片式传感器和共振式传感器. 仿真结果表明: MFC共振式传感器性能远高于MFC贴片式传感器. MFC共振传感器可以有效实现力电耦合, 保证传感信号的传输; 随着激振加速度从10 m/s2增至50 m/s2, 共振式MFC传感器的输出电压响应从8.52 V线性增至42.40 V. 当激振加速度5 m/s2, 悬臂梁基板长度为80 mm时, 计算得到的MFC传感器的谐振频率为67 Hz, 输出电压为4.17 V.
3) 将MFC制备成铝基板传感器, MFC传感器与基板振动具有较好的同频共振特性, 随着驱动激振加速度的增大, MFC传感器的输出电压线性增大. 在铝基板上进行振动激励, MFC传感器测试的谐振频率为74 Hz, 输出电压为3.59 V; 仿真计算的谐振频率为67 Hz, 输出电压为4.17 V. 仿真计算结果可以有效预测MFC传感器的谐振频率的输出电压, 最大误差不超过13.9%. 此外, 实验结构显示MFC悬臂梁在低频工作时具有优异的传感灵敏度, 传感灵敏度为7.35 V/g.
压电纤维复合材料智能传感器的有限元预测与器件性能
Finite element prediction and device performance of piezoelectric fiber composite based smart sensor
-
摘要: 压电纤维复合材料(macro fiber composite, MFC)具有高压电性、高柔韧性和低损耗等优点, 被广泛应用于航空、航天、民用和军事等领域. 然而, 目前MFC传感器的研究主要聚焦于材料应用, 对于MFC传感器件仿真建模还缺乏系统性的研究. 本工作分别建立了代表性体积元模型、直接模型和混合模型, 从细节到整体、从微观到宏观对MFC的有限元模型进行了建模和分析. 一方面通过等效体积元模型, 掌握MFC内部的电场分布规律, 为力-电耦合提供理论依据; 另一方面通过直接模型和混合模型, 对MFC的实体结构进行整体建模和边界条件的加载, 为MFC贴片式传感和共振式传感的分析提供理论依据, 有效预测了MFC智能元件传感器的传感性能. 仿真结果表明, 共振式传感器性能远优于贴片式传感器, 当激振加速度为5 m/s2、悬臂梁基板长度为80 mm时, 计算得到的MFC共振式传感器的谐振频率为67 Hz, 输出电压为4.17 V. 实验结果表明, MFC传感器测试的谐振频率为74 Hz, 输出电压为3.59 V, 仿真计算结果与MFC传感器预测结果基本符合. 此外, MFC传感器在低频工作时具有优异的传感灵敏度, 传感灵敏度为7.35 V/g. 可见, MFC在低频共振时具有优异的传感特性, 构建的3种有限元模型可以有效预测MFC传感器的传感性能, 为MFC传感器的性能预测提供了保障.
-
关键词:
- 压电纤维复合材料(MFC) /
- 传感器 /
- 性能预测 /
- 有限元模型
Abstract: Macro fiber composite (MFC) is extensively utilized in aviation, aerospace, civilian, and military domains due to its high piezoelectricity, flexibility, and minimal loss. Nevertheless, existing research on MFC sensors has focused on material applications, with a conspicuous lack of systematic investigation into the simulation and modeling of MFC sensor devices. In this study, three models, namely, a representative volume element (RVE) model, a direct model, and a Hybrid model are established to analyze the finite element models of MFC, covering the scales from micro to macro. On the one hand, the equivalent RVE model contributes to an understanding of the internal electric field distribution in MFC, thereby establishing a theoretical foundation for force-electric coupling. On the other hand, the application of the direct model and hybrid model accords with the boundary conditions in MFC applications, which lays a theoretical foundation for the stress sensing and resonance sensing mechanisms of MFC. These models constitute effective tools for predicting the sensing performance of MFC smart element sensors. The simulation outcomes indicate that resonant sensors exhibit significantly superior performance compared with patch sensors. Under the conditions where the excitation acceleration is 5 m/s² and the cantilever substrate length is 80 mm, the simulated resonant frequency of the MFC resonant sensor is 67 Hz, with an output voltage of 4.17 V. Experimental results confirm these findings. It is reported that the resonant frequency is 74 Hz and the output voltage is 3.59 V for the MFC sensor. The remarkable consistency between the simulation results and experimental data of the MFC sensor deserves to be emphasized. In addition, the MFC sensor shows excellent sensing sensitivity at low frequencies, with a sensitivity of 7.35 V/g. Obviously, MFC shows remarkable sensing characteristics at low-frequency resonance. The three finite element models established in this work can well predict the sensing performance of MFC sensors, thus ensuring reliable prediction of the performance of such sensors.-
Key words:
- macro fiber composites (MFC) /
- sensors /
- performance prediction /
- finite element model .
-
-
图 1 (a)宏压电纤维复合材料结构; (b)压电纤维复合材料工作模式
Figure 1. (a) Macro fiber composite structure; (b) working mode of macro fiber composite.
图 3 MFC的代表性体积元建模 (a) RVE模型; (b) RVE模型的尺寸参数
Figure 3. Representative volume element modeling of MFC: (a) RVE modeling diagram; (b) dimension parameter of RVE.
图 5 (a) MFC的直接模型; (b) MFC的混合模型
Figure 5. (a) Direct model of MFC; (b) mixed model of MFC.
图 6 MFC传感器 (a)贴片式传感器; (b)共振式传感器
Figure 6. MFC sensor: (a) MFC patch sensor; (b) MFC resonance sensor.
图 8 MFC共振传感器的传感性能 (a)加速度载荷对输出电压的影响; (b)基板长度对输出电压的影响
Figure 8. Sensing performance of MFC resonant sensor: (a) Influence of acceleration load on output voltage; (b) influence of substrate length on output voltage.
图 9 MFC共振式传感器的频率和电压变化
Figure 9. Frequency and voltage variation of MFC resonant sensor.
图 10 PZT-5H基MFC传感器性能 (a)频率响应; (b)加速度响应
Figure 10. Performance of the PZT-5H-based MFC sensor: (a) Frequency response; (b) acceleration response.
图 11 MFC传感器仿真与实验结果对比
Figure 11. Comparison of simulation and experiment results of MFC sensor.
表 1 MFC代表性体积元模型尺寸参数
Table 1. Dimension parameter of RVE of MFC.
建模参数 纤维宽度 纤维高度 环氧
宽度环氧
高度电极宽度 电极高度 电极间距 纤维电极间距 定义符号 Wf Hf We He Wi Hi Si Sf 初始值/mm 0.35 0.45 0.3 0.45 0.1 0.04 0.5 0.04 
下载: 导出CSV
表 2 压电陶瓷的材料参数
Table 2. Material parameters of piezoelectric ceramic.
密度/(kg·m–3) 压电常数/(10–12 C·N–1) 介电常数 柔度矩阵/(10–12 m2·N–1) ρ d33 d31 d15 $\varepsilon_{11 }$ $\varepsilon_{33} $ s11 s12 s13 s33 s44 s66 7750 593 –274 741 3130 3400 16.5 –4.8 –8.5 20.7 43.5 42.6
下载: 导出CSV
表 3 环氧树脂和叉指电极的材料参数
Table 3. Material parameters of epoxy resin and interdigital electrode.
材料 密度/
(kg·m–3)弹性
模量/GPa泊松比 相对介电
常数铜电极 8960 120 0.34 — 环氧树脂 1960 1 0.38 4
下载: 导出CSV
表 4 MFC传感器性能参数
Table 4. Performance parameters of MFC sensor.
性能参数 单位 数值范围 灵敏度(±5%) V/g 0.5—7.35 工作频段(±5%) Hz 1—200 谐振频率 Hz 74 响应时间 ms <1 输出电压 V 0.5—20
下载: 导出CSV
-
[1] Hagood N W, Bent A A 1993 34th Structures, Structural Dynamics and Materials Conference La Jolla, CA, U.S.A, April 19–22, 1993 [2] Aaron A B, Nesbitt W H 1997 J. Intell. Mater. Syst. Struct. 8 903 doi: 10.1177/1045389X9700801101 [3] Bent A A, Hagood N W, Rodgers J P 1995 J. Intell. Mater. Syst. Struct. 6 338 doi: 10.1177/1045389X9500600305 [4] Wilkie W K, Bryant R G, High J W, Fox R L, Hellbaum R F 2000 Industrial and Commercial Applications of Smart Structures Technologies Newport Beach, USA, March 7–9, 2000 [5] Tu J W, Zhang J R, Li Z, Gao K, Liu M Y 2020 Smart Mater. Struct. 29 015038 doi: 10.1088/1361-665X/ab47d5 [6] Lou J Q, Chen T H, Yang Y L, Xu C, Chen H, Ma J, Cui Y G, Li G 2022 J. Vib. Control 28 290 doi: 10.1177/1077546320976917 [7] Lou J Q, Gu T, Chen T H, Yang Y L, Xu C, Wei Y D, Cui Y G 2022 Mech. Syst. Signal Process. 170 108824 doi: 10.1016/j.ymssp.2022.108824 [8] Zhou J J, Zhou J, Chen W, Tian J, Shen J, Zhang P C 2022 Compos. Struct. 299 116019 doi: 10.1016/j.compstruct.2022.116019 [9] Wang X Y, Yuan X, Wu M L, Gao F, Yan X M, Zhou K C, Zhang D 2019 Sensors 19 1809 doi: 10.3390/s19081809 [10] Yan M Y, Yuan X, Zhang Y, Zhang S F, Wang X Y, Gao F, Zhou K C, Zhang D 2019 Smart Mater. Struct. 28 125015 doi: 10.1088/1361-665X/ab4f8c [11] Yuan X, Wang X Y, Yan M Y, Gao F, Zhang S F, Zhou K C, Ji X B, Zhang D 2020 Measurement 154 107500 doi: 10.1016/j.measurement.2020.107500 [12] Zhou J J, Zhou J, Yu Y Y, Shen J, Zhang P C, Chen W 2023 Ceram. Intl. 49 32528 doi: 10.1016/j.ceramint.2023.07.217 [13] Huang R, Zhou J J, Shen J, Tian J, Zhou J, Chen W 2024 Materials 17 3033 doi: 10.3390/ma17123033 [14] Discalea F L, Matt H, Bartoli I, Stefano C, Gyuhae P, Charles F 2006 J. Intell. Mater. Syst. Struct. 18 373 [15] Konka H P, Wahaba M A, Lian K 2013 Sens. Actuators A 194 84 doi: 10.1016/j.sna.2012.12.039 [16] Pearson M R, Eaton M J, Featherston C A, Holford K M, Pullin R 2011 J. Phys.: Conf. Ser. 305 12049 doi: 10.1088/1742-6596/305/1/012049 [17] Grzybek D, Micek P 2017 Sens. Actuators A 267 417 doi: 10.1016/j.sna.2017.10.053 [18] Micek P, Grzybek D 2019 Sens. Actuators A 301 111744 [19] El Najjar J, Mustapha S 2020 J. Civ. Struct. Health Monit. 10 793 doi: 10.1007/s13349-020-00417-0 [20] Glouia Y, Chaabouni Y, El Oudiani A, Maatoug I, Msahli S 2019 Intl. J. Adv. Manuf. Tech. 103 4671 doi: 10.1007/s00170-019-03838-4 [21] Malekimoghadam R, Icardi U 2019 Composites Part B 177 107405 doi: 10.1016/j.compositesb.2019.107405 [22] Marino M, Wriggers P 2019 Comput. Methods Appl. Mech. Eng. 344 938 doi: 10.1016/j.cma.2018.10.016 [23] Yu S, Zhang D T, Qian K 2019 Appl. Composite Mater. 26 65 doi: 10.1007/s10443-018-9707-z [24] Zahid M, Sharma R, Bhagat A R, Abbas S, Kumar A, Mahajan P 2019 Composite Struct. 226 111221 doi: 10.1016/j.compstruct.2019.111221 -
计量
- 文章访问数: 57
- HTML全文浏览数: 57
- PDF下载数: 0
- 施引文献: 0