腔磁子学是最近几年在磁学和光与物质相互领域逐渐兴起的前沿研究方向, 其研究微波谐振腔光子与磁性激发态磁子之间的强耦合作用^[1–15]. 由于磁子可以在室温下操作且磁子具有较小的耗散率, 因此磁子与光子的相互作用被认为在量子调控领域具有较好的应用前景^[16–20]. 目前, 这一领域已经产生了较多的研究成果, 例如超强耦合^[1]、双稳定性^[21–25]、量子纠缠^[26–30]、薛定谔猫态^[31]等奇异的物理结果. 在应用上, 利用磁子与光子耦合制作的换能器(transducer), 既可以实现微波频段之间的转换^[1–20], 也可以实现微波和可见光频段之间的转换^[32–35], 这对于磁子信息的长距离传输是极为有利的.

目前, 磁子与谐振腔光子之间的耦合方式一般有两种. 第1种方式称为相干型耦合, 即通过把钇铁石榴石(YIG)放置在微波谐振腔的波腹处, 磁化与微波磁场通过磁偶极相互作用实现耦合, 从而实现强的磁子-光子耦合^[1–20]. 第2种方式称为耗散型耦合, 一般把钇铁石榴石放在微波谐振腔的波节处, 由于波节处的微波磁场为零, 因此没有磁偶极作用. 然而, 微波谐振腔存在两类光子, 一类是前述的谐振腔光子, 具有驻波特征, 另一类是行波光子. 行波光子在传播的过程中与磁子和谐振腔光子都发生作用, 因此导致了一种间接的耗散型磁子-光子作用^[36,37]. 相干型耦合和耗散型耦合在波导型谐振腔^[36]和微带线谐振腔^[37]的实验中都已经被观测到. 而且, 由于这两种耦合作用之间存在干涉作用, 最近的实验研究观测到了微波透射谱中这种耦合作用干涉引起的零阻尼现象, 这种零阻尼现象在微波透射谱中对应于具有极窄线宽的尖谷^[38], 这对于设计基于磁子的量子传感器件是极为重要的.

目前, 除了单个磁子模式与光子耦合的实验与理论工作之外, 还存在一些多个磁子模式与光子耦合的研究工作^[39–42]. 例如, 多个YIG小球放置在微波谐振腔或者波导中实现磁子-光子耦合^[39–42]; 除了光子之外, 以弹性介质中的声波为媒介的多个磁子之间的耦合也已经实现^[43]. 在磁学领域, 磁性双层或多层膜是可以产生两个或多个磁子模式的, 而且磁子与磁子之间可以通过界面交换耦合作用来实现直接相互作用^[44,45]. 在最近的理论研究中, 我们研究了界面交换耦合的磁双层的两个磁子模式与光子的强耦合作用, 分析了两个磁子模式形成的磁子暗态^[46]. 然而, 该研究仅仅考虑了磁子与光子之间的相干型耦合. 如果磁子与光子之间属于耗散型耦合, 或者相干型与耗散型耦合同时存在, 那么是否会产生新的物理效应? 例如, 前述的零阻尼现象是否会继续存在? 磁双层中界面交换耦合作用如何影响零阻尼现象? 基于这些考虑, 本文从理论的角度进一步研究了微波谐振腔中界面交换耦合的磁双层中的零阻尼现象, 从哈密顿量出发推导了磁子与光子的动力学方程以及微波透射谱, 并给出了数值结果.

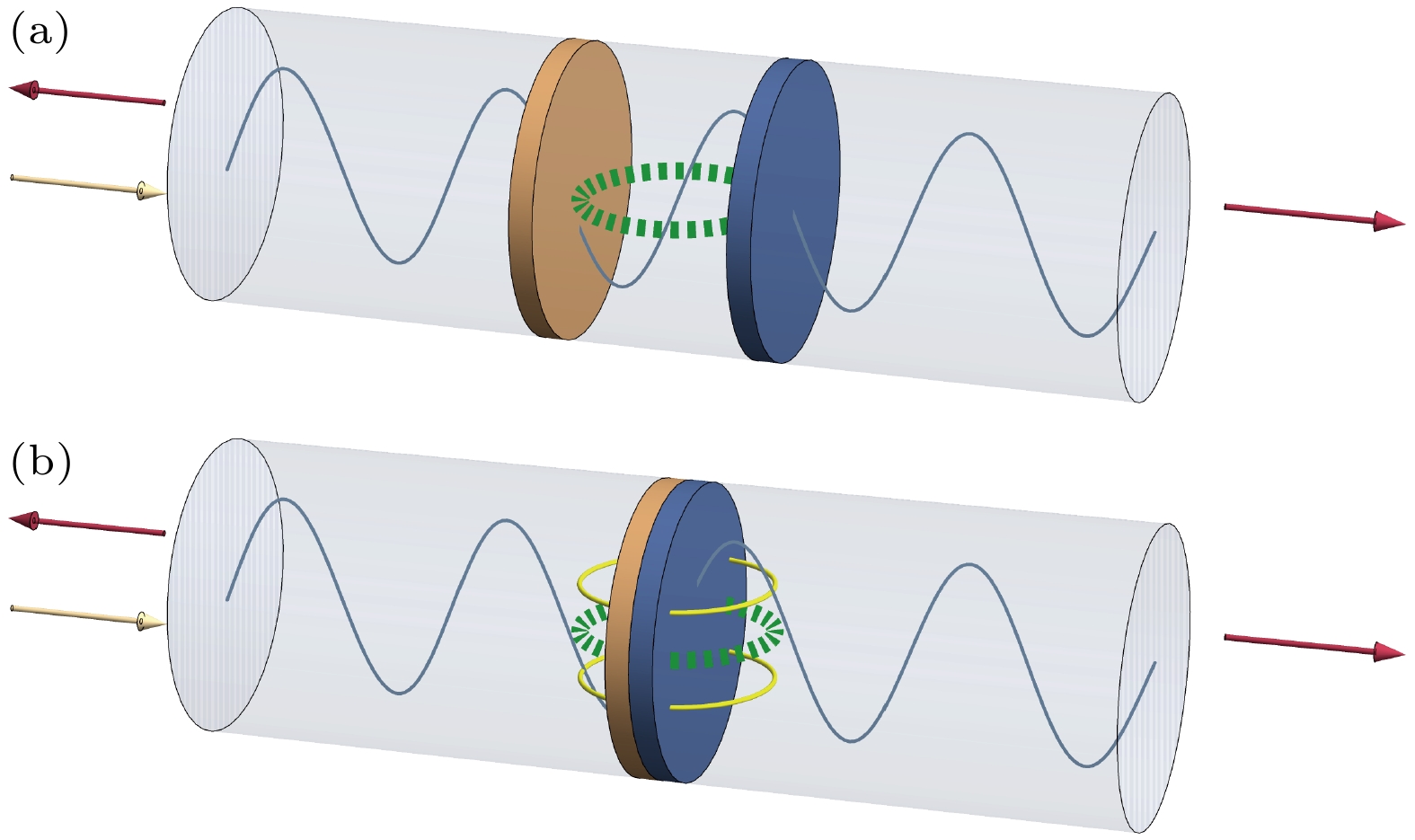
图1所示为铁磁层与微波谐振腔的器件模型. 在图1(a)中, 两个铁磁层放置在微波谐振腔的两个不同的波腹(具有最大的微波磁场)上, 两个磁子模式通过磁偶极作用同时与微波磁场作用, 从而实现由微波谐振腔辅助的磁子-磁子耦合作用, 这一器件模型在腔磁子学领域已经获得了一些关注^[5]. 图1(b)给出了另外一种结构模型, 在微波谐振腔中将两个铁磁层直接放置在一起形成磁双层结构. 相比于图1(a)的结构模型, 磁双层中的界面交换耦合将会导致磁子与磁子形成直接的耦合作用; 同时, 如前所述, 两个磁子与谐振腔作用形成的间接耦合也存在. 因此, 在这一模型中, 磁子与磁子的界面交换直接耦合与谐振腔辅助的间接耦合同时存在, 其哈密顿量可以写为^[40]

其中$ {\omega }_{{\mathrm{c}}} $, $ {\omega }_{{\mathrm{a}}} $和$ {\omega }_{{\mathrm{b}}} $分别为谐振腔光子的共振频率和磁子$ {\mathrm{a}} $与$ {\mathrm{b}} $的频率, $ c\left({c}^{†}\right) $, $ a\left({a}^{†}\right) $和$ b\left({b}^{†}\right) $为光子和磁子的湮灭(产生)算符, $ {G}_{{\mathrm{a}}} $和$ {G}_{{\mathrm{b}}} $分别为磁子$ {\mathrm{a}} $和磁子$ {\mathrm{b}} $分别与谐振腔光子的耦合强度, $ {g}_{{\mathrm{a}}{\mathrm{b}}} $为两个磁子通过界面交换耦合产生的耦合强度. 在(1)式的推导中, 我们对于磁子与光子的磁偶极作用$ \boldsymbol{M}\cdot \boldsymbol{h} $以及磁子与磁子的界面交换耦合作用$ {\boldsymbol{M}}_{{\mathrm{a}}}\cdot {\boldsymbol{M}}_{{\mathrm{b}}} $均采用算符处理, 即将微波磁场$ \boldsymbol{h} $和磁化强度$ \boldsymbol{M} $分别通过电磁场二次量子化^[47]和Holstein-Primakoff变换^[48]表示为光子算符与磁子算符, 并考虑旋波近似去除掉反旋项^[40]. 此外, 我们也引入了一些物理量, $ {\omega }_{{\mathrm{m}}}= {1}/{2}\left({\omega }_{{\mathrm{a}}}+{\omega }_{{\mathrm{b}}}\right) $和$ {\delta }_{{\mathrm{a}}{\mathrm{b}}}= {\omega }_{{\mathrm{a}}}-{\omega }_{{\mathrm{b}}} $表示两个磁子频率的平均值与失谐量, $ {\kappa }_{{\mathrm{c}}} $, $ {\kappa }_{{\mathrm{a}}} $和$ {\kappa }_{{\mathrm{b}}} $为光子与磁子的本征耗散率. 在(1)式中, 磁子与光子的耦合强度$ {G}_{{\mathrm{a}}} $和$ {G}_{{\mathrm{b}}} $为复数, 即$ {G}_{{\mathrm{a}}}= {g}_{{\mathrm{a}}}-{\mathrm{i}}{\varGamma }_{{\mathrm{a}}} $和$ {G}_{{\mathrm{b}}}= {g}_{{\mathrm{b}}}- {\mathrm{i}}{\varGamma }_{{\mathrm{b}}} $. 在常规的磁子与光子耦合实验与理论中^[1–20], $ {G}_{{\mathrm{a}}} $和$ {G}_{{\mathrm{b}}} $一般选为实数, 也就是说磁子与光子的耦合哈密顿量是厄米的. 然而, 如引言所述, 在最近的一些磁子/光子耦合实验中, 研究发现在谐振腔中存在行波光子, 它们同时与谐振腔驻波光子和磁子进行耗散耦合, 其耦合强度为虚数. 当相干型耦合和耗散型耦合同时存在时, 耦合强度一般为复数, 这已经被腔磁子学的实验结果所验证^[36–38]. 不同于复数$ {G}_{{\mathrm{a}}} $和$ {G}_{{\mathrm{b}}} $, 磁子间的界面交换耦合作用是相干作用, 因此在本工作中, 耦合强度$ {g}_{{\mathrm{a}}{\mathrm{b}}} $选为实数. 在最近的一个镍/YIG磁性膜的实验中, 观测到磁子-磁子耦合强度大约在120 MHz^[49]. 基于此, 本工作中$ {g}_{{\mathrm{a}}{\mathrm{b}}} $取值范围选为100—200 MHz.

在哈密顿量(1)式的基础上, 写出运动方程并引入耗散率, 即可写出算符平均值的动力学方程:

式中频率失谐量$ {\delta }_{{\mathrm{c}}{\mathrm{d}}}= {\omega }_{{\mathrm{c}}}-{\omega }_{{\mathrm{d}}} $, $ {\delta }_{{\mathrm{a}}{\mathrm{d}}}= {\omega }_{{\mathrm{a}}}-{\omega }_{{\mathrm{d}}} $和$ {\delta }_{{\mathrm{b}}{\mathrm{d}}}= {\omega }_{{\mathrm{b}}}-{\omega }_{{\mathrm{d}}} $, 其中$ {\omega }_{{\mathrm{d}}} $为谐振腔的驱动频率, $ {c}_{{\mathrm{i}}{\mathrm{n}}} $为驱动场的幅度, $ {\kappa }_{{\mathrm{e}}{\mathrm{x}}} $为外部耗散率.

在稳态条件下, 结合输入输出关系^[46], 可以求出体系的微波透射谱:

其中$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}}= {\omega }_{{\mathrm{m}}}-{\omega }_{{\mathrm{c}}} $和$ {\varDelta }_{{\mathrm{c}}}= {\varDelta }_{{\mathrm{d}}{\mathrm{c}}}= {\omega }_{{\mathrm{d}}}-{\omega }_{{\mathrm{c}}} $. 本工作计算的微波透射谱为S₂₁对$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $和$ {\varDelta }_{{\mathrm{d}}{\mathrm{c}}} $的变化关系图, 并考虑不同的耦合强度$ {G}_{{\mathrm{a}}} $, $ {G}_{{\mathrm{b}}} $和$ {g}_{{\mathrm{a}}{\mathrm{b}}} $的大小对于微波透射谱的影响. 在数值计算中, 一些固定不变的参数包括$ {\kappa }_{{\mathrm{c}}} $= 15 MHz, $ {\kappa }_{{\mathrm{a}}} $= 1 MHz, $ {\kappa }_{{\mathrm{b}}} $= 1 MHz和$ {\kappa }_{{\mathrm{e}}{\mathrm{x}}} $= 880 MHz, 这些参数的大小及$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $和$ {\varDelta }_{{\mathrm{d}}{\mathrm{c}}} $的取值范围均来自于最近的实验结果^[38].

以前的研究结果表明^[38]: 当同时存在耗散型和相干型耦合时, 体系的本征态的阻尼可以变为零, 同时在微波透射谱中出现线宽极窄的尖谷. 这一结果是针对单个磁子模式而言的, 此处将这一结果推广到两个磁子模式的情况. 为了方便解析推导, 考虑两个磁子模式的频率、耗散率和耦合强度都相等, 也就是$ {\delta }_{{\mathrm{a}}{\mathrm{b}}} $= 0, $ {\kappa }_{{\mathrm{a}}}= {\kappa }_{{\mathrm{b}}}= {\kappa }_{{\mathrm{m}}} $和$ {g}_{{\mathrm{a}}}-{\mathrm{i}}{\varGamma }_{{\mathrm{a}}}= {g}_{{\mathrm{b}}}- {\mathrm{i}}{\varGamma }_{{\mathrm{b}}}= g-{\mathrm{i}}\varGamma = G $. 可以推导哈密顿量(1)式的本征频率:

在推导(4)式的过程中, 通过将频率$ \omega $表示为复频率$ \widetilde{\omega }= \omega -{\mathrm{i}}\kappa $的方式来引入耗散率的影响. 此外, 3个模式的耦合作用产生了3个本征频率$ {\widetilde{\omega }}_{\pm } $和$ {\widetilde{\omega }}_{{\mathrm{d}}{\mathrm{a}}{\mathrm{r}}{\mathrm{k}}} $, 其中$ {\widetilde{\omega }}_{{\mathrm{d}}{\mathrm{a}}{\mathrm{r}}{\mathrm{k}}} $的形式说明其与谐振腔光子不耦合, 这是由于两个磁子模式同时与谐振腔光子的耦合发生了干涉相消^[40], 从而产生了磁子暗态. $ {\widetilde{\omega }}_{\pm } $则为干涉相长产生的磁子亮态与谐振腔光子耦合的频率.

零阻尼条件(zero damping condition)对应于$ {\widetilde{\omega }}_{\pm } $的虚部为零, 即Im($ {\widetilde{\omega }}_{\pm } $)= 0. 零阻尼条件在微波透射谱上的表现为零透射系数, 即$ {S}_{21} $= 0. 为了说明这一点, 先将透射谱(3)式改写为

将(4)式代入(5)式, 则有

可看到, 当$ {\varDelta }_{{\mathrm{d}}{\mathrm{c}}}= {\mathrm{R}}{\mathrm{e}}\left({\widetilde{\omega }}_{\pm }\right) $且$ {\rm Im}({\widetilde{\omega }}_{\pm }) = 0 $, 有$ {S}_{21} = 0$. 这一结果表明, 在磁双层中, 零阻尼条件也是存在的. 另外, (6)式也表明微波透射谱$ {S}_{21} $和本征频率$ {\widetilde{\omega }}_{\pm } $都可以体现零阻尼效应. 接下来, 基于微波透射谱和本征频率, 通过调整频率失谐来获取零阻尼条件.

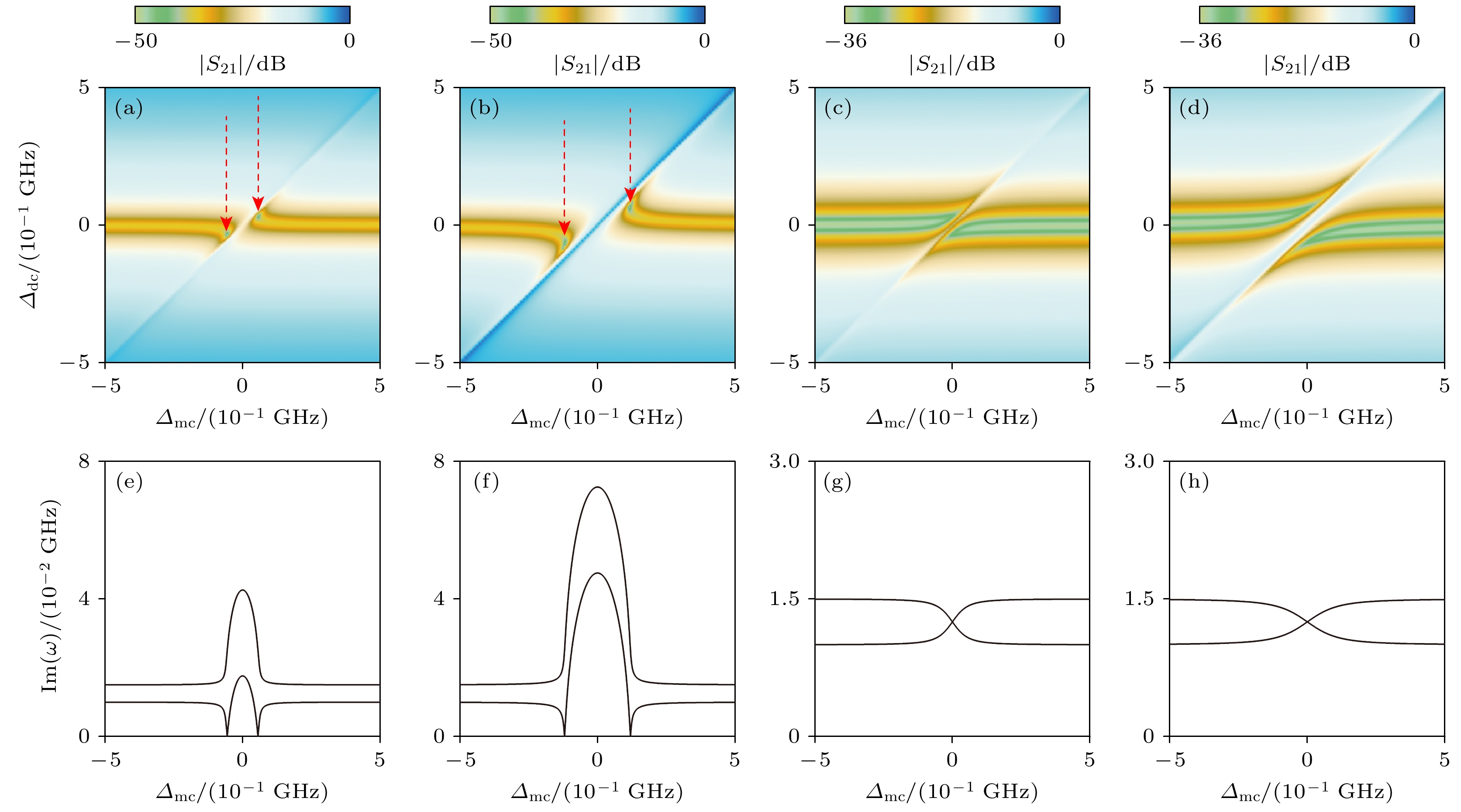
在讨论本文重点关注的磁双层的磁子与光子耦合之前, 首先给出磁单层中的磁子与光子耦合的本征频率和微波透射谱. 对于单个磁子模式, 层间交换耦合带来的相互作用$ {g}_{{\mathrm{a}}{\mathrm{b}}} $= 0, 磁子-光子耦合作用G_a和G_b只需要考虑一个. 图2(a), (b)为纯的耗散型耦合的微波透射谱, 即$ G= -{\mathrm{i}}\varGamma $. 纯的耗散型耦合的微波透射谱表现出明显的能级吸引特征, 共振点附近存在能级靠近的区域, 且随着耦合强度$ \varGamma $的增大, 这一区域的宽度逐渐增大. 除了微波透射谱之外, 在图2(e), (f)中给出了本征频率$ {\widetilde{\omega }}_{\pm } $的虚部, 可以看到在$ {\varDelta }_{{\mathrm{mc}}} $= 0的附近存在两个对称的虚部为零的点, 即零阻尼点. 这一对零阻尼点在微波透射谱中的位置用红色虚线箭头表示. 相比于耗散型耦合, 图2(c), (d)给出的相干型耦合, 即$ G= g $, 表现出了不同的特征. 首先, 微波透射谱给出的是能级排斥的特征, 且能级排斥中的带隙大小等于磁子-光子耦合强度$ g $的2倍. 其次, 本征频率的虚部全都大于零, 不存在虚部等于零的情况, 也就是说纯的相干型耦合不存在零阻尼点. 以前的研究结果表明^[38], 对于单个磁子模式, 磁子-光子耦合强度为复数时, 即$ G= g-{\mathrm{i}}\varGamma $, 零阻尼点也存在. 该结果和本文结果共同表明, 零阻尼的出现主要取决于磁子与光子耦合系统的耗散机制, 即只出现在存在耗散型耦合的系统中.

我们先来推导零阻尼时的频率失谐$ {\varDelta }_{{\mathrm{mc}}, \mp }^{0} $, 以此来估计微波透射谱中的零阻尼点的位置, 同时也可以给出体系是否存在零阻尼的条件. 令(4)式中的本征频率的虚部为零, 即${\mathrm{Im}}( {\widetilde{\omega }}_{\pm }) = 0 $, 可以得到:

由于频率失谐$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}, \mp }^{0} $一定为实数, 因此根号里面的表达式必须大于零, 即

如果要出现零阻尼, (8)式必须要满足.

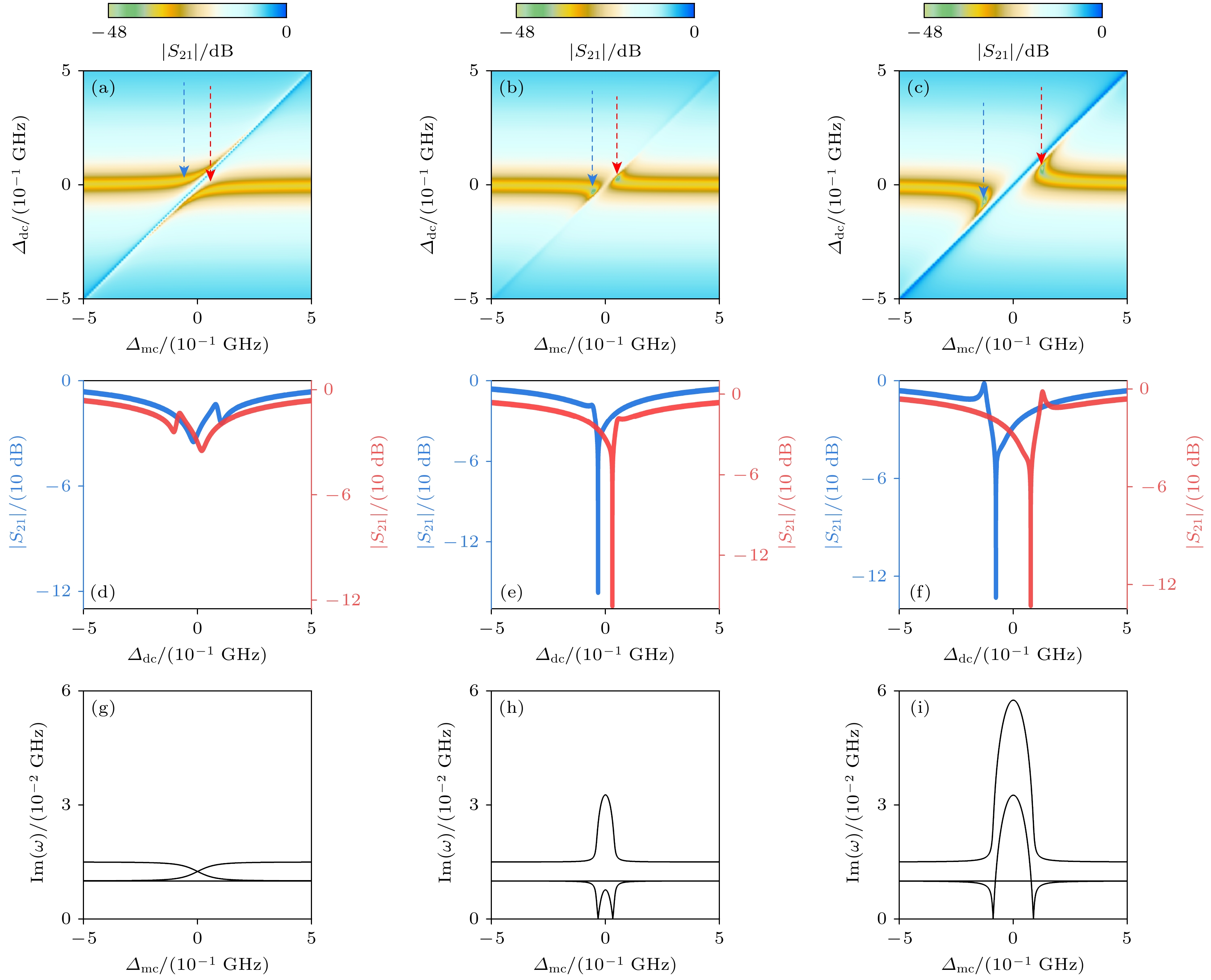
接下来讨论磁双层的数值结果. 如图3(a), (d), (g)给出了磁子与光子相干耦合时的微波透射谱等高线图、随失谐量$ {\varDelta }_{{\mathrm{c}}} $的变化图, 以及本征频率虚部Im($ {\widetilde{\omega }}_{\pm } $)与$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}} $的变化图. 首先考虑没有界面交换耦合$ {g}_{{\mathrm{a}}{\mathrm{b}}} $的情况. 对于相干耦合, 即$ G= g $, 微波透射谱表现出能级排斥的特征, $ {S}_{21} $随$ {\varDelta }_{{\mathrm{c}}} $的变化曲线(图3(d))中的两个尖谷之间的距离反映 了耦合强度. 这里的微波透射谱看上去只有两支, 但是磁双层与谐振腔一共有3个模式, 这种差异 主要是由于暗模式$ {\widetilde{\omega }}_{{\mathrm{d}}{\mathrm{a}}{\mathrm{r}}{\mathrm{k}}} $造成的. 磁子暗模式不与谐振腔光子耦合, 因而不出现在微波透射谱上. 另外, 本征频率的虚部(图3(g))全部大于零, 没有零阻尼现象, 这与磁单层是一样的. 可以根据零阻尼出现的条件, 即(8)式, 来做进一步分析. 相干耦 合的$ g\ne 0 $且$ \varGamma $= 0, 代入(8)式, 根号下的$ 4{g}^{2}{\varGamma }^{2} - {\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}} ({\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}}+2{g}^{2}-{2\varGamma }^{2}) = -{\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}} ({\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}}+2{g}^{2}) < 0 $不满足(8)式, 所以不能产生零阻尼.

图3(b), (e), (h)给出了耗散耦合的结果. 当$ g= $0且$ \varGamma \ne $0时, 零阻尼条件$ 4{g}^{2}{\varGamma }^{2}-{\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}}\left({\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}}+ 2{g}^{2}-{2\varGamma }^{2}\right)= {\kappa }_{{\mathrm{m}}}{\kappa }_{c}\left({2{\varGamma }^{2}-\kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}}\right) $. 若$ {2{\varGamma }^{2} > \kappa }_{{\mathrm{m}}}{\kappa }_{{\mathrm{c}}} $时, 存在零阻尼. 进一步可以计算零阻尼时的频率失谐为

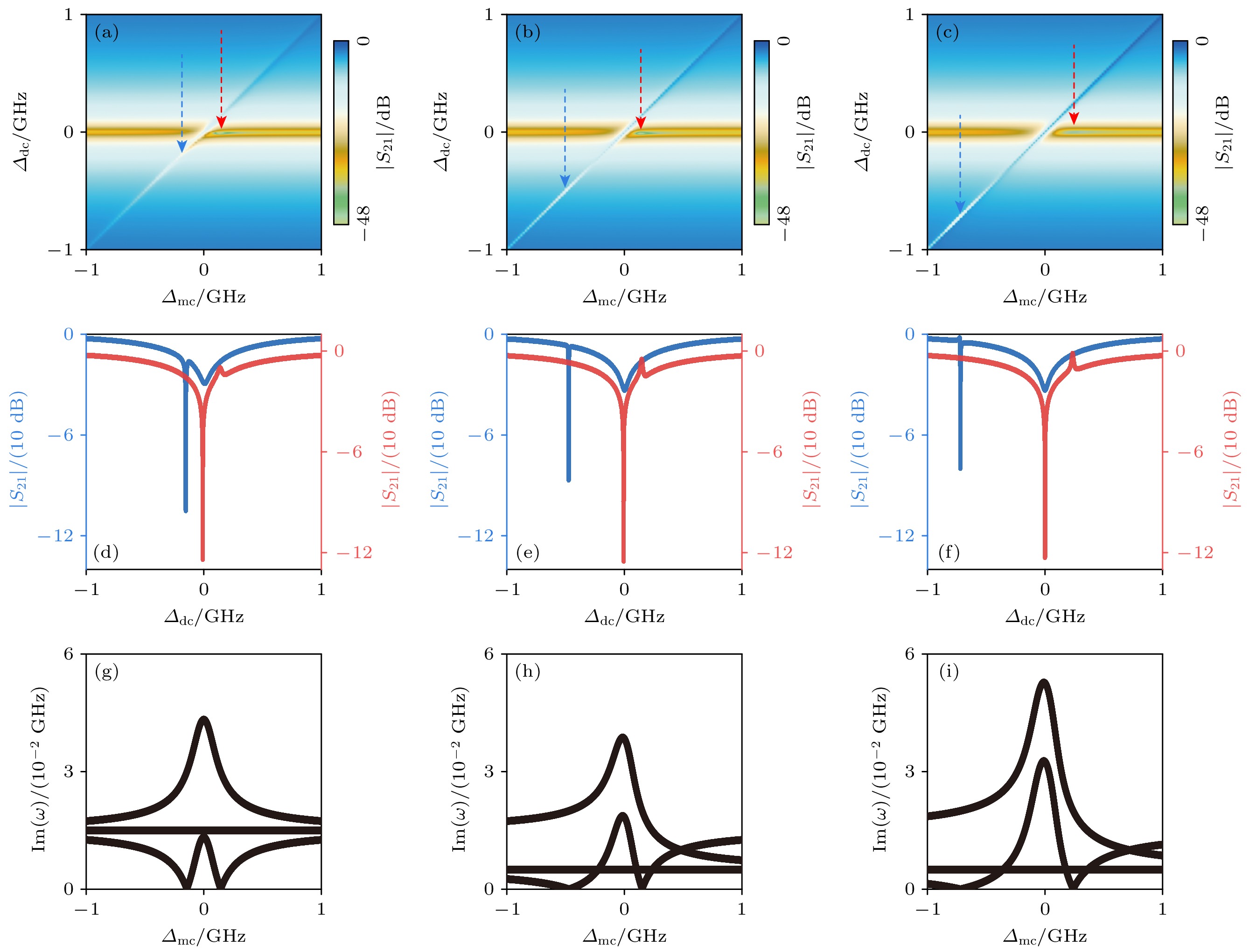
从(9)式可以看出两个特征: 首先, $ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}, \mp }^{0} $一正一负, 且关于$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}}^{0} $= 0对称. 其次, 随着耦合强度$ \varGamma $增大, 两个零阻尼点之间的距离, 即$ {\varDelta }_{{\mathrm{mc}}, +}^{0} $和$ {\varDelta }_{{\mathrm{mc}}, -}^{0} $也会加大. 这两个特征在图3(b), (e), (h)和图3(c), (f), (i)中可以清楚看到.

相比于前述纯的耗散型耦合或纯的相干型耦合的结果, 图4所示为耗散型耦合与相干型耦合同时存在时的混合型耦合的结果. 混合型耦合带来的一个新特征就是零阻尼点不总是关于$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}}^{0} $= 0对称. 首先, 当光子与磁子具有相同的耗散率, 即$ {\kappa }_{{\mathrm{m}}}= { \kappa }_{{\mathrm{c}}} $, 如图4(a), (d), (g)所示, 两个零阻尼点依然保持对称. 这一点可以通过把$ {\kappa }_{{\mathrm{m}}}{= \kappa }_{{\mathrm{c}}} $代入(7)式得到以下频率失谐:

但是, 当$ {\kappa }_{{\mathrm{m}}}{\ne \kappa }_{{\mathrm{c}}} $时, (7)式明显描述了两个不对称的零阻尼点, 这在图4的本征频率虚部的图中可以清楚看到. 其次, 随着耦合强度$ \varGamma $的增大, 两个零阻尼点之间的距离也逐渐增大, 这在(7)式中也能得到体现.

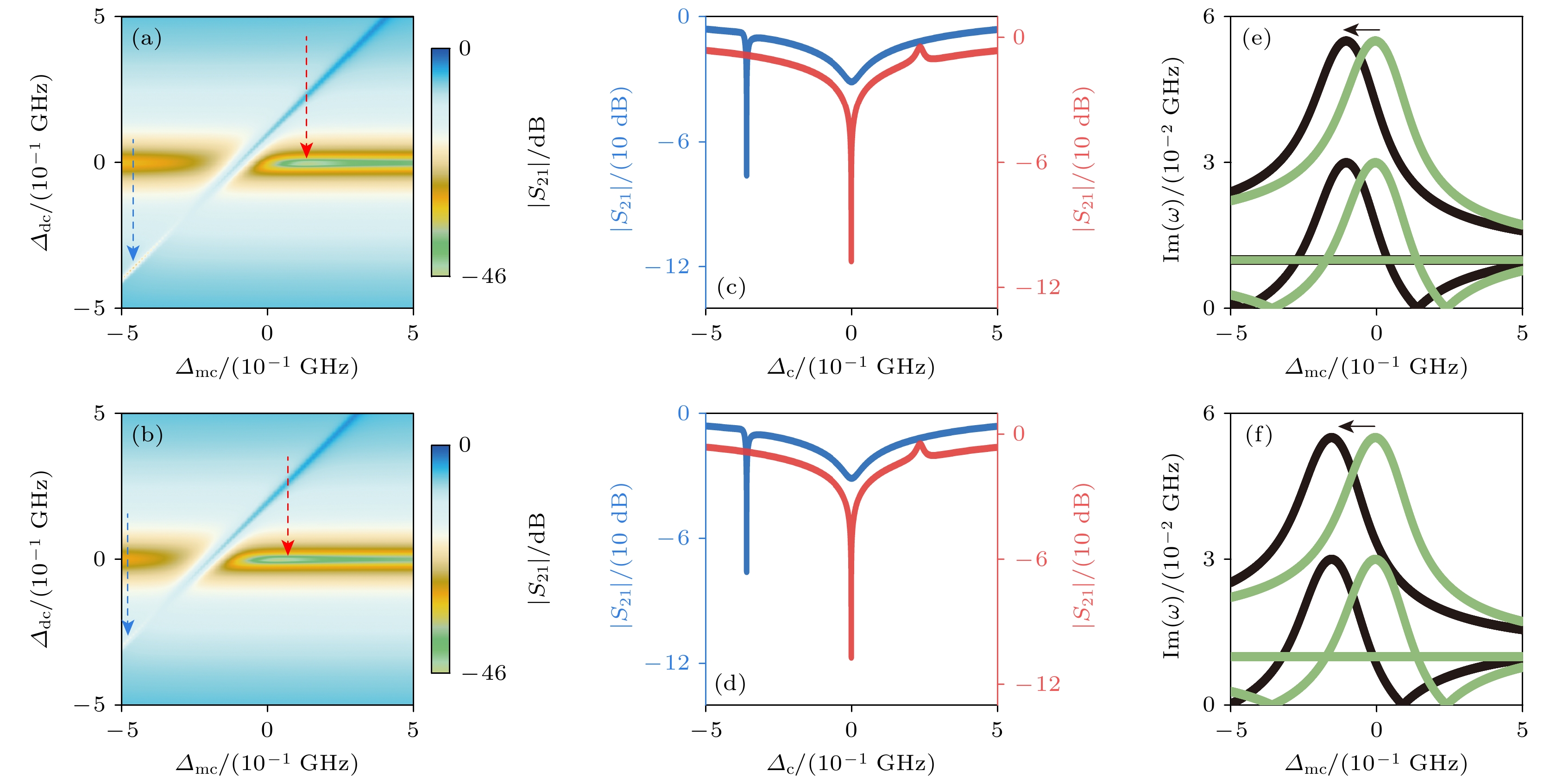
当引入层间交换耦合$ {g}_{{\mathrm{a}}{\mathrm{b}}} $之后, 本征频率和频率失谐都将受到层间交换耦合作用的影响. 本征频率, 即(4)式变为

而零阻尼时的频率失谐, 即(7)式变为

从(12)式可以看到, 层间交换耦合使得频率失谐$ {\varDelta }_{{\mathrm{m}}{\mathrm{c}}, \mp }^{0} $产生了一个$ {g}_{{\mathrm{a}}{\mathrm{b}}} $的整体移动, 因此两个零阻尼点之间的间距并未受到层间交换耦合的影响. 另外, 由于(12)式中的$ {g}_{{\mathrm{a}}{\mathrm{b}}} $前面的负号, 所以层间交换耦合时的本征频率虚部的曲线相比于没有层间交换耦合向左发生平移. 平移量由$ {g}_{{\mathrm{a}}{\mathrm{b}}} $来决定, 因此层间交换耦合作用越强, 平移量越大. 上述这些分析在图5的数值结果中都得到了体现.

尽管本工作研究的是磁性双层膜, 但是研究方法可以直接应用到磁性多层膜, 研究结论对于磁性多层膜具有一定的借鉴作用. 对于磁性多层膜, 哈密顿量将会引入更多的磁子-光子耦合和磁子-磁子耦合, 动力学方程的建立以及微波透射谱的计算方法与磁性双层膜一致. 在物理机制上, 当没有层间交换耦合时, 零阻尼的物理机制与双层膜类似; 当存在层间交换耦合时, 多重耦合机制的叠加使得物理机制变得更为复杂, 这将在未来的工作中进行探讨.

本工作通过计算微波透射谱和分析本征频率, 研究了微波谐振腔中的两个磁子模式的零阻尼效应. 首先推导了两个磁子模式在没有和存在层间交换耦合情况下的动力学方程和微波透射系数的解析表达式, 并根据阻尼为零的条件推导了两个磁子模式与微波谐振腔作用时的零阻尼的解析表达式. 其次, 当两个磁子模式之间没有层间耦合, 即仅仅存在谐振腔辅助耦合的情况, 相干型耦合没有阻尼现象, 只有耗散型耦合才有. 随着耦合强度的增大, 两个零阻尼点之间的距离逐渐增大. 当磁子与光子耦合为混合型耦合时, 相比于纯的耦合方式, 两个零阻尼点变得不再对称. 当引入层间交换耦合时, 层间交换耦合仅仅在零阻尼点的频率失谐上引入一个整体的移动, 这使得本征频率虚部曲线向左发生平移, 而两个零阻尼点之间的距离并不会变化. 由于零阻尼点的线宽非常窄, 因而表现出了极高的灵敏度, 所以本研究结果对于基于两个磁子模式的微波传感和精密测量器件具有一定的意义.