高级搜索

一种基于多目标粒子群算法的太赫兹超材料吸收器快速优化方法

,  ,  ,  , 

downloadPDF

上一篇

下一篇

王玉蓉, 屈薇薇, 李桂琳, 邓琥, 尚丽平. 一种基于多目标粒子群算法的太赫兹超材料吸收器快速优化方法[J]. 物理学报, 2025, 74(5): 057801-1. doi: 10.7498/aps.74.20241684
引用本文: 王玉蓉, 屈薇薇, 李桂琳, 邓琥, 尚丽平. 一种基于多目标粒子群算法的太赫兹超材料吸收器快速优化方法[J]. 物理学报, 2025, 74(5): 057801-1. doi: 10.7498/aps.74.20241684
shu
Yurong WANG, Weiwei QU, Guilin LI, Hu DENG, Liping SHANG. An optimization method for terahertz metamaterial absorber based on multi-objective particle swarm optimization[J]. Acta Physica Sinica, 2025, 74(5): 057801-1. doi: 10.7498/aps.74.20241684
Citation: Yurong WANG, Weiwei QU, Guilin LI, Hu DENG, Liping SHANG. An optimization method for terahertz metamaterial absorber based on multi-objective particle swarm optimization[J]. Acta Physica Sinica, 2025, 74(5): 057801-1. doi: 10.7498/aps.74.20241684
shu

一种基于多目标粒子群算法的太赫兹超材料吸收器快速优化方法

  • 1.

    西南科技大学信息工程学院, 绵阳　621010

  • 2.

    西南科技大学四川天府新区创新研究院, 成都　610299

    • 作者简介: 王玉蓉. E-mail: YurongW_29@126.com .
    通讯作者: E-mail: quweiwei@swust.edu.cn.; 

  • 中图分类号: 78.20.Ci, 81.05.Xj, 78.47.jh

An optimization method for terahertz metamaterial absorber based on multi-objective particle swarm optimization

  • 1.

    School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China

  • 2.

    Tianfu Institute of Research and Innovation, Southwest University of Science and Technology, Chengdu 610299, China

    • Corresponding author: E-mail: quweiwei@swust.edu.cn.; 

  • MSC: 78.20.Ci, 81.05.Xj, 78.47.jh

  • 摘要: 传统太赫兹超材料吸收器设计需多次试错调整, 十分依赖设计人员的经验, 设计时间成本高、效率低, 而目前基于机器学习的设计方法或需要准备大量样本, 或无法并行优化多个目标. 为解决这一问题, 本文提出一种基于多目标粒子群的几何参数优化方法, 以吸收率和品质因子为设计目标寻找符合要求的结构参数和介质厚度, 并以一个由四个角码型金属组成的中心对称结构的吸收器为例进行优化设计. 仿真结果表明, 多目标粒子群所快速获取的结构几何参数可以同时满足高吸收率和高品质因子两个设计目标, 明显优于粒子群算法. 通过该方法设计的吸收器在1.613 THz的吸收率大于99%, 品质因子为319.72, 其传感灵敏度可达264.5 GHz/RIU. 相比于传统设计方法, 此方法设计出的超材料吸收器可以实现高吸收率、高品质因子和高灵敏度, 为超材料吸收器的设计提供了新的思路, 具有广阔的应用前景.
    Abstract: Metamaterials can freely control terahertz waves by designing the geometric shape and direction of the unit structure to obtain the desired electromagnetic characteristics, so they have been widely used in sensing, communication and radar stealth technology. The traditional design of terahertz metamaterial absorber usually requires continuous structural adjustment and a large number of simulations to meet the expected requirements. The process largely relies on the experience of researchers, and the physical modeling and simulation solution process is time-consuming and inefficient, greatly hindering the development of metamaterial absorbers. Therefore, due to its powerful learning ability, deep learning has been used to predict the structural parameters or spectra of metamaterial absorbers. However, when designing a new structure, it is necessary to prepare a large number of training samples again, which is both time-consuming and not universal. Particle swarm optimization algorithm can quickly converge to the optimal solution through the sharing and cooperation of individual information in the group, with no need for prior preparation. Therefore, a method of fast designing terahertz metamaterial absorber is proposed based on multi-objective particle swarm optimization algorithm in this work. Taking a new center symmetric absorber structure composed of four Ls for example, the structure parameters are optimized to achieve rapid and automatic design of metamaterial absorber. The multi-objective particle swarm optimization algorithm takes the absorptivity and quality factor as independent targets to design the structure parameters of the absorber, realizing the dual-objective optimization of the absorber, and overcoming the shortcoming of the multi-objective conflicts that cannot be solved by PSO. When used for refractive index sensing, the optimally-designed absorber achieves perfect absorption at 1.613 THz with a quality factor of 319.72 and a sensing sensitivity of 264.5 GHz/RIU. In addition, the reasons of absorption peaks are analyzed in detail through impedance matching, surface current, and electric field distribution. By studying the polarization characteristics of the absorber, it is found that the absorber is not sensitive to polarization, which is more stable in practical application. In summary, the multi-objective particle swarm optimization algorithm can realize the design according to the requirements, reduce the experience requirement of researchers in the design of metamaterial absorber, thereby improving design efficiency and performance, and has great potential for application in the design of terahertz functional devices.
  • 加载中

  • 图 1  单元结构示意图　(a) 单元结构侧视图; (b) 单元结构俯视图

    Figure 1.  Unit structure diagram: (a) Side view of the unit structure; (b) top view of the unit structure.

    下载: 全尺寸图片 幻灯片

    图 2  自适应网格法步骤　(a)寻找边界; (b)边界扩张; (c)网格划分

    Figure 2.  Adaptive mesh method steps: (a) Boundary finding; (b) boundary expansion; (c) mesh generation.

    下载: 全尺寸图片 幻灯片

    图 3  设计实现流程

    Figure 3.  Implementation flow chart.

    下载: 全尺寸图片 幻灯片

    图 4  经过优化的单元结构及其光谱

    Figure 4.  Optimized cell structure and spectrum.

    下载: 全尺寸图片 幻灯片

    图 5  等效阻抗的实部与虚部

    Figure 5.  The real and imaginary parts of the equivalent impedance.

    下载: 全尺寸图片 幻灯片

    图 6  1.613 THz处表面电流和电场分布图　(a) 1.613 THz处有反射底板表面电流; (b)无反射底板表面电流; (c) 1.613 THz处表面电场分布; (d) 1.613 THz处y = 100平面电场分布; (e) 1.613 THz处x = 100平面电场分布

    Figure 6.  Surface current and electric field distribution at 1.613 THz: (a) Surface current at 1.613 THz of an absorber with reflective backplate; (b) surface current of the absorber without reflective backplate; (c) surface electric field distribution at 1.613 THz; (d) y = 100 plane electric field distribution at 1.613 THz; (e) x = 100 plane electric field distribution at 1.613 THz.

    下载: 全尺寸图片 幻灯片

    图 7  不同折射率下主峰和次峰的谐振频率变化量及拟合曲线　(a)不同折射率下的谐振频率变化量; (b)灵敏度拟合曲线

    Figure 7.  The variation of resonant frequency of main and secondary resonant peaks under different refractive indices and their fitting curves. (a) The variation of resonant frequency under different refractive indices; (b) the sensitivity fitting curve of the resonant peak.

    下载: 全尺寸图片 幻灯片

    图 8  吸收器不同极化角度φ (φ = 15, 30, 45, 60, 75, 90°)的吸收光谱

    Figure 8.  Absorption spectra of the absorber at different polarization angles φ ( φ = 15, 30, 45, 60, 75, 90°).

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  参数优化范围

    Table 1.  Parameter optimization range.

    Parameter d l g h
    Range/μm 10—30 40—85 10—30 10—25
    下载: 导出CSV

    表 2  非支配解集

    Table 2.  Non-dominant solution set.

    g/μml/μmd/μmh/μmA/%Qf0/THz
    12754241848.87473.321.638
    21746252299.99248.311.818
    31468111596.79411.071.707
    42159211899.96277.461.631
    52558221999.56319.721.613
    下载: 导出CSV

    表 3  不同制造误差对性能的影响

    Table 3.  Effect of different manufacturing errors on performance.

    Parameterg/μml/μmd/μmh/μmA/%Qf0/THz
    PA11.24%–2.63%1.65%–3.75%89.96394.951.63
    25.3156.4722.3618.29
    PA21.43%2.06%1.95%–0.86%92.82210.751.6123
    25.3659.2022.4318.84
    PA32.52%3.25%–2.98%3.21%96.92248.101.5992
    25.6359.8821.3419.63
    PA43.66%3.72%–2.74%3.76%95.22234.951.5970
    25.9260.1621.419.72
    下载: 导出CSV

    表 4  其他设计方法与本文方法所设计的吸收器性能对比

    Table 4.  Performance comparison of absorbers designed by other design methods and the method presented in this paper.

    Ref.f0/THzA/%Q仿真次数时间/h
    [13]1.19299.9931.7100072.6
    [18]0.25—0.3599.0843.734806.33
    [28]4.4899.1874.661500—
    [29]1.999.952.18020
    Proposed1.61399.56319.72404.57
    下载: 导出CSV
  • [1] 崔子健, 王玥, 朱冬颖, 岳莉莎, 陈素果 2019 中国激光 46 0614023 doi: 10.3788/CJL201946.0614023 Cui Z J, Wang Y, Zhu D Y, Yue L S, Chen S G 2019 Chin. J. Lasers 46 0614023 doi: 10.3788/CJL201946.0614023
    [2] 金嘉升, 马成举, 张垚, 张跃斌, 鲍士仟, 李咪, 李东明, 刘洺, 刘芊震, 张贻歆 2023 物理学报 72 084202 doi: 10.7498/aps.72.20222336 Jin J S, Ma J C, Zhang Y, Zhang Y B, Bao S Q, Li M, Li D M, Liu M, Liu Q Z, Zhang Y X 2023 Acta Phys. Sin. 72 084202 doi: 10.7498/aps.72.20222336
    [3] Nadège K, Fabrice L, Mathias F, Geoffroy L 2015 Nature 525 77 doi: 10.1038/nature14678
    [4] Meng T H, Hu D, Zhu Q F 2018 Opt. Commun. 415 151 doi: 10.1016/j.optcom.2018.01.048
    [5] 江晓运 2021 博士学位论文(武汉: 华中科技大学) Jiang X Y 2021 Ph. D. Dissertation (Wuhan: Huazhong University of Science and Technology
    [6] 潘学文, 赵全友, 梁晓琳 2021 光电子·激光 32 680 Pan X W, Zhao Y Q, Liang X L 2021 J. Optoelectron. Laser 32 680
    [7] Amirhossein N R, Pejman R 2022 Micro. Nanostruct. 163 107153 doi: 10.1016/j.spmi.2022.107153
    [8] Wang J C, Tu S, Chen T 2024 Physica E 155 115829 doi: 10.1016/j.physe.2023.115829
    [9] 涂建军, 马丁 2023 电子学报 51 3262 doi: 10.12263/DZXB.20220519 Tu J J, Ma D 2023 Acta Electron. Sin. 51 3262 doi: 10.12263/DZXB.20220519
    [10] Ma W, Cheng F, Liu Y M 2018 ACS Nano 12 6326 doi: 10.1021/acsnano.8b03569
    [11] Huo Z Y, Zhang P Y, Ge M F, Li J, Tang T T, Shen J, Li C Y 2021 Nanomaterials 11 2672
    [12] Ma J, Huang Y J, Pu M B, Xu D, Luo J, Guo Y H, Luo X G 2020 J. Phys. D 53 464002 doi: 10.1088/1361-6463/aba3ec
    [13] 谢朝辉, 屈薇薇, 邓琥, 李桂琳, 尚丽平 2023 光学学报 43 1316001 doi: 10.3788/AOS230480 Xie Z H, Qu W W, Deng H, Li G L, Shang L P 2023 Acta Opt. Sin. 43 1316001 doi: 10.3788/AOS230480
    [14] 江晓运 2022 博士学位论文(北京: 北京科技大学) Feng Q 2022 Ph. D. Dissertation (Beijing: University of Science and Technology Beijing
    [15] Arora C, Pattnaik S S 2020 Evol. Intell. 14 801
    [16] Abolfazl M, Hamid R M, Abbas Z 2023 Photonics Nanostruct. 53 101105 doi: 10.1016/j.photonics.2022.101105
    [17] Chen Y, Ding Z X, Zhang M, Li M J, Zhao M, Wang J K 2021 Appl. Opt. 60 9200 doi: 10.1364/AO.438543
    [18] 韩丁, 马子寅, 王俊林, 岳莉莎, 王鑫, 刘苏雅拉图 2019 中国激光 49 1714001 Han D, Ma Z Y, Wang J L, Wang X, Liu S Y 2022 Chin. J. Lasers 49 1714001
    [19] Coello C A C, Pulido G T, Lechuga M S 2004 IEEE Trans. Evol. Comput. 8 256 doi: 10.1109/TEVC.2004.826067
    [20] Leng R, Ouyang A J, Liu Y M, Yuan L W, Wu Z Y 2020 Int. J. Pattern Recognit. Artif. Intell. 34 2059008 doi: 10.1142/S0218001420590089
    [21] 杨佳蓬, 逯景桐, 张帅, 岳莉莎, 许建春, 毕科 2024 电子元件与材料 43 176 Yang J P, Lu J T, Zhang S, Xu J C, Bi K 2024 Electron. Compon. Mater. 43 176
    [22] 葛宏义, 李丽, 蒋玉英, 李广明, 王飞, 吕明, 张元, 李智 2022 物理学报 71 108701 doi: 10.7498/aps.71.20212303 Ge H Y, Li L, Jiang Y Y, Li G M, Wang F, Lü M, Zhang Y, Li Z 2022 Acta Phys. Sin 71 108701 doi: 10.7498/aps.71.20212303
    [23] 曹瑞 2021 硕士学位论文(南京: 南京邮电大学) Cao R 2021 M. S. Thesis (Nanjing: Nanjing University of Posts and Telecommunications
    [24] Lin Q Z, Li J Q, Du Z H, Chen J Y, Zhong M 2015 Eur. J. Oper. Res. 247 732 doi: 10.1016/j.ejor.2015.06.071
    [25] Zhang J, Cho H, Mago P J, Zhang H G, Yang F B 2019 J. Therm. Sci. 28 1221 doi: 10.1007/s11630-019-1133-5
    [26] Xue B, Zhang M J, Browne W. N 2013 IEEE Trans. Cybern. 43 1656 doi: 10.1109/TSMCB.2012.2227469
    [27] 吴小刚, 刘宗歧, 田立亭, 丁冬, 杨水丽 2014 电网技术 38 3405 Wu X G, Liu Z Q, Tian L T, Ding D, Yang S L 2014 Power Syst. Technol. 38 3405
    [28] 梁泽坤 2022 硕士学位论文(成都: 电子科技大学) Liang Z K 2022 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
    [29] 谢朝辉 2024 硕士学位论文(绵阳: 西南科技大学) Xie Z H 2024 M. S. Thesis (Mianyang: Southwest University of Science and Technology
  • 加载中
图( 9) 表( 4)
计量
  • 文章访问数:  99
  • HTML全文浏览数:  99
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-05
  • 刊出日期:  2025-03-05

一种基于多目标粒子群算法的太赫兹超材料吸收器快速优化方法

    通讯作者: E-mail: quweiwei@swust.edu.cn.; 
    作者简介: 王玉蓉. E-mail: YurongW_29@126.com
  • 1. 西南科技大学信息工程学院, 绵阳　621010
  • 2. 西南科技大学四川天府新区创新研究院, 成都　610299
  • 收稿日期:  2024-12-05

摘要: 传统太赫兹超材料吸收器设计需多次试错调整, 十分依赖设计人员的经验, 设计时间成本高、效率低, 而目前基于机器学习的设计方法或需要准备大量样本, 或无法并行优化多个目标. 为解决这一问题, 本文提出一种基于多目标粒子群的几何参数优化方法, 以吸收率和品质因子为设计目标寻找符合要求的结构参数和介质厚度, 并以一个由四个角码型金属组成的中心对称结构的吸收器为例进行优化设计. 仿真结果表明, 多目标粒子群所快速获取的结构几何参数可以同时满足高吸收率和高品质因子两个设计目标, 明显优于粒子群算法. 通过该方法设计的吸收器在1.613 THz的吸收率大于99%, 品质因子为319.72, 其传感灵敏度可达264.5 GHz/RIU. 相比于传统设计方法, 此方法设计出的超材料吸收器可以实现高吸收率、高品质因子和高灵敏度, 为超材料吸收器的设计提供了新的思路, 具有广阔的应用前景.

English Abstract

    全文HTML

    1.   引　言

    • 超材料(metamaterial, MM)是人工单元结构组成的复合材料, 类比于原子或分子周期性排列形成[1], 具有如负折射率、逆多普勒效应、完美透镜效应等[2–4]天然材料不具备的独特性质, 在操控太赫兹波辐射方面具有极大的优势. 超材料吸收器(metamaterial absorber, MMA)可以实现对电磁波的高效吸收, 且可以通过改变其单元结构的几何形状和材料来自由控制吸收频率、吸收幅值等[5], 实现需要的电磁特性, 在传感、隐身雷达、成像和通信技术等领域[6–9]被广泛应用. 目前吸收器的设计主要着重于单元结构的几何形状及其参数设计, 由干涉相消理论可知介质层的厚度会影响电磁波在其中的传播路径长度, 从而改变反射波与入射波之间的相位差. 然而不论是图案还是介质厚度, 都是依靠设计人员的经验决定, 传统方法多通过模拟仿真得到光谱, 然后人工不断试错进行调整来得到所需性能, 设计时间成本高且要求设计人员有丰富的经验和较强的理论知识, 极大地阻碍了超材料吸收器的发展.

      虽然深度学习、神经网络等方法可以根据设计目标逆向设计超材料吸收器结构参数[10–13], 但前期需要准备大量训练样本, 且更换结构就需要重新训练模型, 耗费时间长. 而粒子群算法(particle swarm optimization, PSO)是一种基于群体智能的优化算法, 由James Kennedy和Russell Eberhart在1995年提出[14], 通过模拟鸟群觅食的行为解决优化问题. PSO是一种自适应算法, 无需前期训练数据, 在迭代过程中通过对全局最优和个体最优粒子的学习达到快速收敛, 近年来被广泛应用于超材料的设计. 涂建军等[9]通过PSO优化电磁隐身超表面结构实现预期反射相频特性, 全波仿真结果显示其在中心频率附近均可以得到–10 dB以上的雷达散射截面削减效果. Arora和Pattnaik[15]利用PSO设计了一种超材料圆极化贴片天线, 轴比带宽提高了450 MHz, 天线的增益可达5.2 dBic. Mokhtari等[16]通过PSO优化超宽带超材料吸收器, 优化后的结构在200—4500 nm的波长范围内显示出91.63%的高平均吸收率, 超过90%的吸收带宽为1590 nm. Chen等[17]对比遗传算法、麻雀搜索算法和PSO优化全介质超表面的性能, 结果表明PSO优化后品质因数提高了3倍. 韩丁等[18]用权重线性递减的PSO设计超材料吸波器金属谐振层, 在0.3122 THz处获得吸收率为99.08%的吸收峰, 品质因子为43.73、灵敏度为43.73 GHz/RIU.

      然而, 传统粒子群算法是一种单目标优化方法, 应用于超材料吸收器参数优化时只能分别以吸收率或品质因子作为目标, 无法二者兼顾; 或将两者进行加权处理后作为目标函数, 但对高品质因子的追求会降低吸收率在目标值中的比重, 出现高品质因子低吸收率的现象. 本文在PSO的基础上, 引入多目标优化方法, 针对一个顶层图案由4个角码型金属组成的中心对称超材料吸收器进行优化设计: 以结构参数和介质厚度作为待优化参数, 吸收率和品质因子为优化目标, 采用多目标粒子群算法[19] (multi-objective particle swarm optimization, MOPSO)同时处理两个目标函数, 利用非支配排序、自适应网格等[20]方法进行寻优, 实现超材料吸收器的自适应设计.

    2.   设计方法

      2.1.   结构设计

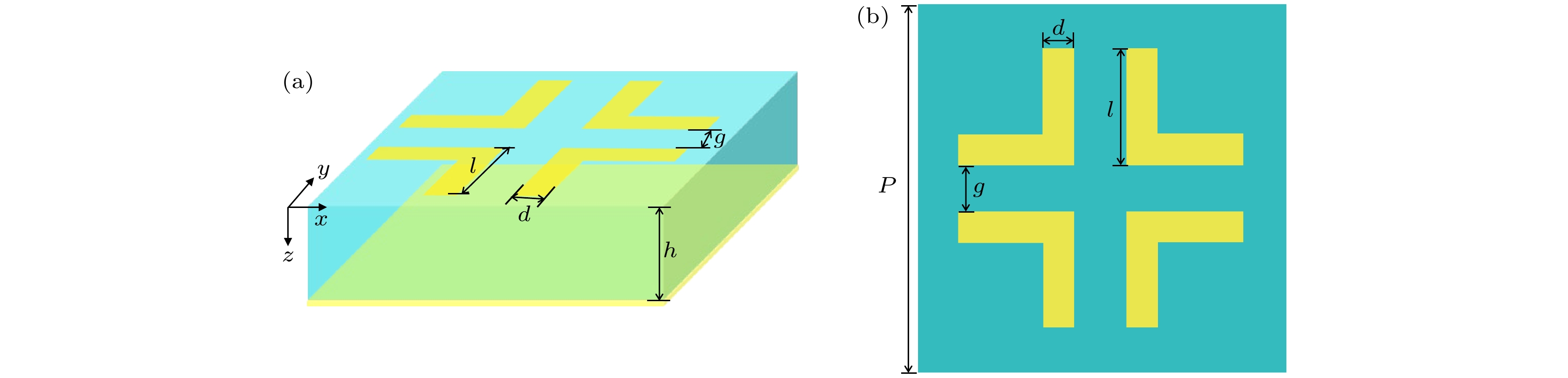
    • 所设计的MMA为典型的三明治结构, 如图1所示, 太赫兹波沿z轴方向垂直入射. 底层是金属底板, 其厚度应远大于金属在该频段内的趋肤深度, 将其设置为0.2 μm; 中间为介质层, 电磁波的能量会被限制在介质层中而表现出吸收特性, 合适的介质层厚度可以使得反射波与入射波的相位差恰好满足干涉相消的条件, 增强吸收效果; 顶层为金属谐振层, 其结构与尺寸决定了吸收器的电磁特性, 本设计中的顶层由四个L型结构组成, 呈中心对称分布. 金属底板和谐振层均使用0.2 μm的纯铜材料, 电导率为5.69×107 S/m[21]; 介质层选用相对介电常数${\varepsilon _{\text{r}}} = $2.1[22]的PTFE聚四氟乙烯, 厚度为h. 结构单元的周期设置为P = 200 μm, 角码型结构的长度为l, 宽度为d, 相邻角码型结构之间的距离为g.

      MMA的吸收特性主要依赖于顶层结构和介质层厚度, 为了使结构设计更加合理, 限制每个结构参数的变化范围如表1所列.

      评价吸收器性能指标主要有吸收率A和品质因子Q, 如(1)式和(2)式所示:

      其中${S_{11}}$表示反射系数; ${S_{21}}$代表透射系数, 由于金属底板的厚度(0.2 μm)远大于金属铜在1—2 THz频段内的趋肤深度(0.0464—0.0656 μm)[23], 所以透射系数为0; ${f_0}$表示谐振频率; $ {X_{{\text{FWHM}}}} $为谐振峰半高宽. 其中吸收率A代表吸收器对入射电磁波能量的吸收能力或效率, 高吸收率意味着能够有效地捕获并转化大部分或几乎全部的入射电磁波能量, 减少电磁波的反射和透射. 品质因子Q反映了谐振峰的损耗程度, Q值越大, 则能量损耗越小, 谐振峰也更加尖锐.

      基于超材料吸收器的传感器能够利用其对光的吸收特性来检测各种物质. 当待测物质与超材料吸收器相互作用时, 会改变其电磁环境, 从而导致谐振峰的频率发生偏移, 偏移量与待测物质的折射率、浓度等有关. 谐振频率偏移量$\Delta f$和待测物折射率的变化量$\Delta n$的比值为灵敏度, 反映了传感器对被测参数变化的灵敏程度:

      • 2.2.   多目标粒子群算法

    • 粒子群算法是一种基于群体智能的优化算法, 粒子之间相互协作在搜索空间中寻找目标函数的最优解, 跟踪个体最优和群体最优不断更新粒子的位置和速度[24]:

      w为惯性权重; c1, c2为加速因子; r1, r2为(0, 1)的随机数; $p_{id}^{(t)}$为第i个粒子在t时刻个体最优位置向量中的第d维分量; $g_d^{(t)}$为t时刻种群全局最优位置向量中的第d维分量; $x_{id}^{(t)}$, $v_{id}^{(t)}$为分别为第i个粒子在t时刻位置和速度向量中的第d维分量.

      超材料吸收器设计希望在近似完美吸收的基础上获得品质因子尽可能高的吸收峰, 然而粒子群算法仅适用于单目标优化, 因此只能将吸收率A和品质因子Q归一化求和作为目标函数. 这种方法可能导致函数值看似达到设计要求, 而实际上A和Q并没有同时满足各自的目标值. 这是因为Q值无上限, 在优化过程中, 某些粒子因其在品质因子Q上的极端优势掩盖了吸收率A在适应度评估中的作用, 使得函数值虽然符合设计要求但吸收率A实际上极低, 从而降低整体优化效果.

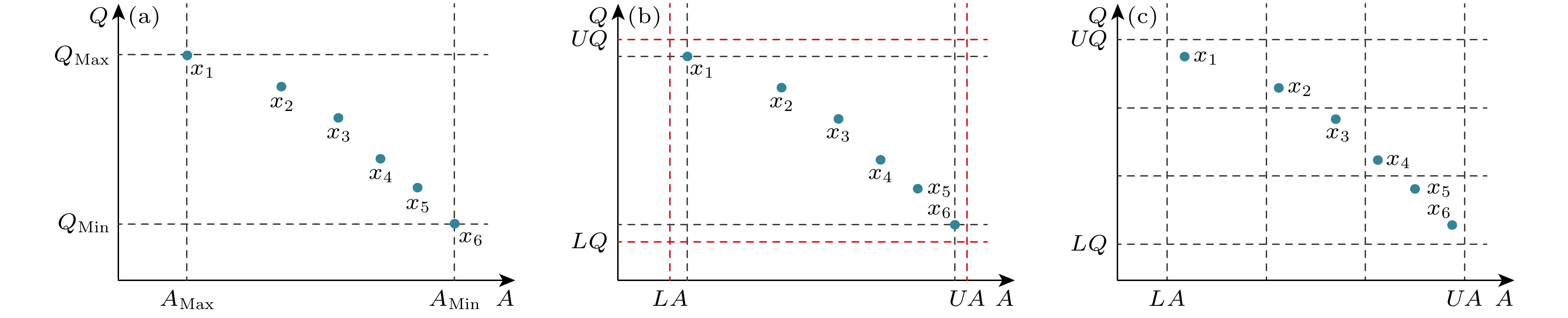
      多目标粒子群算法在粒子群算法的基础上引入了多目标优化策略, 能够直接处理并独立评估多个目标函数[25], 这些函数可能相互冲突, 一个目标的改善可能导致另一个目标的恶化, 所以引入了非支配[19]评价粒子的优劣. 若粒子y在所有目标上都不差于粒子z, 并且在至少一个目标上优于粒子z, 则粒子y支配粒子z; 若粒子y没有在所有目标上都优于粒子z, 则粒子y和z互为非支配关系[26]. 由此可知, 在优化过程中多个粒子之间均会呈现非支配关系, 因此通过非支配排序, 寻找一组非支配解集而不仅仅是单一的最优解, 以求在所有目标函数上达到平衡状态. 种群搜索过程中发现的非支配解均存储在有限大小的外部存档中, 通过计算外部存档中粒子的拥挤密度[27], 对外部存档进行维护以保证非支配解不超出外部存档的大小, 并从中选择全局最优, 引导更新粒子的位置和速度. 本文的设计目标为吸收率A和品质因子Q, 可看作是双目标优化, 采用二维自适应网格来计算拥挤密度. 首先, 找到目标A和目标Q的最大值和最小值作为初始边界, 所有非支配解均应落于边界内部, 如图2(a)所示. 但是可能存在部分非支配解恰好位于边界线上, 因此将边界向外扩展, 以确保所有非支配解都处于网格内部, 如图2(b)所示. 然后, 将边界范围内区域划分为n个栅格, 如图2(c)所示. 每个栅格代表一个区域, 通过计算每个栅格当中粒子的数量来获得该区域的拥挤密度.

      由自适应网格得到的拥挤密度计算栅格被选中的概率${\text{P}}{{\text{R}}_i}$, 通过轮盘赌的方式选择有解存在的栅格, 将该栅格中的解作为全局最优, 若栅格中存在多个解, 则随机选择其中一个作为全局最优, 引导粒子更新.

      其中, Numi为第i个栅格中解的数量; I为有解存在的栅格的数量; β为最佳选择系数, 当β值较大时, ${\text{e}}^{\left( { - {\beta} \cdot {\text{Nu}}{{\text{m}}_i}} \right)}$对Num的敏感性高, 栅格中解数量的增加会显著地降低该栅格被选中的概率, 有助于算法选择较为稀疏的栅格中的解, 从而增加解的多样性.

      • 2.3.   算法实现

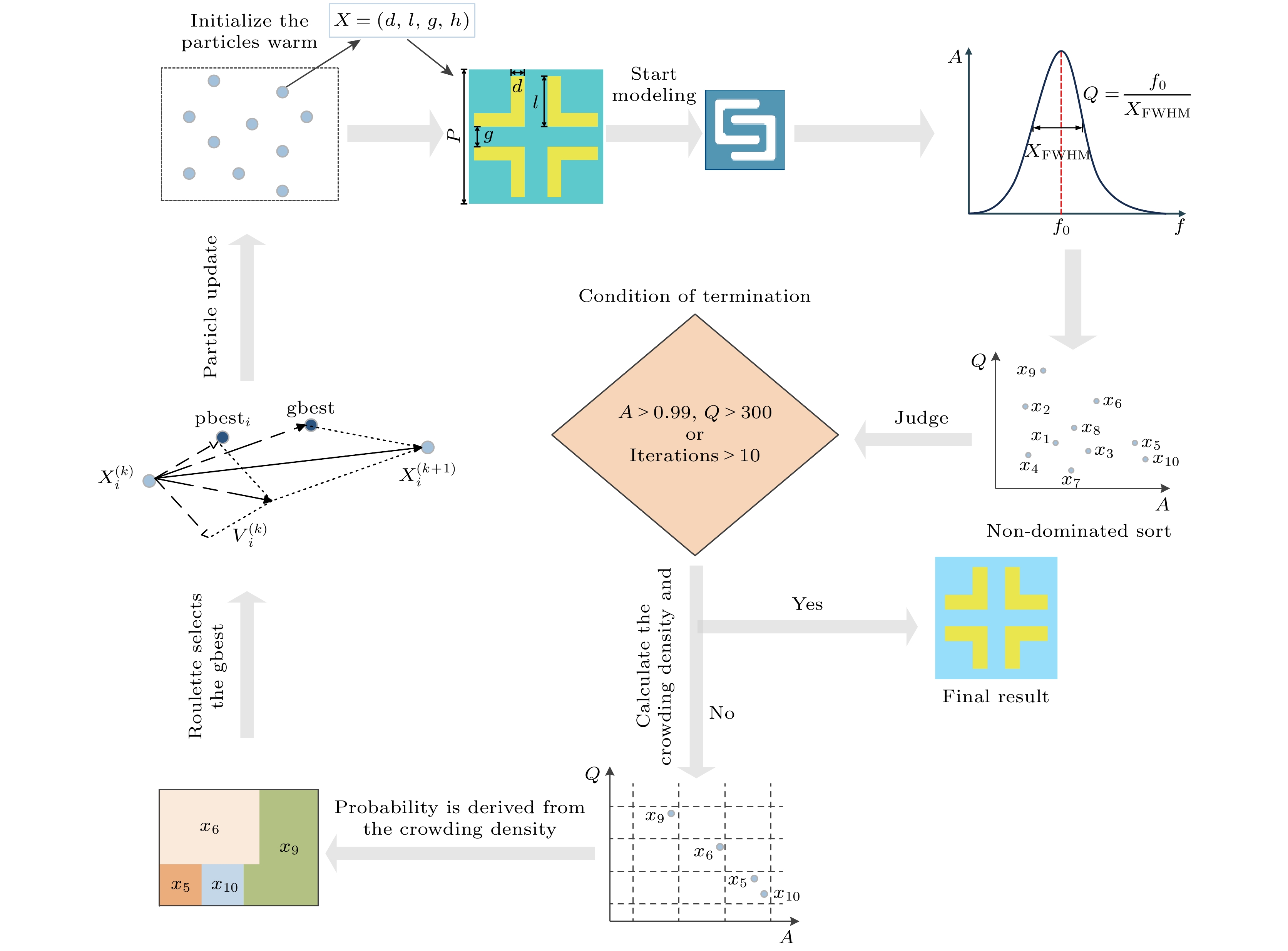
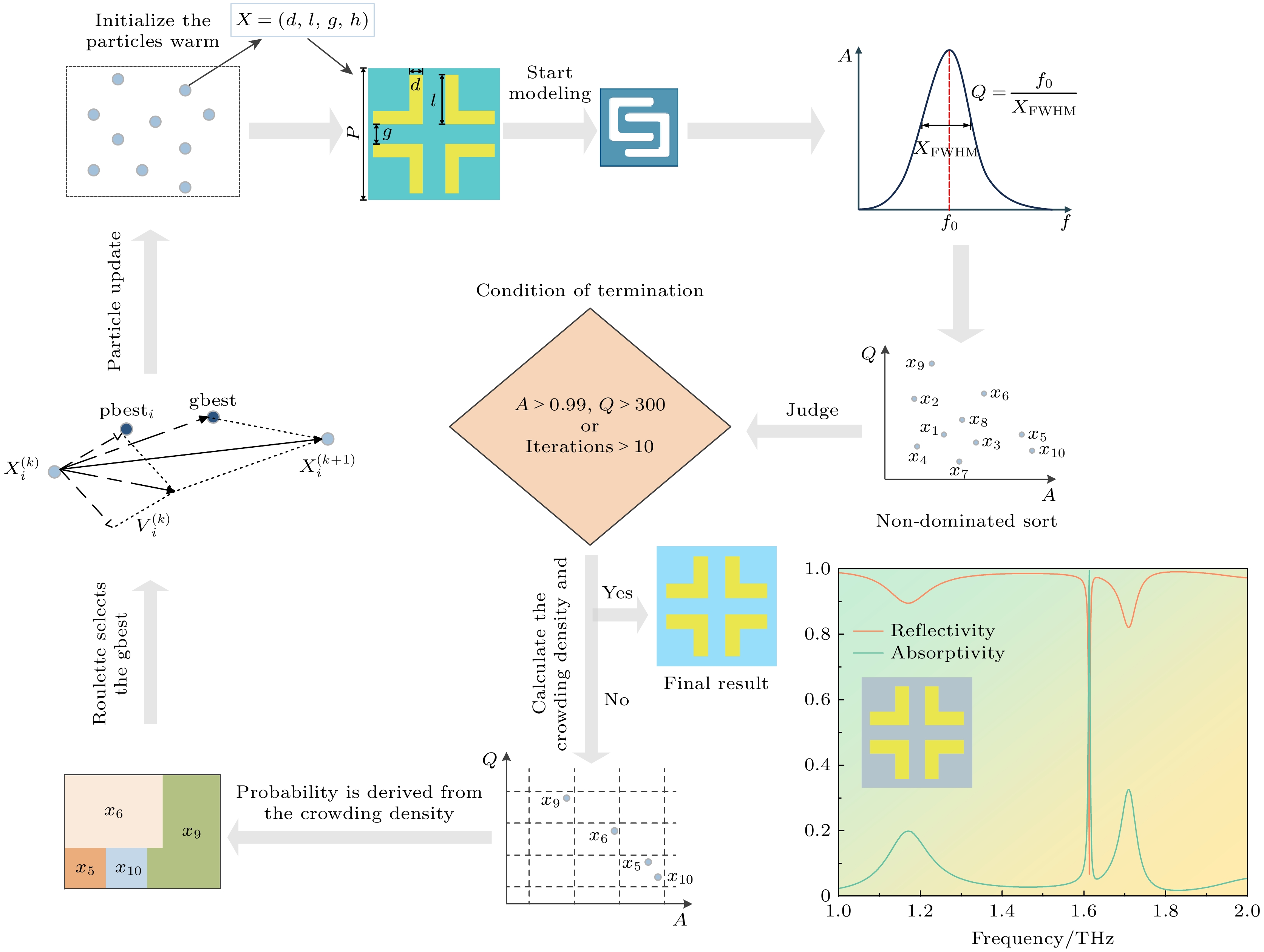
    • 多目标粒子群优化超材料吸收器的流程如图3所示, 根据表1中待优化的结构参数及其范围, 随机生成10个粒子, 每个粒子代表超材料吸收器结构的一个设计方案, 待设计参数有4个, 所以粒子维度为4. 初始化群中每个粒子的位置和速度, 位置信息包含超材料吸收器的结构和厚度信息, 将其值赋予吸收器, 利用仿真软件得到每个粒子对应的吸收光谱, 计算粒子的目标函数值A和Q, 同时更新每个粒子的个体最优解. 根据目标函数值对所有粒子进行非支配排序, 更新非支配解集, 判断其是否满足终止条件, 当达到迭代次数或当前非支配解集中存在满足目标($A \geqslant 0.99$, $Q \geqslant 300$)的粒子, 算法结束; 若不满足终止条件, 则利用自适应网格计算非支配解集中粒子的拥挤密度, 通过轮盘赌的方式选择全局最优. 根据全局最优和个体最优更新每个粒子的速度和位置, 然后重新计算目标函数值继续循环直到满足终止要求.

    3.   结果分析

      3.1.   结构光谱

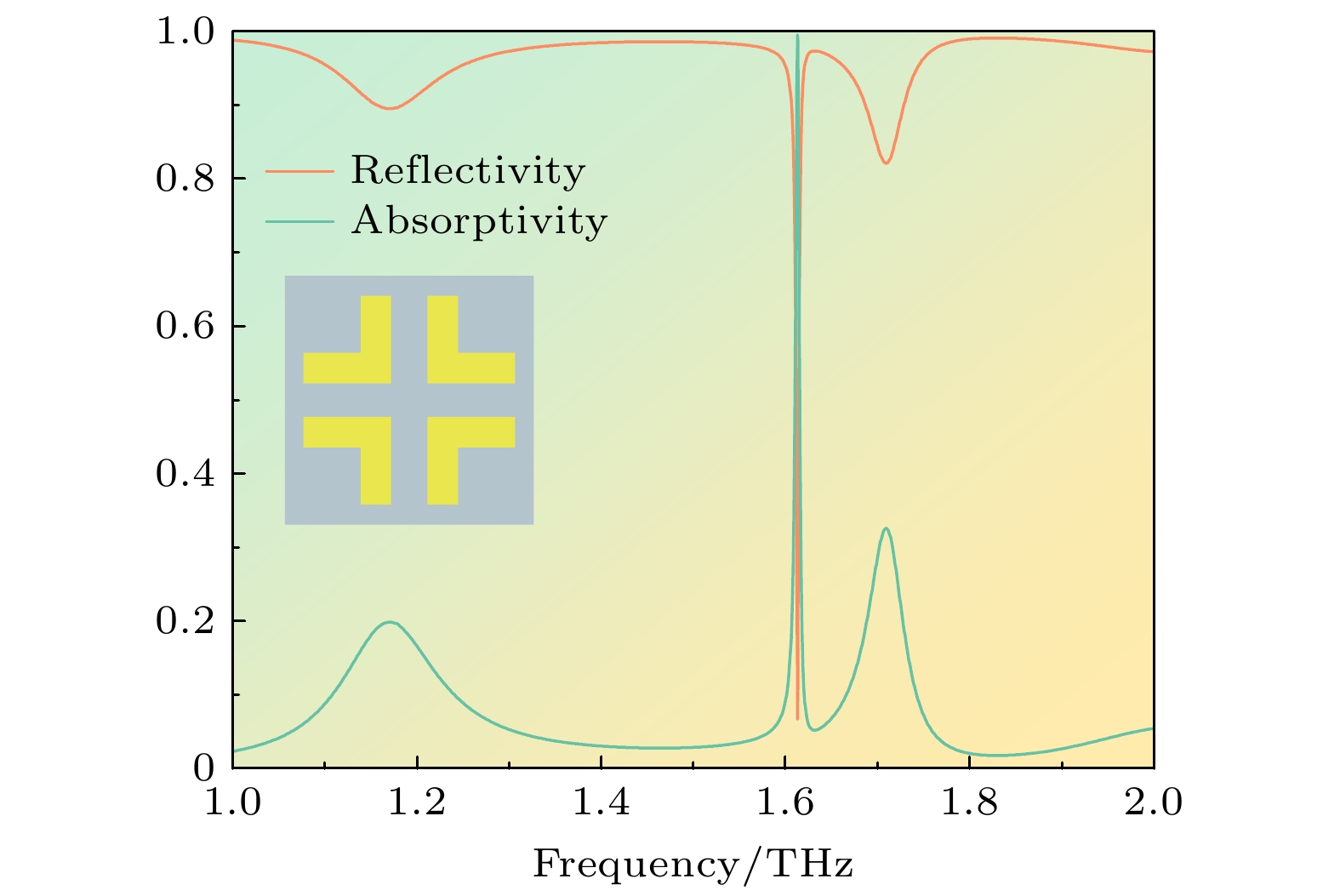
    • 多目标粒子群通过4次迭代, 得到了如表2的非支配解集, 非支配解集如2.2节所述, 并非所有解都满足设计要求, 而是在迭代过程中产生的最优解的解集, 这5个解的吸收率和品质因子互相无法比较大小, 需要根据设计需求进行人工选择. 由表可知, 解1—解4总存在某一目标未达到设计要求, 可以看出解5在1.613 THz处吸收率达到99%以上, 为近似完美吸收, 品质因子为319.72, 二者均达到设计要求, 因此选择解5为最终设计目标. 优化后的单元结构和吸收光谱如图4所示, 虽然在1.708 THz出现了目标以外的次谐振峰, 其吸收率仅为32.76%, 对吸收率有较高的应用需求时该谐振峰会被淘汰, 而1.613 THz处的主谐振峰仍满足设计需求.

      虽然在设计结构时就考虑到了制造误差的问题, 为了使结构设计更加合理, 限制了每个参数的变化范围, 防止设计的吸收器结构参数过小而难以实现加工. 同时, 在算法优化阶段, 对生成的结构参数进行了取整处理, 降低加工精度要求以减少器件的制造误差. 但在实际制造过程中会不可避免地出现制造误差, 为观察制造误差可能对吸收性能产生的影响, 随机生成±4%内的制造误差, 所对应的吸收性能如表3所列. 从表3中可以看出, 共振频率的偏移较小, 最大偏移量仅为0.017 THz; 吸收率的最大变化率为9.6%, 品质因子的变化范围为–34.1%—23.5%. 虽然在第一组制造误差PA1下吸收率稍低于90%, 但其品质因子提升了23.5%. 综上所述, 所设计的太赫兹超材料吸收器能够保持较好的性能, 容错性能较好.

      • 3.2.   电磁特性分析

    • 由阻抗匹配理论可知, 当自由空间的阻抗Z0与超材料吸收器的等效阻抗Z相匹配时, 即Z = 1, 如(7)式, 可以实现对电磁波的完美吸收:

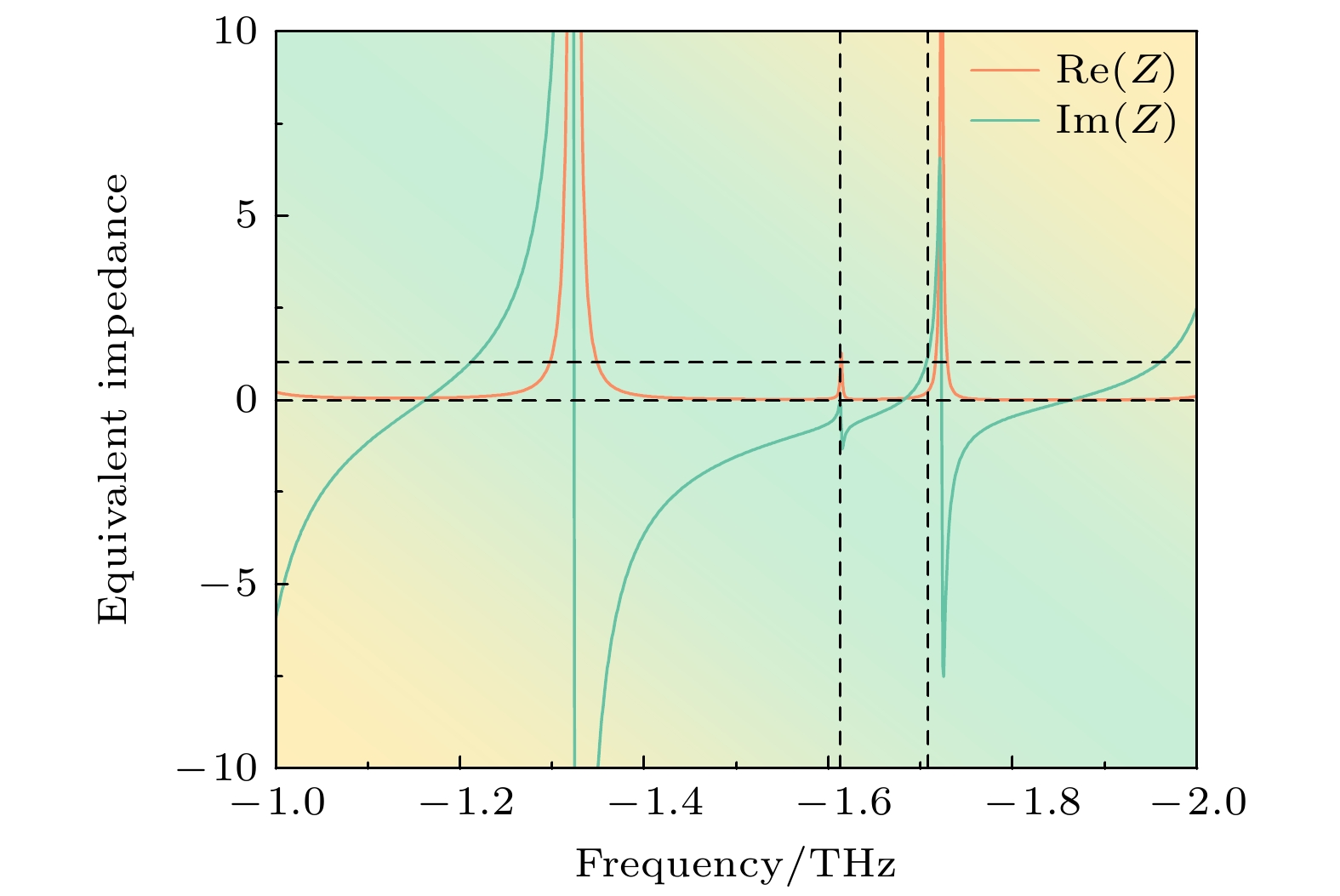
      利用(7)式计算本文设计的吸收器等效阻抗, 如图5所示, 计算结果与阻抗匹配理论完全相符. 在1.613 THz处与实部的交点为Re(Z) = 0.9954, 与虚部的交点为Im(Z) = -0.0646, 吸收器的等效阻抗Z接近于1, 因此在1.613 THz处实现近似完美吸收; 而在1.708 THz处等效阻抗的实部为Re(Z) = 0.2395, 虚部的为Im(Z) = 1.1946, 与自由阻抗不匹配, 所以在1.708 THz只有很小的吸收峰.

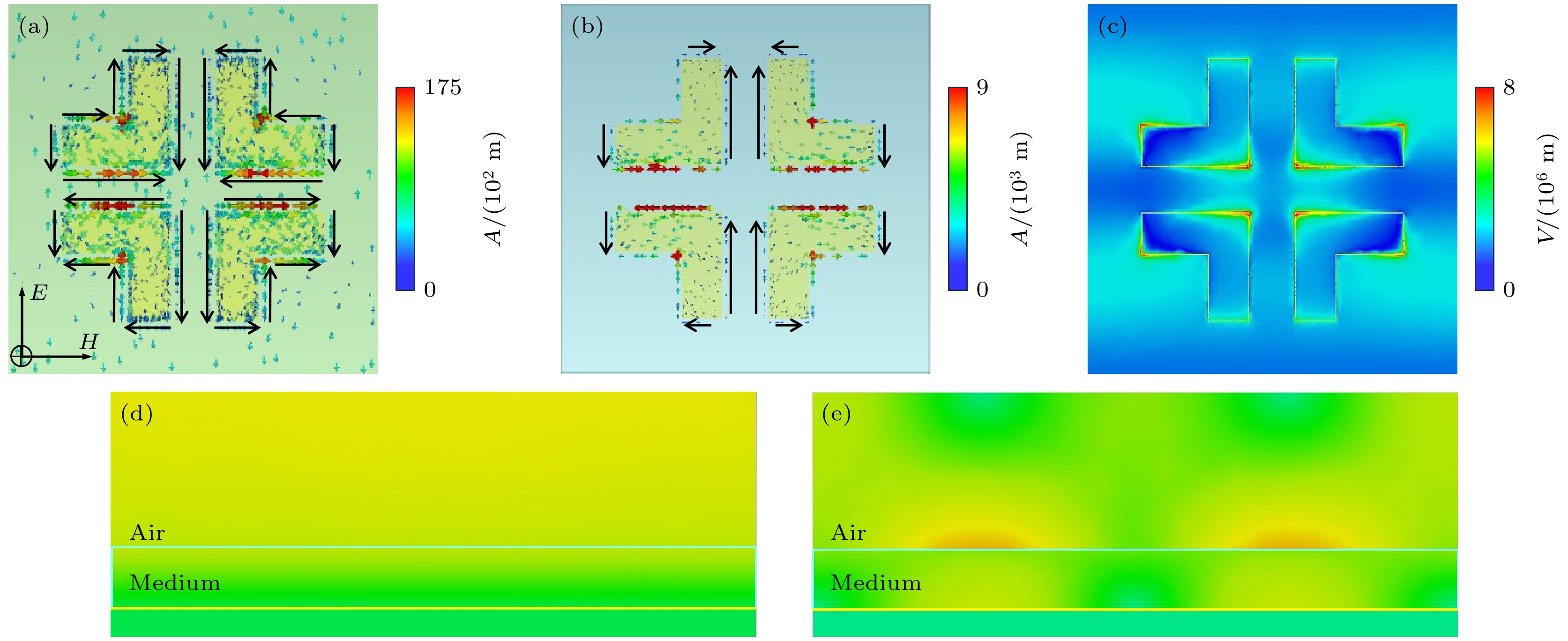
      为了进一步探究吸收器在1.613 THz处产生吸收峰的原因, 仿真了在1.613 THz吸收峰处的电场分布和表面电流分布, 如图6所示. 由图6(a)可以看出, 上半部分左右两边L表面电流轴对称分布, 形成一对偶极子谐振; 同理下半部分也是一对偶极子谐振. 这两对偶极子谐振复合在表面结构上, 形成四极子谐振模式. 为了验证金属底板对吸收峰的产生及其谐振模式的影响, 将吸收器底部金属板移除后其表面电流如图6(b). 对比图6(a)和图6(b)可以看出, 虽然无金属底板的吸收器相较于有金属底板的电流强度十分弱, 但其表面同样也存在四偶极子谐振. 在这两种情况下, 可以看出中间竖直方向的电流方向相反, 这可能是由于金属底板的影响, 使得上下表面的相反电流形成电流回路产生磁偶极子谐振. 表面的四极子谐振和上下表面的磁偶极子谐振使得入射波的能量将以焦耳热的形式被消耗, 实现太赫兹波的高效吸收. 图6(c)为1.613 THz处的结构表面电场分布, 其电场很强且分布于L型金属的直角处和末端, 恰好为电流流向的聚集或分离处, 图6(d)和图6(e)分别为吸收器1.613 THz处y = 100和x = 100的侧面电场分布, 由侧面电场分布可知, 电场被局域在表面结构处, 说明该结构与入射电磁波有充分的耦合, 也印证了上述的阻抗匹配理论, 用作传感时可以实现更好的传感性能.

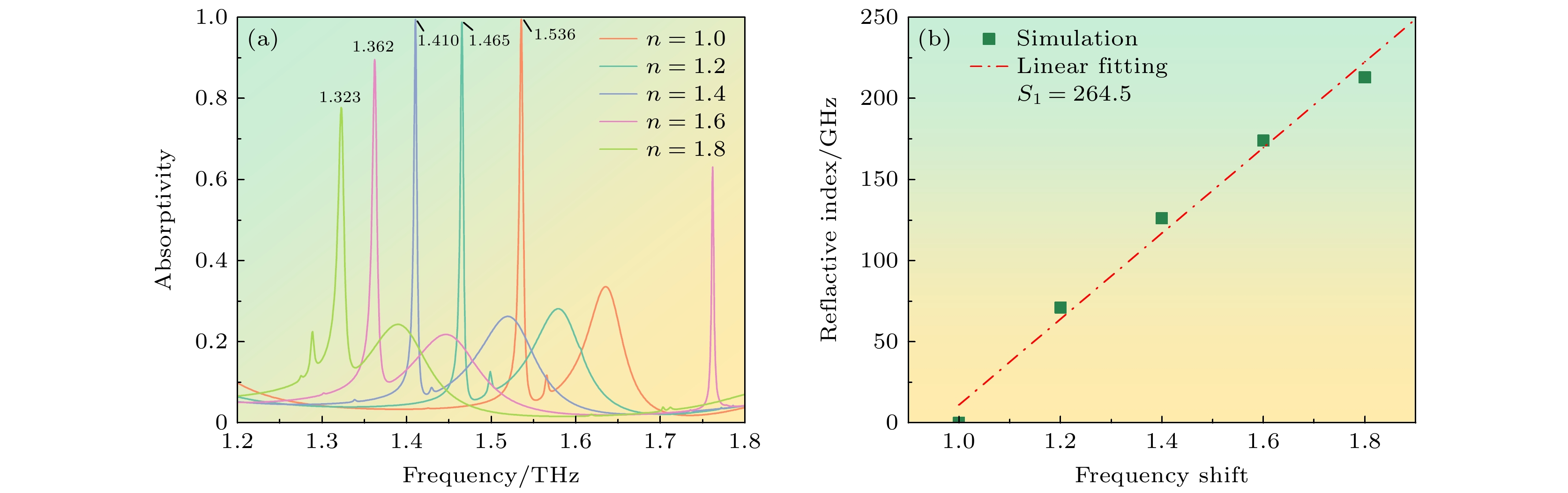
      良好的传感特性与高灵敏度是衡量吸收器在传感探测应用领域具备高实用价值的决定性因素, 因此对所设计吸收器的折射率传感性能进行讨论分析. 将厚度为15 μm的待测物质覆盖于吸收器的表面进行传感性能分析, 如图7(a)所示, 随着待测物折射率的增加, 吸收器的谐振频率出现显著红移. 将频率变化和折射率线性拟合得到如图7(b)所示的拟合曲线, 曲线斜率即为传感器灵敏度, 谐振峰的灵敏度S1近似为264.5 GHz/RIU, 具有极高的灵敏度. 这表明该传感器能够检测到被测参数极其微小的变化, 可以被用于如生物传感、化学分析、环境监测等高精度测量的场景中.

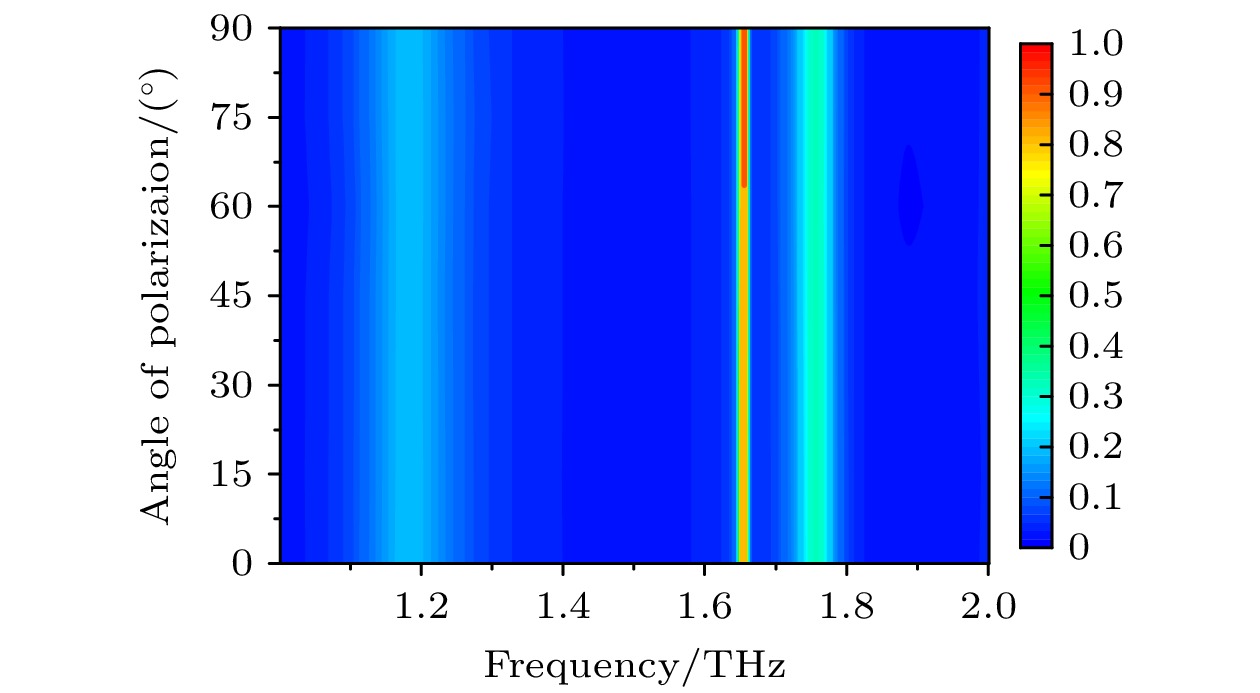
      在实际应用中, 电磁波的极化方向可能会因各种因素而发生变化, 极化角度不敏感的超材料吸收器能够保持稳定的吸收性能, 因此十分有必要探究吸收器在入射波不同极化角度情况下的吸收性能. 图8为对称结构不同极化角度φ的吸收曲线, φ以15°的步长从0°变化为90°. 随着φ的改变, 吸收器的吸收频率和吸收率几乎不变, 在不同φ情况下的谐振频率均在1.613 THz, 对应的吸收率最低为97.75%. 结果表明, 本文设计的吸收器结构具有极化不敏感特性, 该特性源于表面结构的中心对称性, 在任何极化角度下都可以稳定的工作.

      将本文设计的超材料吸收器与其他智能算法设计的超材料吸收器进行对比, 如表4所列. 结果表明, 虽然这些吸收器均能够实现完美吸收, 但本文所用方法可以在更短的时间完成超材料吸收器的设计, 且设计的结构可以实现更高的品质因子, 用于折射率传感时具有极高的灵敏度.

    4.   结　论

    • 本文提出了一种基于多目标粒子群的超材料吸收器的自适应快速设计方法, 并将其应用于一个由4个L型中心对称组成的吸收器结构. 将吸收率和品质因子作为相互独立的优化目标, 通过多目标粒子群算法实现了吸收器的双目标优化. 通过优化设计的吸收器在1.613 THz下实现了完美的吸收, 吸收率超过99%, 品质因子高达319.72, 传感器灵敏度达264.5 GHz/RIU. 本文还利用阻抗匹配、表面电流、电场分布等详细地分析了吸收峰产生的原因. 该吸收器的吸收峰不会随着极化角的变化而变化, 具有极化角不敏感特性, 在实际应用中更具稳定性. 对比其他设计方法, 多目标粒子群算法能在更短的时间内实现更好的性能优化. 多目标粒子群算法能够根据需求实现设计, 降低了超材料吸收器设计对研究人员的经验需求, 克服了其他算法在超材料设计上的缺陷, 提高了设计效率和性能, 在太赫兹功能器件的设计中有极大的应用潜力.

    参考文献 (29)

目录

/

返回文章
返回