高级搜索

扫描波长调制光谱高精度复现分子吸收率函数方法

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

黄知秋, 李启正, 张猛, 彭志敏, 杨乾锁, 杜艳君. 扫描波长调制光谱高精度复现分子吸收率函数方法[J]. 物理学报, 2025, 74(6): 064210-1. doi: 10.7498/aps.74.20241468
引用本文: 黄知秋, 李启正, 张猛, 彭志敏, 杨乾锁, 杜艳君. 扫描波长调制光谱高精度复现分子吸收率函数方法[J]. 物理学报, 2025, 74(6): 064210-1. doi: 10.7498/aps.74.20241468
shu
Zhiqiu HUANG, Qizheng LI, Meng ZHANG, Zhimin PENG, Qiansuo YANG, Yanjun DU. A method of high-precision reproduction of molecular absorbance profile by scanning wavelength modulation spectroscopy[J]. Acta Physica Sinica, 2025, 74(6): 064210-1. doi: 10.7498/aps.74.20241468
Citation: Zhiqiu HUANG, Qizheng LI, Meng ZHANG, Zhimin PENG, Qiansuo YANG, Yanjun DU. A method of high-precision reproduction of molecular absorbance profile by scanning wavelength modulation spectroscopy[J]. Acta Physica Sinica, 2025, 74(6): 064210-1. doi: 10.7498/aps.74.20241468
shu

扫描波长调制光谱高精度复现分子吸收率函数方法

  • 1.

    华北电力大学控制与计算机工程学院, 北京　102206

  • 2.

    中国科学院大学工程科学学院, 北京　100049

  • 3.

    中国科学院力学研究所, 流固耦合系统力学重点实验室, 北京　100190

  • 4.

    怀柔实验室山西研究院, 太原　030032

  • 5.

    清华大学能源与动力工程系, 北京　100084

  • 6.

    北京航天计量测试技术研究所, 北京　100076

    • 作者简介: 黄知秋: huangzhiqiu@imech.ac.cn .
    通讯作者: E-mail: YanjunDu@ncepu.edu.cn.

  • 中图分类号: 42.62.Fi, 33.20.Ea, 42.55.Px

A method of high-precision reproduction of molecular absorbance profile by scanning wavelength modulation spectroscopy

  • 1.

    School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China

  • 2.

    School of Engineering Science, University of Chinese Academy of Science, Beijing 100049, China

  • 3.

    Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

  • 4.

    Shanxi Research Institute of Huairou Laboratory, Taiyuan 030032, China

  • 5.

    Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China

  • 6.

    Beijing Aerospace Institute for Metrology and Measurement Technology, Beijing 100076, China

    • Corresponding author: E-mail: YanjunDu@ncepu.edu.cn

  • MSC: 42.62.Fi, 33.20.Ea, 42.55.Px

  • 摘要: 基于低频三角波扫描加高频正弦波调制的扫描波长调制策略, 提出了一种高精度、免标定分子吸收率函数重构方法. 该方法利用谱线在扫描频率下对应的各次谐波信号重构出以该频率为中心、以调制深度为半宽度频域范围内的透过率信息, 结合低频扫描即可得到谱线透过率信息, 最后对频率重叠区域的透过率进行插值平均即可得到分子吸收率函数. 为验证该方法的测量精度, 利用CO2分子在6330.821 cm–1谱线对不同浓度CO2的吸收率函数进行重构, 并拟合得到浓度, 吸收率拟合残差标准差达到10–5, 强吸收与弱吸收的测量信噪比分别达到503与222. 3000次连续在线浓度测量结果分布直方图表明, 谐波重构法测量稳定性显著优于直接吸收法和二次谐波峰值法, 预期可为谱线参数的高精度标定以及复杂工业现场中弱吸收气体参数高精度在线监测提供新的可靠测量方法.
    Abstract: A high-precision, calibration-free method of reconstructing molecular absorbance profile is introduced in this work. The method employs a scanning wavelength modulation strategy that integrates low-frequency triangular wave scanning with high-frequency sine wave modulation. Specifically, it utilizes harmonic signals corresponding to the spectral lines at the scanning frequency to reconstruct transmittance information centered around that frequency, with the modulation depth used as the half-width frequency range. Combining low-frequency scanning, the transmittance information of the spectral lines can be obtained accurately. Finally, through interpolating and averaging the transmittance in overlapping frequency regions, the molecular absorbance profile is reconstructed. The main content of this paper is divided into three key parts: theoretical derivation of the harmonic reconstruction method, numerical simulation, and experimental validation. In the theoretical derivation, the instantaneous laser frequency is represented as a parameter “x” by using a cosine function and is subsequently substituted into the Fourier expansion of the laser transmittance. Then the transmittance function is reconstructed based on Chebyshev polynomials. In the numerical simulation, we illustrate the complete process of the harmonic reconstruction method, including harmonic detection, data matrix reconstruction, and the interpolation and average of data matrix slices finally obtain the transmittance function. Subsequently, through numerical simulations, the systematic errors in the reconstructed transmittance functions with different harmonic orders and modulation depths are analyzed and compared. The results show that the systematic error decreases with the harmonic order increasing and increases with the modulation depth increasing. In the experimental verification, in order to evaluate the measurement accuracy of this method, we reconstruct the absorbance profiles for different concentrations of CO2 by using the 6330.821 cm–1 spectral line. The standard deviation of the fitting residual of the absorbance profile is on the order of 10–5. The signal-to-noise ratios for the strong absorption and weak absorption, are 503 and 222, respectively. We conduct 3000 consecutive on-line measurements and compare the harmonic reconstruction method with both the direct absorption method and the second harmonic peak method. Statistical analyses are made regarding the standard deviations and Gaussian distributions of the deduced concentration results. These results indicate that the standard deviation from the harmonic reconstruction method is less than half of those from the direct absorption method and the second harmonic peak method, demonstrating significantly superior measurement stability. This method is expected to become a reliable new method to measure spectral line parameters with high accuracy and monitor weakly absorbing gas parameters online in complex industrial environments.
  • 加载中

  • 图 1  激光透过率随时间的变化

    Figure 1.  Temporal variation in laser transmittance.

    下载: 全尺寸图片 幻灯片

    图 2  周期变化透过率的0—5阶谐波频谱

    Figure 2.  The 0th−5th order harmonic spectrum of transmittance with periodic variations.

    下载: 全尺寸图片 幻灯片

    图 3  CO2单谱线0—5阶谐波幅值

    Figure 3.  Amplitude of harmonics in the single spectral line of CO2 ranging from 0th to 5th order.

    下载: 全尺寸图片 幻灯片

    图 4  透过率数据矩阵　(a) 数据矩阵的三维曲面图; (b) 数据矩阵的等高图; (c) 透过率曲线

    Figure 4.  Transmittance data matrix: (a) 3D surface diagram of data matrix; (b) contour map of the data matrix; (c) transmittance profile

    下载: 全尺寸图片 幻灯片

    图 5  第303—323条透过率曲线在波长±2×10–3 cm–1范围内的点的波长散点示意图

    Figure 5.  Scatter diagram of points in the wavelength range of ±2×10–3 cm–1 for the transmittance profile in Section 303–323.

    下载: 全尺寸图片 幻灯片

    图 6  CO2单谱线重构透过率与透过率理论值及残差

    Figure 6.  Reconstruction of the single spectral line transmittance and its theoretical value, as well as the residual.

    下载: 全尺寸图片 幻灯片

    图 7  不同调制深度下, 不同谐波阶次重构透射率及其误差　(a) m = 1.2; (b) m = 2.2

    Figure 7.  Reconstructed transmittance and error analysis for different harmonic orders at various modulation depths: (a) m = 1.2; (b) m = 2.2.

    下载: 全尺寸图片 幻灯片

    图 8  六种不同调制深度下重构透射率及其误差

    Figure 8.  Reconstructed transmittance and its associated error for six distinct modulation depths.

    下载: 全尺寸图片 幻灯片

    图 9  分时测量方案实验装置示意图

    Figure 9.  Experimental device schematic of a time-sharing measurement scheme.

    下载: 全尺寸图片 幻灯片

    图 10  经1次稀释后的CO2标气6330.821 cm–1谱线吸收率函数重构结果　(a) 透过率随时间的变化; (b) H0—H12次谐波信号; (c)重构得到的透过率、吸收率及其拟合残差

    Figure 10.  Reconstruction of the absorption profile for the spectral line at 6330.821 cm–1 of CO2 standard gas following a single dilution: (a) The temporal evolution of transmittance; (b) harmonic signals from H0 to H12; (c) reconstructed transmittance, absorbance and its fitting residuals.

    下载: 全尺寸图片 幻灯片

    图 11  经4次稀释后的CO2标气6330.821 cm–1谱线吸收率函数重构结果　(a) 透过率随时间的变化; (b) H0—H12次谐波信号; (c)重构得到的透过率、吸收率及其拟合残差

    Figure 11.  Reconstruction of the absorption profile for the spectral line at 6330.821 cm–1 of CO2 standard gas after being diluted four times: (a) The temporal evolution of transmittance; (b) harmonic signals from H0 to H12; (c) reconstructed transmittance, absorbance and its fitting residuals.

    下载: 全尺寸图片 幻灯片

    图 12  分束测量方案的实验装置示意图

    Figure 12.  Schematic representation of the experimental setup for beam splitting measurement scheme.

    下载: 全尺寸图片 幻灯片

    图 13  稀释1/16的CO2标气3000次连续在线浓度测量结果, 及其统计分布对比　(a) DAS的浓度测量结果; (b) Scan-WM-RAS的浓度测量结果; (c) DAS的浓度统计分布; (d) Scan-WM-RAS的浓度统计分布

    Figure 13.  Results of 3000 continuous online concentration measurements of CO2 standard gas diluted at a ratio of 1/16 and their statistical distribution comparison: (a) The results of concentration measurements through DAS; (b) the results of concentration measurements through Scan-WM-RAS; (c) the statistical distribution of concentration through DAS; (d) the statistical distribution of concentration through Scan-WM-RAS.

    下载: 全尺寸图片 幻灯片

    图 14  低浓度CO2标气3000次连续在线浓度测量结果, 及其统计分布对比　(a) WMS的浓度测量结果; (b) Scan-WM-RAS的浓度测量结果; (c) WMS的浓度统计分布; (d) Scan-WM-RAS的浓度统计分布

    Figure 14.  Results of 3000 continuous online concentration measurements of low-concentration CO2 standard gas and their statistical distribution comparison: (a) The results of concentration measurements through WMS; (b) the results of concentration measurements through Scan-WM-RAS; (c) the statistical distribution of concentration through WMS; (d) the statistical distribution of concentration through Scan-WM-RAS.

    下载: 全尺寸图片 幻灯片

    表 1  CO2分子6330.821 cm–1处谱线光谱常数

    Table 1.  Spectral constants of the CO2 molecule's spectral line at 6330.821 cm–1.

    $ {\nu }_{0} $/cm–1 S/(cm–2·atm–1) $ {\gamma }_{{\mathrm{a}}{\mathrm{i}}{\mathrm{r}}}/ $(cm–1·atm–1) $ {\gamma }_{{\mathrm{s}}{\mathrm{e}}{\mathrm{l}}{\mathrm{f}}}/ $(cm–1·atm–1) E''/cm–1
    Line 6330.8212 1.522×10–23 0.0725 0.097 163.8684
    下载: 导出CSV

    表 2  4个阶次下6个调制深度透过率重构误差

    Table 2.  Reconstruction error of transmittance at six modulation depths across four orders.

    m = 1.2m = 1.4m = 1.6m = 1.8m = 2.0m = 2.2
    H0—H41.045×10–42.009×10–43.313×10–44.914×10–46.750×10–48.768×10–4
    H0—H81.923×10–64.938×10–61.236×10–52.697×10–55.015×10–58.373×10–5
    H0—H129.197×10–78.450×10–79.185×10–71.754×10–63.591×10–67.469×10–6
    H0—H169.180×10–78.202×10–77.258×10–78.501×10–78.607×10–71.014×10–6
    下载: 导出CSV
  • [1] Adámek P, Olejníček J, Čada M, Kment Š, Hubička Z 2013 Opt. Lett. 38 2428 doi: 10.1364/OL.38.002428
    [2] Goldenstein C S, Spearrin R M, Jeffries J B, Hanson R K 2017 Prog. Energ. Combust. 60 132 doi: 10.1016/j.pecs.2016.12.002
    [3] Witzel O, Klein A, Meffert C, Schulz C, Kaiser S A, Ebert V 2015 P. Combust. Inst. 35 3653 doi: 10.1016/j.proci.2014.06.038
    [4] Fissiaux L, Delière Q, Blanquet G, Robert S, Vandaele A C, Lepère M 2014 J. Mol. Spectrosc. 297 35 doi: 10.1016/j.jms.2014.01.006
    [5] Ghysels M, Durry G, Amarouche N 2013 Spectrochim. Acta A 107 55 doi: 10.1016/j.saa.2013.01.042
    [6] McManus J B, Zahniser M S, Nelson D D, Shorter J H, Herndon S, Wood E 2010 Opt. Eng. 49 111124 doi: 10.1117/1.3498782
    [7] McManus J B, Zahniser M S, Nelson D D, et al. 2015 Appl. Phys. B 119 203 doi: 10.1007/s00340-015-6033-0
    [8] Zhao G, Tan W, Jia M Y, et al. 2016 Sensors 16 1544 doi: 10.3390/s16091544
    [9] Cai W W, Kaminski C F 2014 Appl. Phys. Lett. 104 154106 doi: 10.1063/1.4871976
    [10] Hangauer A, Chen J, Strzoda R, Ortsiefer M, Amann M, 2008 Opt. Lett. 33 1566 doi: 10.1364/OL.33.001566
    [11] Bolshov M A, Kuritsyn Y A, Romanovskii Y V 2015 Spectrochim. Acta B 106 45 doi: 10.1016/j.sab.2015.01.010
    [12] Neethu S, Verma R, Kamble S S, et al. 2014 Sensor. Actuat. B-Chem 192 70 doi: 10.1016/j.snb.2013.10.070
    [13] Werle P A 1998 Spectrochim. Acta A 54 197 doi: 10.1016/S1386-1425(97)00227-8
    [14] Bain J R P, Johnstone W, Ruxton K, Stewart G, Lengden M, Duffin K 2011 J. Lightw. Technol. 29 987 doi: 10.1109/JLT.2011.2107729
    [15] Reid J, Labrie D 1981 Appl. Phys. B 26 203 doi: 10.1007/BF00692448
    [16] Rieker G B, Jeffffries J B, Hanson R K 2009 Appl. Optics. 48 5546 doi: 10.1364/AO.48.005546
    [17] Wang Z H, Fu P F, Chao X 2019 Appl. Sci. 9 2723 doi: 10.3390/app9132723
    [18] Goldenstein C S, Strand C L, Schultz I A, Sun K, Jeffries J B, Hanson R K 2014 Appl. Optics. 53 356 doi: 10.1364/AO.53.000356
    [19] Goldenstein C S, Hanson R K 2015 J. Quant. Spectrosc. RA. 152 127 doi: 10.1016/j.jqsrt.2014.11.008
    [20] Goldenstein C S, Jeffries J B, Hanson R K 2013 J. Quant. Spectrosc. RA. 130 100 doi: 10.1016/j.jqsrt.2013.06.008
    [21] Stewart G, Johnstone W, Bain J, Ruxton K, Duffin K 2011 J. Lightwave Technol. 29 811 doi: 10.1109/JLT.2011.2140930
    [22] Peng Z M, Du Y J, Che L, Li X H, Zheng K J 2011 Opt. Express 19 23104 doi: 10.1364/OE.19.023104
    [23] Peng Z M, Du Y J, Che L, Yang Q S 2012 Opt. Express 20 11976 doi: 10.1364/OE.20.011976
    [24] Rothman L S, Gordon I E, Babikov Y, et al. 2013 J. Quant. Spectrosc. RA. 130 4 doi: 10.1016/j.jqsrt.2013.07.002
    [25] Buchholz B, Böse N, Ebert V 2014 Appl. Phys. B 116 883 doi: 10.1007/s00340-014-5775-4
    [26] Pogány A, Klein A, Ebert V 2015 J. Quant. Spectrosc. RA. 165 108 doi: 10.1016/j.jqsrt.2015.06.023
  • 加载中
图( 14) 表( 2)
计量
  • 文章访问数:  55
  • HTML全文浏览数:  55
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-20
  • 刊出日期:  2025-03-20

扫描波长调制光谱高精度复现分子吸收率函数方法

    通讯作者: E-mail: YanjunDu@ncepu.edu.cn.
    作者简介: 黄知秋: huangzhiqiu@imech.ac.cn
  • 1. 华北电力大学控制与计算机工程学院, 北京　102206
  • 2. 中国科学院大学工程科学学院, 北京　100049
  • 3. 中国科学院力学研究所, 流固耦合系统力学重点实验室, 北京　100190
  • 4. 怀柔实验室山西研究院, 太原　030032
  • 5. 清华大学能源与动力工程系, 北京　100084
  • 6. 北京航天计量测试技术研究所, 北京　100076
  • 收稿日期:  2024-10-20

摘要: 基于低频三角波扫描加高频正弦波调制的扫描波长调制策略, 提出了一种高精度、免标定分子吸收率函数重构方法. 该方法利用谱线在扫描频率下对应的各次谐波信号重构出以该频率为中心、以调制深度为半宽度频域范围内的透过率信息, 结合低频扫描即可得到谱线透过率信息, 最后对频率重叠区域的透过率进行插值平均即可得到分子吸收率函数. 为验证该方法的测量精度, 利用CO2分子在6330.821 cm–1谱线对不同浓度CO2的吸收率函数进行重构, 并拟合得到浓度, 吸收率拟合残差标准差达到10–5, 强吸收与弱吸收的测量信噪比分别达到503与222. 3000次连续在线浓度测量结果分布直方图表明, 谐波重构法测量稳定性显著优于直接吸收法和二次谐波峰值法, 预期可为谱线参数的高精度标定以及复杂工业现场中弱吸收气体参数高精度在线监测提供新的可靠测量方法.

English Abstract

    全文HTML

    1.   引　言

    • 可调谐激光二极管吸收光谱(TDLAS)[1–5], 具有非接触可原位检测气体参数、测量相应速度快、波长选择性强等优点, 其经过多年的发展后形成了直接吸收(DAS)和波长调制(WMS)两种主要测量方法, 其中DAS通过透射光强拟合吸收率函数[6–8], 进而根据其确定气体参数(如浓度、压力、温度)和谱线参数(如碰撞展宽、Dicke收敛系数、线强度)等, 其物理概念清晰, 操作简单, 因此在大气环境监测、工业现场过程分析等领域得到广泛应用, 但容易受到颗粒物、激光强度波动、振动等干扰, 吸收率函数的拟合残差一般在10–4—10–3, 仅适用于强吸收条件下的气体参数测量和谱线参数标定. WMS对目标信号进行高频调制, 而非目标低频噪声信号由于没有经过调制在谐波检测过程中被除去, 因此可以有效地降低其他频率噪声信号的干扰[9–18], 但谐波信号不仅包含了吸收率函数的信息, 还耦合了激光强度、调制频率、相位角、光电放大系数等信息, 传统WMS方法一般通过标定实验, 采用二次谐波峰值来确定待测气体参数, 不仅操作复杂, 而且标定与实际测量工况之间的差异往往会导致较大的误差. 为解决波长调制法难以定量测量的难题, Hanson课题组[19,20]基于剩余幅度调制提出了2f/1f 免标法, 该方法采用一次谐波来修正二次谐波, 消除了激光强度波动、光电放大系数应等因素的影响, 通过拟合并比较2f/1f谐波信号的理论计算与实验测量值来确定气体温度或浓度, 但计算谐波时不仅需要精确标定激光光强调幅系数、频率调制深度、频率调制与光强调制之间相位角等参数, 同时还需要气体组分、光谱常数(碰撞展宽系数、线强度、Dicke收敛系数等)等信息, 上述参数不确定性都会使得谐波信号的理论计算值偏离真实值, 进而导致测量误差. 另外, 2f, 2f/1f免标法仅采用了少量的谐波信息, 难以实现吸收率函数的测量以及谱线参数的标定.

      考虑到吸收率函数的重要性以及WMS方法高信噪比的优点, 近年来, 科研工作者尝试通过高灵敏度的谐波信号提取吸收率函数信息. Stewart 课题组[14,21]提出了一种基于剩余振幅调制的一次谐波信号来复现光谱吸收率函数的方法. 该方法仅在小调制系数(m≤0.2)下效果较好, 此时的一次谐波近似吸收率函数, 随着调制系数的增大, 复现吸收率函数的误差会急剧增大. 为了拓宽该方法的应用范围, 他们引入了一个“形状校正函数”, 用于在大调制系数下复现吸收率函数[22]. 然而, 气体组分浓度、压力、温度以及跃迁本身的固有特性决定了线型形状, 这是计算该校正函数的必要条件. “形状校正函数”在已知气体参数和光谱常数的实验室条件下可以计算得出, 但在气体参数不确定或未知的实际应用工况下难以取得. 事实上, 由于光强调制与频率调制之间相位差的存在, 当忽略光强调制非线性项时, 在谐波检测时通过设定参考信号相位角, 可使得一次谐波X轴分量只含有透过率函数的A0和A2次谐波系数以及光强调制与频率调制相位差. 进而, 当调制系数足够小时, A0趋近于透过率而A2接近于零, 此时一次谐波X轴分量近似于透过率, 如调制系数m = 0.2, 得到的透过率函数在谱线中心频率处相对误差约为0.5%, 但随着调制系数增大而急剧增大, 在调制系数m = 0.5时达到3%. 2012年, Peng等[23]建立了一种基于奇数次谐波信号的吸收率函数重构算法, 该方法利用奇次谐波(包括1次、3次、5次等)在X和Y分量上的数据, 而非单纯依赖于1次谐波RAM信号, 以实现光谱吸收系数的复现. 此方法能够在较大的调制系数下有效降低复现误差. 但该方法需要从实验检测到的透射光强奇数次谐波信号中提取透过率函数的偶数次谐波系数(A0, A2, A4, ···), 数据处理过程复杂, 而且与Stewart方法相似, 重构得到的吸收率函数信噪比主要决定于频率调制与光强调制之间的相位差, 当该相位差趋近于π时, 重构得到的吸收率函数精度较低, 难以用于气体参数或谱线参数高精度测量.

      区别于上述研究, 本文基于扫描波长调制法 建立了一种全新的、高精度、免标定吸收率函数重构方法, 该方法首先利用谱线各频率对应的各次谐波信号(multi-Harmonics)重构特定频率范围内(即频率调制深度)的透过率信息, 然后对频率重 叠区域的透过率进行插值平均, 最终得到透过率函数并对其进行求对数得到吸收率函数. 在验证实验中, 针对CO2在6330.821 cm–1处的谱线, 测量了不同稀释比例不同吸收强度的CO2标气, 初步验证了该方法可行性, 在线90分钟连续测量CO2标气3000次, 验证了该方法在测量稳定性上的优势.

    2.   理论原理推导

    • WMS基本原理在众多研究中已有详尽阐述[20,24–26], 本文提出的一些核心理论为本研究所采用的方法提供了理论基础. 为了生成谐波信号, 将正弦调制的角频率ω施加于缓慢变化的二极管激光器调制电流, 激光频率的瞬时值可表示为

      其中$ \overline \nu $为缓慢扫描的激光频率的中心频率, a为围绕该频率的频率调制深度.

      在均匀介质中, 单色辐射的激光透过率遵循比尔-朗伯定律, 其表达形式可如下展开:

      式中, τ(ν)表示激光透过率, It和I0分别代表激光透过与入射强度, α(ν)为吸收率. 透过率的谐波系数Ak (k = 0, 1, 2, ···)为

      由(1)式可得到

      令$ x = ({{\nu - \overline \nu}})/{a} $, $ x \in \left[ { - 1, 1} \right] $, 则

      将(5)式代入到(2)式中, 可得到透过率函数重构公式如下:

      在(6)式中, 对于某一固定频率$ \overline \nu $, 可重构出 –a—a频率范围(即调制深度)内透过率信息. 在低频扫描范围内, 选取多个频率作为中心, 围绕这些频率以调制深度为宽度重构出多段相互重叠的透过率信息, 将这些透过率信息依序排列成数据矩阵, 对频率重叠部分做插值平均, 得到完整的透过率函数, 再对透过率函数取对数即可得到吸收率函数. 该方法属于波长调制法, 其测量灵敏度与波长调制法相当, 主要取决于谐波信号的测量精度.

    3.   数值模拟

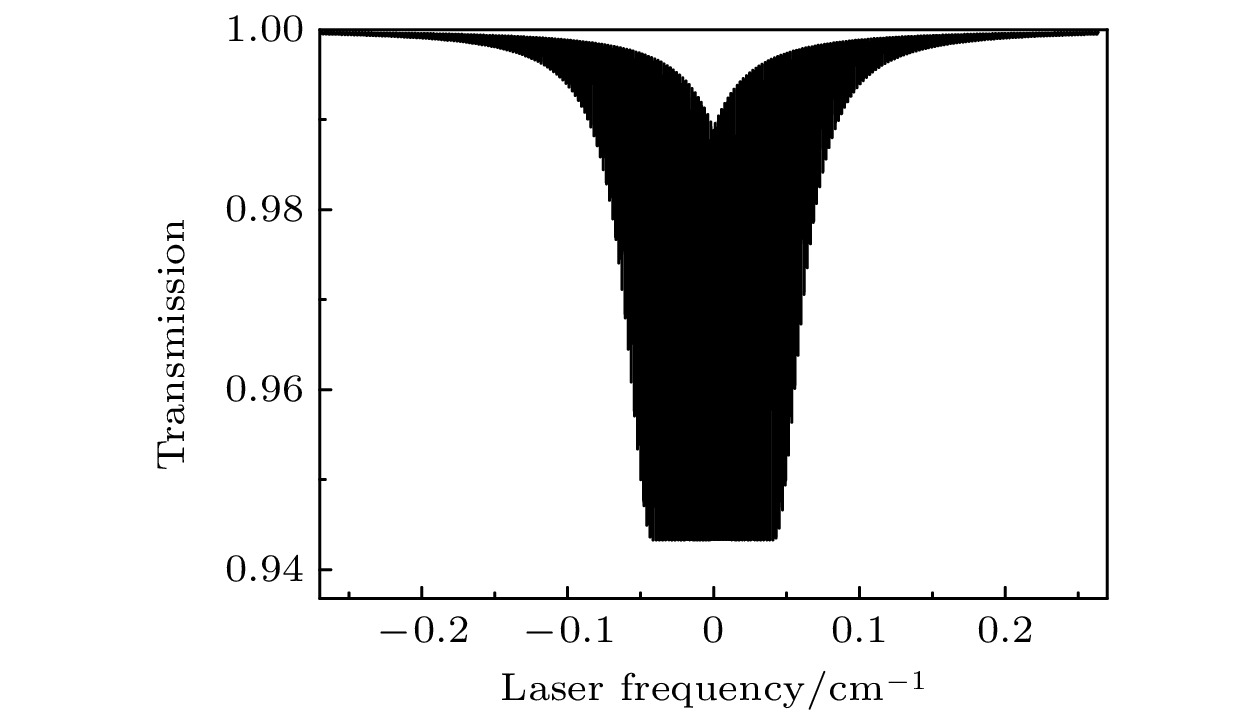
    • 本节通过数值模拟展示上述方法的数据处理流程, 并检验其有效性和准确性. 对CO2的吸收谱线进行仿真, 产生一个带有调制周期变化的透射率信号. 然后, 利用建立的透射率重构方法对信号进行重构. 选择的谱线波数为6330.821 cm–1, 其光谱常数如表1所列, 气体浓度X设定为1, 压力20 kPa, 温度296.15 K, 有效吸收光程长度为50 cm. 根据Voigt线型函数, 计算得到的半高宽为0.0209 cm–1. 扫描频率4 Hz, 波长扫描范围0.5339 cm–1, 调制频率fm为1000 Hz, 调制深度0.041 cm–1, 模拟计算中采用H0—H12阶次的谐波进行信号重构. 随时间周期变化的透过率仿真信号如图1所示, 在实验中可通过透射光强和入射光强比值获得.

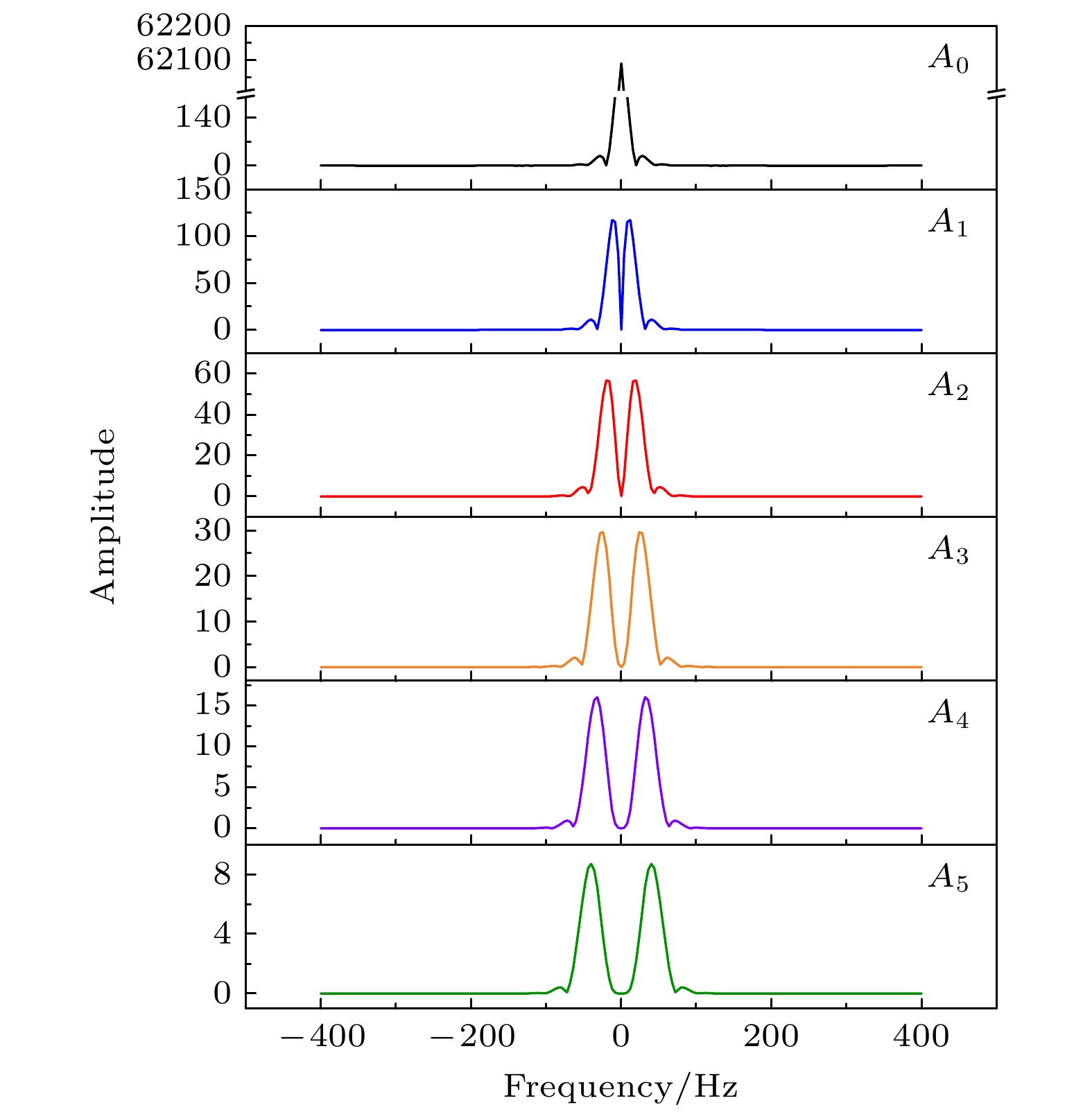
      在谐波检测中, 首先将周期变化的透过率乘上对应阶次的余弦函数, 得到锁相后的透过信号, 再进行快速傅里叶变换(FFT), 可得到各阶次透过率信号的双边对称的频谱特征, 其中0—5阶FFT频谱如图2所示.

      经FFT得到周期变化透过率各阶次谐波频谱后, 对中央特征峰进行截取, 再经过逆快速傅里叶变换(IFFT)后可获得谐波幅值, 0—5阶谐波幅值如图3所示. 在实际测量时, 选取适宜的中心特征频谱的截取宽度尤为重要, 选取过宽容易引入高频噪声, 选取过窄容易丢失有效信息, 均会导致测量精度下降. 对于本节仿真的截取宽度, 0次谐波截取宽度的半宽取23个点, 根据对各阶次特征峰形态观察比较, 阶次每提高1阶, 截取宽度的半宽增加2点, 至第12次谐波, 截取宽度的半宽达到47个点.

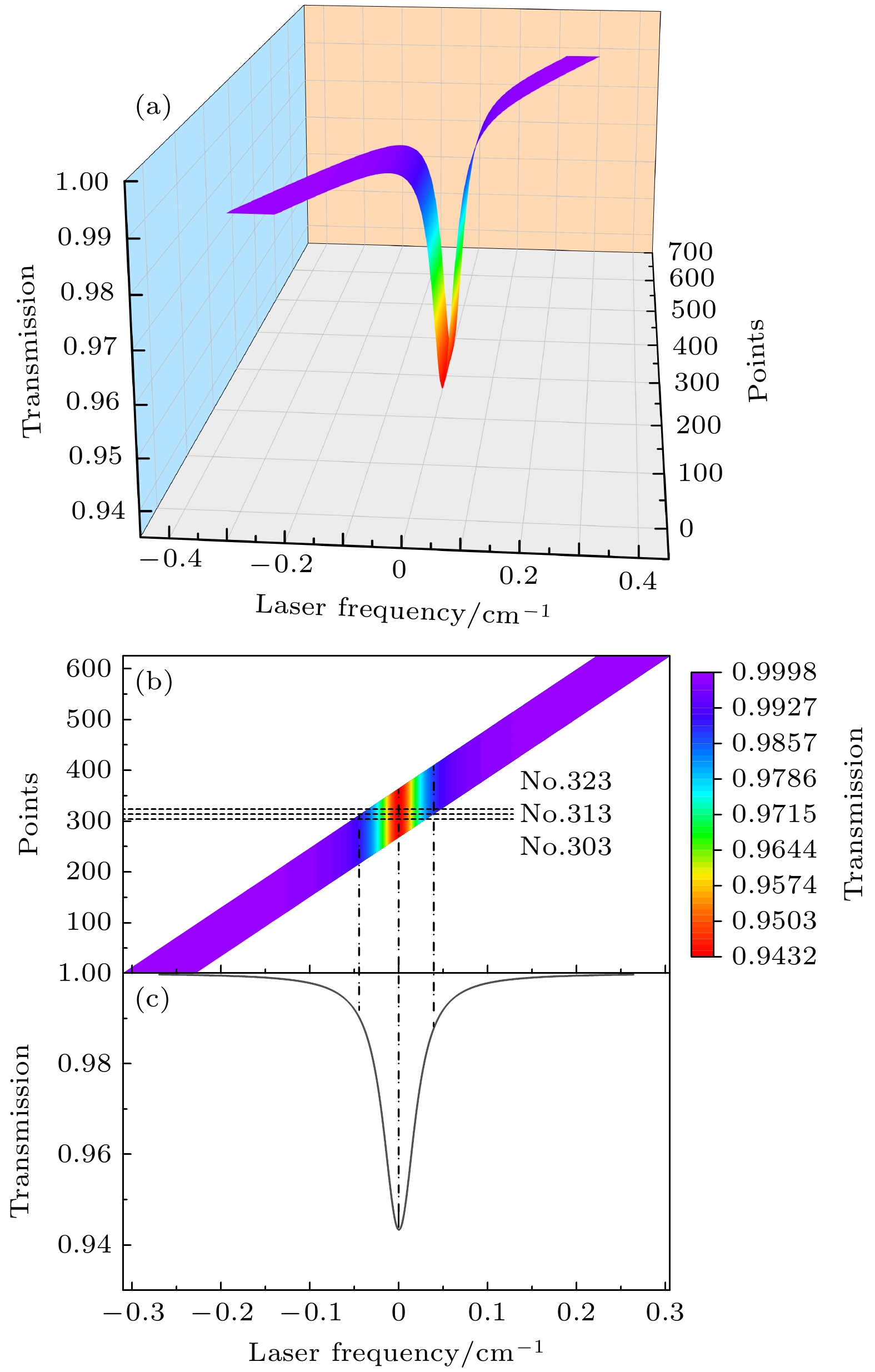
      图3展示了0—5阶谐波分量的幅值, 随着谐波阶次提高, 谐波幅值在不断减小, 在实际实验中, 受实验条件限制, 目前一般采用0—12阶次谐波. 通过FFT谐波检测, 得到各阶次谐波分量幅值后, 将各阶次谐波分量幅值代入透射率重构表达式得到透射率数据矩阵. 重构数据矩阵需要从谐波幅值中挑出足够数量的重构中心点, 本次数值模拟所用取点方案是从第50个点起每隔100取一个点, 总共取625个点, 每次重构出200个点, 最终得到625×200的重构透射率数据矩阵, 如图4所示.

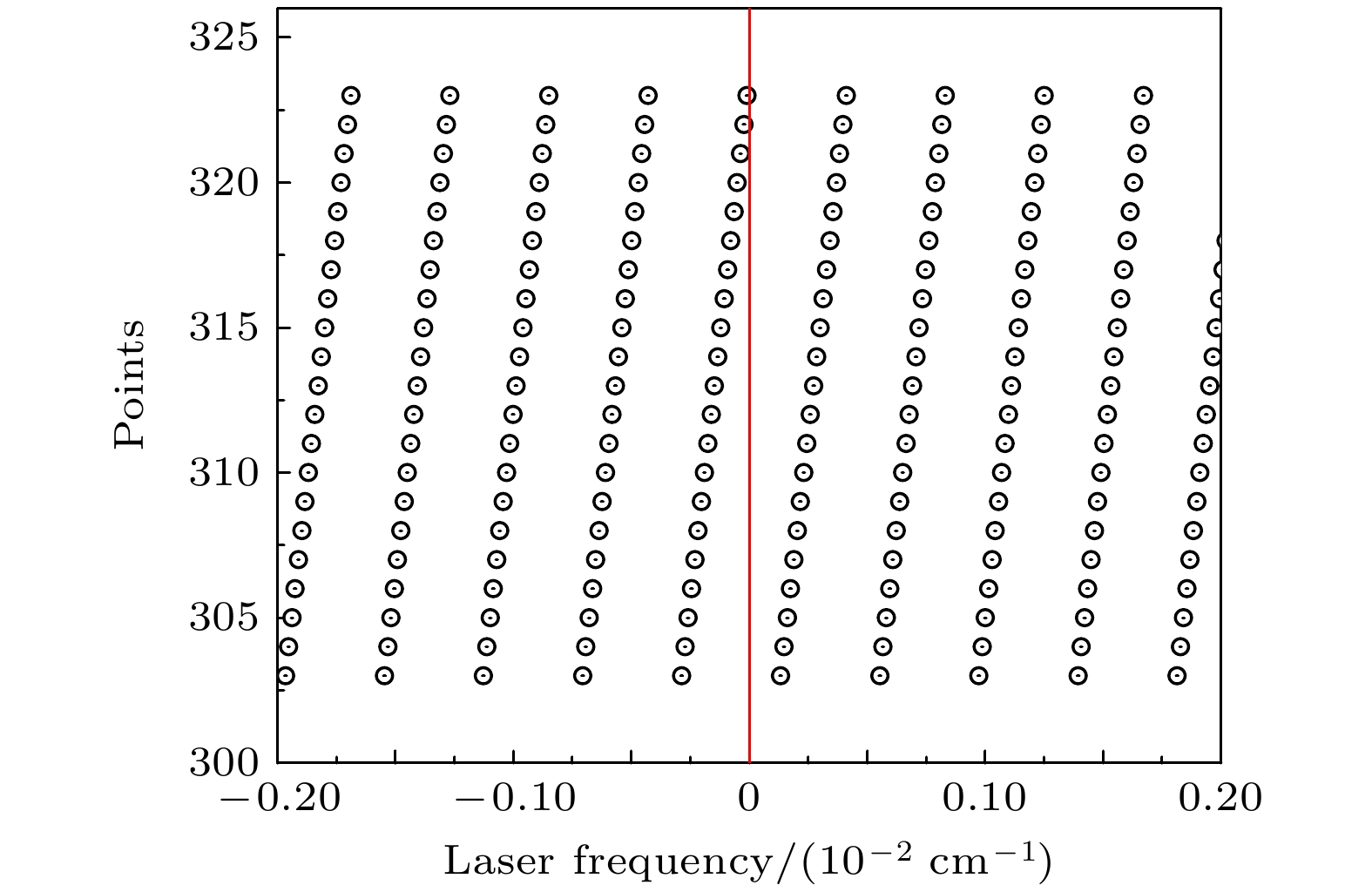
      图4(a)为数据矩阵的三维曲面图, X, Y, Z轴分别为激光波长、重构中心点序数以及透射率大小, 反映了以625个点为中心重构得到的透过率信息, 共101条曲线, 每条曲线频率范围为±0.041 cm–1, 作为数据矩阵的每个切片. 图4(b)是图4(a)的俯视图, 作为数据矩阵的等高图, 透射率大小由不同颜色区分表示, 如在谱线中心频率处, 其透过率约为0.94, 左右均有10个点(303—323)可重构出该点透过率信息, 通过对重叠区域进行平均可提高该点透过率的重构精度. 图4(c)为图4(b)在频域上的投影, 共由625条透过率曲线组成, 每条曲线对应的频率范围即为该点频率调制深度. 由于数据矩阵切片的透过率曲线中心点排列紧密, 重构范围存在大量交叉重叠部分, 对重叠部分取平均则可充分利用所有测量得到的数据来提高透射率重构结果的精度, 但对重叠数据取算术平均需要数据点的波长位置一一对应. 为了对此进行确认, 将谱线中心左右共20个切片在相对波数±2×10–3 cm–1范围内的波长用散点图加以比较, 如图5所示.

      在图5中, 在波长0点处做参照线可以看出相邻切片的波长存在微小错位. 需要采用MATLAB中基于三次多项式的样条插值方法, 对重构前62500个原始数据点的波长用重构数据做插值, 生成列数据, 重构波长范围外的点插值定义为零. 统计每行非零数据个数并求平均, 即得到最终透射率如图6所示, 其中红色和黑色曲线分别为重构得到的透过率及其理论值.

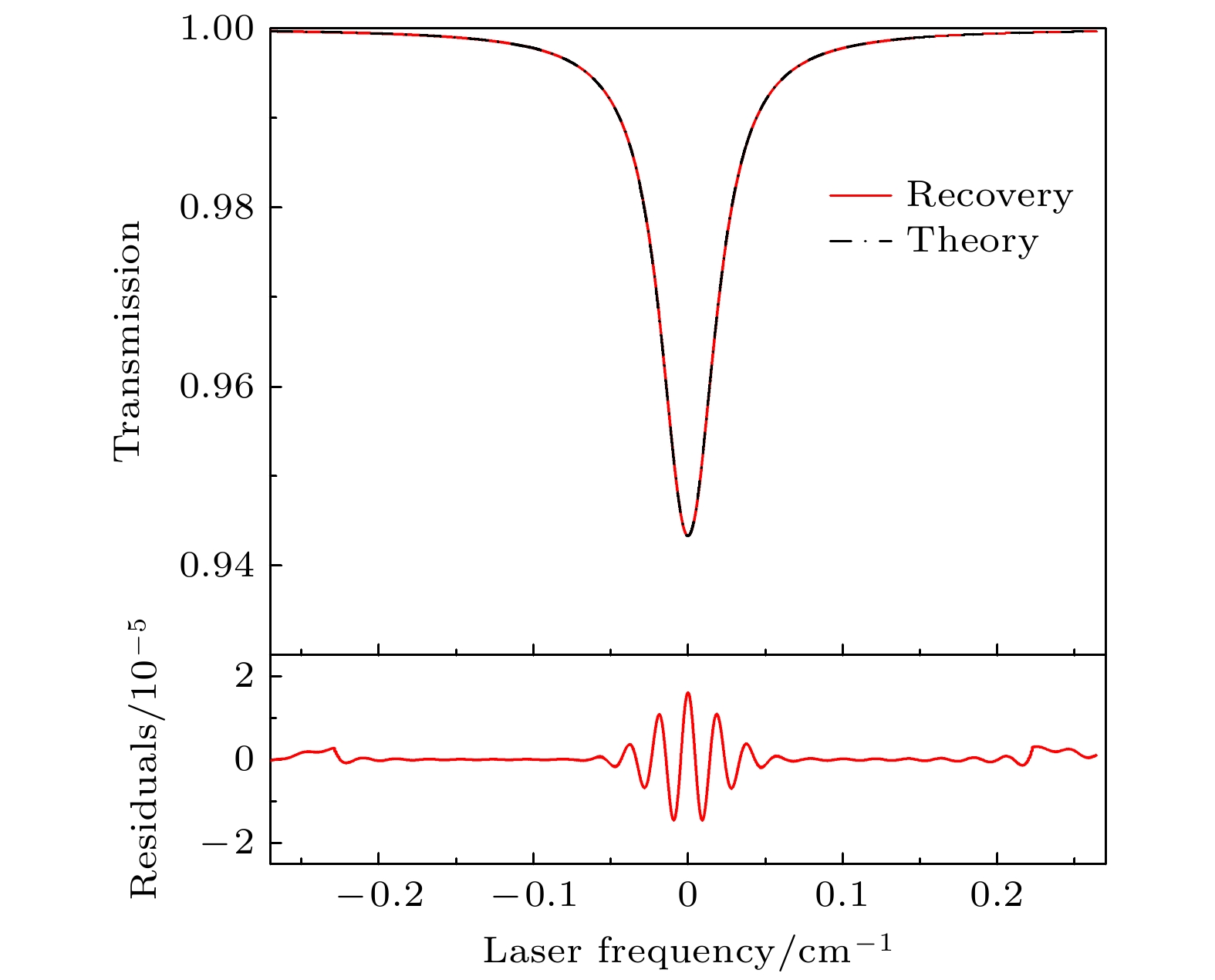
      图6给出了重构透射率数据矩阵插值平均的结果, 并与透射率模拟的理论值进行比较, 同时展示重构结果相对理论值的残差. 可以看出重构结果与理论值吻合较好, 残差均方根误差低至3.13×10–6. 残差反映系统误差特点, 可以看出两端与中心存在一定误差, 两端的误差源于端点处重构透射率数量相比中部有所减少, 中心误差呈现周期变化, 反映重构透射率的结构特点, 通过增大谐波阶次或谐波特征峰截取宽度能减小该误差, 但在实际实验条件下, 受噪声干扰, 可检测的最高谐波阶次以及特征峰截取宽度均受限.

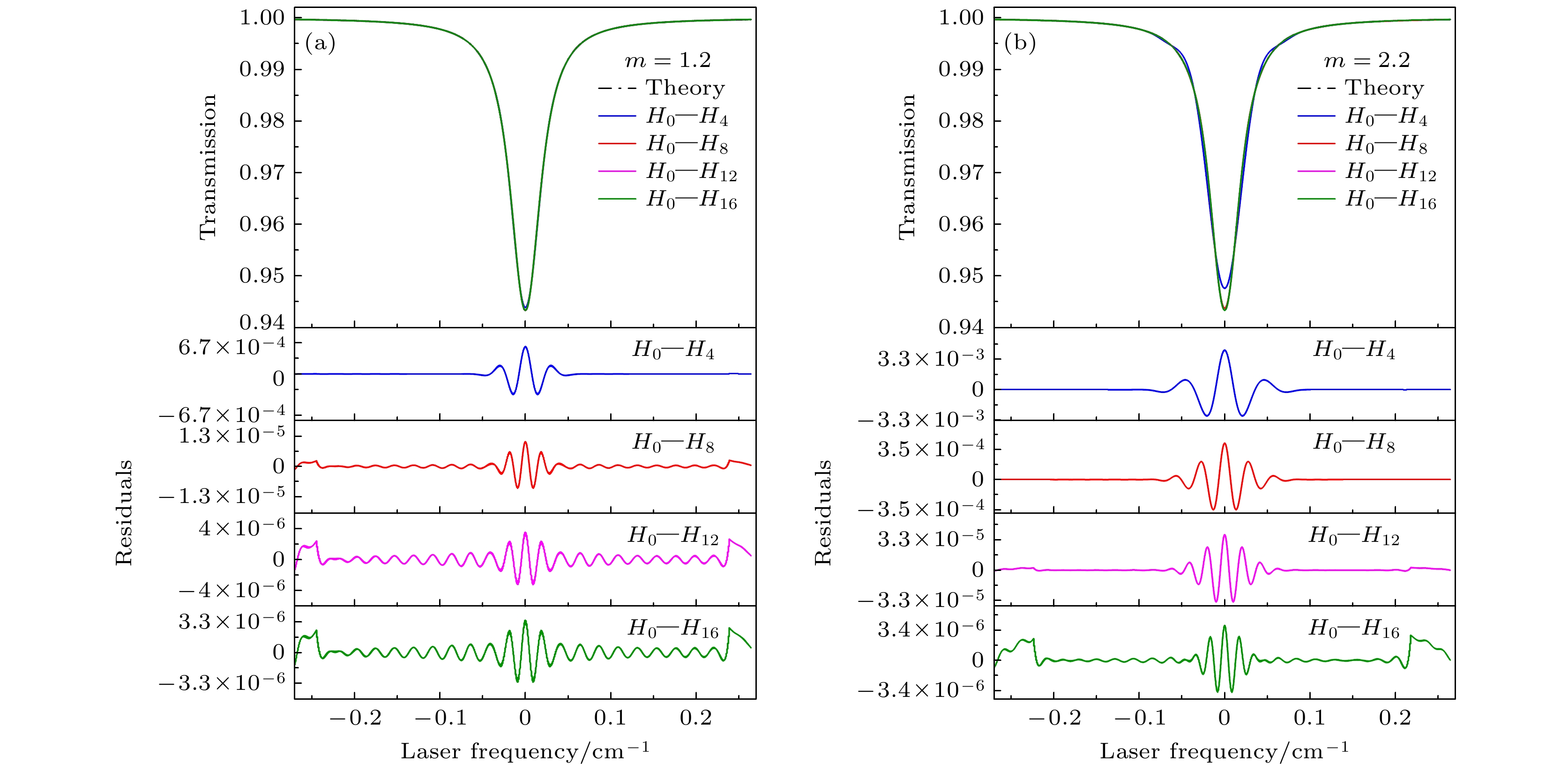
      透射率重构法存在系统误差的主要原因在于: 根据切比雪夫多项式所表达的透射率重构公式((6)式), 理论上需要采用无限阶次的谐波重构透射率, 采用重构的谐波阶次越高结果越精确. 但从图3可以看出, 随着谐波阶次的提高, 谐波幅值迅速减弱, 20阶以上的高阶谐波分量在实际测量中难以精确获取. 图6计算重构结果显示采用H0—H12阶次的谐波进行重构足以满足精度要求. 为了研究透射率重构法系统误差的影响因素, 研究以CO2单谱线为例, 选取了不同谐波阶次和调制深度进行仿真计算, 分析了透射率重构的效果和误差, 其结果如图7、图8和表2所示.

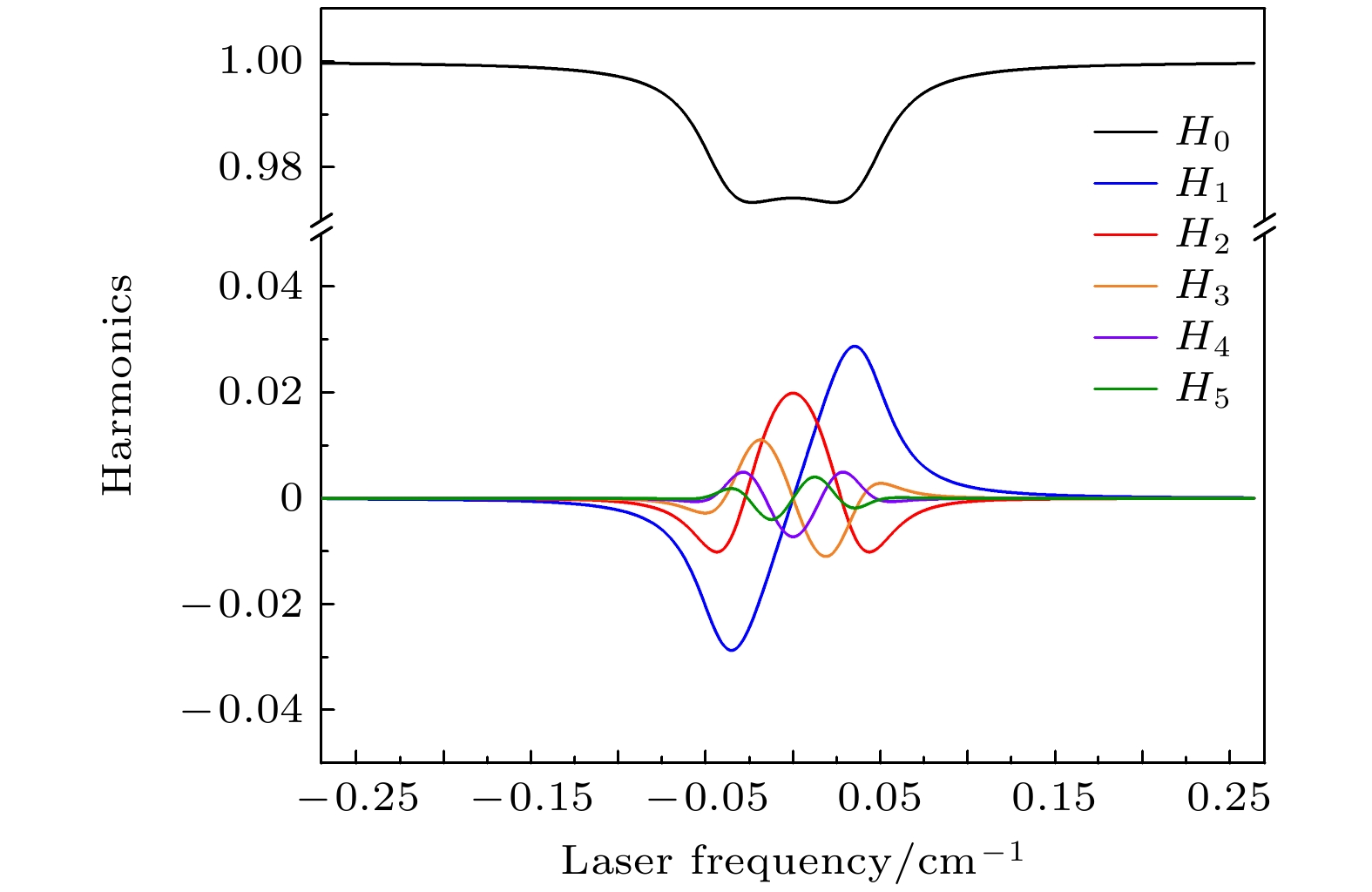
      图7中分别选取调制系数m为1.2和2.2以及谐波阶次H0—H4, H0—H8, H0—H12, H0—H16重构CO2谱线透射率. 结果可以看出调制系数为1.2时仅H0—H8阶次的谐波分量就能获得较高精度, 而调制系数2.2时, 随着重构所用谐波分量阶次的提高(H0—H12), 重构精度也迅速得到提高.

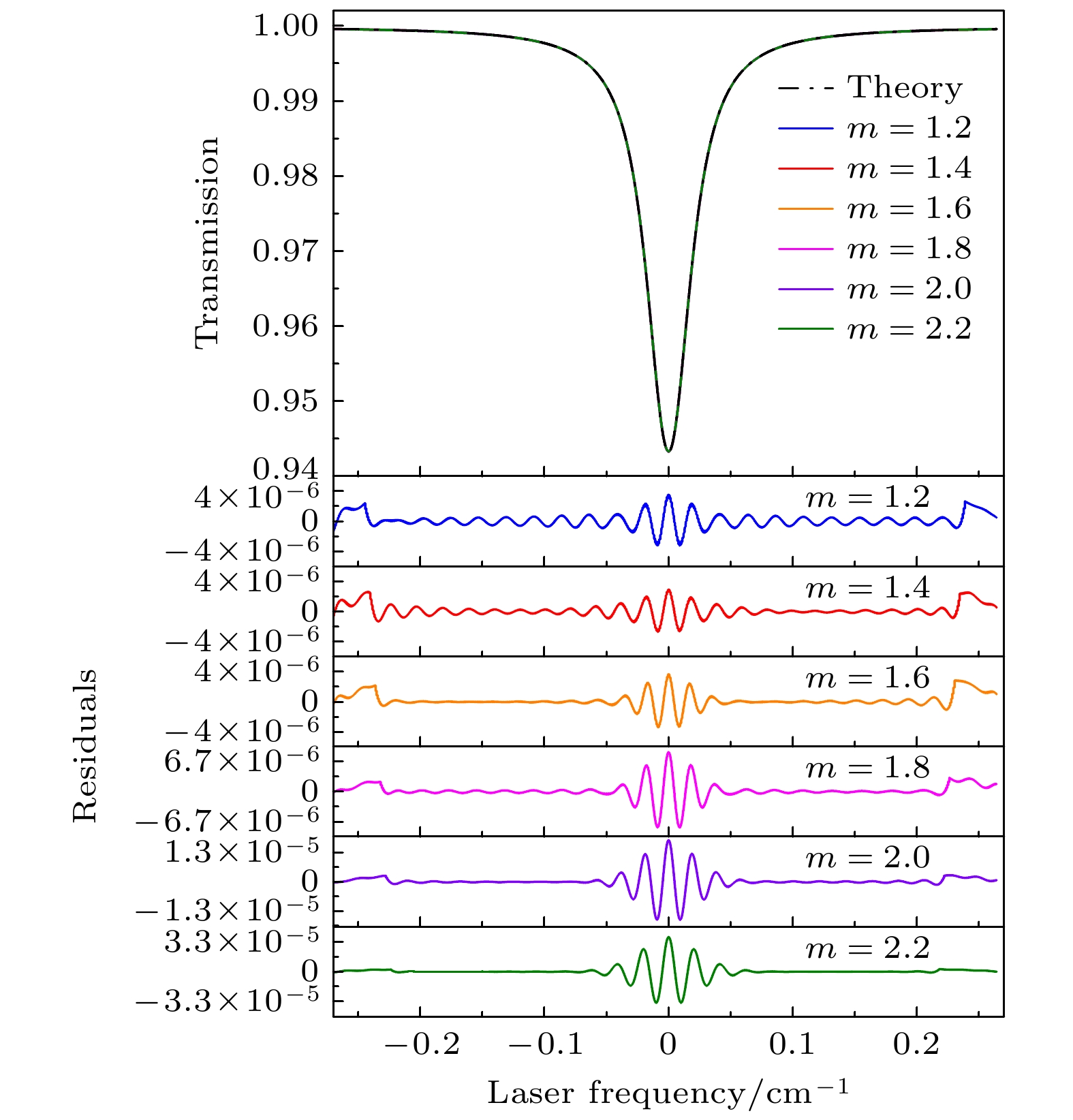
      为了进一步分析调制深度对重构透射率误差的影响作用, 在固定用H0—H12阶次的谐波分量情况下, 调制系数m分别选取1.2, 1.4, 1.6, 1.8, 2.0, 2.2六种不同调制深度进行透射率重构仿真, 模拟结果如图8所示. 由该图下部残差可看出, 随着调制深度的增大, 在谐波阶次不变情况下透射率重构误差会相应增大. 为了全面分析调制深度、谐波阶次对透射率重构系统误差的影响, 对4个阶次、6个调制系数, 总共24个工况进行仿真并计算均方根误差, 结果见表2. 从表2数据可知, 重构精度随着谐波阶次的增加而提升, 但随着调制深度的增大而降低. 在较高阶次谐波的重构中, 调制深度对重构精度的影响变得微乎其微.

      基于上述模拟分析, 揭示了谐波阶次与调制深度对透射率重构结果系统误差的影响规律, 研究成果将为实验方案中谐波阶次和调制系数的选取提供理论依据. 鉴于实验条件的复杂性, 若谐波阶次设置过高, 可能会因高次谐波信噪比不足而引入更多的误差; 另外, 若调制系数设置过低, 则可能导致谐波检测时低次谐波信噪比的下降. 因此, 在下述实验中选定谐波阶次为H0—H12, 调制系数约为2开展实验验证研究.

    4.   实验验证

    • 为验证数据处理方法的可行性和有效性, 分别采用分时测量和分束测量两种实验方案, 其中分时测量用于验证新方法的可行性和吸收率函数测量的信噪比, 分束测量用于连续在线测量来验证测量的稳定性和检测限.

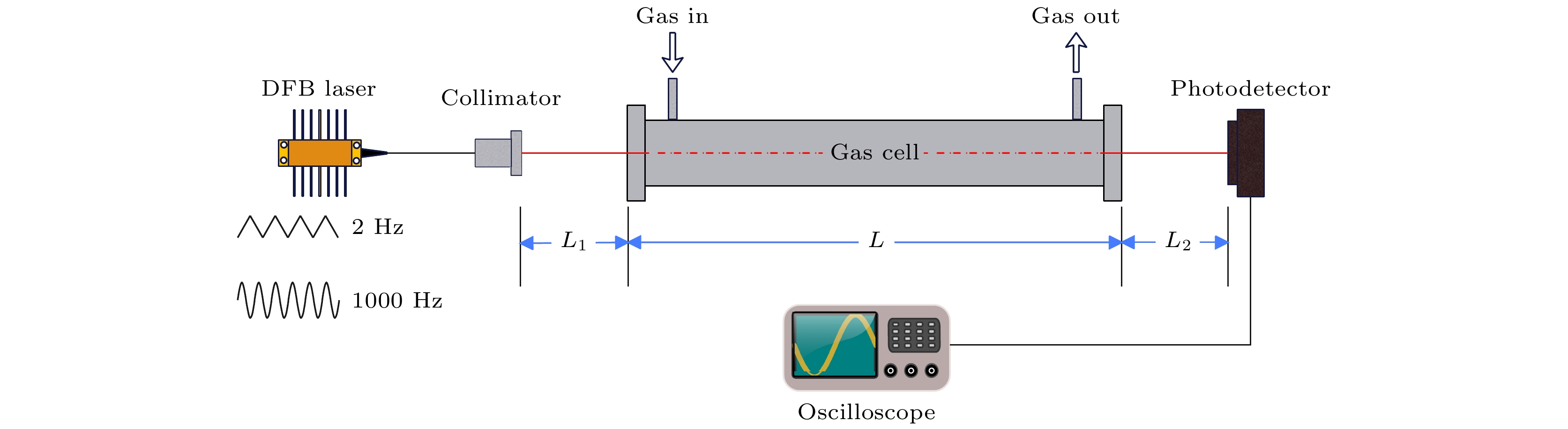
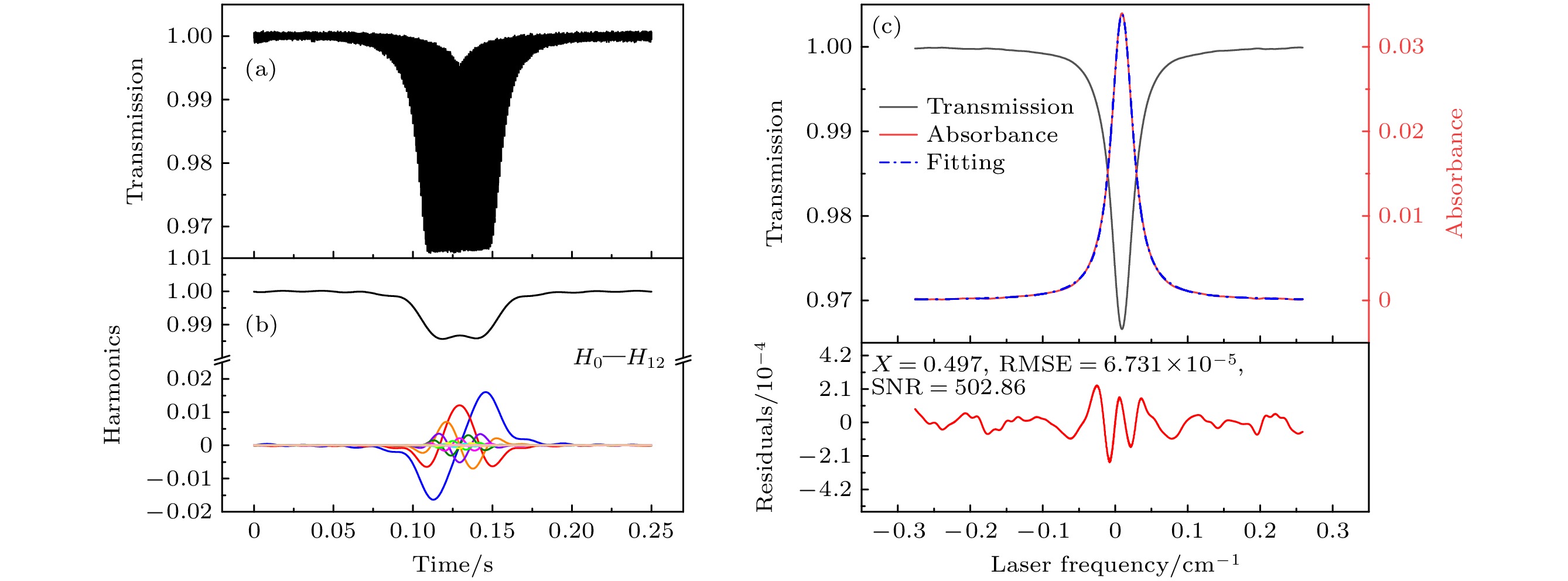
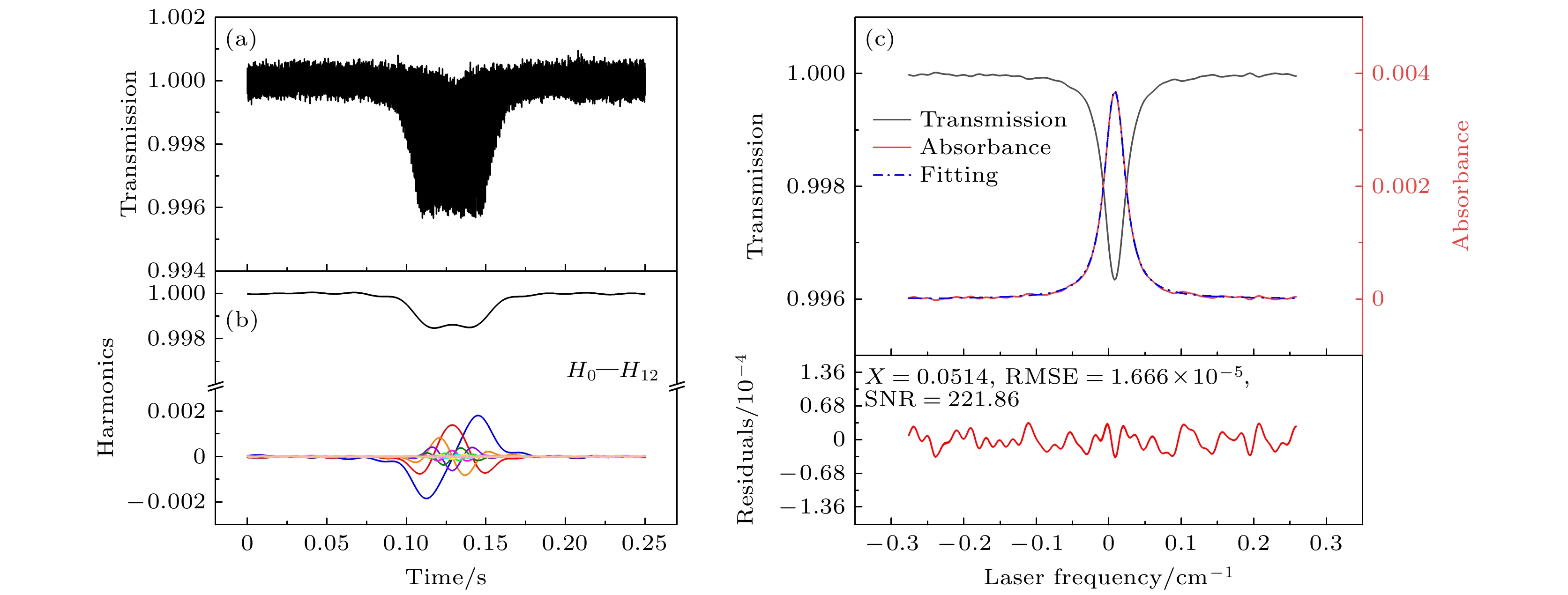
      分时测量实验方案如图9所示, 测量采用了CO2气体在6330.821 cm–1处吸收谱线. 激光光束通过含有样品气体的单程池并由光电探测器接收, 采集总时长0.4 s, 采集速率250 kHz. 测量时首先将气室抽至极低压力(60 Pa), 再对激光器施加2 Hz的三角波扫描信号和1000 Hz的正弦波调制信号进行参考信号测量, 用于消除气室两侧空气中CO2的吸收干扰以及激光自身强度波动的影响; 然后向气室通入纯CO2标气至20 kPa, 待气体稳定后测量吸收信号; 气体浓度配比采用逐级稀释法如向20 kPa的CO2标气气室通入空气至40 kPa, 静置一段时间使气体浓度混合均匀后再抽至20 kPa进行测量, 重复该步骤多次, 可得到多种不同浓度的CO2测量结果. 图10和图11给出CO2纯标气稀释1次和4次两种不同浓度下原始透射率数据、谐波分量, 以及重构的透射率和吸收函数拟合结果.

      图10(a)和图11(a)是根据透射光强和参考光强得到透过率随时间的变化曲线. 对透过率进行 谐波检测可得到H0—H12次谐波信号如图10(b)和图11(b)所示, 其中H12次谐波信噪比较低, 幅值最大值为10–5—10–4, 已接近谐波检测下限. 从谐波信号中提取625个重构中心点, 并将其谐波幅值代入到重构公式(6)中, 可重构出透过率如图10(c)和图11(c)中黑色曲线所示, 当对透过率求对数可得到吸收率函数如图10(c)和图11(c)中红色曲线, 其中图11(c)谱线峰值吸收仅为4×10–3. 图10(c)和图11(c)均展示了利用Voigt线型对重构得到的吸收率函数拟合结果. 拟合时均固定高斯线宽, 强吸收工况下拟合残差均方根误差约为6.7×10–5, 信噪比约为503; 弱吸收工况下拟合残差均方根误差约为1.7×10–5, 信噪比达到222. 相较于传统直接吸收法, 该方法显著提升了吸收率函数的测量信噪比[14,19,23,24], 说明此方法在抗干扰性能和信噪比方面具有优势.

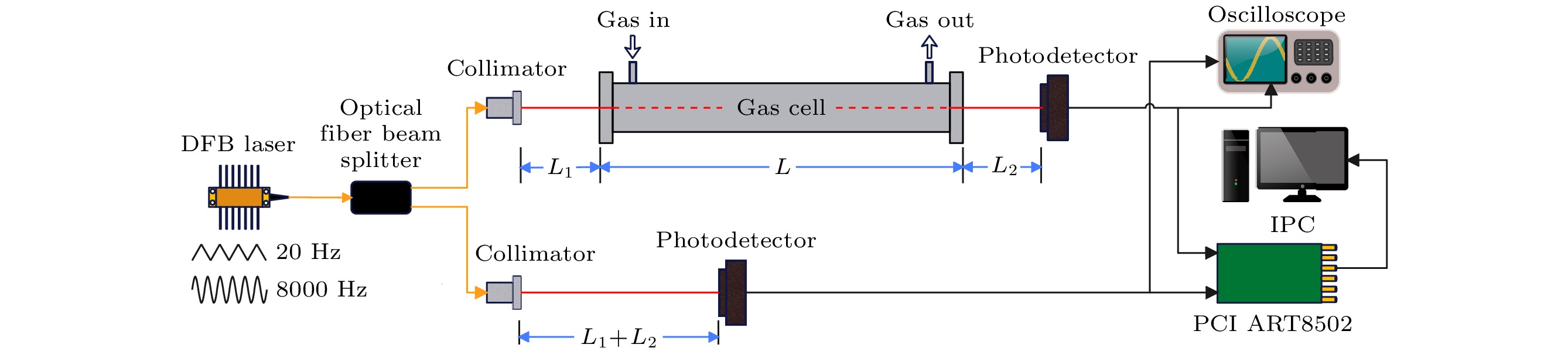
      分束测量的实验方案如图12所示, 激光经1∶1分束光纤分成两束, 一束经过有效吸收路径长度为50 cm的单程池, 另一束作为参考光从准直器发出后经过空气再由探测器接收, 其有效吸收路径长度等于测量光路单程池玻璃窗口距探测器、准直器光程之和, 即L1 + L2. 采集到的数据经Labview程序处理计算后经拟合得到如浓度、洛伦兹半宽等参数. 三角波扫描速率为20 Hz, 正弦波调制速率为8000 Hz, 采集速率2 MHz. 谐波检测得到的谐波序列从第62个点开始每隔125个点取一个重构中心点, 共400重构中心点, 每个重构中心点重构出的切片点数为200, 则数据矩阵总数为400×200即80000个点. 对数据矩阵插值平均时采用的波数序列为–0.2—0.2的200个等间距的点, 略去左右两端重构误差较大的部分, 最后采用Rautian线型函数进行拟合单次测量时间约为1.4 s.

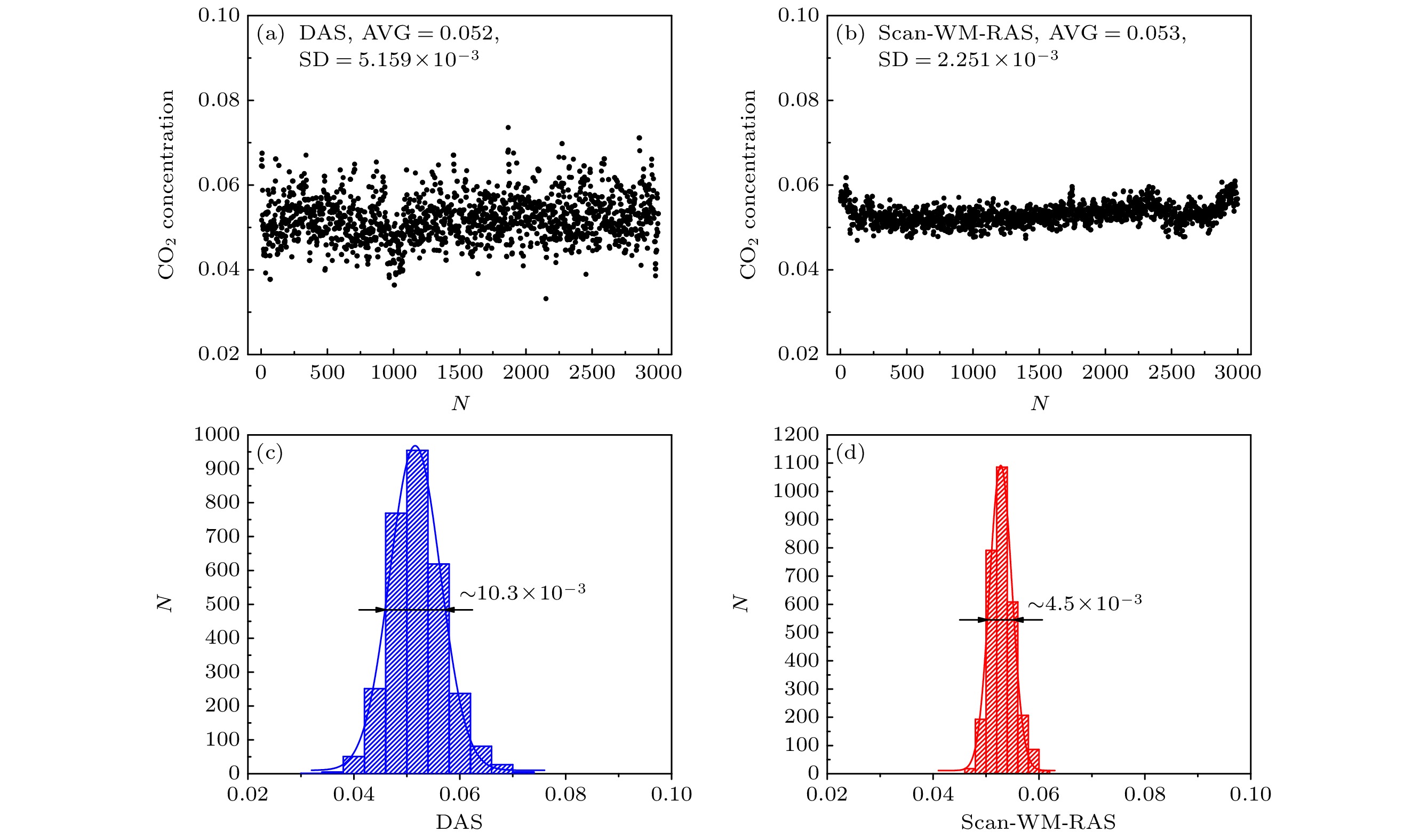
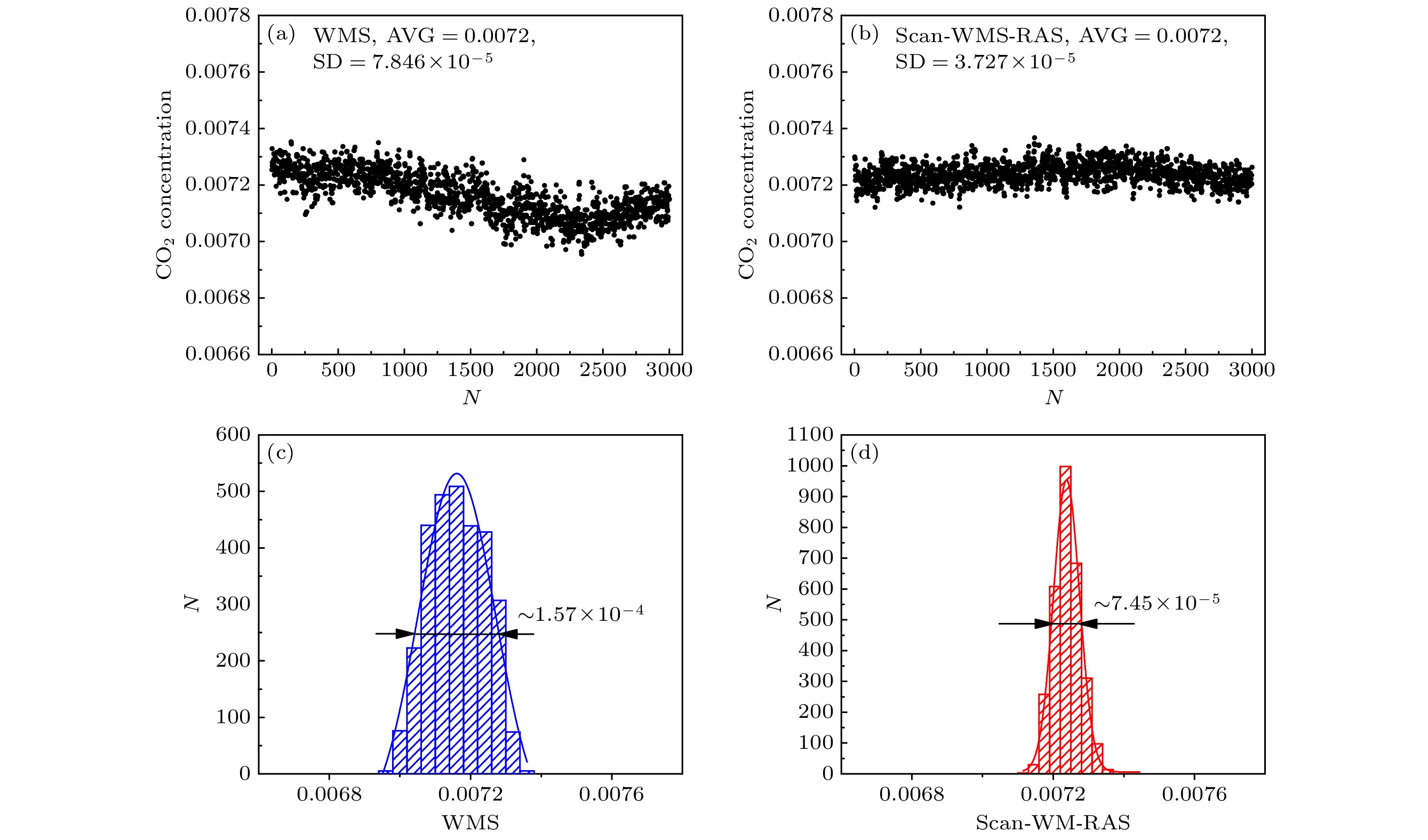
      分束测量实验结果如图13所示, 分别采用直接吸收法和扫描波长调制谐波重构法对稀释至1/16浓度的CO2标准气体进行了3000次连续在线测量. 图13(a)给出了直接吸收法3000次测量结果, 浓度平均值和标准差分别约为0.052和5.2×10–3. 图13(b)为谐波重构法3000次测量结果, 浓度平均值约为0.053, 标准差降低到2.3×10–3. 对图13(a), (b)数据进行分布直方图绘制分别得到图13(c), (d), 其高斯拟合半高半宽即为标准差. 通过比较高斯半高半宽(标准差)可以看出扫描波长调制谐波重构法测量结果的离散程度约为直接吸收法的一半, 这也表明谐波重构法在测量稳定性方面相较于传统的直接吸收法具有明显的优势.

      为验证新方法相对传统波长调制法的优势, 将二次谐波峰值法与扫描波长调制谐波重构法作对比, 实验结果如图14所示. 分束测量方案如下, 将CO2标准气体稀释至约0.72%后通入有效吸收光程为25 m的多次反射池, 分别采用二次谐波峰值法和扫描波长调制谐波重构法同时处理同一批数据, 总共进行了3000次连续在线测量. 图14(a), (b)分别给出了二次谐波峰值法和谐波重构法3000次测量结果, 其浓度平均值均约为0.72%, 其中谐波重构法测量结果更稳定, 其标准差约为3.7×10–5, 仅为二次谐波峰值法的一半. 对图14(a), (b)数据进行分布直方图绘制分别得到图14(c), (d), 其中扫描波长调制谐波重构法测量结果的离散程度显著低于二次谐波峰值法, 表明谐波重构法在测量稳定性方面优于传统二次谐波峰值法, 其原因在于二次谐波峰值法难以消除基线波动、激光频率漂移等问题, 而谐波重构法则通过精确重建吸收率函数轮廓来提高测量的稳定性.

    5.   结　论

    • 波长调制法中谐波信号蕴含了吸收率函数信息, 但同时含有激光强度、调制深度、相位角、光电放大系数等信息. 考虑到吸收率函数的重要性(直接确定气体温度、浓度、谱线参数等)以及波长调制法(高灵敏度、抗干扰能力强)的优点, 本文基于波长调制法建立了一种高精度、免标定的吸收率函数重构方法, 该方法建立了谐波信号与吸收率函数之间的关系, 首先利用谱线某一频率对应的各次谐波信号重构出特定频率范围内(即调制深度)透过率信息, 然后通过低频扫描整条吸收谱线即可得到一系列不同频域范围内的透过率信息, 最后对频率重叠区域的透过率进行插值平均并对其进行求对数可得到完整的吸收率函数. 该方法预期可为谱线物理参数高精度标定、弱吸收条件下气体参数高精度测量以及复杂工业现场中气体监测提供新的测量方法.

    参考文献 (26)

目录

/

返回文章
返回