高级搜索

基于亚多普勒wm-NICE-OHMS的14CO2光谱测量技术理论研究

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

李勇, 周晓彬, 赵刚, 尹润涛, 杨家琪, 闫晓娟, 马维光. 基于亚多普勒wm-NICE-OHMS的14CO2光谱测量技术理论研究[J]. 物理学报, 2025, 74(6): 064209-1. doi: 10.7498/aps.74.20241482
引用本文: 李勇, 周晓彬, 赵刚, 尹润涛, 杨家琪, 闫晓娟, 马维光. 基于亚多普勒wm-NICE-OHMS的14CO2光谱测量技术理论研究[J]. 物理学报, 2025, 74(6): 064209-1. doi: 10.7498/aps.74.20241482
shu
Yong LI, Xiaobin ZHOU, Gang ZHAO, Runtao YIN, Jiaqi YANG, Xiaojuan YAN, Weiguang MA. Theoretical study of 14CO2 spectrum measurement technology based on sub-Doppler wm-NICE-OHMS[J]. Acta Physica Sinica, 2025, 74(6): 064209-1. doi: 10.7498/aps.74.20241482
Citation: Yong LI, Xiaobin ZHOU, Gang ZHAO, Runtao YIN, Jiaqi YANG, Xiaojuan YAN, Weiguang MA. Theoretical study of 14CO2 spectrum measurement technology based on sub-Doppler wm-NICE-OHMS[J]. Acta Physica Sinica, 2025, 74(6): 064209-1. doi: 10.7498/aps.74.20241482
shu

基于亚多普勒wm-NICE-OHMS的14CO2光谱测量技术理论研究

  • 1.

    山西大学, 光量子技术与器件全国重点实验室, 太原　030006

  • 2.

    山西大学, 极端光学协同创新中心, 太原　030006

    • 作者简介: 李勇: liyong328513@163.com .
    通讯作者: E-mail: gangzhao@sxu.edu.cn.;  E-mail: mwg@sxu.edu.cn.

  • 中图分类号: 42.60.Fc, 42.62.Fi, 95.85.Hp

Theoretical study of 14CO2 spectrum measurement technology based on sub-Doppler wm-NICE-OHMS

  • 1.

    State Key Laboratory of Quantum Optics and Quantum Optics Devices, Shanxi University, Taiyuan 030006, China

  • 2.

    Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

    • Corresponding authors: E-mail: gangzhao@sxu.edu.cn.;  E-mail: mwg@sxu.edu.cn.

  • MSC: 42.60.Fc, 42.62.Fi, 95.85.Hp

  • 摘要: 14CO2光谱检测在大气环境学和同位素定年等领域中具有重要应用, 但由于其自然丰度极低且光谱重叠干扰严重, 检测难度极大. 基于亚多普勒光谱的噪声免疫腔增强光外差分子光谱(NICE-OHMS)技术因其具有高的灵敏度和选择性, 有望成为下一代14CO2检测方法. 本文理论分析了亚多普勒NICE-OHMS光谱测量技术. 通过模拟真实大气光谱, 选择2209.108 cm–1处的14CO2跃迁线作为最佳测量目标, 建立了14CO2亚多普勒饱和吸收NICE-OHMS模型, 并与多普勒展宽光谱进行对比, 验证了波长调制(wm-)亚多普勒NICE-OHMS技术可有效抑制光谱重叠干扰, 实现高分辨率的14CO2光谱测量. 最终, 通过数值模拟分析了压强和调制系数等参数对信号幅度的影响, 确定了最佳实验条件, 为高灵敏14CO2光谱测量提供理论依据.
    Abstract: The massive emission of greenhouse gases, particularly CO2, has led to severe damage to the Earth’s ecological environment and poses a threat to human health. Many countries have therefore proposed policies to curb the greenhouse effect. Carbon monitoring is a critical prerequisite for realizing these goals, and tracking carbon emission sources can support the precise implementation and advancement of related policies more effectively. The contribution of fossil fuel combustion to greenhouse gas emissions can be inferred by detecting the abundance of 14C in carbon dioxide in a specific region. Conventional 14CO2 detection methods have significant drawbacks, including complicated operation, high cost and large equipment size. Laser absorption spectroscopy (LAS) offers advantages such as real-time, online in-situ measurement and simple operation, making it suitable for the online detection of isotopes. Among the various LAS techniques, noise immunity cavity enhanced optical heterodyne molecular spectroscopy (NICE-OHMS) is the most sensitive. This method integrates frequency modulation spectroscopy (FMS) into cavity enhanced spectroscopy (CES) to suppress the low-frequency noise while increasing the absorption paths, providing a minimum detectable absorption coefficient as low as 10–13. Additionally, the accumulation of high intracavity laser power in NICE-OHMS can stimulate saturation absorption, which has a narrow spectral width that can mitigate spectral overlap. In this work, we model the spectral signals of 14CO2 at different locations and select the transition line of 14CO2 at 2209.108 cm–1 as an optimal measurement target based on the principles of high-intensity and well-resolution. The theoretical analysis of the NICE-OHMS technique is then carried out, and theoretical simulations of a mixed sample of 14CO2 and its nearby interfering gases (13CO2, 12CO2, and N2O), are performed under the simulated experimental conditions. The results of the simulation show that the Doppler broadened spectral signal of 14CO2 is covered by the other gases’ signals with a very low amplitude, which is adverse to the detection of 14CO2. To eliminate the linear slope of the Doppler broadened signal and to further improve the signal-to-noise ratio, we perform 14CO2 spectral measurements by using wavelength-modulated NICE-OHMS (wm-NICE-OHMS). The results of the simulation show that the spectral lines are effectively separated, and the detection accuracy of the 14CO2 ratio is greatly improved. Finally, the effects of pressure and modulation index on the 14CO2 wm-NICE-OHMS signal are analyzed. The results show that when the pressure is 42 mTorr and the modulation index is 1.07, the signal amplitude of wm-NICE-OHMS reaches its maximum. This work lays a theoretical foundation for the high precision detection of 14CO2 in real-time environmental monitoring. The potential for large-scale application of wm-NICE-OHMS in carbon emission tracking is highlighted, providing a more cost-effective alternative to traditional detection methods. Furthermore, the technology is able to suppress spectral interference from other gases and achieve high resolution in 14CO2 measurements, which will greatly help monitor and reduce greenhouse gas emissions.
  • 加载中

  • 图 1  不同波数的14CO2, N2O, 12CO2, 13CO2混合气体直接吸收模拟信号(黑线), 以及不同波数的14CO2直接吸收模拟信号(红线)

    Figure 1.  Directly absorbed analog signals for 14CO2, N2O, 12CO2, 13CO2 gas mixtures with different wave numbers (black line); directly absorbed analog signals for 14CO2 with different wave numbers (red line).

    下载: 全尺寸图片 幻灯片

    图 2  NICE-OHMS原理图[27]

    Figure 2.  NICE-OHMS schematic[27].

    下载: 全尺寸图片 幻灯片

    图 3  14CO2, N2O, 12CO2和13CO2混合气体的亚多普勒模拟信号

    Figure 3.  Sub-Doppler analog signal for gas mixtures such as 14CO2, N2O, 12CO2, 13CO2.

    下载: 全尺寸图片 幻灯片

    图 4  14CO2, N2O, 12CO2和13CO2混合气体的wm-NICE-OHMS模拟信号

    Figure 4.  wm-NICE-OHMS analog signal for gas mixtures such as 14CO2, N2O, 12CO2, 13CO2.

    下载: 全尺寸图片 幻灯片

    图 5  (a) β = 0.5, 1, 1.5时14CO2 wm-NICE-OHMS信号; (b) 14CO2 wm-NICE-OHMS信号幅度随调制系数β的变化

    Figure 5.  (a) 14CO2 wm-NICE-OHMS signal when β = 0.5, 1, 1.5; (b) variation of 14CO2 wm-NICE-OHMS signal amplitude with β.

    下载: 全尺寸图片 幻灯片

    图 6  (a) 压强为100, 200, 300 mTorr时14CO2 wm-NICE-OHMS信号; (b) 14CO2 wm-NICE-OHMS信号幅度随压强的变化

    Figure 6.  (a) 14CO2 wm-NICE-OHMS signal when pressure is 100, 200, 300 mTorr; (b) variation of 14CO2 wm-NICE-OHMS signal amplitude with pressure.

    下载: 全尺寸图片 幻灯片

    表 1  14CO2, N2O, 12CO2和13CO2光谱的其他参数

    Table 1.  Other parameters of 14CO2, N2O, 12CO2 and 13CO2 spectra.

    波数/cm–1 线强$ /({\rm cm}^{-1}{\cdot}{\rm molecule}^{-1}{\cdot}{\rm cm}^{-2}) $ 跃迁底态能量/cm–1 总配分函数
    14CO2 2209.107679 2.83×10–18 163.8828 2033.395
    12CO2 2209.124896 1.802×10–29 5785.2772 286.09
    13CO2 2209.115876 4.23×10–27 3394.9427 576.64
    13CO2 2209.11747 1.54×10–27 3648.8668 576.64
    N2O 2209.08543 3.41×10–21 1282.3324 4984.9
    N2O 2209.11444 6.61×10–22 654.1553 4984.9
    下载: 导出CSV
  • [1] Zhao X, Ma X, Chen B, Shang Y, Song M 2022 Resour. Conserv. Recycl. 176 105959 doi: 10.1016/j.resconrec.2021.105959
    [2] Kong W, Wan F, Lei Y, Wang C, Sun H, Wang R, Chen W G 2024 Anal. Chem. 96 15313 doi: 10.1021/acs.analchem.4c02865
    [3] Ge H, Kong W P, Wang R, Zhao G, Ma W G, Chen W G, Wan F 2023 Opt. Lett. 48 2186 doi: 10.1364/OL.486417
    [4] Hou X L 2018 J. Radioanal. Nucl. Chem. 318 1597 doi: 10.1007/s10967-018-6258-6
    [5] Hua Q 2009 Quat. Geochronol. 4 378 doi: 10.1016/j.quageo.2009.03.006
    [6] Levin I, Naegler T, Kromer B, Diehl M, Francey R, Gomez-Pelaez A J, Steele P, Wagenbach D, Weller R, Worthy D 2010 Tellus B: Chem. Phys. Meteorol. 62 26 doi: 10.1111/j.1600-0889.2009.00446.x
    [7] Povinec P 2018 J. Radioanal. Nucl. Chem. 318 1573 doi: 10.1007/s10967-018-6248-8
    [8] Maity A, Maithani S, Pradhan M 2021 Anal. Chem. 93 388 doi: 10.1021/acs.analchem.0c04329
    [9] Lehmann B, Wahlen M, Zumbrunn R, Oeschger H, Schnell W 1977 Appl. Phys. 13 153 doi: 10.1007/BF00882474
    [10] Labrie D, Reid J 1981 Appl. Phys. A 24 381 doi: 10.1007/BF00899738
    [11] McCartt A, Jiang J 2022 ACS Sensors 7 3258 doi: 10.1021/acssensors.2c01253
    [12] Zhang Z, Peng T, Nie X Y, Agarwal G S, Scully M O 2022 Light Sci. Appl. 11 274 doi: 10.1038/s41377-022-00953-y
    [13] Chen W P, Qiao S D, Lang Z, Jiang J C, He Y, Shi Y W, Ma Y F 2023 Opt. Lett. 48 3989 doi: 10.1364/OL.497685
    [14] Hashimoto K, Nakamura T, Kageyama T, Badarla V R, Shimada H, Horisaki R, Ideguchi T 2023 Light Sci. Appl. 12 48 doi: 10.1038/s41377-023-01096-4
    [15] Ma Y F, Liang T T, Qiao S D, Liu X N, Lang Z T 2023 Ultrafast Sci. 3 0024 doi: 10.34133/ultrafastscience.0024
    [16] Qiao S D, Ma P Z, Tsepelin V, Han G W, Liang J X, Ren W, Zheng H D, Ma Y F 2023 Opt. Lett. 48 419 doi: 10.1364/OL.482351
    [17] Zhang C, Qiao S D, He Y, Zhou S, Qi L, Ma Y F 2023 Appl. Phys. Lett. 122 241003 doi: 10.1063/5.0157161
    [18] Lang Z T, Qian S D, Ma Y F 2023 Light Adv. Manuf. 4 233 doi: 10.37188/lam.2023.023
    [19] Galli I, Pastor P C, Di Lonardo G, Fusina L, Giusfredi G, Mazzotti D, Tamassia F, De Natale P 2011 Mol. Phys. 109 2267 doi: 10.1080/00268976.2011.614284
    [20] Terabayashi R, Saito K, Sonnenschein V, Okuyama Y, Iwamoto K, Mano K, Kawashima Y, Furumiya T, Tojo K, Ninomiya S, Yoshida K, Tomita H 2022 J. Appl. Phys. 132 083102 doi: 10.1063/5.0101732
    [21] Jiao K, Gao J, Yang J Q, Zhao G, Shi Z, Wang X P, Zhu D, He H Y, Qing J, Yan X J, Ma W G, Jia S T 2024 Microwaves Opt. Technol. Lett. 66 33946 doi: 10.1002/mop.33946
    [22] Galli I, Bartalini S, Ballerini R, Barucci M, Cancio P, De Pas M, Giusfredi G, Mazzotti D, Akikusa N, De Natale P 2016 Optica 3 385 doi: 10.1364/OPTICA.3.000385
    [23] 齐汝宾, 赫树开, 李新田, 汪献忠 2015 光谱学与光谱分析 35 172 doi: 10.3964/j.issn.1000-0593(2015)01-0172-06 Qi R B, He S K, Li X T, Wang X Z 2015 Spectrosc. Spect. Anal. 35 172 doi: 10.3964/j.issn.1000-0593(2015)01-0172-06
    [24] Jiang J, McCartt A D 2022 International Symposium on Molecular Spectroscopy Champaign-Urbana, Illinois, USA, June 20-24, 2022 p1
    [25] Zhou X B, Zhao G, Li Y, Cheng Z W, Jiao K, Zhang B F, Zhang Z H, Li Y K, Yan X J, Ma W G, Jia S T 2024 Opt. Lett. 49 202 doi: 10.1364/OL.507004
    [26] Zak E J, Tennyson J, Polyansky O L, Lodi L, Zobov N F, Tashkun S A, Perevalov V I 2017 J. Quant. Spectrosc. Radiat. Transfer 189 267 doi: 10.1016/j.jqsrt.2016.11.022
    [27] Gagliardi G, Loock H-P 2014 Cavity-Enhanced Spectro- scopyand Sensing (Vol. 179) (Berlin: Springer Berlin Heidelberg) p231
    [28] Foltynowicz A, Ma W, Schmidt F M, Axner O 2009 J. Opt. Soc. Am. B: Opt. Phys. 26 1384 doi: 10.1364/JOSAB.26.001384
    [29] Ma W G, Foltynowicz A, Axner O 2008 J. Opt. Soc. Am. B: Opt. Phys. 25 1144 doi: 10.1364/JOSAB.25.001144
    [30] Foltynowicz A 2009 Ph. D. Dissertation (Sweden: Umeå University
    [31] Šimečková M, Jacquemart D, Rothman L, Gamache R, Goldman A 2006 J. Quant. Spectrosc. Radiat. Transfer 98 130 doi: 10.1016/j.jqsrt.2005.07.003
  • 加载中
图( 6) 表( 1)
计量
  • 文章访问数:  83
  • HTML全文浏览数:  83
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-22
  • 刊出日期:  2025-03-20

基于亚多普勒wm-NICE-OHMS的14CO2光谱测量技术理论研究

    通讯作者: E-mail: gangzhao@sxu.edu.cn.; 
    通讯作者: E-mail: mwg@sxu.edu.cn.
    作者简介: 李勇: liyong328513@163.com
  • 1. 山西大学, 光量子技术与器件全国重点实验室, 太原　030006
  • 2. 山西大学, 极端光学协同创新中心, 太原　030006
  • 收稿日期:  2024-10-22

摘要: 14CO2光谱检测在大气环境学和同位素定年等领域中具有重要应用, 但由于其自然丰度极低且光谱重叠干扰严重, 检测难度极大. 基于亚多普勒光谱的噪声免疫腔增强光外差分子光谱(NICE-OHMS)技术因其具有高的灵敏度和选择性, 有望成为下一代14CO2检测方法. 本文理论分析了亚多普勒NICE-OHMS光谱测量技术. 通过模拟真实大气光谱, 选择2209.108 cm–1处的14CO2跃迁线作为最佳测量目标, 建立了14CO2亚多普勒饱和吸收NICE-OHMS模型, 并与多普勒展宽光谱进行对比, 验证了波长调制(wm-)亚多普勒NICE-OHMS技术可有效抑制光谱重叠干扰, 实现高分辨率的14CO2光谱测量. 最终, 通过数值模拟分析了压强和调制系数等参数对信号幅度的影响, 确定了最佳实验条件, 为高灵敏14CO2光谱测量提供理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 工业革命以来, 温室气体(特别是CO2)大量排放引发的温室效应, 已对地球生态环境造成严重破坏, 严重威胁着人类的生存. 为应对这一挑战, 各国纷纷提出减碳措施以抑制温室效应. 碳监测是碳减排的重要前提, 通过实时监测温室气体浓度, 可以精准核算碳排放量. 然而, 温室气体排放源具有多样性, 包括生物活动(如动植物呼吸)和化石燃料燃烧等, 其中减少化石燃料燃烧是减碳的主要措施之一. 追踪碳排放来源, 特别是评估煤炭、石油、天然气等化石燃料燃烧对温室气体的贡献, 有助于为碳监测提供数据支持, 推动“碳中和、碳达峰”的精准实施[1–3]. 然而直接测量12CO2 (CO2的主要同位素分子, 自然丰度12C/C为98.9%)并不能区分CO2不同的排放源.

      14C是碳的放射性同位素, 其半衰期约为5730年, 主要由宇宙射线与大气中的14N反应生成[4]. 通过衰变耗散, 地球表面14C的自然丰度保持在1.2×10–12 (1.2 ppt)[5]. 由于生态循环, 自然界中动植物体内的14C含量等于自然丰度. 然而, 化石燃料在地下埋藏数百万年, 14C早已消耗殆尽. 化石燃料燃烧不仅释放大量12CO2, 还会导致当地环境中14C丰度的降低. 因此, 通过测量区域内CO2的14C同位素丰度, 可以推断化石燃料燃烧对温室气体排放的贡献[6].

      传统的14CO2检测方法主要有加速质谱法(AMS)和液体闪烁计数法(LSC)[7]. 其中AMS测量仪器价格昂贵, 通常需要数百万美元的投入, 故其存在操作复杂、离线测量、成本高、仪器尺寸大等问题[8]; 而LSC测量仪器虽然成本较低, 但还存在测量周期长以及样品需求量大等问题; 因此这两种技术无法满足14CO2测量的规模化应用.

      1977年以来, 由于激光光谱技术具有实时、在线原位测量和操作简便等优点, 被应用与物质同位素的在线检测[9–18]. 然而, 激光光谱技术应用于大气中14CO2的测量仍面临两个主要挑战. 第一, 14C的自然丰度极低, 要求光谱仪具有极高的灵敏度. 为了提高灵敏度, 通常采用基于高精度光学腔的激光光谱技术, 如腔衰荡光谱(CRDS)[19,20]和光反馈腔增强吸收光谱(OF-CEAS)[21]等, 这些技术通过光学腔中的高反射镜增大激光与气体的作用路径, 从而提升灵敏度. Galli等[22]采用饱和腔衰荡光谱技术(SCAR), 通过长时间平均, 获得了3×10–15 (即0.3 pMC (percent modern carbon))的探测灵敏度, 但样品测量时间长达4 h, 限制了其实时性. 第二, 杂质气体对14CO2产生了严重的谱线干扰, 导致测量误差大. 为解决此问题, 低压采样和低温处理能够有效地减小分子光谱的压力展宽和多普勒展宽, 但低温模块的引入会增加系统成本、体积和操作复杂度[23]. 为此, Jiang等[24]提出双共振腔衰荡光谱技术, 以消除光谱的多普勒展宽, 实现室温条件下14CO2光谱的高灵敏度测量, 但该技术需要两个激光器与高精度腔的锁定, 增加了系统复杂度.

      噪声免疫腔增强光外差分子光谱(NICE-OHMS)技术[25], 在腔增强吸收光谱的基础上引入了频率调制光谱(FMS), 通过抑制低频噪声进一步提高测量灵敏度. NICE-OHMS相比CRDS和OF-CEAS, 具有更高的灵敏度, 因此有望在14CO2检测中实现更高精度的测量. 此外, NICE-OHMS技术通过高精细度光学腔可以无源放大输入激光功率, 在精细度为104的光学腔中, 毫瓦量级的入射激光在腔内可以达到瓦级, 从而激发气体分子的饱和吸收, 通过对亚多普勒光谱的测量, 抑制光谱的重叠干扰. 因此, 基于NICE-OHMS技术, 能够在室温下高选择性地测量14CO2光谱. 目前尚无基于NICE-OHMS测量14CO2光谱的相关报道.

      本文从理论上分析了NICE-OHMS测量14CO2光谱的方法. 首先, 通过光谱重叠度分析筛选了目标光谱谱线, 然后利用跃迁参数确定了饱和参数与光功率之间的关系. 接着, 通过腔传递函数和频 率调制模型, 建立了14CO2的wm-NICE-OHMS光谱模型. 通过模拟证明了亚多普勒光谱能够有效地提升光谱选择性. 最后, 分析了不同实验参数对wm-NICE-OHMS光谱信号的影响, 为大气背景下高灵敏检测14CO2及14C自然丰度(14C/C)奠定了理论基础.

    2.   谱线选择

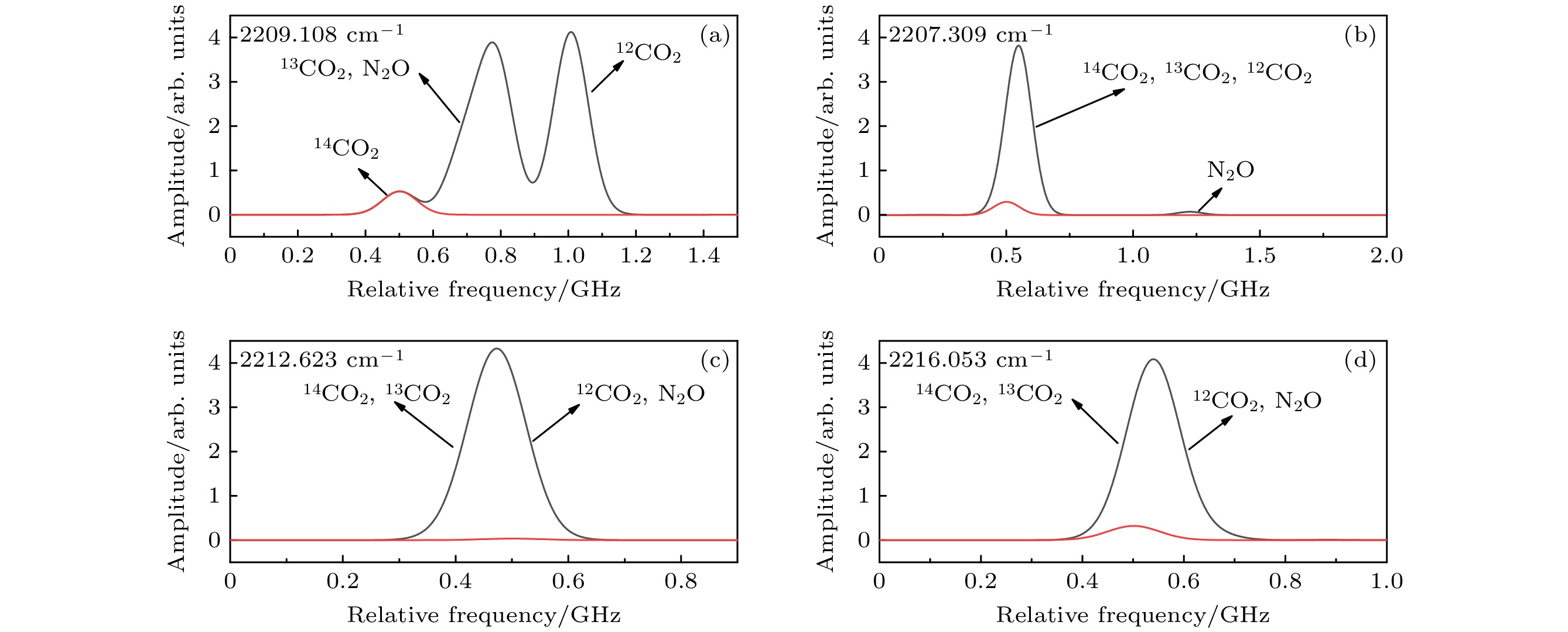
    • 吸收线最强的14CO2光谱位于2200 cm–1(4.5 μm)附近, 对应分子振转能级的基频带跃迁, 由于不对称拉伸带平行于偶极轴的振动运动产生了强偶极矩. 但是, 由于周围其他杂质气体的光谱严重干扰了14CO2光谱, 影响浓度反演的准确性. 因此, 首先模拟了该区域光谱, 分析了光谱重叠干扰, 并借此确定目标14CO2跃迁线. 本节选取四条典型2200 cm–1 附近的14CO2跃迁线为例, 对14CO2及杂质气体(主要为13CO2, 12CO2, N2O)进行直接吸收光谱的仿真, 得到的结果如图1所示, 图中混合气体的吸收线为黑线所示, 14CO2的吸收线为红线所示, 且图1(a)、图1(b)、图1(c)、图1(d)分别对应14CO2在2209.108 cm–1, 2207.309 cm–1, 2212.623 cm–1, 2216.053 cm–1处的跃迁线[26]; 为了模拟真实大气环境, 仿真中14CO2, 13CO2, 12CO2的丰度设置为1.2×10–12, 1.1%, 98.9%, N2O的浓度设置为1×10–8, 其中13CO2, 12CO2, N2O光谱数据来自Hitran数据库, 光学系统的模拟参数符合我们实验室装置条件, 包括腔长为150 cm、压强为100 mTorr (1 Torr = 133 Pa)、温度为296 K.

      从图1可看出, 位于2209.108 cm–1处(图1(a))的14CO2受光谱重叠干扰影响最小, 在14CO2跃迁线中心处, 14CO2吸收信号的贡献最大为99.7%, 其他杂质分子干扰占比仅为0.3%. 而对于其他跃迁线, 14CO2吸收信号在中心频率处的贡献分别为11.1% (图1(b))、0.09% (图1(c))、10.2% (图1(d)), 造成14CO2吸收信号被完全淹没在干扰光谱中. 综上可知, 位于2209.108 cm–1的14CO2的跃迁线受光谱重叠干扰的影响最小, 因此本文选取了位于该跃迁线进行分析与仿真.

    3.   NICE-OHMS理论模型

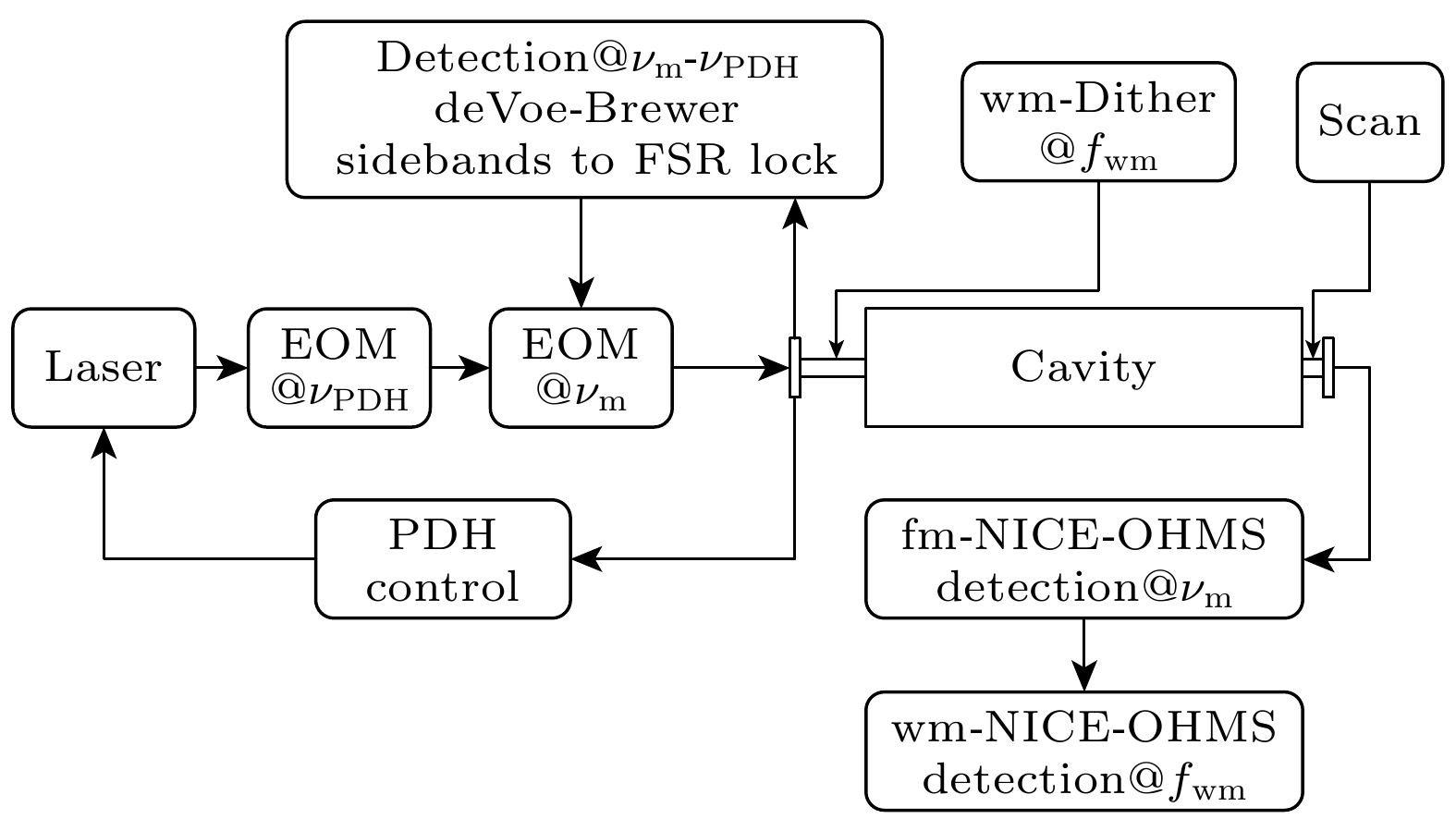
    • 典型的NICE-OHMS原理如图2所示. 一束激光经过两个调制(νPDH和νm)后耦合进入高精细度光学腔, 通过νPDH解调腔反射光, 获取误差信号, 实现激光载频到光学腔的频率锁定; 通过νm-νPDH解调反射光, 获取误差信号, 实现调制频率νm到光学腔自由光谱区的锁定; 然后基于调制频率νm对光学腔透射信号的解调获得fm-NICE-OHMS信号; 最后再对腔长增加一个低频调制信号fwm, 然后对fm-NICE-OHMS信号解调, 获取wm-NICE-OHMS信号.

      • 3.1.   多普勒展宽NICE-OHMS理论模型

    • 根据Foltynowicz等[28]报道可知, fm-NICE-OHMS的理论表达式为

      式中, Δν为激光相对于吸收线中心的频率失谐; $ {\eta }_{{\mathrm{f}}{\mathrm{m}}} $为频率调制的仪器因子; $ {P}_{0} $是入射到探测器上的光功率; F为光学腔的精细度; c为气体浓度; S为目标吸收线强度; P为气体总压强; L为光学腔的长度; $ {{\mathrm{J}}}_{n}\left(\beta \right) $为贝塞尔函数, 其中β为调制系数; vm为调制频率; $ {\theta }_{{\mathrm{f}}{\mathrm{m}}{\mathrm{s}}} $等于$ {\mathrm{\pi }}/2 $的奇数倍时, NICE-OHMS 信号只包含吸收项, 称此时的$ {\theta }_{{\mathrm{f}}{\mathrm{m}}{\mathrm{s}}} $为吸收相位, 当$ {\theta }_{{\mathrm{f}}{\mathrm{m}}s} $等于${{\text{π}} {/ } 2}$的偶数倍时, 只包含色散项, 称$ {\theta }_{{\mathrm{f}}{\mathrm{m}}{\mathrm{s}}} $该为色散相位. $ {\chi }^{{\mathrm{a}}{\mathrm{d}}{\mathrm{s}}} $和$ {\chi }^{{\mathrm{d}}{\mathrm{i}}{\mathrm{s}}{\mathrm{p}}} $分别为谱线的吸收和色散线型函数(单位为cm), 采用Voigt线型, 表达式分别为[29]

      式中C为光速(m/s); W为复误差函数, 表示为

      其中$ s = {\nu _z}/u $, νz为光场传播方向上的速度分量, 由于频率ν的光场只能与玻尔兹曼分布中特定速度的分子相互作用, 所以$ {\nu _z} = c\left( {\nu - {\nu _0}} \right)/{\nu _0} $; G为饱和度. 在Maxwell-Boltzmann分布的情况下, 特定温度下最可几速率为u, 表达式为$u = \sqrt {2{k_{\text{B}}}T/m} $. x为[30]

      y为

      式中ΓD是多普勒展宽(Hz). 对于给定温度T(K)与分子质量m(kg), ΓD表达式为

      其中kB为玻尔兹曼常数, 等于1.380×10–23 J/K; M是分子量, 单位是(u); λ0是光的波长, 单位是(m).

      ΓL为碰撞展宽的半高全宽, 其表达式为

      其中Bp为压力展宽系数. 参考Foltynowicz等[28]报道, 可知wm-NICE-OHMS的理论表达式为

      其中$ \eta_{\mathrm{w}\mathrm{m}} $为波长调制的仪器因子, $ {\nu }_{{\mathrm{a}}} $为调制幅度, 线性函数下标为1表示第一傅里叶函数.

      • 3.2.   亚多普勒展宽NICE-OHMS理论模型

    • 在高精细度光学腔内, 不仅存在往返的载频及调制边带三联体, 同时激光功率被有效放大, 致使分子吸收形成了泵浦-探测结构, 沿透射方向的三联体会观察到高功率反向传播三联体的饱和吸收信号, 因此会在fm-NICE-OHMS信号上出现5个亚多普勒结构, 其中相对幅度依赖于频率νm的调制系数, 相对于多普勒展宽线型, 亚多普勒光谱具有窄线宽结构[30]. 当调制系数β小于0.1时, 可以近似为只有谱线中心亚多普勒结构, 且只有在色散相位时才存在, 该亚多普勒光谱fm-NICE-OHMS信号可以表示为[30]

      式中, x0为面积归一化高斯函数的峰峰值; 与饱和度G相关的参数 Φ(G)决定了亚多普勒信号的幅度, 可以表示为

      其中, $ \omega $为高斯光束光斑半径.

      亚多普勒光谱线型近似为洛伦兹函数的色散部分, 可以表示为

      再者, wm-NICE-OHMS信号可表示为

      式中

      其中, $ {\nu }_{{\mathrm{a}}} $为调制幅度, τ为积分时间.

      • 3.3.   饱和参数的理论计算

    • (2)式中的关键参数为饱和度G, 该值对于利用亚多普勒谱准确反演待测气体浓度至关重要, 可以表示为[29]

      式中, Ic为腔内激光强度; Isat为饱和光强; $ {\varepsilon }_{0} $为介电常数; $ \hbar $为普朗克常数; Bp为压力展宽系数; $ \mu $为跃迁偶极矩; γtt为飞行时间, 其表达式为

      其中, Psat为饱和功率.

      为了获得跃迁偶极矩, 从吸收线强度S出发, 其表达式为[31]

      式中, g2为下能级简并度; c2为第二辐射常数, 值为1.4387769 cm·K; $E'' $为下能级能量; T为温度; $ \sigma $为波数; Q为待测分子的总配分函数; A为爱因斯坦自发辐射系数, 其表达式为

      其中, $ h $为普朗克常量, R为加权跃迁偶极矩的平方, R与偶极矩$\mu $的关系为${\mu ^2} = R$.

      将(20)式代入(19)式中可得跃迁线偶极矩的表达式为

      式中

      其中, J''为低态量子数, gi和gs分别是状态相关和状态无关的核自旋统计权重.

      对于2209.108 cm–1处14CO2的跃迁线[26], 其光谱参数J'' 为19, Bp为0.073 cm–1/atm, S为2.83×10–18 cm–1/(molecule·cm–2), E''为163.8828 cm–1, gigs为7, Q为2033.395[26]. 根据(21)式可得14CO2的下能级简并度为273, 进一步由(20)式可得其偶极矩为225.3 mD, 得到在压力100 mTorr下, 饱和功率是2.8 mW, 当腔内功率为6.33 W时, 14CO2的饱和度为2211. 此外, 对于本课题组搭建的中红外NICE-OHMS测量系统中, 精细度为28000, 调制系数(β)为0.1.

    4.   NICE-OHMS信号仿真

      4.1.   大气14CO2的NICE-OHMS光谱模拟

    • 基于以上14CO2光谱参数以及NICE-OHMS理论模型, 本文对大气提纯的CO2样品的光谱进行了仿真. 在2209.108 cm–1附近包含的主要大气光谱跃迁线及其参数如表1所列[26]. 仿真中, 考虑了丰度为98.9%的12CO2, 以及丰度为1.1%的13CO2和丰度为1.2×10–12的14CO2. 同时由于在位于2209.108 cm–1的14CO2附近有N2O的强吸收线, 尽管使用催化燃烧等手段可以除去一部分N2O, 但仍会有少量残余杂质存在, 故在模拟过程中加入浓度为1.0×10–8的N2O.

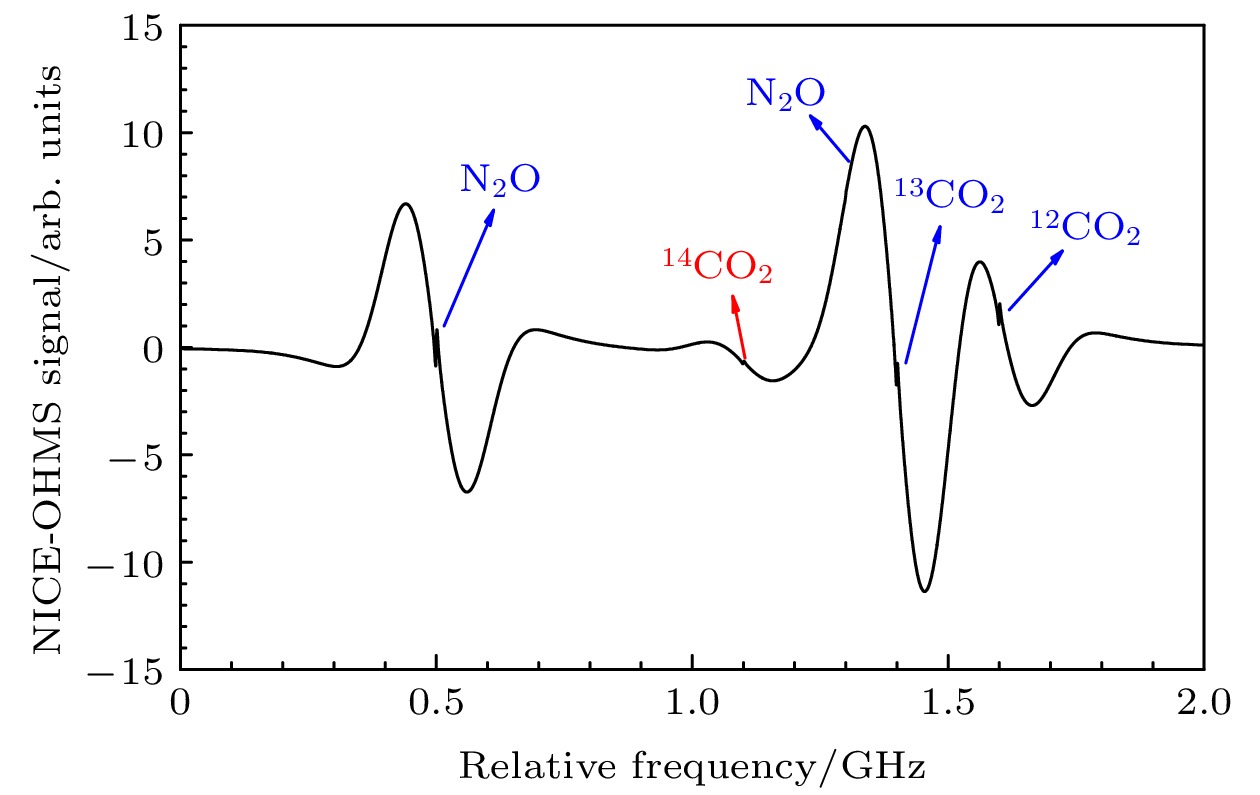
      利用光谱参数仿真获得的fm-NICE-OHMS光谱如图3所示, 频率调制系数约为0.1. 首先从图3可以看出, NICE-OHMS是零背景技术, 当激光频率远离分子跃迁线时, 解调得到的信号为0. 这是促进NICE-OHMS具有超高灵敏度特性的原因之一. 另外, 可以很明显地分辨出N2O, 13CO2和12CO2的吸收信号(如蓝色箭头标识所示), 每一个单一的光谱呈现奇对称形状, 其宽度主要受到多普勒展宽影响, 光谱的半高全宽约为120 MHz; 在光谱中心还可以看到窄线宽的结构, 这是由于饱和吸收造成的亚多普勒光谱信号, 但由于受到背景多普勒光谱的影响, 很难从该信号中准确提取出亚多普勒光谱. 同时14CO2吸收信号(如红色箭头标识所示)较弱, 波束为2209.08543 cm–1, 2209.11444 cm–1的N2O信号最大幅值分别是14CO2的11.6倍和2.25倍, 故在混合气体NICE-OHMS信号中14CO2信号难以观察. 此外14CO2信号在混合气体信号2209.108 cm–1处受到N2O等杂气的多普勒尾翼影响, 14CO2信号不能有效的分离. 因此, 无法准确地分离出14CO2吸收光谱.

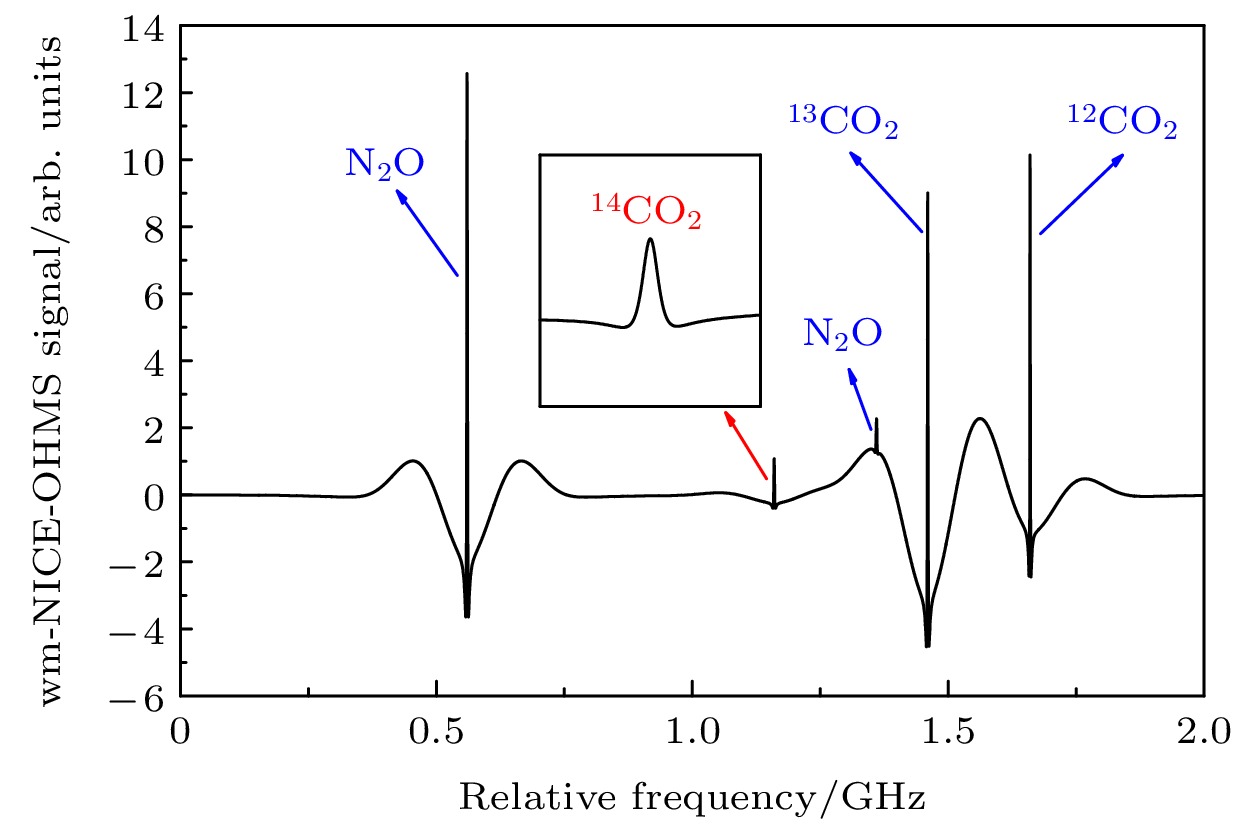
      图4是频率调制系数为0.1时的wm-NICE-OHMS信号, 该过程波长调制幅度设置为0.01 MHz, 使得亚多普勒信号幅度达到最大值, 远小于多普勒展宽的最佳调制幅度, 多普勒展宽被有效抑制. 图4中插图为放大的14CO2亚多普勒光谱, 14CO2谱线展宽仅约为4 MHz. 通过图4中混合气体光谱的零背景可以分析出wm-NICE-OHMS消除了杂质气体的光谱干扰, 因此可以准确提取出14CO2的光谱信号, 通过拟合其亚多普勒光谱可以准确地反演出14CO2的浓度以及其丰度.

      此外, 由(13)式可知, wm-NICE-OHMS信号幅度受调制系数(β)和压强的影响. 下面将分别进行分析讨论.

      • 4.2.   调制系数(β)对14CO2的wm-NICE-OHMS信号的影响

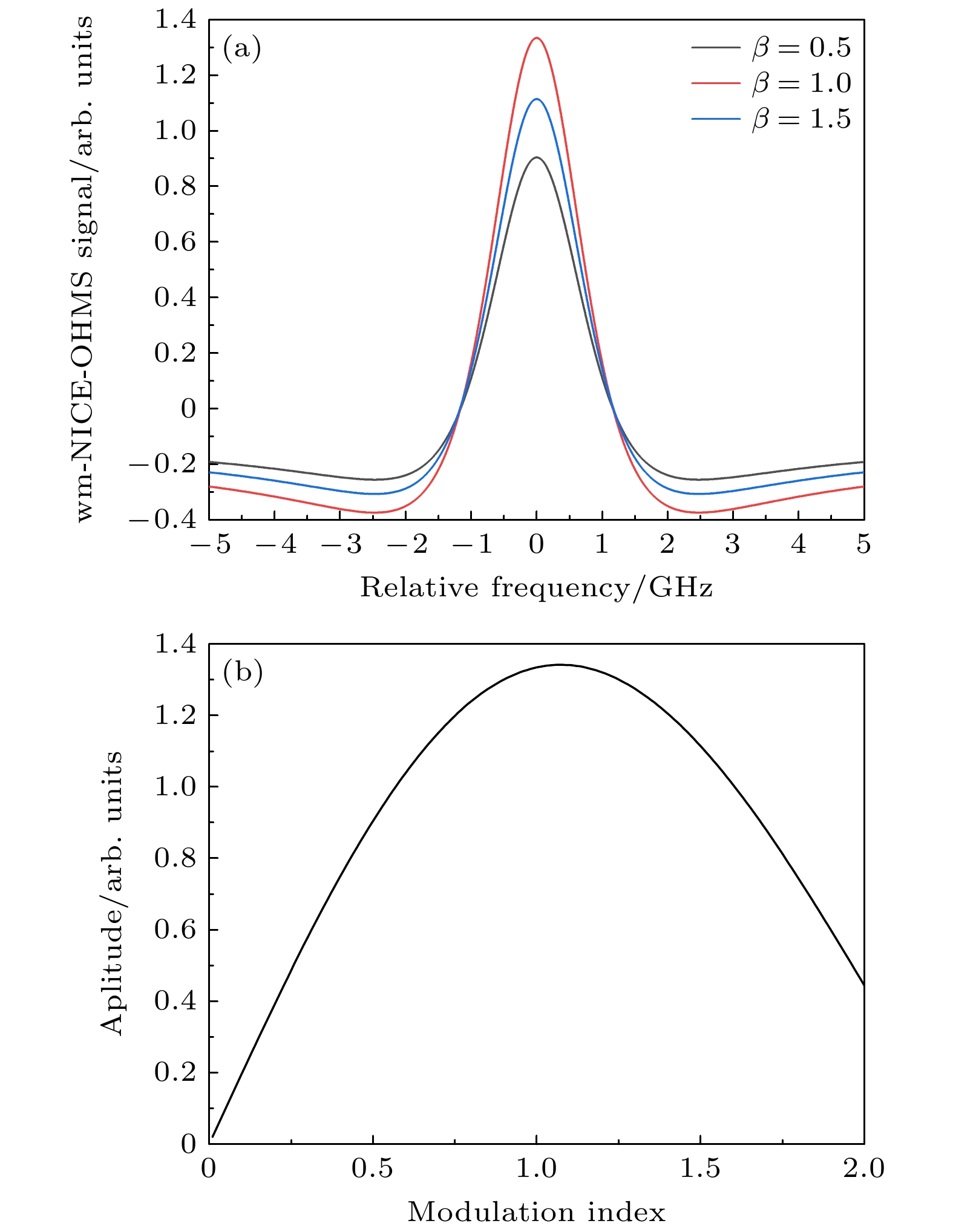
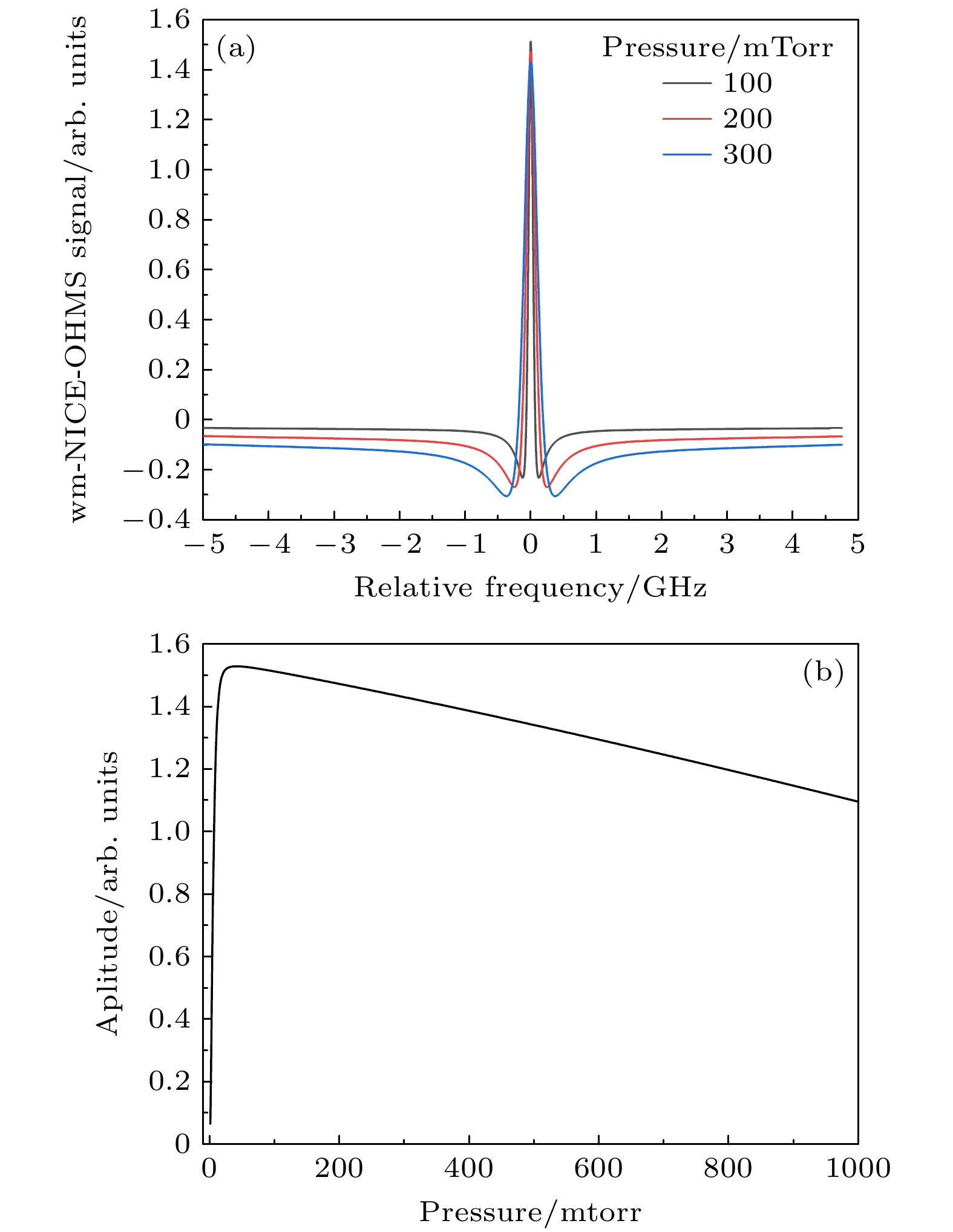
    • 图5(a)中的黑线、红线、蓝线分别是调制系数β为0.5, 1, 1.5时14CO2 的wm-NICE-OHMS仿真信号. 调制系数β主要会影响载波幅度(正比于0阶贝塞尔函数)以及调制边带幅度(正比于1阶贝塞尔函数)的比值, 因此会改变信号的幅度, 但是这种改变并不是单调的. 图5(b)为模拟不同调制系数β下14CO2信号幅度. 可以看出, 随着调制系数β的增加, 信号幅度呈先上升后下降的趋势, 在本模拟系统中, 调制系数β为1.07时信号幅度达到最大, 相较于调制为0.1时, 幅度增大了6.8倍, 因此在同等探测系统噪声下, 可以获得最大的14CO2光谱的信噪比.

      • 4.3.   不同压强对14CO2 wm-NICE-OHMS信号的影响

    • 图6(a)中黑线、红线、蓝线分别对应压强为100, 200, 300 mTorr的14CO2 wm-NICE-OHMS仿真信号. 压强对光谱信号存在三方面影响, 首先压强越大, 分子密度越大, 光谱吸收系数也越大; 其次亚多普勒光谱的饱和度会随着压强的增加而降低; 最后压力增大, 压力展宽会增加, 导致亚多普勒光谱幅度减小. 图6(b)为模拟得到的不同压强下14CO2 wm-NICE-OHMS信号幅度的变化. 可以看出, 随着压强的变化信号幅度呈先上升后下降的趋势, 这是三种影响相互平衡的结果, 在42 mTorr时, 信号幅度达到最大, 是最佳的光谱测量气压.

    5.   结　论

    • 相较于传统的AMS, NICE-OHMS技术可以实现对14C进行高精度实时原位检测, 并且其成本相对较低, 可以满足大规模检测需求. 故本文基于NICE-OHMS技术对模拟实验条件下的12CO2 , 13CO2, 14CO2和N2O的混合样本进行理论仿真, 仿真后得出结论14CO2的多普勒光谱信号被其他气体的信号淹没, 且幅度极低, 不利于14CO2测量. 为了去除多普勒展宽信号的线性斜率, 并且进一步提高信噪比, 我们提出使用波长调制NICE-OHMS进行14CO2光谱测量. 通过模拟可以看出谱线被有效地分离, 极大地提高了14C/C值的检测精度. 之后本文分析了压强与调制系数(β)对14CO2 wm-NICE-OHMS的影响, 得出压强为42 mTorr、调制系数β为1.07时14CO2 wm-NICE-OHMS信号幅度最大, 为后续大气本底下的14CO2高精度检测奠定了理论基础. 尽管本文在理论上验证了wm-NICE-OHMS可以有效抑制气体光谱之间的干扰, 但是我们需要指出如果杂质气体在14CO2光谱处吸收太强, 会影响NICE-OHMS中的频率锁定, 从而影响信号的获取. 通过结合低温测量, 可以有效解决这个问题, 同时进一步提升光谱分辨率.

    参考文献 (31)

目录

/

返回文章
返回