-
电磁波的非互易传输是一种特殊的物理现象, 其本质特征在于电磁波在相反传播方向上的传输特性呈现显著差异, 通常通过打破时间反演对称性来实现. 这种特性可以通过磁偏置、时空调制或非线性效应等方法来实现[1–9], 广泛应用于多个领域. 例如, 在无线通信中, 非互易器件如隔离器和环行器被用于全双工系统中, 实现信号的同时发送与接收而无干扰[10,11]; 在量子计算中, 非互易性用于保护量子态, 防止背向散射或噪声对量子比特系统的破坏[12–16]; 在雷达系统中, 非互易器件通过有效隔离发射和接收通道, 减少自发射信号对接收器的干扰, 从而提高了系统的信噪比和目标检测能力[17,18]. 因此, 深入研究非互易传输的机制和开发新型非互易器件对于推动这些领域的技术进步具有重要意义.
在微波非互易器件的研究领域中, 腔磁子电子学体系凭借磁子出色的调谐特性, 在提升非互易器件性能方面展现出显著优势. 研究者们在腔磁子系统中首次观察到了具有非互易特性的连续域束缚态(bound state in the continuum, BIC), 这一发现使得微波隔离度得到了显著提升, 超过了40 dB[19]. 此外, 通过调整环形天线来控制磁子辐射阻尼, 实现了高达200 MHz的非互易调谐能力[20]. 调节耦合强度能够实现零阻尼条件下的单向传输效应, 展现出高达80 dB的有效隔离度[21]. 这些研究不仅拓展了腔磁子系统的功能, 还通过增强非互易特性, 为信息处理中的信号控制与抗干扰能力提供了有力的技术支持, 进一步巩固了腔磁子电子学体系在非互易性器件和相干信息处理中的关键地位.
近期光诱导磁子态(pump-induced magnon mode, PIM)的发现进一步拓展了磁子动力学的调控维度[22], 不同于常规磁子的调控依赖于电磁边界条件的重构或者磁性样品的选择, PIM的动力学可以很容易地被泵浦波形的振幅、频率所调控, 从而为进一步扩展腔磁子电子学非互易的操控维度描绘了前景. 本研究中, 泵浦这一激励方式的能量来源于微波光子, 即这一磁子态是由微波光子相干诱导产生的. 使用“光诱导”可以明确体现出光子在激发过程中起到的关键作用, 强调了光子与磁子之间的以相干性为代表的相互作用机制. 因此在文中将这一物态称为光诱导磁子态. 在之前的研究中, 基于单个PIM对具有非互易特性的BIC调控, 已展示了对微波非互易传输隔离度操控的可行性[23]. 然而, 在腔磁子系统中实现对微波非互易性的灵活、精确调控以及对非互易频带的高效操控方面仍然存在一定局限. 为解决这一问题, 本研究通过引入多个调制的泵浦信号, 激发多个PIM, 实现与BIC的强耦合, 从而形成多个具有非互易性的混合模式. 通过这种方式, 我们能够精确调控微波非互易通道的数量和隔离区域, 实现具有非互易特性的带通和带阻隔离带. 该方法摆脱了对静磁场调节的依赖, 并通过泵浦信号灵活地调节生成的带通和带阻隔离, 大幅提升了非互易频带的调控能力和系统的灵活性. 这项研究为腔磁子系统中非互易性的精确调控提供了一种新的方法, 同时为多通道、可调谐非互易器件在信息处理领域中的实际应用提供了重要的技术支撑.
-
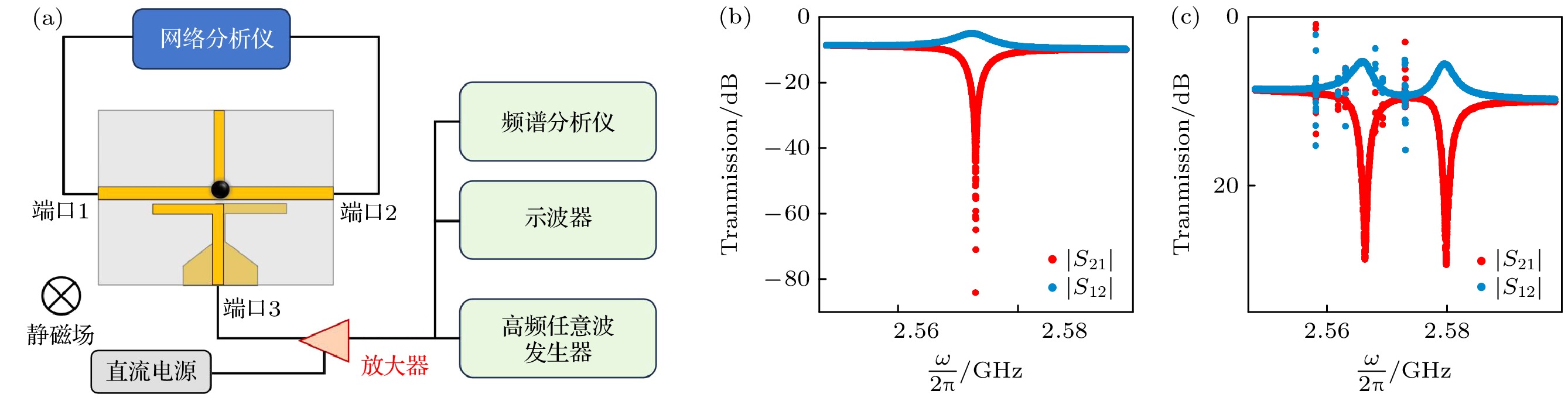
腔磁子系统中的微波非互易性具有单向隔离微波信号的特性, 是设计高性能微波隔离器件的重要基础. 我们设计并构建了一个具备微波非互易特性的腔磁子系统, 如图1(a)所示. 在该系统中, 一个直径为1 mm的钇铁石榴石(YIG)小球被置于微波谐振腔的节点位置. 谐振腔的中心工作频率为2.92 GHz, 采用Rogers 5880基板材料制备, 具有35 μm厚的双面覆铜层, 介质层厚度为0.78 mm, 介电常数为2.2, 损耗因子为 9×10–4, 以确保谐振腔的高品质因数和稳定性能.
为了研究腔磁子系统的微波非互易特性, 利用矢量网络分析仪(VNA)测量了1, 2两个端口之间的传输参数|S21|和|S12|, 从而获取系统的传输谱特性. 端口3连接一个微波贴片天线, 用于送入微波泵浦信号. 实验中, 多个泵浦信号由高频任意波形发生器产生, 经过功率放大器放大后输入端口3, 以提供足够的泵浦功率. 外加静磁场的方向垂直于谐振腔平面, 使微波磁场与静磁场正交, 从而实现对磁矩进动的最强扰动, 提升了磁子模式的激发效率.
如图1(b)所示, 通过调节施加到YIG小球上的外部静磁场强度, 改变YIG中Walker模式的进动频率, 使磁子模式与腔光子模式通过强耦合形成的混合模式达到BIC条件[19]. 在此条件下, 具有BIC特性的混合模式在传输谱|S21|中表现出高达–85 dB的透射损耗, 同时微波非互易性的隔离度ISO = |S21 – S12|也达到最大值, 充分展现了明确的非互易传输特性. 在上述的BIC条件下, 我们从端口3引入微波泵浦信号. 泵浦信号激励YIG小球中未饱和自旋的集体进动, 产生PIM模式[22]. PIM与BIC发生强耦合, 形成新的混合模式, 进一步 丰富了系统的模式结构, 有助于生成新的非互易传输带. 如图1(c)所示, 引入一个泵浦信号可将原本单一的非互易区域分裂成两个非互易带. 这些非互易带的中心频率、带宽和隔离度可以通过调节泵浦信号的频率和功率进行精确控制, 实现对非互易传输特性的灵活调控.
-
在后续的实验中, 通过在端口3送入多个调制的泵浦信号, 以操控微波非互易传输带. 同时, 利用示波器和频谱分析仪对输入的泵浦信号进行实时监测, 确保其频率、功率和波形的精确性. PIM通过输入的微波泵浦信号激发产生, 其共振频率和强度可由泵浦信号的参数灵活调谐.
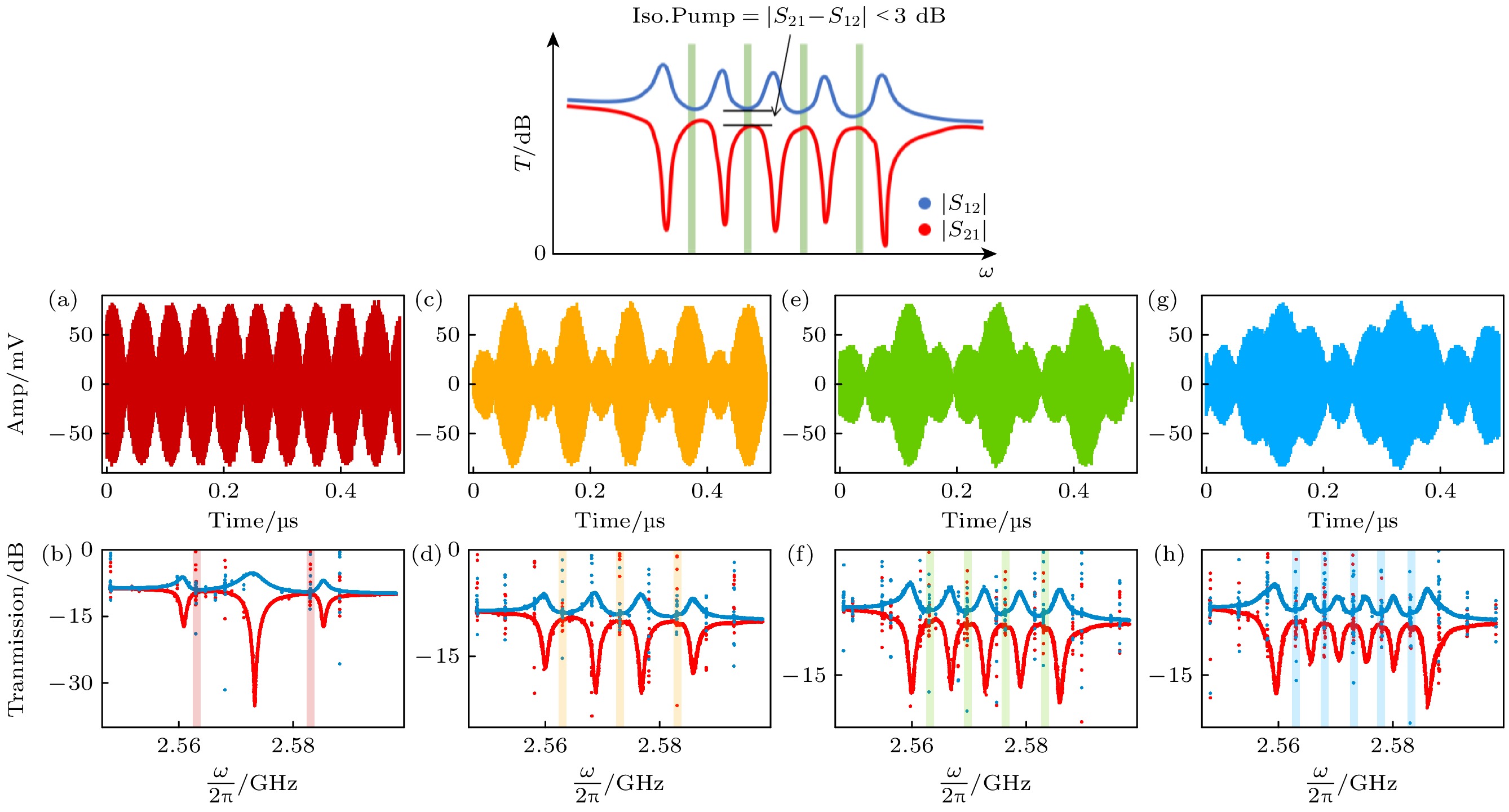
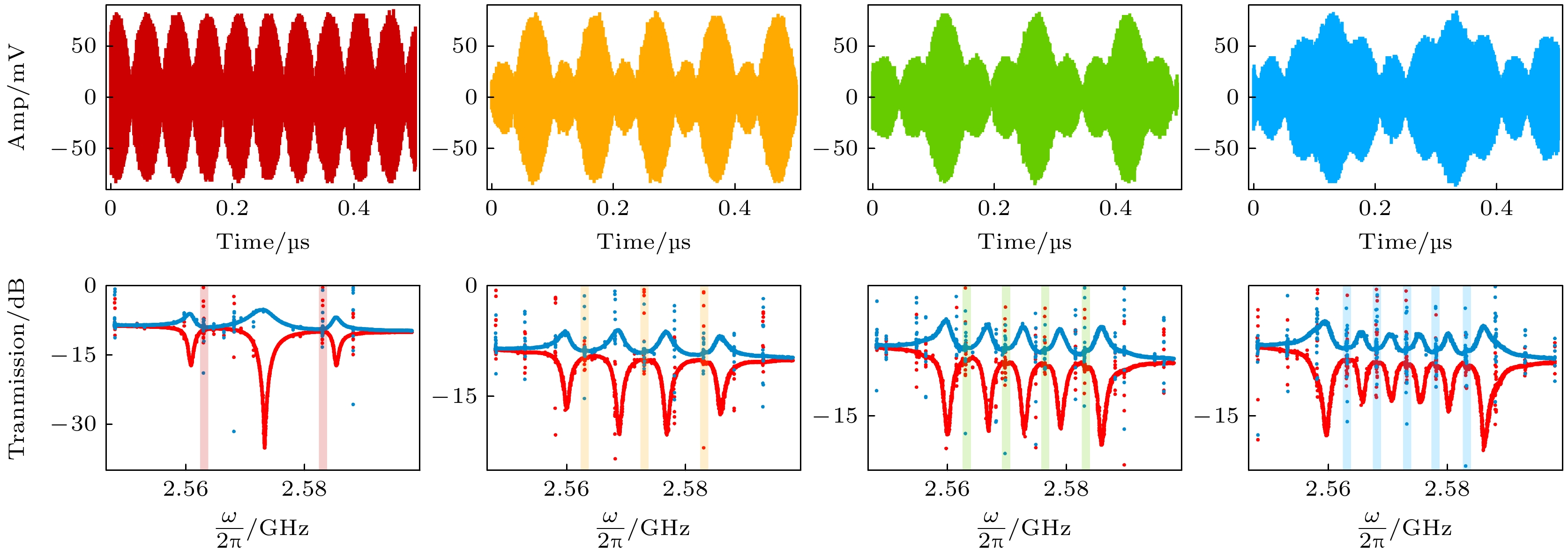
如图2(a), (c), (f)和(g)所示, 我们使用高频任意波形发生器输入多个泵浦信号, 图中展示了输入信号在时域上的波形. 这些波形的主要频率分量在图2(b), (d), (f), (h)中以半透明条带标示, 分别对应在以BIC模式为中心的20 MHz频率范围内, 依次注入2个、3个、4个和5个等间隔、等功率的泵浦信号. 相应地, 图2(b), (d), (f), (h)展示了非互易隔离通道数的变化, 分别形成了3个、4个、5个和6个非互易隔离带. 在图2上方的示意图中, 将泵浦频率处的非互易隔离度记为Iso.Pump, 当Iso.Pump小于3 dB时, 相邻非互易隔离带之间的重叠度较小, 因此可视为独立的隔离通道. 这一标准确保了各通道在非互易传输特性上的独立性和互不干扰性. 值得注意的是, 在图2(b), (d), (f)和(h)中Iso.Pump均小于3 dB, 这些实验结果充分展示了系统在频率分辨率和带宽控制方面的灵活性. 在PIM与BIC的有效耦合区域内, 每个输入的泵浦信号所激发的PIM均与BIC发生强耦合, 形成多个混合模式的非互易区域. 通过这些混合模式的叠加, 可以实现多通道非互易隔离带, 进而灵活控制非互易传输通道数和频率分布. 通过调节泵浦信号的数量、频率间隔和功率, 提升了系统的可调谐性. 该技术不依赖于耦合系统电磁边界条件的重新构建, 也不依赖于材料体系的重新选择, 拓展了非互易隔离带的调控维度.
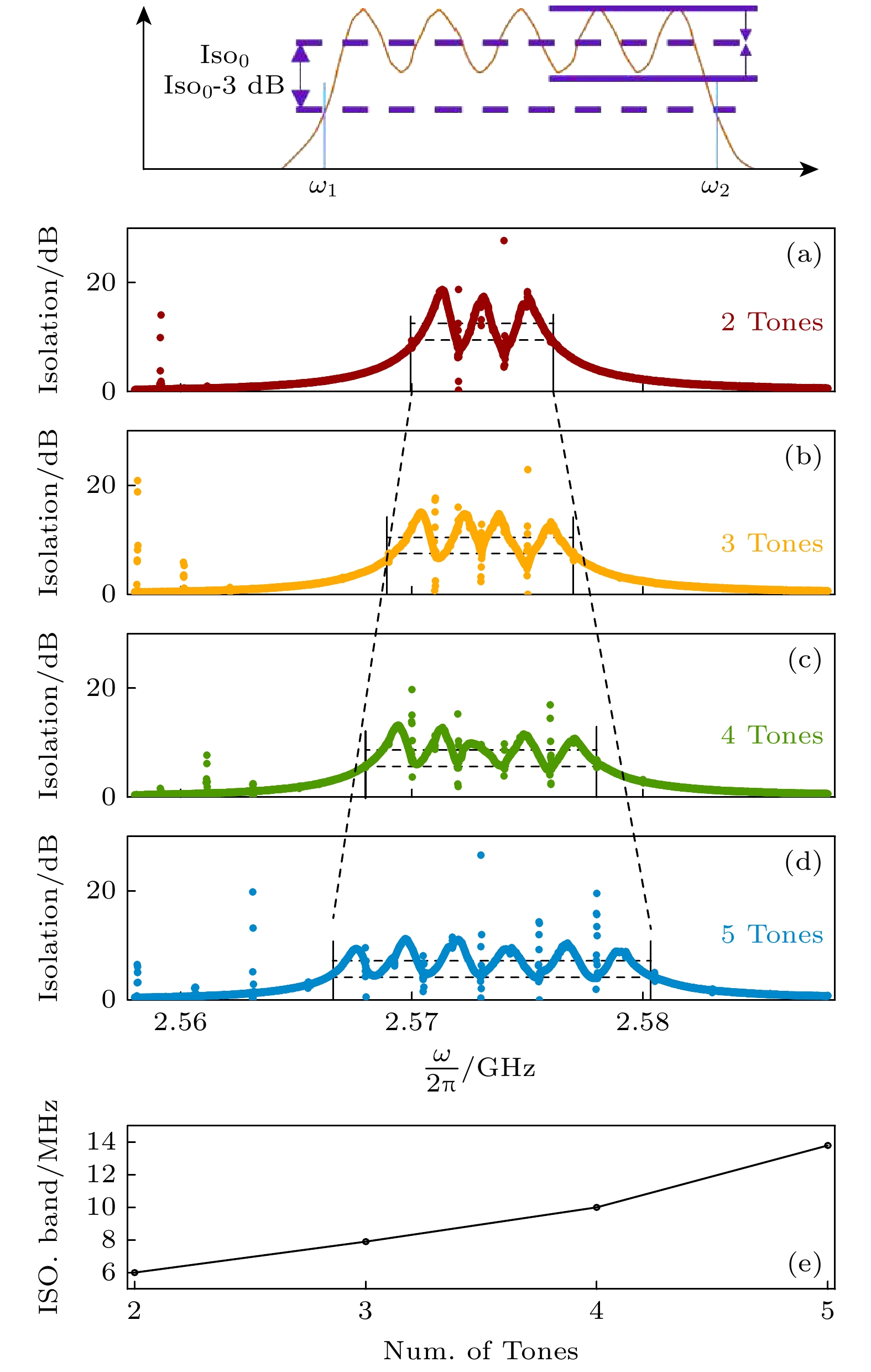
在图2的实验中, 通过调节泵浦信号所对应的频率分量的频率间隔和数目, 实现了独立的多通道非互易隔离带, 从而满足多通道信号独立传输需求, 这种配置有效避免了各非互易通道间的信号干扰. 为了进一步探索非互易隔离带的可调谐性和带宽控制, 我们对输入的泵浦信号在频谱上进行了频率调制. 在图3(a)—(c)中, 以BIC为中心, 依次送入2个、3个和4个泵浦信号, 功率为–10 dBm, 频谱上的泵浦频率间隔设置为2 MHz; 在图3(d)中, 送入5个泵浦信号, 泵浦频率同样以BIC为中心, 但频率间隔调整为2.5 MHz. 当减小泵浦信号的频率间隔, 使相邻非互易隔离带发生重叠时, 泵浦频率对应位置的非互易隔离度超过了3 dB, 表明相邻隔离带之间的独立性逐渐降低. 在此情况下, 相邻通道的带宽出现部分重叠, 最终形成了连续的非互易隔离带. 实验结果如图3(a)—(d)所示, 其中纵轴表示透射谱|S21|与|S12|在对数坐标下的差值, 用于量化非互易性的强度.
由于相邻通道的带宽重叠, 系统形成了更宽的非互易传输区域. 随着输入泵浦信号数目的增加, 连续非互易隔离带的总带宽也相应扩大. 在本文研究中, 由于隔离频带内的隔离度并非恒定值, 采用其隔离度平均值ISO0进行表征, 具体示意如图3最上方的插图所示. 以隔离度值为ISO0-3 dB 处的两个频率ω1和ω2为隔离带的起止点, 其间距定义为隔离带的频宽, 即Iso.band=|ω1 – ω2|. 图3(a)—(d)的演化过程中可以清晰地观察到, 隔离频带逐渐变宽. 具体而言, 图3(e)总结了隔离带宽的演化规律. 实验结果显示, 当输入的泵浦信号数量从2个增加到5个时, 非互易带的隔离带宽从6 MHz扩展至14 MHz.
这一结果表明, 通过增加泵浦信号的数量, 可以有效调控非互易带的带宽, 从而实现对信号频谱的灵活控制. 此外, 图3中的连续可调非互易带宽进一步证明了该腔磁子系统在构建高性能带阻隔离器方面的巨大潜力. 为进一步验证系统的可调控性, 对输入泵浦信号进行了不同的组合调制, 以探索改变非互易隔离区域的可能性.
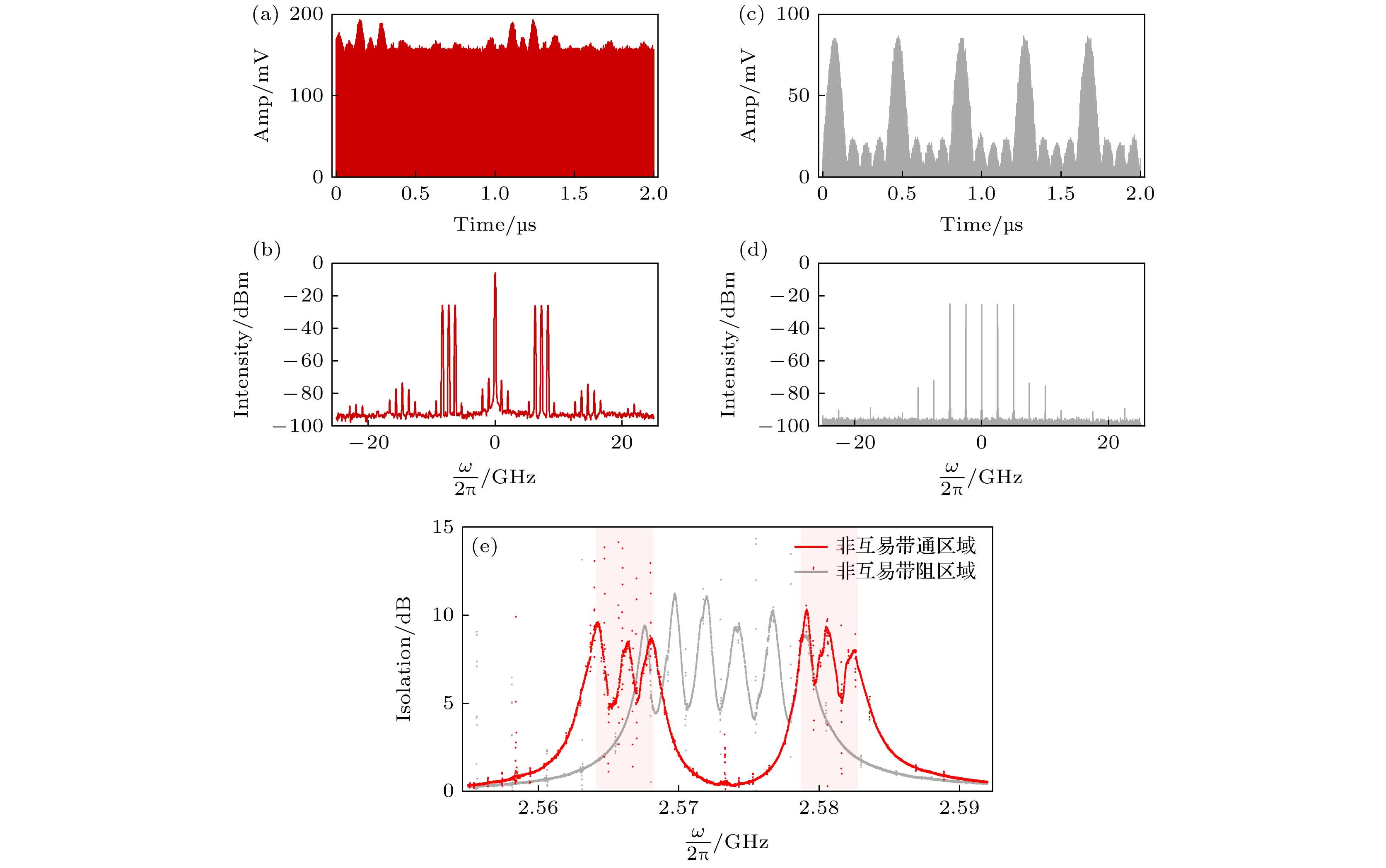
具体而言, 图4(a), (b)分别展示了对应图4(e)中红色带通隔离区域的泵浦信号的时域波形和频谱特性. 在输入泵浦信号的频谱上, 我们在BIC处送入一个较强的泵浦信号, 用于将中间的非互易区域分隔开, 形成较宽的通带; 同时在分隔开的对应非互易区域分别编码3个频率分量, 使得其阻带的带宽增大, 提高了滤波的稳定性. 通过调谐泵浦信号的频率和功率, 利用PIM与BIC的强耦合, 实现了带通性质的非互易隔离区域. 时域波形清晰地显示了泵浦信号的高稳定性和周期性, 确保了PIM的有效激发. 同样地, 图4(c), (d)展示了对应图4(e)中灰色带阻隔离区域的泵浦信号的时域波形和频谱特性. 在这种情况下, 我们调整了泵浦信号的频率、功率等参数, 保持PIM与BIC的强耦合, 同时通过调制泵浦信号改变非互易隔离区域的特性, 从而形成带阻性质的非互易隔离区域.
-
综上所述, 本研究提出了一种通过引入多个调制泵浦信号, 在腔磁子系统中激发PIM并与BIC强耦合的有效方法, 用于灵活调控非互易隔离带宽. 在此前的研究中, 通过单个泵浦信号调控, 已成功验证了微波非互易传输隔离的可行性, 但其隔离带宽和通道数量受限于单一模式的作用范围. 本研究在此基础上, 通过引入多个泵浦信号, 拓展了对非互易隔离通道和带宽的控制能力. 通过该机制, 无需依赖复杂的静磁场调节, 即可实现灵活且精确的非互易性控制, 为微波非互易器件的集成化与功能扩展提供了一条全新的技术路径, 特别是在微波通信和量子信息处理领域展现出广泛的应用潜力. 此外, 通过引入不同的泵浦信号组合, 可根据具体需求定制非互易隔离带的特性, 从而实现特定频段的选择性隔离或透射. 这种灵活性使得该方法在复杂信号处理和通信系统中具备显著优势, 能够满足多样化的应用场景需求. 研究结果表明, 本研究在腔磁子系统中成功实现了多通道、连续可调的非互易隔离带, 并通过泵浦信号调制实现了带宽可调的带通与带阻隔离状态的灵活切换. 相干微波对磁性小球辐照, 经由PIM的产生打破了原有Walker模式的均匀进动, 充当了动力学中的缺陷; 并且PIM对应着稳定的能级差, 能辐射特定频率的电磁波, 故可以被认为是一种特殊的色心, 有望未来进一步在长寿命低耗散的相干信息处理中起到关键作用.
总之, 本研究显著拓展了微波非互易性的调控手段, 提升了系统的功能性与应用性, 为未来多 功能、可调谐的高性能微波器件的设计奠定了坚实的基础. 同时, 本方法为实现更大规模的可编程 集成非互易电路提供了新的方向, 具有重要的应用前景.
光诱导磁子态调控的宽频带非互易传输
Broadband nonreciprocal transmission tuned by pump-induced magnon modes
-
摘要: 本研究提出了一种通过引入多个调制泵浦信号来灵活调控微波非互易隔离带的方法, 从而将常规的单模式的磁子非互易传输拓展到了宽频调节的范畴. 具体地, 本研究通过在腔磁子系统中激发多个光诱导磁子态, 并使其与连续域束缚态发生强耦合, 形成多个杂化模式, 实现了对非互易通道数量和隔离区域的精确控制. 该方法无需依赖静磁场调节, 能够实现独立的多通道非互易隔离带, 以及泵浦可调的带通和带阻隔离, 而不依赖于对系统的重构. 这显著提升了非互易频带的调节能力和系统的灵活性, 为开发多通道、可调谐的非互易器件在信息处理中的应用奠定了技术基础.Abstract: Nonreciprocal electromagnetic wave transmission is essential for wireless communication, quantum computing, and radar systems, traditionally relying on breaking time-reversal symmetry through static magnetic fields or structural modifications, which face limitations in tunability and integration. Recent advancements in cavity magnonics, particularly the use of bound states in the continuum (BIC) and pump-induced magnon mode (PIM), have enhanced the nonreciprocal isolation and dynamic control of magnon dynamics. In this study, a novel method to achieve broadband-tunable microwave nonreciprocal isolation is presented by introducing multiple modulated pump signals, thereby extending traditional single-mode magnon-based nonreciprocal transmission to multi-channel and broadband regimes. The core method involves exciting multiple PIMs in a cavity magnonics system and strongly coupling them with BIC to generate hybrid modes with pronounced nonreciprocal characteristics. The experimental setup is comprised of a 1-millimeter-diameter yttrium iron garnet (YIG) sphere positioned at the node of a microwave resonator (central frequency: 2.92 GHz), with pump signals injected through a microwave patch antenna. By dynamically tuning the frequency, power, and number of pump signals, the precise control over the number of nonreciprocal isolation channels and their spectral positions is realized. Notably, the continuous tuning of the nonreciprocal bandwidth is achieved by increasing the number of pump signals from 2 to 5, expanding the isolation bandwidth from 6 MHz to 14 MHz. Furthermore, by tailoring the spectral distribution of pump signals, the system realizes flexible switching between bandpass and band-stop isolation states. Importantly, this method eliminates the need of static magnetic field adjustments or structural reconfiguration, relying solely on coherent microwave-photon interactions to modulate PIM-BIC coupling. Experimental results highlight two key physical outcomes: 1) Extending conventional single-mode magnonic nonreciprocal transmission to multi-channel and broadband-tunable regimes; 2) achieving microwave nonreciprocal control without the need of static magnetic field adjustments or structural reconfiguration. These advances establish a robust platform for designing reconfigurable multi-channel isolators and circulators, which can be directly applied to microwave communication systems, quantum information processing, and radar technologies.
-
Key words:
- nonreciprocity /
- magnon /
- pump-induced magnon mode (PIM) /
- bound state in continuum (BIC) .
-

-
图 1 (a) 具有非互易特性的腔磁子系统实验装置图, 直径1 mm的YIG小球放置在微波谐振腔上, 通过VNA在1, 2端口测量其透射谱, 在3端口经由微波贴片天线送入泵浦信号; (b) 测量了系统在BIC条件下的|S21|和|S12|透射谱; (c) 在BIC频率(2.573 GHz)处输入一个功率为20 dBm的泵浦信号, 泵浦信号激发的PIM与BIC发生强耦合, 形成两个混合模式
Figure 1. (a) Schematic diagram of the experimental setup for the cavity magnonic system with nonreciprocal characteristics, a 1-mm-diameter YIG sphere is placed at the node of a microwave resonator, the transmission spectra are measured between ports 1 and 2 using a vector network analyzer (VNA), while pump signals are injected into port 3 through a microwave patch antenna; (b) transmission spectra |S21| and |S12| of the system are measured under the BIC condition; (c) a pump signal with a power of 20 dBm is injected at the BIC frequency, exciting PIMs that strongly couple with the BIC, resulting in the formation of two hybrid modes.
图 2 (a), (c), (e), (g)分别为输入的泵浦调制信号在时域上的波形(其主要频率分量, 在频域上20 MHz的带宽内输入2—5个均分带宽的泵浦信号, 在右侧列中用透明条带表示); (b), (d), (f), (h)展示了系统可以调制的不同通道数, 当输入相应的泵浦调制信号时, 在VNA上测量的|S21|和|S12|透射谱
Figure 2. (a), (c), (e), (g) depict the time-domain waveforms of the input modulated pump signals, the main frequency components of these signals are distributed within a 20 MHz bandwidth in the frequency domain, with 2 to 5 evenly spaced pump signals injected, as indicated by the transparent bands on the right; (b), (d), (f), (h) illustrate the number of modulation channels achievable by the system. These results are obtained from the transmission spectra |S21| and |S12| measured on the VNA when the corresponding modulated pump signals are applied.
图 3 (a)—(d) 不同泵浦调制信号下的非互易隔离带, 横轴表示调制的非互易带的隔离区域, 纵轴是器件对微波信号的非互易隔离度; (e) 隔离带宽的大小随输入泵浦信号的数目连续变化, 横轴是输入泵浦信号的数目, 纵轴是非互易隔离带的隔离带宽
Figure 3. (a)–(d) The nonreciprocal isolation bands under different modulated pump signals, the horizontal axis represents the isolation regions of the modulated nonreciprocal bands, while the vertical axis corresponds to the nonreciprocal isolation degree of the device for microwave signals; (e) the variation in isolation bandwidth as a function of the number of input pump signals, the horizontal axis indicates the number of input pump signals, and the vertical axis represents the isolation bandwidth of the nonreciprocal isolation bands.
图 4 (a), (b) 测量的带通隔离器的输入泵浦信号的时域和频域图像; (c), (d) 测量的带阻隔离器的输入泵浦信号的时域和频域图像; (e)红色非互易带区域为带通区域, 灰色部分为带阻区域
Figure 4. (a), (b) The time-domain and frequency-domain representations of the input pump signals for the band-pass isolator; (c), (d) the time-domain and frequency-domain representations of the input pump signals for the band-stop isolator; (e) the red nonreciprocal band corresponds to the band-pass region, while the gray area represents the band-stop region.
-
[1] Yu Z F, Fan S H 2009 Nat. Photonics 3 91 doi: 10.1038/nphoton.2008.273 [2] Lira H, Yu Z F, Fan S H, Lipson M 2012 Phys. Rev. Lett. 109 033901 doi: 10.1103/PhysRevLett.109.033901 [3] Fang K, Yu Z F, Fan S H 2012 Phys. Rev. Lett. 108 153901 doi: 10.1103/PhysRevLett.108.153901 [4] Sounas D L, Alù A 2017 Nat. Photonics 11 774 doi: 10.1038/s41566-017-0051-x [5] Kang M S, Butsch A, Russell P St J 2011 Nat. Photonics 5 549 doi: 10.1038/nphoton.2011.180 [6] Manipatruni S, Robinson J T, Lipson M 2009 Phys. Rev. Lett. 102 213903 doi: 10.1103/PhysRevLett.102.213903 [7] Peng B, Özdemir Ş K, Lei F, Monifi F, Gianfreda M, Long G L, Fan S H, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394 doi: 10.1038/nphys2927 [8] Estep N A, Sounas D L, Soric J, Alù A 2014 Nat. Phys. 10 923 doi: 10.1038/nphys3134 [9] Jalas D, Petrov A, Eich M, Freude W, Fan S H, Yu Z F, Baets R, Popović M, Melloni A, Joannopoulos J D, Vanwolleghem J D, Vanwolleghem M, Doerr C R, Renner D H 2013 Nat. Photonics 7 579 doi: 10.1038/nphoton.2013.185 [10] Reiskarimian N, Krishnaswamy H 2016 Nat. Commun. 7 11217 doi: 10.1038/ncomms11217 [11] Kord A, Sounas D L, Alù A 2017 IEEE Trans. Microw. Theory Tech. 66 911 [12] Abdo B, Sliwa K, Frunzio L, Devoret M 2013 Phys. Rev. X 3 031001 [13] Lecocq F, Ranzani L, Peterson G A, Cicak K, Simmonds R W, Teufel J D, Aumentado J 2017 Phys. Rev. Appl. 7 024028 doi: 10.1103/PhysRevApplied.7.024028 [14] Chapman B J, Rosenthal E I, Kerckhoff J, Moores B A, Vale L R, Mates J A B, Hilton G C, Lalumière K, Blais A, Lehnert K W 2017 Phys. Rev. X 7 041043 [15] Sliwa K M, Hatridge M, Narla A, Shankar S, Frunzio L, Schoelkopf R J, Devoret M H 2015 Phys. Rev. X 5 041020 [16] Ranzani L, Aumentado J 2015 New J. Phys. 17 023024 doi: 10.1088/1367-2630/17/2/023024 [17] Kodera T, Sounas D L, Caloz C 2011 Appl. Phys. Lett. 99 031901 doi: 10.1063/1.3610996 [18] Caloz C, Alù A, Tretyakov S, Sounas D, Achouri K, Deck-Léger Z-L 2018 Phys. Rev. Appl. 10 047001 doi: 10.1103/PhysRevApplied.10.047001 [19] Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202 doi: 10.1103/PhysRevLett.123.127202 [20] Zhao Y T, Rao J W, Gui Y S, Wang Y P, Hu C M 2020 Phys. Rev. Appl. 14 014035 doi: 10.1103/PhysRevApplied.14.014035 [21] Qian J, Rao J W, Gui Y S, Wang Y P, An Z H, Hu C M 2020 Appl. Phys. Lett. 116 031901 doi: 10.1063/1.5136022 [22] Rao J W, Yao B, Wang C Y, Zhang C, Yu T, Lu W 2023 Phys. Rev. Lett. 130 046705 doi: 10.1103/PhysRevLett.130.046705 [23] Chen Z, Rao J, Zhao K X, Yang F, Wang C X, Yao B, Lu W 2024 Appl. Phys. Lett. 125 031901 doi: 10.1063/5.0211263 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: