离子回旋共振加热(ion cyclotron resonance heating, ICRH)是一种利用目标等离子共振频率下的回旋波加热等离子体束流的先进技术, 因其输入功率大、加热效率高、与等离子体无接触等优点广泛应用于托卡马克聚变装置辅助加热、磁等离子体推进等领域^[1–4]. 20世纪70年代, 法国Schmitt^[5]首次观察到了回旋波中钾等离子体同位素选择性加热现象, 从实验上证明了ICR方法分离同位素的可能性. 之后美、法、俄等国陆续开展了ICR分离装置的建造, 并进行了Li, Ca, Pd, Zn, Gd, Yb在内的多种轻、重同位素分离实验, 获得了一定分离效果^[6–12]. 相较于大部分非电磁同位素分离方法, ICR分离方法单级分离系数更高. 相较于传统电磁分离方法, ICR分离方法能耗更低, 产量更高, 适用于丰度需求较低的同位素产品的生产或二次分离中的初次分离过程, 以及乏燃料后处理、稀土元素回收等特殊领域^[13–15].

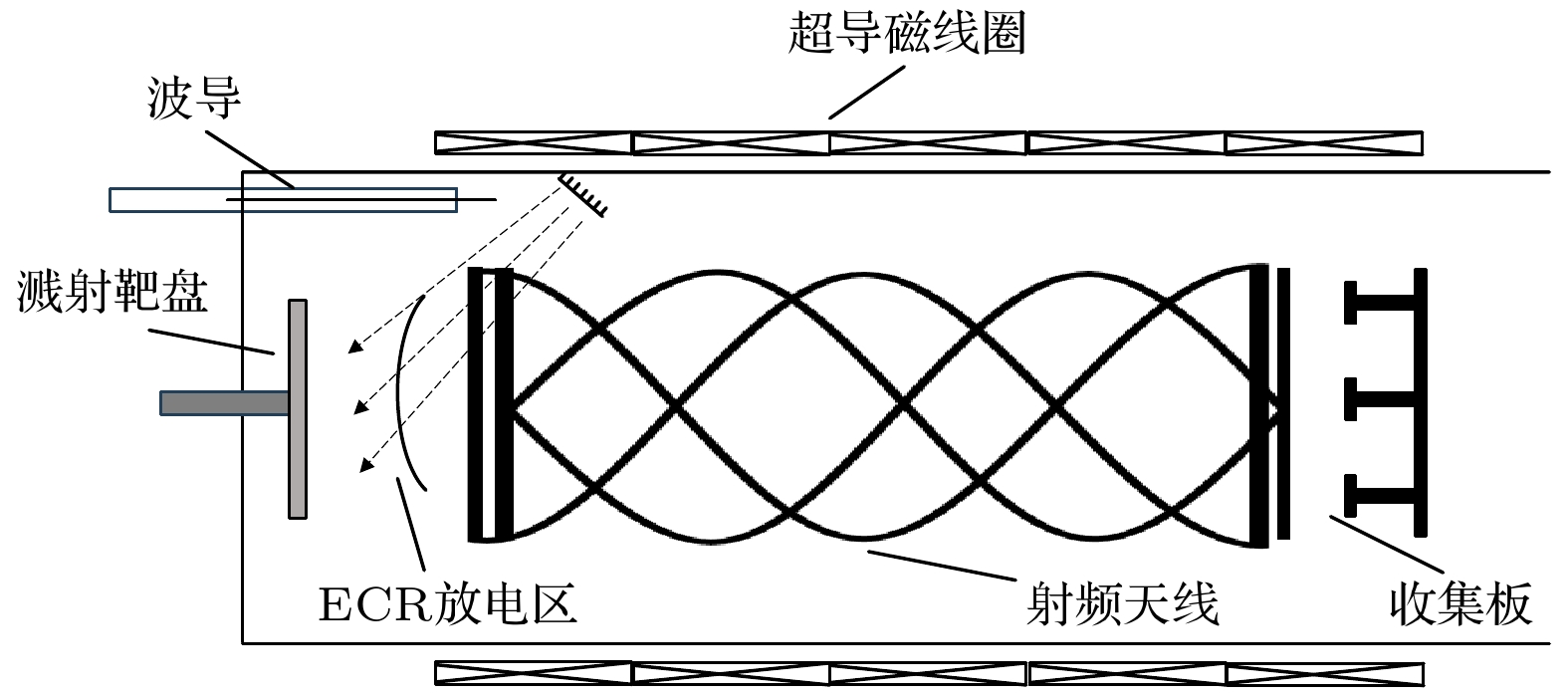
ICR同位素分离装置结构如图1所示, 主要可分为离子源区、共振加热区和收集区三部分. 其中, 离子源区用于产生等离子体, 应用较多的为图1所示的电子回旋共振(electron cyclotron resonance, ECR)离子源结构^[16,17]; 共振加热区用于实现离子的选择性加热, 主要由超导磁线圈和射频天线组成, 分别用于提供稳恒磁场和射频加热电场; 收集区用于精贫料的沉积.

ICR装置分离过程的核心在于离子在共振加热区的选择性加热过程, 装置整体参数设计也主要围绕该过程的加热效果及其选择性开展. 考虑到国外现有ICR研究侧重于实验与装置结构设计, 理论研究相对分散, 而国内ICR同位素分离领域的研究又几乎空白, 本文基于ICR理论研究中常用的单粒子模型对离子在共振区内部的选择性加热过程进行了数值模拟, 详细讨论了ICR分离装置核心参数对选择性加热过程的影响, 为后续ICR分离装置的参数设计奠定基础.

描述等离子体运动状态的方法主要有3种^[18]: 一是单粒子运动, 即在给定电磁场条件下的运动, 不考虑等离子体输运对电磁场的反作用以及带电粒子间的相互作用; 二是流体描述, 即将等离子体中的带电粒子视为电磁流体, 通过流体力学方程组和麦克斯韦方程组描述等离子体束流的运动状态, 但无法描述流体中不同粒子的特性; 三是数值模拟方法, 即直接描述等离子体中实际粒子或等价虚拟粒子随时间的演变. ICR选择性加热过程理论研究和数值模拟普遍采用单粒子模型方法, 理由如下:

单粒子模型应用前提条件主要包括离子间相互作用可忽略和等离子体输运过程感生电磁场相较于外加电磁场可忽略两点. 前者与ICR装置设计理念中减少目标同位素离子与非目标离子间的能量交换相吻合. ICR分离装置设计过程中, 需要保证等离子体与共振区参数取值满足离子平均碰撞时间大于离子在共振区停留时间, 以减小离子间碰撞对选择性加热过程的影响:

式中, $ {T}_{{\mathrm{i}}} $为离子平均能量, 单位eV; $ A $为原子序数; $ {n}_{{\mathrm{i}}} $为等离子体密度, 单位cm^–3; $ L $为共振区长度; $ {v}_{z} $为离子沿磁场方向速度. ICR分离装置中, 离子平均能量在10 eV左右, 沿磁场方向能量5 eV左右, 共振区长度1—3 m, 代入(1)式近似有$ {n}_{{\mathrm{i}}} < {10}^{12}\;{{\mathrm{c}}{\mathrm{m}}}^{-3} $, 基本高于大部分分离实验中应用的等离子体束流密度.

引入等离子体输运过程感生电磁场相较于外加电磁场可忽略的最大等离子体密度$ {n}_{{\mathrm{i}}, {\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $表达式^[19] (等离子体密度低于该值时输入离子回旋波基本维持在圆极化波形式)为

式中$ {m}_{{\mathrm{i}}} $为离子质量, $ c $为光速, $ K $为波数, $ {V}_{{\mathrm{T}}} $为离子热运动速度, $ \omega $为电场频率, 高斯单位制.

代入Siren装置锂同位素分离实验相关参数($ {m}_{{\mathrm{i}}} = {10}^{-23}\;{\mathrm{g}} $, $ K={10}^{-1}\;{{\mathrm{c}}{\mathrm{m}}}^{-1}, \;\omega = 4 \times {10}^{6}\;{{\mathrm{s}}}^{-1}, \; {V}_{{\mathrm{T}}} = 1.6 \times {10}^{6}\;{\mathrm{c}}{\mathrm{m}}/{\mathrm{s}} $)^[20], 可得$ {n}_{{\mathrm{i}}, {\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}\approx {10}^{12}~{{\mathrm{cm}}}^{-3} $, 与忽略粒子间相互碰撞的密度上限相近. 由此证明单粒子模型基本适用于ICR分离装置参数的初步设计.

单粒子模型下, 假设空间中存在沿Z轴方向的均匀磁场$ {\boldsymbol{B}}_{z} $, 与磁场垂直的XY平面存在交变电场$ {\boldsymbol{E}}_{xy} $, 离子运动方程可以表示为

理想情况下, XOY平面交变电场为圆极化波形式, 可表示为(4)式所示的复数形式^[21]:

式中, $ \omega $为交变电场角频率, $ k{v}_{z} $为离子轴向运动引起的Doppler偏移项, $ k=2{\mathrm{\pi }}/\lambda $为射频电场波数.

此时, 离子沿Z轴方向做匀速直线运动, XY平面做周期性回旋运动, 同样以复数形式表示XY平面的速度$ {v}_{xy}={v}_{x}+{\mathrm{i}}{v}_{y} $, (3)式可写为

该方程解可表示为

式中, $ {\omega }_{0}={\mathrm{e}}{B}_{z}/m $, $ {v}_{0}{{\mathrm{e}}}^{{\mathrm{i}}\varphi } $为离子XY方向初始速度. 当$ \omega -k{v}_{z}-{\omega }_{0}=0 $时, 离子发生共振, 持续从外加电场获得能量, $ {v}_{xy}\left(t\right)=\left(\dfrac{{\mathrm{e}}E}{m}t+{v}_{0}{{\mathrm{e}}}^{{\mathrm{i}}\varphi }\right){{\mathrm{e}}}^{-{\mathrm{i}}{\omega }_{0}t} $, 回旋半径持续增大; 当$ \omega -k{v}_{z}-{\omega }_{0}\ne 0 $时, 离子速度周期性变化, 回旋半径存在最大值. 共振区尺寸足够长时, 共振离子与非共振离子回旋半径出现显著性差异, 出现空间上的分离效应.

得到单个离子运动轨迹、能量参数后, 通过理论求解或蒙特卡罗方法即可得到符合一定初始速度分布的等离子体束流出口处参数分布情况. 当考虑磁场不均匀度以及射频天线输出电场实际分布时, 也可基于(3)式利用四阶龙格-库塔方法对离子运动轨迹进行计算.

根据(6)式, 可能影响选择性加热过程的参数可分为共振区长度、磁感应强度、射频电场场强、频率、波数在内的共振加热区参数和离子初始速度分布在内的离子初始参数. 为探究各参数对分离选择性的具体影响, 选择⁶Li为研究对象, 共振区射频天线电场强度$ E=50~{\mathrm{V}}/{\mathrm{m}} $, 波长$ \lambda =0.8~{\mathrm{m}} $, 圆极化波形式; 磁线圈磁感应强度$ {B}_{z}=0.25~{\mathrm{T}} $; 共振加热区长度$ L = 0.8~{\mathrm{m}} $; 离子初始轴向能量$ {T}_{z} = 10~{\mathrm{e}}{\mathrm{V}} $, 横向能量$ {T}_{xy}=5~{\mathrm{e}}{\mathrm{V}} $, 横向速度服从Maxwell分布, 轴向速度形式见(7)式^[22]:

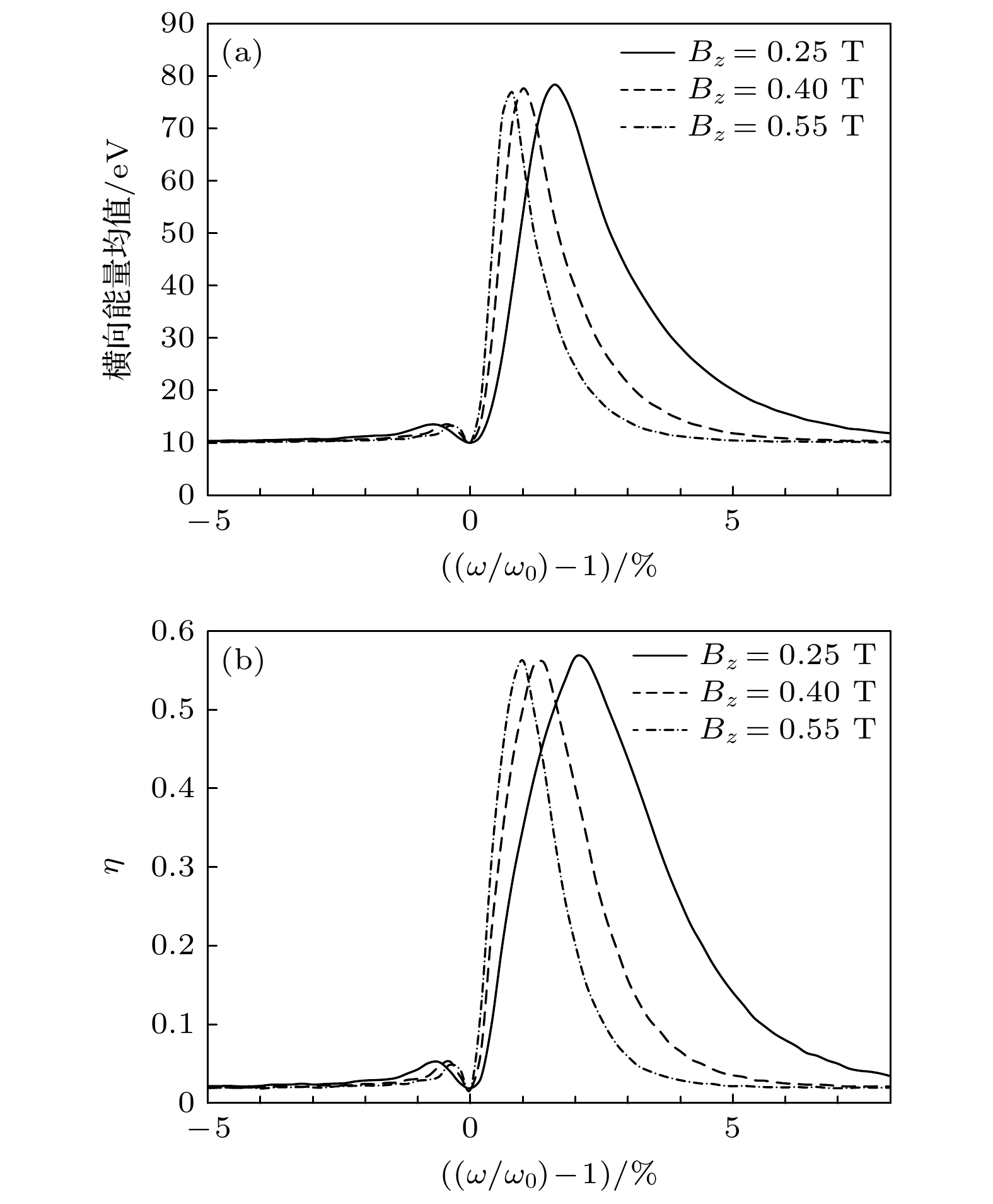
引入平均横向能量、临界分离能量$ {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $(离子离开共振区能量高于该取值时认为离子可以被精料端收集)和加热系数$ \eta $(能量高于$ {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $的离子在共振区出口离子中占比)等参数用于评价选择性加热效果: 横向能量均值曲线越高, 表征该同位素离子加热效果越好, 展宽越小, 表征加热过程选择性效果越明显; 与横向能量均值类似, 加热系数$ \eta $取值越高, 表征离子加热效果越好; 展宽越小, 表征选择性效果越明显. 不同的是横向能量均值侧重于整体加热效果, 当某种同位素中部分离子能量远高于同种同位素离子时, 横向能量分布无法正确反映加热过程的选择性. 而加热系数$ \eta $更侧重描述大部分离子能量状态, 临界分离能量$ {E}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $也需依据横向能量均值选取. 加热效果和选择性效果的评判需综合二者.

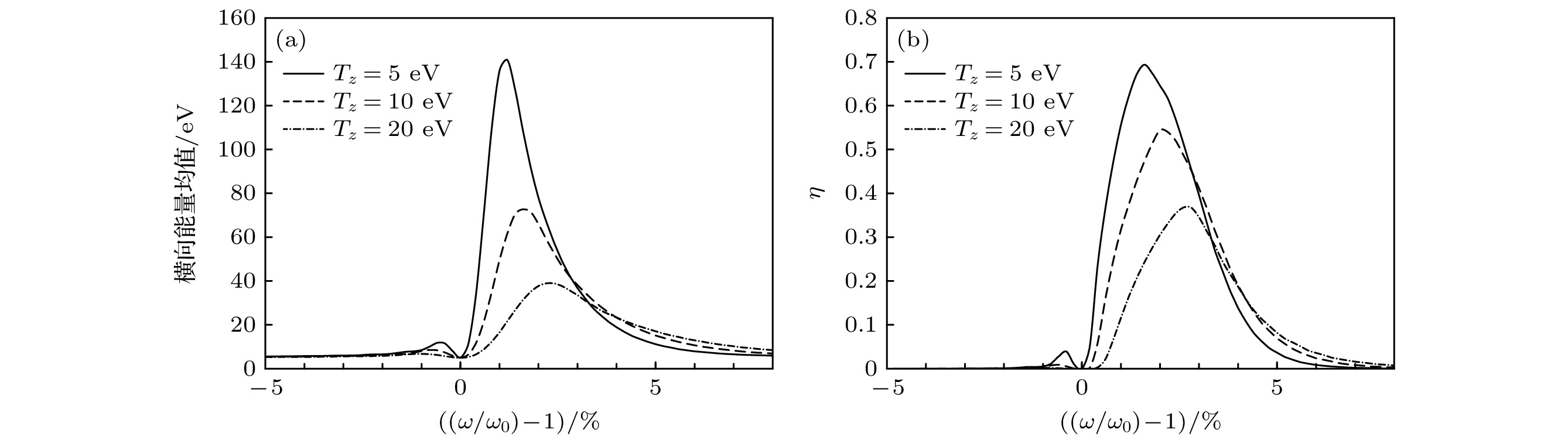
不同磁感应强度下出口离子横向能量均值、加热系数$ \eta $分布曲线分别如图2所示(图中$ {\omega }_{0}= {{\mathrm{e}}{B}_{z}}/{{M}_{6\_{\mathrm{L}}{\mathrm{i}}}} $). 曲线峰值对应频率相较于共振频率右移是由离子自身轴向速度引起的Doppler偏移造成. 曲线的展宽成因有二, 一是离子轴向能量存在一定分布, 导致离子束共振频率不一, 引起横向能量和加热系数分布曲线展宽, 当不考虑离子轴向能量分布时, Doppler偏移引起的展宽完全消失; 二是即使不发生共振, 离子能量以正弦函数形式, $ T= 2{\mathrm{\pi }}/(\omega -k{v}_{z}-{\omega }_{0}) $的周期波动时, 当离子在加热区停留时间$ t=L/{v}_{z}\leqslant T/4 $, 离子仍持续受到外加电场加热作用, 该加热效果同样导致横向能量和加热系数分布曲线存在一定展宽.

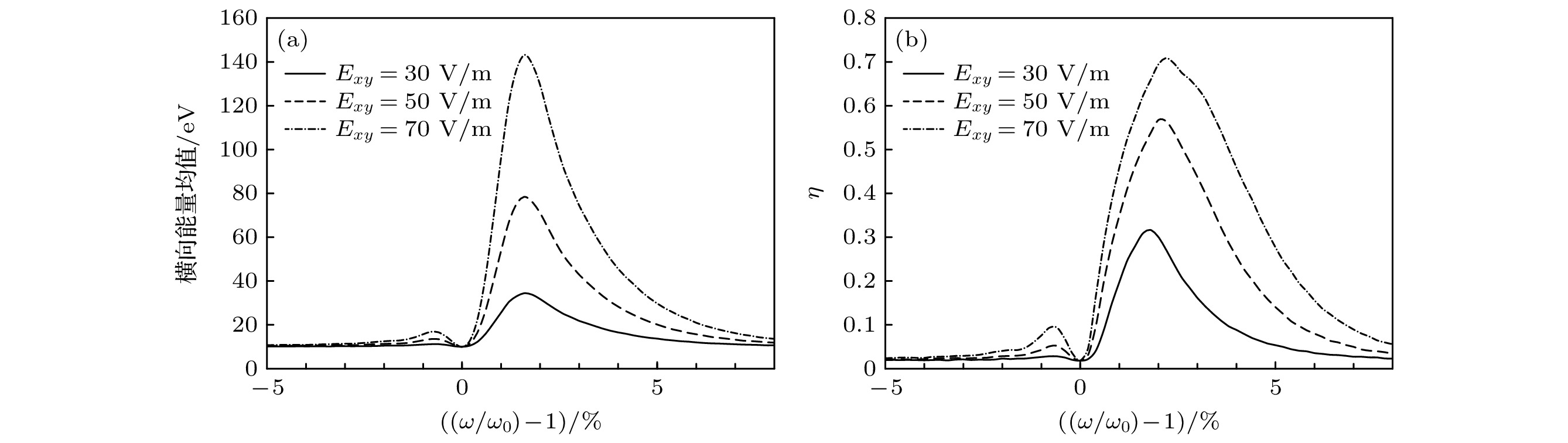
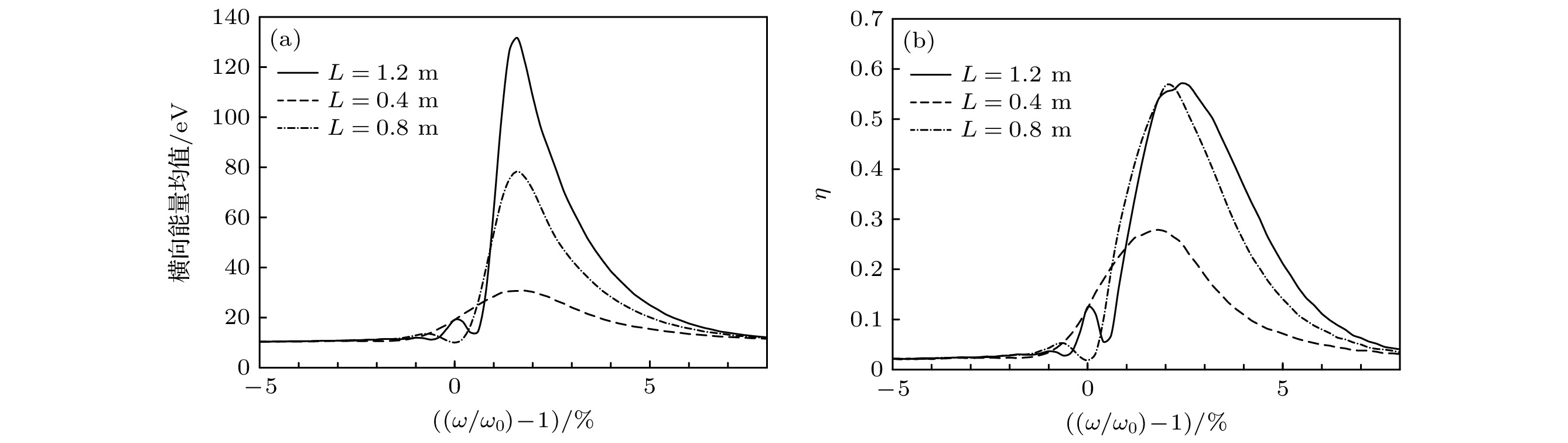
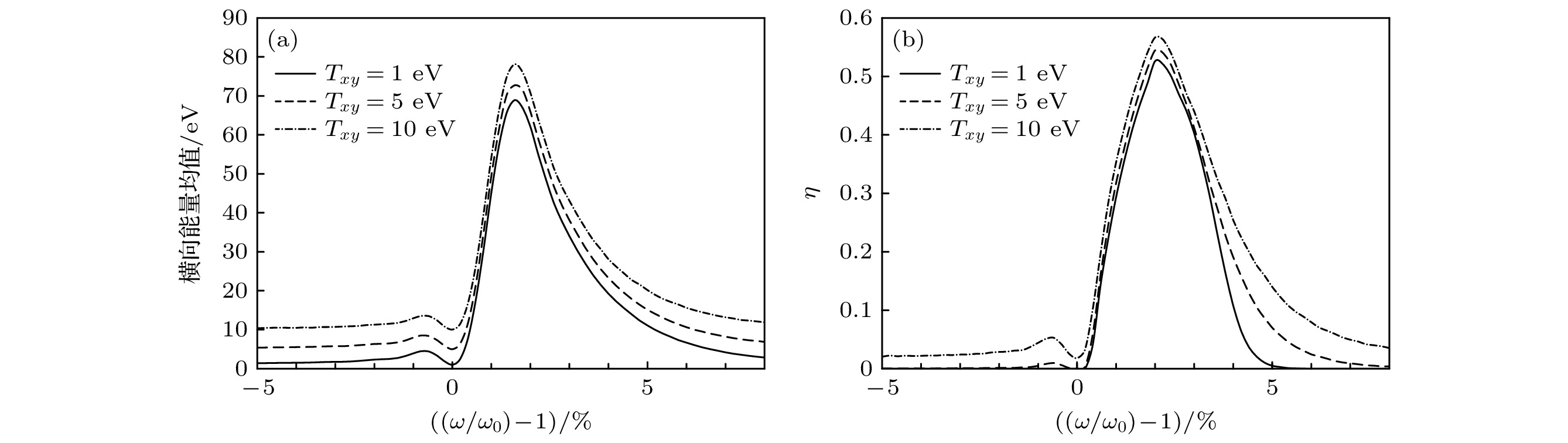
图2表明, 增大磁感应强度, 离子整体加热效果基本不受影响, 选择性效果显著上升. 这是因为磁感应强度增强, 离子在磁场中共振频率$ {\omega }_{{\mathrm{i}}}= {\mathrm{e}}B/{m}_{{\mathrm{i}}} $增大, 轴向运动引起的分布曲线Doppler展宽相较于增大的共振频率变窄, 曲线展宽减小, 选择性效果增强. 但离子在加热区停留时间几乎无变化, 因此加热效果几乎不变. 通常情况下, 目标同位素质量越大, 同位素质量差异相对越小, 相邻同位素共振频率越接近, 对加热过程选择性要求越高, 磁感应强度取值越高. 此外, 共振区内磁感应强度应满足${\Delta B}/{B}\leqslant {\Delta \omega }/{{\omega }_{{\mathrm{i}}}} = {\Delta M}/{{M}_{{\mathrm{i}}}}$ ($ {M}_{{\mathrm{i}}} $为目标核素质量, $ \Delta M $为目标核素与邻近同位素间质量差), 即保证共振区内仅目标同位素发生共振.

电场强度与共振区长度的计算结果如图3和图4所示, 二者均对加热效果产生直接影响, 增强电场强度或提高共振区长度, 整体加热效果有所提升, 能量分布曲线展宽均有一定增大, 选择性效果相对下降, 但二者加热系数变化趋势有所差别. 这是因为电场强度增强, 共振离子与非共振离子最大能量均有所提高; 共振区长度增长, 离子在加热区停留时间延长, 加热效果增强, 但由于非共振离子能量周期性变化, 加热系数不会随共振区尺寸增大而持续增大. 因此, 提高共振区长度时加热系数的增大相较于提高电场强度时存在明显的极限值. 实际装置设计过程时, 除了考虑目标同位素与非目标同位素间能量差异显著性外, 还应综合考虑加热过程中离子平均碰撞频率等因素.

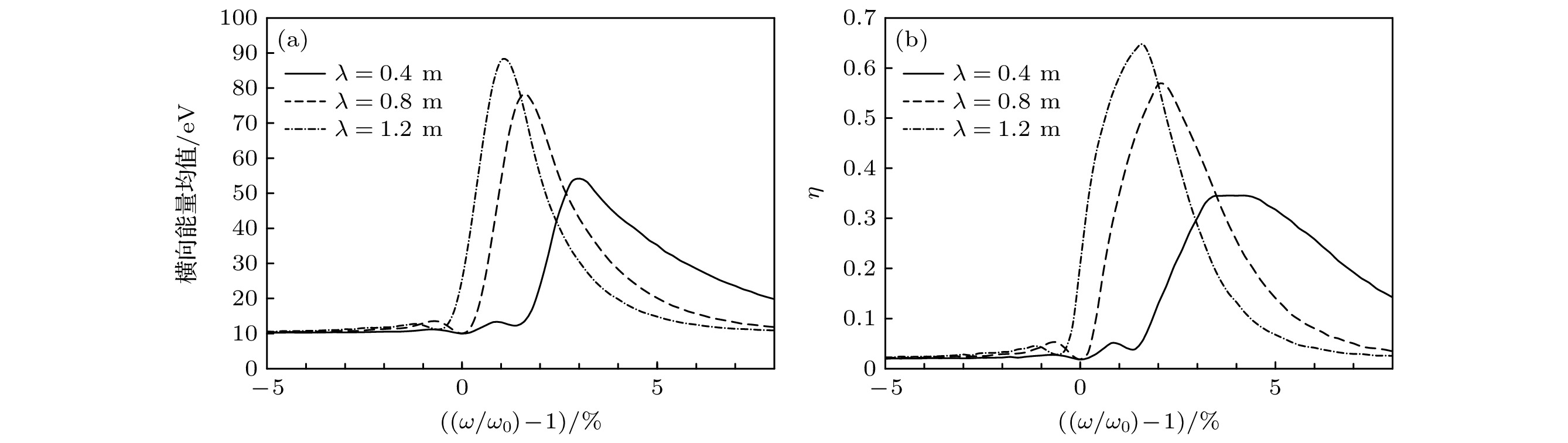
不同射频电场波长下的计算结果如图5所示. 射频电场波长提高, Doppler偏移项$ 2{\mathrm{\pi }}{v}_{z}/\lambda $减弱, Doppler效应引起的展宽减小, 能量随外加电场频率分布更加集中, 导致横向能量峰值左移, 加热效果增强, 选择性提高. 当射频电场波长无限长时, Doppler偏移完全消失, 加热效果和选择性效果达到最佳, 但射频电场波长越长, 微波在等离子体中的穿透性越差. 通常情况下取射频电场波长为加热区长度的两倍^[23].

等离子束流初始参数包括束流尺寸、束流密度、轴向能量分布、横向能量分布等. 在单粒子模型假设下束流尺寸、密度对分离效应几乎无影响. 能量分布方面, 除轴向能量、横向能量大小外, ECR源内部对横向能量分布干扰较小, 可近似为其服从Maxwell分布, 可不考虑其他形式分布; 轴向能量分布干扰较大, 分布形式尚未完全确定, 已有研究中涉及的分布形式较多, 需单独讨论^[21].

不同轴向能量取值计算结果如图6所示, 初始轴向能量增强, Doppler偏移项$ 2{\mathrm{\pi }}{v}_{z}/\lambda $增大, 非共振离子加热效果引起的能量分布曲线展宽增大, 导致能量均值分布峰值右移, 选择性效果下降. 同时, 由于轴向能量提高导致离子在加热区停留时间变短, 离子加热效果变差, 共振离子与非共振离子能量差异变弱, 影响后续收集区的精贫料过程. 适当降低轴向能量有利于提升加热效果, 增大共振离子与非共振离子能量差异, 但轴向能量过低, 离子在加热区停留时间过长, 离子间碰撞加剧, 一般情况下轴向能量取值在5 eV左右.

不同横向能量取值计算结果如图7所示. 初始横向能量增强, 由轴向运动引起的Doppler偏移和离子在共振区停留时间几乎不受影响, 因此对共振区选择性加热过程几乎无影响, 但初始横向能量提高, 导致加热区出口共振离子与非共振离子能量差异变弱, 影响后续收集区的精贫料沉积过程.

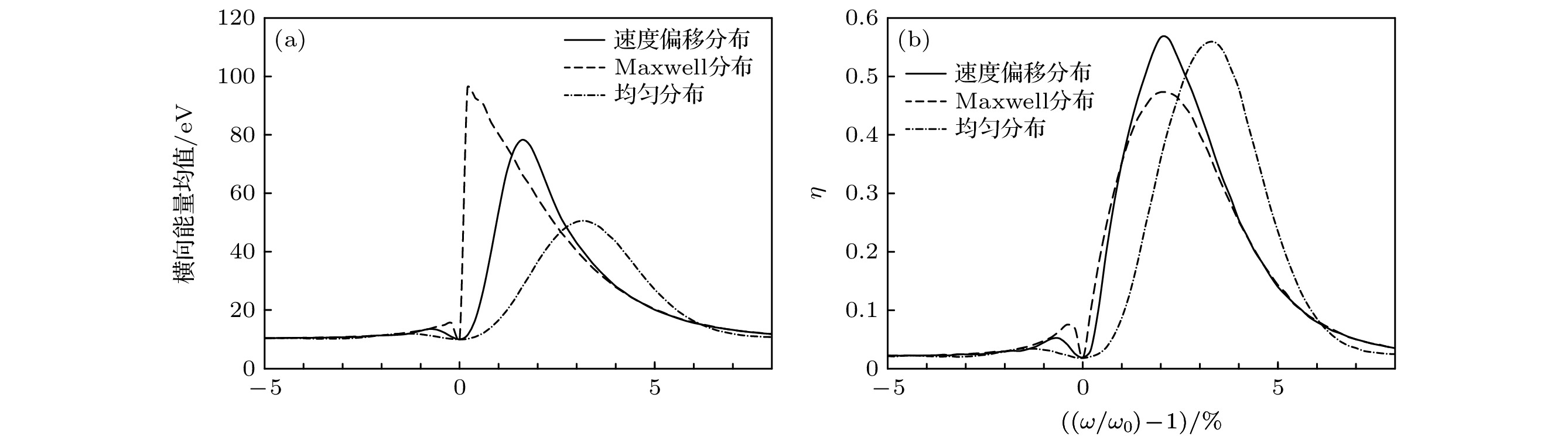
不同轴向能量分布计算结果如图8所示. 平均能量相同的情况下, 束流中低能粒子占比越多, Doppler偏移效应越弱, 离子在共振区停留平均时间越长, 导致能量均值分布峰值越接近共振频率, 整体加热效果越好, 但低能粒子占比过高, 可能导致离子间碰撞加剧, 影响加热选择性. 同时, 束流轴向能量分布展宽越小, 由Doppler偏移效应引起的展宽项越小, 加热过程整体选择性越好.

本文对ICR同位素分离方法分离装置基本结构进行了系统性说明, 基于单粒子模型方法初步讨论了共振加热区参数和等离子体初始参数对分离效应的影响, 主要结论如下:

1)共振区参数中, 束流整体加热效果与共振区尺寸、外加电场强度、波长等参数正相关, 与磁感应强度几乎无关; 加热过程选择性与磁感应强度、外加电场波长正相关, 与共振区尺寸、外加电场强度负相关.

2)等离子体初始能量中, 束流整体加热效果与等离子体轴向能量负相关, 与束流中低能离子占比正相关, 与横向能量几乎无关; 加热过程选择性与等离子体轴向能量、轴向能量分布展宽负相关, 与横向能量几乎无关.

上述模拟工作基于等离子体密度较低的情况开展, 基本适用于小型ICR实验装置的参数设计. 后续将继续完善理论模型, 深入研究等离子体密度过高引起的库仑碰撞和感生电磁场等问题对分离过程的干扰, 并对射频天线、等离子体源等核心组件设计开展研究工作.