惯性约束聚变的主要思想是利用内爆来快速压缩和加热热核燃料, 使其达到高温高密度等离子体状态并发生核聚变反应, 进而利用聚变产物的动能使等离子体自加热, 加速并持续燃烧^[1–5]. 在这一过程中, 当聚变过程产生的能量超过各种物理过程导致的能量损失总和时, 不需要进一步的外部加热就能使热核燃料保持燃烧^[4,5]. 以聚变产生的α粒子为例, 在高能α粒子的输运过程中, α粒子通过频繁与等离子体中的电子和离子碰撞将能量沉积给能量较低的等离子体, 进而加热等离子体. 另一方面, 由于等离子体中电子和离子质量的差异, 高能α粒子沉积给等离子体中电子和离子的能量份额是有显著差异的^[6,7]. 上述过程会影响聚变点火和燃烧过程中中心热斑的温度演化, 进而影响热核燃料自持燃烧的过程和聚变反应率等. 因此, 高能聚变产物的能量沉积和电子离子能量分配对聚变平衡燃烧和非平衡燃烧物理的研究均有着重要应用价值.

在惯性约束聚变点火和自持燃烧阶段, 中心热斑中电子体系的能量密度$ E_\mathrm{e} $的变化可以由下述方程给出^[4,8,9]:

式中$ P_\mathrm{dep} $为聚变产生并沉积的功率密度; $ F_\mathrm{e} $为沉积给电子的能量份额; $ P_\mathrm{ie} $是离子向电子转移能量的功率密度; $ P_\mathrm{me}, P_\mathrm{re} $和$ P_\mathrm{he} $则分别为机械做功、轫致辐射和热传导损失的功率密度. 如果只考虑电子体系动能的贡献, 即$ E_\mathrm{e} = 3 n_\mathrm{e} k_\mathrm{B} T_\mathrm{e} / 2 $, 则可以得到中心热斑内电子的温度演化方程. 这里$ n_\mathrm{e} $和$ T_\mathrm{e} $分别为电子的密度和温度, $ k_\mathrm{B} $是玻尔兹曼常数. 离子的温度演化方程也由类似的方程描述, 详细的细节可参考文献[8,10]. 本文聚焦在方程(1)中电子能量分配因子$ F_\mathrm{e} $这一关键参数上, 它与高能离子的阻止本领和能量沉积密切相关. 在前人的研究^[11]中, 基于高能α粒子能量沉积的理论模型计算电子能量分配因子$ F_\mathrm{e} $后, 对计算结果进行简单插值拟合可以得到以下的近似形式^[11,12](该表达式中温度的单位均为keV):

式中$ T_0 $为某一特征温度, 它与所采用的组织本领模型密切相关; $ T_\mathrm{e} $是电子温度. 在这一拟合中, $ F_\mathrm{e} $被定义为在能量沉积过程中转移给电子的能量占初始α粒子能量的比例. 基于阻止本领的经典两体碰撞模型^[13], Fraley等^[11]给出了电子能量分配拟合公式(2)中$ T_0 = 32 $. 在两体碰撞模型中, 特征温度$ T_0 $的确定与描述粒子碰撞的库仑对数模型密切相关. 基于不同的两体碰撞库仑对数, Atzeni和Meyerter-Vehn^[4]得到的电子能量分配中$ T_0 = 25 $, 而Stanton和Murillo^[6]结合经典两体碰撞模型、德拜势能模型和依赖于高能粒子入射速度的屏蔽长度给出$ T_0 = 16 $.

基于方程(2)的能量分配因子被广泛地应用于惯性约束聚变点火和燃烧的模拟中. 然而, 这一简单的拟合表达式存在多方面的不足. 首先, 电子能量分配因子对密度的依赖关系被忽略了^[12]. 因聚变等离子体涉及的温度密度区间广, 采用不依赖于密度的近似会明显忽略稠密等离子体中密度效应带来的影响, 因此不利于惯性约束聚变点火和燃烧过程的精确模拟. 其次, 目前电子离子能量分配因子的研究主要集中在$ 1—50 \; \mathrm{keV} $的区间^{[4,6,10,11,14]}, 只有少量研究将温度区间扩展到了百keV的量级^[15–17]. 在聚变燃烧阶段等离子体的温度会上升至百keV, 这一过程中α粒子的能量沉积和等离子体升温是同时存在的^[4]. 此外, 以$ {\mathrm{p}}+{\mathrm{B}} \rightarrow 3 {\text{α}} $作为燃料的聚变中, 点火温度约为300 keV^[2]. 因此有必要研究α粒子在百至千keV区间的能量沉积和电子能量分配. 最后, 之前的研究大都采用基于小角度散射假设的阻止本领理论来研究电子离子能量分配^[10,14–16]. 现有研究均表明, 大角度散射对高能粒子的能量沉积有着不可忽视的影响, 尤其是在射程的尾端^[7,18]. 因此, 在能量沉积和电子粒子能量分配因子的研究中必须考虑大角度库仑散射及其累积诱发的横向偏转效应.

本文将基于之前发展的T矩阵扩展模型^[7], 研究高能粒子在宽广温度密度区间等离子体中的能量沉积和电子粒子能量分配因子. 在T矩阵扩展模型中可以自洽地考虑偏转效应对能量沉积和电子粒子能量分配的影响. 本文的结构如下: 首先在第2节中简要回顾阻止本领和能量沉积的T矩阵扩展模型, 以及电子离子能量分配因子的理论; 在第3节中讨论$ \mathrm{p}^{11}\mathrm{B} $和DT等离子体中电子能量分配因子以及偏转效应对电子能量分配因子的影响, 并给出适用于惯性约束聚变模拟的电子能量分配因子的拟合表达式; 第4节对本文的研究工作做简短的总结和展望.

当高能聚变产物或高能粒子束入射到等离子体中时, 入射粒子会经受与背景等离子体中带电粒子的大量碰撞. 这些碰撞的累积不仅会使得入射粒子沿初始速度方向减速, 还会使入射粒子获得垂直于入射方向的动能而产生偏转. 为描述这一过程, 可以将入射粒子的动能$ \varepsilon_\mathrm{T} $和动量$ {\boldsymbol{p}}_\mathrm{T} $按平行和垂直于初始入射方向分解, 即$ \varepsilon_\mathrm{T} = p_\mathrm{T}^2/(2 m_\mathrm{T}) = [(p_\mathrm{T}^{{/ /}})^2 + (p_\mathrm{T}^{\bot})^2]/(2 m_\mathrm{T}) $. 因而, 入射粒子动能随时间的平均变化率可以表述为^[7]

我们前期的研究^[7]表明, 方程(3)左边描述入射粒子动能的变化率, 其与入射粒子的连续慢化(continuous-slowing-down, CSD)阻止本领$ {\rm{d}}E/{\rm{d}}s $相关. 方程(3)右边第1项描述入射粒子平均动量的变化率, 它决定了入射粒子的线性能量转移(linear-energy-transfer, LET)阻止本领$ {\rm{d}}E/{\rm{d}}x $. 方程(3)右边第2项刻画的是入射粒子受背景等离子体作用后垂直初始运动方向的偏转$ {\cal{D}}_\perp $, 即入射粒子在速度空间的横向扩散, 它与入射粒子在等离子体中的热化有密切的联系^[19].

在量子动理学理论的框架下, 通过引入依赖于入射粒子速度的屏蔽势能模型, 发展了描述高能粒子阻止本领的T矩阵扩展模型^[7]. 在这一模型中, LET阻止本领$ \dfrac{{\rm{d}}E}{{\rm{d}}x} = \dfrac{{\boldsymbol{p}}_\mathrm{T}^{{/ /}}}{v_{\mathrm{T}}m_{\mathrm{T}}}\cdot\dfrac{{\rm{d}}}{{\rm{d}}t}\left < {\boldsymbol{p}}_\mathrm{T}^{{/ /}}\right > $由下式给出:

等离子体中不同类粒子阻止本领贡献$ {\rm{d}}E_c/{{\rm d}}x $可从方程(4)中得到, 即方程(4)表征的是$ {\rm{d}}E/{\rm{d}}x = \displaystyle \sum\nolimits_c {\rm{d}}E_c/{\rm{d}}x $. 在方程(4)中$ h_{\mathrm{T}c} = z_{\mathrm{T}}^{2} e^{2}\omega_{\mathrm{pl}, c}^{2}/(4\pi \epsilon_{0} v_{\mathrm{T}}^{2}), \mu_{\mathrm{T}c} = m_{\mathrm{T}}m_{c}/(m_{\mathrm{T}}+m_{c}) $. $ m_\mathrm{T}, z_\mathrm{T} $和$ v_\mathrm{T} $分别为入射粒子的质量、电荷数和速度. $ m_c, z_c, n_c, T_c $和$ \omega_{\mathrm{pl}, c}^2 = z_c^2 e^2 n_c / (\epsilon_0 m_c) $分别为等离子体中$ c $类粒子的质量、电荷数、密度、温度和等离子体频率. $ u = v_\mathrm{T}/v_{\mathrm{th}, c} $和$ z = v_{\mathrm{T}c}/v_{\mathrm{th}, c} $为相对于$ v_{\mathrm{th}, c} = \sqrt{2 k_\mathrm{B} T_c / m_c} $的约化速度. $ {\cal{L}}_{\mathrm{T}c}(u, z) $为描述粒子之间散射的库仑对数, 它与两体碰撞过程中的动量转移截面$ {\cal{Q}}_{\mathrm{T}c}(\nu_{\mathrm{T}}, p) $之间的关系为

式中$ b_{{\mathrm T}c} = z_{\mathrm{T}}z_{c}e^{2}/(4\pi\epsilon_{0}\mu_{{\mathrm T}c} v_{{\mathrm T}c}^{2}) $是库仑散射下的经典碰撞参数. 在本文所讨论的温度密度范围内, 等离子体中的离子都可以看作经典粒子来处理, 因此我们采用经典散射理论计算离子-离子碰撞的动量转移截面:

式中b是碰撞参数; χ是散射角,

其中$ r_0 $是经典转折点. 散射过程中的相互作用势采用依赖于速度的德拜势, 形式为

此处的屏蔽长度是

式中$ x_{\mathrm{T}} = v_{\mathrm{T}}\kappa_{\mathrm{s}}/\omega_{\mathrm{pl, e}}, \kappa_{\mathrm{s}}^{2} = \dfrac{{e}^{2}n_{\mathrm{e}}}{2\epsilon_{0}k_{\mathrm{B}}T_{\mathrm{e}}}\dfrac{F_{-1/2}(\eta_{\mathrm{e}})}{F_{1/2}(\eta_{\mathrm{e}})} , F_{a}(y) = \displaystyle \int_0^\infty \dfrac{x^a}{\exp(x-y)+1} \mathrm{d}x $. 对于离子和电子的碰撞, 由于电子自身的量子特性以及散射过程中可能会形成共振态, 因此需要采用量子散射理论计算. 对应的离子-电子碰撞动量转移截面形式为

式中$ \delta_l(p) $是连续态电子的相移, 需要通过求解薛定谔方程得到, 具体细节见参考文献[7,20–22].

在T矩阵扩展模型中, 入射粒子的横向偏转$ {\cal{D}}_{\perp} = \dfrac{1}{v_{\mathrm{T}}}\cdot\left < \dfrac{({{\boldsymbol{p}}}_{\mathrm{T}}^\perp)^2}{2 m_{\mathrm{T}}}\right > $的表达式如下:

入射粒子的CSD阻止本领$ \dfrac{{\rm{d}}E}{{\rm{d}}s} = \dfrac{1}{v_{\mathrm{T}}}\cdot\dfrac{{\rm{d}}}{{\rm{d}}t}\left < \dfrac{{\boldsymbol{p}}_\mathrm{T}^2}{2 m_{\mathrm{T}}}\right > $则由下式决定:

方程(15)右边第2项描述的是CSD和LET阻止本领之间统计权重的差异: 不同的权重作用在相同的动量转移截面后积分会得到不同的阻止本领. 从这一项可以看出, 横向偏转强烈依赖于$ \mu_{\mathrm{T}c}/m_{\mathrm{T}} $, 因而高能离子的横向偏转只能是由等离子体中的离子引起的. 在以往的研究中通常假设高能离子沿直线运动, 横向偏转带来的影响被认为是不显著的. 然而, 在高能粒子的能量沉积过程中, 带电粒子之间的大角度库仑散射可以起到关键作用. 尤其是在高能粒子射程的尾端, 大角度库仑散射及其累积的多重散射效应会导致CSD和LET阻止本领之间出现显著的差异.

本文讨论的横向偏转效应在文献[10,23]中均有讨论, 然而并没有给出描述横向偏转效应的显示表达式. 此外, 上述文献中对横向偏转的讨论是针对弱耦合等离子体进行的, 相应的阻止本领模型, 如BPS模型^[10]是基于微扰展开建立的, 因而只适用于弱耦合的全电离等离子体. 此外, 常用的Li-Petrasso阻止本领模型^[14]与CSD模型一样, 描述的都是入射粒子动能的阻滞和衰减, 无法描述由多次散射诱发的横向偏转. 当入射粒子的能量非常高时, 入射粒子与等离子体的散射引发的横向偏转并不剧烈, 此时CSD和LET阻止本领的结果之间的差异很小. 随着入射粒子能量的减小, 其与等离子体中的离子之间的碰撞起主导作用, 这些强碰撞会诱发大角度散射, 导致入射粒子产生显著的横向偏转. 我们之前的研究表明, 只有考虑了横向偏转效应带来的影响, 才能揭示低能端能损理论预测和实验测量之间的差异^[7]. 此外, 相较于其他理论模型, T矩阵扩展模型对中等耦合区间等离子体中的能量沉积也能给出更准确的描述.

基于高能粒子阻止本领的理论模型, 可以计算高能粒子慢化过程中沉积给等离子体中$ c $类粒子的能量, 如下式所示^[15]

式中, $ {\rm{d}}E_c/{\rm{d}}x $是等离子体中$ c $类粒子的阻止本领, $ {\rm{d}}E/{\rm{d}}x $是总阻止本领, $ E_{0} $是高能粒子的初始能量, $ E_\mathrm{min} $是需要选取的α粒子的最低能量. 在方程(16)中分别采用LET阻止本领(4)和CSD阻止本领(14)可以考察横向偏转效应对能量分配的影响. 根据方程(16)可得分配给等离子体中$ c $类粒子的能量份额为$ F_c = {E_c}/{E_0} $. 如果简单地认为高能粒子将能量完全沉积给等离子体, 则$ F_\mathrm{e} + F_\mathrm{I} = 1 $, 其中$ F_\mathrm{I} $为分配给等离子体中不同离子的总份额. 这一近似意味着$ E_\mathrm{min} = 0 $, 因而忽略了高能粒子慢化过程中的热化. 考虑热化后, 可分配给等离子体的能量为$ E_\mathrm{dep} = E_0 - E_\mathrm{min} $, 且$ F_\mathrm{e} + F_\mathrm{I} = E_\mathrm{dep}/E_0 < 1 $. 因此, 在满足$ F_\mathrm{e} + F_\mathrm{I} = 1 $的约束下, 等离子体中$ c $类粒子的能量分配因子的定义应修正为

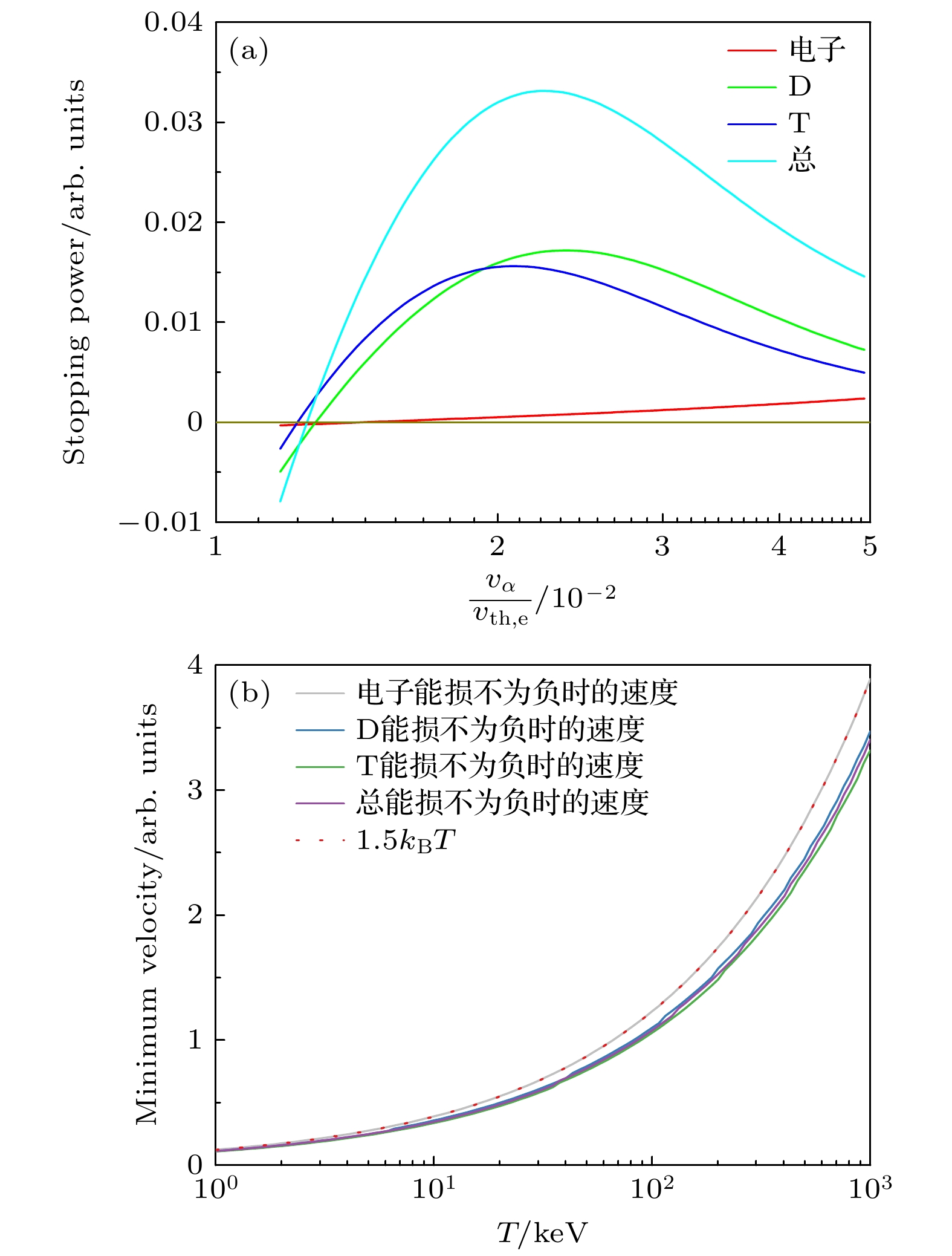
后续的计算需要确定$ E_\mathrm{min} $, 其与给定温度密度条件下等离子体中能量沉积的量有关. 当等离子体的温度远小于入射粒子的能量时, $ E_\mathrm{min} = 0 $是一个简单有效的近似. 高能粒子在等离子体中慢化过程时, 并不能变为完全静止的状态. 当高能粒子的能量低于等离子体的热力学动能时, 它会因与等离子体粒子的碰撞吸收能量而热化, 即入射粒子会被等离子体加热. 这一事实反映在图1(a)中, 当高能粒子的速度低于某一值时, 其阻止本领会发生符号的变化, 且不同等离子体粒子阻止本领符号发生变化时对应的速度或能量有明显差异. 因此能量截止点$ E_\mathrm{min} $选取的不正确会导致电子离子能量分配因子计算的错误.

图1(b)给出了电子密度为$ 10^{25} \; \mathrm{cm^{-3}} $的DT等离子体中, 不同电子温度下不同CSD阻止本领的零点. 可以发现, 在该条件下的DT等离子体中, 电子阻止本领的零点最大, 且与入射粒子动能为$ 3 k_\mathrm{B} T/2 $对应的速度相近. 更细致的对比发现, 在本文研究的温度密度范围内, $ 3 k_\mathrm{B} T/2 $对应的速度始终略大于电子阻止本领的零点. 因此, 在后面的计算中采用$ E_\mathrm{min} = 3 k_\mathrm{B} T/2 $.

本节主要讨论α粒子的能量沉积及其沉积给等离子体中电子的能量份额, 其中α粒子的初始能量为$ 3.54\; \mathrm{MeV} $. 假设电子的温度和离子的温度是相等的. 能量沉积导致的电子离子温度脱离和温度平衡过程^[24,25], 以及其对热斑演化和聚变反应率的影响十分复杂, 将在后续研究中持续深入开展. 本文聚焦在能量沉积过程中的电子离子能量分配因子上.

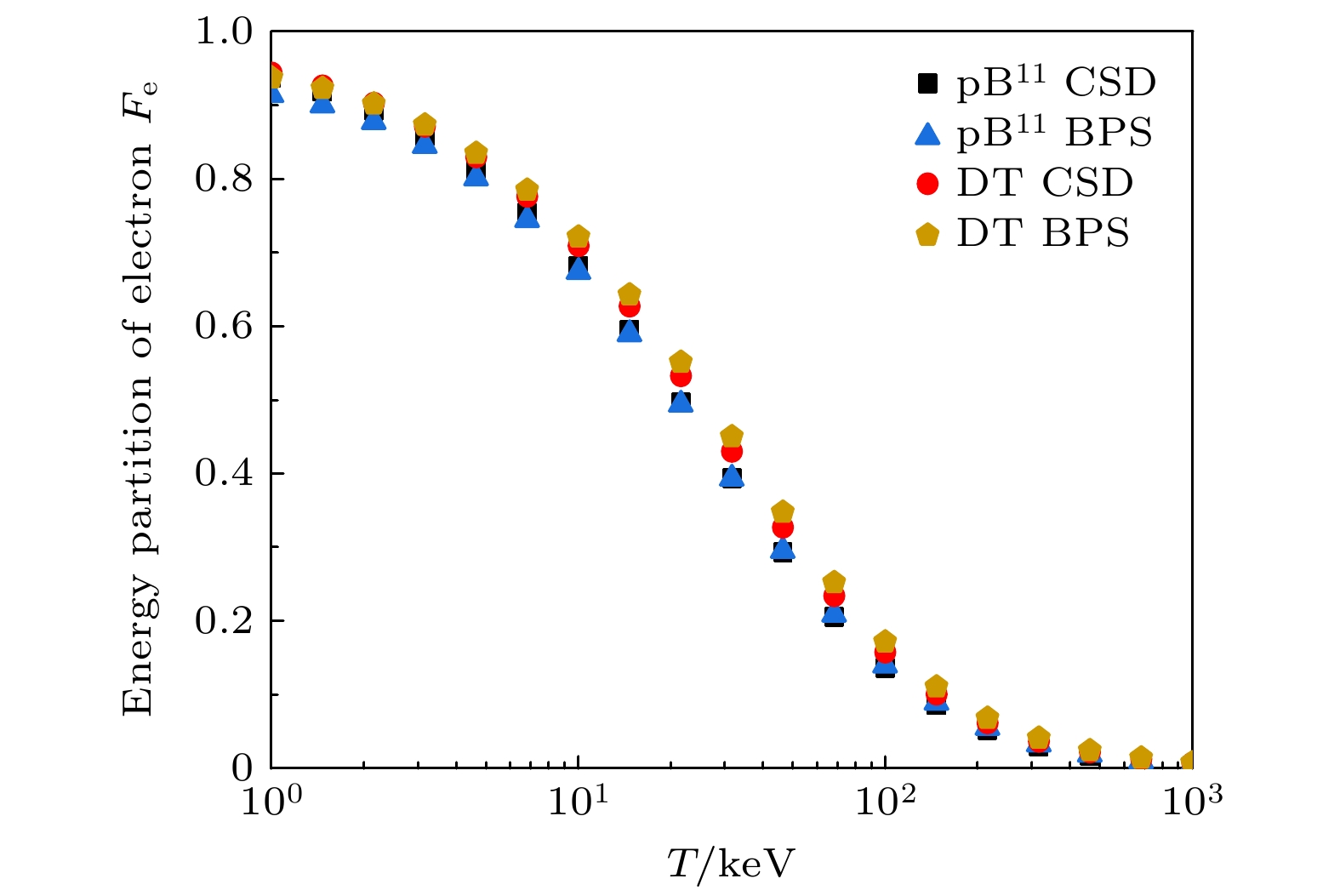
首先研究相同电子密度条件下$ \mathrm{p}^{11}\mathrm{B} $和DT等离子体中电子能量分配因子随温度的变化, 结果如图2所示. 可以发现, 在同种等离子体中, 本文中的CSD模型预测的电子能量分配因子与BPS阻止本领模型给出的结果基本相符合. 这是因为在图2研究的温度范围内, 等离子体均处于弱耦合 等离子体区间. 在弱耦合等离子体区间, 对阻止 本领起主导作用的是粒子之间的库仑散射和等 离子体集体激发效应. 虽然处理的细节不一样, 但 CSD模型和BPS模型对这两种效应均能给出准确的描述, 因而给出的电子能量分配因子之间的差异不大.

从图2还可以发现, 在相同电子密度和温度的$ \mathrm{p}^{11}\mathrm{B} $和DT等离子体中, 根据CSD阻止本领计算的电子能量分配因子之间的差异要小于BPS模型的结果. 此外, 相同电子密度的$ \mathrm{p}^{11}\mathrm{B} $和DT等离子体中, 依据CSD阻止本领模型计算的能量分配因子在10—100 keV的区间呈现出最大约$ 5{\text{%}} $的差异. 这一差异主要来源于DT与$ \mathrm{p}^{11}\mathrm{B} $等离子体中离子质量和电荷的区别. 如何精确描述混合等离子体中离子质量和电荷的差异带来的影响, 并进一步发展便于应用的理论模型, 需要进一步开展更深入的研究. 总的来讲, 图2的结果表明, 相同电子密度和温度条件下, 常用聚变燃料的差异(DT和$ \mathrm{p}^{11}\mathrm{B} $)对电子的能量分配因子的影响相对较小. 接下来将进一步研究DT等离子体中的电子能量分配因子.

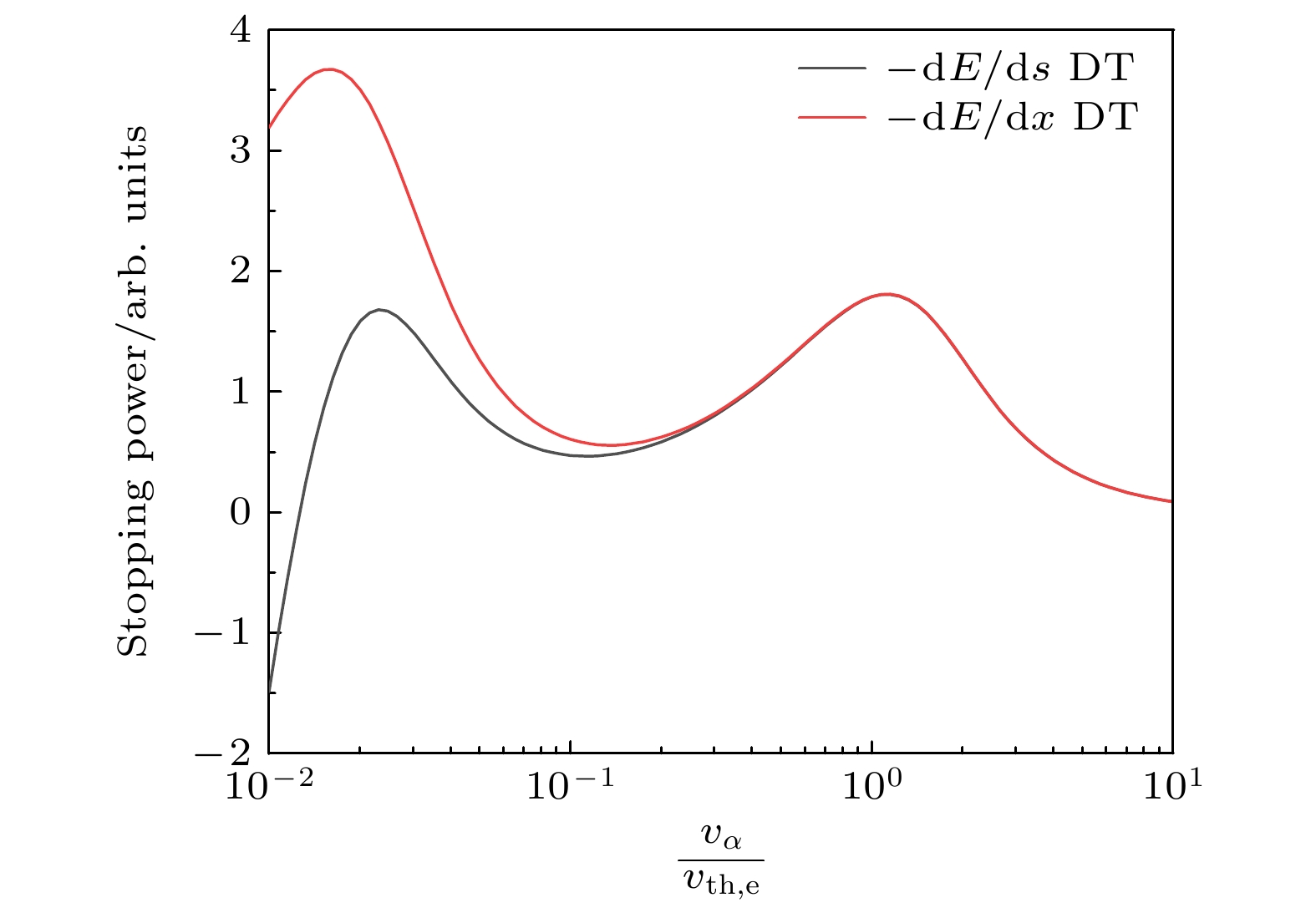
首先研究了偏转效应对阻止本领的影响. 图3给出了α粒子在电子密度为$ 10^{26} \; \mathrm{cm^{-3}} $, 温度为1 keV的DT等离子体中的CSD和LET阻止本领. 如图3所示, 电子阻止本领在高能区占主导地位, 表现为在$ v_{\text{α}}/v_{\mathrm{th, e}}\approx 1 $时存在一个阻止本领的峰值; 而离子阻止本领在低能区占主导地位, 表现为$ v_{\text{α}}/v_{\mathrm{th, e}}\approx m_{\mathrm{DT}}^{-1/2} $处的离子布拉格峰. 随着α粒子能量的衰减, CSD($ {\rm{d}}E/{\rm{d}}s $)和LET($ {\rm{d}}E/{\rm{d}}x $)阻止本领之间的差异越来越显著, 尤其是在射程的尾端, 两者之间的变化趋势有着明显的区别. CSD中多重散射诱发的偏转效应的缺失会对低能区域的阻止本领有显著的影响, 特别是在离子峰附近, LET离子阻止本领显著大于CSD离子阻止本领. 这会导致沉积给离子的能量变多而沉淀给电子的能量变少, 电子能量分配因子也会对应变少. 因此, 偏转效应会显著地影响高能离子能量沉积过程中分配给电子的能量份额. 此外, 不同于LET阻止本领, CSD阻止本领在某个临界速度处会发生符号的变化, 也就是说α粒子不再会往等离子体中沉积能量, 而是会从等离子体中获取能量. 有研究表明, 在电子离子双组分等离子体中, 这一过程与等离子体中不同体系之间的能量弛豫有关^[19]. 对与多组分混合等离子体, 这一问题需要更细致的研究分析.

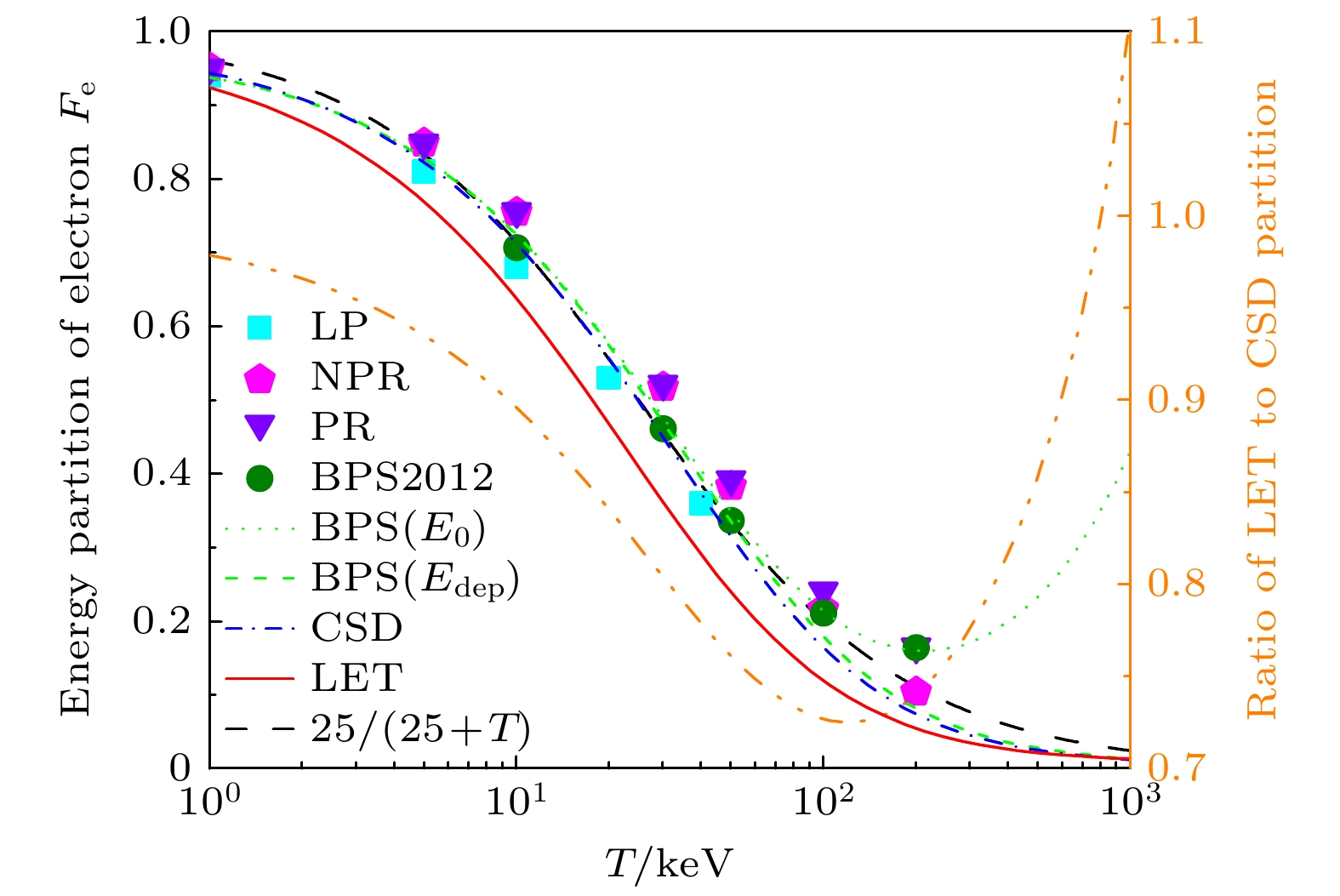
为具体研究偏转对电子能量分配因子的具体影响, 研究了$ n_\mathrm{e} = 10^{26} \; \mathrm{cm^{-3}} $的DT等离子体中, 电子能量分配因子$ F_\mathrm{e} $随温度的变化, 并给出了不同模型之间的对比, 如图4所示. 可以看出, Li-Petrasso模型^[14]给出的电子能量分配因子要低于BPS模型^[10,15]及基于介电函数的阻止本领模型^[16]给出的结果. 在温度大于$ 100 \; \mathrm{keV} $时, 是否考虑入射粒子的反冲效应会带来显著差异. 此外, 通过BPS2012和BPS$ (E_0) $对比发现, 其在温度约为$ 200 \; \mathrm{keV} $时出现拐点. 这一非物理的行为是由于在(17)式中采用$ E_\mathrm{min} = 0 $以及在积分(16)式中采用总阻止本领为零时的能量作为积分下限导致的. 由此可见, 错误的能量截断$ E_\mathrm{min} $会导致不合理的电子能量分配因子. 采用$ E_\mathrm{min} = 3 k_\mathrm{B} T / 2 $后的计算表明, 基于CSD组织本领(14)的电子能量分配因子在$ T = 1 — 1000 \; \mathrm{keV} $的范围与BPS模型的结果符合得比较好. 此外, (2)式中取$ T_0 = 25 $在温度区间$ T = 5— 50 \; \mathrm{keV} $内能很好地复现这一密度下CSD和BPS的计算结果.

进一步的对比可以发现, 大角度散射及其累积效应诱发的横向偏转效应会使得入射粒子将更多的能量沉积给等离子体中的离子体系. 在常用的能量沉积模型如Li-Petrasso^[14], BPS^[10,15]等模型中, 都只考虑了小角度散射对偏转以及能量分配的影响, 而忽略了大角度库仑散射带来的贡献^[7,18]. 从图4可以看出, 横向偏转效应对电子离子能量分配有显著的影响. 在$ n_\mathrm{e} = 10^{26} \; \mathrm{cm^{-3}}, T = 100 \; \mathrm{keV} $的DT等离子体中, 不考虑偏转效应会高估电子能量分配因子, 高估的比例约达到$ 27.5 {\text{%}} $. 因此, 在惯性约束聚变的点火和燃烧研究中, 应充分考虑阻止本领模型的精确性以及电子离子能量分配因子的准确性带来的影响.

为了进一步地获得便于应用的电子分配因子, 需要深入分析温度和密度对电子能量分配因子的影响. 因此, 在CSD和LET阻止本领的框架下计算了宽广温度密度区间($ n_\mathrm{e} = 10^{22}— 10^{27}\; \mathrm{cm^{-3}}, T = 1 —1000 \; \mathrm{keV} $)内的电子分配因子, 并建立了适用的拟合表达式. 这一温度密度涵盖了大多数DT聚变等离子体的情况^[2,4,26,27].

之前的研究表明^[7], 高能粒子的阻止本领随密度的变化基本上呈线性变化, 这是因为碰撞截面基本上与参与散射过程的粒子数目成正比. 根据方程(16)和方程(17)可知, 电子能量分配因子由电子的阻止本领和总的阻止本领之比确定, 故而电子能量分配因子受密度变化的影响很弱. 然而, 温度的变化对电子能量分配因子的影响很强^[11,12]. 根据T矩阵扩展模型, 如方程(14), 温度的变化不仅会影响动量转移截面, 还会显著改变粒子分布函数的形状, 进而改变相应阻止本领的被积函数. 因为电子和离子之间质量的差异, 分布函数的极值位置有显著差别, 因而会影响对高能离子能量沉积的贡献. 综上所述, 温度的变化对电子能量分配因子的影响很强, 而密度变化带来的影响很弱. 因此, 我们建议采用如下的拟合公式:

式中温度的单位为keV, 即$ \widetilde{T} = T / \mathrm{keV} $. 拟合参数$ a_i $均为密度的函数, 并假定由如下拟合公式给出:

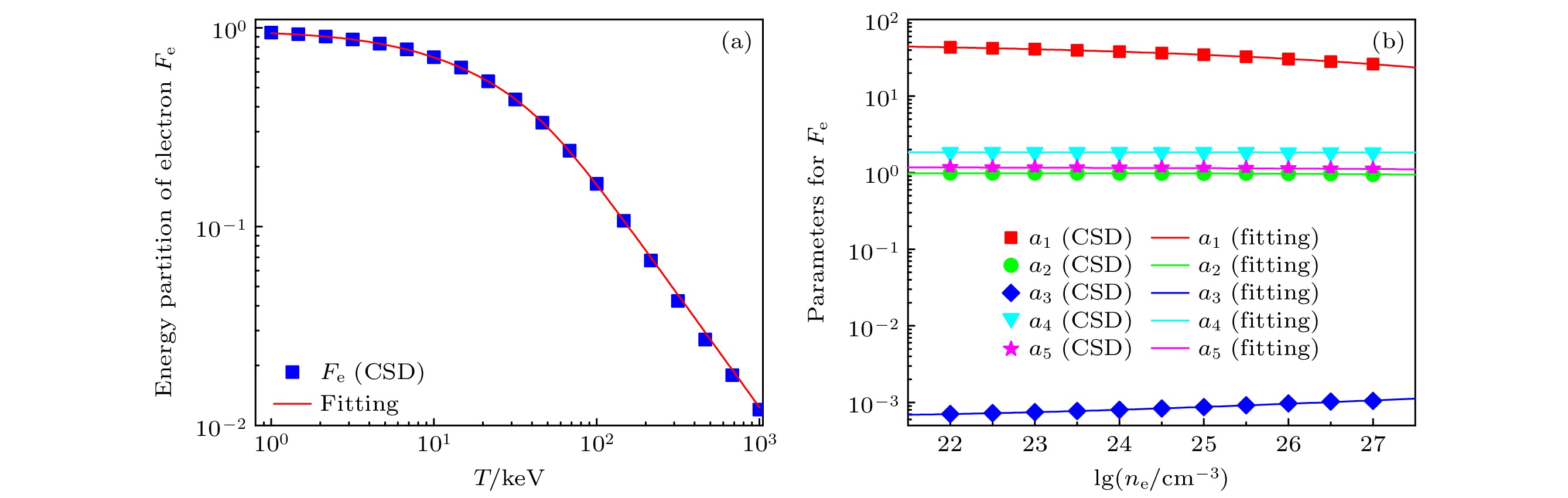
式中约化密度$ \tilde{n}_\mathrm{e} $定义为$ \tilde{n}_\mathrm{e} = \lg({n_\mathrm{e}}/{\mathrm{cm}^{-3}}) $. 图5展现了基于CSD阻止本领计算的电子能量分配因子$ F_\mathrm{e} $及其拟合. 图5(a)给出了电子密度为$ n_\mathrm{e} = 10^{26} \; \mathrm{cm^{-3}} $的DT等离子体中电子能量分配因子$ F_\mathrm{e} $随温度的变化. 可以看出, 基于方程(18)的拟合公式在本文所关心的温度区间都表现优异, 最大的拟合误差约$ 1{\text{%}} $左右. 图5(b)给出了对应的参数$ a_i $随密度的变化. 可以发现, $ a_i $参数随密度的变化均呈现出较弱的变化, 如$ a_1 $在$ n_\mathrm{e} = 10^{22}—10^{27}\; \mathrm{cm^{-3}} $的密度区间有约2倍的变化. 参数$ a_i $能采用方程(19)进行拟合, 相应的拟合参数见表1. 表1也列出了基于BPS阻止本领^[10]的电子能量分配因子的拟合参数.

由于能量分配因子对密度变化的弱依赖性, LET阻止本领给出的电子能量分配因子与CSD的结果之间的比例基本不随密度变化, 而其随温度的变化如图4中右轴所示. 因此, 基于LET阻止本领的电子能量分配因子可以利用下式来计算:

其中$ g(x) $的函数形式如下:

式中$ x = \log_{10} \widetilde{T} $, 各参数取值分别为$ c_0 = 0.98387 $, $c_1 = -0.034894 $, $c_2 = 0.029982 $, $ c_3 = -0.10916 $, $ c_4 = 0.034865 $. 拟合式(20)在宽广温度密度区间($ n_\mathrm{e} = 10^{22}—10^{27}\; \mathrm{cm^{-3}}, \; T = 1 — 1000 \; \mathrm{keV} $)内的最大误差约为$ 2 {\text{%}} $.

在上述拟合公式中, 均没有考虑等离子体中离子质量和电荷的差异带来的影响. 这主要是因为相同电子密度和温度下, 惯性约束聚变中常用燃料之间的差异对电子能量分配因子的影响较小, 如第3.1节中所讨论的那样. 在以前的研究中, 我们发现等离子体中c类粒子对入射粒子横向偏转的贡献正比于$ z_{c}^{2} m_{c}^{1/2}/m_{\mathrm{T}} $^[7]. 因此可以预期, 离子能量分配因子会因自身质量和电荷的差异呈现出明显的区别, 同样也会影响拟合公式(20)中$ g(x) $的形式. 后续将在本文工作的基础上进一步开展混合等离子体中离子能量分配因子的研究.

本文研究了3.54 MeV α粒子在等离子体中的阻止本领和电子能量分配因子. 通过宽温度密度区间的计算, 发展了适用于惯性约束聚变应用研究的电子分配因子拟合公式. 研究发现, 在电子能量分配因子的计算中采用不正确的能量截断会导致电子能量分配因子随温度变化出现非物理的拐点. 这一现象的出现是因为高能粒子慢化中的热化过程没有被正确地纳入计算中. 此外, 本文的研究发现高能粒子慢化过程中的偏转效应会导致高能粒子将更多的能量沉积给等离子体中的离子. 这一发现表明, 基于小角度散射的阻止本领模型无法完备地描述高能粒子的能量沉积和能量分配, 大角度库仑散射及其累积效应对能量沉积和电子离子能量分配过程有明显的影响. 在本文的研究中忽略了能量沉积过程导致的电子离子温度脱离及其平衡过程. 这一处理忽略了非平衡效应带来的影响. 后续将进一步开展双温稠密等离子体中电子离子能量分配以及非平衡温度演化对能量沉积、电子离子能量分配以及热斑演化的影响.