首页
登录
注册
下载:
-
稀土正铁氧体(RFeO3, R为稀土原子)具有自旋重取向、超快磁光存储、自旋开关和超辐射相变等奇异的物理特性而备受关注[1–5]. RFeO3具有正交畸变的钙钛矿结构, 其空间群为
$ D_{2{\text{h}}}^{16} $ -Pbnm [6]. DyFeO3是稀土正铁氧体家族中的一员, 其包含Fe3+和Dy 3+两套磁性离子亚晶格[7], Fe3+-Fe3+, Fe3+-Dy3+, Dy3+-Dy3+之间的相互作用使其展现出丰富的磁学性质. 在Néel温度(~650 K)以下, Fe3+-Fe3+之间的交换作用使得Fe3+自旋磁矩呈现反铁磁有序, 同时由于DM (Dzyaloshinskii-Moriya)相互作用使得磁矩发生微小偏转, 产生微弱的宏观磁化[8,9]. Fe3+-Dy 3+之间的相互作用使得Dy 3+发生极化, 并且极化程度随温度降低而增大, 促使晶体ab平面内的有效各向异性常数减小, 进而导致Fe3+自旋结构发生Γ4(Gx, Ay, Fz)到Γ1(Ax, Gy, Cz)的相变, 通常称为Morin-type自旋重取向(spin-reorientation transition, SRT)[10]. 当温度降低到Dy3+的Néel温度(TN~4.2 K), Dy3+从顺磁性变成反铁磁性, 这意味着Dy3+ 过渡到Γ5(Gx, Ay)自旋结构. 这一变化不仅使Fe3+-Dy3+的相互作用进一步增强, 还破坏了晶体磁结构的反演对称性, 允许线性磁电响应[11].在以往的研究中, 研究人员使用穆斯保尔光谱[12]、拉曼散射[13]、磁光测量[14]、远红外光谱[11]等技术研究DyFeO3中温度和磁场诱导的自旋重取向, 准铁磁(quasi-ferromagnetic mode, q-FM)和准反铁磁(quasi-antiferromagnetic mode, q-AFM)共振等物理现象. Koshizuka和 Hayashi[13]利用拉曼散射实验发现随着温度从室温降至50 K时, DyFeO3中的q-AFM共振频率从0.51 THz降至0.15 THz, 相变之后频率随温度降低而向高频移动, q-FM共振频率则几乎稳定在0.38 THz. Eremenko等[14]的研究发现, 在DyFeO3 Morin相变温度点以上, 沿a轴施磁场会诱导Γ4→Γ24→Γ12→Γ2的相变过程. 该相变顺序中的Γ24→Γ12的过渡为一阶相变, 伴随铁磁矢量F由晶体的ac平面迅速跳变到bc平面. 随后Gnatchenko等[15]和Balbashov等[16]通过磁光技术进一步测定20—80 K范围内Γ12(Γ24)→Γ2二阶相变的临界磁场, 并构建了较为完整的a-cut的H-T相图. Stanislavchuk等[11]使用远红外光谱测量Dy3+原子有序下的q-FM, q-AFM吸收, 发现了电偶极子磁激发. 近年来, 太赫兹时域光谱(THz-TDS)因其在远红外波段优越的信噪比和时域特性在凝聚态物理研究中得到了广泛的应用, 更为重要的是RFeO3 体系的q-FM和q-AFM共振频率都落在太赫兹区域内[17–19].
本文使用THz-TDS研究了70—100 K范围DyFeO3单晶中两种模式的共振频率和振幅强度对外加磁场依赖性. 根据两种共振模式激发规律, 推断样品内磁结构的变化. 当温度高于70 K时, 我们发现了一种新的磁场诱导的相变过程, 即Γ4→Γ24→Γ2→Γ24→Γ2, 该发现鲜有报道.
-
DyFeO3单晶通过光学浮区法生长而来(IRF01-001–05, Quantum Design, Japan). 详细的样品制备过程参见文献[20]. 沿晶体bc平面切割得到a-cut样品, 并两面抛光用于THz测量. 样品最终厚度为1.41 mm. 利用XRD对DyFeO3的晶体结构进行表征, 并通过背散射钨靶劳厄衍射仪(IPX-LC, IPX Co., Ltd, Japan)测定晶轴方向.
THz测量系统基于传统的THz-TDS系统, 该系统与超导磁体(SpectromagPT, Oxford Instruments)相结合, 可提供0—7 T的磁场、1.6—300 K 的温度以及 0.15—2 THz 的光谱范围[21,22]. 系统光源为美国Coherent公司的Astrella一体化钛蓝宝石飞秒激光放大器(中心波长为800 nm, 激光重复频率为1 kHz, 脉宽为35 fs, 单脉冲能量为5 mJ). 利用一对ZnTe晶体作为太赫兹发射和探测晶体, 分别通过光整流和电光采样技术产生和探测THz信号. 为减少水气吸收的影响, 太赫兹光路被密封并冲入干燥的氮气. 产生的线偏振太赫兹脉冲垂直入射到样品表面, 采集不同温度和磁场下样品和参考(空气)的时域信号. 通过傅里叶变化将时域信号变换到频域. 对它们的功率谱进行归一化处理, 得到透射率 (T ). 通过公式α = –lnT/d 计算样品吸收系数(α), 其中d为样品厚度.
-
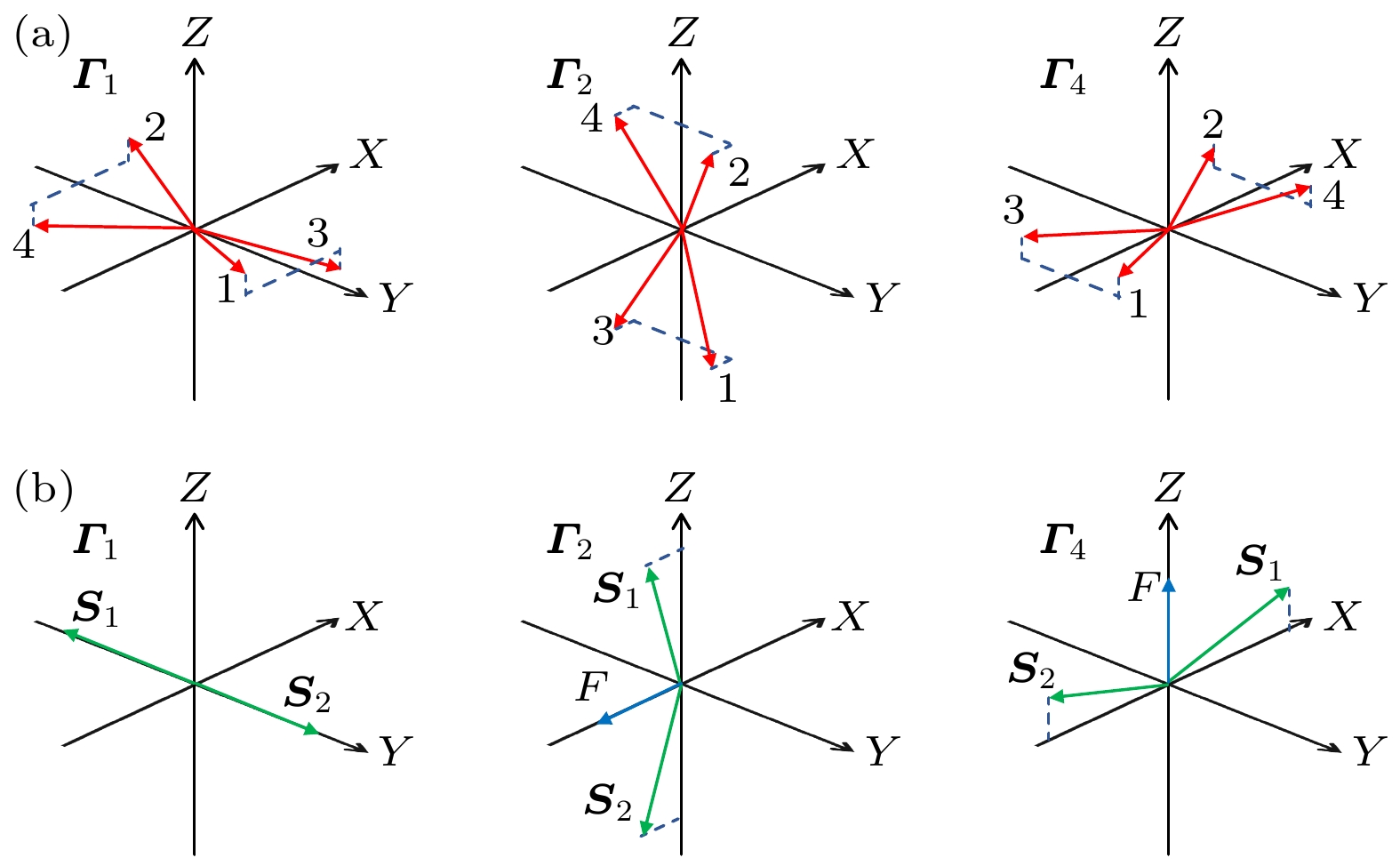
首先介绍法拉第实验构型下q-FM和q-AFM模式的激发规则. 图1(a)为RFeO3 体系3个允许相(Γ1, Γ2, Γ4)的晶胞中Fe3+的4个自旋磁矩. 通常将磁矩1, 3和2, 4合成为S1和S2, 其结果如图1(b). 对于Γ1相, S1和S2沿Y轴反平行排列, 因此对外宏观磁化强度为零, 而Γ2和Γ4分别在X轴和Z轴有宏观磁矩F. DyFeO3样品中q-FM和q-AFM模式在不同构型(Γ1, Γ2, Γ4) 下的激发规则总结在表1中[11,23].
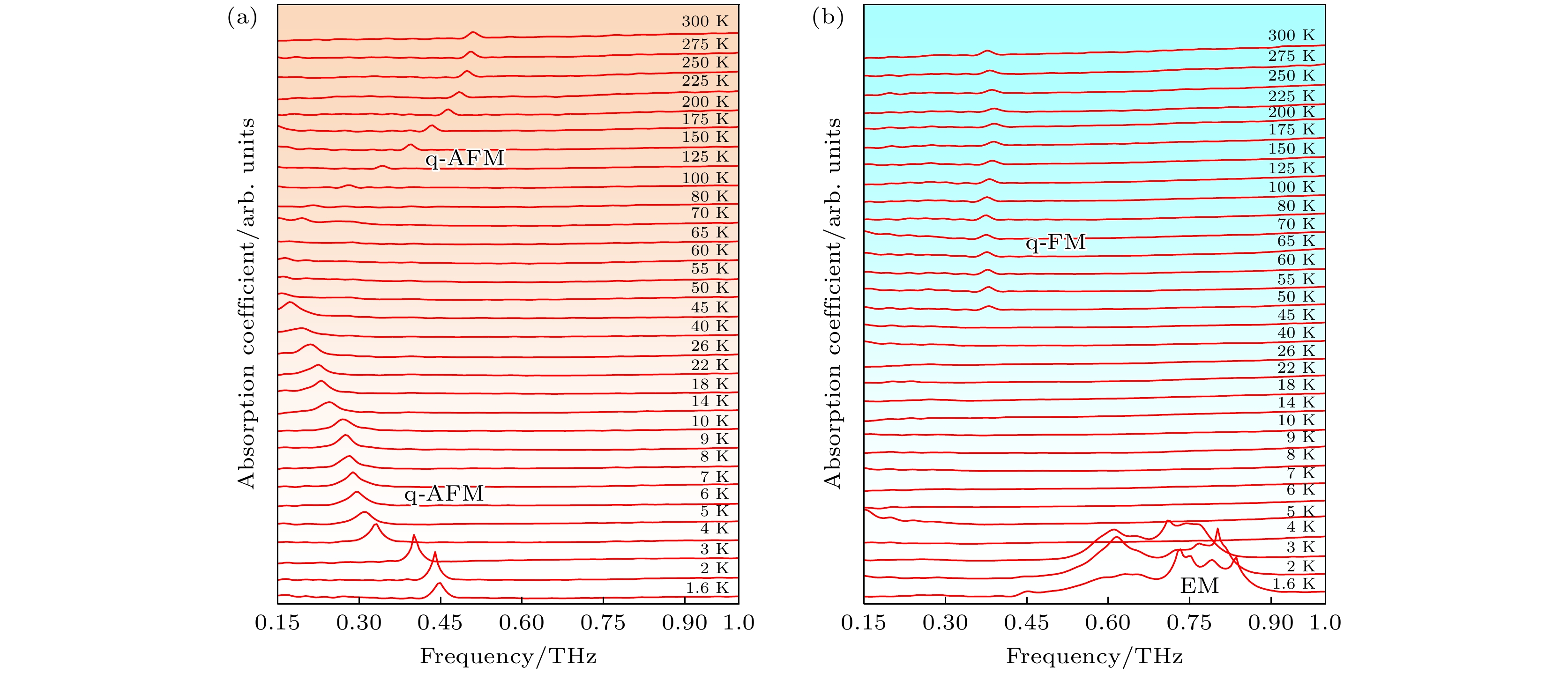
图2(a), (b)分别展示了零磁场下1.6—300 K温度范围内HTHz分别平行样品c轴和b轴的太赫兹吸收光谱. 晶体在300 K温度下处于Γ4相, HTHz 平行于晶体 c 轴和 F 矢量. 因此, q-AFM 模式被激发, 在图2(a)中观察到位于 0.51 THz 的 q-AFM 吸收峰. 随着温度降低到 70 K, q-AFM 共振频率从 0.51 THz 显著软化到 0.2 THz, 峰值强度也逐渐降低. 低于70 K, 当频率降低至 0.15 THz以下时, 受限于我们系统的检测极限, q-AFM 吸收峰无法检测到. 在50—70 K的温度范围内, Fe3+ 的自旋磁结构经历了从Γ4(Gx, Ay, Fz)到 Γ1(Ax, Gy, Cz)的Morin型自选重取向(TM ~ 50 K). 因此, 在50 K以下的Γ1阶段, S1和S2沿b轴反向平行排列, 导致宏观磁矩为零(F = 0). 根据表1中的激发规则, 可以知道Γ1(Ax, Gy, Cz)相下的 q-AFM (q-FM)模式只在HTHz平行c轴(a轴)下激发. 因此, 50 K温度以下的吸收峰归为q-AFM模式, 并且q-AFM频率随着温度下降往高频移动. 当温度降到4 K以下时, q-AFM 频率向更高频率跃迁并且其强度进一步增大. 这是因为 Dy3+ 由顺磁性变为反铁磁性, Fe3+-Dy3+ 之间的相互作用增强, 从而改变了双亚晶格体系的自由能, 影响了 q-AFM 模式的共振频率和强度.
图2(b)展示了HTHz平行晶体b轴的吸收光谱. 在300 K温度下, HTHz与F相互垂直, 激发频率为0.38 THz的q-FM模式. 在 50—300 K 的范围内, q-FM 峰的共振频率略微向低频移动, 而峰值强度基本保持不变. 当温度低于50 K进入Γ1相后, 根据表1可知, 该构型不会激发任何模式的磁共振, 因此光谱没有吸收峰. 当温度低于4 K的时候, 可以观察到从0.45—0.9 THz的宽吸收带. 该吸收带是由于电磁振子吸收所引起的[11], 归因于Γ5相的Dy3+磁结构破坏了反演对称性, 允许线性磁电响应. 沿晶体a轴或b轴施加的强磁场/升高温度会改变Fe3+和Dy3+磁矩的磁相互作用, 使其恢复空间反演对称性, 从而使电磁子吸收消失[11].
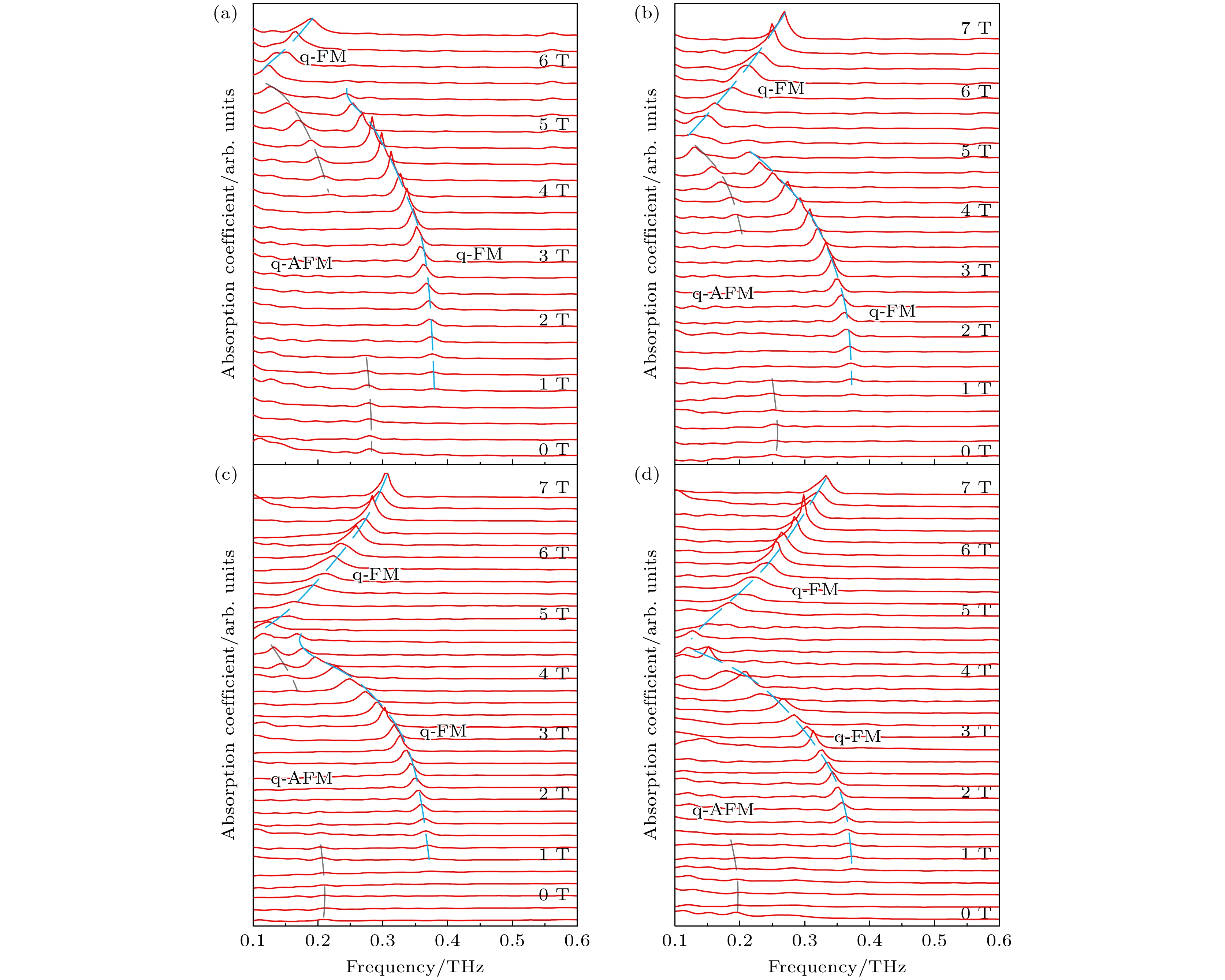
图3显示了在不同温度(70 K, 77 K, 90 K和100 K)下, 当HTHz与晶体的c 轴平行时, a-cut DyFeO3样品磁场从0—7 T的太赫兹吸收光谱. 光谱中各曲线的磁场间隔为0.25 T. 图中灰色(蓝色)虚线代表q-AFM(q-FM)模式的共振频率出现的位置. 图3(a)为100 K时的测量结果. 零磁场下, 样品处于Γ4相且HTHz平行F, 所以激发位于0.28 THz的q-AFM模式. 在1 T以下的磁场中, q-AFM频率和峰值强度保持不变. 在1—2 T的磁场范围内, q-AFM峰值强度逐渐减弱消失, 同时另一频率为0.38 THz的吸收峰出现在光谱中并逐渐增强. 这暗示磁矩F可能在外磁场影响下向a轴偏转. 这时, F与HTHz之间的夹角0° < θ < 90°, 具有平行和垂直于HTHz的分量, 因此同时激发q-AFM和q-FM两种共振模式, 所以在0.38 THz的吸收峰为q-FM模式. 晶体在该磁场范围内为Γ24相. 两个吸收峰短暂共存后, 在磁场大于等于2 T时只剩下q-FM模式的吸收峰, 随着磁场逐渐增大, q-FM频率向低频移动, 并且强度逐渐增强. 这表明F矢量已经从ac平面旋转到a轴, 经历了从Γ24相到Γ2相的转变. 磁场从2—3.5 T时, q-FM峰的得到进一步强化, 表现为强度上升并最终停止. 这表明F向量在这个磁场区间始终位于a轴. 当磁场达到3.75 T, 光谱中出现0.21 THz的吸收峰, 在磁场增大的过程中不仅向低频逐渐移动, 而且强度逐渐增大. 同样该吸收峰可归为q-AFM模式. 3.75—5.5 T范围内双峰共存区间的存在意味着F再次从a轴回到ac平面, 晶相重新回到Γ24相. 当磁场达到5.5 T时, 0.25 THz处的 q-FM吸收峰迅速消失. 在5.5 T以上, 两个吸收峰都消失了并且出现一个新的吸收峰, 其频率和强度随磁场增大而增大, 呈现出与5.5 T以下完全不同的趋势. 这是因为外加磁场超过spin-flop相变的临界值Bcr = 5.5 T, 使得F迅速从ac平面跳转到回到a轴, 即由Γ24相跳变到Γ2相. 这一相变临界磁场与Prelorendjo等[12]的研究一致. 因此, 光谱中高于5.5 T的吸收峰归为q-FM模式. 图3(b)所示为90 K的吸收光谱与100 K时相似, 只是0—1 T范围内的q-AFM模式较弱, 且上述相变过程同样清晰可见.
图3(c), (d)展示了77 K和70 K的吸收光谱, 与90 K, 100 K的光谱有所不同. 77 K的光谱中q-AFM吸收峰非常弱, 而70 K的光谱中q-AFM吸收峰几乎不可见. 参考图2中零磁场下温度依赖的光谱测量结果, 在50—90 K区间的q-AFM吸收峰强度随温度下降而变得微弱并逐渐接近THz系统测量极限(0.15 THz). 通过图2中温度依赖的实验数据, 用灰色虚线标出70 K, 77 K 时q-AFM吸收峰的位置. 总体上来看, 77 K的光谱数据仍然清晰地显示上述相变过程. 综合4张光谱分析, 临界磁场Bcr从100 K的5.5 T降至70 K的4.5 T. 此外, q-AFM和q-FM模式之间的频率间隙随温度降低逐渐增大.
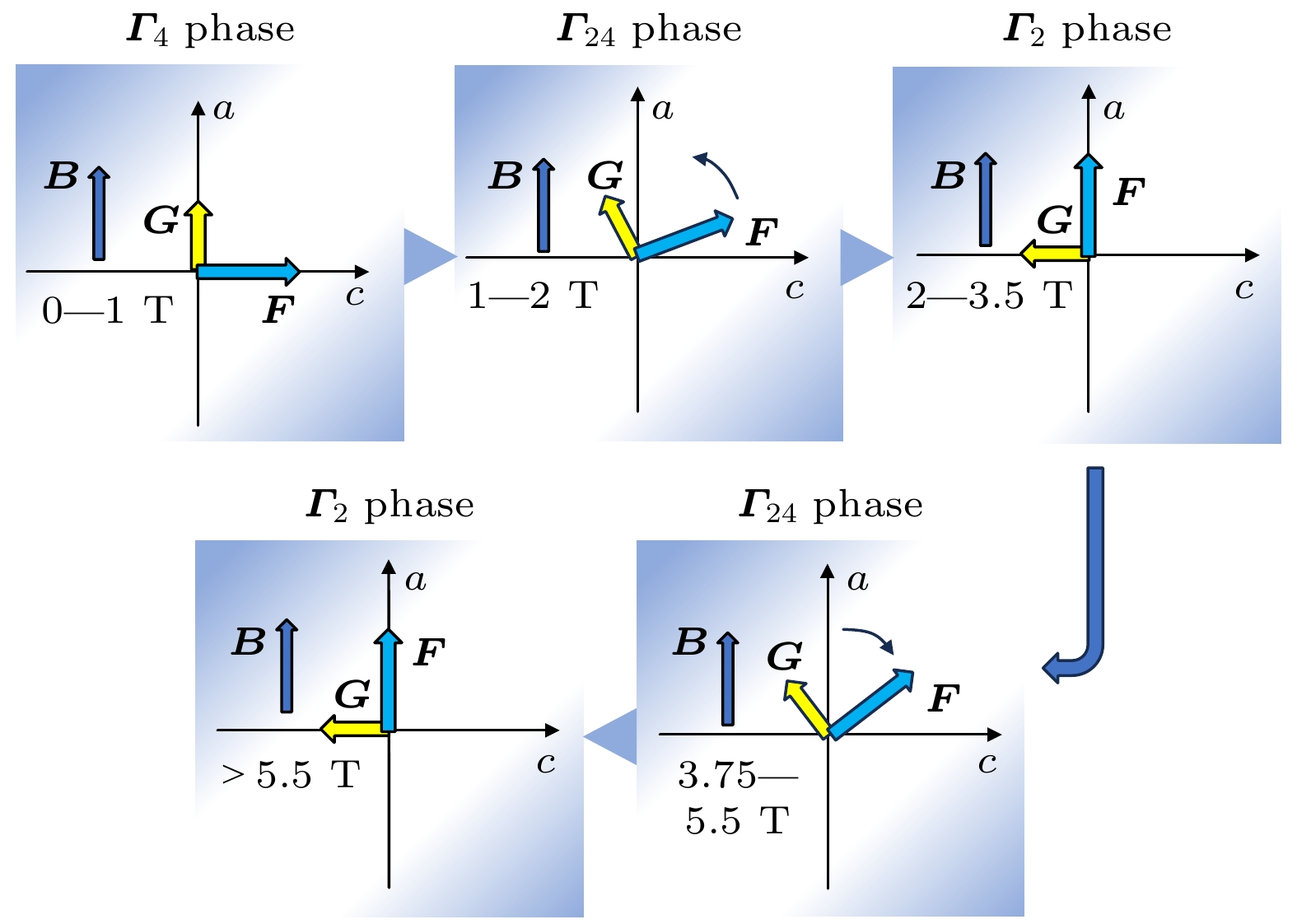
我们的光谱分析表明, 在Morin温度点以上的升磁过程中存在Γ4→Γ24→Γ2→Γ24→Γ2的相变过程, 其相变示意图如图4所示. 根据 Gnatchenko 等[15]的研究, Γ24到Γ12的一阶相变仅存在于50—66 K范围内, 在更高温的条件下并不会出现, 因此排除70—100 K的过渡区间存在Γ12相的可能. Balbashov等 [16]使用光谱仪测定沿DyFeO3晶体 a轴施加磁场的q-FM与q-AFM的频率, 给出了Γ24过渡到Γ4的临界磁场. 但该实验仅测得2 T磁场以上的数据, 缺少低磁场下相关的结果, 因而不能完整分析相变过程. 我们使用THz-TDS测得的共振频率不仅与之高磁场下的数据相符, 还进一步补充了低磁场下的数据, 据此完成分析其相变过程.
DyFeO3有Fe3+和Dy3+两套磁性离子亚晶格, 存在Fe3+-Fe3+, Fe3+-Dy3+, Dy3+-Dy3+三种相互作用, 它们是稀土正铁氧体DyFeO3丰富磁性的来源. Cao等[24]的实验研究发现, 在较大的温度范围内, Dy3+-Dy3+相互作用导致稀土离子磁矩方向倾向与Fe3+磁矩方向反平行排列. 然而, 特定温度和外加磁场能够使两者平行排列, 并引发Fe3+磁矩的自旋翻转等效应. 可见, Dy3+-Fe3+相互作用对DyFeO3磁矩的影响不可忽视. 传统的Herrmann[25]反铁磁理论只关注Fe3+-Fe3+相互作用对磁性的影响. Yamaguchi[7]的有效场理论表明, Fe3+与稀土离子之间磁相互作用的各向异性部分, 即反对称和各向异性对称交换相互作用, 通常是旋转和突变型的自旋重取向的原因. 这些各向异性交换相互作用在垂直于这些自旋的方向上为Fe3+上自旋(S1)产生一个有效场, 在与上述方向相反的方向上对Fe3+下自旋(S2)产生另一个有效场, 这两个有效场的差异会导致磁矩F的旋转. 随着温度的降低或者磁场的改变, 由于稀土磁化强度的增大, 该有效场增大, 当Fe3+自旋与这些有效场的相互作用能超过Fe3+离子自身的各向异性能时, 发生自旋重取向.
根据上述理论, DyFeO3在磁场低于1 T时处于Γ4相, 随着磁场增大, 磁矩F在外磁场影响下向a轴偏转, 在1—2 T范围, 样品处于Γ24相. 在磁场2—3.5 T范围内, F在这个磁场区间旋转到a轴, 即位于Γ2相. 在磁场增强的过程中(3.75—5.5 T), Dy3+磁矩方向与Fe3+磁矩方向从反平行排列逐渐过渡到平行排列, Fe3+-Dy3+相互作用逐渐增强, 其各项异性能对S1和S2产生不同的有效场. 这时, 有效场的作用强于外磁场的作用, 导致样品从Γ2相重新回到Γ24相. 随着磁场的进一步增强, 外磁场对磁矩F的作用逐渐起主导作用, 最终磁矩F再次旋转到a轴, 进入Γ2相. 整个Γ4→Γ24→Γ2→Γ24→Γ2相变过程可以用上述有效场理论解释.
-
本文利用时域太赫兹磁光谱系统测量了a-cut DyFeO3晶体在不同实验构型下的吸收光谱, 结合q-FM和q-AFM共振模式的激发规则, 对其温度依赖性和磁场依赖性数据进行解析. 在零磁场变温实验中, 我们观察到在低于4 K温度下的电磁振子吸收和随温度降低出现在Morin温度(~ 50 K)下的自旋重取向(Γ4→Γ1)现象. 在固定温度(T = 70, 77, 90, 100 K)变磁场实验中, q-FM和q-AFM共振峰呈现复杂变化, 将其归因于一个Γ4→Γ24→ Γ2→Γ24→Γ2的新相变过程. 这一相变过程是由于外磁场和Fe3+-Dy3+的相互作用导致的内部有效场在的相互竞争和协同作用. 本项研究对深入理解稀土铁氧化物的丰富相变和磁电耦合特性具有重要的意义.
DyFeO3中高于Morin温度的新型磁相变
A new magnetic phase transition above Morin temperature in DyFeO3
-
摘要: 稀土正铁氧体(RFeO3, R为稀土原子)包含Fe3+和R3+两套磁性离子亚晶格, 存在Fe3+-Fe3+, Fe3+-R3+, R3+-R3+三种相互作用, 它们是稀土正铁氧体丰富磁性的来源. 本文利用时域太赫兹磁光谱, 在1.6—300 K的温度范围内, 在不同磁场下, 测量a-cut DyFeO3单晶样品的吸收光谱, 并分析光谱中铁磁(FM)和反铁磁共振(AFMR)吸收峰的温度和磁场依赖特性. 在零磁场变温实验中, 我们发现随温度降低在Morin温度(~ 50 K)出现的温度诱导的自旋重取向(Γ4→Γ1), 以及在4 K温度以下存在一个由于电磁振子导致的宽带吸收. 在Morin温度以上, 我们在恒定温度(70, 77, 90, 100 K)下测量了样品在0—7 T磁场范围的吸收光谱. 实验结果表明, 随着磁场的增大, 存在一个新的磁相变过程(Γ4→Γ24→Γ2→Γ24→Γ2), 相变的临界磁场随温度而变化. 这一相变过程是由于外磁场和Fe3+-Dy3+的各向异性交换相互作用导致的内部有效场的相互竞争和对磁矩的协同作用. 本项研究为深入理解稀土铁氧化物的丰富相变和磁电耦合特性, 以及开发相关的自旋电子学器件提供参考.Abstract: Rare-earth orthoferrites (RFeO3) have received significant attention due to their intricate magnetic interactions and potential applications in ultrafast spintronic devices. Among them, DyFeO3 exhibits rich magnetic phase transitions driven by the interplay between Fe3+ and Dy3+ sublattices. Previous studies mainly focused on temperature-induced spin reorientation near the Morin temperature (TM~50 K), but there has been limited exploration of magnetic phase behavior under external fields above TM. This work aims to systematically investigate the temperature- and magnetic-field-dependent magneto-dynamic properties of a-cut DyFeO3 single crystals, with an emphasis on identifying novel phase transitions and elucidating the underlying mechanisms involving Fe3+-Dy3+ anisotropic exchange interactions. High-quality a-cut DyFeO3 single crystals are grown using the optical floating zone method and characterized by X-ray diffraction (XRD) and Laue diffraction. Time-domain terahertz spectroscopy (THz-TDS) coupled with a superconducting magnet (0–7 T, 1.6–300 K) is employed to probe the ferromagnetic resonance (FM) and antiferromagnetic resonance (AFMR) modes. By analyzing the frequency trends in the spectra, the response of internal magnetic moments to external stimuli can be inferred. In the zero magnetic field experiment, it is found that the temperature induced spin reorientation (Γ4→Γ1) occurs at Morin temperature (~50 K) with temperature decreasing. A broadband electromagnetic absorption (0.45–0.9 THz) occurs below 4 K, which is attributed to electromagnons activated by broken inversion symmetry in the Dy3+ antiferromagnetic state. Above the Morin temperature, the absorption spectra of the sample are measured at constant temperatures (70, 77, 90, 100 K) and magnetic fields ranging from 0 to 7 T. The experimental results show that with the increase of magnetic field, a new magnetic phase transition occurs (Γ4→Γ24→Γ2→Γ24→Γ2), and the critical magnetic field of the phase transition varies with temperature. The phase transitions arise from the competition between external magnetic fields and internal effective fields generated by anisotropic Fe3+-Dy3+ exchange. These findings contribute to the further understanding of the magnetoelectric effects in RFeO3 systems and provide a roadmap for using field-tunable phase transitions to design spin-based devices .
-
Key words:
- rare-earth orthoferrite /
- terahertz /
- magnetic resonance /
- magnetic phase transition .
-
-
图 1 (a) RFeO3体系中3个允许相(Γ1, Γ2, Γ4)的晶胞中Fe3+的4个自旋磁矩; (b) 简化后的示意图
Figure 1. (a) The four spin magnetic moments of Fe3+ in the cell of three allowable phases (Γ1, Γ2, Γ4) in the RFeO3 system; (b) simplified schematic diagram.
图 2 零磁场下, a-cut DyFeO3样品在不同温度(1.6—300 K)的太赫兹吸收光谱 (a)HTHz平行于晶体的c轴; (b)HTHz平行于晶体的和b轴, 为清晰起见, 不同温度的光谱垂直偏移
Figure 2. Terahertz absorption spectra of a-cut DyFeO3 samples at different temperatures (1.6–300 K) in zero magnetic field: (a) HTHz parallel to the c-axis of the crystal; (b) HTHz parallel to the b-axis of the crystal, spectra at different temperatures are shifted vertically for clarity.
图 3 在HTHz平行晶体c轴和外加磁场沿晶体a轴方向的实验构型下, a-cut DyFeO3样品在0—7 T磁场下的太赫兹吸收光谱, 温度分别为 (a) 100 K, (b) 90 K, (c) 77 K, (d) 70 K, 清晰起见, 不同磁场的光谱垂直偏移
Figure 3. Terahertz absorption spectra of the a-cut DyFeO3 sample under a magnetic field from 0–7 T at various temperatures of (a) 100 K, (b) 90 K, (c) 77 K, and (d) 70 K, when the directions of HTHz and the applied magnetic field are along the crystal c axis and a axis, respectively. Spectra are vertically offset for clarity.
图 4 温度100 K时, 0—7 T磁场范围内, a-cut DyFeO3单晶中Γ4→Γ24→Γ2→Γ24→Γ2的相变过程
Figure 4. The phase transition process Γ4→Γ24→Γ2→Γ24→Γ2 in the a-cut DyFeO3 single-crystal in a magnetic field range of 0–7 T at 100 K.
-
[1] Johnson C E, Prelorendjo L A, Thomas M F 1980 J. Magn. Magn. Mater. 15 557 [2] Kimel A V, Ivanov B A, Pisarev R V, Usachev P A, Kirilyuk A, Rasing T 2009 Nat. Phys. 5 727 doi: 10.1038/nphys1369 [3] Yuan S J, Ren W, Hong F, Wang Y B, Zhang J C, Bellaiche L, Cao S X, Cao G 2013 Phys. Rev. B 87 184405 doi: 10.1103/PhysRevB.87.184405 [4] Kimel A V, Kirilyuk A, Usachev P A, Pisarev R V, Balbashov A M, Rasing T 2005 Nature 435 655 doi: 10.1038/nature03564 [5] Bamba M, Li X W, Peraca N M, Kono J 2022 Commun. Phys. 5 3 doi: 10.1038/s42005-021-00785-z [6] White R L 1969 J. Appl. Phys. 40 1061 doi: 10.1063/1.1657530 [7] Yamaguchi T 1974 J. Phys. Chem. Solids 35 479 doi: 10.1016/S0022-3697(74)80003-X [8] Moriya T 1960 Phys. Rev. 120 91 doi: 10.1103/PhysRev.120.91 [9] Dzyaloshinsky I 1958 J. Phys. Chem. Solids 4 241 doi: 10.1016/0022-3697(58)90076-3 [10] Balbashov A M, Volkov A A, Lebedev S P, Mukhin A A, Prokhorov A S 1985 Sov. Phys. JETP 61 573 [11] Stanislavchuk T N, Wang Y Z, Janssen Y, Carr G L, Cheong S W, Sirenko A A 2016 Phys. Rev. B 93 094403 doi: 10.1103/PhysRevB.93.094403 [12] Prelorendjo L A, Johnson C E, Thomas M F, Wanklyn B M 1980 J. Phys. C: Solid State Phys. 13 2567 doi: 10.1088/0022-3719/13/13/012 [13] Koshizuka N, Hayashi K 1988 J. Phys. Soc. Jpn. 57 4418 doi: 10.1143/JPSJ.57.4418 [14] Eremenko V V, Gnatchenko S L, Kharchenko N F, Lebedev P P, Piotrowski K, Szymczak H, Szymczak R 1987 Europhys. Lett. 4 1327 doi: 10.1209/0295-5075/4/11/019 [15] Gnatchenko S L, Kharchenko N F, Lebedev P P, Piotrowski K, Szymczak H, Szymczak R 1989 J. Magn. Magn. Mater. 81 125 doi: 10.1016/0304-8853(89)90239-4 [16] Balbashov A M, Marchukov P Y, Nikolaev I V, Rudashevskiĭ E G 1988 Sov. Phys. JETP 67 1910 [17] Peraca N M, Li X W, Moya J M, Hayashida K, Kim D, Ma X X, Neubauer K J, Padilla D F, Huang C L, Dai P C, Nevidomskyy A H, Pu H, Morosan E, Cao S X, Bamba M, Kono J 2024 Commun. Mater. 5 42 doi: 10.1038/s43246-024-00479-3 [18] Lin X, Jiang J J, Jin Z M, Wang D, Tian Z, Han J G, Cheng Z X, Ma G H 2015 Appl. Phys. Lett. 106 092403 doi: 10.1063/1.4913998 [19] Makihara T, Hayashida K, Noe II G T, Li X W, Peraca N M, Ma X X, Jin Z M, Ren W, Ma G H, Katayama I, Takeda J, Nojiri H, Turchinovich D, Cao S X, Bamba M, Kono J 2021 Nat. Commun. 12 3115 [20] Cao Y M, Xiang M L, Zhao W Y, Wang G H, Feng Z J, Kang B J, Stroppa A, Zhang J C, Ren W, Cao S X 2016 J. Appl. Phys. 119 063904 [21] Ju X W, Zhu G F, Huang F, Dai Z R, Chen Y Q, Guo C X, Deng L, Wang X F 2022 Opt. Express 30 957 doi: 10.1364/OE.445724 [22] Ju X W, Hu Z Q, Huang F, Wu H B, Belyanin A, Kono J, Wang X F 2021 Opt. Express 29 9261 doi: 10.1364/OE.418624 [23] Fu Z C, Chen J Y, Shang J M, Lin X, Suo P, Sun K W, Wang C, Li Q X, Luo J L, Wang X B, Wu A H, Ma G H 2024 Appl. Phys. Lett. 125 241102 doi: 10.1063/5.0243672 [24] Cao S X, Chen L, Zhao W Y, Xu K, Wang G H, Yang Y L, Kang B J, Zhao H J, Chen P, Stroppa A, Zheng R K, Zhang J C, Ren W, Íñiguez J, Bellaiche L 2016 Sci. Rep. 6 37529 doi: 10.1038/srep37529 [25] Herrmann G F 1963 J. Phys. Chem. Solids 24 597 doi: 10.1016/S0022-3697(63)80001-3 -
计量
- 文章访问数: 65
- HTML全文浏览数: 65
- PDF下载数: 0
- 施引文献: 0