-
表面等离子体(surface plasmons, SPs)是由金属介质表面的传导电子和光波中的光子进行相互作用而产生[1,2]. 研究人员将表面等离子体按照产生方式主要分成两种类型: 一种是在介质上传播的表面等离子体激元(surface plasmon palaritons, SPPs), 另一种是被束缚的局部表面等离子体[3,4]. 二者都可以将电磁波局域在亚波长范围内, 并增强局部的电场和磁场. 由于其可以突破传统的光学衍射的极限[5], 并且能够在亚波长范围内传播, 一些基于SPPs的各种太赫兹器件被广泛研究, 例如光开关[6]、完美吸收器[7]、调制器[8,9]、传感器[10–12]等. 然而, 这类传统的光学器件存在着两个显著的问题: 一是大部分是以金属介质作为器件的主体架构, 主动可调谐性较差; 其次金属介质的辐射损耗较为严重. 而石墨烯作为一种新型的二维材料, 是由单层碳原子组成的六边形蜂窝状结构[13–15], 自从其被英国曼彻斯特大学的两位教授发现以来, 就引起人们的广泛关注[16–18]. 令人惊喜的是, 相关研究发现石墨烯也具有一定的金属介质所拥有的特性, 例如负介电常数以及较高的载流子迁移率[19], 使得其也可以像金属那样激发并传播SPPs[20,21]. 同时, 研究人员还发现石墨烯有着诸多有趣的现象, 例如对光波更强的压缩能力、比金属更强的局域特性[22,23], 以及更加优异的等离子体诱导透明[24]效应(plasmon induced transparency, PIT).
PIT效应是提高纳米光学器件性能的关键, 通过增强光和物质之间的相互作用, 从而获得更高的耦合效率[25]. 相比于电磁诱导透明(electromagnetically induced transparency, EIT)而言[26], PIT是利用近场耦合模式进行相互作用而产生, 没有严苛的实验条件约束和限制[27], 较强的实用价值使其在光学器件的应用中占据主导地位. 例如, 2021年, Jiang和Chen [28]利用单PIT实现了多功能传感器; 2023年, Zhu和Xiong [29]利用单层石墨烯产生的单PIT实现高折射率传感器; 2024年, Lei等[30]利用十字型的石墨烯图案产生的单PIT实现了偏振不敏感的光开关器件. 如今, 许多器件的应用已经不仅限于单PIT, 各种基于多PIT的光学器件也得到了广泛的研究和应用[31–33]. 然而, 绝大部分的多PIT产生大都是利用两种普遍的方式: 一是在单层图案上简单利用暗模式和多个明模式之间的耦合, 这样单位面积上的石墨烯的组合结构就变得复杂[34]; 二是采取多层石墨烯组合架构[35,36], 导致器件设计的复杂程度以及制造难度的提升, 为器件的实际运用带来了挑战.
本文提出了一个新型的单层图案化石墨烯结构, 其利用3个横向石墨烯条和1个纵向石墨烯带之间的相互作用产生两个单PIT, 两个单PIT之间通过协同效应在太赫兹频率下产生可调谐的三PIT效应. 进一步对归一化电场分布分析表明, 这种协同效应的物理本质可归因于两个单PIT之间的非相干耦合作用. 此外, 通过调控石墨烯的费米能级, 能够实现多频异步光开关之间的相互转换, 其中六频异步光开关所展现的性能非常优异, 当频率点为3.77 THz和6.41 THz时, 调制深度和插入损耗分别达到了99.31%和0.12 dB, 当频率点为4.58 THz时, 退相时间和消光比分别为3.16 ps和21.53 dB. 而且该石墨烯超表面结构具有优异的慢光特性, 其调控范围集中在2.8—3.1 THz, 4.0—4.6 THz, 5.5—6.3 THz, 6.4—7.1 THz频段, 对应群折射率波动范围分别为421 < ng1 < 1212, 402 < ng2 < 425, 452 < ng3 < 791, 431 < ng4 < 601, 超越了大部分传统的慢光器件[37–39]. 基于以上优点, 本文提出的石墨烯结构有望对实现性能优异的光开关和慢光设备提供新的理论指导.
-
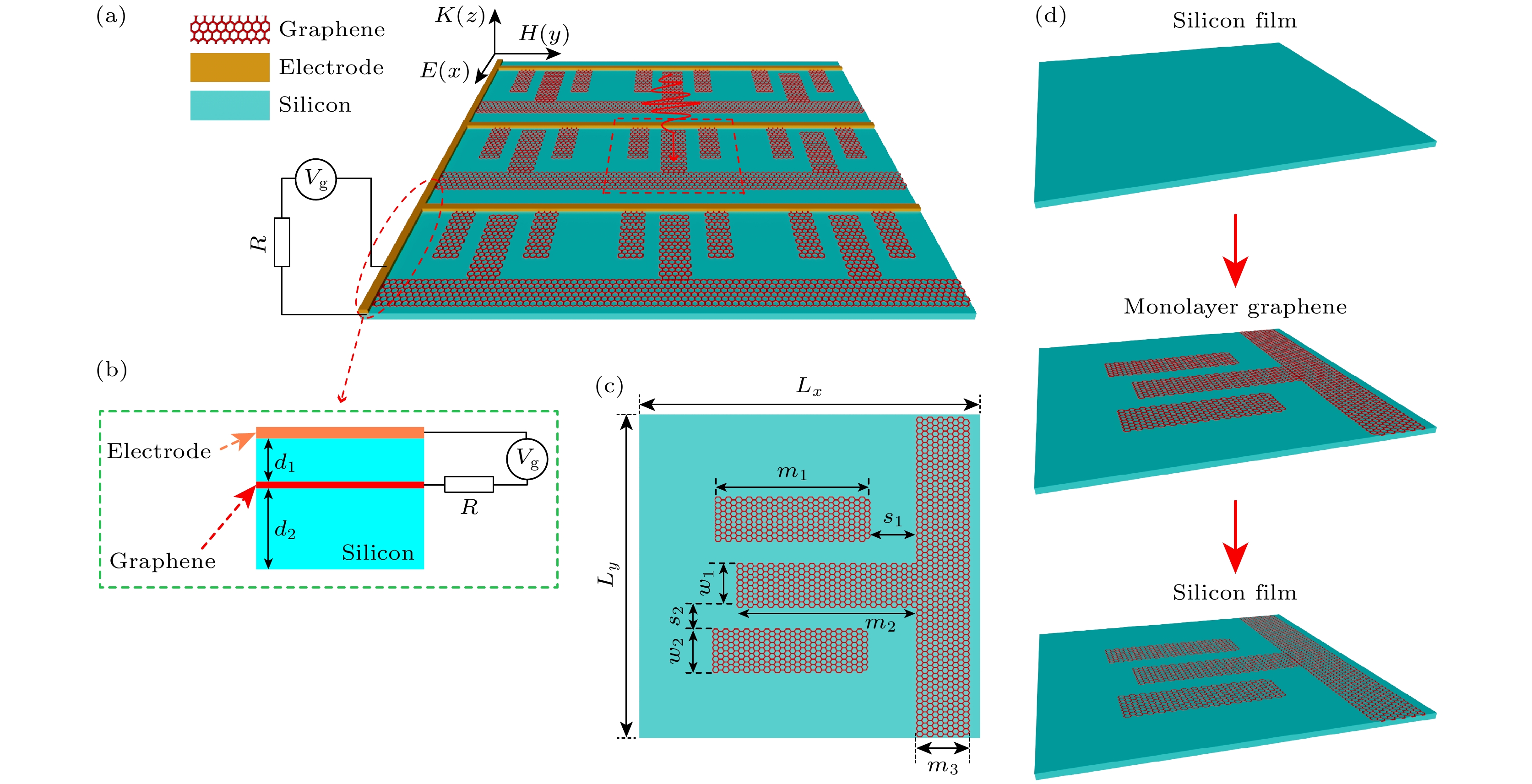
图1(a)为图案化石墨烯结构的整体视图, 3个横向的石墨烯条和纵向的石墨烯带沉积在相对介电常数为11.9的基底硅上, 同时在石墨烯表面覆盖一层相对介电常数相同的硅层, 其作用是防止结构发生氧化, 提高结构的稳定性. 结构的侧视图如图1(b)所示, 顶层和底层的硅层厚度分别为d1 = 10 nm, d2 = 20 nm. 石墨烯组合的几何形状的详细参数如图1(c)所示, 其中, Lx = Ly = 4 μm, m1 = 2.2 μm, m2 = 2.3 μm, m3 = 0.6 μm, s1 = 0.4 μm, s2 = 0.25 μm, w1 = 0.8 μm, w2 = 0.6 μm. 图1(d)为石墨烯器件的制备步骤图, 为器件整体的实际制造提供参考. 石墨烯可以生长在温度高达1000 ℃的铜箔上[40,41], 使用甲烷和氢的混合物进行碳气相沉积[42–44], 然后利用干和湿转移技术将其转移到硅层介质上进行制备[45], 该项制备技术可以在最大程度上减小转移过程中对石墨烯造成的撕裂和损坏, 并且通过该技术制备出来的石墨烯材料相关的性能均处于最佳状态.
在该三重PIT系统中, 单层石墨烯的光学电导率可以利用Kubo模型[46]计算:
当结构的工作温度处于300 K时, 由于
$ {E_{\text{F}}} \geqslant {\text{ }}{k_{\text{B}}}T = {\text{ }}25.85\;{\text{meV}} $ , 带间的石墨烯电导率可以忽略不计, 因此该二维石墨烯的电导率可以进一步简化为Drude模型[47,48]进行表示:式中, e表示电子电荷; EF表示费米能级; τ表示载流子弛豫时间[49], 其中
$ \tau = \mu {E_{\text{F}}}/{\text{ }}(eV_{\text{F}}^{2}) $ , μ表示载流子迁移率, VF = 106 m/s表示费米速度; ω表示入射光的角频率, ћ为约化普朗克常数. 由于石墨烯位于两个介质硅层之间, 因此可以利用电磁场边界条件求解麦克斯韦方程组推导出表面等离子体激元在石墨烯中的传播常数β[50,51]:其中, k0表示入射光的波矢, εsi表示介质硅的相对介电常数, η0表示本征阻抗. 由此得出有效折射率的计算公式:
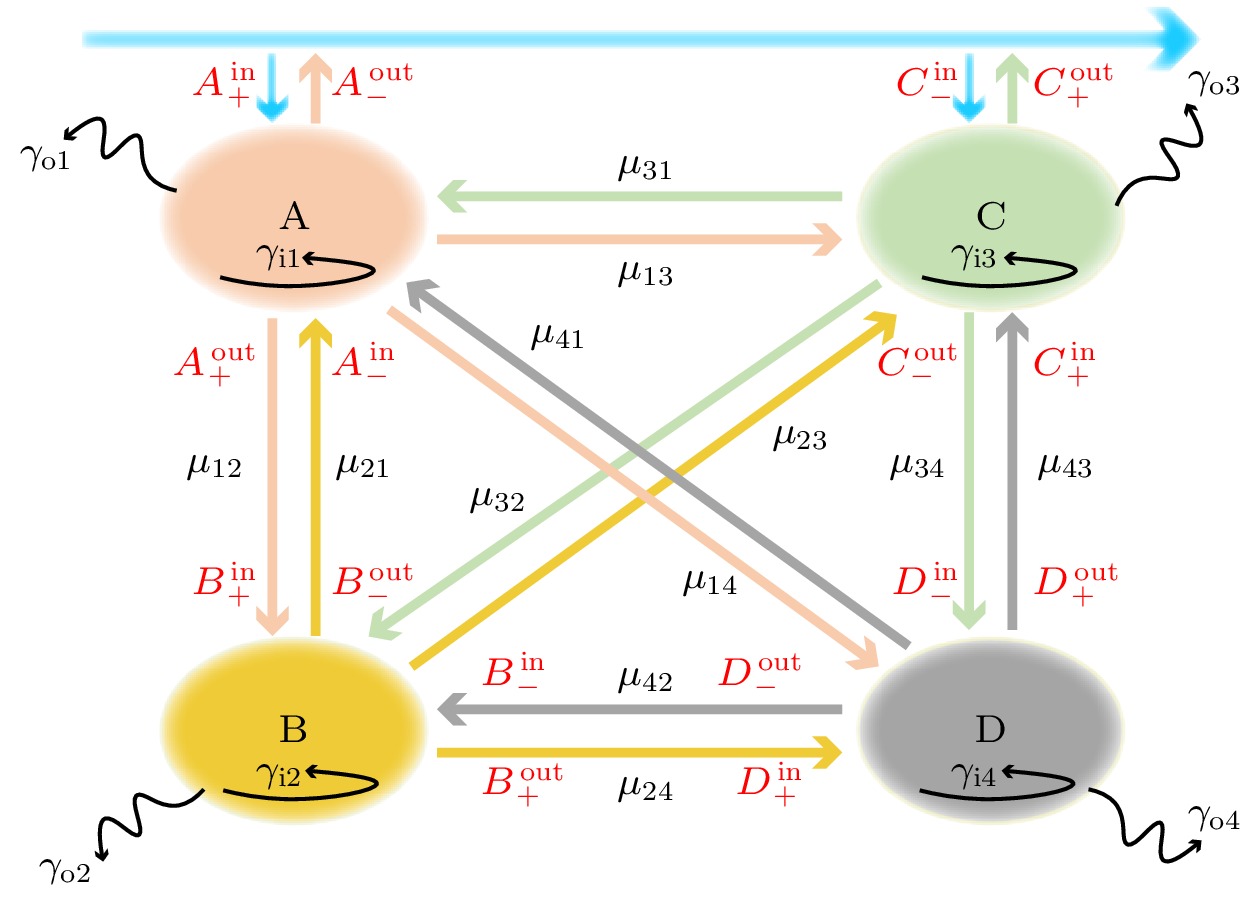
$ {n_{{\text{eff}}}} = {\text{ }}\beta /{k_0} $ .当x偏振光垂直入射到该结构时, 通过非相干耦合和干涉相消机制, 系统产生两个单PIT. 通过非相干耦合作用, 这两个单PIT最终形成一个三重PIT效应. 为深入分析纵向石墨烯带与横向石墨烯条之间的耦合机制, 本研究采用耦合模理论建立了理论模型. 图2展示该耦合模理论的示意图, 其中A, B, C, D对应4种谐振模式, “in”, “out”代表谐振模式信号的输入和输出, “+”和“–”表示信号输入输出的方向. 不同模式的本征损耗系数用
$ {\gamma _{{\text{i}}\left( n \right)}}\left( {n = 1, 2, 3, 4} \right) $ 表示, 模式耦合产生的外部损耗系数用$ {\gamma _{{\text{o}}\left( n \right)}}\left( {n = 1, 2, 3, 4} \right) $ 表示.$ {\mu }_{mn}~(m, n=1, 2, 3, 4 $ 且$m\ne n )$ 则是4个耦合模式的相互耦合系数, 4种模式的耦合关系满足下列表达式:其中,
${\gamma _n} = \left( {{\text{i}}\omega - {\text{i}}{\omega _n} - {\gamma _{{\text{i}}n}} - {\gamma _{{\text{o}}n}}} \right)$ (n = 1, 2, 3, 4)为系统的总损耗系数. 本征损耗系数和外部损耗系数的表达式分别为$ {\gamma }_{\text{i}n} = {\omega }_{n}/\left(2{Q}_{\text{i}n}\right), {\gamma }_{\text{o}n} = {\omega }_{n}/\left(2{Q}_{\text{o}n}\right) $ . 这里ωn表示第n个谐振模式的角频率, Qon和Qin分别表示外部损耗质量因子和内部损耗质量因子. Qtn表示整个系统的损耗质量因子, 其与Qon和Qin满足表达式:$ 1/{Q_{{\text{t}}n}} = 1/{Q_{{\text{o}}n}} + 1/{Q_{{\text{i}}n}} $ , 同时也可以用表达式$ {Q_{{\text{t}}n}} = f/\Delta f $ (f和Δf分别为第n个谐振模式的共振频率和半高宽)进行计算, 内部损耗因子的计算方式为:$ {Q_{{\text{i}}n}} = {\mathrm{Re}}\left( {{n_{{\text{eff}}}}} \right)/ {\mathrm{Im}}\left( {{n_{{\text{eff}}}}} \right) $ (Re(neff)和Im(neff)分别为有效折射率的实部和虚部). 根据能量守恒定理, 4种共振模式的能量关系满足下列方程:$ {\varphi }_{1}, {\varphi }_{2}, {\varphi }_{3} $ 分别为等离子体激元在模式A和B, B和C, C和D之间的相位差, 联立(8)—(14)式可获得透射系数t的计算公式:其中:
由此, 该三PIT系统的透射率T可通过T = t 2获得.
-
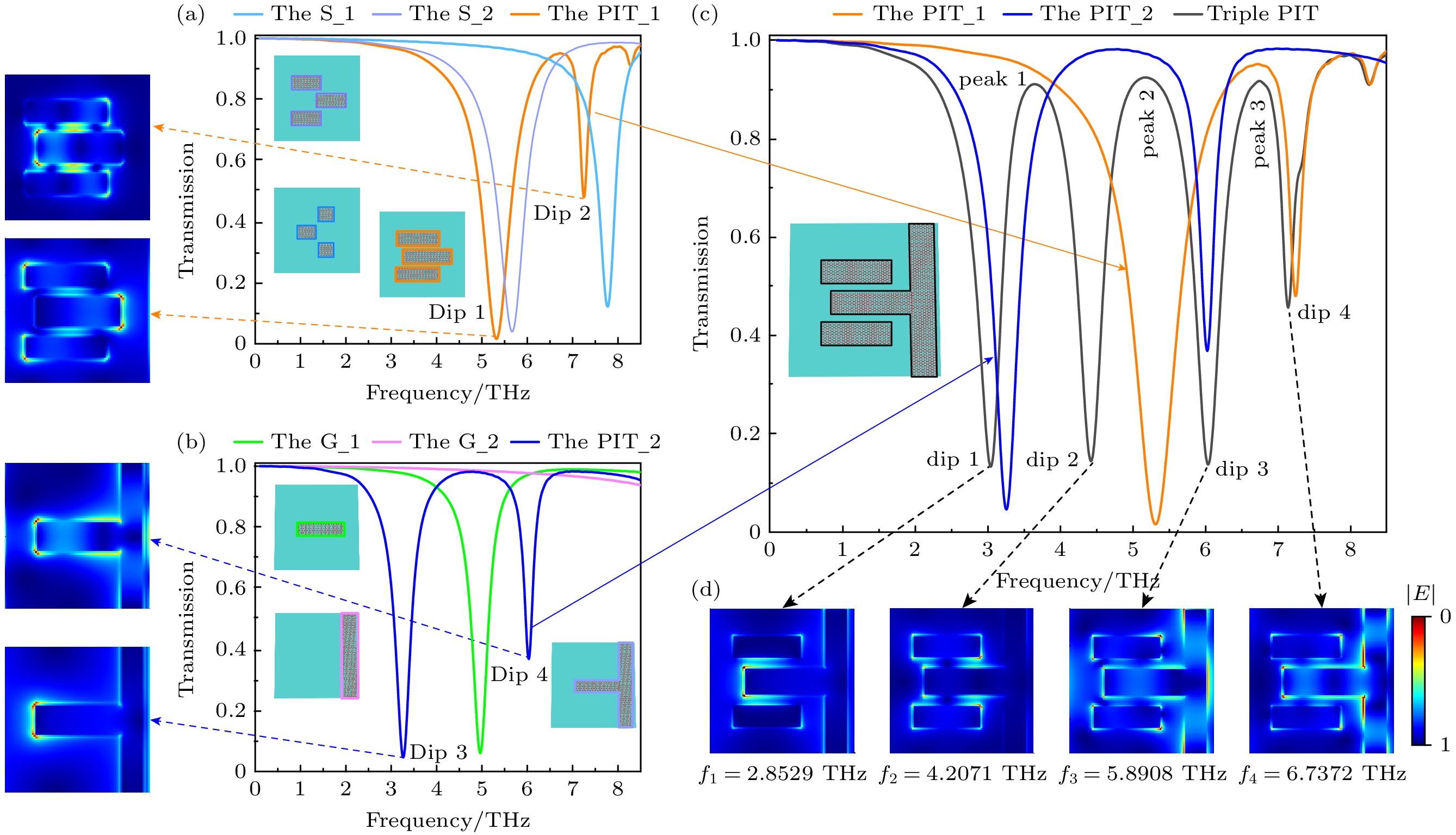
为了清楚地展示三重PIT效应的形成机理, 分析了不同石墨烯超表面产生的透射谱, 如图3所示. 为了方便叙述, 位于结构中心的石墨烯条将其命名为G_1, 它与上下对称的石墨烯条可以拆分成两个结构组合, 分别命名为S_1, S_2, 纵向的石墨烯带命名为G_2.
由于3个横向的石墨烯条边界有着合适的尺寸结构, 当x偏振光照射时, 石墨烯薄层的面电流会在边界上的累积电荷充当电偶极子, 可与光子发生共谐振荡, 从而被入射光直接激发, 显现出宽带亮模式. 相比之下, 纵向的石墨烯带G_2与x偏振光的耦合较弱, 难以被入射光直接激发, 表现出窄带暗模式. 为阐明该三重PIT体系的协同产生机制, 首先对两个独立PIT窗口的形成过程进行系统性分析. PIT_1的形成机制源于两种亮模式间的非相干耦合作用, 该过程区别于传统干涉现象, 其本质在于耦合模式间缺乏稳定的相位匹配条件, 导致电磁场能量呈现非相干的强度叠加特性. 从PIT_1的电场分布特征可以观察到, 左侧透射谷Dip 1的电场能量主要局域在组合结构S_2表面, 这一分布特性表明Dip 1模式的激发主要源于石墨烯组合S_2的贡献; Dip 2的电场能量显著局域于石墨烯组合结构S_1的表面区域, 证实Dip 2的激发主要由S_1贡献. 在单PIT_2体系中, 其形成机制源于明模式与暗模式之间的相干耦合作用. 具体而言, 当入射光激发明模式时, 会同时诱导暗模式的共振响应, 两种模式间产生相干叠加, 最终导致破坏性干涉现象. 然后对PIT_2体系的电场分布进行定量分析, 发现左侧透射谷Dip 3的电场能量显著局域在石墨烯结构G_1的近场区域. 这一空间分布特征表明, Dip 3的形成主要源于石墨烯G_1的贡献. 而右侧透射谷Dip 4的电场能量主要局域在石墨烯结构G_1和G_2的表面区域. 这一空间分布特性表明, Dip 4模式的形成机制源于G_1和G_2的协同耦合作用. 最后, 通过分析三重PIT的电场分布可以进一步理解协同效应, 如图3(d)所示. 由于dip 1与Dip 3的电场分布呈现高度相似的局域特性, dip 4与Dip 2的电场模式表现出类似的分布特征, 而dip 3与Dip 4之间也存在明显的电场分布相似性, 由此可看出dip 1, dip 3, dip 4是由Dip 3, Dip 4, Dip 2非相干耦合而形成. 而dip 2的电场主要与Dip 1相似, 其成因是透射谷Dip 1与暗模式G_2之间发生了非相干耦合. 最终可以得出协同效应的本质是由于PIT_1和PIT_2之间的非相干耦合.
为了体现该超表面动态可调的特性, 相互连接的石墨烯的费米能级通过改变电极上的电压进行调控[9,36], 具体关系满足如下公式[39]:
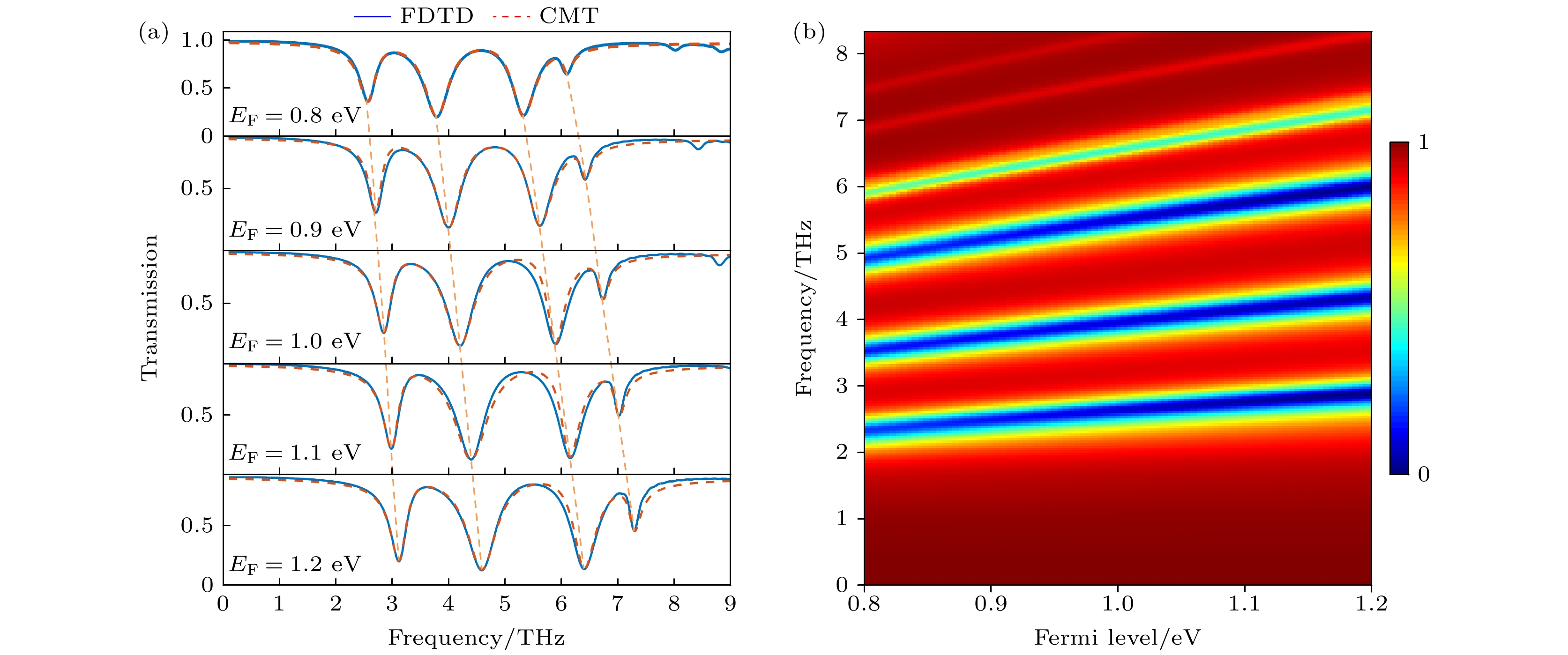
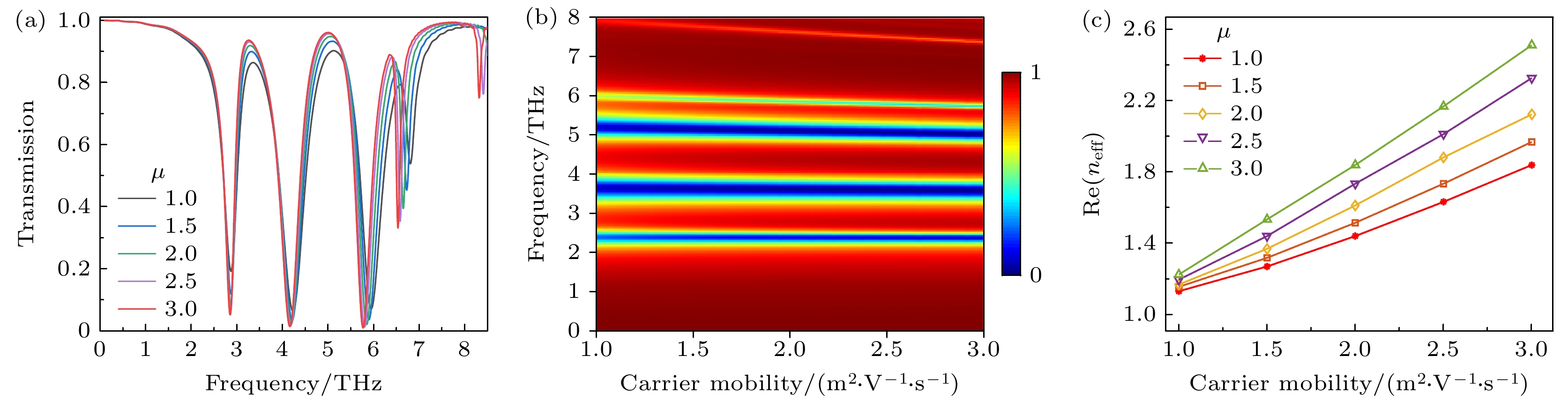
式中vF为费米速度, 其值为106 m/s; d为石墨烯层到电极之间的距离; ε0和εSi分别为真空介电常数和硅的介电常数. 时域有限差分法计算的透射光谱如图4(a)中的蓝色曲线所示, 与红色曲线的耦合模理论结果高度吻合. 当石墨烯的费米能级以0.1 eV的增量变化时, 透射谷几乎呈现出线性的蓝移, 如图4(a)中的橙色线所示. 而图4(b)清晰地展示了透射谱在不同费米能级下的连续演化过程, 进一步证明了该三重PIT的动态可调性.
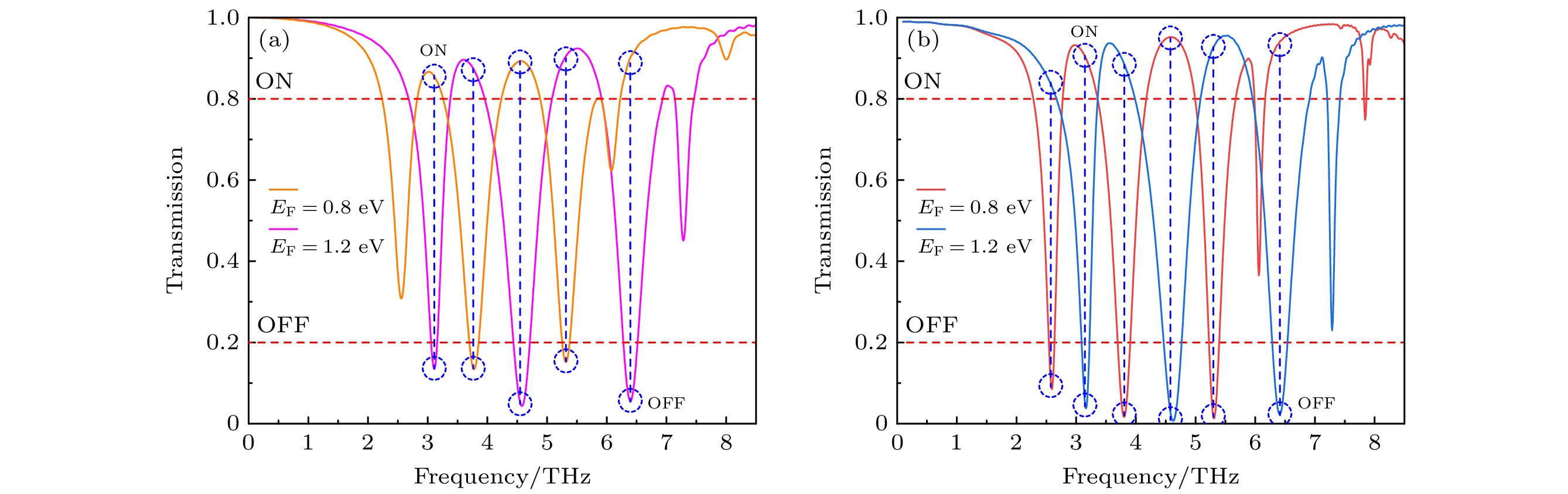
随着费米能级的增大, 透射谱呈现出蓝移, 利用此特性可以实现光开关的操作, 如图5(a)所示. 在光开关设计中, 把透射阈值位于0.2以下和0.8以上分别定义为“OFF”和“ON”. 当费米能级EF = 0.8 eV时, 频率点3.12 THz, 4.58 THz, 6.41 THz表现为“ON”的状态, 而频率点3.77 THz, 5.32 THz则表现为“OFF”的状态. 当费米能级EF = 1.2 eV时, “ON”与“OFF”状态完全反转, 从而实现了五频异步光开关的功能. 同时, 调制深度(DM)、退相时间(TD)、插入损耗(LI)和消光比(RE)是评估光开关性能的重要参数[50,51], 具体可以利用如下公式计算[16,52,53]:
其中, Tmax表示频率点最大透射值, 对应“ON”状态; Tmin则表示最小透射值, 对应光开关“OFF”状态;
$ \Delta f $ 为频谱半高宽. 由此可得五频异步光开关的性能指标: 当频率点为3.12 THz, 3.77 THz, 4.58 THz, 5.32 THz和6.41 THz时, DM分别为85.46%, 86.01%, 96.02%, 84.60%和95.12%; LI分别是0.14 dB, 0.31 dB, 0.11 dB, 0.18 dB和0.26 dB; TD对应为3.57 ps, 4.75 ps, 4.08 ps, 3.19 ps和3.70 ps; RE分别是8.02 dB, 8.12 dB, 13.15 dB, 7.75 dB和12.03 dB.除了通过调节费米能级优化透射谱外, 还可以通过掺杂等方法提升石墨烯的载流子迁移率, 从而进一步改善透射谱特性. 随着载流子迁移率的增大, 透射谱中的高频透射谷出现了轻微的红移, 如图6(a)所示. 产生这种现象的原因是Re(neff)随着载流子迁移率的增大而增大, 从而使得谐振频率的降低, 进而产生红移, 并且这种现象在高频表现得更明显, 如图6(c)所示. 但是由于该结构的Re(neff)较小, 导致红移现象对载流子的变化不敏感. 利用此特性可以对多频异步光开关的性能进行优化, 并且实现多频异步光开关之间的相互转换.
六频异步光开关如图5(b)所示, 当费米能级EF = 0.8 eV时, 频率点2.56 THz, 3.77 THz, 5.32 THz表现为“OFF”, 而频率点3.12 THz, 4.58 THz, 6.41 THz则表现为“ON”, 实现了五频异步光开关向六频异步光开关的动态转变. 此外, 相关性能也得到了显著的优化, 各个频率点的DM分别提升至94.53%, 95.96%, 99.31%, 98.21%, 98.65%, 96.45%; IL对应为0.70 dB, 0.29 dB, 0.17 dB, 0.21 dB, 0.18 dB, 0.12 dB; TD数值为7.12 ps, 5.34 ps, 4.56 ps, 3.16 ps, 5.97 ps, 3.73 ps; 同时RE也分别提升至9.89 dB, 13.77 dB, 17.26 dB, 21.53 dB, 18.24 dB, 16.11 dB. 两种多频异步光开关详细的DM, TD, LI, RE性能参数如表1所列.
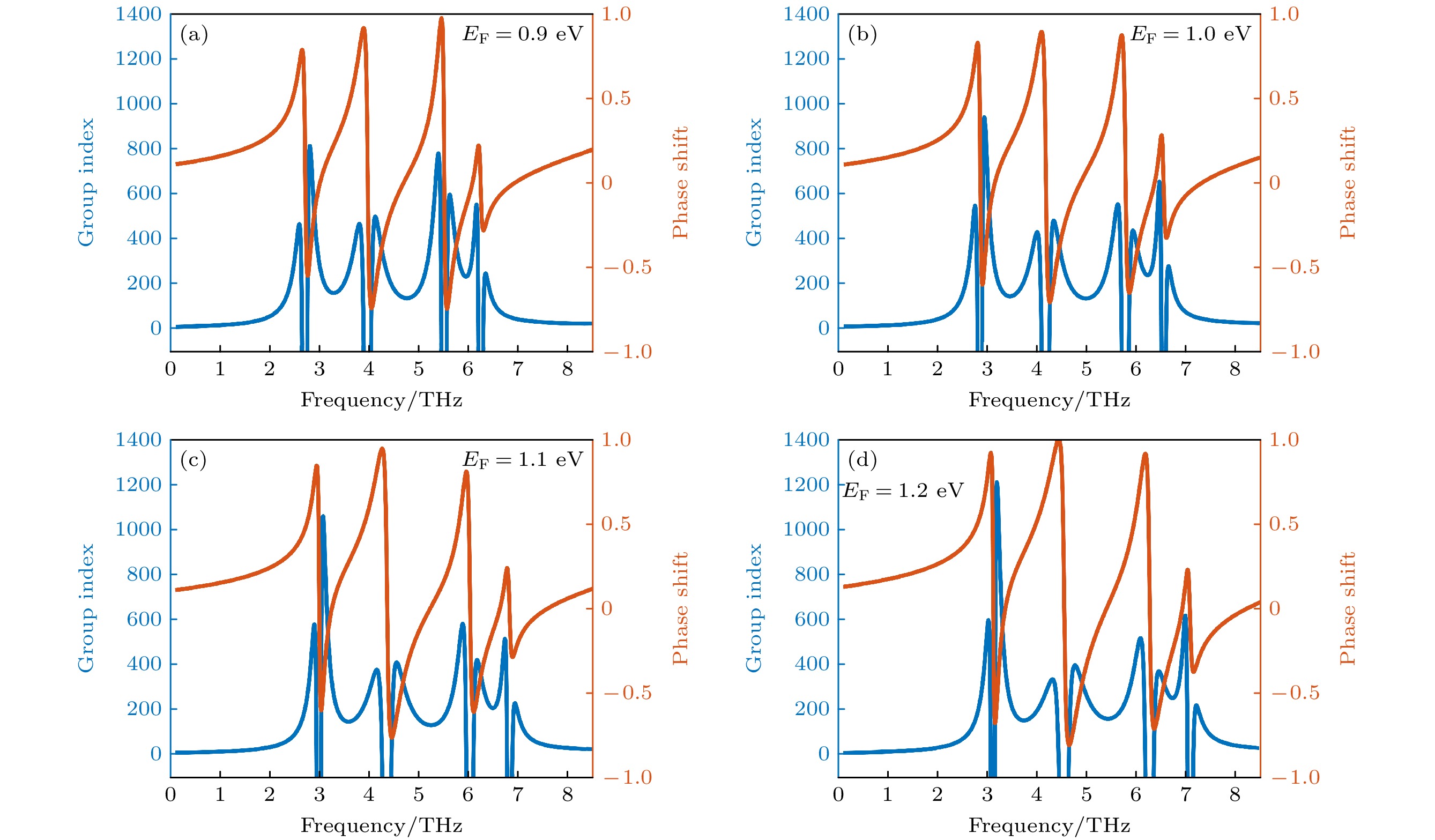
此外, 载流子迁移率增加导致电子活性的增强, 使得透射峰和透射谷的强度有着显著的变化, 如图6(a)所示. 伴随着透射谱压缩, PIT的峰值变得尖锐, 使得结构的色散特性加剧, 引起透射相位的突变. 利用该机理可以实现优异的慢光效应, 而群折射率ng是衡量慢光效应的重要参数. ng越大, 表明器件的慢光效应越好[54]. 而当ng显著减小甚至呈现负值时, 系统表现出快光效应. 由于受到信息速度的限制[55], 尽管群速度可以超过光速, 但是信息速度是由光的相速度决定, 根据相速度公式
$ {v_{\text{p}}} = \omega /k = c/n $ (n为介质折射率)可知, 信息传递速度无法超越真空中的光速. 此外, 由于实现快光的实验条件苛刻, 因此负群折射率的相关研究并不满足器件的实际应用. 其中, 系统的群折射率ng可以利用以下公式计算[56]:式中, c为真空中的光速, vg为群速度, θ(ω) = arg(t)为透射相移, ω为角频率, l为硅衬底的厚度, k为光的波矢. 其中, 石墨烯的载流子迁移率固定为μ = 3.0 m2/(V·s). 通过研究发现, 改变石墨烯的费米能级可以有效地实现对慢光效应的调控, 当费米能级为1.2 eV时, 最大调制范围可以达到2.5—7.1 THz. 同时群折射率均有不同程度上的增强, 最高可以达到1212, 如图7所示. 其中, 慢光性能较强的频率调控范围主要在2.8 THz—3.1 THz, 4.0 THz—4.6 THz, 5.5 THz—6.3 THz, 6.4 THz—7.1 THz波段, 其群折射率波动范围分别为421 < ng1 < 1212, 402 < ng2 < 425, 452 < ng3 < 791, 431 < ng4 < 601.
为了更直观地体现该结构性能的优异, 将其同其他器件进行一系列的对比[30,31,57–63], 如表2所列. 结果表明, 该结构在各个方面性能优势明显. 在制造方面采用单层石墨烯结构, 相较于多层石墨烯来说制备更容易. 此外, 群折射率也相对更高, 所表现出来的慢光特性更加优异. 较大的调制深度, 较小的插入损耗和退相时间使得该结构为优异的光开关制备提供了理论指导.
-
综上所述, 该单层图案化的石墨烯结构能够在太赫兹波段被入射光激发, 表现出显著的三重PIT效应. 理论分析表明, 其成因源于两个单PIT效应之间的协同作用. 通过进一步研究, 揭示了不同费米能级和载流子迁移率对光开关性能的影响, 成功实现了多频光开关之间的动态转换. 其中, 六频光开关所展现的调制深度(94.53% < DM < 99.31%)、插入损耗(0.70 dB < LI < 0.12 dB)、退相时间(7.12 ps < TD < 3.16 ps)和消光比(9.89 dB < RE < 21.53 dB)非常优异. 进一步研究发现, 该石墨烯结构还具有优异的慢光特性, 当其调控范围集中在2.8 THz—3.1 THz频段时, 对应群折射率变化范围分别为421 <ng1 < 1212, 为慢光器件的研究提供了新的思路和潜在应用途径.
基于协同效应的等离子体诱导透明及光开关与慢光应用
Synergy-based plasmon-induced transparency and optical switch and slow light applications
-
摘要: 传统的多重等离子体诱导透明效应(plasmon induced transparency, PIT)的产生依赖于多个明暗模之间的耦合. 然而, 为了打破明暗模这一传统机制, 探索一种新的产生方式迫在眉睫. 本文提出一种由纵向石墨烯带和3个横向石墨烯条组成单层石墨烯超表面, 它能够通过两个单PIT之间的协同效应激发出三重PIT. 深入研究发现, 该三重PIT的物理本质源于两个单PIT之间的非相干耦合. 通过调整石墨烯的费米能级和载流子迁移率, 成功实现五频异步光开关向六频异步光开关的动态转换, 其中六频异步光开关的性能非常优异: 当频率点为3.77 THz和6.41 THz时, 调制深度和插入损耗分别达到99.31%和0.12 dB; 当频率点为4.58 THz时, 退相时间和消光比分别为3.16 ps和21.53 dB. 此外, 当调控范围集中在2.8—3.1 THz波段时, 该三重PIT体系能够展现出高达1212的群折射率. 基于以上结果, 说明该石墨烯结构有望为性能优异的慢光设备、光开关等光学器件设计提供新的理论指导.Abstract: Surface plasmons (SPs) are generated by the interaction of conduction electrons on the surface of a metallic medium with photons in light wave, and they have an important phenomenon called plasmon-induced transparency (PIT). The PIT effect is crucial for improving the performance of nano-optical devices by strengthening the interaction between light and matter, thereby enhancing coupling efficiency. As is well known, traditional PIT is mainly achieved through two main ways: either through destructive interference between bright and dark modes, or through weak coupling between two bright modes. Therefore, it is crucial to find a new excitation method to break away from these traditional approaches. In this work, we propose a single-layer graphene metasurface composed of longitudinal graphene bands and three transverse graphene strips, which can excite a tripe-PIT through the synergistic effect between two single-PITs. We then leverage the synergistic effect between these two single-PITs to realize a triple-PIT. This approach breaks away from the traditional method of generating PIT through the coupling of bright and dark modes. The numerical simulation results are also obtained using the finite-difference time-domain, which are highly consistent with the results of the coupled-mode theory, thereby validating the accuracy of the results. In addition, by adjusting the Fermi level and carrier mobility of graphene, the dynamic transition from a five-frequency asynchronous optical switch to a six-frequency asynchronous optical switch is successfully achieved. The six-frequency asynchronous optical switch demonstrates exceptional performance: at frequency points of 3.77 THz and 6.41 THz, the modulation depth and insertion loss reach 99.31% and 0.12 dB, respectively, while at the frequency point of 4.58 THz, the dephasing time and extinction ratio are 3.16 ps and 21.53 dB, respectively. Additionally, when the tuning range is from 2.8 THz to 3.1 THz band, the triple-PIT system exhibits a remarkably high group index of up to 1212. These performance metrics exceed those of most traditional slow-light devices. Based on these results, the structure is expected to provide new theoretical ideas for designing high-performance devices, such as optical switches and slow-light devices.
-
Key words:
- plasmon-induced transparency /
- synergistic effect /
- optical switch /
- slow-light .
-

-
图 1 (a)石墨烯超材料模型结构的全视图; (b)石墨烯结构侧视图; (c)石墨烯结构俯视图, Lx = Ly = 4 μm, m1 = 2.2 μm, m2 = 2.3 μm, m3 = 0.6 μm, s1 = 0.4 μm, s2 = 0.25 μm, w1 = 0.8 μm, w2 = 0.6 μm; (d)石墨烯结构的制备流程图
Figure 1. (a) Full view of the graphene metamaterial model structure; (b) side view of graphene structure; (c) top view of graphene structure, Lx = Ly = 4 μm, m1 = 2.2 μm, m2 = 2.3 μm, m3 = 0.6 μm, s1 = 0.4 μm, s2 = 0.25 μm, w1 = 0.8 μm, w2 = 0.6 μm; (d) flow chart for the preparation of graphene structures.
图 3 (a), (b)不同石墨烯阵列的透射光谱; (c)整体结构形成的三重PIT透射谱(EF = 1 eV, μ = 1.0 m2/(V·s)); (d) dip 1, dip 2, dip 3, dip 4对应共振频率下的电场分布图
Figure 3. (a), (b) Transmission spectra of the different arrays; (c) triple-PIT transmission spectra formed by the overall structure (EF = 1 eV, μ = 1.0 m2/(V·s)); (d) plot of the electric field distribution at the corresponding resonance frequencies for dip 1, dip 2, dip 3, and dip 4.
图 5 (a)费米能级处于0.8 eV, 1.2 eV时, 载流子迁移率μ = 1.0 m2/(V·s)情况下五频异步光开关的调制, 其中“ON”表示“打开”, “OFF”表示“关闭”; (b)费米能级处于0.8 eV, 1.2 eV, 迁移率μ = 3.0 m2/(V·s)情况下的六频光开关调制
Figure 5. (a) Modulation of a five-frequency asynchronous optical switch with carrier mobility μ = 1.0 m2/(V·s) at Fermi energy levels of 0.8 eV, 1.2 eV, where “ON” means “open”, “OFF” means “close”; (b) six-frequency asynchronous optical switch modulation with Fermi energy levels at 0.8 eV, 1.2 eV and mobility μ = 3.0 m2/(V·s).
表 1 不同频率下DM, TD, LI, RE参数
Table 1. DM, TD, LI, RE parameters at different frequencies.
μ = 1.0 m2/(V·s) μ = 3.0 m2/(V·s) Frequency/THz DM/% LI/dB TD/ps RE/dB Frequency/THz DM/% LI/dB TD/ps RE/dB 3.12 85.46 0.14 3.57 8.02 2.56 94.53 0.70 7.12 9.89 3.77 86.01 0.31 4.75 8.12 3.12 95.96 0.29 5.34 13.77 4.58 96.02 0.11 4.08 13.15 3.77 99.31 0.17 4.56 17.26 5.32 84.60 0.18 3.19 7.75 4.58 98.21 0.21 3.16 21.53 6.41 95.12 0.26 3.70 12.03 5.32 98.65 0.18 5.97 18.24 6.41 96.45 0. 12 3.73 16.11 表 2 不同图案化石墨烯的性能比较
Table 2. Comparison of the properties of different patterned graphene.
Ref./year Modulation mode Material structure Group index DM/% LI/dB TD/ps RE/dB [57]/2020 Dual-frequency Single-layer patterned graphene 358 93.0 0.32 — — [58]/2020 Multiple-frequency Single-layer patterned graphene — 77.7 — — 12.5 [59]/2021 Multiple-frequency Single-layer patterned graphene 321 92.0 — 3.2 — [31]/2022 Multiple-frequency Single-layer patterned graphene — 99.9 0.33 0.848 — [60]/2022 Multiple-frequency Single-layer patterned graphene 1100 97.1 0.04 — — [61]/2023 Multiple-frequency Single-layer patterned graphene — 97.7 5.4 3.86 16.41 [62]/2023 Multiple-frequency Monolayer patterned black phosphorus 219 — — 0.22 — [63]/2024 Multiple-frequency Single-layer patterned graphene 1000 87.5 — — — [30]/2024 Multiple-frequency Single-layer patterned graphene 781 98.0 0.51 — — This work Multiple-frequency Single-layer patterned graphene 1212 99.3 0.120 3.16 21.53 -
[1] Barnes W L, Dereux A, Ebbesen T W 2003 Nature 424 824 doi: 10.1038/nature01937 [2] Ebbesen T W, Genet C, Bozhevolnyi S I 2008 Phys. Today 61 44 doi: 10.1063/1.2930735 [3] He Z H, Li Z X, Li C J, Xue W W, Cui W 2020 Opt. Express 28 17595 doi: 10.1364/OE.395640 [4] Xia S X, Zhai X, Wang L L, Wen S C 2018 Photonics Res. 6 692 doi: 10.1364/PRJ.6.000692 [5] Gramotnev, Dmitri K, Bozhevolnyi, Sergey I 2010 Nat. Photonics 4 83 doi: 10.1038/nphoton.2009.282 [6] Xu H, Chen Z Q, He Z H, Nie G Z, Li D Q 2020 New J. Phys. 22 123009 doi: 10.1088/1367-2630/abcc1c [7] Gao E D, Liu Z M, Li H J, Xu H, Zhang Z B, Luo X, Xiong C X, Liu C, Zhang B H, Zhou F Q 2019 Opt. Express 27 13884 doi: 10.1364/OE.27.013884 [8] Fan X B, Wang G P 2006 Opt. Lett. 31 1322 doi: 10.1364/OL.31.001322 [9] Cui W, Li C J, Ma H Q, Xu H, Yi Z, Ren X H, Cao X L, He Z H, Liu Z H 2021 Physica E 134 114850 doi: 10.1016/j.physe.2021.114850 [10] Li Z L, Xie M X, Nie G Z, Wang J H, Huang L J 2023 J. Phys. Chem. Lett. 14 10762 doi: 10.1021/acs.jpclett.3c02763 [11] Li Z L, Nie G Z, Wang J H, Fang Z, Zhan S P 2024 Phys. Rev. Appl. 21 034039 doi: 10.1103/PhysRevApplied.21.034039 [12] 向星诚, 马海贝, 王磊, 田达, 张伟, 张彩虹, 吴敬波, 范克彬, 金飚兵, 陈健 吴培亨 2023 物理学报 72 128701 doi: 10.7498/aps.72.20230080 Xiang X C, Ma H B, Wang L, Tian D, Zhang W, Zhang C H, Wu J B, Fan K B, Jin B B, Chen J, Wu P H 2023 Acta Phy. Sin. 72 128701 doi: 10.7498/aps.72.20230080 [13] Rodrigo D, Limaj O, Janner D, Etezadi D, García de Abajo F J, Pruneri V, Altug H 2015 Science 349 165 doi: 10.1126/science.aab2051 [14] Chen P Y, Argyropoulos C, Farhat M, Gomez-Diaz J S 2017 Nanophotonics 6 1239 doi: 10.1515/nanoph-2016-0137 [15] D’Apuzzo F, Piacenti A R, Giorgianni F, Autore M, Guidi M C, Marcelli A, Schade U, Lto Y, Chen M W, Lupi S 2017 Nat. commun. 8 14885 doi: 10.1038/ncomms14885 [16] Sun Z P, Martinez A, Wang F 2016 Nat. Photonics 10 227 doi: 10.1038/nphoton.2016.15 [17] Vakil A, Engheta N 2011 Science 332 1291 doi: 10.1126/science.1202691 [18] Jablan M, Buljan H, Soljacic M 2009 Phys. Rev. 80 245435 doi: 10.1103/PhysRevB.80.245435 [19] Wang J Y, Zhao R Q, Yang M M, Liu Z F, Liu Z R 2013 J. Chem. Phys. 138 084701 doi: 10.1063/1.4792142 [20] Gan C H, Chu H S, Li E P 2012 Phys. Rev. B Condens. Matter 85 125431 doi: 10.1103/PhysRevB.85.125431 [21] Grigorenko A N, Polini M, Novoselov K S 2012 Nat. photonics 6 749 doi: 10.1038/nphoton.2012.262 [22] Yan H G, Low T, Zhu W J, Wu Y Q, Freitag M, Li X S, Guinea F, Avouris P, Xia F N 2013 Nat. Photonics 7 394 doi: 10.1038/nphoton.2013.57 [23] Lu H, Liu X M, Mao D 2012 Phys. Rev. A 85 53803 doi: 10.1103/PhysRevA.85.053803 [24] Zhao X L, Zhu L, Yuan C, Yao J Q 2016 Opt. Lett. 41 5470 doi: 10.1364/OL.41.005470 [25] Adato R, Artar A, Erramilli S, Altug H 2013 Nano. Lett. 13 2584 doi: 10.1021/nl400689q [26] Boller K J, Imamoğlu A, Harris S E 1991 Phys. Rev. Lett. 66 2593 doi: 10.1103/PhysRevLett.66.2593 [27] Kim T T, Kim H D, Zhao R K, Oh S S, Ha T, Chung D S, Lee Y H, Min B, Zhang S 2018 Acs. Photonics 5 1800 doi: 10.1021/acsphotonics.7b01551 [28] Jiang W J, Chen T 2021 Diam. Relat. Mater. 118 108531 doi: 10.1016/j.diamond.2021.108531 [29] Zhu J, Xiong J Y 2023 Measurement 220 113302 doi: 10.1016/j.measurement.2023.113302 [30] Lei P L, Nie G Z, Li H L, Li Z L, Peng L, Tang X F, Gao E D 2024 Phys. Scr. 99 075512 doi: 10.1088/1402-4896/ad5120 [31] Zhou X W, Xu Y P, Li Y H, Cheng S B, Yi Z, Xiao G H, Wang Z Y, Chen Z Y 2022 Commun. Theor. Phys. 74 115501 doi: 10.1088/1572-9494/ac8a41 [32] Li J Y, Weng J, Li J Q, Chen S X, Guo Z C, Xu P B, Liu W J, Wen K H, Qin Y W 2022 J. Phys. D 55 445101 doi: 10.1088/1361-6463/ac8be0 [33] Li Y H, Xu Y P, Jiang J B, Cheng S B, Yi Z, Xiao G H, Zhou X W, Wang Z Y, Chen Z Y 2023 Phys. Chem. Chem. Phys. 25 3820 doi: 10.1039/D2CP05368C [34] Li Y H, Xu Y P, Jiang J B, Ren L Y, Cheng S B, Yang W X, Ma C J, Zhou X W, Wang Z Y, Chen Z Y 2022 J. Phys. D 55 155101 doi: 10.1088/1361-6463/ac48b0 [35] Zhang R L, Cui Z R, Wen K H, Lv H P, Liu W J, Li C Q, Yu Y S, Liu R M 2025 Opt. Commun. 574 131083 doi: 10.1016/j.optcom.2024.131083 [36] Zheng S Q, Zhao Q X, Peng L, Jing X 2021 Results Phys. 23 104040 doi: 10.1016/j.rinp.2021.104040 [37] Zhang B H, Li H J, Xu H, Zhao M Z, Xiong C X, Liu C, Wu K 2019 Opt. Express 27 3598 doi: 10.1364/OE.27.003598 [38] Liu C, Li H J, Xu H, Zhao M Z, Xiong C X, Zhang B H, Wu K 2019 J. Phys. D 52 405203 doi: 10.1088/1361-6463/ab2d1e [39] Li M, Xu H, Yang X J, Xu H Y, Liu P C, He L H, Nie G Z, Dong Y L, Chen Z Q 2023 Results Phys. 52 106798 doi: 10.1016/j.rinp.2023.106798 [40] Zheng L, Cheng X H, Cao D, Wang G, Wang Z J, Xu D W, Xia C, Shen L Y, Yu Y H, Shen D S 2014 ACS Appl. Mater. 6 7014 doi: 10.1021/am501690g [41] Zheng L, Cheng X H, Cao D, Wang Z J, Xu D W, Xia C, Shen L Y, Yu Y H 2014 Mater. Lett. 137 200 doi: 10.1016/j.matlet.2014.08.146 [42] Li X S, Cai W W, An J, Kim S, Nah J, Yang D X, Piner R, Velamakanni A, Jung I, Tutuc E, Banerjee S, Colombo L, Ruoff R 2009 Science 324 1312 doi: 10.1126/science.1171245 [43] Yin Y, Alivisatos A P 2005 Nature 437 664 doi: 10.1038/nature04165 [44] Norris D J, Efros A L, Erwin S C 2008 Science 319 1776 doi: 10.1126/science.1143802 [45] Chen Y F, Johnson E, Peng X G 2007 J. Am. Chem. Soc. 129 10937 doi: 10.1021/ja073023n [46] Wu D, Wang M, Feng H, Xu Z X, Liu Y P, Xia F, Zhang K, Kong W J, Dong L F, Yun M J 2019 Carbon 155 618 doi: 10.1016/j.carbon.2019.09.024 [47] Falkovsky L A, Varlamov A A 2007 Eur. Phys. J. B 56 281 doi: 10.1140/epjb/e2007-00142-3 [48] Rouhi N, Capdevila S, Jain D, Zand K, Wang Y Y, Brown E, Jofre L, Burke P 2012 Nano Res. 5 667 doi: 10.1007/s12274-012-0251-0 [49] Cheng H, Chen S Q, Yu P, Duan X Y, Xie B Y, Tian J G 2013 Appl. Phys. Lett. 103 203112 doi: 10.1063/1.4831776 [50] Yu S L, Wu X Q, Wang Y P, Guo X, Tong L M 2017 Adv. Mater. 29 1606128. doi: 10.1002/adma.201606128 [51] Koester S J, Li H, Li M 2012 Opt. Express 20 20330 doi: 10.1364/OE.20.020330 [52] Lee S H, Choi M, Kim T T, Lee S, Liu M, Yin X B, Choi H K, Lee S S, Choi C G, Choi S Y, Zhang X, Min B 2012 Nat. Mater. 11 936 doi: 10.1038/nmat3433 [53] Chen S, Yi X, Ma H, Wang H 2003 Opt. Quantum Electron. 35 1351 doi: 10.1023/B:OQEL.0000009429.14136.3d [54] Lu Q, Wang Z Z, Huang Q Z, Jiang W, Wang Y, Xia J S 2017 J. Lightwave. Technol. 35 1710 doi: 10.1109/JLT.2017.2648819 [55] Boyd R W, Shi Z M 2015 Slow and Fast Light In Photonics: Scientific Foundations, Technology and Applications (Vol. 1) ( John Wiley & Sons, Inc.) pp363–385 [56] Zentgraf T, Zhang S, Oulton R F, Zhang X 2009 Phys. Rev. B 80 195415 doi: 10.1103/PhysRevB.80.195415 [57] Li M, Li H J, Xu H, Xiong C X, Zhao M Z, Liu C, Ruan B X, Zhang B H, Wu K 2020 New J. Phys. 22 103030 doi: 10.1088/1367-2630/abbaea [58] Zhang X, Liu Z, Zhang Z B, Gao E D, Luo X, Zhou F Q, Li H J, Zao Y 2020 Opt. Express 28 36771 doi: 10.1364/OE.410417 [59] Zhang X, Zhou F Q, Liu Z M, Zhang Z B, Qin Y P, Zhuo S S, Luo X, Gao E D, Li H J 2021 Opt. Express 29 29387 doi: 10.1364/OE.433258 [60] Xie Q, Guo L H, Zhang Z X, Gao P P, Wang M, Xia F, Zhang K, Sun P, Dong L F, Yun M J 2022 Appl. Surf. Sci. 604 154575 doi: 10.1016/j.apsusc.2022.154575 [61] Ji C, Liu Z M, Zhou F Q, Luo X, Yang G X, Xie Y D, Yang R H 2023 J. Phys. D: Appl. Phys. 56 405102 doi: 10.1088/1361-6463/ace1fd [62] Chang X, Li H J, Liu C, Li M, Ruan B X, Gao E D 2023 J Opt. Soc. Am. A 40 1545 doi: 10.1364/JOSAA.488335 [63] Xu H Y, Xu H, Yang X J, Li M, Yu H F, Cheng Y X, Zhan S P, Chen Z Q 2024 Phys. Lett. A 504 129401 doi: 10.1016/j.physleta.2024.129401 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: