-
自从Ohtomo和Hwang[1]在LaAlO3/SrTiO3异质结构界面发现高迁移率二维电子气(2DEG)以来, 研究人员在多种氧化物异质结界面相继发现了2DEG的存在[2–7]. 这些发现不仅为量子霍尔效应、界面超导等物理现象的研究提供了重要平台[8–11], 还为高迁移率晶体管和高灵敏度传感器等电子器件的研发提供了新的途径. 目前, 氧化物异质界面的2DEG主要存在于两类体系中: 一类是以钙钛矿氧化物为基底的异质结, 如LaAlO3/SrTiO3[1,12], γ-Al2O3/SrTiO3[4,13], LaTiO3/KTaO3[5]以及EuO/KTaO3[7]等; 另一类则是由二元半导体氧化物 所构成的异质结, 包括MgxZn1–xO/ZnO[2,14,15]和(AlxGa1–x)2O3/Ga2O3[6]等. 对于前者, 其界面上2DEG的导电电子由Ti 3d (或Ta 5d)轨道贡献. 低温下, 导电电子主要分布在能量较低的dxy带上, 因此具有较高的迁移率. 然而, 随着温度的升高, 电子-声子耦合和带间跃迁会使简并的dxz和dyz带参与导电, 导致电子迁移率急剧下降[16,17], 例如, 对于γ-Al2O3/SrTiO3异质结, 在2 K时电子迁移率可达1.4×105 cm2/(V·s), 而在室温则降低到10 cm2/(V·s)以下[4]. 相比之下, 第二类异质结因其导带底由非简并s轨道贡献, 展现出更优异的室温载流子迁移率, 例如, Mgx Zn1–xO/ZnO界面处的2DEG在室温下的迁移率高达250 cm2/(V·s)[2], 而 (AlxGa1–x)2O3/Ga2O3异质结中的2DEG室温迁移率也达到了180 cm2/(V·s)[6], 这些数值远高于以钙钛矿氧化物为基底的异质结. 因此, 为寻找室温下具有高迁移率的2DEG, 有必要探讨其他二元半导体氧化物构成的异质结界面是否也能够产生2DEG. 另一方面, 第一性原理计算解释了多种氧化物异质结界面2DEG的来源问题, 例如, Lee与Demkov[18]利用第一性原理计算, 发现LaAlO3/SrTiO3中的2DEG来源于界面处的极性不连续; Chen等[19]利用第一性原理计算成功解释了Mgx Zn1–xO/ZnO界面处2DEG的产生机制. 因此, 第一性原理计算已经成为探索异质结界面二维电子气起源的重要工具.
SnO2是一种具有金红石结构的直接带隙氧化物半导体, 其带隙值约为3.6 eV[20], 具有较高的室温载流子迁移率[21]. 通常情况, 宽带隙材料与窄带隙材料构成的异质结在界面处会发生能带弯曲现象, 可促进电子向界面附近的积累, 这有利于2DEG的形成[22,23]. HfO2的带隙值(Eg = 5.7 eV[24])比SnO2更宽, 常以单斜相形式存在. 但理论和实验 均表明, 四方相的HfO2也可稳定存在[25,26]. 因此, 本文选用金红石结构的HfO2与SnO2构成异质结构, 系统研究异质结界面的电子结构, 探索材料中的缺陷、表面吸附等对HfO2/SnO2界面电子结构的影响.
-
本文所有计算均使用VASP软件包进行, 计算过程中, 用投影缀加波(PAW)赝势处理离子实与电子之间的相互作用, 选用Perdew-Burke-Ernzerhof (PBE)函数参数化的广义梯度近似(GGA)处理交换关联能, 并用Monkhorst-Pack法对布里渊区进行k点取样[27–30]. 电子能量收敛精度设置为1×10–5 eV, 完全弛豫结构中每个原子上的力小于0.02 eV/Å. 根据收敛测试, k点设置为3×5×1, 平面波截断能设置为420 eV[31].
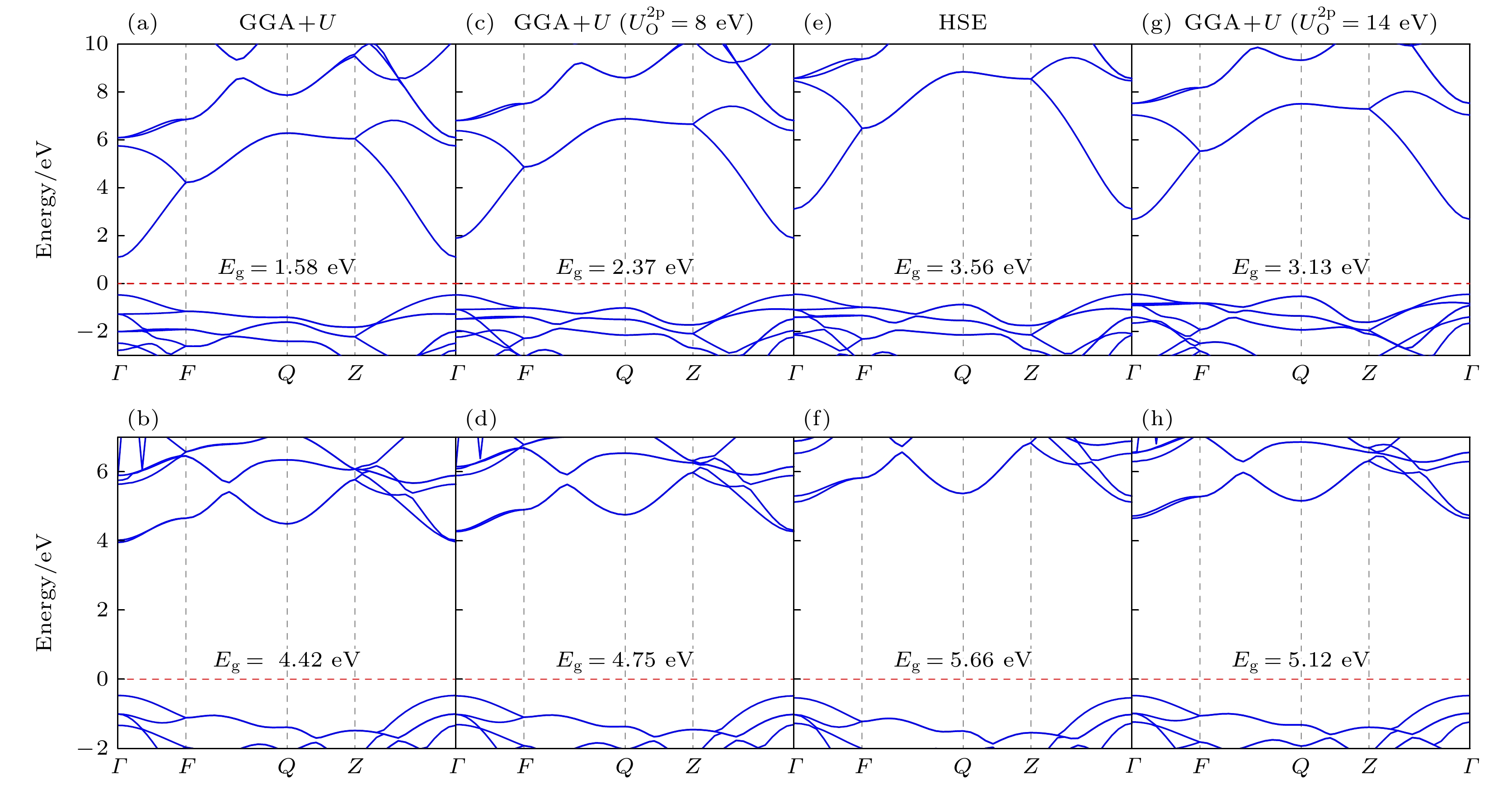
在计算过程中, HfO2/SnO2异质结中Sn, Hf和O原子使用的电子构型分别为5s25p2, 5d26s2及2s22p2, 其中, SnO2中Sn 4d电子态也被当作价态来处理[32–34]. 对于半导体而言, 密度泛函理论(DFT)方法的主要缺陷是低估材料的带隙[35], 因此本文的计算采用GGA+U方法 (这里U为Hubbard 相互作用参数). 根据Singh等[32]和Pavoni等[36]的计算经验, 本工作首先将Sn 4d和Hf 5d轨道的U值分别设定为3.5 eV和5.0 eV, 此U值设置记为GGA+U. 计算所得SnO2和HfO2的带隙值分别为1.58 eV和4.42 eV, 如图1(a)和图1(b)所示, 均分别小于SnO2和HfO2的实验带隙值(Eg(SnO2) = 3.6 eV[20], Eg(HfO2) = 5.7 eV[24]). 近期, Akbar等[37]发现, 在O 2p轨道添加U能够进一步修正SnO2的带隙, 同时, Li等[38]研究的结果也表明, 在O 2p轨道加U同样能进一步增加HfO2的带隙值. 因此, 在固定Sn 4d和Hf 5d轨道的U值的基础上, 进一步在SnO2和HfO2的O 2p轨道加U. 计算结果显示, 随O 2p轨道上U值的增加, SnO2和HfO2的带隙均逐渐增加. 但SnO2价带顶附近的能量-动量色散关系会受到影响, 即价带顶的“F—Q—Z ”高对称点路径处“凸起”, 并且这种“凸起”会随着O 2p轨道上U值的增加而增大. 当O 2p轨道上U值为8.0 eV时, 虽然计算所得到的SnO2和HfO2的带隙值分别为2.37 eV和4.75 eV (仍小于实验带隙值Eg (SnO2) = 3.6 eV[20], Eg (HfO2) = 5.7 eV[24]), 但得到的SnO2和HfO2的能量-动量色散关系(图1(c)和图1(d))与Heyd-Scuseria-Ernzerhof (HSE)方法获得的色散关系(图1(e)和图1(f))基本一致. 我们将此U值设置记
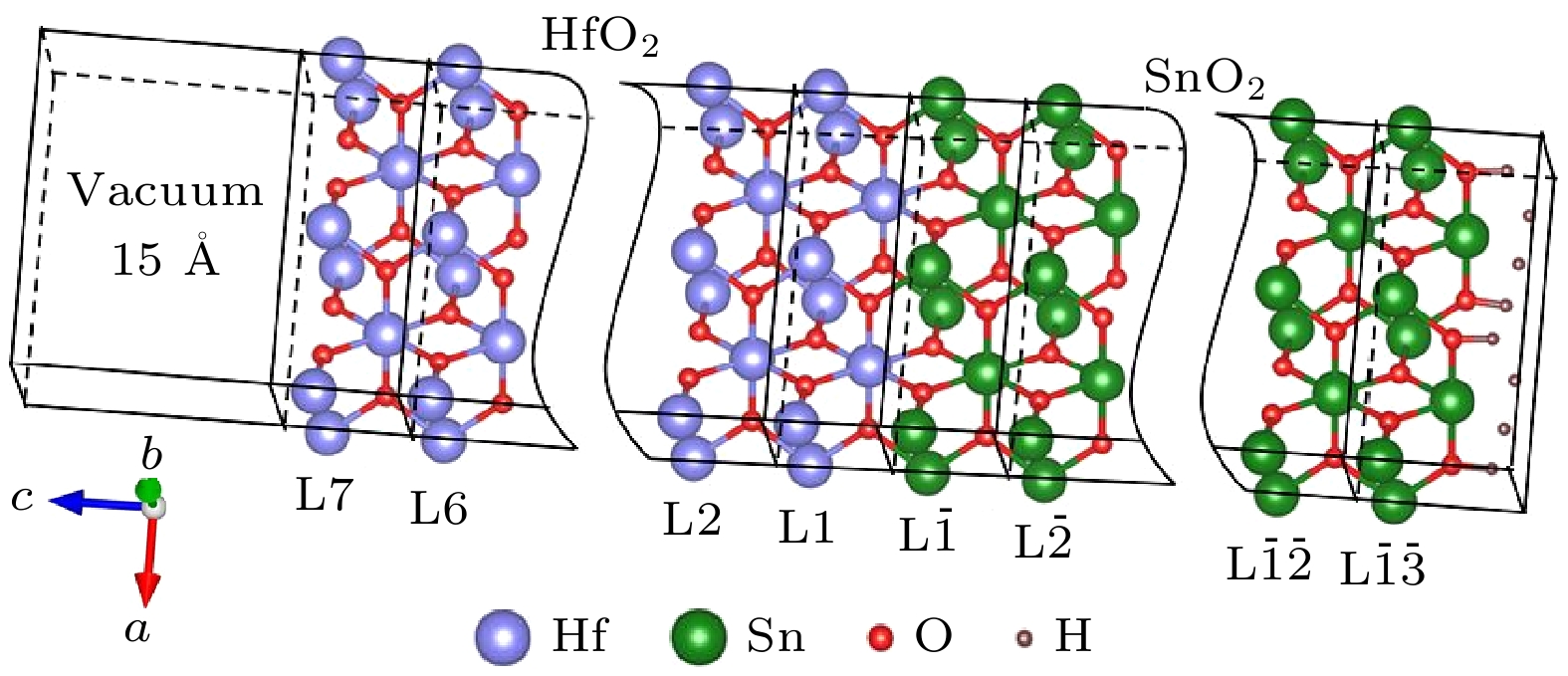
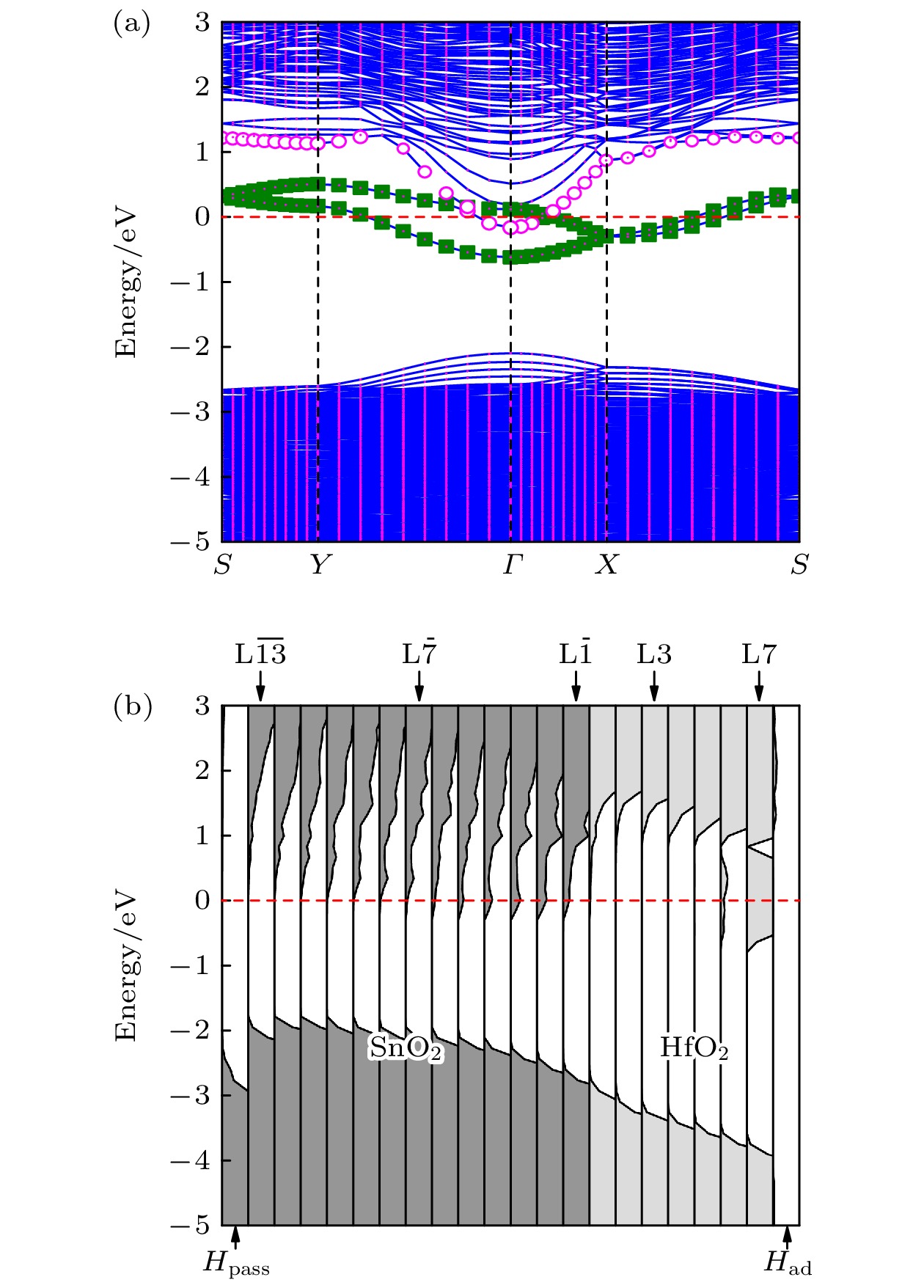
$U_{\text{O}}^{{\text{2p}}}= 8\;{\rm eV}$ 的GGA+U. 由于带边附近的能量-动量色散关系对材料的电输运性质起着至关重要的作用, 因此, 本文若不进行特别说明, 均是采用上述方法计算而得. 此外, 对O 2p轨道U值的测试结果还表明, 进一步增加O 2p轨道的U值能更有效地打开SnO2和HfO2的带隙. 基于此, 我们考虑在保持Sn 4d和Hf 5d轨道U值不变的前提下, 进一步增加O 2p轨道U值. 计算结果显示, O 2p轨道U值的进一步增加对SnO2带隙修正效果比HfO2更明显. 因此, 随O 2p轨道U值的增加, 计算所得SnO2和HfO2的带隙差会逐渐减小. 当O 2p轨道的U值设为14 eV时, 计算所得SnO2和HfO2的带隙差约2.0 eV, 与带隙差的实验值约2.1 eV接近[20,24]; 并且, SnO2和HfO2带隙的计算值分别为3.13 eV和5.12 eV(如图1(g)和图1(h)所示), 与它们带隙的实验值Eg(SnO2) = 3.6 eV[20]和Eg(HfO2) = 5.7 eV[24]分别相差13%和10%, 在可容忍范围. 因此, 为保证对两种材料所构成异质结界面的能带弯曲的准确描述, 将O 2p轨道U值设置为14 eV, 并记为$ U_{\text{O}}^{{\text{2p}}}= 14\;{\rm eV} $ 的GGA+U.为模拟在SnO2衬底上沿c轴生长的HfO2薄层与SnO2衬底所构成的异质结构, 选取了(001)面内2×1 HfO2/SnO2超胞结构. 图2是构建的沿(001)面法线的具有干净HfO2表面的(HfO2)7/(SnO2)13异质结构示意图. 该异质结构含有13 u.c. SnO2层和7 u.c. HfO2 层(这里u.c.为单胞unit cell的简写, 对于SnO2和HfO2(001)法线方向, 1 u.c. = 0.315 nm和0.338 nm), 并沿堆叠方向添加了15 Å真空层. 同时, 在SnO2侧, Sn—O表面端的O和Sn原子分别用带有2/3和4/3电荷的赝H原子进行了钝化. 这种钝化方法成功消除了SnO2侧的表面电子态, 从而能够合理模拟SnO2衬底. 为方便讨论, 对图2所示的异质结构进行编号, 以1 u.c.厚度记为一层, SnO2侧从界面开始到逐渐远离界面编号依次为
${\rm L}\overline {1} $ ,${\rm L}\overline {2} $ , ···,${\rm L}\overline {{13}} $ , HfO2侧从界面开始依次编号为L1, L2, ···, L7. 其中,${\rm L}\overline {1} $ 和L1层形成异质结的界面, L7为异质结的表面层. -
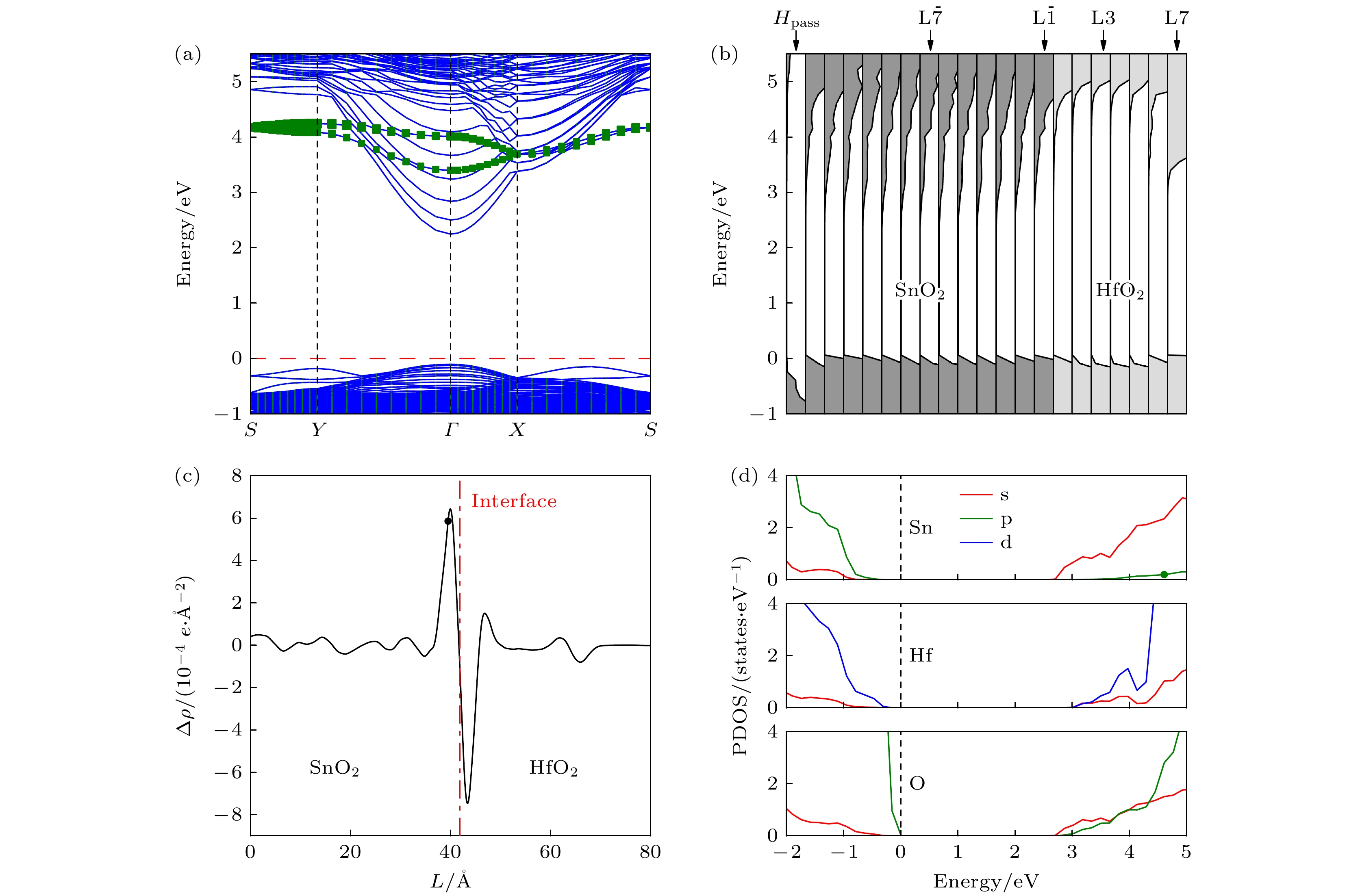
首先来探究具有干净HfO2表面的(HfO2)7/(SnO2)13异质结构的电子结构, 计算结果如图3所示. 图3(a)为(HfO2)7/(SnO2)13异质结构的能带结构. 可以看出, 费米能级位于带隙之中, 价带顶和导带底均位于
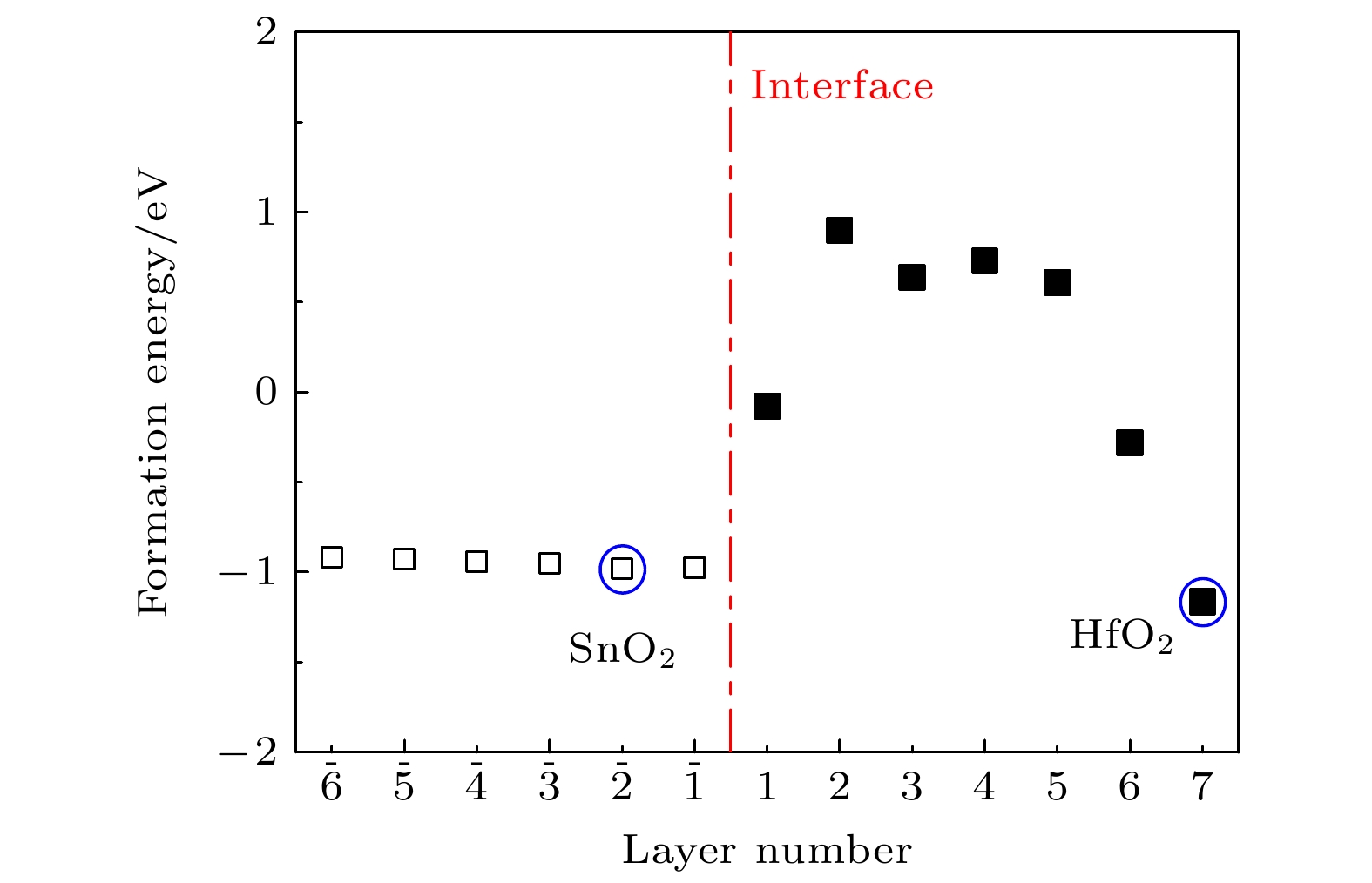
$\varGamma $ 点, 带隙值为2.35 eV, 显示直接带隙半导体特征. 在能带图中, 费米能级以上约3.35 eV到4.50 eV之间存在两条非抛物线能带 (如图中的方形点线所示), 其主要来源于表面层Hf原子的贡献, 这是由于表面不饱和悬键畸变所致. 图3(b)给出了(HfO2)7/(SnO2)13异质结各原子层的电子态密度图. 从图3(b)可以看出, SnO2和HfO2侧的各原子层的导带底均在费米能级以上, 其中SnO2侧${\rm L}\overline 2 $ 层的导带底能量最低, 位于费米能级以上2.17 eV处; 对于HfO2侧, 除HfO2的表面原子层外, 界面处(L1层)的导带底能量最低, 位于费米能级以上3.60 eV处. 上述结果表明, 在界面处SnO2的导带底和HfO2的导带底存在1.43 eV的能量突变, 异质结界面处导带底的不连续, 有利于电子在界面处积累而形成2DEG. 此外, HfO2表面层的导带底位于费米能级以上3.28 eV处, 该值明显低于HfO2侧其他原子层导带底的能量. 这是表面悬键所致, 与图3(a)的能带结果一致. 图3(c)为异质结平面平均电荷密度差. 可以看出, 异质结的界面处存在由HfO2侧向SnO2侧的电荷转移. 这是由于HfO2的费米能级高于SnO2的费米能级, 当两种材料接触形成异质结时, 电子转移会使得HfO2的费米能级下降, 使得SnO2的费米能级升高, 当两种材料的费米能级一致时电子将不再转移. 图3(d)为异质结的Sn, Hf, O原子轨道投影态密度图. 可以看出, 异质结的价带顶来源于O 2p轨道, 导带底主要由非简并的Sn 5s轨道贡献. 相比于导带底由三重简并的d轨道贡献的异质结, 如LaAlO3/SrTiO3和LaTiO3/KTaO3等, 这种非简并的s轨道可以大幅降低带间散射对迁移率的影响[16,39]. 因此, 在该异质结界面附近引入电子, 有望获得s轨道占据的导电电子, 进而得到高室温迁移率的2DEG.上述结果同时表明, 无缺陷的(HfO2)7/(SnO2)13异质结界面处不存在2DEG. 在氧化物异质结中, 氧空位可能会提供额外的电子, 从而改变电荷分布, 在界面处形成2DEG或增强界面处2DEG的浓度, 例如, 无缺陷的MgxZn1–xO/ZnO异质结界面处不会产生2DEG, 但引入氧空位会使界面处形成2DEG[19]; 在LaAlO3/SrTiO3异质结制备过程中, 氧分压越低, 低温下界面电阻越小, 载流子迁移率越高[40]. 同时, 氧空位是氧化物制备过程中的常见缺陷[41,42]. 因此, 我们考虑氧空位对(HfO2)7/(SnO2)13异质结电子结构的影响. 为计算方便, 考虑在(HfO2)7/(SnO2)13超胞中存在一个氧空位的情形. 图4为氧空位在不同位置时的形成能, 这里形成能的计算公式为
$ E_{\text{f}}=E_{\text{V}}-\left(E_0-n\mu_{\text{O}_{ }}\right) $ , 其中${E_{\text{V}}}$ 和${E_{0}}$ 分别为含氧空位和不含氧空位异质结构的总能量,$ \mu_{\text{O}_{ }} $ 为氧原子的化学势,$n$ 为氧空位的个数. 从图4可以看出: 在SnO2侧, 形成能均为负值, 且变化不大; 在HfO2侧, 随着氧空位位置逐渐远离界面, 形成能逐渐增加且为正值, 但在靠近表面时, 氧空位形成能急剧减小, 并且HfO2表面层的形成能甚至低于SnO2侧. 仔细观察发现, SnO2侧和HfO2侧氧空位形成能极小值位置分别位于$\overline {2} $ 层和L7层 (图中圆圈标记位置). 因此, 氧空位更易在界面附近SnO2侧的${\rm L}\overline {2} $ 层和HfO2侧表面(L7层)处形成.我们分别计算了氧空位存在于
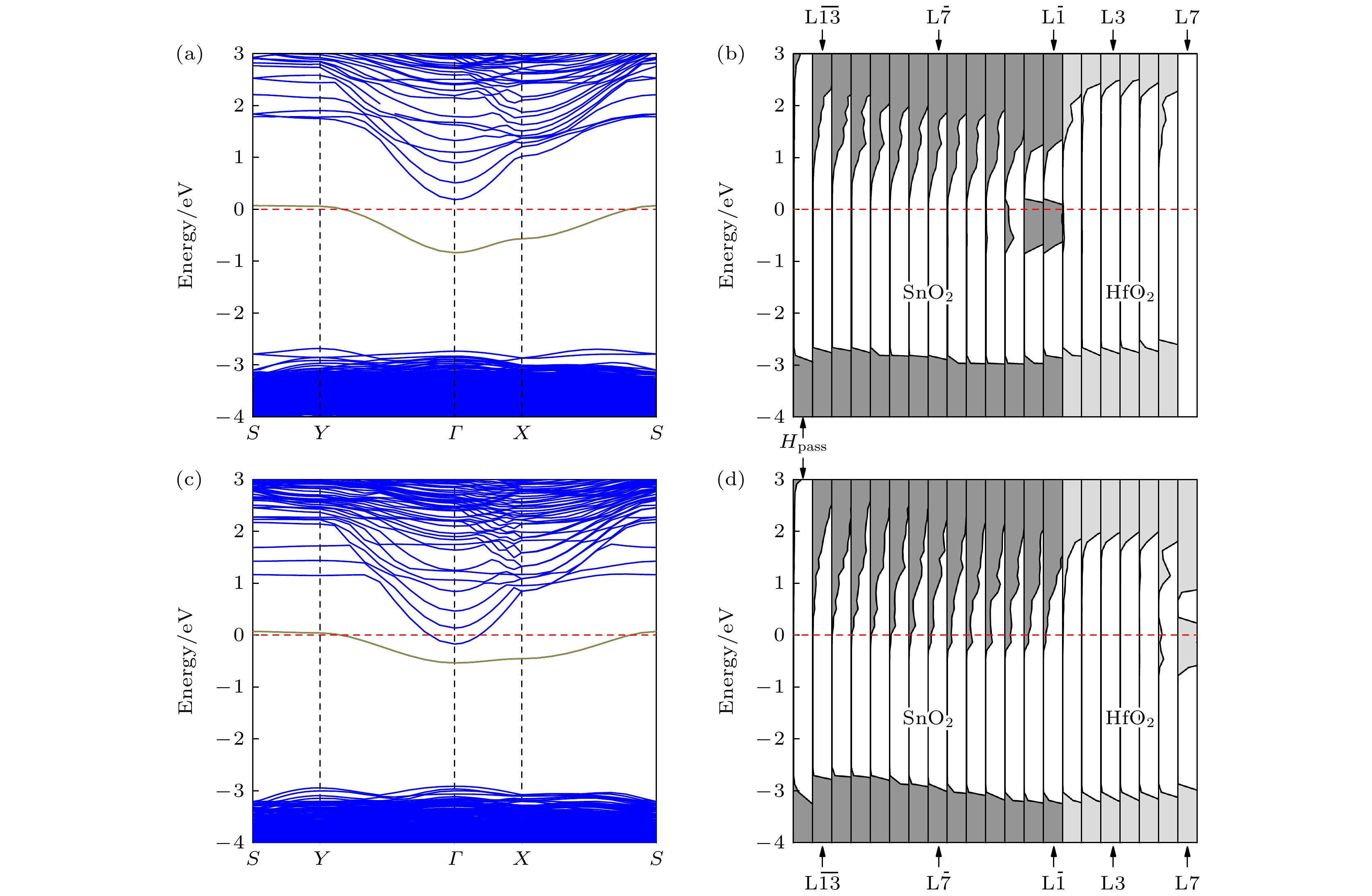
${\rm L}\overline {2} $ 和L7层时, (HfO2)7/(SnO2)13异质结构的电子结构, 为了更准确地描述缺陷能带与导带底的能量状态关系, 计算结果采用能够更好修正带隙的$U_{\text{O}}^{{\text{2p}}}=14 \;{\rm eV}$ 的GGA+U方法所得. 图5(a)和图5(b)分别为氧空位位于${\rm L}{{\overline 2}}$ 层时的(HfO2)7/(SnO2)13异质结的能带结构和原子层分解态密度图. 从图5(a)可以看出,${\rm L}{{\overline 2}}$ 层中空位缺陷引入了一个缺陷能带, 即图中棕实线标记的能带. 该缺陷能带的宽度约0.91 eV, 能带顶位于S点, 与位于Γ点的导带底的能量差为0.12 eV, 费米能级只穿过缺陷能带的顶部. 由于缺陷能带的顶部几乎为平带, 费米能级附近的电子具有很大的有效质量, 因而具有很小的迁移率. 因为缺陷能带靠近导带底, 当系统吸收外界热量时, 缺陷能带上的电子容易获得能量而跃迁到导带中, 从而引发跳跃导电. 综上所述,${\rm L}{{\overline 2}}$ 处存在氧空位会使异质结界面附近随着温度的升高具有一定的导电能力, 但导电性很差. 从图5(b)的分层态密度可以看出, 缺陷能级来自于异质结的${\rm L}\overline {1} $ —${\rm L}\overline {3} $ 层, 而异质结的导带底主要由SnO2侧${\rm L}\overline {4} $ —${\rm L}\overline {9} $ 层所贡献. 因此, 跳跃导电主要发生在界面附近的SnO2侧. 图5(c)和图5(d)分别给出了氧空位位于(HfO2)7/(SnO2)13异质结表面L7层的能带结构和原子层分解态密度图. 从图5(c)可以看出, 当氧空位位于HfO2表面时, 同样在带隙中引入了一条缺陷能带(图5(c)中棕实线标记能带), 且缺陷能带顶部与导带底部发生了交叠, 费米能级进入了导带底部. 此时, 缺陷能带上的电子将部分转移至导带而形成导电电子. 图5(d)的分层态密度图显示, 氧空位在HfO2表面L6和L7层引入缺陷态, 其顶部与该原子层导带底相距0.32 eV, 此时表面层呈半导体特征. 然而, 此时费米能级穿过缺陷态, 即部分缺陷能级高于费米能级. 由图5(d)的分层态密度图还可以看出, 伴随表面缺陷态的引入, 费米能级进入界面附近SnO2侧的导带, 即界面附近SnO2的导带与HfO2表面氧空位的缺陷带发生交叠. 考虑到HfO2的费米能级高于SnO2, 而HfO2侧的表面缺陷态(作为施主态)会进一步提高HfO2侧的费米能级[43], 并且HfO2表面和(HfO2)7/(SnO2)13异质结的界面的距离仅约为2.37 nm. 因此, 缺陷态中的电子并不全部局域在HfO2表面层, 会有一部分电子通过隧穿方式, 转移至SnO2侧. 最终, 在异质结的界面附近, 特别是在SnO2侧的${\rm L}{{\overline 1}}$ —${\rm L}{{\overline 7}}$ 层, 形成了2DEG.近期, Chen等[19]采用第一性原理计算方法, 研究了Mgx Zn1–xO/ZnO异质结中2DEG的来源. 发现Mgx Zn1–xO层较薄时, Mgx Zn1–xO/ZnO异质结中2DEG来源于表面原子或原子团的吸附作用. 由于实验制备过程中SnO2和HfO2等氧化物表面均容易发生原子或原子团的吸附[44–46], 因此, 我们研究了HfO2表面吸附H原子、O原子和OH–原子团对(HfO2)7/(SnO2)13异质结表面和界面电子结构的影响. 当图2所示的(HfO2)7/(SnO2)13异质结构表面分别有H原子、O原子和OH–原子团吸附时, 表面吸附能可通过
${E_{{\text{ads}}}} = {E_{{\text{total}}}} - \left( {{E_{{\text{hetero}}}} + {E_{{\text{atom}}}}} \right)$ 来计算, 这里,${E_{{\text{ads}}}}$ 为表面吸附能,${E_{{\text{total}}}}$ 为原子或原子团吸附后异质结体系的总能量,${E_{{\text{hetero}}}}$ 为未吸附异质结体系的总能量,${E_{{\text{atom}}}}$ 表示孤立原子或原子团的总自由能. 计算结果表明, H原子、OH–原子团和O原子的吸附能分别为–5.17 eV, –3.12 eV和0.12 eV. 吸附能小于零意味着吸附过程放热, 表明吸附系统能量稳定, 故该异质结表面容易吸附H原子和OH–原子团. 首先计算了OH–原子团吸附后, (HfO2)7/(SnO2)13的电子结构. 计算结果表明, 当吸附OH–原子团后, 异质结整体仍具有绝缘体的能带结构, 因此本文对吸附OH–的情况不再进一步讨论. 表面吸附H原子的异质结构型具有更低的表面吸附能, 因此具有更好的热力学稳定性. 下面讨论表面吸附H原子的(HfO2)7/(SnO2)13异质结构的电子结构.图6(a)展示了表面吸附H原子的(HfO2)7/(SnO2)13异质结的能带结构. 与具有干净HfO2表面的(HfO2)7/(SnO2)13异质结的能带结构(见图3(a)) 相比, 表面吸附H原子的异质结的费米能级穿过导带底, 具有类金属(简并半导体)的能带结构. 图6(a)的方形点线标记的两条能带来源于异质结中的HfO2表面原子层 (L6和L7层, 约0.78 nm厚), 这两条缺陷能带与导带底交叠, 为异质结提供导电电子. 图6(b)为表面吸附H原子的 (HfO2)7/(SnO2)13异质结构的原子层分解态密度图. 可以看出, 该异质结在
${\rm L}\overline {1} $ —${\rm L}\overline {7} $ 层中均存在导电电子, 即2DEG分布在厚度约为2.21 nm的SnO2中. 与HfO2表面具有氧空位的情况类似, 杂质带中的电子是通过隧穿的方式传输到异质结界面附近的. 结合图6(a)和图6(b)可知, 尽管(HfO2)7/(SnO2)13异质结在表面吸附H原子时能够像Mgx Zn1–xO/ZnO异质结界面[19]那样产生2DEG, 但H原子提供的电子也在HfO2表面形成了导电层.最后, 我们研究了HfO2的厚度对表面吸附H原子的HfO2/SnO2异质结界面附近电子浓度的影响. 为此, 计算了
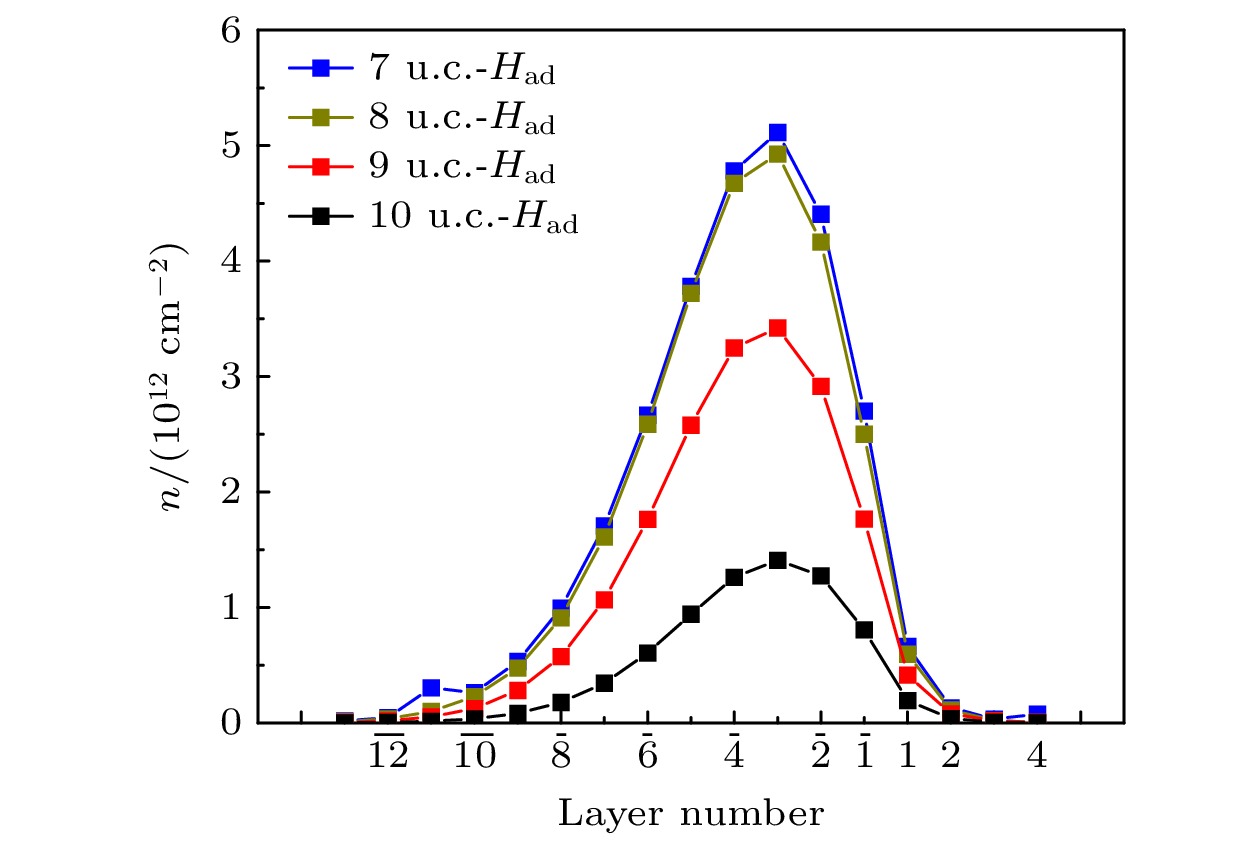
$ {\left( {{\text{Hf}}{{\text{O}}_2}} \right)_l}/{\left( {{\text{Sn}}{{\text{O}}_2}} \right)_{13}} $ (l = 7, 8, 9, 10 u.c.) 异质结构的电子结构, 对费米能级以下电子态密度进行积分, 获得了这些异质结界面附近各个原子层的电子浓度[19,22,47], 结果如图7所示. 从图7可以看出, 这些不同HfO2层厚度的异质结界面处的导电电子均聚集在${\rm L}\overline {1} $ —${\rm L}\overline {7} $ 层中. 当HfO2层厚度固定时, 随着Sn-O层逐渐远离界面, 导电电子浓度开始增大, 在${\rm L}\overline {3} $ 层达到最大值, 然后逐渐减小至0. 随着HfO2层的厚度l的增加, 异质结界面附近各原子层的电子浓度均逐渐减小. HfO2层厚度的增加导致HfO2表面与异质结界面之间的势垒宽度增大, 使表面电子转移到异质结界面附近的概率降低. 该结果进一步说明HfO2表面电子是通过隧穿机制转移到异质结界面附近的. 可以推测, 当HfO2层厚度足够大时, HfO2表面与异质结界面之间的势垒宽度很大, 表面电子向异质结界面转移的概率将很小. 因此, 界面处将不再形成2DEG. 采用$U_{\text{O}}^{{\text{2p}}}=14\;{\rm eV}$ 的GGA+U方法的计算结果与上述结果一致. -
本文采用第一性原理计算的方法研究了(001) HfO2/SnO2异质结构的电子结构. 结果表明: 具有干净HfO2表面的HfO2/SnO2异质结构的能带结构呈现半导体特征; 当异质结构的SnO2侧存在氧空位时, 氧空位会在异质结的导带底以下引入缺陷能带, 使体系出现跳跃导电; 当异质结构的HfO2表面存在氧空位时, 氧空位引入的缺陷态与界面贡献的导带底发生交叠, 使缺陷态中的电子转移至界面, 并在界面处形成2DEG. 此外, HfO2/SnO2异质结构的HfO2表面易吸附H原子. 当HfO2/SnO2异质结构的HfO2层较薄时, 表面吸附的H原子提供的电子部分转移至界面, 从而在界面处形成2DEG. 然而, 随着HfO2层厚度的增加, 表面电子转移到界面的概率逐渐下降, 使界面处的电子浓度逐渐减小.
HfO2/SnO2异质结界面电子结构研究
Electronic structure of interface of HfO2/SnO2 heterostructure
-
摘要: 在SrTiO3基氧化物异质结中, 由于Ti 3d轨道的影响, 界面处的二维电子气(2DEG)室温迁移率较低, 这限制了它们在半导体器件中的应用. 而SnO2的导带底由Sn的5s轨道组成, 因此, 基于SnO2的异质结界面具有形成室温下高迁移率2DEG的潜力. 本文采用第一性原理计算的方法, 对(001) HfO2/SnO2异质结构的界面电子结构进行了系统研究. 计算结果表明, 无缺陷的HfO2/SnO2异质结具有半导体的能带结构, 其界面附近不会形成2DEG. 当异质结界面附近的SnO2侧存在氧空位时, 体系出现跳跃导电, 但其界面附近仍不会出现2DEG. 当氧空位处于异质结的HfO2表面时, 氧空位的存在使表面产生缺陷态. 缺陷态的电子处于局域态, 并不参与导电, 但缺陷态与异质结构的导带底(由界面贡献) 发生交叠, 使异质结表面缺陷态中的电子转移至界面, 并在异质结界面附近形成2DEG. 此外, 对于HfO2层较薄的HfO2/SnO2异质结构, 比如HfO2层为7个单胞(约2.37 nm)厚时, HfO2表面吸附的H原子向异质结提供电子, 这些电子部分转移到界面附近的导带, 形成2DEG. 随着HfO2层厚度的增加, 表面电子转移到界面的概率逐渐下降, 使得界面处的电子浓度逐渐降低.Abstract: In SrTiO3-based oxide heterostructures, the mobility of the two-dimensional electron gas (2DEG) at the interface is relatively low at room temperature due to the influence of Ti 3d orbitals, which limits their applications in semiconductor devices. In contrast, the conduction band bottom of SnO2 is composed of Sn 5s orbitals, and it has been demonstrated that bulk SnO2 exhibits high carrier mobility at room temperature. Therefore, SnO2-based heterostructure interfaces have the potential to form 2DEG with high mobility at room temperature. In this paper, we construct a heterostructure (HfO2)7/(SnO2)13 with $2 \times 1$ supercell in (001) plane and systematically investigate the electronic structure of the heterostructure by using first-principles calculations. The calculation results show that the defect-free (HfO2)7/(SnO2)13 heterostructure has a band structure similar to that of a semiconductor, and there is no 2DEG near the interface of the heterostructure. However, the conduction band bottom is mainly contributed by non-degenerate Sn 5s orbitals in this situation. In the in-plane $2 \times 1$ supercell of the (HfO2)7/(SnO2)13 heterostructure, each layer contains 8 oxygen atoms (the thickness of 1 unit cell is defined as a layer). When an oxygen atom in a layer on the SnO2 side near the interface of the heterostructure is removed, the presence of the oxygen vacancy leads to the formation of a defect band below the conduction band. This will lead to hopping conductivity in the heterostructure. However, 2DEG still does not appear near the heterostructure interface. When the oxygen vacancy is located in the surface layer of the HfO2 in the supercell structure, the presence of the oxygen vacancy leads to the formation of a defect state in the surface. The electrons in the defect state are localized and do not contribute to conductivity. However, the defect band overlaps with the conduction band at the interface, causing the electrons on the surface of HfO2 to tunnel towards the interface. In this scenario, the 2DEG emerges in the vicinity of the heterostructure interface. In addition, for HfO2/SnO2 heterostructures with thinner HfO2 layers, such as HfO2 layer with a thickness of 7 unit cells (about 2.37 nm), the H atoms adsorbed on the HfO2 surface provide electrons for the heterostructure. Some of these electrons transfer to the conduction band near the interface, leading to the formation of a 2DEG in that region. Meanwhile, the remaining electrons stay on the surface, forming a conductive layer with a thickness of approximately 2 unit cells. As the thickness of the HfO2 layer increases, the probability of electrons transferring from the surface to the interface gradually decreases, resulting in a gradual decrease in the electron density at the interface.
-
Key words:
- oxide heterostructures /
- two-dimensional electron gas /
- electronic structure .
-

-
图 1 SnO2和HfO2块体的能带结构图(费米能级设为零点) (a), (b)采用GGA+U所得(a) SnO2和(b) HfO2的能带结构; (c), (d)采用
$U_{\text{O}}^{{\text{2p}}}$ = 8 eV的GGA+U所得(c) SnO2和(d) HfO2的能带结构; (e), (f)采用HSE杂化泛函所得(e) SnO2和(f) HfO2的能带结构; (g), (h)采用$U_{\text{O}}^{{\text{2p}}}$ = 14 eV的GGA+U所得(g) SnO2和(h) HfO2的能带结构Figure 1. Band structure of bulk SnO2 and HfO2. The band structures of (a) SnO2 and (b) HfO2 obtained by GGA+U. (c) SnO2 and (d) HfO2 obtained by GGA+U with
$U_{\text{O}}^{{\text{2p}}}$ = 8 eV. The band structures of (e) SnO2 and (f) HfO2 obtained by HSE hybrid functional. The band structures of (g) SnO2 and (h) HfO2 obtained by GGA+U with$U_{\text{O}}^{{\text{2p}}}$ = 14 eV. The Fermi level is set as zero.图 3 (HfO2)7/(SnO2)13异质结构的电子结构(费米能级设为零点) (a)能带结构图, 方形点线标记能带来源于异质结表面L7层不饱和悬键的畸变; (b)原子层分解态密度图; (c)平面平均电荷密度差, 其中负值和正值分别表示电子的耗尽和积累, L表示沿异质结构的距离, 点划线给出了异质结界面的位置; (d) Sn, Hf, O原子轨道投影态密度
Figure 3. Electronic structure of (HfO2)7/(SnO2)13 heterostructure. (a) The energy band structure. The band marked by the square dots originates from the distortion of the unsaturated dangling bonds of the L7 layer near the heterojunction surface. (b) The partial density of states projected onto atomic planes. (c) The plane-averaged charge density difference. The negative and positive values represent the depletion and accumulation of electrons, respectively. L is noted as the distance along direction of the heterostructure, and the dashed line gives the location of the interface. (d) Projection density of states for Sn, Hf, and O atomic orbitals, where the Fermi level is set as zero.
图 4 (HfO2)7/(SnO2)13异质结表面和界面附近不同原子层的氧空位形成能, 其中点划线给出了异质结界面的位置, 圆圈标记为SnO2侧和HfO2侧的氧空位形成能最低的位置
Figure 4. Formation energies of oxygen vacancies in different atomic layers near the surface and interface of (HfO2)7/(SnO2)13 heterostructure. The dashed line gives the position of the interface of the heterostructure, and the circles mark the lowest oxygen vacancy formation energy on the SnO2 side and the HfO2 side.
图 5 存在氧空位时(HfO2)7/(SnO2)13异质结的能带结构图和原子层分解态密度图 (a), (b)氧空位位于L
$\overline {2} $ 原子层的情况; (c), (d)氧空位位于L7原子层的情况; 棕实线标记能带为氧空位的缺陷能级, 计算结果基于$U_{\text{O}}^{2{\text{p}}}$ = 14 eV的GGA+U方法, 费米能级设为零点Figure 5. Energy band structure and partial density of states projected onto atomic planes of (HfO2)7/(SnO2)13 heterostructure with oxygen vacancy: (a), (b) The cases for oxygen vacancy on the L
$\overline {2} $ layer; (c), (d) the cases for oxygen vacancy on the L7 layer. The band marked by brown solid line are the defective energy levels of the oxygen vacancy. The calculation results are based on the GGA+U method of$U_{\text{O}}^{{\text{2p}}}$ = 14 eV, and the Fermi level is set as zero.图 6 表面吸附H原子的(HfO2)7/(SnO2)13异质结的电子结构(费米能级设为零点) (a)能带结构图, 方形点线标记能带来源于表面处电子, 圆圈标记能带来自界面处电子; (b)原子层分解态密度图
Figure 6. Electronic structure of (HfO2)7/(SnO2)13 heterostructure adsorbed H atoms on the surface. (a) The energy band structure. The band marked by the square dots originates from the surface electrons, and the band marked by the circles comes from electrons at interface. (b) The partial density of states projected onto atomic planes. The Fermi level is set as zero.
图 7 表面吸附H原子
$ {\left( {{\text{Hf}}{{\text{O}}_2}} \right)_l}/{\left( {{\text{Sn}}{{\text{O}}_2}} \right)_{13}} $ (l = 7, 8, 9, 10 u.c.)异质结界面附近的电子浓度Figure 7. Electron density near the interface of
$ {\left( {{\text{Hf}}{{\text{O}}_2}} \right)_l}/ $ $ {\left( {{\text{Sn}}{{\text{O}}_2}} \right)_{13}} $ (l = 7, 8, 9, 10 u.c.) heterostructures adsorbed H atoms on the HfO2 surface. -
[1] Ohtomo A, Hwang H Y 2004 Nature 427 423 doi: 10.1038/nature02308 [2] Tampo H, Shibata H, Matsubara K, Yamada A, Fons P, Niki S, Yamagata M, Kanie H 2006 Appl. Phys. Lett. 89 132113 doi: 10.1063/1.2357588 [3] Hotta Y, Susaki T, Hwang H Y 2007 Phys. Rev. Lett. 99 236805 doi: 10.1103/PhysRevLett.99.236805 [4] Chen Y Z, Bovet N, Trier F, Christensen D V, Qu F M, Andersen N H, Kasama T, Zhang W, Giraud R, Dufouleur J, Jespersen T S, Sun J R, Smith A, Nygård J, Lu L, Büchner B, Shen B G, Linderoth S, Pryds N 2013 Nat. Commun. 4 1371 doi: 10.1038/ncomms2394 [5] Zou K, Ismail-Beigi S, Kisslinger K, Shen X, Su D, Walker F J, Ahn C H 2015 APL Mater. 3 036104 doi: 10.1063/1.4914310 [6] Zhang Y W, Neal A, Xia Z B, Joishi C, Johnson J M, Zheng Y H, Bajaj S, Brenner M, Dorsey D, Chabak K, Jessen G, Hwang J, Mou S, Heremans J P, Rajan S 2018 Appl. Phys. Lett. 112 173502 doi: 10.1063/1.5025704 [7] 颜送灵, 唐黎明, 赵宇清 2016 物理学报 65 077301 doi: 10.7498/aps.65.077301 Yan S L, Tang L M, Zhao Y Q 2016 Acta Phys. Sin. 65 077301 doi: 10.7498/aps.65.077301 [8] Zhang H R, Yun Y, Zhang X J, Zhang H, Ma Y, Yan X, Wang F, Li G, Li R, Khan T, Chen Y S, Liu W, Hu F X, Liu B G, Shen B G, Han W, Sun J R 2018 Phys. Rev. Lett. 121 116803 doi: 10.1103/PhysRevLett.121.116803 [9] Kozuka Y, Tsukazaki A, Maryenko D, Falson J, Akasaka S, Nakahara K, Nakamura S, Awaji S, Ueno K, Kawasaki M 2011 Phys. Rev. B 84 033304 doi: 10.1103/PhysRevB.84.033304 [10] Chen Z, Liu Y, Zhang H, Liu Z R, Tian H, Sun Y Q, Zhang M, Zhou Y, Sun J R, Xie Y W 2021 Science 372 721 doi: 10.1126/science.abb3848 [11] 王继光, 李珑玲, 邱嘉图, 陈许敏, 曹东兴 2023 物理学报 72 176801 doi: 10.7498/aps.72.20230573 Wang J G, Li L L, Qiu G T, Chen X M, Cao D X 2023 Acta Phys. Sin. 72 176801 doi: 10.7498/aps.72.20230573 [12] Thiel S, Hammerl G, Schmehl A, Schneider C W, Mannhart J 2006 Science 313 1942 doi: 10.1126/science.1131091 [13] Chen X H, Li Z Q, Hu Z X, Gao K H 2022 Phys. Rev. B 105 205437 doi: 10.1103/PhysRevB.105.205437 [14] Nakano M, Tsukazaki A, Ueno K, Gunji R Y, Ohtomo A, Fukumura T, Kawasaki M 2010 Appl. Phys. Lett. 96 052116 doi: 10.1063/1.3309699 [15] 张阳, 顾书林, 叶建东, 黄时敏, 顾然, 陈斌, 朱顺明, 郑有炓 2013 物理学报 62 150202 doi: 10.7498/aps.62.150202 Zhang Y, Gu S L, Ye J D, Huang S M, Gu R, Chen B, Zhu S M, Zhen Y D 2013 Acta Phys. Sin. 62 150202 doi: 10.7498/aps.62.150202 [16] Himmetoglu B, Janotti A, Peelaers H, Alkauskas A, Van de Walle C G 2014 Phys. Rev. B 90 241204 doi: 10.1103/PhysRevB.90.241204 [17] Himmetoglu B, Janotti A 2016 J. Phys. Condens. Matter 28 065502 doi: 10.1088/0953-8984/28/6/065502 [18] Lee J, Demkov A A 2008 Phys. Rev. B 78 193104 doi: 10.1103/PhysRevB.78.193104 [19] Chen X H, Li Z Q, Hou D Y, Hu Z X, Gao K H 2023 Phys. Rev. B 107 165411 doi: 10.1103/PhysRevB.107.165411 [20] Sanon G, Rup R, Mansingh A 1991 Phys. Rev. B 44 5672 doi: 10.1103/PhysRevB.44.5672 [21] Toyosaki H, Kawasaki M, Tokura Y 2008 Appl. Phys. Lett. 93 132109 doi: 10.1063/1.2993346 [22] Paudel T R, Tsymbal E Y 2017 Phys. Rev. B 96 245423 doi: 10.1103/PhysRevB.96.245423 [23] Nazir S, Cheng J L, Yang K S 2016 ACS Appl. Mater. Interfaces 8 390 doi: 10.1021/acsami.5b09107 [24] Lee B H, Kang L, Nieh R, Qi W J, Lee J C 2000 Appl. Phys. Lett. 76 1926 doi: 10.1063/1.126214 [25] Seo M, Kim S K, Han J H, Hwang C S 2010 Chem. Mater. 22 4419 doi: 10.1021/cm1010289 [26] Seo M, Kim S K, Min Y S, Hwang C S 2011 J. Mater. Chem. 21 18497 doi: 10.1039/c1jm11763g [27] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [28] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558 [29] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [30] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758 doi: 10.1103/PhysRevB.59.1758 [31] Gilani R, Rehman S U, Butt F K, Haq B U, Aleem F 2018 Silicon 10 2317 doi: 10.1007/s12633-018-9766-7 [32] Singh A K, Janotti A, Schefler M, Van de Walle C G 2008 Phys. Rev. Lett. 101 055502 doi: 10.1103/PhysRevLett.101.055502 [33] Park J, Saidi W A, Chorpening B, Duan Y H 2021 J. Phys. Chem. C 125 22231 doi: 10.1021/acs.jpcc.1c05716 [34] Marcillo F, Stashans A 2015 J. Theor. Comput. Chem. 13 1450069 doi: 10.1142/S0219633614500692 [35] Heyd J, Peralta J E, Scuseria G E, Martin R L 2005 J. Chem. Phys. 123 174101 doi: 10.1063/1.2085170 [36] Pavoni E, Mohebbi E, Stipa P, Mencarelli D, Pierantoni L 2022 Materials 15 4175 doi: 10.3390/ma15124175 [37] Akbar W, Elahi I, Nazir S 2020 J. Magn. Magn. Mater. 511 166948 doi: 10.1016/j.jmmm.2020.166948 [38] Li J P, Meng S H, Yang C, Lu H T, Tohyama T 2018 Chin. Phys. B 27 027101 doi: 10.1088/1674-1056/27/2/027101 [39] Krishnaswamy K, Himmetoglu B, Kang Y, Janotti A, Van de Walle C G 2017 Phys. Rev. B 95 205202 doi: 10.1103/PhysRevB.95.205202 [40] Herranz G, Basletić M, Bibes M, Carrétéro C, Tafra E, Jacquet E, Bouzehouane K, Deranlot C, HamzićA, Broto J M, Barthélémy A, Fert A 2007 Phys. Rev. Lett. 98 216803 doi: 10.1103/PhysRevLett.98.216803 [41] Oh T 2017 Trans. Electr. Electron. Mater. 18 21 doi: 10.4313/TEEM.2017.18.1.21 [42] Liu H Y, Zeng F, Lin Y S, Wang G Y, Pan F 2013 Appl. Phys. Lett. 102 181908 doi: 10.1063/1.4804613 [43] Singh R, Khan M A, Mukherjee S, Kranti A 2018 IEEE Trans. Electron Devices 65 2850 doi: 10.1109/TED.2018.2838546 [44] Bandura A V, Kubicki J D, Sofo J O 2008 J. Phys. Chem. B 112 11616 doi: 10.1021/jp711763y [45] Li L, Huang X, Zhang Y F, Guo X, Chen W K 2013 Appl. Surf. Sci. 264 424 doi: 10.1016/j.apsusc.2012.10.038 [46] Jia H, Liang W H, Zhou M, Cao E S, Yang Z, Hao W T, Zhang Y J 2018 J. Supercond. Novel. Magn. 31 3361 doi: 10.1007/s10948-018-4608-9 [47] Li Y, Phattalung S N, Limpijumnong S, Kim J, Yu J 2011 Phys. Rev. B 84 245307 doi: 10.1103/PhysRevB.84.245307 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: