-
氢作为一种洁净的可再生能源, 因其具有来源广泛、转化效率高、能量密度高的优点, 广泛应用于航空航天、石化、制造业和能源领域[1,2], 有学者预测到2050年, 氢能将占人类消耗总能源的50%[3]. 然而大量的实践与研究表明, 氢会使钢和其他几种金属严重脆化[4], 在低于材料的强度极限的应力作用下, 经过一定时间, 钢突然断裂[5]. 在实际生产中, 工作部件往往受氢与应力协同作用: 在航空航天领域, 储运氢气的压力容器和管道在受氢损伤的同时还承受着高压[6], 在石化领域, 深埋海洋的石油管道受氢损伤的同时还受内压、净水压力作用[7,8]. 在氢能源领域, 氢能源汽车使用的高压氢气罐受气压、振动和氢损伤的联合作用, 氢气罐内衬金属中裂纹更容易萌生与扩展[9]. 应力(应变)诱导氢脆的机制至今尚无统一定论[10], 实践中发现表面吸附氢对氢致裂纹萌生起重要作用, X100管线钢在13.5 MPa氢环境中, 氢致裂纹萌生于试样表面[11], X80钢的氢致塑性损失主要由表面吸附高浓度氢导致[12]. 常见的表面吸附分析技术(LEED, EELS, XPS, AES, STM, SIMS, FIM, UPS)[13–15]为表面能量、结构的分析提供了参考, 但不能真正达到原子尺度的观察, 且在实验过程容易破坏表面结构, 使得表面结构分析的不确定因素增加, 而理论计算可以弥补试验分析中的不足, 是当前研究表面吸附的主流方法[16,17].
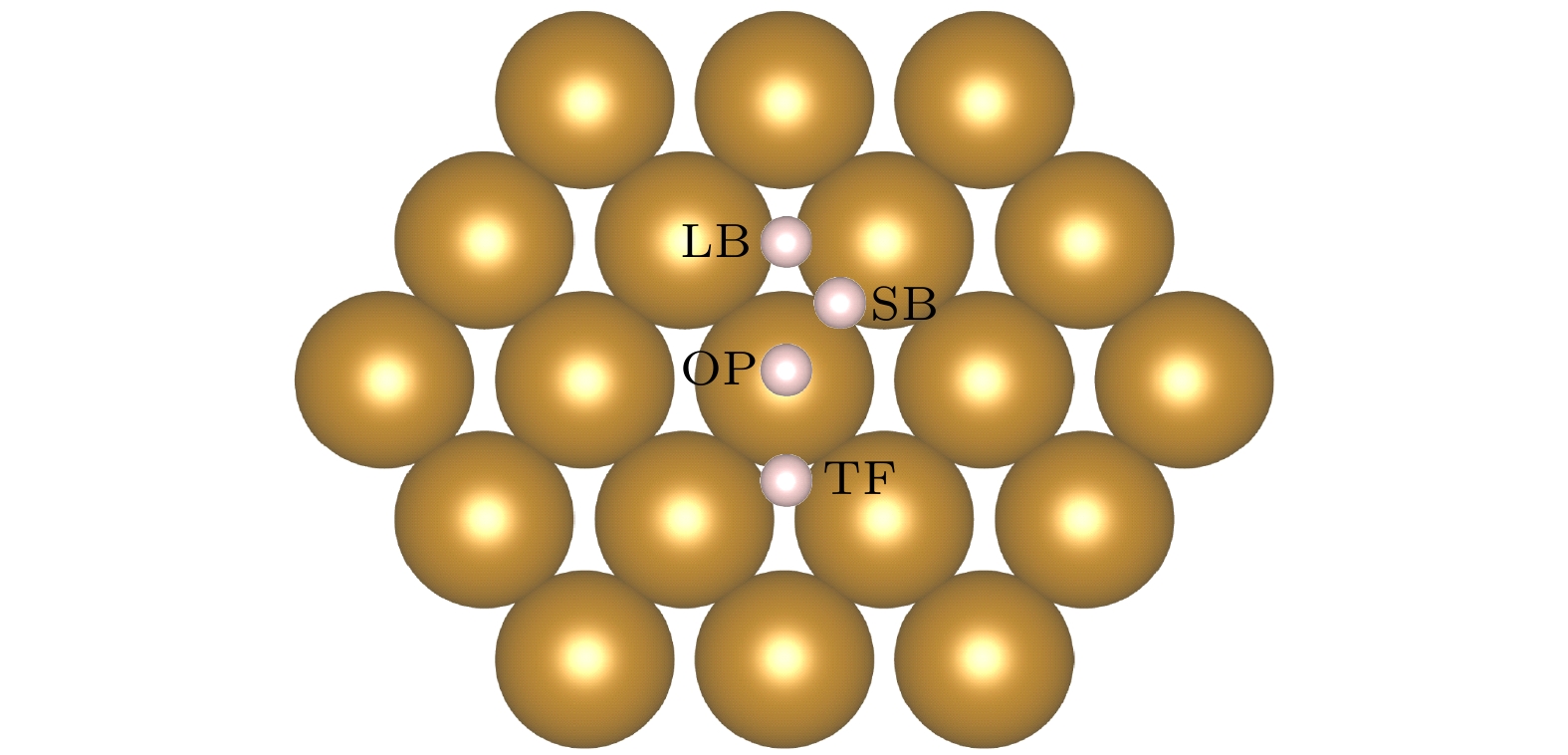
Fe(110)面是α-Fe的密排面, 具有最低的表面能[18–20], 是平衡凝固过程中最容易暴露的表面[21], 因此H与Fe(110)面的相互作用得到较多的理论研究, 但主要是在无应力条件下. Cremaschi等[22]报道了H原子在Fe(110)表面的吸附有4个不同的吸附位点, 如图1所示, 他们的结果与早期实验测试相吻合, H到铁表面距离的实验测试距离为(0.9±0.1) Å[23], 最大可达1.94 Å[24]. H2最稳定的吸附部位是顶部部位[25], 而H原子主要吸附在Fe(110)长桥位或准三重位点[26–28], 且H吸附几乎不会对Fe(110)表面造成任何变形[29]. 由于Fe(100)和Fe(110)表面的吸附能几乎相同[30], Sheikhzadeh等[31]综合密度泛函理论(DFT)和热力学模型, 计算了掺杂各种代表性合金元素(Ni, Ti, W, Mo, Mn, Co, Cr, V, Al和Cu)的Fe(100)表面的H吸附行为, 表明合金元素极大地改变了表面和H原子之间的相互作用.
关于应力加载铁表面的氢吸附报道较少, 李守英等[32]采用基于自旋极化密度泛函理论的第一性原理方法和超软赝势研究H2在Fe(110)表面吸附过程中的势能变化以及不同应变时的吸附, 发现H2的吸附能与应变之间存在近似线性关系, 拉应变使得H2的吸附能更负, 压应变使得吸附能值升高, 这表明拉应力使得H2与Fe(110)面的作用力增强, 压应力减小了H2与Fe(110)面的相互作用. Li等[33]研究了H在双轴应变Fe(110)表面的吸附和扩散, 发现无论Fe(110)表面是压缩状态还是拉伸状态, H在TF位点的吸附最稳定, 存在应变时, 顶部位置的H原子会弛豫到TF位置, 并且压缩使H原子和表面之间的键合强度变弱, 拉伸使H原子和表面之间的键合强度变强, 认为通过表面应变可以控制H在Fe表面的吸附和扩散, 对于研究表面应力对氢脆的影响具有重要意义. 尽管上述工作取得了重要成就, 但这种利用超软赝势来计算Fe等磁性系统不太可靠[34], 并且仍然明显缺乏第一性原理计算用于阐明C掺杂Fe(110)表面时应力对H吸附、扩散的影响. 本文采用密度泛函方法计算预应变下H原子与C掺杂Fe(110)表面的相互作用, 研究不同预应变下H原子在Fe(110)表面的吸附情况, 分析预应变对C掺杂Fe(110)表面结构的影响, 将表面结构变化与最终吸附结构相联系, 从原子空间构型、结合能、电子结构3个方面探究了预应变对H吸附、渗透的影响, 对完善Fe-H体系作用理论具有重要意义.
-
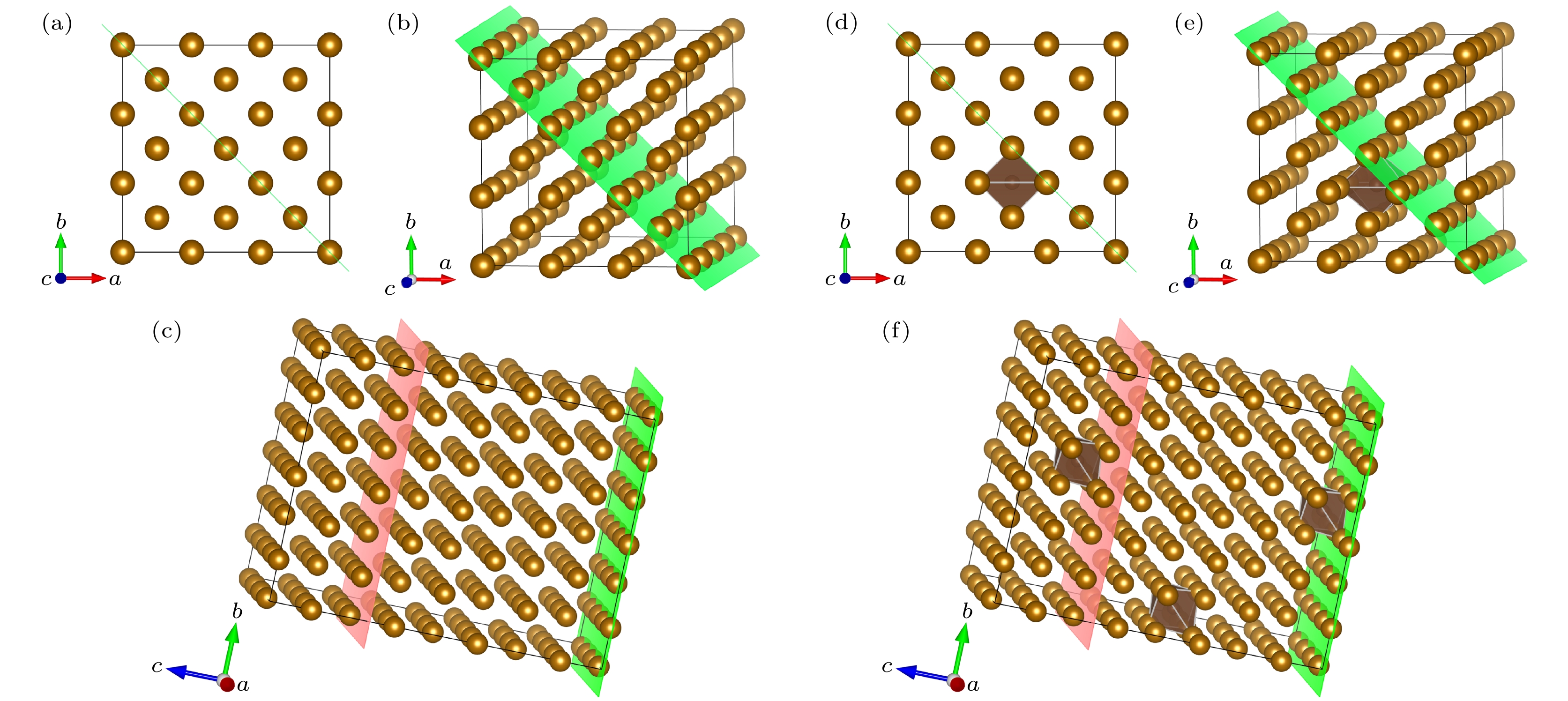
基于自旋极化密度泛函理论的第一性原理方法[35], 采用投影缀加平面波赝势[36]获得电子能量, 交换关联能采用广义梯度近似下Perdew-Burke-Ernzerhof泛函[37], 平面波的截断能设置为520 eV, 结构优化过程中力和能量的收敛准则分别设置为–0.05 eV/Å和10–5 eV, 并考虑Fe原子的磁性. 对BCC铁晶胞进行计算得到了晶格常数为2.806 Å, 与其他DFT计算[38,39]结果(2.832 Å, 2.830 Å)基本一致, 误差为0.918%和0.848%. 将体心立方(BCC)铁晶胞进行3×3×4扩胞(见图2(a)), 然后切(110)面并选择合适的厚度, 充分弛豫以模拟含碳量为0‱的纯铁晶体结构(见图2(c)); 将BCC铁晶胞进行3×3×4扩胞后, 再向超胞的八面体间隙中掺杂1个碳原子(见图2(d)), 然后切(110)面并选择合适的厚度, 充分弛豫以模拟含碳量为29.67‱的中碳钢晶体结构(如图2(f)).
为模拟工作部件受到的单向变形需引入应变ε[40], 对弛豫后的晶体模型的a轴(图2(c), (f)晶体模型的a轴)施加不同程度的应变ε(–5%, –2.5%, 0%, 2.5%, 5%)来改变模型在该方向的尺寸, 然后对整个体系进行结构优化. 优化时采取在保持a轴长度不变的情况下, 让另外两轴自由优化的原则, 从而保证整个体系处于拉伸或压缩状态下的能量最低状态.
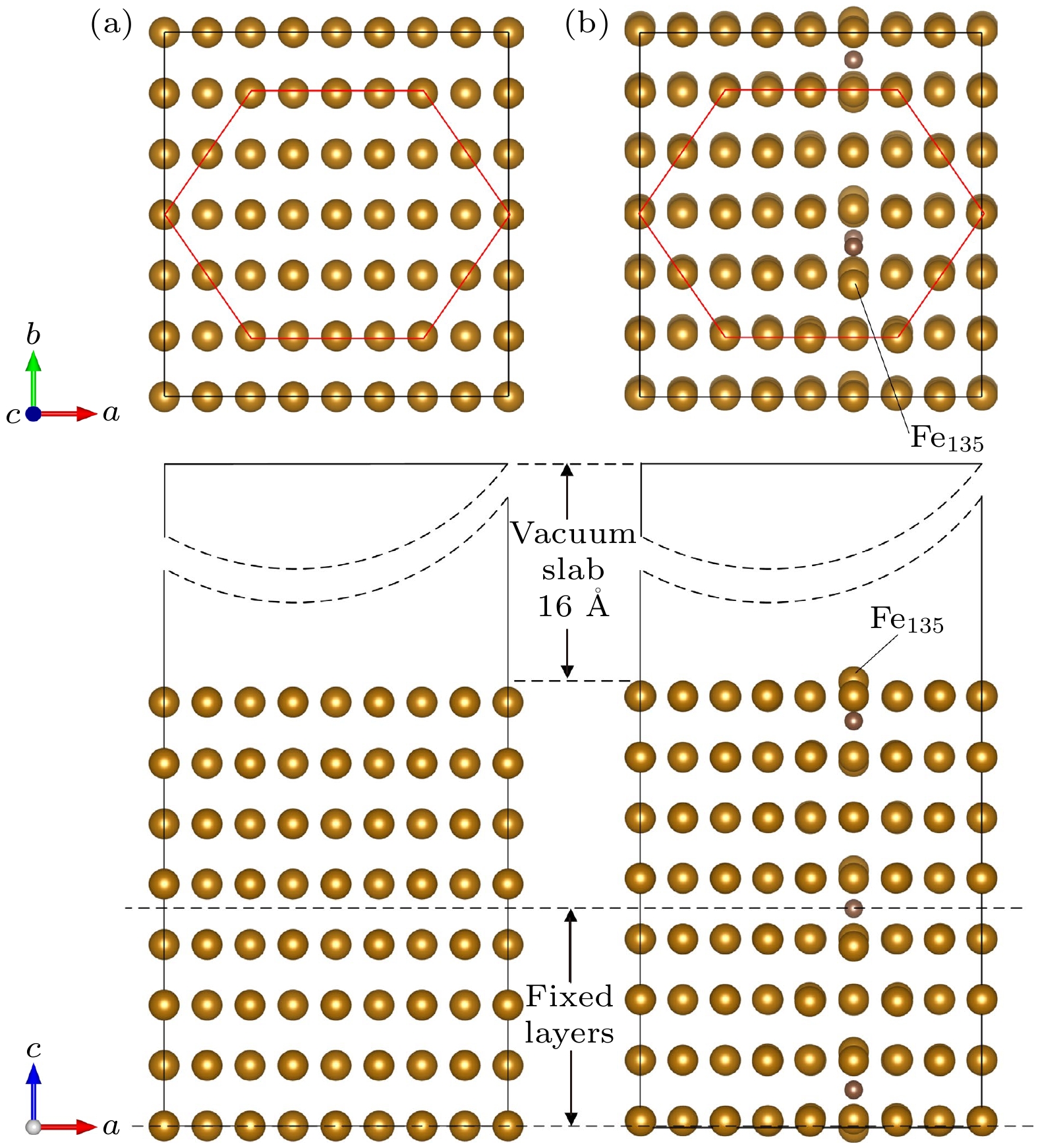
如图3所示, 对优化后的晶体模型进行切割, 在c方向选取1倍晶体长度(8层Fe原子), 然后在切割面上添加16 Å的真空层, 进行弛豫得到基底模型. 弛豫时保持整个体系体积不变, 固定下方4层铁原子(掺杂时额外固定下方2个碳原子), 上方原子不做任何限制. 计算得到0%应力状态下, 未掺杂基底每层大小为a = 11.221 Å, b = 11.874 Å, 共192个Fe原子, 掺杂基底每层大小为a = 11.219 Å, b = 11.952 Å, 共192个Fe原子, 3个掺杂碳(C)原子, 此体系内含碳量略微增大, 为33.37‱, 仍然属于中碳钢结构.
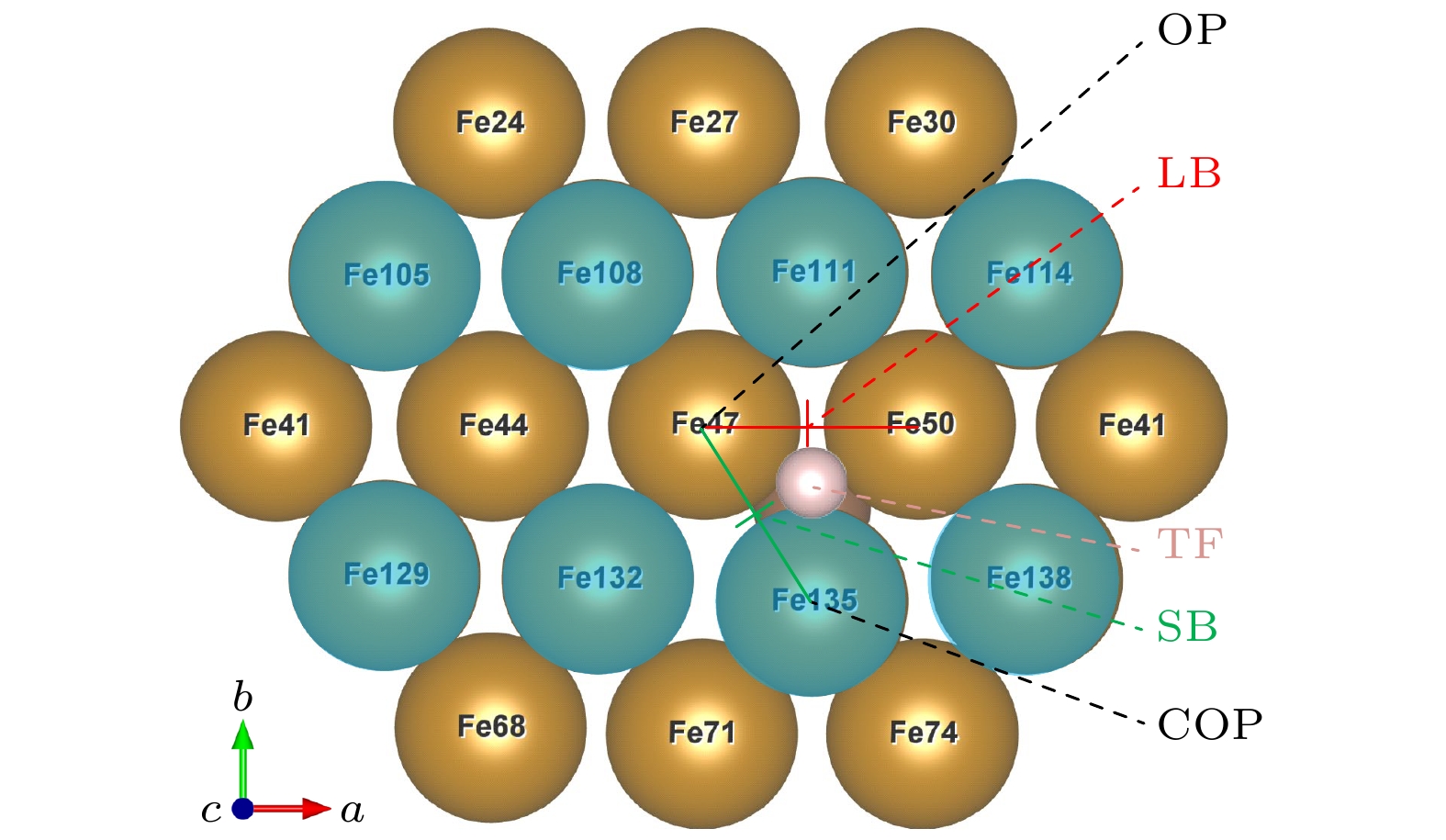
掺杂C原子时, C作为畸变源头, C原子附近的Fe原子存在明显的畸变, 表面上畸变最大的Fe原子为BCC晶体内离掺杂C原子最近的体心原子. 因此, 基底表层原子的顶位吸附位点可分为两类, 一类为体心原子吸附位点(COP), 另一类为顶角原子吸附位点(OP). 两类位点沿着基矢b方向交替排列, 碳原子附近的短桥、长桥发生最大畸变, 图4所示为图3红色区域的表层原子.
H原子吸附在表面时, 由于H原子较小, 可以认为H原子不对整个体系的体积产生影响, 吸附计算过程与基底弛豫过程类似. 以往的DFT研究[41–43]和实验[44,45]都表明, Fe(110)吸附H原子时只有非常小的弛豫, 没有表面重构, 因此, H原子吸附时的结合能(
$ {E_{\text{b}}} $ )可由方程(1)[29]定义:其中,
$ E[{\text{F}}{{\text{e}}_x}{{\text{C}}_y}{\text{H}}] $ 表示吸附模型中所有原子的总能量, x为Fe原子的总数, y为C原子的总数;$ {E_{\text{S}}}[{\text{F}}{{\text{e}}_x}{{\text{C}}_y}] $ 表示基底模型的能量;$ E[{\text{H}}] $ 表示吸附模型中H原子的能量, 计算此能量时需要将吸附模型中的Fe和C原子删除, 只保留吸附模型中的H原子, 并保持H原子位置不变. 结合能是一个负值, 根据(1)式, 更负的Eb代表更强的结合强度. -
在原子尺度上, 由掺杂原子引起的结构畸变往往不能忽略, 表1列出了基底模型表面畸变处的参数. 在应变(ε)加载方向上(b轴方向), 未掺杂模型表面dLB = 2.805 Å, 当ε从0%加载到为–5%, –2.5%, 2.5%, 5%时, 对应dLB变化率分别为–4.99%, –2.50%, 2.50%, 5.03%, dLB变化率与对应加载的ε基本一致, dLB均匀变化; 掺杂模型表面dLB = 2.826 Å, 当ε从0%加载到–5%, –2.5%, 2.5%, 5%时, 对应dLB变化率分别–5.27%, –2.26%, 2.05%, 4.67%, 此时, dLB变化率与对应加载的ε有明显差异. 在c轴方向, 未掺杂模型表面Fe原子到次表面Fe原子的距离(面间距)为1.994 Å, 这与Chohan等[28]的计算结果2.04 Å一致(ε = 0%), 本文还发现面间距随着应变的增大而单调减小; 掺杂模型表面最大畸变处Fe原子到次表面Fe原子的垂直距离dz = 2.418 Å (ε = 0%), 与未掺杂时的状况相比, 掺杂时c方向上发生了膨胀, 且各应变条件下此结论均适用. 在C原子所在的八面体中, ε = 0%时, 表面上C原子与配位Fe原子(Fe47, Fe50和Fe135)之间的键长分别为lFe47/50-C = 1.952 Å, lFe135-C = 1.789 Å, 未掺杂时键长lFe47/50-O = 1.985 Å, lFe135-O = 1.404 Å, 此结果与Liu等[38]的计算结果lFe47/50-C = 1.907 Å, lFe135-C = 1.899 Å, lFe47/50-O = 2.0025 Å, lFe135-O = 1.416 Å一致: lFe47-C < lFe47-O长度, lFe135-C > lFe135-O长度. 这说明C原子使八面体Fe47-C方向收缩, 使Fe135-C方向膨胀, 导致了空间的不均匀变化, 即畸变, 因此空间的一个面(Fe47, Fe50, Fe135组成的三角形区域)也发生了畸变. 未掺杂时, dz与ε呈负相关, lFe47-O与ε呈正相关, 掺杂时在同样的应变条件下却不遵守此规律, 进一步说明了掺杂C原子引起的结构畸变不能忽略.
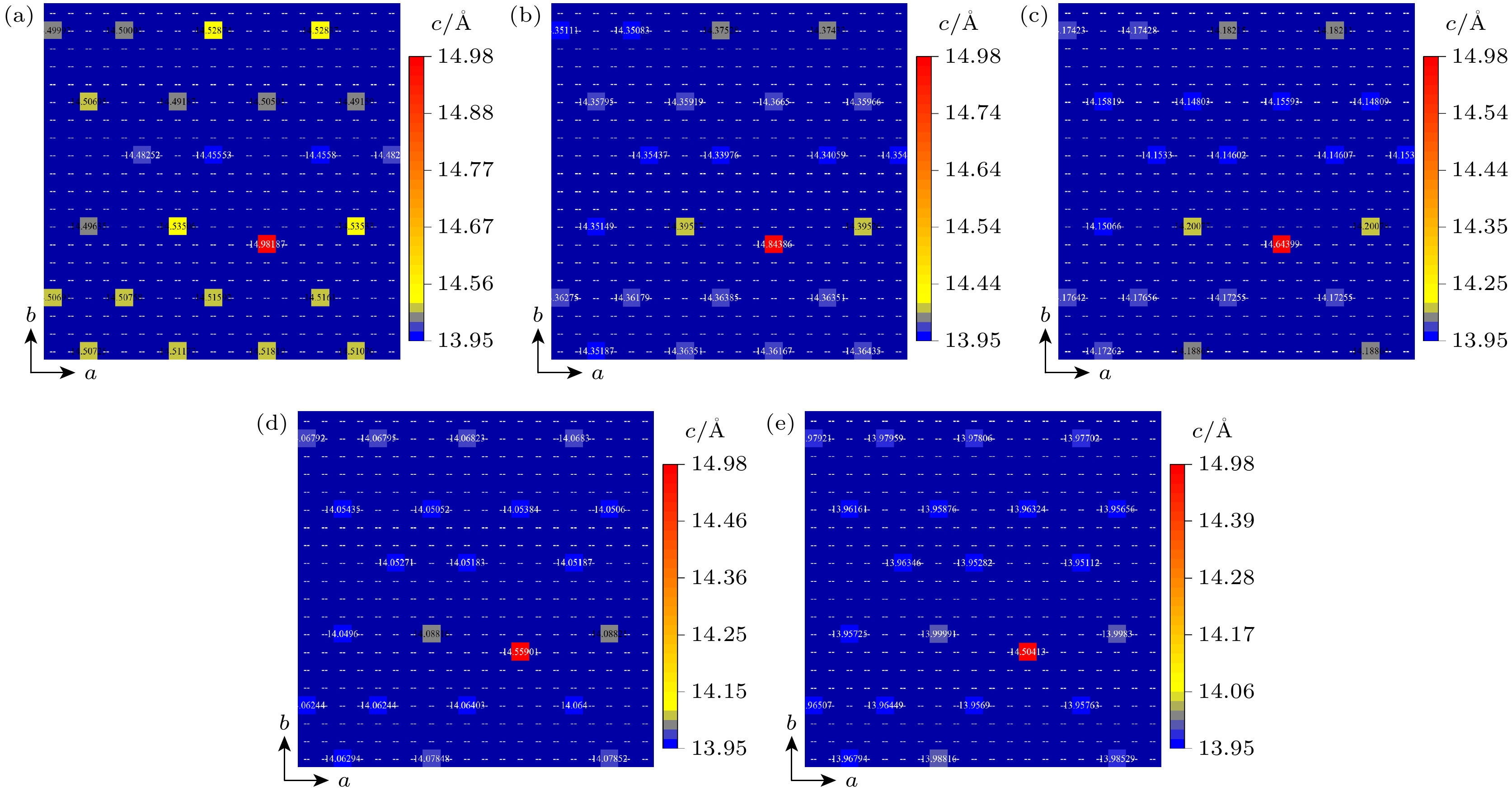
图5为掺杂C原子后整个表面的Fe原子空间位置分布情况, 颜色越暖代表c方向高度越高. 当ε = 0%时, C原子掺杂处的上方的顶角原子(Fe47和Fe50, 为OP位点)和体心原子(Fe135, 为COP位点)在c方向上高度不一致, Fe135在c方向上比表面平均原子高度高0.454 Å. 这与Jiang等[39]的计算结果0.5 Å非常接近, 他们认为这是为了减少C掺杂带来的局部应变. 随着ε从0%减小到–5%, 表面各原子间在c方向上整体高度起落差增大; 随着ε从0%增至5%, 表面上最大畸变原子(Fe135)与周围原子高度差增大, 但其余各原子在c方向上高度起落差减小, 当ε为0%, 2.5%, 5%时, Fe135与Fe47在c方向上对应高度差为0.443 Å, 0.471 Å, 0.504 Å, 应变改变了畸变.
-
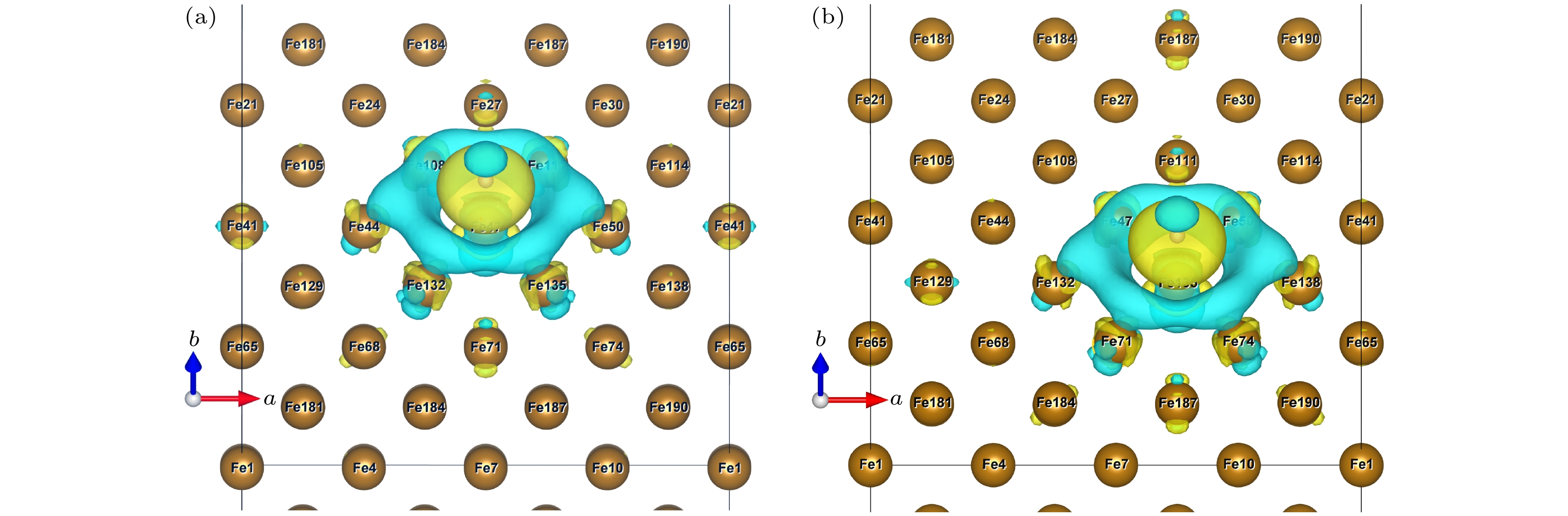
未掺杂C原子时, H原子在不同应变状态下都能稳定地吸附在各个位点上. 图6所示为H吸附时OP位点和COP位点的差分电荷密度空间分布, 发现H原子周围具有对称的差分电荷密度.
在ε为–5%, 0%, 5%的应变条件下对吸附模型进行Bader电荷计算, 发现在相同应变条件下OP, COP位点处H原子得电荷的数目都是一样的, Bader电荷均为1.17e, 1.21e, 1.23e, 配位Fe原子得电荷的数目也基本一样, Fe47为8.18e, 8.09e, 8.07e, Fe135为8.19e, 8.08e, 8.06e, 只相差0.01e. 同时, 计算H吸附时H到配位Fe原子的距离, 发现无应力条件下d = 1.525 Å, 这与Chohan等[28]的计算结果d = 1.55 Å吻合得非常良好, 在ε为–5%, –2.5%, 0%, 2.5%, 5%的应变条件下, OP位点的H到配位Fe原子的距离分为1.483 Å, 1.523 Å, 1.525 Å, 1.541 Å, 1.518 Å, COP位点的H到配位Fe原子的距离分别为1.484 Å, 1.521 Å, 1.521 Å, 1.537 Å, 1.517 Å, 相同应变条件下最大差距仅为0.004 Å, 可忽略不计. 表2为H吸附在各位点处的结合能, 在相同的应变条件下, OP位点和COP位点H原子结合能基本一样, 最大差值为0.02 eV. 由上述分析, 从电子结构、结合能大小, H到配位Fe原子的距离这3个方面来看, OP位点和COP位点的Fe原子对H的作用相同, 两种Fe原子等效.
在无应力条件下, TF位点为能量最小的位点Eb = –2.969 eV, 这与Shen等[46]的计算结果Eb = –2.952 eV吻合, Jiang和Carter [47]的计算结果也证实TF位点是真正的最小值, 而所有其他位点都表现出虚频, 表明在能量上接近准三重位点(TF)的长桥位点(LB)实际上是通向稳定的TF位的过渡态. 由表2还可知, 在不同应变下的Fe(110)表面不同位点插入H原子时, 最小能量均出现在TF位点, H原子在TF位点具有最稳定性, 可以被困在那里. 这与前文Li等[33]发现在双轴应变条件下, 无论Fe(110)表面是压缩状态还是拉伸状态, H在TF位点的吸附最稳定的结论一致.
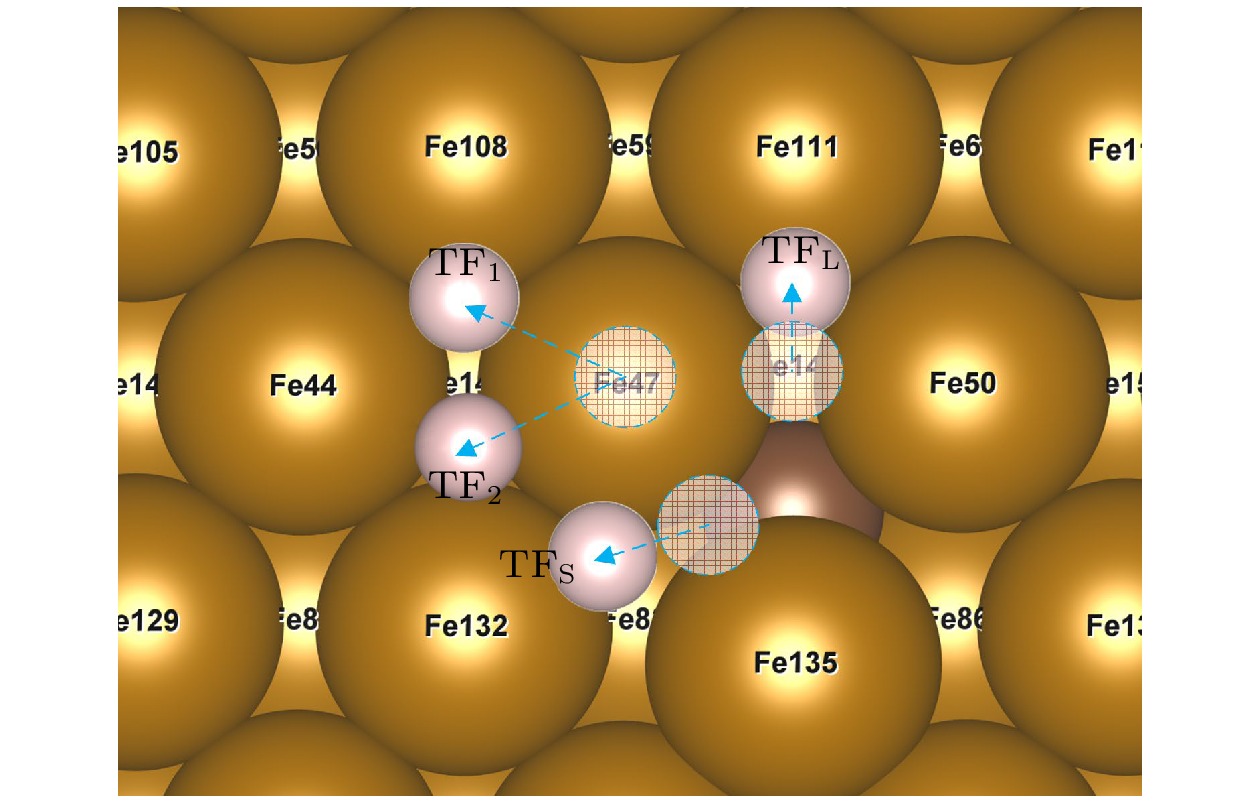
掺杂C原子时, 如图7所示, 各应变情况下, OP, SB, LB位点均为不稳定吸附位点, H原子会向就近的准三重位点移动并最终吸附在那里, 而COP, TF位点的H原子则会稳定地吸附在起始位点上. 同时, 由表2可知在相同的应变条件下COP位点的结合能远高于各准三重位点, 表明H原子在准三重位点处表现出最稳定性, 可以被困在那里.
由上述分析可知, 未掺杂C原子时, 在各应变条件下, OP, COP位点处H吸附完全等价. 掺杂C原子时即使没有应力, OP, COP位点H吸附的结果也不同, 进一步说明表面空间结构的畸变对H吸附结果的影响不可忽略; 而OP处应变大小不同导致H吸附的最终位点不同则反映了C掺杂时畸变空间在应变的作用下再次发生了不规则变化, 原子尺度上空间结构的微小变化导致了H吸附结果的复杂多变.
-
由上述计算结果, 无论是掺杂还是不掺杂C原子, 准三重位点都是H最稳定的吸附位点. 为此, 按照离最大畸变原子远近的程度, 选取掺杂C时TF, TFS, TFL位点和未掺杂C时的TFpure位点(相当于掺杂C时, 离最大畸变原子无穷远处的准三重位点)来研究预应变对H吸附的影响.
-
掺杂C原子使各Fe原子偏离“理想晶格”的点阵结构, 形成了“畸变晶格”[48]. 图8所示为H吸附结构参数. 从图8可以看出, C掺杂使Fe(110)表面不同区域畸变程度不同, Fe(110)表面由多个三角形状的单元表面组成, 本文主要研究离H原子最近的单元表面的变化情况, 它位于H原子下方, 由组成准三重位点的3个Fe原子构成. 其中d为H吸附高度(近似于c方向上H原子到各Fe原子在的平均值); αi为三角形单元表面3个内角. 图8中阴影部分为H原子吸附于TFS位点时, H原子对应的单元表面, 它是由Fe47, Fe132和Fe135构成的三角形, 它也可以作为一个通道, H原子可以穿越此通道扩散进入金属内部.
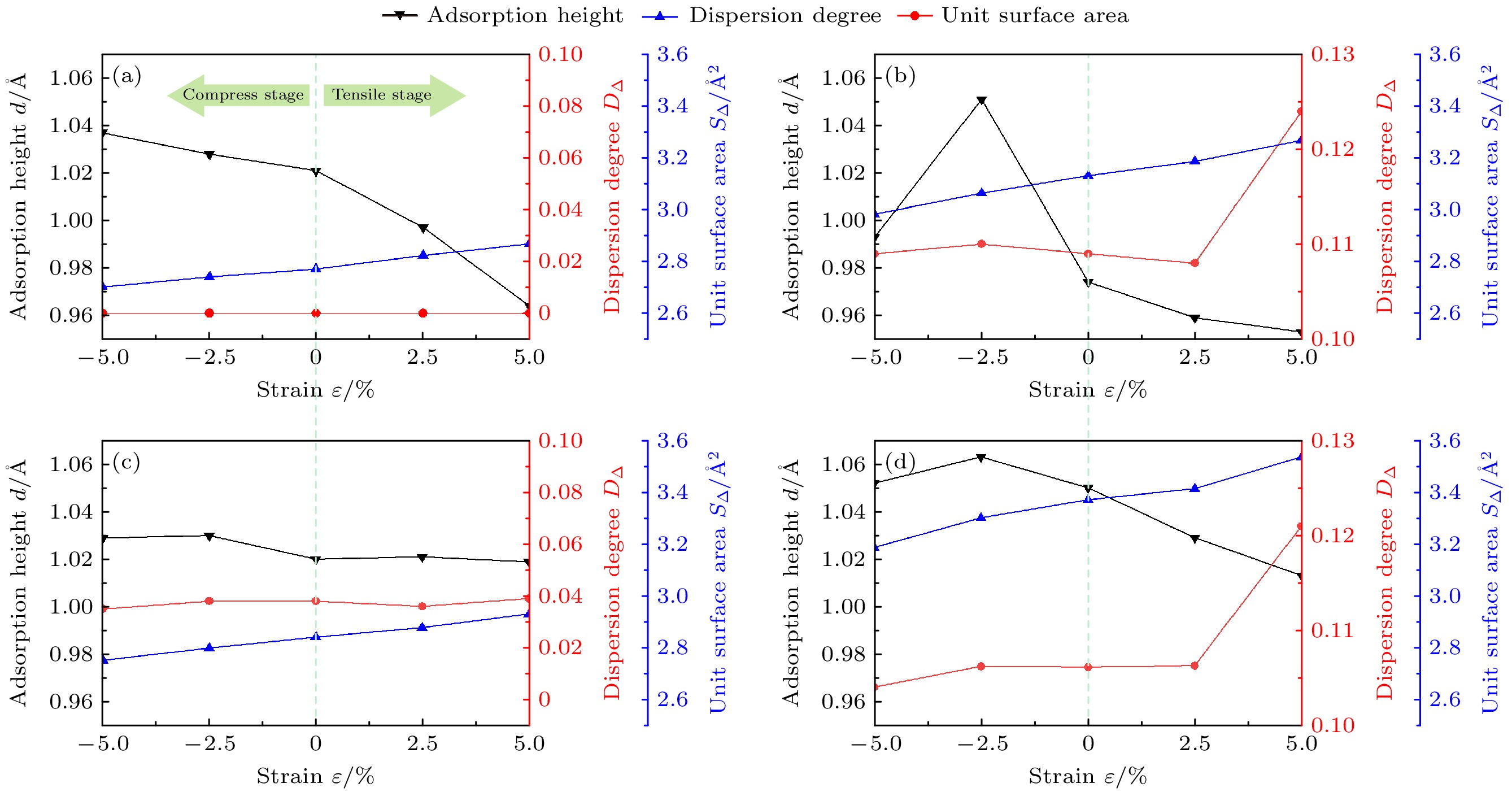
通过在原子尺度上探究应变如何影响畸变晶格微观结构, 继而影响畸变晶格空间电荷分布情况, 最终导致理化性能改变, 期望由此得到基本物理共性规律. 图9为不同位点处预应变对H吸附结果的影响. 单元表面畸变程度(D∆)由方程(2)定义:
其中,
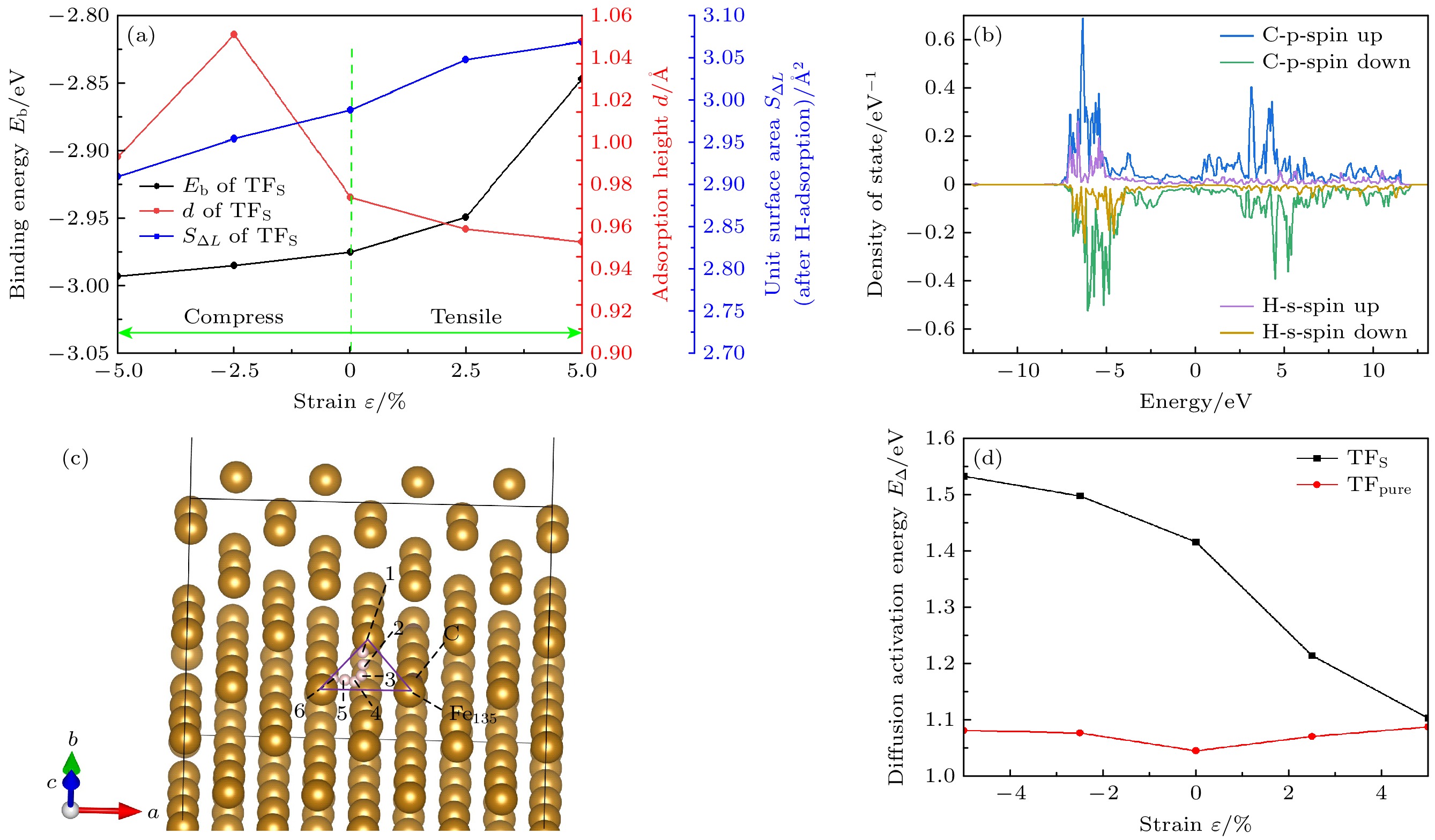
$ \mathop X\nolimits_{ij} $ 表示掺杂C原子时构成单元表面的3个Fe原子的3个坐标分量,$ \mathop {\overline X }\nolimits_{ij} $ 表示未掺杂C原子时构成单元表面的3个Fe原子的3个坐标分量,$ {D_\Delta } $ 的值越大, 畸变程度越大, 形状差异越大.H吸附高度(d)是H吸附在表面时的一个重要的结构参数[49], 其与单元表面积(S∆)和单元表面畸变程度(D∆)有关. 由图9可知, 未掺杂C原子时(TFpure), D∆为0, d不受D∆影响, d与对应的S∆呈负相关. 掺杂C原子时(TFs, TFL, TF), D∆和S∆都不为0: 以ε = 0%为分界线, 压缩时d与D∆呈正相关; 拉伸时d与S∆呈负相关.
S∆和D∆的大小和变化规律与是否掺杂C原子, 以及掺杂C原子后各位点离C原子和最大畸变原子(Fe135)的距离有关. 未掺杂C原子时, TFpure位点处S∆和D∆的值均最小, S∆与ε呈正相关, D∆为0; 掺杂C原子时, TFS, TFL, TF位点处S∆和D∆的值均大于TFpure位点处的值, S∆与ε呈正相关, 压缩时(ε由0%加载到–5%)D∆先增后减, 拉伸时(ε由0%加载到5%)D∆先减后增. 同时, 由于TFL位点处离Fe135较远, S∆和D∆的大小和变化规律与TFpure位点更为接近, 而TFS, TF位点离Fe135较近, S∆和D∆的值明显大于TFL, TFpure位点的值, 这可能是导致掺杂时TFS, TF位点处d对D∆和S∆的变化很敏感的原因. 同时, C原子本身也会对吸附结构产生影响: TF位点的D∆和S∆类似于TFS位点, 两者均较大, 然而TFS位点处d较小, TF位点处d却是4个位点中最大的, 原因是C原子位于TF位点正下方, 又因为C原子到H原子的距离远大于C原子和H原子的成键距离(1.08—1.16 Å), 导致C原子对H原子发生了较大的排斥.
-
三角形单元三个内角的标准差(
$ \mathop S\nolimits_\alpha $ )由方程(3)定义:其中,
$ \mathop \alpha \nolimits_i $ 表示三角形的3个内角,$ \overline \alpha $ 表示3个内角的平均值, 单位均为(°),$ \mathop S\nolimits_\alpha $ 的值越大, 3个内角之间的差异越大, 三角形单元表面越不规则.为分析表面结构与结合能之间的关系, 结合表2绘制出准三重位点处结合能(Eb)与单元表面的3个内角标准差(
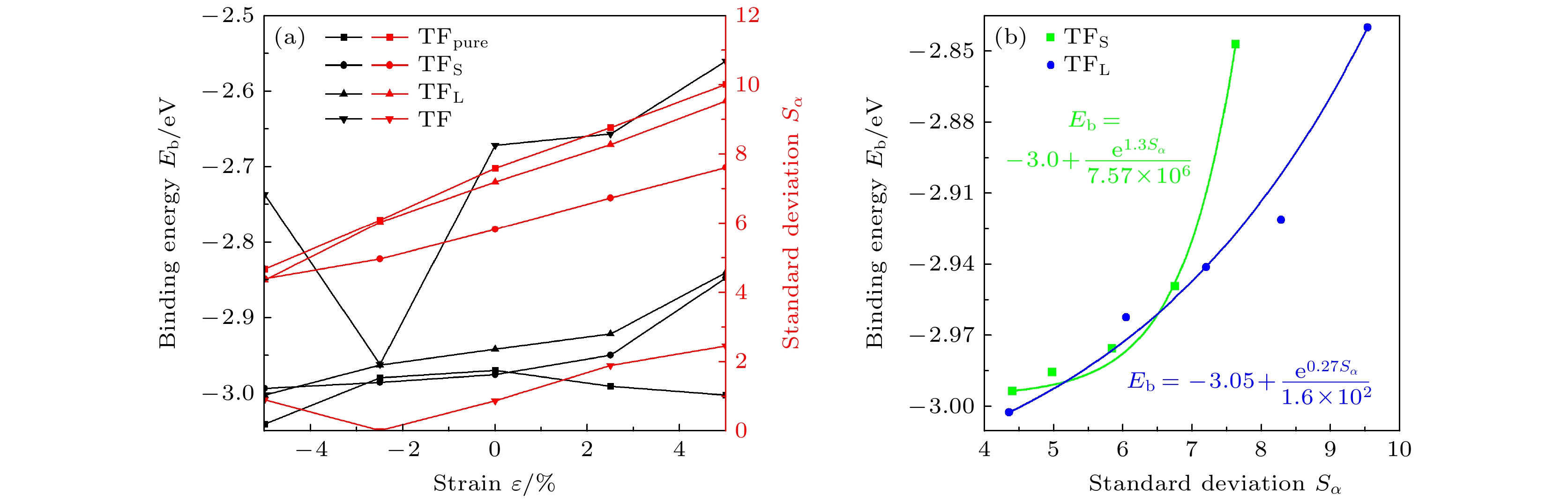
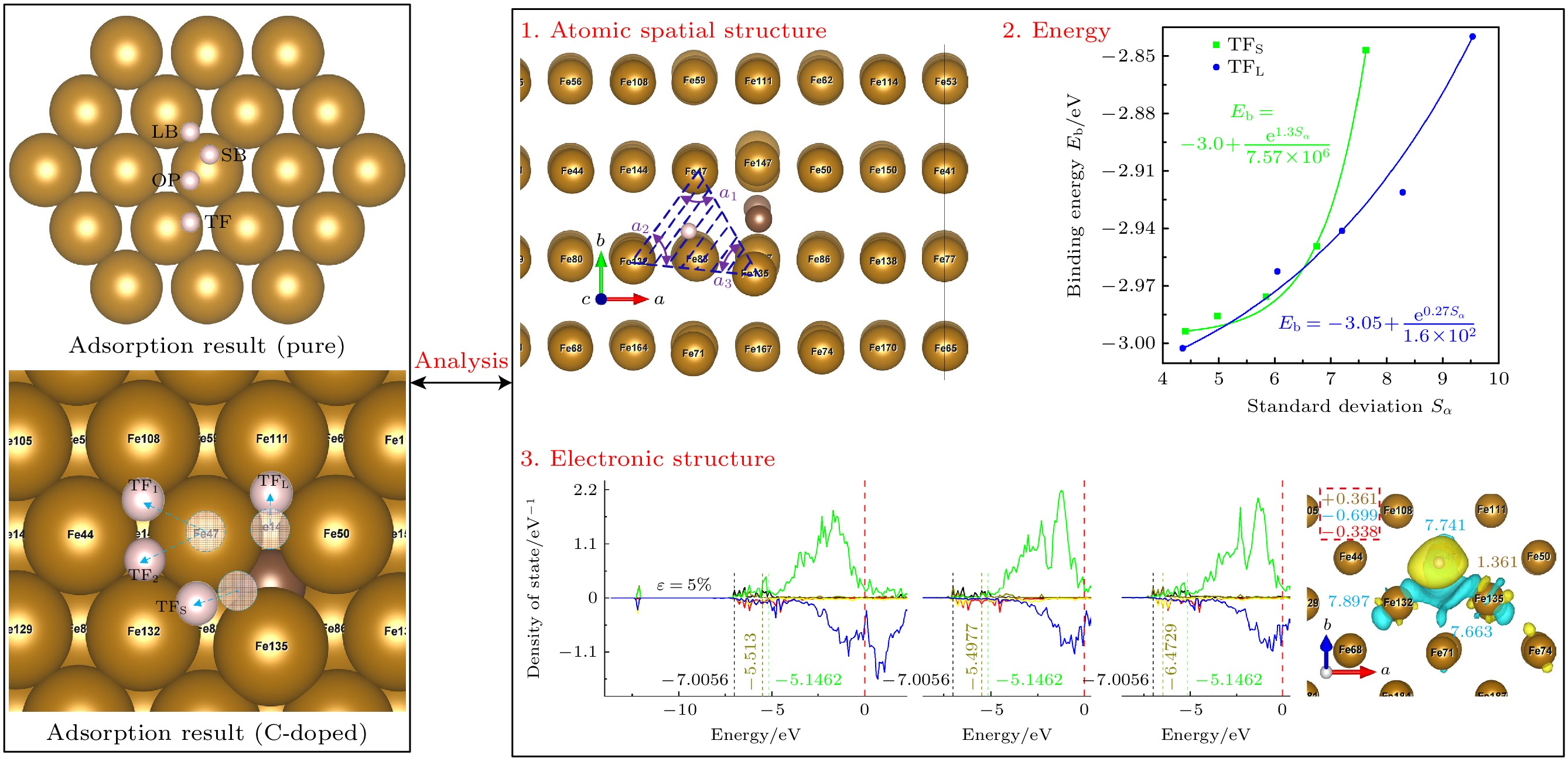
$ \mathop S\nolimits_\alpha $ )在不同预应变(ε)条件下的变化趋势, 如图10(a)所示. 未掺杂C原子时, 当ε由–5%增至5%时, TFpure位点的Eb先增大后减小, 说明ε使得H原子在位点上的结合强度先减小后增大. 掺杂C原子时, 当ε由–5%增至5%时, TF位点的Eb先减小后增大, 说明ε使得H原子在位点上的结合强度先增大后减小; TFS, TFL位点的Eb均单调增大, 说明ε使得H原子在位点上的结合强度单调减小. 掺杂C原子时, 各位点处的Eb与$ \mathop S\nolimits_\alpha $ 的变化趋势呈现出较强的关联性, Eb与$ \mathop S\nolimits_\alpha $ 的大小呈正相关. 利用这种相关性, 虽然H原子的位置难以直接观测, 但可以凭借表面Fe原子的状态判断相关位点处的Eb. 由于TF位置处Eb普遍比TFS, TFL和TFpure处高太多, 其吸附不稳定, 因此在C掺杂时给出TFS, TFL位点处Eb与$ \mathop S\nolimits_\alpha $ 的拟合曲线, 如图10(b)所示, 其函数形式为指数函数, 如(4)式:其中, e为自然常数; A, B, C为常数.
TF位点处, 在ε = –2.5%时, 单元表面的3个内角分别为59.97°, 59.99°, 60.04°,
$ \mathop S\nolimits_\alpha $ 最小, 造成结合能最小, 接近TFS和TFL位点的结合能. 实际上, TFpure, TF, TFS和TFL位点是3类不同的位点: TFpure的H吸附时既不受畸变影响, 也不受C原子的影响, TF的H吸附时既受畸变影响, 也受C原子的直接影响. 这可能是造成TFpure和TF位点上H的Eb在单轴预应变作用下表现出相反趋势的原因. TFS和TFL位点H吸附时受C的影响较小, 主要受Fe原子畸变影响. 这可能是造成TFS和TFL位点处H的Eb在单轴预应变作用下表现出的趋势既不同于无C时的情况, 也不同于直接受C原子作用情况的原因, C原子本身也直接影响预应变条件下结合能的变化趋势. -
Fe(110)表面吸附的H原子向内部扩散, 需要综合考虑H原子在位点处的Eb, d以及S∆L(H吸附后单元表面积). 稳定吸附位点处Eb越大(H原子与表面结合强度越低), d越小, S∆L越大, H原子迁移到子层的机会越大, 原子氢越容易扩散到微观结构中, 对钢构成危险[31]. 表3列出了各准三重位点处H吸附后S∆L的大小, 与吸附前相比, H吸附Fe(110)表面后会造成对应的单元表面积减小.
为探究预应变对C掺杂Fe(110)表面的H原子向内部扩散的影响, 选取TFS位点分析其Eb, d以及S∆L, 如图11所示. 当在拉伸阶段, TFS位点Eb, S∆L持续增大, d持续减小, 说明拉应变使H原子更容易扩散到微观结构中; 在压缩阶段, 虽然d在–2.5%至–5%压缩阶段略有减小, 但是Eb, S∆L持续减小, 说明压缩使H原子更难扩散到微观结构中.
ε = 0%时, 与TFpure处位相比, TFS位点Eb略低, 但差值仅为0.008 eV, 可忽略不计; TFS位点d更小且S∆L更大; 从吸附结构上来看, TFS位点H原子有更容易扩散到微观结构中的可能 性, 然而, H原子从表层扩散到次表层, 还受C原子本身的影响, 如图11(b)所示, C原子p轨道和H原子s轨道存在重叠, 说明C, H原子之间存在相互作用. 在未掺杂时, 体相中H原子通过从四面体间隙向最近的四面体位置迁移而扩散[50], 采用攀爬微动弹性带(CI-NEB)方法[51], 对H从表面扩散到内部的最小能量路径(MEPs)和过渡态 进行了计算. 图11(c)所示为H原子扩散路径. 图11(d)所示为H原子扩散能垒(E∆), 得到TFpure位点从表面到次表面需克服的势垒为1.045 eV, 与Li等[33] (1.05 eV)和Jiang等 [52] (1.02 eV)的研究非常吻和; 而TFS处从表面到次表面需克服的势垒为1.416 eV, 表明C原子掺杂使扩散能垒增大0.371 eV, 这与Zhu等[53]的研究结论一致, C原子掺杂会增大表面到次表面的扩散能垒. 图11(d)显示TFS处E∆随ε增大而减小, 说明压缩应变 使H原子更难扩散到微观结构中, 拉应变使H原子更容易扩散到微观结构中, 此结论与前文分析结论一致. 同时结合图10(a)发现, TFS, TFpure处的E∆和Eb有更强的关联性, 二者随ε变化趋势 相反.
-
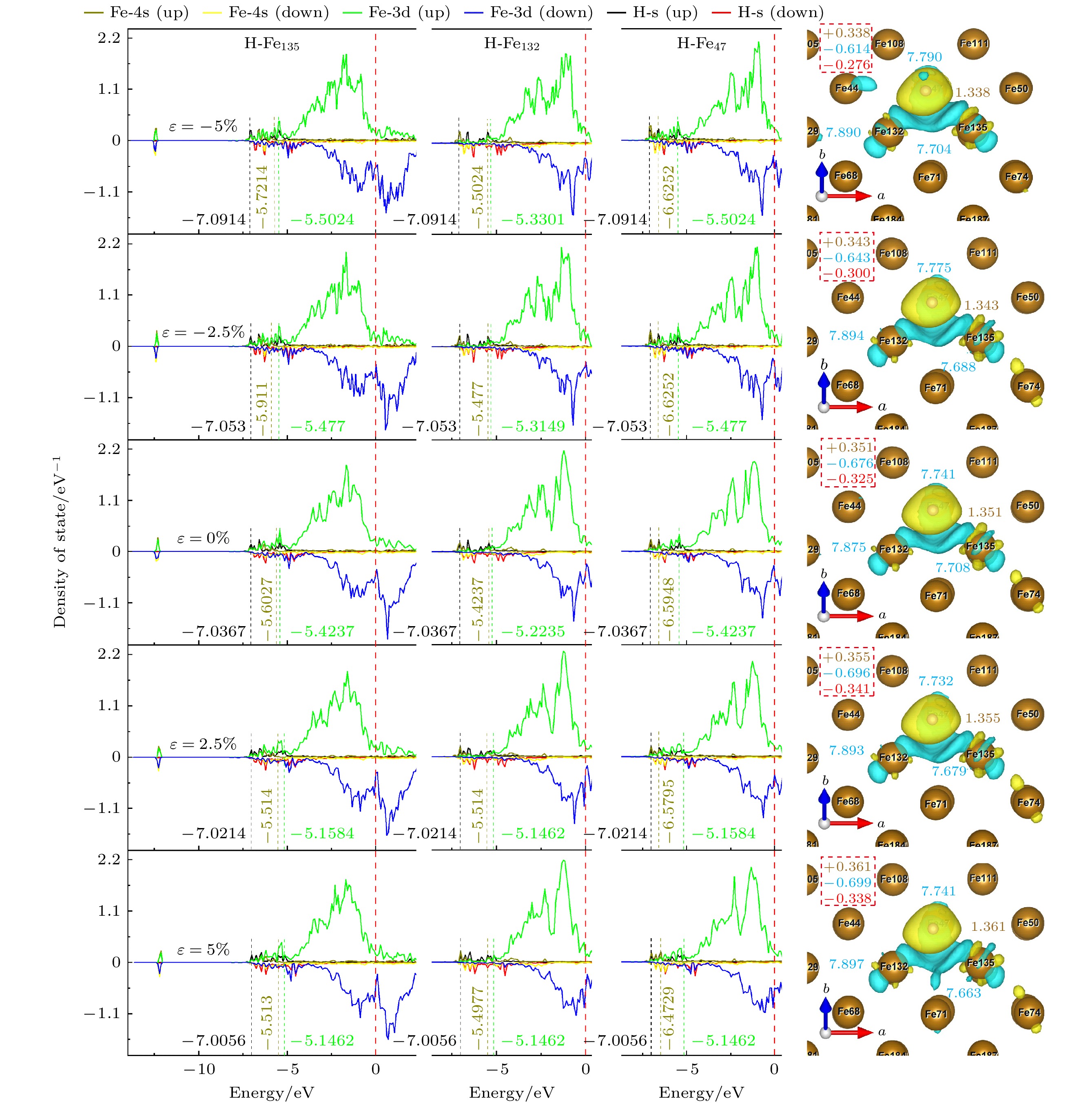
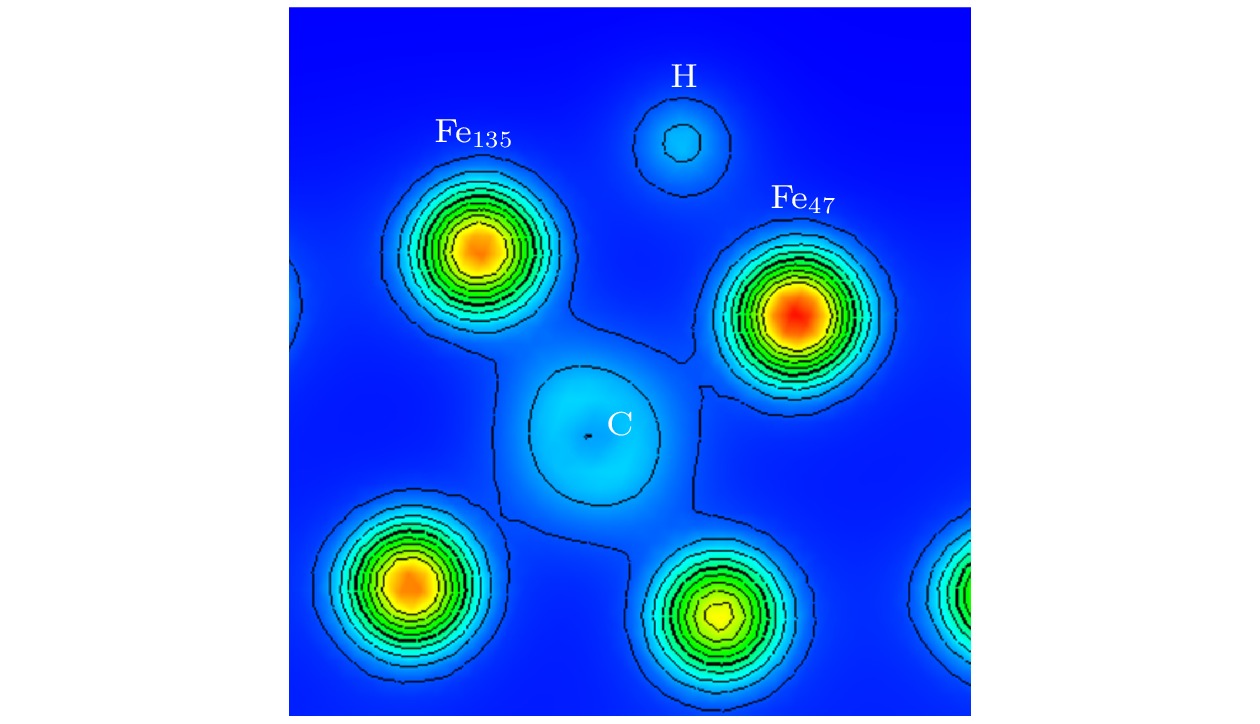
图12所示为ε从–5%增至5%时, TFS位点处原子分波态密度[54]及Bader电荷分布. H原子的s轨道与配位Fe原子的3d, 4s轨道在–7.1至–5 eV之间重叠, Bader电荷空间分布表明H原子得到更多的电荷(从1.338e增至1.361e). 这是与张凤春等[55]在无C掺杂时的研究结果一致, 他们也认为H会从Fe上得到电荷. 在TFS位点处, 3个配位Fe原子电荷分布存在明显差异, 电荷分布不均匀, 产生了极性, H原子得到的总电荷与配位Fe原子失去的总电荷并不相等, 例如在ε = 0%时, Fe原子多失了–0.325e的电荷, 一个可能的原因是这部分电荷被C原子得到了一部分, 因而与H原子发生相斥, 造成位点处H原子难以扩散进入体相内部(与未掺杂C原子相比). 图13所示为ε = 0%时Fe135, H, C原子组成的平面上电荷密度, C原子与Fe原子之间存在键合作用.
综上所述, 远离C原子的H向内部的扩散不受C影响, 而TFS位点处C原子周围的H难以扩散进入钢铁内部, C掺杂使H富集在C杂质周围而导致氢脆, Wang等[56]对钛合金的研究认为随表面H覆盖率升高, 表面能和表面断裂功下降, 可诱发解理断裂, 张江林等[57]也认为H局部积累会导致氢脆. 同时, 预应变增大使掺杂处的空间几何结构和结合能改变(d减小, Eb, S∆L增大), 使H更容易向内部扩散.
-
本文采用第一性原理的计算方法, 原子尺度上, 将H原子吸附表面时预应变导致的表面结构变化与最终吸附结构相联系, 从表面原子空间构型、结合能、电子结构3个方面探究了预应变对H吸附、渗透影响, 并计算了扩散能垒加以验证, 主要得到以下结论.
1)掺杂C原子使Fe(110)晶胞的八面体发生了畸变, 导致表面Fe原子在空间内偏离了原来的理想位点, 继而导致不同位点处H原子在不用预应变条件下的吸附规律不同.
2)当H原子从表面向次表面扩散时, 与TFpure位点(未掺杂C原子的位点)相比, 即使TFS位点(掺杂C原子的位点)处的空间几何结构更适合H原子扩散, 但H原子受C原子本身的排斥作用, TFS处位扩散能垒仍然高于TFpure处, 导致TFS位点处C原子周围的H难以扩散进入钢铁内部, H富集在C杂质周围而导致氢脆.
3) TFS位点处, 随着拉伸应变增大, H原子越容易扩散到钢的微观结构中, 随着压缩应变增大, H原子越难扩散到钢的微观结构中, 可利用压缩应变减小钢中氢脆的发生.
单轴预应变对C掺杂Fe(110)表面H吸附、扩散的影响
Effect of uniaxial pre-strain on H adsorption and diffusion on C-doped Fe (110) surface
-
摘要: 为了从微观结构层次进一步深入研究和完善预应变/预应力与H吸附钢(Fe-C合金)表面的作用机制, 采用第一性原理的方法计算了单轴预应变对C掺杂Fe(110)表面的H吸附和扩散的影响, 从表面原子空间构型、结合能(Eb)、电子结构3个方面探究预应变对H吸附和渗透的影响, 并计算了掺杂和未掺杂C原子时H渗透的扩散能垒. 结果表明, 掺杂的C原子使Fe晶体的八面体空间在不同方向上发生畸变, 从而使Fe(110)表面产生“畸变”, 不同位点处畸变程度(D∆)和离C原子本身的距离不一致, 导致各位点在预应变下的吸附结构(H吸附高度d和单元表面积S∆)与结合能(Eb)变化趋势不一致, 扩散能垒变化趋势与结合能变化趋势相反. 研究发现, H吸附在C掺杂位点时, 吸附结构和结合能计算结果显示H有更容易扩散到内部中的趋势, 而电子结构计算结果显示C原子与H原子相斥, 扩散能垒相较于未掺杂时升高, H原子难以扩散进入体相内部而在C周围富集, 继而诱发氢脆. 吸附结构、结合能、扩散能垒计算结果显示: 在掺杂位点(TFS位点)处, 随着拉伸应变增大, H原子越容易扩散到钢的微观结构中, 随着压缩应变增大, H原子越难扩散到钢的微观结构中, 可利用压缩应变减小钢中氢脆的发生. 这从微观层面解释了实际工程应用中“同等应力情况下, C越多, 钢铁发生氢脆的倾向越严重”的原因, 从电子结构层次完善了预应变下H吸附钢(Fe-C合金)表面的作用机制, 可对氢脆的研究提供参考.Abstract: In order to further investigate and improve the mechanism of the interaction between pre-strain/pre-stress and hydrogen-adsorbed steel (Fe-C alloy) surface at the microstructural level, the first-principles calculations method is used to study the effects of uniaxial pre-strain on hydrogen adsorption and diffusion on C-doped Fe(110) surface. The influence of pre-strain on hydrogen adsorption and permeation is investigated from three aspects: surface atomic spatial configuration, binding energy (Eb), and electronic structure. The diffusion energy barriers for hydrogen permeation are calculated in both doped and undoped C atoms. The results demonstrate that doped C atoms induce octahedral lattice distortion in Fe crystals in different directions, creating “distortion” on the Fe(110) surface. Variations in distortion degree (DΔ) at different sites and their distances from C atom lead to inconsistent trends in adsorption configurations (H adsorption height d and unit surface area SΔ) and binding energy (Eb) under pre-strain. For adsorption configurations, d is coupled by ε and C atom effects: at the TFpure site (non-C-doped site ), d decreases as SΔ increases; under compression (ε decreases from 0% to –5%) at TF (C-doped site with C atom directly beneath the site), TFS (C-doped site located closer to the maximally distorted atom Fe135) and TFL sites (C-doped site located farther from the maximally distorted atom Fe135), d positively correlates with DΔ, while under tension (ε increases from 0% to 5%), d negatively correlates with SΔ. As ε increases from –5% to 5%, Eb peaks at TFpure then declines, whereas Eb at TF decreases initially before rising, and Eb at TFS/TFL monotonically increases. The analysis hows that Eb at TFS/TFL positively is correlated with the standard deviation (Sα) of the three internal angles in the triangular unit. The trend of diffusion energy barrier (E∆) is opposite to that of Eb. When H is adsorbed at C-doped sites, the adsorption configuration and binding energy calculations indicate that H tends to diffuse inward more readily. However, electronic structure analysis reveals repulsion between C and H atoms, accompanied by increased diffusion barriers compared with the scenarios in the undoped cases, causing H atoms to accumulate around C atoms rather than penetrate the bulk phase, thereby leading hydrogen atoms to embrittle. The calculations of adsorption configuration, binding energy, and diffusion barrier indicate that at doped sites (TFS site), increasing tensile strain can contribute to H diffusion into the steel microstructure, whereas compressive strain hinders it. This explains the engineering phenomenon where “higher carbon content exacerbates hydrogen embrittlement tendency under equivalent stress” on an atomic scale. This work elucidates the mechanism of H adsorption on pre-strained Fe-C alloy surfaces from an electronic structure perspective, providing theoretical ideas for studying hydrogen embrittlement.
-
Key words:
- first principles /
- α-Fe(C) /
- pre-strain /
- H adsorption .
-

-
图 1 Fe(110)表面原子排列和吸附位点, H吸附位点分别为长桥位点(LB)、短桥位点(SB)、准三重位点(TF)和顶部位点(OP), 最近的两个Fe原子之间的距离为2.48 Å; LB, SB, TF位点到OT位点的侧向距离分别为2.02, 1.24, 1.52 Å
Figure 1. Atom arrangement and symmetry sites on Fe(110). The H adsorption sites are long bridge site (LB), short bridge site (SB), quasi triple site (TF) and top site (OP), respectively; the distance between the nearest two Fe atoms is 2.48 Å, the lateral distances from LB, SB, TF sites to OT sites are 2.02, 1.24, 1.52 Å, respectively.
图 2 晶体模型 (a) 3×3×4扩胞; (b)切(110)面; (c)纯铁晶体模型; (d) 3×3×4扩胞; (e)切(110)面; (f) 中碳钢晶体模型; 绿色面为(110)面, 粉色面为切割面, 以此为界将晶体模型切割, 后续计算将在切割面上添加真空层
Figure 2. Crystal model: (a) 3 × 3 × 4 cell expansion; (b) cut (110) face; (c) pure iron crystal model; (d) 3 × 3 × 4 cell expansion; (e) cut (110) face; (f) crystal model of medium carbon steel. The green surface is (110) side, the pink surface is the cutting surface, which is used as the boundary to cut the crystal model, subsequent calculations will add a vacuum layer on the cutting surface.
图 4 掺杂吸附模型, 图中蓝色原子表示体心原子; 掺杂时, 整个表面都发生畸变, 以离C原子最近的吸附位点为研究对象: OP位点位于Fe47顶部, COP位点位于Fe135顶部, SB位点位于Fe47和Fe135之间, LB位点位于Fe47和Fe50之间, TF位点位于Fe47, Fe50, Fe135组成的三角形区域
Figure 4. H-adsorption model (C-doped). Blue atoms represent body centered atoms; when doped, the whole surface is distorted, the adsorption site nearest to the C atom is taken as the research object: OP site is at the top of Fe47, COP site is at the top of Fe135, SB site is between Fe47 and Fe135, LB site is between Fe47 and Fe50, TF site is in the triangular region composed of Fe47, Fe50 and Fe135.
图 6 ε = 0%时OP (a)和COP (b)位点差分电荷差分电荷密度空间分布(黄色区域代表得电子, 表示高电子密度; 蓝色区域代表失电子, 表示低电子密度)
Figure 6. Differential charge space distribution of OP (a) and COP (b) at ε = 0%. The yellow area represents electrons, indicating high electron density, and the blue area represents electron loss, indicating low electron density.
图 7 不稳定点吸附结过示意图(掺杂C), 虚圆代表氢原子起始位点, 位于OP位点的H原子在应变为–5%和5%的作用下迁移至TF1位点, 在–2.5%, 0%, 2.5%的情况下迁移至TF2位点; 位于SB位点的H原子迁移至TFS位点; 位于LB位点的氢原子迁移至TFL位点
Figure 7. Adsorption results of unstable site (C-doped). The dotted circles represent the starting site of hydrogen atom, the H atom at the OP site migrates to the TF1 site at the strain of –5% and 5%, and to the TF2 site at the strain of –2.5%, 0%, 2.5%, the H atom located at the SB site migrates to the TFS site, H atom at LB site migrates to TFL site.
图 12 TFS位点态密度和Bader电荷, 其中右图黄色字体为H原子上的电荷, 蓝色字体为3个配位Fe原子的电荷, 虚线框内为H, Fe原子得失总电荷以及它们的差值(红色字体)
Figure 12. State density and Bader charge of TFS site. The charge on the H atom is shown in the right panel by the yellow font, the charge on the three coordinated Fe atoms by the blue font, and the total charge gain or loss of the H and Fe atoms as well as their difference (shown in red type) is included in the dashed box.
表 1 基底表面畸变处参数
Table 1. Parameters of the substrate model at the distortion.
应变ε/% 未掺杂 掺杂 dSB dLB dz lFe47/50-O lFe135-O dSB dLB dz lFe47/50-C lFe135-C –5.0 2.426 2.665 2.044 1.962 1.438 2.731 2.677 2.482 1.915 1.811 –2.5 2.426 2.735 2.016 1.973 1.421 2.761 2.762 2.447 1.935 1.802 0.0 2.423 2.805 1.994 1.985 1.404 2.773 2.826 2.418 1.952 1.789 2.5 2.434 2.875 1.978 2.002 1.393 2.772 2.884 2.421 1.963 1.789 5.0 2.442 2.946 1.952 2.018 1.379 2.806 2.958 2.446 1.976 1.794 注: dSB为短桥距离, 为Fe47和Fe135之间的距离; dLB为长桥距离, 为Fe47和Fe50之间的距离; dz为最大畸变的Fe原子(Fe135)到次表面Fe原子之间的平均垂直距离, lFe-C为C原子与配位Fe原子之间的键长; lFe-O为Fe原子到八面体中心之间的距离; 以上长度单位均为Å. 表 2 结合能Eb (单位为eV)
Table 2. Binding energy Eb (Unit: eV).
ε/% 未掺杂 掺杂 OP COP SB LB TF OP COP SB LB TF –5 –2.419 –2.421 –2.911 –2.901 –3.040 –3.105* –2.438 –2.993* –3.002* –2.736 –2.5 –2.360 –2.358 –2.850 –2.853 –2.979 –3.083* –2.436 –2.985* –2.962* –2.961 0 –2.360 –2.361 –2.829 –2.893 –2.969 –3.059* –2.419 –2.975* –2.941* –2.671 2.5 –2.369 –2.367 –2.841 –2.937 –2.990 –3.051* –2.389 –2.949* –2.921* –2.656 5 –2.387 –2.388 –2.849 –1.411 –3.002 –3.120* –2.290 –2.847* –2.840* –2.560 注: *表示位点不稳定, 最终吸附位点为附近的准三重位点. 表 3 H吸附后单元表面积S∆L
Table 3. Unit surface area of H-adsorption S∆L.
ε/% S∆L/Å2 TFpure TFS TFL TF –5 2.715 2.909 2.751 2.936 –2.5 2.759 2.954 2.797 2.998 0 2.746 2.988 2.83 3.03 2.5 2.812 3.048 2.829 3.047 5 2.856 3.069 2.858 3.061 -
[1] Teng Y, Wang Z D, Li Y, Ma Q, Hui Q, Li S B 2019 Csee J. Power Energy 5 266 doi: 10.17775/CSEEJPES.2019.00190 [2] 张博, 万宏, 徐可忠, 李雪静, 魏寿祥 2017 国际石油经济 25 65 doi: 10.3969/j.issn.1004-7298.2017.01.017 Zhang B, Wan H, Xu K Z, Li X J, Wei S X 2017 Int. Pet. Econ. 25 65 doi: 10.3969/j.issn.1004-7298.2017.01.017 [3] Dodds P E, Mcdowall W 2013 Energy Policy 60 305 doi: 10.1016/j.enpol.2013.05.030 [4] Buzzard R W, Cleaves H E 1951 Hydrogen Embrittlement of Steel-Review of Literature (United States: National Bureau of Standards) p36 [5] 刘松, 王寅岗 2015 中国有色金属学 25 3100 doi: 10.19476/j.ysxb.1004.0609.2015.11.018 Liu S, Wang M G 2015 Trans. Nonferrous Met. Soc. China 25 3100 doi: 10.19476/j.ysxb.1004.0609.2015.11.018 [6] 胡世威, 梁浩, 徐兵 2019 航空学报 40 278 doi: 10.7527/S1000-6893.2019.22796 Hu S W, Liang H, Xu B 2019 Acta Aeronaut. Astronaut. Sin. 40 278 doi: 10.7527/S1000-6893.2019.22796 [7] Cheng A K, Chen N Z 2017 Int. J. Fatigue 96 152 doi: 10.1016/j.ijfatigue.2016.11.029 [8] Cheng A K, Chen N Z 2017 Ocean Eng. 142 10 doi: 10.1016/j.oceaneng.2017.06.057 [9] Meda U S, Bhat N, Pandey A, Subramanya K N, Lourdu Antony Raj M A 2023 Int. J. Hydrogen Energ. 48 17894 doi: 10.1016/j.ijhydene.2023.01.292 [10] Nanninga N, Grochowsi J, Heldt L, Rundman K 2009 Corros. Sci. 52 1237 doi: 10.1016/j.corsci.2009.12.020 [11] Nanninga N E, Levy Y S, Drexler E S, Condon R T, Stevenson A E, Slifka A J 2012 Corros. Sci. 59 1 doi: 10.1016/j.corsci.2012.01.028 [12] Zhou C S, Ye B G, Song Y Y, Cui T C, Xu P, Zhang L 2019 Int. J. Hydrogen Energ. 44 22547 doi: 10.1016/j.ijhydene.2019.04.239 [13] Toofan J, Watson P R 1998 Surf. Sci. 401 162 doi: 10.1016/S0039-6028(97)01031-5 [14] Russell B C, Castell M R 2008 Phys. Rev. B 77 245414 doi: 10.1103/PhysRevB.77.245414 [15] Lord M A, Evans E J, Barnett J C, Allen W M, Barron R A, Wilks P S 2017 J. Phys. Condens. Mat. 29 384001 doi: 10.1088/1361-648X/aa7dc8 [16] 李守英, 胡瑞松, 赵卫民, 李贝贝 王勇 2020 表面技术 49 15 doi: 10.16490/j.cnki.issn.1001-3660.2020.08.002 Li S Y, Hu R S, Zhao W M, Li B B, Wang Y 2020 Surf. Technol. 49 15 doi: 10.16490/j.cnki.issn.1001-3660.2020.08.002 [17] 胡庭赫, 李直昊, 张千帆 2024 物理学报 73 067101 doi: 10.7498/aps.73.20231735 Hu T H, Li Z H, Zhang Q F 2024 Acta Phys. Sin. 73 067101 doi: 10.7498/aps.73.20231735 [18] 赵巍, 汪家道, 刘峰斌, 陈大融 2009 物理学报 58 3352 doi: 10.7498/aps.58.3352 Zhao W, Wang J D, Liu F B, Chen D R 2009 Acta Phys. Sin. 58 3352 doi: 10.7498/aps.58.3352 [19] Yoshida K 1980 Jpn. J. Appl. Phys. 19 1873 doi: 10.1143/JJAP.19.1873 [20] 唐秀艳 2016 硕士学位论文(青岛: 中国石油大学(华东)) Tang X Y 2016 M. S. Thesis (Qingdao: China University of Petroleum (East China) [21] Savoie J, Ray R K, Butron-Guillen M P, Jonas J J 1994 Acta Metall. Mater. 42 2511 doi: 10.1016/0956-7151(94)90332-8 [22] Cremaschi P, Yang H, Whitten J L 1995 Surf. Sci. 330 255 doi: 10.1016/0039-6028(95)00244-8 [23] Bozso F, Ertl G, Grunze M, Weiss M 1977 Appl. of Surf. Sci. 1 103 doi: 10.1016/0378-5963(77)90009-5 [24] Baró A M, Erley W 1981 Surf. Sci. 112 L759 doi: 10.1016/0039-6028(81)90324-1 [25] Xie W W, Peng L, Peng D L, Gu F L, Liu J 2014 Appl. Surf. Sci. 296 47 doi: 10.1016/j.apsusc.2014.01.028 [26] Eder M, Terakura K, Hafner J 2001 Phys. Rev. B 64 115426 doi: 10.1103/PhysRevB.64.115426 [27] Raeker J T, DePristo E A 1990 Surf. Sci. 235 84 doi: 10.1016/0039-6028(90)90109-L [28] Chohan K U, Jimenez M E, Koehler P K S 2016 Appl. Surf. Sci. 387 385 doi: 10.1016/j.apsusc.2016.06.027 [29] Xu L, Kirvassilis D, Bai Y, Mavrikakis M 2018 Surf. Sci. 667 54 doi: 10.1016/j.susc.2017.09.002 [30] Richard T, Zihan X, Balachandran R, Donald W, Wenhao S, Kristin A P, Ping O S 2016 Sci. Data 3 160080 doi: 10.1038/sdata.2016.80 [31] Sheikhzadeh A, Liu J, Zeng Y M, Zhang H 2024 Int. J. Hydrogen Energ. 81 727 doi: 10.1016/j.ijhydene.2024.07.317 [32] 李守英, 赵卫民, 乔建华, 王勇 2019 物理学报 68 217103 doi: 10.7498/aps.68.20190660 Li S Y, Zhao W M, Qiao J H, Wang Y 2019 Acta Phys. Sin. 68 217103 doi: 10.7498/aps.68.20190660 [33] Li S Y, Zhao W M, Wang Y 2020 Chin. J. Struc. Chem. 39 443 doi: 10.14102/J.CNKI.0254-5861.2011-2499 [34] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758 doi: 10.1103/PhysRevB.59.1758 [35] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558 [36] Blochl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [37] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865 [38] Liu X W, Huo C F, Li Y W, Wang J G, Jiao H J 2012 Surf. Sci. 606 733 doi: 10.1016/j.susc.2011.12.018 [39] Jiang D E, Carter A E 2005 Phys. Rev. B 71 045402 doi: 10.1103/PhysRevE.71.057103 [40] Dong N, Zhang C, Liu H, Li J, Wu X L 2014 Comp. Mater. Sci. 90 137 doi: 10.1016/j.commatsci.2014.04.005 [41] Stibor A, Kresse G, Eichler A, Hafner J 2002 Surf. Sci. 507 99 doi: 10.1016/S0039-6028(02)01182-2 [42] Spencer J S M, Hung A, Snook K I, Yarovsky I 2002 Surf. Sci. 515 L464 doi: 10.1016/S0039-6028(02)01975-1 [43] Arya A, Carter A E 2003 J. Chem. Phys. 118 8982 doi: 10.1063/1.1565323 [44] Shih H D, Jona F, Bardi U, Marcus P M 1980 J. Phys. C: Solid State Phys. 13 3801 doi: 10.1088/0022-3719/13/19/021 [45] Xu C, O’Connor D J 1991 Nucl. Instrum. Meth. B 53 315 doi: 10.1016/0168-583X(91)95620-S [46] Shen X J, Chen J, Sun Y M, Liang T S 2016 Surf. Sci. 654 48 doi: 10.1016/j.susc.2016.08.005 [47] Jiang D E, Carter A E 2003 Surf. Sci. 547 85 doi: 10.1016/j.susc.2003.10.007 [48] 杨勇, 赫全锋 2021 金属学报 57 385 doi: 10.11900/0412.1961.2020.00359 Yang Y, He Q F 2021 Acta Metall. Sin. 57 385 doi: 10.11900/0412.1961.2020.00359 [49] Li X J, Lin S Y, Zhou W Z, Ma Y, Jiang N B, Liu Z 2024 Int. J. Hydrogen Energ. 51 894 doi: 10.1016/j.ijhydene.2023.05.338 [50] He Y, Li Y J, Chen C F, Yu H B 2017 Int. J. Hydrogen Energ. 42 27438 doi: 10.1016/j.ijhydene.2017.08.212 [51] Henkelman G, Uberuaga P B, Jónsson H 2000 J. Chem. Phys. 113 9901 doi: 10.1063/1.1329672 [52] Jiang D E, Carter A E 2004 Phys. Rev. B 70 064102. doi: 10.1103/PhysRevB.70.064102 [53] Zhu L X, Luo J H, Zheng S L, Yang S J, Hu J, Chen Z 2023 Int. J. Hydrogen Energ. 48 17703 doi: 10.1016/j.ijhydene.2023.01.150 [54] 刘飞, 文志鹏 2019 物理学报 68 137101 doi: 10.7498/aps.68.20182282 Liu F, Wen Z P 2019 Acta Phys. Sin. 68 137101 doi: 10.7498/aps.68.20182282 [55] 张凤春, 李春福, 文平, 罗强, 冉曾令 2014 物理学报 63 227101 doi: 10.7498/aps.63.227101 Zhang F C, Li C F, Wen P, Luo Q, Ran Z L 2014 Acta Phys. Sin. 63 227101 doi: 10.7498/aps.63.227101 [56] Wang C M, Zhang L J, Ma Y J, Zhang S Z, Yang R, Hu Q M 2023 Appl. Surf. Sci. 621 156871 doi: 10.1016/j.apsusc.2023.156871 [57] 张江林, 王仲民, 王殿辉, 胡朝浩, 王凤, 甘伟江, 林振琨 2023 物理学报 72 168801 doi: 10.7498/aps.72.20230132 Zhang J L, Wang Z M, Wang D H, Hu C H, Wang F, Gan W J, Lin Z K 2023 Acta Phys. Sin. 72 168801 doi: 10.7498/aps.72.20230132 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: