高级搜索

基于信息熵赋权的多通道卷积神经网络节点重要性评估方法

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

姜廷帅, 阮逸润, 李海, 白亮, 袁逸飞, 于天元. 基于信息熵赋权的多通道卷积神经网络节点重要性评估方法[J]. 物理学报, 2025, 74(12): 126401-1. doi: 10.7498/aps.74.20250329
引用本文: 姜廷帅, 阮逸润, 李海, 白亮, 袁逸飞, 于天元. 基于信息熵赋权的多通道卷积神经网络节点重要性评估方法[J]. 物理学报, 2025, 74(12): 126401-1. doi: 10.7498/aps.74.20250329
shu
Tingshuai JIANG, Yirun RUAN, Hai LI, Liang BAI, Yifei YUAN, Tianyuan YU. Entropy-based weighted multi-channel convolutional neural network method for node importance assessment[J]. Acta Physica Sinica, 2025, 74(12): 126401-1. doi: 10.7498/aps.74.20250329
Citation: Tingshuai JIANG, Yirun RUAN, Hai LI, Liang BAI, Yifei YUAN, Tianyuan YU. Entropy-based weighted multi-channel convolutional neural network method for node importance assessment[J]. Acta Physica Sinica, 2025, 74(12): 126401-1. doi: 10.7498/aps.74.20250329
shu

基于信息熵赋权的多通道卷积神经网络节点重要性评估方法

  • 1.

    国防科技大学系统工程学院, 长沙　410073

  • 2.

    吉林大学计算机科学与技术学院, 长春　130012

    • 作者简介: 姜廷帅: jiangtingshuai19@nudt.edu.cn; 阮逸润: ruanyirun@163.com .
    通讯作者: E-mail: ty.yu@nudt.edu.cn.

  • 中图分类号: 64.60.aq, 89.75.Hc, 89.75.Fb

Entropy-based weighted multi-channel convolutional neural network method for node importance assessment

  • 1.

    College of Systems Engineering, National University of Defense Technology, Changsha 410073, China

  • 2.

    College of Computer Science and Technology, Jilin University, Changchun 130012, China

    • Corresponding author: E-mail: ty.yu@nudt.edu.cn

  • MSC: 64.60.aq, 89.75.Hc, 89.75.Fb

  • 摘要: 利用定量分析的方法识别复杂网络中的关键节点, 或者评估某节点相对于其他一个或多个节点的重要程度, 是网络科学研究的热点问题. 针对节点重要性识别中存在的指标权重主观赋值和全局和局部信息融合不足等问题, 本文提出一种基于信息熵赋权的多通道卷积神经网络框架(entropy-based weighted multi-channel convolutional neural network framework, EMCNN). 该方法构建了一种无参熵权分配模型, 通过计算不同节点重要性指标的熵权值, 突破了传统方法依赖经验参数的局限性. 同时, 对全局与局部信息进行解耦重构, 构建多通道特征图, 并结合卷积神经网络的特征提取能力和注意力机制的关键特征融合能力, 实现全局与局部特征的深度融合学习, 从而更精准地识别网络节点的重要性. 为验证该方法的有效性, 本文在9个真实世界网络和3个合成网络上利用SIR模型进行仿真实验, 结果表明EMCNN方法有效克服了评估角度的局限性, 能在不同传播率下对节点的传播影响力进行有效评估, 在相关性及准确性上优于当前主流算法.
    Abstract: Identifying key nodes in complex networks or evaluating the relative node importance with respect to others by using quantitative methods is a fundamental issue in network science. To address the limitations of existing approaches—namely the subjectivity in assigning weights to importance indicators and the insufficient integration of global and local structural information—this paper proposes an entropy-weighted multi-channel convolutional neural network framework (EMCNN). First, a parameter-free entropy-based weight allocation model is constructed to dynamically assign weights to multiple node importance indicators by computing their entropy values, thereby mitigating the subjectivity inherent in traditional parameter-setting methods and enhancing the objectivity of indicator fusion. Second, global and local structural features are decoupled and reconstructed into separate channels to form multi-channel feature maps, which significantly enhance the representational capacity of the network structure. Third, by leveraging the feature extraction capabilities of convolutional neural networks and the integration power of attention mechanisms, the framework extracts deep representations of nodes from the multi-channel feature maps, while emphasizing key structural information through attention-based weighting, thus enabling more accurate identification and characterization of node importance. To validate the effectiveness of the proposed method, extensive experiments are conducted on nine real-world networks by using the SIR spreading model, thereby assessing performance in terms of correlation, accuracy, and robustness. The Kendall correlation coefficient is used as the primary evaluation metric to measure the consistency between predicted node importance and actual spreading influence. Additionally, experiments are performed on three representative synthetic networks to further test the model’s generalizability. Experimental results demonstrate that EMCNN consistently and effectively evaluates node influence under varying transmission rates, and significantly outperforms mainstream algorithms in both correlation and accuracy. These findings highlight the powerful generalization ability and wide applicability of this method in the identification of key nodes in complex networks.
  • 加载中

  • 图 1  EMCNN框架识别过程

    Figure 1.  EMCNN framework identification process.

    下载: 全尺寸图片 幻灯片

    图 2  一跳邻接矩阵${\boldsymbol{E}}$提取示意图, 展示了从一个包含8个节点和11条边的局部网络中, 获取节点3的大小为$L = 5$的一跳邻接矩阵, 首先识别与节点3直接相连的邻居节点(节点1, 2, 4, 6, 7), 并依据其度值${W^{{\text{DC}}}}$进行降序排序, 随后根据排序后的节点顺序构建出节点3的一跳邻接矩阵${{\boldsymbol{E}}_3}$

    Figure 2.  Illustration of one-hop adjacency matrix ${\boldsymbol{E}}$ extraction. The figure shows the process of extracting a one-hop adjacency matrix of size $L = 5$ for node 3 from a local network with 8 nodes and 11 edges, the direct neighbors of node 3 (nodes 1, 2, 4, 6, and 7) are first identified and then sorted in descending order based on their degree values ${W^{{\text{DC}}}}$, finally, the one-hop adjacency matrix ${{\boldsymbol{E}}_3}$ is constructed according to the sorted neighbor order.

    下载: 全尺寸图片 幻灯片

    图 3  参数分析

    Figure 3.  Parameter analysis.

    下载: 全尺寸图片 幻灯片

    图 4  8种方法预测的节点影响力与SIR传播感染节点数的相关性(由于各算法在评分机制和输出尺度上的差异, 横坐标的取值范围不一致)　(a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa

    Figure 4.  Correlation between the node influence predicted by eight algorithms and the number of infected nodes simulated by the SIR model: (a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa. Due to differences in scoring mechanisms and output scales among the algorithms, the horizontal axis values are not on a unified scale.

    下载: 全尺寸图片 幻灯片

    图 5  8种节点排序性方法在9个真实网络上的Kendall相关系数对比　(a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa

    Figure 5.  Comparison of Kendall correlation coefficient for 8 node ranking methods on 9 networks: (a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa.

    下载: 全尺寸图片 幻灯片

    图 6  不同比例节点下8种评估算法的Kendall相关系数对比　(a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa

    Figure 6.  Comparison of Kendall correlation coefficients of 8 node influence evaluation algorithms under different scale nodes: (a) Facebook; (b) Netscience; (c) Protain; (d) Yeast; (e) CA-GrQc; (f) Lesmis; (g) Jazz; (h) USAir; (i) Faa.

    下载: 全尺寸图片 幻灯片

    图 7  合成网络数据集上8种评估算法的Kendall相关系数对比　(a) LFR2000-5; (b) LFR2000-10; (c) BA200-4

    Figure 7.  Comparison of Kendall correlation coefficients of 8 evaluation algorithms on synthetic networks datasets: (a) LFR2000-5; (b) LFR2000-10; (c) BA200-4.

    下载: 全尺寸图片 幻灯片

    表 1  真实网络参数描述

    Table 1.  Parameters description of real networks.

    网络$N$$E$$\langle d\rangle $${\beta _{{\text{th}}}}$$\beta $$\langle k\rangle $$C$$k{s_{\max }}$
    CA-GrQc4158134226.0490.05560.066.45590.55643
    Facebook32422183.0530.04660.0513.6910.46518
    Netscience3799146.0410.12460.134.82320.7418
    Protain278367264.8390.06330.074.4720.0716
    Yeast145819486.8120.14030.152.67210.075
    Lesmis772542.6410.08290.096.59740.5739
    Jazz19827422.2350.02580.0327.6960.61729
    USAir33221262.2730.02250.0312.8070.426
    Faa122624085.9280.13590.143.92820.0674
    下载: 导出CSV

    表 2  合成网络参数描述

    Table 2.  Parameters description of synthetic networks.

    网络$N$$E$$\langle d\rangle $${\beta _{{\text{th}}}}$$\beta $$\langle k\rangle $$C$$k{s_{\max }}$
    LFR2000-52000100345.698360.098360.150.377398
    LFR2000-102000206344.472040.072270.08100.4104111
    BA500-45009963.715120.096170.140.058802
    下载: 导出CSV
  • [1] Lü L Y, Chen D B, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1 doi: 10.1016/j.physrep.2016.06.007
    [2] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200 doi: 10.1103/PhysRevLett.86.3200
    [3] Albert R, Barabási A L 2002 Rev. Modern Phys. 74 47 doi: 10.1103/RevModPhys.74.47
    [4] Zeng Y 2020 Neurocomputing 416 158 doi: 10.1016/j.neucom.2019.05.092
    [5] Albert R, Jeong H, Barabási A L 1999 Nature 401 130 doi: 10.1038/43601
    [6] Lü L, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168 doi: 10.1038/ncomms10168
    [7] Xu X, Zhu C, Wang Q Y, Zhu X Q, Zhou Y 2020 Sci. Rep. 10 2691 doi: 10.1038/s41598-020-59616-w
    [8] Brin S, Page L 1998 Computer Networks and ISDN Systems 30 107 doi: 10.1016/S0169-7552(98)00110-X
    [9] Freeman L C 1977 Sociometry 40 35 doi: 10.2307/3033543
    [10] Sabidussi G 1966 Psychometrika 31 581 doi: 10.1007/BF02289527
    [11] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888 doi: 10.1038/nphys1746
    [12] Bonacich P 1987 Am. J. Sociology 92 1170 doi: 10.1086/228631
    [13] Lü L, Zhang Y C, Yeung C H, Zhou T 2011 PLoS One 6 21202 doi: 10.1371/journal.pone.0021202
    [14] Curado M, Tortosa L, Vicent J F 2023 Inform. Sci. 628 177 doi: 10.1016/j.ins.2023.01.097
    [15] Ullah A, Wang B, Sheng J F, Long J, Khan N, Sun Z J 2021 Expert Syst. Appl. 186 115778 doi: 10.1016/j.eswa.2021.115778
    [16] Liu W Z, Lu P L, Zhang T 2023 IEEE Trans. Comput. Soc. Syst. 11 2105 doi: 10.1109/TCSS.2023.3295177
    [17] Ruan Y R, Liu S Z, Tang J, Guo Y M, Yu T Y 2024 Expert Syst. Appl. 268 126292 doi: 10.1016/j.eswa.2024.126292
    [18] Rezaei A A, Munoz J, Jalili M, Khayyam H 2023 Expert Syst. Appl. 214 119086 doi: 10.1016/j.eswa.2022.119086
    [19] Li X Y, Zhang Z J, Liu J M, Gai K K 2019 Proceedings of the 2019 ACM International Symposium on Blockchain and Secure Critical Infrastructure New York, USA, May 9–12, 2019 p13
    [20] Zhao G H, Jia P, Zhou A M, Zhang B 2020 Neurocomputing 414 18 doi: 10.1016/j.neucom.2020.07.028
    [21] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowl-Based Syst. 198 105893 doi: 10.1016/j.knosys.2020.105893
    [22] Zhang M, Wang X J, Jin L, Song M, Li Z Y 2022 Neurocomputing 497 13 doi: 10.1016/j.neucom.2022.05.010
    [23] 王博雅, 杨小春, 卢升荣, 唐勇平, 洪树权, 蒋惠园 2024 物理学报 73 226401 doi: 10.7498/aps.73.20240937 Wang B Y, Yang X C, Lu S R, Tang Y P, Hong S Q, Jiang H Y 2024 Acta Phys. Sin. 73 226401 doi: 10.7498/aps.73.20240937
    [24] Chen L Y, Xi Y, Dong L, Zhao M J, Li C L, Liu X, Cui X H 2024 Inf. Process. Manag. 61 103775 doi: 10.1016/j.ipm.2024.103775
    [25] Tang J X, Qu J T, Song S H, Zhao Z L, Du Q 2024 J. King Saud Univ. –Comput. Inf. Sci. 36 102183 doi: 10.1016/j.jksuci.2024.102183
    [26] Zhang P, Wang J L, Li X J, Li M H, Di Z R, Fan Y 2008 Physica A 387 6869 doi: 10.1016/j.physa.2008.09.006
    [27] Zhang J X, Chen D B, Dong Q, Zhao Z D 2016 Sci. Rep. 6 27823 doi: 10.1038/srep27823
    [28] Hajarathaiah K, Enduri M K, Dhuli S, Anamalamudi S, Cenkeramaddi L R 2023 IEEE Access 11 808 doi: 10.1109/ACCESS.2022.3232288
    [29] Sheng J F, Dai J Y, Wang B, Duan G H, Long J, Zhang J K, Guan K R, Hu S, Chen L, Guan W H 2020 Physica A 541 123262 doi: 10.1016/j.physa.2019.123262
    [30] Kermack W O, McKendrick A G 1927 Proc. R. Soc. Lond. Ser. A - Contain. Pap. Math. Phys. Charact. 115 700 doi: 10.1098/rspa.1927.0118
    [31] Bae J, Kim S 2014 Physica A 395 549 doi: 10.1016/j.physa.2013.10.047
    [32] Kendall M G 1945 Biometrika 33 239 doi: 10.1093/biomet/33.3.239
    [33] Barabási A L, Albert R 1999 Sci. 286 509 doi: 10.1126/science.286.5439.509
    [34] Dorogovtsev S N, Goltsev A V, Mendes J F F 2006 Phys. Rev. Lett. 96 040601 doi: 10.1103/PhysRevLett.96.040601
    [35] Blagus N, Šubelj L, Bajec M 2012 Physica A 391 2794 doi: 10.1016/j.physa.2011.12.055
    [36] Newman M E J 2006 Phys. Rev. E 74 036104 doi: 10.1103/PhysRevE.74.036104
    [37] Rual J F, Venkatesan K, Hao T, Hirozane-Kishikawa T, Dricot A, Li N, Berriz G F, Gibbons F D, Dreze M, Ayivi-Guedehoussou N, Klitgord N, Simon C, Boxem M, Milstein S, Rosenberg J, Goldberg D S, Zhang L V, Wong S L, Franklin G, Li S M, Albala J S, Lim J, Fraughton C, Llamosas E, Cevik S, Bex C, Lamesch P, Sikorski R S, Vandenhaute J, Zoghbi H Y, Smolyar A, Bosak S, Sequerra R, Doucette-Stamm L, Cusick M E, Hill D E, Roth F P, Vidal M 2005 Nature 437 1173 doi: 10.1038/nature04209
    [38] Jeong H, Mason S P, Barabási A L, Oltvai Z N 2001 Nature 411 41 doi: 10.1038/35075138
    [39] Knuth D E 1993 The Stanford GraphBase: A Platform for Combinatorial Computing (New York: ACM Press
    [40] Gleiser P M, Danon L 2003 Adv. Complex Syst. 6 565 doi: 10.1142/S0219525903001067
    [41] Colizza V, Pastor-Satorras R, Vespignani A 2007 Nat. Phys. 3 276 doi: 10.1038/nphys560
    [42] Kunegis J 2013 Proceedings of the 22nd International Conference on World Wide Web Rio de Janeiro, Brazil, May 13–17, 2013 p1343
    [43] Batagelj V, Mrvar A 1998 Connections 21 47 doi: 10.1007/978-3-642-18638-7_4
  • 加载中
图( 7) 表( 2)
计量
  • 文章访问数:  26
  • HTML全文浏览数:  26
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-12
  • 刊出日期:  2025-06-20

基于信息熵赋权的多通道卷积神经网络节点重要性评估方法

    通讯作者: E-mail: ty.yu@nudt.edu.cn.
    作者简介: 姜廷帅: jiangtingshuai19@nudt.edu.cn ; 阮逸润: ruanyirun@163.com
  • 1. 国防科技大学系统工程学院, 长沙　410073
  • 2. 吉林大学计算机科学与技术学院, 长春　130012
  • 收稿日期:  2025-03-12

摘要: 利用定量分析的方法识别复杂网络中的关键节点, 或者评估某节点相对于其他一个或多个节点的重要程度, 是网络科学研究的热点问题. 针对节点重要性识别中存在的指标权重主观赋值和全局和局部信息融合不足等问题, 本文提出一种基于信息熵赋权的多通道卷积神经网络框架(entropy-based weighted multi-channel convolutional neural network framework, EMCNN). 该方法构建了一种无参熵权分配模型, 通过计算不同节点重要性指标的熵权值, 突破了传统方法依赖经验参数的局限性. 同时, 对全局与局部信息进行解耦重构, 构建多通道特征图, 并结合卷积神经网络的特征提取能力和注意力机制的关键特征融合能力, 实现全局与局部特征的深度融合学习, 从而更精准地识别网络节点的重要性. 为验证该方法的有效性, 本文在9个真实世界网络和3个合成网络上利用SIR模型进行仿真实验, 结果表明EMCNN方法有效克服了评估角度的局限性, 能在不同传播率下对节点的传播影响力进行有效评估, 在相关性及准确性上优于当前主流算法.

English Abstract

    全文HTML

    1.   引　言

    • 网络节点重要性排序是网络科学研究的核心议题, 旨在识别对网络结构和功能影响较大的重要节点[1]. 设计高效、准确的关键节点识别算法在理论和实际应用中均具有重要价值. 例如, 在病毒传播网络中, 通过对关键节点进行干预(如疫苗接种、重点隔离等), 可有效降低传播速度并控制扩散范围[2,3]. 在交通网络中, 找出交通枢纽或高流量路段的关键节点, 并优化其运行, 有助于缓解交通拥堵, 提高通行效率, 并增强应对突发事件的能力. 在电力供应网络中, 识别并加强关键节点的稳定性, 可以降低网络故障风险, 提高电力输送的可靠性, 从而减小大范围停电的可能性, 保障社会正常运作. 因此, 复杂网络理论不仅有助于揭示网络结构的内在机制, 还在优化设计、提升效率及防范网络危机[4]方面具有重要实践价值.

      关于如何挖掘网络关键节点, 已经有了许多研究成果, 传统方法大致可归纳为两类: 基于邻居特征的局部方法、基于路径信息的全局方法. 局部方法主要依赖节点的直接连接信息, 通过邻居数量或邻居质量来评估节点的重要性. 典型代表包括度中心性[5]和H指数[6]等. Xu等[7]提出邻接信息熵方法, 依据节点的邻接程度评估其重要性. Brin和Page[8]提出网页排名中心性(PageRank centrality), 采用随机游走方式对节点进行排名. 全局方法侧重于节点在整体网络结构中的位置与作用, 衡量其在信息传播或路径控制中的地位. 典型代表包括介数中心性[9]、接近中心性[10]和K-shell值[11]等. Bonacich[12]提出特征向量中心性, 通过节点与多个关键节点的连接程度衡量其影响力. Lü等[13]提出了领导者排名中心性(LeaderRank centrality), 通过引入背景节点与所有节点进行双向连接, 在提升排序效果的同时, 提高了对噪声数据的鲁棒性.

      目前也有研究从融合的角度出发, 尝试综合不同的排序指标或结构信息, 以提升节点排序结果的准确性. Curado等[14]提出返回随机游走引力算法, 结合有效距离测度提取局部信息, 并利用通信概率估计获取全局信息. Ullah等[15]提出局部-全局中心性方法, 通过归一化度捕获局部特征, 并结合最短路径长度和邻居度表征全局特征. Liu等[16]提出半局部-全局中心性方法, 基于广义能量熵提取局部信息, 同时结合最短路径长度和聚类系数描述全局特征. Ruan等[17]提出了一种融合全局与局部视角的关键节点识别方法. 该方法先通过聚类识别全局关键节点, 再结合节点邻居的数量与重要性、以及其与全局关键节点的距离综合评估节点影响力.

      近年来, 机器学习和深度学习技术的快速发展推动了多个领域的创新突破, 并为节点重要性评估提供了新的研究视角. Rezaei等[18]提出了扩展机器学习方法(extended machine learning, EML), 该方法利用支持向量回归在部分网络上进行训练, 以预测其他节点的影响力. Li等[19]利用集成学习(ensemble learning, EL), 分析网络鲁棒性并识别关键节点. Zhao等[20]构建基于图卷积网络的深度学习框架(InfGCN), 以4种网络指标和邻居图作为输入, 提高节点影响力评估的精度. Yu等[21]采用卷积神经网络(convolutional neural network, CNN), 将关键节点识别转换为回归任务, 并基于邻接矩阵和节点度提取特征, 以感染规模作为预测目标. Zhang等[22]提出的方法先通过收缩矩阵构建特征矩阵, 再结合图卷积网络和图神经网络预测节点影响力. Wang等[23]提出了多维参数控制的图卷积网络模型, 融合节点属性、邻居关系和结构位置, 通过多层卷积聚合信息, 并引入可调参数以灵活权衡不同维度特征, 从而实现对关键节点的识别. Chen等[24]提出了一种基于transformer的复杂网络中节点影响力识别方法, 该方法以节点自身及其一阶和二阶邻居的特征构建输入序列, 并通过transformer架构实现对节点语义的深度聚合. Tang等[25]提出了一种结合图卷积神经网络与transformer的深度融合模型. 该方法利用图卷积神经网络捕捉节点的局部结构信息, 并结合transformer的自注意力机制以提取网络中的全局依赖关系, 从而构建更加精细的节点表示.

      尽管上述方法在复杂网络节点重要性识别方面取得了一定成效, 但其对经验参数的依赖性较强, 未能充分整合全局与局部信息. 本文基于卷积神经网络, 通过信息熵理论有效融合节点全局与局部特征, 提出了一种基于信息熵赋权的多通道卷积神经网络框架(entropy-based weighted multi-channel convolutional neural network framework, EMCNN). 该方法可以充分挖掘节点结构特征信息, 利用无参熵权分配模型计算各指标的权重, 以优化指标在识别过程中的贡献度分配. 同时对全局与局部信息进行解耦重构, 构建多通道特征图, 并利用卷积神经网络与注意力机制, 实现对全局与局部特征的有效融合和学习, 从而精准评估复杂网络中节点的重要性. 本文提出的EMCNN方法在节点影响力刻画、特征提取及模型泛化能力等方面具有显著优势, 可以为复杂网络分析和优化提供了新的方法论支持.

    2.   相关理论基础

    • 无向无权的复杂网络记为$G$, 其表示形式为$ G = (V, E) $, 其中$V$和$E$分别代表网络中的节点和边. 以往针对节点重要性的研究提出了多种中心性排序方法, 部分结构性指标也常作为辅助特征被引入分析. 本文将对相关方法与指标进行简要论述.

      • 2.1.   度中心性

    • 度中心性[5](degree centrality, DC)是基于局部的网络中心性排序方法, 节点的度由其拥有的相邻节点的个数决定, 度中心性定义如下:

      其中, $ a_{ij} $是网络邻接矩阵中的元素, 表示节点$ i $与节点$ j $之间是否有连接. 度中心性反映了节点的直接影响力, 节点的邻居节点越多, 节点度$ {k_i} $越大.

      • 2.2.   H指数

    • H指数[6](H-index, HI)是为了衡量研究者的科学产出, 表示研究者至少有$h$次引用的$h$篇论文. H指数值越高, 表示研究者的影响力越大, 表示为

      其中, $ {k_{js}} $表示节点$i$的第$s$个邻居的度数, 公式中的运算符$ \xi $返回满足如下条件的最大整数$h$, 即节点$i$至少有$h$个邻居的度数不小于$h$.

      • 2.3.   网页排名中心性

    • 网页排名中心性[8](PageRank centrality, PR)最初被用于网页排名, 认为一个网页的影响力取决于其所获得的反向链接的数量和质量, 其定义如下:

      其中, $ {A_{ij}} $表示邻接矩阵, $ {x_j} $为节点$i$的相邻节点, $ k_j^{{\text{out}}} $为节点$j$的出度, $ \alpha $和$ \beta $为常数.

      • 2.4.   介数中心性

    • 介数中心性[9](betweenness centrality, BC)用于评估某节点在网络中作为“中介桥梁”的能力, 即其在其他节点对之间最短路径上出现的频率. 该指标可表征节点在信息流动过程中的控制力, 计算公式为

      其中, ${g_{st}}$表示在节点$s$与$t$之间的最短路径总数, $n_{st}^i$表示这些最短路径中经过节点$i$的路径条数.

      • 2.5.   接近中心性

    • 接近中心性[10](closeness centrality, CC)衡量的是一个节点与网络中其他节点之间的平均距离. 若某节点与所有其他节点的距离越短, 说明其具有更高的传播效率和更强的中心性, 其计算公式为

      其中, ${d_{ij}}$表示节点$i$与节点$j$之间的最短路径距离, $N$为网络中的总节点数.

      • 2.6.   K-shell值

    • K-shell值[11](K-shell method, KS)用于衡量节点在网络中的结构层级与核心程度. 该方法通过递归剥离低度节点, 将节点划分到不同的壳层中. 具体做法是: 首先移除所有度为1的节点, 并赋予其K-shell值为1. 随着这些节点及其边的删除, 若产生新的度为1的节点, 则继续移除, 直到无此类节点为止. 随后重复该过程, 对度为2, 3等的节点进行处理, 直到网络被完全分解. 最终, 壳层值越大, 表示节点越处于网络的核心位置, 影响力也越强.

      • 2.7.   聚类系数

    • 聚类系数[26](clustering coefficient, CL)用于衡量某一节点邻居之间相互连接的紧密程度, 反映局部网络的聚集性. 对于某节点$i$, 若其邻居之间连接得越密集, 其聚类系数越高. 节点聚类系数的计算公式为

      其中, ${e_i}$表示节点$i$的邻居节点之间实际存在的连接边数, ${k_i}$为节点$i$的度数.

      • 2.8.   投票排名中心性

    • 投票排名中心性[27](VoteRank centrality, VR)是一种基于投票机制选择关键传播节点的算法. 其核心思想是通过投票分数确定最具影响力的传播者, 同时已选中的传播者不再参与后续投票, 并削弱其邻居的投票能力.

      • 2.9.   全局相对平均度

    • Hajarathaiah等[28]基于中心性相对变化扩展了中心性方法, 他们通过观察删除特定节点后中心性的变化, 定义了节点的局部和全局中心性测度. 当采用度中心性作为衡量标准时, 该方法对应的全局指标被称为(global relative average degree, GRAD), 具体定义如下:

      其中, $ {d_v} $表示节点$v$的度. 节点$v$在图$G$中的全局相对平均度可表示为

      其中, $ G_v^\prime $表示在删除节点$v$后得到的图.

      • 2.10.   全局-局部分数

    • 全局-局部分数[29](global-local score, GLS)是一种融合节点全局影响力与局部影响力来衡量其综合影响力的方法. 节点$i$的影响力定义为

      其中, $ {\text{glbinflu}}(i) $代表全局影响力, $ {\text{locinflu}}(i) $代表局部影响力. $ {\varGamma _i} $表示节点$i$的邻居集合, $ \# {\text{Com}}(i, j) $表示节点$i$和节点$ j $之间的共同邻居数, ${\lambda _i}$为常数. $p\left( j \right)$表示节点$j$在节点$i$邻居中的相对度数权重, $ {k_j} $表示节点$j$的度数, $ {k_u} $表示节点$i$的邻居$u$的度数.

      • 2.11.   基于图卷积网络的排序方法

    • 基于图卷积网络的深度学习框架[21](InfGCN)是图卷积网络(graph convolutional network, GCN)的扩展, 由输入层、GCN层、3个全连接层和输出层组成. 该模型采用4种中心性度量(度中心性、接近中心性、介数中心性和聚类系数)来表示节点特征. 节点特征经过包含ELU激活函数的GCN层处理, 同时引入了残差连接和dropout技术. 接着, 特征依次通过3个全连接层进行变换, 其中前两层后接ELU激活函数以增强非线性表达能力. 最终, 模型将输出输入至LogSoftmax分类器, 生成归一化的预测结果.

    3.   算法设计与评价标准

      3.1.   基于信息熵赋权的多通道卷积神经网络框架

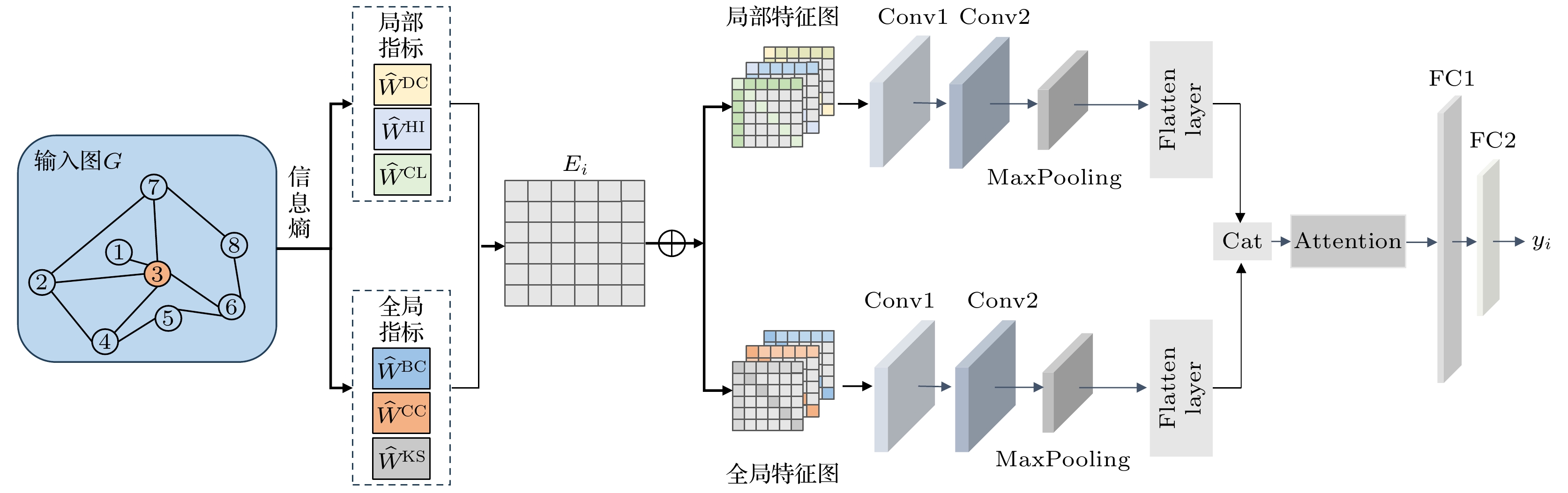
    • 本文针对复杂网络中节点重要性识别存在对经验参数依赖较强、全局与局部结构信息融合不足等问题, 提出了基于信息熵赋权的多通道卷积神经网络框架(EMCNN). 具体而言, 首先通过无参熵权分配模型, 引入信息熵理论对多个网络指标进行客观赋权, 量化各指标的贡献程度; 在此基础上, 构建多通道特征图, 将全局与局部信息解耦重构, 增强特征的可解释性与表达力; 进一步, 通过设计卷积注意力融合模块, 结合卷积操作与注意力机制, 实现全局和局部特征的提取与特征通道的自适应增强, 从而提升模型在关键节点识别任务中的表现. EMCNN的整体框架如图1所示.

      • 3.1.1.   无参熵权分配模型

    • 在复杂网络分析中, 单一指标往往难以全面刻画节点的影响力. 度中心性衡量节点的直接连接数, 反映其基本影响力, 但未考虑连接节点的质量; H指数衡量节点的局部影响力, 结合节点及其邻居的高质量连接, 能够更准确地刻画其在局部网络中的稳定性和重要性; 聚类系数刻画节点所在局部 结构的紧密程度, 反映网络内部的连通性和传播 潜力. 因此, 本文选取度中心性、H指数和聚类系数作为局部指标, 三者结合, 使分析既能关注节点的直接连接情况, 又能衡量其局部影响力和结构特性, 从而更全面地刻画复杂网络的局部特征.

      同时, 选取介数中心性、接近中心性和K-shell值3种指标刻画节点全局特征. 介数中心性衡量节点在最短路径中的重要性, 识别控制网络流通的“桥梁”节点, 反映其在不同群体之间的中介作用; 接近中心性衡量节点到其他所有节点的平均最短路径长度, 揭示其全局可达性和信息传播效率; K-shell识别网络的核心节点, 衡量其在整体结构中的稳固性和影响力. 从全局视角看, 三者结合可以更系统地衡量节点在整个网络中的作用.

      综上, 本文提取了介数中心性(${W^{{\text{BC}}}}$)、接近中心性(${W^{{\text{CC}}}}$)、K-shell值(${W^{{\text{KS}}}}$)、度中心性(${W^{{\text{DC}}}}$)、H-index(${W^{{\text{HI}}}}$)和聚类系数(${W^{{\text{CL}}}}$)六类网络指标. 但在不同类型的复杂网络中, 各指标对节点重要性的贡献不同. 为提高关键节点识别的准确性, 本文在获取六类网络指标后, 引入信息熵来衡量各指标的信息贡献度, 并基于熵权法计算其权重, 计算过程如下.

      首先, 构建决策矩阵. 假设网络包含$c$个节点, 计算每个节点的6个网络指标, 以形成决策矩阵P:

      其中, $ W_i^\theta $表示第$i$个节点的不同网络指标, $\theta \in \left[ {{\text{BC, }} {\text{CC, }} {\text{KS, }} {\text{DC, }} {\text{HI, }} {\text{CL}}} \right]$.

      由于各指标的数值范围不同, 为保证数据的一致性, 对其进行归一化处理, 计算归一化后的值$ \overline W _i^\theta = W_i^\theta \Big/\displaystyle\sum\nolimits_{i = 1}^c {W_i^\theta } $, 得到归一化矩阵R:

      归一化后, 计算每个指标的信息熵:

      式中$ {e^\theta } $反映了每个指标的信息分布情况. 若$ {e^\theta } $大, 说明指标在所有节点上的分布较为均匀, 信息区分度较低, 在关键节点识别中的贡献较小, 因此应赋予较低权重. 反之, 若$ {e^\theta } $小, 则表明指标的分布差异较大, 能够更有效地区分关键节点, 应当赋予较高权重. 因此, 本文基于信息熵计算每个指标的最终权重:

      其中, 权重$ {e^\theta } $表示每个指标的权重. 最后, 根据计算得到的权重对六类网络指标进行加权调整, 得到优化后的指标表示:

      其中, $ \hat W_i^\theta $为每个节点加权后的六类网络指标. 权重的大小反映了对应指标在不同网络中对节点重要性评分的影响程度, 从而提升关键节点识别的精度.

      • 3.1.2.   多通道特征构建

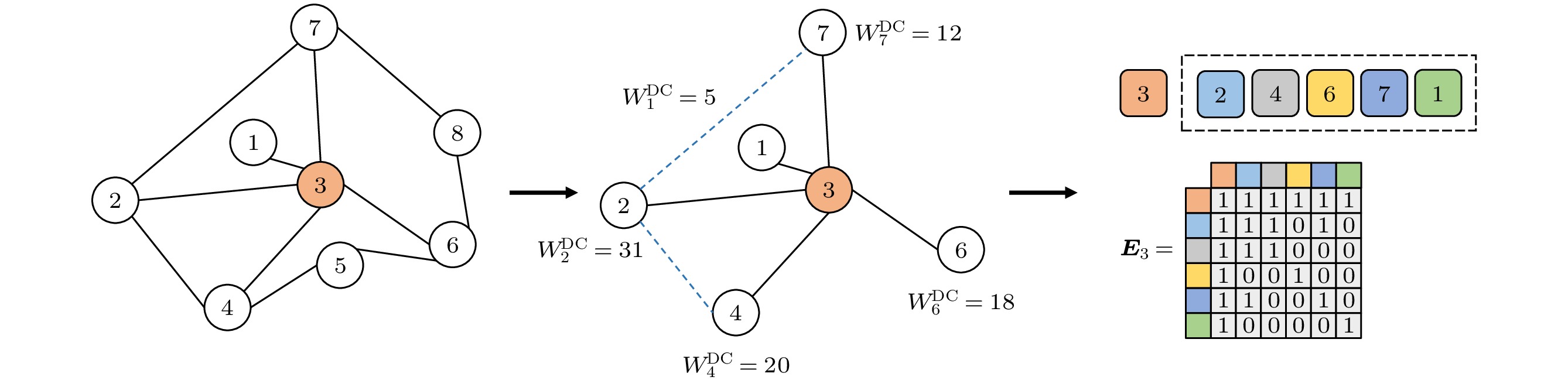
    • 在特征通道构建阶段, 本文设计了一种基于一阶邻域关系的邻接矩阵${\boldsymbol{E}}$生成方法. 具体而言, 对于每个节点, 首先提取其直接邻居, 并按照邻居节点的度值降序排列, 然后从中选取度值最高的$L$个节点构造邻接矩阵${\boldsymbol{E}}$. 在生成的矩阵中, 连接的节点对标记为1, 未连接的节点对标记为0. 若某个节点的邻居数量少于$L$, 则采用零填充以保持矩阵维度一致. 图2展示了一跳邻接矩阵${\boldsymbol{E}}$的生成过程.

      接下来, 将提取的加权指标嵌入一跳邻接矩阵, 为每个节点构建6个特征矩阵, 其定义如下:

      其中, $ {\boldsymbol{E}}_i^{\left( \theta \right)} $表示节点$i$在不同网络指标下构建的一跳邻接特征矩阵, ${a_{nm}}$表示一跳邻接矩阵中第$n$行第$m$列对应的元素, 反映的是排序后邻居节点集合中第$n$个节点与第$m$个节点之间是否存在连接关系. 若两者在网络中有边相连, 则${a_{nm}} = 1$, 否则为0. $\pi \left( n \right)$表示排序后第$n$个邻居节点在网络中的节点编号. 在得到6个特征矩阵后, 将其分为两组特征图, 即基于全局的特征图$F_i^{\left( {{\text{globe}}} \right)} = \{ {\boldsymbol{E}}_i^{\left( {{\text{BC}}} \right)}, {\boldsymbol{E}}_i^{\left( {{\text{CC}}} \right)}, {\boldsymbol{E}}_i^{\left( {{\text{KS}}} \right)} \}$和基于局部的特征图$F_i^{\left( {{\text{local}}} \right)} = \{ {\boldsymbol{E}}_i^{\left( {{\text{DC}}} \right)}, {\boldsymbol{E}}_i^{\left( {{\text{HI}}} \right)}, {\boldsymbol{E}}_i^{\left( {{\text{CL}}} \right)} \}$, 并将其作为输入来训练模型.

      • 3.1.3.   模型预测

    • 本节主要介绍本文设计的基于信息熵赋权的多通道卷积神经网络框架的预测过程. 具体而言, 预测过程包含两个独立的CNN路径, 分别处理全局特征图$F_i^{\left( {{\text{globe}}} \right)}$和局部特征图$F_i^{\left( {{\text{local}}} \right)}$. 每条路径首先通过一个卷积层, 进行初步特征提取, 其中输入通道数为3, 输出通道数为18. 该卷积层主要作用是局部特征的捕捉, 提取初步的空间信息, 并进行通道扩展, 以增强特征表达能力. 随后, 特征图经过Leaky ReLU进行非线性变换, 提升模型的稳定性. Leaky ReLU的数学定义如下:

      其中, $\alpha $是一个小的常数, 取0.1.

      紧接着, 提取的特征进入第2个卷积层, 该层接收来自第1层的18个通道, 并进一步扩展至48个通道, 以提取更深层次的语义信息. 之后跟随一个最大池化层, 用以强化关键特征, 同时保留必要的空间信息, 为后续的处理提供更紧凑、高效的输入表示.

      通过上述卷积与池化操作, 全局特征图$F_i^{\left( {{\text{globe}}} \right)}$和局部特征图$F_i^{\left( {{\text{local}}} \right)}$被有效提取并压缩至更紧凑的表示形式. 随后, 这两个特征图分别经过张量扁平化处理, 转换为一维特征向量, 以便于后续全连接层的输入.

      最终, 模型在特征拼接机制的基础上, 引入注意力机制, 自适应地调整全局特征与局部特征的重要性, 从而实现更高效的特征融合. 具体而言, 全局特征与局部特征在拼接后, 通过一个自适应注意力权重层计算各自的贡献比例, 并进行融合, 使模型能够动态关注最具判别力的信息. 随后, 融合后的特征表示被输入至两层全连接网络, 以进一步学习深层特征. 第1层全连接层采用Leaky ReLU进行非线性变换, 第2层全连接层输出最终的预测值. 训练时采用均方误差作为损失函数, 以最小化模型输出与SIR模型标签之间的误差. 同时, 学习率设为0.001, 确保训练过程稳定高效.

      • 3.2.   评价标准

    • 本文基于易感-感染-恢复模型(susceptible-infected-recovered, SIR)[30]来评估节点的影响力传播过程, 该模型有许多应用, 可以模拟疾病、信息和谣言在社会网络中的传播. SIR模型模拟感染和恢复过程, 通过将节点分为恢复、已被感染和易受感染三类来估计流行病发生的概率. 处于已被感染的节点将以一定的传播率$ \beta $将疾病传播给处于易受感染的邻居节点, 节点被感染后以概率$ \lambda $被治愈呈恢复状态, 此后不再被感染. 当网络中不再有已被感染的节点出现时传播过程终止. 本文所有实验均考虑恢复率$ \lambda = 1 $的情况, 节点经过$M$次信息传播实验后的传播能力定义为

      其中$\varPhi '\left( i \right)$表示其中一次传播实验中, 节点$i$作为起始传播源传播过程终止时处于恢复状态的节点总数.

      为防止过高的感染概率使单个节点影响整个网络并产生不成比例的影响[31], 感染概率参数$ \beta $被调整至网络广泛流行的阈值$ {\beta _{{\text{th}}}} $:

      其中, $ \langle k\rangle $表示网络的平均度, $ \langle {k^2}\rangle $表示网络的二阶平均度. $ {\beta _{{\text{th}}}} $表示网络的临界阈值. 最后本文将$\varPhi \left( i \right)$作为相应节点的标签, 用于模型训练.

      为评估所提算法在节点重要性排序方面的准确性相较其他指标的优势, 本文采用Kendall相关系数[32]来评估不同重要性评估方法的性能, 其定义为

      其中, ${R_1}$和${R_2}$代表$n$个节点的两种不同重要性排序序列, ${n_{\text{c}}}$和${n_{\text{d}}}$分别是这两种排列中同序对和异序对的数量. Kendall相关系数$ \tau $值在[–1, 1]之间变化, $ \tau $值为1表示两个排名完全一致, $ \tau $值为–1表示两个排名完全相反, $ \tau $值为0表示两个排名相互独立.

    4.   实例验证与结果分析

    • 本文通过大量实验验证EMCNN模型的有效性. 由于BA网络在网络科学研究中常作为基准网络, 具备良好的代表性, 能够为模型训练提供可靠基础. 因此在训练阶段, 本文选用具有典型幂律度分布特征、能够较好模拟真实复杂网络结构的BA网络[33] (节点数为1000, 平均度为4)作为输入, 同时以传播率为$\beta = 1.5{\beta _{{\text{th}}}}$的SIR模型生成的节点影响力作为标签. 实验采用Kendall相关系数作为评价指标, 在9种真实网络和3种合成网络上, 与7种基准方法进行对比分析. 最后, 本文结合实验结果对EMCNN模型在不同网络下的表现进行了深入讨论和分析.

      • 4.1.   参数分析

    • 本节围绕EMCNN模型在不同邻居数量配置下的表现开展了参数分析. 实验选取训练网络作为模型输入, 并利用SIR传播模型生成节点的影响力作为标签. 以该网络的训练效果为依据, 评估不同邻居数量设置对关键节点识别准确性的影响.

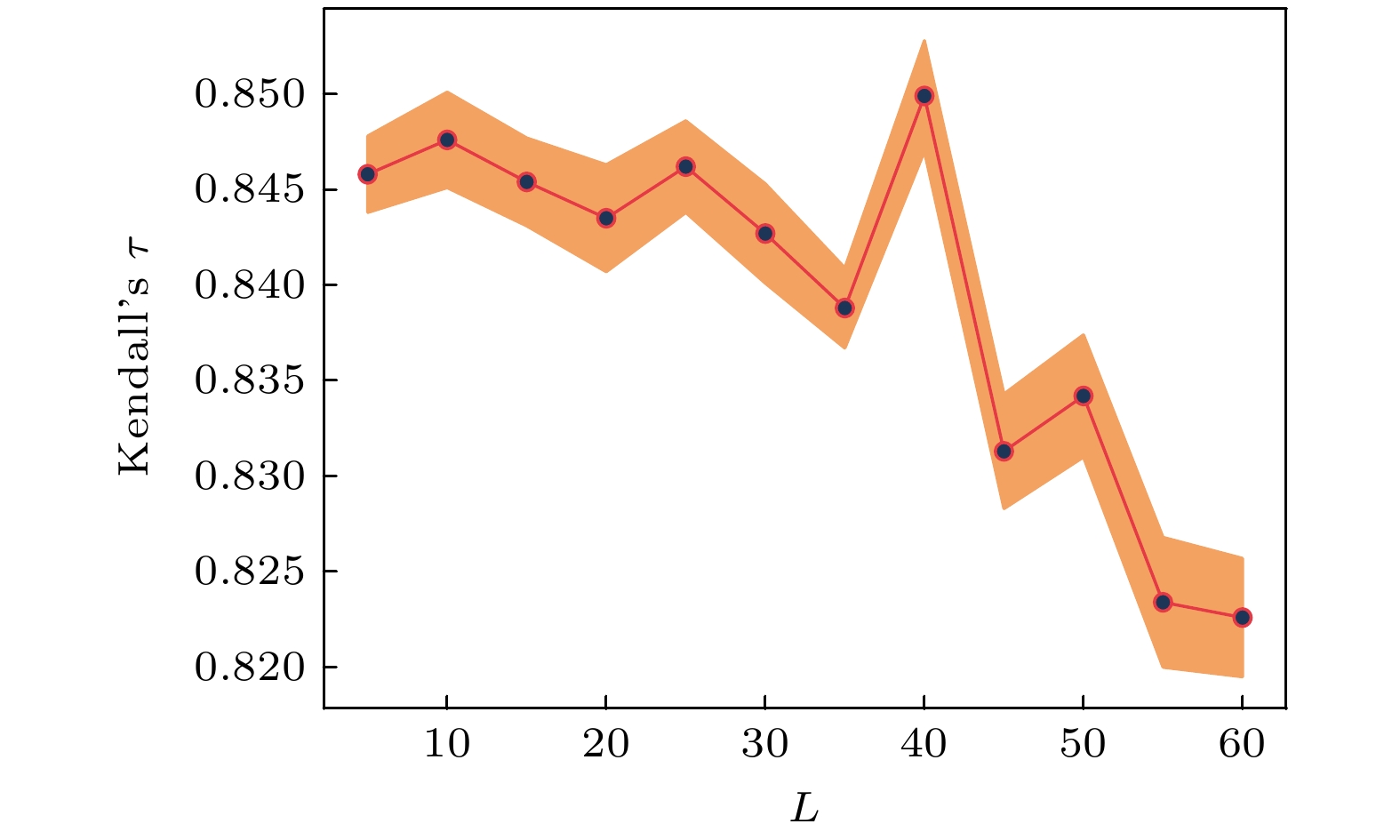
      实验结果如图3所示, 当邻居数量设置$L = 40$时, EMCNN在Kendall相关系数指标上表现最优, 表明在该参数配置下, 模型预测的节点影响力排序与SIR模型生成的真实影响力排序之间具有较高一致性, 排序准确性显著提升. 因此, 本文将$L = 40$作为邻域规模的最优选择, 并在后续实验中采用该参数配置.

      • 4.2.   真实网络验证

    • 为了验证该方法能够普适于不同特征与特性的复杂网络, 本文首先在真实网络数据集中进行验证. 本文选取了9个来自不同领域的真实网络数据集, 应用场景涵盖科研合作网络、社交网络、传染病传播网络和生物网络等网络类型. 分别为CA-GrQc[34](科研合作网络)、Facebook[35](社交关系网络)、Netscience[36](科学家合作关系协作网络)、Protain[37](蛋白质之间相互作用网络)、Yeast[38](蛋白质相互作用网络)、Lesmis[39](小说人物社交网络)、Jazz[40](爵士音乐家关系网络)、USAir[41](美国航空运输网络)和Faa[42](美国联邦航空交通网络). 由于真实世界网络不是完全连通的, 即可能由多个连通分量组成, 因此对9个网络进行处理, 获取每个网络的最大子图, 以减少孤立点或异常情况的影响, 确保实验结果更具统计意义. 关于真实网络的参数介绍见表1, 其中$N$为网络节点个数, $E$为网络边个数, $\langle d\rangle $为平均最短路径长度, ${\beta _{{\text{th}}}}$为SIR模型的感染率阈值, $\beta $为本文设置的感染概率, $\langle k\rangle $为网络平均度, $C$为网络聚类系数, $k{s_{\max }}$为网络的最高度值.

      • 4.2.1.   相关性实验

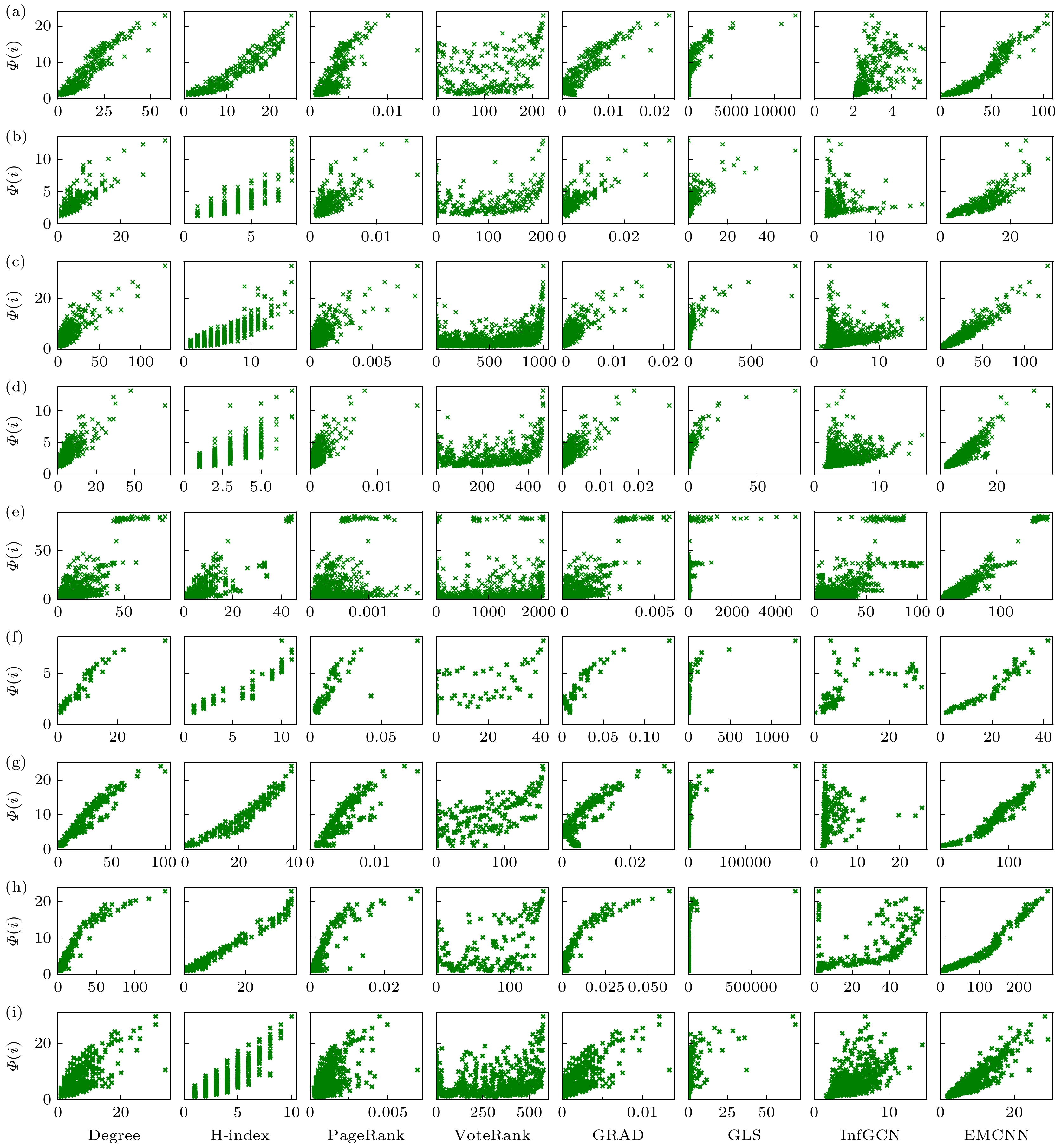
    • 首先分析不同算法预测的节点影响力与SIR模型生成的真实影响力之间的相关性, 按表1中的$\beta $值设置9个网络的感染概率, 独立运行1000次取平均结果, 相关程度越高, 表明相应算法得到的节点重要性排序结果越准确.

      从图4可见, 本文提出的EMCNN与感染数量$\varPhi \left( i \right)$的相关性较高, 且在大多数情况下优于其他算法, 表明该方法能更准确地识别节点的传播影响力. 图中横坐标表示各算法预测的节点影响力值, 纵坐标则为基于SIR模型仿真得到的节点实际感染数量, 即真实传播影响力. 相比之下, 传统度量方法如Degree和H-index与实际影响力的相关性较弱. 这是因为在高度社区化的网络中, 节点间聚集度高, 局部连接限制了度值与全局影响力之间的关联, 从而影响排序精度. PageRank的预测值集中在较小的区间内, 虽然在低影响力区域呈现弱线性关系, 但对高影响力节点的识别效果较差, 主要由于其对随机游走路径的敏感性在强社区化网络中产生偏差, 导致重要节点被低估. 基于深度学习的InfGCN方法表现较差, 原因在于其对全局和局部网络结构信息的融合不够充分, 导致对节点重要性的识别能力不足, 从而影响了预测效果.

      • 4.2.2.   准确性实验

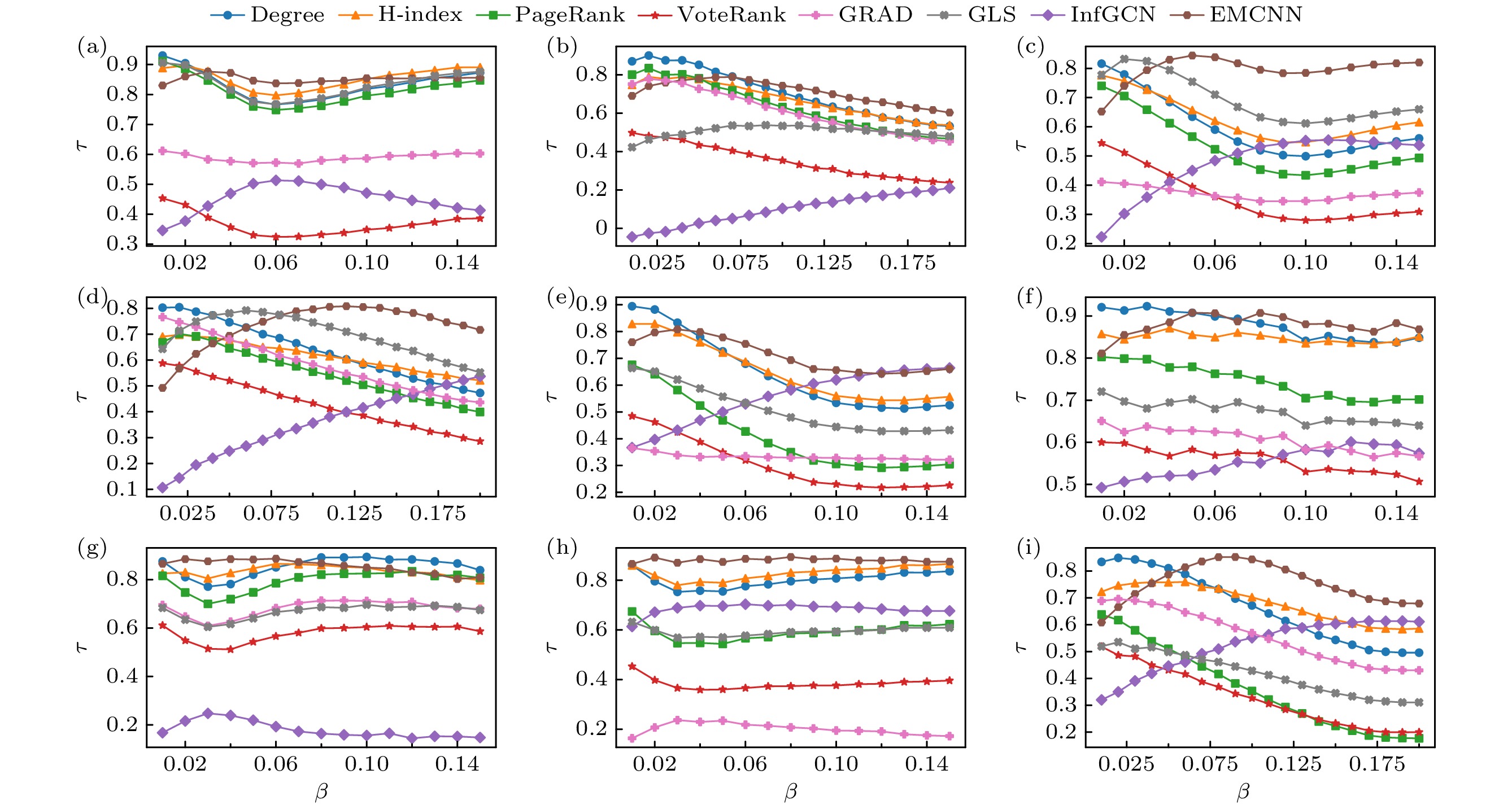
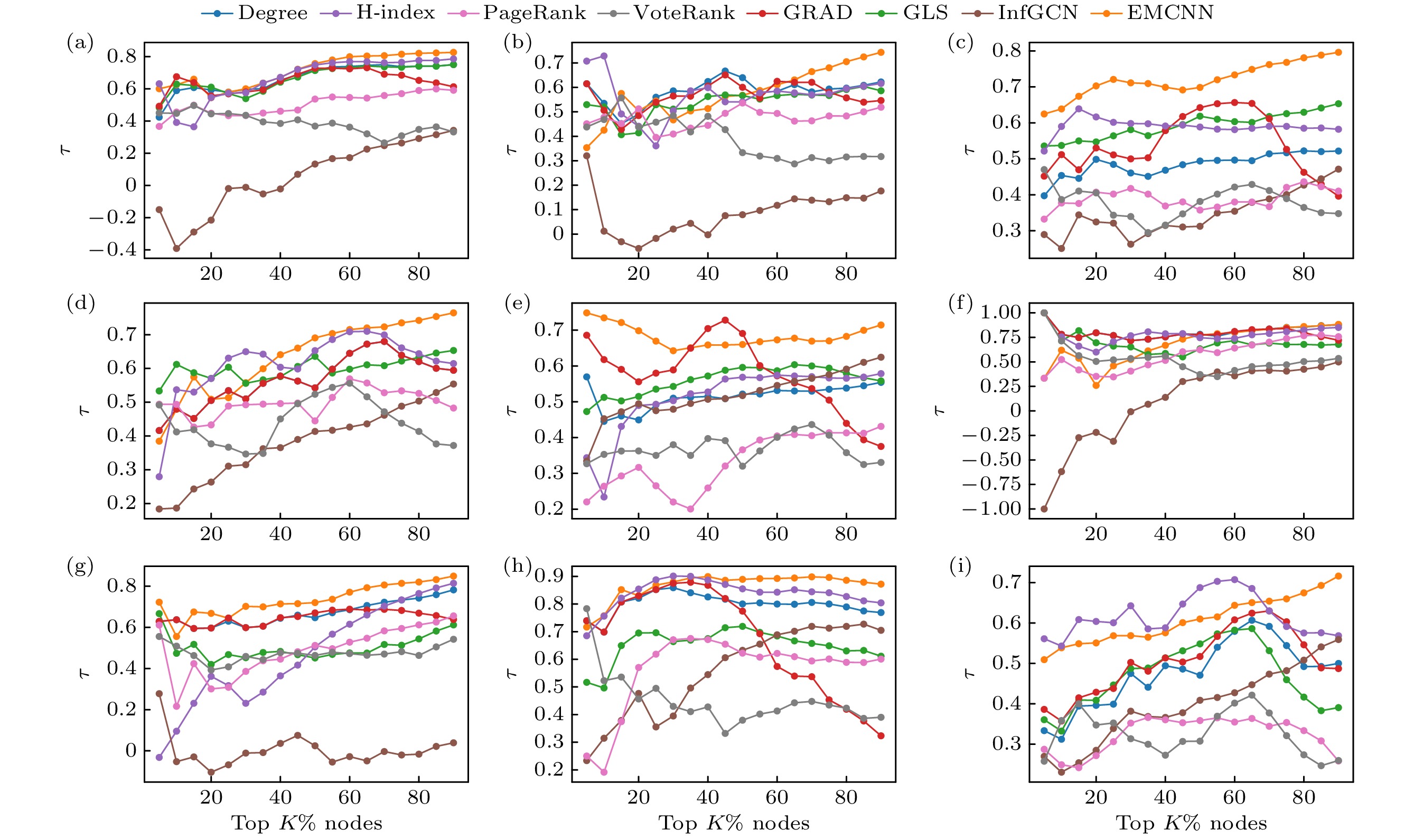
    • 在相关性实验中, 传播率固定, 实验结果仅反映特定传播率下的静态状态. 为了更全面评价各个算法的节点重要性排序精度, 本文采用Kendall相关系数作为准确性度量值, 并将传播率设为$ [0.01, \left|{\beta }_{\text{th}}\right|+7{\text{%}}] $(若$ {\beta }_{\text{th}}\leqslant0.08 $, 传播率区间设为$[ 0.01, 0.15 ]$). 图5展示了实验结果, 其中纵轴表示不同算法预测的节点排序结果与SIR模型生成的真实影响力排序之间的Kendall相关系数. 实验结果表明, EMCNN得到的节点排序结果与真实影响力排序之间的Kendall相关系数在大多数情况下高于其他算法, 证明了其优越性. 尽管PageRank和GRAD方法基于全局信息计算, 但在识别关键节点方面并不具有优势. 同时, Degree和H-index作为局部特征方法, 在传播率较小时表现较好, 因为此时信息传播受限于局部, 主要受邻居数量影响, 即度值越高, 感染范围越广. GLS算法融合了全局和局部影响力来衡量节点的重要性, 但其计算方式主要依赖于邻居节点及其度数, 而未能全面刻画网络的整体拓扑结构, 导致其在识别关键节点时出现偏差. InfGCN也融合全局与局部特征, 但受限于浅层GCN设计, 高阶邻域信息丢失, 且全局与局部特征交互不足, 导致识别性能较差.

      • 4.2.3.   鲁棒性实验

    • 本文调整节点比例范围$K$进一步分析Kendall相关系数的变化, $K$取值为5%—90%. 图6展示了不同算法在各节点采样比例下, 其排序结果与SIR模型生成的真实影响力排序之间的Kendall相关系数. 结果表明, 在较小的$K$值下, EMCNN在Netscience, Yeast和Lesmis网络中的表现略逊于某些特定方法. 这主要是由于这些网络的整体度较低, 导致排名靠前的节点在传播影响力上的差异较小. 在这类低度网络中, 多个高排名节点的传播能力较为接近, 使得不同算法之间的排序差异相对较小, 从而影响了EMCNN在小规模$K$取值下的评估表现.

      然而, 随着$K$值的增大, EMCNN在更广泛的节点排名范围内展现出更稳定的优越性, 能够更准确地识别出对信息传播具有关键作用的节点. 在更大范围的$K$取值下, EMCNN能够充分发挥其优势, 结合全局和局部拓扑信息, 实现对关键传播节点的更精确刻画. 相比之下, 其他算法可能在不同网络结构下表现不够稳定, 尤其在规模较大、结构更复杂的网络中, 排序结果的稳健性较差. 因此, 综合来看, EMCNN在整体排名性能上优于其他算法, 能够在不同类型的网络环境中提供更优的节点重要性评估.

      • 4.3.   合成网络验证

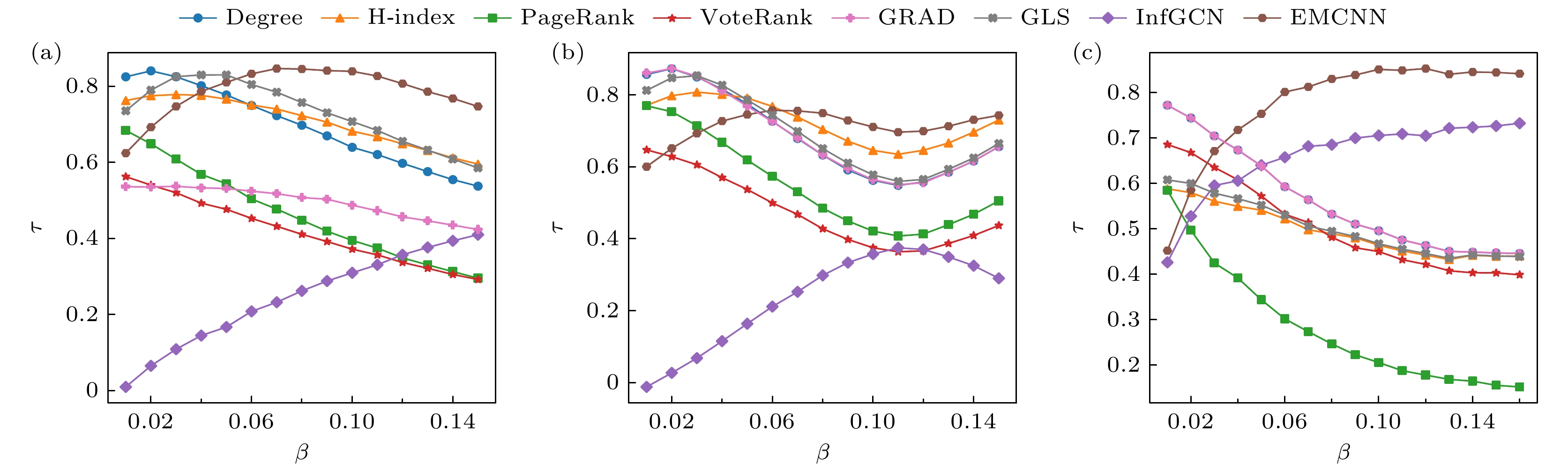
    • 除了9个真实网络数据外, 本文还在Lancichinetti-Fortunato-Radicchi (LFR)[43]模型生成的2个LFR合成网络和1个BA合成网络上比较了不同算法预测的节点排序结果与SIR模型生成的真实影响力排序之间的Kendall相关系数, 传播率区间设为$\left[ {0.01, 0.15} \right]$. 关于合成网络的参数介绍见表2.

      实验结果如图7所示, EMCNN的性能显著优于其他7种算法, 表明其不仅在真实网络中表现出色, 也能在不同的合成网络中有效识别关键节点, 进一步凸显了其优越性. 实验结果进一步表明, EMCNN在更广泛的传播率范围内具有优势. 当传播率较低时, 度中心性和H-index算法表现相对较好, 这与真实数据集上的结果一致. 这一现象的原因在于传播率较低时, 节点的实际影响力主要取决于其度大小.

    5.   结　论

    • 本文提出了一种基于信息熵赋权的多通道卷积神经网络框架(EMCNN)的节点重要性评估方法, 该方法创新性地融合了信息熵理论与多模态学习思想. EMCNN首先利用信息熵计算全局和局部网络指标的权重, 以衡量不同指标对节点重要性的贡献, 从而获得更加合理的加权特征表示. 随后, 基于这些加权指标构建全局特征图和局部特征图, 并将其作为模型输入. 接着, 卷积神经网络与注意力机制被引入, 以实现全局和局部特征的深度融合和非线性表示学习, 进一步提升模型对节点重要性的识别能力. EMCNN相比传统的算法, 考虑到了不同网络指标对节点重要性的贡献度不同, 并且更加全面融合全局和局部特征, 因此在多种网络中表现出更高的效果和适应性.

      在9个真实网络数据集和3个合成网络数据集上的实验结果表明, 与其他方法(如Degree, H-index, PageRank, VoteRank, GRAD, GLS, InfGCN)相比, EMCNN在相关性、准确性和鲁棒性方面均表现出色. 在相关性方面, EMCNN结合了全局与局部网络指标, 学习维度更广, 并利用信息熵理论计算不同指标对节点重要性的贡献度, 从而能够更合理地分配权重, 因此在各类网络上, 其排序结果与真实影响力的相关性更强. 在准确性方面, EMCNN通过卷积神经网络和注意力机制, 充分融合了全局和局部特征图, 在非线性学习的基础上, 提升了对复杂网络结构的表征能力. 实验结果表明, EMCNN的排序结果与节点实际传播能力的Kendall相关系数最高, 能够更加精准地识别出对网络信息传播具有重要影响的核心节点. 鲁棒性方面, EMCNN在不同节点比例下整体表现较优, 尤其在较大比例时优势明显, 而在较小比例时仍能保持较好的识别能力, 进一步证明了该方法的有效性和稳定性.

      然而, 随着网络规模的增长, EMCNN的运行时间和参数量也相应增加, 同时在结构较为简单的网络中, 对排名靠前节点的识别精度仍存在一定局限性. 未来的研究将侧重于优化算法结构和参数设置, 以提升其计算效率和识别精度, 并进一步拓展其应用范围.

    参考文献 (43)

目录

/

返回文章
返回