高级搜索

应变调控反钙钛矿型Li3OCl电子结构和光学性质

,  , 

downloadPDF

上一篇

下一篇

胡宇霄, 李海鹏, 仇康. 应变调控反钙钛矿型Li3OCl电子结构和光学性质[J]. 物理学报, 2025, 74(17): 177101-1. doi: 10.7498/aps.74.20250588
引用本文: 胡宇霄, 李海鹏, 仇康. 应变调控反钙钛矿型Li3OCl电子结构和光学性质[J]. 物理学报, 2025, 74(17): 177101-1. doi: 10.7498/aps.74.20250588
shu
Yuxiao HU, Haipeng LI, Kang QIU. Strain-tuned electronic structure and optical properties of anti-perovskite Li3OCl[J]. Acta Physica Sinica, 2025, 74(17): 177101-1. doi: 10.7498/aps.74.20250588
Citation: Yuxiao HU, Haipeng LI, Kang QIU. Strain-tuned electronic structure and optical properties of anti-perovskite Li3OCl[J]. Acta Physica Sinica, 2025, 74(17): 177101-1. doi: 10.7498/aps.74.20250588
shu

应变调控反钙钛矿型Li3OCl电子结构和光学性质

  • 1.

    中国矿业大学材料与物理学院, 徐州　211116

  • 2.

    徐州医科大学医学信息与工程学院, 徐州　221004

    • 通讯作者: E-mail: haipli@cumt.edu.cn.;  E-mail: qkxzmc@163.com.

  • 中图分类号: 71.15.Mb, 71.20.-b, 78.20.-e

Strain-tuned electronic structure and optical properties of anti-perovskite Li3OCl

  • 1.

    School of Materials Science and Physics, China University of Mining and Technology, Xuzhou 211116, China

  • 2.

    School of Medical Informatics and Engineering, Xuzhou Medical University, Xuzhou 221004, China

    • Corresponding authors: E-mail: haipli@cumt.edu.cn.;  E-mail: qkxzmc@163.com.

  • MSC: 71.15.Mb, 71.20.-b, 78.20.-e

  • 摘要: 反钙钛矿Li3OCl作为极具潜力的新一代固态电解质候选材料, 凭借其优异的离子传导性能与宽电化学窗口, 近年来成为材料领域的研究热点. 然而, 其光电性能的应变调控机制仍未得到充分阐释. 本研究运用第一性原理计算方法, 系统地探究双轴应变和单轴应变分别对Li3OCl材料电子结构及光学性质的调控规律. 研究发现, 相较于本征态, 施加2%单轴拉伸应变时, 材料导带底能量显著降低, 间接带隙从6.26 eV减小至6.02 eV, 光吸收边发生红移; 而2%双轴压缩应变作用下, 带隙增大至6.38 eV, 且间接带隙转变为直接带隙, 光吸收边出现蓝移现象. 通过态密度分析进一步表明, 应变会引发Li-p与O-p/Cl-p 轨道杂化程度增强, 显著优化了光激发载流子的跃迁路径. 此外, 拉伸应变致使介电函数虚部峰值红移, 消光系数起始阈值降至6.02 eV, 有效地拓宽了材料的光响应范围; 压缩应变则导致光学响应蓝移, 并增强了材料在特定能量区间的光吸收强度. 本研究揭示了应变调控晶格常数与轨道杂化来优化光电性能的微观作用机制, 为基于光-力协同策略设计高性能固态电解质提供了重要理论依据.
    Abstract: The lithium-rich anti-perovskite Li3OCl has emerged as an ideal candidate for next-generation lithium-ion batteries (LIBs) due to its excellent ionic conductivity and wide electrochemical stability window. However, achieving ionic conductivity that meets practical application requirements remains challenging. Strain engineering and opto-ionic effects provide new approaches for optimizing the performance, but currently there is a lack of research on the quantitative regulatory mechanisms by which strain influences the electronic structure and optical properties of Li3OCl (both of which are critical for ionic transport and optoelectronic integration). In this study, first-principles calculations are performed using the HSE06 hybrid functional to systematically investigate the effects of biaxial (+2%)and uniaxial (–2%) strains - on electronic structure and optical properties of Li3OCl.In this study, it is found that strain-free Li3OCl exhibits an indirect bandgap of 6.263 eV. Biaxial tensile strain causes a significant downward shift in the energy of the conduction band minimum (Γ point), reducing the bandgap to 6.023 eV (+2% strain) and reinforcing the indirect bandgap characteristics. Biaxial compressive strain (–2%) expands the bandgap to 6.380 eV and triggers off an upward shift in the Γ-point energy level, leading to a transition from an indirect to a direct bandgap. Uniaxial strain exhibits similar trends but with a smaller regulatory magnitude than biaxial strain. The analysis of density of states shows that tensile strain reduces the Li-p state density near the conduction band minimum while enhancing the hybridization of Li-p with O-p/Cl-p orbitals, optimizing carrier transition channels. Compressive strain increases the electron state density near the Fermi level, enhancing the probability of optical transitions. In terms of optical response, tensile strain induces an overall redshift in the complex dielectric function (ε1(ω) and ε2(ω)), absorption coefficient, and extinction coefficient. Compressive strain causes a systematic blue-shift in optical parameters. Despite the expanded bandgap, the optical absorption intensity is significantly enhanced in the ultraviolet region due to the direct bandgap characteristics and the increased state density at the band edges.This study provides new ideas for studying the applications of Li3OCl in optoelectronic devices and solid-state batteries. By precisely regulating its bandgap and light absorption properties through strain engineering, Li3OCl can adapt to the excitation requirements of different wavelengths of light. For example, in light-controlled solid-state batteries, Li3OCl optimized by tensile strain has a wider light response range (red-shifted to lower energy), which can effectively utilize lower-energy photons (such as near-ultraviolet or the edge of visible light) to excite carriers. On the other hand, Li3OCl optimized by compressive strain has higher light absorption efficiency in specific ultraviolet bands, potentially increasing the concentration of carriers excited by photons in these bands. The strain-optimized Li3OCl can synergistically utilize the light field and stress field to enhance ionic conductivity. In addition, its red-shifted light absorption edge makes it promising as an ultraviolet-visible light conversion layer, expanding the range of light energy utilization. However, in practical applications, further research is needed on the synergistic mechanisms of non-uniform strain, temperature effects, and light-force coupling. Moreover, experimental verification of its interfacial stability and cycle performance is required to promote the practical application of high-performance all-solid-state batteries.
  • 加载中

  • 图 1  Li3OCl的单胞结构

    Figure 1.  Unit cell structures of Li3OCl.

    下载: 全尺寸图片 幻灯片

    图 2  双轴/单轴应变下Li3OCl应变能与应变之间关系

    Figure 2.  The relationship between the strain energy and strain of Li3OCl under biaxial/uniaxial strain.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 双轴应变和(b) 单轴应变下Li3OCl的声子色散关系

    Figure 3.  Phonon dispersion relations of Li3OCl under (a) biaxial strain and (b) uniaxial strain.

    下载: 全尺寸图片 幻灯片

    图 4  Li3OCl的能带结构和态密度

    Figure 4.  The band structure and density of states of Li3OCl.

    下载: 全尺寸图片 幻灯片

    图 5  双轴/单轴应变下Li3OCl的带隙

    Figure 5.  The bandgap of Li3OCl under biaxial/uniaxial strain.

    下载: 全尺寸图片 幻灯片

    图 6  (a) 双轴应变和(b) 单轴应变下Li3OCl的能带结构

    Figure 6.  Energy band structure of Li3OCl under (a) biaxial strain and (b) uniaxial strain.

    下载: 全尺寸图片 幻灯片

    图 7  (a) 双轴压缩应变e = –2%时, (b) 无应变e = 0%和(c) 双轴拉伸应变e = 2%时Li3OCl总态密度和分波态密度

    Figure 7.  Total density of states and partial density of states of Li3OCl under (a) –2% biaxial compressive strain, (b) no strain, and (c) 2% biaxial tensile strain.

    下载: 全尺寸图片 幻灯片

    图 8  双轴应变下Li3OCl的介电函数　(a) 介电函数实部; (b) 介电函数虚部

    Figure 8.  Dielectric function of Li3OCl under biaxial strain: (a) Real part of the dielectric function; (b) imaginary part of the dielectric function.

    下载: 全尺寸图片 幻灯片

    图 9  双轴应变下Li3OCl的(a) 吸收系数、(b) 折射率、(c) 消光系数和(d) 反射率

    Figure 9.  (a) Absorption coefficients, (b) reflection index, (c) extinction coefficient, and (d) reflectivity of Li3OCl under biaxial strain.

    下载: 全尺寸图片 幻灯片
  • [1] Lü X, Wu G, Howard J W, Chen A, Zhao Y, Daemen L L, Jia Q 2014 Chem. Commun. 50 11520 doi: 10.1039/C4CC05372A
    [2] Luo X, Li Y, Zhao X 2024 Energy Environ. Mater. 7 e12627 doi: 10.1002/eem2.12627
    [3] Wang Q, Liu B, Shen Y, Wu J, Zhao Z, Zhong C, Hu W 2021 Adv. Sci. 8 2101111 doi: 10.1002/advs.202101111
    [4] Zhu J, Li S, Zhang Y, Howard J W, Lü X, Li Y, Wang Y, Kumar R S, Wang L, Zhao Y 2016 Appl. Phys. Lett. 109 101904 doi: 10.1063/1.4962437
    [5] 余启鹏, 刘琦, 王自强, 李宝华 2020 物理学报 69 228805 doi: 10.7498/aps.69.20201218 Yu Q P, Liu Q, Wang Z Q, Li B H 2020 Acta Phys. Sin. 69 228805 doi: 10.7498/aps.69.20201218
    [6] Lu J, Li Y 2021 J. Mater. Sci. Mater. Electron. 32 9736 doi: 10.1007/s10854-021-05699-8
    [7] Wang Y, Chen D, Zhuang Y, Chen W, Long H, Chen H, Xie R 2021 Adv. Opt. Mater. 9 2100624 doi: 10.1002/adom.202100624
    [8] Zhao Y, Daemen L L 2012 J. Am. Chem. Soc. 134 15042 doi: 10.1021/ja305709z
    [9] Abdulchalikova N R, Aliev A E 1995 Synth. Met. 71 1929 doi: 10.1016/0379-6779(94)03112-J
    [10] Aliev A É, Krivorotov V F, Khabibullaev P K 1997 Phys. Solid State 39 1378 doi: 10.1134/1.1130083
    [11] Bachman J C, Muy S, Grimaud A, Chang H H, Pour N, Lux S F, Paschos O, Maglia F, Lupart S, Lamp P, Giordano L, Shao-Horn Y 2016 Chem. Rev. 116 140 doi: 10.1021/acs.chemrev.5b00563
    [12] Tsymbalov E, Shi Z, Dao M, Suresh S, Li J, Shapeev A 2021 Npj Comput. Mater. 7 76 doi: 10.1038/s41524-021-00538-0
    [13] Kahlaoui S, Belhorma B, Labrim H, Boujnah M, Regragui M 2020 Heliyon 6 e03713 doi: 10.1016/j.heliyon.2020.e03713
    [14] Itoh M, Inaguma Y, Jung W, Chen L, Nakamura T 1994 Solid State Ionics 70–71 203
    [15] Wei J, Ogawa D, Fukumura T, Hirose Y, Hasegawa T 2015 Cryst. Growth Des. 15 2187 doi: 10.1021/cg501834s
    [16] Shen H, Wang Q, Chen Z, Rong C, Chao D 2023 Materials 16 4266 doi: 10.3390/ma16124266
    [17] Li F, Li J, Zhu F, Liu T, Xu B, Kim T H, Kramer M J, Ma C, Zhou L, Nan C W 2019 Matter 1 1001 doi: 10.1016/j.matt.2019.05.004
    [18] Zuo X, Zhu J, Müller-Buschbaum P, Cheng Y J 2017 Nano Energy 31 113 doi: 10.1016/j.nanoen.2016.11.013
    [19] Tippens J, Miers J C, Afshar A, Lewis J A, Cortes F J Q, Qiao H, Marchese T S, Di Leo C V, Saldana C, McDowell M T 2019 ACS Energy Lett. 4 1475 doi: 10.1021/acsenergylett.9b00816
    [20] Defferriere T, Klotz D, Gonzalez-Rosillo J C, Rupp J L M, Tuller H L 2022 Nat. Mater. 21 438 doi: 10.1038/s41563-021-01181-2
    [21] Wu M, Xu B, Lei X, Huang K, Ouyang C 2018 J. Mater. Chem. A 6 1150 doi: 10.1039/C7TA08780B
    [22] Emly A, Kioupakis E, Van Der Ven A 2013 Chem. Mater. 25 4663 doi: 10.1021/cm4016222
    [23] Pegolo P, Baroni S, Grasselli F 2022 Npj Comput. Mater. 8 24 doi: 10.1038/s41524-021-00693-4
    [24] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 doi: 10.1016/0927-0256(96)00008-0
    [25] Kresse G, Furthmüller J, Hafner J 1994 Phys. Rev. B 50 13181 doi: 10.1103/PhysRevB.50.13181
    [26] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [27] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188
    [28] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207 doi: 10.1063/1.1564060
    [29] Krukau A V, Vydrov O A, Izmaylov A F, Scuseria G E 2006 J. Chem. Phys. 125 224106 doi: 10.1063/1.2404663
    [30] Paier J, Marsman M, Hummer K, Kresse G, Gerber I C, Ángyán J G 2006 J. Chem. Phys. 124 154709 doi: 10.1063/1.2187006
    [31] Qin H, Zuo Y, Jin J, Wang W, Xu Y, Cui L, Dang H 2019 RSC Adv. 9 24483 doi: 10.1039/C9RA03426A
    [32] Li L, Guo X, Lu X, Ren J, La P 2023 Mater. Sci. Semicond. Process. 154 107189 doi: 10.1016/j.mssp.2022.107189
    [33] Tignon J, Voisin P, Delalande C, Voos M, Houdré R, Oesterle U, Stanley R P 1995 Phys. Rev. Lett. 74 3967 doi: 10.1103/PhysRevLett.74.3967
    [34] Silveirinha M G 2011 Phys. Rev. B 83 165119 doi: 10.1103/PhysRevB.83.165119
    [35] Ou Y, Hou W, Zhu D, Li C, Zhou P, Song X, Xia Y, Lu Y, Yan S, Zhou H, Cao Q, Zhou H, Liu H, Ma X, Liu Z, Xu H, Liu K 2025 Energy Environ. Sci. 18 1464 doi: 10.1039/D4EE04282D
    [36] Xiao Y, Miara L J, Wang Y, Ceder G 2019 Joule 3 1252 doi: 10.1016/j.joule.2019.02.006
  • 加载中
图( 9)
计量
  • 文章访问数:  38
  • HTML全文浏览数:  38
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-05-01
  • 刊出日期:  2025-09-05

应变调控反钙钛矿型Li3OCl电子结构和光学性质

    通讯作者: E-mail: haipli@cumt.edu.cn.; 
    通讯作者: E-mail: qkxzmc@163.com.
  • 1. 中国矿业大学材料与物理学院, 徐州　211116
  • 2. 徐州医科大学医学信息与工程学院, 徐州　221004
  • 收稿日期:  2025-05-01

摘要: 反钙钛矿Li3OCl作为极具潜力的新一代固态电解质候选材料, 凭借其优异的离子传导性能与宽电化学窗口, 近年来成为材料领域的研究热点. 然而, 其光电性能的应变调控机制仍未得到充分阐释. 本研究运用第一性原理计算方法, 系统地探究双轴应变和单轴应变分别对Li3OCl材料电子结构及光学性质的调控规律. 研究发现, 相较于本征态, 施加2%单轴拉伸应变时, 材料导带底能量显著降低, 间接带隙从6.26 eV减小至6.02 eV, 光吸收边发生红移; 而2%双轴压缩应变作用下, 带隙增大至6.38 eV, 且间接带隙转变为直接带隙, 光吸收边出现蓝移现象. 通过态密度分析进一步表明, 应变会引发Li-p与O-p/Cl-p 轨道杂化程度增强, 显著优化了光激发载流子的跃迁路径. 此外, 拉伸应变致使介电函数虚部峰值红移, 消光系数起始阈值降至6.02 eV, 有效地拓宽了材料的光响应范围; 压缩应变则导致光学响应蓝移, 并增强了材料在特定能量区间的光吸收强度. 本研究揭示了应变调控晶格常数与轨道杂化来优化光电性能的微观作用机制, 为基于光-力协同策略设计高性能固态电解质提供了重要理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 锂离子电池(lithium-ion batteries, LIBs)凭借其高能量密度、高功率容量、快充放速率及长循环寿命等显著优势[1,2], 在便携式电子设备和电动汽车等关键领域展现出广泛应用前景. 然而, 现有商业化LIBs普遍采用液态有机电解质, 不仅存在泄漏和燃烧风险, 其有机成分在充放电过程中还易与活性金属锂负极发生副反应, 导致电池容量衰减和循环寿命缩短[3]. 为解决上述问题, 采用无机固态电解质替代液态电解质成为重要的研究方向[4]. 固态电解质不仅能够有效地避免液态电解质的安全与环境风险, 还可与金属锂负极匹配, 构建具有更高能量密度和功率密度的全固态电池. 因此, 兼具高能量密度、长寿命和高安全性的全固态锂离子电池已成为当前研究的热点[5].

      在众多固态电解质中, 钙钛矿型化合物(ABX3, 其中A, B为阳离子, X为阴离子)因其独特的晶体结构与离子传导特性而广受关注. 然而, 钙钛矿型固态电解质仍面临与锂金属接触稳定性不足及界面电阻过高等关键问题[6]. 与钙钛矿结构异曲同工却巧妙实现阴阳离子反转的反钙钛矿型化合物(M3AB, M = Li, Na; A = O, S; B = Cl, Br, BH4等), 凭借高离子电导率、稳定性及相容性等特性, 成为极具潜力的固态电解质候选材料. 受富氟钙钛矿高温超离子导体 NaMgF3启发[7], Zhao和Daemen[8]设计合成了新型三维锂离子传导固态电解质富锂反钙钛矿(lithium-rich antiperovskite, LiRAP). 其中, 富含锂的反钙钛矿型固态电解质Li3OCl在过去十几年中逐渐成为全固态锂金属电池领域的重要候选材料. 该电解质在室温下表现出超离子特性, 具有较高的离子电导率; 其组成元素轻质、成本低廉且环境友好, 同时具备不易燃性和良好的循环性能[9]. 此外, Li3OCl的宽电子带隙特性赋予其极低的电子导电率, 并形成了宽电化学稳定性窗口, 从而显著地提升了电池体系的安全性[10]. 更为关键的是, 该电解质对锂金属沉积展现出优异的化学稳定性, 可有效地抑制因锂枝晶生长引发短路问题, 为提升电池长期循环性能提供了重要保障.

      然而固态电解质产业化仍面临关键性技术瓶颈. 其核心问题在于现有材料的室温离子电导率(10–9—10–2 S/cm)远低于实际应用需求(>10–3 S/cm)[11]. 研究者提出了掺杂改性、界面优化及应变调控等协同优化策略. 例如, 弹性应变工程通过调控载流子迁移率和带隙宽度[12], 有效地调节固态电解质的离子输运行为, 其机制在于通过晶格畸变诱导原子重排和缺陷重构过程[13], 从而显著地降低离子扩散势垒与迁移活化能; Itoh等[14]实验证实A位稀土离子置换(Sm<Nd<Pr<La)产生的晶格应变可使钙钛矿型电解质的锂离子电导率提升2个数量级; Wei等[15]也观察到在 NdGaO3衬底上, 晶格失配引起的应变导致了Li0.33La0.5TiO3薄膜离子传导的各向异性. 实际上, 电池循环过程中电极体积变化(如硅基电极嵌锂过程中体积膨胀近400%[16])引发的机械应力与界面应变(Li0.33La0.5TiO3电解质在富锂层状电极外延界面处应变达5%—10%[17]), 已成为影响固态电解质结构稳定性的关键因素[18,19]. 此外, 光场调控技术为突破固态电解质离子迁移率瓶颈提供了新思路. Defferriere等[20]通过实验证实, 在250 ℃条件下, 多晶陶瓷材料的离子电导率通过光学照明可增加近4倍, 而特定波长的光场可使固态电解质陶瓷燃料电池中的晶界电导率提升3.5倍, 其机制源于光诱导晶界空间电荷势垒的降低, 从而增强离子迁移效率. 这种“光离子效应”可拓展至锂离子固态电解质领域, 通过优化光场参数(如波长、强度与照射模式), 有望在锂电池中实现光控离子传输路径的精准设计, 提升充电速率与循环稳定性.

      目前反钙钛矿电解质Li3OCl的研究以固态电解质的离子输运特性与电化学稳定性为核心, 其光电性质研究尚处起步阶段. Wu等[21]基于HSE06杂化泛函计算表明, Li3OCl基态为间接带隙结构(带隙为6.26 eV), 价带顶与导带底分别位于布里渊区M点和Γ点, 宽禁带特性赋予其优异电化学稳定性与极低电子电导率. 导带电子态对晶格常数变化高度敏感, 尤其在高对称点处表现显著. 当晶胞晶格常数压缩约1% (至3.865 Å)时, 带隙类型由间接转变为直接带隙, 且价带顶与导带底均位于M点, 这与Emly等[22]的计算结果一致, 表明压缩应变可有效调控材料能带特征. 分波态密度分析显示, 费米能级附近电子态主要来源于O原子, 导带电子态则主要由Li原子贡献, 结合Bader电荷分析(Li, O, Cl的Bader电荷分别为+0.88|e|, –1.71|e|, –0.93|e|, 与价电子数高度吻合), 证实Li3OCl化学键具有高度离子性. Pegolo等[23]在HSE06理论水平下计算Li3ClO电子能带结构, 发现其在布里渊区M点呈现直接带隙6.46 eV, 显示宽带隙绝缘体属性和良好的电化学稳定性.

      尽管应变工程与光场调控技术为固态电解质性能优化开辟了新路径, 但现有研究仍存在两方面空白: 其一, 反钙钛矿材料的应变响应机制尚未系统阐明, 特别是晶格畸变如何通过能带演化影响光电性能亟待深入解析; 其二, Li3OCl作为典型反钙钛矿电解质, 其光电响应与应变敏感性的定量关系缺乏理论支撑, 难以指导实际应用中的参数优化. 针对上述问题, 本研究基于密度泛函理论方法计算了Li3OCl晶体的电子结构和光学性质, 探究双轴/单轴应变对其电子结构及光学性质的调控机理. 本研究定量地揭示了应变通过调控晶格常数与轨道杂化优化光电性能的微观机制, 阐明了应变诱导能带演化与光吸收特性的定量关系, 对推动下一代全固态电池实用化具有重要意义.

    2.   模型与方法

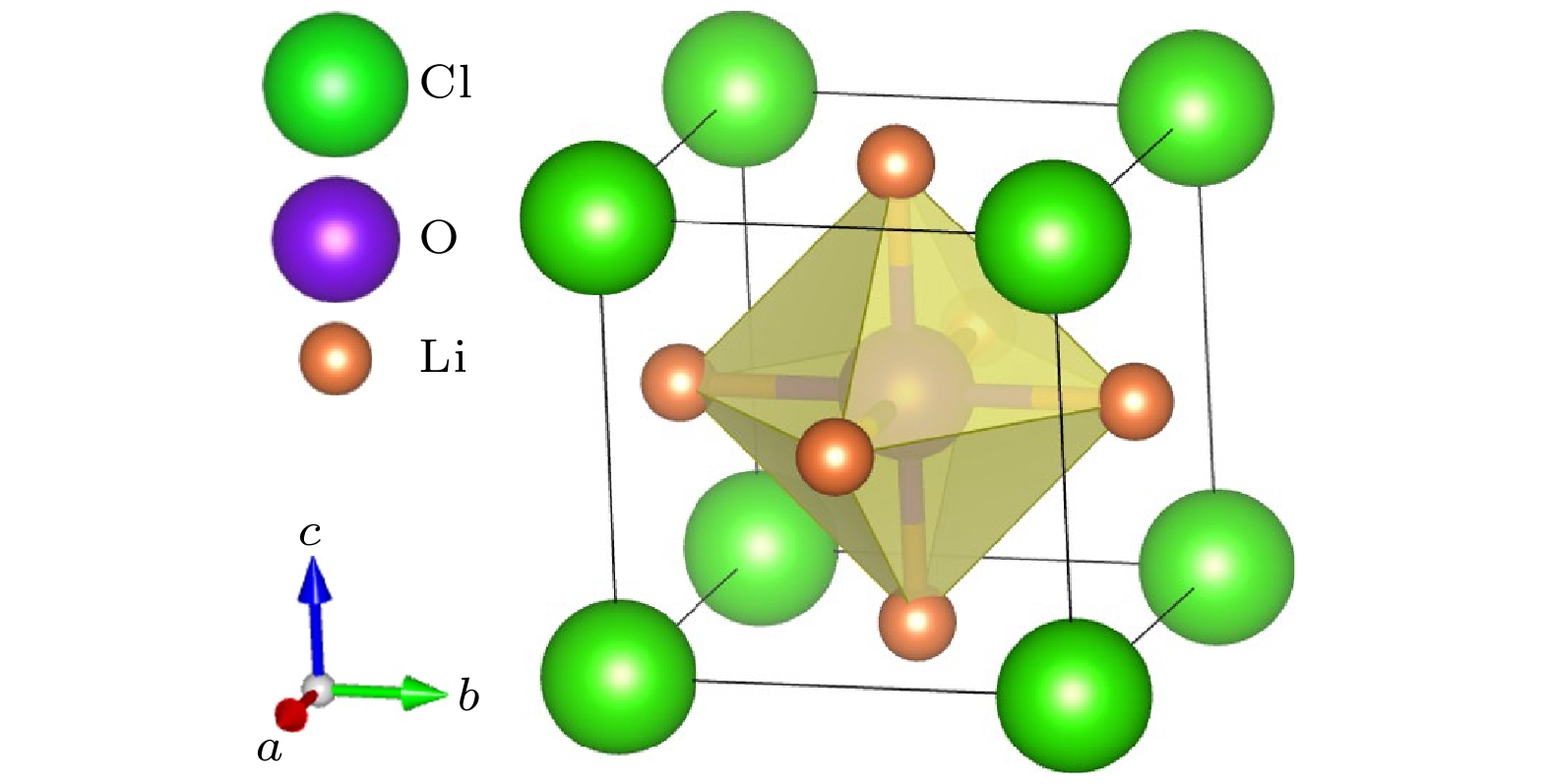
    • 如图1所示, 反钙钛矿Li3OCl具有典型的立方晶体结构, 即a = b = c, α = β = γ = 90°, 属于$ Pm\overline{3}m $空间群. 在该结构中, O2–离子占据体心位置, Li+离子则围绕O2–离子分布在面心位置, 形成稳定的Li6O八面体配位结构, 而卤素元素则占据晶格的角落位置, 构成完整的晶体框架.

      本文基于密度泛函理论(density functional theory, DFT)第一性原理计算采用VASP (Vienna ab-initio simulation package)[24,25]软件完成. 在对Li3OCl进行结构优化时, 连续步骤之间的能量差低于10–8 eV, 并且原子上的力低于10–2 eV/Å. 所采用的泛函为广义梯度近似(generalized gradient approximation, GGA)下的PBE (Perdew Burke-Ernzerhof)泛函[26], 平面波截断能设置为600 eV. 在计算中第一布里渊区采样使用以Γ为中心的Monkhorst-Pack[27]方法生成11 × 11 × 11的网格进行积分, 优化的晶格常数为3.908 Å, 与文献报道的理论和实验结果(3.91 Å)一致[8,21-23]. 在电子结构计算中, 采用杂化泛函(Heyd-Scuseria-Ernzerhof, HSE06)[28-30]计算能带结构. 交换关联能$ {E}_{\mathrm{X}\mathrm{C}}^{\mathrm{H}\mathrm{S}\mathrm{E}} $的表述公式如下:

      式中, 下标X和c分别表示交换泛函和关联泛函; $ {E}_{\mathrm{X}}^{\mathrm{H}\mathrm{F}, \mathrm{S}\mathrm{R}} $是短程的HF交换项$ ; {E}_{\mathrm{X}}^{\mathrm{P}\mathrm{B}\mathrm{E}, \mathrm{S}\mathrm{R}} $和$ {E}_{\mathrm{X}}^{\mathrm{P}\mathrm{B}\mathrm{E}, \mathrm{L}\mathrm{R}} $分别是PBE的短程和长程交换项, 其中$ {E}_{\mathrm{X}}^{\mathrm{P}\mathrm{B}\mathrm{E}, \mathrm{S}\mathrm{R}} $和$ {E}_{\mathrm{X}}^{\mathrm{P}\mathrm{B}\mathrm{E}, \mathrm{L}\mathrm{R}} $的和等于1; α是HF的成分比例, 设置为0.25; ω为筛选参数, 设置为0.20 Å–1. $ {E}_{\mathrm{C}}^{\mathrm{P}\mathrm{B}\mathrm{E}} $是PBE的库仑相关项. 使用以Γ为中心的Monkhorst-Pack网格, 沿布里渊区高对称路径的K点间隔设置为0.03 Å–1.

      材料的光学性质可通过计算介电函数并构建相应的关联响应函数来系统推导[31-34]. 具体而言, 通常采用密度泛函理论结合Kramers-Kronig变换关系, 通过求解Maxwell方程组与材料极化响应的本构关系, 建立复介电函数$ \varepsilon \left(\omega \right)={\varepsilon }_{1}\left(\omega \right)+ \mathrm{i}{\varepsilon }_{2}\left(\omega \right) $的实部和虚部表达式, 进而解析出吸收系数$ \alpha \left(\omega \right) $、折射率$ \eta \left(\omega \right) $、消光系数$ k\left(\omega \right) $和反射率$ R\left(\omega \right) $等关键光学参数:

    3.   结果与分析

      3.1.   几何结构

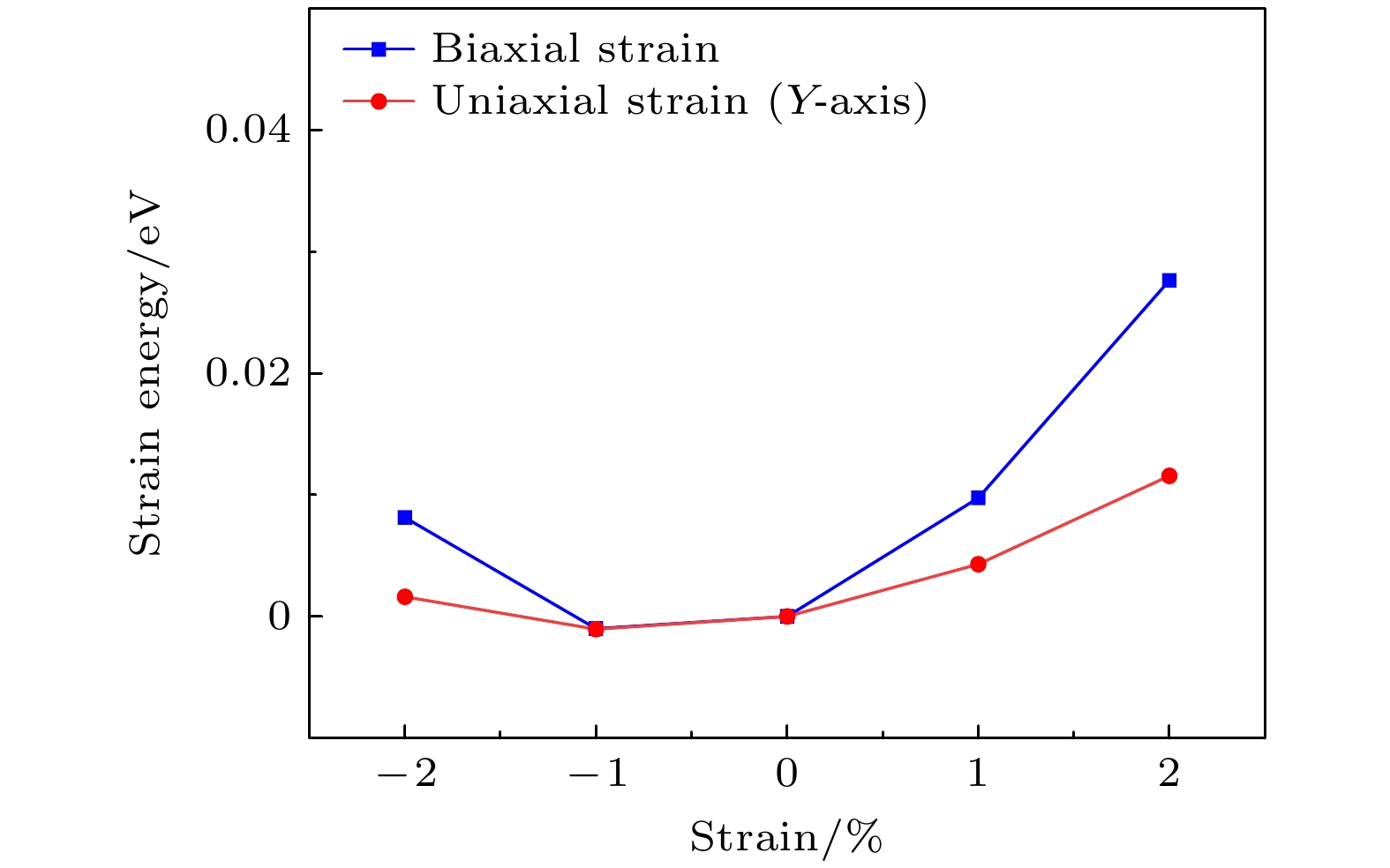
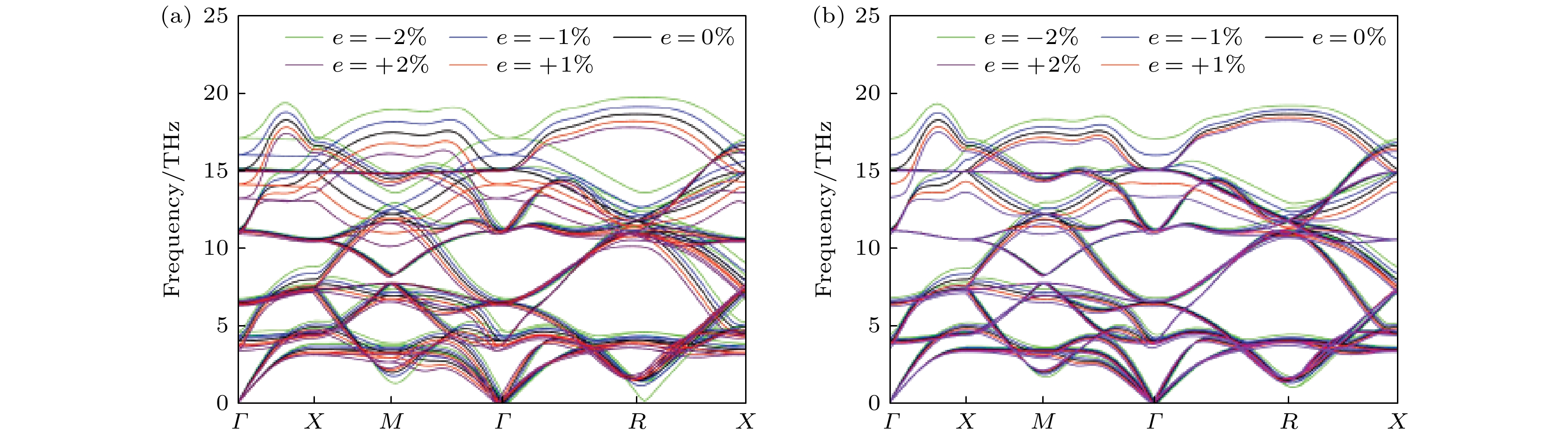
    • 我们研究了Li3OCl的弹性应变范围及其对压缩应变和拉伸应变的响应特性. 研究表明, 应变能与双轴应变之间呈现显著的二次关系, 这一发现充分体现了系统固有的结构柔性. 图2为Li3OCl晶体的应变能随双轴应变和单轴应变的关系. 模拟实验中, 将施加的应变e范围设定在–2%至2%之间. 我们计算了–2%至2%范围内双轴与单轴应变下的声子色散关系(图3), 未出现虚频, 表明在此应变范围内结构是稳定的.

      • 3.2.   电子性质

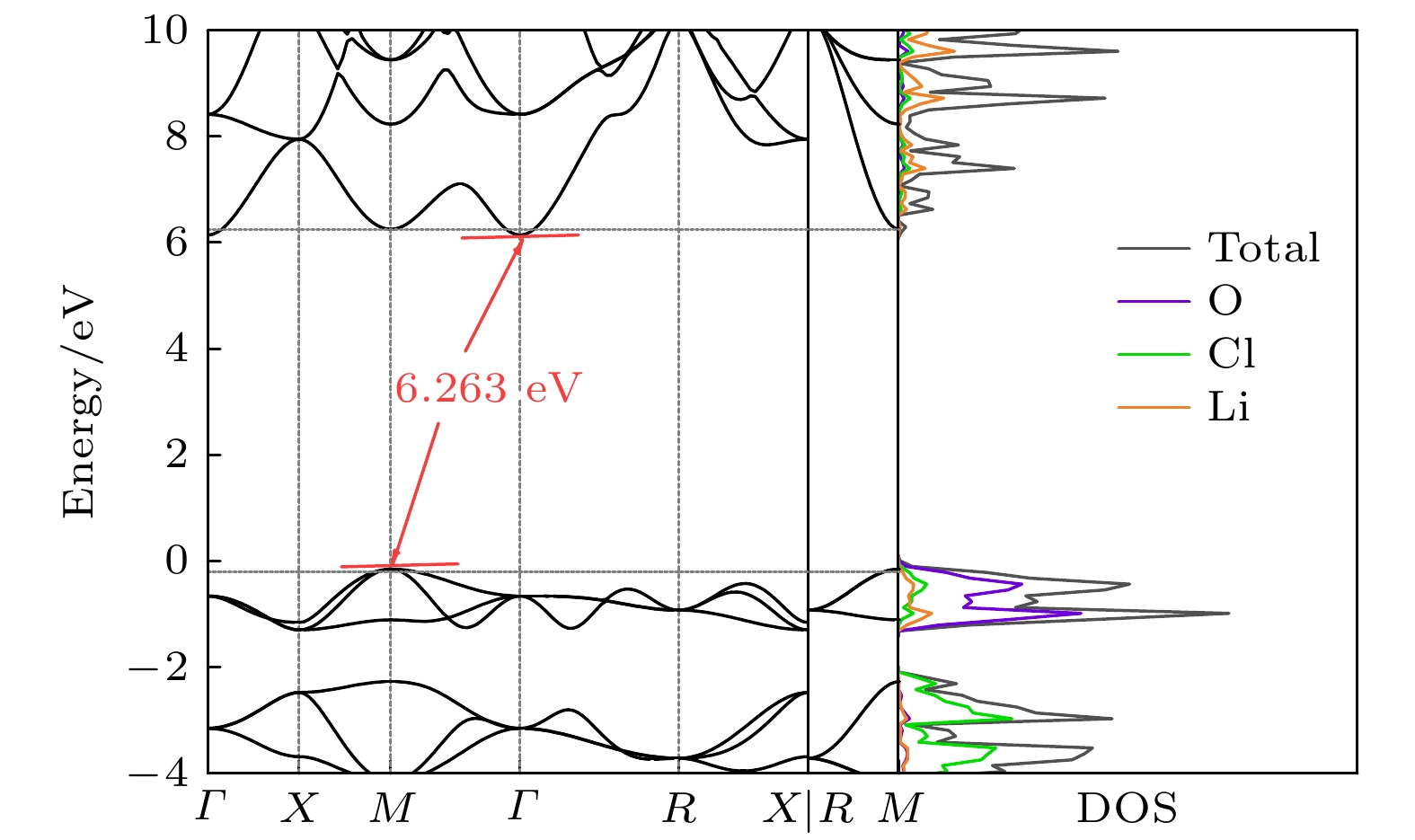
    • 当固体电解质的带隙与电池的电压范围相匹配时, 才是有效的电解质. 由于高压阴极工作在4 V左右[35], 大于5 eV的带隙被认为适合用于锂离子电池[36]. 图4给出了无应变的Li3OCl的电子能带结构和态密度(density of states, DOS). 电子能带结构计算显示价带顶和导带底分别位于M点和Γ点, 间接带隙为6.263 eV, 这与Wu等[21]计算的间接带隙值(6.26 eV)十分吻合. Li3OCl的带隙对晶格常数非常敏感, 当Li3OCl的晶格常数略微压缩至3.865 Å时, 变为直接带隙且带隙值为6.46 eV. 因此, Li3OCl是一种宽禁带的绝缘体, 具有良好的电化学稳定性.

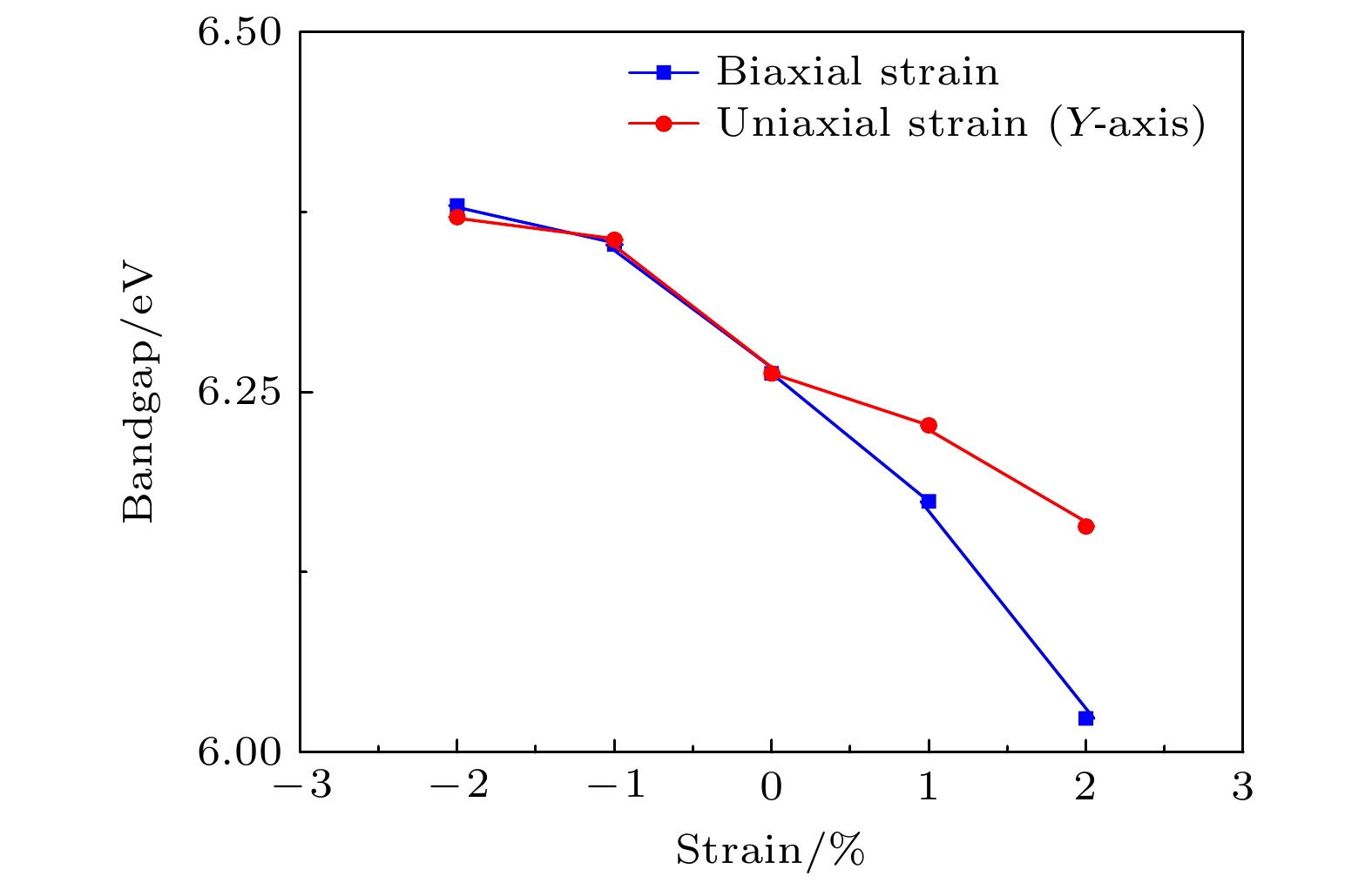
      图5给出了Li3OCl在双轴/单轴应变下带隙随应变量的变化情况. Li3OCl的带隙对拉伸应变的敏感性高于压缩应变. 随着双轴拉伸应变由e = 0增加到e = 2%, 带隙由6.263 eV减小到6.023 eV; 随着双轴压缩应变由e = 0增加到e = –2%, 带隙由6.263 eV增加到6.380 eV. 对于单轴应变, 带隙的变化趋势与双轴应变类似, 但变化的幅度和敏感性有所不同. 在单轴拉伸应变下, 带隙也呈现下降趋势, 但下降的幅度较双轴应变更为平缓.

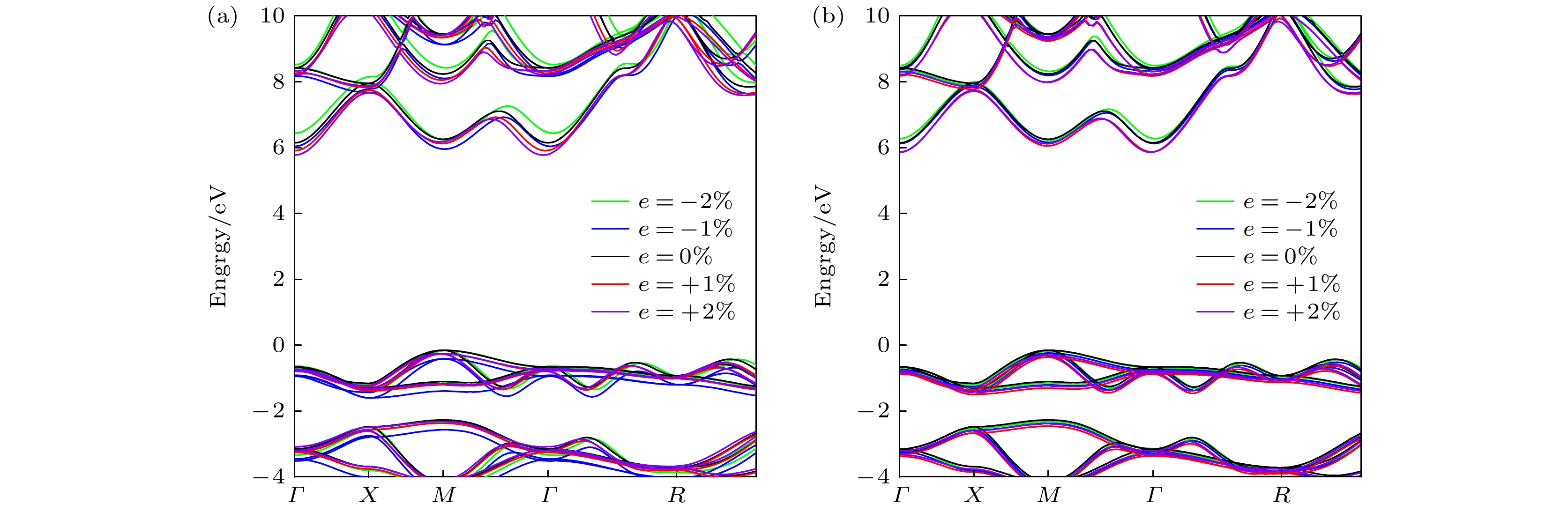
      图6给出了Li3OCl在双轴/单轴应变下的能带结构. 价带顶几乎不受压缩应变和拉伸应变的影响, 但导带底却因拉伸应变而明显降低. 在无应变状态下, 导带底在M点和Γ点的能量相近. 拉伸应变会略微提高M点的能量, 而降低Γ点的能量, 强化了Li3OCl的间接带隙特性. 相反, 压缩应变提高了Γ点的能级, 导致Li3OCl从间接带隙转变为直接带隙.

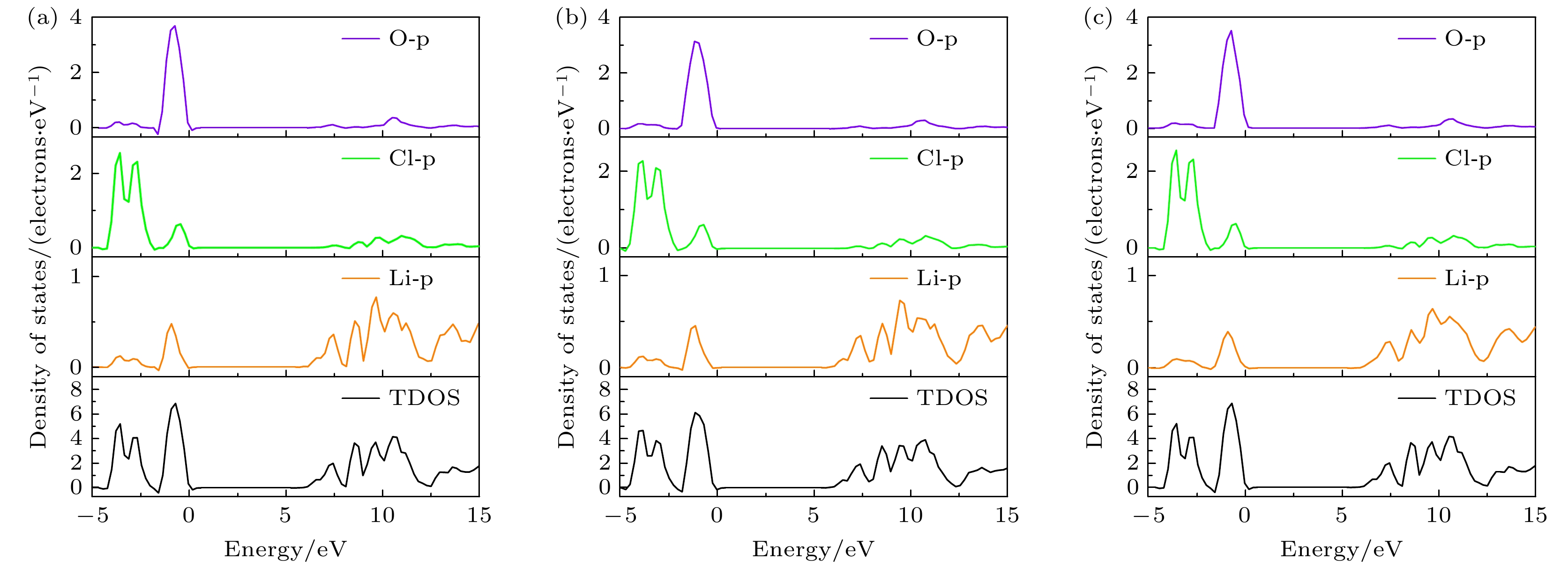
      在e = 0—2%的双轴拉伸应变过程中, Li3OCl导带底附近的DOS持续降低, 如图7所示. 无应变Li3OCl的导带底附近存在高密度的Li-s/p电子态分布, 其主要由Li原子的电子态贡献; 而在费米能级附近, Cl原子和O原子的电子态则表现出更显著的峰形特征, 表明其对费米能级区域的电子行为具有主导作用. 该原子特异性电子分布决定了光激发跃迁的起始和终止态, 直接影响光激发跃迁过程. Cl-p和O-p态在费米能级附近的高态密度, 显著增强了光激发时电子跃迁的概率与数量, 而Li-p态则作为跃迁的“桥梁”, 主导了Li-p↔O-p/Cl-p之间的本征跃迁通道(满足偶极选择定则). 这一机制揭示了拉伸应变下Li3OCl价带和导带边缘的电子结构的动态演化规律, 为调控其光电性能提供了关键理论依据.

      • 3.3.   光学性质

      3.3.1.   介电函数

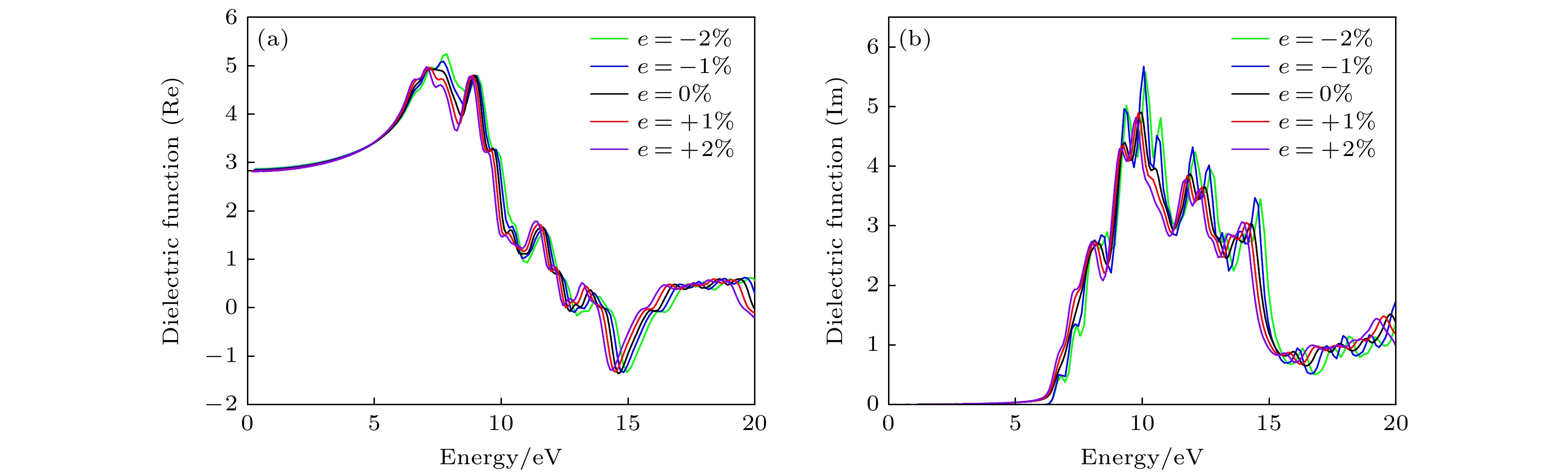
    • 作为典型反钙钛矿材料, Li3OCl的宽禁带特性和可调带隙表明其在光电领域的潜在应用价值. 对于固体材料来说, 介电函数ε(ω) = ε1(ω) + iε2(ω)作为带间跃迁微观物理过程与固体电子结构之间的桥梁, 能够反映固体的能带结构信息. 每个介电峰的产生与材料的电子结构息息相关. 双轴均匀拉伸应变下, Li3OCl的复介电常数实部ε1(ω)和虚部ε2(ω)随外场频率ω变化的情况如图8所示. 无应变时, Li3OCl的静态介电常数实部ε1(0)为2.749. 当施加–2%至2%的双轴/单轴应变时, 静态介电常数实部ε1(0)的变化较小, 表明材料在低能区域对电场的响应能力受应变影响有限. 然而, 随着外场频率大于5 eV, 介电函数实部ε1的变化明显. 施加双轴拉伸应变时, ε1曲线整体红移. 而施加双轴压缩应变时, ε1曲线整体蓝移.

      介电函数的虚部如图8(b)所示, 其反映了材料对光的吸收程度, 其值的大小与电子跃迁的强度有关. 无应变时, 当外场能量大于6.26 eV后, ε2迅速上升, 并在外场能量为9.97 eV处达到峰值4.90, 随后ε2逐渐下降, 在频率为15 eV趋于稳定. 相比于无应变情况, 当施加双轴拉伸应变时, ε2的吸收带红移.

      • 3.3.2.   光吸收系数

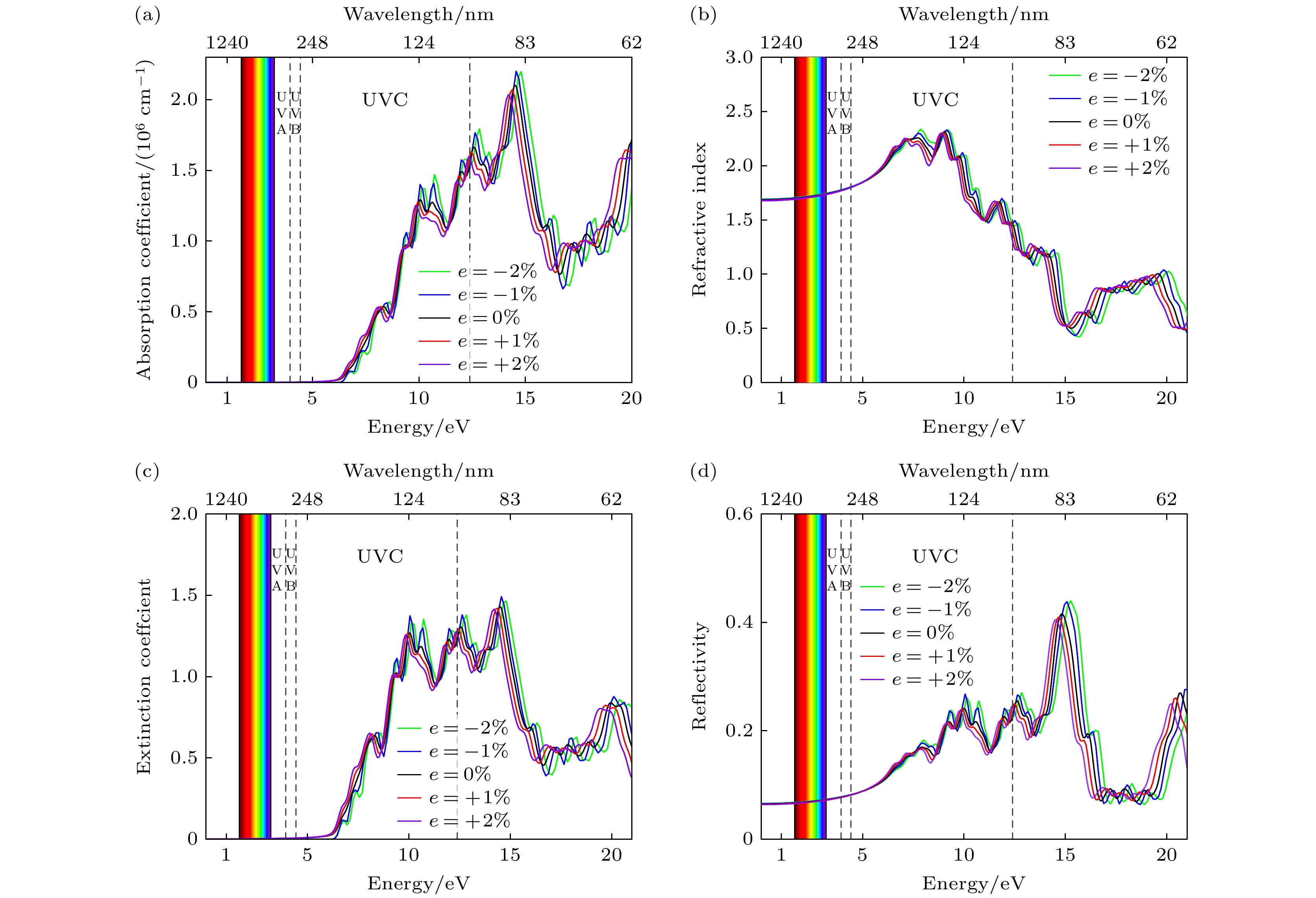
    • 紫外线(UV)区域主要分为三个区域, 即短波紫外线(ultraviolet C, UVC: 4.4—12.4 eV)、中波紫外线(ultraviolet B, UVB: 3.8—4.4 eV)和长波紫外线 (ultraviolet A, UVA: 3.1—3.8 eV). 吸收系数能够测定光波在介质中衰减的程度. 在可见光区域和紫外区域的光吸收强度对光学器件的设计应用有非常重要的影响. 如图9(a)所示, 无论是无应变还是施加应变后的Li3OCl, 均在紫外区域(UVC)展现出较强的光子吸收能力. 双轴拉伸应变后带隙减小, 光子受激后更容易跃迁, 使光吸收边从约198.1 nm(对应能量为6.26 eV)红移至205.9 nm(对应能量为6.02 eV), 拓宽Li3OCl的光响应范围, 从而为其在可见光区域的应用提供了潜在的可能性. 这种调控机制对光控固态电池至关重要, 因为拓宽光吸收范围可增强材料对不同波长光的利用率, 为提升光激发载流子浓度, 进而优化离子传输性能提供可能性. 无应变条件下的Li3OCl在12.74和18.18 eV处存在两个较为明显的吸收峰, 这表明材料在这些能量范围内具有较高的光吸收效率. 当施加双轴拉伸应变后, 无应变时的12.74和18.18 eV处的吸收峰均出现了明显的红移现象, 且峰值随着应变程度的增加而逐渐降低. 当施加双轴压缩应变后, 吸收峰均出现明显的蓝移现象, 且峰值增大.

      • 3.3.3.   光折射率、反射率和消光系数

    • 图9(b)显示, 无应变条件下, Li3OCl的静折射系数为1.803, 且在紫外区域的7.76和9.09 eV处分别达到2.25和2.31的峰值, 表明材料在紫外区域(UVC)具有较强的光折射能力. 施加双轴拉伸应变后, 折射峰表现出明显的红移现象, 且峰值略微下降. 根据介电函数理论, 材料的带隙与介电响应密切相关. 通常, 宽带隙材料在低频区域的介电函数较小, 折射率相对较低; 而窄带隙材料由于更易发生电子跃迁, 介电函数可能增大, 从而表现出较高的折射率. 本研究发现, 双轴拉伸应变(0%—2%)使Li3OCl的带隙从6.26 eV减小至6.02 eV. 尽管带隙变窄理论上应提升介电响应, 但计算结果却显示介电函数和折射率整体降低. 这一反常现象源于应变的双重效应: 一方面, 晶格膨胀缩小了带隙; 另一方面, 应变诱导的Li-p轨道电子态密度降低(图7)削弱了电子对光场的极化能力. 此外, 间接带隙的加深进一步抑制了直接光跃迁概率. 这些竞争机制共同导致介电函数和折射率随应变增加而下降, 揭示了应变调控光电性能的复杂性. 此外, 施加双轴压缩应变后, 折射峰表现出明显的蓝移现象, 且峰值略微上升. 这一现象与拉伸应变下的变化形成对比, 其内在机制同样源于压缩应变对电子结构和带隙性质的调控: 一方面, 晶格收缩增大了带隙, 导致介电响应的特征峰向更高能量(蓝移)移动; 另一方面, 压缩应变诱导了Li3OCl从间接带隙向直接带隙的转变, 显著增强了高对称点附近的直接光跃迁概率. 同时, 压缩应变下导带底附近Li-p态密度相对增加, 这有助于增强电子对光场的极化响应. 这些因素(带隙增大导致的蓝移趋势, 与直接跃迁增强和态密度变化导致的介电响应增强)的竞争结果, 最终表现为折射峰蓝移的同时峰值略微上升.

      对于带隙大的材料, 只有当光的能量足够高时, 消光系数才会显著增大, 即才会具有明显的消光系数. 由图9(c)所示, 我们发现在光子能量增加的过程中, 由于2%拉伸应变下的带隙最小, 因此最先在较低的光子能量下具有消光系数. 消光系数在8.43到12.74 eV之间保持较为稳定且大于1, 说明Li3OCl在紫外区域(UVC)对光的衰减能力较强. 施加双轴拉伸应变后, 消光系数表现出明显的红移现象, 且峰值略微下降. 而施加双轴压缩应变后, 消光系数表现出明显的蓝移现象, 且峰值略微上升. 图9(d)显示了Li3OCl的反射特性, 无应变状态下Li3OCl在紫外区表现出较强的反射特性, 双轴拉伸应变使反射峰红移且反射强度略有下降, 而压缩应变作用使反射峰蓝移且反射强度略有上升.

      我们发现施加–2%的双轴压缩应变后的Li3OCl, 其光吸收系数、介电函数、折射率和反射率均达到最高值. 从态密度分析可以看出, 施加–2%的压缩应变后的Li3OCl在价带和导带附近存在更为密集的电子态分布, 主要由Li原子贡献; 同时Cl和O原子在费米能级附近呈现出更显著的态密度峰. 这种电子结构特征显著增强了Li-p, O-p和Cl-p轨道之间的跃迁概率, 使得光子受激跃迁时的数量更多, 从而大幅提升了材料的光吸收强度.

    4.   结　论

    • 本研究通过第一性原理计算研究了双轴/单轴应变对反钙钛矿材料Li3OCl电子结构及光学响应的调控规律. 拉伸应变下呈现显著的带隙收缩效应: 当双轴拉伸应力从0%增至2%时, 带隙由6.263 eV线性降至6.023 eV, 主要归因于导带底的显著下移, 而价带顶位置保持稳定. 压缩应变则导致带隙增大并诱导能带类型转变: 施加2%双轴压缩应变时, 带隙增大至约6.380 eV. 更为关键的是, 压缩应变显著提高了Γ点的能级, 导致材料从间接带隙转变为直接带隙. 态密度分析进一步揭示, 应变类型深刻影响电子态分布与轨道杂化. 拉伸应变不仅降低了导带附近Li-p态密度, 同时增强了Li-p与O-p/Cl-p轨道的杂化作用, 从而优化了光激发载流子的跃迁通道. 压缩应变则导致价带和导带附近(尤其在费米能级附近)的电子态密度相对增强, 主要由Li, O, Cl原子贡献, 这为更强的光吸收提供了电子结构基础. 在光学性质方面, 应变诱导了显著的光谱偏移与强度变化. 拉伸应变诱导的带隙窄化导致介电函数实部ε1(ω)和虚部ε2(ω)光谱曲线整体红移, 光吸收边向低能方向移动, 使材料的光响应范围有望拓展至可见光区域. 在2%拉伸应变下, 消光系数在6.02 eV处即出现显著光衰减效应, 这一现象与带隙收缩导致的光子吸收阈值降低直接相关. 压缩应变则引起介电函数和光学参数(吸收系数、消光系数、反射率)整体蓝移, 光吸收边向高能方向移动. 值得注意的是, 尽管带隙增大, 压缩应变后的Li3OCl在紫外区域(UVC)特定能量范围展现出更强的光吸收强度、更高的介电函数峰值、折射率峰值和反射率峰值. 这主要归因于压缩应变下价带和导带附近更高的电子态密度以及诱导产生的直接带隙特性, 显著增强了特定能量光子的跃迁概率和材料的光学响应强度. 这为通过应变工程平衡光吸收效率与带隙调控提供了新视角.

      本文研究结果为Li3OCl在光电器件和固态电池中的应用研究提供了新思路. 通过应变工程精准调控其带隙和光吸收特性, 使其适配不同波长的光激发需求, 例如在光控固态电池中, 拉伸应变优化的Li3OCl具有更宽的光响应范围(红移至较低能量), 可有效利用更低能量的光子(如近紫外或可见光边缘)激发载流子; 而压缩应变优化的Li3OCl则在特定紫外波段具有更高的光吸收效率, 可能提升该波段光子激发载流子的浓度. 应变优化的Li3OCl协同利用光场与应力场提升离子电导率; 此外, 红移的光吸收边使其有望作为紫外-可见光转换层, 拓宽光能利用范围. 然而, 实际应用中需进一步研究非均匀应变、温度效应及光-力耦合的协同机制, 并结合实验验证其界面稳定性和循环性能, 以推动高性能全固态电池的实用化.

    参考文献 (36)

目录

/

返回文章
返回