-
2019年, 斯坦福大学Hwang团队[1]成功制备了Nd0.8Sr0.2NiO2薄膜, 并观测到约15 K临界温度的超导转变, 这是首次在镍氧化物中观测到超导电性. 2023年, Sun等[2]发现双层Ruddlesden-Popper(RP)相La3Ni2O7在14 GPa以上压力下呈现出转变温度
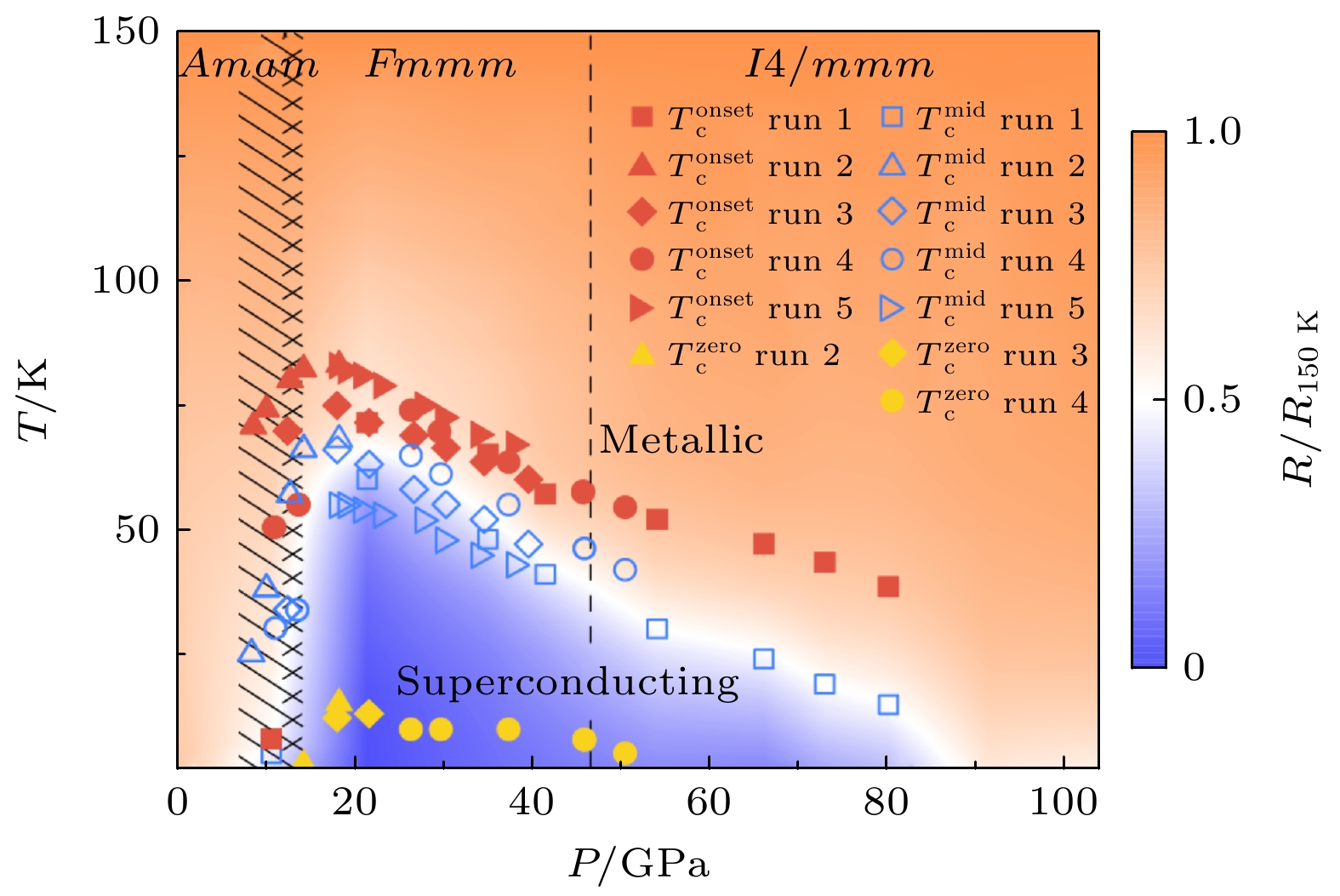
$ T_{{\mathrm{c}}} $ 接近80 K的超导电性, 这一发现立即吸引了广泛的实验[3–19]和理论[16,20–50]研究. RP相镍酸盐La3Ni2O7具有双层Ni-O八面体结构, 其中, 镍原子的平均价态为${\rm{Ni}} ^{2.5+} $ ($ 3 {\mathrm{d}}^{7.5} $ ), 为介于$ 3 {\mathrm{d}}^{8} $ 和$ 3 {\mathrm{d}}^{7} $ 之间的混合价态. 费米能附近$ 3{\mathrm{ d}}_{3 z^2-r^2} $ 和$ 3 {\mathrm{d}}_{x^2-y^2} $ 轨道分别呈现近似半填充和1/4填充. 考虑到其具有3个费米口袋和多轨道特性, La3Ni2O7更接近于铁基超导体的情形. 相比之下, 无限层镍酸盐中并不存在顶角氧, 形成Ni-O方平面结构. 因此, 其镍的电子构型为${\rm{Ni}} ^{1+} $ ($ 3 {\mathrm{d}}^{9} $ ), 更接近铜酸盐中具有Cu-O方平面结构的${\rm{Cu}} ^{2+} $ ($ 3 {\mathrm{d}}^{9} $ )[1,51]. 目前, 针对La3Ni2O7提出的理论模型表明, Ni的$ 3 {\mathrm{d}}_{3 z^2-r^2} $ 轨道间强烈的垂直层间耦合对形成库珀对具有重要作用, 可能形成$ s_\pm $ 波配对对称性[21–23,28–30,33,36,37,42,43]或d波配对对称性[32,35,44,45,48]. 目前, La3Ni2O7的超导机制仍尚无定论. 研究表明, 基于电声耦合机制得到的超导转变温度趋于0 K[52], 而实验测得的超导转变温度远远超过McMillan极限[53]. 因此, 可以排除常规的电声耦合机制. 近期的理论研究主要基于巡游电子图像[23,43,54–58]或局域自旋图像[29,33,34,47,59]开展. Zhou等[60,61]和Ko等[62]分别发现双层RP相镍酸盐(La,Pr)3Ni2O7薄膜和La3Ni2O7薄膜在常压下的超导起始转变温度突破40 K, 确立了镍酸盐成为继铜基、铁基之后的第3类常压高温超导体.最近, Li等[63]将La3Ni2O7高压实验研究的压力范围扩展至104 GPa. 研究发现, 在0—14 GPa压力范围, La3Ni2O7呈现弱绝缘特性; 当压力超过14 GPa时出现结构相变, 在18 GPa时超导转变温度最高, 为83 K, 随后随着压力的增大单调递减, 形成近直角三角形
$ T_{{\mathrm{c}}} $ -压力相图(图1). 该相图与铜氧化物超导体和铁基超导体中掺杂或压力下的穹顶形超导相图明显不同[64–66]. 解释该反常相图对揭示La3Ni2O7的超导机制至关重要. 我们分别从巡游电子图像和局域自旋图像出发, 探讨超导转变温度的压力依赖性. 利用泛函重整化群(FRG)方法深入研究了巡游电子图像下压力对电子关联效应与超导电性的影响. 同时, 基于局域自旋图像, 对超导转变温度的压力依赖性进行了估算. 通过将两种图像的理论结果与实验结果进行对比, 为揭示其超导机制提供线索. 目前该研究成果已发表[57], 本文对其加以介绍并拓展讨论. -
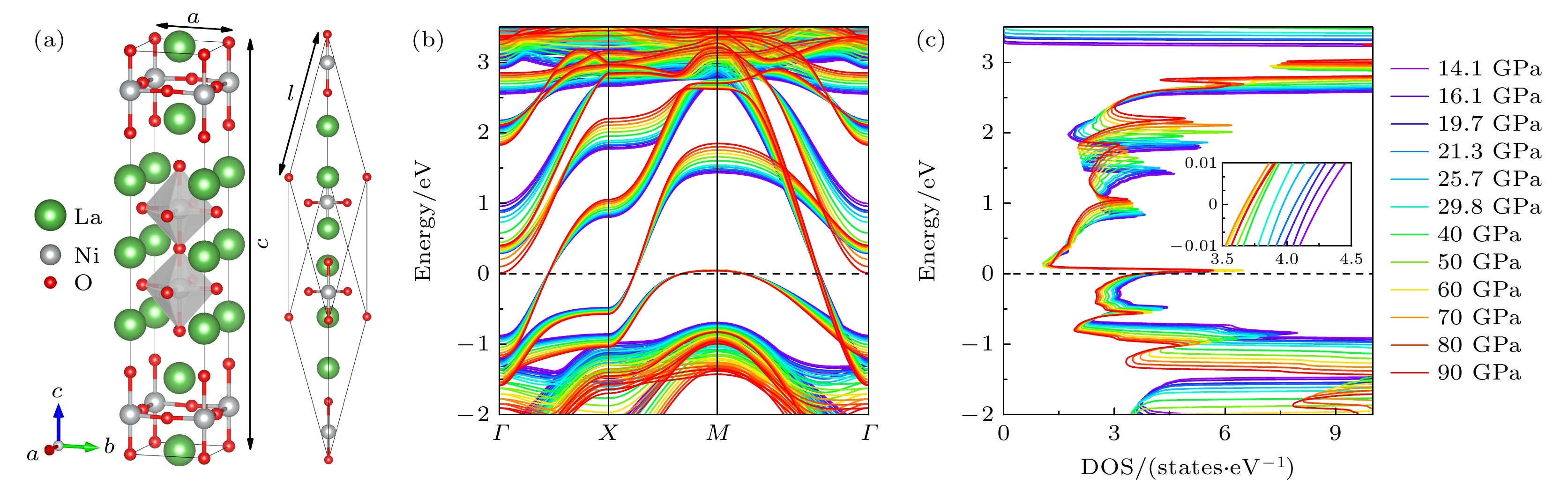
图2(a)展示了高压下La3Ni2O7的晶体结构. 基于密度泛函理论进行电子结构计算, 更多计算细节参见文献[57]. 能带结构和态密度分析(图2(b), (c))显示费米能级
$ E_\mathrm{F} $ 附近的能带结构基本不变, 而远离$ E_\mathrm{F} $ 的能带色散显著增强导致带宽增大, 同时态密度在70 GPa前后呈现先降后升的非单调变化(图2(c)插图). 轨道投影分析证实$ E_\mathrm{F} $ 附近的电子态主要来源于Ni的$ 3 {\mathrm{d}}_{3 z^2-r^2} $ 和$ 3 {\mathrm{d}}_{x^2-y^2} $ 轨道, 这与已有研究结论一致[2,20,22,23,43]. 值得注意, 上述结果都给出了一个能带结构的重要特征, 即M点存在空穴口袋. 理论研究认为, 压力的增大使得原本位于费米能级以下的能带穿过了费米能级, 在M点形成了空穴口袋, 与此同时形成了金属化的σ键[2], 这被认为是导致超导电性的重要原因. 目前, 常压下的角分辨光电子能谱的结果表明, La3Ni2O7不存在M点的空穴口袋[14]. 另一方面, 在最近关于常压下Pr掺杂La3Ni2O7薄膜的角分辨光电子能谱实验表明, M点空穴口袋是否存在似乎并不影响超导电性[67,68]. 因此, 需要进一步的理论和实验研究M点空穴口袋和超导电性的内在关联.由于Ni的
$ 3{\mathrm{ d}}_{3 z^2-r^2} $ 和$ 3 {\mathrm{d}}_{x^2-y^2} $ 轨道在整个超导压力区间主导$ E_\mathrm{F} $ 附近的电子态, 因此, 基于最大局域化Wannier函数方法[69], 我们构建了基于Ni原子$ 3 {\mathrm{d}}_{3 z^2-r^2} $ 和$ 3 {\mathrm{d}}_{x^2-y^2} $ 的双层两轨道模型:其中,
$ t_\delta^{ab} $ 表示格点i的a轨道与格点i+δ的b轨道之间的跃迁矩阵元, σ代表自旋,$ \varepsilon_a $ 为a轨道的在位能. 为简化表述, 下文以x和z分别代表$ 3 {\mathrm{d}}_{x^2-y^2} $ 和$ 3 {\mathrm{d}}_{3 z^2-r^2} $ 轨道. 不同压力下的在位能及跃迁参数列于表1, 其中z轨道间的垂直层间跃迁$ t_{\left(00\tfrac12\right)}^{zz} $ 强度最大, 这与La3Ni2O7已有研究结果一致[20,22,23,57]. -
我们通过引入原子多轨道库仑相互作用来研究电子关联效应, 其相互作用哈密顿量表示为
其中U表示轨道内Hubbard排斥势,
$ U' $ 为轨道间库仑相互作用,$ J_{\mathrm{H}} $ 是洪特耦合,$ J_{\mathrm{P}} $ 为配对跃迁相互作用. 根据Kanamori关系[70], 轨道间排斥势满足$ U = U'+2 J_{\mathrm{H}} $ , 且轨道间配对跃迁$ J_{\mathrm{H}} = J_{\mathrm{P}} $ . 通过约束无规相近似[71]估算得到U的特征值范围为2.0—3.4 eV, 表明电子关联处于中等强度, 因此, 本研究选取轨道内Hubbard排斥势U = 2 eV和U = 3 eV进行计算.奇异模泛函重整化群(SM-FRG)是一种先进的量子多体非微扰方法, 可以无偏地处理超导(SC)、自旋密度波(SDW)和电荷密度波(CDW)3个通道的竞争及相互作用, 在弱至中等耦合强度范围内具有较好的计算结果. 该方法的核心在于对Wetterich方程进行截断处理, 得到单粒子不可约四点顶角函数
$ \varGamma_{\varLambda} $ 随着红外截断能标Λ演化的流动方程(忽略自能修正和频率依赖性). 通过将$ \varGamma_{\varLambda} $ 重新投影至SC, SDW和CDW通道并进行因式分解, 可获得费米子双线性算符间的散射矩阵. 通过迭代求解流动方程, 我们得到依赖能标的散射矩阵最负奇异值$ S_{\varLambda} $ . 当$ S_{\varLambda} $ 在某个通道中首次发散时, 标志着相变的发生, 其相由散射通道和散射矩阵奇异模式决定, 相变温度$ T_{\mathrm{c}} $ 正比于发散能标$ \varLambda_{\mathrm{c}} $ . SM-FRG的优势在于消耗较少计算资源的同时得到较为精确的系统的失稳性质, 例如$ T_{\mathrm{c}} $ 、超导配对对称性、密度波序配对形式等. 综上, SM-FRG方法不仅能够平等处理所有可能的有序态, 还具有直接获得转变温度$ T_{\mathrm{c}}\sim \varLambda_{\mathrm{c}} $ 的优势. 因此, 我们采用奇异模泛函重整化群(SM-FRG)方法来确定系统的序. 更多技术细节可参考文献[57]. 下文将首先展示3种典型情况下的FRG计算结果, 继而系统讨论$ T_{\mathrm{c}} $ 的压力依赖性.图3(a)展示了在14.1, 50和90 GPa压力下, U = 3 eV,
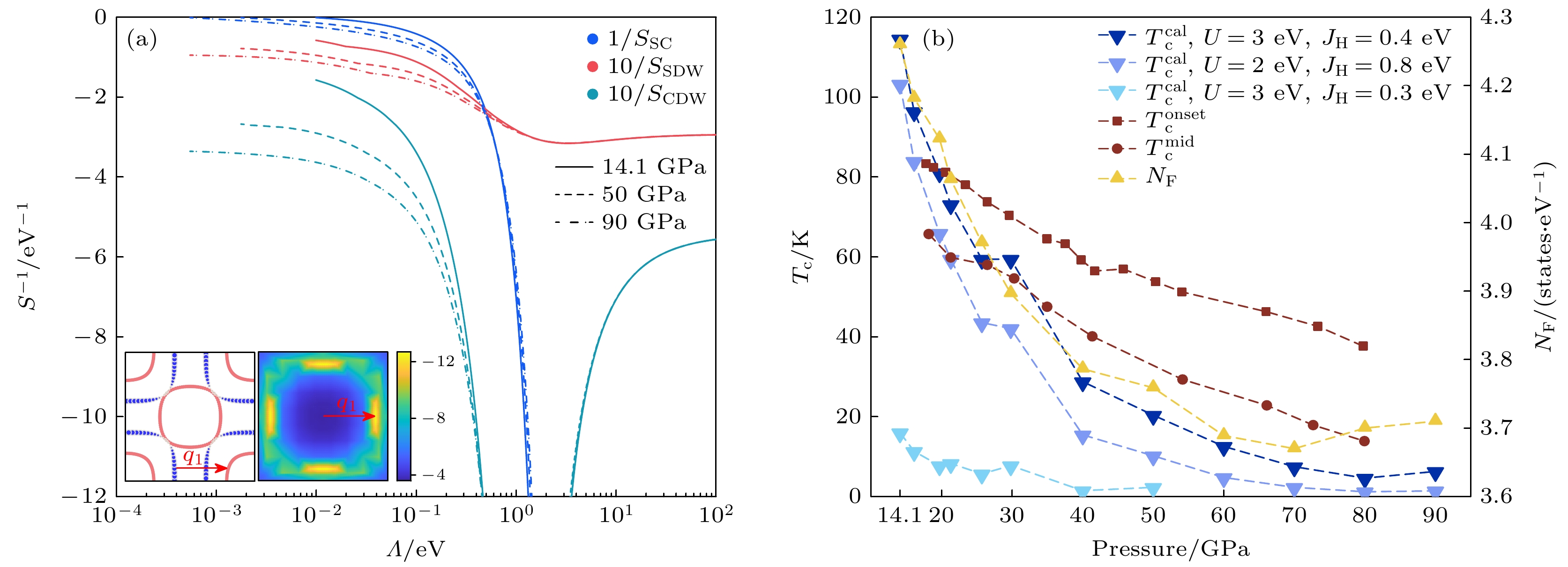
$ J_{\mathrm{H}} $ = 0.4 eV时, SC, SDW和CDW通道中$ S^{-1} $ 随Λ的变化关系. 3种压力下高能标区域的初始FRG流行为相似, 此时裸相互作用占主导地位, 表现为SDW通道较强而CDW通道因库仑屏蔽而衰减. 然而, 在低能标区域, 由于低能粒子-空穴激发的相空间受限, SDW和CDW通道变为次要通道并趋于饱和(图3(a)右插图展示出SDW通道动量依赖的本征值, 在(1,0)和(0,1)方向呈现峰值). 在中能标区域, 随着SDW通道增强, SC和CDW通道通过通道耦合开始被增强. SC通道最终通过Cooper机制发散, 这是以自旋涨落为媒介的超导电性的典型表现. 表1所列所有压力情况均获得类似结果. 通过分析SC通道的本征散射模式, 我们获得费米口袋上的配对能隙函数(图3(a)左插图), 显示为$ {\mathrm{s}}_\pm $ 波对称性. 在$ C_{4 v} $ 对称性下, 存在连接两个具有相反配对符号费米口袋的特征动量$ {{\boldsymbol{q}}_{1}} $ , 该动量恰好对应SDW通道的峰值动量(图3(a)右插图), 再次证实了配对与自旋涨落的关联性.从图3(a)可以观察到, U = 3 eV,
$ J_{\mathrm{H}} $ = 0.4 eV时, 随着压力从14.1 GPa增至50 GPa和90 GPa, 临界能标$ \varLambda_{\mathrm{c}} $ 显著降低, 这一现象与自旋涨落的减弱(在FRG流方程求解的最终阶段)直接相关. 这表明转变温度$ T_{\mathrm{c}}\sim \varLambda_c $ 对压力具有高度敏感 性. 为此, 针对表1所列压力序列进行了系统的SM-FRG计算, 获得转变温度$ T^{{\mathrm{cal}}}_{\mathrm{c}} $ 的压力依赖性(图3(b)中倒三角符号). 作为对比, 图中同时展示了实验测量的超导起始温度$ T^{{\mathrm{onset}}}_{\mathrm{c}} $ (实心方块)和中间温度$ T^{{\mathrm{mid}}}_{\mathrm{c}} $ (实心圆)数据[63]. 为验证SM-FRG结果的稳健性, 通过改变U和$ J_{\mathrm{H}} $ 参数进行系统计算. 图3(b)中给出了3套U和$ J_{\mathrm{H}} $ 参数下超导$ T_{\mathrm{c}} $ 随压力的变化规律. 结果表明, 除最低$ J_{\mathrm{H}} $ 对应最低$ T_{\mathrm{c}} $ (体现洪特耦合的重要性)外, 其他两种情况$ T_{\mathrm{c}} $ 随着压力的增大逐渐降低, 与实验中$ T^{{\mathrm{onset}}}_{\mathrm{c}} $ 和$ T^{{\mathrm{mid}}}_{\mathrm{c}} $ 的变化规律定性相似. 这里要说明的是, SM-FRG中计算的超导通道发散能标$ \varLambda_{\mathrm{c}}\sim T_{\mathrm{c}} $ 对应的是材料完全进入超导态的临界温度, 即零电阻温度$ T^{{\mathrm{zero}}}_{\mathrm{c}} $ . 通过和Li等[63]实验相图(见图1)对比可以看到, 实验测得的零电阻温度$ T^{{\mathrm{zero}}}_{\mathrm{c}} $ 与我们采用(U,$ J_{\mathrm{H}} $ ) = (3,0.3) eV计算的$ T^{{\mathrm{zero}}}_{\mathrm{c}} $ 曲线高度符合. 由于材料的电子相互作用参数U和$ J_{\mathrm{H}} $ 无法严格确定, 因此计算得到的$ T_{\mathrm{c}} $ 是近似结果. 但是我们计算的$ T_{\mathrm{c}} $ 随压力的变化趋势与实验相符. 另外, 值得注意的是, 虽然80 GPa时正常态DOS (黄色三角)高于70 GPa, 但理论$ T_{\mathrm{c}} $ 并未跟随DOS变化趋势, 而是与实验相符. 这表明必须如我们的FRG计算那样, 对能带结构和关联效应进行系统处理才能正确描述这一物理现象. 以上研究表明, 基于巡游电子图像可以很自然地得到与实验定性一致的超导转变温度-压力相图. -
基于电子局域自旋图像(例如多轨道t-J模型), 超导转变温度的粗略估计式为
$ T_{{\mathrm{c}}} \sim \exp\left[-\dfrac{1}{N_{\mathrm{F}} J}\right] $ , 其中J为有效自旋交换能,$ N_{\mathrm{F}} $ 为$ E_\mathrm{F} $ 处的电子态密度. 考虑到$ J \propto t^2 $ 且$ N_{\mathrm{F}} \propto 1/t $ (t为代表性跃迁积分), 而静水压条件下t必然增大, 这将导致J和$ N_{\mathrm{F}} J $ 同时增大, 从而预测$ T_{\mathrm{c}} $ 应随压力升高而增大—这与实验结果[63]明显不符. 当然, 这只是粗略的估计, 有待更深入的理论研究. -
通过结合密度泛函理论和奇异模泛函重整化群计算, 本文系统研究了La3Ni2O7超导区域不同压力下的电子结构、紧束缚模型、配对机制及配对对称性. 研究发现体系始终呈现
$ {\mathrm{s}}_\pm $ 波配对对称性, 该配对源于自旋涨落, 而涨落强度随压力增强逐渐减弱, 从而导致超导转变温度下降. 这一结论说明基于巡游电子图像, 可以很自然地得到与实验一致的结果; 而基于局域自旋图像, 简单估计发现超导转变温度的压力依赖性与实验结果相反. 因此, 实验和理论结果表明, 至少在超导区域, 超导转变温度随着压力的演化规律更倾向于巡游电子图像. 当然, 我们只是基于局域自旋图像做了简单估计, 不一定准确. 目前, 暂时还没有基于此图像研究压力依赖性的详细报道, 期待从该图像出发有进一步更细致的研究. 最近, 有研究表明, 通过考虑强关联巡游电子图像与电声耦合的叠加效应, 存在增强超导的可能性[56]. 这为理解双层镍基超导体中的高温超导提供了新视角和潜在的理论机制, 值得进一步研究讨论此机制下的压力依赖性.
双层镍酸盐La3Ni2O7超导转变温度的压力依赖: 巡游电子与局域自旋图像
Pressure dependence of superconducting transition temperature in bilayer nickelate La3Ni2O7: Itinerant electrons and local spin picture
-
摘要: 对于双层Ruddlesden-Popper相镍酸盐La3Ni2O7, 近期的实验研究表明, 在超导区, 随着压力增大, 其超导转变温度从18 GPa压力下的83 K单调下降, 表现出近直角三角形的超导转变温度-压力相图, 与铜氧化物超导体和铁基超导体中掺杂或压力下的穹顶形超导相图不同. 解释该反常相图对揭示La3Ni2O7的超导机制至关重要. 由于电声耦合机制无法解释镍基超导体的高超导转变温度, 因此, 本文从巡游电子和局域自旋图像出发, 探讨超导转变温度的压力依赖性. 通过将理论结果与实验结果进行对比, 为揭示其超导机制提供线索.
-
关键词:
- Ruddlesden-Popper相双层镍酸盐 /
- 超导相图 /
- 泛函重整化群 /
- 巡游电子图像 /
- 局域自旋图像
Abstract: Recent experimental studies on the bilayer Ruddlesden-Popper phase nickelate La3Ni2O7 have shown that in the superconducting region, its superconducting transition temperature decreases monotonically from 83 K at 18 GPa as pressure further increases, exhibiting a nearly right-triangular temperature-pressure phase diagram that is different from the dome-shaped diagrams observed in cuprates and iron-based superconductors under either doping or pressure. It is important to understand this anomalous phase diagram in elucidating the superconducting mechanism of La3Ni2O7. Since the electron-phonon coupling mechanism cannot account for the high superconducting transition temperatures in nickelate superconductors, in this work, the pressure dependence of the transition temperature is investigated from the perspective of the itinerant electrons picture and the local spin picture. By combining the density functional theory (DFT) and the unbiased singular-mode functional renormalization group (SM-FRG) method, it is found that the pairing symmetry is consistently an $s_\pm$-wave, driven by spin fluctuations that become progressively weakened under pressure, thereby decreasing in the superconducting transition temperature, which is in qualitative agreement with the experimental observation. On the other hand, we estimate that the pressure dependence in the local spin picture contradicts with the experimental result. Therefore, the pressure dependence of superconducting transition temperature is more consistent with the itinerant electrons picture. Admittedly, we only made a rough estimation based on the local spin picture. It is expected that further and more detailed research will be conducted on the pressure dependence of superconducting transition temperature from the local spin picture, providing deeper insights into the underlying superconducting mechanism of La3Ni2O7. -

-
图 2 (a) 高压下La3Ni2O7的晶胞与原胞结构示意图; (b) 不同压力下原胞的能带结构及(c) 态密度(DOS)分布, 其中插图展示了费米能级
$ E_\mathrm{F} $ 附近的DOS特征[57]Figure 2. (a) Conventional cell and primitive cell for La3Ni2O7 under high pressure; (b) band structure and (c) DOS under different pressures for primitive cell, the insert shows the DOS near the
$ E_\mathrm{F} $ [57].图 3 (a) La3Ni2O7在14.1, 50和90 GPa压力下, U = 3 eV,
$ J_{\mathrm{H}} $ = 0.4 eV时, 超导(SC)、自旋密度波(SDW)和电荷密度波(CDW)通道中$ S^{-1} $ 随Λ变化的FRG流方程计算结果, 左插图展示50 GPa压力下费米面上的能隙函数分布, 右插图显示同压力下SDW通道最负奇异值$ S({\boldsymbol{q}}) $ 的空间分布特征[57]; (b) La3Ni2O7超导转变温度$ T_{\mathrm{c}} $ 随压力的相图[57],$ T^{{\mathrm{onset}}}_{\mathrm{c}} $ 和$ {\mathrm{T}}^{{\mathrm{mid}}}_{\mathrm{c}} $ 引自实验数据[63]用于对比, 费米能处态密度也展示出来用于对比Figure 3. (a) FRG flows of
$ S^{-1} $ versus Λ in the SC, SDW, and CDW channels of La3Ni2O7, respectively, at pressures 14.1, 50, and 90 GPa with U = 3 eV,$ J_{\mathrm{H}} $ = 0.4 eV; the left subfigure present the gap function on the Fermi surfaces, the right subfigure presents the leading negative$ S({\boldsymbol{q}}) $ in the SDW channel, both subfigures are the results at pressure 50 GPa[57]; (b) phase diagram of superconducting$ T_{\mathrm{c}} $ versus pressure of La3Ni2O7[57], the$ T^{{\mathrm{onset}}}_{\mathrm{c}} $ and$ T^{{\mathrm{mid}}}_{\mathrm{c}} $ are extracted from the experimental work[63] for comparison, the DOS at the$ {E}_{\mathrm{F}}$ ($ {N}_{\mathrm{F}} $ ) versus pressure is also shown for comparison.表 1 不同压力下La3Ni2O7双层双轨道紧束缚模型的在位能
$ \varepsilon_a $ 与跃迁积分$ t_\delta^{ab} $ 参数表(其中x和z分别表示$ 3 {\mathrm{d}}_{x^2-y^2} $ /$ 3 {\mathrm{d}}_{3 z^2-r^2} $ 轨道, 垂直层间距设定为1/2). 压力单位为GPa,$ \varepsilon_a $ 与$ t_\delta^{ab} $ 单位均为eV[57]Table 1. On-site energies
$ \varepsilon_a $ and hopping integrals$ t_\delta^{ab} $ of the bilayer two-orbital tight-binding model for La3Ni2O7 under different pressures. Here, x and z denote the$ 3 {\mathrm{d}}_{x^2-y^2} $ /$ 3 {\mathrm{d}}_{3 z^2-r^2} $ orbitals, respectively. Note that the vertical interlayer distance is assigned as 1/2. The unit of pressure is GPa, and the unit of$ \varepsilon_a $ and$ t_\delta^{ab} $ are eV[57].Pressure $ \varepsilon_x $ $ \varepsilon_z $ $ t_{(100)}^{x x} $ $ t_{(100)}^{z z} $ $ t_{(100)}^{x z} $ $ t_{\left(00\frac{1}{2}\right)}^{x x} $ $ t_{\left(00\frac{1}{2}\right)}^{z z} $ $ t_{(110)}^{x x} $ $ t_{(110)}^{z z} $ $ t_{\left(10\frac{1}{2}\right)}^{x z} $ 14.1 0.728 0.402 –0.470 –0.118 0.235 0.008 –0.623 0.071 –0.018 –0.036 16.1 0.737 0.407 –0.476 –0.119 0.238 0.009 –0.629 0.071 –0.018 –0.037 19.7 0.747 0.411 –0.483 –0.121 0.242 0.009 –0.637 0.071 –0.018 –0.037 21.3 0.749 0.412 –0.486 –0.123 0.243 0.008 –0.640 0.071 –0.018 –0.037 25.7 0.761 0.416 –0.495 –0.125 0.247 0.009 –0.647 0.072 –0.018 –0.037 29.8 0.769 0.417 –0.501 –0.126 0.249 0.010 –0.651 0.072 –0.018 –0.036 40.0 0.803 0.426 –0.521 –0.134 0.259 0.009 –0.674 0.071 –0.015 –0.040 50.0 0.833 0.437 –0.535 –0.139 0.269 0.010 –0.698 0.073 –0.016 –0.042 60.0 0.847 0.435 –0.552 –0.145 0.273 0.011 –0.703 0.075 –0.016 –0.040 70.0 0.871 0.447 –0.566 –0.149 0.283 0.010 –0.723 0.073 –0.017 –0.041 80.0 0.896 0.453 –0.580 –0.153 0.287 0.009 –0.738 0.072 –0.015 –0.045 90.0 0.918 0.461 –0.593 –0.155 0.293 0.008 –0.753 0.071 –0.016 –0.046 -
[1] Li D F, Lee K, Wang B Y, Osada M, Crossley S, Lee H R, Cui Y, Hikita Y, Hwang H Y 2019 Nature 572 624 doi: 10.1038/s41586-019-1496-5 [2] Sun H L, Huo M W, Hu X W, Li J Y, Liu Z J, Han Y F, Tang L Y, Mao Z Q, Yang P T, Wang B S, Cheng J G, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7 [3] Liu Z, Huo M W, Li J, Li Q, Liu Y C, Dai Y M, Zhou X X, Hao J H, Lu Y, Wang M, Wen H H 2024 Nat. Commun. 15 7570 doi: 10.1038/s41467-024-52001-5 [4] Hou J, Yang P T, Liu Z Y, Li J Y, Shan P F, Ma L, Wang G, Wang N N, Guo H Z, Sun J P, Uwatoko Y, Wang M, Zhang G M, Wang B S, Cheng J G 2023 Chin. Phys. Lett. 40 117302 doi: 10.1088/0256-307X/40/11/117302 [5] Zhang Y N, Su D J, Huang Y E, Shan Z Y, Sun H L, Huo M W, Ye K X, Zhang J W, Yang Z H, Xu Y K, Su Y, Li R, Smidman M, Wang M, Jiao L, Yuan H Q 2024 Nat. Phys. 20 1269 doi: 10.1038/s41567-024-02515-y [6] Zhang M X, Pei C Y, Wang Q, Zhao Y, Li C H, Cao W Z, Zhu S H, Wu J F, Qi Y P 2024 J. Mater. Sci. Technol. 185 147 doi: 10.1016/j.jmst.2023.11.011 [7] Wang G, Wang N, Wang Y, Shi L, Shen X, Hou J, Ma H, Yang P, Liu Z, Zhang H, Dong X, Sun J, Wang B, Jiang K, Hu J, Uwatoko Y, Cheng J 2023 arXiv: 2311.08212[cond-mat.supr-con] [8] Wang L H, Li Y, Xie S Y, Liu F Y, Sun H L, Huang C X, Gao Y, Nakagawa T, Fu B Y, Dong B, Cao Z H, Yu R Z, Kawaguchi S I, Kadobayashi H, Wang M, Jin C Q, Mao H K, Liu H Z 2024 J. Am. Chem. Soc. 146 7506 doi: 10.1021/jacs.3c13094 [9] Zhou Y Z, Guo J, Cai S, Sun H L, Li C Y, Zhao J Y, Wang P Y, Han J Y, Chen X T, Chen Y J, Wu Q, Ding Y, Xiang T, Mao H K, Sun L L 2025 Matter Radiat. Extremes 10 027801 doi: 10.1063/5.0247684 [10] Cui T, Choi S, Lin T, Liu C, Wang G, Wang N N, Chen S R, Hong H T, Rong D K, Wang Q Y, Jin Q, Wang J O, Gu L, Ge C, Wang C, Cheng J G, Zhang Q H, Si L, Jin K j, Guo E J 2024 Commun. Mater. 5 32 doi: 10.1038/s43246-024-00478-4 [11] Chen K, Liu X, Jiao J, Zou M, Jiang C, Li X, Luo Y, Wu Q, Zhang N, Guo Y, Shu L 2024 Phys. Rev. Lett. 132 256503 doi: 10.1103/PhysRevLett.132.256503 [12] Wang H Z, Chen L, Rutherford A, Zhou H D, Xie W W 2024 Inorg. Chem. 63 5020 doi: 10.1021/acs.inorgchem.3c04474 [13] Dong Z H, Huo M W, Li J, Li J Y, Li P C, Sun H L, Gu L, Lu Y, Wang M, Wang Y Y, Chen Z 2024 Nature 630 847 doi: 10.1038/s41586-024-07482-1 [14] Yang J G, Sun H L, Hu X W, Xie Y Y, Miao T M, Luo H L, Chen H, Liang B, Zhu W P, Qu G X, Chen C Q, Huo M W, Huang Y B, Zhang S J, Zhang F F, Yang F, Wang Z M, Peng Q J, Mao H Q, Liu G D, Xu Z Y, Qian T, Yao D X, Wang M, Zhao L, Zhou X J 2024 Nat. Commun. 15 4373 doi: 10.1038/s41467-024-48701-7 [15] Wang G, Wang N N, Shen X L, Hou J, Ma L, Shi L F, Ren Z A, Gu Y D, Ma H M, Yang P T, Liu Z Y, Guo H Z, Sun J P, Zhang G M, Calder S, Yan J Q, Wang B S, Uwatoko Y, Cheng J G 2024 Phys. Rev. X 14 011040 doi: 10.1103/PhysRevX.14.011040 [16] Wang M, Wen H H, Wu T, Yao D X, Xiang T 2024 Chin. Phys. Lett. 41 077402 doi: 10.1088/0256-307X/41/7/077402 [17] Lei Y H, Wang Y H, Song J H, Ge J X, Wu D R, Zhang Y L, Li C J 2024 Chin. Phys. B 33 096801 doi: 10.1088/1674-1056/ad6a0d [18] 沈瑶 2024 物理学报 73 197104 doi: 10.7498/aps.73.20240898 Shen Y 2024 Acta Phys. Sin. 73 197104 doi: 10.7498/aps.73.20240898 [19] Huang X, Zhang H Y, Li J Y, Huo M W, Chen J F, Qiu Z Y, Ma P Y, Huang C X, Sun H L, Wang M 2024 Chin. Phys. Lett. 41 127403 doi: 10.1088/0256-307X/41/12/127403 [20] Luo Z H, Hu X W, Wang M, Wú W, Yao D X 2023 Phys. Rev. Lett. 131 126001 doi: 10.1103/PhysRevLett.131.126001 [21] Yang Q G, Wang D, Wang Q H 2023 Phys. Rev. B 108 L140505 doi: 10.1103/PhysRevB.108.L140505 [22] Sakakibara H, Kitamine N, Ochi M, Kuroki K 2024 Phys. Rev. Lett. 132 106002 doi: 10.1103/PhysRevLett.132.106002 [23] Gu Y H, Le C C, Yang Z S, Wu X X, Hu J P 2025 Phys. Rev. B 111 174506 doi: 10.1103/PhysRevB.111.174506 [24] Christiansson V, Petocchi F, Werner P 2023 Phys. Rev. Lett. 131 206501 doi: 10.1103/PhysRevLett.131.206501 [25] Wú W, Luo Z H, Yao D X, Wang M 2024 Sci. China Phys. Mech. Astron. 67 117402 doi: 10.1007/s11433-023-2300-4 [26] Cao Y, Yang Y F 2024 Phys. Rev. B 109 L081105 doi: 10.1103/PhysRevB.109.L081105 [27] Chen X J, Jiang P H, Li J, Zhong Z C, Lu Y 2025 Phys. Rev. B 111 014515 doi: 10.1103/PhysRevB.111.014515 [28] Liu Y B, Mei J W, Ye F, Chen W Q, Yang F 2023 Phys. Rev. Lett. 131 236002 doi: 10.1103/PhysRevLett.131.236002 [29] Lu C, Pan Z M, Yang F, Wu C J 2024 Phys. Rev. Lett. 132 146002 doi: 10.1103/PhysRevLett.132.146002 [30] Zhang Y, Lin L F, Moreo A, Maier T A, Dagotto E 2024 Nat. Commun. 15 2470 doi: 10.1038/s41467-024-46622-z [31] Oh H, Zhang Y H 2023 Phys. Rev. B 108 174511 doi: 10.1103/PhysRevB.108.174511 [32] Liao Z G, Chen L, Duan G J, Wang Y M, Liu C L, Yu R, Si Q M 2023 Phys. Rev. B 108 214522 doi: 10.1103/PhysRevB.108.214522 [33] Qu X Z, Qu D W, Chen J, Wu C, Yang F, Li W, Su G 2024 Phys. Rev. Lett. 132 036502 doi: 10.1103/PhysRevLett.132.036502 [34] Yang Y F, Zhang G M, Zhang F C 2023 Phys. Rev. B 108 L201108 doi: 10.1103/PhysRevB.108.L201108 [35] Jiang K, Wang Z, Zhang F C 2024 Chin. Phys. Lett. 41 017402 doi: 10.1088/0256-307X/41/1/017402 [36] Huang J, Wang Z D, Zhou T 2023 Phys. Rev. B 108 174501 doi: 10.1103/PhysRevB.108.174501 [37] Tian Y H, Chen Y, Wang J M, He R Q, Lu Z Y 2024 Phys. Rev. B 109 165154 doi: 10.1103/PhysRevB.109.165154 [38] Qin Q, Yang Y F 2023 Phys. Rev. B 108 L140504 doi: 10.1103/PhysRevB.108.L140504 [39] Xia C L, Liu H Q, Zhou S J, Chen H H 2025 Nat. Commun. 16 1054 doi: 10.1038/s41467-025-56206-0 [40] Ouyang Z, Wang J M, Wang J X, He R Q, Huang L, Lu Z Y 2024 Phys. Rev. B 109 115114 doi: 10.1103/PhysRevB.109.115114 [41] Qu X Z, Qu D W, Li W, Su G 2023 arXiv: 2311.12769[cond-mat.str-el] [42] Zheng Y Y, Wú W 2025 Phys. Rev. B 111 035108 doi: 10.1103/PhysRevB.111.035108 [43] Wang Y, Jiang K, Wang Z, Zhang F C, Hu J 2024 Phys. Rev. B 110 205122 doi: 10.1103/PhysRevB.110.205122 [44] Fan Z, Zhang J F, Zhan B, Lv D, Jiang X Y, Normand B, Xiang T 2024 Phys. Rev. B 110 024514 doi: 10.1103/PhysRevB.110.024514 [45] Luo Z H, Lv B, Wang M, Wu W, Yao D X 2024 npj Quantum Mater. 9 61 doi: 10.1038/s41535-024-00668-w [46] Shen Y, Qin M L, Zhang G M 2023 Chin. Phys. Lett. 40 127401 doi: 10.1088/0256-307X/40/12/127401 [47] Xue J R, Wang F 2024 Chin. Phys. Lett. 41 057403 doi: 10.1088/0256-307X/41/5/057403 [48] Jiang R S, Hou J N, Fan Z Y, Lang Z J, Ku W 2024 Phys. Rev. Lett. 132 126503 doi: 10.1103/PhysRevLett.132.126503 [49] Huo Z H, Luo Z H, Zhang P, Yang A Q, Liu Z T, Tao X R, Zhang Z H, Guo S M, Jiang Q W, Chen W X, Yao D X, Duan D F, Cui T 2025 Sci. China Phys. Mech. Astron. 68 237411 doi: 10.1007/s11433-024-2583-y [50] Yang Y F 2025 Chin. Phys. Lett. 42 017301 doi: 10.1088/0256-307X/42/1/017301 [51] Zhang F C, Rice T M 1988 Phys. Rev. B 37 3759 doi: 10.1103/PhysRevB.37.3759 [52] Ouyang Z, Gao M, Lu Z Y 2024 npj Quantum Mater. 9 80 doi: 10.1038/s41535-024-00689-5 [53] McMillan W L 1968 Phys. Rev. 167 331 doi: 10.1103/PhysRev.167.331 [54] Zhan J, Le C, Wu X, Hu J 2025 arXiv: 2503.18877 [cond-mat.supr-con] [55] Wang Y, Chen Z, Zhang Y, Jiang K, Hu J 2025 arXiv: 2501.08536 [cond-mat.str-el] [56] Zhan J, Gu Y H, Wu X X, Hu J P 2025 Phys. Rev. Lett. 134 136002 doi: 10.1103/PhysRevLett.134.136002 [57] Jiang K Y, Cao Y H, Yang Q G, Lu H Y, Wang Q H 2025 Phys. Rev. Lett. 134 076001 doi: 10.1103/PhysRevLett.134.076001 [58] Liu Y Q, Wang D, Wang Q H 2025 arXiv: 2505.07341 [cond-mat.supr-con] [59] Zhang J X, Zhang H K, You Y Z, Weng Z Y 2024 Phys. Rev. Lett. 133 126501 doi: 10.1103/PhysRevLett.133.126501 [60] Zhou G D, Lv W, Wang H, Nie Z H, Chen Y Q, Li Y Y, Huang H L, Chen W Q, Sun Y J, Xue Q K, Chen Z Y 2025 Nature 640 641 doi: 10.1038/s41586-025-08755-z [61] 陈卓昱, 黄浩亮, 薛其坤 2025 物理学报 74 097401 doi: 10.7498/aps.74.20250331 Chen Z Y, Huang H L, Xue Q K 2025 Acta Phys. Sin. 74 097401 doi: 10.7498/aps.74.20250331 [62] Ko E K, Yu Y, Liu Y, Bhatt L, Li J, Thampy V, Kuo C T, Wang B Y, Lee Y, Lee K, Lee J S, Goodge B H, Muller D A, Hwang H Y 2025 Nature 638 935 doi: 10.1038/s41586-024-08525-3 [63] Li J, Peng D, Ma P, Zhang H, Xing Z, Huang X, Huang C, Huo M, Hu D, Dong Z, Chen X, Xie T, Dong H, Sun H, Zeng Q, Mao H k, Wang M 2025 Natl. Sci. Rev. nwaf220 [64] Stewart G R 2011 Rev. Mod. Phys. 83 1589 doi: 10.1103/RevModPhys.83.1589 [65] Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 doi: 10.1103/RevModPhys.78.17 [66] Sun J P, Matsuura K, Ye G Z, Mizukami Y, Shimozawa M, Matsubayashi K, Yamashita M, Watashige T, Kasahara S, Matsuda Y, Yan J Q, Sales B C, Uwatoko Y, Cheng J G, Shibauchi T 2016 Nat. Commun. 7 12146 doi: 10.1038/ncomms12146 [67] Wang B Y, Zhong Y, Abadi S, Liu Y, Yu Y, Zhang X, Wu Y M, Wang R, Li J, Tarn Y, Ko E K, Thampy V, Hashimoto M, Lu D, Lee Y S, Devereaux T P, Jia C, Hwang H Y, Shen Z X 2025 arXiv: 2504.16372[cond-mat.supr-con] [68] Li P, Zhou G, Lv W, Li Y, Yue C, Huang H, Xu L, Shen J, Miao Y, Song W, Nie Z, Chen Y, Wang H, Chen W, Huang Y, Chen Z H, Qian T, Lin J, He J, Sun Y J, Chen Z, Xue Q K 2025 Natl. Sci. Rev. nwaf205 doi: 10.1093/nsr/nwaf205 [69] Pizzi G, Vitale V, Arita R, Blügel S, Freimuth F, Géranton G, Gibertini M, Gresch D, Johnson C, Koretsune T, Ibañez-Azpiroz J, Lee H, Lihm J M, Marchand D, Marrazzo A, Mokrousov Y, Mustafa J I, Nohara Y, Nomura Y, Paulatto L, Poncé S, Ponweiser T, Qiao J, Thöle F, Tsirkin S S, Wierzbowska M, Marzari N, Vanderbilt D, Souza I, Mostofi A A, Yates J R 2020 J. Phys.: Condens. Matter 32 165902 doi: 10.1088/1361-648X/ab51ff [70] Castellani C, Natoli C R, Ranninger J 1978 Phys. Rev. B 18 4945 doi: 10.1103/PhysRevB.18.4945 [71] Vaugier L, Jiang H, Biermann S 2012 Phys. Rev. B 86 165105 doi: 10.1103/PhysRevB.86.165105 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: