首页
登录
注册
-
建筑结构在施工和服役期间，除受到自重、风等常规荷载的作用外，还有可能遭遇冲击、碰撞等偶然低速冲击荷载的作用，而降低建筑结构在此类荷载作用下连续倒塌风险的一个有效措施就是增强结构构件的承载能力和耗能能力。纤维增强树脂复合材料（FRP）具有较高的比强度及比吸能（材料的强度及吸能与其表观密度之比），同时具有良好的环境耐受能力[1]，采用FRP增强钢结构中常用的建筑圆钢管可以很好地综合两种材料的特点，使复合而成的构件在具有较高承载能力和耗能能力的同时具有较轻的质量和较好的环境耐受能力，因此在土木工程领域具有良好的应用前景。
近年来，国内外学者针对FRP增强金属构件在低速冲击、碰撞等荷载作用下的响应开展了大量研究。Zhi等[2]针对高强GFRP（Glass Fiber Reinforced Plastic）增强Q235B圆钢管构件在轴向低速冲击荷载作用下的响应进行了试验及仿真研究，分析了GFRP壁厚、钢管壁厚、冲击速度、试件长度等因素对试件极限承载能力和耗能能力的影响；Batuwitage等[3]采用CFRP材料增强了方钢管构件，并针对其轴向抗冲击性能开展研究，发现CFRP材料对增强方钢管构件的轴向耗能能力有很好的效果；Alam等[4]提出了CFRP增强钢管的侧向冲击仿真方法，发现CFRP材料可以显著限制钢管构件的塑性位移发展；李洋等[5]研究了横向冲击荷载作用下GFRP-钢组合悬臂梁的响应，发现包裹2.7 mm厚GFRP能有效地降低钢管的冲击作用；Kadhim等[6–7]针对CFRP增强钢管构件在侧向冲击荷载作用下的响应展开了试验研究，讨论了加载速率对试件性能的影响，发现CFRP的增强效果在较高加载速率下更为明显。
此外，随着对冲击等偶然荷载的研究成为热点，材料的动态力学行为也引起了广泛关注。金属材料对应变率效应较为敏感，一般采用J-C模型[8]或Z-A模型[9]进行模拟，其中J-C模型由于可以同时考虑应变率效应、温度效应及应力三轴度而被后续学者广泛应用及改进[10–12]。对于FRP材料，由于其力学性能较为复杂，目前关于其在低速冲击荷载作用下损伤演化的研究多基于Hashin准则[13]或Puck准则[14]展开，忽略了应变率效应的影响[15–16]。
本研究首先通过轴压试验及轴向低速冲击试验的结果对比，分析了GFRP增强建筑圆钢管构件的应变率效应敏感性；随后通过仿真的方法，将不考虑应变率效应、只考虑钢管应变率效应、只考虑GFRP应变率效应以及考虑钢管及GFRP应变率效应4种情况下的结果进行对比分析。
-
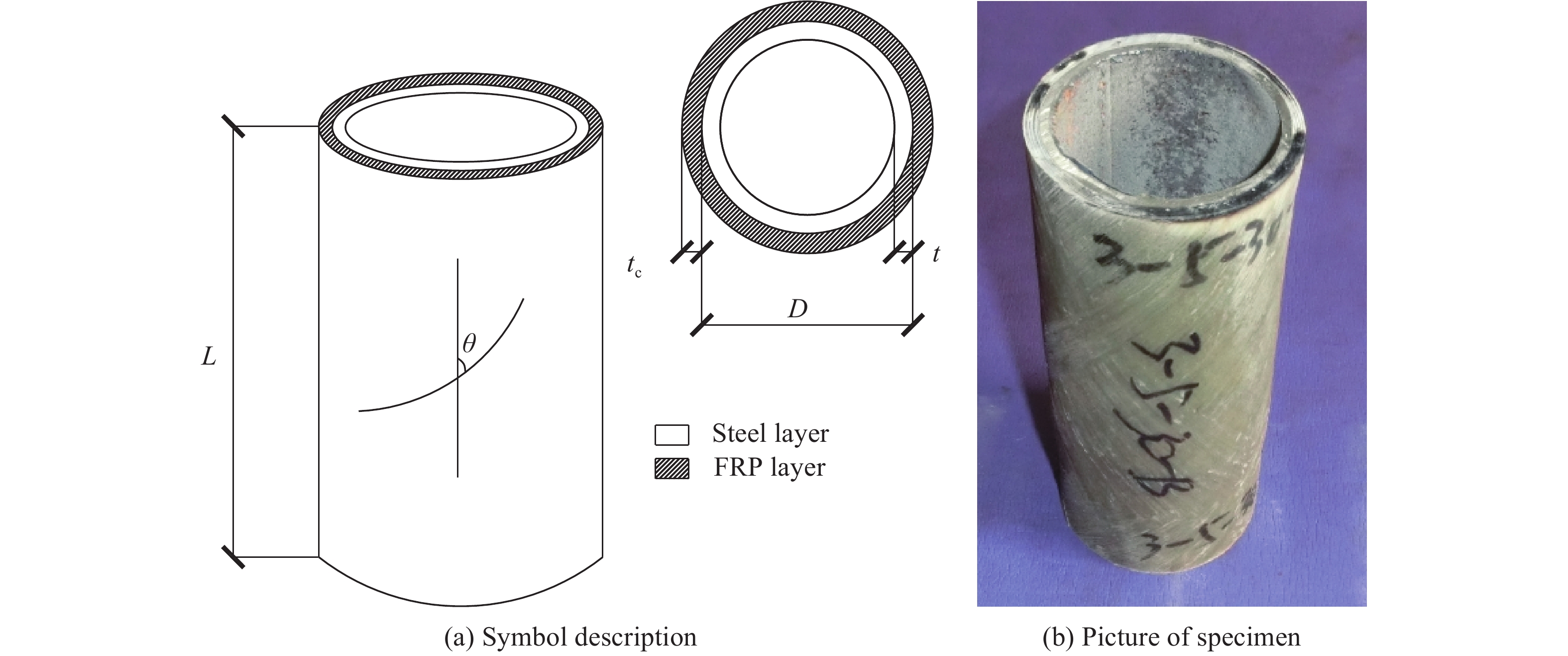
缠绕成型具有生产效率高、产品性能好的优点，同时对于GFRP增强圆钢管构件，其内部钢管可以直接充当芯模而不需要脱模，适合土木领域的大规模应用。因此，本研究采用此种成型工艺进行了试件的加工，且GFRP采用性价比较高的S2-1200玻璃纤维增强E-51环氧树脂，钢管采用应用较广泛的Q235B直缝圆焊管。试件的符号说明及实物图如图1所示，其中D为钢管外径，t为壁厚，
$\theta$ 和n为GFRP缠绕角度和层数，tc为GFRP层厚度，L为试件长度，v为冲击速度。为对比分析构件在准静态及低速冲击情况下的应变率效应，针对设计尺寸如表1所示的构件，分别开展了轴压试验和低速冲击试验。相较准静态轴压试验，冲击试验的数据采集更为困难，试件的响应更为剧烈，故为验证试验方案的可重复性，对于试件D-58-1.5-30-3.0开展了3组重复试验。 -
轴压试验中，试件的两端采用钢槽配合
$\alpha$ 高强石膏进行嵌固，同时在其下部支座的4个角点处布置4个竖向位移计（LVDT），用来测量其轴向压缩量。试验的加载过程通过30 t液压千斤顶配合反力系统实现，加载装置如图2所示。轴压试验采用先力控制后位移控制的方式进行加载，加载工艺流程如下：（1）荷载达到峰值之前，力加载速度为5 kN/min；（2）荷载达到峰值后，改为位移控制加载，加载速度减为1 mm/min。低速冲击试验在哈尔滨工业大学落锤式冲击试验系统上完成，此试验系统可以满足不同冲击质量（400.19～1063.30 kg）及不同冲击高度（0～20.6 m）的试验要求。本研究所进行的低速冲击试验采用的冲击能量为4052.03和1800.90 J，即落锤质量为400.19 kg，冲击速度分别为3.0和4.5 m/s。试验过程中，试件的底部采用钢槽及
$\alpha$ 高强石膏锚固，其位移及冲击荷载分别采用磁栅线位移测量系统及60 t压电式力传感器进行测量，试验装置如图3所示。 -
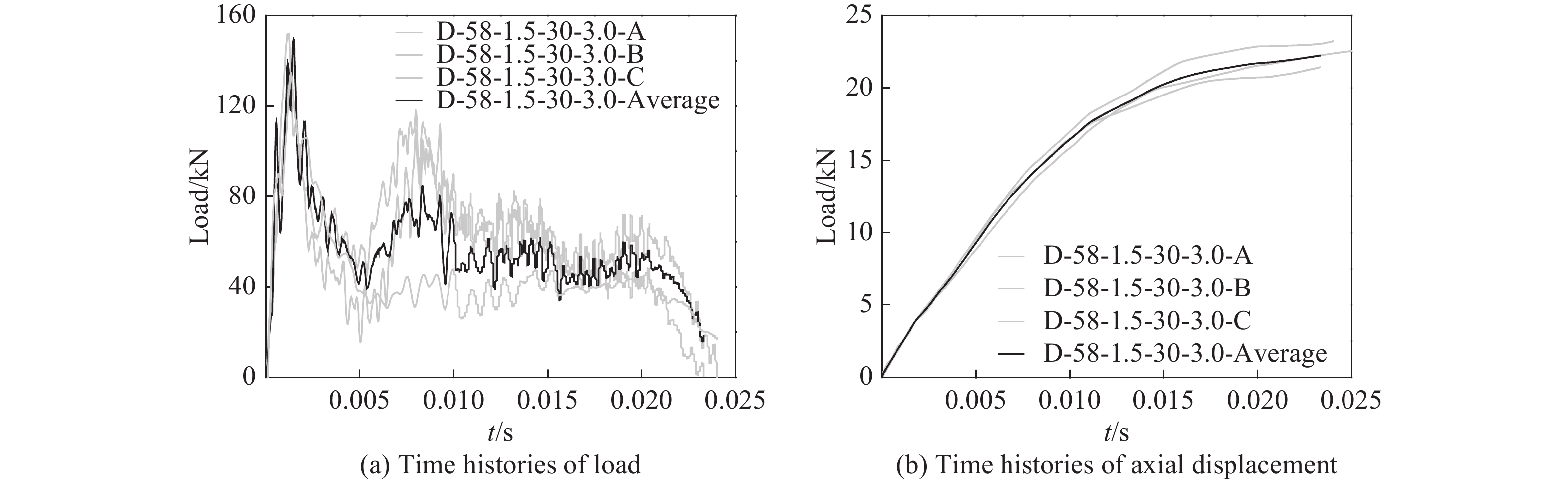
试件D-58-1.5-30-3.0的3组重复试验结果及其平均结果如图4所示。考虑到冲击荷载的特性，试验所得曲线存在较大的波动，但整体而言试验结果仍存在良好的可重复性。
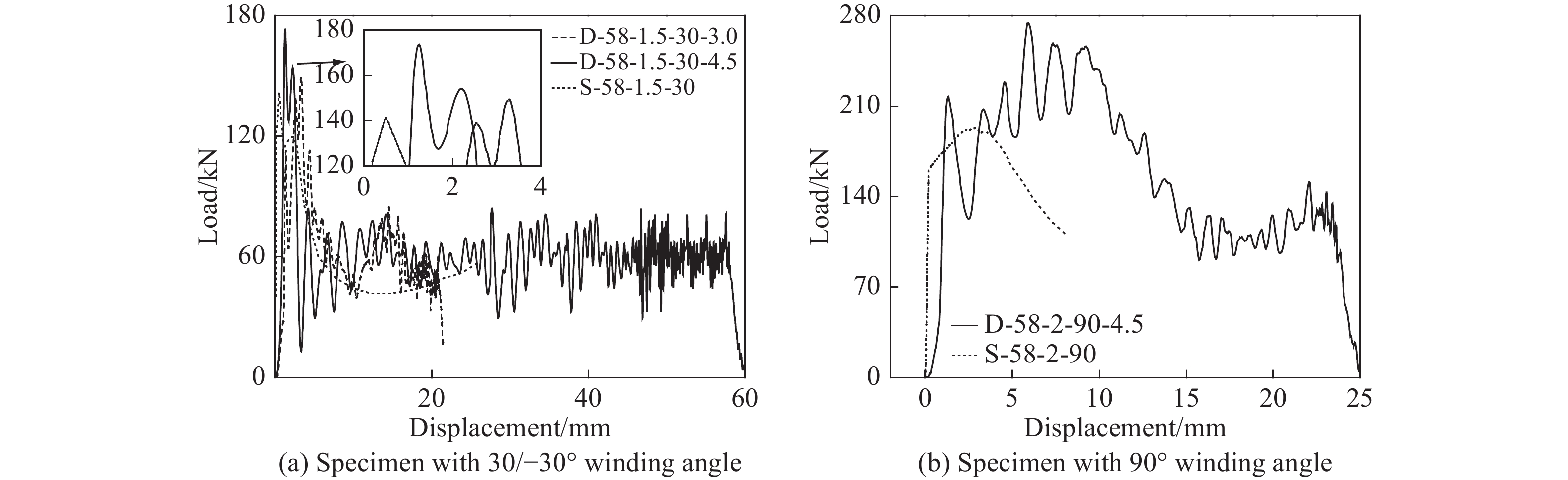
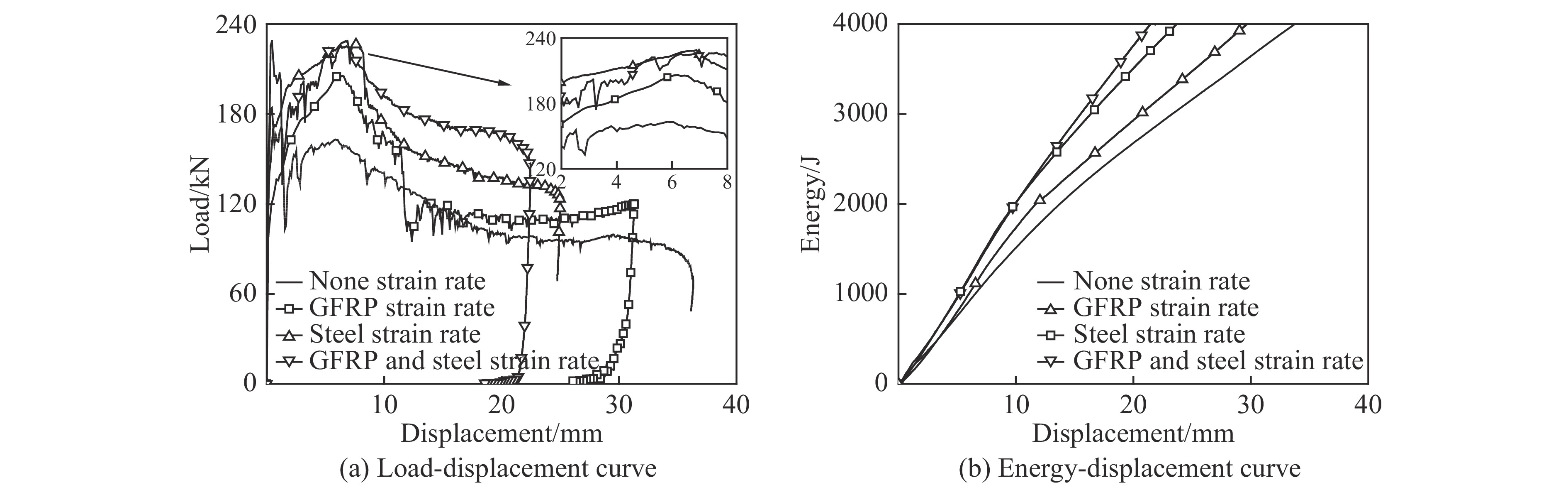
轴压试验与轴向低速冲击试验的结果（荷载-轴向位移曲线）对比如图5所示，得到以下结论：（1）在两种荷载作用下，试件的弹性段刚度相差不多，表明在低速冲击范围内，GFRP增强钢管构件的弹性段刚度对于应变率效应不敏感；（2）随着冲击速度的增加（冲击速度为3.0和4.5 m/s时对应的最大应变率分别为9.5、21.1 s–1），GFRP增强钢管构件的峰值荷载有所增加，且大于承受准静态轴压荷载作用的试件，表明在低速冲击范围内，构件的强度对于应变率效应较为敏感；（3）试件的荷载-位移曲线在低速冲击荷载作用下具有相似的形状及趋势，仅破坏位移有所增大，表明冲击速度的增加对试件的失效模式影响不大。
然而，由于在试验过程中不可避免地存在一些不可控参数，如试件实际几何尺寸与设计几何尺寸的差异、试件初始缺陷的差异以及试件组成材料性能的差异等，故仅通过试验并不能很好地分析应变率效应对试件性能的影响。鉴于上述原因，本研究提出了可考虑钢材及GFRP应变率效应的仿真方法，开展了关于GFRP增强圆钢管构件的应变率效应分析。
-
在仿真中，试件的各层依次建模，并通过一阶特征值屈曲的形式施加由实测得到的最大初始缺陷，同时为了简化分析，将试件的锚固段简化为刚域，有限元模型如图6所示。对于准静态轴压过程，采用ABAQUS的Explicit（显式）求解器进行拟静力分析，即缓慢地施加外力以消除惯性效应，通常拟静力分析中的加载时间取构件最低阶模态周期的10倍以上[17]，对于本研究试件，加载时间取为0.1 s。此外，为与轴压试验吻合，试件两端采用了固接的边界条件，并在其顶部采用光滑步骤（Smooth Step）以位移的形式施加轴压荷载。对于冲击过程，为与实际试验吻合，试件采用了底部固接顶部自由的边界条件，并建立了与实际落锤相同的模型（如图7所示）对试件模型施加冲击荷载。
-
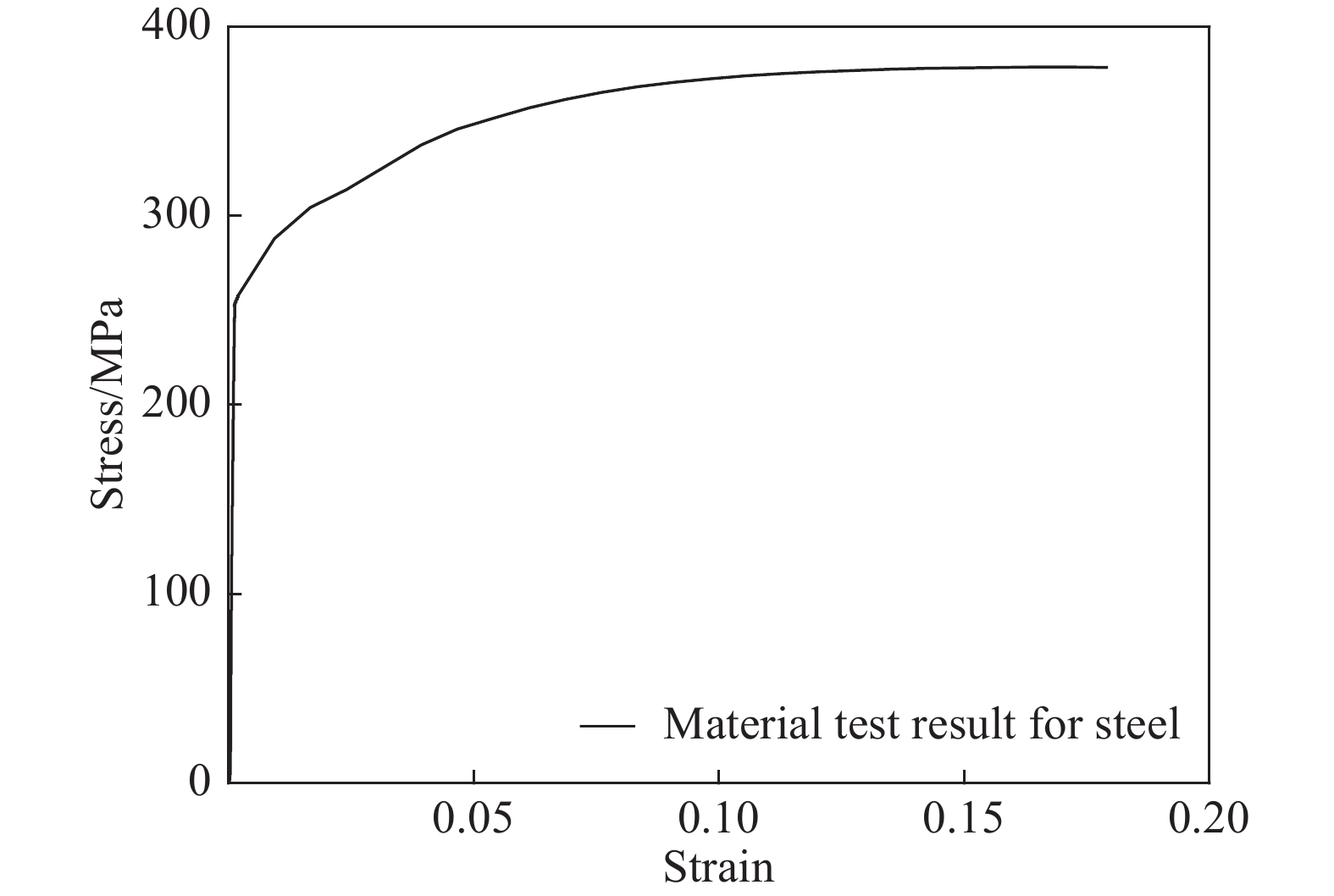
在ABAQUS中，一般采用Isotropic Elasto-Plasticity模型[17]模拟钢材的准静态力学行为，所需参数通过材性试验获得，如图8所示。在低速冲击仿真中，为讨论钢材的应变率效应，采用J-C模型[8]，即
式中：A、B、C、m、n及D1～D5均为材料有关系数，如表2、表3所示。材性参数均来源于Zhi等[2]的研究。
GFRP具有正交各向异性的材料特点，其本构模型较为复杂，本研究在文献[2]提出的关于GFRP增强钢管在冲击荷载作用下仿真方法（失效模式及损伤演化法则如表4所示，GFRP材料力学参数如表5所示，各层间界面性能如表6所示）的基础上，引入了Shokrieh等[18]关于GFRP应变率效应的模型
式中：
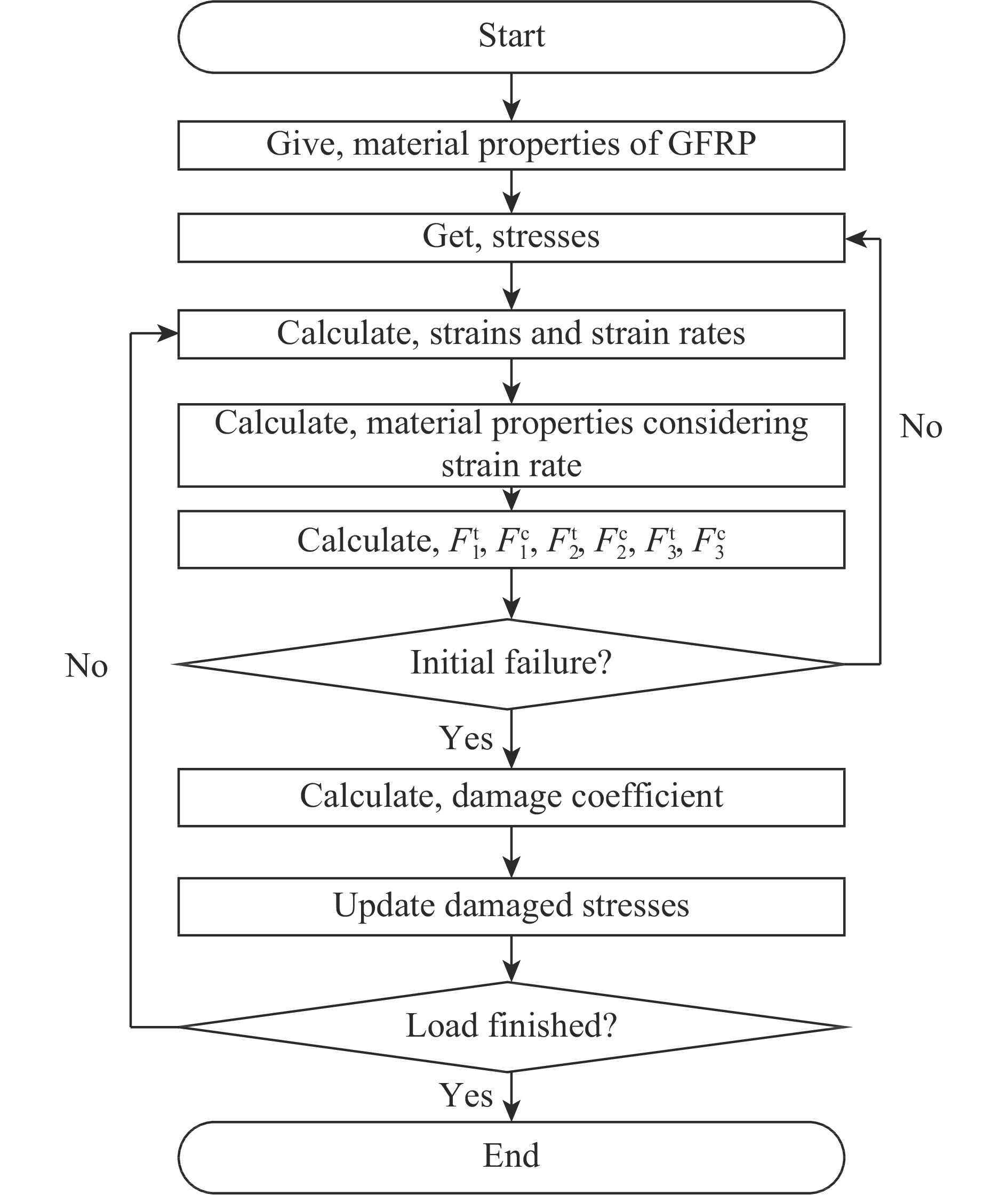
$\alpha$ 为GFRP单向板材性参数，$\beta $ 及$\gamma$ 为应变率效应系数，如表7所示。因此得到了可用于模拟GFRP 6种初始失效模式（纤维拉伸/压缩失效、树脂拉伸/压缩失效以及层内拉伸/压缩失效）及相应损伤演化，并能考虑GFRP应变率效应的VUMAT子程序，流程图如图9所示。此外，冲击过程中认为落锤保持弹性，其材料性能定义为E=217 GPa，
$\mu$ =0.3；落锤与试件之间的接触采用罚刚度方法进行模拟，取平均摩擦系数为0.3。 -
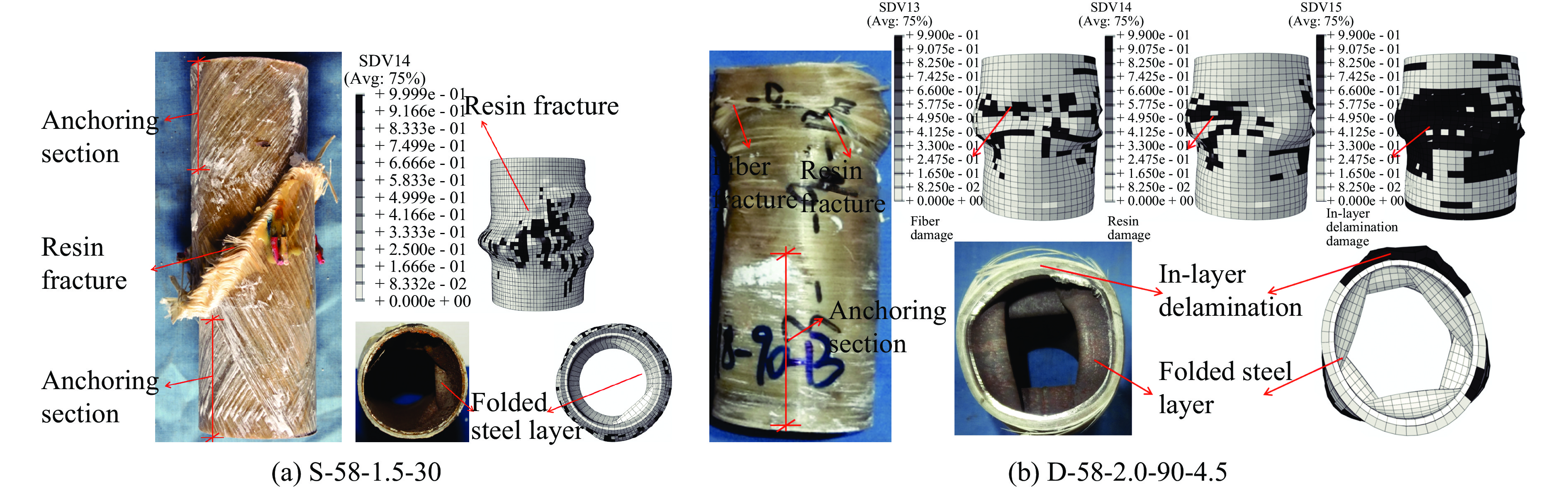
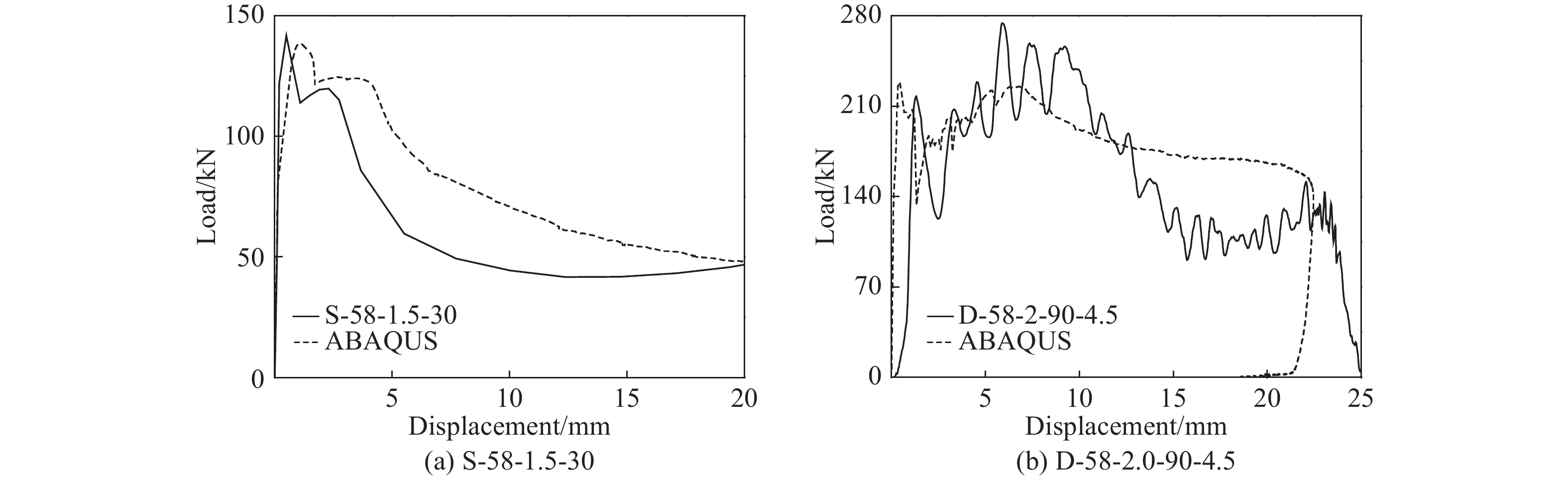
轴压试件的边界条件为两端嵌固，而低速冲击试件的边界条件为一端嵌固一端自由，故其破坏模式存在一些差异。以S-58-1.5-30及D-58-2.0-90-4.5为例，前者在跨中部位发生外部GFRP的树脂断裂及内部钢管的叠缩，而后者则在顶部发生了包括钢管叠缩、树脂断裂、纤维断裂及GFRP层内分层失效的破坏，这些破坏模式通过本文介绍的有限元模拟方法可以得到很好的仿真，如图10所示。此外，S-58-1.5-30及D-58-2.0-90-4.5的仿真及试验荷载-位移曲线对比如图11所示，可知有限元模拟结果与试验结果在弹性段及荷载下降段均吻合良好，为后续关于应变率的分析奠定了基础。
-
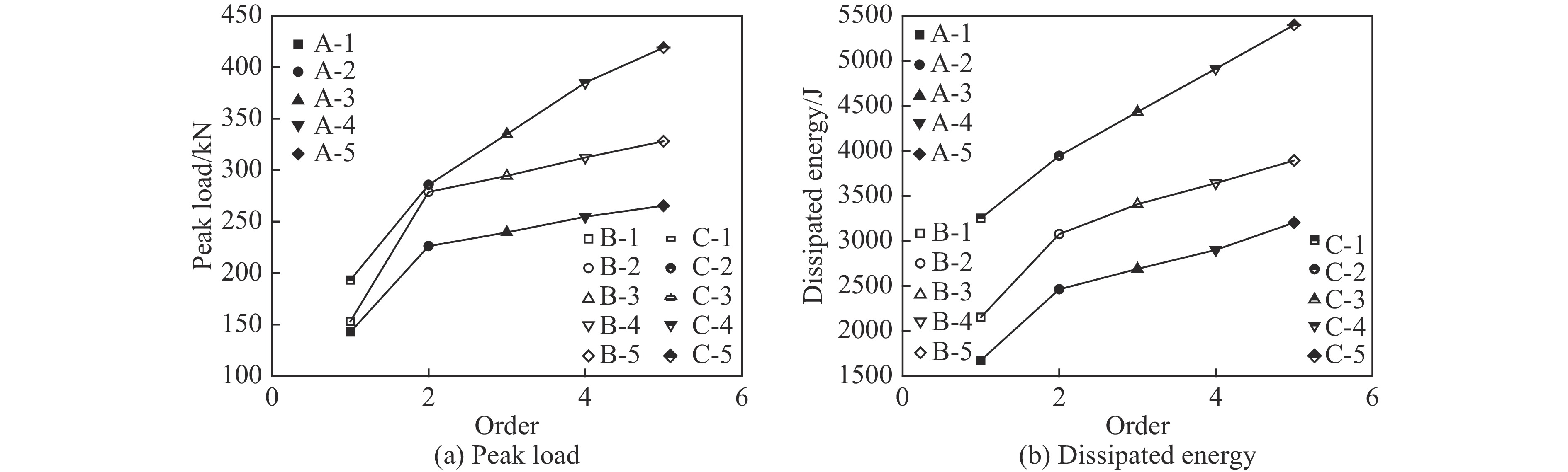
由Zhi等[2]的研究结果可知，对于发生叠缩式破坏的GFRP增强圆钢管试件，缠绕角度为90°时具有较好的耗能能力，故针对缠绕角度为90°的试件展开应变率效应分析。图12所示为试件D-58-2.0-90-4.5在不同情况下的仿真结果对比，包括考虑钢管及GFRP应变率效应、仅考虑钢管应变率效应、仅考虑GFRP应变率效应以及不考虑应变率效应4种情况。通过对比得到如下结论：（1）考虑应变率效应后试件的承载能力（如图12（a）所示）及耗能能力（相同轴向位移下消耗的能量，如图12（b）所示）均有所提高，故在低速冲击荷载作用下，试件的应变率效应不应忽略；（2）同时考虑GFRP及钢管应变率效应时的结果最大，但比仅考虑钢管应变率效应时的结果提升不多，由此可知在低速冲击范围内，钢管的应变率效应对于构件的影响更为显著。
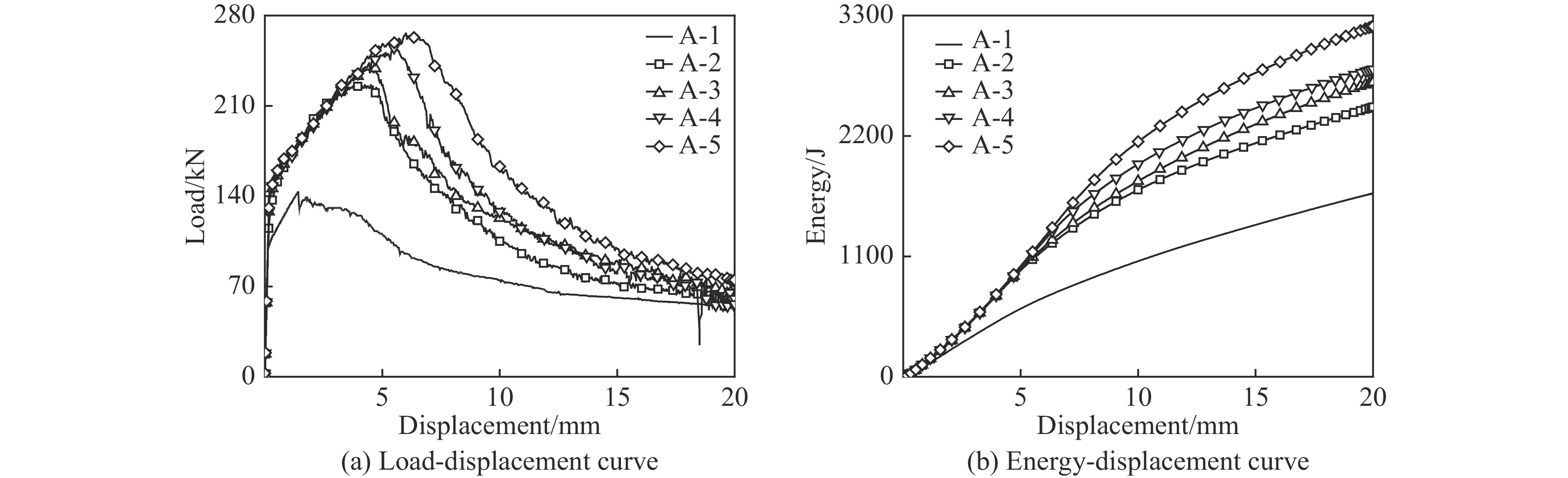
为进一步讨论低速冲击范围内，应变率效应对GFRP增强圆钢管试件性能的影响，针对恒定速率加载过程开展了一系列有限元模拟研究，试件设计参数及加载工况如表8所示。对比试件A-1～试件A-5的仿真结果（图13）可以得到如下结论：（1）试件在准静态及动态轴压荷载作用下具有相似的荷载-位移曲线形式，说明材料应变率效应对试件破坏模式的影响不大；（2）除准静态过程外，其余试件的荷载上升段随加载速率的增大变化不大，但峰值荷载明显增大，说明材料应变率效应与试件极限强度有正相关的关系，但对试件刚度影响不大；（3）随着加载速率增大，试件的耗能能力明显增大。此外，通过不同的钢管及GFRP壁厚试件结果的对比（图14）可知，在低速冲击范围内，钢管壁厚较大试件的峰值荷载及耗能能力随着加载速率增大具有更明显的增大效果，表明相对GFRP而言，钢管的应变率效应更为明显。
-
通过试验结果对比可知，由于应变率效应的影响，在低速冲击荷载作用下，GFRP增强圆钢管构件的强度较承受准静态轴压荷载的构件有明显提升。介绍了一种可以考虑GFRP及钢材应变率效应的有限元仿真方法，并通过数值模拟对比分析了考虑钢管及GFRP应变率效应、仅考虑钢管应变率效应、仅考虑GFRP应变率效应以及不考虑应变率效应4种情况下试件的性能，得到在低速冲击荷载作用下，试件应变率效应不应忽略，且相较GFRP而言，钢管的应变率效应对于构件的影响更为明显。最后，通过一组仿真研究进一步讨论了应变率效应对构件的影响，得出结论：（1）材料应变率效应对试件破坏模式影响不大；（2）材料应变率效应与试件极限强度有正相关的关系，但对试件刚度影响不大；（3）随着加载速率增大，试件的耗能能力明显增大。
GFRP增强圆钢管在低速冲击荷载作用下的应变率效应
Strain Rate Effect of GFRP-Reinforced Circular Steel Tube under Low-Velocity Impact
-
摘要: 讨论了玻璃纤维/环氧树脂复合材料（Glass Fiber Reinforced Plastic，GFRP）增强Q235圆钢管在低速冲击荷载作用下的应变率效应。通过轴压试验和轴向低速冲击试验获得了试件在准静态和低速冲击状态下的力学响应（轴向荷载及轴向位移），为后续仿真工作提供了依据。编写了可以考虑初始失效、损伤演化及应变率效应的GFRP材料子程序（VUMAT），并基于ABAQUS对构件的轴压及轴向冲击过程进行了仿真再现。通过仿真将不考虑应变率效应、只考虑钢管应变率效应、只考虑GFRP应变率效应、考虑钢管及GFRP应变率效应4种情况下的结果进行了对比分析。
-
关键词:
- 应变率效应 /
- 钢管 /
- 玻璃纤维/环氧树脂复合材料 /
- 低速冲击试验 /
- 有限元模拟
Abstract: This paper discussed the strain rate effect of glass fiber/epoxy resin composite (GFRP)-reinforced Q235 circular steel tube under low-velocity impact load. Firstly, the responses (axial load and displacement) of GFRP-reinforced steel tube under quasi-static and low-velocity impact load were obtained through axial compression tests and low-velocity impact tests respectively, which provided gist for the subsequent simulation. Secondly, a VUMAT subroutine considered initial failure modes, damage evolution and strain rate effect of GFRP was introduced; then the axial compression and low-velocity impact processes were simulated. Finally, the results under 4 situations (ignoring strain rate effect, considering the strain rate effect of steel tube, considering the strain rate effect of GFRP and considering the strain rate effect of both steel tube and GFRP) was compared using simulation. -
-
图 5 轴压试验及低速冲击试验结果对比
Figure 5. Comparison of test results between compression test and low-velocity impact test
图 6 GFRP增强圆钢管有限元模型
Figure 6. Finite element model of GFRP reinforced circular steel tube
图 11 仿真及试验荷载-位移曲线对比
Figure 11. Compared load-displacement curves between simulation and low-velocity impact test
图 12 D-58-2.0-90-4.5在不同情况下的仿真结果
Figure 12. Simulated results of D-58-2.0-90-4.5 with different situations
表 1 试件设计尺寸
Table 1. Design size of tested specimens
Specimen D×t/(mm×mm) [ $\theta$ /(°)]n
tc/mm L/mm Type of test v/(m·s−1) Maximum strain rate/s−1 S-58-1.5-30 58.0×1.5 [30/–30]3 2.0 100.0 Compression S-58-2.0-90 58.0×2.0 [90]6 2.0 100.0 Compression D-58-1.5-30-3.0 58.0×1.5 [30/–30]3 2.0 100.0 Impact 3.0 9.5 D-58-1.5-30-4.5 58.0×1.5 [90]6 2.0 100.0 Impact 4.5 21.1 D-58-2.0-90-4.5 58.0×2.0 [90]6 2.0 100.0 Impact 4.5 21.1 
下载: 导出CSV
A/MPa B/MPa n m Tm/K Tr/K 272.28 899.7 0.94 0.1515 1795 293
下载: 导出CSV
D1 D2 D3 D4 D5 –43.408 44.608 0.016 0.0145 –0.046
下载: 导出CSV
Failure modes Initial failure criterions Damage evolution laws Fiber tensile failure $F_1^{\rm t} = {\left( {\dfrac{{\sigma {}_1}}{{{X_{\rm t}}}}} \right)^2} + {\left( {\dfrac{{\sigma {}_4}}{{{S_{12}}}}} \right)^2} + {\left( {\dfrac{{\sigma {}_6}}{{{S_{13}}}}} \right)^2} \geqslant 1{\rm{ }}$ 
$D_1^{\rm t} = \dfrac{{\varepsilon _1^{\rm {ft}}}}{{\varepsilon _1^{\rm {ft}} - \varepsilon _1^{\rm {it}}}}\left( {1 - \dfrac{{\varepsilon _1^{\rm {it}}}}{{{\varepsilon _1}}}} \right)$ 
Fiber compression failure $F_1^{\rm c} = {\left( {\dfrac{{\sigma {}_1}}{{{X\rm_c}}}} \right)^2} \geqslant 1$ 
$D_1^{\rm c} = \dfrac{{\varepsilon _1^{\rm{fc}}}}{{\varepsilon _1^{\rm{fc}} - \varepsilon _1^{\rm{ic}}}}\left( {1 - \dfrac{{\varepsilon _1^{\rm{ic}}}}{{{\varepsilon _1}}}} \right)$ 
Resin tensile failure $F_2^{\rm t} = {\left( {\dfrac{{\sigma {}_2}}{{{Y_{\rm t}}}}} \right)^2} + {\left( {\dfrac{{\sigma {}_4}}{{{S_{12}}}}} \right)^2} + {\left( {\dfrac{{\sigma {}_5}}{{{S_{23}}}}} \right)^2} \geqslant 1{\rm{ }}$ 
$D_2^{\rm t} = \dfrac{{\varepsilon _2^{\rm{ft}}}}{{\varepsilon _2^{\rm {ft}} - \varepsilon _2^{\rm{it}}}}\left({1 - \dfrac{{\varepsilon _2^{\rm{it}}}}{{{\varepsilon _2}}}} \right)$ 
Resin compression failure $F_2^{\rm c} = {\left( {\dfrac{{{\tau _{nt}}\left( \theta \right)}}{{S_{23}^{\rm A} + {\mu _{nt}}{\sigma _n}\left( \theta \right)}}} \right)^2} + {\left( {\dfrac{{{\tau _{nl}}\left( \theta \right)}}{{{S_{12}} + {\mu _{nl}}{\sigma _n}\left( \theta \right)}}} \right)^2}$ 
$D_2^{\rm c} = \dfrac{{\gamma_{\rm r}^{\rm f}}}{{\gamma _{\rm r}^{\rm f} - \gamma _{\rm r}^{\rm i}}}\left( {1 - \dfrac{{\gamma _{\rm r}^{\rm i}}}{{{\gamma _r}}}} \right)$ 
Stretch in-layer delamination $F_3^{\rm t} = {\left( {\dfrac{{{\sigma _3}}}{{{Z_{\rm t}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _6}}}{{{S_{13}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _5}}}{{{S_{23}}}}} \right)^2}$ 
$D_3^{\rm t} = \dfrac{{\varepsilon _3^{\rm ft}}}{{\varepsilon _3^{\rm ft} - \varepsilon _3^{\rm it}}}\left( {1 - \dfrac{{\varepsilon _3^{\rm it}}}{{{\varepsilon _3}}}} \right)$ 
Compression in-layer delamination $F_3^{\rm c} = {\left( {\dfrac{{{\sigma _3}}}{{{Z_{\rm c}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _6}}}{{{S_{13}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _5}}}{{{S_{23}}}}} \right)^2}$ 
$D_3^{\rm c} = \dfrac{{\varepsilon _3^{\rm fc}}}{{\varepsilon _3^{\rm fc} - \varepsilon _3^{\rm ic}}}\left( {1 - \dfrac{{\varepsilon _3^{\rm ic}}}{{{\varepsilon _3}}}} \right)$ 
下载: 导出CSV
Modulus/GPa Poisson’s ratio Strength/MPa Fracture energy/(N·mm) E1=41.29; E2=E3=4.21; ${\nu}$ 12=
${\nu}$ 13=0.31;
Xt =884.5; Xc =837.17; Yt=Zt=37.38; ${\varGamma _1^{\rm t} = 28.25}$ ;
${\varGamma _1^{\rm c} = 80.1}$ ;
G12=G13=3.16; G23=3.0 ${\nu}$ 23=0.42
Yc =Zc=145; S12=S13=44.765; S23=50.88 ${\varGamma _2^{\rm t} = \varGamma _3^{\rm t}= 0.36}$ ;
${\varGamma_2^{\rm c} = \varGamma_3^{\rm c}=7.24}$ 
下载: 导出CSV
Elastic properties/GPa Strength/MPa Fracture toughness/(N·mm−1) B-K parameter Knn =4210; Ktt=3160; Kll=3160 Tn =37.380; Tt=44.765; Tl=44.765 Gn =0.36; Gt=1.33; Gl=1.33 $\eta$ =2.6
下载: 导出CSV
表 7 GFRP应变率效应模型所需参数
Table 7. Parameters for the model considering the strain rate effect of GFRP
Parameter ${\alpha}$ 
${\;\beta }$ 
${\gamma}$ 
Parameter ${\alpha}$ 
${\;\beta }$ 
${\gamma}$ 
E11/GPa 41.29 1.139 0.276 Xt/MPa 837.17 7.721 0.886 E22/GPa 4.21 0.437 0.262 Yt/MPa 37.38 13.088 0.131 G12/GPa 3.16 –0.941 0.054 Yc/MPa 145 0.11 1.278 Xt/MPa 881.5 7.721 0.886 S/MPa 44.756 15.656 0.086
下载: 导出CSV
表 8 仿真试件设计
Table 8. Design of simulated specimens
Specimen D/mm t/mm [ $\theta$ /(°)]n
tc/mm L/mm Displacement/mm Loading speed/(m·s−1) A-1 58.0 2.0 [90]6 2.0 100 20.0 Quasi-static A-2 58.0 2.0 [90]6 2.0 100 20.0 2.0 A-3 58.0 2.0 [90]6 2.0 100 20.0 4.0 A-4 58.0 2.0 [90]6 2.0 100 20.0 6.0 A-5 58.0 2.0 [90]6 2.0 100 20.0 8.0 B-1 58.0 2.0 [90]6 3.0 100 20.0 Quasi-static B-2 58.0 2.0 [90]6 3.0 100 20.0 2.0 B-3 58.0 2.0 [90]6 3.0 100 20.0 4.0 B-4 58.0 2.0 [90]6 3.0 100 20.0 6.0 B-5 58.0 2.0 [90]6 3.0 100 20.0 8.0 C-1 58.0 3.0 [90]6 2.0 100 20.0 Quasi-static C-2 58.0 3.0 [90]6 2.0 100 20.0 2.0 C-3 58.0 3.0 [90]6 2.0 100 20.0 4.0 C-4 58.0 3.0 [90]6 2.0 100 20.0 6.0 C-5 58.0 3.0 [90]6 2.0 100 20.0 8.0
下载: 导出CSV
-
[1] 岳清瑞, 杨勇新. 纤维增强复合材料加固结构耐久性研究综述 [J]. 建筑结构学报, 2009, 30(6): 8–15. YUE Q R, YANG Y X. Introduction to durability of concrete strengthened with fiber reinforced polymers [J]. Journal of Building Structures, 2009, 30(6): 8–15. [2] ZHI X D, WU Q J, WANG C. Experimental and numerical study of GFRP-reinforced steel tube under axial impact loads [J]. International Journal of Impact Engineering, 2018, 122: 23–37. doi: 10.1016/j.ijimpeng.2018.07.018 [3] BATUWITAGE C, FAWZIA S, THAMBIRATNAM D, et al. Impact behaviour of carbon fibre reinforced polymer (CFRP) strengthened square hollow steel tubes: a numerical simulation [J]. Thin-Walled Structures, 2018, 131: 245–257. doi: 10.1016/j.tws.2018.06.033 [4] ALAM M I, FAWZIA S. Numerical studies on CFRP strengthened steel columns under transverse impact [J]. Composite Structures, 2015, 120: 428–441. doi: 10.1016/j.compstruct.2014.10.022 [5] 李洋, 王俊, 刘伟庆. 纤维复合材料-钢组合柱侧向冲击试验和有限元仿真分析 [J]. 钢结构, 2017, 32(2): 21–26. LI Y, WANG J, LIU W Q. Experimental study and FE simulation of the anti-impact performance of GFRP-steel column subjected to transverse impact [J]. Steel Construction, 2017, 32(2): 21–26. [6] KADHIM M M A, WU Z J, LEE S C. Loading rate effects on CFRP strengthened steel square hollow sections under lateral impact [J]. Engineering Structures, 2018, 171: 874–882. doi: 10.1016/j.engstruct.2018.04.066 [7] KADHIM M M A, WU Z J, LEE S C. Experimental study of CFRP strengthened steel columns subject to lateral impact loads [J]. Composite Structures, 2018, 185: 94–104. doi: 10.1016/j.compstruct.2017.10.089 [8] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large Strains, high strain rates and high temperatures [C]//Proceedings of the Seventh International Symposium on Ballistics. The Hague, Netherlands, 1983: 1–7. [9] ZERILLI F J, ARMSTRONG R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816–1825. doi: 10.1063/1.338024 [10] LIN L, FAN F, ZHI X D. Dynamic constitutive relation and fracture model of Q235A steel [J]. Applied Mechanics and Materials, 2013, 274: 463–466. doi: 10.4028/www.scientific.net/AMM.274 [11] ZHANG D N, SHANGGUAN Q Q, XIE C J, et al. A modified Johnson-Cook model of dynamic tensile behaviors for 7075-T6 aluminum alloy [J]. Journal of Alloys and Compounds, 2015, 619: 186–194. doi: 10.1016/j.jallcom.2014.09.002 [12] TAN J Q, ZHAN M, LIU S, et al. A modified Johnson-Cook model for tensile flow behaviors of 7050-T7451 aluminum alloy at high strain rates [J]. Materials Science and Engineering:A, 2015, 631: 214–219. doi: 10.1016/j.msea.2015.02.010 [13] HASHIN Z. Failure criterion for unidirectional fiber composite [J]. Journal of Applied Mechanics, 1980, 47: 329–334. doi: 10.1115/1.3153664 [14] PUCK A, SCHURMANN H. Failure analysis of FRP laminates by means of physically based phenomenological models [J]. Composites Science and Technology, 2001, 62: 1633–1662. [15] SINGH H, NAMALA K K, MAHAJAN P. A damage evolution study of E-glass/epoxy composite under low velocity impact [J]. Composites Part B: Engineering, 2015, 76: 235–248. doi: 10.1016/j.compositesb.2015.02.016 [16] LIAO B B, LIU P F. Finite element analysis of dynamic progressive failure of plastic composite laminates under low velocity impact [J]. Composite Structures, 2017, 159: 567–578. doi: 10.1016/j.compstruct.2016.09.099 [17] Dassault Systèmes Simulia Corp. ABAQUS 6.11 user’s manual [Z]. Providence, RI: Dassault Systèmes Simulia Corp, 2011. [18] SHOKRIEH M M, KARAMNEJAD A. Investigation of strain rate effects on the dynamic response of a glass/epoxy composite plate under blast loading by using the finite difference method [J]. Mechanics of Composite Materials, 2014, 50(3): 295–310. doi: 10.1007/s11029-014-9415-1 -
图( 14) 表( 8)
计量
- 文章访问数: 3154
- HTML全文浏览数: 3154
- PDF下载数: 17
- 施引文献: 0