高级搜索

多孔材料温压状态方程计算简要评述

, 

downloadPDF

上一篇

下一篇

陈俊祥, 耿华运. 多孔材料温压状态方程计算简要评述[J]. 高压物理学报, 2019, 33(3): 030111-1. doi: 10.11858/gywlxb.20190767
引用本文: 陈俊祥, 耿华运. 多孔材料温压状态方程计算简要评述[J]. 高压物理学报, 2019, 33(3): 030111-1. doi: 10.11858/gywlxb.20190767
shu
Junxiang CHEN, Huayun GENG. Review on Evaluation of Temperature-Pressure Equation of State of Porous Materials[J]. gaoyawli, 2019, 33(3): 030111-1. doi: 10.11858/gywlxb.20190767
Citation: Junxiang CHEN, Huayun GENG. Review on Evaluation of Temperature-Pressure Equation of State of Porous Materials[J]. gaoyawli, 2019, 33(3): 030111-1. doi: 10.11858/gywlxb.20190767
shu

多孔材料温压状态方程计算简要评述

  • 中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳　621999

    • 作者简介: 陈俊祥（1933－），男，研究员，主要从事实验物态方程研究. E-mail: cjx621@163.com .

  • 中图分类号: O521.2

Review on Evaluation of Temperature-Pressure Equation of State of Porous Materials

  • National Key Laboratory of Shock Wave and Detonation Physics, Institute of Fluid Physics, CAEP, Mianyang 621999, China

  • MSC: O521.2

  • 摘要: 多孔材料是一种重要的结构和功能材料，在过滤、催化、屏蔽和冲击防护等重要工程领域具有广泛的应用。多孔材料的物理力学行为极其复杂，虽然经过多年研究，但是仍未完全理解其在极端条件下的响应行为。以冲击加载下多孔材料的压力和温度变化特点为例，对目前常用的几种具有代表性的以密实材料Hugoniot为参照线的多孔材料物态方程模型进行深入分析，并对多种模型的优劣进行比较，在此基础上提出了一种分段处理多孔材料冲击波数据的方法。以多孔Cu为例，展示了该方法的有效性。这种方法将为发展更为精细严格的多孔材料状态方程理论提供有益的参考。
    Abstract: As an important structural and functional material, porous material has been widely used in the engineering fields such as filtration, catalysis, shielding and impact protection. Because of its complex physical-mechanical behavior, even with years of research, its response under extreme conditions still has not been fully understood. Taking the characteristics of pressure and temperature change of porous materials under shock loading as an example, this paper makes an in-depth analysis of several typical models of equation of state for porous materials by choosing Hugoniot of the dense material as the reference line and compares them. On the basis of this analysis, an approach of piecewise processing the shock data of porous materials is proposed and its effectiveness is demonstrated for porous copper. This approach may be helpful in developing an accurate and rigorous theory of the equation of state of porous materials.
  • 加载中

  • 图 1  多孔Cu的Trunin方程计算与实验数据的比较[13]

    Figure 1.  Hugoniot of porous Cu calculated by Trunin’s equation compared to experimental data[13]

    下载: 全尺寸图片 幻灯片

    图 2  W-J方程计算多孔Cu与实验数据比较

    Figure 2.  Compression curve of porous Cu calculated by W-J equation of state compared to experimental data

    下载: 全尺寸图片 幻灯片

    图 3  通过推广的W-J方程计算多孔Cu压强与实验结果比较

    Figure 3.  Compression curve of porous Cu calculated by improved W-J equation of state compared to experimental data

    下载: 全尺寸图片 幻灯片

    图 4  通过推广的W-J方程计算多孔Cu温度与其他计算结果比较

    Figure 4.  Shock temperature of porous Cu calculated by improved W-J equation of state compared to other calculated data

    下载: 全尺寸图片 幻灯片

    图 5  计算压强曲线[18]与Viljoen等结果[13]的比较

    Figure 5.  Compression curve calculated[19]compared to the results of Vilioen et al.[13]

    下载: 全尺寸图片 幻灯片

    图 6  冲击温度和压强的计算结果[18]

    Figure 6.  The calculated shock temperature and pressure[18]

    下载: 全尺寸图片 幻灯片

    图 7  低孔隙度Cu的冲击压强线

    Figure 7.  Compression curve of Cu with ultra-low porosity

    下载: 全尺寸图片 幻灯片

    图 8  低孔隙度Cu的冲击温度线

    Figure 8.  Calculated shock temperature curve of Cu with ultra-low porosity

    下载: 全尺寸图片 幻灯片

    图 9  低孔隙度多孔Cu的D-u曲线

    Figure 9.  The D-u curves of Cu with different ultra-low porosities

    下载: 全尺寸图片 幻灯片

    图 10  低孔隙度多孔Cu的p-$\rho $曲线

    Figure 10.  The p-$\rho $ curves of Cu with different ultra-low porosities

    下载: 全尺寸图片 幻灯片

    图 11  大孔隙度Cu冲击压缩T-p线

    Figure 11.  The calculated shock T-p curves of Cu with a high porosity

    下载: 全尺寸图片 幻灯片

    表 1  不同孔隙度Cu的D-u数据拟合参数

    Table 1.  The parameters for the D-u data of Cu with high porosity

    ${\rho _{00}}$/(g·cm–3)mc0/(km·s–1)$\lambda $$\lambda $'
    7.9001.131.920 462.414 25–0.146 04
    7.3151.221.168 502.684 83–0.199 24
    6.3261.410.421 782.694 98–0.183 45
    5.7421.560.247 992.476 93–0.117 16
    4.5081.980.090 922.105 15–0.080 52
    下载: 导出CSV

    表 2  低孔隙度Cu冲击固相温度与液相温度函数参数

    Table 2.  The parameters for the shock temperature in the solid and liquid phases of Cu with low porosity

    ${{\rho _{00}}}$/(g·cm–3)${T_{\rm H}=a+b p_{\rm H}+c p_{\rm H}^2+d p_{\rm H}^3}$${T_{\rm L}=a+b p_{\rm L}+c p_{\rm L}^2+d p_{\rm L}^3}$
    abcdabcd
    7.900722.153 20–17.753 260.735 67–0.002 685911.275 89–84.108 460.597 35–8.591 44×10–4
    7.315868.336 33–26.095 541.312 99–0.006 913603.769 33–55.517 720.537 68–9.226 82×10–4
    6.3261195.581 88–61.546 114.200 98–0.044 56–1936.853 5854.373 03–0.072 412.025 16×10–4
    5.7421342.781 34–71.452 266.891 94–0.107 30–519.446 3145.078 97–0.040 801.391 05×10–4
    4.508–150.530 7252.113 33–0.158 495.409 68×10–4
    下载: 导出CSV

    表 3  高孔隙度Cu的D-u数据处理参数

    Table 3.  The fitted parameters to the D-u experimental data of porous Cu with different porosities

    ${\rho _{00}}$/(g·cm–3)mc0/(km·s–1)$\lambda $$\lambda'$
    3.57202.50.041.6450.01
    2.976730.0411.456 80.026 5
    2.073 321.182 4210–9
    2.55143.50.0681.344 80.035 1
    2.232540.1121.30.023
    2.966 170.866 160.015 61
    1.63885.450.2251.141 310.038 64
    1.24037.20.346 830.993 520.052 32
    下载: 导出CSV
  • [1] 刘培生. 多孔材料引论[M]. 北京: 清华大学出版社, 2004.
    [2] GIBSON L J, ASHBY M F. Cellular solids: structure and properties [M]. Cambridge: Cambridge University Press, 1999.
    [3] 赵信峰, 方炎. 金属铜纳米孔洞阵列膜制备方法研究 [J]. 物理学报, 2016, 55(7): 3785–3789. ZHAO X F, FANG Y. Metal nano-hole array copied from AAO template [J]. Acta PhysicaSinica, 2016, 55(7): 3785–3789.
    [4] 张华伟, 李言祥. 金属熔体中气泡形核的理论分析 [J]. 物理学报, 2007, 56(8): 4864–4871. doi: 10.3321/j.issn:1000-3290.2007.08.082 ZHANG H W, LI Y X. Study on bubble nucleation in liquid metal [J]. Acta PhysicaSinica, 2007, 56(8): 4864–4871. doi: 10.3321/j.issn:1000-3290.2007.08.082
    [5] ROSA M E. An introduction to solid foams [J]. Philosophical Magazine Letters, 2008, 88(9-10): 637–645. doi: 10.1080/09500830802302014
    [6] 谭华. 实验冲击波物理导引[M]. 北京: 国防工业出版社, 2007: 56.
    [7] 经福谦. 实验物态方程导引[M]. 北京: 科学出版社, 1986: 134.
    [8] 李西军, 龚自正, 刘福生. 铁高压熔化线的测量——熔化机理的影响 [J]. 高压物理学报, 2001, 15(3): 221–225. doi: 10.3969/j.issn.1000-5773.2001.03.009 LI X J, GONG Z Z, LIU F S. A problem in measurements of high pressure melting curve of iron: influenceof melting mechanism on the melting temperature [J]. Chinese Journal of High Pressure Physics, 2001, 15(3): 221–225. doi: 10.3969/j.issn.1000-5773.2001.03.009
    [9] LI X J, GONG Z Z, JING F Q, et al. Sound velocities in porous iron shocked to 177 GPa and the implications for shock melting [J]. Chinese Physics Letters, 2001, 18(12): 1632. doi: 10.1088/0256-307X/18/12/327
    [10] WU Q, JING F Q. Thermodynamic equation of state and application to Hugoniot predictions for porous materials [J]. Journal of Applied Physics, 1996, 80(8): 4343. doi: 10.1063/1.363391
    [11] BOSHOFF M L, VILJOEN H J. Comparative study of analytical methods for Hugoniot curves of porous materials [J]. Journal of Applied Physics, 1999, 86(3): 1245. doi: 10.1063/1.370878
    [12] GENG H Y, WU Q, TAN H, et al. Extension of the Wu–Jing equation of state for highly porous materials: Calculations to validate and compare the thermoelectron model [J]. Journal of Applied Physics, 2002, 92(10): 5917–5923. doi: 10.1063/1.1516618
    [13] TRUNIN R F, SIRNAKOV G V, SUTULOV Y N, et al. Compressibility of porous metals in shock waves [J]. Soviet Physics–JETP, 1989, 69(3): 580–588.
    [14] TRUNIN R F, MEDVEDEV A B, FUNTIKOV A I, et al. Shock compression of porous iron, copper, and tungsten, and their equation of state in the terapascal pressure range [J]. Soviet Physics–JETP, 1989, 68(2): 356–361.
    [15] 耿华运, 吴强, 谭华. 热力学物态方程参数的统计力学表示 [J]. 物理学报, 2001, 50(7): 1334. doi: 10.3321/j.issn:1000-3290.2001.07.027
    [16] 耿华运, 谭华, 吴强. 比容可分性及其在自由电子气体模型中的应用 [J]. 高压物理学报, 2001, 15(3): 199–204. doi: 10.3969/j.issn.1000-5773.2001.03.006 GENG H Y, TAN H, WU Q. Aeparability of specific wolume and its application to free-GAS model of thermoelectrons [J]. Chinese Journal of High Pressure Physics, 2001, 15(3): 199–204. doi: 10.3969/j.issn.1000-5773.2001.03.006
    [17] GENG H Y, WU Q, TAN H, et al. Bulk sound velocity of porous materials at high pressures [J]. Chinese Physics, 2002, 11(11): 1188. doi: 10.1088/1009-1963/11/11/317
    [18] 陈俊祥, 于继东, 耿华运, 等. 多孔材料的温度和压强计算 [J]. 物理学报, 2017, 66(5): 056401. doi: 10.7498/aps.66.056401 CHEN J X, YU J D, GENG H Y, et al. Temperature and pressure calculation of porous materials [J]. Acta Physica Sinica, 2017, 66(5): 056401. doi: 10.7498/aps.66.056401
    [19] CAO X X, CHEN J X, YU Y, et al. An equation of state for abnormal expansion of shocked porous materials [J]. Journal of Applied Physics, 2018, 124(21): 215903. doi: 10.1063/1.5047233
    [20] 陈俊祥. 《实验物态方程导引》附录(内部资料)[Z]. 2019.
    [21] 于渌, 郝柏琳, 陈晓松. 相变和临界现象[M]. 北京: 科学出版社, 2005: 27.
    [22] 汤文辉, 张若棋. 物态方程理论及计算概论 [M]. 北京: 高等教育出版社, 1999.
  • 加载中
图( 11) 表( 3)
计量
  • 文章访问数:  3559
  • HTML全文浏览数:  3559
  • PDF下载数:  33
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-04-28
  • 刊出日期:  2019-06-01

多孔材料温压状态方程计算简要评述

    作者简介: 陈俊祥（1933－），男，研究员，主要从事实验物态方程研究. E-mail: cjx621@163.com
  • 中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳　621999
  • 收稿日期:  2019-04-28

摘要: 多孔材料是一种重要的结构和功能材料，在过滤、催化、屏蔽和冲击防护等重要工程领域具有广泛的应用。多孔材料的物理力学行为极其复杂，虽然经过多年研究，但是仍未完全理解其在极端条件下的响应行为。以冲击加载下多孔材料的压力和温度变化特点为例，对目前常用的几种具有代表性的以密实材料Hugoniot为参照线的多孔材料物态方程模型进行深入分析，并对多种模型的优劣进行比较，在此基础上提出了一种分段处理多孔材料冲击波数据的方法。以多孔Cu为例，展示了该方法的有效性。这种方法将为发展更为精细严格的多孔材料状态方程理论提供有益的参考。

English Abstract

    全文HTML

  • 多孔材料因其特殊的几何结构和能量吸收特性，在冲击防护等许多工程领域有着广泛的应用[1–5]。多孔材料在冲击压缩下会发生空隙塌缩，伴随体积的巨大变化和外部做功，最终的冲击温度特别高，所以多孔材料是研究高温高压物质热力学状态的重要手段之一[6–10]。但是大多数多孔材料是由粉末烧结而成的具有不同孔隙度的工程材料，密度分布很不均匀，精细的实验测量比较困难，所获数据往往具有分散性大、误差大的问题，给后续理论分析带来巨大挑战，其热力学状态量的计算也比较困难。

    20世纪末，Boshoff等[11]对多孔材料的实验和理论研究进行了评述，其中以密实材料的物态方程（主要是冲击绝热线，即Hugoniot线）为基准，利用Grüneisen系数外推得到多孔材料的压强数据。该方法对孔隙度较低的材料比较有效，但当孔隙度增大后，模拟结果与实验结果相差甚远。他们对5种常用的疏松材料状态方程模型进行了比较，认为吴-经（W-J）方程最好。21世纪初，耿华运等[12]进一步改进了W-J方程，提出了热电子贡献项的物理模型及计算方法，使W-J方法计算的压强更加接近实验结果，获得了与实验基本一致的冲击温度和声速。近年来，中国工程物理研究院流体物理研究所冲击波物理与爆轰物理实验室陆续发展了从多孔材料本身的参数入手研究多孔材料物态方程的简易方法，找到了由冲击波速度-粒子速度（D-u）实验数据获得完全物态方程的途径。这一方法对密实材料和多孔材料均适用，对Hugoniot状态和Off Hugoniot状态也都可用。在此基础上，我们用这种方法研究了5组低孔隙度材料和6组高孔隙度材料的冲击压强和温度，得到了与实验一致的结果。本文首先对多孔材料温压热力学状态性质的计算方法进行简单评述，然后对新方法做重点介绍，最后总结并展望后续可能的发展。

1.   多孔材料温压性质计算评述

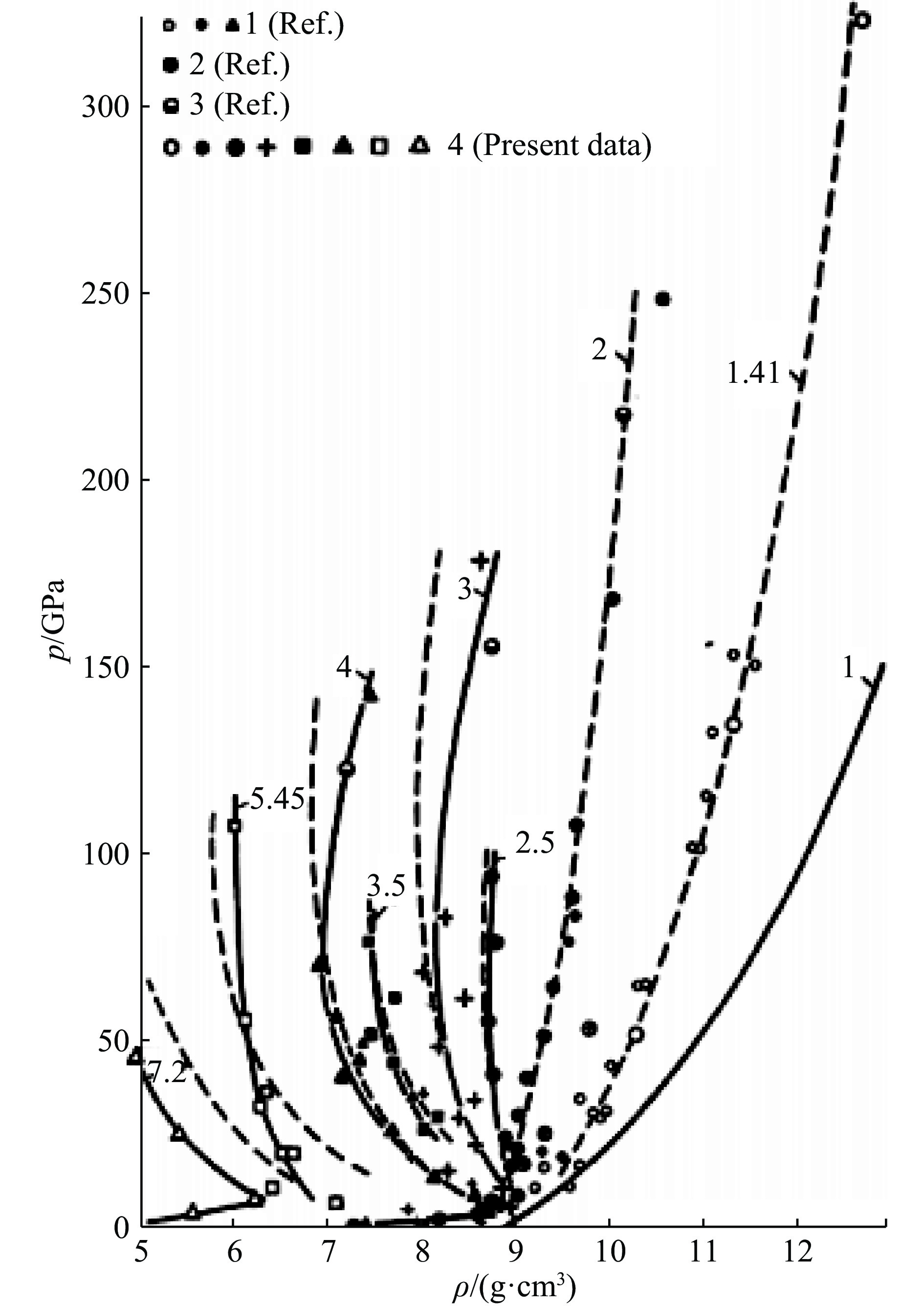
  • 鉴于实验技术所面临的困难，在目前已发表的文献中大部分多孔材料高温高压实验数据均来源于俄罗斯早期的冲击实验。20世纪60年代至80年代，Trunin等[13–14]陆续发表了多种材料大孔隙度的实验数据。这些数据具有两个特点。第一个特点是根据孔隙度（m=${\rho _0}$/${\rho _{00}}$，其中${\rho _0}$为密实材料的初始密度，${\rho _{00}}$为多孔材料的初始密度）的大小可将数据分为两类：m<2时为小孔隙度数据，满足v<v0（v为比容，v0为初始比容）；m>2时为大孔隙度数据，满足v>v0。第二个特点是，大孔隙度数据显示材料状态由压缩转为反向膨胀，膨胀到一定程度后又转为压缩。图1为文献[13]给出的实验数据与计算曲线，其中实线为实验数据，虚线表示计算数据，可见m=4时的数据明显可分为3个阶段。

    Trunin等[13–14]提出了膨胀曲线方程

    式中：c0为零压下的声速，${\gamma _0}$为Grüneisen系数，$\xi$为等效的Grüneisen系数，p为压力，下标 $\Gamma $ 表示密实参考线上的量。压缩曲线方程为

    图1中由(3)式计算得到的大孔隙度的结果（虚线）均与实验结果（实线）相差较远。

    Trunin等在推导时利用了公式

    式中：E代表比内能。这是基于Grüneisen状态方程模型和热力学Grüneisen系数 $\gamma $ 的定义，即

    对于疏松材料的冲击压缩，沿Hugoniot线有

    Trunin等还特别假设了多孔材料膨胀到理想气体状态时$\gamma $=2/3，进一步增加压力使得材料由膨胀转变为压缩状态。实际上这个假设有待商榷，因为当材料体积膨胀到一定程度后，抵抗外部压缩的热压迅速减弱，再升高外部加载压力后材料已没有膨胀余地，只能转变为压缩状态，其膨胀-压缩转变点依赖于孔隙度。小孔隙度材料的冲击压缩不出现膨胀是因为原来留下的空隙很小，体积塌缩产生的热量少，不足以驱动材料发生反向膨胀。

    1999年，Boshoff等[11]对多孔材料的冲击压缩计算进行了评述，列举了5种计算方法，可分为两类。一类是基于Grüneisen方程，即

    式中：$\gamma_v(v)$为Grüneisen系数，$\Delta $表示多孔材料与密实材料物理量之差，E(v)为比内能。另一类是基于W-J状态方程，即

    式中：R(p)为W-J系数，H(p)为比热焓。这两类方程都是以密实材料的冲击压缩曲线作为参考，通过密实材料的Grüneisen系数 $\gamma_v(v)$ 进行计算。需要指出，其中W-J系数R(p)是用$\gamma_v(v)$换算得到的，即

    因而两类方程是基于同一热力学原理、同一热力学参数，只是方程形式、所用参数的表现形式和简化程度不同而已。但是，通常所用的Grüneisen系数并不考虑温度的影响，事实上它应该是温度的函数，而多孔材料冲击响应的特点恰恰是冲击温度变化特别大，因此在实际应用中这两类方程对大孔隙度材料的计算结果相差甚远。文献[13]对5种方法进行综合比较后，认为W-J方程最好。

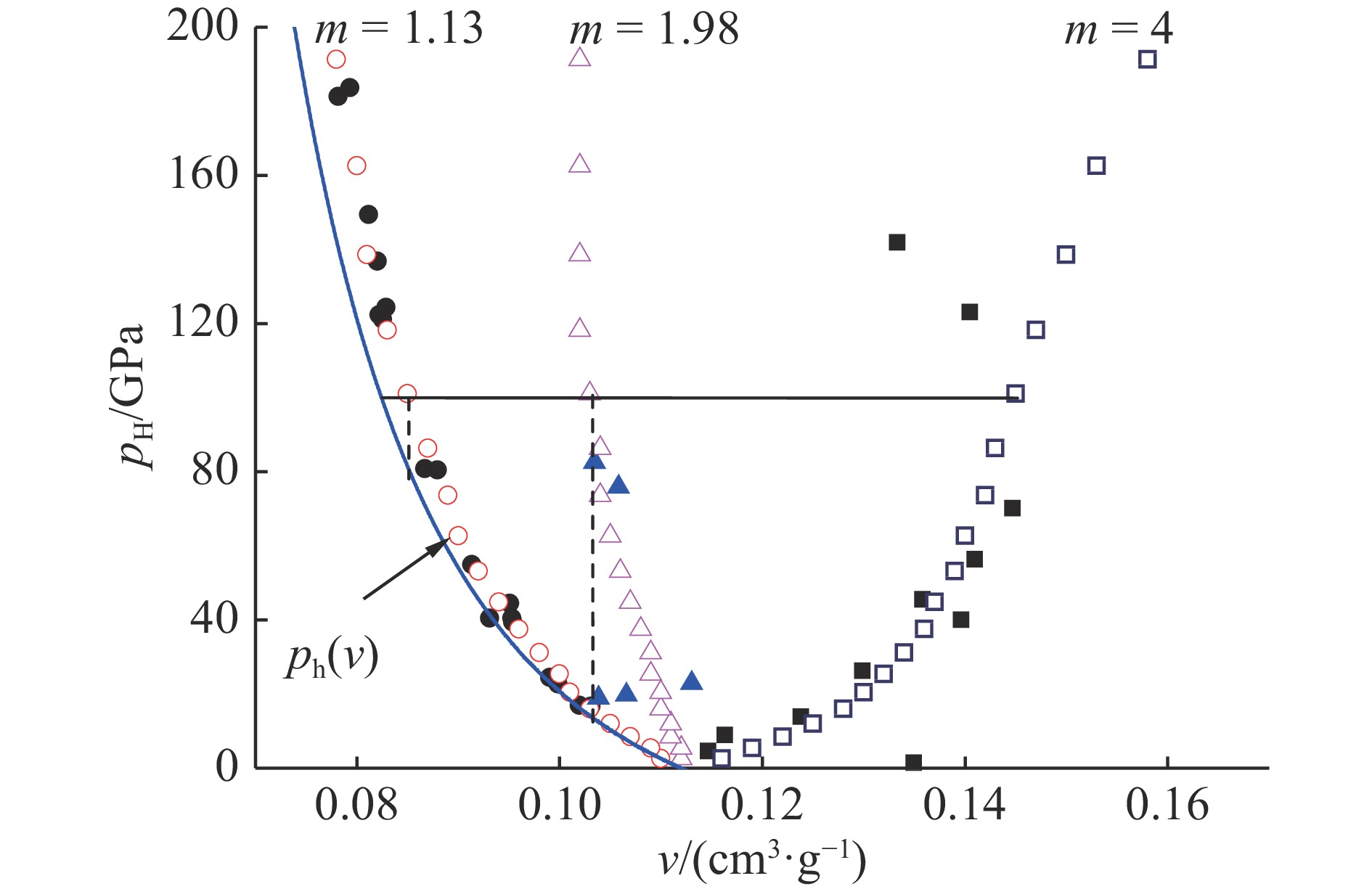
    一个有趣的问题是：W-J方程也利用了Grüneisen系数，为什么结果要好一些？主要原因在于这两种方法的计算路径是不同的。如图2所示，其中实心点是实验数据，空心点是W-J方程计算得到的结果，实线是计算参考线。由路径比较可得以下信息。

    （1）W-J方程沿等压路径从密实参考线导出多孔材料的Hugoniot线，即从ph(v)实线向右，可计算到v>v0区域。图2给出了采用W-J方程计算m=4时的数据，在膨胀区仍然与实验数据符合得很好。而Grüneisen方程沿等容路径导出多孔材料的Hugoniot曲线，即从ph(v)实线向上计算，只能计算v<v0区域的数据。特别地，由于在v>v0区域没有密实材料的参考线，也没有相应的$\gamma $v(v)参数，所以Grüneisen方程无法计算此区域的大孔隙度数据。

    （2）对于斜率陡峭的Hugoniot线，多孔材料的pH(v)线与密实材料的ph(v)线之间沿等压路径时距离较短，而沿等容路径时距离较长。如果用同样的物性参数进行近似计算，则沿路径较长时误差较大。且随着m增大，温度变化剧烈，导致这种影响越来越严重。图2中，m=1.98时的计算结果非常明显地体现了这一点。

    纵观自20世纪80年代以来对多孔材料冲击压缩状态的计算，几乎都是以密实材料的物态方程和物性参数为参照进行外推。这种方法只在近区（即较短的计算路径）有效，而在远区或跨越不同相区时计算精度急剧下降，需要利用积分方程求解，而非差分方程外推。

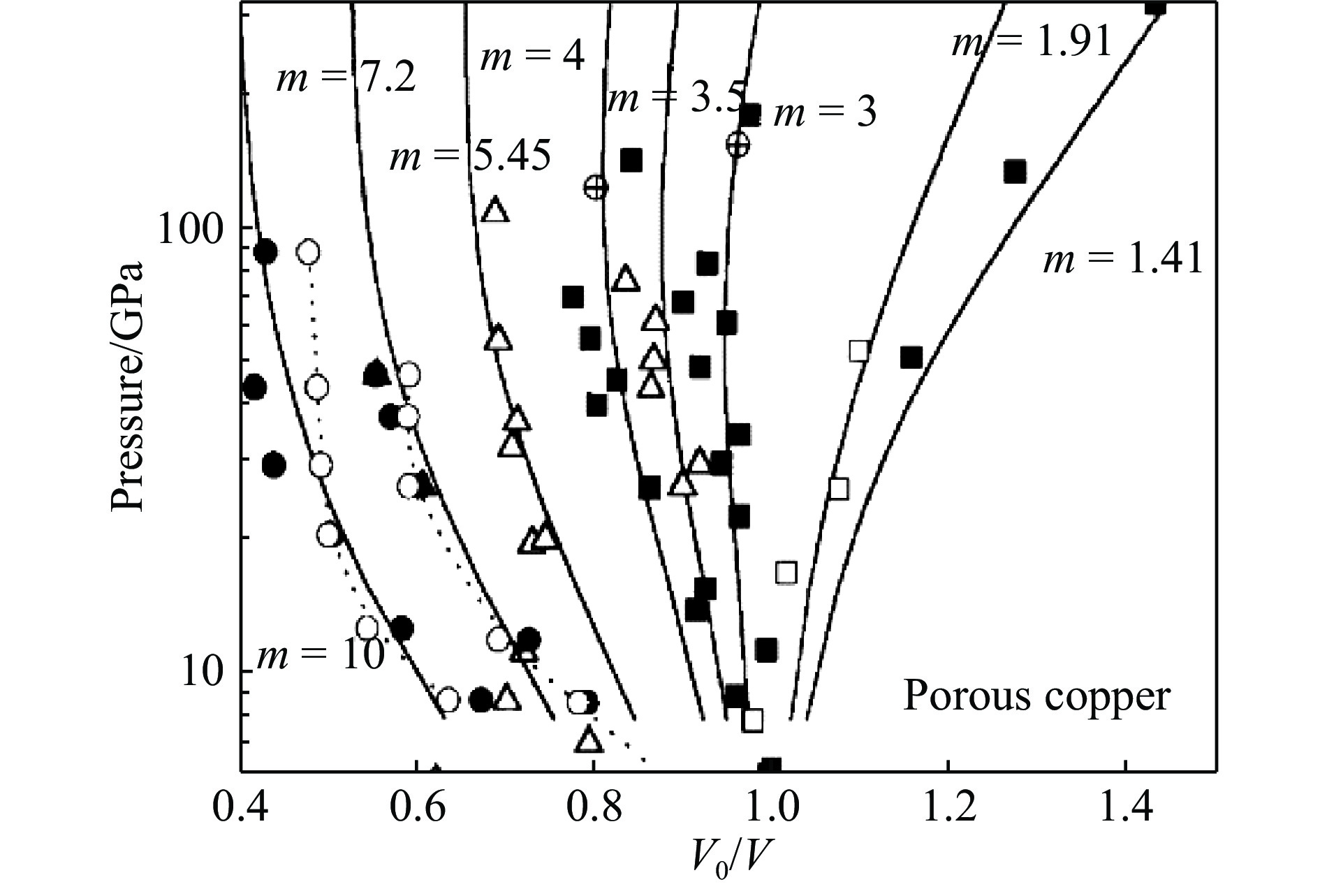
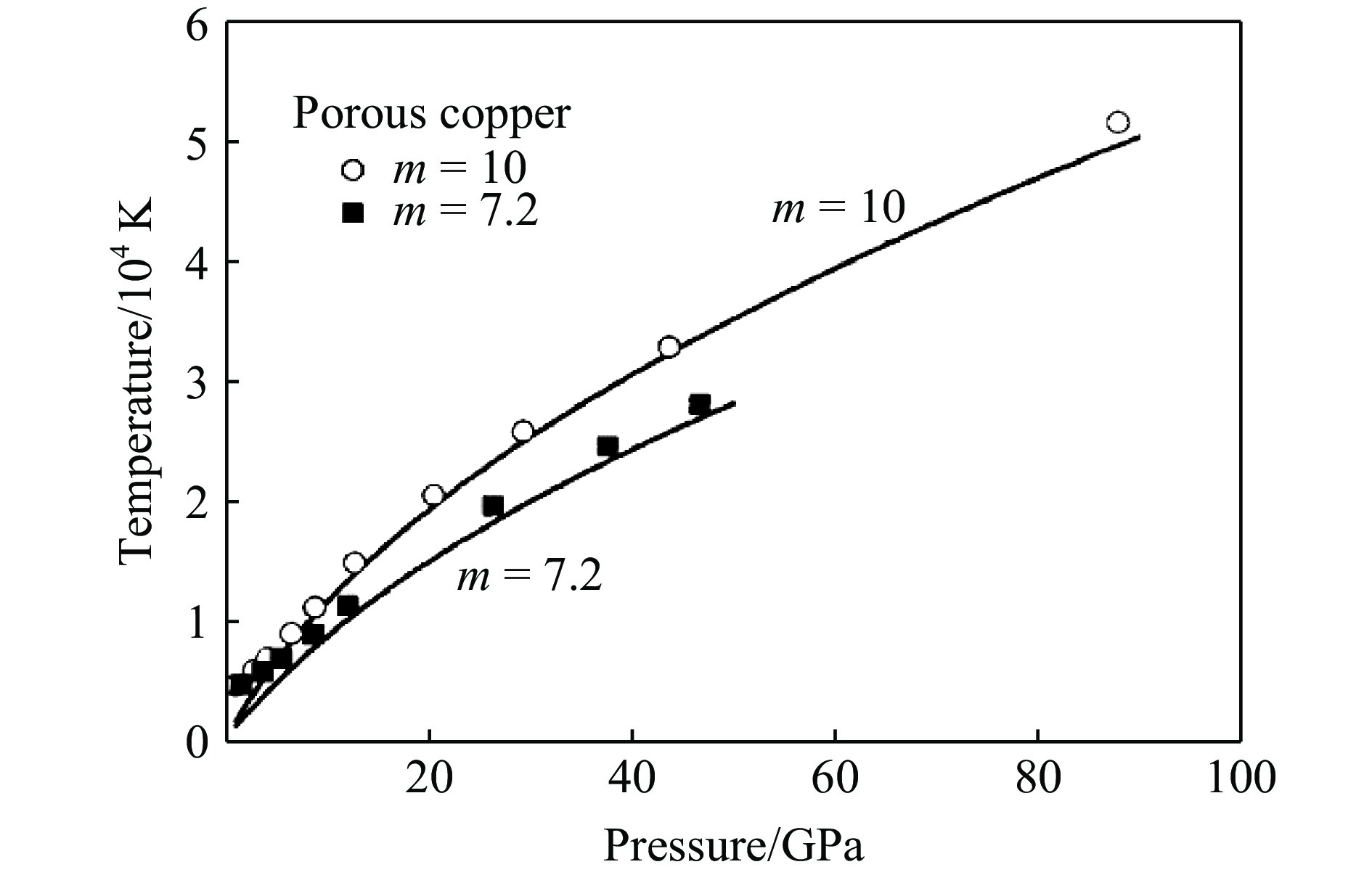
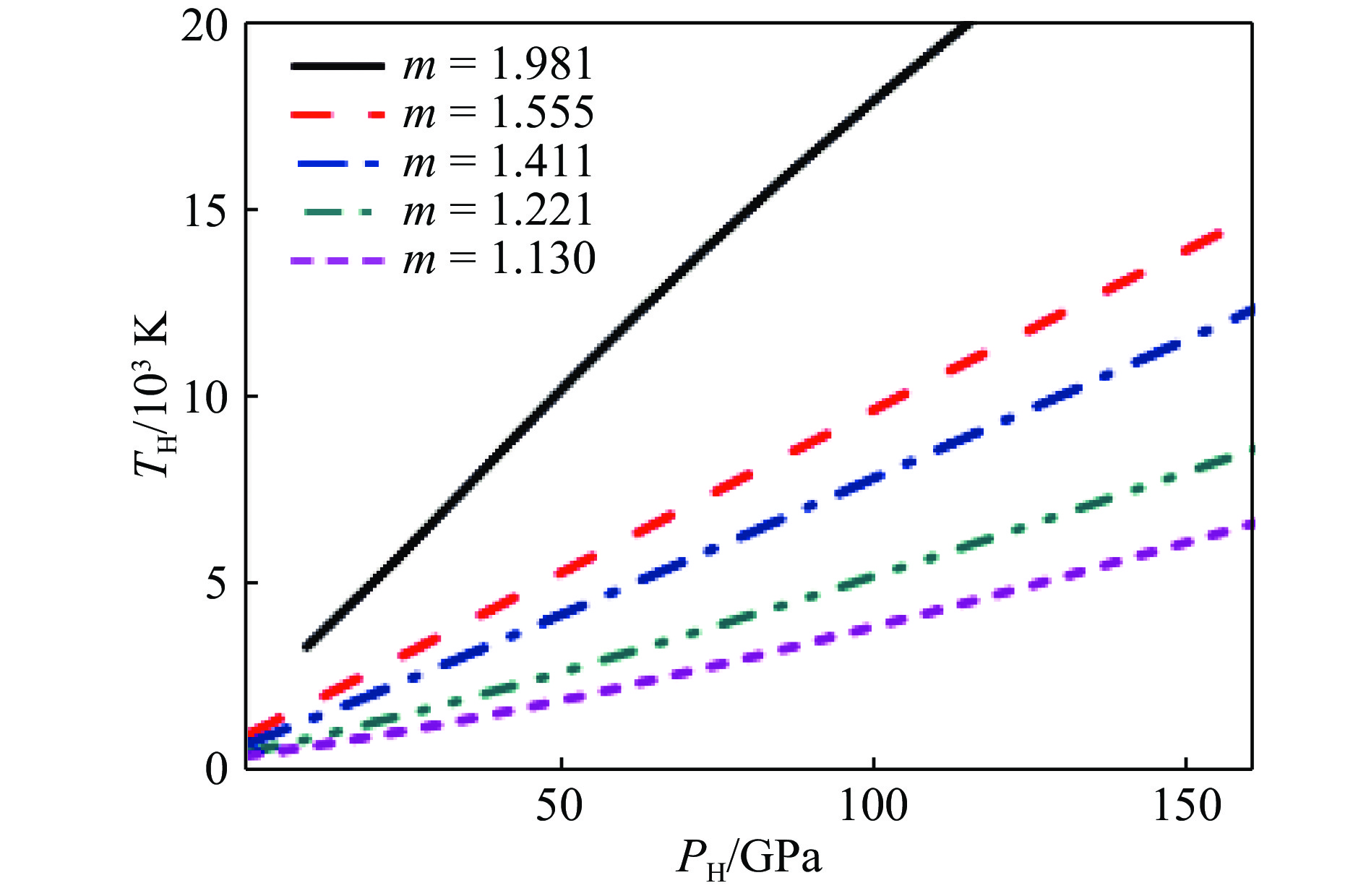
    2002年耿华运等[12]发表了“推广的W-J方程”，主要增加了温度的影响，并用体积拆分方法给出了热电子的贡献[15–16]，从而使W-J方程的计算结果更加接近实际，如图3所示。同时计算了冲击体声速[17]和冲击温度，获得了与其他研究相近的结果，如图4所示。

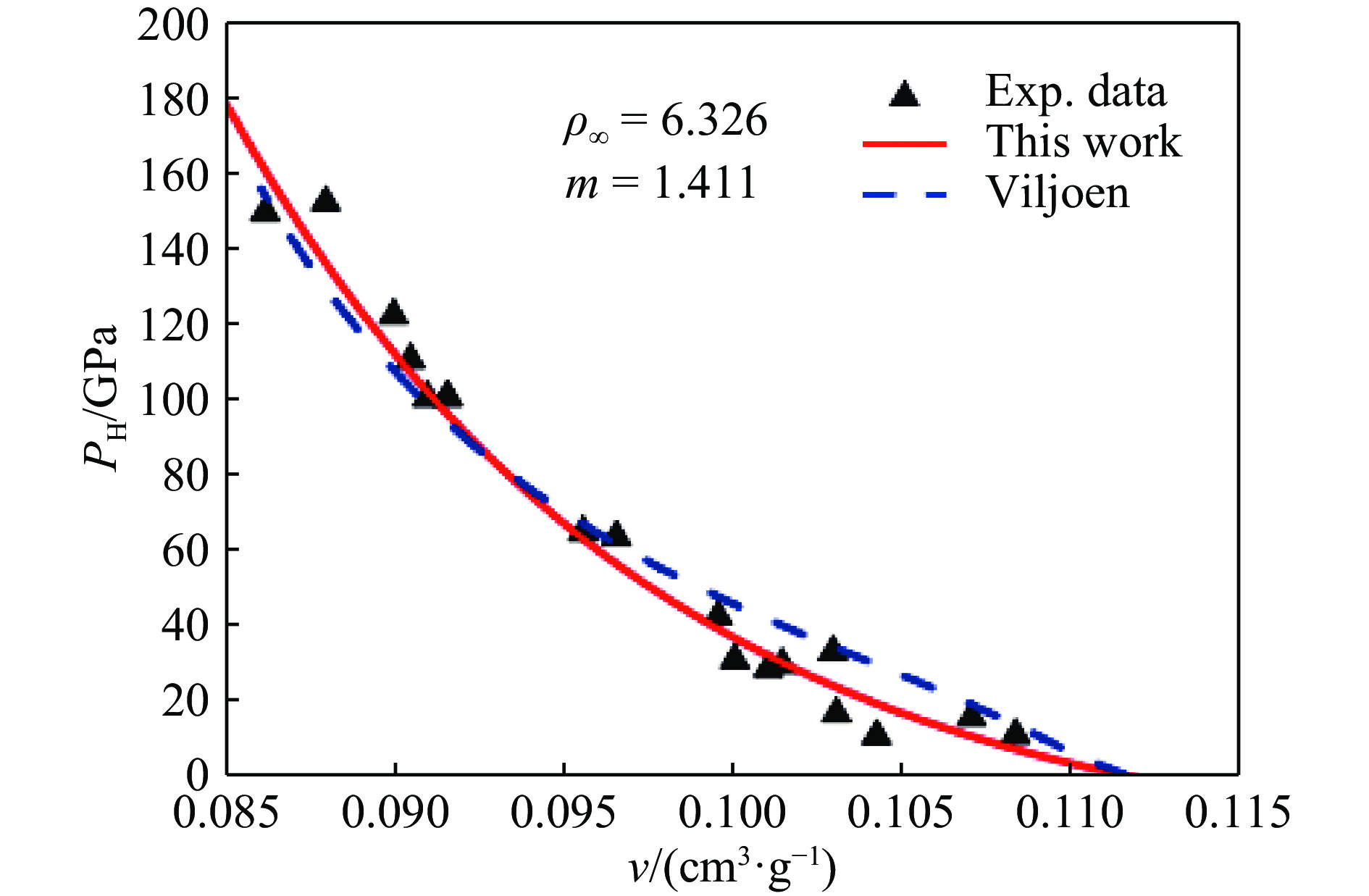
    2017年于继东等将德拜温度函数$\varTheta $(v)拓展到多孔材料的膨胀区，得到了多孔材料的等熵温度线，并利用多孔材料与密实材料在0 K下等熵功相等的原理得到了多孔材料的等熵压强线，从而建立了多孔材料自身的物态方程参考线，改进了计算方法，提高了计算的可信度[18]。这一方法是先计算温度，再由温度计算压强。由图5可见，获得的压强数据与实验符合很好，而Viljoen等[11]的方法却偏离实验值较远。通过与实验数据比较，验证了所计算压强的合理性，从而可推测图6中给出的温度线是可信的。但是这种方法只能用于m<2时的低孔隙度材料，对高孔隙度材料无效。

    2018年，操秀霞等[19]提出了一种处理冲击波速度D和粒子速度u数据的新方法，适用于各种孔隙度材料。随后向士凯等又提出了根据Hugoniot物态方程标定冷压函数pc(v)和比热函数Cv(v, T)的方法，从而找到了一种从D-u数据建立完全物态方程的途径[20]。充分挖掘D-u数据的潜力，不仅能直接得到压强方程，而且能计算温度和其他状态量。这种依据实验数据自身的计算方法，不仅适用于密实材料，也适用于多孔材料，而且适用于各种孔隙度。我们用这种方法处理了5组低孔隙度和6组高孔隙度的实验数据，获得了很好的结果，后续将作详细介绍。

2.   多孔材料D-u数据的一种处理方法

  • 多孔材料实验数据分为两类。一类是冲击终态在v<v0的固液相区，D-u二次式（即$D = {c_0} + \lambda u + \lambda '{u^2}$）中的系数$\lambda'$<0，压强函数为

    式中：c0为零压下的声速。另一类是冲击终态在v>v0区域的固气共存区，D-u二次式中的$\lambda'$>0，压强函数为

    通常多孔材料实验用样品的初始密度分布很不均匀，实验测量得到的p-v数据特别分散，误差很大，很难从p-v数据中找到其规律性。但D-u数据的误差只与冲击波速度和粒子速度的测试有关，与${\rho _{00}}$无关，只是由于孔隙闭合阶段的冲击波不稳定，粒子速度测量不准确，因而对拟合零压声速c0的影响较大。因此研究多孔材料的实验物态方程，关键在于仔细分析和甄别D-u实验数据，注意剔除那些不符合物理规律的数据，再严格按照D-u二次式关系拟合，从而确保得到合理的拟合参数。

    • 2.1.   低孔隙度材料的冲击压强和温度

  • 美国洛斯阿拉莫斯国家实验室（LASL）给出了5种低孔隙度Cu的D-u数据拟合参数，见表1。

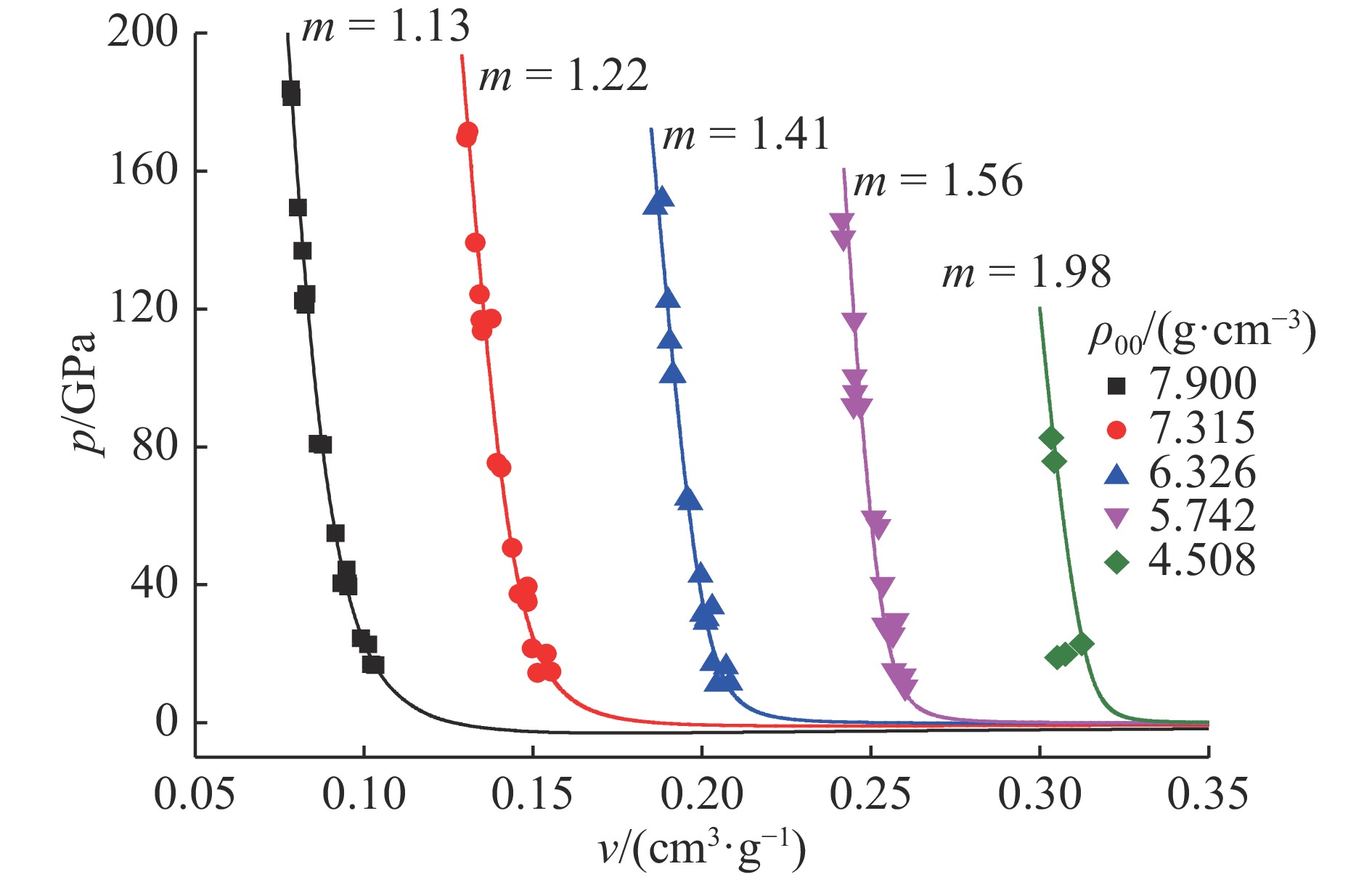
    为了便于统一分析和比较，需将多孔材料的比容v坐标换成密实材料的体应变x坐标。设多孔材料体应变$\eta = 1 - v/{v_{00}} = u/D$、压力$p = {\rho _{00}}Du$，密实材料体应变为x=1–v/v0，则$x=1- {\rho _0}( 1 - $ $u/D)/{\rho _{00}}$。因此低孔隙度材料的压强方程为

    式中：p0是x=0处的压强，即p(v0)。根据表1中的拟合参数，5组低孔隙度多孔Cu的压强线如图7所示, 图中每条曲线相对前一条v坐标平移了0.05 cm3/g，其中压强线从固相区直伸到液相区。

    固相区温度计算以密实Cu的冷压线作为参考，冲击压力为

    式中：TH为冲击温度。进入熔化区的温度按熔化线计算

    液相区温度按液态金属物态方程计算

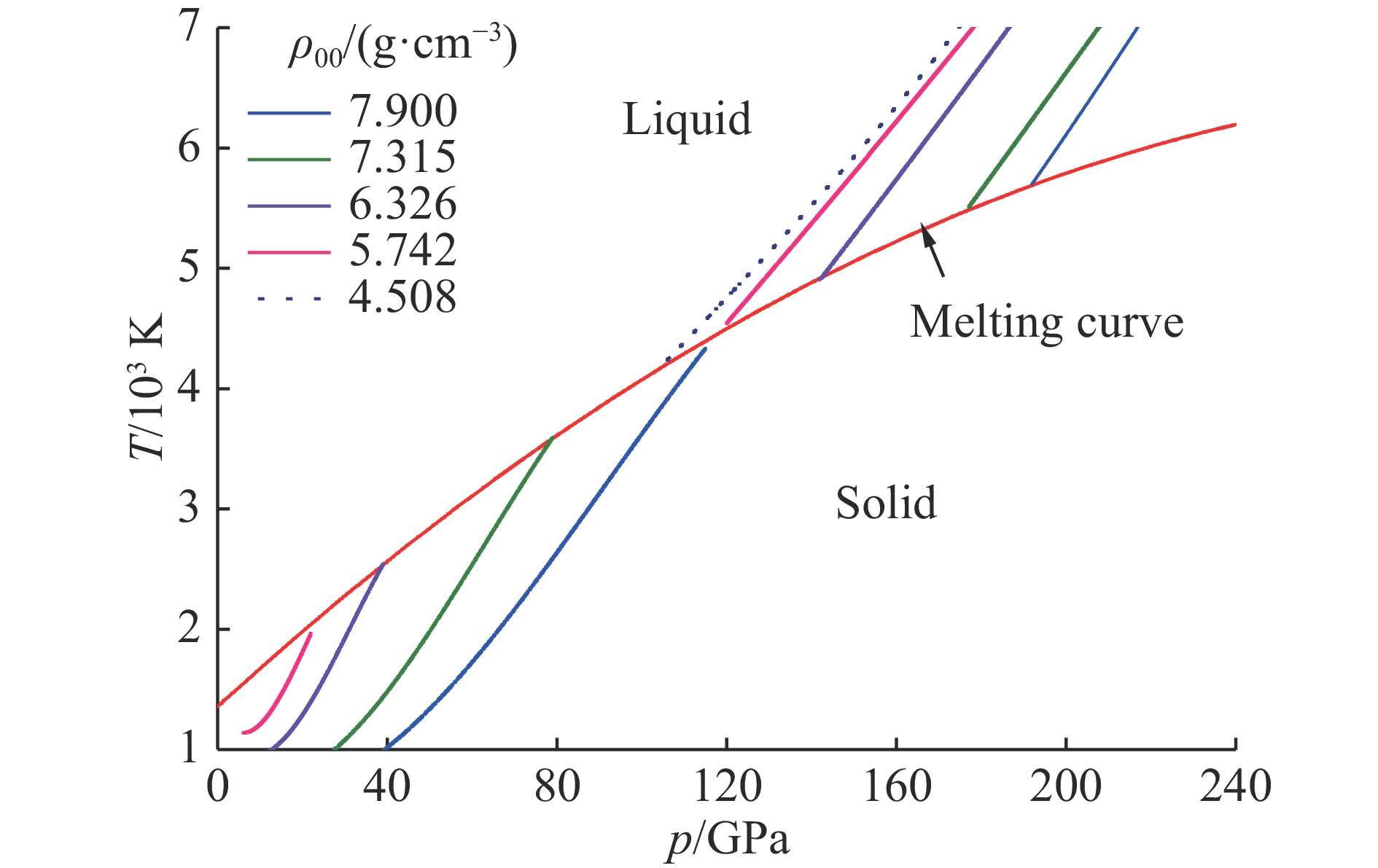
    计算温度所用到的参考函数pc(x)、Cv(x, T)、Tm(p)、Tm(x)、${\gamma _{\rm{m}}}$(x)、$\Delta s$(x)和$\tau $(x)全部取自文献[20]，计算结果见表2，温度与压强的关系曲线如图8所示。

    由图7可知，孔隙度m=1.98的多孔材料中，p-v线近似垂直上升，冲击状态已经进入液态，在图8中只有液相温度线。当m>2后，多孔材料的冲击加载使材料直接进入气态。

    • 2.2.   高孔隙度材料的冲击压强和温度

  • 高孔隙度材料的冲击温度特别高，冲击后经孔隙塌缩直接进入反向态膨胀区，在足够高的强冲击下可转变为等离子态。将这类材料的D-u数据按单相物质绝热静水压状态处理，假定$\lambda' $>0。其Hugoniot压强方程为

    式中：xm为最大体应变；p<p(xm)时冲击终态传播为压缩波，p>p(xm)时冲击终态传播为膨胀波。

    针对Trunin等[13]发表的6组高孔隙度多孔Cu的D-u数据，重新处理后的结果列于表3。

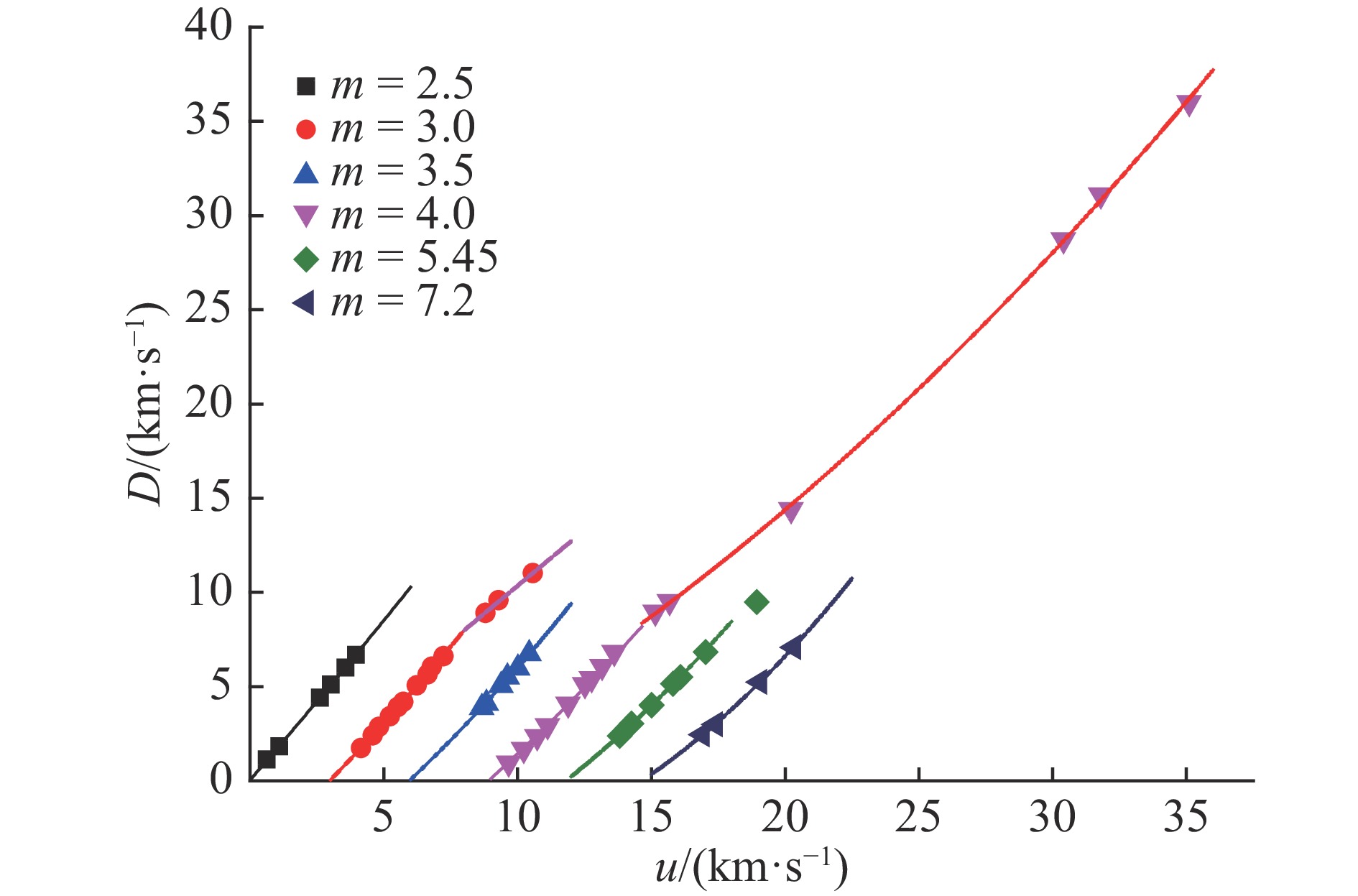
    由于各组数据较为分散，误差很大，初步拟合的压强趋势互不协调，以致出现压强线交叉的情况。因此，对多组数据的处理要考虑曲线趋势是否协调合理，需对拟合参数做适当调整。表3是调整后的拟合参数，得到的D-u线和p-$\rho $线分别见图9和图10。

    表3中两种孔隙度m=3和m=4有两列(c0, $\lambda $, $\lambda $')参数：第1列对应图10中连续光滑的气相压强线，在xm点由压缩转为膨胀，斜率发生反转；第2列参数对应图10中转折进入第二相区的pH线（即将数据进行分段处理）。其中m=5.45的最后一个数据不属于第一相区，在图9中可见最后一个数据不在D-u曲线上，如果将它与其他数据放在一组数据中进行拟合，则图10中的p-$\rho $曲线与前后的p-$\rho $曲线不协调，需要将其划入第二相区。

    大孔隙度材料的冲击压缩终态，已进入v>v0的固气共存区[21]。固气共存区的温度可用实际气体Y-A状态方程计算

    式中：ay是材料常数，材料为Cu时取ay=3500 GPa·(cm3/mol)2[22]，R为摩尔气体常数。

    由于冲击下多孔材料的高温气态同时又是Hugoniot状态，因此其内能满足Hugoniot关系式

    利用(17)式和(18)式相等这一条件，解出冲击温度及其变化率

    假设这一变化关系可以近似地拓展至低温低压条件，取边界条件v=v00、T=T0，积分后可得

    进行坐标变换v=v00(1–x)，则有

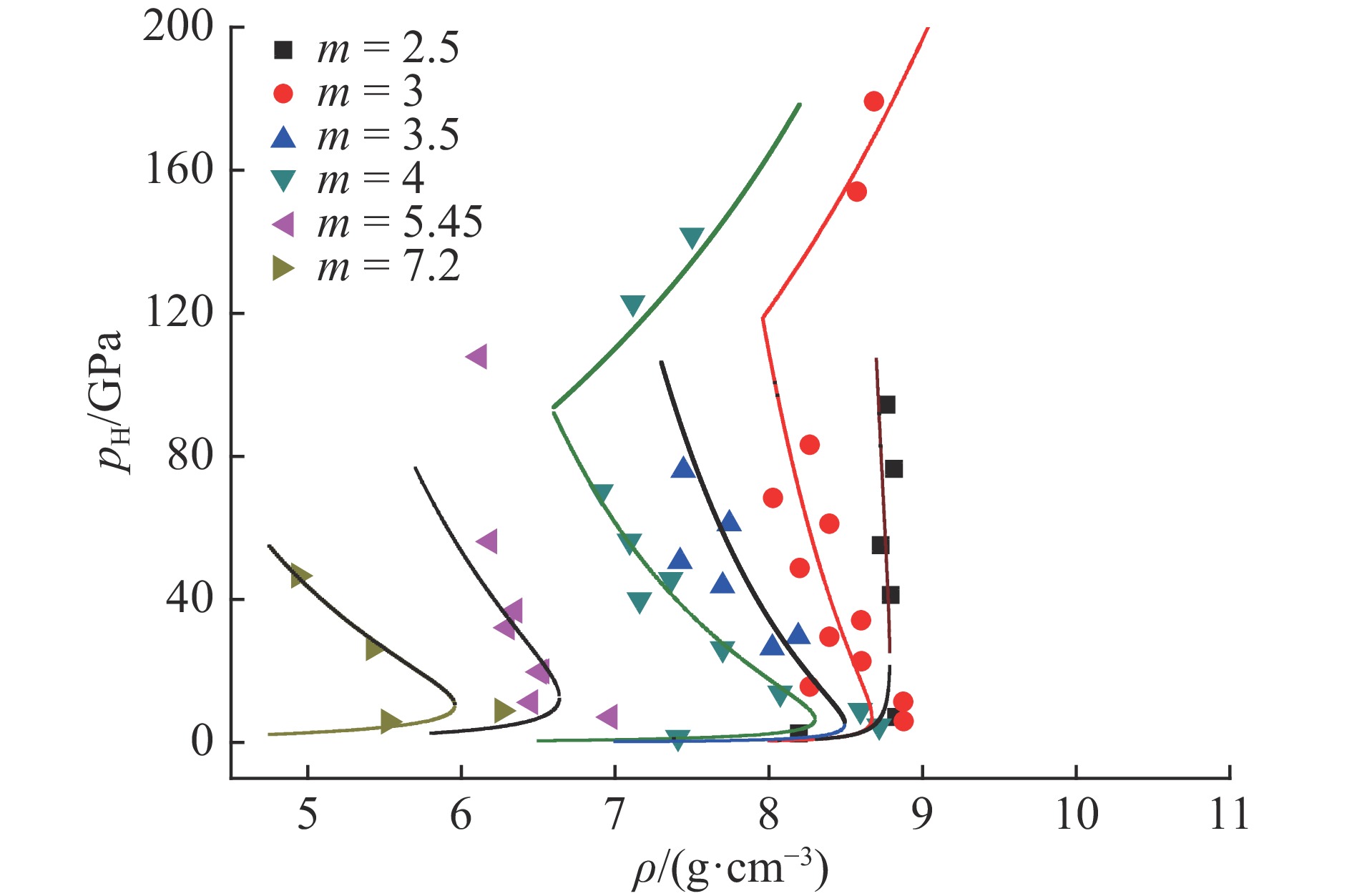
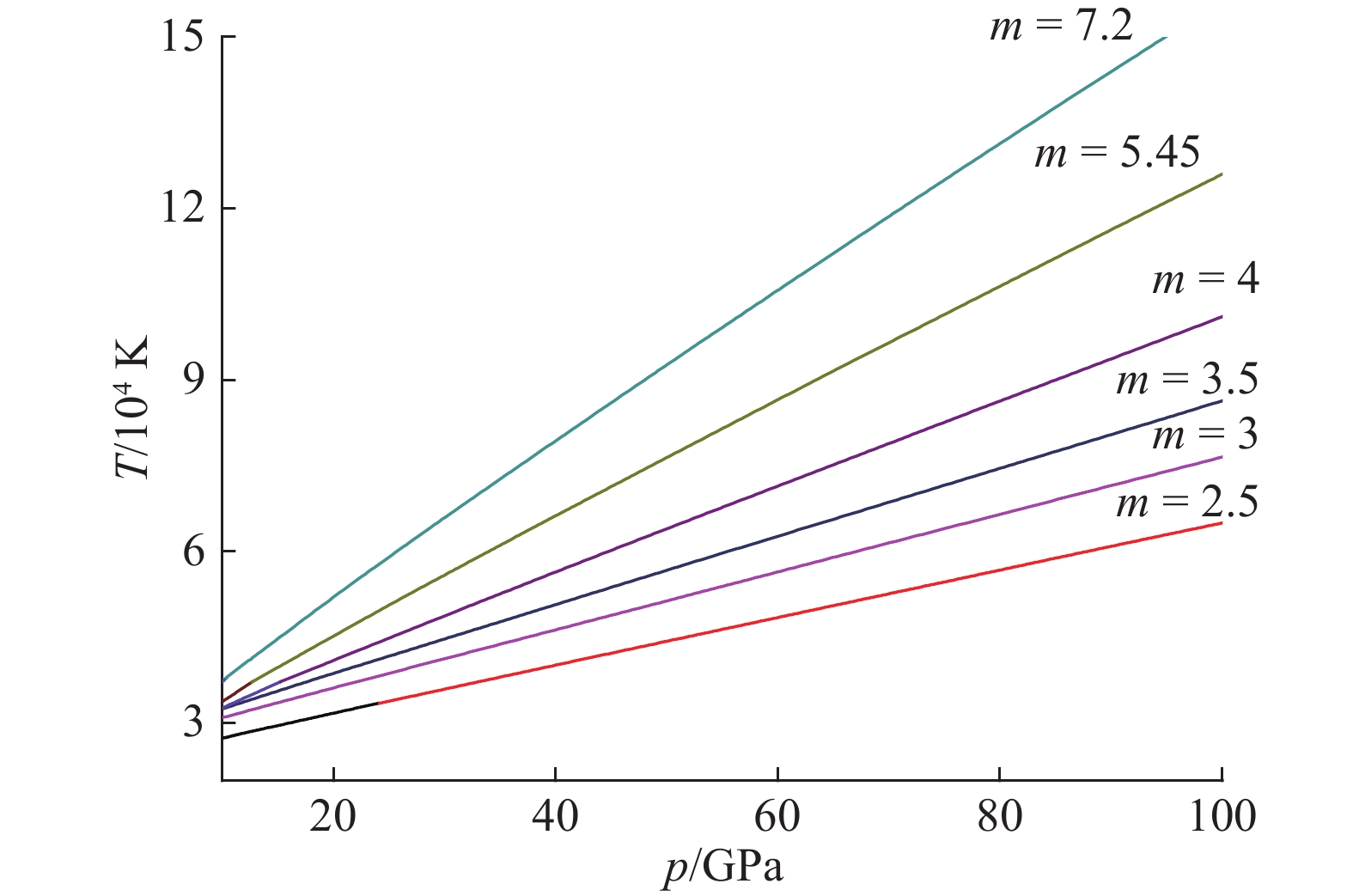
    利用表3中6组参数的pH(x)函数，由(22)式近似计算气相区的冲击温度TH，绘制曲线如图11所示。6组高孔隙度多孔Cu的冲击压缩实验数据中，除m=4和m=3的少数高压数据外，压强均只有几十吉帕，温度在几万开范围。计算结果表明，用Y-A方程近似计算高孔隙度多孔材料的冲击温度在定性的意义上具有一定的可行性。m=4和m=3的第二区域数据，已进入电离区，应由电离区温度方程计算，因实验数据太少，未能进行深入研究。例如m=3的第二区域仅有2个数据，所以压强方程只能作参考，不能用于计算冲击温度。

    • 3.   结　语

  • 多孔材料的物理建模和理论模拟远谈不上完善，上述简单讨论仅限于孔隙塌缩后热力学状态的唯象描述（可能仅在定性的意义上成立），其不足显而易见：对声子和电子的贡献仅以简单的唯象模型计入，未考虑可能存在的熔化、汽化或固-固相变及相应潜热等影响，也未考虑实际过程中材料发生的冲击弹塑性转变和孔隙塌缩过程，更未对孔隙大小、固体颗粒间的结合方式、颗粒大小、孔隙表面能以及填充气体的影响等进行分析和考虑。虽然进行了大量的近似，且有种种不足，但从现象学和唯象理论的角度，本文讨论的模型和方法对高温高压下多孔材料的冲击响应行为提供了一种在物理上有一定理论支撑的简易描述手段，且其结果在一定程度上是合理可信的，通过对模型参数的适当修正，甚至可以获得可以与实验进行定量比较的结果，具有一定的参考价值，这在动态加载领域可满足大多数实际应用的需求。后续工作需要在此基础上将模型进一步精细化，逐一考虑那些被忽略的效应和过程。这将进一步提高对多孔材料的理论描述能力和计算精度，但这尚在探索实践中，需要不断完善，希望本文的简单评述可以为这一方向的发展提供一些有益的参考。

参考文献 (22)

目录

/

返回文章
返回