磁场作用下的双扩散对流涉及流场、温度场、浓度场以及磁场的多物理场耦合, 这种多物理场耦合的对流现象广泛存在于自然界和工业生产之中. 例如, 磁对流下太阳黑子的形成^[1], 磁约束下的受热核聚变^[2,3], 电磁冶金^[4,5]以及磁场辅助下的材料焊接^[6,7]等. 对磁场作用下液态金属双扩散自然对流现象的研究不仅有利于揭示磁场对流动和传热传质的影响机理, 也对实际的工业运用有着重要的意义.

关于磁场强度对流动的影响, 有研究指出, 磁场的作用导致等温线趋向于热传导曲线 ^[8], 磁场通过降低流速来抑制流动和传热^[8,9]. 对于左右两侧施加正弦波形的封闭腔体, 等温线向垂直侧壁移动, 并形成两条对称的等温线^[9]. 对于左侧壁面上3个不同位置的热源的热对流情形, Manogaran和Anbalagan ^[10]获得了类似的结论, 发现传热传质效率随哈特曼数(Ha, 表征磁场强度的无量纲参数)的增大而减小. 无论对于高宽比为2∶1矩形腔体^[11]还是梯形腔体^[12]内的热对流问题, 研究者们均发现磁场抑制了流体的总动能, 抑制程度与磁场强度成正比^[11], 传热传质效率随着磁场强度的增大而降低^[12]. 关于磁场下双扩散毛细对流, 文献[13]研究发现当磁场强度足够大时能实现晶体生长所需要的条件. Uddin 等^[14]还发现不同类型的磁场对传热的影响不同, 如均匀磁场下对流的传热传质效果优于非均匀磁场. 磁场方向对流动也有一定的影响, 表现在流型上导致了腔内多涡的存在^[15]. 通过对比气体、水、液态金属镓, 研究者发现磁场方向和强度对腔内流动影响很大, 但相比于其他两种流体, 液态金属镓对磁场强度的变化响应最小^[16]. Makayssi 等^[17]发现磁场方向在0°—180°范围内变化时, 传热和传质效率随磁场方向的变化呈倒三角形, 且在180°—360°的范围内重现. 随后, Liao等^[18]通过数值研究不同瑞利数和磁场强度下的对流换热模式, 给出了用以描述磁场方向影响的关联式, 但其并不是普适的. 对于带热源的情形, 前人发现通过固定腔体倾斜角, 传热效率在磁场角度平行于流体流动方向时达到最大^[19]. 最近, Moolya和Satheesh ^[20]发现在浮力比$N = 1$时, 传热最强对应的磁场角度是60°, 而浮力比$N = - 1$时, 最佳角度为30°. 后来, 他们使用方差分析方法确定了所考虑参数的显著性, 并优化了所选定参数对传热和传质的影响^[21]. 针对三维立方体和锥形体, 研究均发现磁场显著抑制流体运动, 从而抑制热传递, 且抑制程度与磁场方向有关^[22,23]. 随后, 通过探讨左右壁面平行、上下壁面为波纹壁的腔体内的热对流, Yasin等^[24]发现热传递速率在较大和垂直磁场处达到最大.

事实上, 大多数研究是针对特定磁场方向进行的, 特别是常见的水平磁场或垂直磁场. 对于水平磁场, 研究者发现磁场会产生和法向相反方向的力从而阻碍对流, 当瑞利数较小且磁场强度相对较小时, 传热效率强烈地依赖于腔体倾角^[25]. 振荡发生在足够大的雷诺数下, 并且会引起涡对的不稳定性^[26]. Ghosh等^[27]模拟研究了低Prandtl数下导电流体热对流的转变, 尝试揭示热运输增强的原因和不同流型的起源. Listratov等 ^[28]研究揭示了雷诺数和哈特曼数对异常高振幅温度波动的影响. Ren 等^[29]还计算了洛伦兹力的分布, 以解释实验中所观察到的复杂对流现象. 针对垂直磁场, 在某些特定情形下, 流体介质的最大传热量与瑞利数无关 ^[30]. Han 等^[31]发现随着瑞利数的增大, 系统经历了两个连续的过渡, 一种是叉形分岔, 一种是根据系统参数不同而决定的. 对于低Prandtl数下的磁对流, Zürner 等^[32]给出了4种不同的磁对流区域, 分别用磁场强度和流动中的湍流水平来进行区分. 研究者还在强磁场下模拟获得了3种磁对流状态, 即胞状、柱状和湍流形式, 发现前两种状态是磁约束的, 第3种状态中受洛伦兹力的影响较小^[33].

综上可以发现, 前人对于强磁场的流动问题进行了大量研究, 并取得了丰富的研究成果, 但已有研究表明, 在对流发生的临界磁场强度附近, 流动模态更难预测, 流动结构更加复杂有趣, 且水平磁场与垂直磁场的对比研究鲜见报道. 本文针对水平磁场和垂直磁场两种磁场情形, 在较大的磁场强度范围内, 探讨磁场强度、Prandtl数、Lewis数和腔体尺寸等对流动和传热传质的影响, 通过对比研究揭示磁场对流动和传热传质的影响机制.

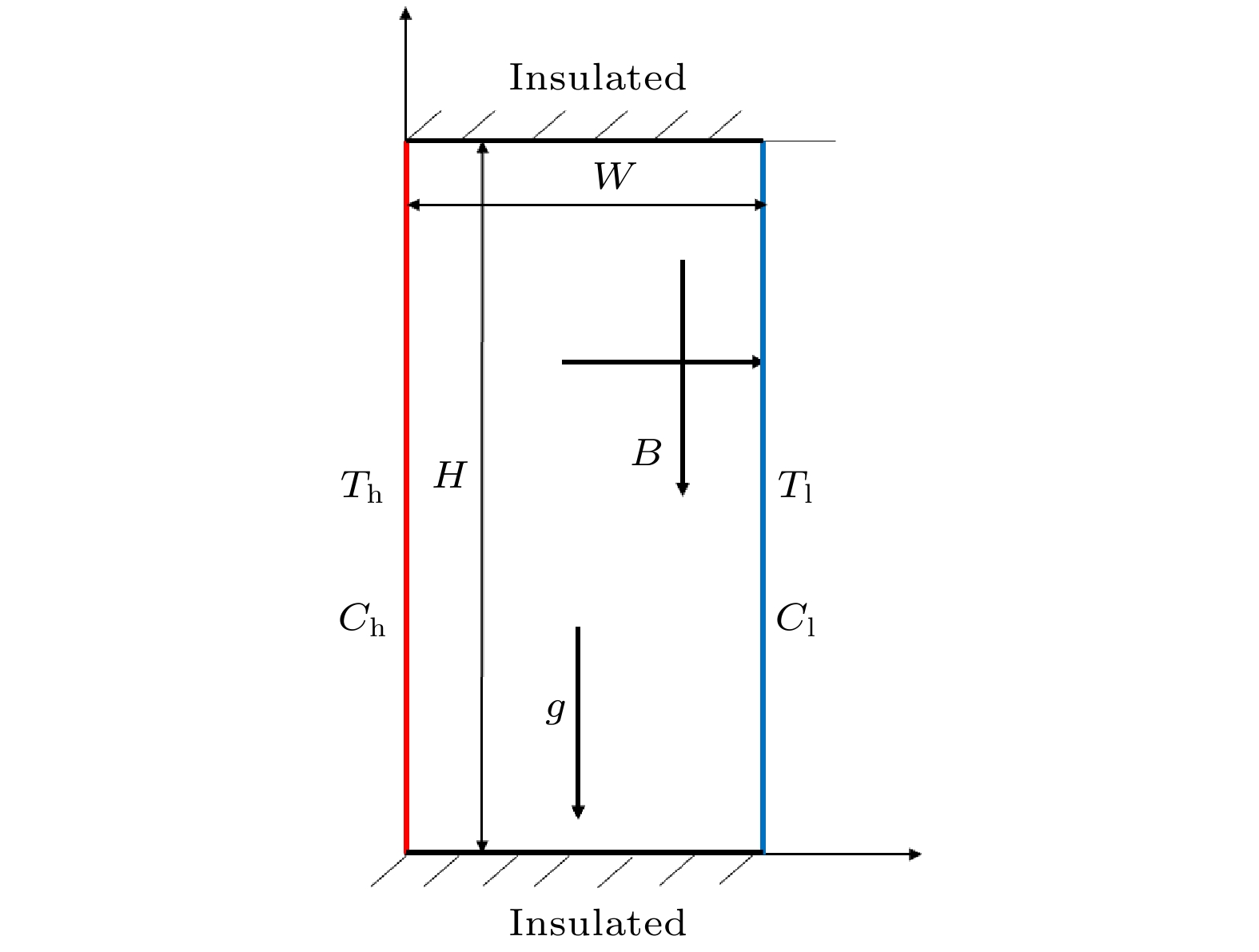
物理模型如图1所示, 其中腔体高为$H$, 宽为$W$, 高宽比为$ A = H/W $. 上、下壁面是绝热的, 左侧壁面温度(T_h)和浓度(C_h)高于右侧壁面的温度(T_l)和浓度(C_l), $B$表示水平和垂直方向施加的磁场. 假设感应磁场和总外磁场$B$之比的磁雷诺数远小于1, 则可以忽略电磁感应现象产生的感应磁场.

假设流体满足Bonssinesq假设, 则流体密度$\rho $, 温度$T$和浓度$C$的关系状态方程为

其中${\varphi _{\text{T}}} = - \dfrac{1}{{{\rho _0}}}\dfrac{{\partial \rho }}{{\partial T}}\Big|_{{C_0}},~ {\varphi _{\text{C}}} = - \dfrac{1}{{{\rho _0}}}\dfrac{{\partial \rho }}{{\partial C}}\Big| _{{T_0}}$分别为热膨胀系数和浓度膨胀系数, 式中${T_0}, {C_0}, {\rho _0}$分别为参考温度、参考浓度和参考密度. 选取$W$为特征长度, ${W^2}/{\kappa _{\text{T}}}$为特征时间(其中${\kappa _{\text{T}}}$为热扩散系数), 只考虑水平和垂直磁场的情形, 引入以下无量纲量:

可得描述磁场作用下的双扩散对流系统的无量纲方程为^[11,16](为书写方便, 这里去掉无量纲量的上标*号) :

其中$u, v$分别表示$x, y$方向的速度, $p$为流体压力, $ \beta $为磁场方向(取值$ \beta = 0^\circ $或$90^\circ $). 无量纲参数瑞利数$Ra, $Prandtl数Pr, Lewis数$Le$, 浮力比$N$, 以及哈特曼数$Ha$的定义为

其中$\nu$为运动学黏性系数, ${\kappa _{\text{C}}}$为浓度扩散系数, $B$为磁感应强度, $ \sigma $为电导率. 为消除压力$p$引入流函数$\psi $和涡量$\omega $, 具体表达式为

由此方程(2)—(6)可写为

相应的无量纲边界条件为

用Nusselt数表示传热效率, Sherwood数表示传质效率, 热壁上的传热传质分别用平均$Nu$和$Sh$来描述:

本文采用高精度高分辨率的差分方法进行直接数值模拟^[34]. 该方法针对非线性对流项的离散采用了优化的四阶迎风紧致格式, 扩散项的离散采用四阶Pade格式, 流函数泊松方程采用四阶高精度格式进行离散并使用多重网格进行加速, 用三阶TVD型Runge-Kutta方法进行时间推进, 方法的理论分析和检验已在前面的工作中完成^[34,35].

为了选取合适的网格, 针对不同的磁场大小$\left( {\beta = 0^\circ , \beta = 90^\circ } \right)$, 以及不同磁场强度$( Ha = 5, Ha = 10 )$进行网格无关性验证, 时间步长取${10^{ - 5}}$, 其他参数固定为$Ra = {10^4}, \;Pr = 0.025, \; N = 0.8, Le = 2,\; A = 2$. 通过表1和表2可以看出, 选取 41×81的网格进行计算, 其与精细网格的误差小于2%, 误差相对较小, 考虑计算精度以及计算效率, 故选用$41 \times 81$的网格. 后续计算若未特别提及, 均使用上述参数进行计算.

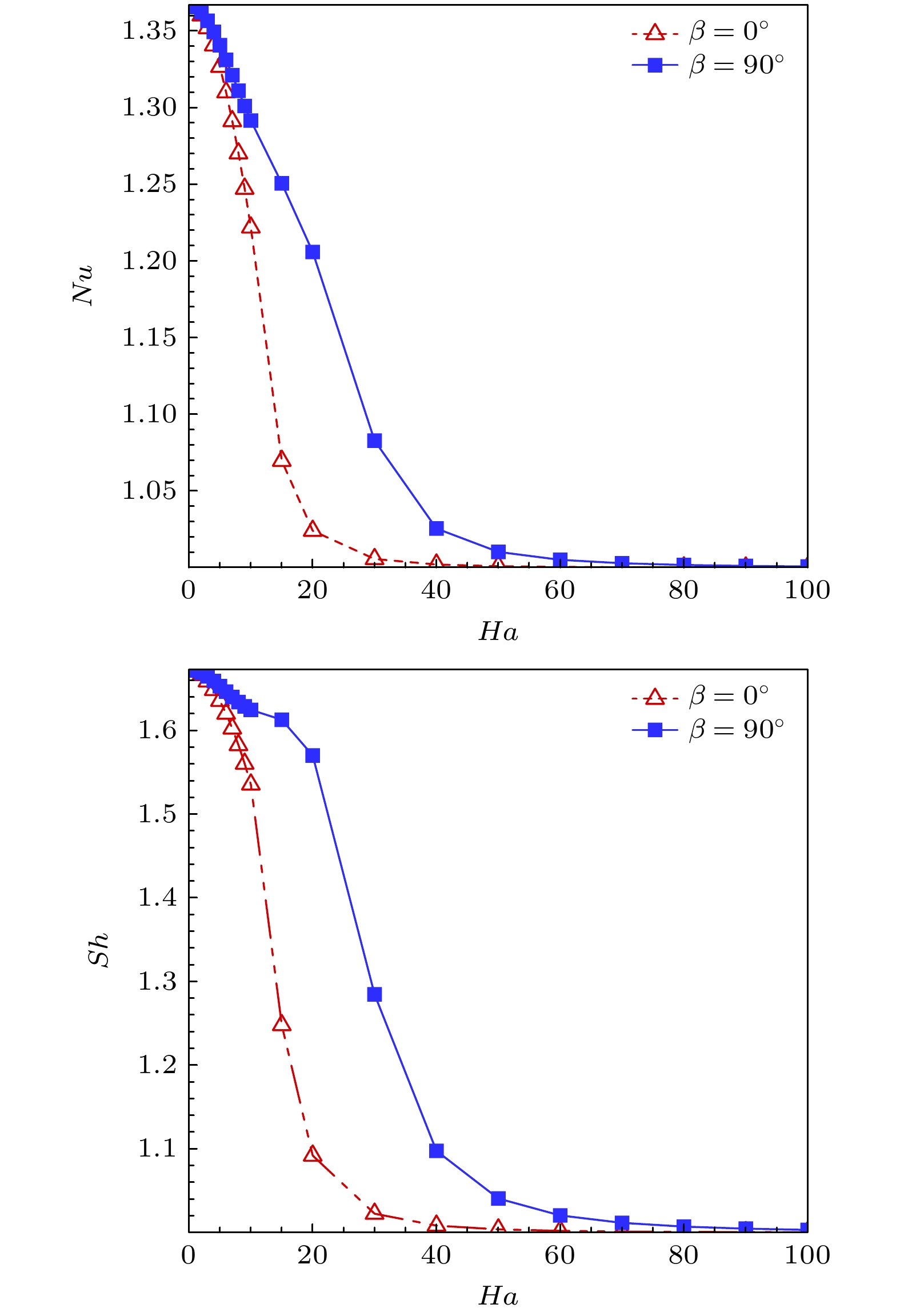
不同方向磁场下热壁面Nusselt数随磁场强度哈特曼数的变化情况如图2所示. 由图可以看出, Nusselt数随着Ha的增大而逐渐减小, 表明外加磁场起到抑制对流的作用, 且随着磁场强度的增大, 这种抑制作用增强且使传热逐渐减弱. 水平磁场($\beta = 0^\circ $)和垂直磁场($\beta = 90^\circ $)作用下对流换热的效率有明显的不同, 水平磁场下Nusselt数曲线始终位于垂直磁场Nusselt数曲线的下方, 意味着同等强度下水平磁场对流动和传热的抑制作用强于垂直磁场. 这是因为在水平磁场下, 磁场力的方向与流体速度方向相反, 从而减小了流体运动的速度, 这种阻尼作用会抑制涡旋的形成, 使热对流减弱. 而在垂直磁场下, 磁场引起的洛伦兹力导致流体发生横向的位移和加速度分布的变化, 也会对流体运动产生一定的阻尼作用, 但与水平磁场相比, 垂直磁场对流动的阻尼作用较小、热对流较强.

在本文关注的磁场强度范围内($0 \leqslant Ha \leqslant 100$), 随着磁场强度Ha的增大, 两条Nusselt数曲线表现为先分开后合并的变化过程. 磁场较弱时($0 \leqslant Ha \leqslant 10$), 由于弱磁场产生的洛伦兹力较小, 此时温度和浓度梯度引起的浮力占主导地位, 磁场方向对流动和传热的影响较小, 故两种方向磁场 下Nusselt数相近, 区别不明显. 随着Ha的增大, 当$10 < Ha \leqslant 60$时, 水平磁场下传热Nusselt数和垂直磁场下传热Nusselt数之间的差距逐渐拉大, 在$15 \leqslant Ha \leqslant 20$之间二者差距最大, 此时磁场方向对流动和传热的影响最大; 在此哈特曼数范围内, 浮力和洛伦兹力的竞争最为激烈, 往往导致流动十分复杂、不易稳定, 从而发展为时间依赖的非定常对流状态. 随着哈特曼数的进一步增大 ($Ha > 60$), 磁场洛伦兹力进一步增强, 磁场占主导地位, 强磁场的抑制作用使得流动较弱, 相对于磁场强度, 此时磁场方向对流动的影响相对较小. 因此, 在实际应用中为有效实现抑制流动, 在中等强度磁场时, 可以考虑通过改变磁场角度进行调控.

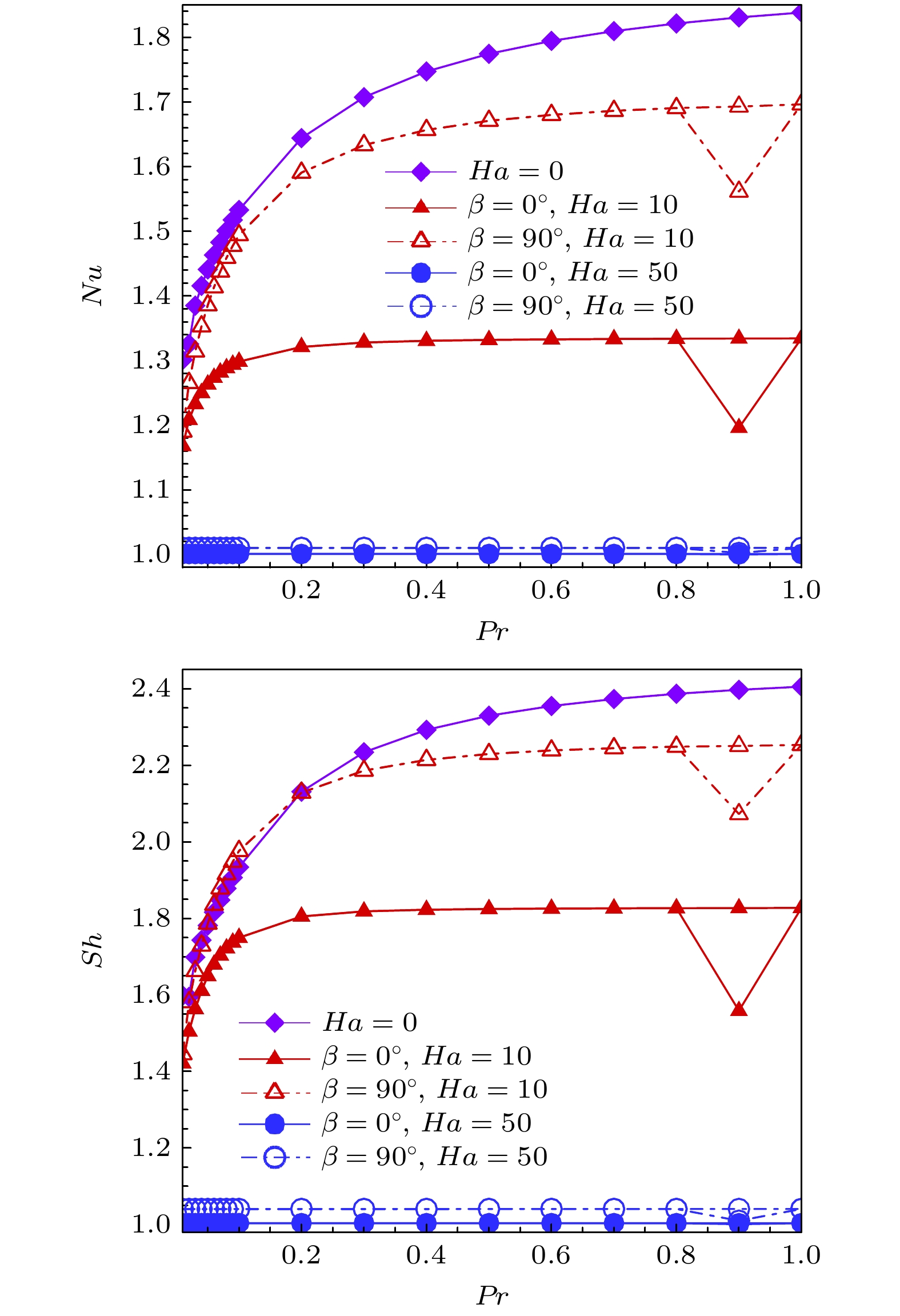
整体上而言, 随着Pr数的增长, 传热传质效率均随着Pr数的增大而增大, 如图3所示. 在$0.01 < Pr < 0.1$的范围内, 传热传质效率增长剧烈, 如在较小的磁场强度下($\beta = {90^\circ }, Ha = 10$), $Nu$增长了25.5%, $Sh$增长了36.7%. 对于$Ha = 10$的影响相对较大.

在$Pr = 0.1$的时候, 垂直磁场较水平磁场的传热传质效率分别高出了15%和13%. 这说明垂直磁场作用下, 腔内对流更加激烈, 洛伦兹力和腔内浮力耦合作用更强. 当$Pr > 0.1$时, 传热传质效率受到磁场强度和磁场方向影响的增长速度缓慢. 无磁场时, 传热效率始终优于有磁场的情况, 表明磁场起到了抑制传热的作用; 传质效率在$Pr < 0.2$时与弱垂直磁场($Ha = 10$)下的传质效率相当, 在$Pr > 0.2$时则高于有磁场时的传质效率. 与有磁场时不同, 无磁场时Nu和Sh曲线是光滑的, 且不存在解的分岔现象.

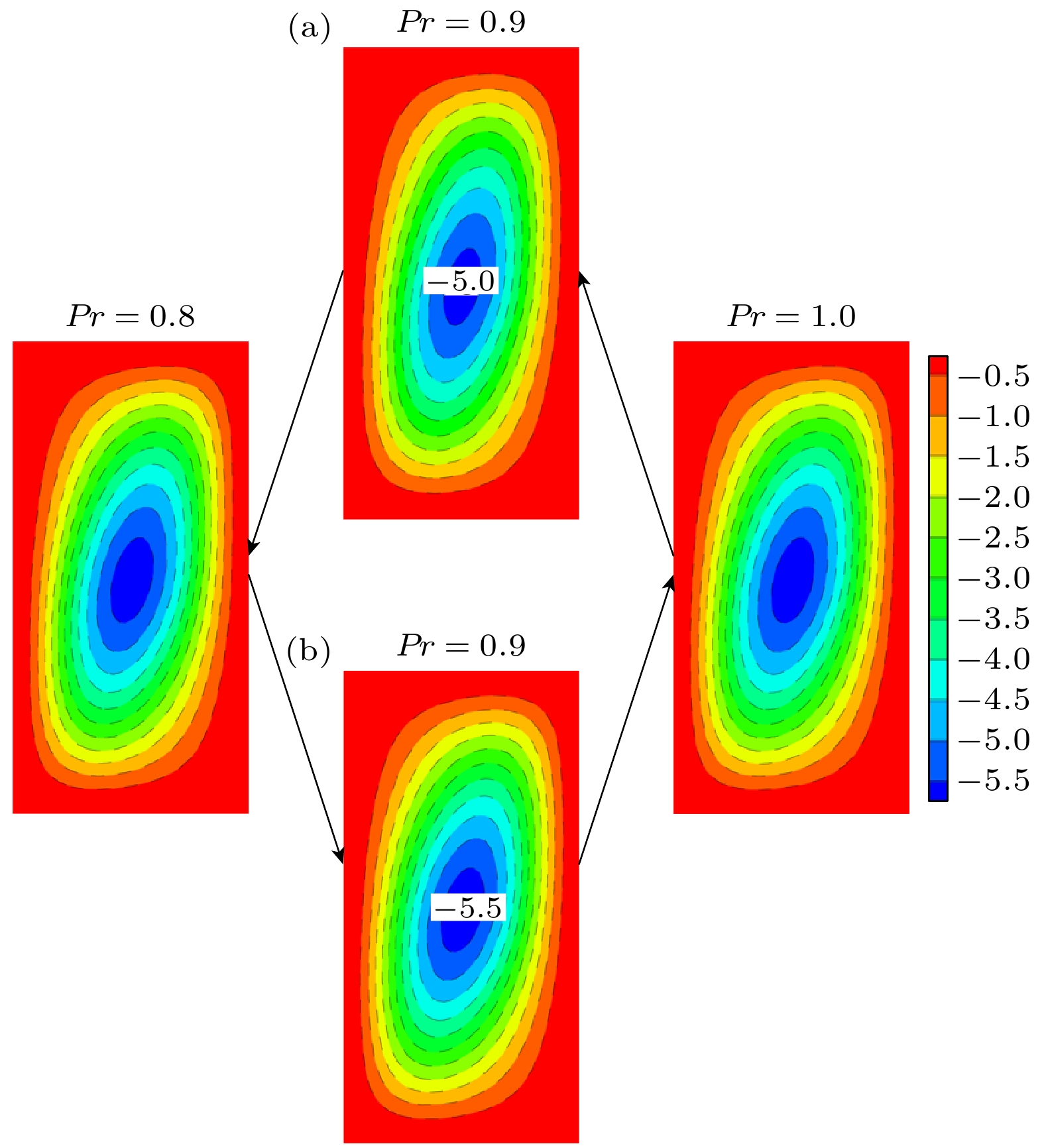
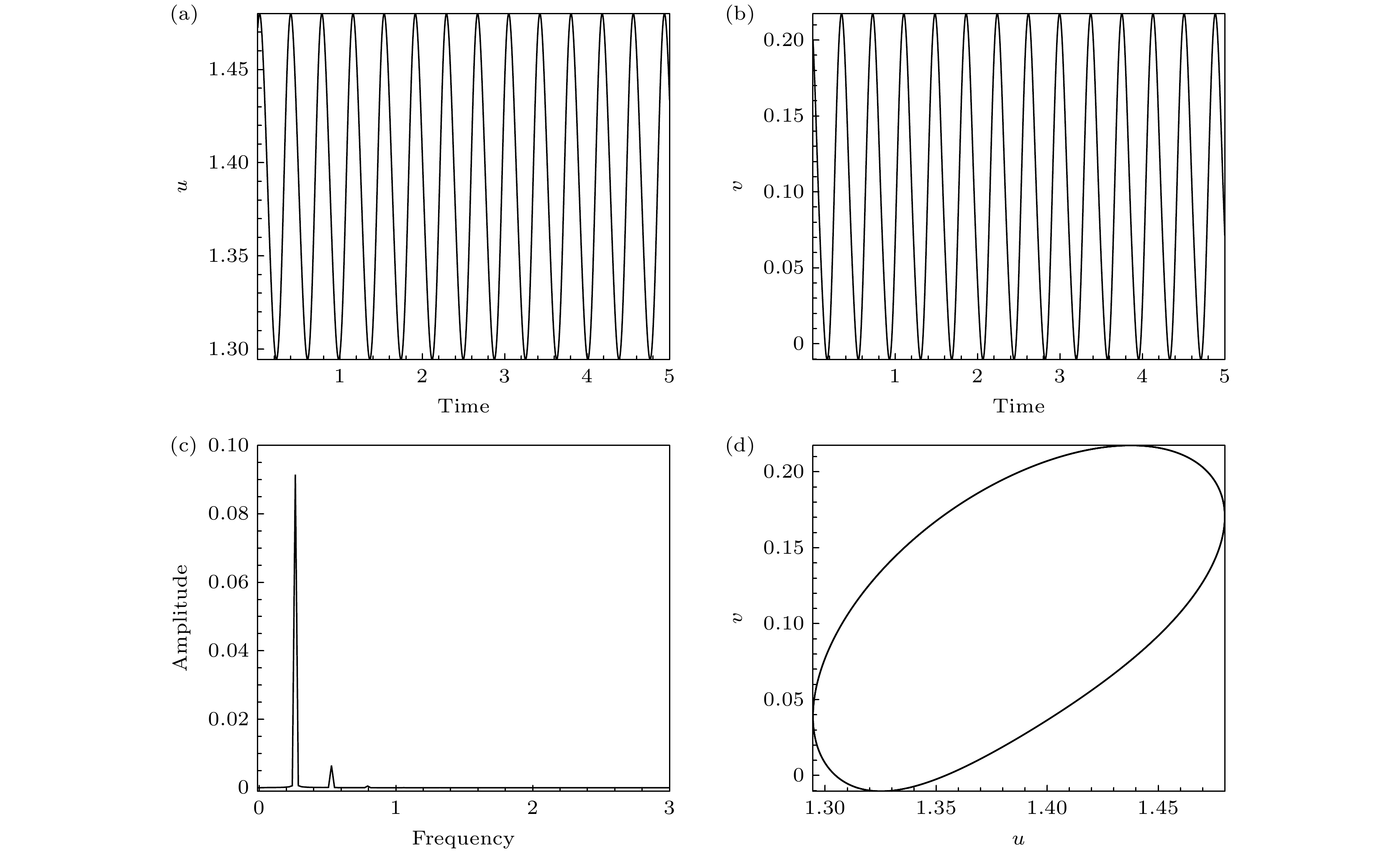
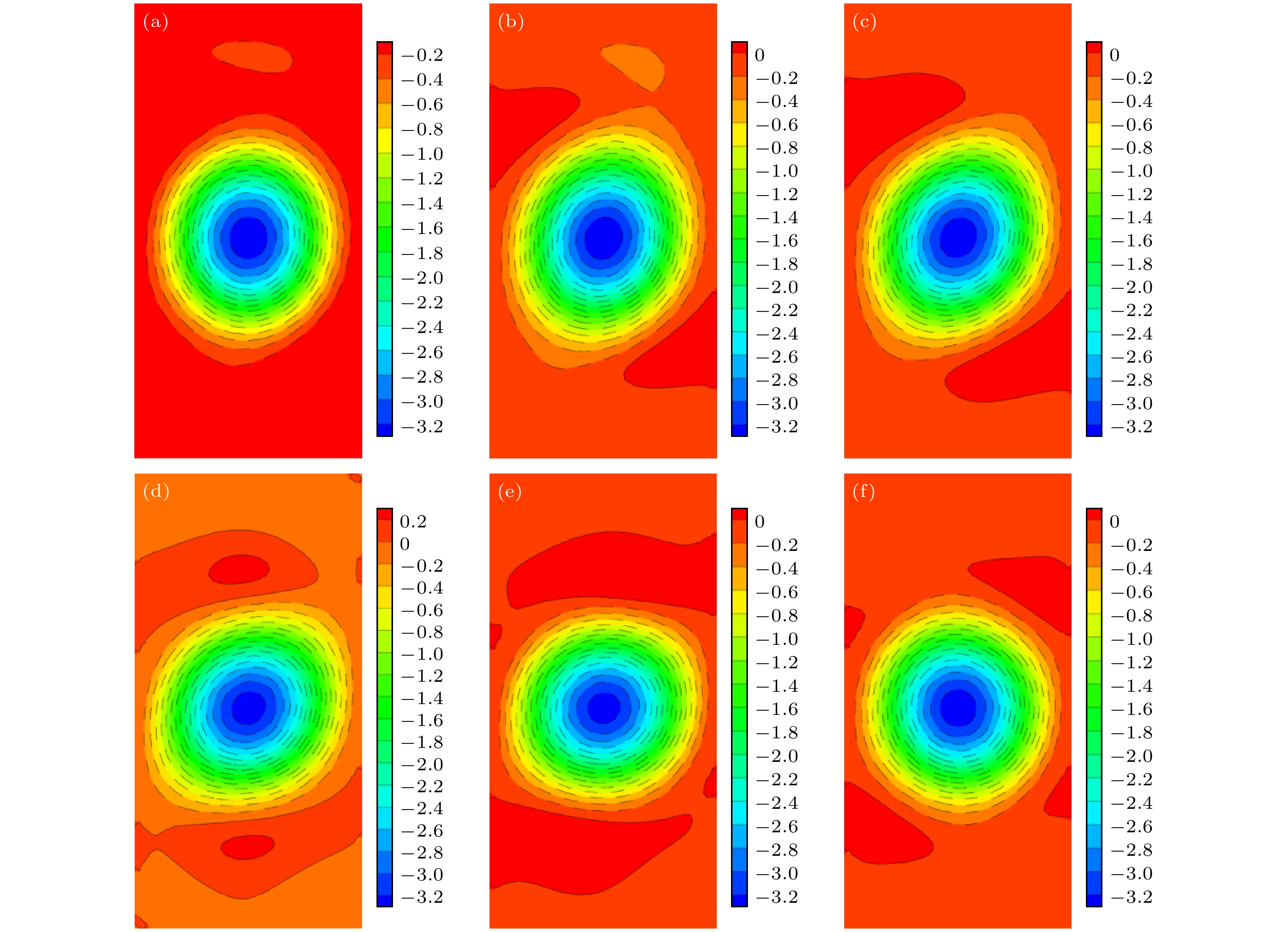
有磁场时, 在Pr = 0.9处系统出现了两个不同的解, 选取$\beta = 0^\circ , Ha = 10$对这种多解的情况进行了探讨, 如图4所示. 随着Prandtl数的增大, 传热效率呈现递增的趋势. 当使用较小Prandtl数为初值向更高Prandtl数计算时, 结果为图4中的下部分支, 计算至Pr = 0.9时传热效率出现了显著的减小, 最大流函数的值为–5.5, 此时流场结构对应图4(b). 沿着该分支继续增大Prandtl数到Pr = 1时, 解的分岔消失; 从Pr = 1减小Prandtl数到Pr = 0.9, 在Pr = 0.9处得到另一解如图4中的上部分支, 最大的流函数值为–5, 流场结构如图4(a)所示, 沿着上部分支继续减小Prandtl数, 在Pr = 0.8时, 上下两分支重合, 解的分岔消失. 此外, 我们还发现, Pr = 0.01时, 当$\beta = 90^\circ , Ha = 10$时, 流场结构为周期流动. 这种流动的代表性情形的各特征量变化如图5所示($ Ha = 10, \beta = 0^\circ $), 速度分量$u, v$的时间序列呈周期变化(见图5(a), (b)), 相位图为如图5(d)所示一个封闭的环, 此时周期演化的主频为0.264, 倍频为0.528, 如图5(c), 周期为3.7825.

图6(a)—(f)给出了一个周期内不同时刻流场的瞬时结构. 整个周期变化过程的特征是: 来自左侧壁面的高温度流体向上向右流动, 来自右侧壁面的低温度流体向下向左流动, 从而在中心形成一个顺时针涡卷(主涡). 由于腔体竖直方向的空间更大, 中心主涡在竖直方向洛伦兹力的作用下被拉长, 为椭圆形状(见图6(a)); 尽管如此, 主涡仍不足以覆盖整个腔体, 于是在剪切力和壁面黏性的作用下, 流场中出现了两个逆时针旋转的二次涡(见图6(b)); 二次涡逐渐成长 (见图6(c)), 其覆盖区域逐渐增大, 并挤压中心主涡(见图6(d)); 最终使中心主涡在竖直方向受限并被压回到圆形(见图6(e)); 与此同时, 二次涡控制的区域达到最大, 但其强度不足以维持这种状态, 在竖直方向洛伦兹力的作用下, 二次涡逐渐衰退、中心主涡再次成长, 如图6(f)所示, 进入了下一个循环.

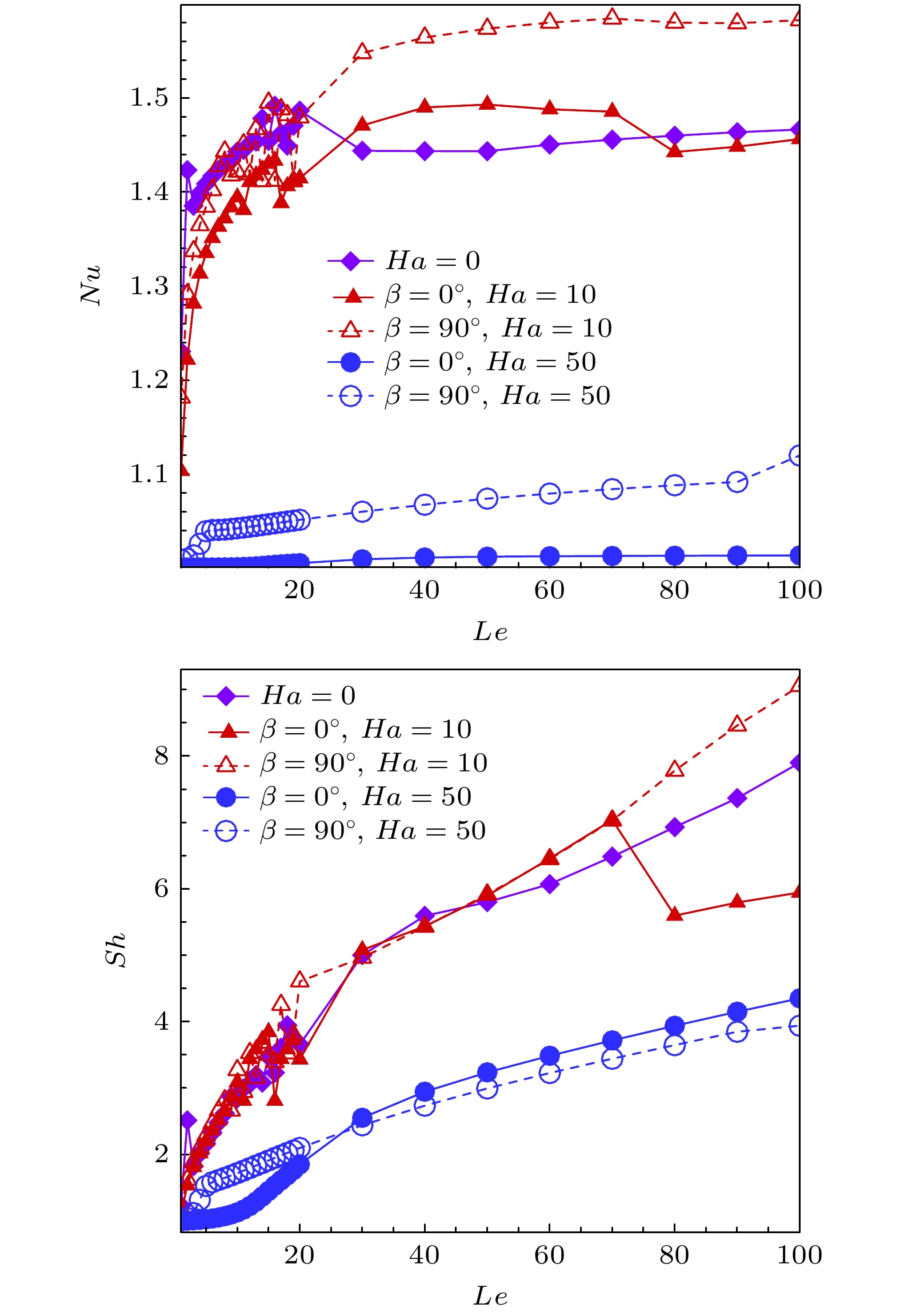
本节给出了流动和传热传质特性随Lewis数的变化情况. 由前面的分析可知, 磁场较弱(如$Ha = 10$)时流动往往更为复杂, 随着Lewis数的增大, 流动从定常状态过渡到周期状态. 具体地, 如表3所示, 水平磁场下, 随着Lewis数的增大, 在$1 \leqslant Le \leqslant 8$时, 流动是定常的, $Le \geqslant 9$时流动是周期的; 垂直磁场下, 在$1 \leqslant Le \leqslant 6$时, 流动是定常的, $Le \geqslant 7$时是周期的. 相比于水平磁场, 施加的垂直磁场加速了周期解的到来, 流动从定常向周期状态过渡的临界Lewis数更小.

Nusselt数随Lewis数的变化如图7所示. 在无磁场的情况下, 当Le数较小时($Le < 20$), 传热效率随Lewis数的变化表现出较大的波动, 但在$Le > 30$变得相对稳定, 这表明低Le数对传热的影响更为显著, 而高Le数的影响较小. 对较弱磁场($Ha = 10$)而言, 当$1 < Le < 20$时, 不论是水平磁场还是垂直磁场, Nusselt数曲线均呈现一定程度的振荡, 垂直磁场下的振荡更为剧烈. 而$Le > 20$时, Nu呈现先增大后减小的趋势, 在$Le = 80$附近达到最小. 对于较强磁场($Ha = 50$), 在本文所研究的Lewis数范围内, 两种方向磁场下Nusselt数单调增大, 且垂直磁场下Nu的增速快于水平磁场. 传质效率的变化更为复杂, 主要表现在: 无磁场时, 传质效率与弱垂直磁场下的传质效率接近, 而在$Le > 50$之后, 无磁场的传质效率总是低于弱磁场的传质效率. 对于弱磁场, 当$Le \leqslant 70$时, 传质效率随Lewis数的增大整体上呈增大的趋势, 两条Sherwood数曲线离得很近, 在$30 < Le < 70$的范围内几乎重合, 表明磁场方向对传质的影响并不显著; 当$Le > 70$时, 水平磁场下的传质效率急速下降之后再缓慢增大, 而垂直磁场下仍然是递增的. 对于较强磁场, 在整个Le数范围内, 两种磁场下传质效率总是随着Le的增大而增大; 在$1 < Le < 20$的范围内, 垂直磁场下流动的传质效率相对更强(Sh数更大), 在$Le = 25$附近二者接近, 之后则水平磁场下的传质效率更强. 值得注意的是, $Le = 80$处Nu和Sh突然下降, 这是因为尽管$Le = 70$和$Le = 80$时流动均是周期性的, 且都是从单涡结构发展到三涡结构、再回到单涡结构的循环往复, 但是$Le = 80$时单涡结构存在的时间长, 而$Le = 70$时三涡结构存在的时间长. 由于涡卷数目越多则传热传质效率更强, 于是$Le = 80$的Nu和Sh值比$Le = 70$时的小很多, 从而导致了$Le = 80$处Nu和Sh的突然下降. 如果继续增大Lewis数时, 三涡结构存在的时间又会缓慢增加, 故$Le > 80$之后, Nu和Sh随着Le的增大而缓慢增大.

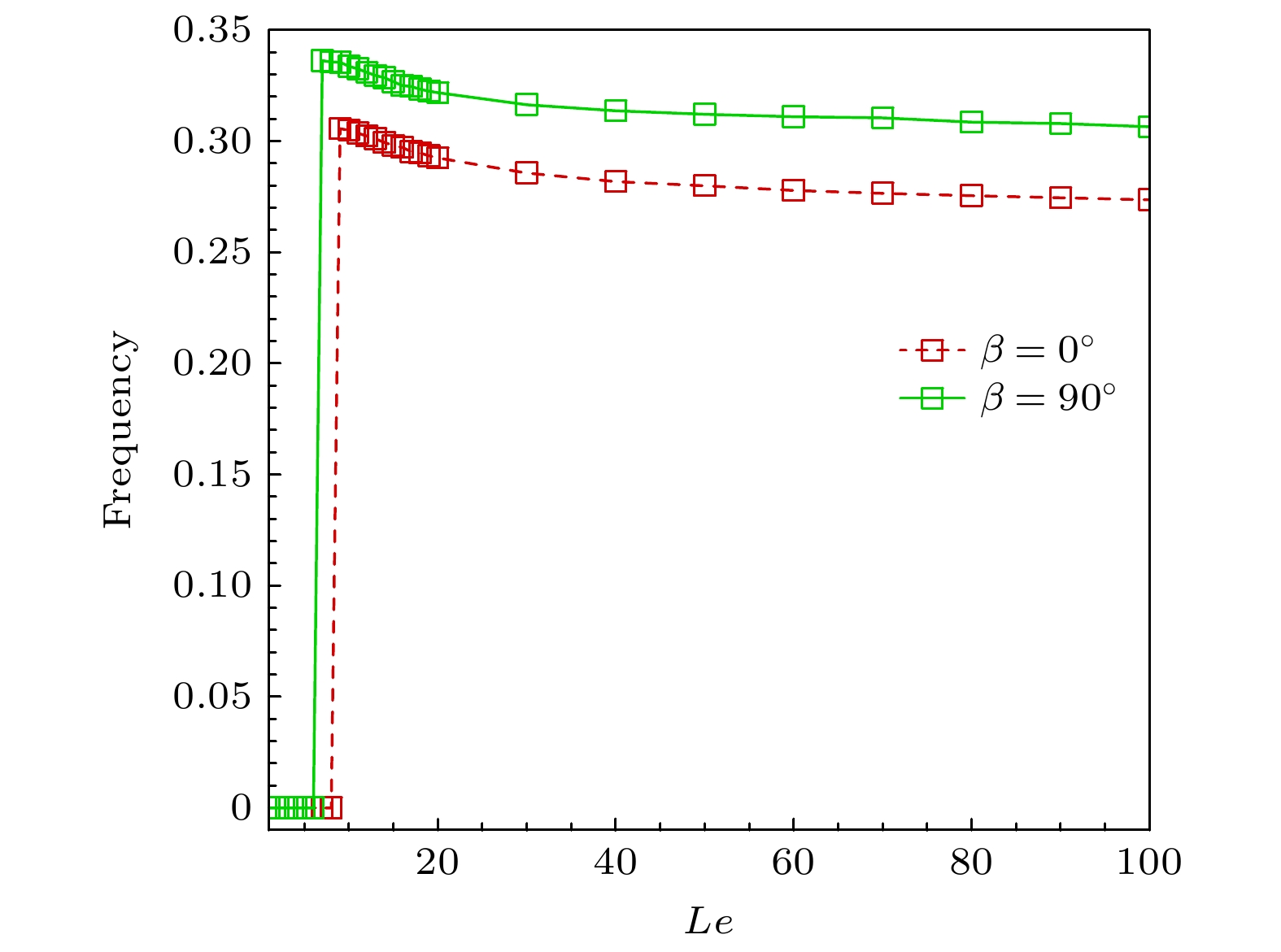
根据图7中所呈现的变化趋势并结合表3中定常解和周期解的范围, 我们给出了腔体几何中心处速度$u$的频率随Lewis数的变化, 如图8所示. 可以看出, 不论何种方向的磁场, 速度$u$的频率均是随着Le数的增大而单调递减, 表明流体的热扩散系数越大, 则周期性流动的周期越长; 相同Le数时, 相比于垂直磁场, 水平磁场下的频率更小, 表明水平磁场通过有效地抑制流动的速度和速度波的传播频率, 实现了对传热的更强抑制作用(Nusselt数更小, 见图7). 事实上, Lewis数和磁场强度、磁场方向等对流动的耦合作用机制较为复杂, 这里仅给出了初步的结果, 未来需进一步深入研究.

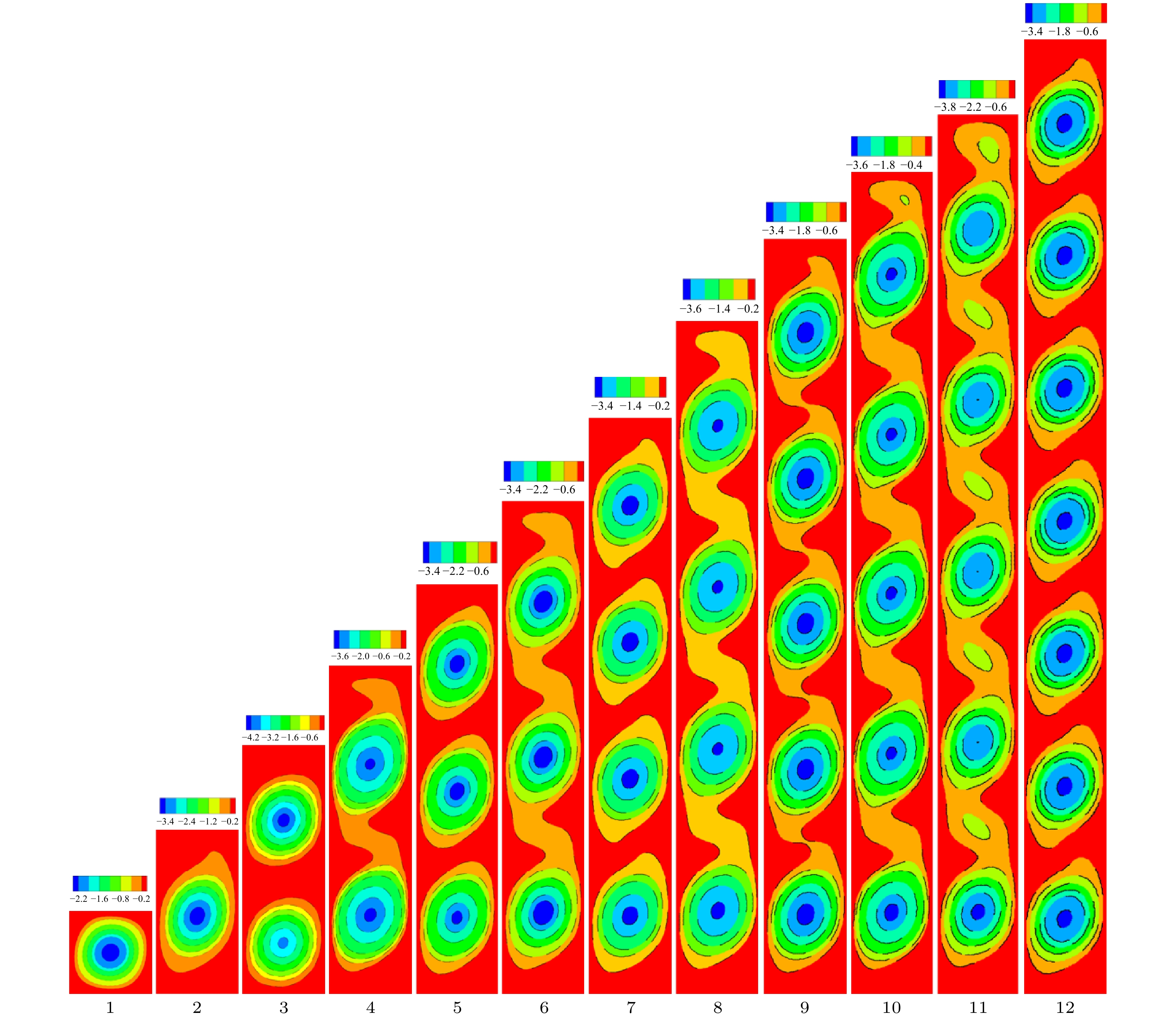
在高宽比为$1 \leqslant A \leqslant 12$的范围内研究了腔体尺寸对流动和传热传质的影响, 腔体尺寸对传热传质的影响如图9所示. 无磁场时, 传热传质曲线随着高宽比的增大出现振荡现象, 且基本都高于对应的有磁场的情形. 较弱磁场($Ha = 10$)时, 传热传质效率也呈现一定程度的上下摆动. 在$1 < A < 3$的范围内, 水平磁场比垂直磁场下的传热传质效率高, 而$A \geqslant 3$时, 垂直磁场比水平磁场下的传热传质效率高. 对于较强磁场($Ha = 50$), 对于任意高宽比的腔体, 水平磁场下流动几乎被完全抑制($Nu \approx 1.0, \;Sh \approx 1.0$), Nusselt数和Sherwood数曲线近乎为一条直线; 垂直磁场下传热传质效率则呈现先增大后减小的变化趋势, 见图9中蓝色实线, 在$A = 5$附近达到最强. 无论何种高宽比的腔体, 对于相同的磁场强度, 垂直磁场下的传热传质效率强于水平磁场, 例如$A = 5$时, 垂直磁场下的传热效率相较水平磁场下传热效率增长了约13%.

图10给出了$Ha = 10$垂直磁场下不同高宽比腔体内的流场结构. 当$A = 1, 2$时流场为单涡结构, 对应的模态为单涡奇模态, $A = 3, 4$时为双涡结构(两涡偶模态), $A = 5, 6$为三涡结构, $A = 7, 8$为四涡结构, A = 9—11为五涡结构, $A = 12$时流场为七涡结构. 可以看出, 在不同的高宽比范围内, 流场中涡卷的个数不同, 对应的临界模态的奇偶性不同, 且奇偶性随着高宽比的增加而交替变化^[36]. 结合图9进一步发现, 对于相同涡卷数量的流动, 高宽比A较小时传热和传质效率最强, 这也意味着, 保持在相同的涡卷数情况下, 增大腔体比例, 流动的传热传质能力会减弱.

本文对磁场作用下二维腔体内液态金属双扩散对流进行了高精度数值模拟, 研究了磁场、流体特性参数、以及高宽比对流动和传热传质的影响. 发现随着磁场强度的增大, 流动逐渐被抑制, 传热传质逐渐减小, 同等强度下水平磁场对流动和传热传质的抑制作用强于垂直磁场. 在本文关注的磁场强度范围内, 强磁场下的传热比无磁场时减小了36%, 而传质减小了约60%. Lewis数会影响周期解的存在范围, 施加垂直磁场时, 会在较小的Lewis数达到周期解的状态. 此外, Lewis数对传质的影响十分明显, 如水平弱磁场下最大Lewis数的传质效率约为最小Lewis数的6倍, 垂直弱磁场下约为9倍; 相比而言, 对传热的影响作用要小得多.

Prandtl数对传热和传质的影响规律相同, 无磁场时传热传质效率随Prandtl数单调增大, 最大Prandtl数下的传热传质效率比最小Prandtl数时增大了约45%; 施加磁场会降低传热传质的增幅, 且当磁场强度达到一定程度后, 洛伦兹力占绝对主导地位, Prandtl数对传热传质的影响变得非常小. 虽然磁场具有抑制对流的作用, 但也会导致在某些Prandtl数时出现解的分岔现象, 这在实际应用中需特别关注. 高宽比对流场结构和临界模态有明显的影响, 涡卷数量的变化也会影响传热传质效率, 相同涡卷数时, 腔体尺寸越小传热传质效率越大. 这些结果对有助于深入揭示二元流体双扩散对流的动力学特性, 并可推广到混合流体Rayleigh-Bénard对流等其他情况.