-
半导体量子点量子计算与传统的微电子工艺兼容, 可拓展性强, 是实现固态量子计算的重要路线之一[1–3]. 用于半导体量子点量子计算的材料体系主要有Ⅲ-Ⅴ族GaAs/AlGaAs[4,5], InAs[6]或InSb纳米线[7], Ⅳ族的Si MOS[8], Si/SiGe二维异质结电子气[9]、Ge/SiGe二维异质结空穴气[10]、原子掺杂的Si材料[11]和Ge量子线[12–16]等. 早期研究主要围绕着Ⅲ-Ⅴ族的GaAs/AlGaAs材料[17]开展, 但栅控量子点中电子因受到电子自旋和核自旋超精细作用的影响[4], 退相干时间最高仅为94 ns[17]. 相比于Ⅲ-Ⅴ材料, IV族硅、锗材料中具有核自旋的稳定同位素丰度低(29Si: 4.67%, 73Ge: 7.76%)且可以通过同位素纯化进一步获得无核自旋的28Si和72Ge (或70Ge, 74Ge, 76Ge), 大幅提高退相干时间, 实现高保真度门操作的量子比特.
在上述的众多用于半导体量子计算的IV族材料中, Si/SiGe异质结二维电子气材料因具有高的迁移率及易于扩展和集成而备受关注, 近年来得到了快速的发展. 2016年, Takeda 等[18]基于非纯化的Si/SiGe异质结实现了电子自旋量子比特的电偶极自旋操控(EDSR), 门操控保真度达到99.6%. 基于同位素纯化的28Si/SiGe异质结, 该课题组在2018年将单比特门保真度进一步提高到大于99.9%[19]. 2022年, Xue 等[20]、Takeda 等[21]和Mills等[22]3个团队基于28Si/SiGe异质结分别实现了两比特门保真度大于99%. 而且, Philips 等[23]基于纯化的28Si/SiGe异质结实现了线性排列的六量子比特.
高质量材料是进一步提升比特性能的关键. 目前用于量子点量子计算的Si/SiGe二维异质结材料主要是通过化学气相沉积(CVD)的生长方法获得, 工业级CVD制备的材料迁移率可以达到4.2×105 cm2·V–1·s–1[24], 实验室用于制备量子点的材料迁移率记录值为6.5×105 cm2·V–1·s–1[25]. 分子束外延(MBE)是获得高迁移率异质结薄膜的主要手段, 基于MBE生长的 GaAs/AlGaAs异质结二维电子气的迁移率达到4.4×107 cm2·V–1·s–1[26]. 然而, 基于MBE技术生长的掺杂型Si/SiGe目前报道的最高迁移率还只有3.2×105 cm2·V–1·s–1[27], MBE外延非掺杂型Si/SiGe异质结研究工作也鲜有报道. 对于Si/SiGe异质结, 理论和实验研究表明界面台阶可以调节谷分裂能[28]. 分子束外延技术在界面调控具有显著优势, 将有助于研究更精细的谷态物理性质. 本研究利用MBE技术在Si基SiGe虚拟衬底上外延了Si/SiGe异质结结构, 并利用扫描隧道显微镜(STEM), 原子力显微镜(AFM)和X射线衍射(XRD) 等表征技术分析了材料的界面、表面形貌、组分及应变. 通过微纳加工技术制备霍尔器件并进行低温输运测量, 二维电子气迁移率达到20.21×104 cm2·V–1·s–1. 提取了渗透密度、载流子有效质量, 分析了载流子浓度和迁移率的幂指数关系和丁格比等. 本研究对MBE生长的Si/SiGe材料进行了系统的研究, 对进一步提升异质结材料迁移率及其在半导体量子点量子计算应用具有重要意义.
-
如图1(a)所示, 虚线框里的外延结构是MBE制备, 下面的硅基Si0.73Ge0.27虚拟衬底由北京超弦存储器研究院王桂磊研究员和中国科学院微电子研究所孔真真团队通过减压化学气相沉积(RPCVD)制备. 利用RPCVD在Si(001)衬底上渐变沉积Si1–xGex (x = 0—0.27)缓慢释放应变, 随后生长 固定Si0.73Ge0.27缓冲层, 采用化学机械抛光工艺(chemical mechanical polishing, CMP)提高表面平整度(均方根粗糙度为0.292 nm). 经过RCA标准清洗工艺去除表面杂质, 再使用5%氢氟酸漂洗1 min, 去除表面氧化层并形成氢键钝化的表面. 传入分子束外延设备进行后续外延生长, 生长腔室背景真空为6×10–11 mbar (1 bar =105 Pa). 首先将衬底温度升至400 ℃除气15 min, 再将衬底温度升至700 ℃使表面氢键脱附, 然后在500 ℃以Si 0.41 Å/s, Ge 0.15 Å/s的生长速率依次沉积400 nm Si0.73Ge0.27缓冲层, 12 nm应变Si层, 30 nm Si0.73Ge0.27间隔层以及2 nm Si盖层, 其中量子阱生长背景真空为1.5×10–9 mbar.
器件的制备方面, 利用激光直写和反应离子刻蚀将异质结材料加工成纵向长度为800 μm, 横向宽度为200 μm 的霍尔器件. 欧姆接触采用离子注入工艺, 将磷(P)元素注入到欧姆接触特定位置, 并在700 ℃温度下进行退火30 s激活. 通过电子束蒸发技术沉积Ti/Au层(10 nm/70 nm)作为金属电极, 通过原子层沉积技术生长30 nm Al2O3作为介电层. 最后, 通过电子束蒸发沉积Ti/Au层 (10 nm/70 nm)作为顶栅电极, 形成Hall-bar结构. Si/SiGe异质结霍尔器件的电输运测试是在最低温度可到250 mK的无液氦低温系统中完成.
-
对样品进行聚焦离子束(FIB)制样后, 使用STEM-HAADF对样品进行表征. 如图1(b)所示, 底部区域可以看到明显的CVD和MBE外延的界面. 界面上部是MBE制备的固定Ge含量的Si0.73Ge0.27薄膜层, 截面HAADF图像中没有观察到位错的存在, 表明薄膜具有高的晶体质量. 图1(b)顶部区域可以看到明显的Si量子阱(黑色)和Si0.73Ge0.27层的界面. 图1(c), (d)分别表示与高倍的STEM-HAADF图1(e)相对应的量子阱附近Si, Ge元素的能谱(EDS), 图像的明暗程度定性反映相对应元素分布量多少, 图中可以清晰看到界面处的明暗交界. 图1(f)是量子阱上界面高倍原子尺度成像, 观察到从应变Si层到SiGe间隔层界面厚度仅有几个原子层, 并且在图像上没有看到缺陷信息, 说明生长的量子阱结构界面清晰, 质量高. 量子阱中硅原子的排列和Si0.73Ge0.27薄膜层中原子排列完全共格, 处于完全应变状态. 实验同时根据误差函数拟合[29]硅含量变化的EDX数据, 量子阱上界面特征长度为0.53 nm, 定量验证了外延制备的原子级尖锐的Si/SiGe异质结界面.
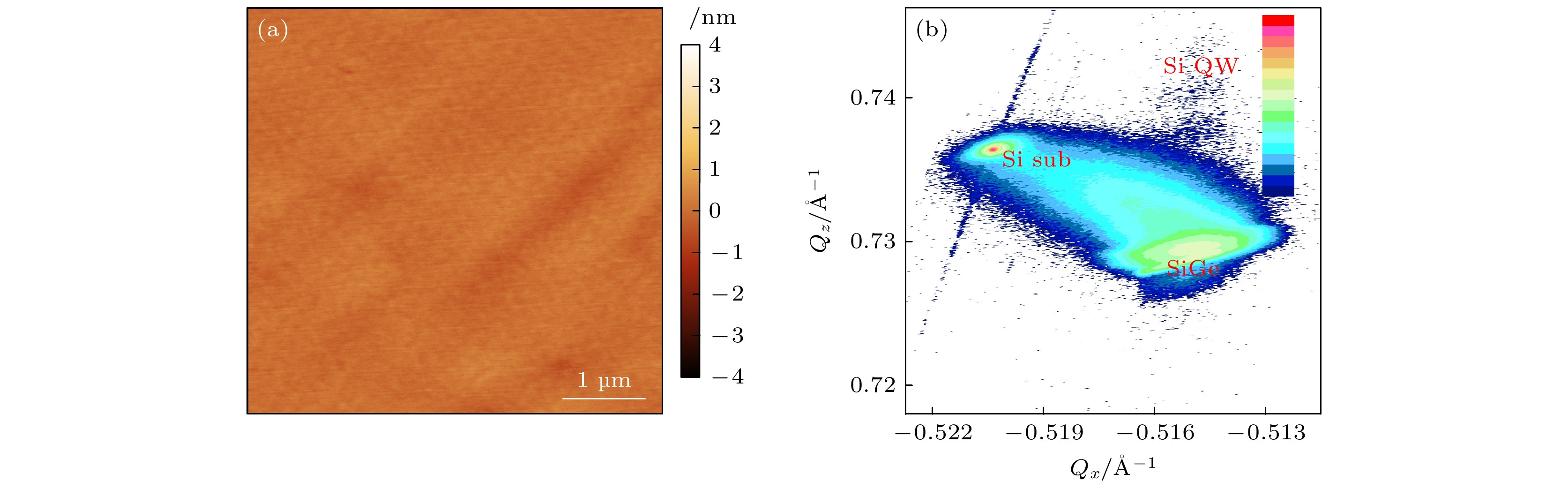
图2(a)展示了材料表面5 μm×5 μm的AFM图像. 样品表面起伏小, 平整度高, 其均方根粗糙度(RMS roughness)仅为0.44 nm. 图2(b)是沿着
$ \text{(}\bar{2}, \bar{2}\text{, 4)} $ 方向对材料进行X射线衍射倒易空间图像(XRD-RSM), 横坐标Qx纵坐标Qz分别是衍射矢量在面内、面外的分量. 从图像可以分析材料生长结构为硅衬底逐渐渐变到锗含量为0.27的Si0.73Ge0.27薄膜层. 分子束外延的固定含量的SiGe薄膜层和CVD的SiGe薄膜层信号重合, 两者锗含量一致. 在Si0.73Ge0.27信号峰的上方, 有微弱的硅量子阱信号峰. 多个信号峰的出现是由于X射线信号在量子阱界面引起了干涉效应. 硅量子阱处于Si0.73Ge0.27薄膜信号峰正上方, 表明处于面内完全拉应变状态, 应变值为1.03%. -
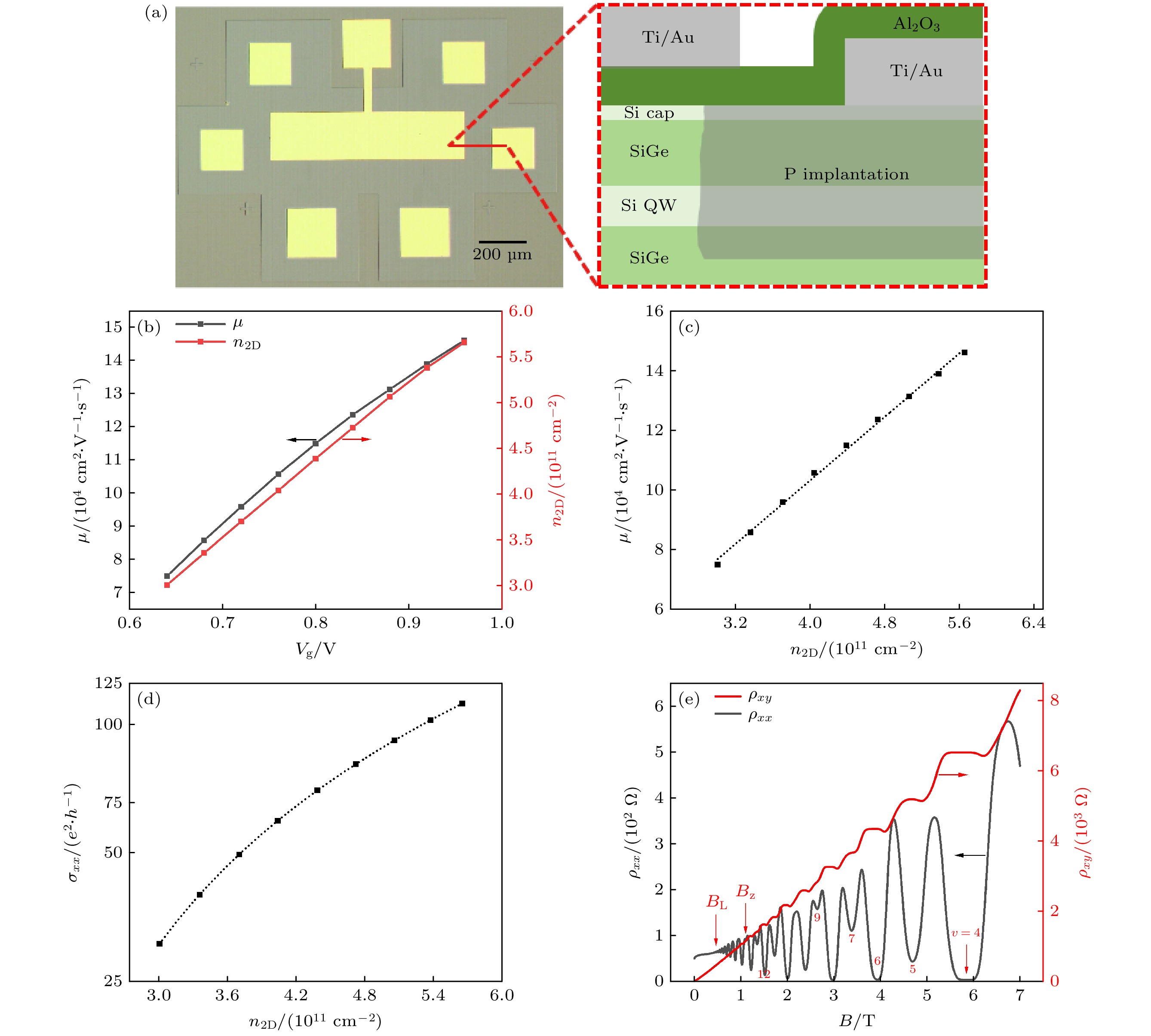
低温电学测量可通过调节栅极电压来调节硅量子阱沟道中的载流子浓度. 图3(a)是霍尔器件的光显图及截面示意图, 源漏极分别在器件的两侧. 截面示意图从左到右显示的是光显图中红线代表的从栅极到漏极的截面结构. 图3(b)显示了250 mK的温度下载流子浓度n2D和迁移率μ随栅极电压Vg变化时的曲线. 根据Vg-n2D斜率拟合得出电容为4.0133×10–11 F/cm2, 而根据平行板电容器模型计算电容为4.5013×10–11 F/cm2, 实际结果与理论结果基本一致. 250 mK温度下μ随着n2D变化的关系如图3(c)所示, 根据载流子浓度和迁移率关系的幂律函数公式
$ \mu \propto {n}_{2{\mathrm{D}}}^{\alpha } $ 拟合, 幂指数拟合值α = 1.026. 数值介于背景散射对应理论值0.5和氧化物/半导体界面远端散射对应理论值1.5中间, 这表明3.2×1011—5.6×1011 cm–2范围内的载流子迁移率主要受背景散射和半导体/氧化物界面散射共同影响[30]. 图3(d)是以电导率σxx, 载流子浓度n2D为坐标轴的图像, 黑点是实际σxx与n2D对应的数据点, 虚线是根据[31]渗透理论$ {\sigma }_{xx}\propto {({n}_{2{\mathrm{D}}}-{n}_{{\mathrm{p}}})}^{1.31} $ 拟合出的曲线. 由公式拟合得出[32]渗透密度np = 1.465×1011 cm–2. 进一步增大栅极电压到2 V, 250 mK温度条件下测量ρxx, ρxy随着B变化的关系, 结果见图3(e). 可以观察到经典的SdH振荡(Shubnikov de Haas oscillations), 在B = 0.3745 T时是SdH起振点, B = 1.104 T时出现了塞曼分裂点. 计算得到载流子浓度为6.265×1011 cm–2, 载流子迁移率峰值为20.21 × 104 cm2·V–1·s–1.进一步, 通过下面的公式拟合SdH振荡的热阻尼曲线, 可以提取电子的有效质量:
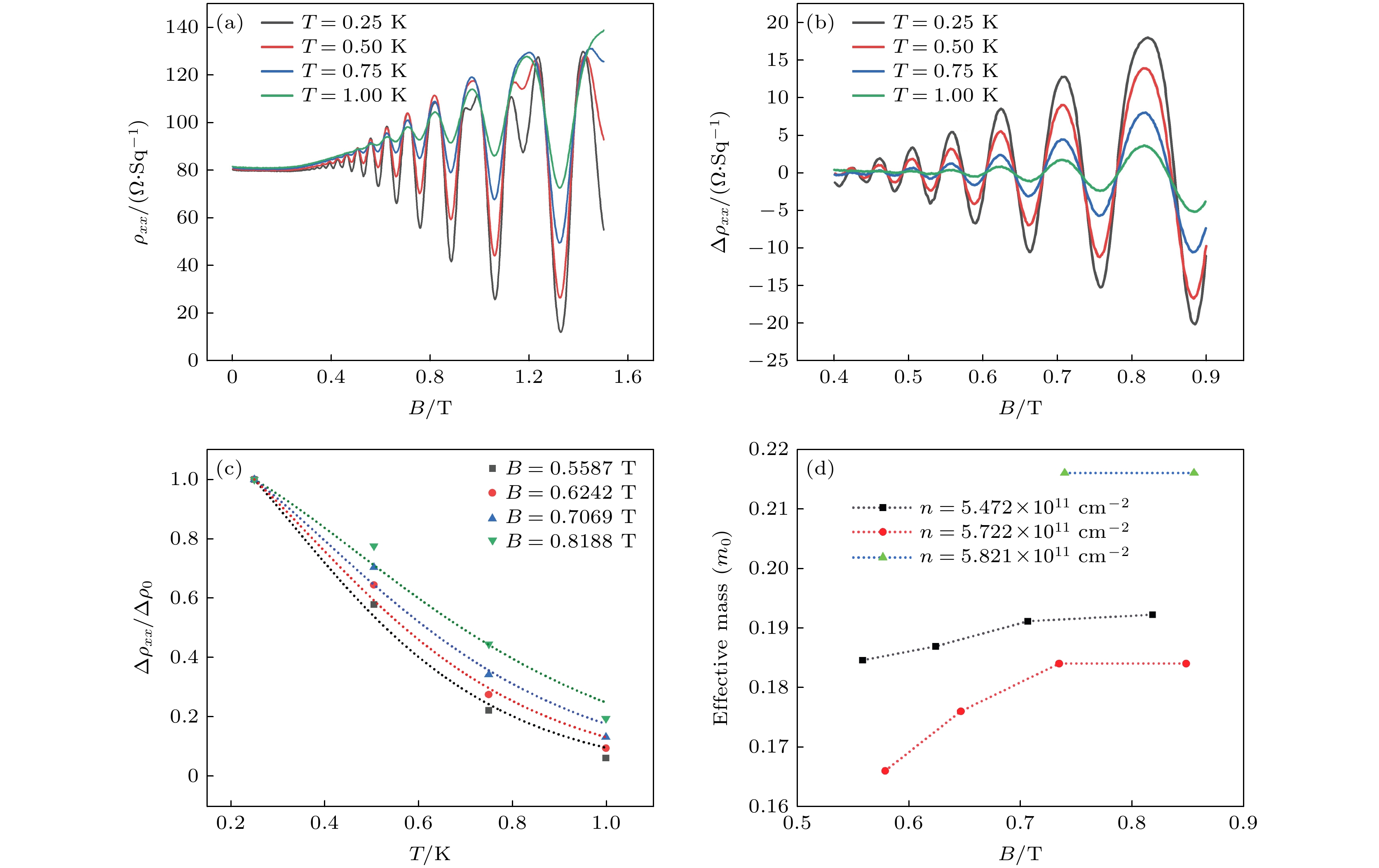
式中, Δρ0是去除背景噪声后场强为零时的电阻率, T0是测量振荡时的最低温度, 这里T0 = 0.25 K, 式中
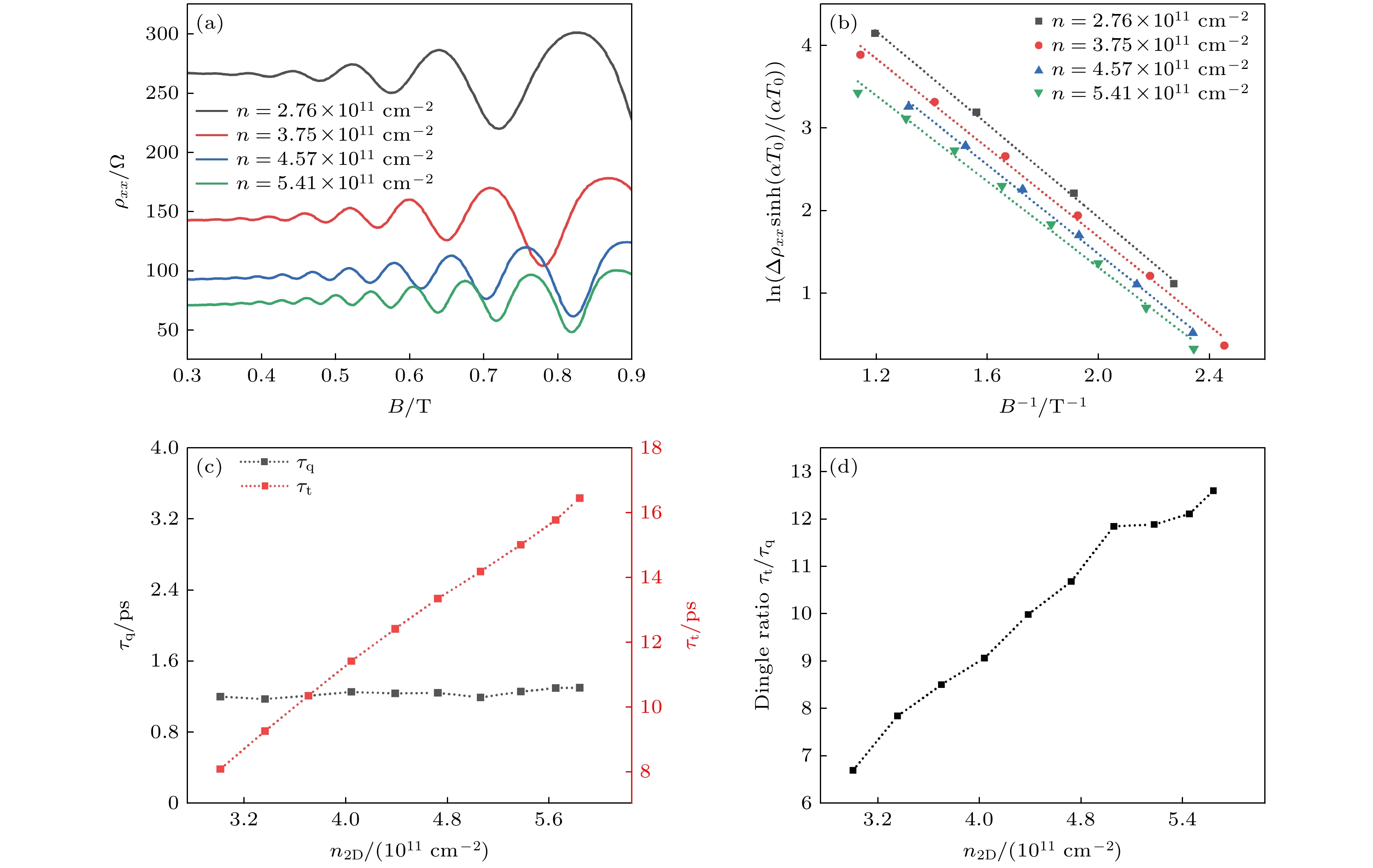
$ \varphi =\dfrac{2{{\mathrm{\pi }}}^{2}{k}_{{\mathrm{B}}}{m}^{*}}{\hslash eB} $ , 其中$ {k}_{{\mathrm{B}}} $ 是玻尔兹曼常数,$\hbar $ 是约化的普朗克常量, e是电子电荷. 图4(a)显示载流子浓度为5.472×1011 cm–2时不同温度条件下的SdH振荡曲线, 图4(b)则是去除背景噪音[33,34]后不同温度下的SdH振荡曲线. 图4(c)是Δρxx/Δρ0在不同磁场强度的条件下随着温度变化的数据点, 虚线是根据拟合得到的曲线. 根据拟合曲线计算在该磁场强度下的有效质量m*. 通过变换栅极电压改变载流子浓度, 测量不同载流子浓度下有效质量m* 随磁场的变化(图4(d)). 计算得到有效质量变化范围为0.17m0—0.21m0, 和文献中[34]基本一致. 有效质量数值低, 表明电子主要填充在因应变导致硅六重简并分裂后的二重简并态的能谷处.图5(a)显示T = 0.25 K时, 不同载流子浓度在低磁场下的SdH振荡曲线. 载流子浓度越高, 振荡周期越小. 由图4(d)可知, 二维电子气有效质量在0.17m0—0.21m0, 有效质量只在较小范围内波动, 可以推断出有效质量的变化对计算量子寿命τq的影响很小. 假设有效质量m*是一个定值[34], 大小为0.21 m0, 根据以上假设得到
$\ln \Big(\dfrac{\Delta \rho_{xx} {\rm sinh}(\alpha T_0)}{\alpha T_0}\Big) $ 随着1/B变化的曲线图5(b). 通过拟合得到图5(b)中的斜率k, 计算出量子寿命τq. 根据公式$ {\tau }_{{\mathrm{t}}} = \mu {m}^{*}/e $ 可以获得载流子的输运寿命τt. 如图5(c)所示, τq几乎不随载流子浓度变化, 而τt随着载流子浓度的升高不断变大[35]. 根据图5(c)可以得到丁格比随着载流子浓度变化(图5(d)). 随着载流子浓度升高, 丁格比逐渐增大. 丁格比在7—13之间, 表明二维电子气载流子迁移率主要受背景杂质散射和半导体/氧化物界面散射影响[36]. -
研究通过分子束外延技术在Si 基SiGe虚拟衬底上外延制备了表面高平整度、原子级尖锐界面的Si/SiGe异质结结构, 界面特征长度仅为0.53 nm. 低温电学测量显示载流子浓度6.265×1011 cm–2时, 迁移率达到20.21×104 cm2·V–1·s–1, 渗透密度为1.465×1011 cm–2. 载流子浓度和迁移率的幂指数关系(1.026)和丁格比(7—13)表明目前载流子主要受到背景散射和氧化物/半导体界面的散射. 研究为进一步优化材料、研究更精细的谷态物理性质和后续制备量子点量子计算器件提供了基础.
非掺杂型Si/SiGe异质结外延与表征
Epitaxy and characterization of undoped Si/SiGe heterojunctions
-
摘要: 以自旋为编码单元的硅基半导体量子计算与传统微电子工艺兼容, 易拓展且可以同位素纯化提高退相干时间, 因而备受关注. 本研究工作通过分子束外延生长了高质量非掺杂型Si/SiGe异质结并测试了二维电子气迁移率. 球差电镜观察到原子级尖锐界面, 原子力显微镜表征显示其表面均方根粗糙度仅为0.44 nm, 低温下迁移率达到20.21×104 cm2·V–1·s–1. 不同栅压下载流子浓度和迁移率的幂指数为1.026, 材料丁格比值在7—12之间, 表明载流子主要受到背景杂质散射和半导体/氧化物的界面散射.
-
关键词:
- Si/SiGe异质结 /
- 二维电子气 /
- 霍尔迁移率 /
- 硅基量子计算
Abstract: Silicon-based semiconductor quantum computing with spin as the encoding unit is compatible with traditional microelectronic processes, easy to expand, and can improve isotope purification and decoherence time, thus attracting much attention. There are fewer reports on the work related to undoped Si/SiGe heterostructures grown by molecular beam epitaxy than those on chemical vapor deposition. An undoped Si/SiGe heterostructure is grown by molecular beam epitaxy (see the attached figure below). The results from scanning transmission electron microscopy and energy-dispersive spectroscopy mapping show an atomic-scale interface with a characteristic length of 0.53 nm. The surface root-mean-square roughness measured by atomic force microscope is 0.44 nm. The X-ray diffraction data show that the Si quantum well is fully strained and the in-plane strain is 1.03%. In addition, the performance of the two-dimensional electron gas is evaluated by low-temperature Hall measurements, which are conducted in the Hall-bar shaped field-effect transistor. The peak mobility is 20.21×104 cm2·V–1·s–1 when the carrier density is about 6.265×1011 cm–2 at 250 mK. The percolation density is 1.465×1011 cm–2. The effective mass of the two-dimensional electron gas is approximately 0.19m0. The power exponential between carrier density and mobility at different gate voltages is 1.026, and the Dingle ratio of the two-dimensional electron gas is in a range of 7–12, indicating that the electrons are scattered by background impurities and semiconductor/oxide interfaces charges. The atomically sharp interface of Si/SiGe heterostructures created by molecular beam epitaxy is beneficial for studying the valley physics properties in silicon. The structural and transport characterizations in this paper lay the foundation for the optimization of Si-based semiconductor quantum dot quantum computing materials. -

-
图 1 (a) 硅基Si/SiGe异质结结构示意图; (b) MBE 制备SiGe/Si QW/SiGe/Si 结构的 STEM-HAADF图; (c), (d) 量子阱附近Si, Ge元素的EDS谱; (e) SiGe/Si/SiGe 高倍STEM-HAADF图像; (f) Si 量子阱上界面的STEM-HAADF原子图像
Figure 1. (a) Schematic of Si/SiGe heterostructure on Si (001); (b) STEM-HAADF of SiGe/Si QW/SiGe/Si heterostructure grown by MBE; (c), (d) EDS of Si and Ge distribution around quantum well; (e) magnified STEM-HADDF of SiGe/Si/SiGe; (f) atomic-scale STEM-HADDF image of the Si/SiGe interface.
图 3 (a) 霍尔器件的光显图和截面示意图; (b) 载流子浓度和载流子迁移率随栅极电压变化的曲线; (c) 载流子迁移率与载流子浓度的对应关系曲线; (d) 纵向电导率随载流子浓度变化的关系(虚线是根据渗透理论拟合的曲线); (e) 栅极电压为2 V时的纵向电阻率和横向电阻率随磁场的变化
Figure 3. (a) Optical microscope diagram and cross-sectional schematic view of Hall device; (b) carrier density and mobility as a function of the gate voltage Vg; (c) density-dependent mobility; (d) density-dependent conductivity, the dashed line is a fit based on the percolation theory; (e) transverse Hall resistivity and longitudinal resistivity as a function of the magnetic field.
图 4 (a) 不同温度下SdH振荡曲线; (b) 不同温度下去除噪音的SdH振荡曲线; (c) Δρxx/Δρ0在不同磁场强度下随温度的变换曲线; (d) 不同载流子浓度下有效质量m*随磁场B的变化
Figure 4. (a) Longitudinal resistivity as a function of magnetic field for different temperatures; (b) oscillation amplitude of the longitudinal resistivity as a function of the magnetic field; (c) Δρxx/Δρ0 for different temperatures, different colors represent different magnetic fields from 0.55 T to 0.82 T, dashed lines are the fits for extracting effective mass; (d) effective mass as a function of the magnetic field at various densities.
图 5 (a) 不同载流子浓度下的Sdh振荡曲线; (b) 不同载流子浓度下
$\ln \Big(\dfrac{\Delta \rho_{xx} {\rm sinh}(\alpha T_0)}{\alpha T_0}\Big) $ 随1/B的变化曲线; (c) 量子寿命τq, τt随着载流子浓度变化的曲线; (d) 丁格比(τq/τt)随载流子浓度的变化曲线Figure 5. (a) Longitudinal resistivity as a function of magnetic field under various carrier densities; (b) the variation curve of
$\ln \Big(\dfrac{\Delta \rho_{xx} {\rm sinh}(\alpha T_0)}{\alpha T_0}\Big) $ with 1/B under different carrier densities; (c) τq and τt at different carrier densities; (d) carrier density-dependent Dingle plot (τq/τt). -
[1] 王宁, 王保传, 郭国平 2022 物理学报 71 230301 doi: 10.7498/aps.71.20221900 Wang N, Wang B C, Guo G P 2022 Acta Phys. Sin. 71 230301 doi: 10.7498/aps.71.20221900 [2] Zhang J J, Li H O, Guo G P 2024 Sci. Sin. Inf. 54 102 doi: 10.1360/SSI-2023-0333 [3] 张结印, 高飞, 张建军 2021 物理学报 70 217802 doi: 10.7498/aps.70.20211492 Zhang J Y, Gao F, Zhang J J 2021 Acta Phys. Sin. 70 217802 doi: 10.7498/aps.70.20211492 [4] Petta J, Johnson A, Taylor J, Laird E, Yacoby A, Lukin M, Marcus C, Hanson M, Gossard A 2005 Science 309 2180 doi: 10.1126/science.1116955 [5] Yoneda J, Otsuka T, Nakajima T, Takakura T, Obata T, Pioro-Ladrière M, Lu H, Palmstrøm C J, Gossard A C, Tarucha S 2014 Phys. Rev. Lett. 113 267601 doi: 10.1103/PhysRevLett.113.267601 [6] Nadj-Perge S, Frolov S M, Bakkers E P, Kouwenhoven L P 2010 Nature 468 1084 doi: 10.1038/nature09682 [7] van den Berg J W G, Nadj-Perge S, Pribiag V S, Plissard S R, Bakkers E P A M, Frolov S M, Kouwenhoven L P 2013 Phys. Rev. Lett. 110 066806 doi: 10.1103/PhysRevLett.110.066806 [8] Li R, Hudson F E, Dzurak A S, Hamilton A R 2015 Nano Lett. 15 7314 doi: 10.1021/acs.nanolett.5b02561 [9] Borselli M G, Eng K, Croke E T, Maune B M, Huang B, Ross R S, Kiselev A A, Deelman P W, Alvarado-Rodriguez I, Schmitz A E, Sokolich M, Holabird K S, Hazard T M, Gyure M F, Hunter A T 2011 Appl. Phys. Lett. 99 063109 doi: 10.1063/1.3623479 [10] Hendrickx N W, Lawrie W I L, Russ M, van Riggelen F, de Snoo S L, Schouten R N, Sammak A, Scappucci G, Veldhorst M 2021 Nature 591 580 doi: 10.1038/s41586-021-03332-6 [11] Madzik M T, Asaad S, Youssry A, Joecker B, Rudinger K M, Nielsen E, Young K C, Proctor T J, Baczewski A D, Laucht A, Schmitt V, Hudson F E, Itoh K M, Jakob A M, Johnson B C, Jamieson D N, Dzurak A S, Ferrie C, Blume-Kohout R, Morello A 2022 Nature 601 348 doi: 10.1038/s41586-021-04292-7 [12] 高飞, 冯琦, 王霆, 张建军 2020 物理学报 69 028102 doi: 10.7498/aps.69.20191407 Gao F, Feng Q, Wang T, Zhang J J 2020 Acta Phys. Sin. 69 028102 doi: 10.7498/aps.69.20191407 [13] Xu G, Gao F, Wang K, Zhang T, Liu H, Cao G, Wang T, Zhang J J, Jiang H W, Li H O, Guo G P 2020 Appl. Phys. Express 13 065002 doi: 10.35848/1882-0786/ab8b6d [14] Xu G, Li Y, Gao F, Li H O, Liu H, Wang K, Cao G, Wang T, Zhang J J, Guo G C, Guo G P 2020 New J. Phys. 22 083068 doi: 10.1088/1367-2630/aba85a [15] Wang K, Xu G, Gao F, Liu H, Ma R L, Zhang X, Wang Z, Cao G, Wang T, Zhang J J, Culcer D, Hu X, Jiang H W, Li H O, Guo G C, Guo G P 2022 Nat. Commun. 13 206 doi: 10.1038/s41467-021-27880-7 [16] Watzinger H, Kukučka J, Vukušić L, Gao F, Wang T, Schäffler F, Zhang J J, Katsaros G 2018 Nat. Commun. 9 3902 doi: 10.1038/s41467-018-06418-4 [17] Stano P, Loss D 2022 Nat. Rev. Phys. 4 672 doi: 10.1038/s42254-022-00484-w [18] Takeda K, Kamioka J, Otsuka T, Yoneda J, Nakajima T, Delbecq M R, Amaha S, Allison G, Kodera T, Oda S, Tarucha S 2016 Sci. Adv. 2 e1600694 doi: 10.1126/sciadv.1600694 [19] Yoneda J, Takeda K, Otsuka T, Nakajima T, Delbecq M R, Allison G, Honda T, Kodera T, Oda S, Hoshi Y, Usami N, Itoh K M, Tarucha S 2018 Nat. Nanotechnol. 13 102 doi: 10.1038/s41565-017-0014-x [20] Xue X, Russ M, Samkharadze N, Undseth B, Sammak A, Scappucci G, Vandersypen L M K 2022 Nature 601 343 doi: 10.1038/s41586-021-04273-w [21] Takeda K, Noiri A, Nakajima T, Kobayashi T, Tarucha S 2022 Nature 608 682 doi: 10.1038/s41586-022-04986-6 [22] Mills A R, Guinn C R, Gullans M J, Sigillito A J, Feldman M M, Nielsen E, Petta J R 2022 Sci. Adv. 8 5 doi: DOI:10.1126/sciadv.abn5130 [23] Philips S G J, Mądzik M T, Amitonov S V, de Snoo S L, Russ M, Kalhor N, Volk C, Lawrie W I L, Brousse D, Tryputen L, Wuetz B P, Sammak A, Veldhorst M, Scappucci G, Vandersypen L M K 2022 Nature 609 919 doi: 10.1038/s41586-022-05117-x [24] Paquelet Wuetz B, Bavdaz P L, Yeoh L A, Schouten R, van der Does H, Tiggelman M, Sabbagh D, Sammak A, Almudever C G, Sebastiano F, Clarke J S, Veldhorst M, Scappucci G 2020 NPJ Quantum Inf. 6 43 doi: 10.1038/s41534-020-0274-4 [25] Mi X, Cady J V, Zajac D M, Stehlik J, Edge L F, Petta J R 2017 Appl. Phys. Lett. 110 043502 doi: 10.1063/1.4974536 [26] Chung Y J, Villegas Rosales K A, Baldwin K W, Madathil P T, West K W, Shayegan M, Pfeiffer L N 2021 Nat. Mater. 20 632 doi: 10.1038/s41563-021-00942-3 [27] Weitz P, Haug R J, von Klitzing K, Schäffler F 1996 Surf. Sci. 361-362 542 doi: 10.1016/0039-6028(96)00465-7 [28] Goswami S, Slinker K A, Friesen M, McGuire L M, Truitt J L, Tahan C, Klein L J, Chu J O, Mooney P M, van der Weide D W, Joynt R, Coppersmith S N, Eriksson M A 2007 Nat. Phys. 3 41 doi: 10.1038/nphys475 [29] Zhang D D, Lu J, Liu Z, Wan F S, Liu X Q, Pang Y Q, Zhu Y P, Cheng B W, Zheng J, Zuo Y H, Xue C L 2022 Appl. Phys. Lett. 121 6 [30] Laroche D, Huang S H, Nielsen E, Chuang Y, Li J Y, Liu C W, Lu T M 2015 AIP Adv. 5 107106 doi: 10.1063/1.4933026 [31] Tracy L A, Hwang E H, Eng K, Ten Eyck G A, Nordberg E P, Childs K, Carroll M S, Lilly M P, Das Sarma S 2009 Phys. Rev. B 79 235307 doi: 10.1103/PhysRevB.79.235307 [32] Kim J S, Tyryshkin A M, Lyon S A 2017 Appl. Phys. Lett. 110 123505 doi: 10.1063/1.4979035 [33] Coleridge P T 1990 Semicond. Sci. Technol. 5 961 doi: 10.1088/0268-1242/5/9/006 [34] Mi X, Hazard T M, Payette C, Wang K, Zajac D M, Cady J V, Petta J R 2015 Phys. Rev. B 92 035304 doi: 10.1103/PhysRevB.92.035304 [35] Wang K, Li H O, Luo G, Zhang X, Jing F M, Hu R Z, Zhou Y, Liu H, Wang G L, Cao G, Jiang H W, Guo G P 2020 Europhys. Lett. 130 27001 doi: 10.1209/0295-5075/130/27001 [36] Monroe D, Xie Y H, Fitzgerald E A, Silverman P J, Watson G P 1993 J. Vac. Sci. Technol. B: Microelectron. Nanometer Struct.—Process. Meas. Phenom. 11 1731 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: