-
阿秒脉冲由于其超短的持续时间, 成为分析测量原子或分子内部电子超快动力学的有力工具[1]. 它在自然时间尺度上提供了更高的测量精度, 为观察和控制原子分子中电子运动奠定了基础. 近年来, 随着激光技术的快速发展, 出现了多种产生阿秒脉冲的方法[2–4], 其中通过近红外(NIR)飞秒激光与气体相互作用形成极紫外(XUV)波段高次谐波(HHG)驱动的阿秒脉冲合成方案被认为是目前最成熟的方法[5–7]. 这种方法成功产生并测量了阿秒脉冲串(attosecond pulse trains, APTs)和孤立阿秒脉冲(isolated attosecond pulses, IAPs), 标志着阿秒科学成为新的前沿研究领域[8–11]. 由于传统电子学手段所能测量的时间尺度局限于皮秒量级, 不能直接获取阿秒脉冲的时域脉冲信息, 因此实验上采用了测量阿秒脉冲与飞秒激光共同作用的光电子能谱的间接方式. 对于孤立阿秒脉冲, 通常采用的方案是阿秒条纹相机(attosecond streak camera)[12], 而测量阿秒脉冲串的方案被称为双光子跃迁干涉重构阿秒拍频(reconstruction of attosecond beating by interference of two-photon transition, RABBITT)技术[13,14]. 这两种方法都基于阿秒泵浦-飞秒探测方案. 其原理是阿秒脉冲电离气体喷嘴中惰性气体原子的价电子, 飞秒探测脉冲对释放的电子进行调制, 导致光电子能谱随阿秒脉冲和飞秒脉冲的时间延迟发生周期性变化, 区别在于飞秒激光的强度不同. 对于阿秒条纹相机来说, 惰性气体原子的电子吸收一个XUV光子后电离, 其电子波包的初始动量携带阿秒脉冲频率信息, 不同初始动量的光电子电离的先后时间携带了阿秒脉冲的相位信息, 而末动量光电子的计数携带了阿秒脉冲的强度信息, 这些信息反映在经过飞秒脉冲电场调制后的光电子谱中. 对于RABBITT来说, 阿秒脉冲串产生的光电子跨越了飞秒激光的不同半周期, 这导致光电子的能谱分布在不同谐波阶次两边产生边带, 并随延时变化形成稳定的干涉. 同一个边带的电子来自相邻高次谐波阶次的光电子吸收或释放了一个NIR光子后相干叠加产生, 因此RABBITT是典型的双光子过程.
阿秒脉冲的时域信息可以从阿秒条纹相机或RABBITT方法得到的能谱图中提取, 但方法不同. 阿秒条纹相机方法的相位通过反演程序迭代提取[15–19]; 而RABBITT方法由于其干涉性质, 可以直接从边带的振荡频率提取不同高次谐波阶次的相位差, 也可以结合具有不同近似的迭代算法反演阿秒脉冲串的完整相位, 从而对其进行表征. 从实验角度来看, 阿秒脉冲串的产生难度要比孤立阿秒脉冲小得多, 因此常使用阿秒脉冲串研究电子的动力学. 由于RABBITT实验本身就是泵浦探测过程, 其能谱图中同样也包含了被电离原子中的电子动力学信息, 可以用来研究自旋-轨道作用、双电离过程和共振等[20–23]. 例如, 通过提取相位信息, 可以得到不同能级电子电离的时间延时[24], 在这种情况下, 需要从RABBITT能谱图中提取更精细的相位信息.
本文主要研究了阿秒脉冲串的产生、测量和相关表征. 通过自主设计和搭建的飞秒钛宝石再生放大器来产生高次谐波, 并利用共线阿秒极紫外束线进行RABBITT实验[25–27]. 在阿秒脉冲的时域重建和表征方面, 首先采用RABBITT边带相位方法得到高次谐波相位差, 从而直接完成了阿秒脉冲串的重建. 同时, 还使用了阿秒重建频率分辨光学开关法(complete reconstruction of attosecond burst, FROG-CRAB)[15]和扩展层析重建迭代引擎(extended phase retrieval and iterative engine, ePIE)算法[28]来完整地重建阿秒脉冲串的相位信息. 除此之外, 还尝试使用遗传算法来提取相位信息, 并对不同的方法进行比较和讨论. 本工作对进一步进行电子动力学测量并解释其演化规律具有重要的指导意义.
-
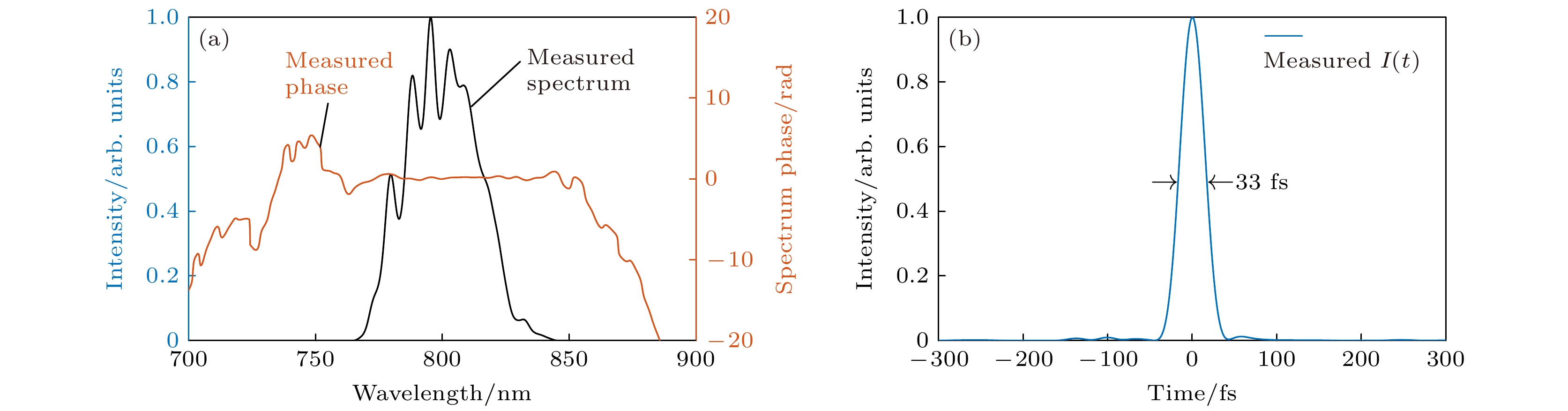
本实验采用一台自行搭建的钛宝石啁啾脉冲放大器作为光源. 与商业放大器相比, 自建放大器能够根据需求灵活调整结构, 例如在再生放大器谐振腔中添加光阑以得到更好的光束质量, 以及通过可编程声光色散滤波器进行光谱预整形以补偿增益窄化, 同时精密控制其光谱相位, 以得到更好的脉冲时间质量等. 自建振荡器输出15 fs种子脉冲, 经过再生放大后输出脉冲能量2 mJ、脉冲宽度33 fs、重复频率1 kHz的飞秒激光[26]. 通过Wizzler (Fastlite Inc.)得到的光谱与脉冲的测量数据如图1所示.
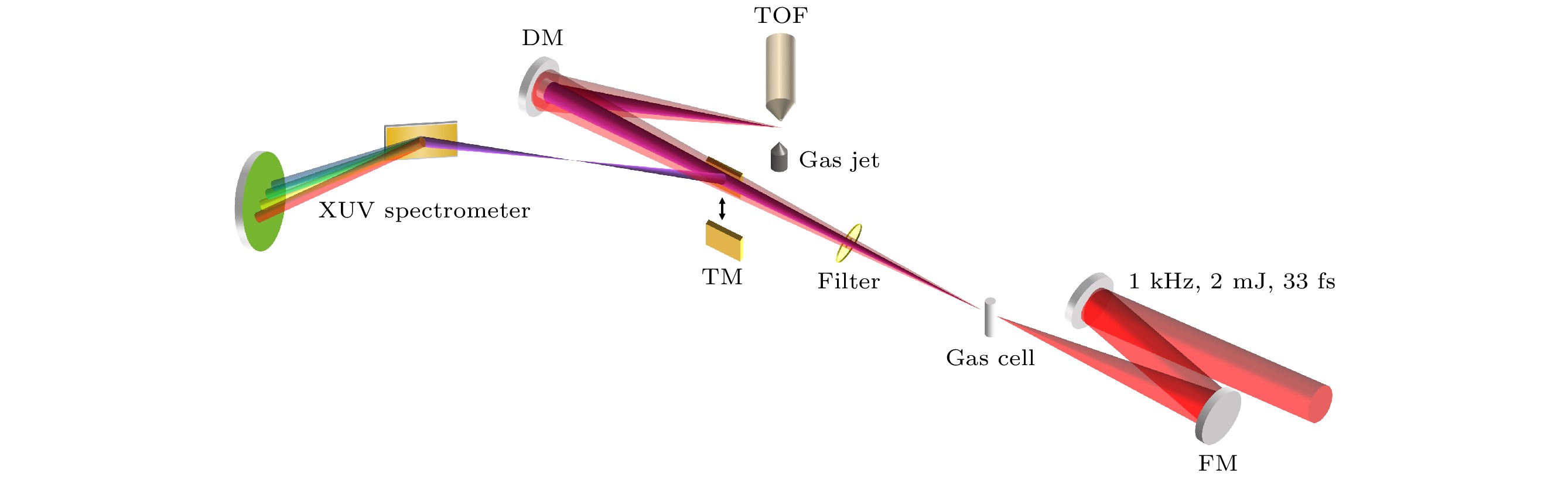
由于高次谐波的频谱范围在极紫外和软X射线波段, 产生的高能光子无法在空气中传播, 所以需要在真空中进行相关实验. 实验所用的自行搭建的共线阿秒脉冲产生和测量束线[25–27]结构如图2所示, 后续实验均在真空腔内完成. 如图2所示, 实验时飞秒激光作为驱动光源通过f = 300 mm凹面银镜聚焦到由铜管制成的厚度为0.5 mm 的气体靶上(gas cell), 焦点处的峰值功率约为2.7×1015 W/cm2. 其中气体靶充入背压40 kPa左右的氖气, 通过优化气体靶相对驱动激光焦点的位置、入射口处光阑的大小、以及气压的大小来改变气体靶中高次谐波产生过程相位匹配条件, 从而在XUV光谱仪上观察到强度较强的高次谐波信号. 经过傅里叶变换可知这种分立的光谱在时域上正是阿秒脉冲串. 然后驱动光和阿秒脉冲串共线穿过电动光阑进入测量腔, 腔内有镀金的轮胎镜(TM)、内外镜(DM)、气体喷嘴(gas jet)、金属膜(filter)和飞行时间谱仪(TOF). 金属膜用于过滤和控制驱动光强度, 还可以补偿阿秒脉冲的正色散部分, 并通过金属膜的截止边对XUV光谱仪进行标定. 通过移动轮胎镜的位置可以将光导入后面的XUV光谱仪进行光谱测量, 或者在测量腔内进行RABBITT实验. 在TOF口处放置惰性气体喷 嘴, 内外镜分别将阿秒和飞秒脉冲聚焦在喷嘴上方, 产生的光电子经TOF收集并记录其飞行时间和计数. 通过调节内外镜的相对位置可以改变阿秒脉冲和飞秒激光的延时, 扫描延时并测量不同延时下的光电子谱, 得到RABBITT实验的光电子能谱图.
-
在 RABBITT 光电子谱中, 边带作为泵浦-探测延时的振荡函数可以表示为[14]
其中
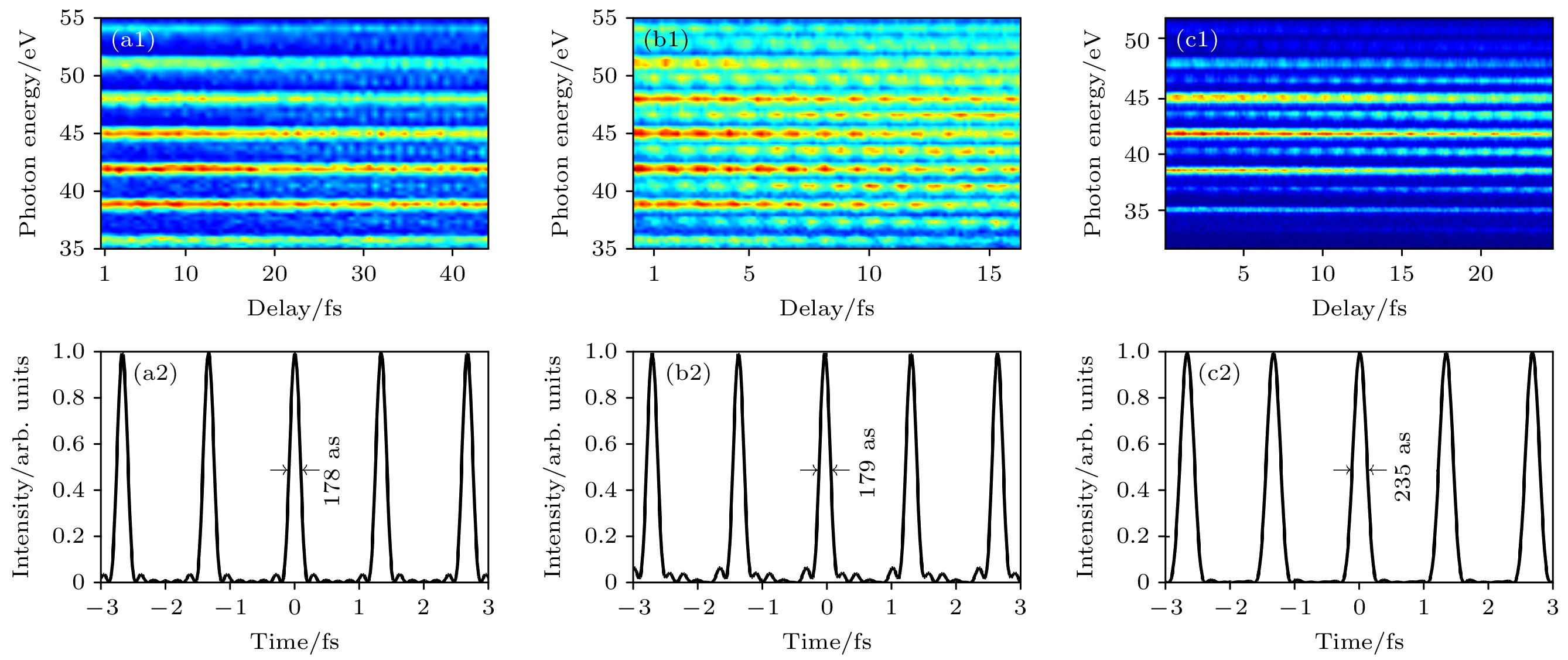
$ \alpha $ 和$ \beta $ 是与$ \tau $ 无关的强度项,$ \tau $ 是阿秒脉冲与红外飞秒脉冲的时间延时.$ 2\omega {\tau }_{2 q} = {{\Delta }}{\phi }_{2 q} = {\phi }_{2 q+1} - {\phi }_{2 q-1} $ 表示相邻谐波$ {{\mathrm{H}}}_{2 q-1} $ 和$ {{\mathrm{H}}}_{2 q+1} $ 之间的相位差, 与边带中不同量子路径的相关跃迁振幅相位差相关.$ {\tau }_{\theta }={{\Delta }}{\theta }_{2 q}/2\omega $ 是电离过程中原子散射相位${\Delta } {\theta }_{2 q}$ 导致的固有时间延时[29]. 这个时间延时由两个部分组成: Wigner时间延时$ {\tau }_{\rm W}$ 和连续态-连续态时间延时$ {\tau }_{{\mathrm{C}}{\mathrm{C}}} $ [24], Wigner时间延时$ {\tau }_{{\mathrm{W}}} $ 衡量的是电子波包在短程库仑势影响下相对于具有相同动能的自由电子所经历的群延时. 而连续态-连续态时间延时$ {\tau }_{{\mathrm{C}}{\mathrm{C}}} $ 对应在红外探测脉冲影响下两个连续电子态之间产生的额外量子跃迁[30]. 在阿秒脉冲串反演时, 通常倾向于选择产生于远离共振区、电离自同一能级的电子的边带, 并且光电离时间延时的测量往往采用飞行时间谱仪等角度积分技术, 所以在一个特定的能量范围内, 相对于高次谐波本身的相位, 这些原子相位差通常是可以被忽略的. 采用傅里叶变换分析来确定两个边带之间的相对相位$ {{\Delta }}{\phi }_{2 q} $ . 将各级边带分别纵向积分得到的原始振荡图, 快速傅里叶变换后获得一阶信号的频率和相位, 再通过逆傅里叶变换得到去除噪声后的边带振荡图, 从中提取边带相位差就可以知道相应的高次谐波之间的相位差. 设最低阶的高次谐波相位为0, 则可以知道其他高次谐波的相位, 再结合高次谐波的强度就可以反演出阿秒脉冲串. 通过改变延时的步长进行实验, 一共测到了3组RABBITT能谱图. 其中第1组的延时步长为66.7 as, 总共扫描了66步; 第2组步长设定为16.7 as, 总共扫描了99步; 第3组步长设定为13.3 as, 总共扫描了184步. 此外前两组实验中TOF的透镜电压设置为300 V, 而第3组实验的TOF的透镜电压设置为150 V, 以增加信号的对比度. 通过上述方法重建的阿秒脉冲串结构如图3所示.虽然通过边带提取相位差可以直接重建阿秒脉冲串, 但这个方法只能估计高次谐波各阶次中心, 也就是2q+1处的相位, 而实际中各阶次中心附近的相位仍对时域脉冲的形貌有贡献, 因此通过这个方法重建的脉冲串并不能代表实际的形貌. 在泵浦-探测实验中, 有时需要知道泵浦光或者探测光的真实时域形貌, 才能在实验数据中区分电子动力学信息和阿秒脉冲本身的信息, 此时需要对阿秒脉冲进行时域重建. 目前已经有多种算法用于孤立阿秒脉冲的重建, 比如FROG-CRAB[15], PROOF[17], VTGPA[19]等, 这类算法通过迭代可以反演出阿秒脉冲和提供延时扫描的飞秒脉冲的信息, 也可以用来反演RABBITT, 进行阿秒脉冲串的重建. 但需要注意的是这类算法要求实验数据尽可能多地采集不同延时下的数据, 具体来说如果扫描延时的过程没有把飞秒脉冲的包络扫描完整, 则反演得到的飞秒脉冲的信息是不完整的. 对于孤立阿秒脉冲测量来说, 由于其时域脉宽远小于飞秒脉冲, 即使在飞秒脉冲没有扫描完全的情况下也仍有可能存在冗余信息来提取阿秒脉冲的相位. 但阿秒脉冲串的总体时间宽度在飞秒量级, 在扫描的延时过程中处于脉冲串前沿和后沿的阿秒脉冲大部分时间并没有和飞秒脉冲形成时间重叠, 也就没有和飞秒脉冲共同产生光电子. 如果延时扫描没能覆盖阿秒脉冲串的整体宽度, 上述这些阿秒脉冲的信息就不能完整地出现在RABBITT能谱图中, 算法提取出的信息也就是不完整不准确的.
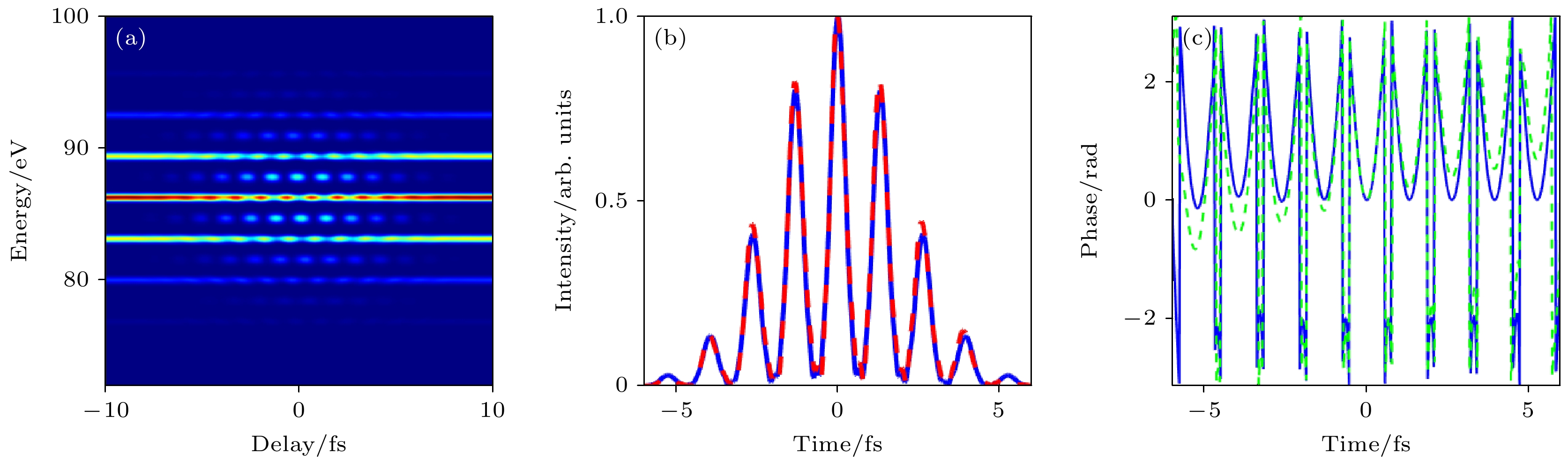
首先尝试通过FROG-CRAB提取阿秒脉冲串的时域信息. FROG-CRAB具有原理简单、迭代速度快等优点, 常用于阿秒条纹相机实验中孤立阿秒脉冲相位恢复. 该算法通过物理约束和强度约束, 通过对测量得到的电子能谱进行多次迭代重建, 也可以实现对阿秒脉冲串的表征. 通过FROG-CRAB反演了一组理论模拟的RABBITT能谱图, 结果如图4所示.
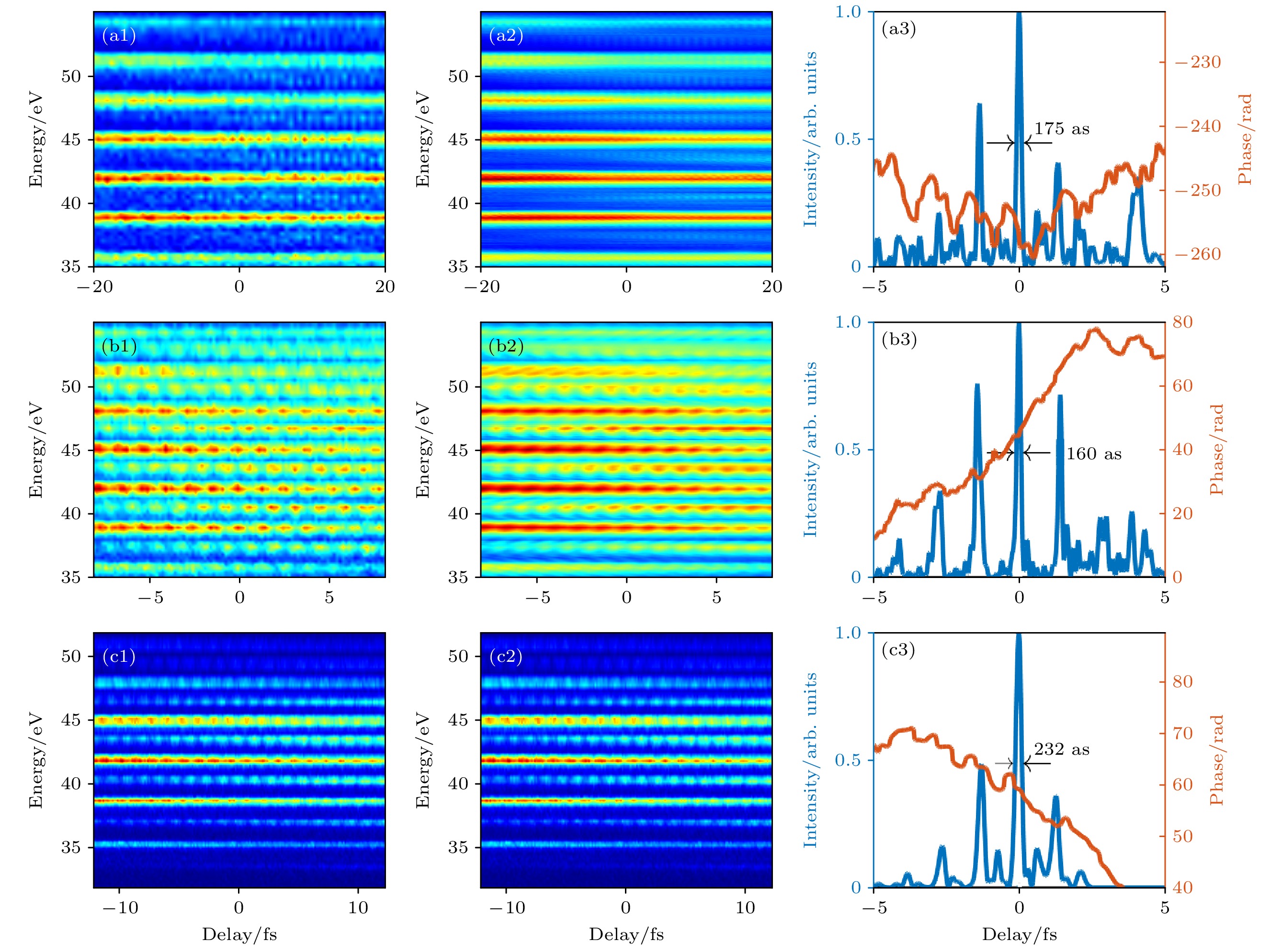
通过图4可以看到FROG-CRAB成功从RABBITT能谱图重建了阿秒脉冲串. 因此用FROG-CRAB对上述3组实验数据也进行了反演, 结果如图5所示. 可以看到重构的RABBITT呈现了实验能谱图的特征, 并且与直接从边带提取相位的方法比较, FROG-CRAB反演得到的时域阿秒脉冲串不再是强度接近的梳齿分布, 在脉冲串之上出现了包络. 从物理上说出现这样的包络是因为飞秒脉冲每半个周期产生一个阿秒脉冲, 由于飞秒脉冲不同时间处的强度不同, 激发的高次谐波阶次不同, 叠加后在时域上就会出现这样的分布, 因此通过FROG-CRAB反演得到的时域阿秒脉冲串与边带提取相位相比确实包含了更多的物理信息.
为了比较FROG-CRAB的准确性和计算效率, 还测试了ePIE方法, 这是一种在无透镜成像中广泛使用的, 从层析成像中衍生出来的相位恢复方案. 在层析技术中, 对于一个真实的空间物体, 尤其是对于它的振幅和相位, 采用一系列远场衍 射测量迭代的形式进行重建. 将光照射到物体上, 并且在垂直于光束传播方向的平面上移动物体或者移动照明光束, 记录每一次移动得到的信号. 即使照明光束未知, 也可以将其轮廓和物体一起重建. 这个算法和FROG-CRAB在反演过程采用了相同的物理公式, 所以物理层面的约束是相同的, 区别是ePIE中的延时轴坐标和两个脉冲的时间轴坐标是各自独立的, 计算时不需要额外的约束关系和插值计算, 因此提高了计算效率. 此外, ePIE中有两个参数分别用于控制阿秒脉冲串和飞秒脉冲的搜寻速度, 为优化过程提高了灵活性. 为测试 ePIE反演RABBITT的能力, 用一组理论模拟的RABBITT能谱图进行测试, 结果如图6所示.
可以看到与FROG-CRAB相比较ePIE同样具备反演RABBITT能谱图的能力, 因此采用ePIE对3组实验数据进行了反演, 结果如图7所示.
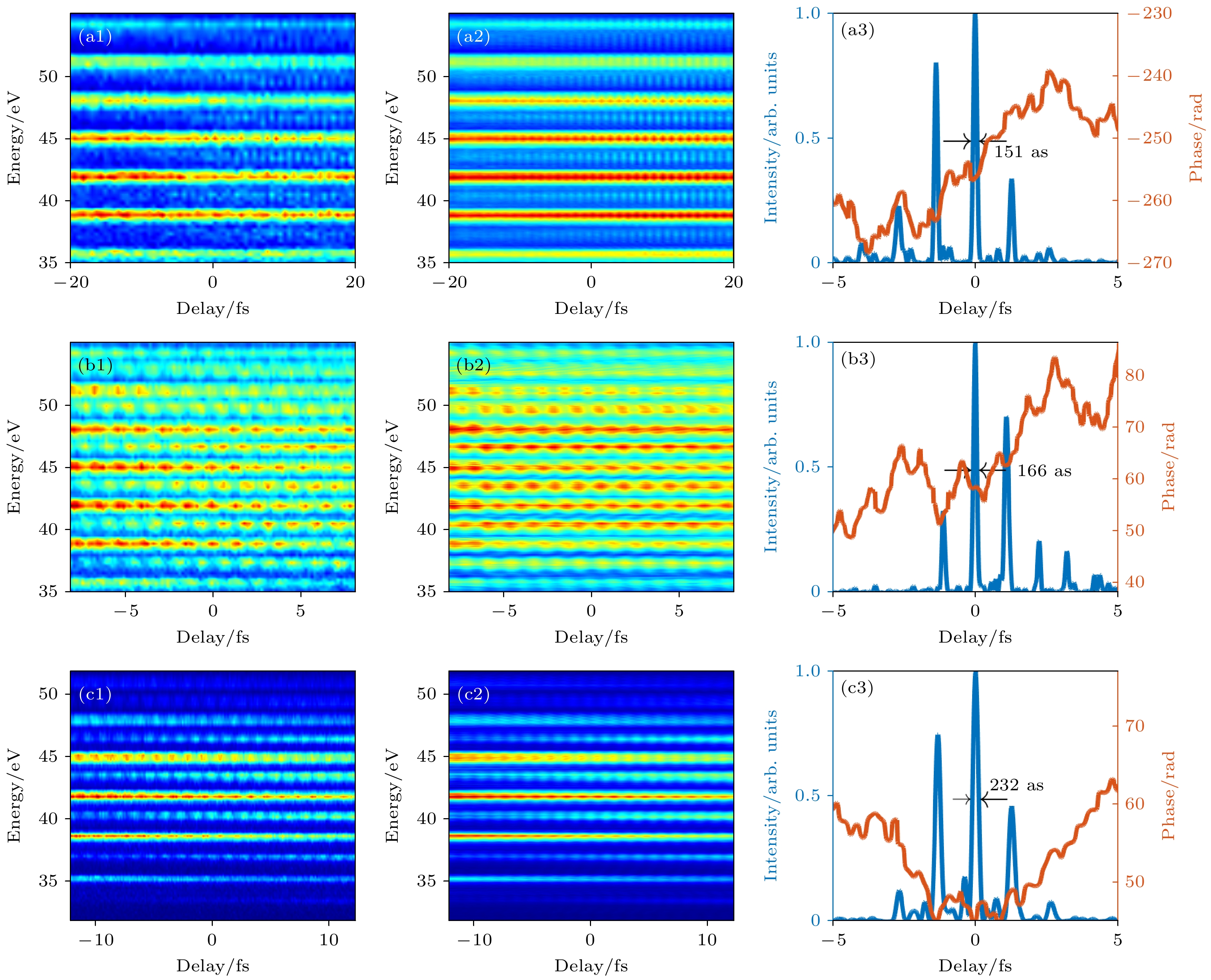
从图7可以看到ePIE重构的RABBITT同样呈现了实验能谱图的特征, 且得到了与FROG-CRAB方法类似形貌的时域阿秒脉冲串. 将3种反演方法的结果放在一起对比, 可以发现第3组实验数据的脉冲宽度在3种反演算法下给出的结论相差不大, 而第1组实验数据的反演结果则差异明显, 第2组实验数据次之. 这是因为第1组实验数据虽然时间延时范围足够大, 但延时步长扫描的间隔也较大, 边带的精细结构没有被实验数据很好的记录下来, 这增加了反演的难度, 降低了反演的精确程度, 所以反演的结果不够理想. 第2组实验数据虽然扫描的时间延时间隔大, 但相应的总延时范围不够大, 且实验数据含有大量的噪声, 同样增加了程序的反演难度. 因此想要从实验数据重建理想的阿秒脉冲, 需要在实验过程中注意扫描延时的步长和总长度均在合理的范围, 并提高信号的强度, 提高实验数据信噪比.
由于FROG-CRAB以及ePIE这两种算法物理约束上有相似之处, 还尝试了使用遗传算法处理RABBITT实验数据. 遗传算法中将阿秒脉冲串的相位作为未知参数, 将猜测的相位代入公式得到理论的RABBITT能谱图与实验测量的RABBITT能谱图的差异构造衡量相位准确性的误差函数, 也叫做适应度. 遗传算法的优化过程将相位作为模拟种群的生物遗传信息, 将误差函数作为生物“物竞天择”的标准, 种群的每一代繁衍即一次迭代. 每一次迭代模拟了种群的遗传信息交叉变异的过程, 因此新的一代种群在继承上一代优点的同时也增加了随机的搜索范围, 最终幸存下来的种群所携带的遗传信息即要搜寻的相位. 与前两种反演算法相比较, 遗传算法的约束程度更高, 除了在迭代过程中使用强场近似下能谱图计算公式之外, 遗传算法还可以约束阿秒脉冲串的光谱信息以及飞秒脉冲的时域强度和相位信息. 由于上述信息均可以通过实验手段直接获得, 因此遗传算法将更多的物理约束作为先验信息代入到反演过程, 缩小了参数搜寻空间, 使得得到的结果更符合物理规律. 用遗传算法处理了第3组实验数据, 为了使用较少的参数表示光谱相位, 采取了样条插值的思想, 在谱中每一个峰的峰值和峰中间的位置各取一个点, 这样得到的一组点集再经过样条插值就可以得到一条足够复杂的曲线. 采用遗传算法搜寻设计的相位参数, 得到的结果如图8所示.
可以看到, 遗传算法反演的实验结果并不理想. 分析认为, 首先在反演过程中使用的是理论模拟的高斯型脉冲, 因此能谱图中由真实的飞秒脉冲产生的特征会干扰程序的收敛. 其次遗传算法对理论计算能谱图与实验能谱图的差异高度敏感, 而理论能谱计算公式采用的强场近似会引入误差, 且理论计算的过程没有考虑实验数据采集过程中引入的散粒噪声等引起的误差, 因此也会干扰程序收敛. 除此之外, 用于相位参数的构造也是一个难题, 不同于孤立阿秒脉冲的光谱, 阿秒脉冲串的光谱相位更复杂, 但过多的参数又会增加算法搜寻的难度, 降低搜寻结果的精确度. 所以遗传算法仍然有进步的空间.
-
本文研究了阿秒脉冲串的产生、测量和表征, 通过自主设计和搭建的飞秒钛宝石再生放大器来产生阿秒脉冲串, 并利用共线阿秒极紫外束线进行RABBITT实验, 得到了3组实验数据. 在阿秒脉冲的时域重建和表征方面, 通过采用RABBITT边带相位方法得到边带相位差, 从而直接完成了阿秒脉冲串的重建. 此外, 还使用了阿秒重建频率分辨光学开关法和扩展层析重建迭代引擎算法来完整地重建理论和实验的阿秒脉冲串相位信息并对其进行了比较. 发现想要得到理想的反演结果的前提是实验数据的时间延时步长足够小, 扫描范围足够大, 才能采集到更丰富的信息用于反演. 最后还尝试使用遗传算法来提取阿秒脉冲串的光谱相位信息. 这项工作对于进一步进行电子动力学测量并解释其演化规律具有重要的指导意义.
阿秒脉冲串产生和相位信息重构的对比研究
Comparative study on generation of attosecond pulse train and phase information reconstruction
-
摘要: 阿秒脉冲为研究原子、分子和电子的超快动力学提供了前所未有的测量精度. 目前最成熟的方法是使用飞秒激光与气体相互作用产生阿秒脉冲串和孤立阿秒脉冲. 阿秒脉冲的时域信息以及电子的动力学信息可以通过阿秒条纹相机或基于双光子跃迁干涉的重构阿秒拍频(RABBITT)方法从能谱图中提取. 本文研究了阿秒脉冲串的产生、测量和表征, 通过自主设计建造的钛宝石放大器和阿秒束线进行实验获得光电子能谱图, 并采用不同方法重构阿秒脉冲串的相位信息. 这对于深入理解电子动力学并进行相关测量具有重要意义.Abstract:
Attosecond pulses provide higher measurement precision for analyzing ultrafast dynamics in atoms, molecules, and electrons, laying the foundation for studying electronic motion in atomic and molecular systems. The most important method currently is to generate attosecond pulse trains and isolated attosecond pulses through the interaction of femtosecond lasers with gases. The temporal information of attosecond pulses and the dynamic information of electrons can be extracted from spectrograms by using attosecond streak camera or the reconstruction of attosecond beating by interference of two-photon transitions (RABBITT) method based on two-photon transition interference. Although the differences in phase among different high-order harmonics can be directly extracted from the oscillation frequencies of sidebands, the iterative algorithm of attosecond streak camera can provide complete phase information of attosecond pulse trains to better support the study of electron dynamics in atoms. Research purpose This work is dedicated to the investigation of the generation, measurement, and characterization of attosecond pulse train (APT), which are essential for probing ultrafast dynamics in atomic, molecular, and electronic systems. The focus is on the generation of APTs through interactions between femtosecond lasers and gases, as well as the extraction of temporal and dynamic information from these pulses by using advanced spectroscopic techniques such as the RABITT method. Methods The experimental approach involves the use of a homebuilt femtosecond titanium sapphire regenerative amplifier to produce high-order harmonics, leading to the generation of APTs. The setup includes the homebuilt titanium sapphire chirped pulse amplifier and a collinear attosecond pulse generation and measurement beamline, which are used to conduct RABITT experiments. The process requires the interaction of femtosecond lasers with gas targets to generate high-energy photons in the extreme ultraviolet and soft X-ray spectral ranges. By optimizing the phase-matching conditions within the gas target, strong high-order harmonic signals are observed on an XUV spectrometer. The temporal information of the attosecond pulses is indirectly measured through the photoelectron spectrum produced by the interaction of attosecond pulses with femtosecond lasers. The research also employs the FROG-CRAB algorithm and the extended phase retrieval and iterative engine (ePIE) algorithm for temporally reconstructing APTs and attempts to use a genetic algorithm to extract phase information. Results The study yields three sets of RABITT spectrograms, which are analyzed by using the RABITT sideband phase method to directly reconstruct APTs. Fourier transform analysis is used to extract phase differences between sidebands, offering insights into the phase differences between corresponding high-order harmonics. This method, however, provides an estimation of the phase in the center of each harmonic order, which does not fully represent the actual pulse shape. The FROG-CRAB algorithm and ePIE algorithm successfully reconstructs the attosecond pulse trains from the RABITT spectrograms, revealing similar temporal pulse train morphologies. In contrast, the genetic algorithm, despite its potential for high constraint optimization, does not yield satisfactory results, possibly due to the sensitivity of the algorithm to discrepancies between theoretical simulations and experimental data. Conclusions The research concludes that achieving ideal inversion results for APTs necessitates small time delay steps and a wide scanning range in the experimental data collection process to ensure a rich dataset for inversion. The FROG-CRAB algorithm and ePIE algorithm demonstrate their effective performance in reconstructing APTs, with ePIE showing higher computational efficiency. The genetic algorithm, while offering a high degree of constraint, faces challenges and requires to be further refined. The study underscores the importance of the signal-to-noise ratio in experimental data for the accuracy of inversion results. This work provides significant guidance for future measuring electron dynamics and explaining their evolution patterns, contributing valuable experimental methods and data analysis techniques to the field of attosecond science. -
Key words:
- attosecond pulse trains /
- phase reconstruction /
- RABBITT method /
- attosecond streaking camera .
-

-
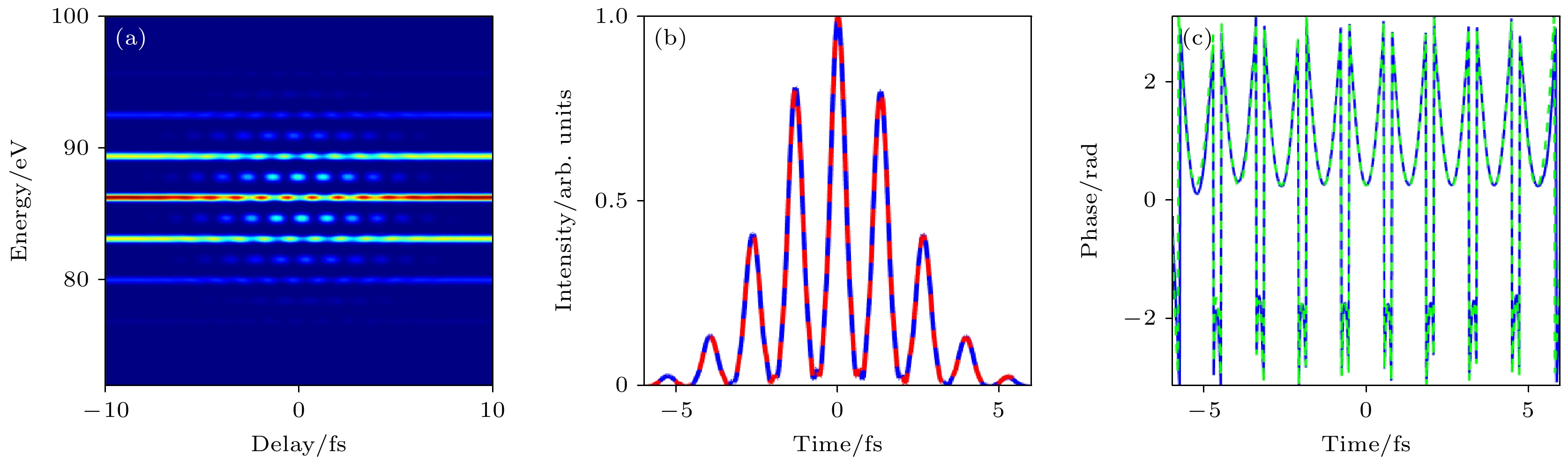
图 4 FROG-CRAB反演理论模拟的RABBITT能谱图重建阿秒脉冲串结果 (a)模拟的能谱图; (b), (c)中蓝线表示理论产生的阿秒脉冲串和相位, (b)中红线表示FROG-CRAB通过反演重建的阿秒脉冲串, (c)中绿线代表FROG-CRAB在RABBITT能谱图中提取到的相位
Figure 4. Reconstruction results of RABBITT spectrogram using FROG-CRAB. The simulated spectrogram is displayed in panel (a). The blue lines in panel (b) and (c) represent the theoretically generated attosecond pulse train and phase, respectively. The red line in panel (b) indicates the attosecond pulse train reconstructed by FROG-CRAB, and the green line in panel (c) represents the phase extracted by FROG-CRAB from the RABBITT spectrogram.
图 5 FROG-CRAB反演实验RABBITT能谱图重建阿秒脉冲串结果 (a1), (b1), (c1)实验测到的3组RABBIT能谱图; (a2), (b2), (c2)根据反演脉冲重建的能谱图; (a3), (b3), (c3)反演得到的时域阿秒脉冲串和相位
Figure 5. Results of reconstructing attosecond pulse trains using FROG-CRAB from RABBITT spectrogram: (a1), (b1), (c1) Three sets of RABBITT spectrograms measured in the experiment; (a2), (b2), (c2) the reconstructed spectrograms based on the inverted pulses; (a3), (b3), (c3) the time-domain attosecond pulse trains and phases obtained from the inversion.
图 6 ePIE反演理论模拟的RABBITT能谱图重建阿秒脉冲串结果 (a)模拟的能谱图; (b), (c)蓝线表示理论产生的阿秒脉冲串和相位, (b)中红线表示ePIE通过反演重建的阿秒脉冲串, (c)中绿线代表ePIE在RABBITT能谱图中提取到的相位
Figure 6. Reconstruction results of RABBITT spectrogram using ePIE. The simulated spectrogram is displayed in panel (a). (b), (c) The blue lines represent the theoretically generated attosecond pulse train and phase, respectively. The red line in panel (b) indicates the attosecond pulse train reconstructed by ePIE, and the green line in panel (c) represents the phase extracted by ePIE from the RABBITT spectrogram.
图 7 ePIE反演实验RABBITT能谱图重建阿秒脉冲串结果 (a1), (b1), (c1)实验测到的3组RABBIT能谱图; (a2), (b2), (c2)根据反演脉冲重建的能谱图; (a3), (b3), (c3)反演得到的时域阿秒脉冲串和相位
Figure 7. Results of reconstructing attosecond pulse trains using ePIE from RABBITT spectrogram: (a1), (b1), (c1) Three sets of RABBITT spectrograms measured in the experiment; (a2), (b2), (c2) the reconstructed spectrograms based on the inverted pulses; (a3), (b3), (c3) the time-domain attosecond pulse trains and phases obtained from the inversion.
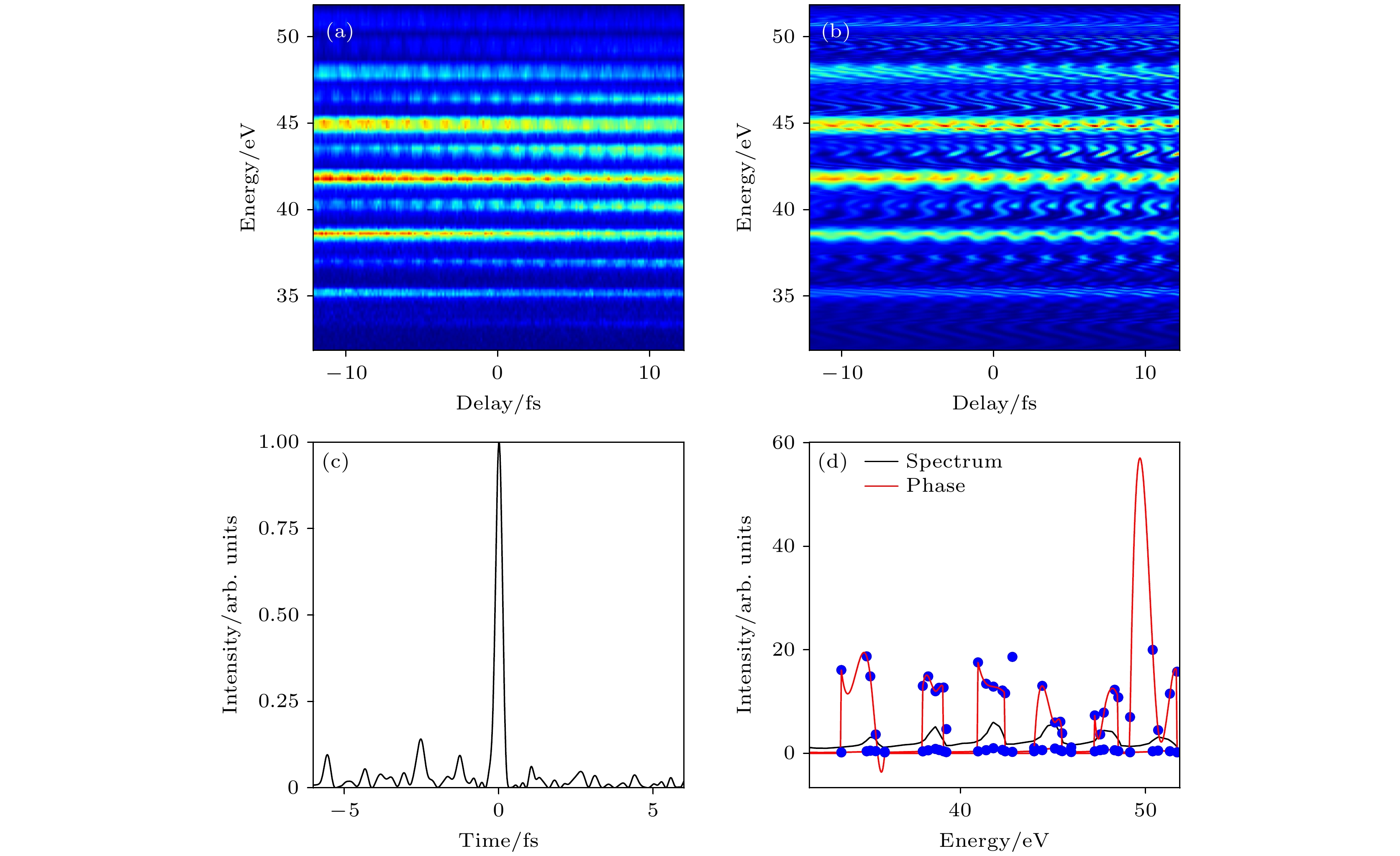
图 8 遗传算法反演第3组实验RABBITT能谱图重建阿秒脉冲串结果 (a)第3组实验的能谱图; (b)遗传算法反演的能谱图; (c)遗传算法反演的时域脉冲串; (d)遗传算法在RABBITT能谱图中提取到的相位
Figure 8. Results of reconstructing the attosecond pulse train of the third experimental RABBITT spectrogram using genetic algorithm: (a) The spectrogram of the third experimental RABBITT spectrogram; (b) the spectrogram inverted by the genetic algorithm; (c) the time-domain pulse train inverted by the genetic algorithm; (d) the phase extracted by the genetic algorithm from the RABBITT spectrogram.
-
[1] Borrego-Varillas R, Lucchini M, Nisoli M 2022 Rep. Prog. Phys. 85 066401 doi: 10.1088/1361-6633/ac5e7f [2] Zholents A, Zolotorev M 2008 New J. Phys. 10 025005 doi: 10.1088/1367-2630/10/2/025005 [3] Nees J, Naumova N, Power E, Yanovsky V, Sokolov I, Maksimchuk A, Bahk S W, Chvykov V, Kalintchenko G, Hou B 2005 J. Mod. Opt. 52 305 doi: 10.1080/0950034042000297285 [4] Kaplan A 1994 Phys. Rev. Lett. 73 1243 doi: 10.1103/PhysRevLett.73.1243 [5] McPherson A, Gibson G, Jara H, Johann U, Luk T S, McIntyre I, Boyer K, Rhodes C K 1987 JOSA B 4 595 doi: 10.1364/JOSAB.4.000595 [6] Ferray M, L'Huillier A, Li X, Lompre L, Mainfray G, Manus C 1988 J. Phys. B: At. Mol. Opt. Phys. 21 L31 doi: 10.1088/0953-4075/21/3/001 [7] Chini M, Zhao K, Chang Z 2014 Nat. Photonics 8 178 doi: 10.1038/nphoton.2013.362 [8] Krausz F, Ivanov M 2009 Rev. Mod. Phys. 81 163 doi: 10.1103/RevModPhys.81.163 [9] Antoine P, L'huillier A, Lewenstein M 1996 Phys. Rev. Lett. 77 1234 doi: 10.1103/PhysRevLett.77.1234 [10] Sansone G, Benedetti E, Calegari F, Vozzi C, Avaldi L, Flammini R, Poletto L, Villoresi P, Altucci C, Velotta R 2006 Science 314 443 doi: 10.1126/science.1132838 [11] Hentschel M, Kienberger R, Spielmann C, Reider G A, Milosevic N, Brabec T, Corkum P, Heinzmann U, Drescher M, Krausz F 2001 Nature 414 509 doi: 10.1038/35107000 [12] Itatani J, Quéré F, Yudin G L, Ivanov M Y, Krausz F, Corkum P B 2002 Phys. Rev. Lett. 88 173903 doi: 10.1103/PhysRevLett.88.173903 [13] Muller H G 2002 Appl. Phys. B 74 s17 doi: 10.1007/s00340-002-0894-8 [14] Paul P M, Toma E S, Breger P, Mullot G, Augé F, Balcou P, Muller H G, Agostini P 2001 Science 292 1689 doi: 10.1126/science.1059413 [15] Mairesse Y, Quéré F 2005 Phys. Rev. A 71 011401 doi: 10.1103/PhysRevA.71.011401 [16] Gagnon J, Goulielmakis E, Yakovlev V S 2008 Appl. Phys. B 92 25 doi: 10.1007/s00340-008-3063-x [17] Chini M, Gilbertson S, Khan S D, Chang Z 2010 Opt. Express 18 13006 doi: 10.1364/OE.18.013006 [18] Zhao X, Wei H, Wu Y, Lin C D 2017 Phys. Rev. A 95 043407 doi: 10.1103/PhysRevA.95.043407 [19] Keathley P D, Bhardwaj S, Moses J, Laurent G, Kaertner F X 2016 New J. Phys. 18 073009 doi: 10.1088/1367-2630/18/7/073009 [20] Månsson E P, Guénot D, Arnold C L, Kroon D, Kasper S, Dahlström J M, Lindroth E, Kheifets A S, L’huillier A, Sorensen S L 2014 Nat. Phys. 10 207 doi: 10.1038/nphys2880 [21] Jordan I, Huppert M, Pabst S, Kheifets A S, Baykusheva D, Wörner H J 2017 Phys. Rev. A 95 013404 doi: 10.1103/PhysRevA.95.013404 [22] Kotur M, Guenot D, Jiménez-Galán Á, Kroon D, Larsen E W, Louisy M, Bengtsson S, Miranda M, Mauritsson J, Arnold C 2016 Nat. Commun. 7 10566 doi: 10.1038/ncomms10566 [23] Haessler S, Fabre B, Higuet J, Caillat J, Ruchon T, Breger P, Carré B, Constant E, Maquet A, Mével E 2009 Phys. Rev. A 80 011404 doi: 10.1103/PhysRevA.80.011404 [24] Klünder K, Dahlström J, Gisselbrecht M, Fordell T, Swoboda M, Guenot D, Johnsson P, Caillat J, Mauritsson J, Maquet A 2011 Phys. Rev. Lett. 106 143002 doi: 10.1103/PhysRevLett.106.143002 [25] Zhan M J, Ye P, Teng H, He X K, Zhang W, Zhong S Y, Wang L F, Yun C X, Wei Z Y 2013 Chin. Phys. Lett. 30 093201 doi: 10.1088/0256-307X/30/9/093201 [26] Jiang Y J, Liang Y Y, Gao Y T, Zhao K, Xu S Y, Wang J, He X K, Teng H, Zhu J F, Chen Y L, Wei Z Y 2020 Chin. Phys. B 29 013206 doi: 10.1088/1674-1056/ab6315 [27] Zhong S Y, Teng H, Zhu X X, Gao Y T, Wang K J, Wang X Z, Wang Y M, Yu S, Zhao K, Wei Z Y 2023 Chin. Opt. Lett. 21 113201 doi: 10.3788/COL202321.113201 [28] Lucchini M, Brügmann M, Ludwig A, Gallmann L, Keller U, Feurer T 2015 Opt. Express 23 29502 doi: 10.1364/OE.23.029502 [29] Kheifets A S, Bray A W 2021 Phys. Rev. A 103 L011101 doi: 10.1103/PhysRevA.103.L011101 [30] Cattaneo L, Vos J, Lucchini M, Gallmann L, Cirelli C, Keller U 2016 Opt. Express 24 29060 doi: 10.1364/OE.24.029060 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: