高级搜索

超晶格电子阻挡层周期数对AlGaN基深紫外发光二极管性能的影响

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

刘举, 曹一伟, 吕全江, 杨天鹏, 米亭亭, 王小文, 刘军林. 超晶格电子阻挡层周期数对AlGaN基深紫外发光二极管性能的影响[J]. 物理学报, 2024, 73(12): 128503-1. doi: 10.7498/aps.73.20231969
引用本文: 刘举, 曹一伟, 吕全江, 杨天鹏, 米亭亭, 王小文, 刘军林. 超晶格电子阻挡层周期数对AlGaN基深紫外发光二极管性能的影响[J]. 物理学报, 2024, 73(12): 128503-1. doi: 10.7498/aps.73.20231969
shu
Ju Liu, Yi-Wei Cao, Quan-Jiang Lv, Tian-Peng Yang, Ting-Ting Mi, Xiao-Wen Wang, Jun-Lin Liu. Influence of period number of superlattice electron barrier layer on the performance of AlGaN-based deep ultraviolet LED[J]. Acta Physica Sinica, 2024, 73(12): 128503-1. doi: 10.7498/aps.73.20231969
Citation: Ju Liu, Yi-Wei Cao, Quan-Jiang Lv, Tian-Peng Yang, Ting-Ting Mi, Xiao-Wen Wang, Jun-Lin Liu. Influence of period number of superlattice electron barrier layer on the performance of AlGaN-based deep ultraviolet LED[J]. Acta Physica Sinica, 2024, 73(12): 128503-1. doi: 10.7498/aps.73.20231969
shu

超晶格电子阻挡层周期数对AlGaN基深紫外发光二极管性能的影响

  • 1.

    江苏大学材料科学与工程学院, 镇江　212013

  • 2.

    圆融光电科技股份有限公司, 马鞍山　243000

  • 3.

    马鞍山杰生半导体有限公司, 马鞍山　243000

    • 作者简介: 刘举: Juuuuz@163.com .
    通讯作者: Email: lvquanjiang@ujs.edu.cn.;  E-mail: liujunlin@ujs.edu.cn

  • 中图分类号: 85.60.Jb, 73.61.Ey, 78.20.Bh

Influence of period number of superlattice electron barrier layer on the performance of AlGaN-based deep ultraviolet LED

  • 1.

    School of Materials Science and Engineering, Jiangsu University, Zhenjiang 212013, China

  • 2.

    Epitop Optoelectronic Co., Ltd., Ma’anshan 243000, China

  • 3.

    Ma’anshan Jason Semiconductor Co., Ltd., Ma’anshan 243000, China

    • Corresponding authors: Email: lvquanjiang@ujs.edu.cn;  E-mail: liujunlin@ujs.edu.cn

  • MSC: 85.60.Jb, 73.61.Ey, 78.20.Bh

  • 摘要: 在AlGaN基深紫外发光二极管(DUV-LEDs)中设计了具有不同周期数的超晶格电子阻挡层(SL-EBL)结构, 研究了SL-EBL周期数对DUV-LEDs发光效率、I-V特性、可靠性及有源区载流子复合机制的影响. 研究结果表明, 随着SL-EBL的周期数增加, DUV-LEDs的光输出功率(LOP)、外量子效率(EQE)和电光转换效率 (WPE)均呈先上升后下降的趋势, 同时泄漏电流减小, 可靠性提升. 当周期数为7时(厚度为28 nm), DUV-LEDs裸芯的EQE和WPE均达到最大值, 在7.5 mA注入电流下分别为3.5%和3.2%. 能带模拟结果证明了增加SL-EBL周期数可以有效提升电子势垒高度, 而几乎不改变空穴势垒高度. 然而, 当SL-EBL超过一定厚度时, 抑制了空穴向有源区的注入, 导致EQE和WPE随SL-EBL周期数变化出现拐点. 研究了SL-EBL周期数对DUV-LEDs载流子复合机制的影响, 发现增加SL-EBL周期数可以有效地降低有源区内载流子非辐射复合.
    Abstract: The development of AlGaN-based deep ultraviolet light emitting diodes (DUV-LEDs) is currently limited by poor external quantum efficiency (EQE) and wall-plug efficiency (WPE). Internal quantum efficiency (IQE), as an important component of EQE, plays a crucial role in improving the performance of DUV-LEDs. The IQE is related to the carrier injection efficiency and the radiation recombination rate in the active region. In order to improve the IQE of AlGaN-based DUV-LEDs, this work proposes a scheme to optimize the period number of superlattice electron barrier layer (SL-EBL) to achieve better carrier injection efficiency and confinement capability. The effect of the period number of SL-EBL on the luminous efficiency, reliability and carrier recombination mechanism of AlGaN-based DUV-LEDs with an emission wavelength of 273 nm are investigated. The experimental results show that the light output power (LOP), external quantum efficiency (EQE) and wall-plug efficiency (WPE) of the DUV-LEDs tend to first increase and then decrease with the period number of SL-EBL increasing, while the leakage current decreases and the reliability is enhanced. The maximum EQE and WPE of the DUV-LED are 3.5% and 3.2%, respectively, at an injection current of 7.5 mA when the period number of SL-EBL is fixed at 7 (the thickness is 28 nm). Meanwhile, the numerical simulation results show that the electron potential barrier height is enhanced with the period number of SL-EBL increasing, and the variation of the hole potential barrier height is negligible. Therefore, increasing the period number of SL-EBL is beneficial to shielding the dislocations and suppressing the leakage of electrons into the p-type layer, which improves the luminous efficiency and reliability of DUV-LEDs. However, when the period number of SL-EBL exceeds 7, the excessively thick hole potential barrier prevents the holes from entering into the activation region and reduces the radiative recombination efficiency. Therefore, EQE and WPE will show an inflection point with the variation of the period number of SL-EBL. In addition, to investigate the carrier recombination mechanism of the active region, the experimental EQE curves are fitted by the ABC model as well as the different slopes in logarithmic light output power-current (L-I ) curves are calculated after aging. It can be found that increasing the period number of SL-EBL can effectively suppress the non-radiative combination of carriers in the active region. This investigation can provide an alternative way to enhance the photoelectric performance of DUV-LEDs.
  • 加载中

  • 图 1  AlGaN基DUV-LEDs外延结构示意图(右)和四组不同的SL-EBL周期数(左)

    Figure 1.  Schematic of epitaxial structure for AlGaN-based DUV-LEDs (right) and the schematic of four different period numbers of SL-EBL (left).

    下载: 全尺寸图片 幻灯片

    图 2  不同SL-EBL周期数样品的实验结果　(a)光输出功率以及外量子效率随电流的变化; (b)电光转换效率随电流的变化; (c) I-V曲线; (d)在100 mA注入电流下发光强度随峰值波长的变化

    Figure 2.  Experimental results for different samples: (a) LOP, EQE and (b) WPE as a function of current density; (c) experimentally measured I-V curves in logarithmic coordinates; (d) EL emission spectrums of DUV-LEDs at 100 mA.

    下载: 全尺寸图片 幻灯片

    图 3  (a)—(d)不同老化时间下样品A, B, C和D的 EQE 随电流的变化; 具有不同SL-EBL周期数的样品A, B, C和D在老化过程中测得的在(e)小电流以及(f)工作电流下的归一化光输出功率, (f)中插图为样品A在不同老化时间下的归一化电致发光光谱

    Figure 3.  The EQE characteristic curves of samples (a) A, (b) B, (c) C, and (d) D after aging; (e) the normalized output power of (e) low injection current and (f) working current of samples A, B, C and D during aging period; the illustration in panel (f) shows the electroluminescence spectra of sample A under different stress time.

    下载: 全尺寸图片 幻灯片

    图 4  电流密度为75 A/cm2 时模拟的不同周期数SL-EBL DUV-LEDs样品的能带示意图　(a) 样品A; (b) 样品B; (c) 样品C; (d) 样品D

    Figure 4.  Calculated band structure and the Femi energy level in EBL under current density of 75 A /cm2 for sample (a) A, (b) B, (c) C and (d) D.

    下载: 全尺寸图片 幻灯片

    图 5  (a)样品A和样品C的 EQE曲线与ABC模型的理论拟合, 其中实验数据用点表示, ABC模型拟合数据用实线表示; (b)样品A和样品C在老化前后双对数坐标L-I 曲线; (c)样品A和样品C在老化前后的S值

    Figure 5.  (a) Experimentally measured EQE vs. current density (solid dot) and theoretical ABC model (solid line) fits for sample A and C; (b) LOP and (c) slope (S ) as functions of current density for sample A and C.

    下载: 全尺寸图片 幻灯片
  • [1] 冯丽雅, 路慧敏, 朱一帆, 陈毅勇, 于彤军, 王建萍 2023 物理学报 72 048502 doi: 10.7498/aps.72.20222004 Feng L Y, Lu H M, Zhu Y F, Chen Y Y, Yu T J, Wang J P 2023 Acta Phys. Sin. 72 048502 doi: 10.7498/aps.72.20222004
    [2] Kneissl M, Seong T Y, Han J, Amano H 2019 Nat. Photonics 13 233 doi: 10.1038/s41566-019-0359-9
    [3] Du P, Shi L, Liu S, Zhou S J 2022 Micro Nanostruct. 163 107150 doi: 10.1016/j.spmi.2022.107150
    [4] Hu H, Zhou S, Liu X T, Gao Y L, Gui C Q, Liu S 2017 Sci. Rep. 7 44627 doi: 10.1038/srep44627
    [5] Sharif M N, Niass M I, Liou J J, Wang F, Liu Y 2021 Superlattice. Microstruct. 158 107022 doi: 10.1016/j.spmi.2021.107022
    [6] Nagasawa Y, Hirano A 2018 Appl. Sci. (Basel) 8 1264 doi: 10.3390/app8081264
    [7] Zhang D Y, Chu C S, Tian K K, Kou J Q, Bi W G, Zhang Y H, Zhang Z H 2020 AIP Adv. 10 065032 doi: 10.1063/5.0007460
    [8] Lobo-Ploch N, Mehnke F, Sulmoni L, Cho H K, Guttmann M, Glaab J, Hilbrich K, Wernicke T, Einfeldt S, Kneissl M 2020 Appl. Phys. Lett. 117 111102 doi: 10.1063/5.0015263
    [9] Sun Y H, Xu F J, Xie N, Wang J M, Zhang N, Lang J, Liu B Y, Fang X Z, Wang L B, Ge W K, Kang X N, Qin Z X, Yang X L, Wang X Q, Shen B 2020 Appl. Phys. Lett. 116 212102 doi: 10.1063/5.0008339
    [10] Hu H P, Tang B, Wan H, Sun H D, Zhou S J, Dai J N, Chen C Q, Liu S, Guo L J 2020 Nano Energy 69 104427 doi: 10.1016/j.nanoen.2019.104427
    [11] Meneghini M, La Grassa M, Vaccari S, Galler B, Zeisel R, Drechsel P, Hahn B, Meneghesso G, Zanoni E 2014 Appl. Phys. Lett. 104 113505 doi: 10.1063/1.4868719
    [12] Tian K K, Chu C S, Shao H, Che J M, Kou J Q, Fang M Q, Zhang Y H, Bi W G, Zhang Z H 2018 Superlattice. Microstruct. 122 280 doi: 10.1016/j.spmi.2018.07.037
    [13] Sun J, Sun H Q, Yi X Y, Yang X, Liu T Y, Wang X, Zhang X, Fan X C, Zhang Z D, Guo Z Y 2017 Superlattice. Microstruct. 107 49 doi: 10.1016/j.spmi.2017.03.055
    [14] Yu H B, Chen Q, Ren Z J, Tian M, Long S B, Dai J N, Chen C Q, Sun H D 2019 IEEE Photonics J. 11 1 doi: 10.1109/jphot.2019.2922280
    [15] Cao Y W, Lv Q J, Yang T P, Mi T T, Wang X W, Liu W, Liu J L 2023 Micro Nanostruct. 175 207489 doi: 10.1016/j.micrna.2022.207489
    [16] So B, Kim J, Kwak T, Kim T, Lee J, Choi U, Nam O 2018 RSC Adv. 8 35528 doi: 10.1039/C8RA06982D
    [17] Zhao F Y, Wei J, Dong H L, Jia Z G, Li T B, Yu C Y, Zhang Z X, Xu B S 2022 Aip Adv. 12 125003 doi: 10.1063/5.0127070
    [18] Wang L Y, He W, Zheng T, Chen Z X, Zheng S W 2019 Superlattice. Microstruct. 133 106188 doi: 10.1016/j.spmi.2019.106188
    [19] Usman M, Jamil T, Malik S, Jamal H 2021 Optik 232 166528 doi: 10.1016/j.ijleo.2021.166528
    [20] Cao Y W, Lv Q J, Yang T P, Mi T T, Wang X W, Liu W, Liu J L 2023 J. Lumin. 257 119699 doi: 10.1016/j.jlumin.2023.119699
    [21] Kim K S, Han D P, Kim H S, Shim J I 2014 Appl. Phys. Lett. 104 091110 doi: 10.1063/1.4867647
    [22] Cao X A, Teetsov J M, D’evelyn M P, Merfeld D W, Yan C H 2004 Appl. Phys. Lett. 85 7 doi: 10.1063/1.1767280
    [23] 王福学, 叶煊超 2017 发光学报 38 6 doi: 10.3788/fgxb20173801.0057 Wang F X, Ye X C 2017 Chin. J. Lumin. 38 6 doi: 10.3788/fgxb20173801.0057
    [24] Schubert M F, Schubert E F 2010 Appl. Phys. Lett. 96 131102 doi: 10.1063/1.3373610
    [25] Lv Q J, Gao J D, Tao X X, Zhang J L, Mo C L, Wang X L, Zheng C D, Liu J L 2020 J. Lumin. 222 117186 doi: 10.1016/j.jlumin.2020.117186
    [26] Grillot P N, Krames M R, Zhao H, Teoh S H 2006 IEEE Trans. Device Mater. Rel. 6 564 doi: 10.1109/TDMR.2006.887416
    [27] 毛清华, 江风益, 程海英, 郑畅达 2010 物理学报 59 8078 doi: 10.7498/aps.59.8078 Mao Q H, Jiang F Y, Cheng H Y, Zheng C D 2010 Acta Phys. Sin. 59 8078 doi: 10.7498/aps.59.8078
    [28] Dai Q, Shan Q F, Wang J, Chhajed S, Cho J, Schubert E F, Crawford M H, Koleske D D, Kim M H, Park Y 2010 Appl. Phys. Lett. 97 133507 doi: 10.1063/1.3493654
    [29] Yun J, Shim J I, Hirayama H 2015 Appl. Phys. Express 3 8 022104 doi: 10.7567/APEX.8.022104
    [30] Cao X A, Stokes E B, Sandvik P M, Leboeuf S F, Kretchmer J, Walker D 2002 IEEE Electr. Device Lett. 23 535 doi: 10.1109/LED.2002.802601
    [31] Lv Q J, Liu J L, Mo C L, Zhang J L, Wu X M, Wu Q F, Jiang F Y 2019 ACS Photonics 6 130 doi: 10.1021/acsphotonics.8b01040
    [32] Yamaguchi M, Yamamoto A, Tachikawa M, Itoh Y, Sugo M 1988 Appl. Phys. Lett. 53 2293 doi: 10.1063/1.100257
  • 加载中
图( 5)
计量
  • 文章访问数:  201
  • HTML全文浏览数:  201
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-12-14
  • 刊出日期:  2024-06-20

超晶格电子阻挡层周期数对AlGaN基深紫外发光二极管性能的影响

    通讯作者: Email: lvquanjiang@ujs.edu.cn.; 
    通讯作者: E-mail: liujunlin@ujs.edu.cn
    作者简介: 刘举: Juuuuz@163.com
  • 1. 江苏大学材料科学与工程学院, 镇江　212013
  • 2. 圆融光电科技股份有限公司, 马鞍山　243000
  • 3. 马鞍山杰生半导体有限公司, 马鞍山　243000
  • 收稿日期:  2023-12-14

摘要: 在AlGaN基深紫外发光二极管(DUV-LEDs)中设计了具有不同周期数的超晶格电子阻挡层(SL-EBL)结构, 研究了SL-EBL周期数对DUV-LEDs发光效率、I-V特性、可靠性及有源区载流子复合机制的影响. 研究结果表明, 随着SL-EBL的周期数增加, DUV-LEDs的光输出功率(LOP)、外量子效率(EQE)和电光转换效率 (WPE)均呈先上升后下降的趋势, 同时泄漏电流减小, 可靠性提升. 当周期数为7时(厚度为28 nm), DUV-LEDs裸芯的EQE和WPE均达到最大值, 在7.5 mA注入电流下分别为3.5%和3.2%. 能带模拟结果证明了增加SL-EBL周期数可以有效提升电子势垒高度, 而几乎不改变空穴势垒高度. 然而, 当SL-EBL超过一定厚度时, 抑制了空穴向有源区的注入, 导致EQE和WPE随SL-EBL周期数变化出现拐点. 研究了SL-EBL周期数对DUV-LEDs载流子复合机制的影响, 发现增加SL-EBL周期数可以有效地降低有源区内载流子非辐射复合.

English Abstract

    全文HTML

    1.   引　言

    • 近年来, GaN基深紫外发光二极管(deep ultraviolet light-emitting diodes, DUV-LEDs)在消毒杀菌、空气净化、气体传感、紫外光疗以及非视距通信等领域的应用日趋成熟, 受到了广大研究人员的青睐[1–4]. 尤其是在全球新型冠状病毒肺炎(COVID-19)爆发期间, 有研究团队已经证明了经过发光波长为270—280 nm的DUV-LEDs照射可以有效地杀死新型冠状病毒[5]. 此外, 根据国际水俣公约, 传统的汞灯等紫外光源必将退出市场[6], 而相比于传统汞灯, DUV-LEDs具有无毒环保、体积小、寿命长、能耗低以及波长可调等优点[7]. 然而, 尽管研究人员已经在外延生长、结构设计以及封装技术等领域付出了巨大的努力, 但是DUV-LEDs的发展仍然受限于较低的外量子效率(external quantum efficiency, EQE)和电光转换效率(wall plug efficiency, WPE)[8,9]. 目前, 一般DUV-LEDs的EQE低于10%, WPE低于5%, 远低于InGaN基蓝光LED(＞80%)[5,10]. 因此, 提升DUV-LEDs的发光效率以及可靠性已经成为重要的研究课题.

      AlGaN基DUV-LEDs的EQE取决于内量子效率(internal quantum efficiency, IQE)和光提取效率(light extraction efficiency, LEE), 其中, IQE与载流子注入效率和有源区的载流子辐射复合效率有关[11]. 除了采取改善外延层晶体质量[12]、提高Mg掺杂效率[13]以及增加电子和空穴的波函数重叠[14]等方式提高IQE以外, 优化电子阻挡层(electron-blocking layer, EBL)[15]同样可以依靠改善载流子注入情况提升IQE. 目前, 研究人员已经提出了许多EBL优化方案来提高载流子注入效率和限制能力. So等[16]采用了渐变超晶格EBL (GSL-EBL)结构代替传统的单层EBL结构, 通过仿真研究表明GSL-EBL的极化电场有利于增加空穴浓度, 在80 mA时能将DUV-LED的光功率提升17倍. Zhao等[17]设计了阶梯式电子阻挡层来提高DUV-LED的性能, 仿真结果表明, 所开发的EBL结构改善了界面极化场, 有效缓解了导带和价带弯曲, 提高了辐射复合率, 发射强度提高了153.8%. 此外, 还有研究人员通过设计W形EBL[18]、倒梯形EBL[19]以及优化EBL厚度[15]来改善载流子注入, 提高内量子效率. 综上所述, 超晶格EBL (SL-EBL)结构已经广泛应用于DUV-LEDs中, 并在提高发光效率方面取得了不错效果, 但对SL-EBL的周期数的优化需要进一步探讨.

      本研究制备了具有不同周期数SL-EBL (Al0.75 Ga0.25N/Al0.85Ga0.15N)的AlGaN基DUV-LEDs, 研究了SL-EBL的周期数变化对DUV-LEDs的光输出功率(light output power, LOP), EQE, I-V特性以及可靠性的影响. 为了更深入研究器件性能变化的物理机制, 对能带结构进行了模拟. 此外, 通过ABC模型对EQE曲线进行拟合和老化后对数坐标L-I 曲线的斜率S的计算, 探讨了SL-EBL周期数变化对DUV-LEDs有源区载流子复合机制的影响. 为高效AlGaN基DUV-LEDs的EBL结构设计提供了参考.

    2.   实　验

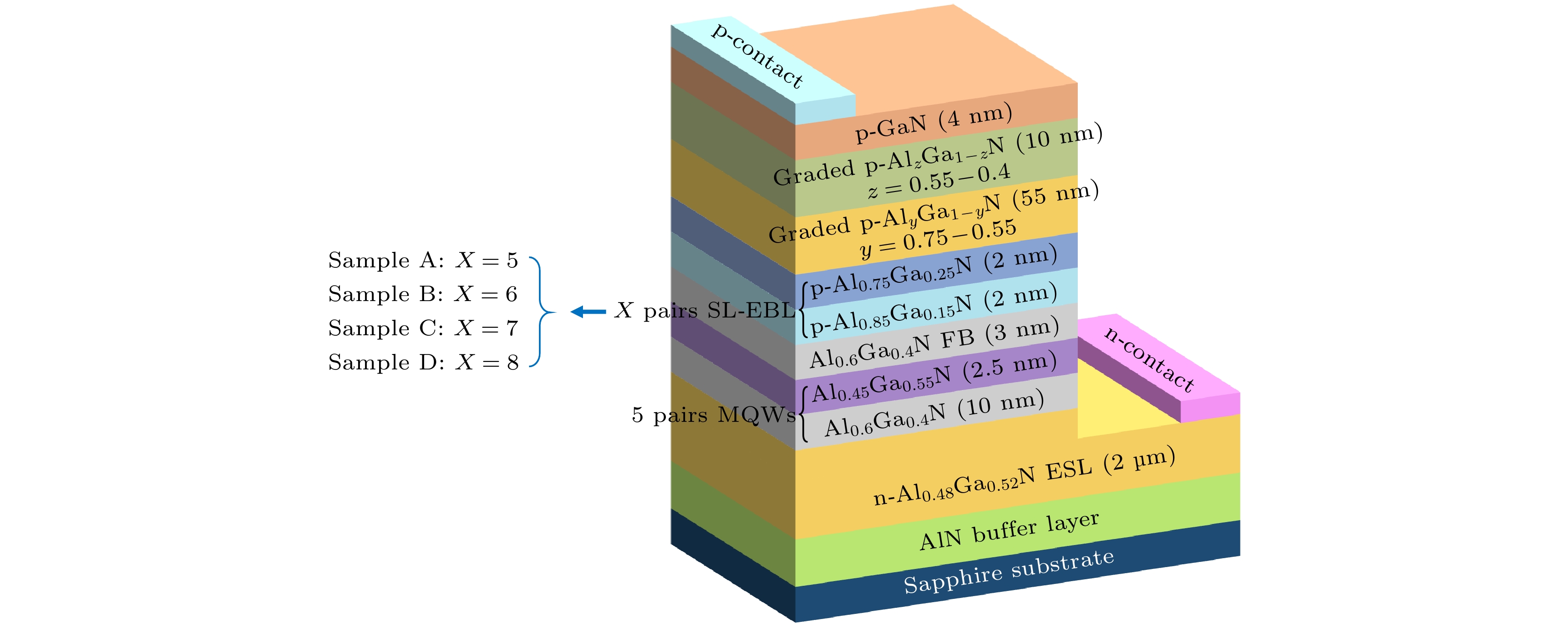
    • 在蓝宝石衬底上生长DUV-LEDs外延片, 依次生长: AlN缓冲层, 2 μm的n-AlGaN电子注入层(ESL, Si掺杂浓度为5×1018 cm–3), 由10 nm的Al0.60Ga0.40N量子垒(Si掺杂浓度为3×1018 cm–3)和2.5 nm的Al0.45Ga0.55N量子阱组成的5个周期的多重量子阱有源区(MQWs), 3 nm非掺杂的末垒(FB), 多周期的Al0.85Ga0.15N(2 nm)/Al0.75Ga0.25N(2 nm)超晶格EBL(SL-EBL, Mg掺杂浓度为1×1018 cm–3), 55 nm的Al组分梯度渐变p-Al0.75→0.55Ga0.25→0.45N(Mg掺杂浓度为3×1018 cm–3)空穴注入层(HIL)以及10 nm的p-Al0.55→0.40Ga0.45→0.60N过渡层(Mg掺杂浓度为3×1019 cm–3), 最上层为4 nm的p-GaN欧姆接触层(Mg掺杂浓度为2×1020 cm–3). 为了研究SL-EBL的周期数对AlGaN基DUV-LEDs光电性能的影响, 设计了SL-EBL周期数分别为5, 6, 7和8的4组样品, 分别对应样品A, B, C和D, 如图1所示. 所有外延片制备完成后, 采用统一的芯片制造工艺制备成500 μm×500 μm的倒装DUV-LEDs芯片. 采用透明的导电薄膜ITO和Ni/Au合金作为p型电极, Cr/Al/Ti/Au合金作为n型电极. 在本研究中, 为排除封装工艺对LED可靠性的影响, 将切割后的芯片固定在封装支架上, 样品不灌胶、无透镜进行测试. 室温条件下, 利用Keithley 2450源表、远方HAAS-2000高精度快速光谱辐射计和积分球对DUV-LEDs光电性能进行表征. 可靠性测试选择多只DUV-LEDs进行裸芯老化, 电流设置为100 mA(电流密度为40 A/cm2). 此外, 为了研究相关的物理机制, 利用计算机辅助设计(TCAD)仿真程序对其能带结构进行仿真研究, 仿真所用到的Ⅲ-Ⅴ族氮化物半导体的参数已经在本课题组发表的文献[20]中报道过.

    3.   结果与讨论

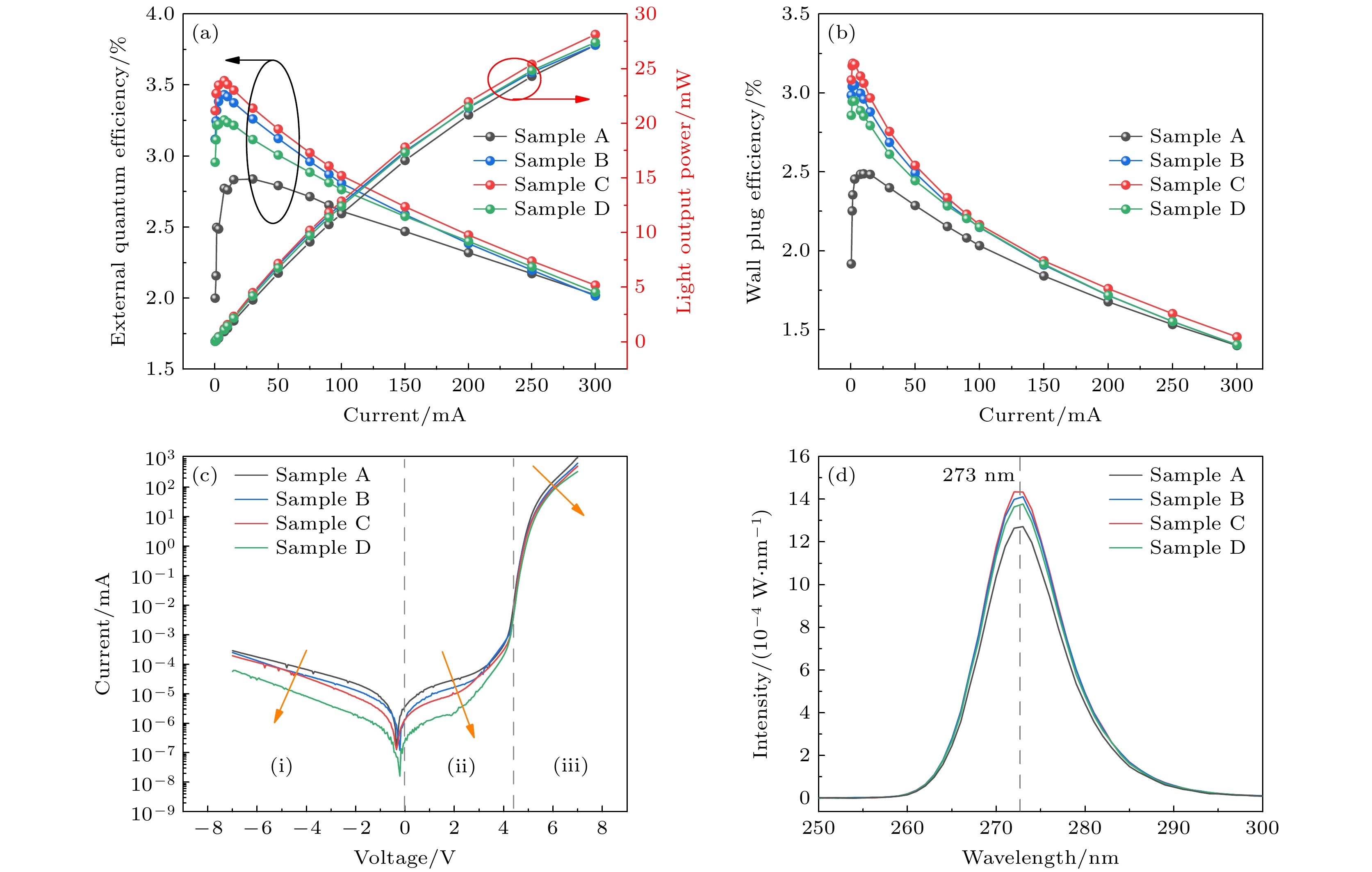
    • 图2(a), (b)分别给出了4种DUV-LEDs样品的LOP, EQE和WPE的实验结果. 由图2(a)可知, 4种样品的EQE随测试电流增大的变化趋势分为两个阶段: EQE先随测试电流的增加而达到最大值, 即Emax, 之后随注入电流增大而逐渐减小. 样品A, B, C和D均在7.5 mA时达到Emax, 分别为2.8%, 3.4%, 3.5%和3.2%, 随着SL-EBL周期数的增加呈现先增大后减小的趋势. 图2(b)中WPE的变化趋势与EQE变化趋势一致. 随着SL-EBL周期数的增加, 可以有效抑制穿透位错等缺陷, 由这些缺陷主导的陷阱辅助隧穿和非辐射复合降低, 有效阻挡了电子泄漏, 增大了有效辐射复合率[15]. 但当SL-EBL周期数增加, EBL厚度也随之增大, 空穴势垒厚度增大, 会产生阻碍空穴注入的负面作用, 使有效辐射复合率降低[19]. 最终在增强电子阻挡能力和阻碍空穴注入两种因素的共同作用下, EQE随SL-EBL周期数的增加表现出上述趋势.

      将图2(c)中的I-V曲线分为3个区域: (i)反向偏压区, (ii)低正向偏压区(0—4.2 V), (iii)开启电压以上的正向偏压区(＞4.2 V). 在(i)反向偏压区和(ii)低正向偏压区, DUV-LEDs的泄漏电流随SL-EBL周期数增加而逐渐减小, 周期数为8的样品D比周期数为5的样品A在–5 V电压下的反向漏电流低一个数量级. 反向漏电流与耗尽区的缺陷态密切相关[9], 由于AlGaN外延层和衬底之间的晶格失配和热失配, 导致AlGaN外延层中产生大量穿透位错等缺陷[21], 这些缺陷会辅助载流子隧穿, 形成跨越有源区的电子泄漏通道[14]. 在正向偏压下, 这种泄漏电流的存在是由于有源区内或周围产生的点缺陷对陷阱辅助隧穿和非辐射复合的促进作用[10]. 基于正偏压下 I-V曲线从10–5—10–4 mA 的线性部分来计算理想因子, 样品A, B, C和D理想因子分别为63.1, 59.5, 21和20.5, 均远大于2, 这主要是由于上述讨论的深能级缺陷和载流子隧穿泄漏的影响[22,23]. 同时可以发现随着SL-EBL周期数的增加, 泄漏电流不断减少, 理想因子也随之减小, 其可能原因在于增大超晶格电子阻挡层的厚度可以有效屏蔽位错. 在(iii)高于4.2 V的正向偏压区的电流也表现出随着SL-EBL周期数的增加而降低的现象, 电流的降低主要是由于SL-EBL厚度增大导致具有高Al组分的高阻层增加, 串联电阻增大. 由图2(d)可以发现4组样品的电致发光的峰值波长均在273 nm左右, 保证了实验测试结果不受波长差异的影响.

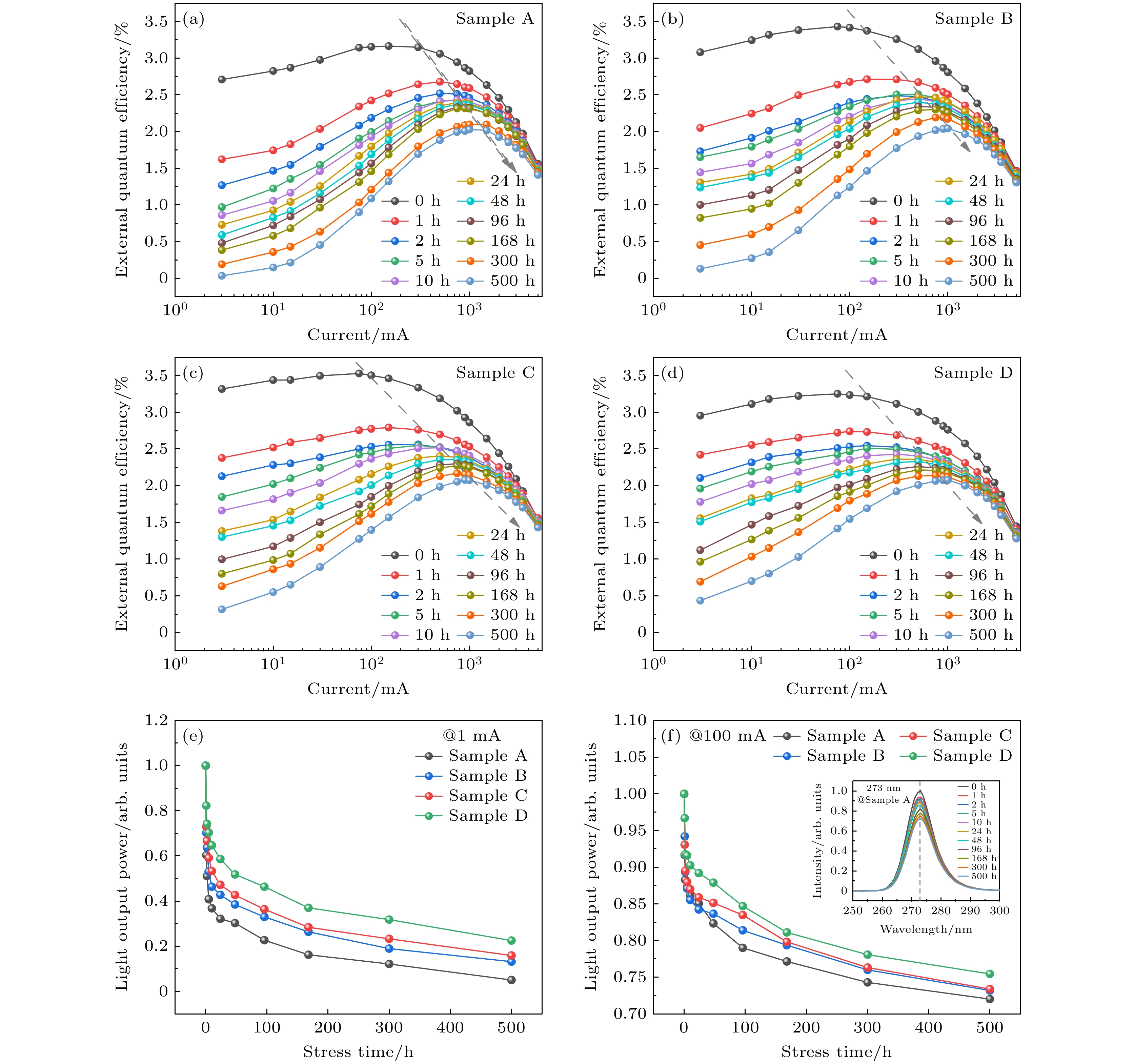
      为了评估不同SL-EBL周期数的4种DUV-LEDs结构的可靠性, 在室温下对4种DUV-LEDs的裸芯在恒定电流100 mA下进行可靠性实验. 经恒流老化500 h后4组样品的EQE整体变化趋势基本相同, 如图3(a)—(d)所示. 从该组EQE特性曲线的变化可以看出: 在小电流(1 mA)下, 长时间的电流应力导致DUV-LEDs的EQE显著下降; 对于大电流(100 mA), 老化后EQE的下降明显减小.

      从图3(e), (f)的归一化光输出功率曲线可以清晰看出, SL-EBL周期数不同的样品光衰差异较大. 其中, SL-EBL周期数最大的样品D 的光输出功率衰减最少, 可靠性最佳, 表明优化SL-EBL周期数是提高LED器件可靠性的有效方法. 通过增加SL-EBL周期数能有效的屏蔽位错, 降低电子泄漏, 提高器件可靠性. 同时, 比较图3(e), (f)可以发现, 4组样品的光输出功率均在小电流下退化的更加明显. 以样品A为例, 经过500 h的老化后, 1 mA下光输出功率退化至未老化时光输出功率的5%, 100 mA下测得光输出功率依然维持在初始值的72%. 随着老化的进行, 电流流经有源区的位错缺陷会造成晶格振动产生热量, 导致有源区内缺陷增生, 晶体质量变差[24]. 在小电流下, 随着老化的进行, 越来越多的载流子被禁带中的缺陷能级所俘获并通过非辐射复合的方式进行复合, 导致实际参与辐射复合发光的载流子数变少, 使得4组样品的发光强度在小电流下显著下降[25]. 而在大电流下, 缺陷中心可能会因高注入密度的载流子而饱和, 导致实际参与辐射复合发光的载流子数不会发生明显变化, 无法显著限制DUV-LEDs的发光强度[26]. 除此之外, 图3(f)中插图显示峰值波长均保持在273 nm, 未发生变化(仅示出具有代表性的样品A的电致发光光谱, 其他样品老化后的光谱相似, 因此这里没有显示).

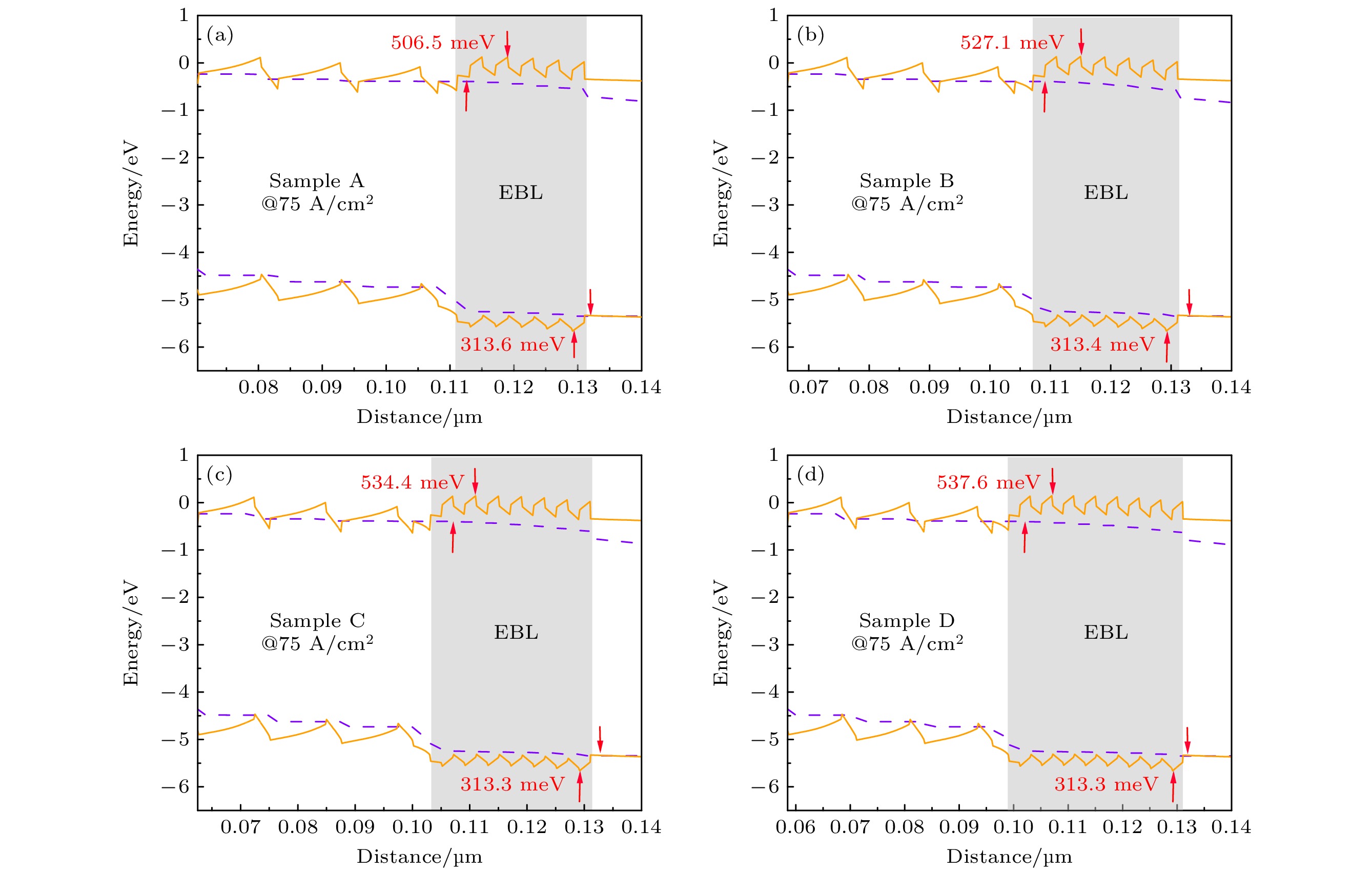
      如图2(a)所示, 未老化前样品A的EQE与其他样品相差较大, 引起这种现象的一种可能原因是有源区和EBL之间的导带偏移较小, 造成电子从有源区向p型层泄漏的概率增加. 为了证明我们的猜想并探究影响DUV-LEDs性能的物理机制, 对4组结构的能带结构进行了模拟计算. 图4(a)—(d)分别示出了4种不同EBL结构在75 A/cm2电流密度下计算得到的能带(粉色实线)和准费米能级(蓝色虚线). 可以观察到, 随着SL-EBL周期数(厚度)增加, 4组结构的EBL电子势垒高度(Φe)分别为506.5, 527, 534.4, 537.6 meV. 显然, 增加SL-EBL周期数能有效地提高EBL的电子势垒高度. 与样品A相比, 样品C和样品D的电子势垒高度分别提高了5.5%和6.1%, 这也使样品C和样品D能更有效地限制电子, 防止电子向p型层泄漏. 此外, 随着SL-EBL周期数增加, EBL空穴势垒高度(Φh)分别为313.6, 313.4, 313.3, 313.3 meV, 4组结构之间的空穴势垒高度无明显变化. 在所设计的DUV-LEDs中, SL-EBL周期数分别从5(样品A)增大到7(样品C)时, 空穴势垒高度不变的同时电子势垒高度增大了5.5%. 因此, 实现了样品C的光电性能的显著提高, 如图2所示. 此外, 势垒厚度的变化对载流子注入的影响也不容忽视, 增加SL-EBL的周期数虽然可以有效地调节DUV-LEDs的势垒高度, 但样品D的EBL厚度由初始的20 nm增大到了32 nm, 更厚的空穴势垒不利于空穴的带内隧穿, 妨碍了空穴向有源区的注入, 使有源区内的空穴浓度降低, 导致样品D的EQE下降[27]. 有研究表明[15], 在FB/EBL/HIL异质结中, EBL的电场会影响空穴注入效率, 随着EBL厚度增大, 电场强度降低, 所以空穴注入效率会随着EBL厚度增大而下降. 综上所述, 增大SL-EBL的周期数会导致电子势垒高度增大, 抑制了电子泄漏; 空穴势垒高度变化可以忽略不计, 对空穴注入的影响很小. 然而, 增加SL-EBL的周期数等同于增大了EBL厚度, 导致空穴势垒的厚度增大, 阻碍了空穴由p型层向有源区注入.

      为了研究SL-EBL周期数对DUV-LEDs的载流子复合机制的影响, 可以利用载流子复合模型(ABC模型)对测试的EQE曲线进行拟合. 在ABC模型中包括5个变量: SRH非辐射复合系数(A)、辐射复合系数(B)、俄歇复合系数(C )、有效激活区厚度(d)以及光提取效率(γ ). 电流密度方程如下[28]:

      其中q为基本电荷, n为注入载流子浓度. 由此, IQE和EQE可以表达为

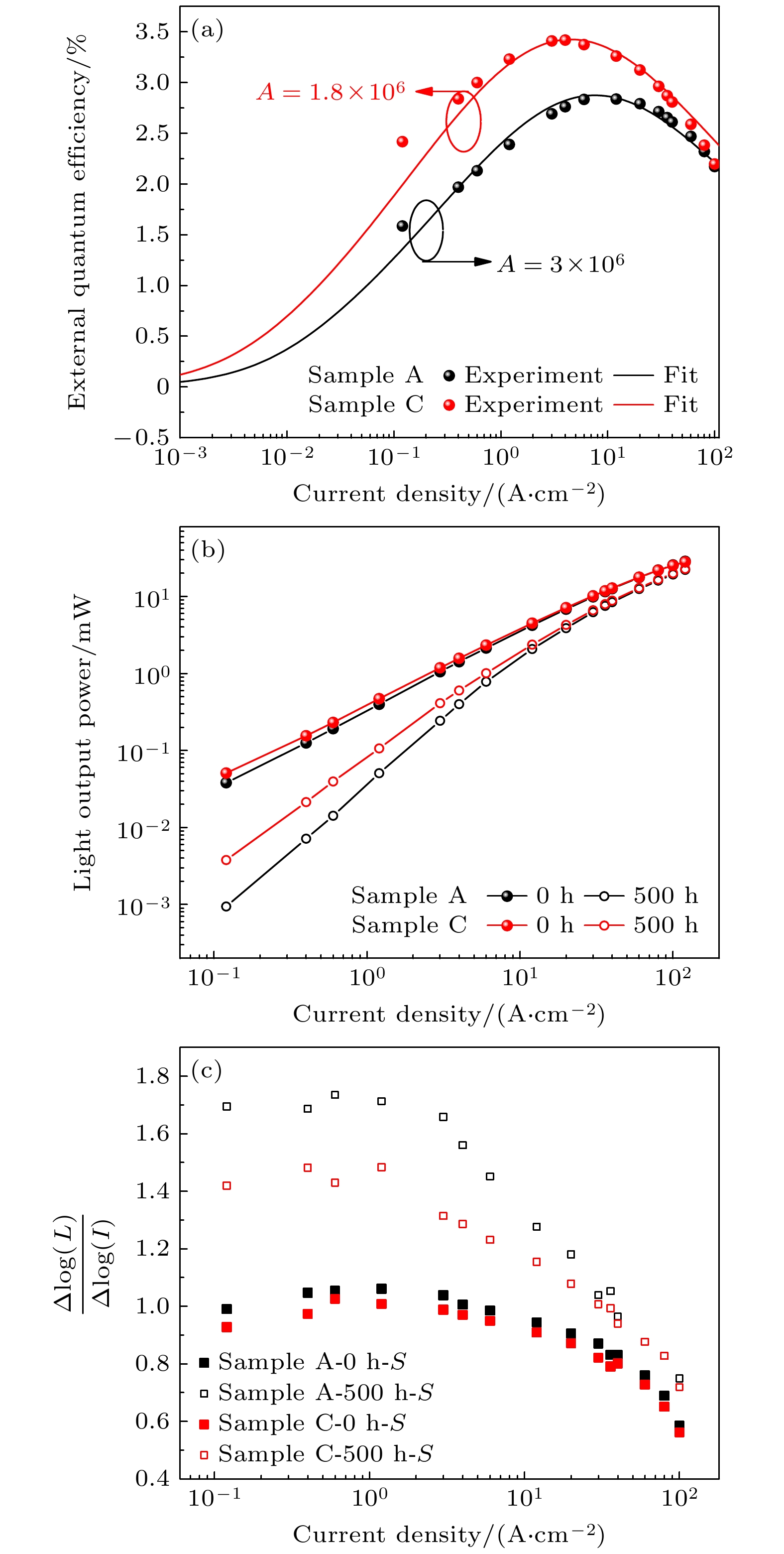
      在DUV-LEDs中, 由于空穴质量远大于电子的质量, 造成了电子和空穴传输的不对称性, 所以电子和空穴的复合主要发生在靠近EBL的末阱中. 因此, 在ABC模型中设置d值为2.5 nm与末阱厚度相等. 由于晶格缺陷的存在, DUV-LEDs器件的SRH非辐射复合系数相对较高, 在室温下通常在 106—108 s–1 之间[29]. 此外, 由于在4组样品中除了SL-EBL的周期数不同, 其余结构完全一致, 所以在拟合过程中假定B, C和γ相同, 而由于SL-EBL厚度对载流子注入效率的影响, 对样品C的载流子浓度向下进行微调. 如图5(a)所示, 经过对样品A和样品C的EQE曲线进行拟合, 得到SRH非辐射复合系数分别为3×106 s–1和1.8×106 s–1. 随着SL-EBL周期数增加, SRH非辐射复合系数明显降低.

      图5(b)为样品A和样品C在老化前后测量的双对数坐标L-I曲线, 其中L为光输出功率. 可以看出, 与具有较低SRH非辐射复合系数的样品C相比, 样品A经过500 h的老化后表现出更强烈的光输出功率下降. 为了进一步推断两个样品在老化前后发光过程中主要的载流子复合机制, 根据Kim等[21]的研究, 引入参数S. 在对数坐标中, S值就是L-I曲线在一定电流范围内的斜率, 计算公式为

      通常在小电流时, 有源层中的非辐射复合过程占主导, S = 2; 当电流继续增大, 自由载流子的辐射复合过程或俄歇复合过程占主导时, S值分别接近于1和0.67[21]. 图5(c)的散点图示出了样品A和样品C老化前后的S值, 老化前用实心方框表示, 老化后用空心方框表示. 在老化之前, 样品A和样品C的S值在小电流密度范围内均接近于1, 表明老化前辐射复合过程占主导地位. 经过500 h的老化后, 在小电流范围内对数L-I曲线的斜率均向 2移动(样品A和样品C分别为1.7和1.4), 表明非辐射复合对于整体复合的占比增大[21,30]. 晶体初始缺陷引入的非辐射复合中心会在器件退化中发挥作用, 长期老化会使器件有源区域内缺陷增生, 导致非辐射复合增加. 此外, 老化后样品A的S值较样品C更接近于2, 进一步证明老化后样品A在小电流下的SRH非辐射复合更强. 产生这种现象的主要原因是由于高Al组分的EBL层生长温度更高, 在同样的生长速率下, SL-EBL周期数较多的样品对有源区的热处理时间更长. 对于整个量子阱区域, 尤其是距离最近且主要发生辐射复合发光的末阱和末垒, 可以利用相对较高的温度以及热应力促进位错的湮灭和合并, 减少非辐射复合中心[31–32].

    4.   结　论

    • 本文研究了SL-EBL周期数对发光波长为273 nm的AlGaN基DUV-LEDs的发光效率、I-V特性、可靠性以及有源区载流子复合机制的影响. 实验结果表明: 随着SL-EBL周期数增加, DUV-LEDs的EQE和WPE呈先增大后下降的趋势. 当周期数设计为7 (厚度为28 nm)时, DUV-LEDs的峰值EQE和WPE分别为3.5%和3.2%, 对比周期数为5的结构提升了24%和28%. 通过I-V曲线可以发现, 泄漏电流随着SL-EBL的周期数增加而减小, 4组样品的理想因子均远大于2, 主要原因是由于存在深能级缺陷和载流子隧穿泄漏. 可靠性测试结果表明, SL-EBL的周期数增加有利于屏蔽位错, 降低电子缺陷辅助隧穿泄漏, 减少缺陷对载流子的捕获, 降低非辐射复合, 提高了DUV-LEDs的可靠性. 通过模拟能带结构, 发现SL-EBL周期数增加提高了电子势垒高度, 可以起到抑制电子泄漏的作用, 但是空穴势垒厚度的增大会阻碍空穴向有源区注入. 利用ABC模型对样品A和样品C的EQE曲线进行了拟合, 得到SRH非辐射复合系数分别为3×106 s–1和1.8×106 s–1, SL-EBL周期数的增加可显著降低非辐射复合系数, 同时经过500 h老化后S值的增幅更小(样品A和样品C分别为1.7和1.4), 最终表现为更低的光功率衰减, 本文为实现高光效高可靠性的AlGaN基DUV-LEDs提供了新思路.

    参考文献 (32)

目录

/

返回文章
返回