-
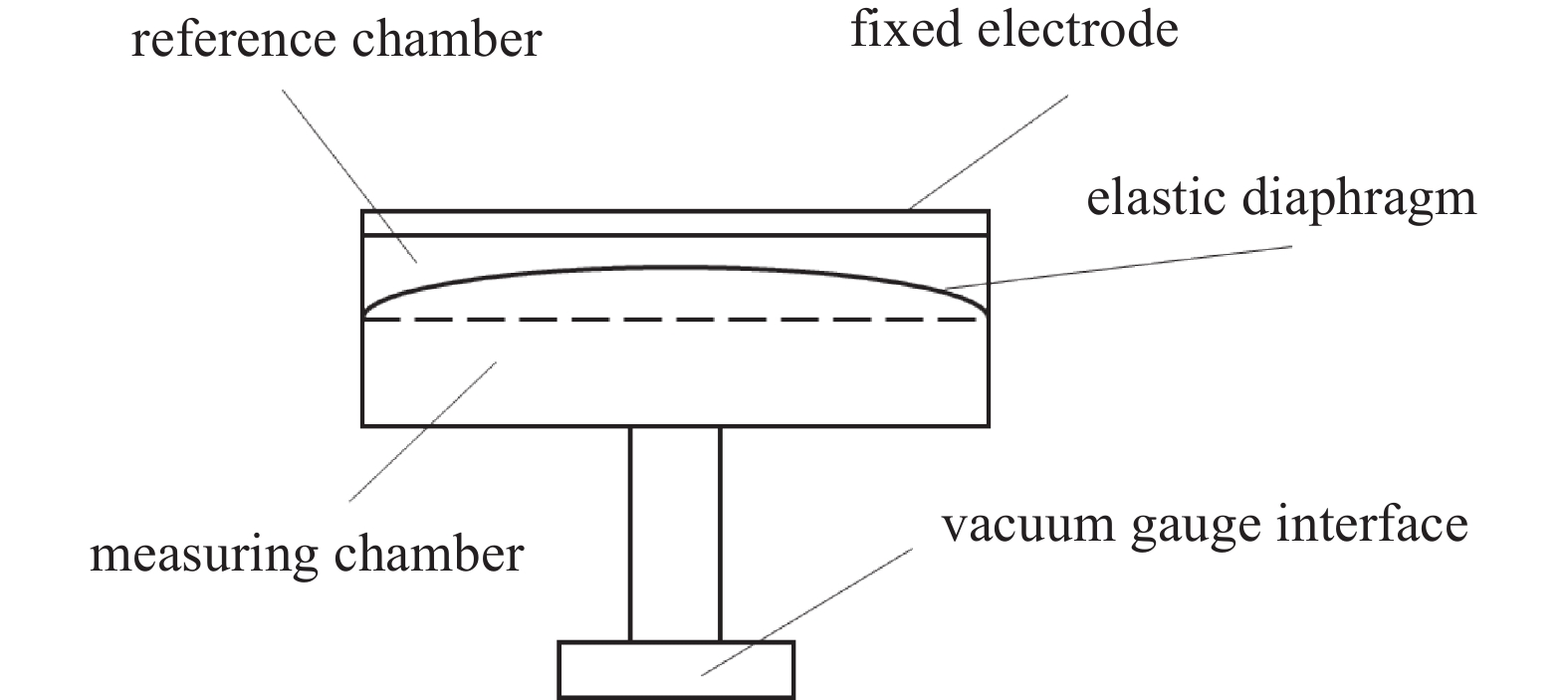
在粗低真空环境中,当需要精确测量气体的真空度时,通常选用电容薄膜真空计(Capacitance Diaphragm Gauge, CDG)[1-3]。CDG的测量原理如图1所示,主要由弹性膜片、固定电极、参考腔以及测量腔构成。真空参考腔通常抽至真空状态,并用吸气剂维持其真空环境。当测量腔与参考腔处于同样的真空状态时,弹性膜片处于平衡位置,此时固定电极与膜片之间的电容C最小;当测量腔真空度增大时,弹性膜片逐渐偏向固定电极一侧,使得电容C增大。通过测量电容C即可实现对测量腔真空度的测量[4-5]。
相较于其他类型的真空计,CDG具有较高的测量精度和稳定性,测量精度可达读数的0.5%甚至更低[6]。但是当真空计的测量环境温度发生变化时,测量结果会发生一定的偏移。各CDG生产厂商通常将真空计的零点温度效应和满量程温度效应单独给出,并未将温度效应计算入真空计的测量精度中。在考虑温度效应的情况下,部分真空计的测量精度将大大降低。
为了改善真空计的温度效应问题,CDG研发公司对真空计的结构进行了优化,并通过加装恒温装置,将真空计的环境温度维持到室温以上,以保持真空计测量结果的稳定。结构的优化也难以完全抑制温度对CDG测量精度的影响,加装恒温装置虽然很好的抑制了温度的影响,但温度梯度的产生导致了真空系统出现了热传导效应,CDG测量腔中的压力与实际被测压力存在一定的偏差。研究者针对CDG的热传导效应开展了大量的研究工作,对其测量结果进行修正,但恒温式CDG的另一些弊端仍然无法解决[7-9]。恒温装置给真空系统带来了一定的热量,对真空系统会产生一定的影响。而恒温式CDG在温度较低的情况下进行测量时,其功率会增大,当功率无法满足时,CDG仍然会发生温度漂移的现象。近来研究表明,CDG在高温烘烤恢复后其测量结果与烘烤之前表现出较高的一致性 [10],环境温度与其造成的误差具有一定的关系。为研究温度补偿解决上述问题的可行性,本文对CDG的温度特性开展了相关的研究工作。
-
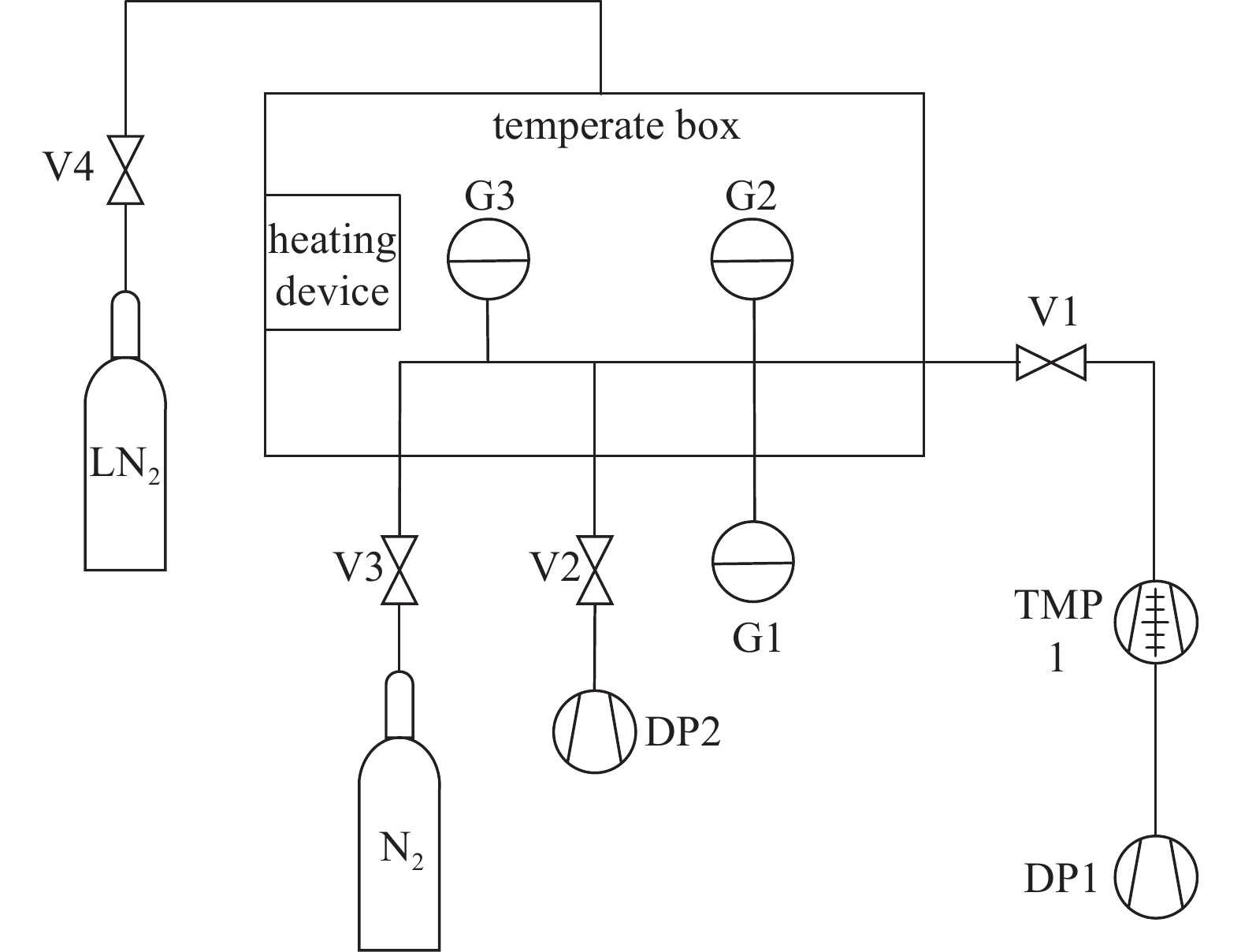
实验所采用的实验装置如图2所示,研究对象保温型真空计G2、非保温型真空计G3放置于恒温箱内,保温型真空计G1放置于室温环境中用于和G2、G3进行比对。升温时通过恒温箱中的加热装置将恒温箱中的温度提升至所需温度;降温时,通过电磁阀V4将液氮引入恒温箱,液氮的蒸发使得恒温箱温度下降。真空系统的真空度通过V1、V2、V3进行调节。
G1、G2以及G3均为1333 Pa类型的普通金属型CDG,其薄膜由镍铬合金3J53制成。实验利用99.9%的N2对真空计性能进行测试。由于真空计通过橡胶圈连接至真空系统中,温度过低会造成密封橡胶圈失效,使得系统无法维持真空,因此恒温箱中的温度最低限定为−30℃。保温型真空计G2的恒温温度为45℃,温度高于45℃时G2的恒温装置无法工作,G2可视为普通型CDG,其特性与G3相同,因此考虑将实验的最高温度设置为50℃。实验包含升温过程与降温过程,每隔5℃改变真空系统内的压力进行一组实验。
实验时,首先打开V1,将真空系统的压力抽至CDG的测量下限,并记录G1、G2与G3的值,之后将温度调节至需要测量的点,等待30 min后开始调节真空系统的压力。调节真空度时,关闭V1并打开V3,将N2引入系统,将真空度调节至1200 Pa左右,之后关闭V3打开V2开始抽气,在G1大致达到1100、900、700、500、300、100、90、70、50 Pa时,记录真空计G2以及G3的读数,此时机械泵抽气速度缓慢,关闭V2,打开V1继续对真空系统进行抽气,在G1示数在30、10、9、7、5、3 Pa以及真空度达到G1的测量下限时,记录G2以及G3的值。完成一组实验后,改变恒温箱的温度,进行下一组实验。
-
参考真空计G1在实验过程中始终处于室温环境,表1为真空计G1在零点时的离差,可以看出测量值与零点的平均值之间的差值小于0.08 Pa,小于满量程的0.006 %,说明G1的测量结果具有很好的稳定性,恒温箱内温度的变化对其测量结果几乎没有影响。
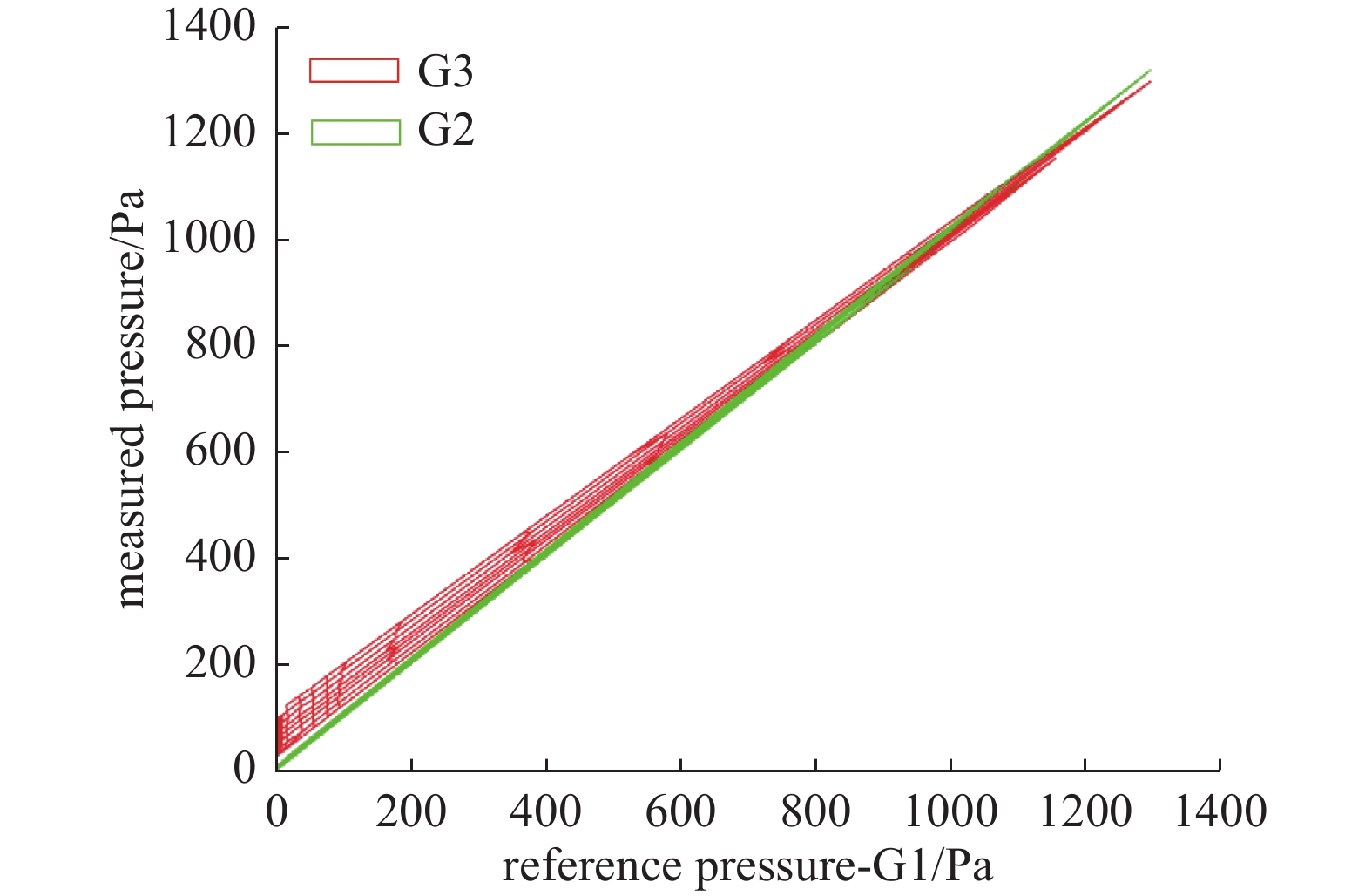
CDG的测量结果如图3所示,横坐标轴为用于对比的标准真空计G1,纵坐标轴为放置在恒温箱中的真空计。通过实验结果可以看出,在不同的温度下,保温型真空计G2的测量结果一致性较好,而没有保温装置的真空计G3的零点和满量程均出现了较大的漂移情况。
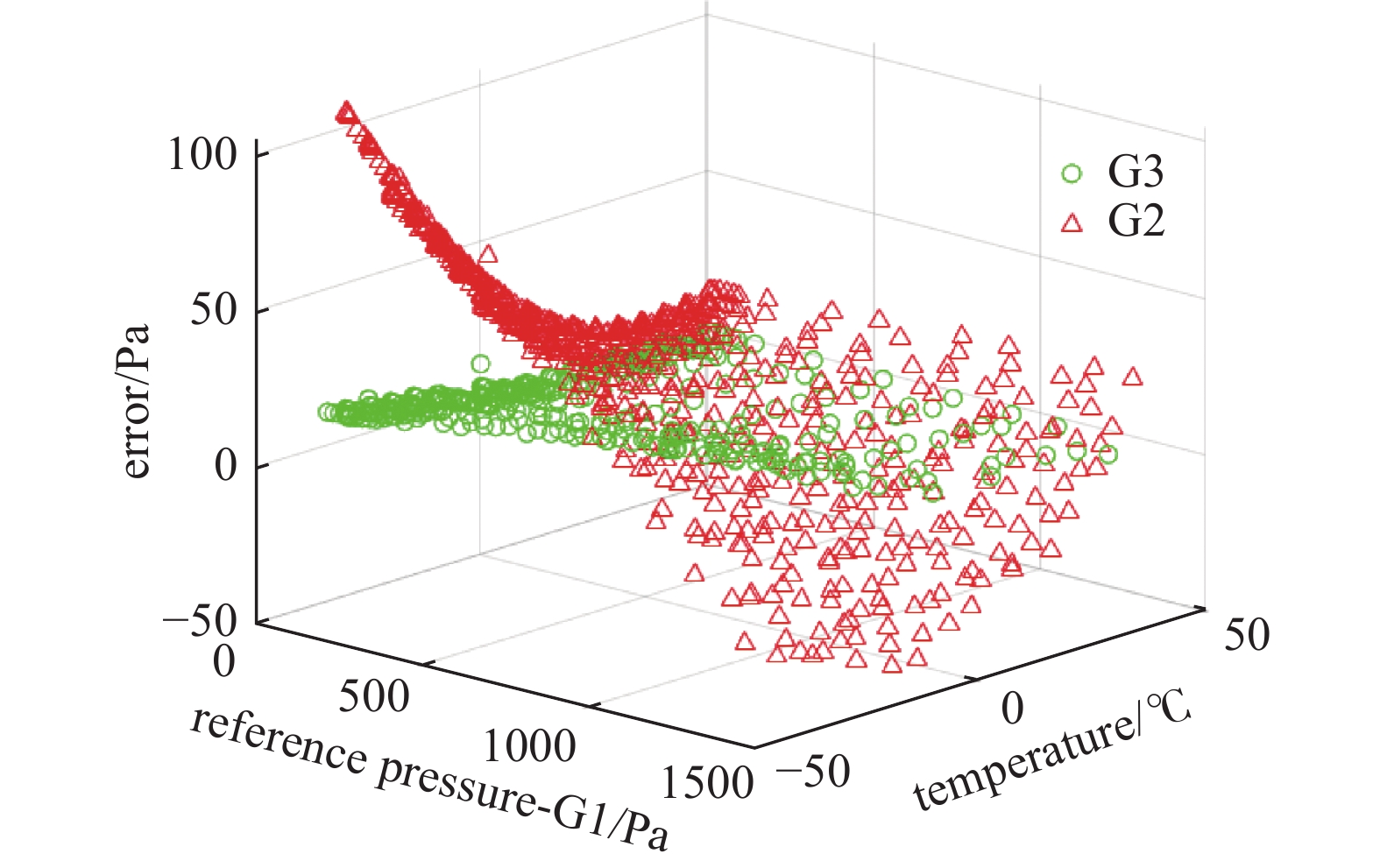
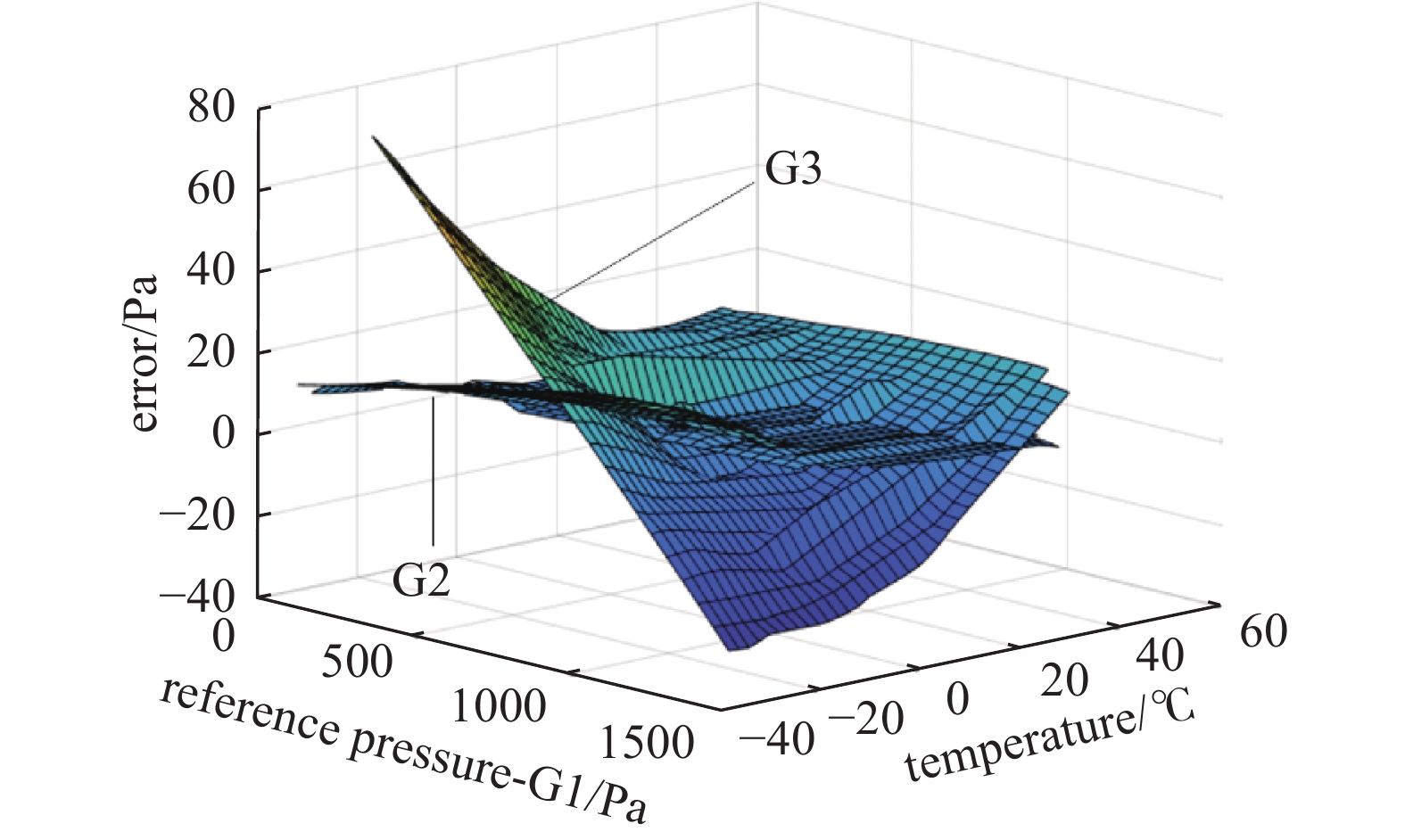
为了更加清晰的了解CDG示数随环境温度的变化情况,考察了真空计G2、G3与参考真空计G1之间的误差变化情况,并将其绘制在三维坐标系中如图4 所示。根据测试结果可以看出,保温型真空计G2与G1之间的误差较小,可近似视为恒定值,误差大小与环境温度、真空度变化情况无关;而非保温型的真空计G3与G1之间的存在较大的误差,这种误差随着温度和真空系统中压力的变化而变化。从多次实验的结果可以看出,G3与G1的误差随着温度与真空系统中压力的变化表现出一定的重复性,因此可以研究温度对非保温型真空计测量误差的影响情况,进而提高G3的测量精度。
-
在修正温度对G3测量结果的影响时,需要获得任意温度、压力下真空计产生的误差值。通过实验获得的数据均为离散的值,若要获得真空计在任意温度、压力下的误差,可利用插值的方法对所需点的误差进行估计。在实验过程中,每组实验的温度可视为一致,但是真空系统的压力很难在每次测量时调节为恒定值,因此无法划定均匀的网格对真空计进行双线性插值处理。因此考虑使用基于Delaunay 三角剖分的线性插值方法获取每个点的误差值[11]。
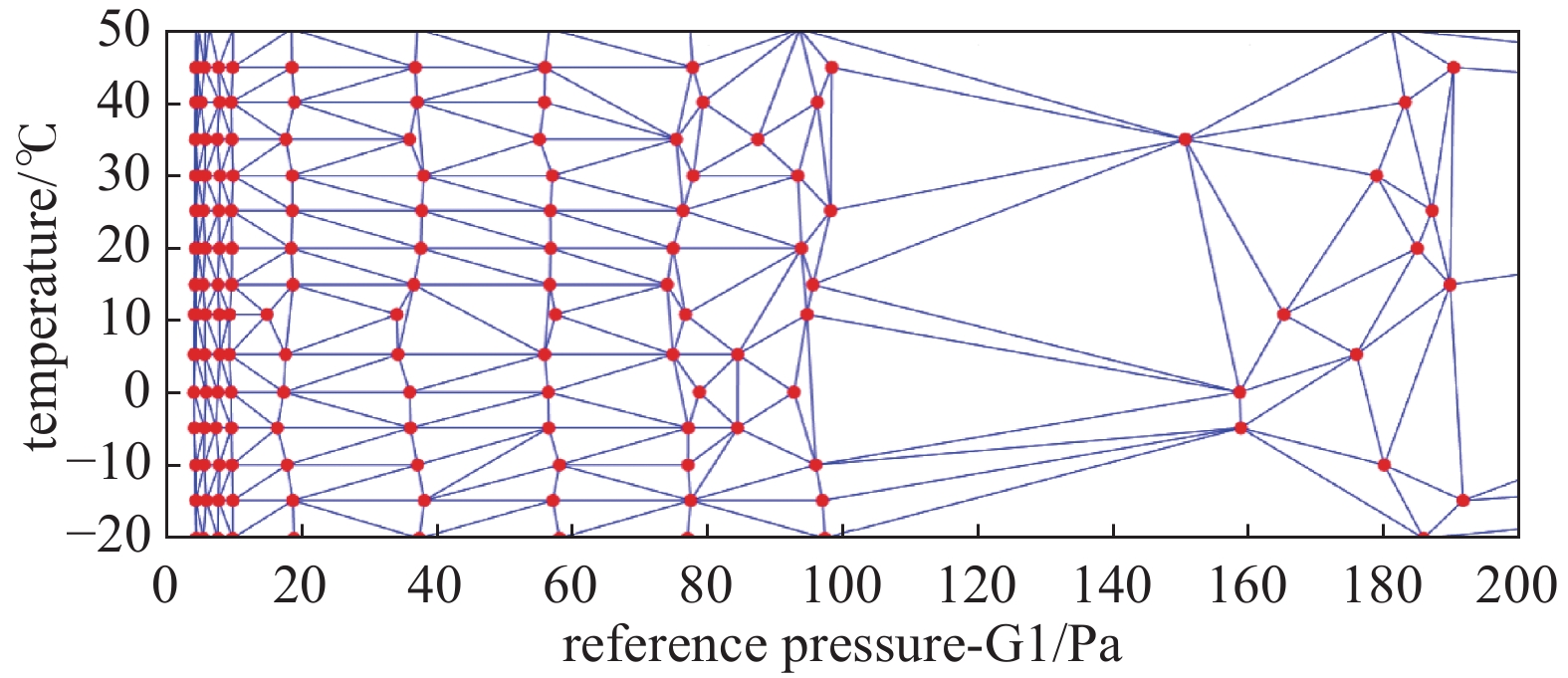
如图5所示,利用Delaunay 三角剖分方法可以将数据压力-温度坐标平面划分互不相交的三角形区域。在这些三角形中,任意一个三角形的外接圆不包含该三角形以外的点。Delaunay三角剖分所形成的三角形集合具有的最小角最大的特点,目前得到了广泛的应用。在完成对平面网格的划分后,即可用三角形顶点坐标的值计算可以在三角形区域内任意一点对应的误差的值。记三维坐标系中,三角形三个顶点及其对应的误差值为A(p1,T1,e1)、B(p2,T2,e2)和C(p3,T3,e3),假设在三角区域内每个点的坐标均在同一平面,则设该平面为:
式中a、b和c为平面的参数,p为压力,T为温度,e为CDG在(p,T)点处产生的误差值。由于三角形三个点均在该平面上,因此可以得到:
其中e为误差向量,a为参数向量,X为三角形坐标矩阵,通过矩阵运算可以得到参数向量a的值,进而求解出三角形内任意一点D(p, T)的误差值e。
-
通过上节方法,可以计算出每个所需点的误差值,绘制出的CDG的坐标曲面如图6所示,其更加直观的显示了真空计的误差在不同压力点、不同温度下的变化情况。
真空计G2在其正常工作范围内(0℃~45℃)时误差最小,而温度低于0℃后,其误差有随着温度的降低而逐渐变大的趋势;真空计G3在常温时(20℃~30℃)的误差相对较小,随着温度的升高或降低,真空计的误差均有变大的趋势,这种现象在零点尤为明显,在−30℃时最大误差达到了100 Pa,温度产生的读数误差达到了满量程的7.5%,这种误差对于一些较为精密的实验影响相当大。
-
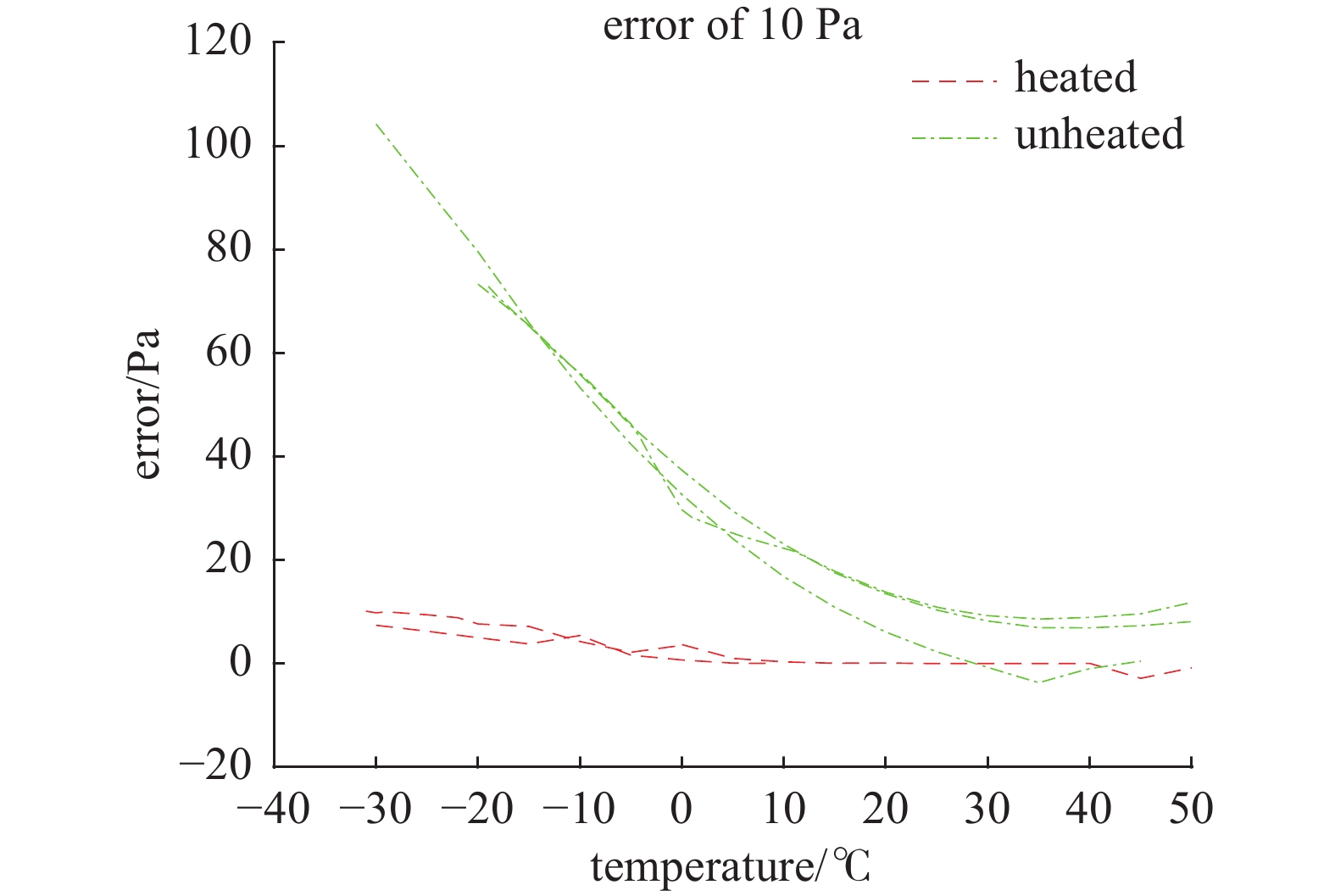
零点温度温度系数和满量程温度系数是衡量CDG测量准确度的重要指标,从图6所示的误差曲面中可以截取得到CDG在零点以及满量程附近温度造成的误差曲线。
图7为CDG在10 Pa时的温度误差曲线,该曲线表征了CDG测量误差在零点时受到温度影响的情况。可以看出保温型真空计的误差受到温度干扰很小,在10℃~50℃范围内时,G2与G1的误差几乎保持不变,表现出很好的温度稳定性。当温度小于0℃后,随着温度的降低,真空计G2与G1的误差逐渐增大,这可能是由于真空计的加热功率已经达到最大,无法继续将真空计的温度维持到设定温度造成。
非保温型的真空计受到温度的影响较大,并表现出一定的非线性。真空计G3与G1的误差在30℃~50℃时较为恒定,随着温度的持续降低,G3与G1之间的误差也越来越大。当CDG接近零点位置时,薄膜两侧的压差较小,此时薄膜几乎不发生弹性形变。温度变化造成的零点漂移可能是由电极与薄膜具有不同的热膨胀系数,当环境温度降低时,电极与薄膜之间的间隙减小,进而使得电容变大,测得的结果偏大。除此之外,真空计的检测电路也会受到温度的影响,图7中G3在30℃ ~ 50℃时,误差有先减小后增大的趋势,这种现象可能是传感器与检测电路共同作用的结果。
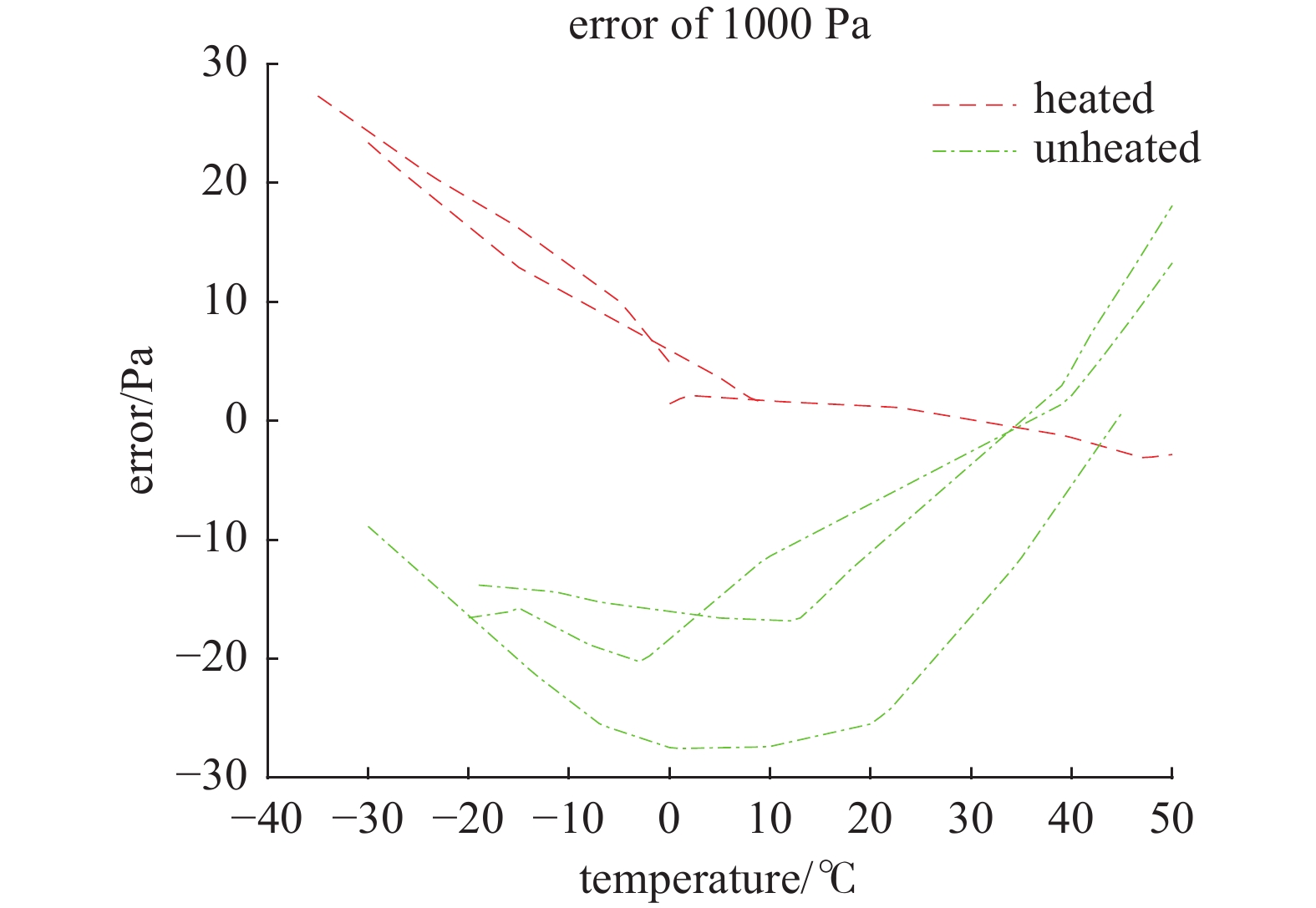
图8显示了CDG在接近满量程时的误差变化情况。保温型CDG误差在小于0℃时依然较小,但是在小于0℃时,误差随着温度的降低而逐渐增大,这种现象进一步印证了保温型CDG在低温环境中存在功率不足的问题。非保温型的CDG在满量程附近明显出现了先减小后增大的趋势,相较于在零点,非保温型的CDG误差明显有所减小,除了薄膜与电极之间的间隙以及电路放大倍数随温度发生变化外,薄膜的挠度变化也是造成这种现象的因素之一。
对比图7与图8可以发现,在-30℃ 时非保温型CDG的误差在满量程时下降了约110 Pa,当温度为50℃ 时满量程误差上升了约5 Pa。即在同样的压力下,温度越低,非保温型CDG的挠度变化越小,反之则挠度变化增大。
-
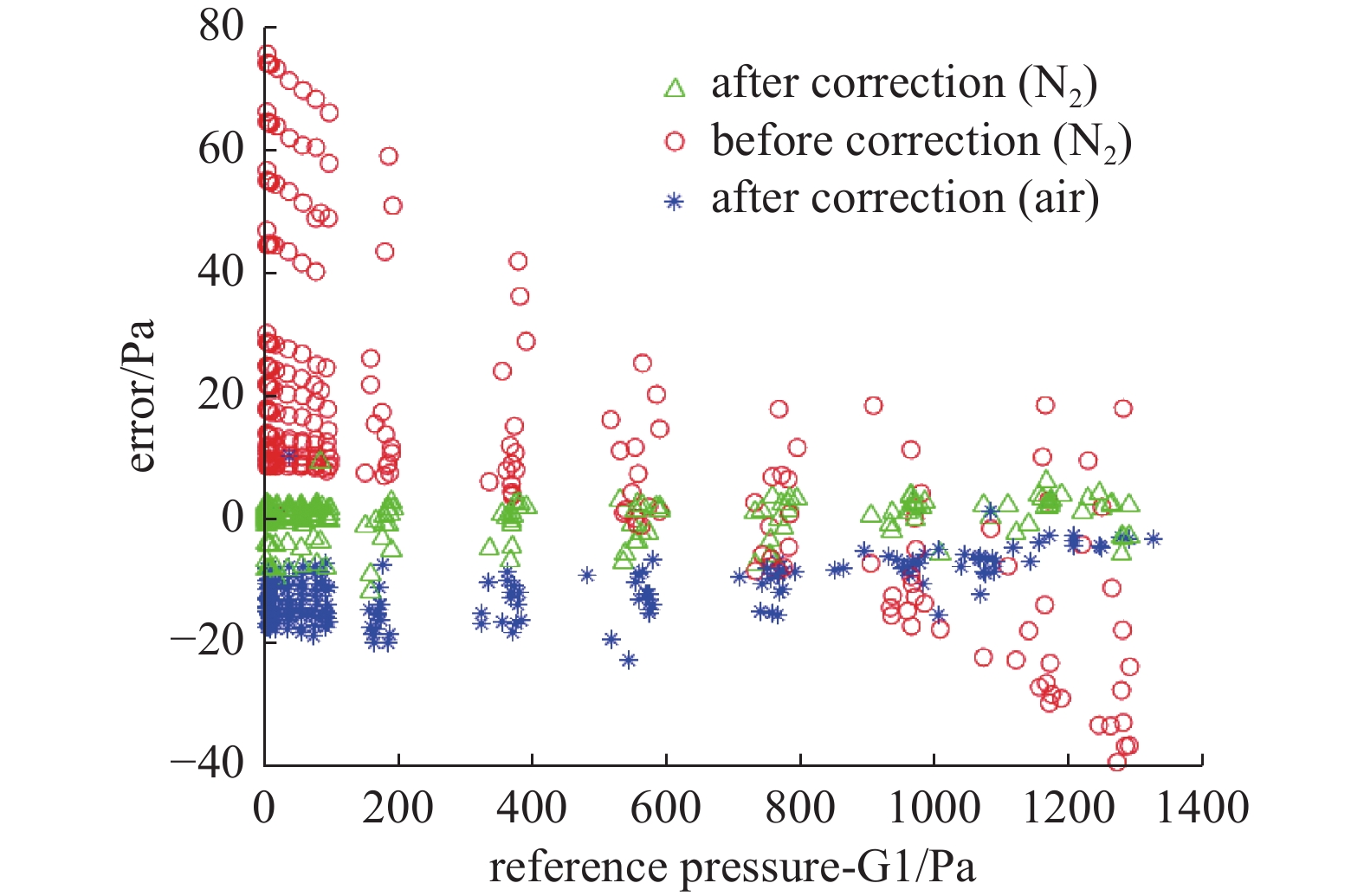
为验证温度-压力误差曲面修正的效果,采用一组温度实验的数据绘制温度-压力误差曲面。得到修正曲面后,对分别用氮气和空气进行实验的数据进行修正,修正前后的误差如图9所示。
修正结果显示,该方法具有良好的效果,在利用N2进行的实验中,非保温型CDG的测量误差从修正前最大6%(F.S.)下降到了0.75%(F.S.),测量精度得到了大幅提升。CDG是一种绝对型真空计,其测量结果与被测气体种类无关。从图9中可以看出,利用温度误差曲面修正后的空气组实验数据同样具有较好的修正效果,但其误差整体上向负方向漂移了5 Pa左右,造成这种现象是由于空气组实验相较于其他两组实验晚两个月进行,CDG的膜受到应力影响产生了一个固定的误差,这个误差后期可以通过定期的校准进行消除。
利用误差曲面修正的方法显现出了优异的修正效果。相较于给CDG添加保温装置,该方法不仅避免了向真空系统中增加热源,同时也解决了保温型CDG只能在特定温度区间内稳定测量的缺陷。
-
本文针对保温型CDG和非保温型真空计开展了 −30℃~50℃ 的温度效应实验,实验发现保温型真空计在额定温度 0℃~45℃ 范围内时具有较好的测量精度,超出温度范围后真空计的测量结果出现了一定的误差。温度对非保温型CDG的影响较大,利用基于三角剖分的插值方法获得真空计的误差曲面,可以对真空计的测量误差进行修正,使其在不同温度、压力下均达到较好的测量结果。
电容薄膜真空计的温度特性研究
Temperature Characteristics of Capacitance Diaphragm Gauge
-
摘要: 电容薄膜真空计(Capacitance Diaphragm Gauge, CDG)是一种常用的粗低真空测量传感器,具有较高的测量精度和稳定性。温度是影响真空计量准确性的重要因素之一,环境温度的变化会导致CDG的测量结果发生较大的偏移。为探究温度对CDG测量结果的影响情况,开展了温度环境实验,考察了保温型与非保温型CDG在 −30℃~50℃ 环境中测量结果的变化情况。实验结果表明,保温型CDG在额定温度 0℃~45℃ 环境中测量结果较为稳定,温度高于或低于该区间范围时,测量结果会发生一定程度的偏移;温度对非保温型CDG造成的影响较大,利用温度-压力误差曲面可以修正CDG误差,提高真空计测量精度。
-
关键词:
- 电容薄膜真空计 /
- 温度特性 /
- Delaunay三角剖分插值
Abstract: Capacitance Diaphragm Gauge (CDG) is a type of sensor commonly used under low vacuum with high accuracy and stability. Temperature is one of the most important factors affecting its measurement accuracy. When the ambient temperature changes, the measurement results of CDGs will also drift accordingly. We experimented with the effect of temperature on CDGs and quantified the measurement errors of heated and unheated CDGs in the environment of −30℃~50℃. The experimental results show that the measurement results of the heated CDGs are stable at the rated temperature 0℃~45℃, and the measurement accuracy will deteriorate if the temperature exceeds this range. The error caused by the temperature for the unheated CDG is relatively large. The temperature-pressure error surface proposed in this paper can effectively reduce the measurement error of the unheated CDG and improve its accuracy. -

-
表 1 G1在不同温度下零点测量值与平均值间的离差
Table 1. Deviation between the zero-point measured value and the mean value of G1 at different temperatures
T/℃ p/Pa △p%(F.S.) −20 0.071333 0.0054% −15 0.051333 0.0039% −10 0.041333 0.0031% −5 0.021333 0.0016% 0 −0.048667 −0.0037% 5 −0.058667 −0.0044% 10 −0.078667 −0.0059% 15 0.001333 0.0001% 20 −0.008667 −0.0007% 25 −0.008667 −0.0007% 30 0.031333 0.0024% 35 −0.018667 −0.0014% 40 0.001333 0.0001% 45 −0.028667 −0.0022% 50 0.031333 0.0024% -
[1] Song P,Ma Z,Ma J,et al. Recent progress of miniature MEMS pressure sensors[J]. Micromachines,2020,11(1):56 doi: 10.3390/mi11010056 [2] Hyland R W,Shaffer R L. Recommended practices for the calibration and use of capacitance diaphragm gages as transfer standards[J]. Journal of Vacuum Science & Technology A:Vacuum, Surfaces, and Films,1991,9(6):2843−2863 [3] Feldman J,Paul M,Xu G,et al. Effects of natural zeolites on field-scale geologic noble gas transport[J]. Journal of Environmental Radioactivity,2020,220:106279 [4] Jousten K,Naef S. On the stability of capacitance-diaphragm gauges with ceramic membranes[J]. Journal of Vacuum Science & Technology A:Vacuum, Surfaces, and Films,2011,29(1):011011 [5] Patra J C,Panda G,Baliarsingh R. Artificial neural network-based nonlinearity estimation of pressure sensors[J]. IEEE Transactions on Instrumentation and Measurement,1994,43(6):874−881 doi: 10.1109/19.368082 [6] Sullivan J J. Development of variable capacitance pressure transducers for vacuum applications[J]. Journal of Vacuum Science & Technology A:Vacuum, Surfaces, and Films,1985,3(3):1721−1730 [7] Nishizawa S I,Hirata M. DSMC analysis of thermal transpiration of capacitance diaphragm gauge[J]. Vacuum,2002,67(3-4):301−306 doi: 10.1016/S0042-207X(02)00212-9 [8] Daudé B,Elandaloussi H,Janssen C. On the gas dependence of thermal transpiration and a critical appraisal of correction methods for capacitive diaphragm gauges[J]. Vacuum,2014,104:77−87 doi: 10.1016/j.vacuum.2014.01.002 [9] Setina J. New approach to corrections for thermal transpiration effects in capacitance diaphragm gauges[J]. Metrologia,1999,36(6):623 doi: 10.1088/0026-1394/36/6/27 [10] Scherschligt J,Barker D,Eckel S,et al. Stability of bakeable capacitance diaphragm gauges[J]. Vacuum,2022,197:110801 doi: 10.1016/j.vacuum.2021.110801 [11] Amidror I. Scattered data interpolation methods for electronic imaging systems: a survey[J]. Journal of electronic imaging,2002,11(2):157−176 doi: 10.1117/1.1455013 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: