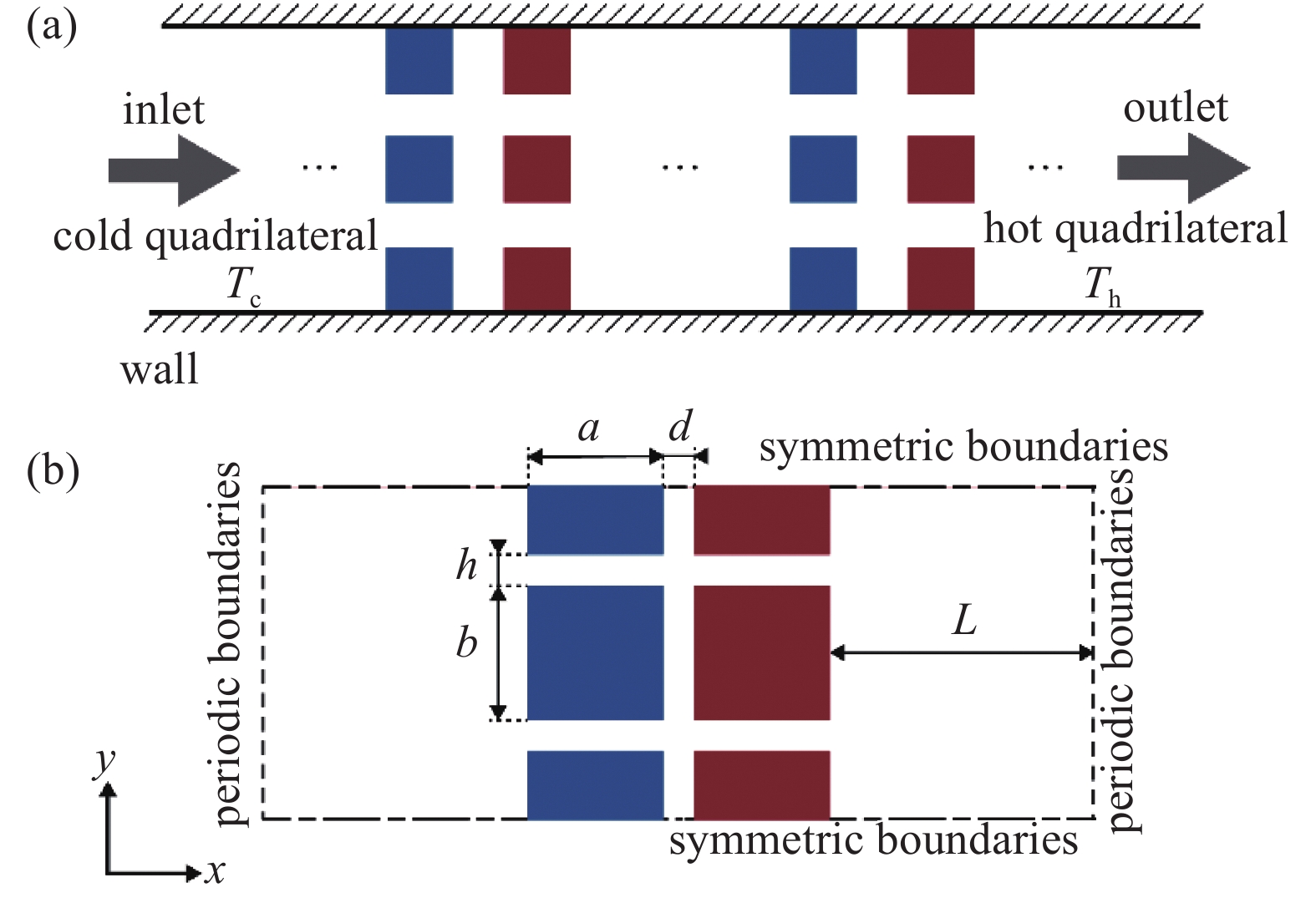
本文研究了具有不同温度四边形的二维微通道内氦气的流动过程。微通道内的四边形是四棱柱的横截面，假设四棱柱的长度远大于其横截面尺寸，所以只进行二维结构的数值模拟就能够合理的表征微通道的泵送能力。图1（a）示意性的展示了微通道的结构，微通道上下两侧为壁面，两壁面之间包含一系列排列整齐的温度为${T_{\text{c}}}$的低温四边形和温度为${T_{\text{h}}}$的高温四边形。每一竖列低温四边形和与其距离相近的高温四边形组成一组，沿壁面（$x$方向）可以有多组四边形。箭头方向为气体流动方向，低温四边形一侧（左侧）为气体入口，高温四边形一侧（右侧）为气体出口。微通道内一个低温四边形和与其邻近的一个高温四边形作为一个单元，则本文只需研究其中一个单元即可满足研究需求。图1（b）展示了数值模拟的计算域，计算域包含了一个完整的单元和与其上下相邻的两个单元的二分之一，其中高温和低温四边形的宽度都为$a$，高度都为$b$。每一行中，相邻两个不同温度四边形之间的距离为$d$。每一列中，相邻两个相同温度四边形之间的距离为$h$。计算域上下两侧的边界除了四边形的部分以外都为对称边界，而计算域的左右两侧则为周期边界。四边形与周期边界的距离为$L$。计算域内空白区域为气流通道。表1给出了计算域内各参数的值。针对不同的温差和Knudsen数对计算域内的氦气进行了数值模拟分析。

Knudsen泵中的热驱流动以过渡流为主，传统的Navier-Stokes（NS）方程并不适合求解此类问题，而采用Boltzmann方程求解得到的结果会更加准确可靠，但是鉴于Boltzmann方程的复杂性，在进行研究时多采用Boltzmann方程的各种简化形式，但是DSMC方法则另辟蹊径，这种方法利用大量粒子模拟真实气体分子，通过对粒子的统计来得到Boltzmann方程的解。DSMC方法的计算结果已经被验证与实验数据的结果非常一致^[12]，其缺点是计算效率低^[13]，目前已经成为解决稀薄气体流动问题的主要数值模拟方法之一^[14-15]。与传统的计算流体力学方法类似，DSMC方法的计算域需要划分为网格单元，通过对每个网格单元内的粒子采样统计，最终得到气流的宏观流动特性。在DSMC方法中，每个DSMC粒子代表大量的物理原子或分子。在计算开始时，模拟粒子均匀分布在网格单元中。随着时间步的推进，粒子以各自的速度运动，相互碰撞或与边界相互作用，然后进行采样统计。

为了得到准确的数值模拟结果，需要在DSMC求解器中设置一系列工作参数。本研究采用无时间计数器(no-time-counter, NTC)碰撞方法来选择碰撞对进行计算。本文借助于面向对象的CFD开源程序OpenFOAM（Open Source Field Operation and Manipulation）中发布的DSMC求解器——dsmcFoam+^[12]展开数值模拟计算。在该程序中，采用可变径硬球（variable hard sphere，VHS）模型来描述分子间的碰撞过程^[14-15]。划分的网格中，每个网格中的模拟粒子数量控制在20个以上。网格的最大尺寸$e$不得大于$\lambda /3$，$\lambda $为氦气分子运动的平均自由程，可由式(1)得到：

式中，$\theta {\text{ = 2}}{\text{.33}} \times {\text{1}}{{\text{0}}^{{{ - 10}}}} \;{\text{ m}}$为VHS模型中氦气粒子参考直径，${T_{{\rm{ref}}}}{{ = 300 \;{\rm{K}}}}$为参考温度，$\omega $为粘性指数，标准情况下（101325 Pa和0℃）氦气的粘性指数为0.66。另外，模拟的时间步长则应该小于$e/{u_0}$，其中${u_0} = \sqrt {2{k_B}{T_{\text{c}}}/m} $为微通道中粒子的特征速度，$m= {\text{ 6}}{\text{.65}} \times {\text{1}}{{\text{0}}^{{{ - 27}}}}\;{\text{ kg}}$为氦气的分子质量，${k_{\rm{B}}}$为玻尔兹曼常数。

本文研究了微通道内气流无量纲化温度$T/{T_{\text{c}}}$、气流结构、速度$u/{u_0}$和质量流量$M/{M_0}$随无量纲化温差$\Delta T/{T_{\text{c}}}$和Knudsen数的变化情况，其中，

${W_{{\rm{eff}}}}$为气体流动的特征尺寸，可由下式得到：

无量纲质量流量可由下式得到：

式中，$n$为气体粒子的数密度，下标0代表初始时刻对应参数的值。

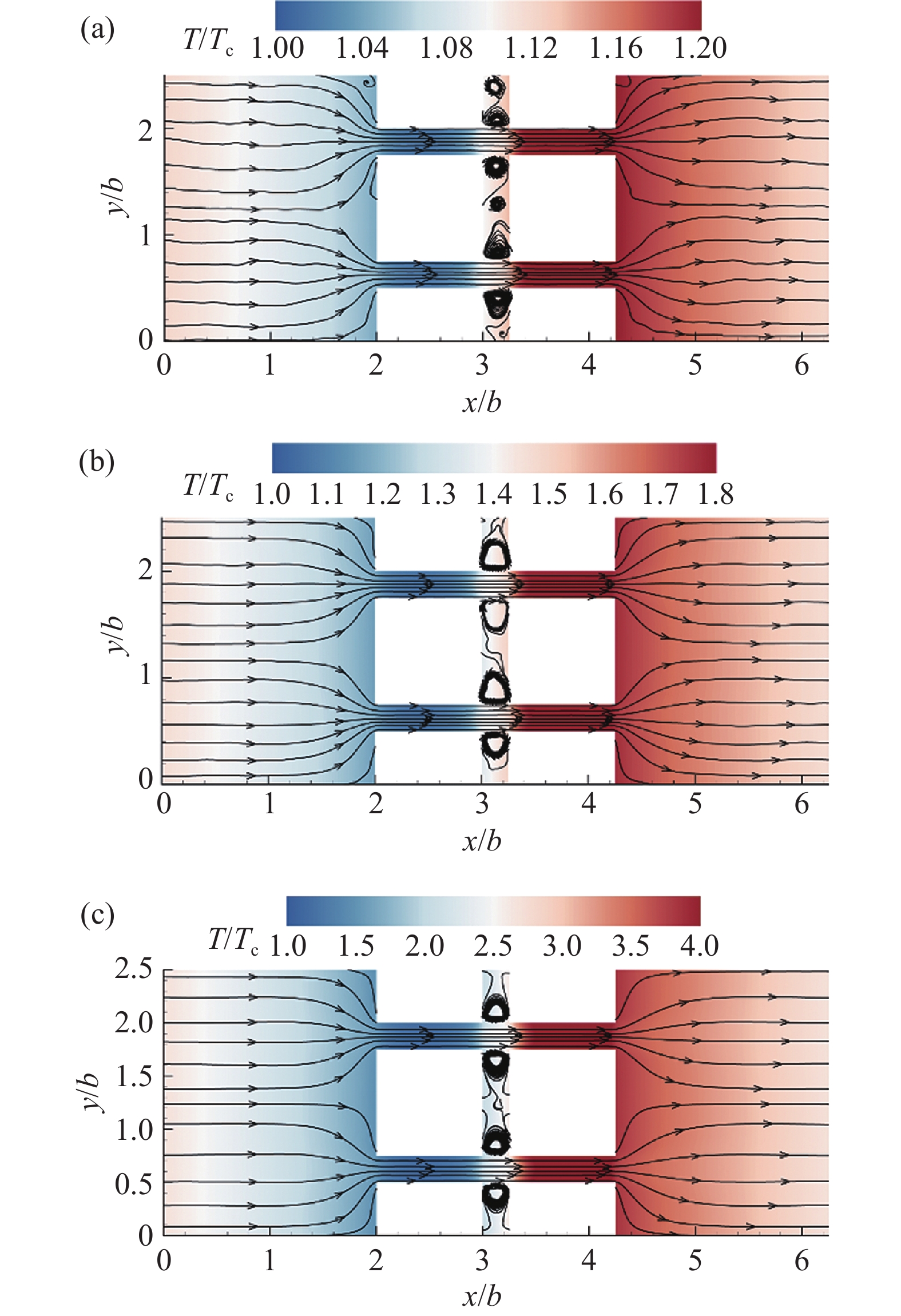
本节内容研究了温差对微通道内气体流动特性的影响，其中Knudsen数保持不变，即$Kn \equiv 0.5$。通过维持低温四边形的温度不变，改变高温四边形的温度来获取不同的温差进行研究。图2展示了在不同温差下微通道内的温度分布云图和速度流线图。可以看出，在不同温差下，微通道内的温度分布规律是相同的，即低温四边形附近的温度较低，高温四边形附近的温度较高，因此在四边形周围形成了温度梯度，进而产生了热蠕效应，最终形成了沿壁面的“类似热蠕流”。“类似热蠕流”是热驱流动的其中一种形式，顾名思义，其形成机理与热蠕流动类似，热蠕流动是由具有温度梯度的壁面诱导产生的，而“类似热蠕流”是由恒温壁面诱导产生的。从速度流线可以看出，在不同温差下，微通道内的速度流线均从左侧指向右侧，说明微通道内气体的净流动方向从低温指向高温，这一结果与棘轮形微通道的结果^[16-17]相同。另外，在温差较大的情况下（$\Delta T/{T_{\text{c}}} \geqslant 1$），速度流线比较平滑和顺畅，而在温差较小时（$\Delta T/{T_{\text{c}}} = 0.25$），速度流线较粗糙。说明温差会对气流结构造成一定的影响，温差越高越有利于气体流动。图中还可以发现，在高低温四边形之间的狭窄通道内存在大量涡流，并且随着温差的增大，较小的多个涡流逐渐合成一个较大的涡流，这是因为随着温差的增大也就是温度梯度的增大，微通道内的热蠕效应增大了，使得“类似热蠕流”增强了，气体粒子运动速度加快，气流结构趋于稳定。高低温四边形之间的狭窄通道内气体粒子运动方向也趋于一致，导致多个小涡流逐渐合成一个大涡流。

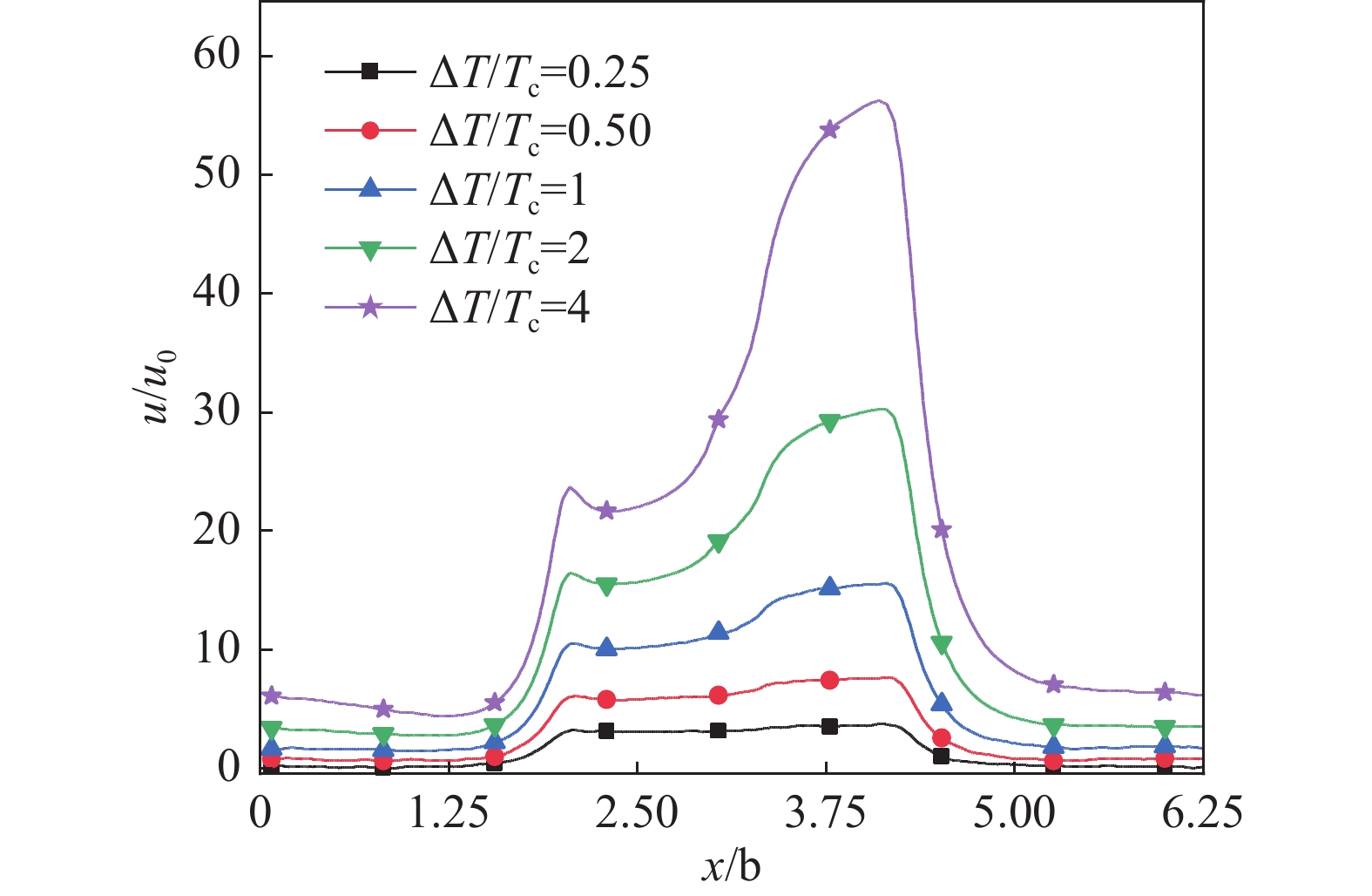
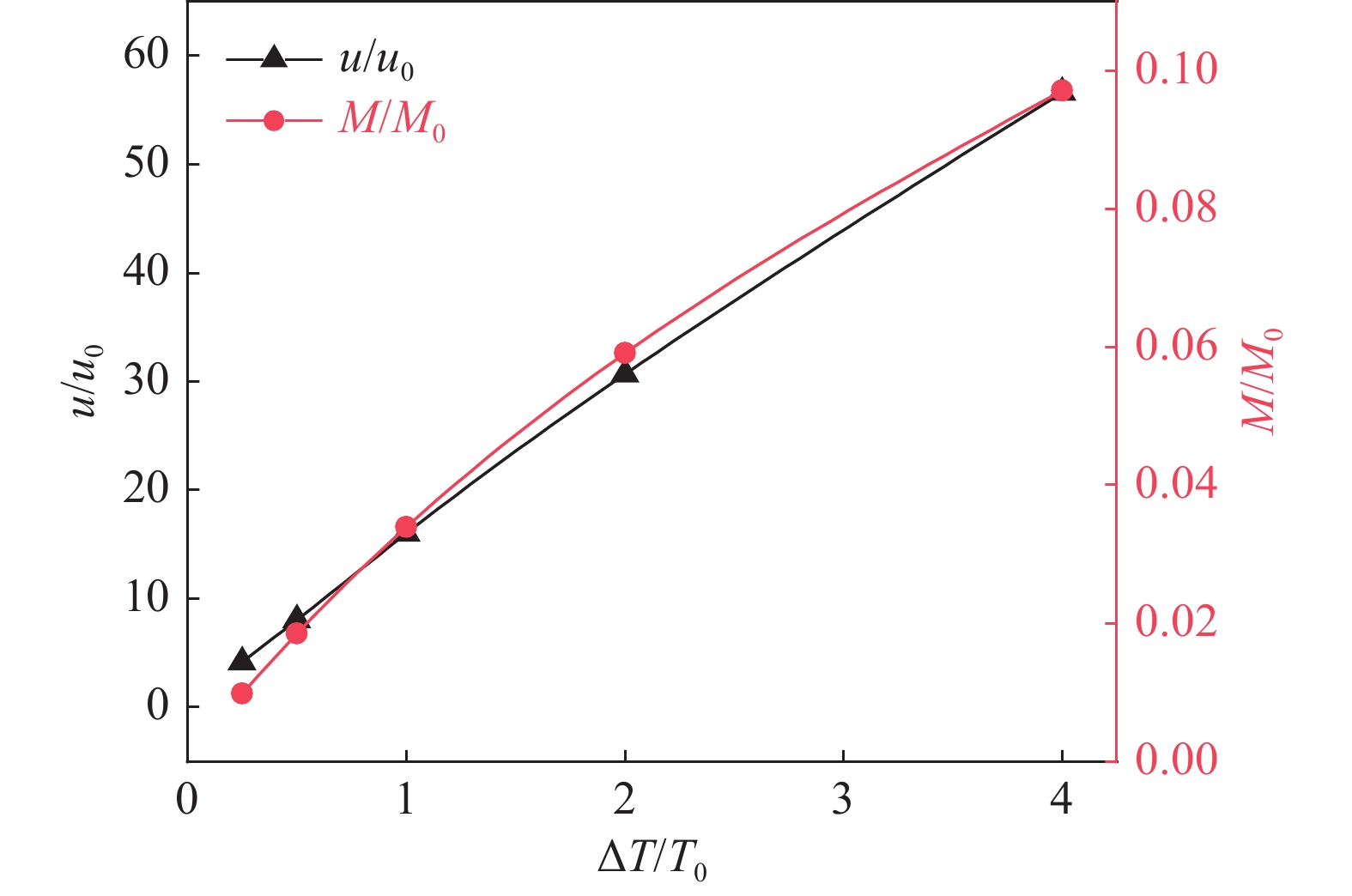
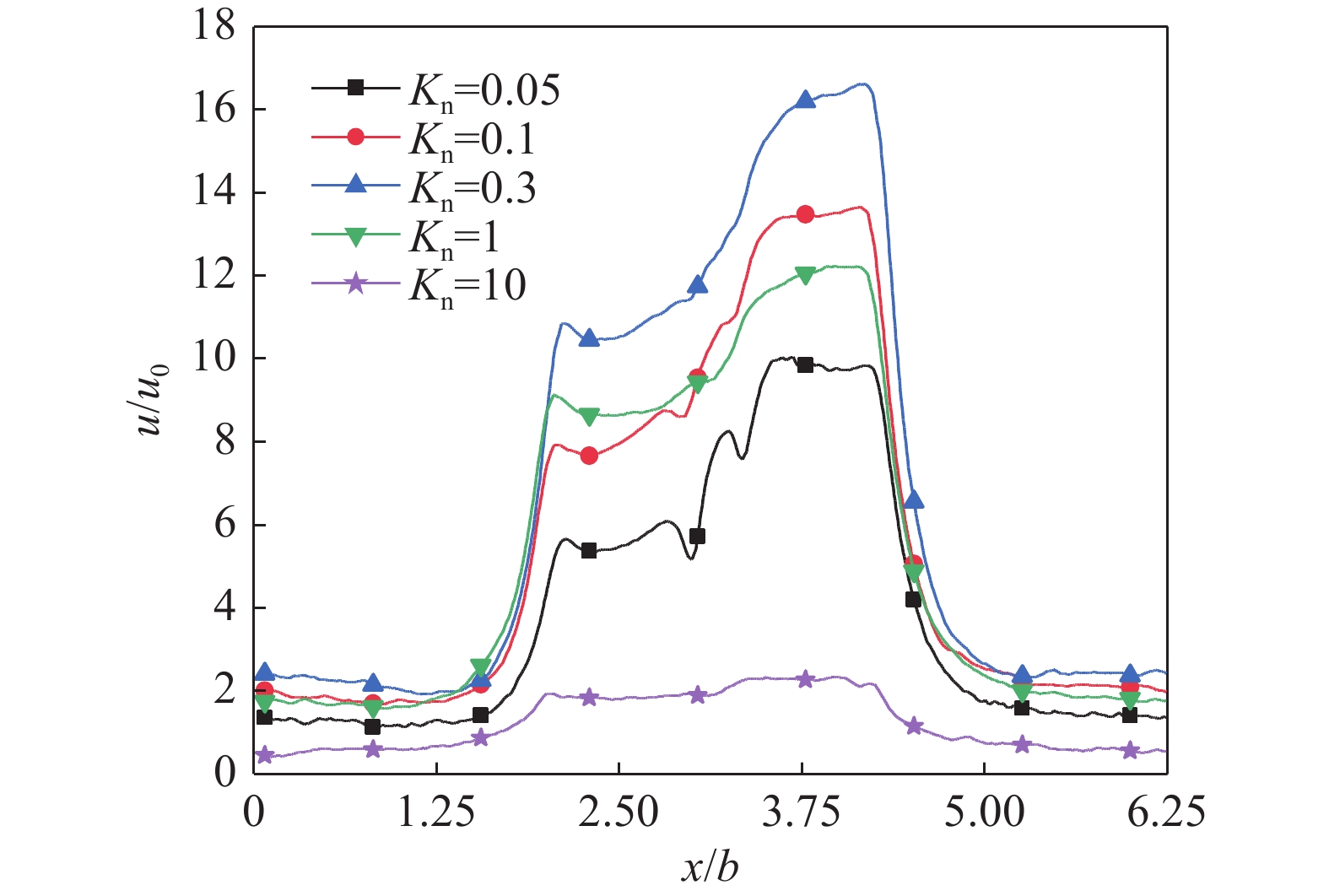
图3展示了微通道内沿$x$轴方向在不同温差下速度分布曲线。可以看出，在任何温差下，微通道左右两侧（低温四边形的左侧和高温四边形的右侧）的速度都很小，而在四边形附近速度急剧增大，尤其是在高温四边形附近速度达到最大值。这是因为四边形附近的温度梯度大，“类似热蠕流”强，尤其是高温四边形附近的“类似热蠕流”最强。另外，气体流速随着温差的增大而增大，在四边形附近速度变化的程度更为明显。同时，高温与低温四边形附近的流速差随着温差的增大也增大了，例如，$\Delta T/{T_{\text{c}}} = 0.25$时高低温四边形附近的流速几乎相等，但是当$\Delta T/{T_{\text{c}}} = 4$时高低温四边形附近的速度差相差一倍以上。这是因为温差的改变是由高温四边形的温度改变引起的，而低温四边形的温度始终保持不变。所以随着温差的增大，低温四边形附近的气流速度变化不大，但是高温四边形附近的气流速度随之增大。

与图3相比，图4更直观的展示了气体流速随温差变化的规律。由图可知，气体流速随温差的增大呈线性增大。质量流量最能直观的展示微通道的泵送能力，图4还展示了质量流量随温差的变化趋势。质量流量随温差的变化规律与气体流速随温差的变化规律相似，但是随着温差的增大，其对于提高微通道泵送能力的影响有削弱的趋势。这一结果与棘轮形微通道的结果^[16]相同。$\Delta T/{T_{\text{c}}} = 4$时的质量流量是$\Delta T/{T_c}{\text{ = 0}}{\text{.25}}$时的10倍。可以预见的是，如果温差继续增大，质量流量的值也会相应的增大，也就是说，微通道的泵送能力也会相应的增强，但是过高的温差也会提高微通道的制作成本。综上，在实际应用中为提高微通道泵送性能而选择合适的温差时，还应考虑壁材的导热系数和热阻等问题。

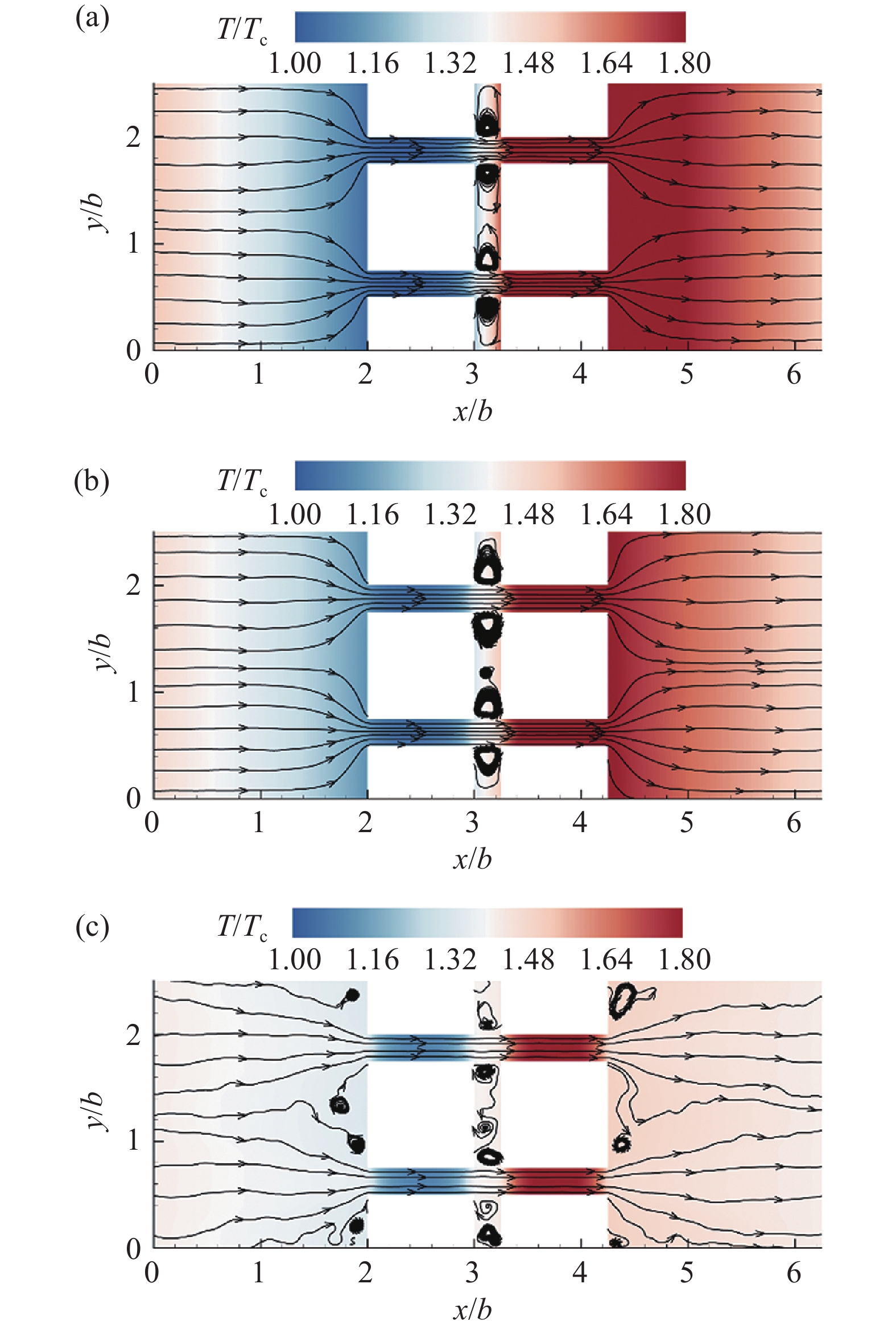
本节内容研究了Knudsen数对微通道气体流动特性的影响，其中温差保持不变，即$\Delta T/{T_{\text{c}}} \equiv 1$。图5展示了在不同Knudsen数下微通道内的温度分布云图和速度流线图。微通道内的温度分布受Knudsen数的影响较大，随着Knudsen数的增大，气体的温度变得越来越小，这是因为随着Knudsen数增大，气体变得稀薄，气体粒子与壁面总的碰撞概率降低，因此与壁面的热交换率降低，气体从壁面获得的能量减少，气体的温度随之降低。气体温度的降低进而导致微通道内的温度梯度减小，“类似热蠕流”变弱。从图中可以看出，Knudsen数较小时，速度流线比较平滑，而当$Kn = 10$时，速度流线变得粗糙且混乱，在四边形左右两侧形成了很多没有规律的涡流。这是因为“类似热蠕流”强度减弱，进而对气体粒子的驱动力减弱，同时气体过于稀薄，导致气体粒子数量大量减少。

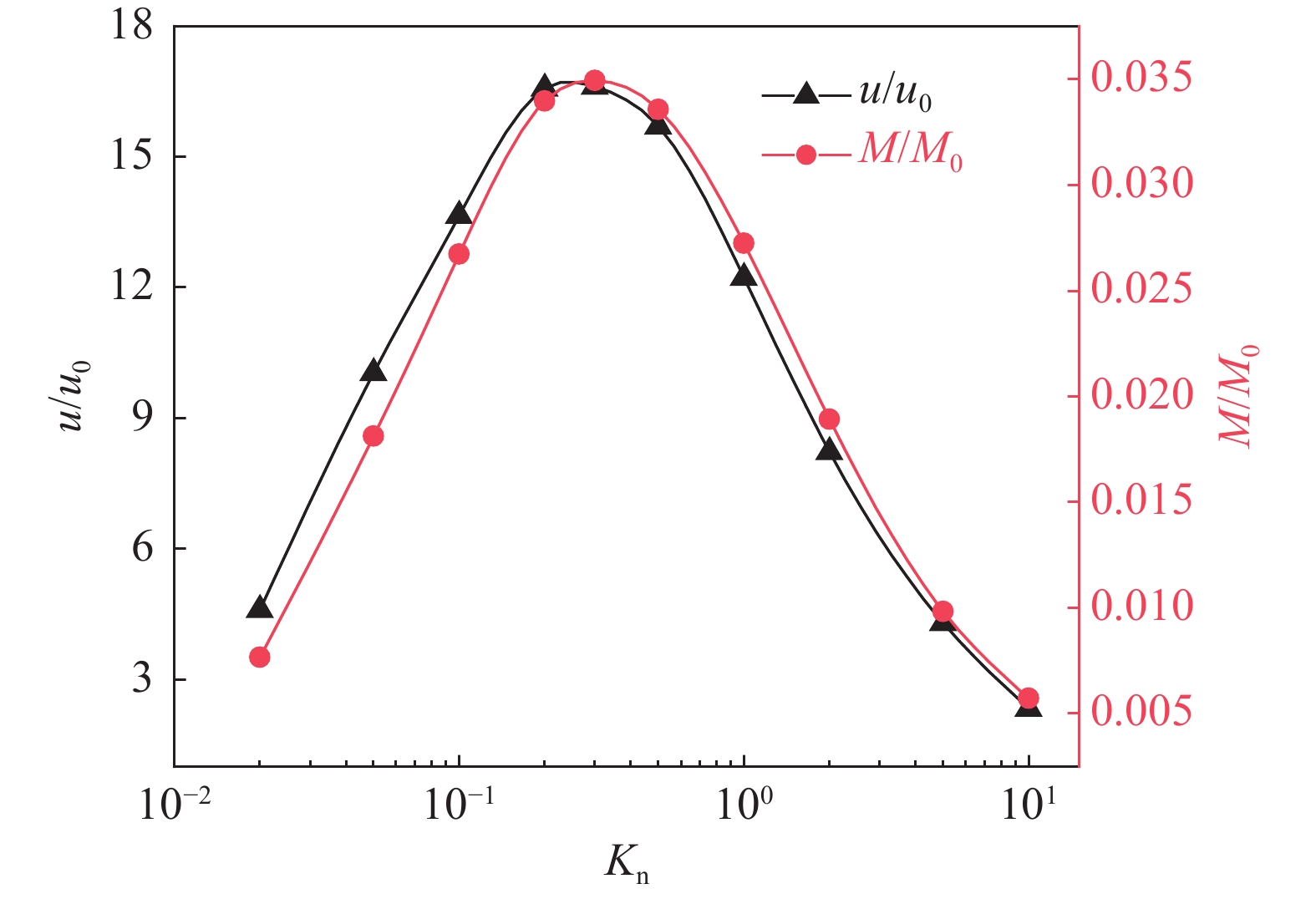
图6展示了微通道内沿$x$方向在不同Knudsen数下速度分布曲线。与图3相似，在各Knudsen数下，高低温四边形附近的速度很高，而微通道两侧的速度很低，这是因为四边形附近的温度梯度远高于微通道两侧的温度梯度，并且高温四边形附近的速度同样明显高于低温四边形附近的速度。由图5可知，Knudsen数越小，高温四边形附近的温度越高，但是图6显示气流速度却不是随着Knudsen数的减小而提高。$Kn = 0.3$时速度达到最大值，自此，Knudsen数增大或减小，气流速度均逐渐减小。尤其是当$Kn = 10$时，四边形附近的速度几乎等于微通道两侧的速度，且接近于0。在Knudsen数较低时气流速度也较低是因为热驱流动需要在稀薄气体中才能产生，当Knudsen数变小时，气流状态逐渐接近连续流态，将会难以产生热驱流动；在Knudsen数较高时气流速度较低则是因为气体过于稀薄，气体粒子数量太少，与壁面碰撞的总概率降低，无法将壁面的能量传递给气体，进而导致热驱流动减弱，气流速度降低。

图7展示了气流速度和质量流量随Knudsen数变化的曲线。在Knudsen数约为0.3时气流的无量纲速度达到最大值16.614。在$Kn \geqslant 0.{\text{3}}$时，气流速度随着Knudsen数的增大而减小，可以预见，当Knudsen数大到一定程度时，随着Knudsen数的增大，气流速度的变化量会很小且速度值无限接近于零；在$Kn < 0.{\text{3}}$时，气流速度随着Knudsen数的减小几乎呈线性减小。这一变化规律与棘轮形微通道的结果相同^[16]。质量流量随Knudsen数变化的规律与流速随Knudsen数变化的规律相似，同样在Knudsen数约为0.3时达到最大值。这是因为在Knudsen数较小时，气流接近连续流态，热驱流动弱，因此质量流量较小；而在Knudsen数较大时，一方面是因为温度梯度较小导致的热驱流动较弱，另一方面是因为气体稀薄程度大，气体粒子数量少，所以传输的气体质量就小。这说明了在过渡流态微通道的泵送能力比在连续流态和自由分子流态都好。这一结果与其他Knudsen泵^[16]得到结果相同。

另外，将本文提出的微通道与典型的矩形微通道^[11]在相同条件下做了对比，发现本文所提出微通道的无量纲质量流量是矩形微通道的62倍。本文所提微通道既降低了工业制造难度，又提高了气体泵送能力。

本文提出了一种新的内部带有恒定且不同温度四棱柱的微通道型Knudsen泵，它摆脱了需要在同一壁面上设置温度梯度和在同一组件不同壁面处设置不同温度的限制，降低了工业制造难度，采用DSMC方法对该二维微通道内的气体流动特性进行了数值模拟研究。研究表明，微通道内气体从低温四边形流向了高温四边形，证明了微通道的气体泵送能力，同时也验证了由温度梯度引起的热驱流动使得气体从低温区流向高温区。相同工况下该微通道的无量纲质量流量是传统矩形Knudsen泵的62倍。本文所解决的关键问题在于提出一种新型微通道构型，该微通道即降低了工业制造难度，又提高了气体传输性能。

微通道内的温差会影响气体流动特性，在75 ~ 1200 K范围内时，温差越高，气体流线越平滑，速度越快，质量流量越大，说明温差越高，微通道的气体泵送能力越强，并且质量流量随着温差的升高几乎呈线性增大。温差在1200 K时质量流量是温差在75 K时的10倍。气体的稀薄程度，也就是Knudsen数在0.05~10范围内时，受“类似热蠕流”强度和气体分子数量的影响，最大气体流速和质量流量均出现在$Kn = 0.3$时，说明在过渡流态微通道的气体泵送能力最强。