混沌是非线性系统在一定条件下产生的复杂动力学行为^[1]. 由于混沌系统具有初值敏感性、伪随机性和不可预测性, 因此得到了学者们的深入探索, 并广泛应用在工业界^[2,3]. 与连续混沌系统相比, 离散混沌映射具有简单的代数结构和较高的计算效率, 因此受到越来越多的关注^[4,5]. 作为Lorenz大气对流模型的简化版本, Henon映射是目前研究最广泛的离散混沌映射之一^[6]. 近年来, 关于Henon映射的研究不断取得新的进展. 例如, Lv等^[7]构建了一种新的具有复杂动力学行为和良好随机性的广义二维Henon映射, 从数学意义上研究了系统的Lyapunov指数和空间动力学行为, 并给出相应的定理和推论, 最后基于该系统设计一种伪随机数发生器. Fu等^[8]提出一种改进的Henon映射, 并通过分岔图、Lyapunov指数谱和样本熵等分析该系统丰富的动力学行为, 最后利用PSIM电路仿真验证了该模型的物理可实现性.

忆阻器作为一种非线性记忆元件, 为混沌系统的设计和应用带来了新的方向^[9]. 自从HP实验室首次成功地制造出忆阻器以来^[10], 该元件被广泛应用于非线性电路^[11,12]、信息安全^[13]、人工神经网络^[14–16]等领域. 此外, 忆阻器在多模态神经形态计算中的应用^[17]也展现出显著的优势, 进一步证明了其在处理复杂非线性系统中的潜力. 局部有源忆阻器是蔡少棠于2014年提出的^[18], 由于它可以产生比无源忆阻器更复杂的动力学行为, 因此具有更广阔的应用前景. 近年来, 研究者提出许多类型的局部有源忆阻器, 例如Ma等^[19]提出一种具有符号函数的局部有源离散忆阻器, 并将其引入超混沌映射, 显著提高原系统的复杂度. Li等^[5]将连续忆阻器离散化, 得到一种局部有源离散忆阻器, 将其引入混沌映射中, 产生丰富的动力学行为. 因此, 研究基于局部有源忆阻器的混沌系统具有重要意义.

多稳定性是指混沌系统在不同初始条件下产生具有不同位置或拓扑结构的共存吸引子^[20]. 同质多稳定性是指系统能在不同位置生成具有相同拓扑结构的共存吸引子^[21]. 同质多稳定性的混沌系统提供的混沌序列持续且稳定, 并对初始条件和外部干扰具有较强的鲁棒性, 这为许多基于混沌的工程应用带来了便利^[9]. 另外, 共存吸引子的数量也会影响保密通信的性能. 因此, 在非线性系统中引入多稳定性并对其加以控制是必要的^[22].

由于记忆效应, 分数阶微积分比整数阶微积分更能准确地描述对象^[23]. 近年来, 分数阶微积分在理论研究和工程应用方面都得到快速发展^[24,25]. 然而分数阶微积分的数值模拟繁琐且耗时, 相比之下, 分数阶差分的模拟较为简单, 因此受到更多的关注. Caputo, Riemann-Liouville和Grunwald-Letnikov是3种常见的分数阶微分定义, 其中Caputo定义因其物理意义明确和易于工程实现而被广泛使用^[26]. 分数阶差分最早由Edelman引入混沌映射, 随后关于分数阶混沌映射的动力学分析^[27]、同步控制^[28]和图像加密^[29]等方面的研究不断取得新的进展. 例如, Wang等^[30]根据稳定性理论引入两个一维分数阶混沌映射, 并实现它们的同步. Ma等^[31]提出一种具有简单代数形式的二维混沌映射, 并分析了该模型在整数阶和分数阶形式下的动力学行为.

作为人与人之间交流的主要媒介之一, 视频的安全传输已成为当下的研究热点. 混沌因其固有的高随机性和初始值敏感性, 广泛应用在视频加密中, 并取得了显著的成果^[32,33]. 例如, Tabash和Izharuddin ^[34]基于上下文自适应二进制算术编码和Logistic映射, 提出一种视频加密算法, 该算法具有效率高和计算复杂度低等优点. Karmakar等^[35]设计一种基于DNA编码的视频加密方案, 该方案在视频帧上引入稀疏编码, 并与DNA编码相结合, 获得了较高的安全性. Liu等^[36]开发一种基于超混沌映射的快速视频加密算法, 该算法采用置乱-扩散-置乱的加密策略, 提高了算法的安全性. Li等^[37]基于Lorenz系统提出一种视频加密方案, 该方案在帧图像的三维通道Y, Cb和Cr上采用不同的加密算法, 不仅提高算法的安全性还提升了加密效率.

本文利用局部有源离散忆阻器构建一种具有可控多稳定性的分数阶忆阻Henon映射, 并基于该映射设计一种视频加密算法. 本文的主要贡献如下:

1)利用多分段非线性函数构造一种渐近稳定点数量可控的分数阶局部有源离散忆阻器, 然后基于该忆阻器构造一种分数阶忆阻Henon映射.

2)该分数阶忆阻Henon映射能够产生期望数量的同质共存吸引子, 这意味着在该系统中出现了可控的同质多稳定性. 此外, 该系统还能产生各种周期和混沌吸引子、倍周期分岔等特殊现象.

3)为了拓展分数阶忆阻Henon映射的应用, 利用该系统产生的可控的共存混沌序列设计一种视频加密方案. 实验结果表明, 该方案具有良好的安全性.

为了产生更多共存吸引子, 可以在混沌系统中引入额外的控制器, 如周期函数或绝对值函数. 然而, 这种方法不仅会增加系统的设计成本, 还会对基于混沌的工程应用产生不利影响^[21]. 本节构造一种具有多分段非线性函数的局部有源离散忆阻器, 通过控制不动点的数量来实现多稳定性的控制. 该模型表示为

其中$ \gamma $, $ c $和$ d $表示忆阻器参数. $ i(n) $, $ v(n) $和$ z(n) $代表第$ n $次迭代时忆阻器的电流、电压和状态变量的值. $ u(z(n))={u}_{1}(z(n))或{u}_{2}(z(n)) $, 表示为

其中$f$是正参数, ${I_1}$和${I_2}$是非负整数. 通过分别在$ {u_1}(z(n)) $和$ {u_2}(z(n)) $中选择不同的$ {I_1} $或$ {I_2} $值, 可以产生任意奇数或偶数个共存吸引子. 由Caputo分数阶差分算子^[38]和差分方程^[39]的定义得到方程(1)的分数阶形式:

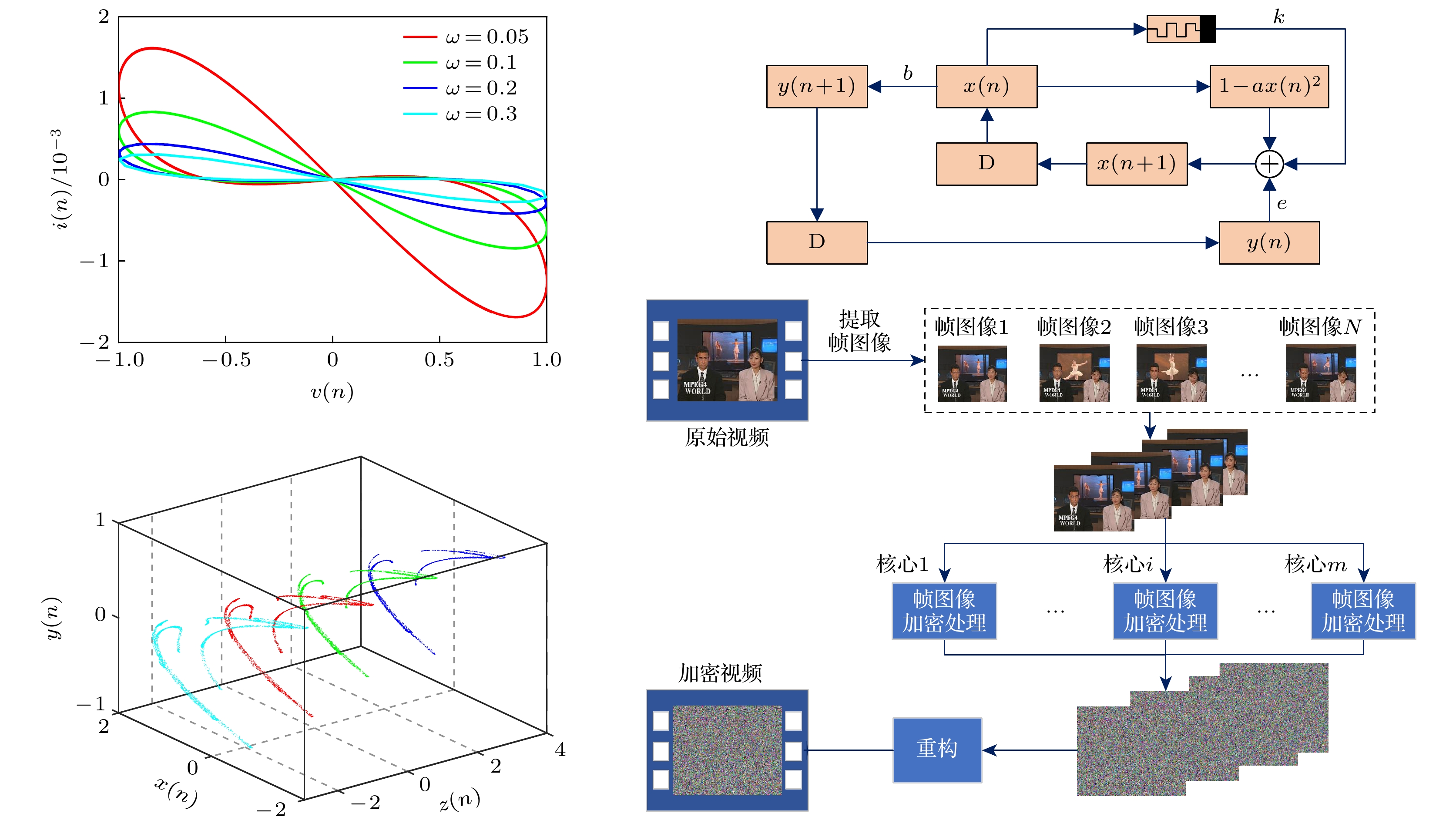
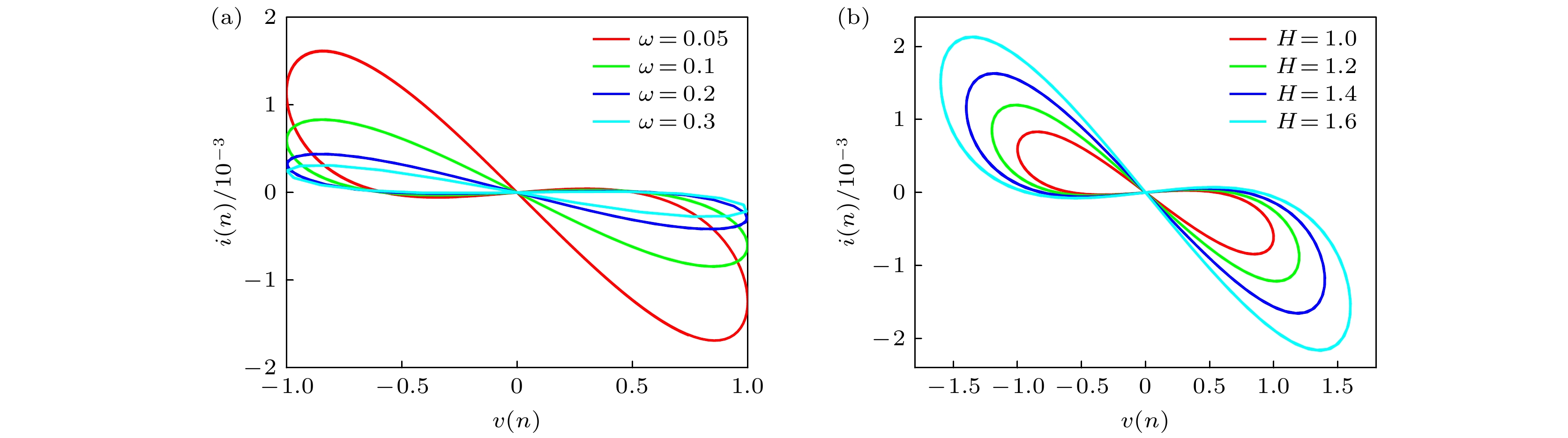
其中$ \varGamma ( \cdot ) $表示Gamma函数. 为了研究该忆阻器模型的磁滞回线特征, 设方程(2)和方程(3)的参数为$ {I_1} = 0 $, $ q = 0.95 $, $ \gamma = - 1.26 $, $ f = 200 $, $ c = 1 \;\times {10^{ - 4}} $, $ d = 1 \times {10^{ - 7}} $. 驱动信号为$ v(n) = $$ H\sin (\omega n) $时, 该模型在不同频率$ \omega $和振幅$ H $下的紧磁滞回线如图1所示. 图1清楚地表明了该离散模型满足广义忆阻器的定义.

局部有源忆阻器的非易失性可以通过断电图(power-off plot, POP)来判断. 设方程(3)中的$ v(n) = 0 $和$ i(n) = 0 $, 则其可以改写为

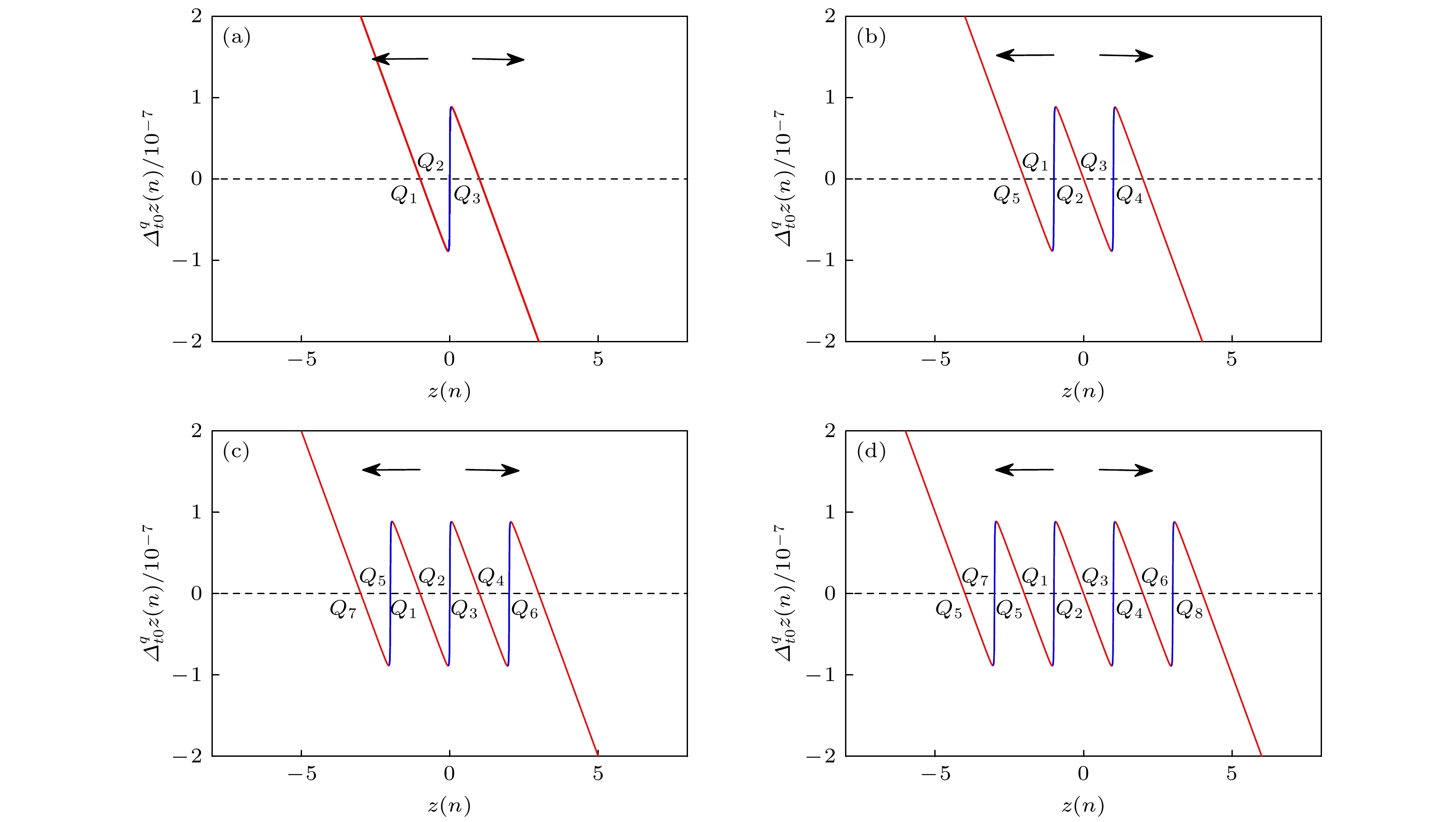
其中$ ^{\text{c}}\varDelta _{{t_0}}^q $是阶数为$q$的Caputo分数阶差分算子, ${t_0}$为起始点. 设$ d = 1 \times {10^{ - 7}} $, 当$ {I_1} = 0, 1 $和$ {I_2} = 0, 1 $时, 该忆阻器的POP如图2所示. 从图2可以看出, 随着$ {I_1} $和$ {I_2} $的增大, 该忆阻器的POP和$ x $轴之间分别产生3, 5, 7和9个交点, 其中$ {Q_1}( - 2, 0) $, $ {Q_3}(0, 0) $, $ {Q_5}(2, 0) $, $ {Q_7}(4, 0) $和$ {Q_9}( - 4, 0) $斜率为负, 是渐近稳定点, $ {Q_2}( - 1, 0) $, $ {Q_4}(1, 0) $, $ {Q_6}(3, 0) $和$ {Q_8}( - 3, 0) $斜率为正, 是不稳定点. 而且, 新生成的交点沿着$ x $轴向两侧展开. 由上述分析可知, 当$ u(z(n)) = $$ {u_1}(z(n)) $时, 该忆阻器可以产生$ 2{I_1} + 2 $个渐近稳定点; 当$ u(z(n)) = {u_2}(z(n)) $时, 该忆阻器可以产生$ 2{I_2} + 3 $个渐近稳定点. 这些点导致了可控多稳定性的产生, 具体讨论见3.2节和4.1节. 此外, 该忆阻器的POP图有两个或两个以上的负斜率, 根据非易失定理^[40], 该忆阻器具有非易失性.

此外, 该分数阶离散忆阻器的局部有源特性可通过静态电压-电流(DC voltage-current, DC v -i)特性曲线来判断. 设方程(3)中的$ ^{\text{c}}\varDelta _{{t_0}}^qz(n) = 0 $, 则其可以改写为

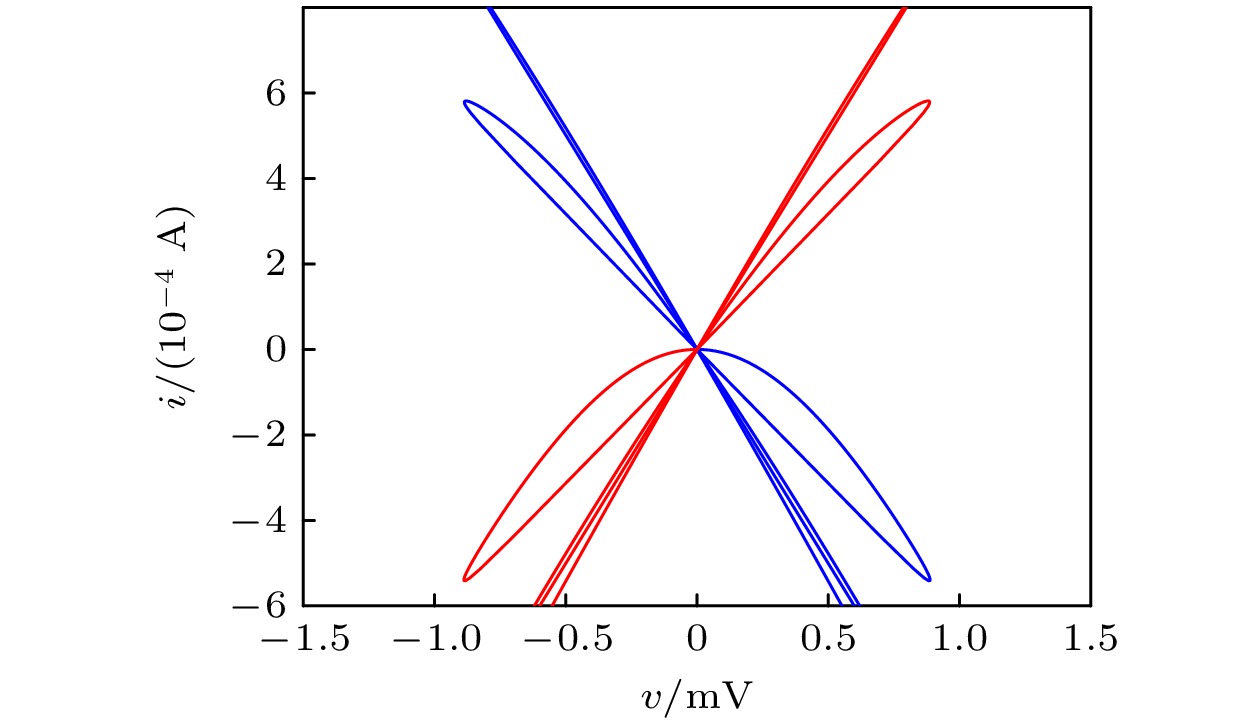
设$ d = 1 \times {10^{ - 7}} $, $ \gamma = - 1.26 $, 当$ {I_1} = 1 $时, 该分数阶模型的DC v - i图如图3所示, 其中蓝色曲线表示斜率为负的部分, 红色曲线表示斜率为正的部分. 图3清楚地表明该分数阶忆阻器具有局部有源特性.

综上所述, 该分数阶离散模型满足局部有源忆阻器的特性, 当参数$ f $为某个定值时, 该忆阻器的内部状态变量函数可以被视为三角波函数, 通过控制参数$ {I_1} $和$ {I_2} $, 可以产生任意数量的三角波.

本节首先构造一个分数阶忆阻混沌映射, 通过图解法, 研究该映射的不动点随着参数$ {I_1} $和$ {I_2} $变化的规律, 然后分析系统在不动点处的稳定性.

经典Henon映射的方程可以表示为

其中$ a $, $ b $和$ e $表示系统参数, $ x(n) $和$ y(n) $分别表示第$ n $次迭代时的状态变量. 将第2节提出的分数阶局部有源离散忆阻器引入Henon映射, 系统的方程表示为

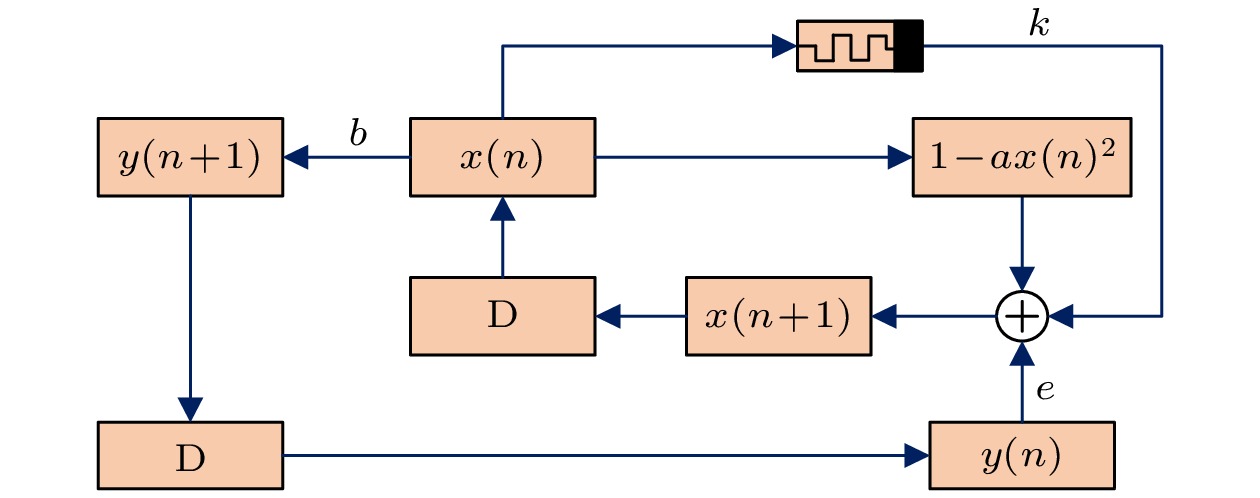
其中$ k $表示耦合系数. 方程(7)的结构如图4所示, 其中, D代表此次迭代已完成, 开始下一次迭代.

方程(7)的分数阶形式为

其中$ x(0) $, $ y(0) $和$ z(0) $表示分数阶忆阻Henon映射的初始值. 方程(8)表明$ x(n) $, $ y(n) $和$ z(n) $的值和过去的状态有关, 因此该系统具有记忆效应.

该分数阶忆阻Henon映射的不动点$ (x, y, z) $可以由下式计算:

为了求解方程(9), 可以将其改写为

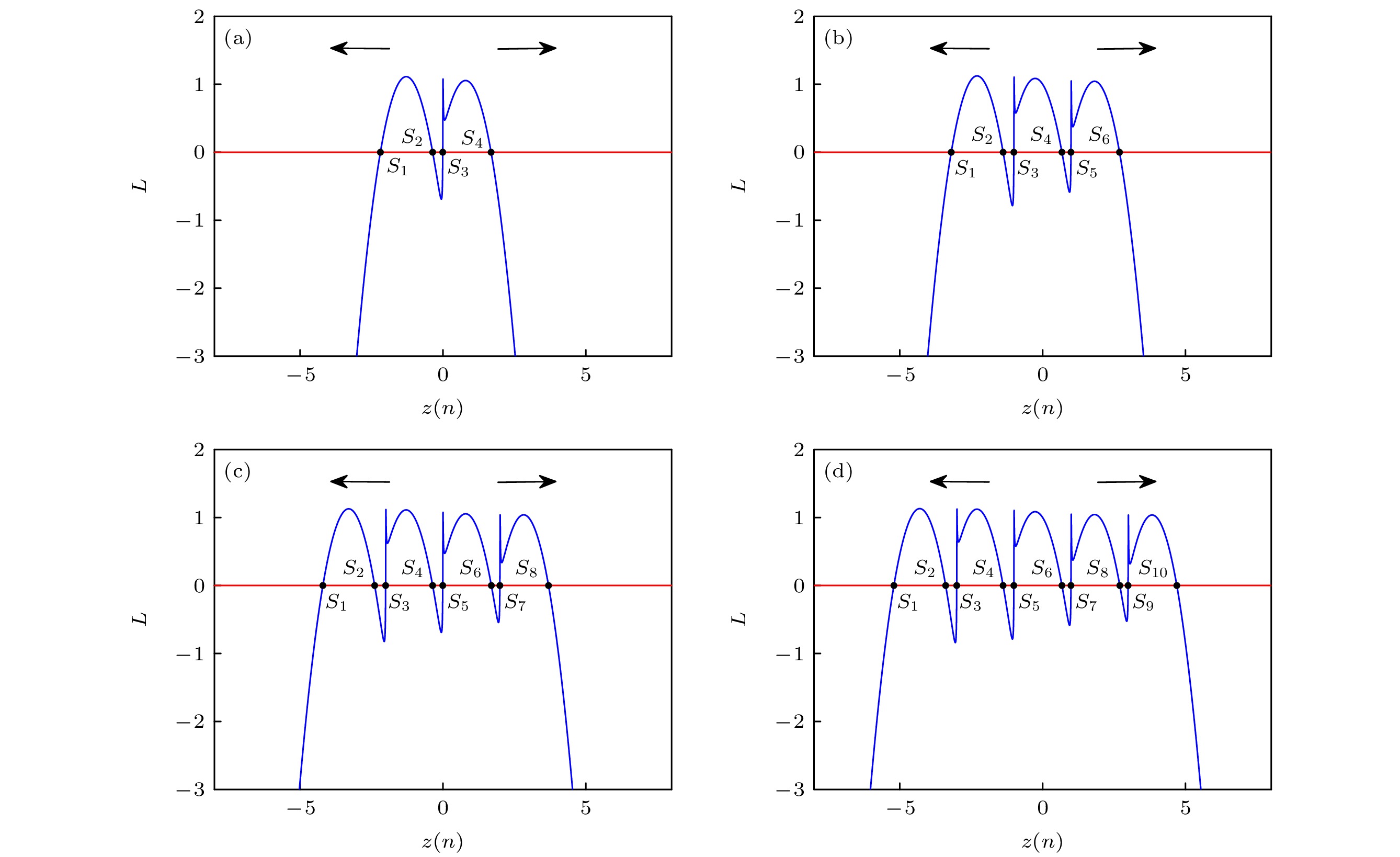
则曲线$ L $和直线$ L = 0 $的交点即为方程(10)的解, 以此可以求出系统的不动点. 设$ a = 1.01 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ k = 0.2 $和$ f = 200 $, 当$ {I_1} $和$ {I_2} $分别取不同值时, 曲线$ L $和直线$ L = 0 $的交点变化情况如图5所示. 从图5可以看出当$ {I_1} = 0 $, $ {I_2} = 0 $, $ {I_1} = 1 $和$ {I_2} = 1 $时, 系统分别产生4, 6, 8和10个不动点, 这些不动点分为两列并沿着$ z $轴排列. 在第2节中, 当$ u(z(n)) = {u_1}(z(n)) $或$ {u_2}(z(n)) $时, 分数阶局部有源离散忆阻器能够生成$ 2{I_1} + 2 $或者$ 2{I_2} + 3 $组渐近稳定点. 同理, 当$ u(z(n)) = {u_1}(z(n)) $时, 该系统可以产生$ 2{I_1} + 2 $组不动点; 当$ u(z(n)) = {u_2}(z(n)) $时, 该系统可以产生$ 2{I_2} + 3 $组不动点, 其中每一组包含两个不动点.

该分数阶系统在不动点处的Jacobi矩阵J可以表示为

其中$ u{(z)'} $表示$ u(z) $的导数. 根据Jacobi矩阵J可以求出不动点处的特征值.

定理1　分数阶混沌映射在不动点处渐近稳定当且仅当$ |{\lambda _i}| < |{\omega _i}| $, $ {\varphi _i} \in \varphi _i^{\text{f}} $.

其中$ q \in (0, 2) $, $ |{\lambda _i}| $和$ {\varphi _i} $分别表示不动点处的特征值的模和辐角.

根据定理1, 当$ {I_2} = 1 $和$ q = 0.95 $时, 系统产生的10个不动点中, $ {S_1} $是稳定的, 而$ {S_2} $, $ {S_3} $, $ {S_4} $, $ {S_5} $, $ {S_6} $, $ {S_7} $, $ {S_8} $, $ {S_9} $和$ {S_{10}} $是不稳定的.

本节利用相图、分岔图、MLE和吸引盆等方法研究该分数阶忆阻Henon映射的动力学行为, 如可控多稳定性、分数阶阶次对系统动力学的影响以及系统参数的动力学行为等.

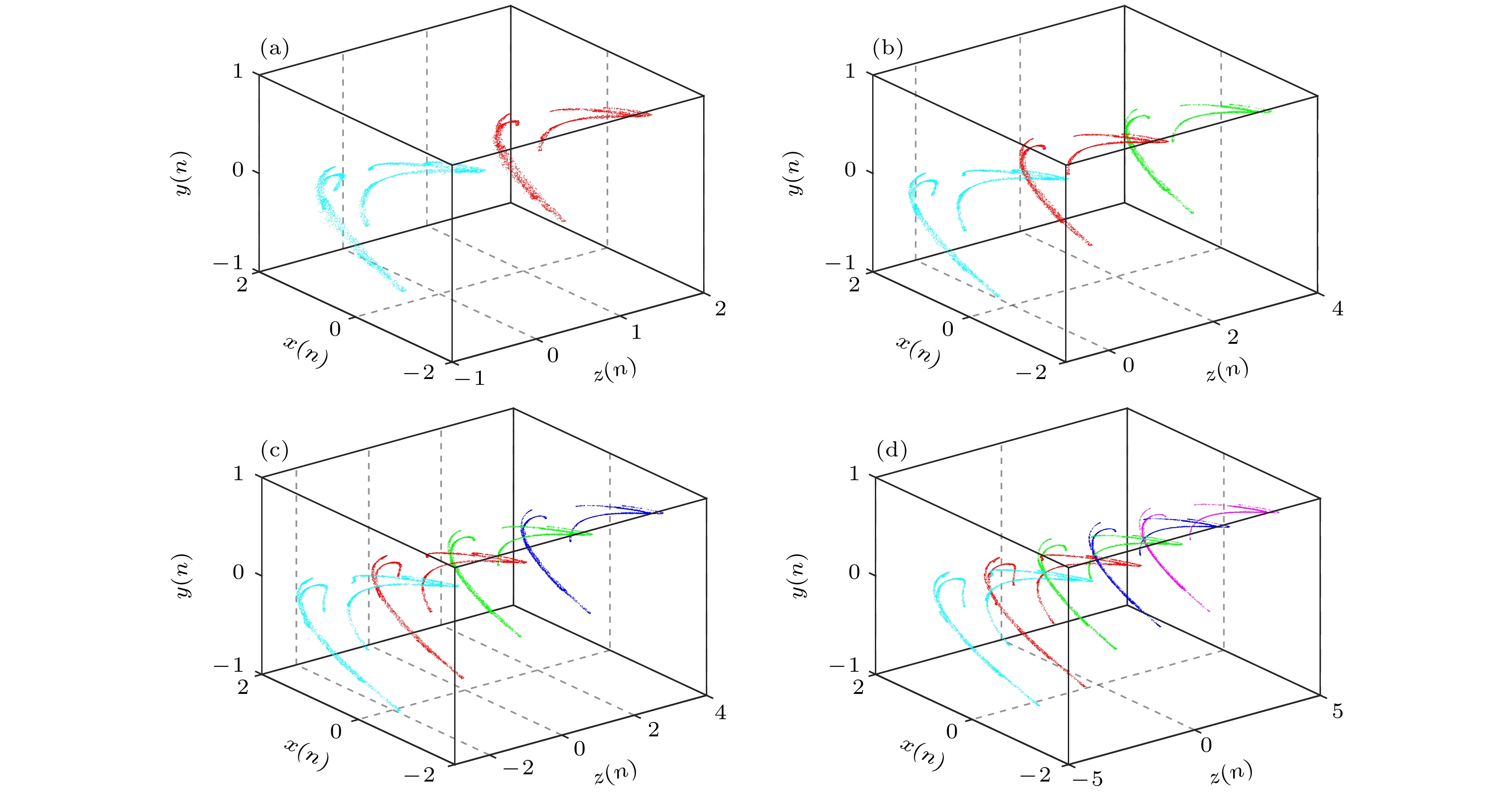
为了展示分数阶忆阻Henon映射的可控多稳定性, 设系统(7)的参数为: $ a = 1.01 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ k = 0.2 $, $ q = 0.95 $和$ f = 200 $, 初始值为$ (0.4, 0.5, z(1)){\text{ }}(z(1) = \pm 6, \pm 4, \pm 2, 0) $. 从图6可以看出, 当$ {I_1} = 0 $, $ {I_2} = 0 $, $ {I_1} = 1 $和$ {I_2} = 1 $时, 该系统产生了2, 3, 4和5个共存的混沌吸引子(MLE约为0.23), 这些共存吸引子具有相同 的拓扑结构, 并且随着参数$ {I_1} $和$ {I_2} $的增大, 新生成的共存吸引子将沿着$ z $轴向两侧延伸. 这些现象表明通过改变初始值$ z(1) $, 可以使共存吸引子发生偏置. 此外, 共存吸引子的数量与参数$ {I_1} $和$ {I_2} $有关, 证明该分数阶忆阻Henon映射具有可控多稳定性.

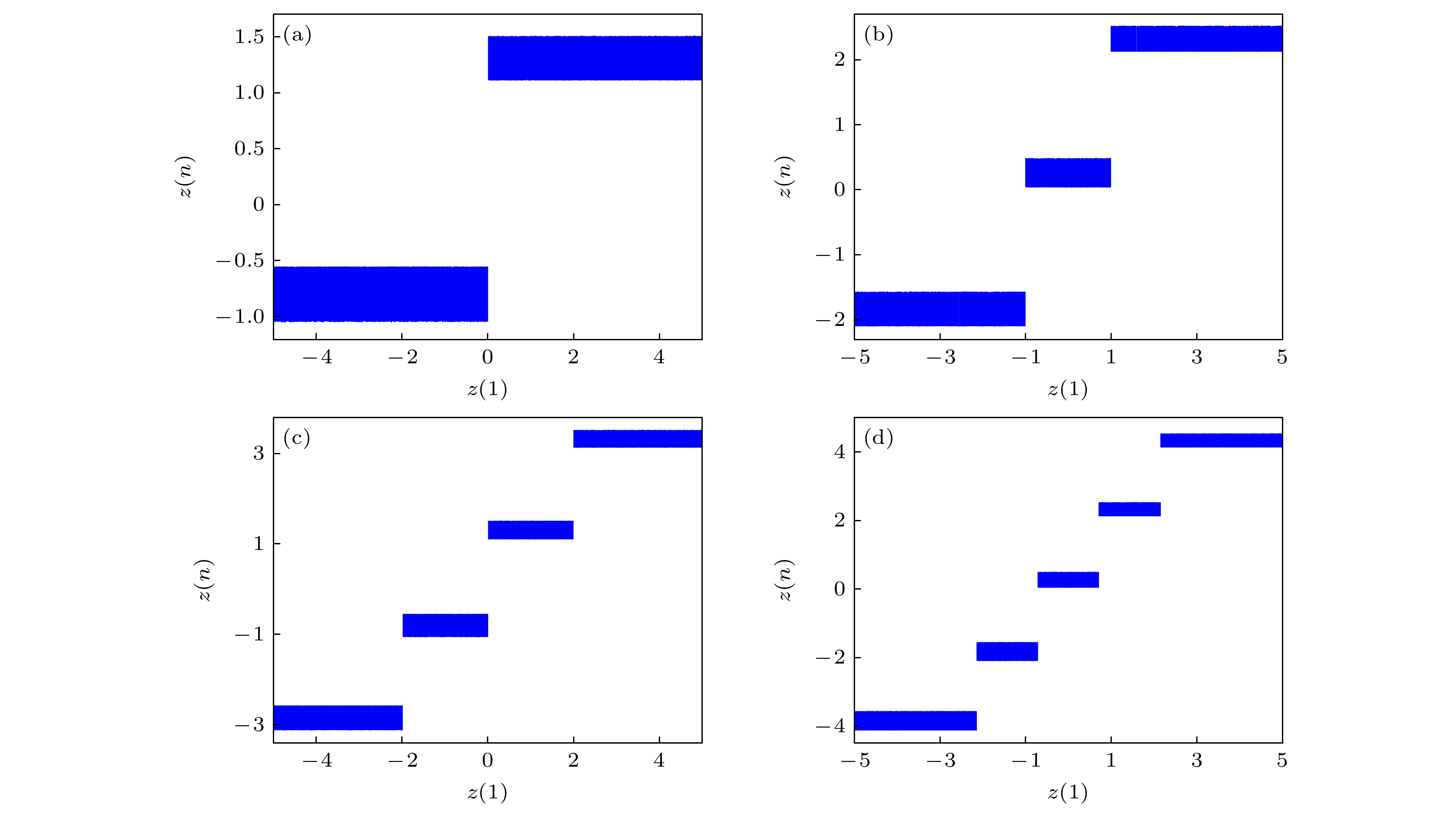
为了进一步研究可控多稳定性的产生机理, 保持参数不变, 当参数$ {I_1} $和$ {I_2} $取不同值时, 图7给出了初始值$ z(1) $在[–5, 5]内变化的分岔图. 从图7也可看出, 当参数$ {I_1} = 0 $, $ {I_2} = 0 $, $ {I_1} = 1 $和$ {I_2} = 1 $时, 初始值$ z(1) $从–5增大到5的过程中, 该系统分别产生了2, 3, 4和5个共存吸引子, 这与图6的分析结果一致. 此外, 共存吸引子的数量是由参数$ {I_1} $和$ {I_2} $决定的, 不受初始值$ z(1) $的影响. 随着区间上界的增大和下界的减小, 该分数阶忆阻Henon映射不会产生新的共存吸引子.

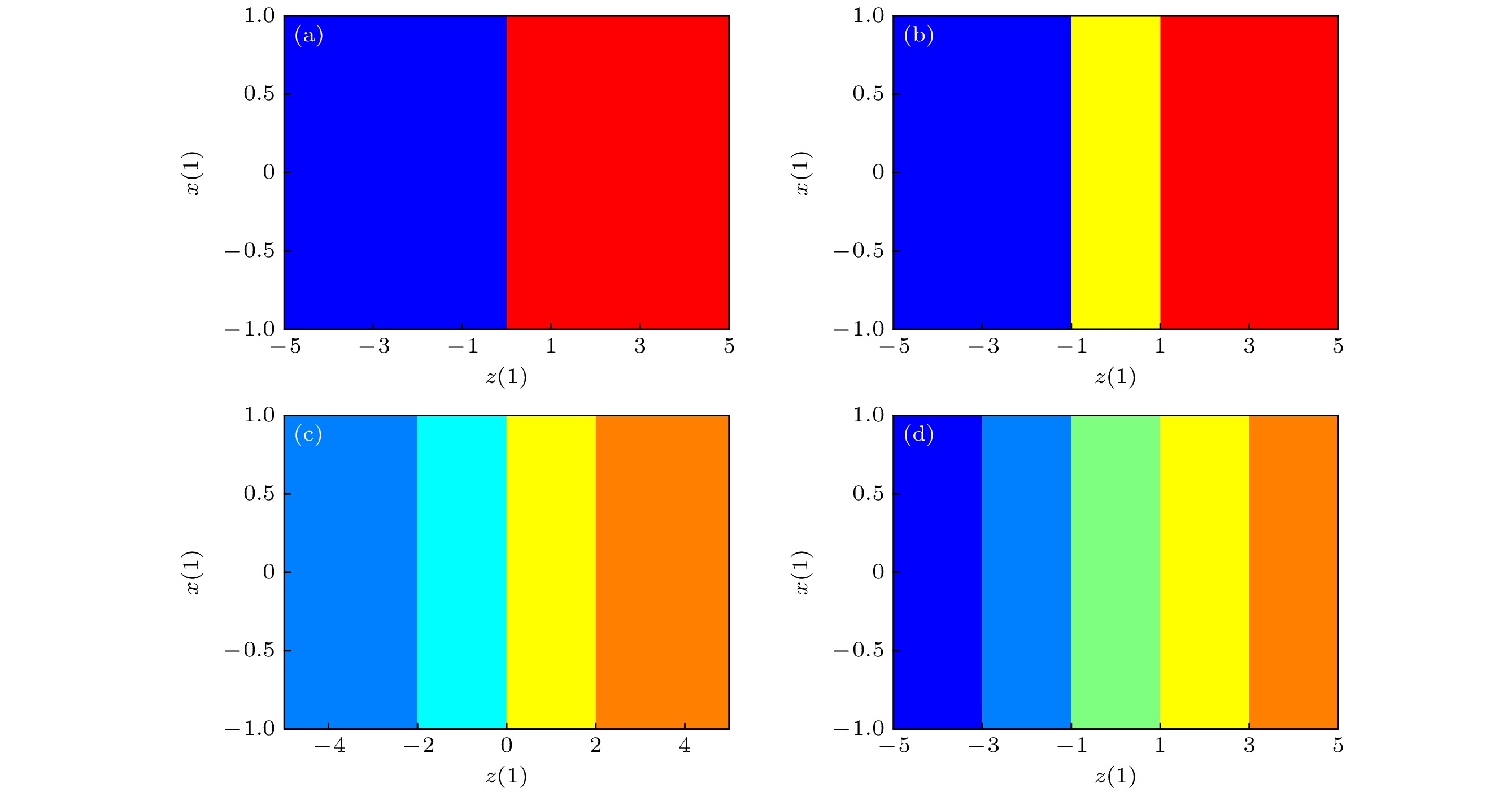
在3.2节的分析中, 分数阶忆阻Henon映射产生了$ 2{I_1} + 2 $或$ 2{I_2} + 3 $组不动点. 在本例中, 当参数$ {I_1} = 0 $, $ {I_2} = 0 $, $ {I_1} = 1 $和$ {I_2} = 1 $时, 该系统分别产生了2, 3, 4和5个共存吸引子, 并且共存吸引子的数量由参数$ {I_1} $和$ {I_2} $决定. 因此, 可以得出结论, 当$ u(z(n)) = {u_1}(z(n)) $时, 该系统可以产生$ 2{I_1} + 2 $个共存吸引子; 当$ u(z(n)) = {u_2}(z(n)) $时, 该系统可以产生$ 2{I_2} + 3 $个共存吸引子, 其中每组不动点对应于1个共存吸引子.

吸引盆能够更直观地反映共存吸引子的数量, 不同类型的吸引子可以通过不同的颜色区分. 保持其他参数不变, 当参数$ {I_1} $和$ {I_2} $取不同值时, 初始值$ x(1) $和$ z(1) $分别在区间[–1, 1]和[–5, 5]变化的吸引盆如图8所示. 图8清楚地表明, 当参数$ {I_1} = 0 $, $ {I_2} = 0 $, $ {I_1} = 1 $和$ {I_2} = 1 $时, 该系统分别产生了2, 3, 4和5个共存吸引子, 验证了上述的结论.

文献[41, 42]介绍了一种有限数量吸引子的共存, 如周期和混沌吸引子之间的共存. 文献[43, 44]介绍了一种具有周期函数的混沌系统, 该系统能够产生初始偏置的极端多稳定性, 即无穷多个吸引子的共存. 与上述的研究相比, 本文构建的分数阶忆阻Henon映射所展现的多稳定性有一个显著的特点, 即共存吸引子的数量可以灵活调节. 这意味着该映射可以产生所需数量的共存吸引子. 此外, 随着初始条件的改变, 系统不会出现分岔行为, 始终处于混沌状态. 这种特性使得系统能够产生连续且稳定的混沌序列, 这在工程实践中具有重要的应用价值. 综上所述, 该分数阶系统能够产生所需数量的共存吸引子, 吸引子的数量由参数$ {I_1} $和$ {I_2} $决定. 更重要的是, 当参数$ {I_1} $和$ {I_2} $趋近于无穷大时, 该系统能够产生无穷多个共存吸引子, 此时该系统能够生成可控的极端多稳定性.

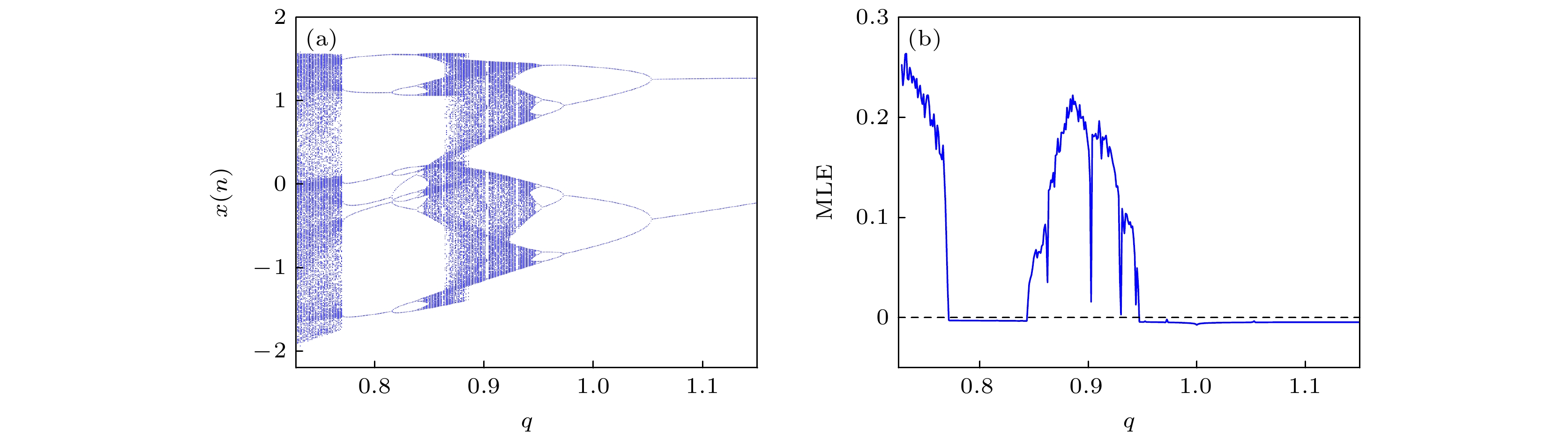
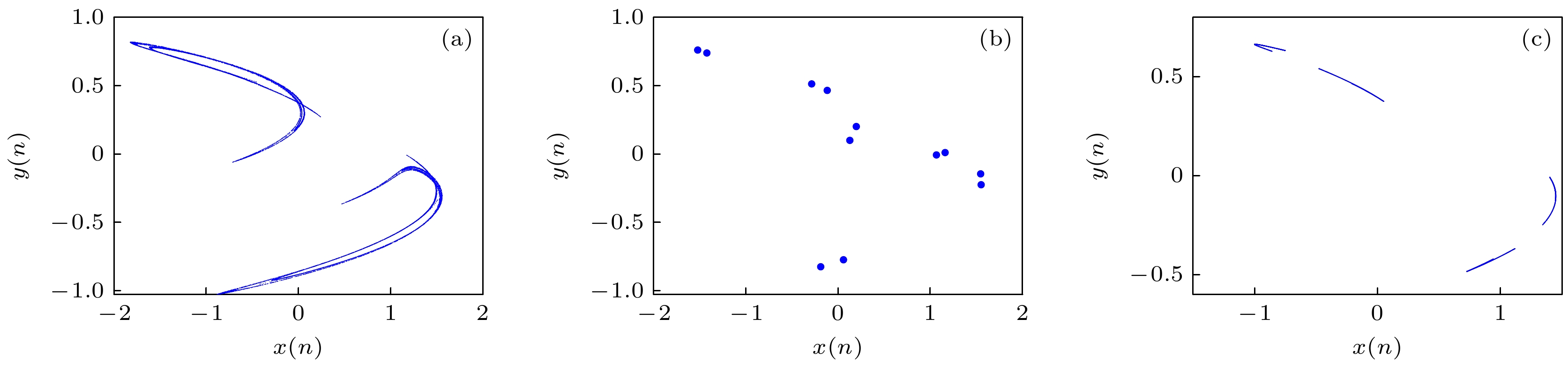
由于记忆效应的存在, 与整数阶系统相比, 分数阶系统往往表现出更复杂的动力学行为. 因此, 分析分数阶阶次$ q $的变化对系统动力学演化过程的影响是非常有必要的. 设系统(7)的参数为: $ a = 0.93 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ k = 0.2 $和$ f = 200 $, 初始值为$ (0.4, 0.5, 0.5) $, 当分数阶阶次$ q $在区间$ [0.728, 1.15] $内变化时, 系统(7)的分岔图和相应的MLE如图9所示. 从图9(a)可以看出: 开始时, 系统处于混沌状态, 随着$ q $的增大, 当$ q = 0.77 $时, 系统变为周期6, 并在$ q = 0.816 $处通过倍周期分岔变为周期11; 当$ q = 0.844 $时, 系统再次进入混沌, 并在$ q = 0.946 $处离开混沌状态, 变为周期7, 最后通过反向被周期分岔变为周期2. 当$ q \in [0.860, 0.863] $, $ q \in [0.901, 0.904] $和$ q \in [0.928, 0.931] $时, 分岔轨迹上存在3个窄的周期窗口. 图9(b)中的MLE与图9(a)中的结果一致. 图10展示了$ q $取不同值时, 该映射产生的吸引子.

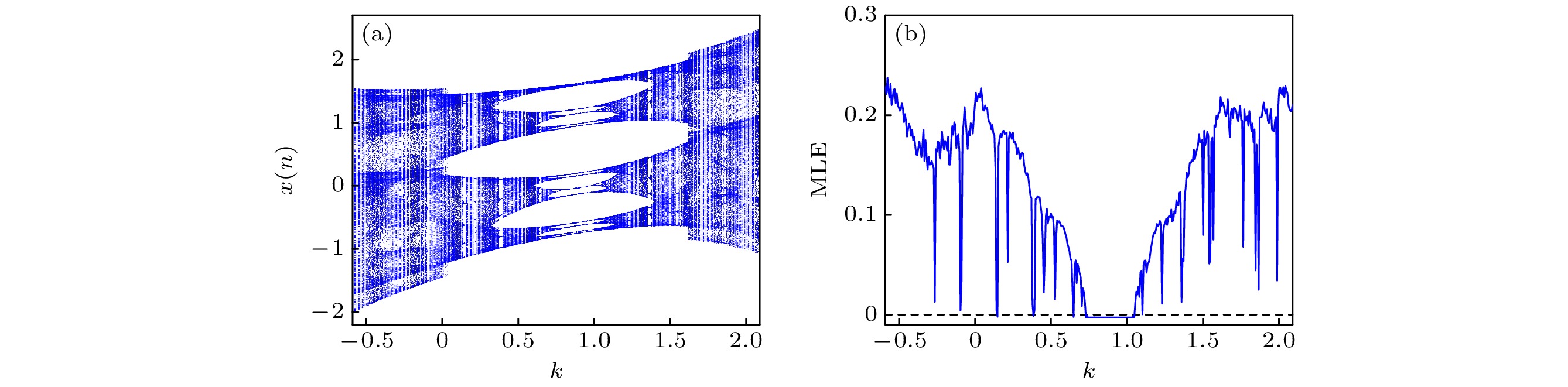
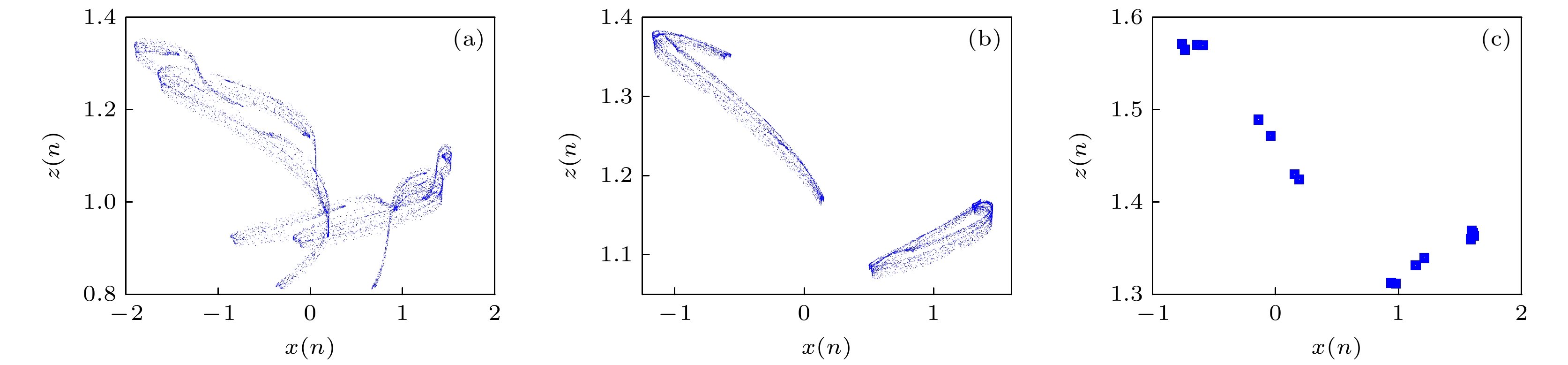
系统(7)的参数为: $ a = 0.93 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ f = 200 $和$ q = 0.91 $, 初始值为$ (0.4, 0.5, 0.5) $, 当耦合系数$ k $在区间$ [ - 0.59, 2.09] $内变化时, 系统的动力学演化轨迹和相应的MLE如图11所示. 从图11(a)可以看出: 开始时, 系统处于混沌状态, 随着$ k $的增大, 当$ k = 0.033 $时, 一条宽的混沌带分为两条, 并在$ k = 0.331 $处再分为4条; 当$ k = 0.73 $时, 系统通过反向倍周期分岔离开混沌, 并在$ k = 1.055 $处通过正向倍周期分岔再次进入混沌. 此外, 系统的动力学演化过程几乎关于直线$ k = 0.89 $对称, 图11(b)的MLE也证明了该现象. 当耦合系数$ k $取不同值时, 分数阶忆阻Henon映射生成的混沌和周期吸引子如图12所示.

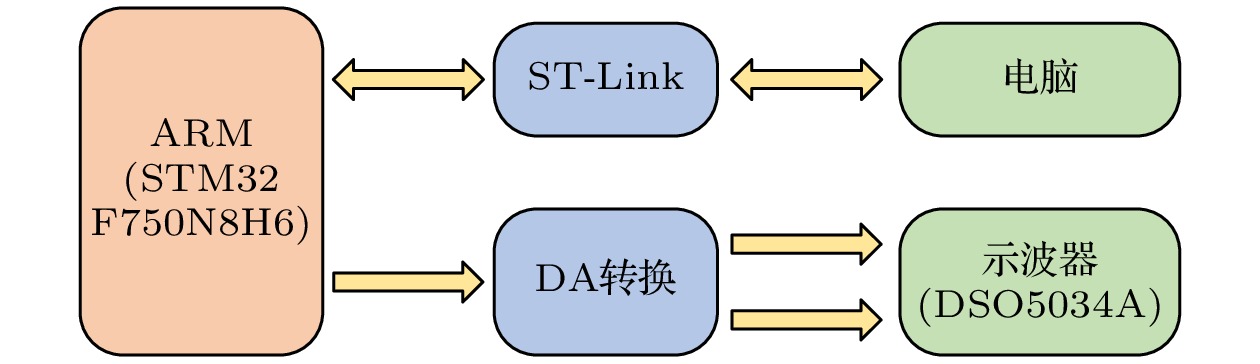
基于ARM的硬件实现具有速度快和成本低等优点. 因此, 本节在32位微控制器STM32F750N8H6平台上实现该分数阶忆阻Henon映射, 结果显示在数字示波器(DSO5034A)上. 图13给出了硬件实现的基本框架.

首先初始化系统参数和用于迭代计算的数组, 经过计算后等比例放大数组元素, 计算结果经过DA转换后显示在示波器上. 设$ a = 0.93 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ k = 0.2 $和$ f = 200 $, 初始值为$ (0.4, 0.5, 0.5) $, 当分数阶阶次$ q $取不同值时, 该系统产生的吸引子如图14所示, 这与图10(a), (c)中的仿真结果一致, 因此基于ARM的硬件实现验证了理论分析的正确性.

本节基于分数阶忆阻Henon映射的可控多稳定性设计一种视频加密算法. 值得注意的是, 加密方案的每一步都是用不同的混沌序列.

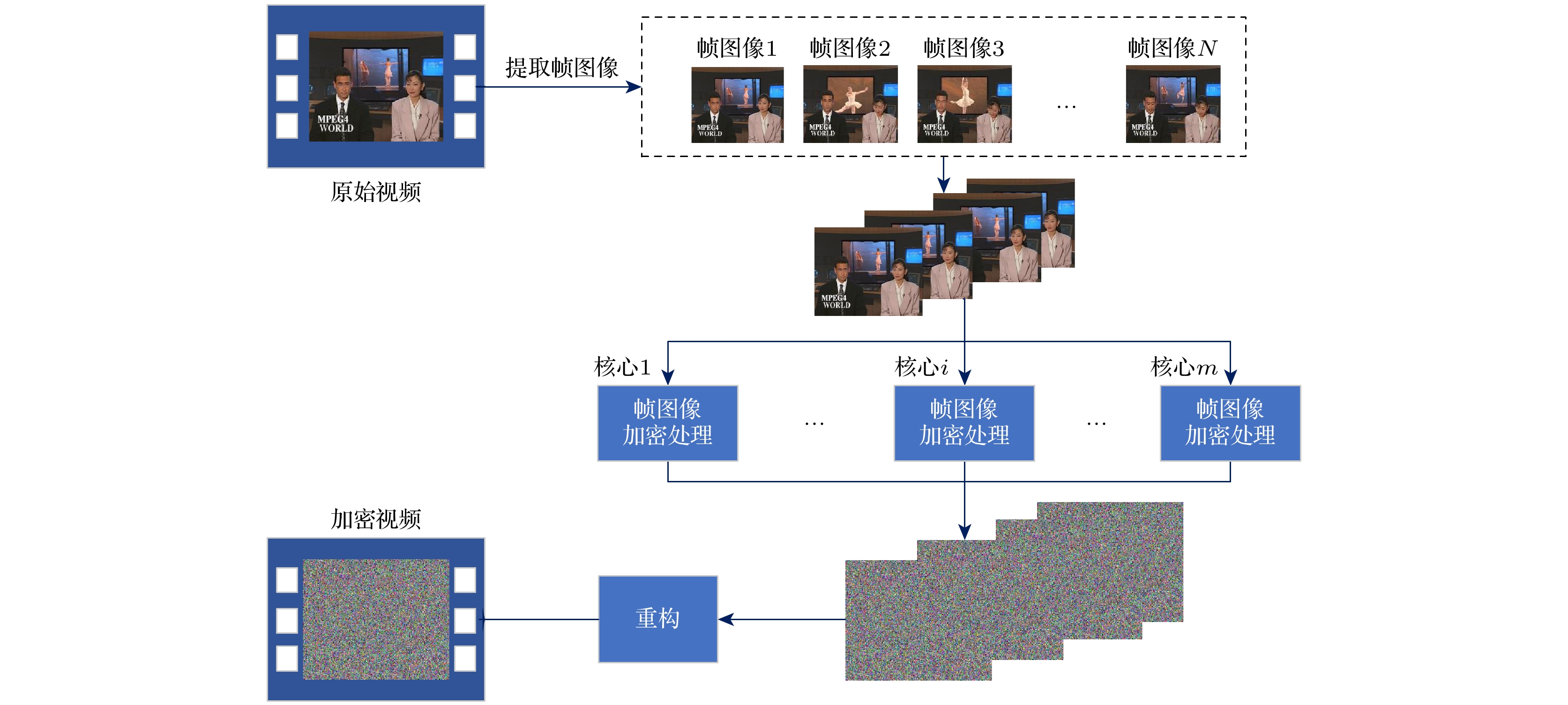
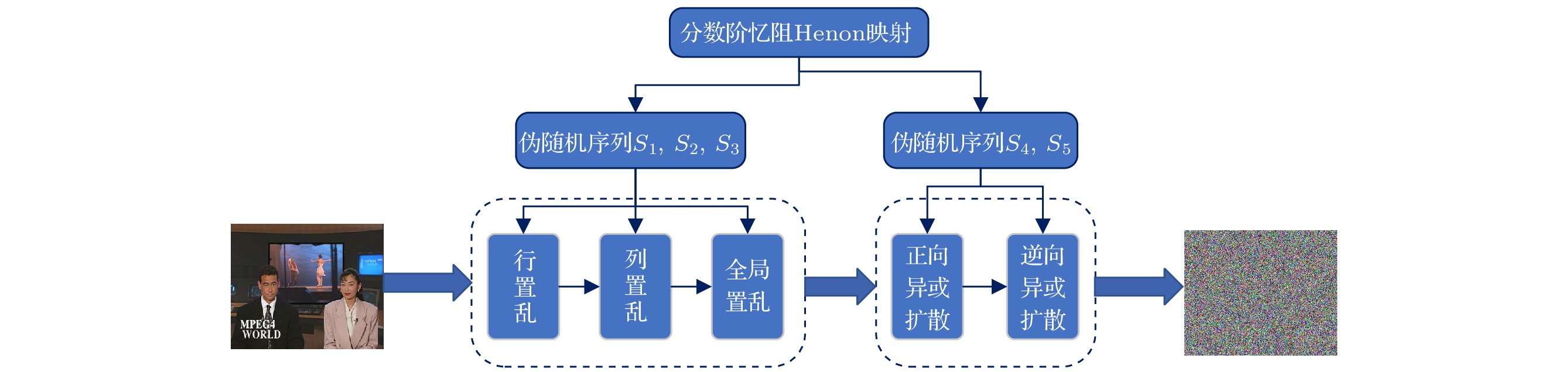
该加密方案主要是基于CPU的多核心多线程的基本原理, 具体的加密流程如图15所示. 首先从原始视频中提取出所有帧, 然后利用CPU的多核心对提取的帧图像进行并行加密处理, 最后将加密后的帧图像重构为视频. 帧图像加密处理的基本流程如图16所示, 具体的操作如下.

系统(7)的参数为: $ a = 1.01 $, $ b = 0.443 $, $ c = 0.17 $, $ d = 0.2 $, $ k = 0.2 $, $ q = 0.95 $, $ f = 200 $和$ {I_2} = 1 $, 初始值为$ (0.4, 0.5, z(1)){\text{ }}(z(1) = \pm 6, \pm 4, \pm 2, 0) $. 分数阶忆阻Henon映射的迭代次数为$ M \times $$ N + 1000 $. 为消除系统的瞬态效应, 确保所生成的伪随机数具有良好的随机性, 丢弃前1000个值, 最终产生5组可控的共存混沌序列$ {z_i}(i = 1, 2, \cdots , 5) $, 其中$ M $和$ N $分别为帧图像的行数和列数. 接着对5组混沌序列执行下述操作:

其中$ i = 1, 2, \cdots, 5 $. 通过上述操作即可获得伪随机序列$ {S_i} $.

对视频的帧图像处理的流程如图16所示. 利用伪随机序列${S_i}(i = 1, 2, \cdots , 5)$分别对帧图像像素进行置乱和异或扩散操作, 具体的步骤如下.

步骤1　将提取的帧图像$ {P_j}(j = 1, 2, \cdots ) $分解为$ {{\boldsymbol{P}}_{j{\text{R}}}} $, $ {{\boldsymbol{P}}_{j{\text{G}}}} $和$ {{\boldsymbol{P}}_{j{\text{B}}}} $三个像素矩阵.

步骤2　将伪随机序列$ {S_1} $的前$ M $个元素按升序排列, 获得索引向量A₁. 然后令$ {{\boldsymbol{B}}_{\text{R}}}(k, :) = {{\boldsymbol{P}}_{j{\text{R}}}}({{\boldsymbol{A}}_1}(k), :) $, $ {{\boldsymbol{B}}_{\text{G}}}(k, :) = {{\boldsymbol{P}}_{j{\text{G}}}}({{\boldsymbol{A}}_1}(k), :) $, $ {{\boldsymbol{B}}_{\text{B}}}(k, :) = {{\boldsymbol{P}}_{j{\text{B}}}}({{\boldsymbol{A}}_1}(k), :), k = 1, 2, \cdots , M $, 对3个像素矩阵的行进行置乱.

步骤3　将伪随机序列$ {S_2} $的前$ N $个元素按降序排列, 获得索引向量A₂. 然后令$ {{\boldsymbol{C}}_{\text{R}}}(:, l) = {{\boldsymbol{P}}_{j{\text{R}}}}(:, {{\boldsymbol{A}}_2}(l)) $, $ {{\boldsymbol{C}}_{\text{G}}}(:, l) = {{\boldsymbol{P}}_{j{\text{G}}}}(:, {{\boldsymbol{A}}_2}(l)) $, $ {{\boldsymbol{C}}_{\text{B}}}(:, l) = {{\boldsymbol{P}}_{j{\text{B}}}} (:, {{\boldsymbol{A}}_2}(l)), l = 1, 2, \cdots , N $, 对3个像素矩阵的列进行置乱.

步骤4　将伪随机序列$ {S_3} $的前$ M \times N $个元素按升序排列, 获得索引向量A₃, 接着像素矩阵$ {{\boldsymbol{C}}_{\text{R}}} $, $ {{\boldsymbol{C}}_{\text{G}}} $和$ {{\boldsymbol{C}}_{\text{B}}} $转换为一维向量$ {{\boldsymbol{D}}_{\text{R}}} $, $ {{\boldsymbol{D}}_{\text{G}}} $和$ {{\boldsymbol{D}}_{\text{B}}} $. 然后令$ {{\boldsymbol{E}}_{\text{R}}}(m) = {{\boldsymbol{D}}_{\text{R}}}({{\boldsymbol{A}}_3}(m)) $, $ {{\boldsymbol{E}}_{\text{G}}}(m) = {{\boldsymbol{D}}_{\text{G}}}({{\boldsymbol{A}}_3}(m)) $,$ {{\boldsymbol{E}}_{\text{B}}}(m) = {{\boldsymbol{D}}_{\text{B}}}({{\boldsymbol{A}}_3}(m)) $, 对像素矩阵$ {{\boldsymbol{C}}_{\text{R}}} $, $ {{\boldsymbol{C}}_{\text{G}}} $和$ {{\boldsymbol{C}}_{\text{B}}} $进行全局置乱.

步骤5　对伪随机序列$ {S_4} $和$ {S_5} $执行如下操作, 得到$ [0, 255] $范围内的伪随机序列:

接着对向量$ {{\boldsymbol{E}}_{\text{R}}} $执行如下正向异或扩散运算:

其中$ n = 2, 3, \cdots , MN $, $ {F_{0 R}} = 0 $. 然后对向量$ {{\boldsymbol{E}}_{\text{G}}} $和$ {{\boldsymbol{E}}_{\text{B}}} $也执行上述操作, 获得向量F_G和F_B. 接着对向量F_R执行如下逆向异或运算:

其中$ n = MN - 1, \cdots , 2, 1 $, $ {H_{0 R}} = 0 $. 然后对向量F_G和F_B也执行上述操作, 获得向量H_G和H_B. 最后将向量H_R, H_G和H_B重塑为加密矩阵$ {\boldsymbol{P}}_{j{\text{R}}}' $, $ {\boldsymbol{P}}_{j{\text{G}}}' $和$ {\boldsymbol{P}}_{j{\text{B}}}' $.

步骤6　将步骤5中得到的加密矩阵$ {\boldsymbol{P}}_{j{\text{R}}}' $, $ {\boldsymbol{P}}_{j{\text{G}}}' $和$ {\boldsymbol{P}}_{j{\text{B}}}' $转换为加密后的帧图像$ {\boldsymbol{P}}_j' $. 通过上述过程执行逆操作即可获得解密后的帧图像.

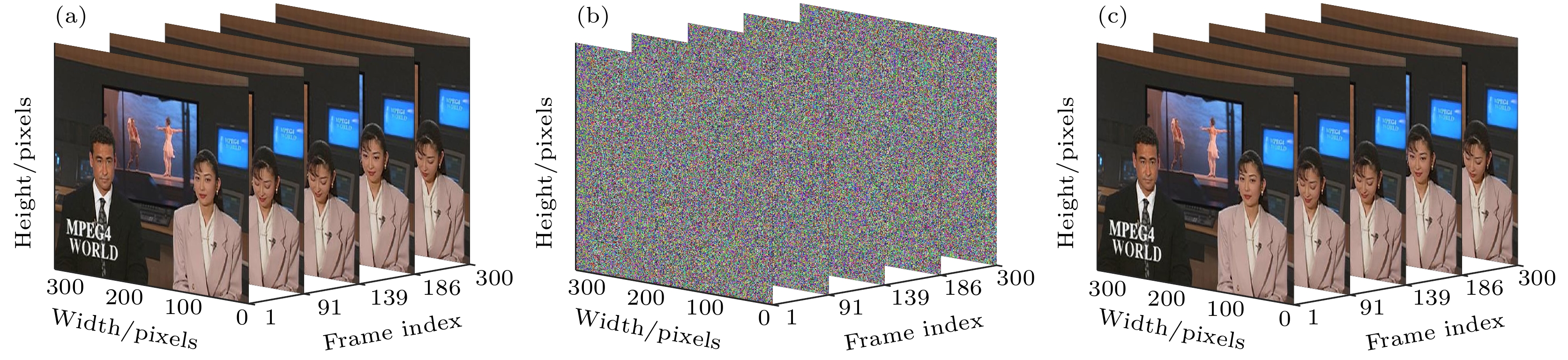
使用样本视频News对该加密方案进行测试, 以验证算法的安全性. 样本视频不同帧的测试结果如图17所示. 从图17可以看出, 原始视频和加密视频之间没有任何相关性, 并且无法从加密视频中获得任何有用的信息, 所有的加密视频都可以被正确解密.

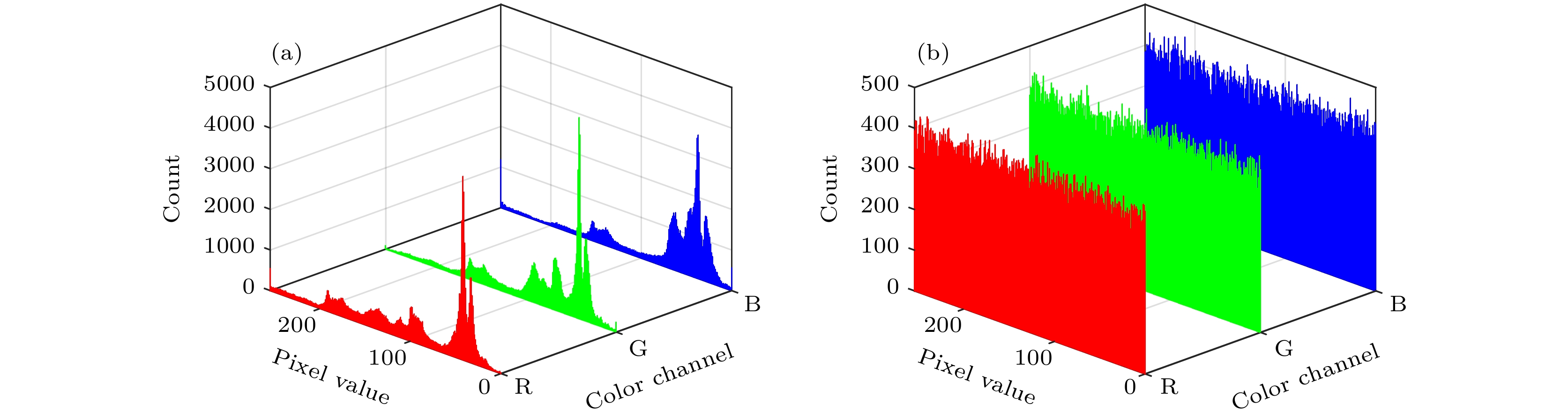
直方图是评估加密算法安全性的重要指标, 反映了帧图像像素值的整体分布情况. 本文以News第91帧为例, 测试帧图像的像素值分布情况, 其直方图如图18所示. 从图18可以看到, 相比原始帧, 加密帧图像的像素值分布很均匀, 原有的统计特征被有效隐藏, 这说明该加密方案很难被破解.

帧图像的水平、垂直和对角线3个方向上相邻像素值的相关性可以用相关系数表示. 通常原始帧图像的相关系数接近于1, 而加密帧图像的相关系数接近于0. 相关系数$ r(x, y) $定义为

其中$ E(x) = \dfrac1 N \displaystyle \sum\nolimits_{i = 1}^N {{x_i}} $, $ E(y) = \dfrac 1 N \displaystyle \sum\nolimits_{i = 1}^N {{y_i}} $, $ {x_i} $和$ {y_i} $两个相邻的像素值, $ N $表示像素值的总数.

为了评估加密方案的性能, 这里在News第91帧的3个方向上随机选择5000对相邻像素值, 并计算其相关系数, 如表1所列. 从表1可以看出, 原始帧图像的相关系数非常接近1, 而加密帧图像的相关系数则趋近于0.

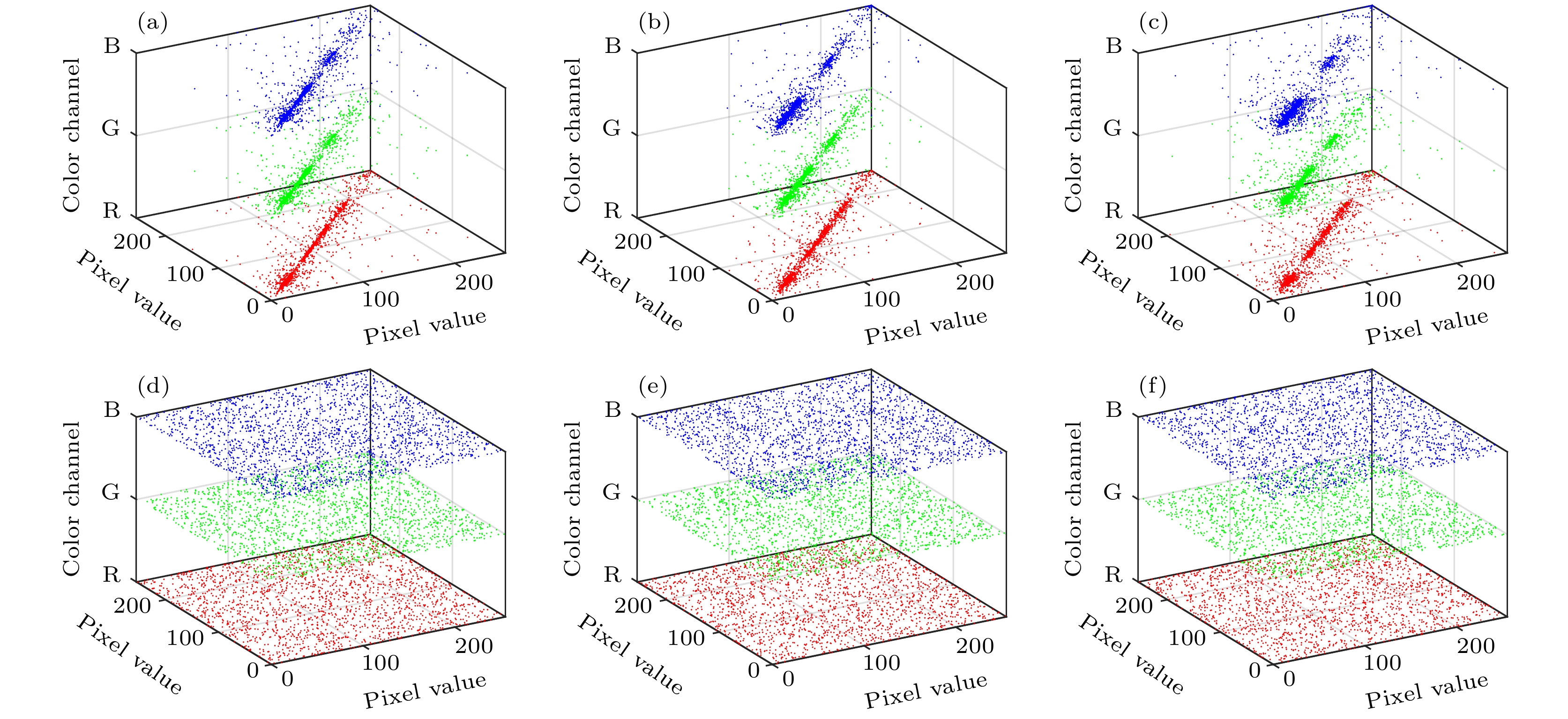
图19更直观地展示了3个方向上的相邻像素值的相关性. 图19(a)—(c)清楚地表明原始帧图像在3个方向上的相邻像素值高度相关. 而图19(d)—(f)则表明加密帧图像像素值分布均匀, 在3个方向上的相邻像素值之间几乎没有相关性.

信息熵是一种用来定量表征信号的不确定性的指标, 也可以用来评估帧图像像素值的随机性. 帧图像的像素值分布越均匀, 其信息熵越接近理论值8. 信息熵$ H $的定义如下:

其中$ p(j) $是像素值$ j $出现的概率, $ L $是帧图像中像素值的总数. News第91帧在加密前后的信息熵如表2所列. 从表2可以看出, 加密后帧图像的信息熵非常接近理论值8, 这表明该加密方案能够有效的加密视频信息.

密钥空间表示在一个加密算法中可以被使用的所有可能的密钥的数量. 密钥空间越大, 加密算法抵御穷举攻击的能力越强, 因此一个优秀的加密算法必须拥有足够大的密钥空间. 该加密方案使用参数$ a $, $ b $, $ c $, $ d $, $ k $, $ q $和初始值$ x(1) $, $ y(1) $, $ z(1) $作为密钥. 如果计算机为双精度, 则该加密算法的密钥空间为$ {({10^{16}})^9} = {10^{144}} \approx {2^{478}} $, 远远大于2¹⁰⁰. 因此该加密方案密钥空间非常大, 能够有效抵御暴力攻击. 如表3所列, 该方案的密钥空间与其他方案相比也具有优势.

加密方案对密钥的敏感性是指当密钥发生微小的变化时, 加密结果也发生很大的变化. 这里以News第91帧为例, 来说明该加密算法对密钥的敏感性, 实验结果如图20所示. 从图20可以看出, 密钥的微小变化($ {10^{ - 16}} $), 也会导致无法得到正确的解密帧图像. 因此, 该加密方案对密钥的敏感性很高.

加密后的视频在信道中传输的过程中, 噪声干扰或者数据丢失的情况不可避免. 因此, 一个优秀的加密算法必须具有很好的鲁棒性, 以确保信息特征在传输过程中不被破坏. 这里以News为例, 分别在其中引入不同强度的椒盐噪声和数据丢失, 并将第91帧展示在图21和图22中. 从图21和图22可以看出, 在不同强度的椒盐噪声和数据丢失的影响下, 解密后的帧图像仍然可以被视觉识别, 并且能够获得大部分的有效信息. 因此, 该加密方案对噪声影响和数据丢失有良好的容错能力, 有很好的鲁棒性.

本文利用多段非线性函数构建一种渐近稳定点可控的分数阶局部有源离散忆阻器. 然后将其引入Henon映射中, 构建了一种分数阶忆阻Henon映射. 仿真结果表明系统不动点的数量由忆阻器参数控制, 并且不动点与共存吸引子的数量存在对应关系, 从而产生可控的同质多稳定性. 通过相图、分岔图和MLE等分析方法, 详细阐述了分数阶忆阻Henon映射的复杂动力学行为, 如各种周期轨道、混沌吸引子和倍周期分岔等. 接着基于ARM数字平台实现了该系统, 实验结果与仿真结果完全一致, 验证了理论分析的正确性. 最后, 利用从分数阶忆阻Henon映射迭代过程中生成的混沌序列设计了视频加密算法. 安全性分析表明, 该加密算法能够有效地加密视频信息.

研究结果表明分数阶忆阻Henon映射呈现复杂的动力学行为和良好的混沌特性, 值得进一步探索. 此外, 该系统在伪随机数生成和保密通信等领域有潜在应用, 因此设计和实现可控多稳定性的分数阶混沌系统意义重大. 未来, 我们将继续探索构建可控多稳定性的混沌或超混沌系统, 并研究其电路实现、同步控制及混沌工程应用.