-
圆环换能器又称为圆管换能器, 使用压电陶瓷环实现机电转换, 是最为常见的水声换能器之一[1]. 传统的压电圆环换能器通常利用径向振动模态(又称呼吸模态)进行工作, 例如空气背衬的压电薄圆环水听器[2-4], 或大功率溢流圆环发射换能器[5,6]等. 研究者们对呼吸模态的研究已较为成熟, 相关理论可以较好地阐述其振动特性[7-13].
随着声学换能器的发展与需要, 除了呼吸模态, 国内外学者对压电圆环的弯曲振动也进行了相关研究. Huang等[14]研究了轴向极化圆环的
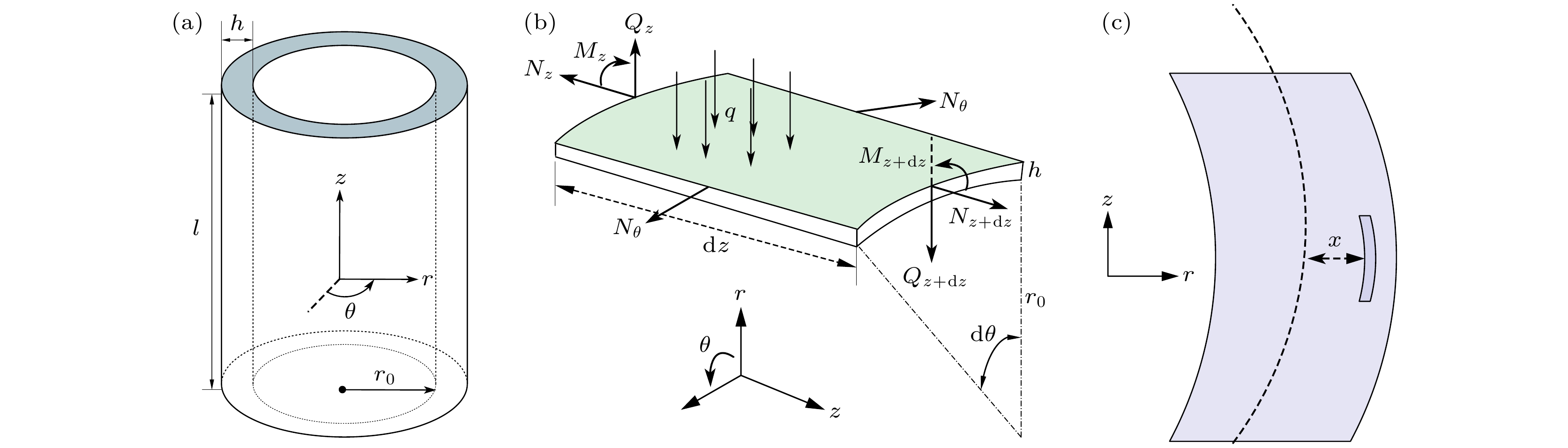
$ r \text- \theta $ 方向面外弯曲振动(振型如图1(a)所示), 利用板壳假设推导了非轴对称的横振动频率方程及多阶解析解. Aronov[15]使用能量法推导了压电圆环的$ r \text- \theta $ 方向面内弯曲振动(振型如图1(b)所示), 该振动模态的谐振频率相比呼吸模态大幅下降, 可使圆环用于超低频发射.然而, 对于压电圆环径向弯曲振动即
$ r \text- z $ 面内振动, 由于该模态的振动反相区较大、辐射能力差等原因往往未引起人们重视, 相关研究较少(振型如图1(c)所示), 相关理论缺失. 但一方面, 对于普通压电圆环水声换能器的设计, 需要使弯曲模态的谐振频率远离工作区间, 以避免响应曲线出现凹谷. 确认弯曲模态谐振频率对压电圆环换能器的响应分析及具体设计均有直接帮助. 另一方面, 由于压电圆环的大功率特性, 人们往往考虑引入其他结构与圆环换能器耦合, 例如圆环弯张换能器[16], 此时径向弯曲模态将不可避免. 因此, 对径向弯曲模态特性及激励原理进行相关研究具有重要意义. -
对于压电圆环, 如果壁厚
$ {h} $ 远小于曲率半径$ {r_0} $ , 在力学上可视为薄壳. 在呼吸模态[17]的计算中, 通常认为径向正应力$ {T_{rr}} $ 和切应力$ {T_{rz}} $ 是一个相对小量, 即所谓的薄膜理论. 本文所讨论压电圆环的弯曲振动, 属于薄壳的小挠度振动, 径向正应力$ {T_{rr}} $ 同样可以忽略, 但切应力$ {T_{rz}} $ 应该被保留. 结合轴对称性质, 作出假设如下: 1)环上各点径向位移为挠度$ w $ , 且忽略径向正应力, 即$ {\eta }_{r}(r, z, t)= w(z, t), \;{T}_{rr}=0 $ ; 2)${\boldsymbol{\theta }}$ 方向切应力与切应变为0, 即$ {S}_{\theta r}={S}_{\theta z}=0, \;{T}_{\theta r}={T}_{\theta z}=0 $ .Timošenko[18]在其《板壳理论》一书中给出了图2(a)圆柱壳体的静力平衡方程:
式中N, Q, M分别表示对厚度积分的正力、剪力和力矩. 这些面力与应力张量T的关系如下:
式中
$ x $ 为被积分点到中性面的距离, 如图2(c) 所示.引入惯性力项, 将(1)式改写并化简为动力平衡方程. 由于薄壳的转动惯性力矩
$ I\dfrac{{{\partial ^2}\theta }}{{\partial {t^2}}} $ 可以忽略[19], 同时考虑法向振动w是弯曲模态的主要组成, 忽略z方向的惯性力项$ \rho h\dfrac{{{\partial ^2}{\eta _z}}}{{\partial {t^2}}} $ (即不考虑径长耦合), 将方程简化为 -
由板壳理论, 将距离中性面x处的纤维轴向正应变
${S_{zz}}$ 与切向正应变表示为挠度w的形式, 即几何方程:对于本文讨论的压电材料, 其本构方程由压电方程组描述[20], 式中
$ {{\boldsymbol{d}}_{\text{t}}} $ 为压电耦合矩阵$ {\boldsymbol{d}} $ 的转置:讨论径向极化压电圆环, 定义z,
$\theta $ , r分别为1, 2, 3轴(避免对相关矩阵进行空间变换). 将应力与应变张量用6个独立变量表示:$ {S}_{1}={S}_{zz}, \;{S}_{2}= {S}_{\theta \theta },\; \;{S}_{3}={S}_{rr}, $ ${S}_{4}=2{S}_{\theta r},\; \;{S}_{5}=2{S}_{rz}, \;\;{S}_{6}=2{S}_{z\theta } $ , 且$ {D_1} = {D_z},\;{D_2} = {D_\theta }, \;{D_3} = {D_r} $ . 考虑压电陶瓷的横向各向同性, 有本构方程: -
由(5)式及
$ {T_{rr}} = 0 $ , 轴向与切向正应变可以表示为将其代入几何方程
$ {S}_{zz}=-x\dfrac{{\partial }^{2}w}{\partial {z}^{2}}, \;{S}_{\theta \theta }=-w/{r}_{0} $ , 令$ {v_{12}} = - {{s_{{12}}^{\text{E}}} {/ } {s_{{{11}}}^{\text{E}}}} $ 为$\theta \to z$ 方向的泊松比, 则:因此, 平衡方程中的弯矩为
可以发现,
$ {T_{zz}} $ 的后两项对弯矩并无贡献. 即压电圆环弯曲时其抗弯刚度$ D = \dfrac{{{h^3}}}{{{12}s_{{{11}}}^{\text{E}}(1 - v_{12}^2)}} $ 与无源材料相同, 不受到压电效应影响.已知
$ {N_\theta } = \displaystyle\int_{ - h/2}^{ + h/2} {{T_{\theta \theta }}{\text{(1}} - {x {/ } r}{)}} {\text{d}}x \approx h{T_{\theta \theta }} $ , 由(6)式和(4)式可得由(3)式和(2)式可得
$ \dfrac{{\partial {T_{zz}}}}{{\partial z}} = \dfrac{{1}}{h}\dfrac{{\partial {N_z}}}{{\partial z}} = 0 $ ,$ {T_{zz}} = {\text{const}}{.} $ . 由于弯曲振动其轴向自由, 应力较小, 不妨认为$ {T_{zz}} = {0} $ . 联立(11)式得 -
对于内外壁接地的径向极化圆环(有电极), 在两电极相距较近时使压电陶瓷内部场强为零, 即
$ {E_r} = 0 $ . 将(12)式代入(10)式可得电学短路振动方程: -
若径向极化的圆环内外壁悬空(无电极), 或者两电极相距较远时, 压电陶瓷内部不满足
$ {E_r} = 0 $ 条件. 由于电压陶瓷为非导电介质, 内部无自由电荷, 则应满足无源静电场中的麦克斯韦方程(柱坐标):而由基本假设中
$ {T_{\theta r}} = 0 $ 和本构方程(6)得到:而
$ 2{S_{\theta r}} = s_{{44}}^{\text{E}}{T_{\theta r}} + {d_{15}}{E_\theta } = 0 \Rightarrow {E_\theta } = 0 $ 即$ {D_\theta } $ = 0. 将本构方程(6)中的电位移$ {D_r} $ ,$ {D_z} $ 分量展开, 代入(14)式得:对该电学方程进行一些必要简化: 对于该薄壳模型认为电场、应力在
$r$ 方向均匀, 即物理量关于$r$ 的一阶导为0. 由于径向极化加电, 忽略z方向电场, (16)式变为将(18)式代入(17)式, 然后结合(12)式可以得到关于
$ {T_{\theta \theta }} $ 的方程组:消去
$ {E_r} $ , 得令机电耦合系数满足
$ k_{31}^2 = \dfrac{{d_{31}^2}}{{\varepsilon _{{33}}^{\text{T}}s_{{11}}^{\text{E}}}} $ , 将(20)式代入(10)式得电学开路振动方程: -
(13)式和(21)式形式相似, 令径向位移
$ w(z, t) = W(z){{\text{e}}^{ - {\text{i}}\omega t}} $ , 有频域振动方程:式中声速
$ p $ 为大于0的正实数, 且考虑令波速$ c = 1/\sqrt {\rho s_{11}^{\text{E}}} $ , 波数$k = {\omega {/ } c}$ , 其中方程(22)通解可以表示为
-
考虑压电圆环在水中工作时两端往往保持自由. (9)式展示了压电效应对弯矩没有贡献, 则两端自由边界表示为
$ \dfrac{{\partial }^{2}w}{\partial {z}^{2}}=0, \text{ }\dfrac{{\partial }^{3}w}{\partial {z}^{3}}=0(z=0或l) $ . 可得A = C, B = D, 且有方程组:令
$ \left| N \right| = 0 $ 得频率方程:设超越方程
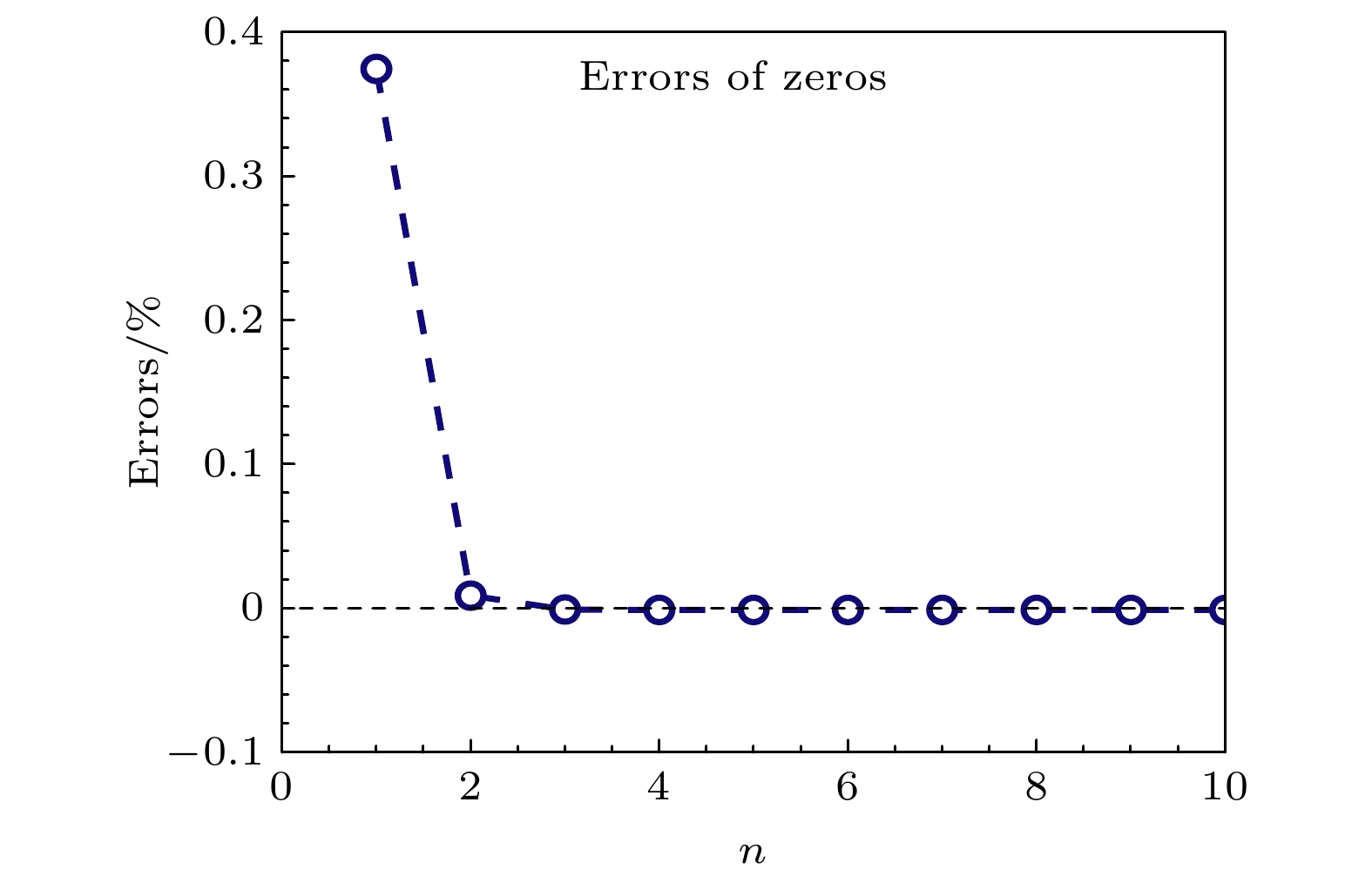
$ \cos (x)\cosh (x) = 1 $ 解为${\mu _n}$ , 其有近似解${\mu _n} \approx \dfrac{{3{\text{π}}}}{2} + (n - 1){\text{π}} = \dfrac{{(2 n + 1){\text{π}}}}{2}$ , 代入不同n计算可发现误差较小, 如图3所示.将频率参量
${p_n} = \dfrac{{{\mu _n}}}{l} \approx \dfrac{{3{\text{π}} + (n - 1){\text{π}}}}{{2 l}}$ 代入(23)式, 可以得到电学短路和电学开路下谐振频率.电学短路谐振频率为
电学开路谐振频率为
若为固定、简支、载荷等其他条件使用对应边界即可, 这里不再赘述.
-
依旧考虑两端自由边界, 由(25)式得
随着阶数的增高, 其比值会愈发接近
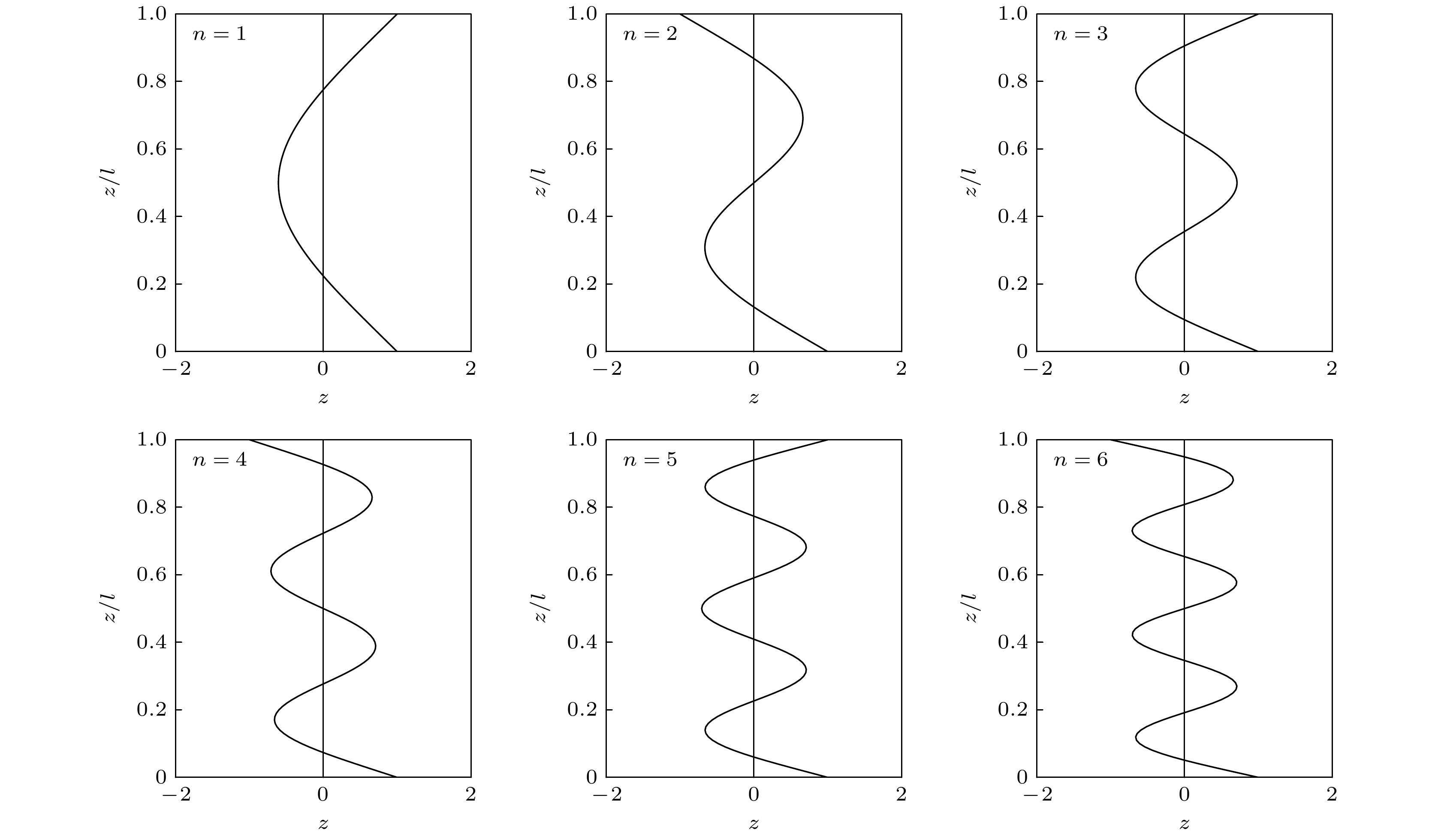
$ - {1} $ . 令${B {/ } A} = Y(n)$ , 第n阶振型函数为频域振动方程的解(24)式应表示为多阶模态的叠加:
-
令
$ {W_n}(z) = 0 $ , 使用数值法求得前几阶模态的节点位置在表1列出. -
对于一个特定物理结构, 其往往具有无穷多个振动模态, 然而模态的激发取决于激励本身. 在水声换能器领域, 压电陶瓷的模态激发理论一直未能明晰, 潘瑞等[21]基于等效电路方法给出了压电细棒的多阶模态单端激励理论, 论证了对细棒的1/s部分进行电压激励, 可以激发出前2s – 1阶模态. 而本文所讨论的压电圆环径向弯曲采用常规激励方式(内外壁均匀加电)不易激发, 下面通过模态理论来进行研究.
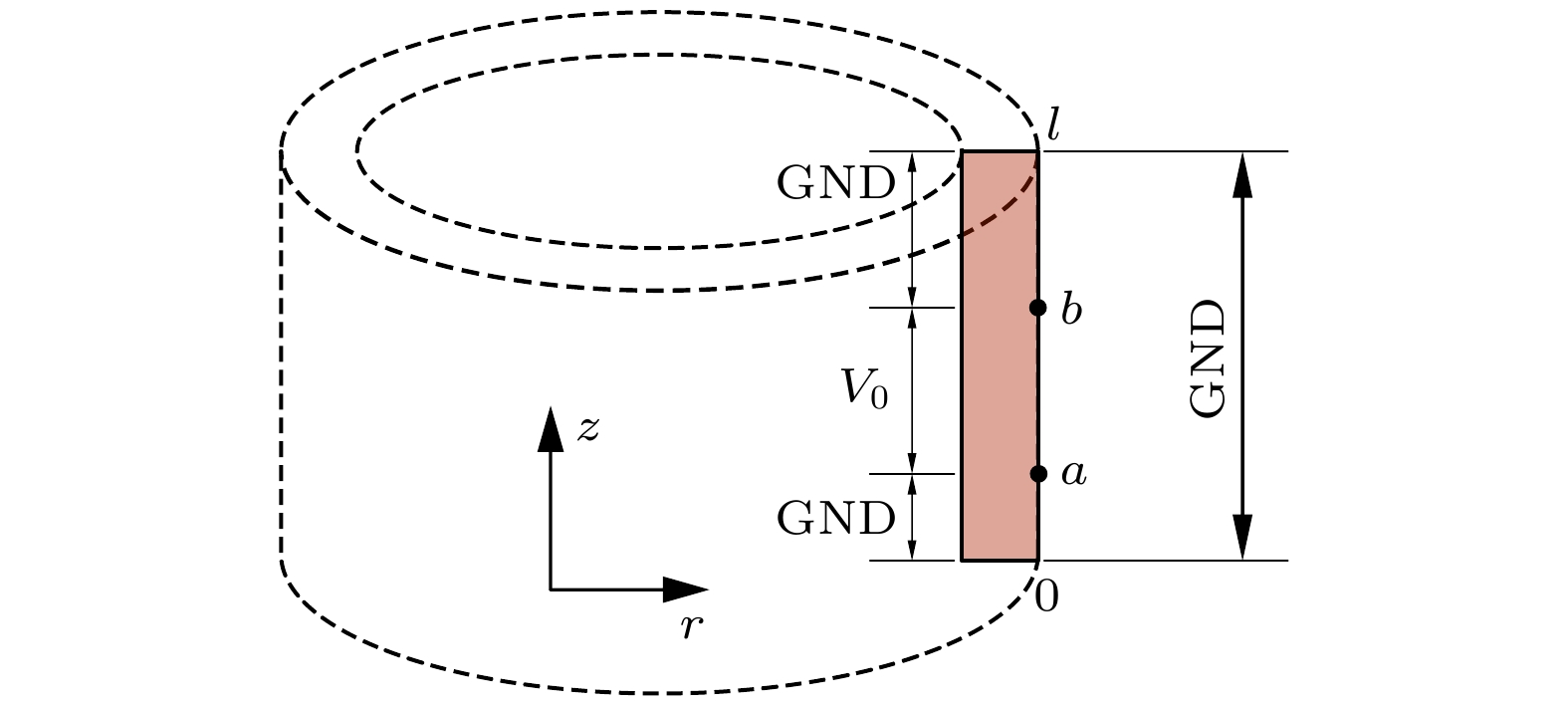
由于电学开路和短路条件只影响谐振频率而不影响对应振型, 两种条件下满足同一激发原理. 令外壁电势为0, 内壁施加电压分布
$V(z){{\text{e}}^{ - {\text{i}}\omega t}}$ , 电压幅值$V(z)$ 是关于$z$ 的函数. 将${E_r}(z, t) = \dfrac{{V(z)}}{h}{{\text{e}}^{ - {\text{i}}\omega t}}$ 代入(12)式, 使自由振动方程(13)变为受迫振动下的非齐次方程:其中,
$ {{{d_{31}}V} {/ } {s_{{{11}}}^{\text{E}}{r_0}}} $ 为$2{\text{πd}}\theta {\text{d}}z$ 微元上所受面力, 可以将$N = {{{d_{31}}} {/ } {s_{{{11}}}^{\text{E}}{r_0}}}$ 定义为机电转换系数.进一步, 对(32)式有稳态方程:
由模态理论, 不同阶的振型函数(30)式共同构成一个线性空间, 其正交完备(该振型与梁的弯曲类似[22], 其正交完备性容易证明). 此时坐标z为物理坐标, 而(31)式中振型系数
${A_n}$ 为简正坐标, 定义以振型$ {W_n}(z) $ 为基向量的积分变换$ \mathcal{T} $ :实际上若圆环两端为固定边界, 其基向量为三角函数, 对应的
$ \mathcal{T} $ 是更常见的空间傅里叶变换. 对(33)式作$ \mathcal{T} $ 变换, 使稳态方程在简正坐标中求解, 得展开(35)式并考虑到三角函数与双曲函数的求导关系
$ \dfrac{{{{\text{d}}^4}{W_n}(z)}}{{{\text{d}}{z^4}}} = p_n^4{W_n}(z) $ , 该积分变换可将四阶微分方程(33)变为简正坐标中的代数方程:考虑正交性, (36)式可变换为
令
$ \displaystyle\int_0^l {{W_n}(z){W_n}(z)\text {d} z = \delta (n)} $ , 有$ \delta (1)=0.8901, \delta (2)=1.0796\cdot \cdot \cdot $ ,$ \delta (n) $ 是只与振型函数相关的非零量, 因此(37)式充分反映了激励源对于不同阶模态的影响. 一方面分母中$ p_n^4 - {p^4} $ 表示激励频率与第n阶谐振频率相差越远, 则该阶振型系数$ {A_n} $ 越小, 由于模型中未考虑阻尼,$ p_n^4 - {p^4} $ =0时该模态系数$ {A_n} \to \infty $ ; 另一方面$ {A_n} $ 取决于电压分布$ V(z) $ , 即激励对不同模态的强弱作用. 对(37)式, 电压可以顺利激发出第n阶模态的条件:$ \displaystyle\int_0^l {V(z){W_n}(z)\text {d} z} \ne 0 $ . 定义$ {G_n} = \displaystyle\int_0^l {V(z){W_n}(z)\text {d} z} $ 为第n阶的模态权值(即简正坐标中的广义电压), 以反映电压分布对不同阶振型系数的影响. -
由于模态的正交性, 当电压分布与第m阶振型相同即
$ V(z) = {V_0}{W_m}(z) $ 时, 有因此如果采用和第n阶振型函数相同的电压分布函数进行激励, 则压电圆环只会激发出第n阶弯曲模态, 而不会激发出其他阶. 依据此方法可以获得纯粹的单阶振动.
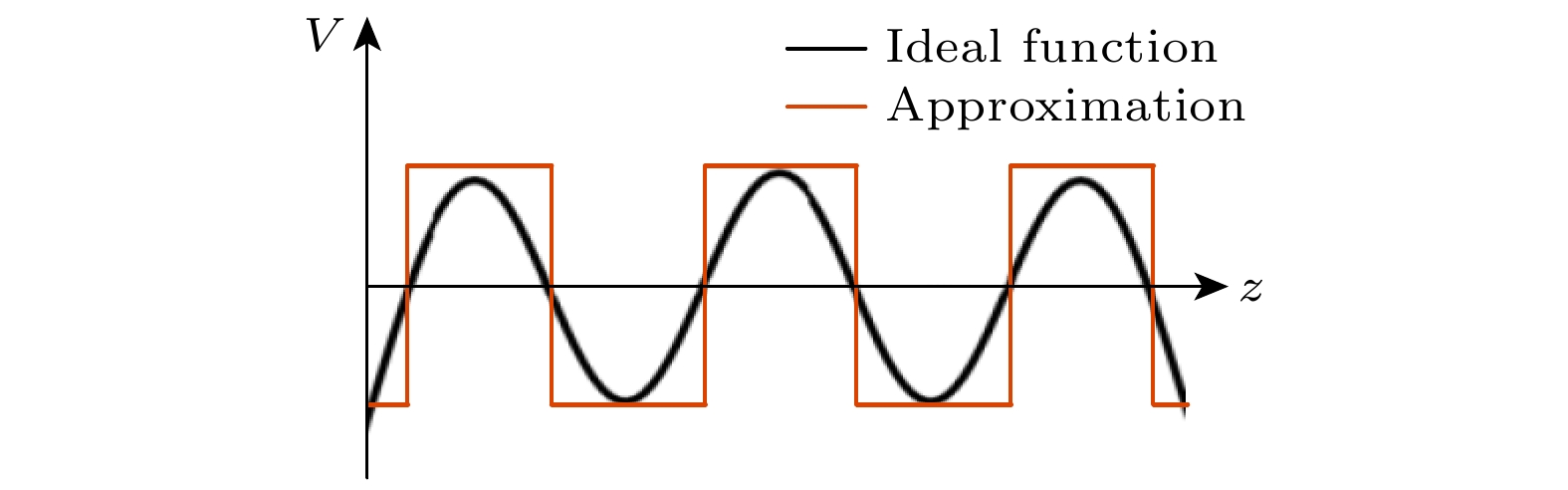
在实际情况中, 对压电材料施加连续的电压分布较为困难, 可以采用如图5所示的近似激励方法, 将连续化的电压函数变为不连续的分段函数. 显然, 分段数越多, 其激励效果将越接近理论值. 后文将实验证明该方法对于单模态激励的可行性.
-
考虑对压电圆环z方向上只有部分内外壁施加电压激励(依然轴对称, 只在z方向上加电不均匀, 具有激励段与非激励段), 假设对压电圆环在b–a的长度上施加等幅电压激励,
$V(z)$ 满足(39)式, 图6是其示意图.则有
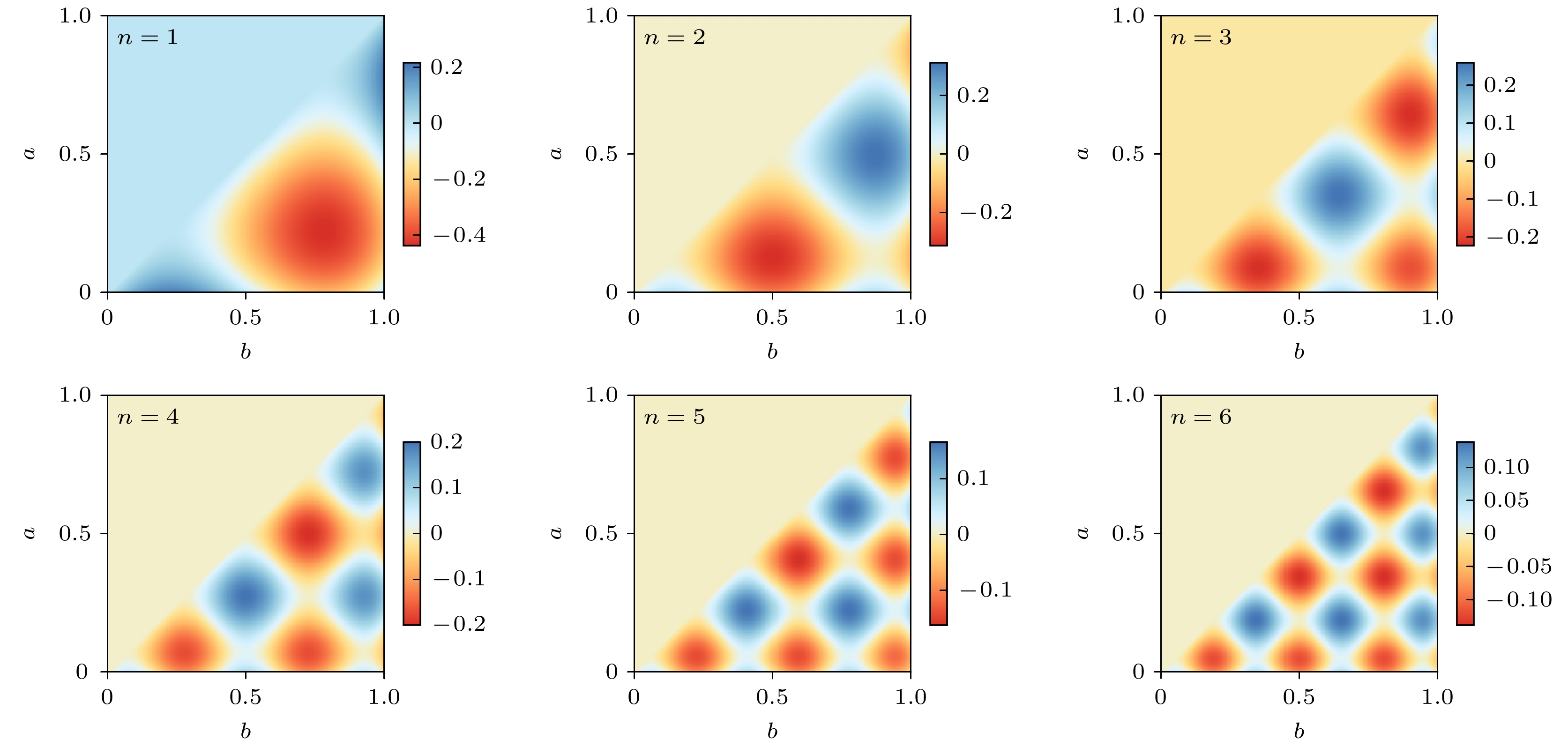
取
$ {V_0} = 1 $ , 可以得到积分的数值解. 图7是不同的激励区间[a, b]对前六阶模态的作用情况. 采用局部等幅激励的方式, 要使得某一模态的振动较强, 需要选取合适的a与b使模态权值Gn最大. -
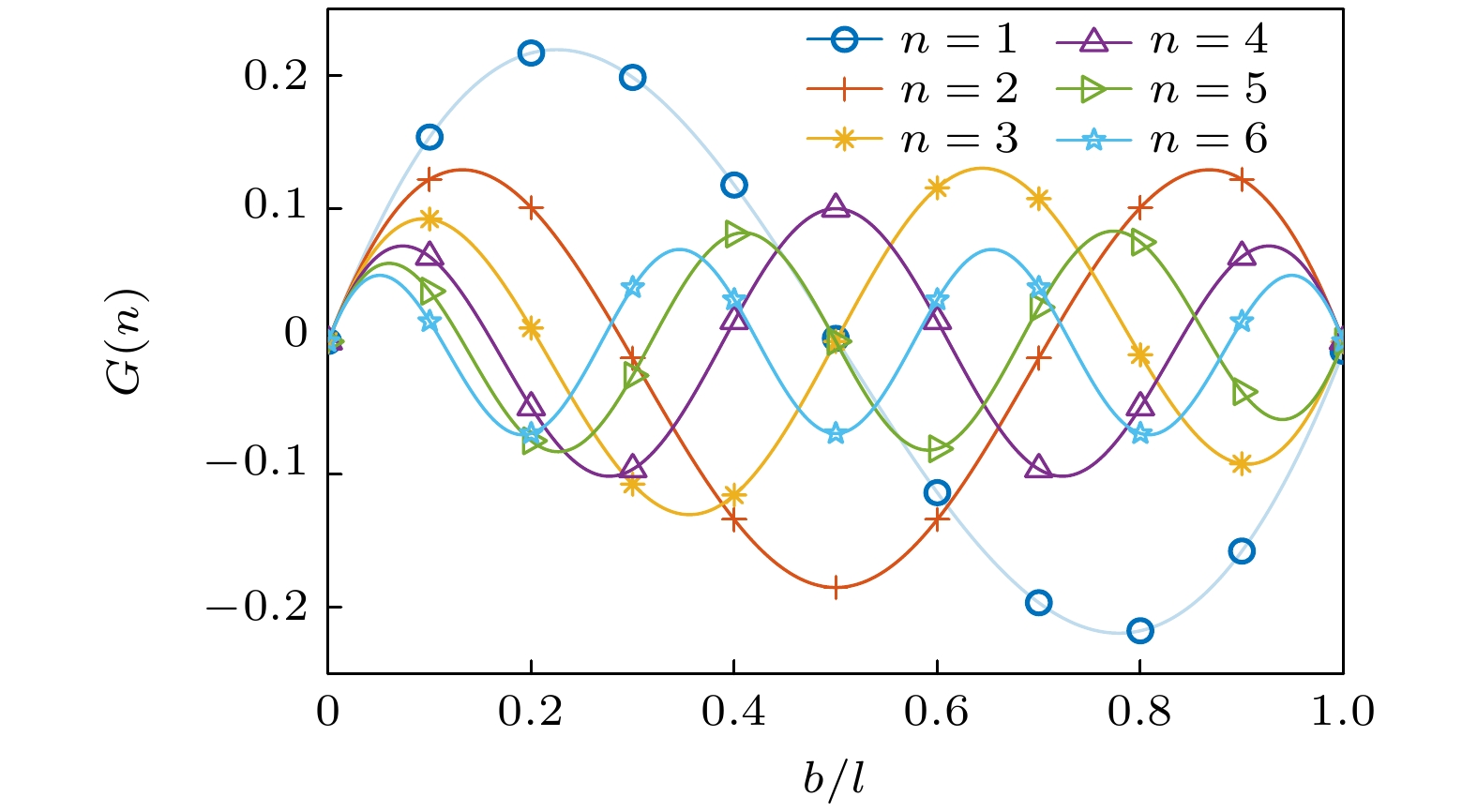
进一步考虑a = 0的特例情况, 即单端激励. 可得到不同的激励长度对所能激发的模态强弱的影响, 如图8所示. 可以发现对于单端激励, 激励长度对不同阶模态的影响是不一样的. 在
$b/l = 1$ 时, 由于各振型系数皆为0, 因此用常规全激励的方法无法激发出弯曲模态.通过数值法可以求得, (40)式中, 当
$n = 5$ 时,$ {V_0}\displaystyle \int_0^b {{W_n}(z) \text{d} z} $ 第一个$b \ne 0$ 的零点${b_{{\text{zero}}}} \approx 0.1322$ . 当$b/l < 0.1322$ , 此时必定可激发出前五阶的所有模态. 表2为采用单端激励方法激发出前n阶模态的激励长度约束.与前文单模态激励只激发某阶特定模态相对应, 采用单端激励方法, 可以激发出前n阶所有模态. 从图8可以看到: 1)对于同一长度单端激励, 越高阶的模态权值越小, 即越高阶振动越微弱; 2)对于不同长度单端激励, 激励长度越短, 可激发出模态阶数越多, 但所有模态的振动也更弱.
在满足可激发条件下, 为了达到有效的模态激发效果, 应该选取合适激励长度使目标模态的Gn取极大值, 而对多个模态实现精细化调控则可采用分段多激励方式.
-
多激励驱动一直是水声换能器领域关于驱动方面的研究重点, 可以实现拓宽带宽、调节模态等功能[23]. 考虑在
$[{a_1}, {\text{ }}{b_1}], {\text{ }}[{a_2}, {\text{ }}{b_2}] \cdots , {\text{ }}[{a_n}, {\text{ }}{b_n}]$ 等区间施加等幅电压激励, 显然根据积分的可加性:即多激励的模态权值
$ {G_n} $ 是不同局部等幅激励的线性叠加, 采用该方式可更大限度调节各个模态强弱分量. 对于一些简单激励如双激励、三激励等, 其计算较为方便, 具有较大的应用价值. -
在前文对激励电压的讨论中可知, 激励源只会影响到模态权值
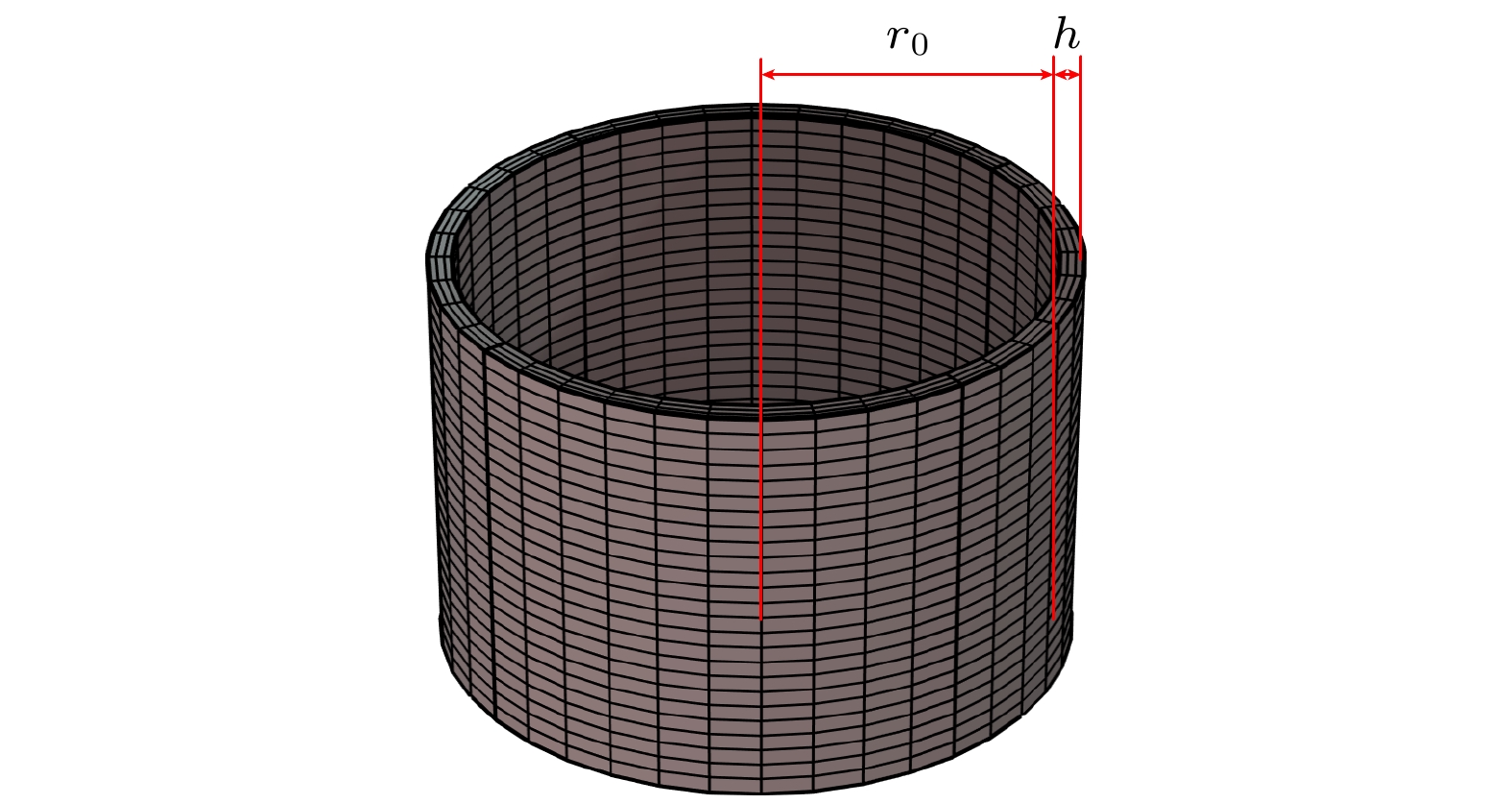
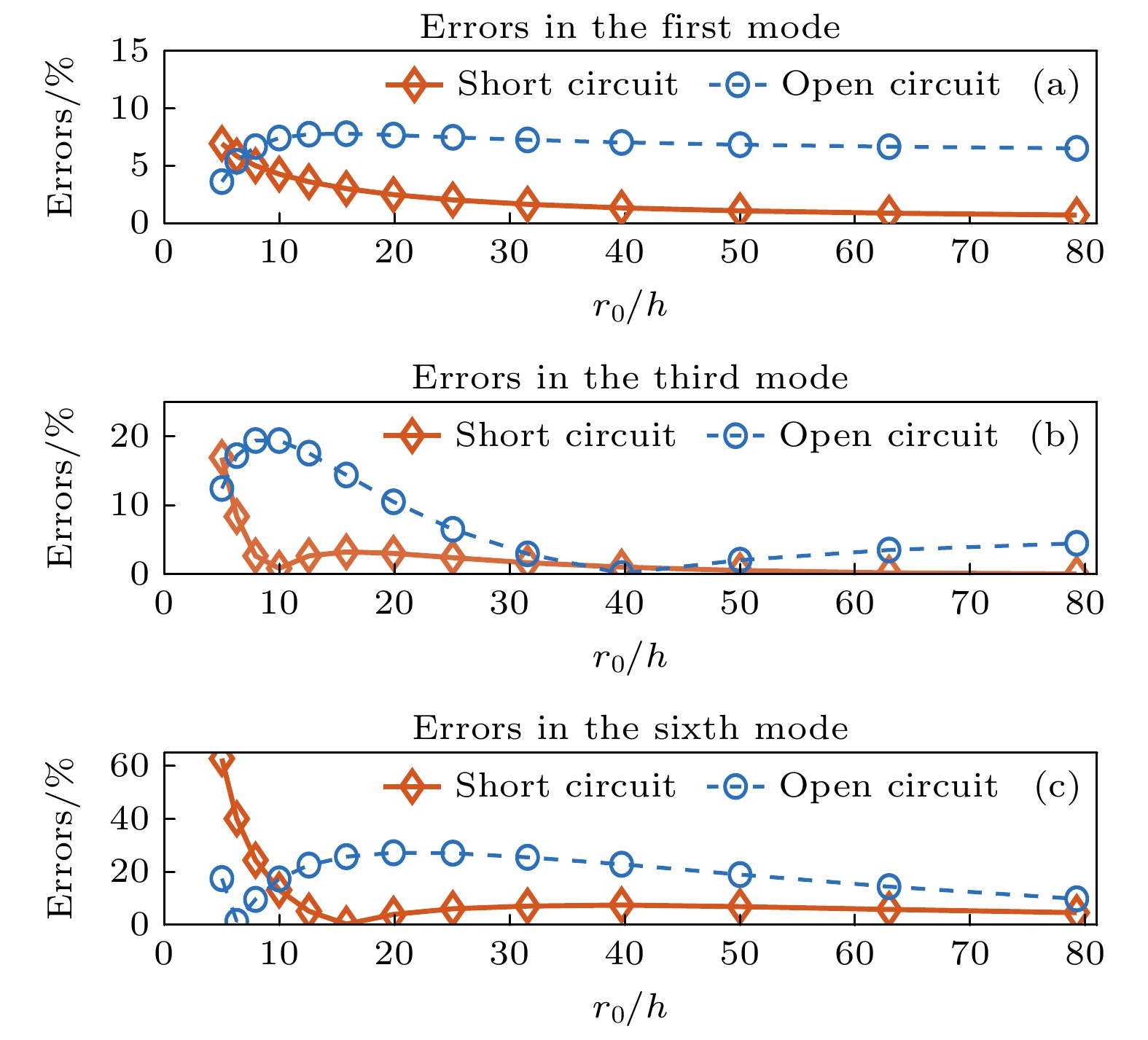
$ {G_n} $ , 即模态的激发与否和强弱, 而不会影响压电圆环的谐振频率. (27)式和(28)式得到了关于压电圆环弯曲模态谐振频率的两种表达, 即电学短路谐振频率$ f_{{\text{short}}}^{(n)} $ 与电学开路谐振频率$ f_{{\text{open}}}^{(n)} $ . 由于径向弯曲振动时存在大小几乎一致的反相区,$r, z$ 两方向振动方程耦合弱, 文中相关结论在不同长径比压电圆环中仍然适用.而圆环的径厚比对电学短路、开路条件以及薄壳理论本身的适用范围均有较大影响, 在有限元仿真(FEM)中对这两式的适用性进行讨论, 有限元模型如图9所示. 对于不同径厚比的压电圆环(内外壁均有电极),
$ f_{{\text{short}}}^{(n)} $ ,$ f_{{\text{open}}}^{(n)} $ 与有限元所计算特征模态的误差如图10所示, 具体信息见附录A.可以发现当壳较薄即两电极较近时, 更接近电学短路条件, 反之更接近电学开路条件, 式中两者具有不同的适用范围. 通过有限元仿真计算得出, 在
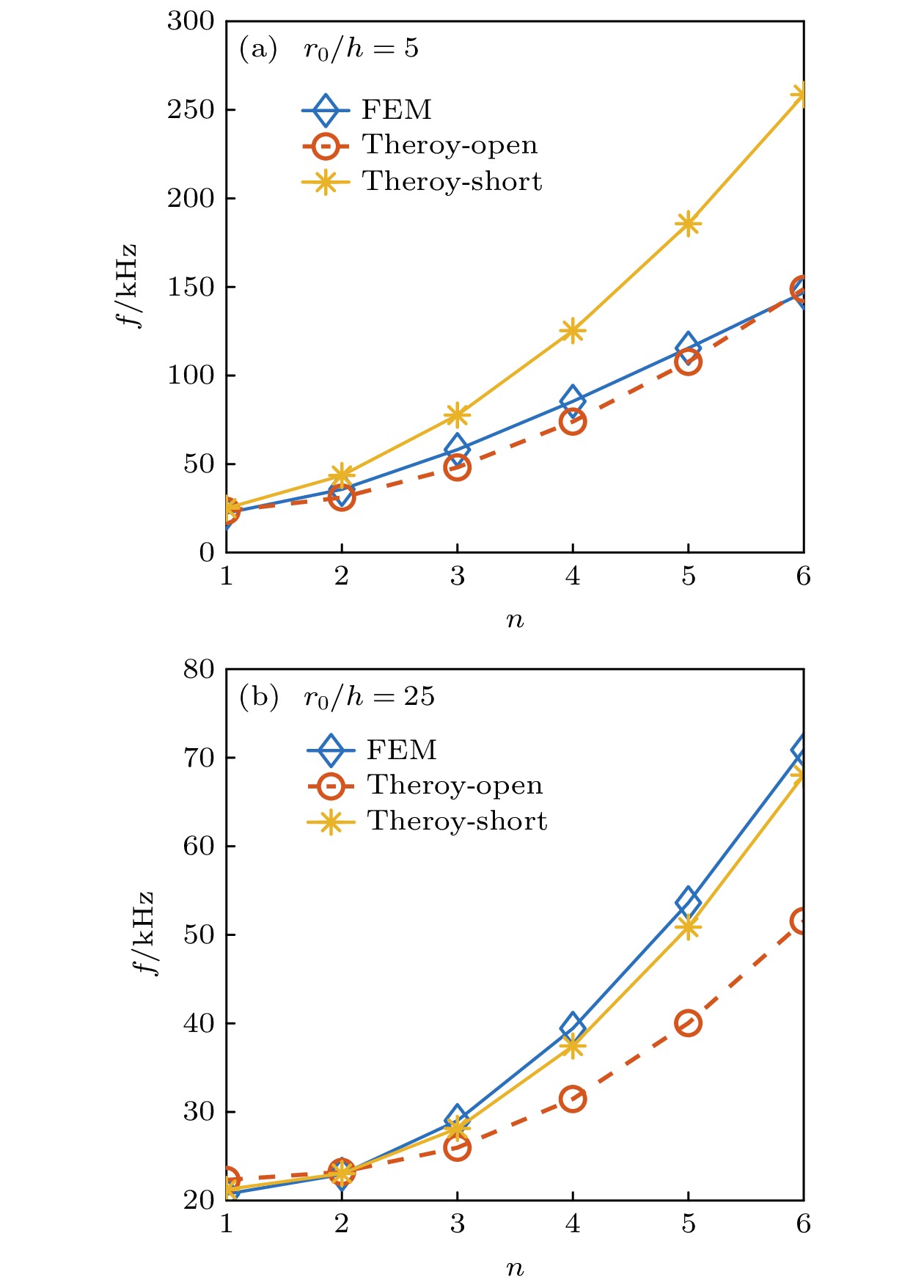
${r_0}/h > 7$ 时, 短路频率(27)式更加适用; 在$4.5 < {r_0}/h < 7$ 时, 开路频率(28)式更加适用, 图11分别为${r_0}/h = 5$ 与${r_0}/h = 25$ 时理论预测与有限元计算的吻合情况.此处未谈及薄壳理论本身的局限, 实际上本文的开路理论认为电场沿r均匀, 会使得谐振频率偏低, 一定程度上修正了薄壳理论在壳较厚时谐振频率偏高的误差. 当
${r_0}/h < 4.5$ 时, 由于模型已完全不满足薄壳条件, 使电学开路时的频率估计误差较大; 而当${r_0}/h > 20$ 时, 薄壳理论足够精确、电学短路条件较为满足, 使得理论预测足够准确(前六阶误差皆小于5%). -
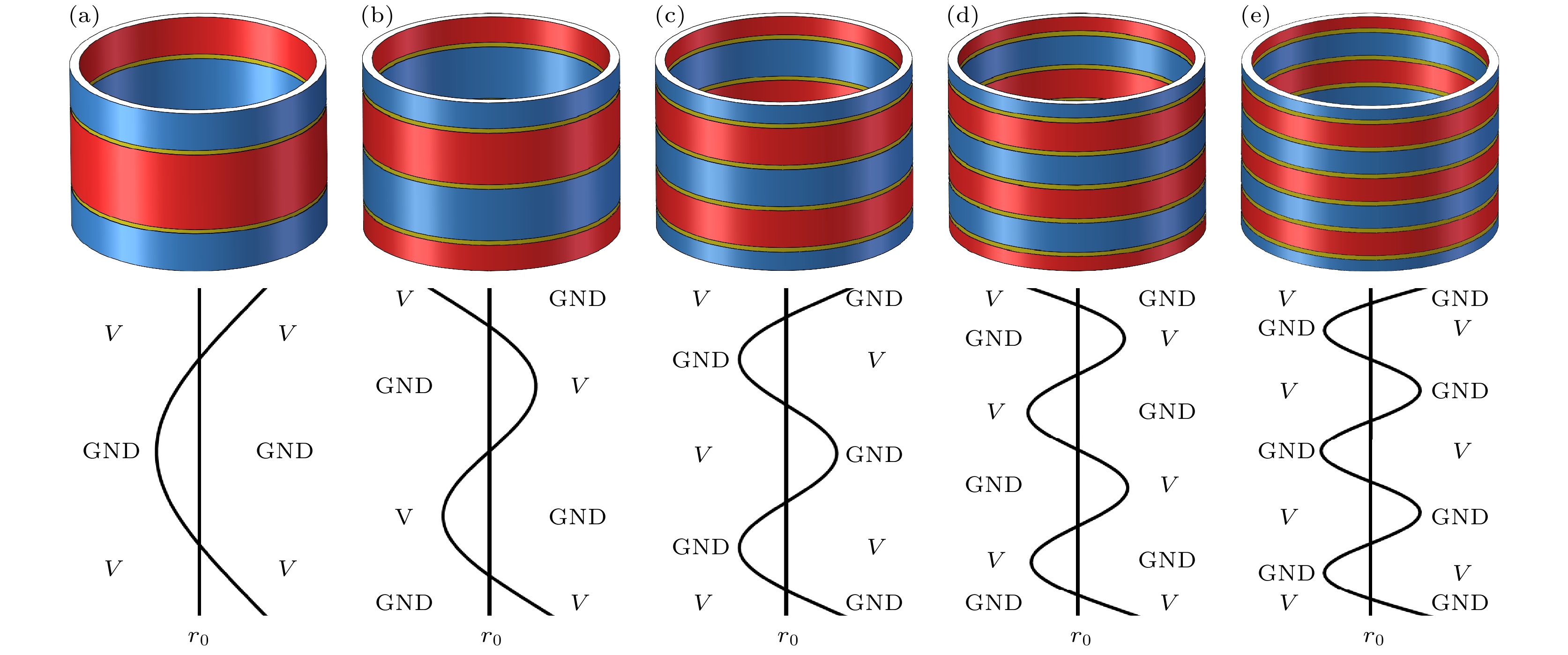
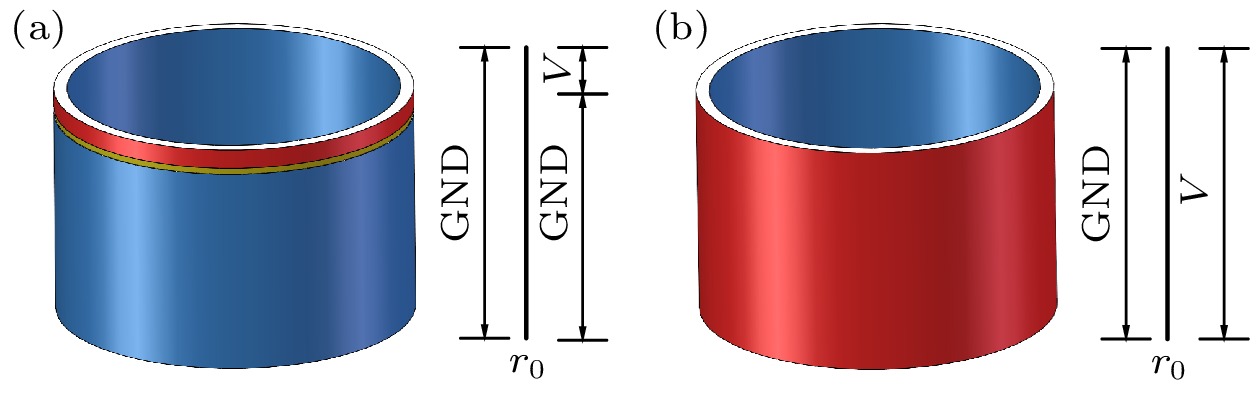
针对压电圆环的前五阶弯曲模态进行实验测试. 使用径向极化PZT-46压电圆环, 尺寸Φ54×Φ50×36 mm, 表3是PZT-46压电陶瓷的相关参数. 图12中样品A, B, C, D, E在内外壁进行银层切缝处理, 切缝位置处于弯曲振动节点处, 以实现单模态激励. 另有样品F在其距离顶部3 mm处进行银层切缝处理, 进行单端激励, 此时满足单端激励长度
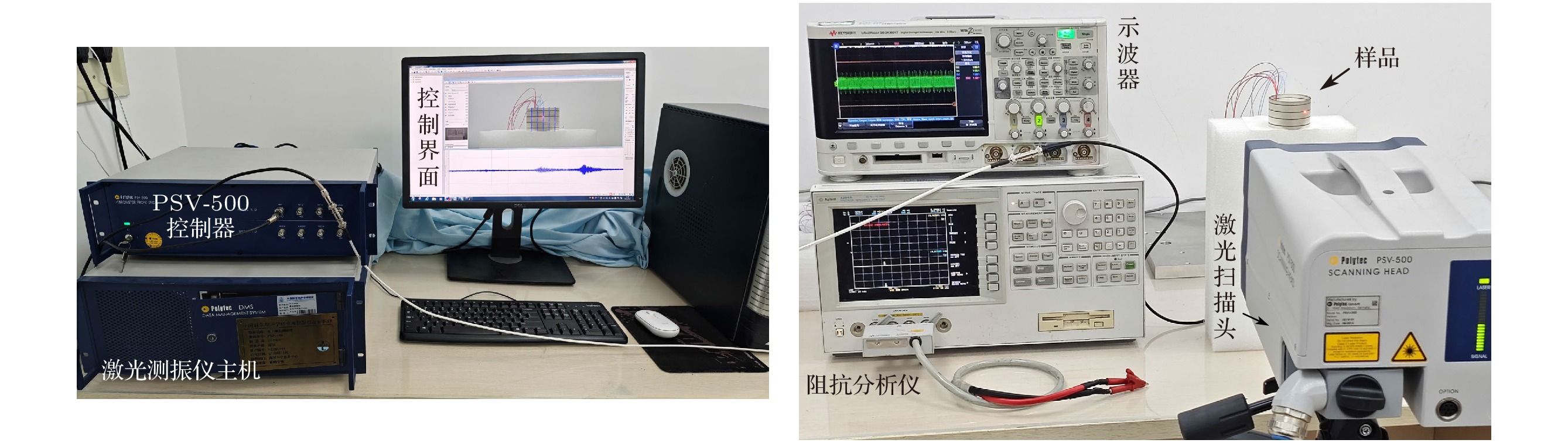
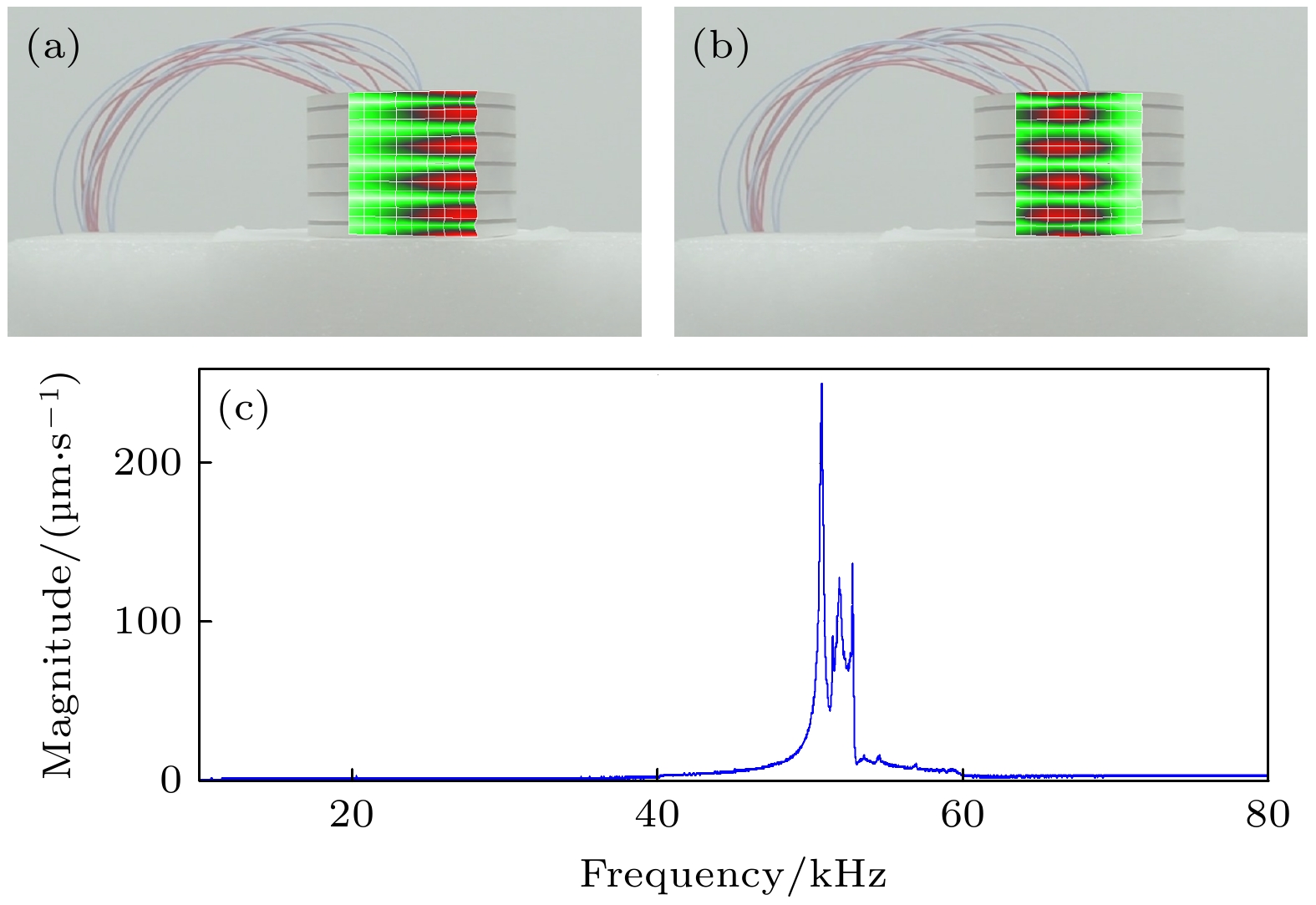
$ b/l = {1}/{{12}} < {(b/l)_{\max }} = 0.13 $ , 即理论上可以激发出前五阶所有模态. 图13和图14为这些压电圆环的电压激励示意图.图15为实验现场图. 使用阻抗分析仪测量各个压电圆环电导曲线, 并提取峰值处频率, 利用激光测振仪判断该阶弯曲模态是否被激发. 激光测振得到的单端激励振型及振速响应如图16所示, 通过该单端激励的方法同时激发出了前五阶弯曲模态, 且越低阶模态振动越强, 与激励理论一致. 图17是单端激励圆环和完整圆环的电导曲线与理论计算频率对比, 因为环的径厚比满足前文讨论的电学短路条件, 谐振频率与
$ f_{{\text{short}}}^{{(}n{)}} $ 较为吻合, 可以看到电导谐振峰与理论值一一对应, 通过激光测振仪的振型图16判断, 第1, 5个峰分别为圆环的呼吸模态与轴向纵振模态.通过振型图佐证, 该压电圆环的弯曲谐振频率分别为19.7, 24.7, 36.1, 52.6, 72.8 kHz; 呼吸谐振频率18.8 kHz, 轴向谐振频率45.4 kHz. 表4为实验测试与有限元仿真、理论计算对比, 可以发现理论计算精确度较高(误差低于5%).
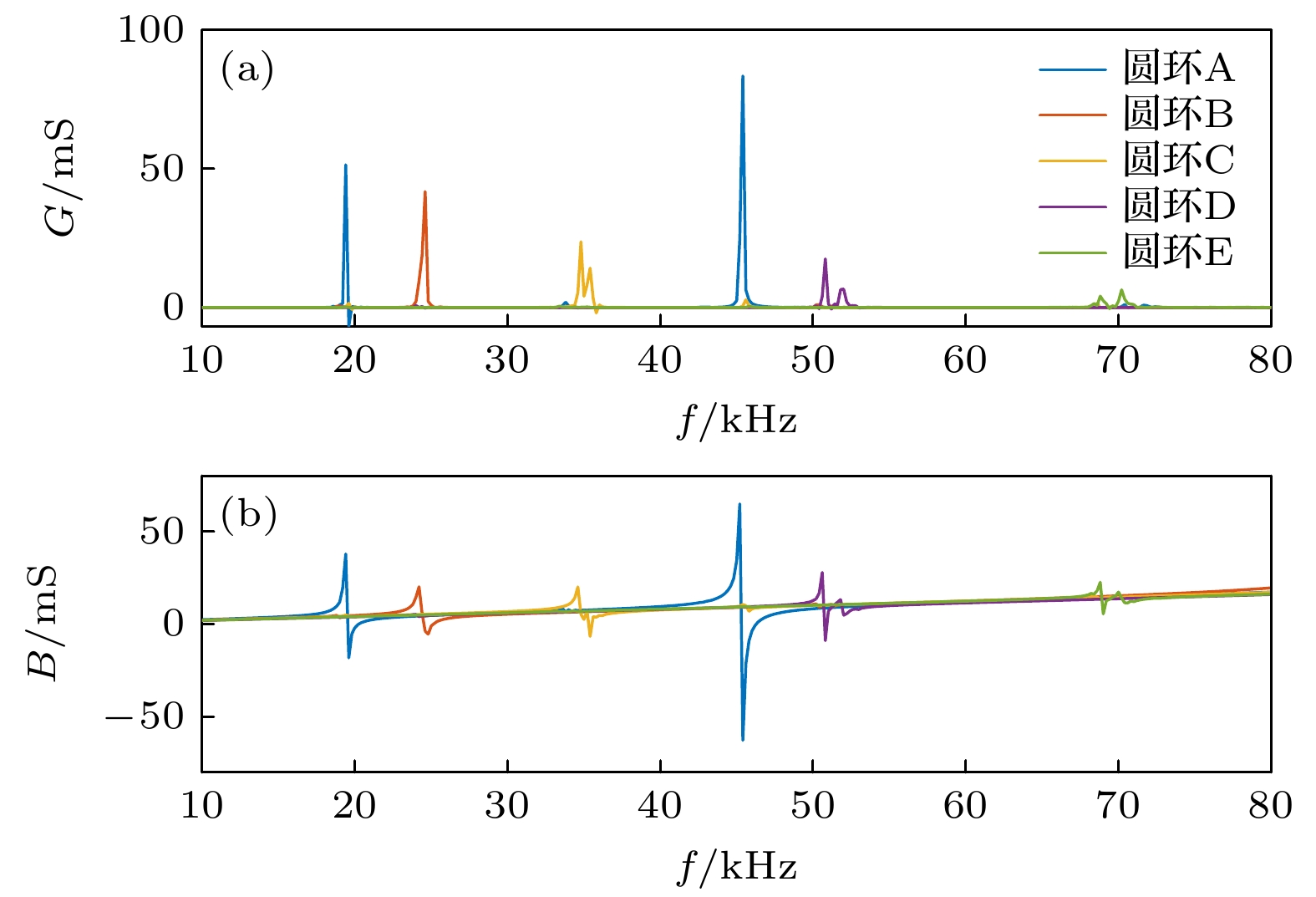
图18为单模态激励压电圆环的电导纳曲线, 发现虽然图13所示电势分布并未严格与振型分布相同, 而只是采用宽泛的近似, 但模态的激发符合预期: 每个单模态激励圆环主要激发了对应弯曲模态, 而其他阶的弯曲模态分量较小或未激发. 注意到, 处于45.4 kHz的轴向纵振模态仅被圆环A所激发, 这是一阶弯曲振型与纵振振型相似导致, 同时所有圆环皆规避了常规激励方法下的呼吸模态.
值得说明的是, 在单端激励与单模态激励实验中, 图16(h)、图17(a)和图18皆展示了高阶弯曲模态的电导曲线与振速幅频曲线在谐振峰处有“分叉”现象. 文中理论采用轴对称模型, 而压电圆环样品周向存在不均匀度, 这也是表4中有限元计算理论误差的主要来源. 经测量最薄处为2.1 mm, 最厚处为2.2 mm, 由弯曲谐振频率(27)式和(28)式可知阶数n越大, 厚度h对谐振频率影响越大, 即样品的周向不均匀使得高阶谐振处电导更容易“分叉”.
图19是圆环D单模态激励时谐振附近两振速峰的激光测振图, 这种周向不对称性体现得较为明显.
-
本文对压电圆环径向弯曲振动进行相关研究, 结合有限元仿真和实验测试, 得出以下结论.
1)得到的电学短路与开路条件下压电圆环径向弯曲的谐振频率表达式, 经验证误差较小, 可适用于压电圆环的弯曲模态频率估计.
2)提出的压电圆环单模态激励、单端激励方法在实验中成功激励出了目标模态. 单模态激励圆环只激发了其对应的弯曲模态, 而单端激励方法激发了前五阶的所有弯曲模态, 模态强弱特征符合理论预测. 结合线性叠加特性, 该激励方法和理论可用于多个弯曲模态的精细化调节.
本文虽然仅具体讨论了径向极化、两端自由的压电圆环, 但通过材料矩阵的方向变换、改变边界条件可直接得出不同极化方向压电圆环在不同条件下的相关参量. 而关于模态激发原理的讨论由简正空间与物理空间的积分变换关系得到, 由于大部分结构振动模态具备正交完备性, 因此相关激励方法可拓展至纵向振动、板壳弯曲等多种声学换能器振动形式. 这些声学换能器结构与本文讨论的压电圆环相比仅有振型函数的区别, 相应积分变换的基向量换为对应振型即可, 文中相关结论具备一致性.
-
表A1列出了径厚比
${r_0}/h$ 对电学开路与电学短路理论的影响.
压电圆环径向弯曲振动与激励研究
Study of radial bending vibration and excitation of piezoelectric rings
-
摘要: 针对压电圆环换能器的径向弯曲振动问题, 从薄壳理论出发进行相关数理推导, 讨论了压电效应的影响及电学短路与开路下的弯曲振动方程. 进行相关解析求解, 给出了两种条件下的多阶谐振频率预测公式, 并利用有限元法分析了两式的适用范围. 使用模态理论, 定义模态权值函数, 研究了电学激励条件对多阶弯曲振动模态的具体影响, 得到了单模态激励、局部等幅激励和单端激励等作用于多个目标模态的有效方法. 经有限元仿真(FEM)、实验与理论对比验证, 三者吻合较好, 相关结论可以为压电圆环弯曲振动模态识别、模态激励的精细化调控提供理论基础.Abstract: Piezoelectric ring transducer is one of the most common underwater transducers, and its radial vibration, bending vibration in-plane $r \text- \theta $ and out-of-plane $r \text- \theta $ have been widely studied. However, the current research on the bending vibration in the plane $r \text- z$ of the ring is insufficient, although it may have a noticeable influence on the applicability of the underwater transducers. In this study, mechanical analysis and related mathematical calculations of the bending vibrations in the plane $r \text- z$ are carried out by using the thin-shell theory. Herein, the following three aspects are studied: 1) free vibration theory solution, 2) forced vibration: multi-order modal excitation theory, and 3) related finite element calculations and experimental verification. In this study, the bending vibration equations under electrical short and electric open condition are derived, and the multi-order resonance frequency prediction formulas and shape functions for both conditions are obtained by analytical solution and function fitting. Using the finite element method, the influence of piezoelectric effect and the range of applicability of these two electrical conditions are analyzed. The non-homogeneous equations under forced vibration are solved. By utilizing the orthogonal completeness of the vibration mode function, an integral transformation with the vibration mode function can be defined as the basis vector, so that the equation is solved in a simple positive space, and the results reveal the relationship between the coefficients of the modes of different orders and the voltage distribution. By modal theory, the effects of electrical excitation conditions on the multistep bending vibration modes are investigated, and effective methods such as unimodal excitation, partial excitation and single-ended excitation acting on several different target modes are obtained. The proposed piezoelectric ring unimodal excitation and single-ended excitation methods successfully excite the target modes in the experiments: the unimodal excited ring excites only one of its corresponding bending modes, while the single-ended excitation method excites all the bending modes of the first five orders, and its modal strength characteristics are in accordance with the theoretical predictions. This study involves finite element simulation, experimental and theoretical comparative verification, which are in good agreement. The relevant conclusions can provide a theoretical basis for identifying the vibration modes of piezoelectric ring and the fine tuning of modal excitation.
-
Key words:
- piezoelectric ring transducer /
- bending vibration /
- thin shell theory /
- modal excitation .
-

-
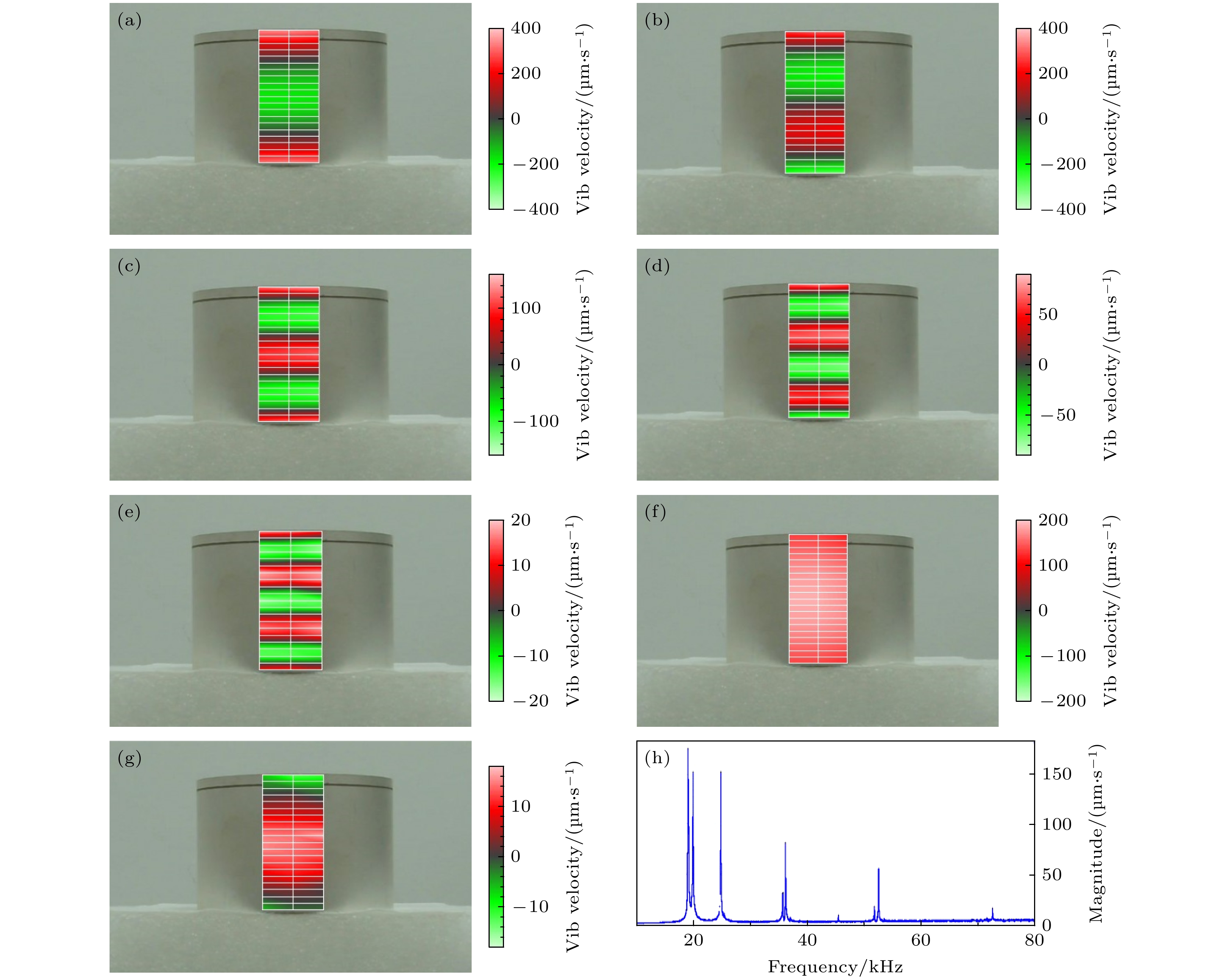
图 16 单端激励的激光测振图 (a) f = 19656 Hz; (b) f = 24656 Hz; (c) f = 36094 Hz; (d) f = 52594 Hz; (e) f = 72813 kHz; (f) f = 18750 Hz; (g) f = 45500 Hz; (h) 平均振速幅频响应
Figure 16. Vibration with single-ended excitation: (a) f = 19656 Hz; (b) f = 24656 Hz; (c) f = 36094 Hz; (d) f = 52594 Hz; (e) f = 72813 kHz; (f) f = 18750 Hz; (g) f = 45500 Hz; (h) mean amplitude-frequency response of the vibration rate.
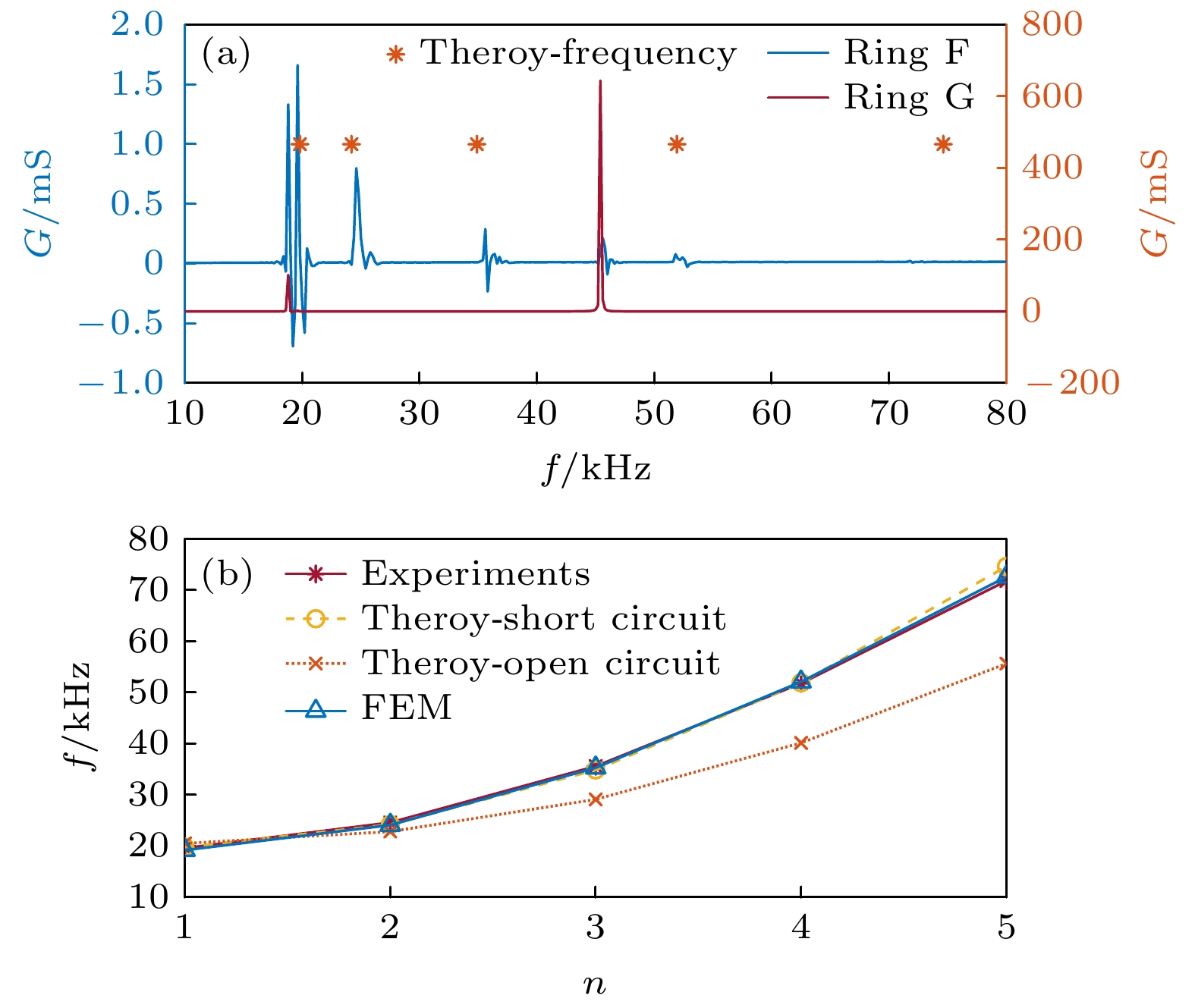
图 17 单端激励实验电导曲线及谐振频率 (a) 单端激励、全激励电导曲线与理论计算弯曲谐振频率; (b) 理论计算、有限元仿真与实验的谐振频率对比
Figure 17. Experimental conductance curves and resonance frequencies for single-ended excitation: (a) Single-ended excitation, full excitation conductance curves and theoretically calculated bending resonance frequencies; (b) comparison of theoretically calculated, finite element simulation and experimental resonance frequencies.
表 1 n阶模态对应的第m个节点位置z/l
Table 1. The m-th node positions z/l corresponding to n-th order modes.
n m 1 2 3 4 5 6 7 1 0.2250 0.7788 — — — — — 2 0.1321 0.5000 0.8677 — — — — 3 0.0944 0.3558 0.6441 0.9076 — — — 4 0.0735 0.2768 0.4997 0.7298 0.8749 — — 5 0.0601 0.2265 0.4091 0.5909 0.7727 0.9545 — 6 0.0509 0.1916 0.3462 0.5000 0.6538 0.8077 0.9615 表 2 单端激励激发出前n阶模态对应激励长度
Table 2. Excitation lengths of the first n order modes with single-ended excitation.
n 1 2 3 4 5 $ b/{l_{\max }} $ 0.5019 0.2904 0.2077 0.1616 0.1322 表 3 PZT-46压电陶瓷的材料参数
Table 3. Material parameters of PZT-46 piezoelectric ceramics.
$ s_{11}^{\text{E}}/{\text{P}}{{\text{a}}^{ - {1}}} $ $ \rho /({\text{kg}} {\cdot} {{\text{m}}^{ - {3}}}) $ $ \varepsilon _{{33}}^{\text{T}}/({\text{F}} {\cdot} {{\text{m}}^{ - {1}}}) $ $ {d_{31}}/\left( {{\text{C}} {\cdot} {{\text{N}}^{ - {1}}}} \right) $ $ {d_{15}}/ ({{\text{C}} {\cdot} {{\text{N}}^{-{1}}}}) $ ${v_{12}}$ ${k_{31}}$ 14.31×10–12 7750 11.51×10–9 –1.56×10–10 4.96×10–10 0.33 0.365 表 4 前五阶弯曲模态谐振频率对比
Table 4. Comparison of the first five orders resonance frequencies of bending modes.
阶数n 实验/Hz FEM/Hz 理论/Hz FEM误差/% 理论误差/% 1 19656 19423 19795 1.19 0.71 2 24656 24162 24192 2.00 1.88 3 36094 35537 34881 1.54 3.36 4 52594 52182 51921 0.78 1.28 5 72813 72685 74623 0.18 2.49 表 A1 径厚比
${r_0}/h$ 对电学开路与电学短路理论的影响Table A1. Influence of diameter to thickness ratio on the theory of electrical open circuit and electrical short circuit.
阶数 ${r_0}/h$ 5.0 6.3 7.9 10.0 12.6 15.8 19.9 25.1 31.5 39.7 50.0 62.9 79.2 1 有限元/Hz 23427 22319 21596 21154 20905 20778 20726 20717 20731 20754 20781 20807 20830 短路频率/Hz 25053 23626 22678 22060 21661 21405 21242 21138 21073 21031 21005 20989 20978 开路频率/Hz 24276 23525 23038 22725 22526 22399 22319 22268 22236 22215 22202 22194 22189 短路误差/% 6.94 5.85 5.01 4.28 3.62 3.02 2.49 2.03 1.65 1.34 1.08 0.87 0.71 开路误差/% 3.63 5.40 6.68 7.43 7.75 7.80 7.68 7.48 7.26 7.04 6.84 6.67 6.52 2 有限元/Hz 40544 35696 31597 28337 25888 24139 22944 22156 21653 21340 21149 21037 20973 短路频率/Hz 43504 36827 31904 28361 25878 24180 23044 22298 21814 21503 21304 21178 21098 开路频率/Hz 35260 31081 28126 26090 24719 23814 23225 22845 22602 22447 22349 22287 22248 短路误差/% 7.30 3.17 0.97 0.08 0.04 0.17 0.44 0.64 0.74 0.76 0.73 0.67 0.60 开路误差/% 13.03 12.93 10.99 7.93 4.51 1.35 1.22 3.11 4.38 5.19 5.67 5.94 6.08 3 有限元/Hz 66373 58089 50260 43279 37378 32638 29010 26349 24478 23211 22368 21823 21477 短路频率/Hz 77602 62943 51593 42915 36389 31585 28135 25721 24074 22974 22252 21784 21484 开路频率/Hz 58123 48095 40510 34885 30813 27939 25963 24635 23759 23189 22822 22587 22438 短路误差/% 16.92 8.36 2.65 0.84 2.65 3.23 3.02 2.38 1.65 1.02 0.52 0.18 0.03 开路误差/% 12.43 17.21 19.40 19.39 17.56 14.40 10.50 6.51 2.94 0.09 2.03 3.50 4.47 4 有限元/Hz 95852 85373 74406 63912 54400 46191 39426 34073 30016 27075 24983 23555 22608 短路频率/Hz 125279 100324 80701 65355 53452 44327 37442 32352 28680 26098 24329 23143 22362 开路频率/Hz 91537 73949 60265 49730 41737 35787 31458 28390 26270 24839 23892 23275 22877 短路误差/% 30.70 17.51 8.46 2.26 1.74 4.03 5.03 5.05 4.45 3.61 2.62 1.75 1.09 开路误差/% 4.50 13.38 19.00 22.19 23.28 22.52 20.21 16.68 12.48 8.26 4.37 1.19 1.19 5 有限元/Hz 127550 115393 101969 88402 75470 63752 53614 45168 38422 33276 29389 26593 24652 短路频率/Hz 185694 148051 118288 94818 76386 61997 50865 42363 35979 31287 27924 25576 23976 开路频率/Hz 134507 107689 86595 70092 57284 47455 40031 34535 30563 27765 25845 24557 23707 短路误差/% 45.59 28.30 16.00 7.26 1.21 2.75 5.13 6.21 6.36 5.98 4.98 3.82 2.74 开路误差/% 5.45 6.68 15.08 20.71 24.10 25.56 25.33 23.54 20.45 16.56 12.06 7.66 3.83 6 有限元/Hz 158793 146882 131735 115583 99537 84429 70872 59146 49430 41762 35690 31123 27819 短路频率/Hz 258551 205769 163943 130846 104712 84144 68040 55526 45907 38625 33218 29298 26528 开路频率/Hz 186616 148846 118998 95479 77029 62653 51559 43114 36802 32189 28902 26620 25073 短路误差/% 62.82 40.09 24.45 13.21 5.20 0.34 4.00 6.12 7.13 7.51 6.93 5.87 4.64 开路误差/% 17.52 1.34 9.67 17.39 22.61 25.79 27.25 27.11 25.55 22.92 19.02 14.47 9.87 -
[1] Butler J L, Sherman C H 2016 Transducers and Arrays for Underwater Sound (Cham: Springer International Publishing) p191 [2] 滕舵, 王龑, 解柯柯 2018 陕西师范大学学报(自然科学版) 46 30 doi: 10.15983/j.cnki.jsnu.2018.03.235 Teng D, Wang Y, Xie K K 2018 J. Shaanxi Norm. Uni. (Nat. Sci. Ed. ) 46 30 doi: 10.15983/j.cnki.jsnu.2018.03.235 [3] 周利生, 许欣然 2021 声学学报 46 1250 doi: 10.15949/j.cnki.0371-0025.2021.06.045 Zhou L S, Xu X R 2021 Acta Acust. 46 1250 doi: 10.15949/j.cnki.0371-0025.2021.06.045 [4] 张鸿磊 2018 硕士学位论文 (哈尔滨: 哈尔滨工程大学) Zhang H L 2018 M. S. Thesis (Harbin: Harbin Engineering University [5] 柴勇, 莫喜平, 刘永平, 潘耀宗, 张运强, 李鹏 2017 声学学报 42 619 doi: 10.15949/j.cnki.0371-0025.2017.05.013 Chai Y, Mo X P, Liu Y P, Pan Y Z, Zhang Y Q 2017 Acta Acust. 42 619 doi: 10.15949/j.cnki.0371-0025.2017.05.013 [6] 宋哲, 严由嵘 2018 水下无人系统学报 26 498 Song Z, Yan Y R 2018 J. Unmanned Underw. Systems 26 498 [7] 林书玉 2023 声学学报 28 102 doi: 10.15949/j.cnki.0371-0025.2003.02.002 Lin S Y 2023 Acta Acust. 28 102 doi: 10.15949/j.cnki.0371-0025.2003.02.002 [8] 穆廷荣 1979 声学学报 3 161 doi: 10.15949/j.cnki.0371-0025.1979.03.001 Mu Y R 1979 Acta Acust. 3 161 doi: 10.15949/j.cnki.0371-0025.1979.03.001 [9] Been K, Nam S, Lee H, Seo H seon, Moon W 2017 J. Acoust. Soc. Am. 141 4740 doi: 10.1121/1.4986937 [10] Lee J, Been K, Moon W 2023 J. Acoust. Soc. Am. 154 A228 doi: 10.1121/10.0023365 [11] Rogers P H 2005 J. Acoust. Soc. Am. 77 S16 doi: 10.1121/1.2022199 [12] Butler J L 1976 J. Acoust. Soc. Am. 59 480 doi: 10.1121/1.380863 [13] Sherman C H, Parke N G 2005 J. Acoust. Soc. Am. 38 715 doi: 10.1121/1.1909792 [14] Huang C H, Ma C C, Lin Y C 2005 IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 52 1204 doi: 10.1109/TUFFC.2005.1509779 [15] Aronov B S 2013 J. Acoust. Soc. Am. 134 1021 doi: 10.1121/1.4812760 [16] 胡久龄 2023 博士学位论文 (哈尔滨: 哈尔滨工程大学) Hu J L 2023 Ph. D. Dissertation (Harbin: Harbin Engineering University [17] 滕舵 2016 水声换能器基础 第233页 Teng D 2016 Fundamentals of Hydroacoustic Transducers (Northwestern Polytechnical University Press) p233 [18] Timošenko S P, Woinowsky-Krieger S 1996 Theory of Plates and Shells (New York: McGraw-Hill) p580 [19] 曹志远 1989 板壳振动理论 (北京: 中国铁道出版社) 第462页 Cao Z Y 1989 Plate and Shell Vibration Theory (Beijing: China Railway Press) p462 [20] 栾桂冬 2005 压电换能器和换能器阵 (北京: 北京大学出版社) 第479页 Luan G D 2005 Piezoelectric Transducers and Transducer Arrays (Beijing: Peking University Press) p479 [21] 潘瑞, 柴勇, 莫喜平, 刘文钊, 张秀侦 2024 应用声学 43 719 doi: 10.11684/j.issn.1000-310X.2024.04.002 Pan R, Chai Y, Mo X P, Liu W Z, Zhang X Z 2024 Appl. Acoust. 43 719 doi: 10.11684/j.issn.1000-310X.2024.04.002 [22] 张海澜 2012 理论声学(北京: 高等教育出版社) 第139页 Zhang H L 2012 Theoretical Acoustics (Beijing: Higher Education Press) p139 [23] 单影, 许龙, 周光平 2022 压电与声光 44 316 doi: 10.11977/j.issn.1004-2474.2022.02.033 Dan Y, Xu L, Zhou G P 2022 Piezoelectr. Acoustoopt. 44 316 doi: 10.11977/j.issn.1004-2474.2022.02.033 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: