声图测量是适用于近场的噪声源无源定位方法, 可获得辐射噪声源的空间位置分布图, 简称声图^[1], 目前被广泛应用于发动机噪声源定位和故障诊断^[2]、水下舰船辐射噪声定位^[3]等问题的研究中。常规声图测量是通过聚焦波束形成实现, 不同于远场波束形成仅能给出方位信息, 聚焦波束形成在近场条件下按照球面波假设计算时延得到聚焦输出, 可同时实现对方位和距离的测量。其分辨力受信号频率和阵列孔径的限制, 在有限阵列孔径下对较低频率声源分辨能力差。实际应用中对声源分辨力、定位精度和计算效率的要求日渐提高, 亟需具有高分辨性能的快速声图测量方法。

目前典型的高分辨声图测量算法有最小方差无畸变(MVDR)高分辨声图测量^[4]、多重信号分类(MUSIC)^[5]声图测量, 基于压缩感知的聚焦波束形成处理^[3]等。其中, MVDR类和MUSIC类算法在水中阵列流形存在误差的情况下稳健性会有所下降。基于压缩感知的水下目标无源测距方法的计算量大, 多用于后置处理分析。陈新华等提出复域感知矩阵近场声图测量模型^[6], 相比频域压缩感知方法, 低信噪比下性能得到较大提升。近年来, 反卷积算法在远场目标方位估计中的稳健高分辨性能已得到验证^[7-8], 其在近场声源定位中的作用也逐渐受到重视。反卷积高分辨噪声源无源定位方法在空气声学中发展较早, 典型方法为反卷积声源成像方法(DAMAS)^[2,9], 适用于中高频声源的识别并对噪声具有较好的适应性。Chu等比较了三种卷积核的反卷积近场聚焦算法, 并提出了卷积近似矩阵乘法来降低计算复杂度以实现高分辨率声成像实时测量^[10]。总体而言, DAMAS方法更适用于高信噪比的环境, 而R-L (Richardson-Lucy)反卷积算法更适用于水下的较低信噪比环境。基于R-L反卷积的近场高分辨算法已在高分辨三维成像^[11]、远近场混合源的分离^[12]、近场低频声源无源定位^[13]等方面取得进展。文献[14]通过结合MVDR声图测量与R-L反卷积处理进一步提升了分辨效果。水下近场声图测量是空域移变模型, 文献[13]提出的水下移变模型的二维反卷积声图测量方法无需使目标位于近似移不变区域, 而直接利用移变模型反卷积求解, 文献[15]结果表明扩展的RL反卷积算法(Ex-RL) 应用于二维移变反卷积声图测量问题，可以取得良好的分辨效果。但当扫描区域较大时, 二维移变模型的反卷积处理方法计算量较大, 所需点扩散函数(PSF)存储空间大, 使其在工程应用上受限。

针对反卷积声图测量快速处理问题, 本文提出了一种在极坐标系将二维移变反卷积降维为两个一维反卷积的处理方法。首先, 证明了极坐标下声图在方位和距离维扫描具有近似可分离特性; 然后, 将声图测量二维反卷积转换为分别对方位和距离维进行一维反卷积求解; 再利用方位维的近似空域移不变性对方位维采用移不变快速处理, 仅对距离维采用一维移变处理; 最后, 综合方位和距离维结果。该方法的处理性能与原二维方法相近, 但显著减少了PSF存储空间和算法计算量。

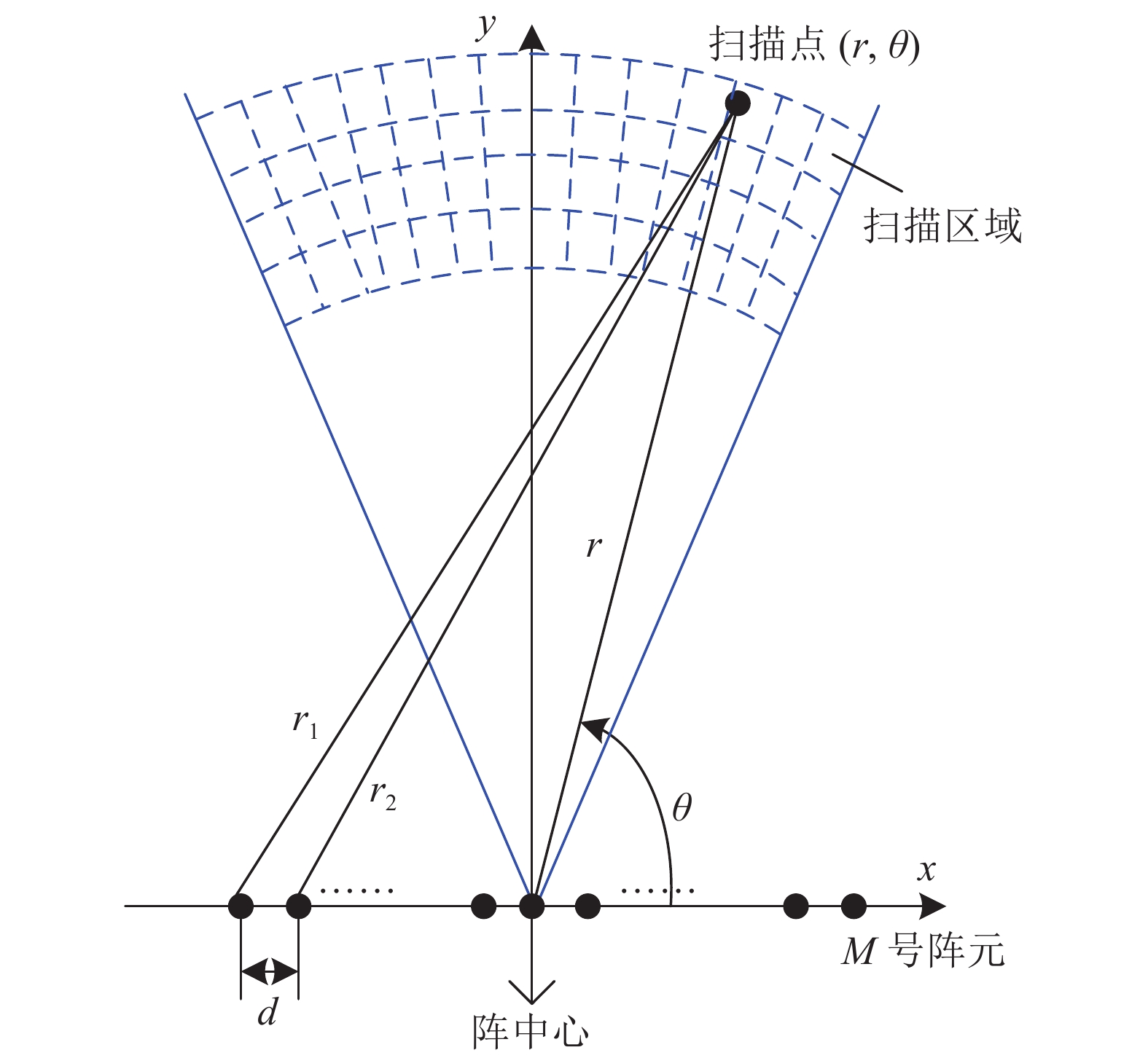
利用$M$元的均匀声压线列阵接收的近场声信号通过聚焦波束形成方法可获得常规的声图测量噪声源空间分布。极坐标系下的聚焦波束形成声图测量基本原理如图1所示。

建立测量坐标系, 取阵中心为坐标原点, 阵列位于$x$轴, 阵元位置坐标为$ ({x}_{m}, {y}_{m})=\left(\left[m-(M + 1)/2\right]d,0\right) $, $d$为阵元间距, $m$为阵元序号, $m = 0,1, \cdots ,M$。各扫描点极坐标为$(r,\theta )$, 其中$r$为目标斜距, $\theta $为目标水平方位角(定义为与$x$正半轴的夹角)。阵列接收信号可表示为

其中, ${{\boldsymbol{x}}}\left( t \right) = {\left[ {{x_1}\left( t \right), \cdots ,{x_m}\left( t \right), \cdots ,{x_M}\left( t \right)} \right]^{\text{T}}}$为$M$元接收阵的接收信号向量矩阵, ${{\boldsymbol{s}}}\left( t \right) = {[{s_1}\left( t \right), \cdots ,{s_p}\left( t \right), \cdots ,{s_P}\left( t \right)]^{\text{T}}}$为声源信号向量矩阵, $P$为声源的个数, ${{\boldsymbol{n}}}\left( t \right) = {\left[ {{n_1}\left( t \right), \cdots ,{n_m}\left( t \right), \cdots ,{n_M}\left( t \right)} \right]^{\text{T}}}$为噪声向量矩阵, ${{\boldsymbol{A}}}\left( {r,\theta } \right) = \left[ {{{\boldsymbol{a}}}\left( {{r_1},{\theta _1}} \right), \cdots ,{{\boldsymbol{a}}}\left( {{r_p},{\theta _p}} \right), \cdots ,{{\boldsymbol{a}}}\left( {{r_P},{\theta _P}} \right)} \right]$为各声源信号方向向量矩阵, $ {{\boldsymbol{a}}}\left( {{r_p},{\theta _p}} \right) = {\left[ {{{\rm e}^{ - {\rm j}2\pi f{\tau _{p1}}}}, \cdots ,{{\rm e}^{ - {\rm j}2\pi f{\tau _{pm}}}}, \cdots ,{{\rm e}^{ - {\rm j}2\pi f{\tau _{pM}}}}} \right]^{\text{T}}} $, $ {\tau _{pm}} = {r_{pm}}/c $为第$ p $个声源信号传播到第$m$个阵元的时延, $ {r_{pm}} $为第$ p $个声源到第$m$个阵元的距离:

此时, 常规聚焦波束形成声图测量输出可表示为

其中, ${{\boldsymbol{w}}}\left( {r,\theta } \right) = {{\boldsymbol{a}}}\left( {r,\theta } \right)/M$为常规聚焦波束形成权向量, ${{{\boldsymbol{R}}}_{x}}$为阵列接收信号的协方差矩阵。$ {{\boldsymbol{a}}}\left( {r,\theta } \right) = {\left[ {{{\rm e}^{ - {\rm j}2\pi f{\tau _1}}}, \cdots ,{{\rm e}^{ - {\rm j}2\pi f{\tau _m}}}, \cdots ,{{\rm e}^{ - {\rm j}2\pi f{\tau _M}}}} \right]^{\text{T}}} $, $ {\tau _m} = {r_m}^\prime /c $, $ {r_m}^\prime $为各个扫描点到第$m$个阵元的距离:

反卷积处理可改善声图测量效果, 但二维移变模型处理计算量较大^[13]。声图测量中, 常规聚焦波束形成输出的声图可表示为阵列近场二维空间指向性函数(波束图)和噪声源空间分布函数的叠加积分:

其中, $(\zeta ,\vartheta )$表示假定指向的极坐标位置(即扫描点位置), $\left( {r,\theta } \right)$表示近场聚焦波束形成输出的空间位置, ${{\boldsymbol{S}}}(\zeta ,\vartheta )$的峰值位置和数值代表噪声源在空间的位置和强度, 理想情况下是二维德尔塔函数, 因此具有高分辨效果。${{\boldsymbol{R}}}(\left. {r,\theta } \right|\zeta ,\vartheta )$表示空间位置坐标指向$(\zeta ,\vartheta )$时的阵列近场聚焦波束形成空间指向性函数, 也称为反卷积的点扩散函数(PSF)字典。上述过程是二维移变PSF广义卷积, 利用反卷积求解可得对目标函数${{\boldsymbol{S}}}(\zeta ,\vartheta )$的估计结果, 迭代公式如下:

对于二维移变模型的反卷积求解, 其PSF字典是一个四维函数, 所需存储空间大, 计算量较大。为此先分别对声图的方位维和距离维反卷积, 再综合处理, 以降低计算量。

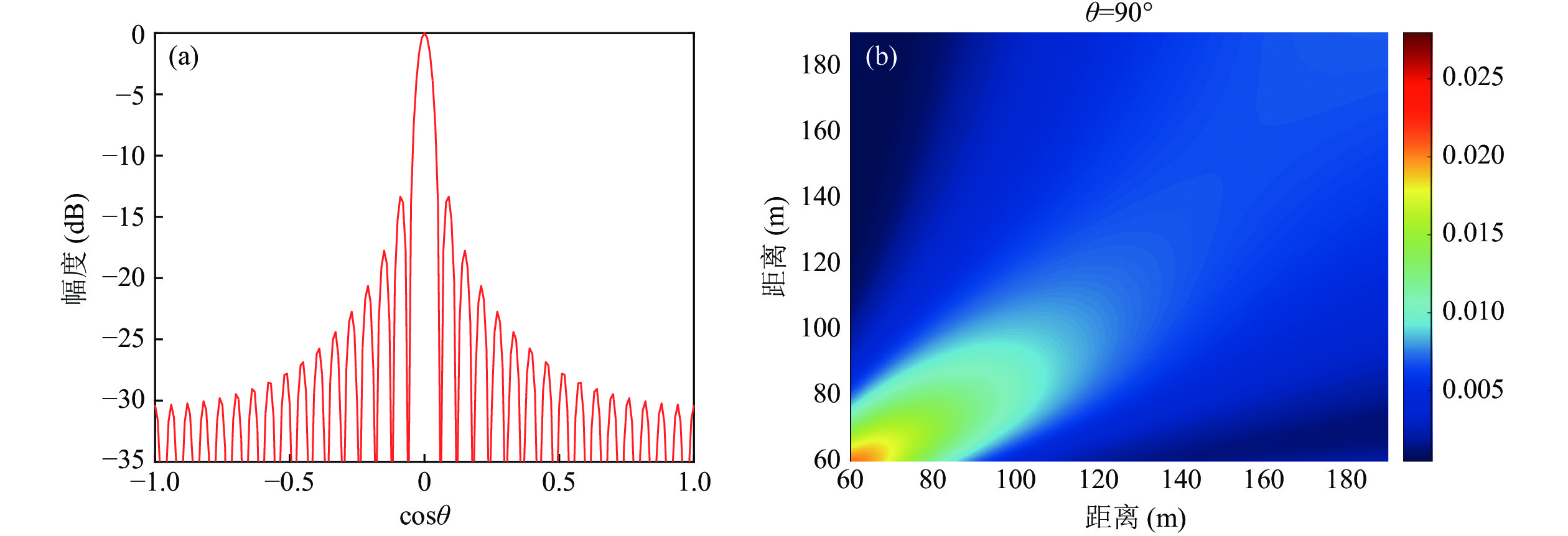
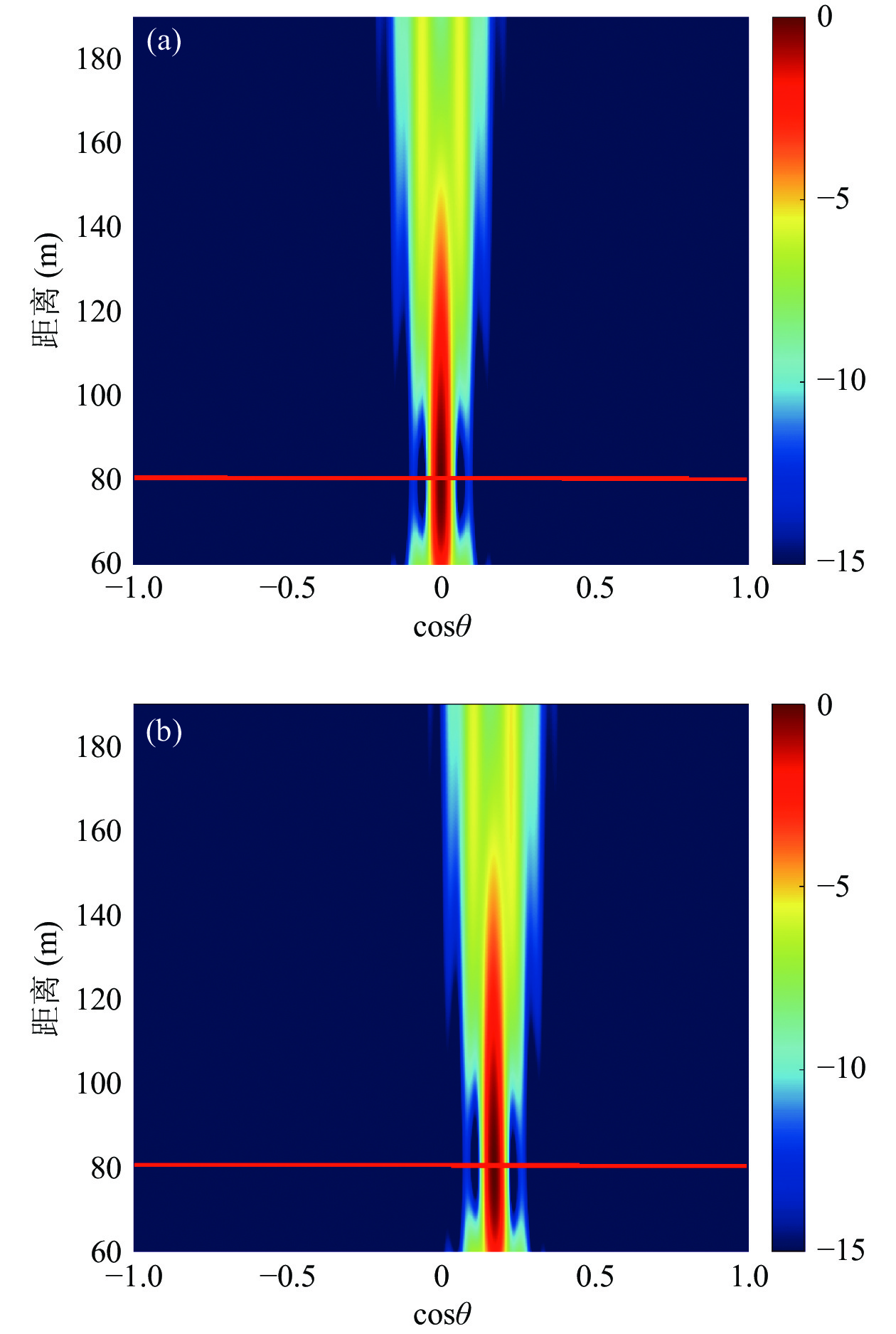
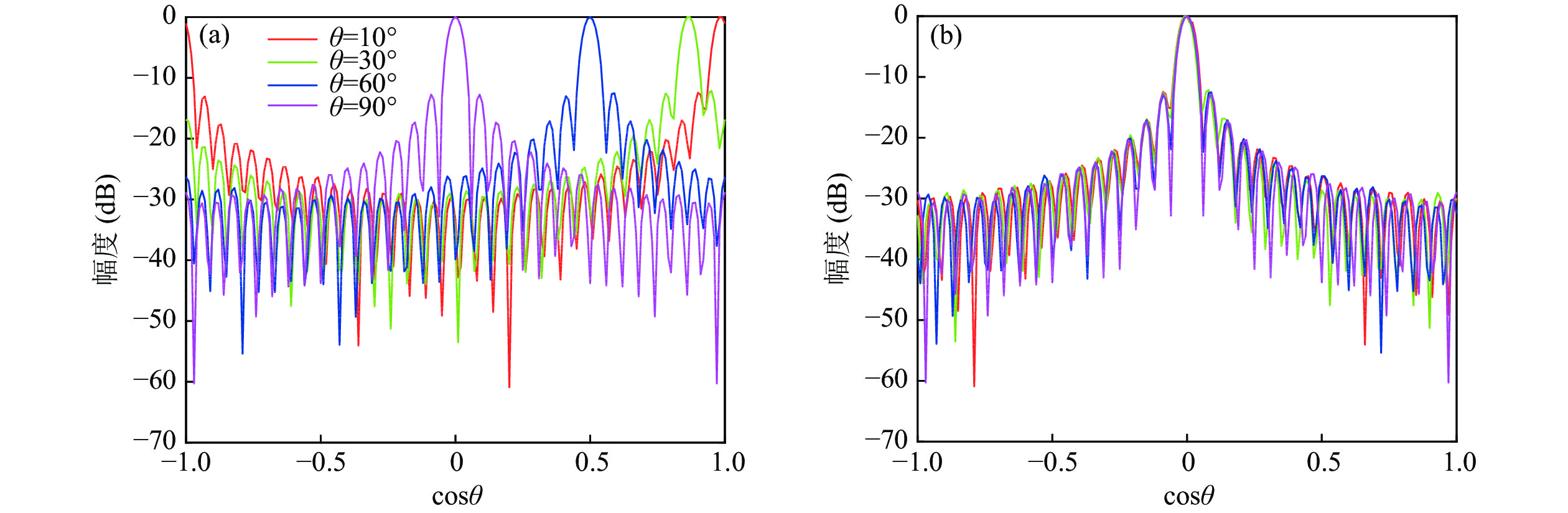
分析声图PSF在方位维和距离维的分布特点。相同距离情况下方位维PSF关于$ \cos \theta $近似移不变。以33元半波间距直线阵的声图测量为例, 目标距离$r$为80 m时, 相同距离不同角度的声图测量结果如图2所示, 声图PSF在方位维具有移不变特性。将图3(a)中不同角度目标声图的方位维PSF切片对齐, 如图3(b)所示, 四条曲线相差不大, 即对相同距离、不同角度的目标其PSF具有近似移不变的特性。因此可将声图的方位维进行一维移不变反卷积处理, 进而减小近场聚焦反卷积声图测量的计算量。

图4是33元半波间距直线阵的声图对不同距离处目标PSF的波束宽度对比结果。当目标距离大于1倍阵长时, 不同距离的方位维PSF也是近似移不变的。根据不同方位和不同距离目标的方位维PSF移不变性, 计算过程中可仅存储一个方位维PSF曲线, 在节省存储空间同时移不变反卷积的计算量也更小。

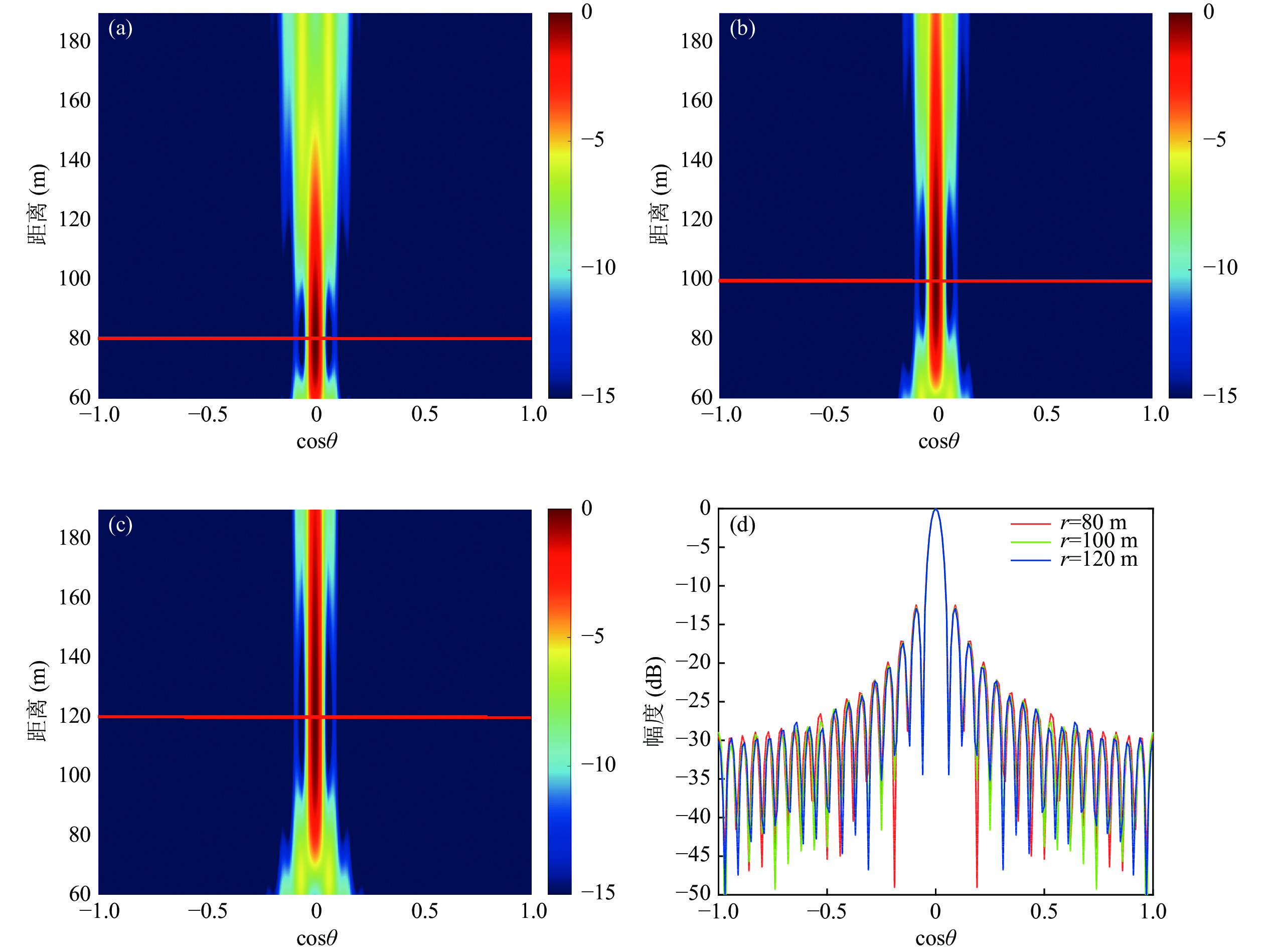
分析距离维反卷积PSF的分布规律。在33元半波间距直线阵条件下, 不同距离情况下的距离维声图PSF以及相同距离情况下不同方位目标对应的距离维PSF对比如图5所示。由图5(a)(b)可见, 不同距离目标的聚焦峰尺度明显不同, 说明声图测量的距离维度PSF是空间移变的。由图5(c)可见, 相同距离情况下, 不同方位目标的距离维PSF仍具有近似移不变性, 因此单独距离维反卷积是一维移变模型, 但不同方位目标可共用相同的距离维PSF字典。目标所在方位的距离维PSF字典如图5(d)所示, 目标距离越近聚焦峰值越尖锐。

根据近场声图测量的特点, 新方法求解过程如下:

(1)声图方位维移不变反卷积处理

声图方位一维反卷积是对每个距离的声图方位曲线切片进行一维反卷积处理, 由于其方位维关于$ \cos \theta $的近似移不变, 因此将卷积公式转换为$ \cos \theta $域表示, 其在距离$ {r_i} $处的卷积模型为

方位维$ {\boldsymbol R}({r_i},\cos \theta - \cos \vartheta ) $的计算公式为

$ {r_i} $每次为固定常数, 进一步简写为一维形式:

$ {{\boldsymbol S}_{{r_i}}}(\cos \vartheta ) $表示距离$ {r_i} $处声图关于方位维的目标函数。利用R-L算法进行反卷积迭代求解:

由于其具有近似空域移不变的特点, 可以利用FFT-RL快速算法^[16]进行反卷积求解, 将迭代公式中的卷积积分过程利用FFT转换至变换域, 通过乘积的方式求解, 进一步提高计算速度, 简化计算过程。

(2)声图距离维移变反卷积处理

声图距离一维反卷过程是对每个方位的声图距离曲线切片进行一维反卷积处理, 其在方位$ {\theta _j} $处的卷积模型为

距离维$ {\boldsymbol R}(\left. r \right|\zeta ,\cos {\theta _j}) $的计算公式为

$ {\theta _j} $每次为固定常数, 进一步简写为一维形式:

利用R-L算法进行反卷积求解, 迭代公式为

其在距离维不具有空域移不变性, 因此$ {{\boldsymbol R}_{\cos {\theta _j}}}(\left. r \right|\zeta ) \ne {{\boldsymbol R}_{\cos {\theta _j}}}(r - \zeta ) $, 只能写作上述叠加积分的形式, 不能写为移不变的卷积形式, 需要采用移变模型字典求解。

(3)方位反卷声图和距离反卷声图乘法综合

分别对方位维和距离维求解, 得$ {{\boldsymbol S}}_{{}_{{r}_{i}}}^{(\alpha + 1)}(\mathrm{cos}\vartheta )= {{\boldsymbol S}}_{{}_{}}^{(\alpha + 1)}({r}_{i}, \mathrm{cos}\vartheta ) $, $ {{\boldsymbol S}}_{{}_{\mathrm{cos}{\theta }_{j}}}^{(\alpha + 1)}(\zeta )={{\boldsymbol S}}_{{}_{}}^{(\alpha + 1)}(\zeta , \mathrm{cos}{\theta }_{j}) $, 二者维度相同, 将对应点取几何平均数, 即可得到最终的反卷积声图测量结果:

其中, “·”表示对应点相关。

实现过程如表1所示。

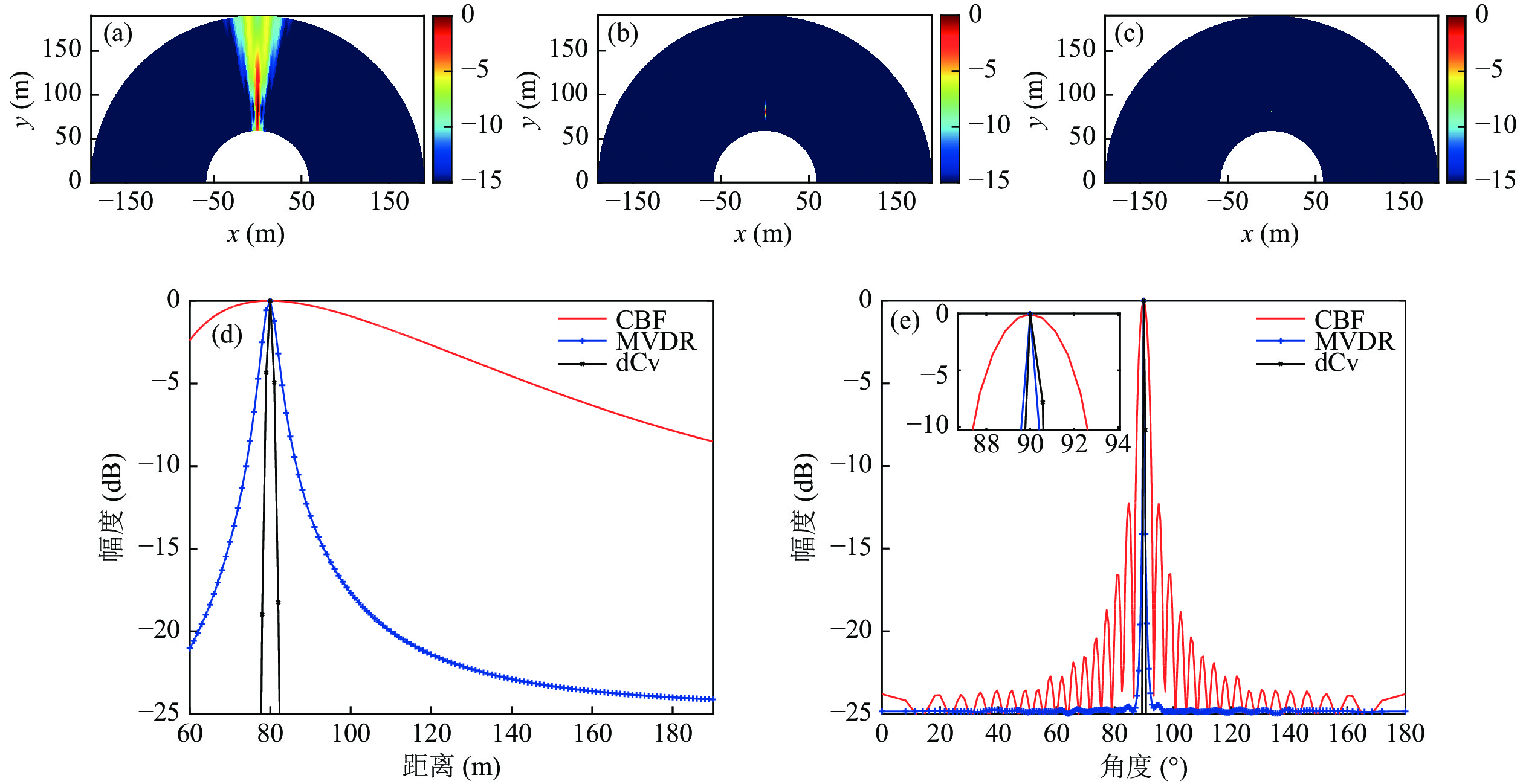
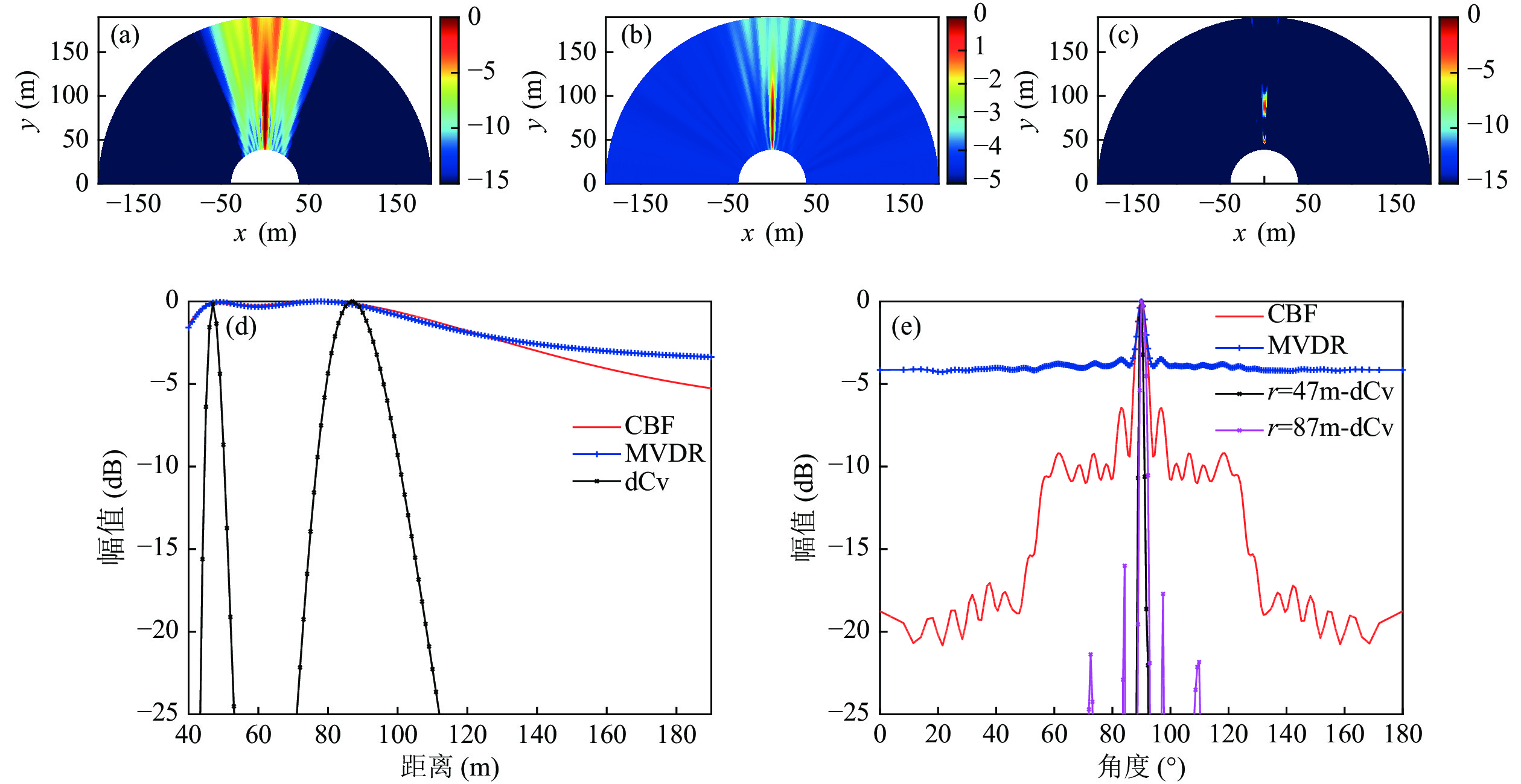
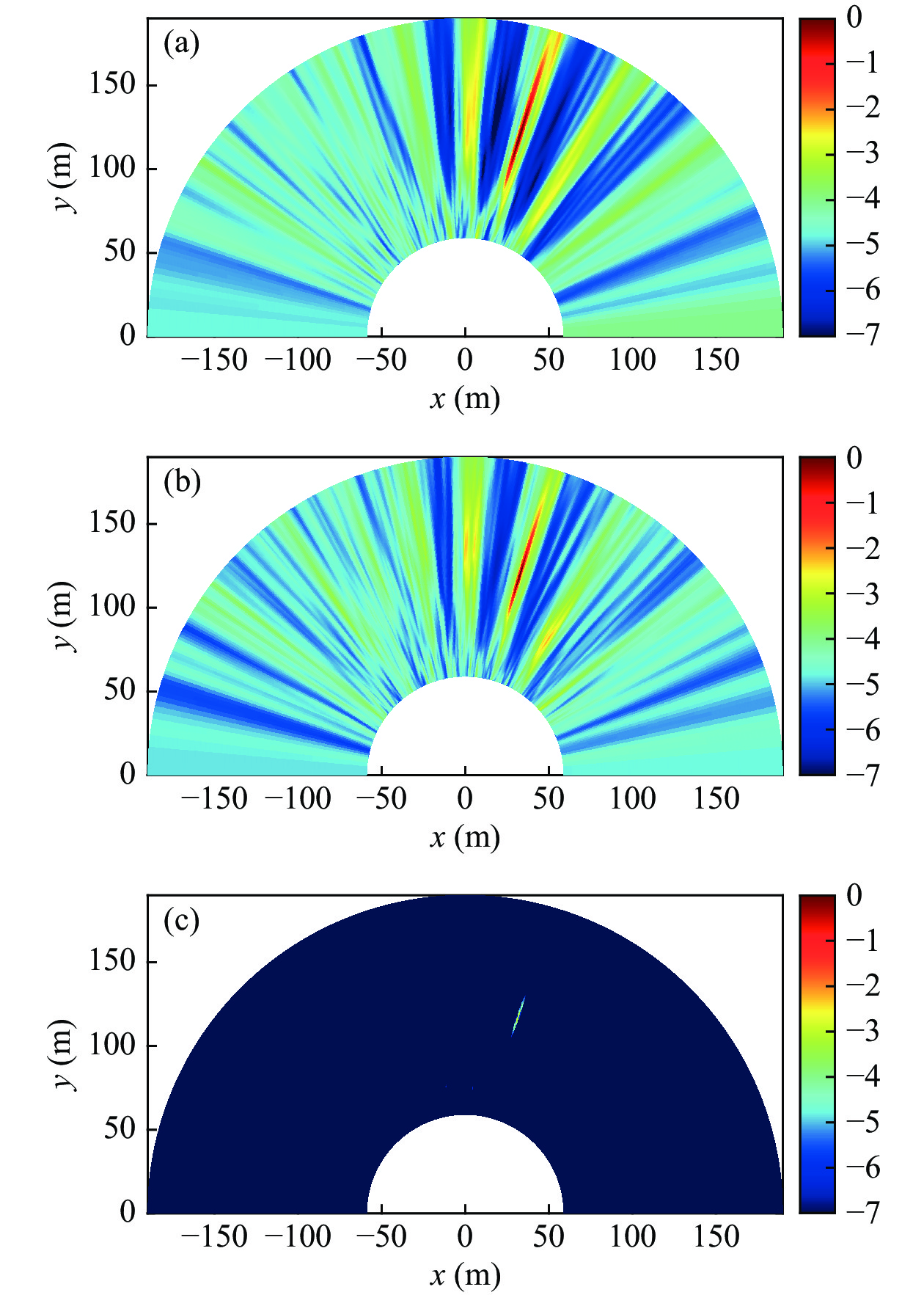
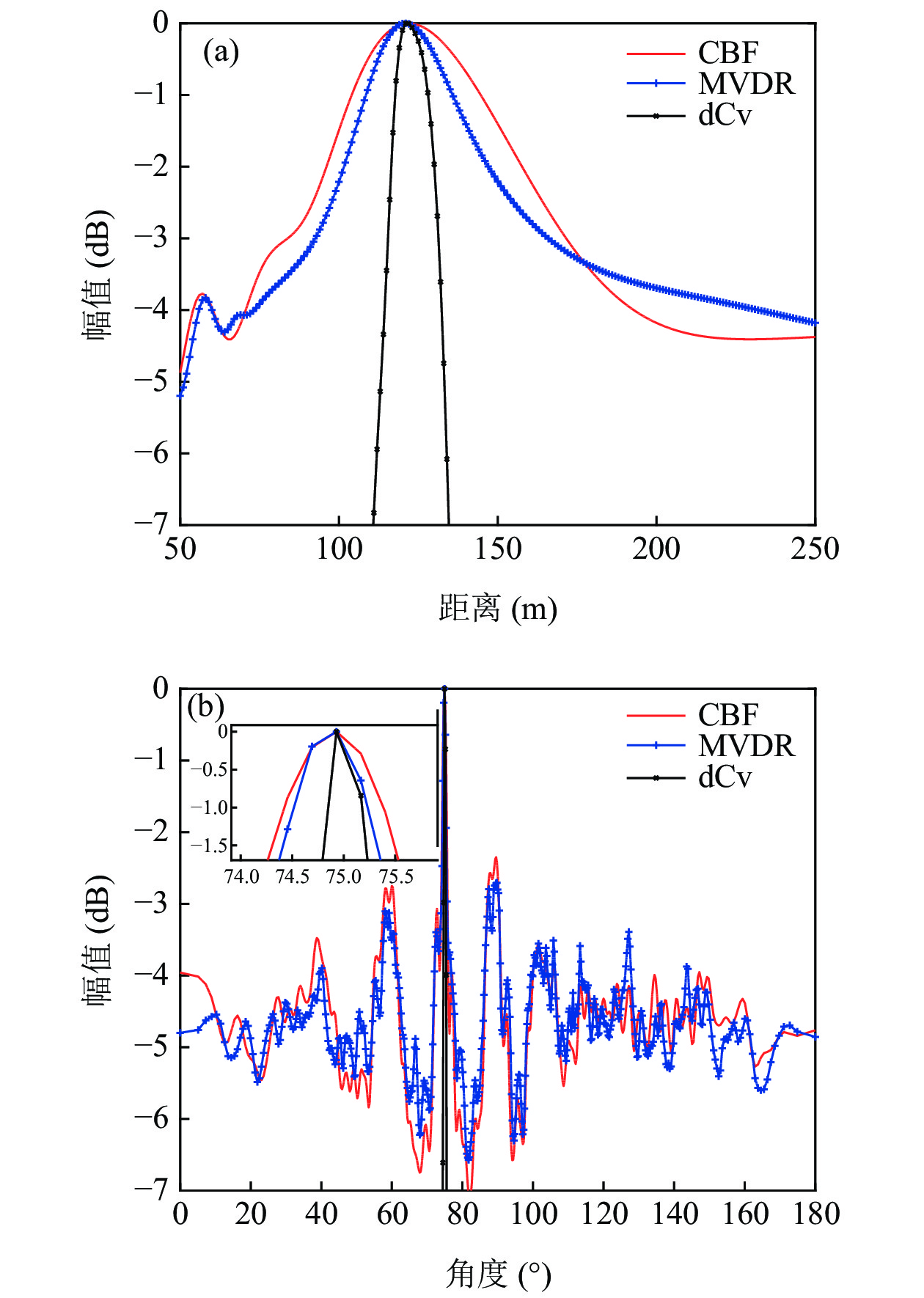
仿真参数: 信号频率500 Hz, 阵元数33, 阵元间距$d = 1.5{\text{ m}}$, 距离扫描区域$r \in \left[ {{\text{6}}0{\text{ m}}:1{\text{ m}}:190{\text{ m}}} \right]$, 方位扫描$\cos \left( \theta \right) \in \left[ { - 1:0.01:1} \right)$, 单目标情况目标位置坐标为$\left( {{\text{8}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$。根据式(8)和式(12)得到方位维和距离维PSF字典, 如图6所示。

图7是信噪比10 dB情况下单目标近场常规波束形成(CBF)、最小方差无畸变(MVDR)声图^[5]以及快速反卷积声图测量结果对比, 其中dCv 表示反卷积方法。声图测量主要在近场进行, 目标距离近, 信噪比相对较高, 因此采用了高信噪比仿真。由图7(a)(c)可见, 相比于CBF声图和MVDR声图, 极坐标系下快速反卷积声图能够实现近场声源所在位置的距离和方位的高分辨估计, 明显减小聚焦峰尺度。比较CBF、MVDR与极坐标系下反卷积声图测量在距离维及方位维的波束形成结果, 如图7(d)(e)所示, 高信噪比条件下反卷积算法能够明显降低距离维及方位维的波束形成旁瓣级。

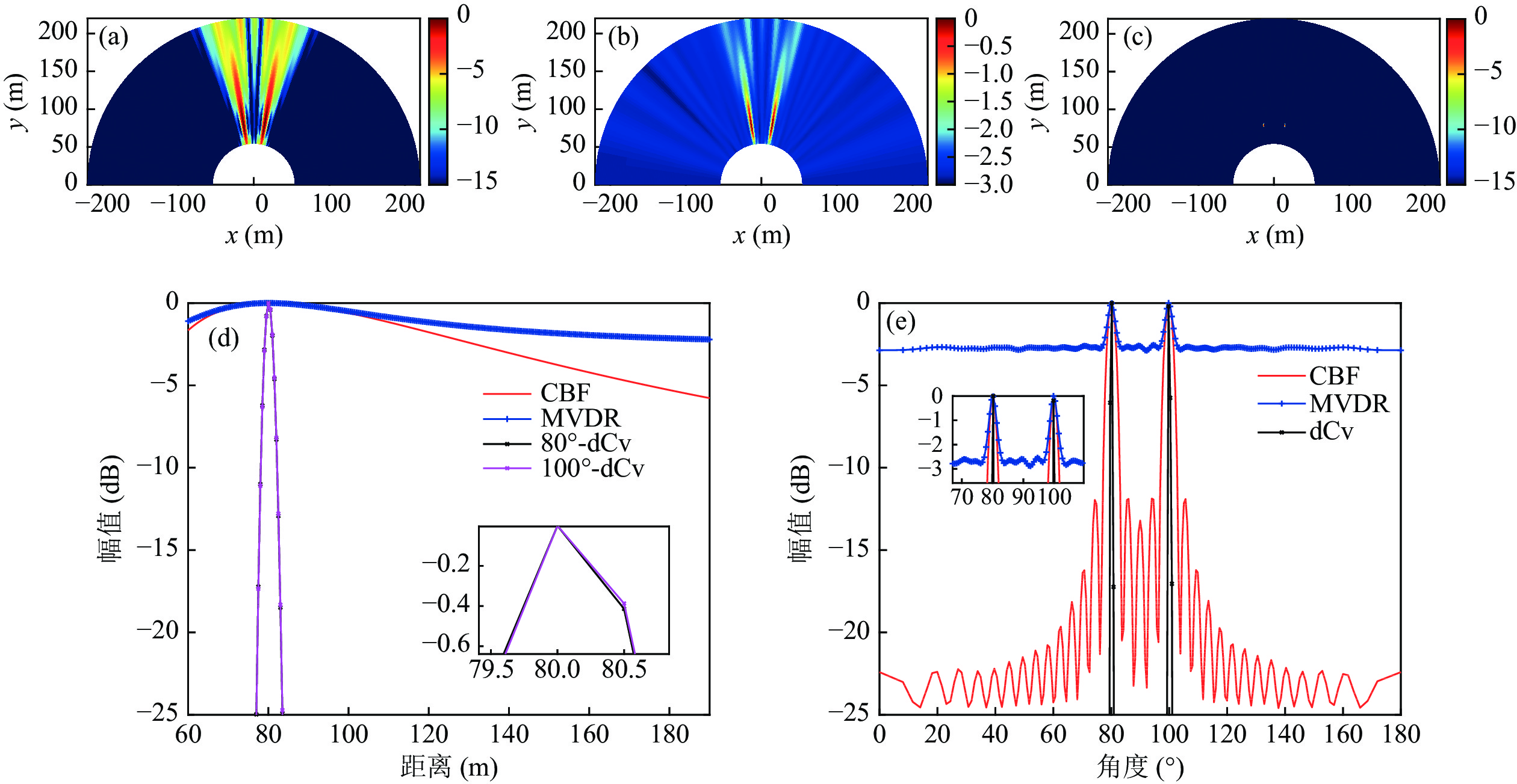
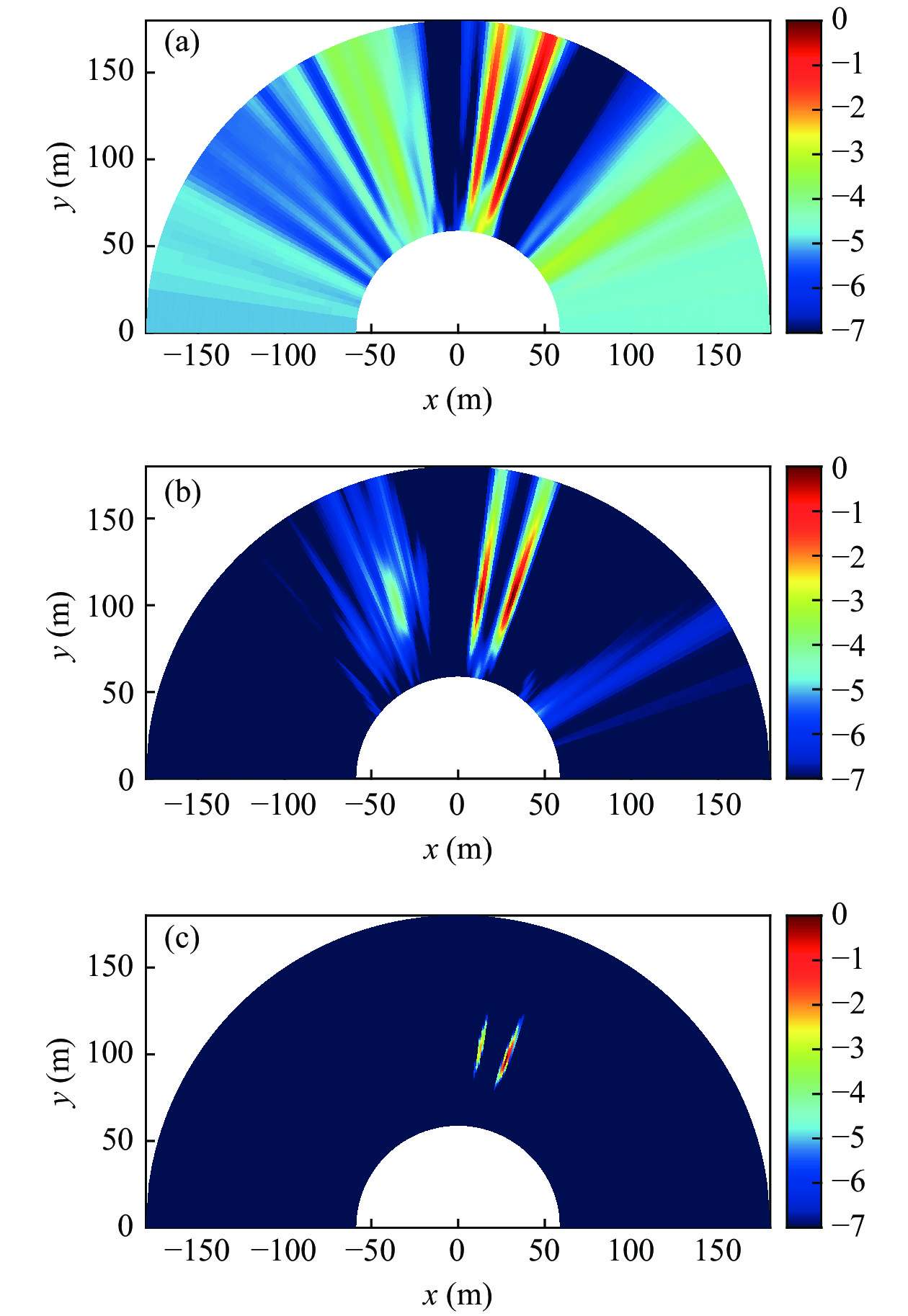
三种算法对等强度同频相干双目标的分辨能力对比如图8和图9所示, 两声源均为单频信号, 频率为500 Hz, 其他仿真参数与上述单频仿真条件相同。图8中目标1位置坐标$\left( {80{\text{ m}},8{{\text{0}}{\text{°}} }} \right)$, 目标2位置坐标$\left( {80{\text{ m}},{\text{10}}{{\text{0}}{\text{°}} }} \right)$, 信噪比均为10 dB。

由图8可见, 极坐标系快速反卷积高分辨声图测量方法可有效实现双目标近场距离维与方位维的声图测量, MVDR算法由于不能解相干, 在同频相干双目标分辨中性能较差。图8(d)是距离维结果, 极坐标系快速反卷积高分辨声图测量方法在距离维利用一维移变模型实现了距离维的高分辨定位, 相比CBF及MVDR, 距离维主瓣宽度明显变窄。图8(e)为两目标的方位剖面对比, 快速反卷积在方位维对双目标具有高分辨和低旁瓣处理效果。

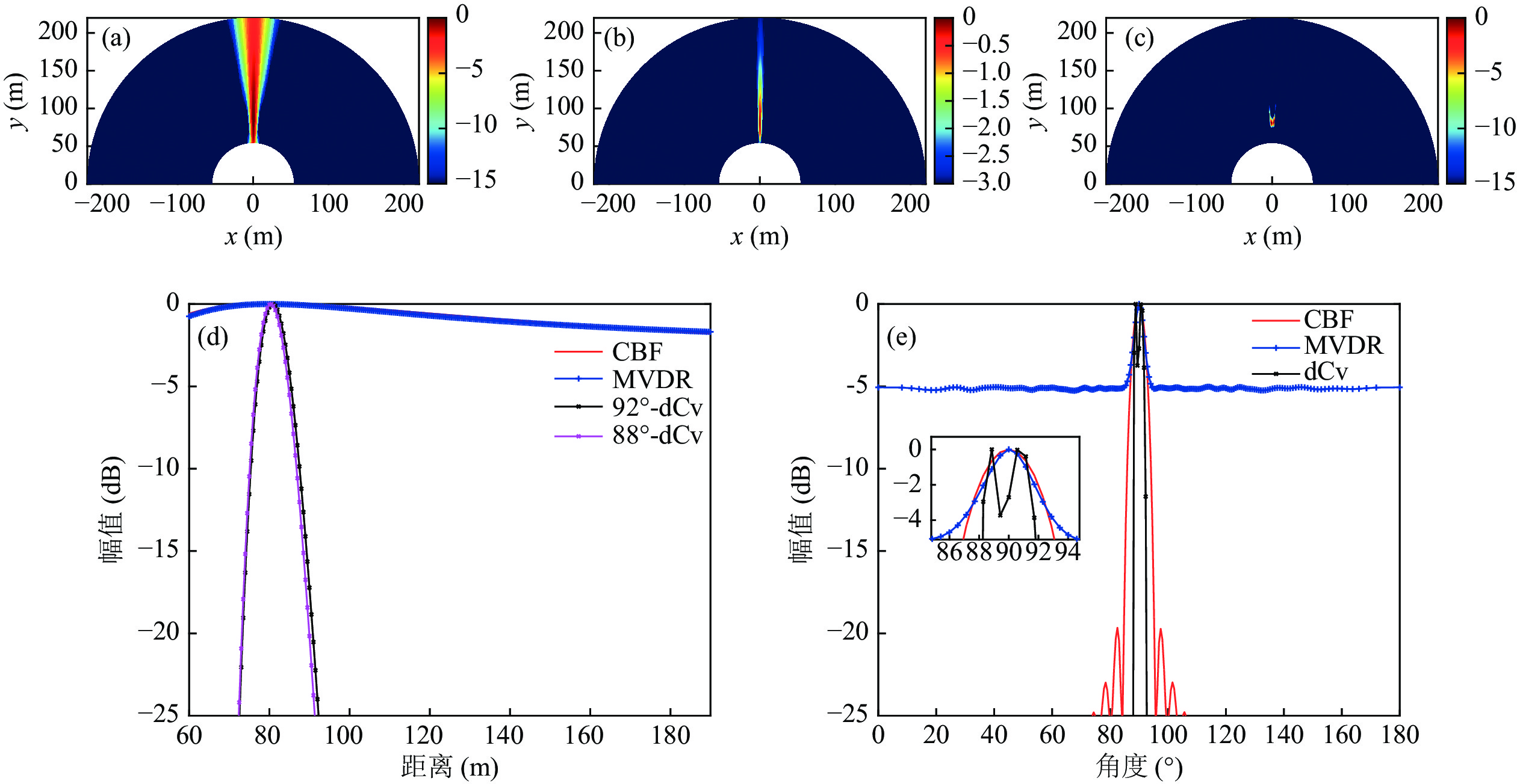
图9是三种方法对近场双目标方位维极限分辨力的比较, 除两目标位置外仿真条件与上述双目标仿真相同, 目标1位置坐标$\left( {80{\text{ m}},8{{\text{8}}{\text{°}} }} \right)$, 目标2位置坐标$\left( {80{\text{ m}},{\text{9}}{{\text{2}}{\text{°}} }} \right)$, 信噪比均为10 dB。由图9(a-c)可见, 当双目标在方位维相距极近时, 相比于CBF和MVDR算法, 极坐标系快速反卷积高分辨声图测量方法的估计结果中可以看到两个亮点, 而常规声图测量结果中无法分辨。由图9(d)(e)可见, 当前仿真条件下, 极坐标系快速反卷积高分辨声图测量方法可对相同距离、相距4°的双目标进行方位维的分辨, 而常规声图测量结果在方位维已不可区分。

对双目标距离分辨力进行仿真对比。信号为单频信号$f = 500{\text{ Hz}}$, 信噪比为10 dB, 阵元数33, 阵元间距1.5 m, 距离扫描区域$r \in \left[ {{\text{3}}0{\text{ m}}:1{\text{ m}}:{\text{25}}0{\text{ m}}} \right]$, 方位扫描$\cos \theta \in \left[ { - 1:0.01:1} \right)$, 双目标所在位置为$\left( {{\text{45 m, 9}}{{\text{0}}{\text{°}} }} \right)$和$\left( {{\text{9}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$。如图10(a-c)所示, 相同角度情况下, 极坐标系快速反卷积声图测量相比常规声图测量的距离分辨能力更好。根据图10(d)(e)所示双目标声图测量的峰值处距离维和方位维反卷积声图测量剖面可知, 在常规声图测量无法区分两个相隔较近的声源时, 本文方法可实现相同角度不同距离的双目标定位, 较近位置的方位维反卷积旁瓣更低。

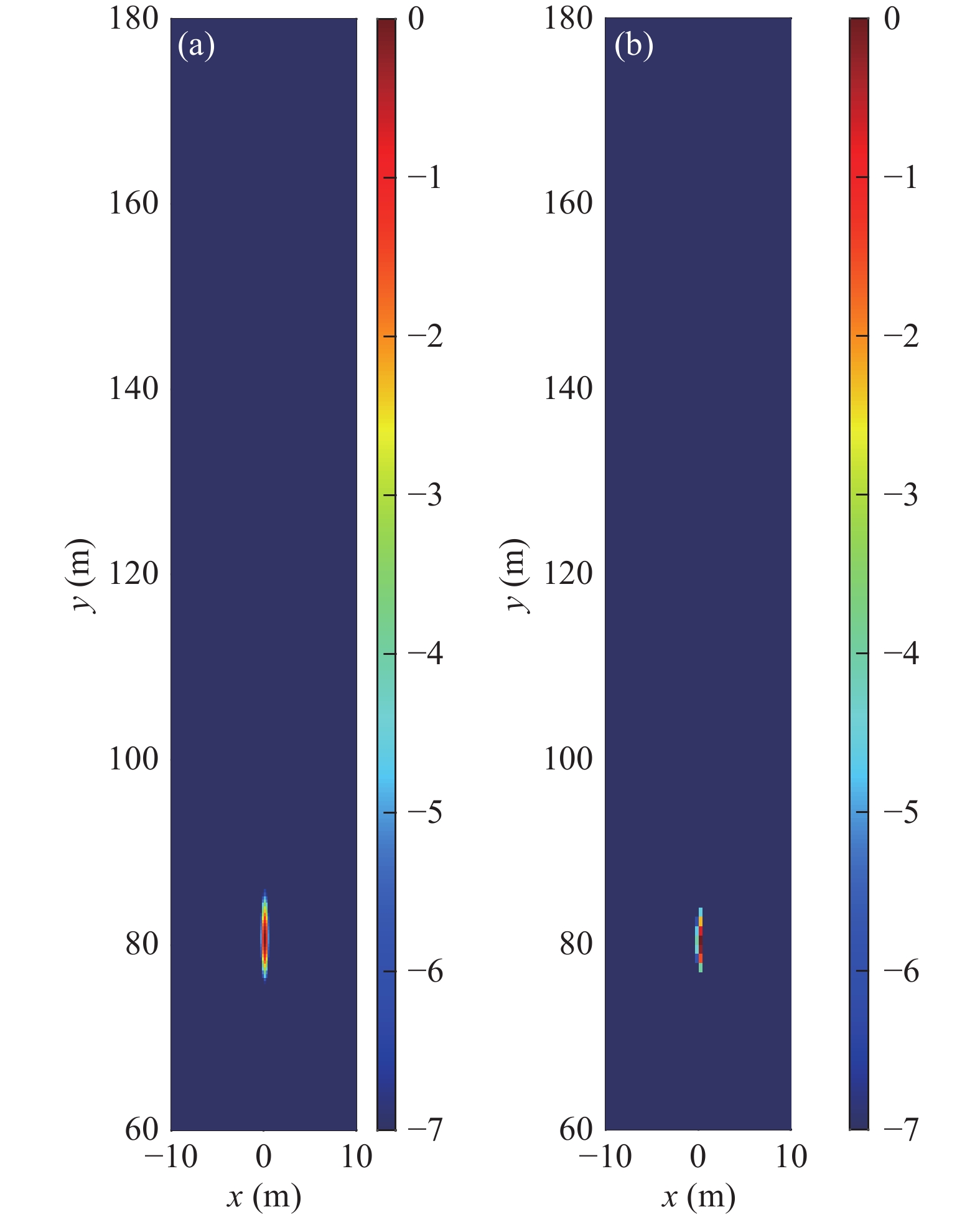
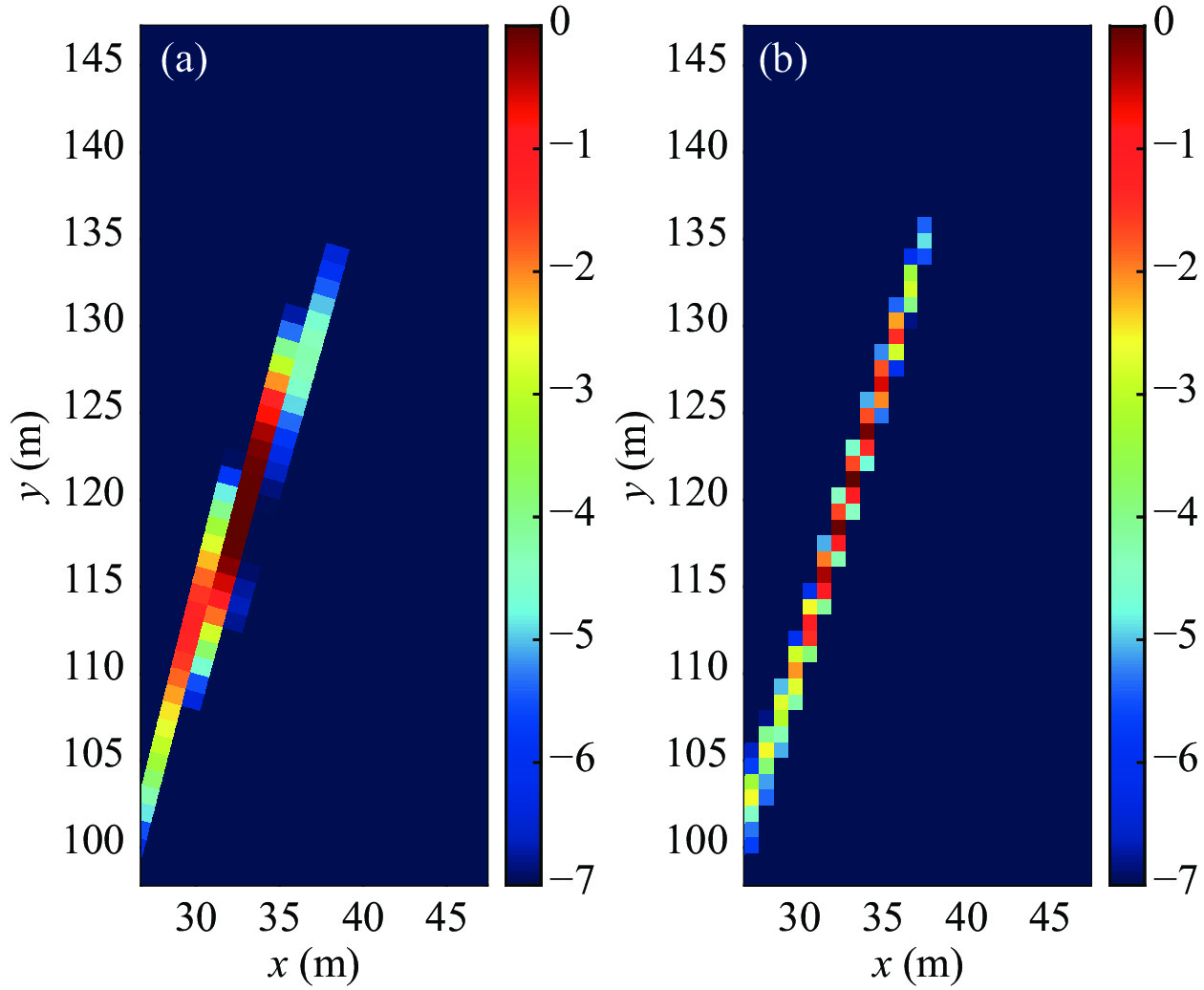
直角坐标系下声图测量算法是二维移变的反卷积聚焦算法, 计算量较大。选择了较小区域范围进行计算, 结果如图11所示。仿真参数: 信号频率500 Hz, 阵元数33, 半波间距直线布阵, 极坐标系下距离扫描区域$r \in \left[ {{\text{6}}0{\text{ m}}:1{\text{ m}}:190{\text{ m}}} \right]$, 方位扫描$\cos \left( \theta \right) \in \left[ { - 1:0.01:1} \right)$; 直角坐标系下扫描区域$x \in [ { - 10{\text{ m}}:0.{\text{1 m}}:10{\text{ m}}} ]$, $y \in [ {60{\text{ m}}:1{\text{ m}}:190{\text{ m}}} ]$。单目标情况目标位置坐标为$( 80{\text{ m}}, \; 0{\text{°}} )$, 反卷积迭代次数均为500。

图11(a)为直角坐标系下dCv聚焦结果, 其中横向−3 dB聚焦峰尺度为0.6 m, 纵向−3 dB聚焦峰尺度为6 m; 图11(b)为极坐标系dCv聚焦结果转换至直角坐标系下的结果, 其中横向−3 dB聚焦峰尺度为0.45 m, 纵向−3 dB聚焦峰尺度为9 m。可见二者在处理性能上是比较接近的。

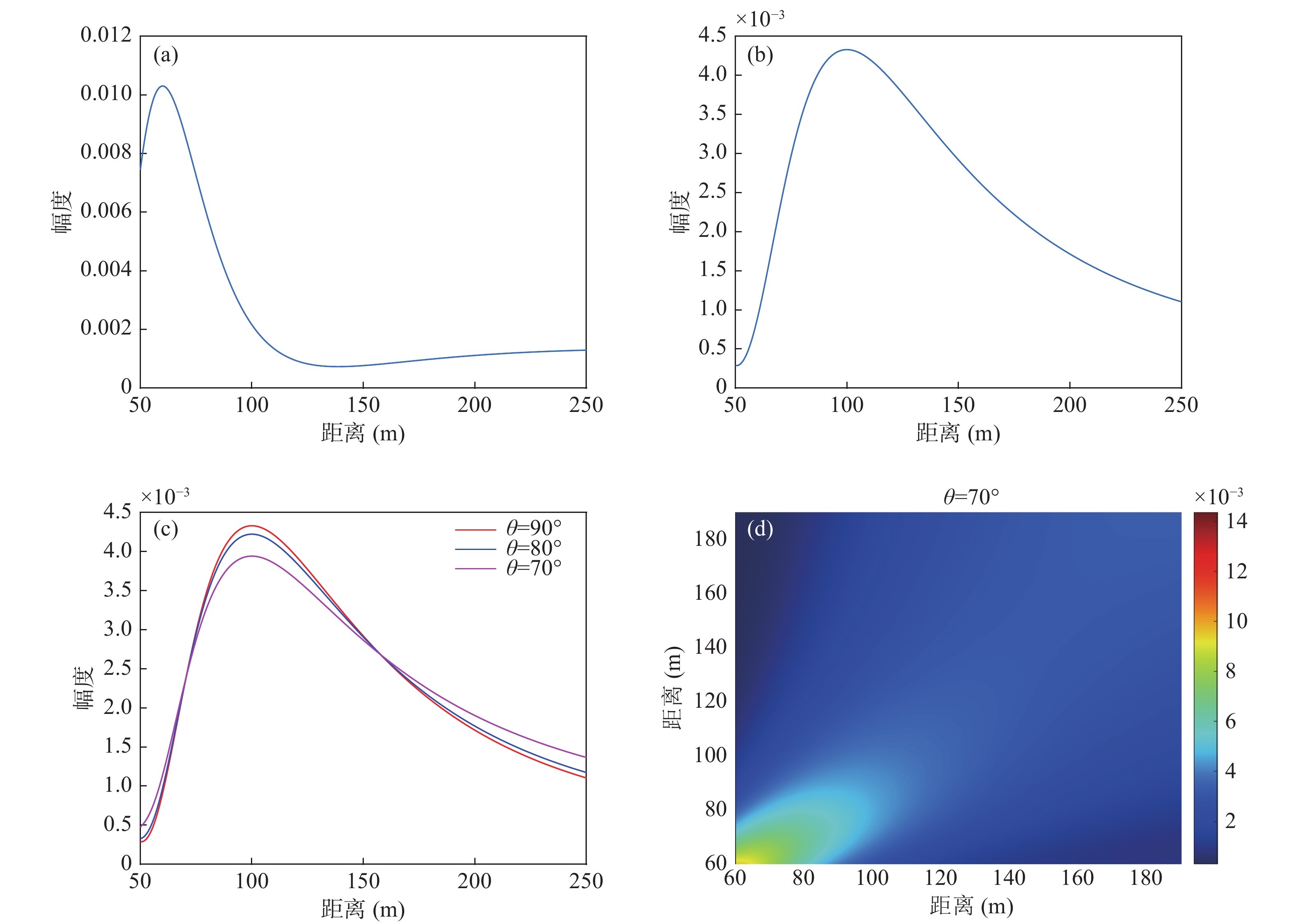
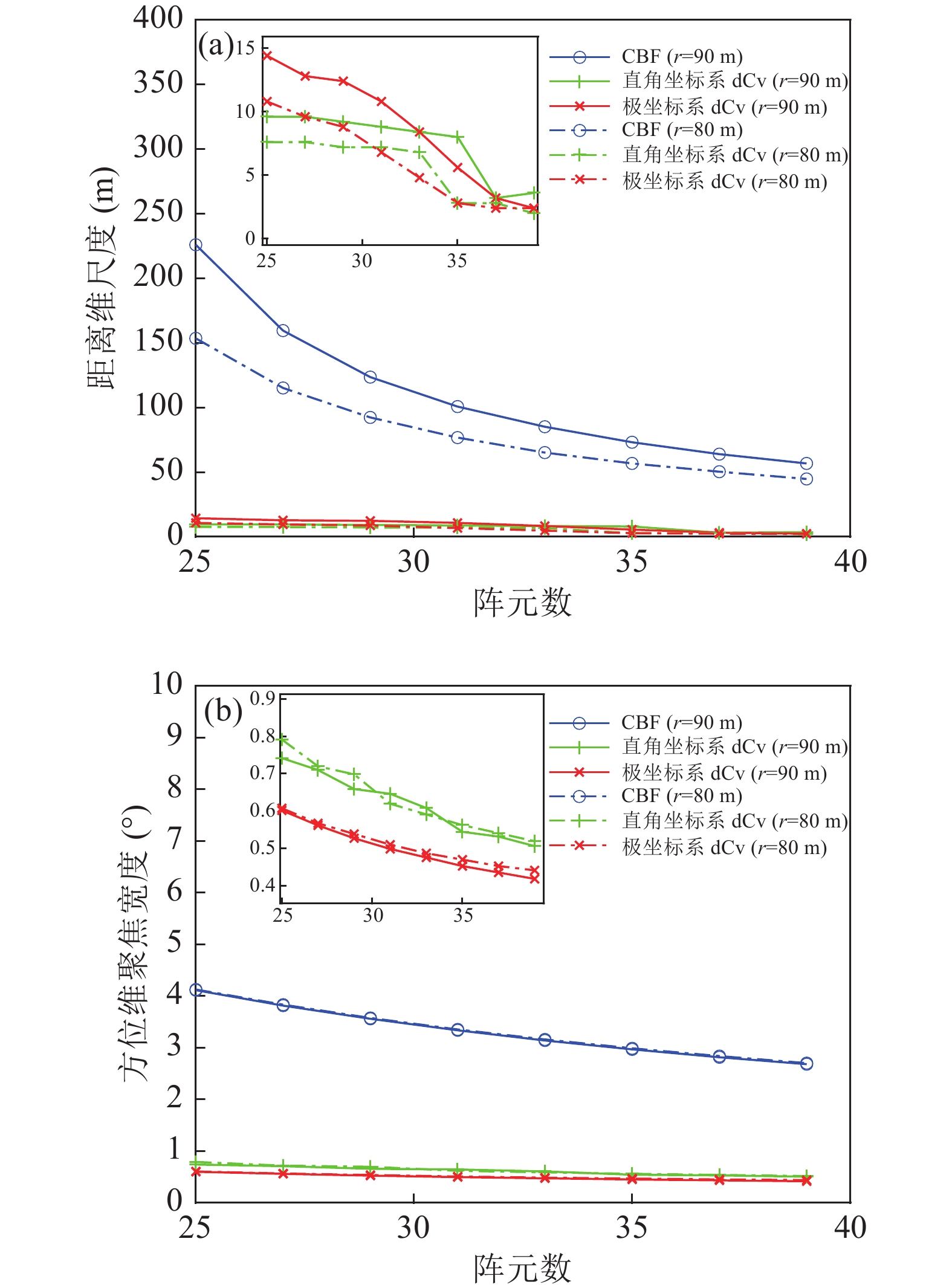
分析极坐标系快速反卷积高分辨声图测量方法的−3 dB聚焦峰尺度, 结果如图12所示。仿真参数: 信号频率为500 Hz, 极坐标系下计算方法的距离扫描区域$r \in \left[ {{\text{6}}0{\text{ m}}:0.4{\text{ m}}:190{\text{ m}}} \right]$, 方位扫描$\cos \left( \theta \right) \in \left[ { - 1:0.0{\text{00}}1:1} \right)$; 直角坐标系下计算方法的距离扫描区域$y \in \left[ {{\text{6}}0{\text{ m}}:0.4{\text{ m}}:190{\text{ m}}} \right]$, $x \in [ {{ - 2}}0{\text{ m}}:0.005{\text{ m}}: 20{\text{ m}} ]$; 单目标位置坐标为$\left( {{\text{9}}0{\text{ m,9}}{{\text{0}}{\text{°}} }} \right)$/$\left( {{\text{8}}0{\text{ m,9}}{{\text{0}}{\text{°}} }} \right)$, R-L反卷积迭代次数均为500。

图12为反卷积声图测量与常规声图测量的距离维以及方位维尺度的对比曲线, 其中实线为$\left( {{\text{9}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$处的结果, 虚线为$\left( {{\text{8}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$处的结果。由图12(a)可见, 随着阵元数增加两种方法距离维聚焦峰尺度都逐渐减小, 常规声图测量的距离维−3 dB聚焦峰尺度整体高于反卷积高分辨声图测量方法。由图12(b)可见, 随着阵元数的增加, 反卷积高分辨声图测量方法方位维的−3 dB聚焦峰尺度呈下降趋势, 但总体变化较小, 而常规声图测量的方位维聚焦峰尺度明显变小。

比较直角坐标系下二维移变反卷积与极坐标系快速反卷积声图测量方法在距离维和方位维的聚焦峰尺度曲线可知, 两种方法都能够有效减小聚焦峰尺度, 极坐标系快速反卷积算法方位维的聚焦峰尺度更小。声源位于$\left( {{\text{9}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$时各算法距离维聚焦峰尺度相比声源位于$\left( {{\text{8}}0{\text{ m, 9}}{{\text{0}}{\text{°}} }} \right)$时大, 而方位维聚焦峰尺度变化较小。

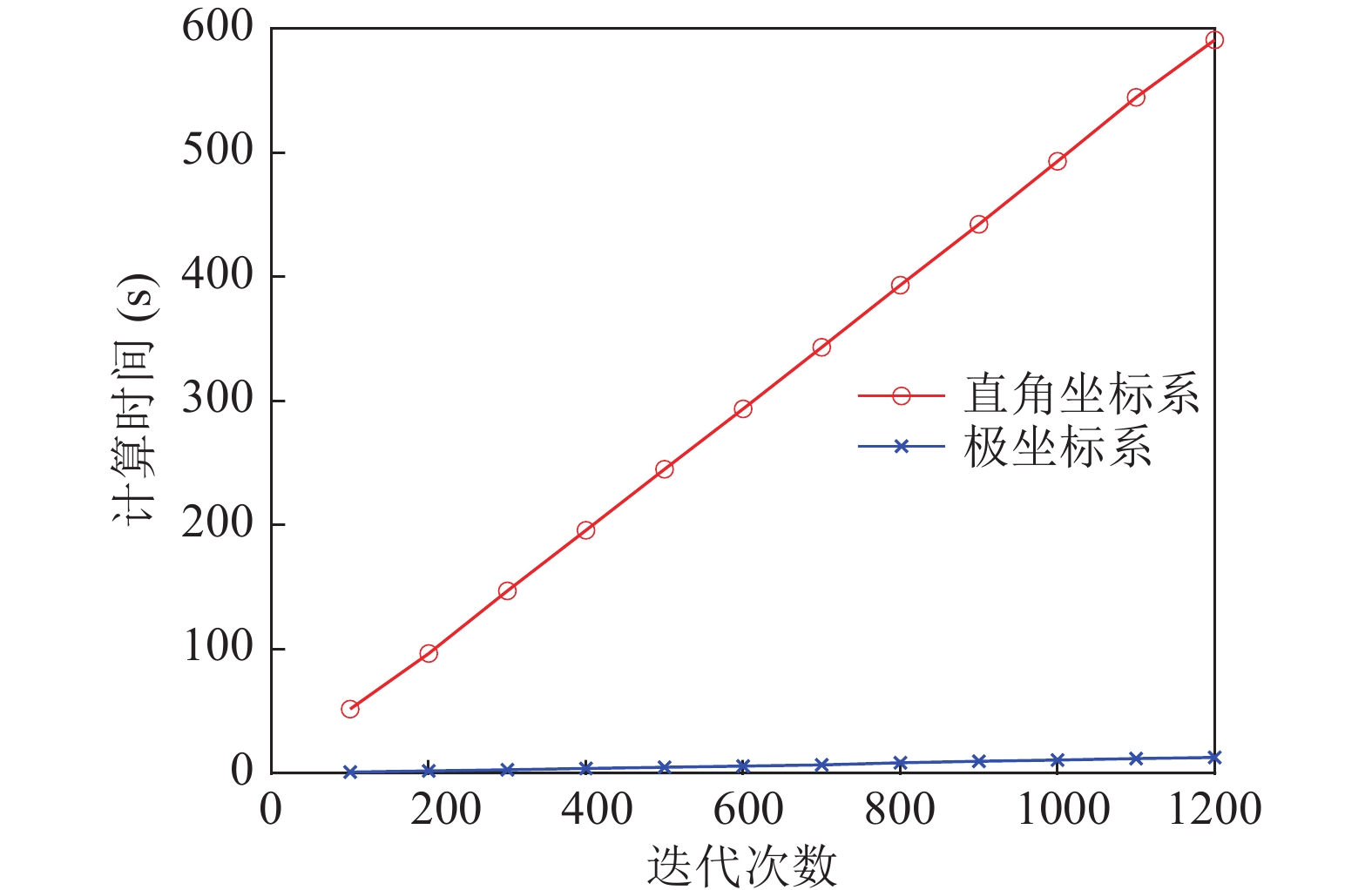
保持直角坐标系与极坐标系下反卷积算法的网格数相同, 即极坐标系下方位维网格数为$ M $, 距离维网格数为$ N $, 直角坐标系下$ x $方向的网格数为$ M $, $ y $方向的网格数为$ N $。统计仿真信号频率$f = 500{\text{ Hz}}$, 目标位于极坐标系$\left( {80{\text{ m}},{{90}{\text{°}} }} \right)$处即直角坐标系$\left( {0{\text{ m}},80{\text{ m}}} \right)$的位置, 极坐标系下计算方法的距离扫描区域$r \in \left[ {{\text{5}}0{\text{ m}}:1{\text{ m}}:180{\text{ m}}} \right]$, 方位扫描$\cos \theta \in [ { - 1:0.01:1} )$, 直角坐标系下计算方法的距离扫描区域$y \in \left[ {{\text{5}}0{\text{ m}}:1{\text{ m}}:180{\text{ m}}} \right]$, $x \in \left[ {{{ - 1}}0{\text{ m}}:0.1{\text{ m}}:10{\text{ m}}} \right]$。该仿真条件下两方法的网格数相同, 使用处理器为Intel(R) Core(TM) i7-855U CPU @ 1.80 GHz 1.99 GHz、内存16 GB的计算机测试两种方法计算时间, 对比结果如图13所示。极坐标系快速反卷积算法相比直角坐标系二维移变反卷积计算量显著下降, 计算时间明显减少, 尤其当扫描网格点较多时, 计算量反映在计算时间上的改善更明显。

(1) 直角坐标系直角二维移变反卷积运算PSF存储量及计算量分析

直角坐标二维卷积积求解迭代计算公式为

其中

存储量分析: 根据式(16), 假设扫描空间范围为$M \times N$时, 需存储$M \times N$个$M \times N$维的声图结果作为点扩散函数(PSF) ${{\boldsymbol{p}}}\left( {x,y\left| {X,Y} \right.} \right)$, 因此PSF的存储量为$ (M\times N{)}^{2} $。

计算量分析: 计算时使用离散的西格玛求和计算迭代积分, 每次反卷积迭代计算过程中乘加运算量为${\left( {M \times N} \right)^3}$次, 除法运算量为${\left( {M \times N} \right)^2}$次。乘法分别对应$M \times N$次${{{\boldsymbol{B}}}^{\left( r \right)}}\left( {x,y} \right)$求解积分乘加运算; $M \times N$次$\left( {x,y} \right)$维度${{\boldsymbol{B}}}\left( {x,y} \right){{\boldsymbol{p}}}\left( {x,y\left| {X,Y} \right.} \right)/{{{\boldsymbol{B}}}^{\left( r \right)}}\left( {x,y} \right)$积分运算是$M \times N$次的$\int_{{x_{\min }}}^{{x_{\max }}} {\int_{{y_{\min }}}^{{y_{\max }}} {} } {\text{d}}x{\text{d}}y$乘加运算; $M \times N$次与$\left( {X,Y} \right)$维度的对应点乘加运算。${\left( {M \times N} \right)^2}$次除法分别对应$\left( {x,y} \right)$维度的$M \times N$次对应点除和$\left( {X,Y} \right)$维度的$M \times N$次逐点运算。

(2) 极坐标系两次一维反卷积PSF存储量及计算量分析

极坐标系下的反卷积可以转换为两次一维运算, 方位维及距离维的计算公式如式(10)和式(14)所示。

存储量分析: 根据距离维和方位维的反卷积迭代公式, 假设扫描空间网格数同样为$M \times N$时, 点扩散函数(PSF)的存储量为$M + M{N^2}$, 其中$M$为方位维PSF, 只需存储一条移不变曲线, $M{N^2}$是距离维PSF, 距离维是移变的, 每个角度存储一组${N^2}$距离维矩阵。

计算量分析: 离散化卷积迭代运算, 总的乘加法运算量约为$MN\left( {{M^2} + {N^2}} \right)$, 除法$MN\left( {M + N} \right)$次。方位维迭代运算的乘运算为${M^3}$, 需做$N$个距离的运算, 距离维运算为${N^3}$, 需要做$M$个距离维。方位维需要做$N$个${M^2}$次除法, $M$个${N^2}$次除法。

直角坐标系下移变反卷积声图及本文方法存储量及计算量总结如下: (i) PSF存储空间对比。扫描空间范围都为$M \times N$时, 直角坐标系下PSF存储量为$ (M\times N{)}^{2} $, 本文方法的PSF存储空间为$M + M{N^2}$, 约为原方法的${1 \mathord{\left/ {\vphantom {1 M}} \right. } M}$。(ii) 计算量对比。直角坐标一次迭代计算量为${\left( {M \times N} \right)^3}$次乘加运算, 本文方法计算量为$MN\left( {{M^2} + {N^2}} \right)$次乘加运算, 比值为$({M^2} + {N^2})/{M^2}{N^2}$。此外, 本文方法在方位维反卷积求解时还可使用FFT算法, 将卷积运算转换为频域FFT, 进一步降低计算量^[16]。

利用一组浅海海试数据分析所提方法的性能。试验中采用阵元间距为5 m的10元等间隔直线阵, 目标源信号有两种: 小型快艇单点声源和双体船双桨声源目标。信号处理频段为1~1.5 kHz和400~700 Hz。

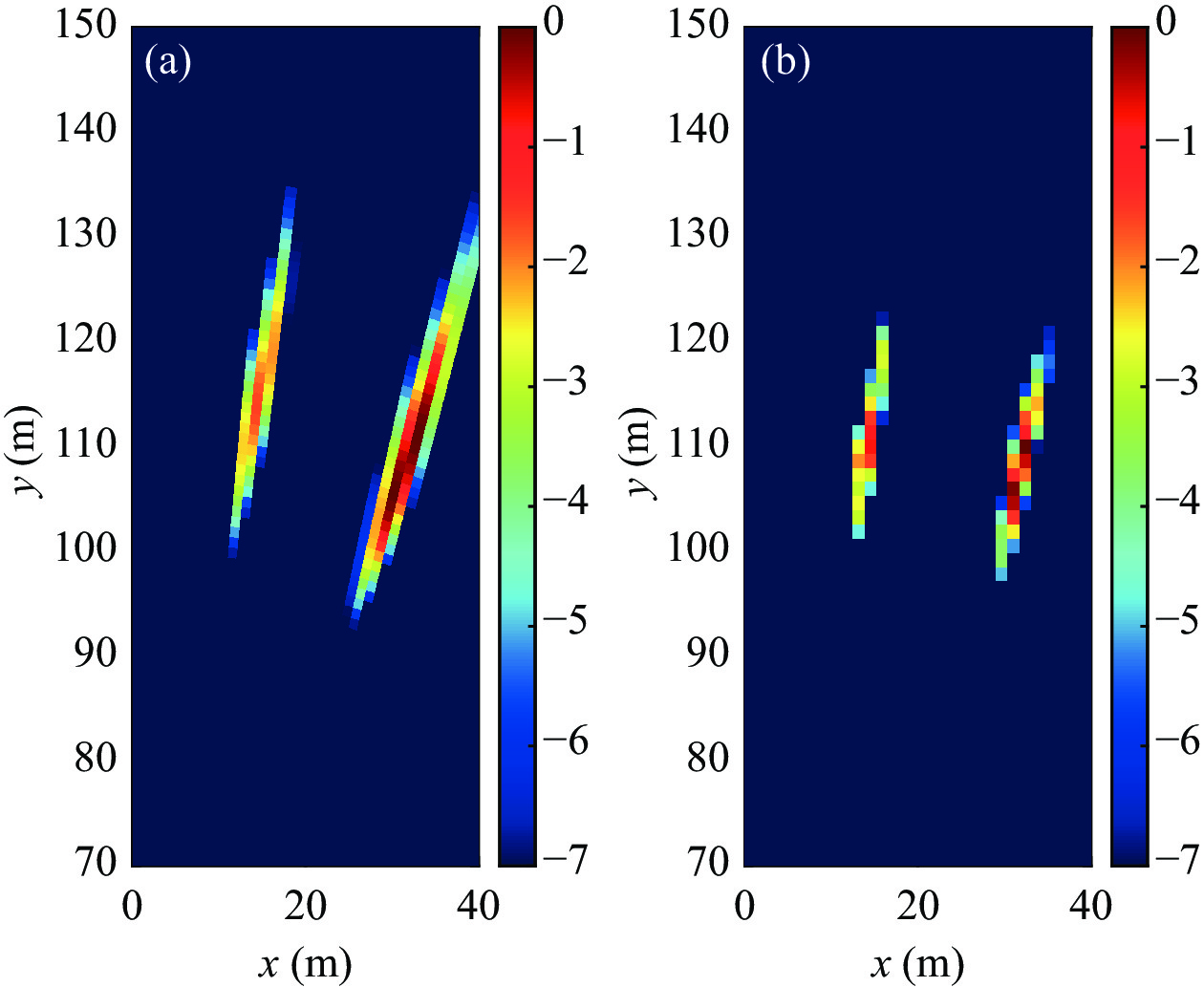
单目标反卷积声图结果如图14—图15所示。常规声图测量受阵列稀疏导致的高合成旁瓣的影响, 不利于判别目标个数以及确定目标位置。对于宽带信号, 不同频率信号的栅瓣位置不同、主瓣位置相同, 不会形成等强度栅瓣, 而是体现为高合成旁瓣, 宽带信号本身具有抗稀疏性能, 其抑制效果与带宽和稀疏度有关。MVDR声图的距离维和方位维主瓣宽度较CBF声图小。相比CBF和MVDR算法, 极坐标快速反卷积能够明显改善聚焦尺度, 降低旁瓣, 净化图像, 更利于探测定位目标。反卷积处理能够降低阵列稀疏带来的高合成旁瓣的影响, 是因为生成PSF时稀疏阵PSF也是与之匹配的, 因此反卷积迭代时会对栅瓣形成的高旁瓣有抑制效果。

图16是双目标的反卷积声图测量结果。同样, 双目标情况下受阵列稀疏的影响, 栅瓣会形成高合成旁瓣, 对常规声图目标个数造成干扰, 但由于双目标的频段低于单目标, 阵稀疏度低, 因此所受影响小于单目标情况。MVDR算法可降低旁瓣, 但无法消除栅瓣的影响, 由于栅瓣的形成和合成, 其旁瓣仍然较高。而快速反卷积的聚焦效果明显优于另两种方法。

极坐标快速反卷积和文献[13]直角坐标系反卷积声图处理结果如图17—图18所示。受直角坐标二维反卷积计算量的影响, 声图定位时往往在给定小范围区域内进行, 即在目标区域附近划定扫描网格区间，结果见图17(b)和图18(b)。图17(a)及图18(a)为取极坐标快速反卷积相应的区域的结果, 二者的聚焦峰尺度大小相近, 与仿真结论一致。

本文提出了一种极坐标系下方位距离维分离的快速反卷积声图测量方法, 模拟仿真了单声源、双声源情况, 并利用小型快艇单点声源和双体船双桨声源海试数据对该方法的性能进行了验证。结果表明, 与原方法相比, 所提方法对PSF存储空间要求和计算量都显著降低, 且可获得与原算法方位聚焦尺度相接近、距离聚焦尺度更佳的测量效果。