-
海底沉积物是一种复杂的频散介质, 其声速和声衰减随频率的变化具有明显的非线性特征。作为海洋声场的下边界, 海底沉积物的声学频散特性一直是海底沉积声学以及地球物理勘探领域关注的重点, 影响到声速、衰减系数、反射系数、掠射角等声传播特性参数的获取, 进而影响海洋底质调查[1-3]。通过海底沉积物的声学频散特性可对沉积物的土工参数进行反演, 评估海床地基的承载力和稳定性; 在海底含气沉积物中, 通过分析气泡对声波激振频率的不同响应, 还能够无损探测施工区域沉积物中赋存的高压气体, 规避工程灾害[4-7]。
声传播理论建模是海底沉积物声学研究的重要内容。传统声传播模型基于流体理论或弹性理论[8-9], 不能反映沉积物的频散特性; 随着对海洋精细化探测的需要, 传统理论的局限性凸显[10]。Biot[11-13]首先注意到饱和多孔介质中孔隙流体相对固体骨架黏性流动所产生的能量耗散, 即Biot流耗散, 提出了Biot理论, 认为多孔介质的频散特性与流固之间相互作用密切相关, 并预测了三类体波的存在。Stoll[14]将Biot理论应用于海底沉积物频散性的分析, 考虑了浅表层沉积物颗粒胶结弱、固结程度低的特点, 在Biot理论基础上, 引入骨架颗粒内部相互摩擦所产生的能量损耗机制, 即骨架耗散, 建立了Biot-Stoll模型。Williams等[15]在应用Biot-Stoll模型预测沉积物纵波频散时, 发现可忽略骨架模量的影响, 将多孔介质简化为等效密度流体介质, 提出了等效密度流体模型(EDFM)。Chotiros等[16]考虑了未胶结沉积物颗粒接触间的弛豫过程, 认为接触间隙流体薄膜的喷流和拖曳会产生进一步的能量耗散, 基于Biot-Stoll模型提出了附加接触喷流与剪切拖曳的Biot-Stoll 模型(BICSQS模型), 同时参照Biot流高频校正方式, 给出了剪切拖曳机制的高频校正系数。Kimura[17]分析了颗粒接触刚度和沉积物整体骨架模量之间的关系, 结合Biot模型和Hertz接触理论建立了考虑接触间隙刚度修正的Biot模型(BIMGS模型)。
声传播模型的适用性是准确预测沉积物声学频散特性的前提。为研究海底浅表层低固结、高渗透率砂质沉积物的频散特性, 本文采用由Biot理论发展而来的Biot、Biot-Stoll和BICSQS模型, 对典型砂质沉积物的声学频散特性进行对比预测分析, 从耗散机制角度揭示三者间的差异, 并结合现场实测数据分析不同模型对饱和砂质沉积物纵横波频散特性的预测性能。
-
利用Lagrange方程和耗散函数, Biot建立了饱和多孔介质中弹性波传播的一般理论框架, 并将该理论直接应用于预测饱和多孔介质的声速和衰减系数等声传播特性参数, 即为Biot模型。根据该模型, 沉积物中三类体波的一维平面波解可用如下特征方程组[18]描述:
其中,
$ \rho $ 为沉积物平均体积密度, 与孔隙流体密度$ {\rho }_{f} $ 、颗粒密度$ {\rho }_{r} $ 、孔隙度$ \beta $ 之间满足关系式$ \rho = \beta {\rho }_{f} + \left(1-\beta \right){\rho }_{r} $ ;$ {m}{{'}} $ 为总有效质量, 与弯曲度$ \alpha $ 、孔隙流体动力黏滞系数$ \eta $ 、Biot高频黏滞系数校正因子$ F $ (与临界频率$ {f}_{r}=\beta \eta /2\pi {\rho }_{f}\kappa $ 和孔隙尺寸$ a $ 相关, 其物理意义及计算见文献[12])、渗透率$ \kappa $ 之间满足关系式$ {m}{{'}}=(\alpha {\rho }_{f}/\beta ) + \mathrm{i}\eta F/\kappa \omega $ ;$ {l}_{p} $ 为纵波的复波数,$ {l}_{s} $ 为横波的复波数;$ H $ ,$ C $ ,$ M $ ,$ {\mu }_{b} $ 为Biot弹性模量, 其中$ {\mu }_{b} $ 为骨架剪切模量, 其余弹性模量满足下列关系[13]:其中,
$ {K}_{\mathrm{s}\mathrm{a}\mathrm{t}} $ 为流体饱和介质不排水条件下的体积模量,$ A $ 为Biot系数,$ {K}_{r} $ ,$ {K}_{b} $ ,$ {K}_{f} $ 分别为介质颗粒、骨架以及流体的体积模量。由波数与波速、衰减系数之间的关系[18], Biot模型中快纵波、慢纵波与横波的相速度
$ {c}_{p1} $ ,$ {c}_{p2} $ ,$ {c}_{s} $ 及衰减系数$ {\alpha }_{p1} $ ,$ {\alpha }_{p2} $ ,$ {\alpha }_{s} $ 分别为由式(8)—式(11)可知, Biot模型预测的海底沉积物中纵波、横波速度与衰减系数均与频率相关。其中, 波数的实部反映了速度随频率的变化特性即频散性; 波数的虚部反映了衰减系数随频率的变化特性即频率相关性, 衰减系数的频率相关性满足
$ \alpha ={kf}^{n} $ 的幂律关系[14],$ k $ 为衰减因子; 两者可统一表述为速度与衰减系数的频散关系。 -
Stoll[14]应用Biot理论研究了低固结海底沉积物中的声波传播, 在Biot模型的基础上引入了复骨架体积模量
$ \overline{{K}_{b}} $ 和复骨架剪切模量$ \overline{{\mu }_{b}} $ , 以此反映骨架内部颗粒相互摩擦所引起的平均声能衰减, 建立了Biot-Stoll模型。同时, Stoll给出了弹性模量$ H $ ,$ C $ ,$ M $ 与复骨架剪切模量$ \overline{{\mu }_{b}} $ 、复骨架体积模量$ \overline{{K}_{b}} $ 、颗粒体积模量$ {K}_{r} $ 以及孔隙流体体积模量$ {K}_{f} $ 之间的显式关系:其中, 复骨架剪切模量
$ \overline{{\mu }_{b}} $ 与复骨架体积模量$ \overline{{K}_{b}} $ 为复常数, 包含了无耗散体积模量$ {K}_{b} $ 、剪切模量$ {\mu }_{b} $ 与耗散项$ {\delta }_{k} $ ,$ {\delta }_{\mu } $ , 分别为$ \overline{{\mu }_{b}} $ = μb(1−δμi/π)与$ \overline{{K}_{b}} $ = Kb(1−δki/π)。 -
Chotiros[16,19]在Biot-Stoll模型的基础上更详细地讨论了骨架耗散过程, 引入了附加接触喷流与剪切拖曳衰减机制, 即BICSQS模型。该模型认为, 对于流体饱和的低固结沉积物而言, 在颗粒不连续接触间隙中, 流体薄膜的动力响应会影响接触性质, 进而改变骨架模量。
经简化后, 接触间隙流体薄膜的相互作用可由体积弛豫和剪切弛豫过程反映, 其中剪切弛豫过程被定义为Couette流。弛豫过程将分别产生接触喷流耗散与剪切拖曳耗散, 可用弹簧和黏壶所构建的接触模型描述。
基于上述弛豫过程和耗散机制, Chotiros对Biot-Stoll模型中的复骨架模量进行如下修正[16]:
其中,
$ {K}_{c} $ 和$ {G}_{c} $ 分别为低频极限时沉积物的骨架体积模量和剪切模量;$ {K}_{y} $ 为高低频骨架极限体积模量的差值;$ {F}_{1s} $ 为BICSQS高频校正因子, 用于校正接触间隙流体在高频情况下因惯性效应所导致的Couette流失效, 与接触间隙尺寸$ {a}_{1} $ 相关, 接触间隙越小则校正因子的影响越小, 当$ {a}_{1} $ 小于0.1 μm时, 在1 MHz范围内可不考虑高频校正因子的影响, 式(17)退化为$ \overline{{\mu }_{b}}={G}_{c}\left(1-\mathrm{i}\omega /{\omega }_{\mu }\right) $ ,$ {F}_{1s} $ 的具体物理意义及计算见文献[16];$ {\omega }_{k} $ 和$ {\omega }_{\mu } $ 分别为体积弛豫频率和剪切弛豫频率。 -
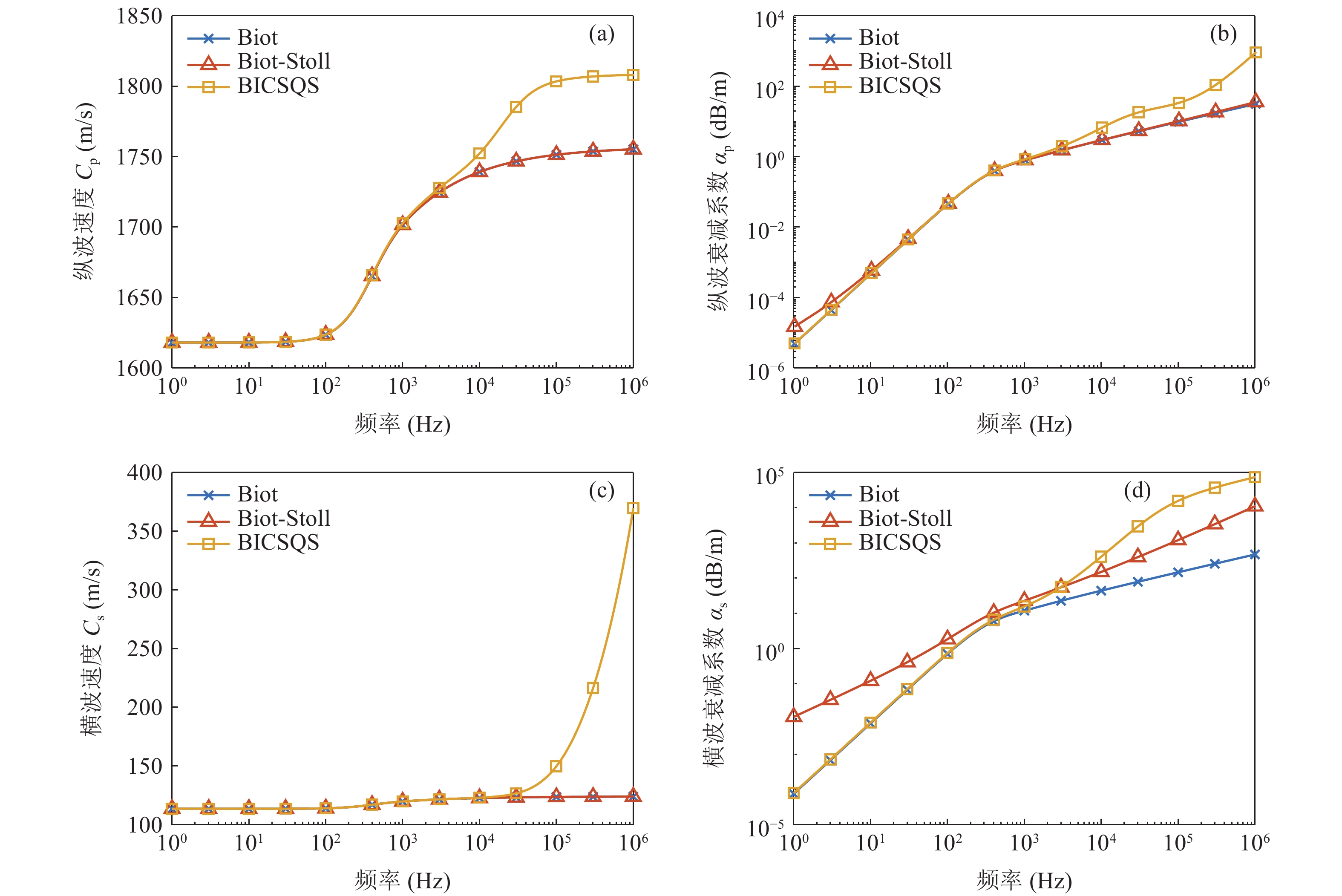
基于表1典型砂质沉积物[20-21]的Biot、Biot-Stoll、BICSQS模型参数, 分别计算并绘制三种模型对于纵波和横波频散关系的预测曲线, 如图1所示。相对慢纵波, 饱和沉积物中快纵波与横波频散关系预测更具有工程意义, 因此本文只针对这两类体波的频散关系进行研究, 下文纵波均指快纵波。
由图1可知, 对于典型砂质沉积物, 全频段内, Biot与Biot-Stoll模型对纵波、横波频散的预测基本一致; 纵波衰减系数预测的差异主要在10 Hz频段内, 而横波衰减系数预测在中间频段较为接近, 在低频和高频段则有明显差异。在中低频段内, Biot模型与BICSQS模型对纵波、横波频散关系的预测基本一致, 但在高频范围内, BICSQS模型预测出更为显著的频散特性。
对于Biot和Biot-Stoll模型而言, 纵波的频散程度远大于横波, 但表现出相同的阶梯状频散特征, 主要频散区间在100 Hz~10 kHz内; 在Biot模型中, 纵波、横波衰减系数的幂律关系相同, 在低于约600 Hz时均与
$ {f}^{2} $ 成正比, 高于该值时与$ {f}^{0.5} $ 成正比; 而Biot-Stoll模型在低于10 Hz时, 纵波衰减系数的频率相关性的幂律指数接近于1.6, 横波衰减系数在全频段内几乎都与$ {f}^{1} $ 成正比, 仅在100 Hz~1 kHz附近衰减系数略有增大。在BICSQS模型中, 纵波速度表现出两个明显的频散区间, 分别位于100 Hz~10 kHz、10~100 kHz频带附近, 呈二级阶梯状; 横波频散也表现出两个区间, 但不呈二级阶梯状分布, 在低于10 kHz时频散关系与Biot、Biot-Stoll模型的频散关系一致, 当高于该频率时频散程度加剧, 且未表现出收敛趋势; 纵波和横波衰减系数在低于600 Hz附近时与频率相关性的幂律关系与Biot模型相同。随着频率增加, 纵波衰减系数逐渐过渡到与
$ {f}^{2} $ 成正比, 而横波衰减系数则先过渡到与$ {f}^{2} $ 成正比, 再过渡到与$ {f}^{1} $ 成正比。综上所述, 部分频段内三种模型耗散机制总的作用效果相近, BICSQS模型新引入的耗散机制主要影响砂质沉积物高频段时的声频散关系。由同一模型的声频散关系预测曲线可知, 相同耗散机制对纵波和横波的作用效果不同, 需进一步深入分析。
-
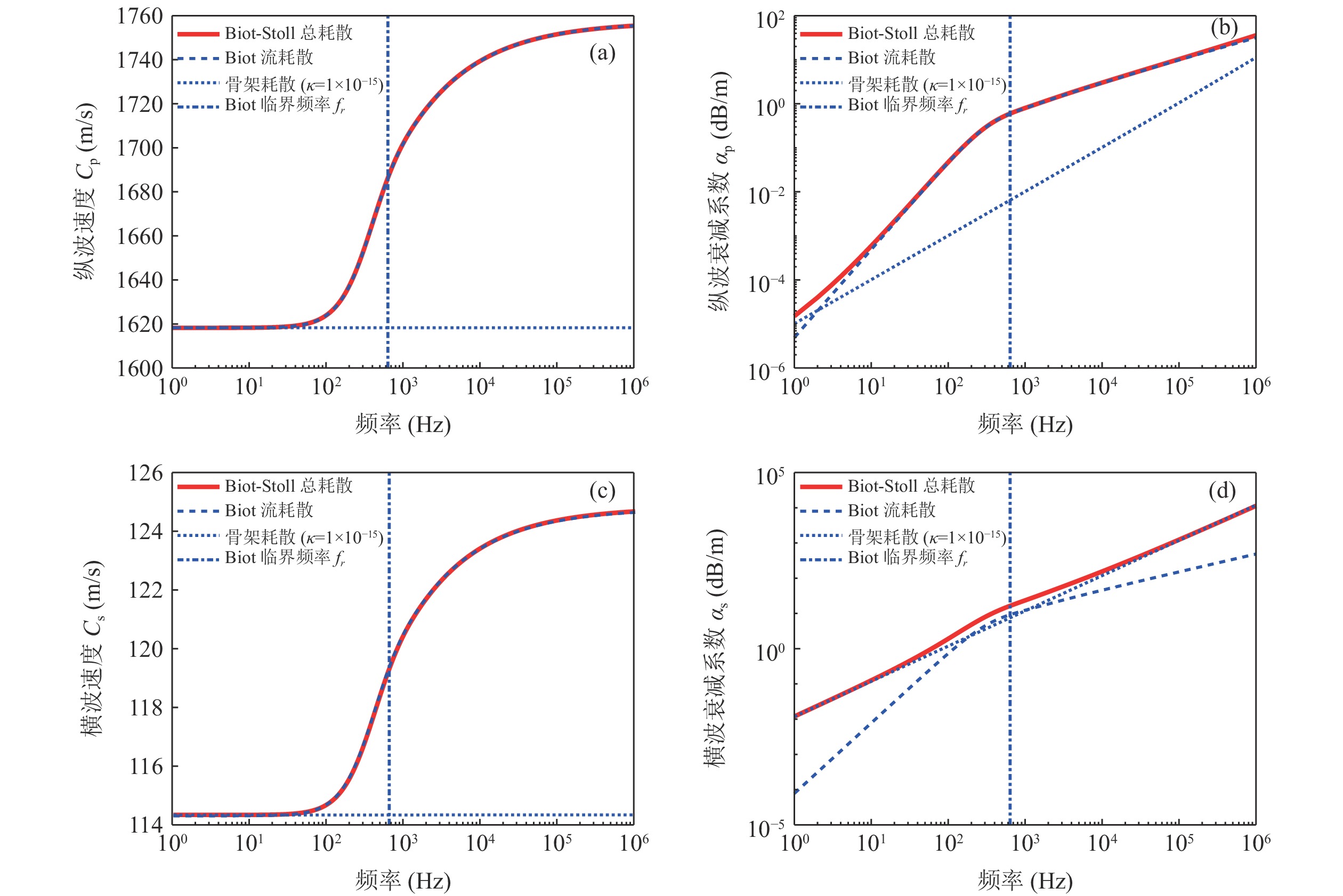
Biot-Stoll模型中包含Biot流和骨架耗散两种耗散机制, 在渗透率足够低的不排水和渗透率足够大的排水条件下, Biot流机制都将失效[14,22], 此时Biot-Stoll模型对声频散关系的预测仅反映骨架耗散机制的作用; 当不考虑骨架的黏弹性, 只取Biot-Stoll模型复骨架模量的实部时, 仅有Biot流机制, Biot-Stoll模型退化为Biot模型[14]。图1中Biot模型的频散关系曲线即反映了Biot流耗散的影响。以表1中Biot、Biot-Stoll模型的相关参数为基础, 通过控制渗透率κ = 1 × 10−15 m2, 讨论不排水条件下的骨架耗散机制对模型整体预测结果的影响, 如图2所示。
由图2(a)(c)可知, 单纯骨架耗散情况下的纵波和横波不发生频散, 其值处于Biot-Stoll模型的低频极限; Biot流机制是Biot-Stoll模型中纵波和横波频散的主要原因。由图2(b)(d)可知, 对于纵波而言, 在低于2 Hz的频带附近, 骨架耗散所产生的纵波衰减高于Biot流耗散, 起主要作用; 此时, 衰减系数与频率相关曲线的切线斜率向1倾斜, 而剩余频段均由Biot流耗散起主要作用, 衰减系数在2 Hz至Biot临界频率
$ {f}_{r} $ 范围内逐渐过渡为与$ {f}^{2} $ 成正比, 大于Biot临界频率$ {f}_{r} $ 后则与$ {f}^{0.5} $ 成正比。对于横波而言, Biot流机制仅在Biot临界频率$ {f}_{r} $ 附近起主要作用, 其余频段均为骨架耗散起主要作用, 衰减系数的频率相关性的幂律指数接近于1, 而在Biot临界频率$ {f}_{r} $ 附近, 幂律关系在两种耗散机制之间过渡。因此, 衰减系数与频率相关性曲线中幂律关系的变化可反映声传播模型中主要耗散机制的变化。 -
BICSQS模型将骨架耗散替换为接触喷流与剪切拖曳耗散, 属于接触间隙内的局部流动形式。为讨论接触喷流与剪切拖曳耗散对声频散关系的影响, 分别考虑两种特殊情况: (1) 剪切弛豫频率趋于无穷而体积弛豫频率有限, 此时的频散关系曲线反映了Biot流和接触喷流耗散的影响; (2) 体积弛豫频率趋于无穷而剪切弛豫频率有限, 此时的频散关系曲线反映了Biot流和剪切拖曳耗散的影响。在此基础上, 若渗透率足够小, Biot流失效, 仅反映接触喷流或剪切拖曳耗散的影响。
-
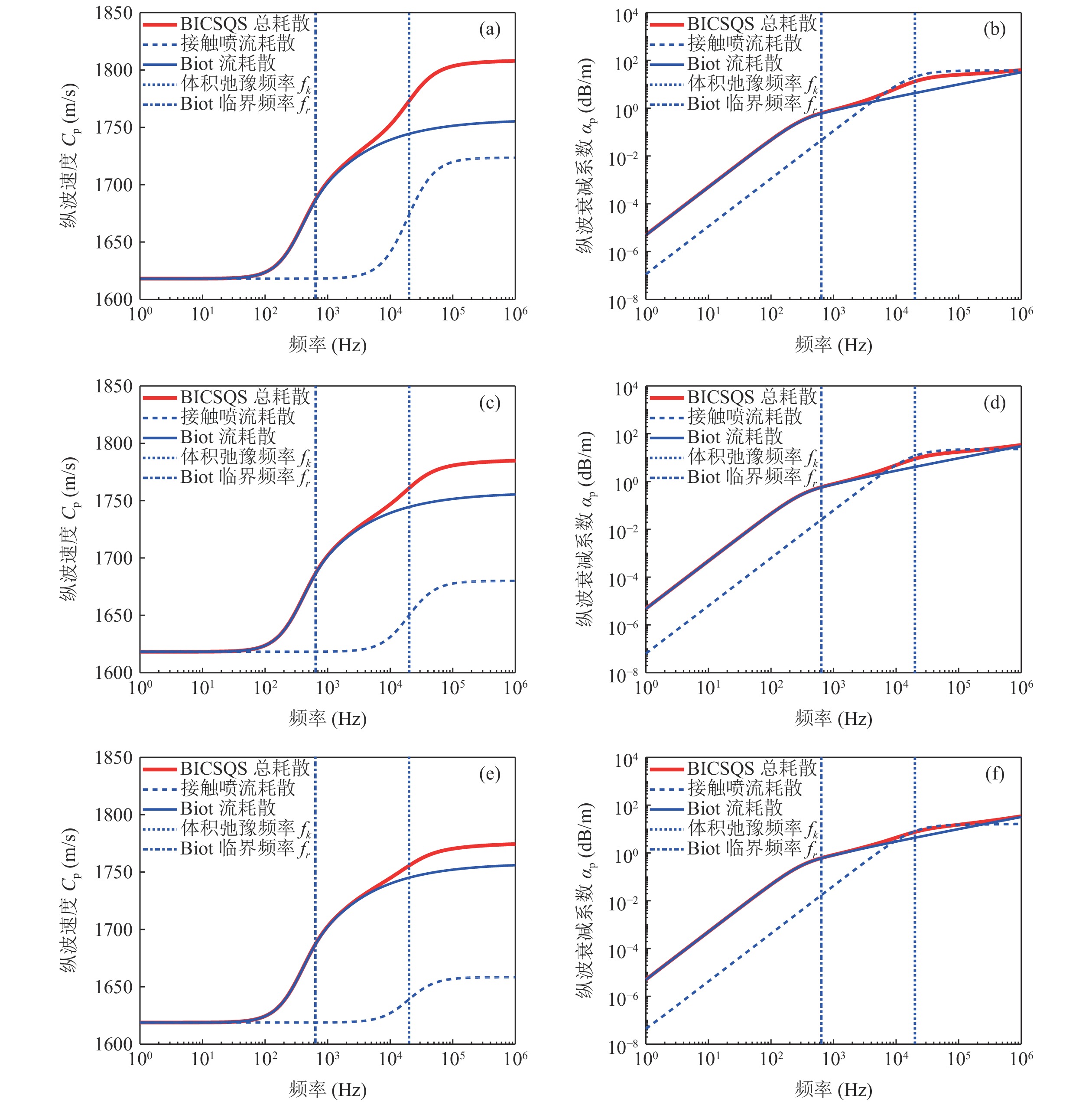
图3和图4分别给出了仅有体积弛豫时Biot流耗散与接触喷流耗散机制对纵波和横波频散关系曲线的影响, 用Biot临界频率
$ {f}_{r} $ 和体积弛豫频率$ {f}_{k} $ 划分为三个区间, 相关模型参数见表1。此外, 为分析骨架体积模量高低频极限差Ky对频散关系的影响, 考虑不同的Ky取值。由图3可知, 接触喷流机制使纵波速度在
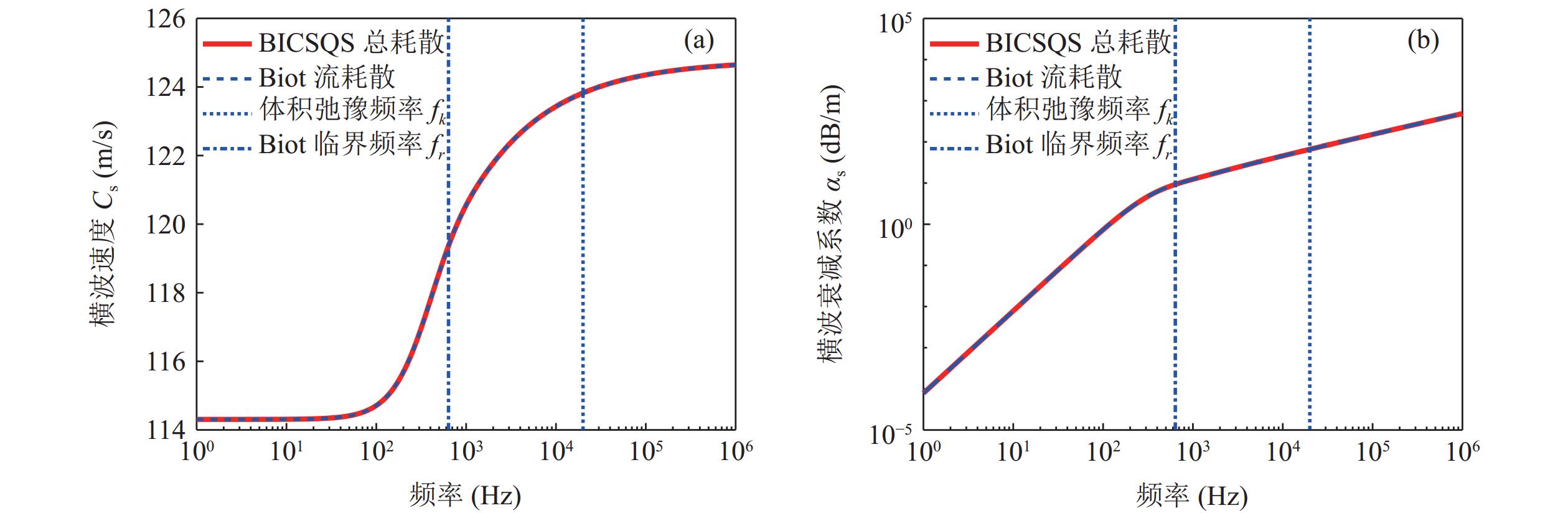
$ {f}_{k} $ 附近产生显频散, 作用效果与Biot流相近, 呈阶梯状, 使纵波速度在大于$ {f}_{r} $ 后进一步频散; 接触喷流所引起的纵波衰减在低于$ {f}_{k} $ 时与$ {f}^{2} $ 成正比, 高于$ {f}_{k} $ 后斜率趋于0, 仅在$ {f}_{k} $ 附近时接触喷流引起的声衰减系数大于Biot流耗散引起的声衰减系数。同时, 接触喷流对纵波频散关系的影响还与骨架体积模量高低频极限差Ky相关, 随着Ky的降低, 接触喷流散所产生的频散程度逐渐降低, 且在总耗散中的影响也逐渐降低。在图4中, BICSQS总耗散与Biot流耗散情况下的横波频散关系曲线一致, 表明接触喷流耗散对横波速度与衰减系数的频散关系不产生影响。 -
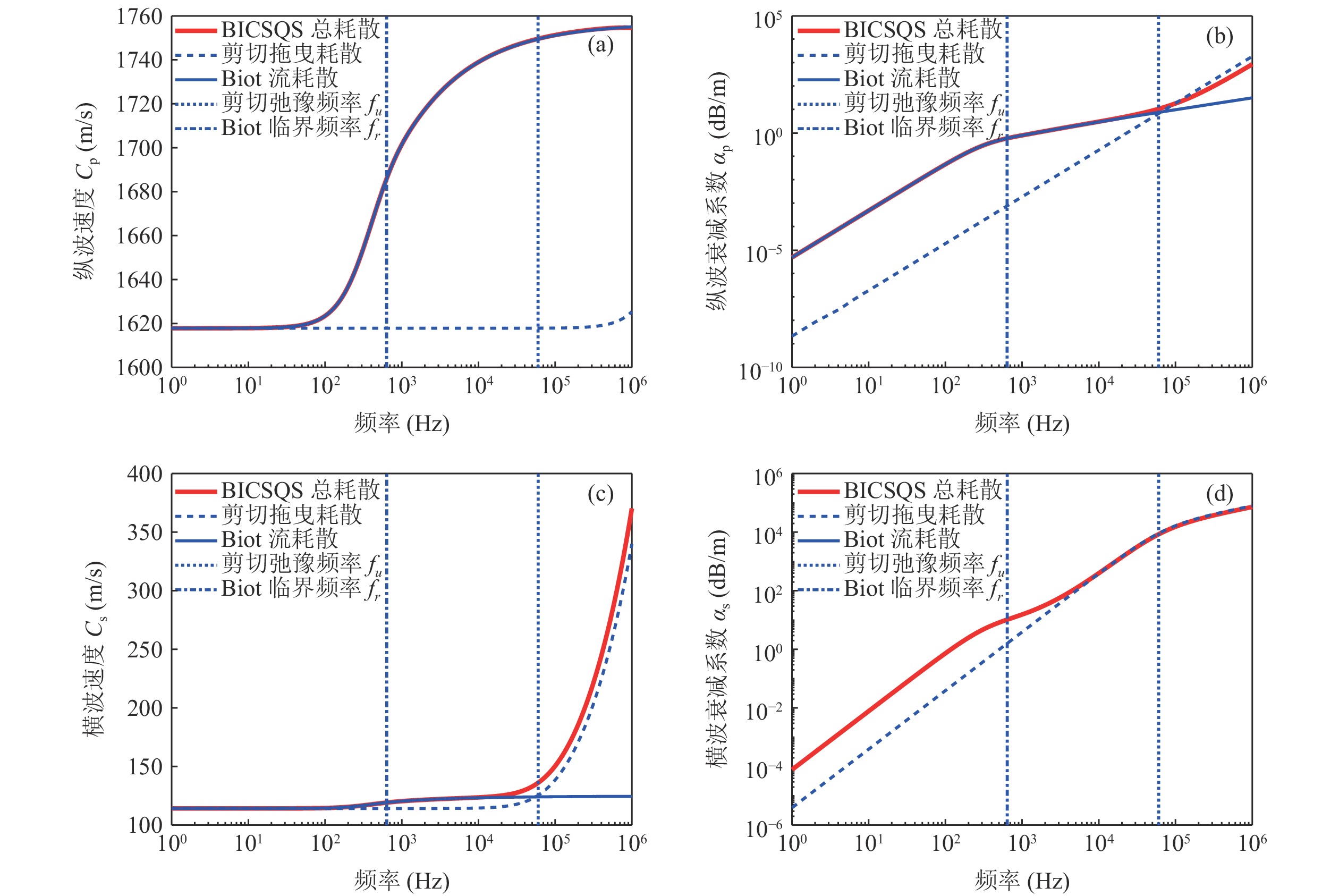
当仅有剪切弛豫过程时, Biot流耗散与剪切拖曳耗散对纵波和横波频散关系的影响如图5所示。由图可知, 剪切拖曳耗散机制对纵波、横波的速度和衰减系数均有影响。其中, 剪切拖曳耗散仅在频率大于200 kHz时使纵波速度产生轻微频散, 而横波速度则在剪切弛豫频率
$ {f}_{u} $ 附近随频率的增大而迅速提升。同时, 剪切拖曳耗散对纵波和横波衰减系数的影响也表现出较大差异。对纵波而言, 衰减系数在1 Hz~1 MHz的宽频范围内均与$ {f}^{2} $ 成正比, 且在低于$ {f}_{u} $ 的频带范围内Biot流耗散衰减高于剪切拖曳耗散; 对横波而言, 剪切拖曳耗散的主要作用频带范围相对纵波更广, 衰减系数在低于$ {f}_{u} $ 的频带范围时与$ {f}^{2} $ 成正比、高于$ {f}_{u} $ 时与$ {f}^{0.5} $ 成正比, Biot流机制则主要在频率低于$ {f}_{r} $ 时占主要作用, 影响范围较小。 -
分别应用Biot、Biot-Stoll和BICSQS模型对不同类型浅表层砂质沉积物的声频散关系进行预测, 并结合实测结果对比讨论三种模型的适用性。由前述可知, Biot与Biot-Stoll模型仅在横波衰减系数的预测上表现出明显差异, 因此仅在该预测效果对比中讨论Biot、Biot-Stoll与BICSQS模型的适用性, 而在其他频散关系的预测效果对比中讨论Biot-Stoll与BICSQS模型的适用性。
-
1999年, Stoll[23]、Buckingham等[24]在Fort Walton海滩, 针对埋深1~2 m厚的中细粒径砂质沉积物, 开展了SAX99系列原位声学试验, 测试了125 Hz~400 kHz和2.6~400 kHz频段内的纵波速度与衰减系数。Williams等[25]针对SAX99试验, 给出了Biot-Stoll模型中沉积物的相关物理参数, 提供了可靠的Biot-Stoll模型验证数据。但当前关于横波频散数据的报道较少, 多数情况下仅有少量几个频点的实测数据。Kimura等[18]基于弯曲元试验, 依据差距测量原理, 同时测得了饱和细粒硅砂中的横波速度和衰减系数频散数据, 覆盖频段范围为4~20 kHz。此后, Lee等[26]通过双压电陶瓷换能器阵列, 在Currituck湾浅水区埋深30 cm内的中细粒砂质沉积物中开展了原位声学试验, 测得了0.3~1 kHz低频范围内的横波频散数据。
-
以SAX99原位纵波试验数据、Kimura室内横波试验数据、Lee原位横波试验数据为例, 对由多孔介质理论发展起来的三种声传播模型频散关系预测性能及其耗散机制进行对比讨论。在此之前, 需选取合适的模型参数, 使其与待测沉积物相匹配。不同类型砂质沉积物的模型参数, 如表2所示。
由表1可知, Biot、Biot-Stoll与BICSQS模型的相关参数可分为三组, 包括与孔隙流体相关的物理参数: 孔隙流体密度
$ {\rho }_{f} $ 、孔隙流体体积模量$ {K}_{f} $ 及孔隙流体黏滞系数$ \eta $ , 这类参数随海水的温度、压力和盐度不同有轻微变化, 但对声传播模型的最终预测结果影响较小、取值较固定, 可被认为是常数; 与沉积物颗粒相关的物理参数: 颗粒密度$ {\rho }_{r} $ 与颗粒体积模量$ {K}_{r} $ , 这类参数和沉积物颗粒的矿物成分相关, 对于特定类型的沉积物而言也可认为是常数, 在砂质沉积物中, 体积模量取值范围为32~49 GPa, 颗粒密度可直接通过试验测量; 其他参数均为与沉积物骨架相关的物理参数, 除孔隙度可直接测量外, 需通过经验公式[27]或拟合得出。表2中, SAX99原位试验、Kimura室内试验与Lee原位试验中的模型参数取值于参考文献[25][18][26], 并结合表1典型砂质海底沉积物的相关参数确定。其中, Lee原位试验中沉积物的骨架剪切模量
$ {\mu }_{b} $ 由密度$ \rho $ 和横波速度$ {c}_{s} $ 的关系式$ {\mu }_{b}=\rho {c}_{s}^{2} $ 计算得到。 -
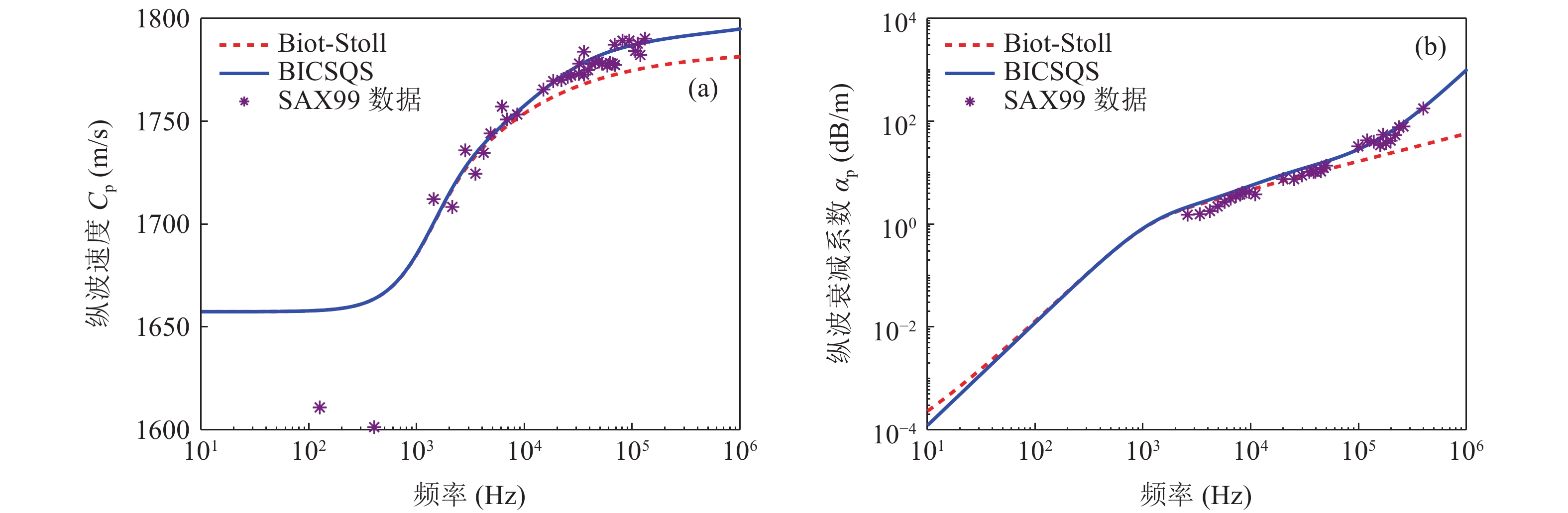
SAX99原位试验与Biot-Stoll、BICSQS模型预测的对比结果如图6所示。结合对模型耗散机制的分析可知, 在125 Hz~10 kHz时, Biot-Stoll模型与BICSQS模型的纵波主要耗散机制均为Biot流机制, 此时两模型对纵波速度和衰减系数的预测效果接近, 除125 Hz与400 Hz两个频点离散性较大外, 1~10 kHz内的预测值均能够较好地与实测纵波频散吻合, 最大误差小于0.63%, 而衰减系数的预测结果由2.2 dB/m增大至6.1 dB/m, 均大于实测值; 在10~100 kHz时, Biot-Stoll模型的主要耗散机制仍为Biot流机制, 而BICSQS模型的主要耗散机制为Biot流机制与接触喷流机制, 其中接触喷流机制使BICSQS模型在该频段内的纵波速度预测值由1758 m/s进一步频散至1787 m/s, 较Biot-Stoll模型而言更趋近于实测结果, 但接触喷流对纵波衰减系数的影响较低, 使BICSQS模型的预测结果在该频段内仅略大于Biot-Stoll模型, 实测衰减数据处于两模型预测的区间范围内; 大于100 kHz时, BICSQS模型的主要耗散机制为剪切拖曳机制, Biot-Stoll模型的主要耗散机制不变, 此时衰减系数的实测数据与BICSQS模型预测更为吻合, 且显著高于Biot-Stoll模型的预测结果。
-
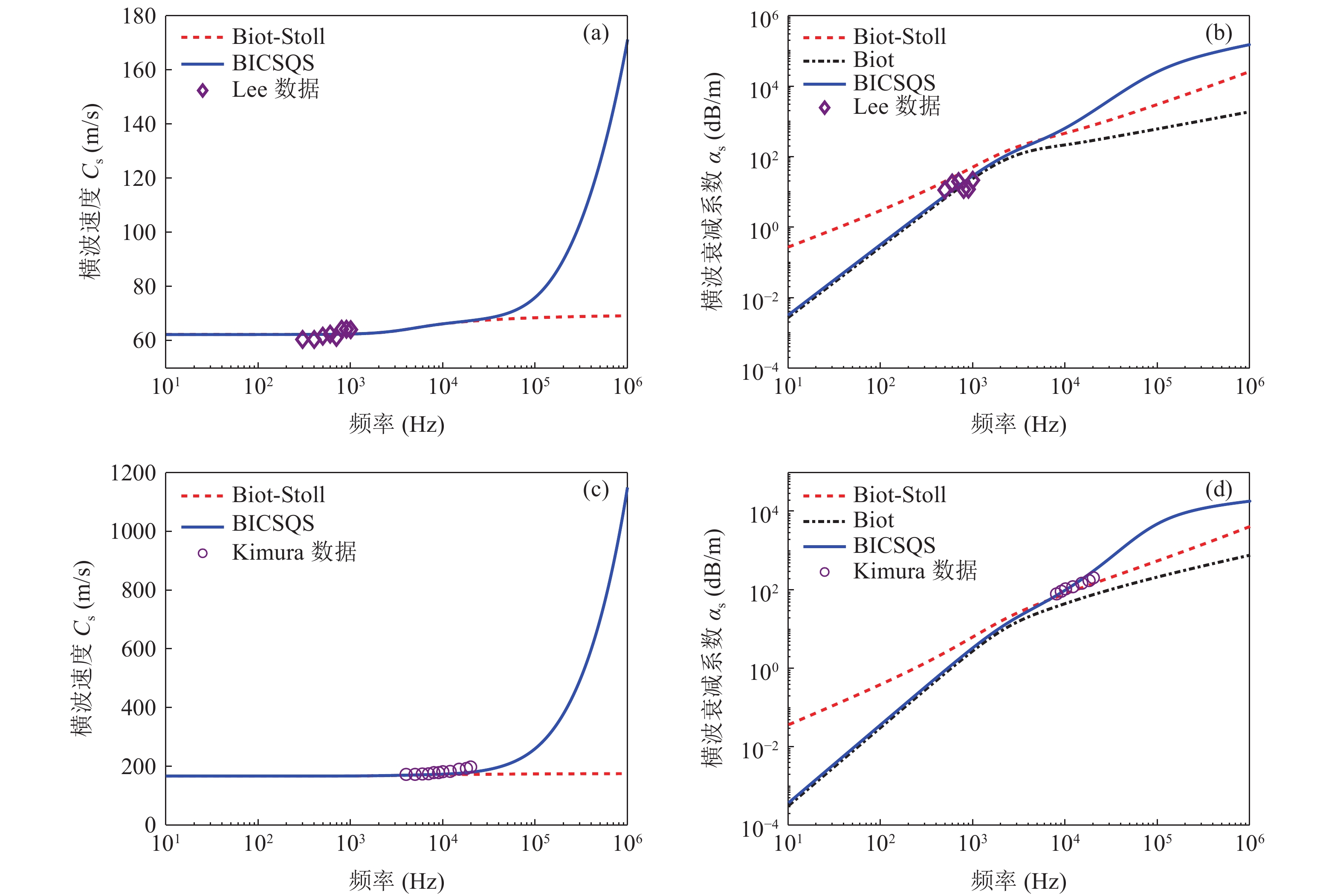
Lee原位试验、Kimura室内试验结果与Biot、Biot-Stoll、BICSQS模型预测结果如图7所示。由图7(a)(b)可知, 对于Currituck湾的中细粒砂质沉积物而言, 在0.3~1 kHz频段内, 实测横波频散较小, 增幅小于5.6%, 此时Biot-Stoll与BICSQS模型中引起横波频散的主要耗散机制均为Biot流机制, 两者预测效果相同, 与实测结果吻合较好, 最大误差小于3%; 实测横波衰减系数则处于11.8~22.5 dB/m之间, 较好地落在了BICSQS与Biot模型的预测曲线附近, 而均低于Biot-Stoll模型的预测。结合其耗散机制可知, 该频段内横波衰减系数的频率相关性主要受骨架耗散机制的影响, 而此时BICSQS与Biot模型中仍为Biot流机制起主要作用。这表明在低频范围内, 此类砂质沉积物中由于骨架内部颗粒相互摩擦而产生的损耗并不显著, Biot流耗散对横波衰减系数频率相关性的解释具有合理性, 而BICSQS模型中剪切拖曳机制的作用需在更高频段内进一步验证。
由图7(c)(d)可知, 在Kimura室内试验的饱和细粒硅砂试样中, Biot-Stoll模型与BICSQS模型对横波频散预测的差异主要发生在大于7 kHz的频段上, 而实测数据覆盖频段范围为4~20 kHz。4~7 kHz频段, 频散由Biot流决定, 实测横波速度在174.1~183.2 m/s范围内, 与Biot-Stoll模型、BICSQS模型预测值均能较好地吻合; 7~20 kHz频段, 频散由剪切拖曳机制决定, 实测横波速度由183.2 m/s递增为199.3 m/s, 与BICSQS模型预测的最大误差小于8.5%, 而与Biot-Stoll模型预测的误差则逐渐扩大至14.5%。在整个实测频段范围内, BICSQS模型预测的横波衰减系数均大于Biot模型与Biot-Stoll模型, 且此时Biot、Biot-Stoll与BICSQS模型中的主要耗散分别为Biot流、骨架耗散与剪切拖曳。实测横波衰减系数位于77.4~200 dB/m范围内, 与BICSQS模型预测结果更为接近, 说明了BICSQS模型中剪切拖曳耗散对横波作用的合理性。
综上所述, Biot流耗散机制在中低频范围内具有一定的适用性, 使得Biot模型或Biot-Stoll模型的预测结果与实测结果较好吻合; 但随着频率的增大, 实测纵波、横波速度与衰减系数均有高于Biot-Stoll模型预测的趋势, 而BICSQS模型的接触喷流与剪切拖曳机制可合理地解释该趋势, 与实测结果更好地吻合。
-
(1) 声传播模型对声频散关系的预测与其对沉积物内部耗散机制的不同描述相关。在以Biot流机制为主要耗散机制的频段内, Biot、Biot-Stoll与BICSQS模型的预测结果相近, 而BICSQS模型新引入的耗散机制使其在高频段预测出更为显著的频散性。
(2) 耗散机制对纵波、横波频散关系的影响效果不同。在Biot-Stoll模型中, 均主要受Biot流机制的影响, 而横波衰减系数的频率相关性则主要受骨架耗散机制的影响。在BICSQS模型中, 纵波速度、衰减系数的频散关系均受Biot流、接触喷流与骨架耗散机制的影响, 各机制的主要作用频段不同; 而横波频散特性则不受接触喷流机制的影响。
(3) Biot、Biot-Stoll与BICSQS模型的预测和实测结果对比发现, 在海底浅表层砂质沉积物中, 随着频率的增加, 纵波与横波均表现出高频散、高衰减的趋势, 相对于Biot模型和Biot-Stoll模型, BICSQS模型可更有效地预测并解释该趋势, 初步验证了BICSQS模型具有更好的适用性。
基于Biot理论的饱和砂质沉积物声传播模型及耗散机制分析
Analysis of acoustic propagation models and dissipation mechanisms of saturated sandy sediments based on the Biot theory
-
摘要: 为研究海底浅表砂质沉积物的频散特性, 利用由多孔介质理论发展而来的Biot模型、Biot-Stoll模型和附加接触喷流与剪切拖曳的Biot-Stoll模型(BICSQS模型), 对比三种声传播模型描述下的典型砂质沉积物中纵波和横波频散特性, 分析了模型中不同耗散机制对其声频散关系的影响; 结合实测数据探讨了各模型对砂质沉积物的适用性。结果表明, 沉积物的声频散特性是不同耗散机制共同作用的结果, 不同频段内的主要耗散机制不同, 相同频段内耗散机制对纵波和横波的传播影响亦不同; 随着频率的增加, 相比Biot和Biot-Stoll模型的预测结果, 砂质沉积物的实测声速和衰减系数表现出更高的频散趋势, 而BICSQS模型可更合理地预测和解释试验现象, 适用性更好。Abstract: To investigate the dispersion characteristics of shallow sandy sediments on the seabed, a comparative analysis was conducted on the longitudinal and transverse wave dispersion features in typical sandy sediments described by the three acoustic propagation models using the Biot model, the Biot-Stoll model and the Biot-Stoll with contact squirt flow and shear drag (BICSQS) model developed from the theory of porous media. The effects of different dissipation mechanisms in the models on the acoustic dispersion relationship were revealed. Furthermore, the applicability of the models to sandy sediments was explored using integrating empirical data. The results indicate that the acoustic dispersion characteristics of sediments are the result of different dissipation mechanisms, which are different in different frequency bands and have different effects on the propagation of longitudinal and transverse waves in the same frequency band. As the frequency increases, the measured acoustic speed and attenuation of sandy sediments exhibit higher dispersion trends than those predicted by the Biot and Biot-Stoll models. In contrast, the BICSQS model demonstrates a more reasonable prediction and interpretation of experimental phenomena with better applicability.
-
Key words:
- Sandy sediments /
- Biot theory .
-

-
参数 单位 Biot Biot-Stoll BICSQS 颗粒密度 $ {\rho }_{r} $ 

kg/m3 2650 2650 2650 颗粒体积模量 $ {K}_{r} $ 

GPa 36 36 36 流体密度 $ {\rho }_{f} $ 

kg/m3 1000 1000 1000 流体体积模量 $ {K}_{f} $ 

GPa 2.25 2.25 2.25 流体黏滞系数 $ \eta $ 

Pa·s 0.001 0.001 0.001 孔隙度 $ \beta $ 

— 0.4 0.4 0.4 渗透率 $ \kappa $ 

m2 1 × 10−10 1 × 10−10 1 × 10−10 弯曲度 $ \alpha $ 

— 1.25 1.25 1.25 骨架体积模量 $ {K}_{b}\left({K}_{c}\right) $ 

MPa 44 44 44 骨架剪切模量 $ {\mu }_{b}\left({G}_{c}\right) $ 

MPa 26 26 26 体积耗散系数 $ {\delta }_{k} $ 

— — 0.143 — 剪切耗散系数 $ {\delta }_{\mu } $ 

— — 0.151 — 骨架体积模量高低频极限差 $ {K}_{y} $ 

MPa — — 950 体积弛豫频率 $ {f}_{k} $ 

kHz — — 20 剪切弛豫频率 $ {f}_{\mu } $ 

kHz — — 60 表 2 不同类型砂质沉积物的模型参数
分组 模型参数 单位 SAX99中细砂[25] Kimura细砂[18] Lee中细砂[26] 沉积物颗粒 颗粒密度 $ {\rho }_{r} $ 

kg/m3 2690 2659 2633.3 颗粒体积模量 $ {K}_{r} $ 

GPa 32 36 38 孔隙流体 流体密度 $ {\rho }_{f} $ 

kg/m3 1023 998.2 997.7 流体体积模量 $ {K}_{f} $ 

GPa 2.395 2.193 2.15 流体黏滞系数 $ \eta $ 

Pa·s 0.00105 0.00105 0.00105 沉积物骨架 孔隙度 $ \beta $ 

— 0.385 0.368 0.44 渗透率 $ \kappa $ 

m2 2.5 × 10−11 6.423 × 10−12 2.07 × 10−11 弯曲度 $ \alpha $ 

— 1.35 1.86 1.16 Biot模型 骨架体积模量 $ {K}_{b} $ 

MPa 43.6 — — 骨架剪切模量 $ {\mu }_{b} $ 

MPa 29.2 58 7.4 Biot-Stoll模型 体积耗散系数 $ {\delta }_{k} $ 

— 0.15 — — 剪切耗散系数 $ {\delta }_{\mu } $ 

— 0.19 0.12 0.15 BICSQS模型 骨架体积模量高低频极限差 $ {K}_{y} $ 

MPa 240 — — 低频骨架剪切模量 $ {G}_{c} $ 

MPa 29.2 58 7.4 低频骨架体积模量 $ {K}_{c} $ 

MPa 43.6 — — 体积弛豫频率 $ {f}_{k} $ 

kHz 20 — — 剪切弛豫频率 $ {f}_{\mu } $ 

kHz 60 300 90 注: 未标注参数为对模型的横波频散预测结果无影响的参数。 -
[1] 于盛齐, 王飞, 郑广赢, 等. 海底沉积物声学特性研究进展与探讨. 哈尔滨工程大学学报, 2020; 41(10): 1571−1577 doi: 10.11990/jheu.202007049 [2] Best A I, Huggett Q J, Harris A J K. Comparison of in situ and laboratory acoustic measurements on Lough Hyne marine sediments. J. Acoust. Soc. Am., 2001; 110(2): 695−709 doi: 10.1121/1.1382616 [3] 王飞. 宽频段沙质沉积物声速频散和衰减特性研究. 博士学位论文, 哈尔滨: 哈尔滨工程大学, 2019 [4] Klein G, Bohlen T, Theilen F, et al. Acquisition and inversion of dispersive seismic waves in shallow marine environments. Mar. Geophys. Res., 2005; 26(2-4): 287−315 doi: 10.1007/s11001-005-3725-6 [5] 黄必桂, 李家钢, 周庆杰, 等. 基于浅地层剖面的海底浅表层沉积物物理性质参数反演技术研究—以渤海海底管线路由区为例. 海洋学报, 2022; 44(9): 156−164 doi: 10.12284/hyxb2022113 [6] 黄林, 王勇, 邹大鹏, 等. 重塑砂质含气沉积物的声响应特性与模型预测分析. 声学学报, 2022; 47(1): 61−68 doi: 10.15949/j.cnki.0371-0025.2022.01.007 [7] Anderson A L, Hampton L D. Acoustics of gas-bearing sediments I. Background. J. Acoust. Soc. Am., 1980; 67(6): 1865−1889 doi: 10.1121/1.384453 [8] 李燕, 刘浩杰, 王玉梅. Gassmann模型机理分析及其应用. 勘探地球物理进展, 2010; 33(1): 16−20 [9] Mavko G, Mukerji T, Dvorkin J. The rock physics handbook. Cambridge: Cambridge University Press, 2020 [10] 阚光明, 邹大鹏, 孙蕾, 等. 浅海沉积声学原位探测系统研制及深海功能拓展. 海洋测绘, 2014; 34(5): 79−82 doi: 10.3969/j.issn.1671-3044.2014.05.022 [11] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am., 1956; 28(2): 168−178 doi: 10.1121/1.1908239 [12] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am., 1956; 28(2): 179−191 doi: 10.1121/1.1908241 [13] Biot M A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys., 1962; 33(4): 1482−1498 doi: 10.1063/1.1728759 [14] Stoll R D. Acoustic waves in ocean sediments. Geophysics, 1977; 42(4): 715−725 doi: 10.1190/1.1440741 [15] Williams K L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory. J. Acoust. Soc. Am., 2001; 110(5): 2276−2281 doi: 10.1121/1.1412449 [16] Chotiros N P, Isakson M J. High-frequency dispersion from viscous drag at the grain-grain contact in water-saturated sand. J. Acoust. Soc. Am., 2008; 124(5): 296−301 doi: 10.1121/1.2987465 [17] Kimura M. Velocity dispersion and attenuation in granular marine sediments: Comparison of measurements with predictions using acoustic models. J. Acoust. Soc. Am., 2011; 129(6): 3544−3561 doi: 10.1121/1.3585841 [18] Kimura M. Shear wave speed dispersion and attenuation in granular marine sediments. J. Acoust. Soc. Am., 2013; 134(1): 144−155 doi: 10.1121/1.4809679 [19] Chotiros N P, Isakson M J. A broadband model of sandy ocean sediments: Biot-Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am., 2004; 116(4): 2011−2022 doi: 10.1121/1.1791715 [20] 曹正良, 张叔英, 马在田. BICSQS模型与Biot-Stoll模型海底界面声波反射和散射的比较. 声学学报, 2006; 31(5): 389−398 doi: 10.15949/j.cnki.0371-0025.2006.05.002 [21] Chotiros N P. Biot model of sound propagation in water-saturated sand. J. Acoust. Soc. Am., 1995; 97(1): 199−214 doi: 10.1121/1.412304 [22] Song J, Xu C S, Li L. The Influence of permeability on the propagation characteristics of the waves in different saturated soils. Appl. Sci., 2021; 11(17): 8138 doi: 10.3390/app11178138 [23] Stoll R D. Velocity dispersion in water-saturated granular sediment. J. Acoust. Soc. Am., 2002; 111(2): 785−793 doi: 10.1121/1.1432981 [24] Buckingham M J, Richardson M D. On tone-burst measurements of sound speed and attenuation in sandy marine sediments. IEEE J. Oceanic Eng., 2002; 27(3): 429−453 doi: 10.1109/JOE.2002.1040929 [25] Williams K L, Jackson D R, Thorsos E I, et al. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media. IEEE J. Oceanic Eng., 2002; 27(3): 413−428 doi: 10.1109/JOE.2002.1040928 [26] Lee K M, Ballard M S, McNeese A R, et al. In situ measurements of sediment acoustic properties in Currituck Sound and comparison to models. J. Acoust. Soc. Am., 2016; 140(5): 3593−3606 doi: 10.1121/1.4966118 [27] Kimura M. Study on the Biot-Stoll model for porous marine sediments. Acoust. Sci. & Tech., 2007; 28(4): 230−243 doi: 10.1250/AST.28.230 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: