高级搜索

基于高阶非厄密物理的磁共振无线电能传输研究进展

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

王利凯, 王宇倩, 郭志伟, 江海涛, 李云辉, 羊亚平, 陈鸿. 基于高阶非厄密物理的磁共振无线电能传输研究进展[J]. 物理学报, 2024, 73(20): 201101-1. doi: 10.7498/aps.73.20241079
引用本文: 王利凯, 王宇倩, 郭志伟, 江海涛, 李云辉, 羊亚平, 陈鸿. 基于高阶非厄密物理的磁共振无线电能传输研究进展[J]. 物理学报, 2024, 73(20): 201101-1. doi: 10.7498/aps.73.20241079
shu
Li-Kai Wang, Yu-Qian Wang, Zhi-Wei Guo, Hai-Tao Jiang, Yun-Hui Li, Ya-Ping Yang, Hong Chen. Research progress of magnetic resonance wireless power transfer based on higher-order non-Hermitian physics[J]. Acta Physica Sinica, 2024, 73(20): 201101-1. doi: 10.7498/aps.73.20241079
Citation: Li-Kai Wang, Yu-Qian Wang, Zhi-Wei Guo, Hai-Tao Jiang, Yun-Hui Li, Ya-Ping Yang, Hong Chen. Research progress of magnetic resonance wireless power transfer based on higher-order non-Hermitian physics[J]. Acta Physica Sinica, 2024, 73(20): 201101-1. doi: 10.7498/aps.73.20241079
shu

基于高阶非厄密物理的磁共振无线电能传输研究进展

  • 1.

    同济大学物理科学与工程学院, 教育部先进微结构材料重点实验室, 上海　200092

  • 2.

    同济大学电子与信息工程学院, 上海　201804

    • 作者简介: 王利凯: 2230977@tongji.edu.cn .
    通讯作者: E-mail: 2014guozhiwei@tongji.edu.cn; 

  • 中图分类号: 11.30.Er, 42.25.Bs, 03.65.Vf

Research progress of magnetic resonance wireless power transfer based on higher-order non-Hermitian physics

  • 1.

    MOE Key Laboratory of Advanced Micro-structured Materials, School of Physics Sciences and Engineering, Tongji University, Shanghai 200092, China

  • 2.

    School of Electronic and Information Engineering, Tongji University, Shanghai 201804, China

    • Corresponding author: E-mail: 2014guozhiwei@tongji.edu.cn.; 

  • MSC: 11.30.Er, 42.25.Bs, 03.65.Vf

  • 摘要: 近年来, 基于宇称-时间(parity-time, PT)对称的非厄密物理机制在磁谐振式无线电能传输(wireless power transfer, WPT)领域取得了显著进展. 非厄密物理不仅有效地解释了当前WPT领域基于电路理论分析的主要实验结果, 而且为进一步提升WPT器件的传输效率、距径比、鲁棒性等方面提供了全新的原理支撑. 本文主要综述了基于PT对称、高阶PT对称、高阶Anti-PT对称等条件下的高效稳定磁谐振式WPT的研究进展, 揭示了非厄密物理在该领域的独特作用机制及重要应用. 最后对非厄密物理在WPT领域的应用前景进行了展望.
    Abstract: In recent years, wireless power transfer (WPT) leveraging parity-time (PT) symmetry has made significant progress , in terms of enhancing efficiency, transfer distance, and robustness. This paper overviews magnetic resonance WPT systems utilizing ideal, asymmetric, high-order, and anti-PT symmetry.The first section discusses the second-order PT symmetry, evolving from inductive to resonant WPT. Active tuning and nonlinear saturation gain techniques optimize frequency and spontaneously achieve efficient WPT. These methods improve transmission efficiency, especially with the change of dynamic transfer distance. The second section focuses on the third-order PT and anti-PT symmetry. The third-order PT systems maintain a fixed eigenfrequency, making stable energy transfer possible. Generalized PT symmetry harnesses bandgaps for further efficiency. The BIC in asymmetric systems reveals a pure real mode for stable WPT. The anti-PT symmetry’s ‘level pinning’ maintains stability in dynamic changes. The final section summarizes high-order PT symmetry for long-range WPT. Heterojunction coupling and topologically non-trivial chains enhance efficiency and stability. Examples include long-range WPT via relay coils and directional WPT using asymmetric topological edge states.In summary, this review emphasizes the pivotal role of various forms of PT symmetry in improving the performance and reliability of magnetic resonance WPT systems. By improving transmission efficiency, range, and stability, these symmetries pave the way for wider applications in fields such as smart homes, medical devices, and electric vehicles. The synthesis of current research results provides valuable insights and references for the future development of WPT technology.
  • 加载中

  • 图 1  (a) 感应式和谐振式模型及能量分布; (b) 谐振式模型的传输特性; (c) 频率随距离劈裂现象(电路方程解); (d) 非厄密物理PT对称相图(哈密顿量解)

    Figure 1.  (a) Inductive and resonant models and energy distribution; (b) the transmission characteristics of resonant model; (c) frequency splitting phenomenon with distance (circuit equation solution); (d) phase diagrams of PT-symmetric non-Hermitian system (Hamiltonian solution).

    下载: 全尺寸图片 幻灯片

    图 2  (a) 由射频放大器组成的频率追踪式磁耦合谐振式WPT的示意图[27]; (b) 固定驱动频率系统与自适应频率调谐系统随距离变化的传输效率对比图[27]; (c) 4种不同情形下的实验传输效率对比[28]

    Figure 2.  (a) Schematic diagram of frequency tracking magnetic coupling resonant WPT composed of RF amplifiers[27]; (b) comparison of transmission efficiency between fixed frequency system and auto-tuned system with distance[27]; (c) comparison of experimental transmission efficiency in four cases[28].

    下载: 全尺寸图片 幻灯片

    图 3  (a) PT对称WPT的电路模型[32]; (b) 频率及稳态增益随耦合强度(距离)的变化[32]; (c) PT对称WPT的电压比[32]; (d) 理论(黑线)、电路仿真(品红虚线)和实验结果(蓝色圆点)对比[32]; (e) 无人机WPT传输示意图[35]; (f) 无人机平台原边副边传输效率及总体效率[35]

    Figure 3.  (a) The Circuit model of PT symmetric WPT[32]; (b) frequency and steady-state gain as a function of coupling strength (distance)[32]; (c) voltage ratio of PT symmetric WPT[32]; (d) comparison of theoretical (black line), circuit simulation (magenta dashed line), and experimental results (blue dots)[32]; (e) schematic of UAV WPT transmission[35]; (f) UAV platform primary-side secondary-side transmission efficiency and overall efficiency[35].

    下载: 全尺寸图片 幻灯片

    图 4  三阶PT对称WPT系统[38]　(a) 三阶PT对称模型图; (b) 三阶PT对称系统效率随频率和耦合强度变化关系; (c) 二阶和三阶PT对称系统传输实部虚部相图对比

    Figure 4.  Third-order PT-symmetric WPT system[38]: (a) Diagram of the third-order PT-symmetric model; (b) variation of the efficiency of the third-order PT-symmetric system with frequency and coupling strength; (c) comparison of the phase diagrams of the real and imaginary parts of the transmission of the second- and third-order PT-symmetric systems.

    下载: 全尺寸图片 幻灯片

    图 5  三阶PT对称WPT系统的实现　(a) 分离型三阶系统电路图; (b) 合成型三阶系统电路; (c) 小车三阶WPT演示图[23]; (d) 三阶系统实部随耦合和损耗的演化轨迹[23]; (e) 理想情况下三阶和二阶系统效率对比图[23]; (f) (b)图对应实验图[38]; (g) 三阶系统反射率随频率和耦合强度的变化关系[38]; (h) 不同本征损耗下效率与传输距离变化图[38]

    Figure 5.  Realization of the third-order PT symmetric WPT system: (a) Circuit diagram of the separated third-order system; (b) circuit of the synthesized third-order system; (c) demonstration diagram of the third-order WPT of the cart[23]; (d) evolution trajectory of the real part of the third-order system with coupling and loss[23]; (e) comparison of the efficiencies of the third-order and the second-order systems in the ideal case[23]; (f) experimental plots corresponding to the diagrams in (b)[38]; (g) variation of the reflectivity of the third-order system with frequency and coupling strength[38]; (h) different intrinsic losses in the efficiency versus transmission distance plots[38].

    下载: 全尺寸图片 幻灯片

    图 6  (a) 三阶PT非对称结构图; (b) 三阶PT非对称系统实部随${\kappa _{23}}$变化相图; (c) 三阶PT非对称系统虚部随${\kappa _{23}}$变化相图; (d) 同(b)但关于耦合${\kappa _{12}}$${\kappa _{23}}$三维实部相图演化; (e) 同(c)但关于耦合${\kappa _{12}}$${\kappa _{23}}$三维虚部相图演化; 三阶非厄密WPT系统本征频率实部, 虚部和系统效率在不同增益损耗比下的演化: (f) 增益损耗比例为0.5; (g) 增益损耗比例为2[40]

    Figure 6.  (a) Third-order PT asymmetric structure; (b) phase diagram of the real part of the third-order PT asymmetric system as a function of the variation; (c) phase diagram of the imaginary part of the third-order PT asymmetric system as a function of the variation; (d) same as in figure (b) but with respect to the coupling three-dimensional real phase diagram evolution; (e) same as in figure (c) but with respect to the coupling Three-dimensional imaginary phase diagram evolution; evolution of the real and imaginary parts and the system efficiency of the characteristic frequencies of the third-order non-Hermitian WPT system for different gain-loss ratios: (f) gain-loss ratio of 0.5; (g) gain-loss ratio of 2[40].

    下载: 全尺寸图片 幻灯片

    图 7  (a) 基于偶极-单极类比的广义奇偶性的局部和全局奇偶性分解[41]; (b) 高维参数空间$(g, \gamma , {\kappa _{12}}, {\kappa _{23}})$中WPT 系统的能带理论解释[41]; (c) 标准PT对称电子二聚体的示意图[42]; (d) 由两个增益(红色)单元和一个损耗(蓝色)单元组成的三阶赝厄密系统[42]; (e) 增益单元和损耗单元对应的等效电路[42]; (f) 图(d)模型的实验装置示意图[42]; (g) 稳态频率${f_{\text{s}}}$(上图), 电压比$ {V_1}/{V_2} $(左侧红色y轴)和$ {V_3}/{V_2} $(右侧蓝色y轴)(中间图), 以及传输效率${\eta _{{\text{PTE}}}}$(下图), 作为耦合系数$\kappa $的函数. 理论, 模拟和实验结果分别用实线、虚线和空心圆表示. 阴影区域表示$\kappa \geqslant \gamma =0.078$[42]

    Figure 7.  (a) Local and global parity decomposition based on the generalized parity of the dipole-monopole analogy[41]; (b) band theory explanation of the WPT system in high-dimensional parameter space $(g, \gamma , {\kappa _{12}}, {\kappa _{23}})$[41]; (c) schematic diagram of a standard PT-symmetric electronic dimer[42]; (d) third-order pseudo-Hermitian system composed of two gain (red) units and one loss (blue) unit[42]; (e) equivalent circuit corresponding to the gain and loss units[42]; (f) schematic diagram of the experimental setup for the model in Figure (d)[42]; (g) steady-state frequency ${f_{\text{s}}}$(upper panel), voltage ratios $ {V_1}/{V_2} $ (left red y-axis) and $ {V_3}/{V_2} $ (right blue y-axis) (middle panel), and transmission efficiency ${\eta _{{\text{PTE}}}}$ (lower panel), as functions of the coupling coefficient $\kappa $. Theoretical, simulated, and experimental results are represented by solid lines, dashed lines, and hollow circles, respectively. The shaded area represents $\kappa \geqslant \gamma =0.078$[42].

    下载: 全尺寸图片 幻灯片

    图 8  (a) 由3个耦合谐振器构成的Anti-PT对称模型[48]; (b) “能级钉扎”原理图[48]; (c) 反共振系统中本征频率实部的演化[48]; (d) 等效电路图[48]; (e) 实物图[48]; (f) 系统中本征频率实部随耗散耦合($\gamma $)和相干耦合($\kappa $)的演化[48]; (g) 合成三阶Anti-PT对称中本征频率计算(测量)的实部[48]; (h) WPT系统待机功率损耗[48]; (i) 具有RTC(ATC)的匹配WPT系统在追踪工作频率下的传输效率[48]

    Figure 8.  (a) Anti-PT symmetry model consisting of three coupled resonators[48]; (b) “energy level pinning” schematic[48]; (c) evolution of the real part of the eigenfrequency in the anti-resonant system[48]; (d) equivalent circuit diagram[48]; (e) physical diagram[48]; (f) evolution of the real part of the eigenfrequency in the system with dissipative coupling $\gamma $ and coherent coupling $\kappa $[48]; (g) real part of the computed (measured) eigenfrequency in the synthesized third-order inverse PT symmetry[48]; (h) standby power loss of the WPT system[48]; (i) transmission efficiency of the matched WPT system with RTC (ATC) at the tracking operating frequency[48].

    下载: 全尺寸图片 幻灯片

    图 9  (a) 高阶PT对称系统机制演示[50]; (b) 当负载线圈移动时, 不同位置中性原子耦合强度变化[50]; (c) 系统本征频率随位移的变化[50]; (d) 异质结型电路示意图[50]; (e) 实验PCB元件图[50]; (f) 柔性负载谐振器实物图[50]; (g) 高阶系统高效区域的可视化[50]; (h) 系统从远端位移获得的恒定电压增益[50]; (i) 二极管在远端和横向位移下通过组织对负载谐振器进行可靠的WPT演示[50]

    Figure 9.  (a) Demonstration of the higher-order PT symmetric system mechanism[50]; (b) variation of the neutral atom coupling strength at different locations when the load coil is moved[50]; (c) variation of the system intrinsic frequency with displacement[50]; (d) schematic diagram of a heterogeneous junction-type circuit[50]; (e) diagram of the experimental PCB components[50]; (f) physical diagram of a flexible loaded resonator[50]; (g) visualization of the efficient region of the higher-order system[50]; (h) the system’s gain from distal displacements with a constant voltage gain[50]; (i) reliable WPT demonstration of the loaded resonator by organization of the diode under far-end and lateral displacements[50].

    下载: 全尺寸图片 幻灯片

    图 10  (a) PT对称的多线圈复合二聚链WPT系统示意图[59]; (b) 等效三阶 PT 对称(绿色)和等效二阶 PT 对称(橙色)拓扑二聚体链的特征值谱[59]; (c) 等效三阶 PT 对称的复合拓扑二聚体链中的三种拓扑模式的归一化强度分布[59]; (d) 拓扑二聚体链在工作和待机状态下的反射谱[59]; (e) 图(d)在工作状态下实验演示[59]; (f) 图(d)在待机状态下实验演示[59]; (g) 一维 Harper 链左右两端的传输比[60]; LED 灯组成汉字的“同”和“济”的定向 WPT 的演示实验 (h) 左向演示[60]; (i) 右向演示[60]

    Figure 10.  (a) Schematic diagram of the PT-symmetric multi-coil WPT system[59]; (b) eigenvalue spectra of the equivalent third-order PT-symmetric (green) and equivalent second-order PT-symmetric (orange) topological dimer chains[59]; (c) normalized intensity distributions of the three topological modes in the equivalent third-order PT-symmetric composite topological dimer chain[59]; (d) reflection spectra of the topological dimer chain in the operating and standby states[59]; (e) demonstration of experiment in working condition in figure (d) [59]; (f) demonstration of experiment in standby condition in figure (d) [59]; (g) transmission ratio between left and right ends of one-dimensional Harper chain[60]; demonstration of directional WPT with LEDs forming Chinese characters “Tong” and “Ji”; (h) left-oriented demonstration[60]; (i) right-oriented demonstration[60].

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Tesla N 1914 U. S. Patent 1 119 732 [1914-12-1]
    [2] Hui S Y R, Zhong W X, Lee C K 2013 IEEE Trans. Power Electron. 29 4500
    [3] Wang C S, Covic G A, Stielau O H 2004 IEEE Trans. Ind. Electron. 51 148 doi: 10.1109/TIE.2003.822038
    [4] Ho S L, Wang J, Fu W N, Sun M 2011 IEEE Trans. Magn. 47 1522 doi: 10.1109/TMAG.2010.2091495
    [5] Shen D, Du G P, Zeng W, Yang Z J, Li J J 2020 IEEE Access 8 59648 doi: 10.1109/ACCESS.2020.2983612
    [6] Kurs A, Karalis A, Moffatt R, Joannopoulos J D, Fisher P, Soljacic M 2007 Science 31 75834
    [7] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 doi: 10.1103/PhysRevLett.80.5243
    [8] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11 doi: 10.1038/nphys4323
    [9] Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, Xu B, Chen J, Wang J, Fan S, Qiu C W, Alù A, Chen L 2023 Nat. Nanotechnol. 18 706 doi: 10.1038/s41565-023-01408-0
    [10] Feng L, El-Ganainy R, Ge L 2017 Nat. Photonics 11 752 doi: 10.1038/s41566-017-0031-1
    [11] Özdemir K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783 doi: 10.1038/s41563-019-0304-9
    [12] Zhang S M, Jin L, Song Z 2022 Chin. Phys. B 31 010312 doi: 10.1088/1674-1056/ac364a
    [13] 唐原江, 梁超, 刘永椿 2022 物理学报 71 171101 doi: 10.7498/aps.71.20221323 Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101 doi: 10.7498/aps.71.20221323
    [14] 祝可嘉, 郭志伟, 陈鸿 2022 物理学报 71 131101 doi: 10.7498/aps.71.20220842 Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101 doi: 10.7498/aps.71.20220842
    [15] Cao W, Wang C, Chen W, Hu S, Wang H, Yang L, Zhang X 2022 Nat Nanotechnol. 17 262 doi: 10.1038/s41565-021-01038-4
    [16] Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101(R
    [17] Li H, Yin S, Galiffi E, Alù A 2021 Phys. Rev. Lett. 127 153903 doi: 10.1103/PhysRevLett.127.153903
    [18] Yang X, Li J, Ding Y, Xu M, Zhu X F, Zhu J 2022 Phys. Rev. Lett. 128 065701 doi: 10.1103/PhysRevLett.128.065701
    [19] Chen P Y, Sakhdari M, Hajizadegan M, Cui Q, Cheng M M C, El-Ganainy R, Alù A 2018 Nat. Electron. 1 297 doi: 10.1038/s41928-018-0072-6
    [20] Zeng C, Guo Z W, Zhu K J, Fan C F, Li G, Jiang J, Li Y H, Jiang H T, Yang Y P, Sun Y, Chen H 2022 Chin. Phys. B 31 010307 doi: 10.1088/1674-1056/ac3815
    [21] Song M, Jayathurathnage P, Zanganeh E, Krasikova M, Smirnov P, Belov P, Kapitanova P, Simovski C, Tretyakov S, Krasnok, A 2021 Nat. Electron. 4 707 doi: 10.1038/s41928-021-00658-x
    [22] Song M, Belov P, Kapitanova P 2017 Appl. Phys. Rev. 4 021102 doi: 10.1063/1.4981396
    [23] Sakhdari M, Hajizadegan M, Chen P Y 2020 Phys. Rev. Res. 2 013152 doi: 10.1103/PhysRevResearch.2.013152
    [24] Guo Z W, Chen H 2024 Physics 53 33 [郭志伟, 陈鸿 2024 物理 53 33] doi: 10.7693/wl20240104 Guo Z W, Chen H 2024 Physics 53 33 doi: 10.7693/wl20240104
    [25] Miri M A, Alù A 2019 Science 363 7709 doi: 10.1126/science.aar7709
    [26] Ding K, Fang C, Ma G 2022 Nat. Rev. Phys. 4 745 doi: 10.1038/s42254-022-00516-5
    [27] Sample A P, Meyer D T, Smith J R 2010 IEEE Trans. Ind. Electron. 58 544
    [28] Park J, Tak Y, Kim Y, Kim Y, Nam S 2011 IEEE Trans. Antennas Propag. 59 1769 doi: 10.1109/TAP.2011.2123061
    [29] Li Y, Wang M, Zhang W, Zhao M, Liu J 2019 Energies 12 2626 doi: 10.3390/en12132626
    [30] Song M, Baryshnikova K, Markvart A, Belov P, Nenasheva E, Simovski C, Kapitanova P 2019 Phys. Rev. Appl. 11 054046 doi: 10.1103/PhysRevApplied.11.054046
    [31] Lerosey G 2017 Nature 546 354 doi: 10.1038/546354a
    [32] Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387 doi: 10.1038/nature22404
    [33] Guo Z, Jiang H, Li Y, Chen H, Agarwal G. S 2018 Opt. Express 26 627 doi: 10.1364/OE.26.000627
    [34] Fan S H , Suh W, Joannopoulos J D 2003 J. Opt. Soc. Am. A 20 569
    [35] Zhou J, Zhang B, Xiao W, Qiu D, Chen Y 2019 IEEE Trans. Ind. Electron. 66 4097 doi: 10.1109/TIE.2018.2864515
    [36] Assawaworrarit S, Fan S 2020 Nat. Electron. 3 273 doi: 10.1038/s41928-020-0399-7
    [37] Zeng C, Sun Y, Li G, Li Y, Jiang H, Yang Y, Chen H 2020 Phys. Rev. Appl. 13 034054 doi: 10.1103/PhysRevApplied.13.034054
    [38] Guo Z, Jiang J, Wu X, Zhang H, Hu S, Wang Y, Li Y, Yang Y, Chen H 2023 Fundam. Res. 11 2667
    [39] Xie Y, Zhang Z, Lin Y, Feng T, Xu Y 2021 Phys. Rev. Appl. 15 044024 doi: 10.1103/PhysRevApplied.15.044024
    [40] Zhang H, Guo Z, Li Y, Yang Y, Chen Y, Chen H 2024 Front. Phys. 19 43209 doi: 10.1007/s11467-023-1388-x
    [41] Wu Y, Kang L, Douglas H. Werner 2022 Phys. Rev. Lett. 129 200201 doi: 10.1103/PhysRevLett.129.200201
    [42] Hao X, Yin K, Zou J, Wang R, Huang Y, Ma X, Dong T 2023 Phys. Rev. Lett. 130 077202 doi: 10.1103/PhysRevLett.130.077202
    [43] Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404 doi: 10.1103/PhysRevB.99.054404
    [44] Wu H C, Jin L, Song Z 2021 Phys. Rev. B 103 235110 doi: 10.1103/PhysRevB.103.235110
    [45] Peng P, Cao W, Shen C, Qu W, Wen J, Jiang L, Xiao Y 2016 Nat. Phys. 12 1139 doi: 10.1038/nphys3842
    [46] Zhang H, Huang R, Zhang S D, Li Y, Qiu C W, Nori F, Jing H 2020 Nano Lett. 20 7594 doi: 10.1021/acs.nanolett.0c03119
    [47] Ke S, Zhao D, Liu J, Liu Q, Liao Q, Wang B, Lu P 2019 Opt. Express 27 13858 doi: 10.1364/OE.27.013858
    [48] Guo Z, Yang F, Zhang H, Wu X, Wu Q, Zhu K, Jiang J, Jiang H, Yang Y, Li Y, Chen H 2024 Natl. Sci. Rev. 11 172 doi: 10.1093/nsr/nwae172
    [49] Ozaki T, Ohta N, Jimbo T, Hamaguchi K 2021 Nat. Electron. 4 845 doi: 10.1038/s41928-021-00669-8
    [50] Kim H, Yoo S, Joo H, Lee J. An D, Nam S, Han H, Kim D H, Kim S 2022 Sci. Adv. 8 4610 doi: 10.1126/sciadv.abo4610
    [51] Shu J C, Cao M S, Zhang M, Wang X X, Cao W Q, Fang X Y, Cao M Q 2020 Adv. Funct. Mater. 30 1908299 doi: 10.1002/adfm.201908299
    [52] Gutruf P, Krishnamurthi V, Vázquez-Guardado A, Xie Z, Banks A, Su C J, Xu Y, Haney C R, Waters E A, Kandela I, Krishnan S R, Ray T, Leshock J P, Huang G Y, Chanda D, Rogers J A 2018 Nat. Electron. 1 652 doi: 10.1038/s41928-018-0175-0
    [53] Gutruf P, Yin R T, Lee K B, Ausra J, Brennan J A, Qiao Y, Xie Z, Peralta R, Talarico O, Murillo A, Chen S W, Leshock J P, Haney C R, Waters E A, Zhang C X, Luan H, Huang Y G, Trachiotis G, Efimov I R, Rogers J A 2019 Nat. Commun. 10 5742 doi: 10.1038/s41467-019-13637-w
    [54] Lyu H, John M, Burkland D, Greet B, Post A, Babakhani A, Razavi M 2020 Sci. Rep. 10 2067 doi: 10.1038/s41598-020-59017-z
    [55] Yoo S, Lee J, Joo H, Sunwoo S H, Kim S, Kim D H 2021 Adv. Healthcare Mater. 10 2100614 doi: 10.1002/adhm.202100614
    [56] Kim J, Banks A, Xie Z, Heo S Y, Gutruf P, Lee J W, Xu S, Jang K I, Liu F, Brown G, Choi J, Kim J H, Feng X, Huang Y, Paik U Rogers, J A 2015 Adv. Funct. Mater. 25 4761 doi: 10.1002/adfm.201501590
    [57] Khan S R, Pavuluri S K, Cummins G, Desmulliez M P 2020 Sensors 20 3487
    [58] Zhong W X, Lee C K, Ron Hui S Y 2013 IEEE Trans. Ind. Electron. 60 261 doi: 10.1109/TIE.2011.2171176
    [59] Song J, Yang F, Guo Z, Wu X, Zhu K, Jiang J, Sun Y, Li Y, Jiang H, Chen H 2021 Phys. Rev. Appl. 15 014009 doi: 10.1103/PhysRevApplied.15.014009
    [60] Yang F, Song J, Guo Z, Wu X, Zhu, K, Jiang J, Sun Y, Jiang H, Li Y, Chen H 2021 Opt. Express 29 7844 doi: 10.1364/OE.417887
    [61] Zhang L, Yang Y, Jiang Z, Chen Q, Yan Q, Wu Z, Zhang B, Huangfu J, Chen H, 2021 Sci. Bull. 66 974 doi: 10.1016/j.scib.2021.01.028
    [62] Lu L, Joannopoulos J D, Soljacic M 2014 Nat. Photonics 8 821 doi: 10.1038/nphoton.2014.248
    [63] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
    [64] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 doi: 10.1103/RevModPhys.91.015006
    [65] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
    [66] Guo Z, Wang Y, Ke S, Su X, Ren J, Chen H 2024 Adv. Phys. Res. 3 2300125 doi: 10.1002/apxr.202300125
    [67] Guo Z, Zhang T, Song J, Jiang H, Chen H 2021 Photonics Res. 9 574 doi: 10.1364/PRJ.413873
    [68] Zangeneh‐Nejad F, Fleury R 2020 Adv. Mater. 32 2001034 doi: 10.1002/adma.202001034
    [69] Feis J, Solymar L, Shamonina E 2023 J. Appl. Phys. 133 22
    [70] Puchnin V M, Matvievskaya O V, Slobozhanyuk A P, Shchelokova A V, Olekhno N A 2023 Phys. Rev. Appl. 20 024076 doi: 10.1103/PhysRevApplied.20.024076
    [71] Guo Z, Jiang H, Sun Y, Li Y, Chen H 2018 Opt. Lett. 43 51425
    [72] Wu H C, Xu H S, Xie L C, Jin L 2024 Phys. Rev. Lett. 132 083801 doi: 10.1103/PhysRevLett.132.083801
    [73] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025 doi: 10.1016/j.chip.2022.100025
    [74] Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187 doi: 10.1038/nature23280
    [75] Maamache M, Kheniche L 2020 Prog. Theor. Exp. Phys. 12 123A01
    [76] Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J, Alù A, Fan S, Qiu C W 2019 Science 364 170 doi: 10.1126/science.aaw6259
    [77] Yang Y, Wang Y P, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2020 Phys. Rev. Lett. 125 147202 doi: 10.1103/PhysRevLett.125.147202
    [78] Kim D H, Ahn D 2019 IEEE Trans. Power Electron. 35 11391
    [79] Ma W, Liu Z, Kudyshev Z A, Boltasseva A, Cai W, Liu Y 2021 Nat. Photonics 15 77 doi: 10.1038/s41566-020-0685-y
    [80] Genty G, Salmela L, Dudley J M, Brunner D, Kokhanovskiy A, Kobtsev S, Turitsyn S K 2021 Nat. Photonics 15 91 doi: 10.1038/s41566-020-00716-4
    [81] Nadell C C, Huang B, Malof J M, Padilla W J 2019 Opt. Express 27 27523 doi: 10.1364/OE.27.027523
  • 加载中
图( 11)
计量
  • 文章访问数:  681
  • HTML全文浏览数:  681
  • PDF下载数:  10
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-02
  • 刊出日期:  2024-10-20

基于高阶非厄密物理的磁共振无线电能传输研究进展

    通讯作者: E-mail: 2014guozhiwei@tongji.edu.cn; 
    作者简介: 王利凯: 2230977@tongji.edu.cn
  • 1. 同济大学物理科学与工程学院, 教育部先进微结构材料重点实验室, 上海　200092
  • 2. 同济大学电子与信息工程学院, 上海　201804
  • 收稿日期:  2024-08-02

摘要: 近年来, 基于宇称-时间(parity-time, PT)对称的非厄密物理机制在磁谐振式无线电能传输(wireless power transfer, WPT)领域取得了显著进展. 非厄密物理不仅有效地解释了当前WPT领域基于电路理论分析的主要实验结果, 而且为进一步提升WPT器件的传输效率、距径比、鲁棒性等方面提供了全新的原理支撑. 本文主要综述了基于PT对称、高阶PT对称、高阶Anti-PT对称等条件下的高效稳定磁谐振式WPT的研究进展, 揭示了非厄密物理在该领域的独特作用机制及重要应用. 最后对非厄密物理在WPT领域的应用前景进行了展望.

English Abstract

    全文HTML

    1.   引　言

    • 无线电能传输(wireless power transfer, WPT)为人们提供了无需电缆的全新用电方式, 其中非辐射型WPT因其应用场景的通用型以及较高的安全性而受到了人们的广泛关注[1,2]. 传统的磁耦合WPT为纯感应式, 主要基于变压器原理, 通过磁近场耦合进行能量传输. 然而当传输距离增大时, 由于磁感应线在空间中发散非常迅速, 发射线圈和接收线圈间的互感系数会显著降低, 进而极大地限制了感应式WPT的传输距离. 因此, 感应式WPT通常只适用于近距离、同轴、且无异物的场景[3–5]. 而谐振式WPT利用共振耦合原理, 当发射线圈和接收线圈处于谐振状态时, 可以对线圈附近磁感线进行很好的约束, 用以实现中距离、异位(不同轴)和有障碍物的WPT. 2007年, Kurs等[6]首次实现了7 in (1 in = 2.54 cm)大约40%的中距离谐振式WPT, 这是一项极具开创性的工作. 然而, 由于近场耦合的局限性, 导致了谐振式WPT存在稳定性和高效率难以平衡的问题. 一方面, 在近距离(强耦合区)条件下, 它对于距离的变化极其敏感, 强烈的近场耦合会导致工作频率劈裂, 进而严重影响系统的稳定性, 需利用频率追踪技术来维持较高的传输效率. 另一方面, 在远距离(弱耦合区)条件下, 由于本征频率虚部的迅速增长而导致传输效率急剧下降.

      非厄密物理中的宇称-时间(parity-time, PT)对称性为构造具有纯实数本征值的WPT系统提供了全新的物理思路. 1998年, Bender 和Boettcher[7] 指出满足PT对称的非厄密哈密顿量在一个相变点之下, 同样具有纯实数的本征能量, 相关研究结果极大地促进了非厄密物理的发展[8–14]. 利用非厄密物理及PT对称的概念[15–20]可以清晰地解释当前WPT系统局限性的物理起源, 这为实现高性能WPT提供了可能[20–24].

      本文综述了近年来受非厄密物理, 特别是高阶PT对称和Anti-PT对称启发的WPT技术的前沿进展. 主要分为三个部分: 第一部分探讨了在二阶PT对称系统中实现高效WPT的特殊工作模式, 包括利用调谐电路追频来实现高效WPT, 以及利用非线性增益实现自发的二阶PT对称WPT等; 第二部分介绍了三阶PT对称系统和非对称系统、广义PT对称系统以及Anti-PT系统的稳定高效WPT技术; 第三部分讨论了高阶PT对称系统长程稳定WPT技术. 通过引入PT对称, 不仅提升了系统的能量传输效率, 还扩大了传输距离, 减少了能量损耗. 同时, PT对称为设计新的传输方案提供了理论基础和实践指导, 使得WPT技术在实际应用中更加可行和可靠. 因此, PT对称为下一代高性能WPT技术的发展奠定了坚实的基础, 预示着未来在智能家居、医疗设备、电动汽车等领域的广泛应用前景.

    2.   基于二阶PT对称的WPT

      2.1.   感应式到共振式的演化及物理机制

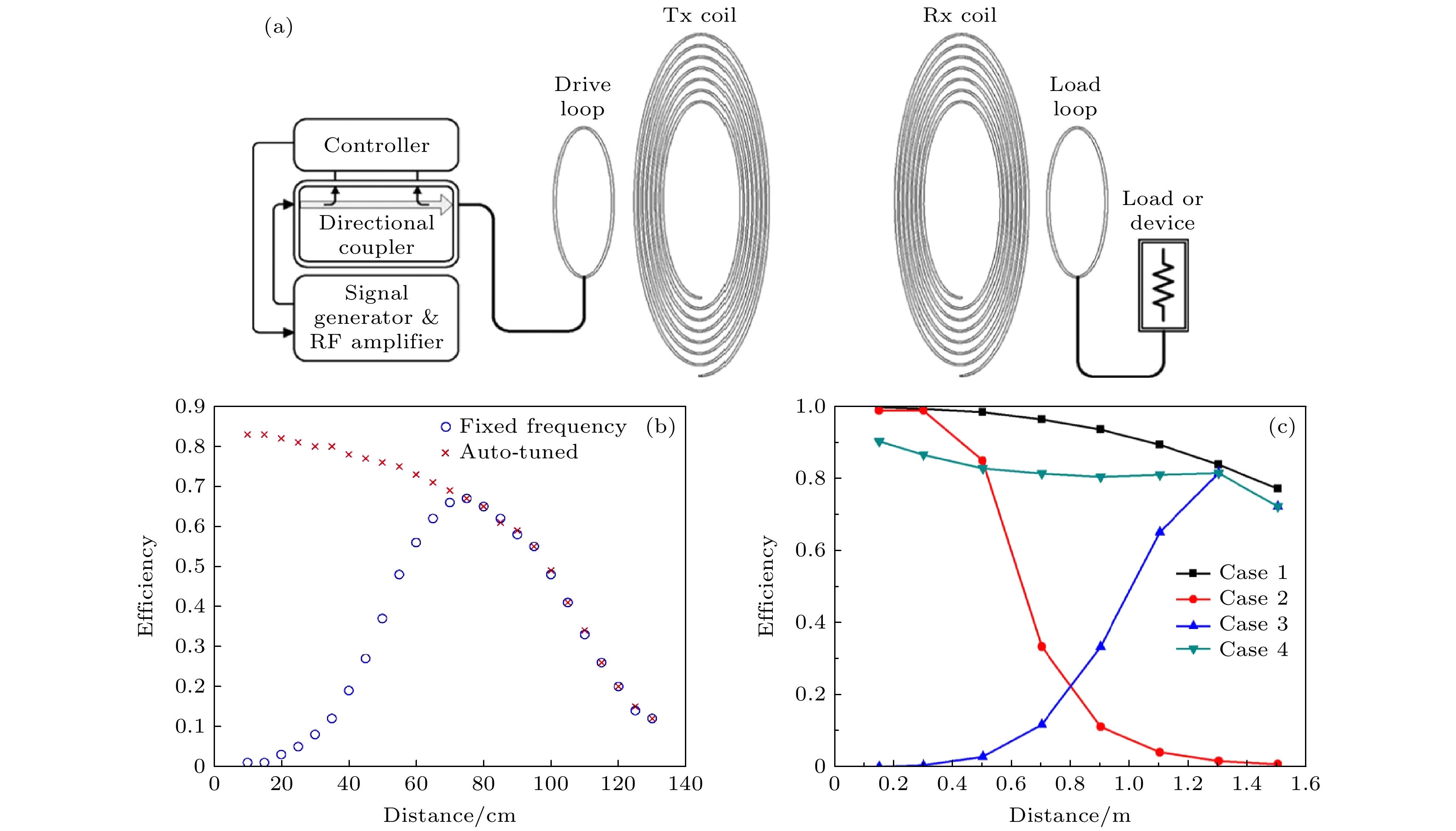
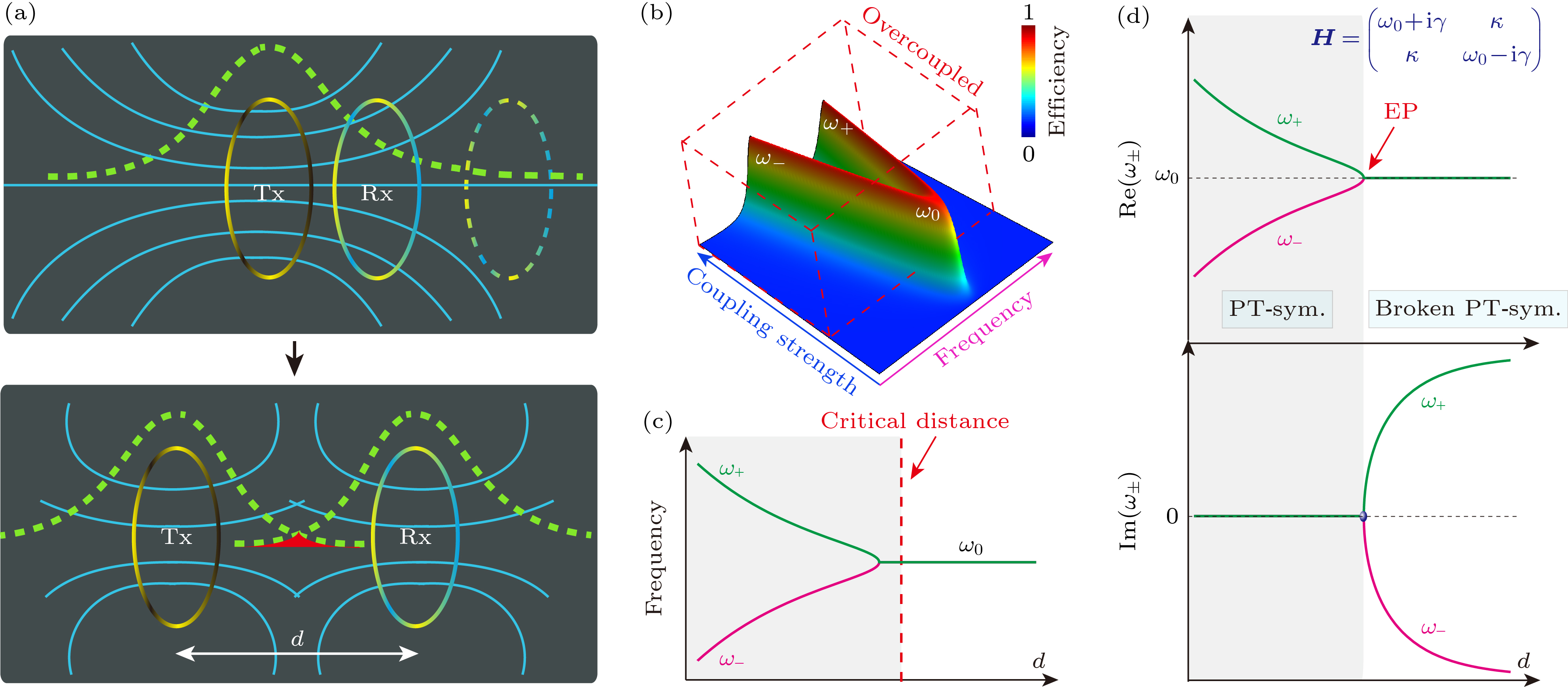
    • WPT技术极大地改变了人们的生产生活方式. 然而, WPT是否能成为一项通用技术, 仍面临一些关键挑战, 如传输距离、传输效率、传输功率及电磁环境等问题亟需解决. 感应式WPT基于电磁感应原理, 其能量主要集中于发射线圈中, 如图1(a)上图所示, 效率受位置偏离的影响剧烈, 通常仅适用于近距离WPT. 而谐振式WPT基于能量耦合原理, 其能量分布于共振的发射(接收)线圈中, 如图1(a)下图所示, 这种方式突破了距离的限制, 可以实现中距离的WPT.

      对于二阶谐振系统, 其频率劈裂现象如图1(b)所示, 色标代表效率强度, 可以看到高效率点总是分布在这两支劈裂的频率上. 图1(c)展示了其随距离变化的二维图. 非厄密物理学的引入可以很好地解释这一现象中的频率劈裂、简并问题. 这里需要强调的是, 频率劈裂现象也可以从阻抗匹配与传输效率角度进行理解. 在电工学里频率劈裂被解释为阻抗匹配条件变化导致的传输效率波动. 结合这两种方法, 可以全面解析频率劈裂现象, 既揭示其物理本质, 又指导WPT系统的优化设计与性能提升. 二阶谐振系统可以简化为图1(d)右上角所示的哈密顿量形式, 通过求解得到的本征频率的实部和虚部分别如图1(d)上图和下图所示. 将频率发生简并的点称为奇异点(exceptional point, EP), 它将相图分成了PT对称相和PT破缺相[25,26]. 利用非厄密物理及PT对称的概念, 可以很好地解释谐振WPT系统的传输特性和局限性的物理本质: 1)传输相的频率劈裂主要是来源于强耦合(过耦合)条件的频率劈裂; 2)对于临界耦合(即EP)可以实现单频传输, 但是鲁棒性弱; 3)弱耦合条件下, 尽管系统工作模式因为固定的实数本征值得以稳定, 但是此时本征值存在虚部, 因此导致了传输效率的下降. 因此非厄密物理和WPT的结合为进一步理解和优化该系统提供了新的思路和方法.

      • 2.2.   利用调谐电路追踪纯实本征频率

    • 通过在系统中加入合适的控制电路, 可以在强耦合区实现较理想的传输功率和传输效率, 使系统能够自动追踪最大效率对应的工作频率, 而无需精确的手动调节[27]. 利用系统在强耦合区频率劈裂的特性, 在放大器和驱动环路之间引入定向耦合器, 如图2(a)所示. 发射系统通过连续测量入射和反射功率随频率的变化来实现动态调节. 由于该系统形成了传输线, 未被负载消耗或寄生电阻损耗的功率会被反射回发射端.

      图2(b)为固定频率$ {f_0} = 7.65{\text{ MHz}} $和自动频率调节情况下传输效率随距离变化的曲线图. 当启用频率调谐时, 控制器拾取最大谐振峰, 并随着接收器远离发送端而进行追踪. 从图2(b)中可以看出, 与固定频率的情况相比, 频率追踪在强耦合区内系统的传输效率显著提升. 随着距离的增加, 效率缓慢下降, 直到临界耦合点, 两种模式融合, 系统进入弱耦合区.

      另外, 还有一种基于将自适应阻抗匹配与自动追频相结合的方法, 可有效提高弱耦合区的传输效率[28]. 具体来说, 该方法不设定输入端的输出阻抗为50 Ω, 而是设置为目标距离下的最佳阻抗, 然后利用追频电路进行能量传输. 具体的实验分为以下4种情形, 结果如图2(c)所示. 情形1: 频率固定, 同时满足匹配条件的实验; 情形2: 采用50 Ω负载阻抗的频率追踪方法; 情形3: 实验频率固定, 设定最佳负载阻抗在1.5 m处; 情形4: 采用改进的频率追踪法, 并设定最佳负载阻抗为1.5 m处. 可以明显看到, 情形1所实现的传输效率最高, 但其要求时刻针对距离变化时满足阻抗匹配条件, 这在实际应用中很难实现. 情形2中仅在强耦合区是有效的, 在强耦合区外传输效率急剧下降. 情形3也仅在接近1.5 m目标距离时传输效率较高. 而情形4, 即改进的频率追踪方法, 在目标距离为1.5 m以内均具有较高的传输效率.

      • 2.3.   利用非线性PT电路实现自动追频

    • 如果可以在保持高效率的同时消除主动调谐的需求[29], 将大大拓宽WPT技术的应用领域, 例如行驶中车辆的动态充电[30,31]. 本节主要介绍如何利用PT对称和非线性饱和增益相结合的物理机制, 自动选择最大传输效率对应的工作频率, 从而在较远的传输距离范围内实现最优传输效率, 而无需像之前方案进行任何主动调谐[27].

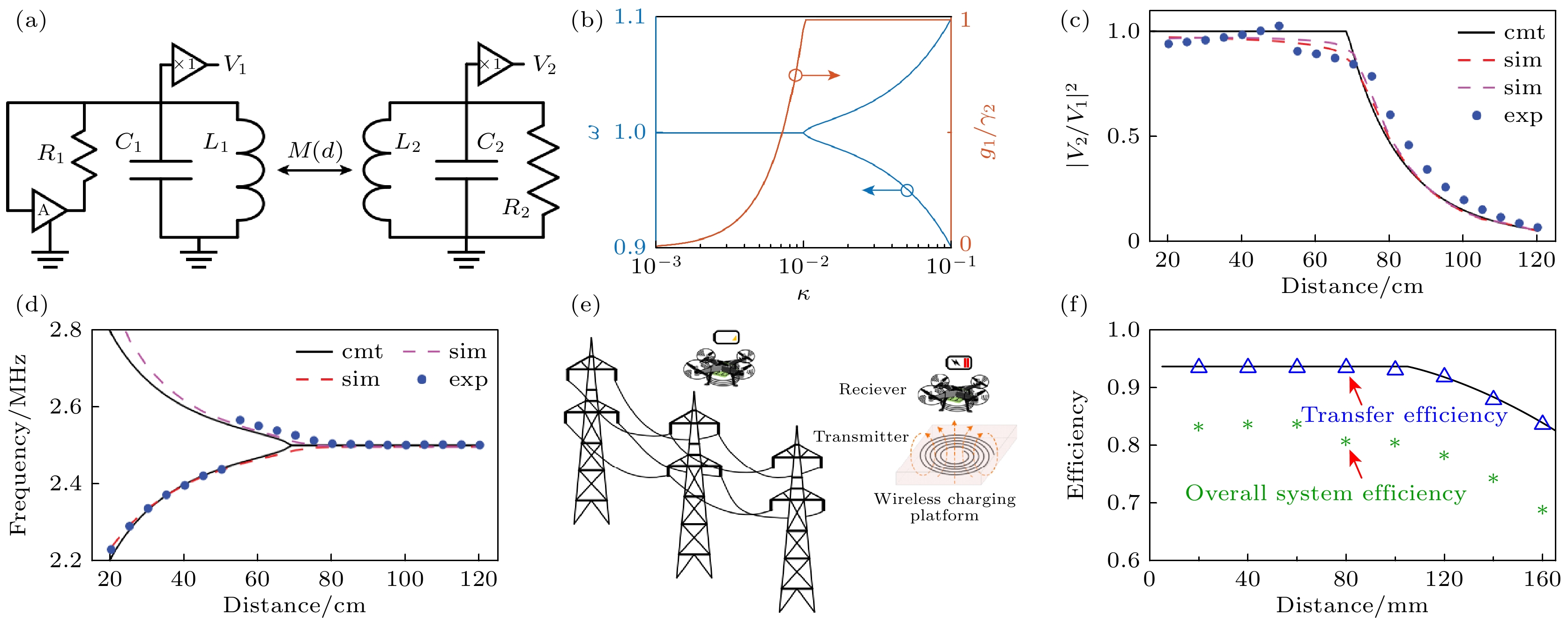
      之前的方案为了保证最优的传输效率, 必须时刻调整源输入输出耦合强度或工作频率, 以适应传输距离的变化. 而这里提出的包含非线性饱和增益的PT对称电路, 作为设备损耗的时间反演对应项[32], 有效地解决了这一问题. 该电路中的非线性饱和增益元件由电压放大器A和反馈电阻${R_1}$组成, 如图3(a)所示的全电路模型的源侧增益元件提供了负电阻. 图3(b)显示了PT对称和非线性饱和增益相结合的物理机制可以自适应选择最大效率对应的工作频率, 从而保证在较远的传输距离范围内实现最优传输效率.

      进一步地, 为了更具体地理解如何利用PT对称和非线性饱和增益实现WPT, 基于电路模型分析了由源谐振器耦合到接收谐振器的双谐振系统. 这里采用的是PP电路模型, 源谐振器和接收机谐振器的固有谐振频率均为${\omega _1}$, 两个谐振器以互感M耦合, 其中M是源到接收器之间距离的函数. 能量通过耦合传输到接收器之前是通过其增益元件直接馈入源.

      根据基尔霍夫方程可得

      其中下标t(或R)表示源(或接收器); ${U_{{\text{in}}}}$定义为输入电压值, 系统的传输效率用电压比来表示, 如图3(c)所示.

      根据耦合模理论和电路方程的关系, 其系统动力学方程描述为

      类似于线性PT系统, 在$\kappa ={\gamma _2}$处也观察到模态频率实部的劈裂(图3(b)中蓝色线段). 匹配共振${\omega _1}={\omega _2}={\omega _0}$, 且非线性饱和增益${g_1}$初始值需要略大于接收器谐振器的损耗${\gamma _2}$, 此时系统处于稳态时的传输效率也可以用耦合模公式表示为[33,34]

      从(2b)式可以看到的是, 系统在强耦合区($\kappa > {\gamma _2}$)时, 传输效率是一个与耦合强度无关的常数. 因此, 传输效率对传输距离或方向的波动具有鲁棒性, 而这两者均可以改变$\kappa $. 其传输效率与传统的基于两个谐振器的最优效率(其需对每个$\kappa $值进行频率调谐)相匹配. 这里利用非线性饱和增益实现的PT对称稳态强耦合区, 自动实现了最佳工作频率的WPT. 当系统工作在弱耦合区时, 传输效率会随着耦合强度的减小而降低. 将该机制应用于无人机的WPT技术[35], 其模型如图3(e)所示. 其传输效率如图3(f)所示, 其中耦合的原副边效率可达90%以上, 整体效率则维持80%以上.

      为解决运算放大电路的低效增益元件存在固有损耗而导致系统的总效率较差的问题, 提出了一种使用低功耗开关型与电流敏感反馈放大器的PT对称电路. 在这个电路中, PT对称性确保了有效负载阻抗放大器保持不变, 从而使系统在传输距离变化时仍能维持高传输效率[36].

    3.   基于三阶PT以及Anti-PT对称/非对称WPT

      3.1.   三阶PT对称

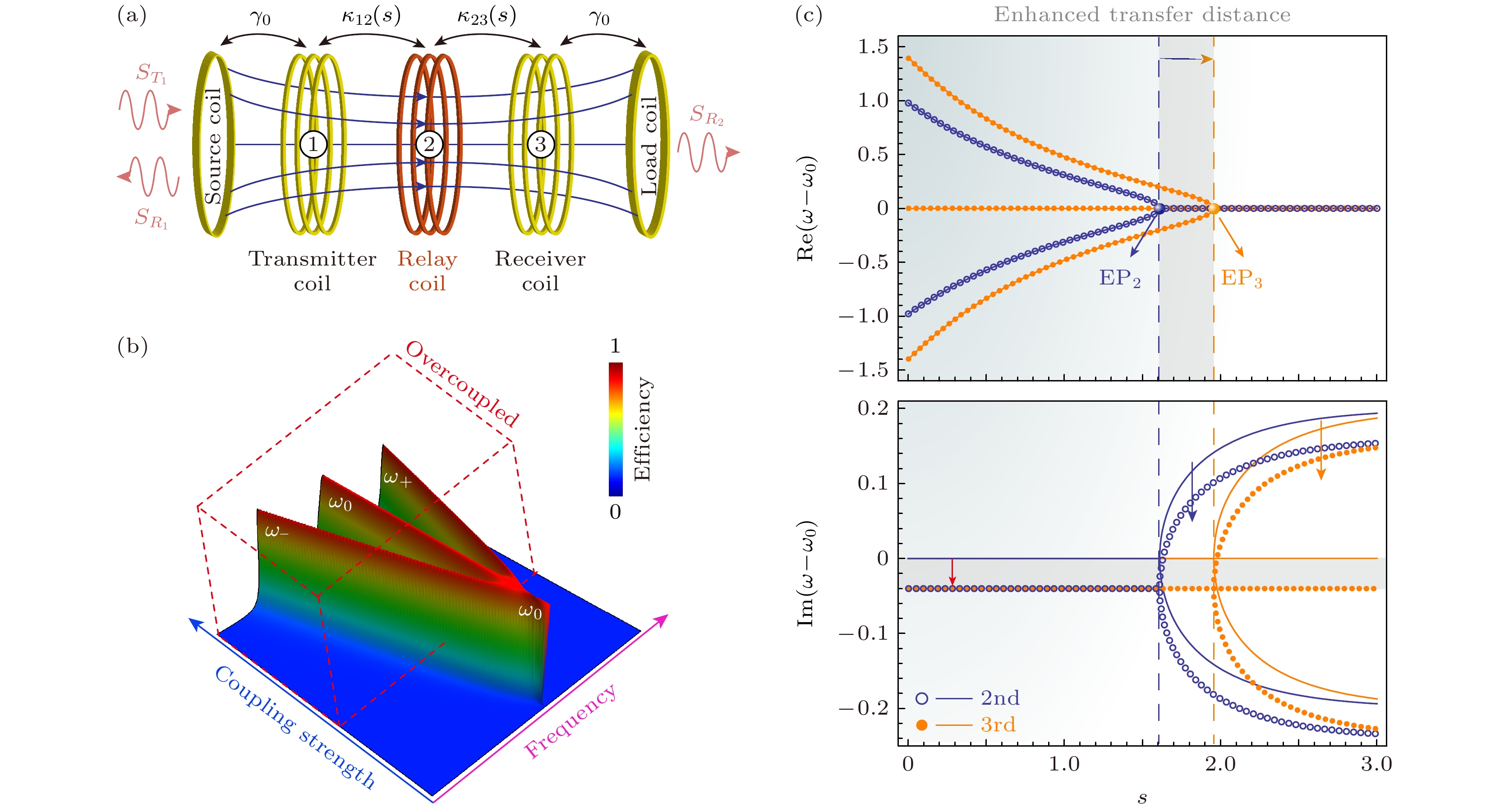
    • 在标准的三阶PT对称系统中, 始终存在一个纯实本征频率不随距离的变化而改变, 这对于高效WPT是十分有利的[23,37]. 其标准模型如图4(a))所示, 通过基尔霍夫方程计算其传输效率与频率和耦合强度的变化关系如图4(b)所示. 其哈密顿量为形式为

      如(3)式所示, 当${\gamma _1}={\gamma _2}=\gamma $时求解特征方程可得系统的本征频率为

      从图4(c)可以明显看到, 相比较于二阶系统, 三阶系统中存在不随距离改变的纯实本征频率, 这是一种无需频率追踪的高效实用的WPT技术[38].

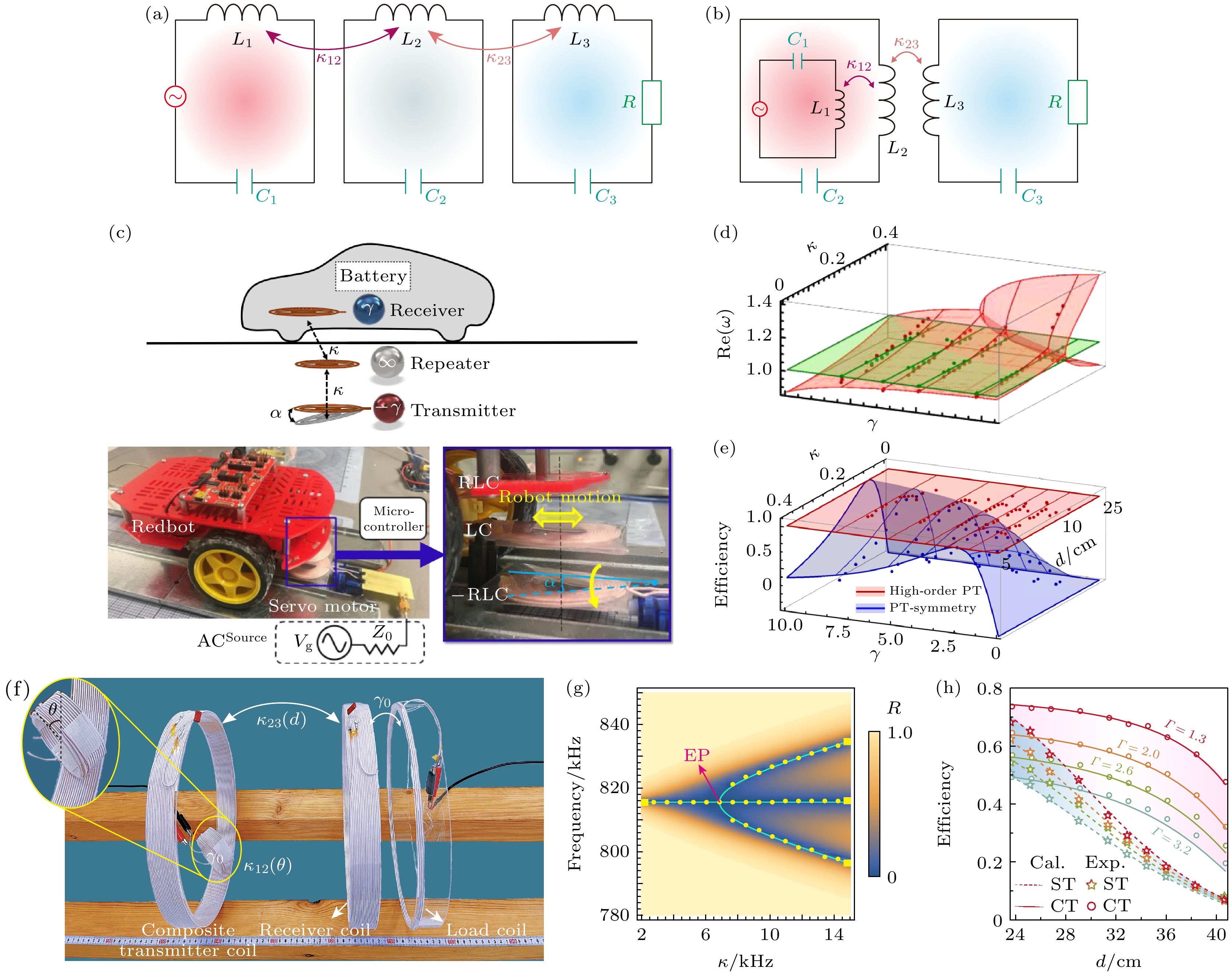
      接下来考虑三阶PT对称系统的实际应用, 三阶WPT系统电路模型如图5(a)和图5(b)所示, 二者分别为分立型三阶WPT系统和合成型三阶WPT系统. 二者的基本原理是相同的, 但合成型系统极大地减少了体积, 增加了一定的自由度. 它们的基尔霍夫方程可写为

      当考虑${\kappa _{12}}={\kappa _{23}}=\kappa ({M_1} = {M_2} = M)$的对称情况时, 其系统构成一个标准的三阶PT对称系统. 通过适当近似和变换后可得其等效哈密顿量如(3)式所示. 其中图5(e)为分立型系统在小车无线充电中的实际应用, 发射线圈和中继线圈被固定在地面之下, 而接收线圈则被安装在小车上. 通过调整合适的距离(耦合), 可以实现对小车的高效WPT. 图5(d)展示了三阶系统的实部随耦合和损耗变化的相图, 图5(e)对比了高阶(三阶)系统和二阶系统的传输效率, 其中上面的小球代表实验结果. 图5(f)为图5(b)电路的实验图, 和图5(c)不同的是, 这里发射线圈和中继线圈被集成在一个线圈中, 通过调节二者之间的角度改变${\kappa _{12}}$使它和${\kappa _{23}}$保持相等. 相较于前者, 这种设计减少了整体体积, 并使调节更为灵活, 更适用于小微装置的WPT. 图5(g)为系统反射率与耦合和工作频率的关系, 在系统的三支本征频率上反射率接近为零. 实验测得系统传输效率在不同本征损耗下随距离变化关系如图5(h)所示.

      • 3.2.   三阶PT非对称系统的BIC

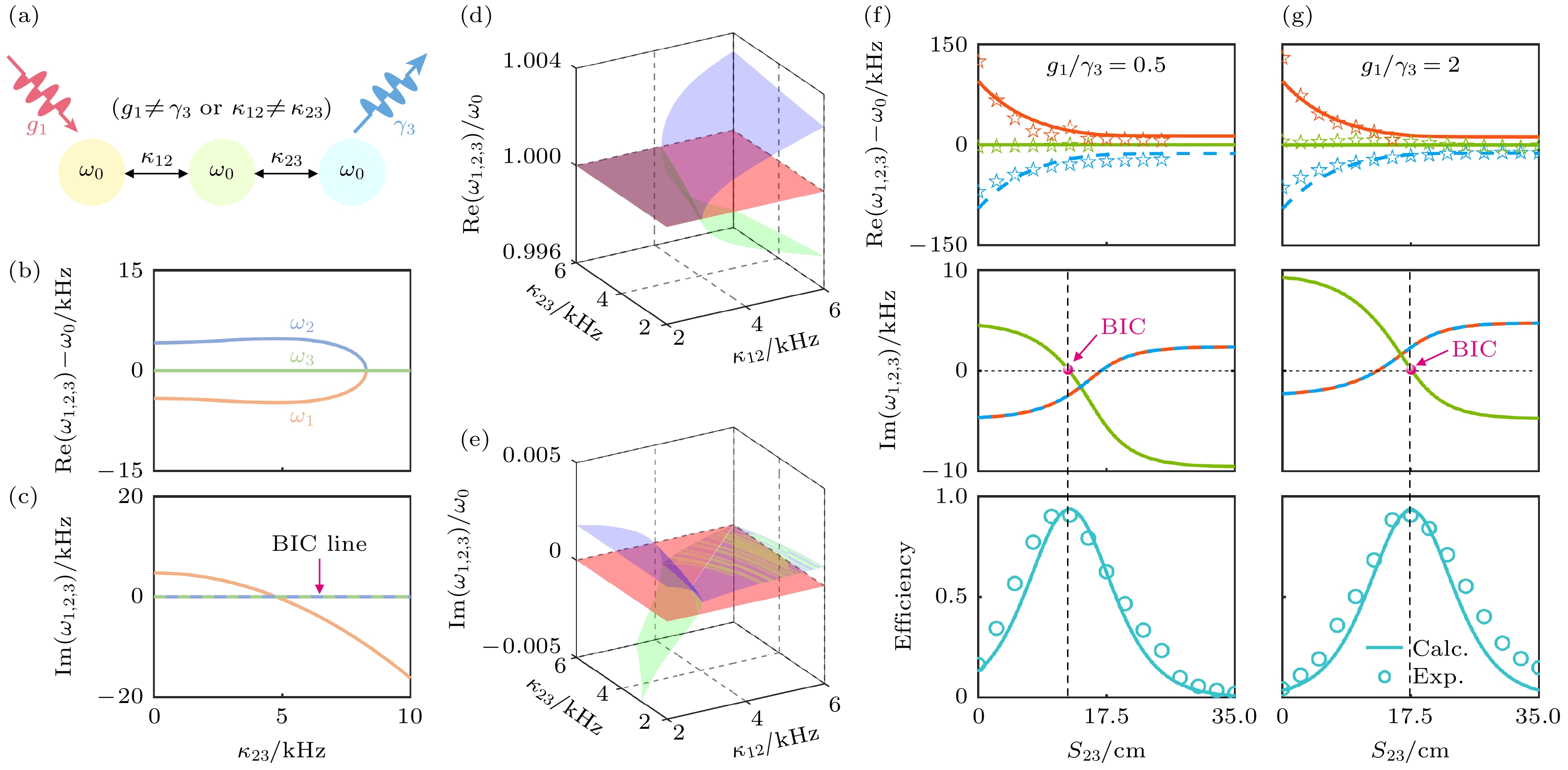
    • 在PT对称破缺相中, 由于本征频率虚部的存在, 传输效率的下降一直是一个棘手的问题. 而这里借助隐藏在PT非对称系统弱耦合区域连续域中的束缚态(bound states in the continuum, BIC)模式可以实现高效稳定的WPT, 打破了PT对称具有平衡增益和损耗的严格限制. 考虑一个三阶PT非对称(损耗不等于增益或者耦合不相等)WPT系统, 如图6(a)所示, 其中谐振线圈间通过近场电磁相互作用耦合, 发射线圈以速率${g_1}$接收能量输入(发射器), 中继线圈传递能量, 接收线圈向负载(接收器)以速率${\gamma _3}$提供能量. 其哈密顿量可描述为

      为满足BIC条件, 系统需满足内在条件:

      在固定${\kappa _{12}}$只调节${\kappa _{23}}$的情况下, 此类系统的本征频率的实部和虚部分别如图6(b)和图6(c)所示, 其始终存在一条BIC线. 图6(d)和图6(e)分别为系统在PT非对称时本征频率实部和虚部随耦合${\kappa _{12}}$和耦合${\kappa _{23}}$演化的情况. 图6(f)和图6(g)分别为增益小于损耗和增益大于损耗时, 本征频率实部, 虚部和系统传输效率随耦合强度的演化. 可以看到, 当满足BIC条件时, 系统将呈现良好的阻抗匹配, 从而实现高效稳定的WPT[39,40]. 在进一 步调控和优化BIC模式以实现高效WPT的过程 中, 关键在于精确调整增益、损耗以及耦合强度等系统参数以满足BIC条件. 比如可以通过采用可调控的增益和损耗元件, 结合反馈控制系统实时 调整参数值, 确保系统处于最佳工作状态. 同时, 优化耦合配置, 确保谐振器之间的互感系数精确且稳定.

      • 3.3.   广义PT对称系统

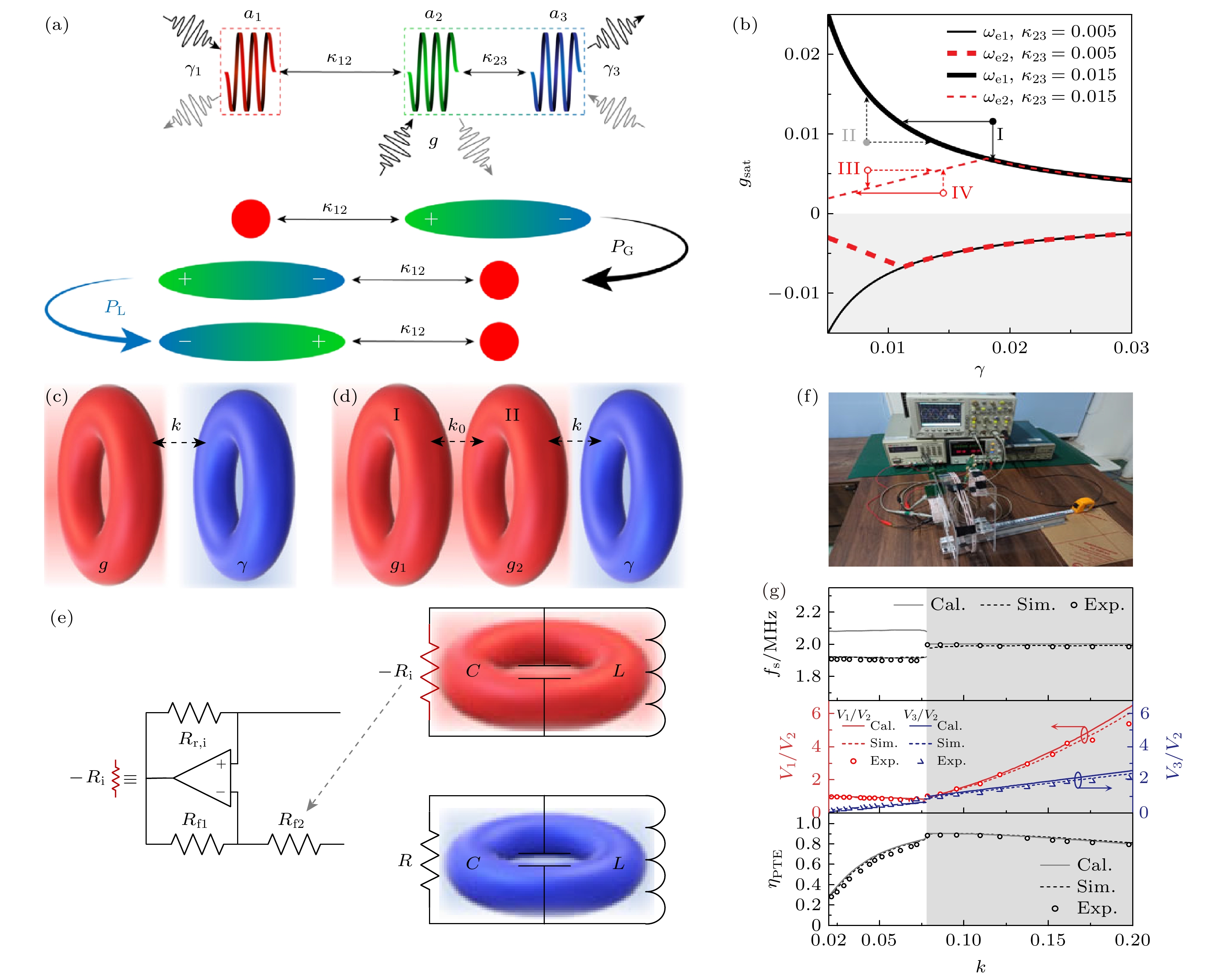
    • 利用动态饱和增益[41], 可在不平衡(非 PT 对称)高阶WPT系统中实现广义 PT(generalized PT, GPT)对称. 从演化的角度来看, 三体WPT系统可以被视为广义的两体WPT系统, 特别是当$ {\kappa _{12}} \ne {\kappa _{23}} $时. 如图7(a)所示, Tx被类比为具有正输入速率(增益)的“单极子”(红色球体), 而Ix和Rx被共同类比为一个“偶极子”, 其极性由两极的不平衡输入和输出(通常情况下$g \ne \gamma $)定义. 因此, 广义宇称反转操作$\hat P$可以直观地分解为全局宇称反转(${\hat {\boldsymbol{P}}_{\text{G}}}$)和局部宇称反转(${\hat {\boldsymbol{P}}_{\text{L}}}$). ${\hat {\boldsymbol{P}}_{\text{G}}}={\sigma _x}$是基于单极子和偶极子之间的位置反转($\hat {\boldsymbol{P}}_{\text{G}}^\dagger {\hat {\boldsymbol{r}}_{\text{G}}}{\hat {\boldsymbol{P}}_{\text{G}}} = - {\hat {\boldsymbol{r}}_{\text{G}}}$对应$\left[ {1, (2, 3)} \right] \to \left[ {3, (1, 2)} \right]$), ${\hat{\boldsymbol{ P}}_{\text{L}}}={\sigma _x}$反转偶极子的两极($ \hat {\boldsymbol{P}}_{\text{L}}^{\text{\dagger }}{\hat {\boldsymbol{r}}_{\text{L}}}{\hat {\boldsymbol{P}}_{\text{L}}} = - {\hat {\boldsymbol{r}}_{\text{L}}} $对应$ (2, 3) \to (3, 2) $), 且同时满足$ {\hat {\boldsymbol{T}}^\dagger }{{t}}\hat {\boldsymbol{T}} = - t $. 三体系统的哈密顿量可写为

      其中局部${H_{\text{L}}}$描述了在局部坐标定义下的偶极子内部相互作用. 与二体WPT系统相比, 三体拓扑等效于在一个极点嵌入局部二体系统的全局二体拓扑, 这表明GPT对称三体拓扑和PT对称二体拓扑在全局上是等效的.

      此外, GPT 对称态可被描述为高维参数空间$\left( {\gamma , g, {\kappa _{12}}, {\kappa _{23}}} \right)$中的带内稳态, 其具有饱和增益${g_{{\text{sat}}}}$. 相对于带内GPT对称态, 可以利用能带理论来充分解释参数空间中的不完美态[30]. 这里设置${\kappa _{12}}= 0.01$, $ {\kappa }_{23}=0.005, \text{ }0.015 $, 如图7(b)所示包含两个耦合区域, 上半部[下半部(灰色))]表示在Rx主导(Tx主导)的耦合${\kappa _{12}} < {\kappa _{23}}$(${\kappa _{12}} > {\kappa _{23}}$). 黑色(红色虚线)曲线表示第一稳态的${g_{{\text{sat}}1}}(\gamma )$(第二和第三稳态${g_{{\text{sat}}2, 3}}(\gamma )$). 对于${\kappa _{12}} < {\kappa _{23}}$的情况, 当$g(\gamma ) = {g_{{\text{sat}}}}(\gamma )$时, 系统在具有最大传输效率的能带(黑线)上工作, 而其他态则处于效率折中的带外态. 具体来说, 第一个带外态由黑点(I)表示, 对应于$\gamma $和$g$的过饱和参数, 被定义为过饱和态, 它可以被认为是由速率为$g$的外部刺激诱导的“激发态”. 该态可以通过“受激发射”($g$减小, 由向下的黑色实线箭头指示)或“动量匹配”($\gamma $减小, 由向左的黑色实线箭头指示)转变为带内“基态”. 相反, 由灰点(II)表示的态被归类为不饱和态, 其在没有额外的“馈源”的情况下不能直接过渡到为带上态. 此外, 当系统满足$g(\gamma ) > {g_{{\text{sat}}}}(\gamma )$, $\gamma (g) < {\gamma _{{\text{sat}}}}(g)$或$g(\gamma ) < {g_{{\text{sat}}}}(\gamma )$, $\gamma (g) > {\gamma _{{\text{sat}}}}(g)$ (图7(b)中分别为红色圆圈(III)和(IV))时, 它处于杂化态或半饱和态. 当${\kappa _{12}} > {\kappa _{23}}$时, 可以实现类似的分析. GPT 对称性可以显着提高不平衡耦合条件下WPT系统的鲁棒性和传输效率[41], 其在强耦合区域和弱耦合区域均具有最佳传输效率.

      在实验上则通过非线性增益饱和元件组成实现了三阶赝厄密(GPT)双发射-单接收WPT系统[42]. 在不同的耦合系数下, 系统仍具有真实的本征频率. 其在强耦合区始终存在一支本征频率不随耦合系数变化. 首先考虑从标准的二阶PT对称WPT系统(图7(c)构造三阶WPT系统, 其哈密顿量是三对角矩阵. 根据耦合模理论, 二阶PT对称系统的哈密顿量可以写为

      其中$ {H_{11}} = H_{22}^ * = {\omega _0}(1 + {\text{i}}\gamma ) $. 如果元素${H_{11}}$或${H_{22}}$被替换为与${H_{{\text{std}}}}$形式相同的二阶矩阵, 并且仅考虑相邻谐振器的耦合, 即$ {H_{21}} = H_{12}^{\text{T}} = \left[ {{\kappa _{13}}, {\kappa _{23}}} \right] $(${\kappa _{13}} = 0$), 就可以得到三阶系统, 其可以由图7(d)所示的双发射-单接收系统组成. 由于每个谐振器可以是有增益的、有损的或无损的, 因此相应的哈密顿量一般是非厄密对称矩阵, 其对角线元素可以是复数并且非对角线元素都是实数. 图7(d)系统的哈密顿量表示为

      这里, ${g_1}$和${g_2}$分别表示发射谐振器I和II中的增益强度; $\gamma $是接收谐振器的损耗常数; ${\kappa _0}$表示两个增益谐振器之间的耦合系数; $\kappa $表示发射谐振器II和接收谐振器之间的耦合系数. 所有谐振器的固有谐振频率被调谐为${\omega _0}$. 此外, 即使它不是 PT 对称的, (10)式仍然可以具有实本征值[43]. 通过求解特征方程, 在强耦合区即$\kappa \geqslant \gamma $, 存在三个模式, 其对应的本征值为

      $\tilde \kappa =\kappa _0^2{+}{\kappa ^2}{+}{g_1}{g_2} - \gamma ({g_1} + {g_2})$, $c = {g_1} + {g_2} - \gamma $. 当满足$ ({g_1}{g_2} + \kappa _0^2)\gamma = {\kappa ^2}{g_1} $时, 无论${\omega _{2, 3}}$是复数还是实数, 均可存在$\omega ={\omega _1}$, 从而提供了很大的设计自由度. 当$\kappa < \gamma $时, 弱耦合区中只存在两个实本征值, 对应的本征频率为

      ${\omega _1}={\omega _0} - {{{\text{i}}c} {/ } 2}$表示不稳定态, 当满足$( {g_1}{g_2}\gamma + \kappa _0^2\gamma - {\kappa ^2}{g_1} ){c^{ - 1}} = - \tilde \kappa $时, 支持弱耦合下的稳频模式. 因此, 可以通过改变$\gamma $和${\kappa _0}$来控制耦合区域, 从而使相变与负载无关.

      接下来通过电路仿真对两发射一接收系统的实验进行验证, 其实验装置示意图如图7(f)所示. 所有线圈的谐振频率均为2 MHz, 初始增益分别为${g_{1 i}} = 0.113$和${g_{2 i}} = 0.005$. 由于${\omega _{2, 3}}$是复数, 因此在强耦合区域中仅呈现单个稳态$ {\omega _1}={\omega _0} $. 图7(g)显示了稳态工作频率${f_{\text{s}}}$、谐振器电压比以及功率传输效率${\eta _{{\text{PTE}}}}$与耦合系数$\kappa $的关系. 实验结果与模拟和理论结果吻合良好. 当耦合系数$\kappa $在强耦合区域从0.078变化到大约0.2时, 无需对电路进行任何调谐, 工作频率始终保持在大约2 MHz. 且在强耦合区域, 系统具有几乎稳定的传输效率. 此外, 随着$\kappa $的增加, 由于过耦合, 效率会略有下降. 仿真和实验结果都表明稳态频率在$\kappa =\gamma $附近发生转变, 这表明系统中存在频带间隙. 由于谐振器的振幅比在转变点$\kappa =\gamma $处不连续, 因此传输效率出现轻微的突变. 这种转变只会在弱耦合区域引起频率和效率的微小变化, 不会影响WPT系统的稳定运行. 通过优化损耗常数$\gamma $和/或耦合系数${\kappa _0}$, 可以进一步提高所提出的系统的效率和鲁棒性. 此外, 对于有损线圈, 假设附加增益${g_2} = - {\gamma _{{\text{s}}2}}$, 只要发射器的增益为${g_1} = {{\kappa _0^2\gamma } {/ } {\left( {{\kappa ^2} + {\gamma _{{\text{s}}2}}\gamma } \right)}}$, 就可以实现频率稳定的三线圈WPT系统.

      • 3.4.   三阶Anti-PT对称:“能级钉扎”效应

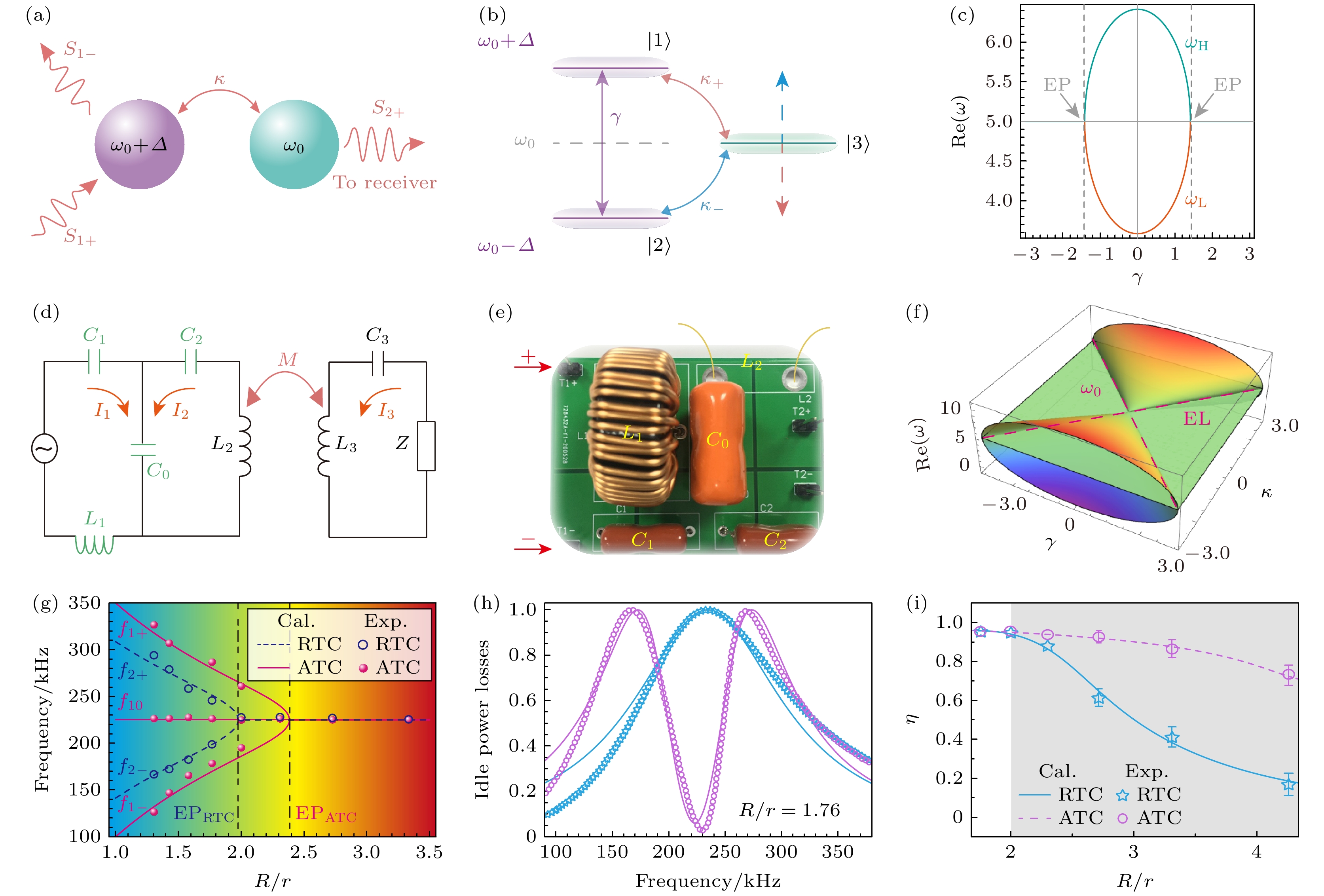
    • 之前的WPT系统大都是在PT对称的条件下进行研究的, 而在Anti-PT对称的条件下($(PT)\boldsymbol{H}(PT)^{-1} = -\boldsymbol{H}$)实现高效能量传输的讨论较少[44–47]. 这里介绍一种新的具有反谐振发射器的磁共振WPT方案[48] , 它的物理模型如图8(a)所示, 与典型方案“RTC-NFC-RRC”不同, 其中RTC(resonance transmitter coil), NFC(near-field coupling)和RRC(resonance receiver coil)分别表示谐振发射器线圈、近场耦合和谐振接收器线圈. 这里基于近场耦合的关键配置对应“ATC-NFC-RRC”, 其中ATC(anti-resonance transmitter coil)表示反谐振发射线圈. 在由ATC和RRC构成的等效非厄密WPT系统中构建了具有“能级钉扎”效应的三阶Anti-PT对称系统. 这里的“能级钉扎”源自两种近场耦合机制的竞争抵消. 1)反共振模式的“能级吸引”: 随着发射端两个模式间的虚耦合$\gamma $(即耗散耦合)增强, 失谐的两个模式(对应透射峰)逐渐接近, 表现出“能级吸引”; 2)反共振模式和共振模式的“能级排斥”: 随着发射端-接收端两个模式间的实耦合$\kappa $(即相干耦合)增强, 劈裂的两个模式(对应透射峰)逐渐远离, 表现出“能级排斥”. 正是系统“能级吸引”和“能级排斥”的竞争抵消导致了新奇的“能级钉扎”效应(如图8(b)所示). 这里的耗散耦合和相干耦合分别对应LRC电路中的阻性耦合和容性(感性)耦合(如图8(d)). 在Anti-PT对称系统中, “能级钉扎”效应由于具有稳定性, 所以系统在动态变化场景下的高效WPT也可以得以保证, 其主要归因于耗散耦合与相干耦合之间的动态平衡. 这种平衡机制通过抵消不同耦合类型对工作频率的影响, 确保系统在外部环境变化时维持固定的工作频率.

      系统的基尔霍夫方程可写为(其中源${U_1} = - IZ$):

      令${L_1} = {L_2} = {L_3} = L$, ${C_3} = C$, ${1}/{C} = {1}/{{{C_1}}} + {1}/{{{C_0}}}$, 由电路方程与耦合模公式间关系[33], (13)式改写为

      这里$M=\xi L$表示合成的ATC和TC的互感; $\xi = {{ - C} {/ } {{C_0}}}$为不同负载的耦合因子, 可得到ATC和RC耦合系统的动力学方程. 用幺正变换及${a_3} = {a_0}$, 系统的动力学方程可表示为

      假定$\varDelta ={1 {/ } {2\omega {C_0}L}}$以及${\gamma _0} = {{ - Z} {/ } {(2 L)}}$, 即可得到(15)式所示的哈密顿量:

      正是由于非对角项中的实部和虚部耦合系数使得系统的哈密顿量满足Anti-PT对称条件, 从而使得纯实本征频率可用于有效的能量传输. 通过求解系统哈密顿量(16)式可以得到本征频率为

      其中$A = 3\left( {4\gamma - {\varDelta ^2} - 2{\kappa ^2}} \right)$, $ B = 54\gamma \left( {{\varDelta ^2} - 2{\kappa ^2}} \right) $.

      由于竞争耦合的存在, 谐振频率处的工作频率锁定总是会发生“能级钉扎”, 而一般非厄密系统的纯实本征值是无法保证的. 这里其本征频率实部随耗散耦合的演化如图8(c)所示. 特别地, 当耗散耦合不为零时, 由(17)式可以确定在${\omega _0}$处的纯实本征频率的条件为$\varDelta =\sqrt {2\kappa } $. 因此, 系统中两种不同类型耦合的共存至关重要. 一方面, 它们之间的竞争抵消导致了“能级钉扎”, 保证了工作频率稳定. 另一方面, 由哈密顿量(16)式得到, 实(虚)耦合系数是构成Anti-PT对称WPT系统的关键组成部分, 保证了在工作频率$ \omega ={\omega _0} $下基于纯实本征值的高效能量传输.

      实验上选取了合成反谐振WPT系统与传统谐振WPT系统作为对比, 图8(g)为实本征频率, 图8(i)为传输效率[38]. RTC (ATC) WPT系统的计算和测量结果分别由蓝色实线(粉红色虚线)和蓝色五角星(粉红色圆)显示. 从图8(e)可以看到与采用不同半径比${R {/ } r} = 1.76\left( {2.31} \right)$系统的工作频率分别为198.3 kHz(225 kHz). 与追踪最佳工作频率的RTC情况不同, 合成Anti-PT对称的WPT系统的工作频率始终固定225 kHz, 并且ATC系统的实本征频率在${R {/ } {r = 2.41}}$的EP ATC处简并. 而对于RTC情况, 本征频率在${R {/ } {r = 1.98}}$的EP RTC处会发生简并, 而$ {R {/ } r} $偏离这一临界值会导致传输效率迅速下降. 在相同频率下, ATC系统中EP的半径比大于RTC系统. 此外, 由图8(f)所示, 新型三阶Anti-PT对称WPT系统的传输效率比较稳定. 而在传统谐振WPT系统中, 当系统对应于弱耦合区域时, 传输效率急剧下降, 如阴影区域(${R {/ } {r = 1.98}}$). 并且基于RTC(ATC)的谐振(反共振)WPT系统的待机功率损耗的计算及实验结果如图8(e), 分别用实心青(紫)线和青(紫)符号表示. 可以明显看出, Anti-PT对称WPT系统在工作频率附近的待机功率损耗明显小于共振情况[15]. 这有利于无线间歇充电, 在实际应用中具有更好的安全性. “反共振-共振”型WPT具有更高的安全性、稳定性、传输效率和灵活性, 此外兼具更低的待机功率损耗. 因此具有Anti-PT对称性的三阶非厄密WPT系统为研究比传统谐振WPT方案具有更高性能(更高的传输效率和更低的待机功率损耗)的非厄密WPT提供了良好的平台.

    4.   基于高阶PT对称的WPT

      4.1.   耦合链的WPT: 多中继线圈(五聚体)实现长距离传能

    • 目前的WPT系统的理想传输距离大多有限, 且易受运行环境变化的影响, 这极大地阻碍了其在动态环境中的应用[23,49]. 为了克服这些局限性, 这里介绍了一种具有PT对称性的中继单元横向排列的WPT系统, 该系统可以在中继单元个数为N的情况下拓宽工作区域[50], 实现长距离能量传输. 与传统的多输入单输出WPT系统相比, 这种新系统由于中继单元的幅值仅由耦合电容控制, 显著降低了系统复杂度. 同时, 工作频率自动调整为PT对称系统的实本征值, 从而实现高电压增益和高传输效率, 使系统具有更强的鲁棒性.

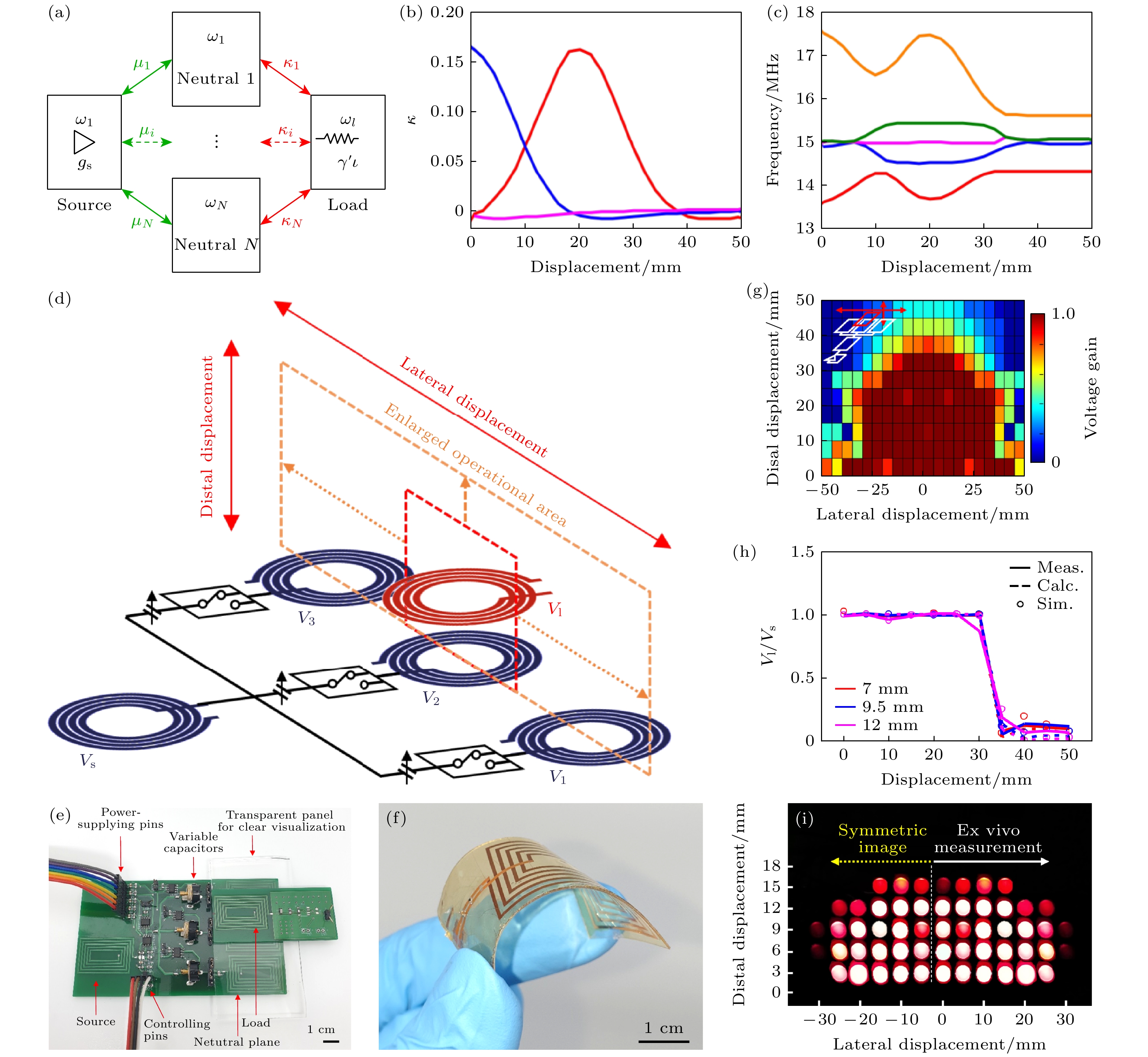
      如图9(a)引入高阶PT对称系统, 在源(左)和负载(右)之间布置多个横向对齐的中继单元(中心), 用于长距离鲁棒高效WPT. 源和负载的谐振器中的线圈与中继单元中的线圈具有相同的尺寸. 第i个中继单元与负载和源谐振器分别进行能量耦合, 耦合率分别为${\mu _i}$和${\kappa _i}$. 为了使系统满足PT对称条件, 需要控制源和中继谐振器之间的耦合电容使得${\mu _i} = {\kappa _i}$. 具体来说, 系统包括5个单元, 1个源、1个负载和3个中继单元, 组成一个五聚体系统, 其结构图如图9(d)所示, 实验PCB如图9(e)所示. 当负载线圈发生横向位移时, 系统3个位置的中继单元与其耦合强度变化如图9(b)所示, 对应的5个本征频率变化如图9(c)所示. 通过保持5个单元之间的PT对称性, 五聚体系统的电压增益可以在最大面积上保持不变(如图9(g)所示).

      这里其电路方程可写为

      对电路方程变形, 其哈密顿量可以表示为

      这里下标s和l分别表示源和负载, 数值下标i (i = 1, 2 ,···, N)表示第i个中继单元. 同样, ${\omega _m}$(m = 1, 2 ,···, N)表示每个谐振器的自谐振频率, $\Delta {\omega _m}$是由于谐振器之间的耦合而在耦合模理论模型中可能出现的频率偏移. ${\kappa _{ij}}$表示在第i个和第j个中继单元之间的耦合率. 这里的中继点个数N = 3, 随着负载沿黑色箭头方向横向偏移, 第1, 2个中继谐振器(位于底部/中心的神经单元)与负载之间的距离增大, 导致耦合率速率减小. 另一方面, 随着负载靠近第三个中继谐振器, 顶部与负载谐振器之间的耦合率增加. 根据这个位移, 调节耦合使整个系统满足PT对称条件. 除了匹配耦合强度外, 增益$ -{R}_{\text{S}}({g}_{\text{S}}) $恰好补偿WPT系统为满足PT对称条件而产生的损耗${R_{\text{l}}}$. WPT系统的增益元件由非线性放大器实现, 其中增益饱和中的非线性动力学确保WPT系统达到稳态振荡, 而不是幅值发散到无穷大. 电路的实际工作频率是WPT系统在稳态时的振荡频率. 具体来说, 在众多稳态模式中, 对于一个可变增益${g_{\text{S}}}$, 选择需要最低增益${g_{\text{S}}}$的模式作为工作模式. 这里通过连接源和中继点的可变电容来实现可控电容耦合, 由于不需要机械运动部件, 这种设计更有利于消费电子和生物医学电子[51]. 类似于二聚体的情况, 这是一个中继分子为PT对称的低聚物体系, 它保证了源和负载之间的等幅分布, 从而具有较高的传输效率. 对于负载的每次位移, 需要手动调节耦合率、翻转元件和源电容, 以满足PT对称条件. 测量了实验中当负载谐振器沿横向移动时系统的响应如图9(h)所示, 在横向移动30 cm的范围内, 可以看到系统获得了几乎恒定的电压比(效率).

      目前植入式生物电子器件已被广泛用于监测生理和电生理信号(例如: 心脏信号, 血糖和血压)和/或刺激器官和神经(例如: 心脏和听觉神经) [52–54]. 然而, 这些设备大多依赖于需要周期性手术更换的电池[52,55,56]. 由于包括电池在内的器件是刚性的, 与柔软的人体之间会发生机械不匹配, 从而对目标组织施加持续的应力, 可能引起炎症反应. 这里可以将上述高阶PT系统的接收端设计为柔性负载谐振器(图9(f)), 其在提高植入式生物电子器件的效率和鲁棒性上有很大的应用潜力[57]. 最后将其置于猪肉表面模拟向人体内传感器传能过程, 负载为发光二极管(图9(i)所示), 实验结果显示, 在该区域内发光均匀效果良好.

      • 4.2.   高阶拓扑二聚链WPT

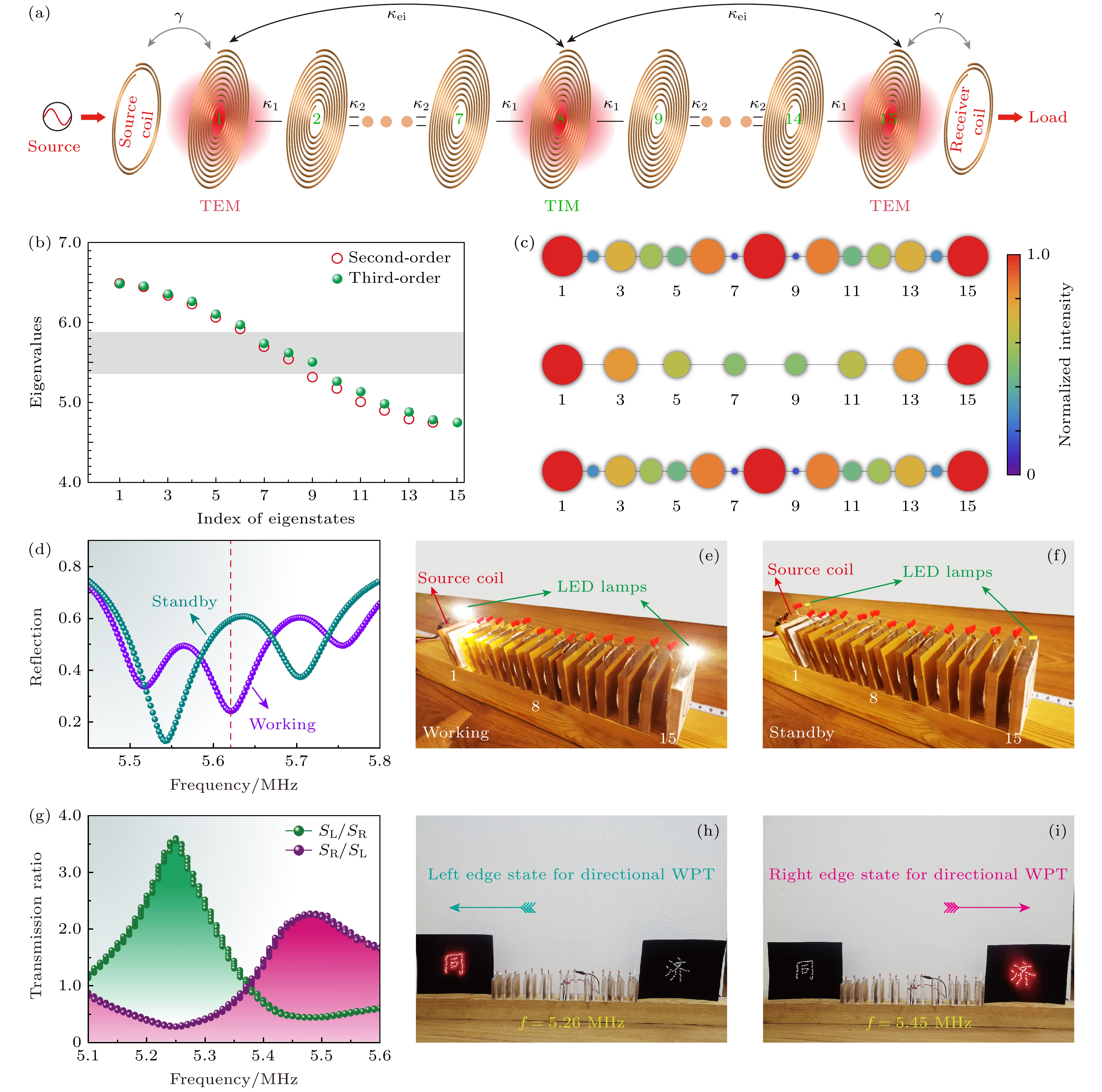
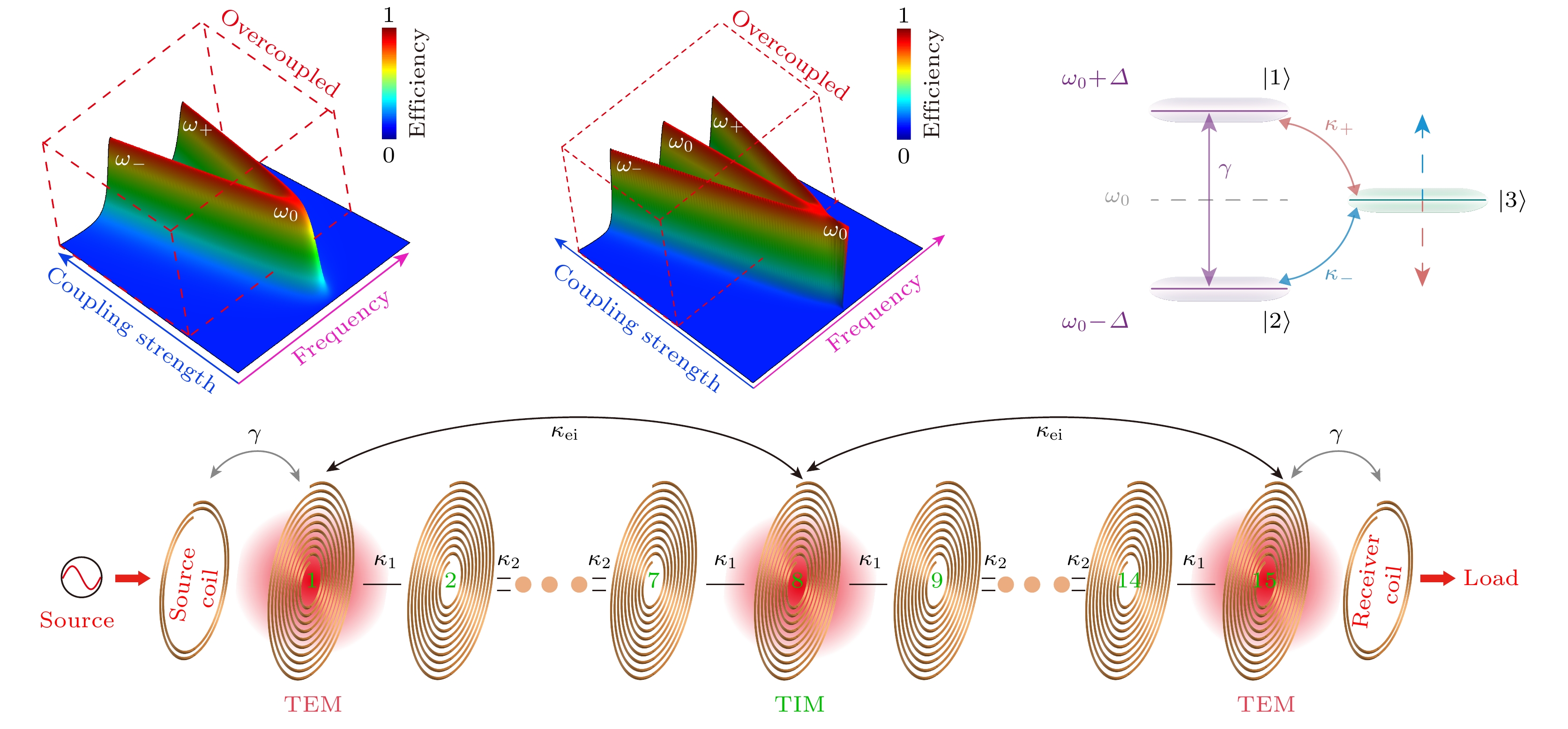
    • 对于一些复杂的传能通道需求(机械臂等), 通常需要多个谐振线圈组成的多米诺骨牌结构来实现[58]. 然而简单的多线圈系统存在的诸多技术局限: 1)系统存在多重劈裂, 工作频率影响因素复杂; 2)多线圈均加载磁场, 损耗增大; 3)目前的研究结果已经发现优化设计为非均匀分布, 但是其中的机理不清楚. 非厄密拓扑物理[59–65]为解决多线圈构造的长程WPT技术提供了全新的解决方案. 本部分将介绍利用深亚波长谐振线圈以及基于紧束缚模型来设计具有高阶PT对称的一维二聚体链, 并将拓扑链的拓扑边界模式应用于长程鲁棒性应用[66–70]. 图10(a)展示了由15个共振单元组成的两个拓扑二聚体链组成的复合链. 这里两个二聚体链中的所有谐振线圈都是相同的, 相应的谐振频率为 5.62 MHz, 其取决于加载的集总电容器$C$和线圈具体的几何参数. 改变原胞内耦合强度${\kappa _1}$和原胞间耦合强度${\kappa _2}$的相对大小可以实现从拓扑平庸到拓扑非平庸的拓扑相变.

      图10(a)中任一条二聚链等效电路的基尔霍夫方程可以写为

      所有的电感值${L_n}$和电容值${C_n}$都相等, 互感值${M_n}$与耦合强度相对应(交替变化).

      进一步地, 将该系统可以等效为非厄密近场耦合系统, 其等效哈密顿量可以写成:

      其中${\kappa _{{\text{ee}}}}$指边界态间等效耦合系数; ${\gamma _{\text{a}}}$和${\gamma _{\text{b}}}$分别是左右边界态的等效增益和损耗. 由(21)式可以发现, 当满足${\gamma _{\text{a}}} = {\gamma _{\text{b}}}$的条件时, 系统哈密顿量满足 $(PT)\boldsymbol{H}(PT)^{-1} = \boldsymbol{H}$. 因此拓扑二聚体链中两个边界态所实现的等效二阶非厄密系统是满足二阶 PT 对称的.

      类似地, 将两个拓扑二聚体链进行复合后, 就可以实现等效的三阶PT对称拓扑链中边界模式. 其等效哈密顿量可以写为[37,59]

      此时带隙中两个边界模式和一个界面模式近场耦合产生三种拓扑模式, 如图10(b)所示. 两种拓扑模式的频率偏离工作频率, 而另外一种拓扑模式是固定的, 这类似于简单的三线圈WPT系统. 三种拓扑模式的归一化强度分布分别如图10(b)所示. 第二种拓扑模式固定在工作频率上, 可用于实现长程稳定WPT. 从图10(c)可以看出, 第二种拓扑模式的场幅值在链的两端对称局域化, 而链的内部强度较低. 此外, 这种设计还解决了待机功率损耗问题. 如图10(d)所示为等效三阶 PT 对称系统在工作和待机状态下的反射谱. 与工作状态不同的是, 待机状态是系统移去最右端的一个谐振单元. 从图中可以看到, 当系统处于工作状态时, 系统的反射较低, 相反, 当系统处于待机状态, 系统的反射较高, 这意味着具有等效三阶 PT 对称性的拓扑二聚体链的待机功率损耗较小. 实验上系统的低待机功率特性如图10(e)和图10(f)所示, 发射线圈放在链的左端, 链的两端分别加载两个 LED 灯. 当系统处于工作状态时, 两个 LED 灯都亮. 相反, 当系统处于待机状态时, 两个 LED 灯在工作频率下仍然是暗的. 这证明了具有等效三阶 PT 对称系统的拓扑二聚体链的待机功率非常小.

      另外如果改变耦合强度的分布, 还可以得到非对称拓扑边界态即Harper 链来实现定向传输[60,71–73]. 图10(g)展示了拓扑Harper 链中两个拓扑边界态的传输比, 左边界态和右边界态的传输比(SL/SR)用绿线标记, 右边界态和左边界态的传输比(SL/SR)用紫线标记. 对于左边界态($f = 5.26$MHz), SL/SR显著高于SR/SL, 对于右边界态($f = 5.45$MHz), SR/SL显著高于SL/SR, 这表明拓扑边界态在不同频率下选择性地局域在准周期链的左端或右端[66]. Harper链是一种不对称结构, 它不仅导致左、右边界态的不同分布, 而且还导致左、右边界态的传输效率不同. 因此, 基于Harper链中的非对称拓扑边界态可以实现了定向 WPT. 如图10(h)所示, 在链的左右两端放置非谐振线圈, 分别连接由 LED 灯组成的“同”和“济”两个汉字. 可以看到在左边界态的工作频率($f = 5.26$MHz)下, 准周期链左端的汉字“同”亮起, 而链右端的汉字“济”则没有被点亮. 图10(i)的现象则恰好相反.

    5.   结　论

    • 本文围绕共振式WPT, 详细介绍了基于高阶非厄密PT对称的WPT相关发展及其应用, 其主要分为三个部分: 第一部分涵盖了从感应式WPT到共振式WPT的发展历程, 主动调谐电路追频实现高效WPT, 利用非线性饱和增益追频实现自发的二阶PT对称实现高效WPT; 第二部分探讨了利用三阶PT对称自身具有的不随距离变化的工作频率(固有谐振频率)实现高效WPT, 利用广义PT对称下的带隙实现高效WPT, 利用三阶PT非对称系统的BIC纯实模式实现高效WPT, 利用Anti-PT对称下的“能级钉扎”效应实现高效WPT; 第三部分涉及基于异质结耦合的高阶PT对称下实现宽横移范围的高效WPT, 利用拓扑非平庸链高阶PT中存在的鲁棒性边界态实现高效及定向WPT等. 总之, 本文主要综述了基于PT对称、PT非对称系统的BIC、广义PT对称、高阶PT对称、Anti-PT对称下的高效稳定磁耦合谐振式WPT, 揭示了非厄密物理在磁耦合谐振式WPT方面的独特作用机制及重要应用.

      基于本文介绍的PT对称的WPT的研究方法、相关实验测量平台及实验测量手段, 未来仍有诸多需要进一步深入研究的方向, 比如:1)探索在PT对称下的高效传能与高灵敏传感相结合的系统, 例如利用奇异点高灵敏度[74]以及高阶PT对称系统中的多个模式的分信道传递等, 可以实现能信同传以及通感一体化的功能; 2)在Anti-PT对称的背景下, 研究如何将先前在 PT对称条件下获得的结论应用于新的系统, 以拓展理论和实际应用[75–77]; 3)进一步探索一对多/多对一的高阶传能系统, 以提升系统的灵活性和应用范围[78]; 4)结合机器学习技术来优化非厄密WPT系统的设计与控制策略[79–81], 通过动态环境适应性、预测与提前调整、多目标优化、复杂系统建模与控制以及实时监控与故障检测等方面的应用, 机器学习可以有效地应对复杂和动态变化的环境, 提升系统的传输效率、稳定性和鲁棒性. 此外, 机器学习算法还能通过多目标优化实现设计的全局最优或帕累托最优解, 并简化高阶系统的建模与控制过程, 从而确保非厄密WPT系统的高效可靠运行. 然而, 尽管PT对称WPT系统的理论已相对完善, 但在高功率应用的实验、系统稳定性与可靠性以及异物检测与自动处理等方面, 仍然存在挑战. 未来的研究应综合考虑理论与实践的结合, 探索PT对称涉及的更加丰富的物理原理, 结合新物理原理并通过多方面的实验验证和技术优化, 推动新型的WPT技术得以实际应用.

    参考文献 (81)

目录

/

返回文章
返回