脉冲等离子体推力器(pulsed plasma thruster, PPT)是一种利用脉冲弧放电使推进剂电离而产生等离子体, 并加速等离子体产生推力的电磁型推力器, 因无储供机构、系统简单紧凑、可靠性高、运行功率低、元冲量精细可调等诸多优点, 近年来已成为微小卫星在轨控制任务动力装置的探索焦点^[1–5]. 但是, PPT的能量转化效率(即每个放电脉冲消耗的电能转化为羽流脉冲动能的比例)普遍较低^[6–8], 限制了其工程应用前景. 为提升PPT效率, 研究人员从放电电极结构^[9,10]、工质馈入方式^[11]、工质成分^[12,13]等方面开展工艺优化研究, 实现了PPT能量效率的一定程度提升. 也有研究通过PPT的能量转化过程和机制, 以期在认清PPT能量转化动力学基础上, 探索能量转化途径的优化设计及干预能量分配途径的技术手段, 如通过分析PPT推进剂烧蚀^[14–16]过程、放电电路的参数布局^[17]和放电能量分配优化^[18]等, 优化注入能量用于推进剂烧蚀的比例以及放电电流的时间行为, 提升总体能量转化效果. 总之, 清晰认识PPT放电过程中能量转化途径以及机制是探索PPT能量效率有效提升方法的基础.

机-电模型^[19]和磁流体动力学 (magnetohydrodynamic, MHD)数值模型^[20,21]是研究PPT等离子体羽流加速机制的常用物理模型. 其中, 机-电模型将PPT放电回路及相应电能消耗过程等效为一种RLC电路及其导电行为, PPT放电通道部分既是RLC电路的构成元件, 也是借助于电磁力产生羽流动能和元冲量的力学单元. 机-电模型中对于电磁加速体的加速过程有两种不同物理模型, 即弹丸模型(slug model)和雪犁模型(snowplow model). 电磁加速过程中, 若加速体可以视为质量基本不变的, 即质量恒定的“弹丸”, 则采用弹丸模型, 适用于加速通道内无气体的固体推进剂PPT. 雪犁模型中, 电磁加速体则像一个质量逐渐积累的“雪犁”, 在加速过程中由于不断电离“扫过”的气体, 而增加质量, 适用于以预填充气体为推进剂的PPT放电等离子体的电磁加速过程. 相较于MHD模型, 机-电模型结构分明、过程清晰、控制方程求解计算量较小, 尤其是电路模型能够再现PPT放电维持阶段的伏安波形, 利用波形仿真可得PPT放电回路等效元件参数, 因此成为一种分析PPT工艺条件与放电行为关联机制的可靠途径.

1968年, Jahn^[19]首先基于等离子体弹丸假设提出了针对平行板电极结构PPT的一维机-电模型, 将PPT装置等效为RLC放电电路与等离子体“弹丸”加速机构组成的机-电装置. 其中, PPT放电回路被模型化为离散、时变的RLC放电电路, 而PPT羽流的加速被假设为具有一定质量的薄电流片在安培力作用下以“弹丸”形式加速喷出的过程, 不涉及工质的烧蚀过程及其产物的热膨胀过程. 实际上, PPT羽流的加速不仅包括安培力对带电成分的加速, 而且还包括热膨胀气动加速过程. Vondra等^[22]考虑了羽流的热膨胀气动力, 在电流片的“弹丸”动力学方程中引入气动力项, 提出了一种修正机-电模型, 但这种修正的机-电模型不再封闭, 需要羽流气压及温度等热力学参数作为补充, 实际上已扩展为一种机-电-热模型. 魏荣华^[23]考虑到放电等离子体通道的有限几何尺寸, 将薄电流片修正为厚度随放电电流改变的扩散电流片, 这种修正虽然是针对薄电流片模型的局限性, 但是作为一种基于经验的唯像修正, 并不能帮助理解电流片形态的演变及其影响. Gatsoni等^[24,25]通过施加外部磁场以影响放电通道等离子体受到的安培力, 优化羽流加速过程, 但需要在电流片的“弹丸”动力学方程中引入阻尼项, 以确保羽流最终速度收敛.

为提高机-电模型中动力学方程的理论可解析性, Laperriere^[26]将平行板电极结构的PPT放电回路的电感元件具体化为一个准无限宽、理想导电薄片组成的单匝导电管, 提出了PPT回路电感的解析表达式以及等离子体“弹丸”的电阻表达式, 并且将“弹丸”电阻与电子温度、密度关联起来, 其目的是建立PPT电路参数与等离子体参数之间的关联机制, 仍然采用与文献[24,25]相同的薄电流片“弹丸”动力学方程.

PPT放电等离子体在加速喷出及飞行过程中其形态是持续演变的, 因此, 基本机-电模型中将放电通道视为一维薄“弹丸”等离子体片, 并以此形成的PPT羽流电磁加速机制存在不可避免的缺陷. 为了反映PPT放电通道“弹丸”的质量变化, 吴建军等^[27,28]考虑了推进剂的材料学和热学性质, 提出了聚四氟乙烯工质的一种烧蚀模型, 将烧蚀产物的实时积累以可变质量的方式纳入“弹丸”动力学方程, 可一定程度上体现电磁加速过程中“弹丸”质量的改变. 与此同时, 也有许多学者为了更有效地避开机-电模型中“弹丸”的缺陷, 将磁流体力学应用于描述PPT放电等离子体的磁流体加速过程, 开辟了PPT羽流加速机制的另一类理论研究途径. 与机-电模型中将工质烧蚀过程与羽流加速过程分割开来的处理方法不同, 在磁流体(MHD)模型中无法将放电等离子体力学过程与工质表面烧蚀过程分割开来. Mikellides等^[29,30]假定推进剂表面存在饱和蒸气, 并以此界定推进剂表面与等离子体之间的烧蚀层热力学状态, 将烧蚀过程与磁流体过程耦合在一起, 在形式上建立了烧蚀过程与磁流体加速过程的兼容模型. Keidar和Boyd^[31,32]则认为推进剂表面烧蚀会形成所谓Knudsen层, 作为推进剂表面与等离子体之间的过渡层, 建立了K-B模型. Yang等^[33,34]在弹丸模型中计入羽流等离子体质量积累和气动力效应, 优化了机-电模型中的动力学方程, 并考虑了烧蚀层内的化学反应并对K-B模型修正, 阐述了聚四氟乙烯在PPT中的烧蚀与电离过程. 虽然理论上MHD模型可以避开机-电模型电流片假设的缺陷, 其动量与能量方程既反映等离子体羽流携带动能及动量的演化机制, 又体现其加速历程, 但是MHD模型的求解, 需要可靠的初始和边界条件, 这些条件的可靠性决定了模型计算结果的可信性. 但对于PPT放电等离子体而言, MHD模型的初始与边界条件往往基于经验或者简化假设而设定, 不具有普遍合理性. 况且MHD主控方程数量多、形式复杂, 求解计算耗时大. 对于PPT性能优化的工艺设计期望而言, MHD模型的复杂性形成了很大挑战, 丧失了解析功能的MHD模型, 降低了对工程产品迭代研制的支撑作用.

对于PPT设计以及工艺优化研究而言, 作为一种高效分析预测手段, 机-电模型仍然具有不可替代的价值. 如前所述, 为了克服基本机-电模型的某些局限性, 虽然许多学者提出了机-电模型改进思路, 但这些改进聚焦于对PPT羽流形成及加速过程的补充. 如为了纳入羽流热膨胀加速过程, 必须引入推进剂烧蚀模型. 而关于推进剂烧蚀的实验数据很少, 过程机制仍然不明确, 只能借用某些现成烧蚀模型以保证方程组的封闭性, 在一定程度上降低机-电模型的可靠性. 机-电模型的基本目标是基于PPT放电电路模型构建羽流的电磁加速机制, 对PPT能量转化过程进行模型分析预测. 到目前为止, 对机-电模型中的PPT电路模型以及电流片电磁加速模型存在的固有局限性进行改进研究的报道不多.

本文针对机-电模型的电路及电流片模型的固有局限性, 提出如下改进思路: 1)现有机-电模型中, 认为PPT放电的等效RLC电路各等效元件的参数是固定的, 目的是为了能够获得电路方程的解析解. 但实际上, 等效电阻与电感随PPT放电历程而变化, 而且电阻与电感变化在PPT放电波形中有所体现, 因此将PPT电路修正为变参数RLC电路, 提出了求解变参数电路方程的一种方法. 2)现有机-电模型将PPT放电通道视为一维电流片, 无论是薄电流片还是有限厚电流片, 均为垂直于极板方向的一维平直构型. 实际上, PPT放电通道形状是复杂变化的, 为此, 将放电通道模型修正为二维电流片, 通过分析放电通道的电磁受力以及加速过程, 提出了二维电流片受电磁加速而获得动能的理论与计算方法. 并将上述改进后的机-电模型用于PPT样机不同工况的能量转化过程及机-电效率分析, 改进型机-电模型保留了模型结构简单、计算量不大的优点, 而且适用性得到提升.

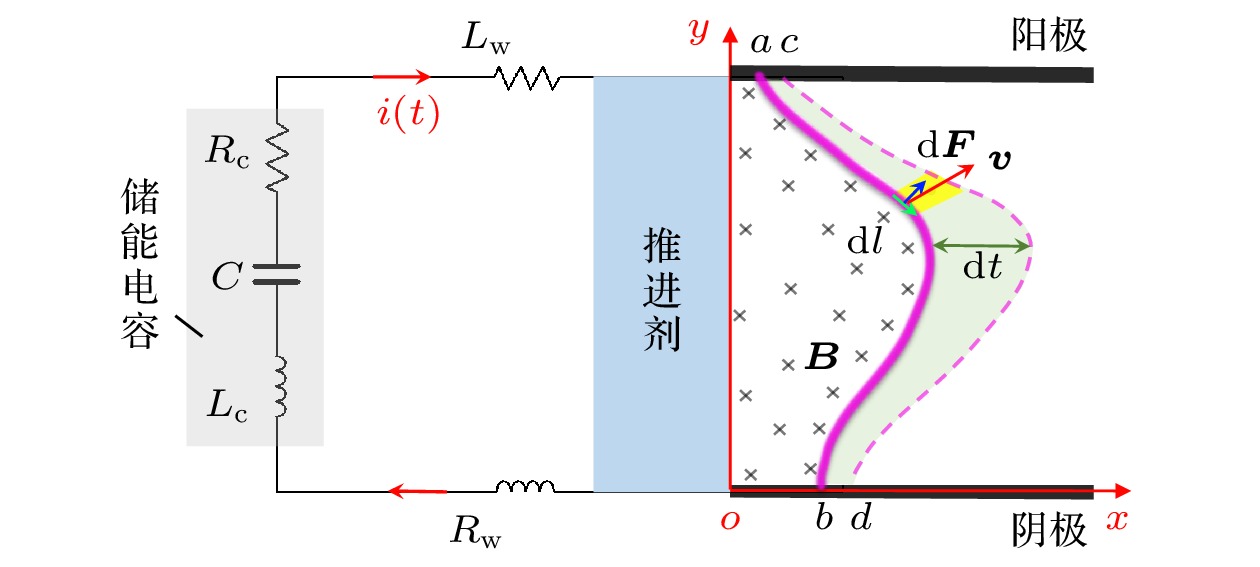
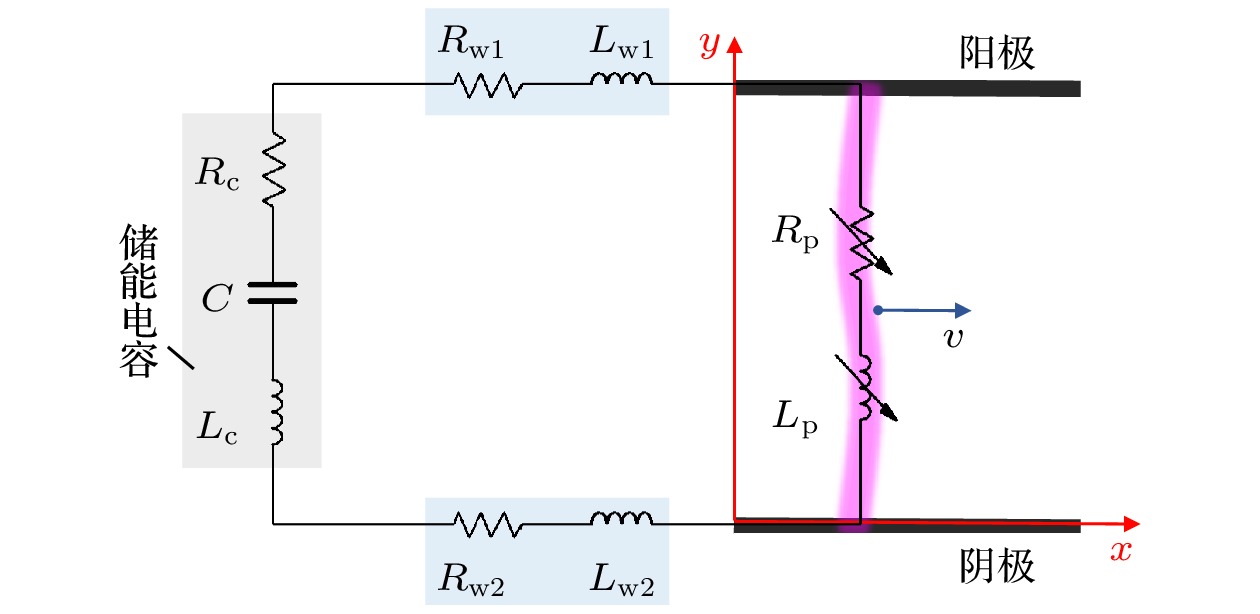
所谓基本机-电模型是针对平行板构型PPT提出的, 其电路模型将PPT放电回路视为离散元件构成的RLC电路, 示意如图1所示. 等效电感$ {L}_{{\mathrm{e}}{\mathrm{q}}}(t)={L}_{{\mathrm{c}}}+{(L}_{{\mathrm{w}}1}+{L}_{{\mathrm{w}}2})+{L}_{{\mathrm{p}}}(t) $, 等效电阻$ {R}_{{\mathrm{e}}{\mathrm{q}}}(t)={R}_{{\mathrm{c}}}+{(R}_{{\mathrm{w}}1}+{R}_{{\mathrm{w}}2})+{R}_{{\mathrm{p}}}(t) $, 均由三部分构成. 其中, $ {R}_{{\mathrm{c}}} $和$ {L}_{{\mathrm{c}}} $分别为储能电容寄生电阻和寄生电感; $ {R}_{{\mathrm{w}}1}, {R}_{{\mathrm{w}}2} $和$ {L}_{{\mathrm{w}}1}, {L}_{{\mathrm{w}}2} $分别为正负电极及连接导线的电阻和电感; $ {R}_{{\mathrm{p}}}(t) $, $ {L}_{{\mathrm{p}}}(t) $是PPT放电通道的等效电阻和电感. 回路电容即储能电容$ C $, 即$ {C}_{{\mathrm{e}}{\mathrm{q}}}=C $为常数.

根据基尔霍夫定律, PPT放电过程中, 电路的电压方程为

其中, $ {V}_{{\mathrm{c}}}\left(t\right) $为储能电容的极板间电压, $ i\left(t\right) $为回路电流, 定义电容放电电流为正电流. 若电容电量为$ Q\left(t\right) $, 则$ {V}_{{\mathrm{c}}}\left(t\right)=\dfrac{Q\left(t\right)}{C} $, $ i\left(t\right)=-\dfrac{{\mathrm{d}}Q\left(t\right)}{{\mathrm{d}}t} $. 代入(1)式消去$ {V}_{{\mathrm{c}}}\left(t\right) $和$ i\left(t\right) $得到:

(2)式即是PPT的模型电路方程. 基本机-电模型中认为回路电感和电阻不随时间变化, 视电路R, L, C参数为常数, 所以(2)式简化为常系数微分方程:

PPT放电通道是机-电模型中的移动单元, 是实现电能转化为机械能的核心. 放电通道被近似为以垂直于电极方向的平直构型向喷口加速喷出的薄电流片, 该电流片在回路电流激励的磁场中受到安培力作用而加速, 称为“弹丸”. 电流片沿图1中x轴方向加速喷出, 形成羽流. 电流片“弹丸”的动力学方程为

其中, $ m $为电流片质量为常数, 忽略推进剂烧蚀电离导致的电流片质量变化; $ \boldsymbol{x}\left(t\right) $为电流片的位置, 则$ \dot{\boldsymbol{x}}\left(t\right) $为电流片速度; $ \boldsymbol{F} $为电流片受力, 机-电模型认为安培力是电流片唯一受力.

电流片所受的安培力可以根据虚功原理计算. 当PPT回路电流为$ i\left(t\right) $时, 则回路储存的磁能$ {E}_{{\mathrm{L}}}=\dfrac{1}{2}{L}_{{\mathrm{e}}{\mathrm{q}}}{\left[i (t)\right]}^{2} $. 根据虚功原理, 若电流片发生虚位移$ \delta x $, 则虚功为$ \delta W=\delta {E}_{{\mathrm{L}}}=\delta \left[\dfrac{1}{2}{L}_{{\mathrm{e}}{\mathrm{q}}}{\left[i(t)\right]}^{2}\right]= \dfrac{1}{2}\delta {L}_{{\mathrm{e}}{\mathrm{q}}}{\left[i(t)\right]}^{2} $, $ \delta {L}_{{\mathrm{e}}{\mathrm{q}}} $是虚位移过程导致的回路自感虚增量, 一维电流片所受安培力$ {\boldsymbol{F}}_{{\mathrm{L}}} $的大小可表示为

其中, $ {L}_{{\mathrm{e}}{\mathrm{q}}x}'=\dfrac{\delta {L}_{{\mathrm{e}}{\mathrm{q}}}}{\delta x} $为电流片沿$ x $方向移动单位长度导致的回路电感增量, 即电感梯度.

基本机-电模型利用电感定义^[26]获得电感梯度, 回路电感与电感梯度可以表示为

其中, $ {\mu }_{0} $为真空磁导率, h为平行板极间距, $ w $为电极宽度(远大于极间距h和电流片厚度$ \delta $). 将(7)式代入(5)式可得

(8)式代入电流片动力学方程(4)可得

在PPT一次放电脉冲的持续时间内对(9)式进行积分, 可得到PPT在一个放电脉冲内产生的元冲量:

其中, $ {t}_{{\mathrm{e}}{\mathrm{n}}{\mathrm{d}}} $表示PPT放电结束时刻.

(3)式与(10)式构成基本机-电模型的控制方程:

在PPT维持放电阶段, 一般满足$ {R}_{{\mathrm{e}}{\mathrm{q}}} < 2\sqrt{\dfrac{{L}_{{\mathrm{e}}{\mathrm{q}}}}{C}} $, 故(11)式中电路方程为欠阻尼振荡方程, 有解析解:

其中, $ {Q}_{0}=C{V}_{0} $为PPT放电维持阶段开始时刻的电容电量, $ {V}_{0} $为该时刻的电容电压; $ \alpha =\dfrac{{R}_{{\mathrm{e}}{\mathrm{q}}}}{2{L}_{{\mathrm{e}}{\mathrm{q}}}} $; $ \omega = \Big(\dfrac{1}{{L}_{{\mathrm{e}}{\mathrm{q}}}C}-\dfrac{{R}_{{\mathrm{e}}{\mathrm{q}}}^{2}}{4{L}_{{\mathrm{e}}{\mathrm{q}}}^{2}}\Big)^{1/2};\;\beta ={\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}} \Big(\dfrac{4{L}_{{\mathrm{e}}{\mathrm{q}}}}{{R}_{{\mathrm{e}}{\mathrm{q}}}^{2}C}-1 \Big)^{1/2} $.

对基本机-电模型的两处基本缺陷进行改进: 1)为了解析法求解电路方程, 忽略PPT放电模型电路回路电感和电阻的时间变化; 2) PPT放电通道被简化为一维平直电流片.

基本机-电模型控制方程(11)中, 电路方程将回路等效电阻和电感视为不随时间改变的常数, 而电流片动力学方程则认为回路等效电感是变化的, 可见两个控制方程之间并不自洽. 事实上, PPT回路的$ {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $和$ {R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $均随时间而变, 所以电路方程应该采用含时电路参数的方程(2)的形式, 并改写为

其中$ R\left(t\right)={R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right)+\dfrac{{\mathrm{d}}{L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right)}{{\mathrm{d}}t} $为PPT电路的形式电阻.

电路方程(14)是一个变系数二阶微分方程, 目前尚无解析求解方法. Riazantsev等^[35]最近提出了利用最小二乘法和逆向解法求解方程(14)的方案. 在最小二乘法方案中, 需要假设回路电阻和电感均是随时间的线性函数, 针对实测放电波形进行拟合, 以确定回路电感以及电阻的时间函数形式, 但是该方案掩盖了PPT放电可能存在的非线性电路动态特性. 而逆向求解方案中, 将微分方程离散化差分方程, 从而转化为线性代数求解问题, 虽然通过数值方法求解该差分问题, 但是需要PPT放电开始与结束时刻的准确回路电感和电阻作为初始条件. 该算法对信号噪声敏感, 信号误差可导致计算结果不稳定.

本文提出方程(14)一种新求解方法. 在PPT放电的维持阶段, 虽然等效电阻和电感随时间而变, 但是累计变化量并不大, 因为PPT放电实际波形基本呈现为欠阻尼振荡波形. 由此, 在PPT放电持续时间[0, $ {t}_{{\mathrm{e}}{\mathrm{n}}{\mathrm{d}}} $]内, 若将[0, $ {t}_{{\mathrm{e}}{\mathrm{n}}{\mathrm{d}}} $]分成多个时间间隔足够小的时间单元, 在每个时间单元内, 回路电感和电阻均可以作为常数, 则方程(14)可作为常系数二阶微分方程, 即:

在[0, $ {T}_{1} $]内, (14)式可写为$ {L}_{1}\dfrac{{{\mathrm{d}}}^{2}Q\left(t\right)}{{\mathrm{d}}{t}^{2}}+ {R}_{1}\dfrac{{\mathrm{d}}Q\left(t\right)}{{\mathrm{d}}t}+\dfrac{Q\left(t\right)}{C}=0 $, $ {L}_{1} $, $ {R}_{1} $为常数;

在[$ {T}_{1} $, $ {T}_{2} $]内, (14)式可写为$ {L}_{2}\dfrac{{{\mathrm{d}}}^{2}Q\left(t\right)}{{\mathrm{d}}{t}^{2}}+ {R}_{2}\dfrac{{\mathrm{d}}Q\left(t\right)}{{\mathrm{d}}t}+\dfrac{Q\left(t\right)}{C}=0 $, $ {L}_{2} $, $ {R}_{2} $为常数;

······

在[$ {T}_{n-1} $, $ {T}_{n} $]内, (14)式可写为$ {L}_{n}\dfrac{{{\mathrm{d}}}^{2}Q\left(t\right)}{{\mathrm{d}}{t}^{2}}+ {R}_{n}\dfrac{{\mathrm{d}}Q\left(t\right)}{{\mathrm{d}}t}+\dfrac{Q\left(t\right)}{C}=0 $, $ {L}_{n} $, $ {R}_{n} $为常数.

每个时间片段内, 利用方程(14)的通解形式, 拟合PPT实际波形, 可得各时间片段内的$ {R}_{i} $, $ {L}_{i} $. 本文中各时间片段得到的电路参数与该片段中间时刻对应, 以这些离散参数体现PPT放电回路电感和电阻的动态变化. 将这些离散数据视为时间演变函数$ {R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) , {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $的插值点, 进行插值拟合, 得到$ {R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) , {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $的函数形式. 将得到$ {R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) , {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $的函数代回(14)式, 利用数值解法便可以实现对PPT的放电波形的仿真, 并于实测波形对比, 以验证$ {R}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) , {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $函数形式的可靠性.

基本机-电模型中的平直电流片“弹丸”与PPT放电通道实际形态有明显差别, 根据PPT放电通道的二维形貌特点, 将PPT放电通道视为厚度可忽略的“弧线”型二维电流片, 如图2中的粉色弧线所示, 电流片在垂直于纸面方向上视为延伸足够远. 曲线ab表示$ {t}_{1} $时刻电流片的形态与位置, 曲线cd表示电流片经过$ {\mathrm{d}}t $时间运动后的形态与位置, 运动中电流片的形态有变化但基本保持弧形. 为了分析电流片的安培力作用过程, 假设放电中某一时刻的回路电流为$ i\left(t\right)=I $, 方向如图2中绿色箭头所示, 回路电流形成的磁场也示于图2中. 在电流片中任取一个电流元$ I{\mathrm{d}}\boldsymbol{l} $(绿色箭头所示), $ {\mathrm{d}}\boldsymbol{F} $为该电流元所受安培力, 此刻该电流元速度为$ \boldsymbol{v} $, 黄色区域为电流元在$ {\mathrm{d}}t $时间内扫过的面积, 绿色区域为电流片在$ {\mathrm{d}}t $时间内扫过的面积.

该电流元所受安培力为

其中, $ \boldsymbol{B} $是PPT放电回路中除该电流元以外的其他电流元在“当地”所产生的磁感强度. 安培力对电流元做功的瞬时功率$ {\mathrm{d}}P $为

电流片ab所对应的曲线路径记为$ \varSigma $, 安培力对该电流片做功的瞬时功率$ P $为(16)式对该路径的积分, 即:

在$ {\mathrm{d}}t $时间内安培力对电流片所做的功$ {\mathrm{d}}W $:

其中, $ \boldsymbol{v}{\mathrm{d}}t\times {\mathrm{d}}\boldsymbol{l} $表示电流元在$ {\mathrm{d}}t $时间内扫过的面积, 图2中黄色区域. 图2中浅绿色区域则表示电流片由ab在$ {\mathrm{d}}t $时间内到达cd扫过的面积$ {\mathrm{d}}{S}_{\varSigma }= \displaystyle\int _{\varSigma }(\boldsymbol{v}{\mathrm{d}}t\times {\mathrm{d}}\boldsymbol{l}) $. 而$ \displaystyle\int _{\varSigma }\boldsymbol{B}\cdot \left(\boldsymbol{v}{\mathrm{d}}t\times {\mathrm{d}}\boldsymbol{l}\right)={\mathrm{d}}{\phi }_{\varSigma } $则是$ {\mathrm{d}}t $时间内电流片位移过程扫过的磁通量, 即PPT放电回路在$ {\mathrm{d}}t $时间内由于电流片从位置ab移动到cd所导致的磁通增量. 若PPT回路自感用$ {L}_{{\mathrm{e}}{\mathrm{q}}} $表示, 在$ {\mathrm{d}}t $时间内由于电流片从位置ab移动到cd所导致的回路自感增量用$ {\mathrm{d}}{L}_{{\mathrm{e}}{\mathrm{q}}} $表示, 则磁通增量$ {\mathrm{d}}{\phi }_{\varSigma } = \displaystyle\int _{\varSigma }\boldsymbol{B}\cdot \left(\boldsymbol{v}{\mathrm{d}}t\times {\mathrm{d}}\boldsymbol{l}\right)=I{\mathrm{d}}{L}_{{\mathrm{e}}{\mathrm{q}}} $, 那么由(18)式得

安培力对电流片所做功转化为电流片的动能, 所以, 在PPT的一个放电脉冲期间, 安培力做功所产生的动能为

与安培力做功过程对应, 在PPT的一个放电脉冲期间内, 电流片所受安培力的冲量转化为电流片的元冲量, 但由于电流片为弧形, 不同位置电流元所受安培力方向各异, 电流片的元冲量作为矢量只有x方向分量才能成为PPT的反推冲量. 但是该冲量分量难以与回路参数关联起来, 所以用安培力加速电流片的动能方程作为机-电模型中的动力学方程. 因此, 二维电流片机-电模型控制方程如下:

根据该模型, 利用2.2.1节的算法求解其中的电路方程, 可以得到PPT回路等效电感的时间函数$ {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right) $, 进而可以利用(21)式中的第2个方程计算电磁加速产生的动能. 该动能与储能电容初始储能的比值即为评价PPT能量效率的指标, 定义该比值为PPT的机-电效率:

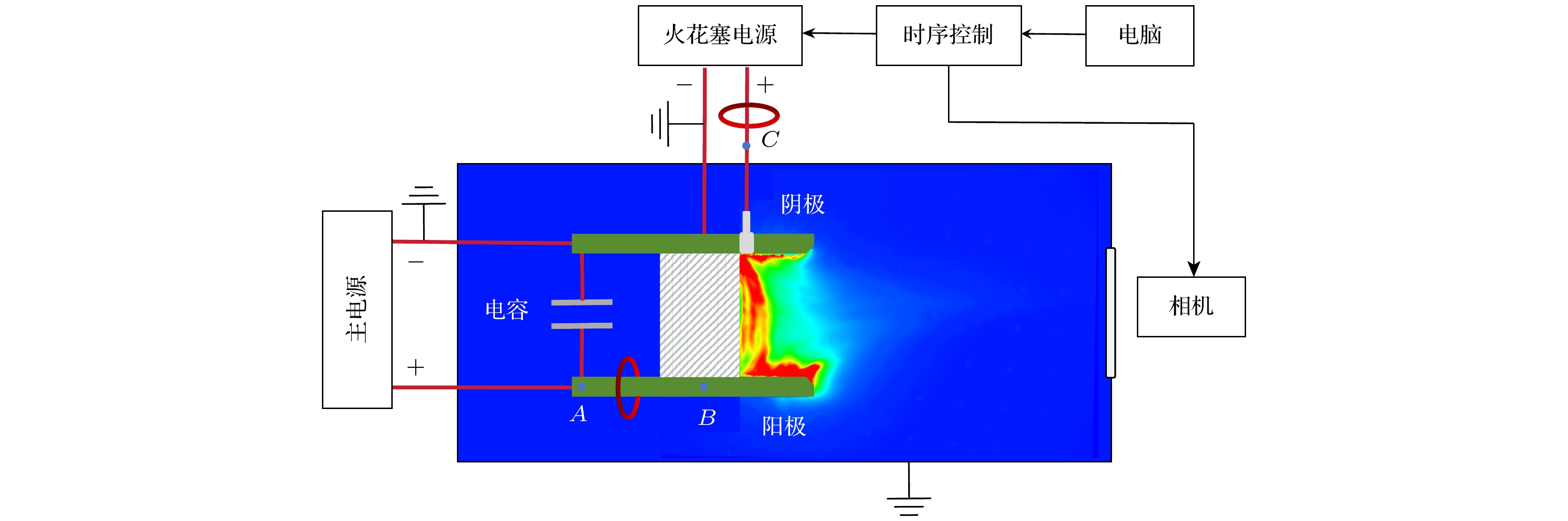
为验证改进机-电模型, 基于图3所示PPT样机实验装置, 测量了多种工况的PPT放电波形, 利用改进模型计算各种工况下PPT的电磁加速 动能及机电效率, 分析机电效率与工况条件的关系, 以判断模型的可靠性. 所用平行板PPT样机包括火花塞、平行极板、储能电容、推进剂, 样机置于10^–3 Pa的真空舱内. 样机推进剂为聚四氟乙烯棒, 与电极宽度和电极间隙适配. 电极板为紫铜板, 电极间隙h为30—40 mm, 电极加速长度为25 mm. 储能电容为3 μF(内阻为10 mΩ), 充电电压$ {V}_{0} $为1.0—2.0 kV可变. 火花塞固定在阴极上且贴近推进剂表面, 以外触发控制的脉冲电源驱动. 为了对PPT放电通道及羽流高速成像, 利用时序控制器可产生两路TTL信号, 一路触发火花塞电源, 另一路为高速相机提供快门信号, 两路控制信号的延迟可调以保证高速相机快门与PPT点火同步. PPT放电、电流波形通过电压探头(Tek P5100)和电流探头(优测 LS-T-1000)测量, 并用示波器(Tek DPO3034)记录. 在A, B, C三个不同位置监测电压: 电容的输出电压(A点), PPT放电间隙电压(B点), 火花塞电压(C点). PPT放电电流和火花塞电流测量位置示于图3中红色椭圆. 火花塞的点火电压幅值1.2 kV, 单次放电能量为50 mJ.

采用二维电流片模型改进的机-电模型, 需通过求解电路方程, 得到PPT回路等效电感的时间变化行为, 才能进行电磁加速动能及机-电效率的计算分析. 本节对不同工况下测得的PPT放电波形, 利用2.2.1节阐述的电路方程解法, 进行放电波形仿真, 得到等效电感及其时变特性.

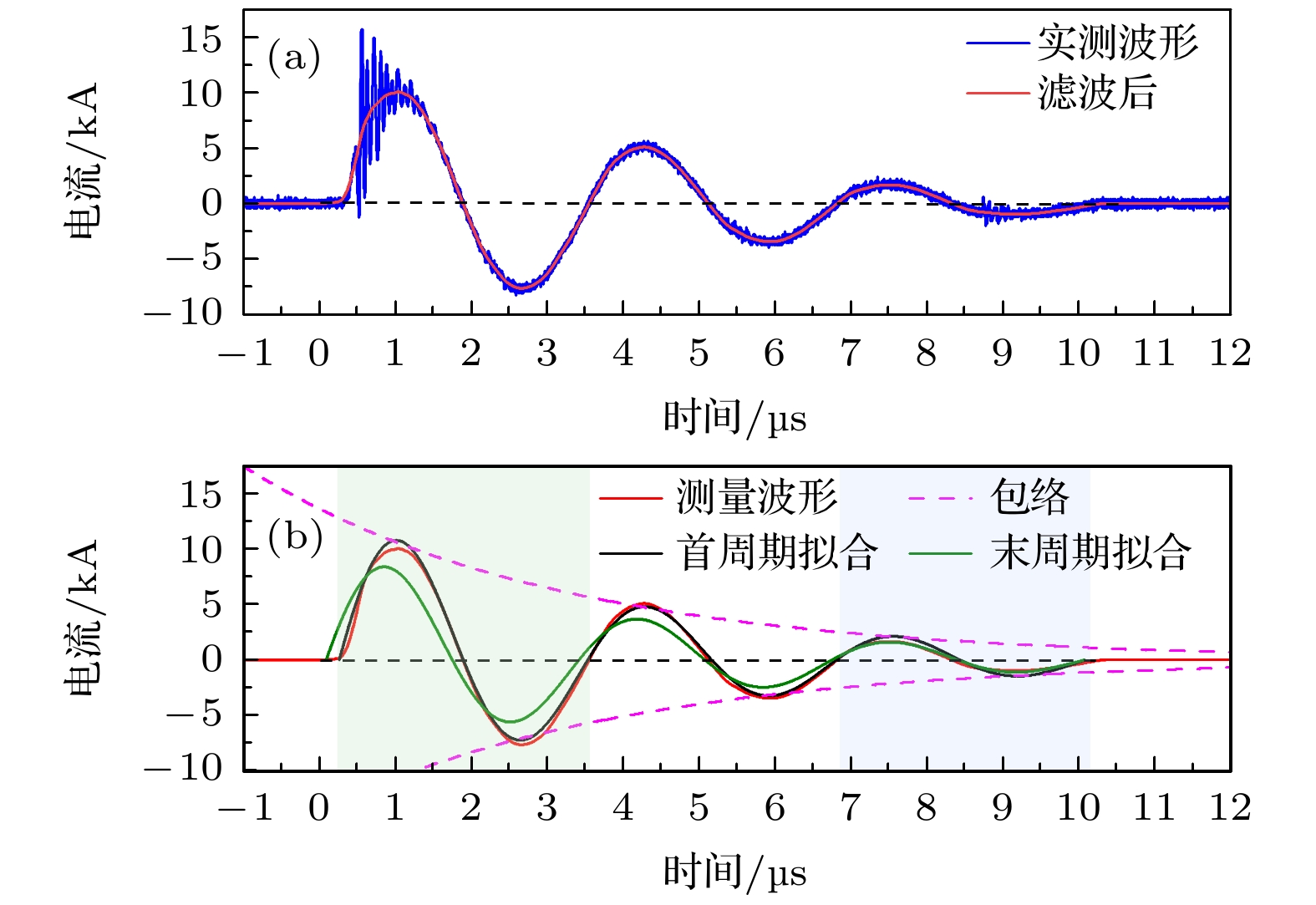
图4展示了典型的PPT电流波形图(工况为h = 40 mm, $ {V}_{0} $= 2 kV). 图4(a)中的蓝色波形为原始测量波形, 为一欠阻尼衰减振荡波形. 可以看出在放电初期, 由于发生击穿导致电流波形叠加了高频振荡干扰, 为了开展数值拟合计算, 对原始波形进行数值滤波处理, 得到图4(a)中红色波形, 该波形与原始波形的平均轮廓吻合.

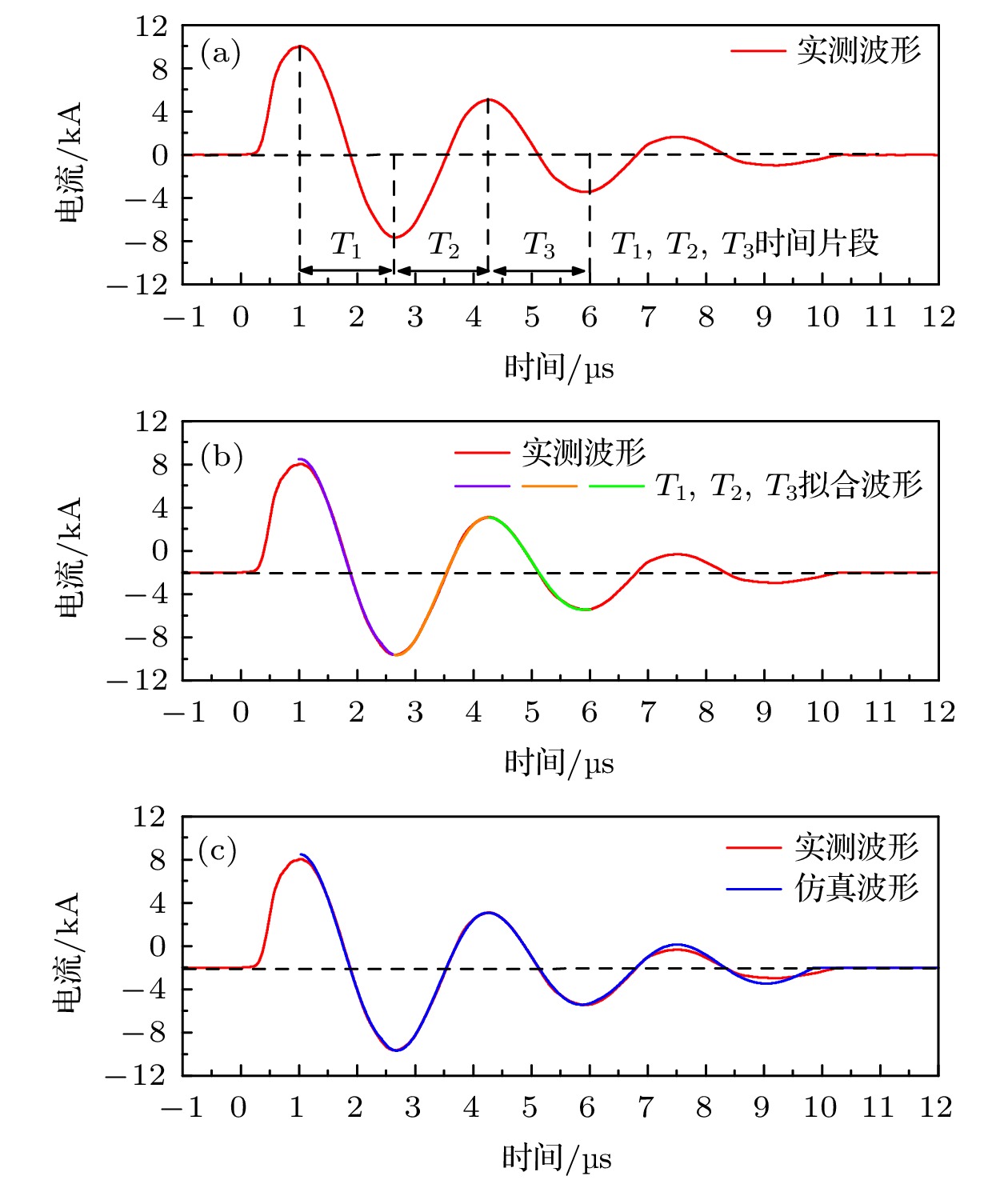
虽然模型方程(21)中的电路方程以电量$ Q\left(t\right) $为函数, 但考虑(12)式和(13)式, 电量$ Q\left(t\right) $与电流$ i\left(t\right) $有相似通解形式, 所以后续计算过程直接针对PPT电流波形. 为了直观显示PPT回路电感的变化, 图4(b)展示了对电流波形进行不同拟合效果的对比. 图4(b)红色波形即图4(a)红色波形, 粉色虚线是红色波形的衰减轮廓线(对应于(13)式的指数函数部分), 黑色波形是以红色波形首周期(即图中浅绿色区域)为拟合目标, 根据(13)式拟合得到的; 绿色波形则是以红色波形末周期(即图中浅蓝色区域)为目标的拟合波形. 对比发现, 黑色波形在放电前段与红色波形吻合, 但后期不重合, 绿色波形则相反, 在放电后期与红色波形吻合, 而前期波形则存在波形错位, 绿色波形周期大于黑色波形周期. 这表明放电过程前后期, 电流波形周期不一致, 即回路电感随时间变化.

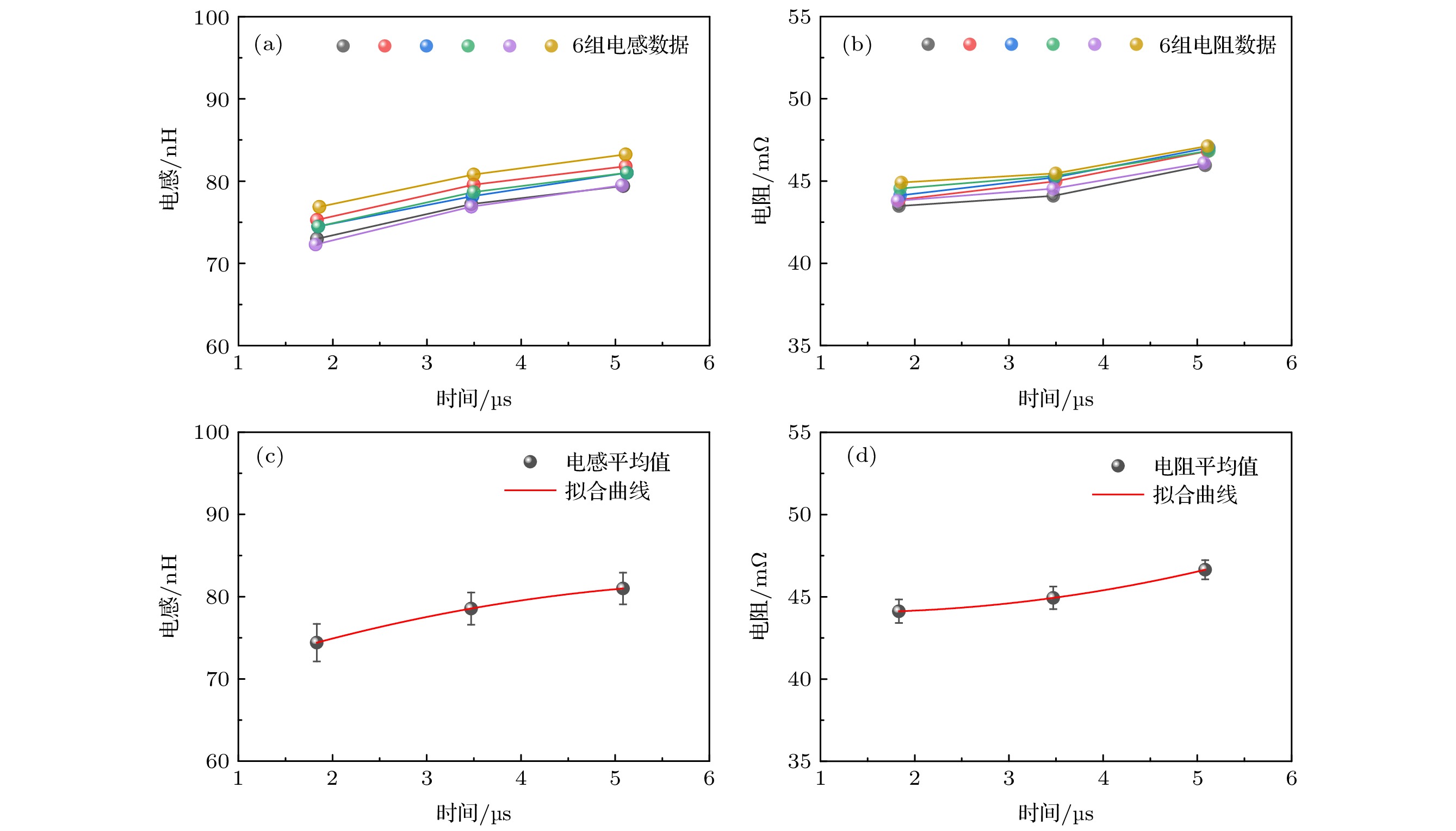
根据2.2.1节所述求解系数含时电路方程的方法, 需要对PPT电流波形进行分时间段拟合, 可以得到回路电感与电阻的时间变化特性. 虽然图4(b)显示PPT回路电感随时间改变, 但是电流波形的周期改变并不大(3个半周期的时间跨度内, 波形错位小于1/4周期), 所以将PPT电流波形划分为多个时间片段, 在每个时间片段内可以视为回路电感和电阻不变. 虽然划分的时间片段越小, 波形畸变程度越小, 但是时间片段越小, 参与拟合的数据点越少, 无法保证拟合精度, 所以选择时间片段长度为1/2周期. 图5(a)显示了3个时间片段, 标记为$ {T}_{1} $, $ {T}_{2} $, $ {T}_{3} $片段. 图5(a)波形的首个1/4周期未划入任何拟合片段, 因为这个时段对应PPT放电通道的建立阶段, 不属于PPT放电维持阶段. 为了将波形的衰减轮廓拟合与波形周期拟合分离进行, 首先对PPT波形全时段波形轮廓利用(13)式指数衰减函数进行拟合获得衰减系数$ \alpha $, 然后分片段进行波形拟合. 在片段波形拟合时轮廓拟合得到的衰减系数, 从而获得各时间片段内的回路电感和电阻, 并且与时间片段的中间时刻对应, 构成回路电感、电阻的随时间变化函数关系. 图5(b)展示了分段拟合波形(不同颜色对应不同时间片段)与实测波形(红色)的符合情况, 各片段的拟合优度高于0.99. 为了进行放电波形的仿真验证, 将得到的回路电感、电阻的时间函数及回路电容$ C=3{\mathrm{\mu }}{\mathrm{F}} $带回电路方程(14), 利用MATLAB中自带的ODE45求解器对该工况的电路方程进行数值求解, 可以得到该工况的电流仿真波形, 如图5(c)的蓝色波形所示(同时显示实测电流波形以对比), 表明仿真波形和实验波形的吻合程度明显优于图4(b)的吻合程度, 可见含时回路电感、电阻的电路方程的仿真精度得到了改善. 另外, 对于仿真波形值得提出的是: 在放电初期和末期的仿真波形与实测波形有差别, 其中放电初期的1/4周期的波形未进行仿真, 因为该时段为PPT放电通道的形成阶段, 不是放电维持阶段, 电路方程(14)并不适用于该时段. 放电末期的两个半周期波形也不够吻合, 这是因为放电临近结束时, 放电电流过小, 放电通道逐渐呈现出不能充分维持的状态, 因此电路方程(14)的适用性逐渐变低, 导致仿真精度下降.

为进一步考察时间片段拟合方案的可靠性, 对图5工况(h = 40 mm, V₀ = 2 kV)下PPT的6次独立放电波形进行仿真计算, 获得的6组电感、电阻数据展示在图6中. 其中图6(a), (b)显示分别是仿真计算得到的回路电感、电阻数据, 为了体现随时间的变化趋势, 同一组数据用相同颜色显示并连以折线. 可以看出, 1) 6次放电中, 回路电感和电阻分别随时间呈现相似的增大趋势, 与文献[36]预测结论一致; 2)确定工况下的6次PPT放电中, 回路电感和电阻的数值略有差异, 但不超过5%, 这些差异是PPT放电起伏以及数据误差共同产生的. 对6组数据进行平均, 可以得到同一工况下PPT放电的回路电感、电阻数据, 显示于图6(c), (d)中, 图中同时显示了数据的起伏范围. 对图6(c), (d)中电感、电阻数据以多项式进行时间分布拟合, 当回路电感、电阻随时间的关联函数, 分别为$ {L}_{{\mathrm{e}}{\mathrm{q}}}\left(t\right)= -3.12\times {10}^{11}\cdot {t}^{2}+4.19\times {10}^{6}\cdot t+67.78 $ (nH), $ R(t) = 1.73\times {10}^{11}\cdot {t}^{2}-4.23\times {10}^{5}\cdot t+44.32 $ (mΩ)时, 拟合优度可达0.999. 另外, 针对在其他工况下(h =30, 35 mm和l =15, 25, 35 mm)的PPT放电波形, 同样进行了类似计算过程, 拟合得到回路电感、电阻的时间函数均为二次多项式, 且拟合优度高. 由此可见, PPT放电回路电感、电阻的时间函数可用二次多项式$ y=A{t}^{2}+Bt+C $表达.

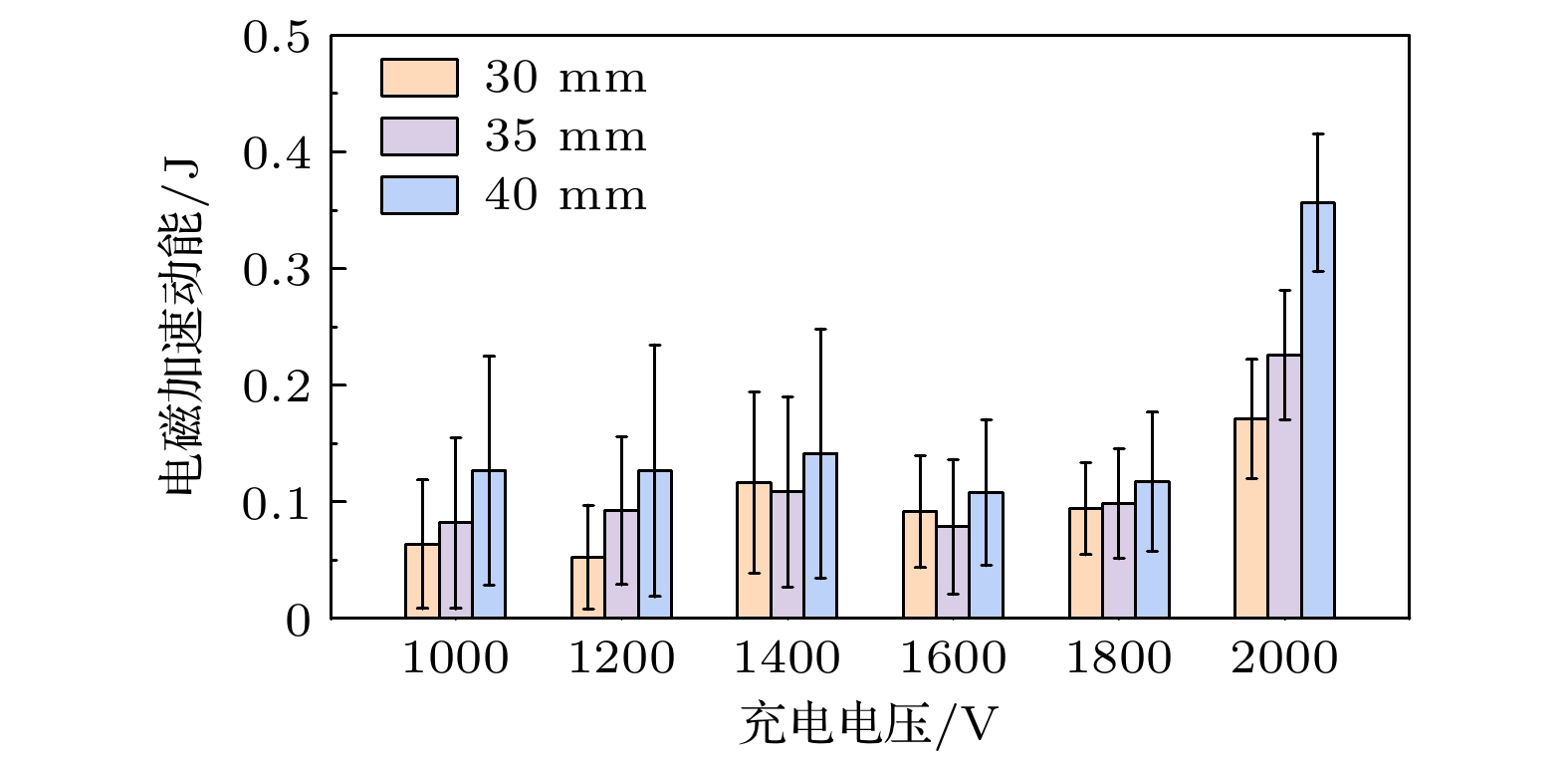
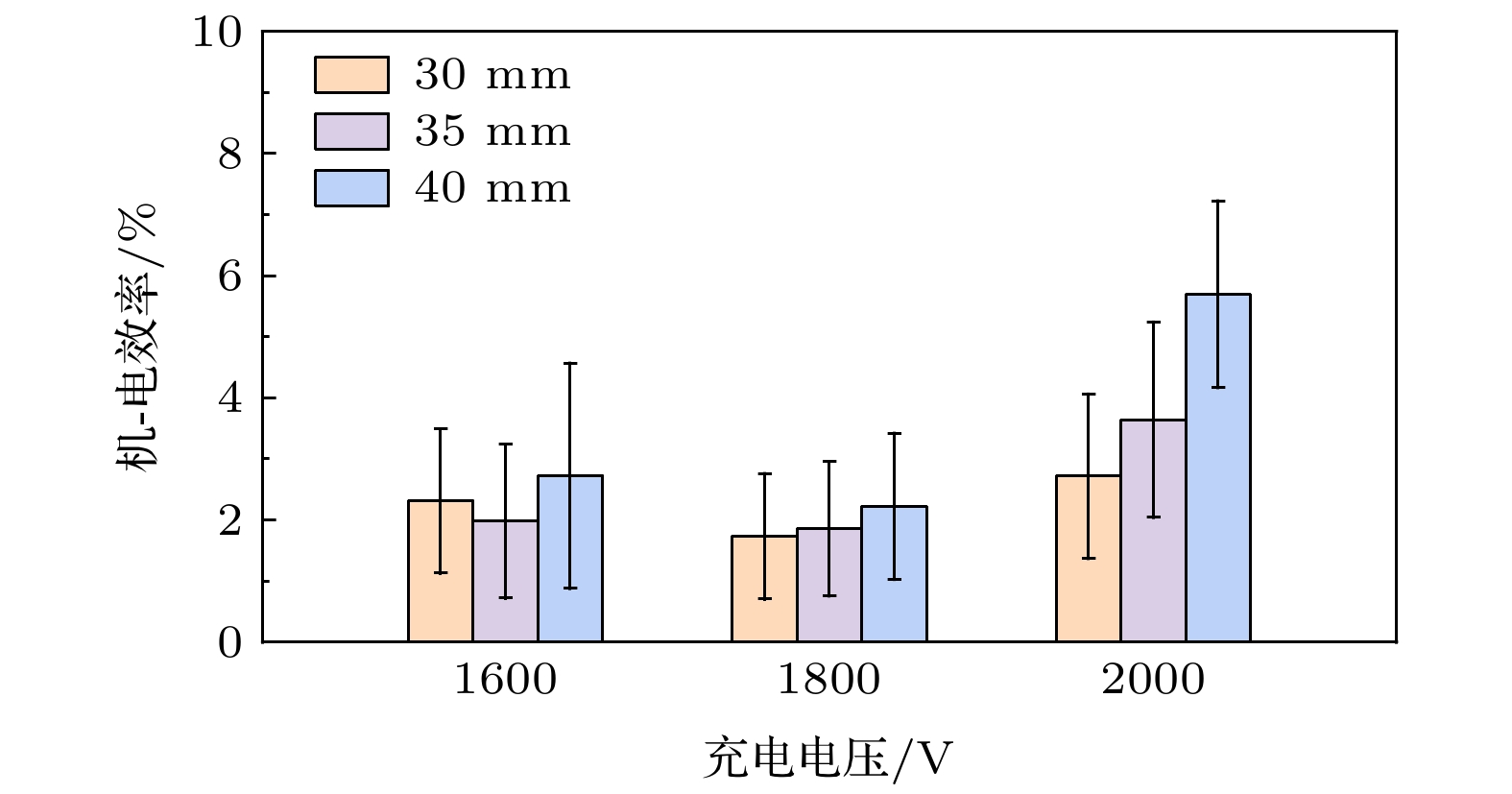
利用3.2节的PPT电路方程仿真方法, 通过对PPT放电波形进行分段拟合, 可得到不同工况下PPT放电的回路电感时间特性, 进而利用方 程(20)可以计算PPT放电通道等离子体在安培力作用下获得的动能, 即PPT羽流的电磁加速动能, 图7以柱状图展示了计算得到的不同工况下PPT羽流电磁加速动能. 图7所示的工况范围内, PPT羽流获得的电磁加速动能在50—370 mJ之间. 图7的数据表明: 1)在相同充电电压条件下, 随着电极间距增大, 电磁加速动能大致呈现逐步增大趋势, 这是因为电极间隙越大, 放电通道对应电流片长度越大所致. 但是, $ {V}_{0}= $1.4 kV, 1.6 kV且h = 30 mm工况的电磁加速动能计算结果偏大, 其原因在于: 电磁加速动能的大小取决于多个工况参数, 不同参数的影响机制复杂多变. 其中电流片长度的影响最为直接, 所以随电极间隙增大, 电磁加速动能的增大趋势比较明显. 但是充电电压的影响比较复杂, 因为充电电压不但对放电通道的形貌有影响, 而且也影响放电通道维持时间. 2)若保持电极间距不变, 充电电压1.0—2.0 kV范围内, 电磁加速动能随充电电压的增加趋势只是1.6 kV以上的工况才较为明确. 在较低充电电压(1.0—1.4 kV之间)时, 由于电容初始储能较小, 相应的电磁加速动能应该低于1.6 kV工况, 然而却有多个计算结果高于1.6 kV工况的, 这种“反常”计算结果表明(20)式的适用条件, 即PPT放电电流通道须符合薄电流片模型. 而1.0—1.4 kV PPT放电通道可能与薄电流片模型差距较大, 使得(20)式中使用的针对薄电流片定义的电感不再成立, 而且电路方程中的回路电感也不能与之等价. 因为低放电电压条件相应的放电能量低, 导致放电通道发展不充分, 形态分散, 电流强度分布不集中, 不宜将电流通道视为边界清晰的薄电流片模型; 与之相反, 若PPT放电能量足够大, 则放电通道形态清晰, 放电电流集中, 符合电流片模型. 当PPT放电通道不宜采用电流片模型时, 尽管放电波形仍然可以采用PPT电路方程(14)进行仿真计算, 并得到等效回路电感等参数, 但(14)式中的回路电感等价于(20)式使用的电感.

根据计算出的PPT羽流电磁加速动能, 由(22)式可得PPT机-电效率. 虽然对各工况均可进行(22)式的计算, 但电流片模型不适用的工况下(22)式的计算结果会反常. 根据图7的结果, 图8仅显示了薄电流片模型基本符合得1.6—2.0 kV各工况的机-电效率计算结果, 充电电压为1.6—2.0 kV的9种工况下, PPT机-电效率均小于6%, 且绝大部分工况的电效率为2%—4%. 文献[22]报道了储能电容2 μF、充电电压1360 V工况下PPT的机-电效率, 文中使用Langmuir探针、微波干涉仪和Faraday杯等工具, 表征了羽流等离子体参数和羽流速度, 并据此估算了羽流的平均动能, 结果表明机-电效率大约3 %, 与图8中充电电压1.6 kV的结果相符, 这表明(22)式的计算结果是可靠的.

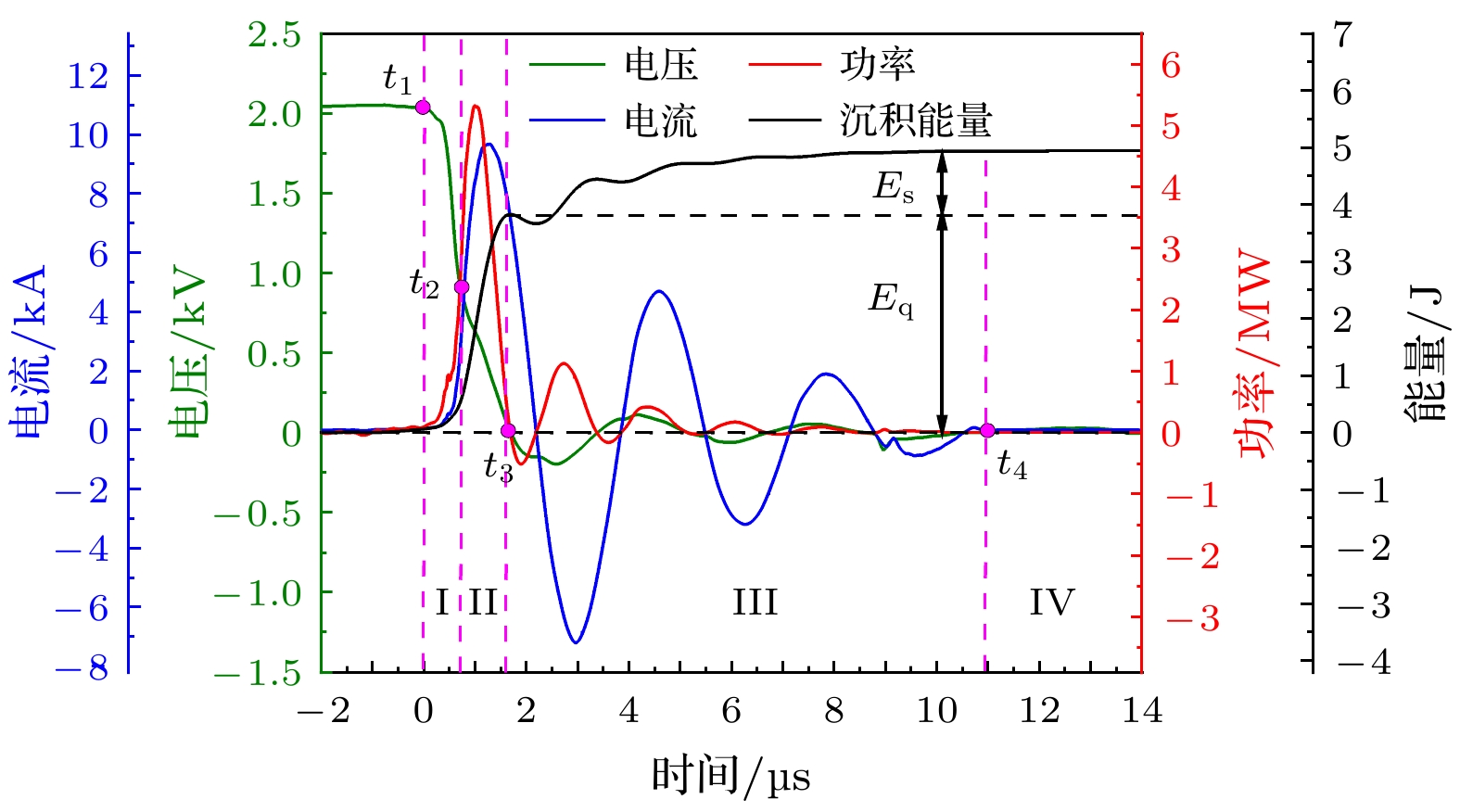
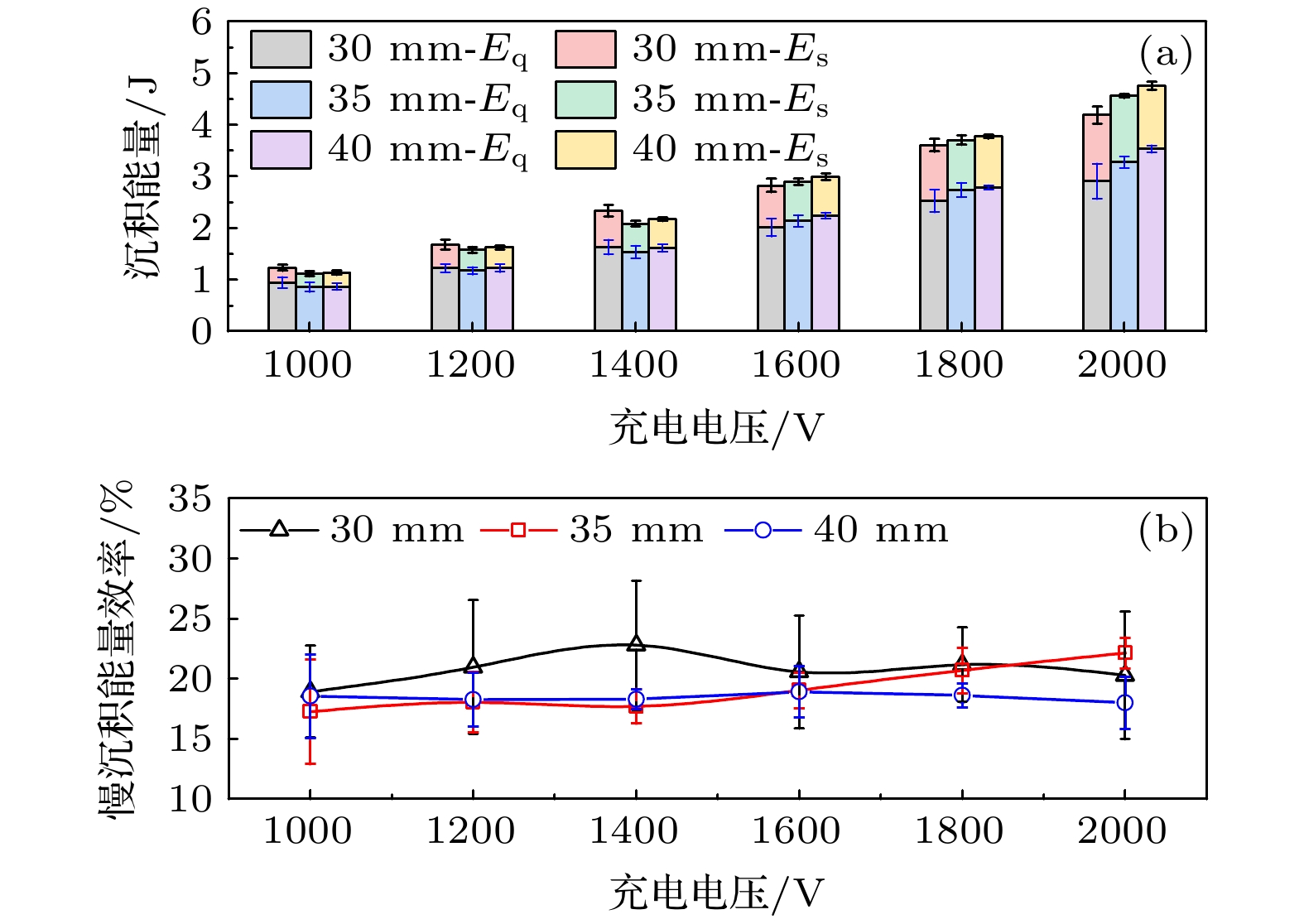
文献[22]提出PPT机-电转化效率低是由于绝大部分放电能量用于推进剂烧蚀、电离和放电通道的热维持, 而用于电磁加速等离子体羽流的部分很少. 图8结果表明通过提高电压或者加大放电间隙不能显著提高PPT机-电效率, 其原因可能是仅仅改变这两个参数不能显著影响放电能量分配过程. 为了阐述PPT放电能量转化过程的特点, 图9的绿、红波形显示了h = 40 mm, $ {V}_{0}= $2.0 kV工况下PPT放电电压(绿) $ {V}_{{\mathrm{p}}}\left(t\right) $与放电电流波形(红) $ i\left(t\right) $, 其中电压波形是在图3所示B点测量的PPT放电间隙电压波形. 注入放电通道的功率波形根据$ {P}_{{\mathrm{a}}{\mathrm{r}}{\mathrm{c}}}\left(t\right)={V}_{{\mathrm{p}}}\left(t\right)i\left(t\right) $得到, 如图9红色波形. 即时注入放电能量根据$ {E}_{{\mathrm{a}}{\mathrm{r}}{\mathrm{c}}}\left(t\right)=\displaystyle \int _{0}^{t}{P}_{{\mathrm{a}}{\mathrm{r}}{\mathrm{c}}}\left(t \right){\mathrm{d}}t = \displaystyle \int _{0}^{t}{V}_{{\mathrm{p}}}\left(t \right)i\left(t \right){\mathrm{d}}t $计算, 如图9黑色波形, 称为放电通道沉积能量. 根据PPT放电电压波形可以区分3个放电阶段, 图9绿色波形上标注了4个特殊时刻, 分别为: t₁, PPT开始放电(即图中时间零点); t₂, PPT放电状态突变; t₃, 电压首次过0; t₄, 放电结束. 其中, t₁—t₂为PPT放电通道形成时段(I), 即击穿阶段, 过程快, 持续时间短; t₂—t₃为放电增长阶段(II), 能量快速注入, 放电通道温度与电离度快速升高, 放电电流快速增长, 电压快速下降, 形成电弧通道, 为能量快沉积阶段^[37], 相应注入能量构成快沉积能量; t₃—t₄为电弧维持阶段(III), 沉积功率变小, 由于电路参数约束导致的周期性振荡, 导致沉积功率小幅振荡直至放电结束. 该时段的放电能量沉积相较于(I), (II)阶段慢许多, 故称为慢沉积能量. 所以, 图9黑色波形可以划分为两个阶段, 黑色虚线所示区分为能量快、慢沉积阶段. 对于图9的PPT工况, 可以计算, PPT放电的快沉积能量$ {E}_{{\mathrm{q}}}\approx 3.6 $ J占放电过程总沉积能量(4.6 J)的78%; 而慢沉积能量$ {E}_{{\mathrm{s}}}\approx1.0 $ J, 约占总沉积能量的22%. 其中, 能量快沉积阶段对应于推进剂的烧蚀、电离和放电通道成长过程, 快沉积能量消耗在这些过程中. 而能量慢沉积阶段持续时间较长, 能量消耗用于放电通道加热维持与电磁加速转化为机械能. 可见, PPT放电能量的注入过程决定了能量分配比例, 用于推进剂烧蚀、电离(阶段I+II)与用于放电通道的成长、维持及电磁加速(阶段III)的能量是互相竞争的. 其中, 阶段I+II决定等离子体密度, 即电流片质量, 而阶段II决定电磁加速动能大小, 所以放电注入能量在阶段I+II与III之间的分配需要调控优化, PPT的机-电效率才可能最大化.

图10展示了不同工况下PPT放电能量以及慢沉积能量占比. 图10(a)的每个数据柱分为上下两段, 下段为快沉积能量$ {E}_{{\mathrm{q}}} $, 上段为慢沉积能量$ {E}_{{\mathrm{s}}}$. 图10(a)表明: 1)随着充电电压升高, 快、慢沉积能量均上升; 2)随电极间隙的增大, 快、慢沉积能量在不同电压下的趋势则有所不同. 充电电压为1—1.4 kV范围内, 电极间隙的作用趋势不明朗, 似乎小电极间隙有利于放电能量注入. 而充电电压1.6—2 kV范围内, 极间隙的作用趋势清晰, 较大极间距使得放电通道延长, 推进剂烧蚀面增大, 有利于快沉积能量的注入, 这与文献[38]结果相吻合, 即在较大放电能量时, 放电间隙增大能够有效提升推进剂烧蚀量. 图10(b)显示了图10(a)各工况下的慢沉积能量占比(按照$ {\eta }_{{\mathrm{s}}}=100{\text{%}} \times \dfrac{{E}_{{\mathrm{s}}}}{{E}_{{\mathrm{s}}}+ {E}_{{\mathrm{q}}}} $计算), 表明: 不同工况下慢沉积能量占比在17%—22%之间, 变化幅度不大. 而能量慢沉积阶段是电磁加速形成羽流机械能的主要时段, 所以提高慢沉积能量占比才有可能显著提高PPT机-电效率, 提高充电电压和优化极间隙工艺改进之外, 需要开展PPT放电能量分配机制和调控技术的探索.

本文针对基本PPT机-电模型中电路方程和放电通道电流片的简化模型导致的局限性, 提出了体现放电通道形态特征的改进型二维电流片模型. 基于二维电流片模型分析了放电通道受力情况以及电磁自加速过程, 推导了PPT羽流电磁加速动能与放电等效回路电感变化率的定量关系; 针对含时系数电路方程提出了时间分段拟合放电波形得到等效回路电感变化率的计算方法, 形成了基于放电波形仿真计算PPT羽流电磁加速动能的分析方案. 将该机-电模型用于PPT样机的能量转化及机-电效率分析以开展验证. 结果表明, 改进型机-电模型通过修正基本机-电模型的过度简化, 使得电流片模型更接近放电通道实际形态, 电路方程更符合放电回路的真实表现. 所以改进后的机-电模型对PPT放电通道形貌的适用范围扩大, 改进后的电路方程的仿真程度更高. 改进型机-电模型计算结果表明PPT样机的机-电效率很低, 符合预期, 而且与其他文献的结果相符. PPT样机系列工况下机-电效率计算结果界定了改进型机-电模型的适用条件. 分析了PPT放电沉积能量的分配机制, 阐述了导致PPT机-电效率低的原因, 仅改变PPT放电工况不能大幅度提高机-电效率, 须探索PPT放电能量分配机制和调控技术, 寻找大幅度提升PPT机-电效率的思路.