二维材料在微纳电子和光电器件制造中具有广泛应用前景. 自2004年首次成功合成石墨烯以来, 由于其高达10⁶ cm²/(V·s)的载流子迁移率, 引起了人们的广泛关注^[1]. 然而, 石墨烯零禁带宽度的特性限制了其应用. 在对石墨烯进行调整改进这项工作中, 人们尝试了很多种方法. Su等^[2]对石墨烯进行原子替换, 得到二维$ { \mathrm{BC_{3} }} $和$ { \mathrm{C_{3}N }} $, 通过GGA-PBE泛函发现其带隙分别为0.70 eV和0.41 eV. 进一步探究了其在300 K下的电子和空穴迁移率. $ { \mathrm{BC_{3} }} $的电子迁移率为6.56 × 10² cm²/(V·s), 空穴迁移率为9.60 × 10¹ cm²/(V·s); $ { \mathrm{C_{3}N }} $的电子迁移率为8.54 × 10² cm²/(V·s), 空穴迁移率为3.26 × 10³ cm²/(V·s). 虽然带隙被打开, 但载流子迁移率显著降低, 仍难以满足高性能器件的需求. 因此, 寻找具有高载流子迁移率的半导体材料成为研究重点. 例如, Qu等^[3]报道了同构型的二维ZrNBr不仅具有极高的载流子迁移率, 并在下一代高性能和低功耗NMOS和PMOS器件应用中表现出优异的性能. 此外, 作为第四代半导体材料的氧化镓, 其本征迁移率数值可达300 cm²/(V·s). Li等^[4]通过镓基液态金属掺杂铜的方式, 使用表面生长法制备了P型氧化镓, 并且打印设计了高功率同质结二极管. 在此基础上, 最近的研究还表明, 二维金属卤化物在超低功耗的新型MOSFET中同样具有巨大的应用潜力. Guo等^[5]研究了卤化硼烯(Bx, x = F, Cl, Br)在5 nm高性能MOSFET中的量子输运特性, 发现其高度各向异性的半导体电子结构可以在超缩尺度下实现优异的器件性能. Shi等^[6]对各向异性单层GaSCl的电子特性和输运性能进行了研究, 发现其在10 nm通道长度下的p型FET可实现高性能和低功耗的表现, 有望成为下一代高效P型通道材料.

Song等^[7]通过高通量筛选方法, 在替换CrSBr中发现得到了340多个MXX ' (M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, Hf, Ta, W, Re, Os, Ir, Pt, Au; X = S, Se, Te; X ' = F, Cl, Br, I)化合物, 其中发现45种半导体, 并且在这些半导体中, 得到同时兼具好的热稳定性和较高的载流子迁移率的材料. 根据形变势理论(DPT), 他们发现这些材料的载流子迁移率将近10³ cm²/(V·s), 空穴在y方向的迁移率高达10⁵ cm²/(V·s)(PBE方法).

本文首先使用声子色散曲线和第一性原理 分子动力学(AIMD)验证了材料在300 K下的稳定性. 利用形变势理论方法^[8–10], 通过计算单层IrSCl和IrSI的弹性模量、形变势和有效质量, 推导了其载流子迁移率. 进一步探索了双轴应变对IrSCl和IrSI能带宽度以及有效质量的影响^[11], 展示了应变工程在调控材料性能中的潜力. 最后, 基于玻尔兹曼方程精确计算了载流子迁移率, 发现迁移率结果与DPT结果在同一个数量级, 表明使用DPT计算迁移率具有一定参考价值.

形变势模型是预测载流子迁移率的一种半经验模型. 这一模型最早由Bardeen和Shockley于1950年提出, 适用于各向同性的材料^[12], 对于各向异性二维材料, 迁移率公式修改为^[13]

式中e是电子电荷量; $\hbar $是约化普朗克常数; $ C_{x}, C_{y}$是弹性模量; $ {k_\text{B}} $是玻尔兹曼常数; T是温度; m^*是有效质量; E是形变势. 从(1)式可以看出, x方向的迁移率仅与x方向的弹性模量和形变势有关. 实际上, 载流子会被声子往每个方向散射^[14], 如果考虑到弹性模量和形变势的各向异性, 则修正之后的迁移率公式为^[13,15]

在实际计算中, 二维材料的载流子迁移率可以简化为^[11]

式中$m_{\mathrm{e}}^{\ast }$是有效质量, 由公式$m_{\mathrm{e}}^{\ast } = \pm \hbar ^{2} \left ( \dfrac{\mathrm{d}^{2} E_{\mathrm{k}} }{\mathrm{d}k^{2} } \right )^{-1} $可以得到, 其中$ \left ( \dfrac{\mathrm{d}^{2} E_{\mathrm{k}} }{\mathrm{d}k^{2} } \right )$的值是通过能量$E_{\mathrm{k}}$与 倒易向量$\boldsymbol k $二次拟合得到的. $m_{\mathrm{d}}$是平均有效质 量, 由公式$m_{\mathrm{d}} = \sqrt{m_{x}^{\ast } m_{y}^{\ast }} $得到. 弹性模量$C_{2\mathrm{D}} = \dfrac{1}{S_{0} } \dfrac{\partial^{2}\left (E-E_{0} \right ) }{\partial \varepsilon ^{2} } $, 其中$E-E_{0} = \Delta E$为总能量变化, ε为单轴应变量, $S_{0}$是x-y平面的晶格面积. 可利用E的表达形式对弹性模量进行如下变形^[10,16]:

式中p表示体系的压强; h代表二维材料之间的真空层厚度; a和b是二维材料的晶格常数; $ \Delta V $代表体系的体积变化量; $ a_{0} $是初始状态下a方向的晶格常数; 应变ε定义为长度变化量与初始长度的比值, 即$\varepsilon = l-l_{0} $, 其中l是变化后的长度, $ l_{0} $是初始长度; 形变势$E_{\mathrm{d}} = \mathrm{d}E_{\mathrm{edge}} /\mathrm{d}\varepsilon $, 通过拟合能带边缘随形变一次函数得到. T设置为300 K.

玻尔兹曼输运方程(BTE)描述了载流子分布函数$f_{nk} $的时间演化. 从电场漂移并从晶格散射的载流子将倾向于偏离其平衡状态($ f_{nk}^0 $). 在稳定状态下, BTE可以简化为如下公式^[17–19]:

式中漂移项可以写为$\left ( \dfrac{\partial f_{nk} }{\partial t} \right ) _{{\mathrm{drift}}} = \dfrac{e}{\hbar }E\cdot \nabla _{k}f_{nk}$, 其中E表示电场. 散射项可以表示为$\left ( \dfrac{\partial f_{nk} }{\partial t} \right ) _{{\mathrm{scatt}}} = -\dfrac{f_{nk} -f_{nk}^{0} }{\tau _{nk} } $. 载流子迁移率可用下式计算^[20]:

式中, n是载流子浓度, $nk$表示第一布里渊区中k网格的数量, $\varOmega $是单位晶胞的体积. 分布函数对电场的导数由下式给出:

式中$ \nu_{nk} = \hbar^{-1} \partial \varepsilon_{nk} / \partial k $是能量$ \varepsilon_{nk} $下的电子速度; $ {1}/{\tau _{nk} } $表示由声子散射引起的跃迁概率; $\hbar \omega _{q\lambda }$是λ模式的声子能量; q网格是指在布里渊区内用来计算电声耦合矩阵元的一组离散k点, $N_{q}$是第一布里渊区中q网格的数量; $ n_{\pm q\lambda} $是由玻色-爱因斯坦分布确定的声子的平均数量, +/–表示声子的吸收/发射; $g_{mn\lambda } \left ( k, q \right ) $表示载流子通过模式为λ的声子从$nk$态到m态的跃迁概率, 可分为短程(S)和长程(L)部分^[21,22]. 在方程(10)中, $\dfrac{\partial f_{mk+q} }{\partial E_{\alpha } } $必须通过迭代方法求解, 也称为迭代玻尔兹曼输运方程(IBTE). 如果弛豫时间取Fan-Migdal电子自能的虚部, 通过$\dfrac{1}{\tau _{nk} } = 2 {\mathrm{Im}} { \displaystyle\sum\nolimits_{nk}^{FM}} $, 则由自能弛豫时间近似(SERTA)得到的迁移率表达式可以描述为^[23]

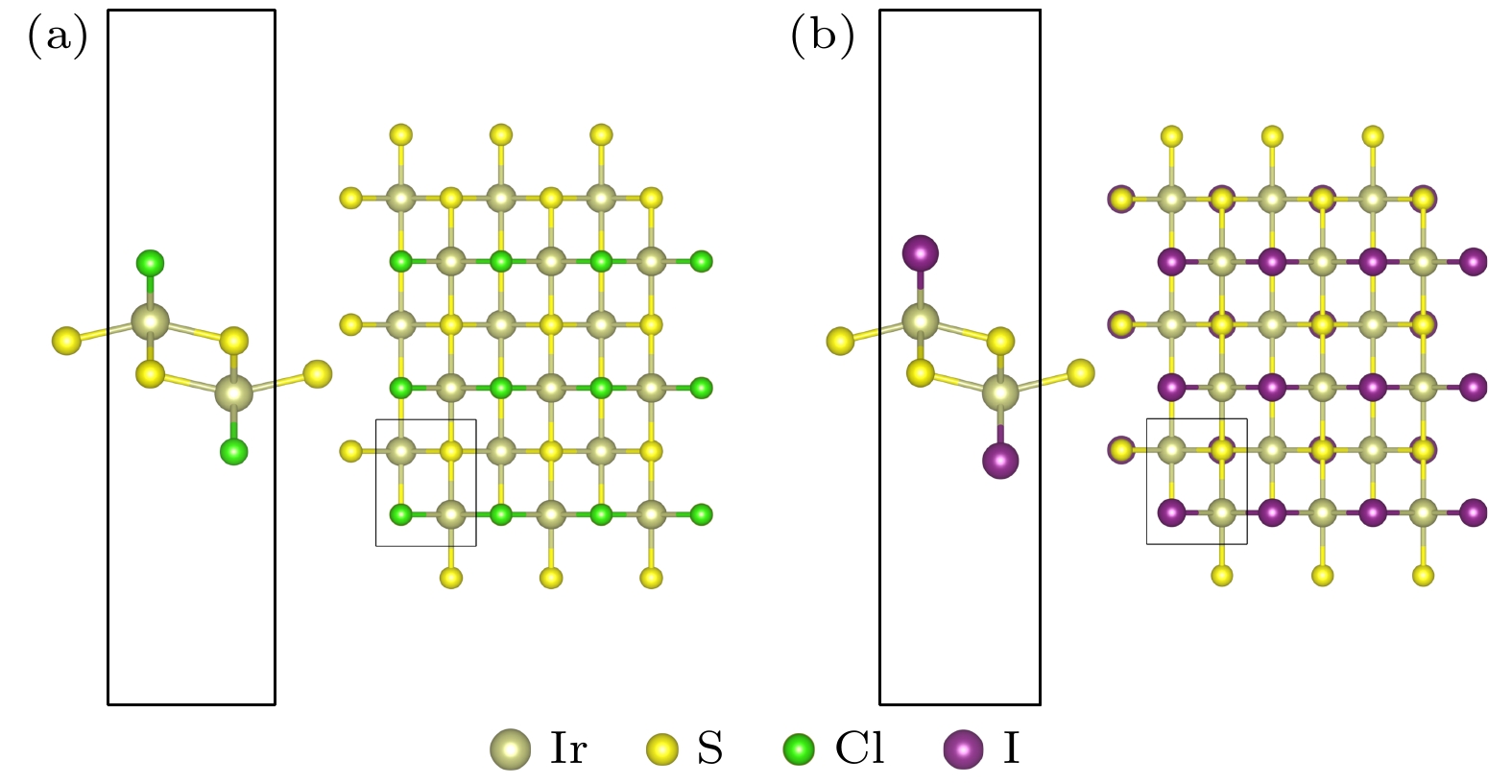
首先对结构进行优化计算, 使用Norm-conserving (NC)赝势^[24]和Perdew-Burke-Ernzerhof (GGA-PBE)交换关联泛函^[25]在quantum espresso软件^[26]中进行. 设置平面波截断能为70 Ry, 电荷密度截断能为280 Ry. 布里渊区采用8×6×1的k点网格. 图1(a)给出了单层的IrSCl的晶胞结构, 由两个Ir原子、两个S原子和两个Cl原子组成. 将x轴定义为水平向右, y轴定义为垂直向上. 在z轴方向设置20 Å 的真空层以避免层间相互作用. 原子完全弛豫至每个原子上的力小于10^–3 Ry/Bohr. 计算得到单层IrSCl的晶格常数为a = 3.56 Å, b = 4.66 Å, 与之前Song等^[7]报道的结果一致. 图1(b)显示了单层IrSI的晶胞结构, 由两个Ir原子、两个S原子和两个I原子组成. 坐标轴和计算参数 定义同上. 计算得到单层IrSI的晶格常数为a = 3.75 Å, b = 4.46 Å, 与之前报道的结果一致^[7]. 布里渊区的高对称点选取Γ(0, 0), X(0.50, 0), M(0.50, 0.50), Y(0, 0.50). 在此基础上, 使用密度泛函理 论计算声子谱, 考虑了极化效应和自旋轨道耦合效应^[27]. 利用Wannier插值方法计算了电子-声子耦合矩阵元, 从而得到单层IrSCl和IrSI的载流子迁移率^[28].

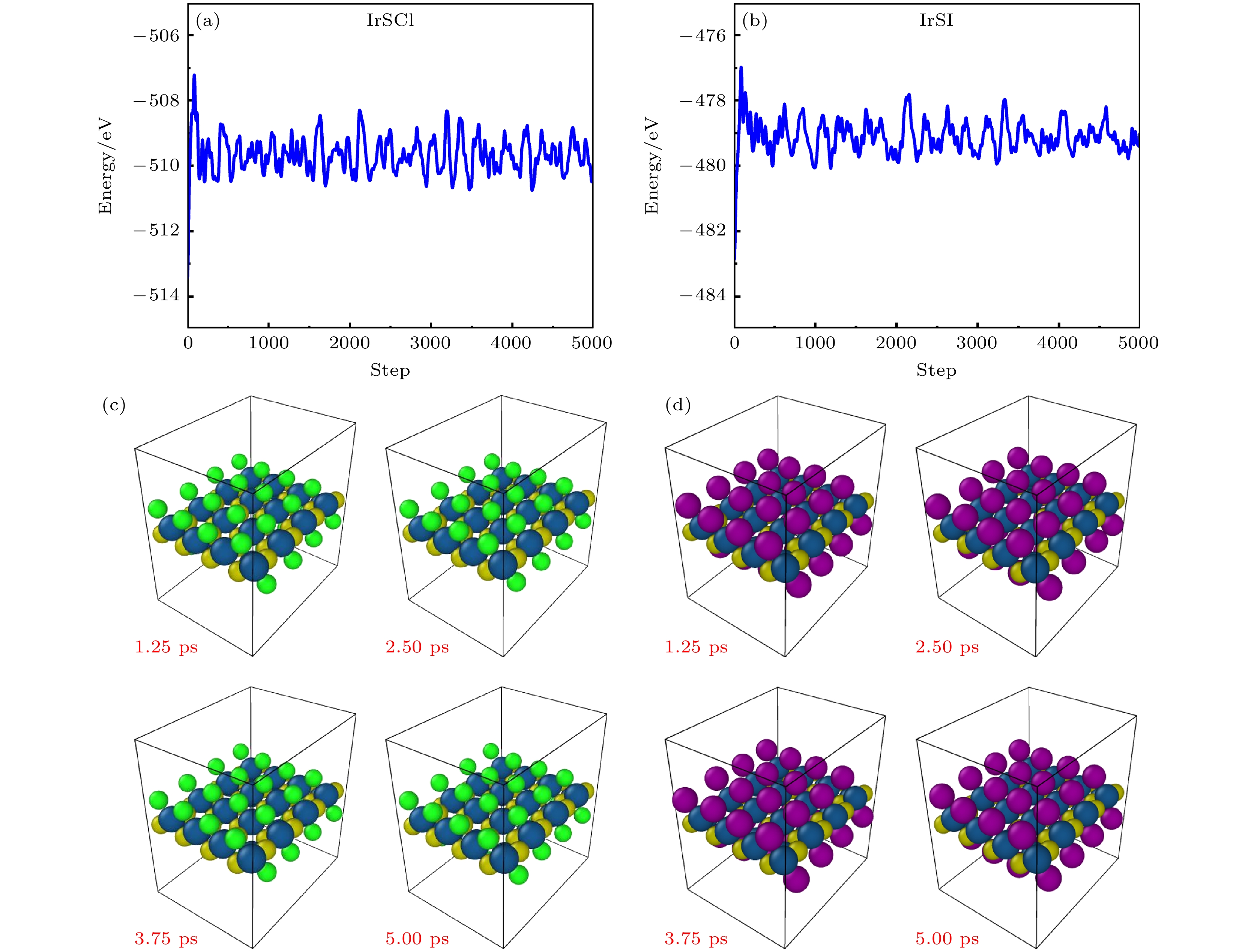
为了研究IrSCl和IrSI化合物的热稳定性, 本工作首先对两种化合物的弛豫后结构进行了分 子动力学模拟. 模拟温度设为300 K, 总步数为5000步, 时间步长为1 fs, 截断能设为500 eV, 收敛精度设置为10^–4 eV. 图2(a)和图2(b)显示, 在5 ps内, 两种化合物的总能量波动在5 eV范围内, 趋于稳定状态, 未出现大幅度能量变化. 图2(c)和图2(d)分别展示了IrSCl和IrSI在模拟的1.25, 2.5, 3.75和5 ps时刻的原子构型. 可以看出, 在5 ps时间内, 每个原子仅在其原位置附近振动, 未发生明显的原子重排, 表明在300 K下IrSCl和IrSI均具有良好的热稳定性. 上述分子动力学模拟结果证实, 在常温条件下, IrSCl和IrSI化合物的原子结构具有热力学稳定性.

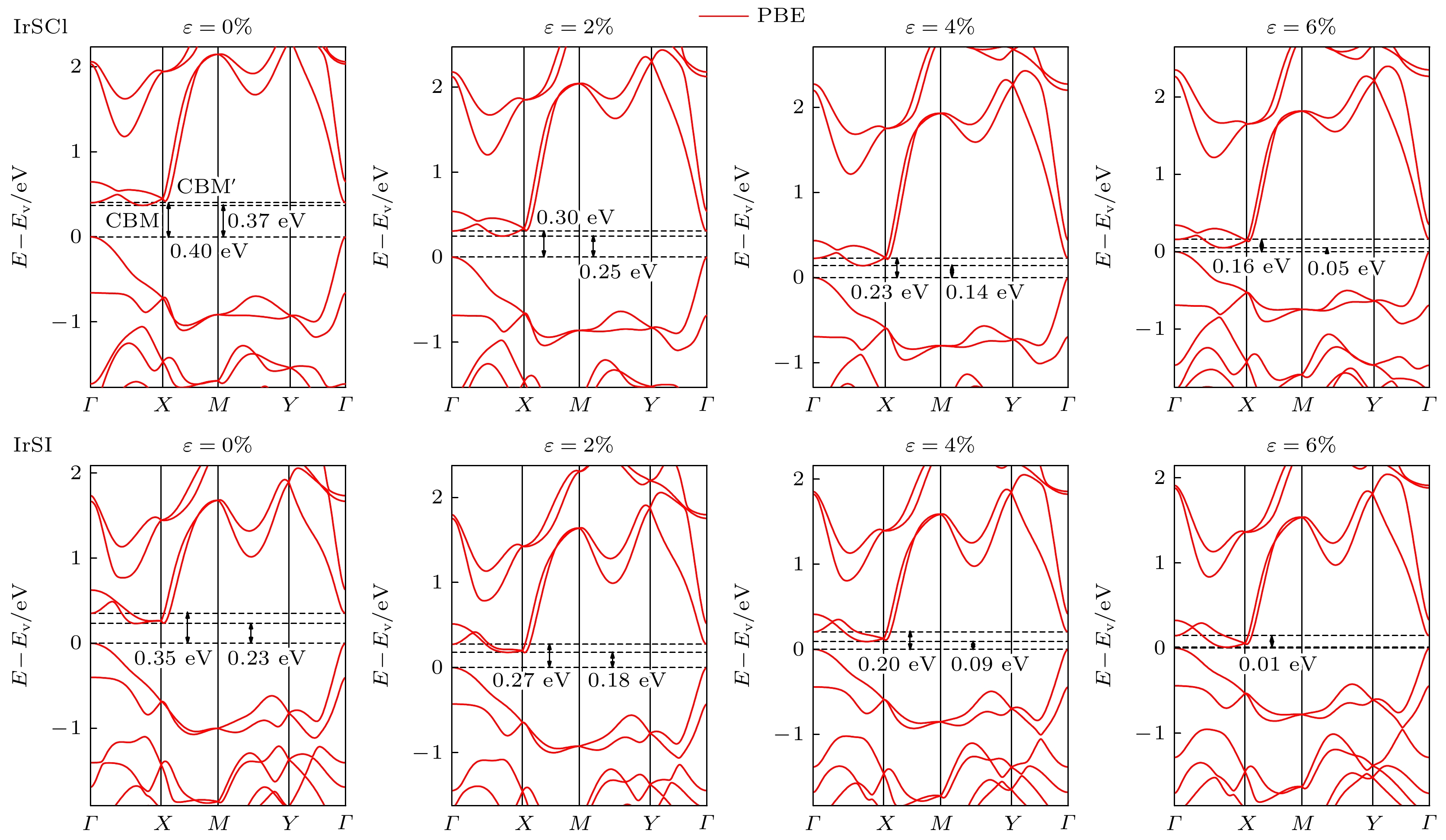
基于GGA-PBE泛函理论, 本文探讨了单层IrSCl和IrSI在双轴应变作用下的能带结构变化, 具体结果如图3所示. 两种材料均为间接带隙半导体, 价带顶(VBM)位于Γ点, 导带底(CBM)位于Γ点与X点之间, 且导带中存在一个与导带底相近的次级导带底(CBM'). 在无应变条件下, GGA-PBE计算得到IrSCl和IrSI的禁带宽度分别为0.37 eV和0.23 eV, 与文献报道的值(0.3 eV和0.2 eV)符合较好^[7]. 由于GGA-PBE泛函通常低估半导体的禁带宽度, 因此这里进一步采用HSE06泛函对能带间隙进行了修正. 图4给出了基于HSE06泛函计算的IrSCl和IrSI的能带结构. 修正后, IrSCl的能带间隙为1.58 eV, IrSI为1.36 eV. HSE06计算结果表明, 两种材料的能带间隙均大于1 eV, 显示出在下一代电子器件中潜在的应用前景, 更符合实验结果和实际应用的需求.

在双轴应变作用下, IrSCl和IrSI的禁带宽 度随应变增大而逐渐减小. 对于IrSCl, 当应变为2%, 4%和6%时, 禁带宽度分别降至0.25, 0.14和0.05 eV; 而对于IrSI, 禁带宽度相应为0.18, 0.09和0.01 eV. 结果表明, 双轴应变显著改变了IrSCl和IrSI的电子结构特性.

为了准确计算载流子有效质量, 本文通过对价带顶和导带底附近数据进行高密度采样的方法来进行计算. 根据有效质量公式$m^{\ast } = \left ( \hbar ^{2} \Big/\dfrac{\partial ^{2} E}{\partial k^{2} } \right ) $, 价带顶和导带底附近的数据可以拟合为$E = Ak^{2} + Bk+C$, 进而得到$m^{\ast } = \left ( \hbar ^{2} /2 A \right )$, A为二次拟合的二次项系数. 可以计算IrSCl和IrSI在不同应变条件下载流子的有效质量. 在无应变情况下, 二维IrSCl的价带顶空穴有效质量分为$m_{x} = 1.839 m_{\mathrm{e}} $和$m_{y} = 0.232 m_{\mathrm{e}} $; 导带底电子的有效质量为$m = 2.081 m_{\mathrm{e}} $, 次级导带底电子的有效质量为$m_{x} = 3.300 m_{\mathrm{e}} $和$m_{y} = 0.179 m_{\mathrm{e}} $. 对于二维的IrSI, VBM空穴的有效质量为$m_{x} = 2.295 m_{\mathrm{e}} $和$m_{y} = 0.244 m_{\mathrm{e}} $; CBM'电子的有效质量为$m_{x} = 1.337 m_{\mathrm{e}} $和$m_{y} = 0.238 m_{\mathrm{e}} $. 随着双轴应变的增加, IrSCl中除$m_{x, {\rm{h}}} $外, 其他有效质量均有所增加. 在ε = 6%时, 分别上升为$m_{x, {\rm{e}}} = 3.861 m_{\mathrm{e}} $, $m_{y, {\rm{h}}} = 0.379 m_{\mathrm{e}} $, $m_{y, {\rm{e}}} = 0.196 m_{\mathrm{e}} $. 而IrSI中, $ m_{x, {\rm{h}}} $和$ m_{y, {\rm{e}}} $有效质量下降, $ m_{x, {\rm{e}}} $和$ m_{y, {\rm{h}}} $有效质量上升, 在$ \varepsilon = 6{\text{%}} $时分别为$ m_x = 2.134 m_{\mathrm{e}} $, $ m_y = 0.205 m_{\mathrm{e}} $, $ m_x = 1.512 m_{\mathrm{e}} $和$ m_y = 0.300 m_{\mathrm{e}} $. 不同应变下的有效质量列于表1. 根据有效质量与迁移率的关系, 随着有效质量的增大, 载流子迁移率大概率呈现下降趋势. 综合考虑有效质量变化规律, 本文只计算了两种材料在原长条件下的迁移率. 上述计算结果表明, 双轴应变能显著调控二维IrSCl和IrSI的能带间隙.

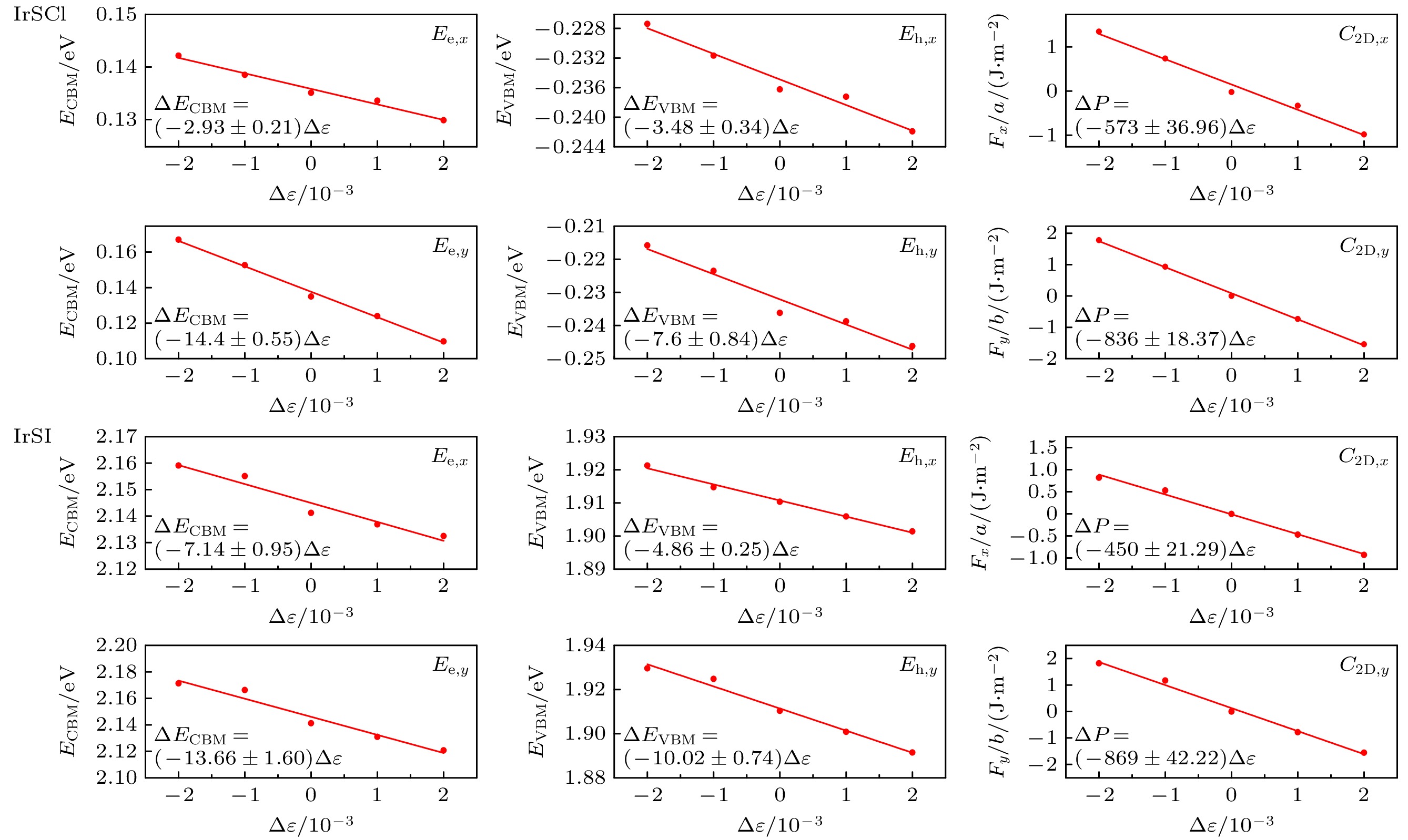
根据形变势模型: $\mu _{2{\mathrm{ D}}} = \dfrac{e\hbar ^{3}C_{{\rm{2 D}}} }{k_{{\rm{B}}} Tm_{\mathrm{e}}^{\ast }m_{{\rm{d}}} E_{{\rm{d}}}^{2}}$. 想要通过公式计算二维材料载流子迁移率, 首先需要知道该材料的形变势、弹性模量等参数. 本文通过对IrSCl和IrSI施加单轴微小应变, 获得了能带边缘随应变的变化关系, 应变范围设置为–0.2%—0.2%, 间隔为0.1%, 具体结果如图5所示, 通过线性拟合的斜率得到形变势. 弹性模量可由$C_{{\rm{2 D}}} = h\dfrac{\partial p}{\partial \varepsilon } $得到. 对于IrSCl材料, 电子沿x方向和y方向的形变势分别为2.93 eV和14.4 eV, 空穴沿x方向和y方向的形变势分别为3.48 eV和7.6 eV; 弹性模量方面, x方向和y方向的值分别为114.6 J/m²和167.2 J/m². 对于IrSI材料, 导电子沿x方向和y方向的形变势分别为7.14 eV和13.66 eV, 空穴沿x方向和y方向的形变势分别为4.86 eV和10.02 eV. 弹性模量方面, x方向和y方向的值分别为90 J/m²和173.8 J/m². 将以上参数代入形变势模型, 可以计算出二维材料的载流子迁移率. 这些结果对理解二维材料的电子输运性质和器件应用具有重要意义.

根据形变势模型的计算结果, 得到单层IrSCl和IrSI的载流子迁移率如表2所列. 由于次级导带底与导带底之间能量值相近, 且从能带图(图3)的变化趋势来看, 次级导带底附近的有效质量明显更小, 因此本文仅计算了该部分的迁移率, 以评估迁移率上限值. 对于IrSCl材料, 其x方向和y方向的值分别为112.84 cm²/(V·s)和161.88 cm²/(V·s). 空穴迁移率由VBM决定, x方向和y方向的值分别为168.50 cm²/(V·s)和407.77 cm²/(V·s). 对于IrSI材料, 电子迁移率由CBM' 决定, 其x方向和y方向的值分别为50.14 cm²/(V·s)和148.90 cm²/(V·s). 空穴迁移率由VBM决定, x方向和y方向的值分别为47.49 cm²/(V·s)和202.64 cm²/(V·s). 可以看出, 这两种二维材料均存在各向异性, y方向上的载流子迁移率明显大于x方向.

尽管形变势模型是一种广泛应用的半经验预测半导体材料性质的方法, 但其中不可避免存在一定的误差. 相比之下, 基于玻尔兹曼输运理论计算电子-声子耦合矩阵元的方法, 能够更加直接和准确地预测材料的载流子迁移率. 为了节省计算时间并获得可靠的结果, 本文采用Wannier函数插值方法, 精确计算了所有电声耦合矩阵元, 并通过玻尔兹曼输运方程计算单层IrSCl和IrSI的载流子迁移率.

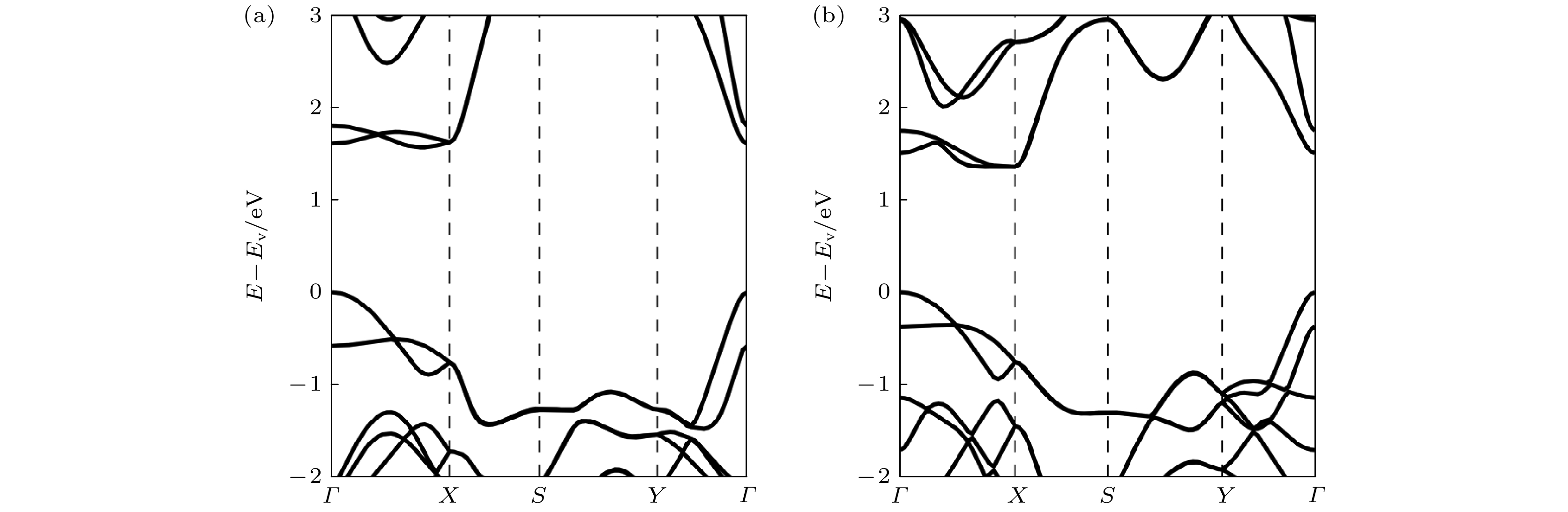
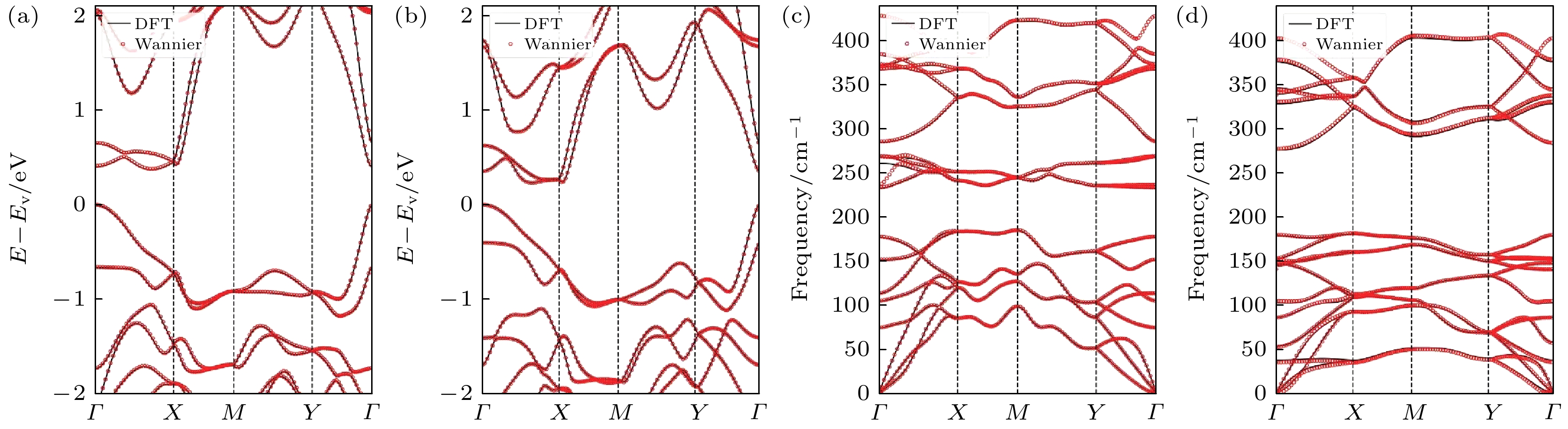
为确保计算的精确性, 采用精细的k点网格(16×8×1)和q点网格(8×6×1). 首先, 将基于Wannier插值方法计算得到的能带结构和声子色散与DFT结果进行对比, 结果如图6所示. 可以发现, 两种方法所得的能带图和声子色散基本一致, 验证了计算的可靠性. 从声子谱中也可以看出, 该二维材料具有稳定的晶体结构.

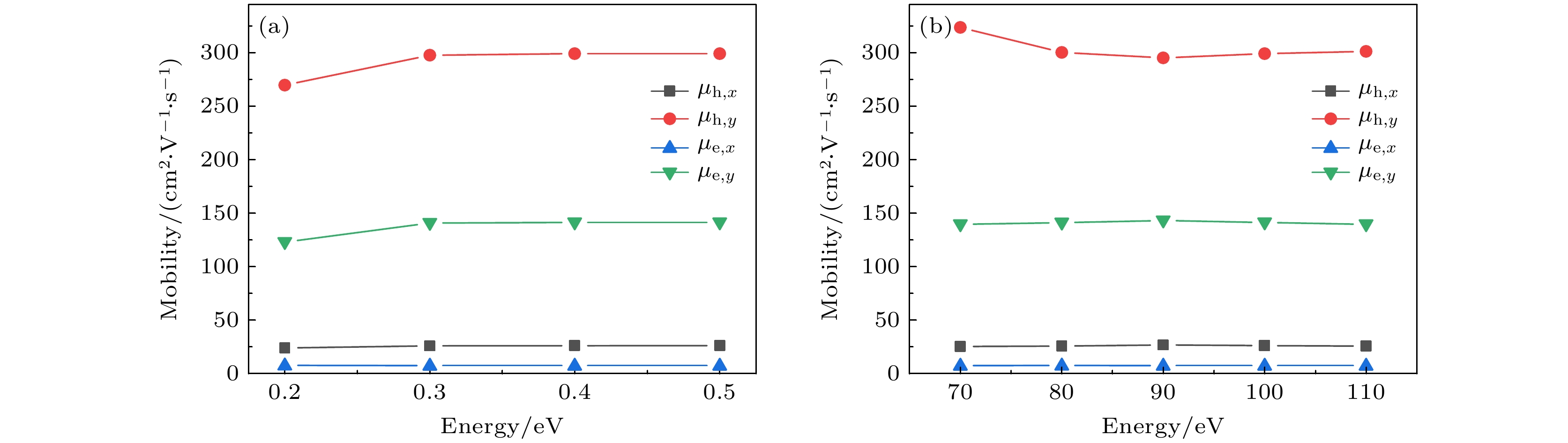
随后, 以IrSCl为例进行了Wannier插值深度的测试, 结果如图7(a)所示. 对于插值深度的测试, 选取了0.2—0.6 eV的范围, 步长为0.1 eV. 可以发现, 在进入深度为0.4 eV及以上时, 计算结果趋于稳定. 接下来测试了不同的插值密度, 范围从70 × 70到110 × 110, 步长为10 × 10, 如图7(b)所示. 结果表明, 在该范围内误差基在1%以内. 因此, 本文最终选择的能量深度为0.4 eV, 插值密度设置为100 × 100.

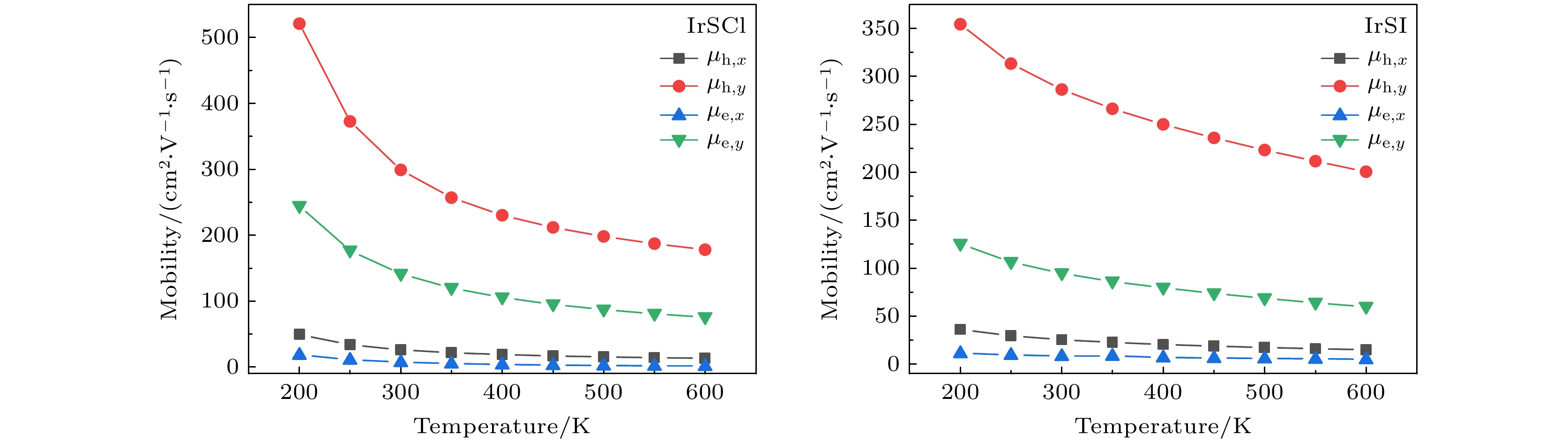
基于玻尔兹曼输运方程, 计算了单层IrSCl和IrSI在300 K下的载流子迁移率, 结果如表3所列. 对于IrSCl, 电子的迁移率为$ \mu _{{\rm{e}}, x} $ = 7.57 cm²/(V·s), $ \mu _{{\rm{e}}, y} $ = 141.39 cm²/(V·s), 空穴的迁移率为$ \mu _{{\rm{h}}, x} $ = 26.20 cm²/(V·s), $ \mu _{{\rm{h}}, y} $ = 299.44 cm²/(V·s). 而对于IrSI, 电子的迁移率为$ \mu _{{\rm{e}}, x} $ = 8.44 cm²/(V·s), $ \mu _{{\rm{e}}, y} $ = 94.75 cm²/(V·s), 空穴的迁移率为$ \mu _{{\rm{e}}, x} $ = 8.44 cm²/(V·s), $ \mu _{{\rm{e}}, y} $ = 94.75 cm²/(V·s). 同时, 探究了在200—600 K不同温度下两种材料的载流子迁移率, 结果如图8所示. 可以看出, 随着温度的升高, 迁移率逐渐下降. 这两种材料在y方向上的迁移率明显高于x方向, 差别达到一个数量级, 可能的原因是y方向的有效质量远大于x方向的有效质量.

本文基于密度泛函理论, 系统地研究了单层IrSCl和IrSI的载流子迁移率. 在计算迁移率前, 首先验证了二维材料IrSCl和IrSI的稳定性. 通过计算两种材料的声子色散关系, 发现得到的声子频率均大于0, 证明材料在0 K下是稳定存在的. AIMD模拟结果表明, 在5 ps内, 两种化合物的总能量波动在5 eV范围内, 未出现大幅能量变化并且每个原子仅在其原位置附近振动, 未发生明显的原子重排, 表明在300 K下IrSCl和IrSI均具有良好的热稳定性. 通过能带结构的计算, 发现IrSCl有着0.37 eV的禁带宽度, IrSI有着0.23 eV的禁带宽度, 均为半导体材料. 通过双轴应变, 发现随着应变的增加, 能带间隙逐渐减小. 通过形变势理论模型计算了IrSCl和IrSI的载流子迁移率, IrSCl在x方向和y方向的电子迁移率分别为112.84 cm²/(V·s)和161.88 cm²/(V·s); x方向和y方向的空穴迁移率分别为168.50 cm²/(V·s)和407.77 cm²/(V·s). 对于IrSI, x方向和y方向的电子迁移率分别为50.14 cm²/(V·s)和148.90 cm²/(V·s); x方向和y方向的空穴迁移率分别为47.49 cm²/(V·s)和202.64 cm²/(V·s). 从结果来看, y方向的迁移率远大于x方向, 说明两种材料存在明显的各向异性. 接着通过求解电声耦合矩阵元的方法计算了IrSCl和IrSI的本征迁移率, 并探究了不同温度下载流子迁移率的变化. 在300 K时, 对于IrSCl, $ \mu _{{\rm{e}}, x} $ = 7.57 cm²/(V·s), $ \mu _{{\rm{e}}, y} $ = 141.39 cm²/(V·s), $ \mu _{{\rm{h}}, x} $ = 26.20 cm²/(V·s), $ \mu _{{\rm{h}}, y} $ = 299.44 cm²/(V·s); 对于IrSI, $ \mu _{{\rm{e}}, x} $ = 8.44 cm²/(V·s), $ \mu _{{\rm{e}}, y} $ = 94.75 cm²/(V·s), $ \mu _{{\rm{h}}, x} $ = 25.44 cm²/(V·s), $ \mu _{{\rm{h}}, y} $ = 266.34 cm²/(V·s). 根据本文研究发现, 二维IrSCl和IrSI在300 K下表现出良好的热稳定性, 并且具有较高的载流子迁移率及较为合适的能带宽度, 有望成为电子器件候选材料.