-
量子存储器可以实现光量子比特的存储[1-3], 基于量子存储的量子中继[4,5]可以有效地克服信道损耗, 从而建立起长程的量子纠缠网络[6,7]. 此外, 量子存储器还可以支持多光子产生[8-11]、高效率光子探测[12,13]以及分布式量子计算[14]等任务的实现. 稀土掺杂晶体[15,16]是目前被广泛使用于量子存储的固体材料, 其优异的光学及超精细跃迁相干特性能够支持长寿命的量子存储[17-22], 并且还具备大带宽[23,24]和多模式[24-27]存储等优点. 稀土掺杂晶体作为固体材料, 天然地具备易于加工和实现集成化应用的优点. 飞秒激光加工[28-32]、聚焦离子束[33-36]和电子束曝光[37,38]等加工技术已成功应用于稀土掺杂晶体, 实现可集成的量子存储器件.
Eu3+离子具有长达6 h的核自旋相干时间以及1 h的相干光存储时间[19,22], 成为了长寿命量子存储的重要候选介质[21,22]. 在飞秒激光加工技术的推动下, 151Eu3+:Y2SiO5波导的量子存储研究也取得了系列进展[29-31]. 近期的工作已成功在151Eu3+:Y2SiO5晶体中实现了可集成的自旋波量子存储[39]. 相比于飞秒激光加工, 聚焦离子束的加工精度更高, 在稀土掺杂晶体中可以实现纳米量级的加工精度[33,34]. 聚焦离子束可以在晶体表面刻蚀出三角形的悬梁臂结构(triangular nanobeam)[40]. 该悬梁臂由于具有高折射率特性, 能够使光束在其中发生全反射, 从而有效束缚激光沿悬梁臂传播. 此前, Yb3+[36], Nd3+[41,42]和Er3+[34,43]离子已通过聚焦离子束技术加工出微纳结构, 并成功实现可集成的量子存储器和单个离子的探测. 然而, Eu3+离子的光学跃迁波长相对较短, 使其在聚焦离子束加工方面面临更大的挑战[35]. 聚焦离子束加工的波导中的Eu3+离子的光跃迁和超精细跃迁特性仍缺乏表征, 这阻碍了聚焦离子束技术在基于Eu3+离子的可集成量子存储及单离子探测方面的应用[36,41].
本文利用聚焦离子束技术在151Eu3+:Y2SiO5晶体中刻蚀出三角形的悬梁臂波导, 对波导内151Eu3+离子的光学和超精细跃迁特性进行了详细表征, 具体包括基于荧光手段测量的光学上能级布居数寿命、光学与自旋非均匀展宽, 基于瞬态光谱烧孔测量的光学均匀线宽, 以及基于自旋回波序列测量的自旋相干寿命, 以探索聚焦离子束这一工艺路线对于151Eu3+:Y2SiO5晶体加工的适用性和可行性.
-
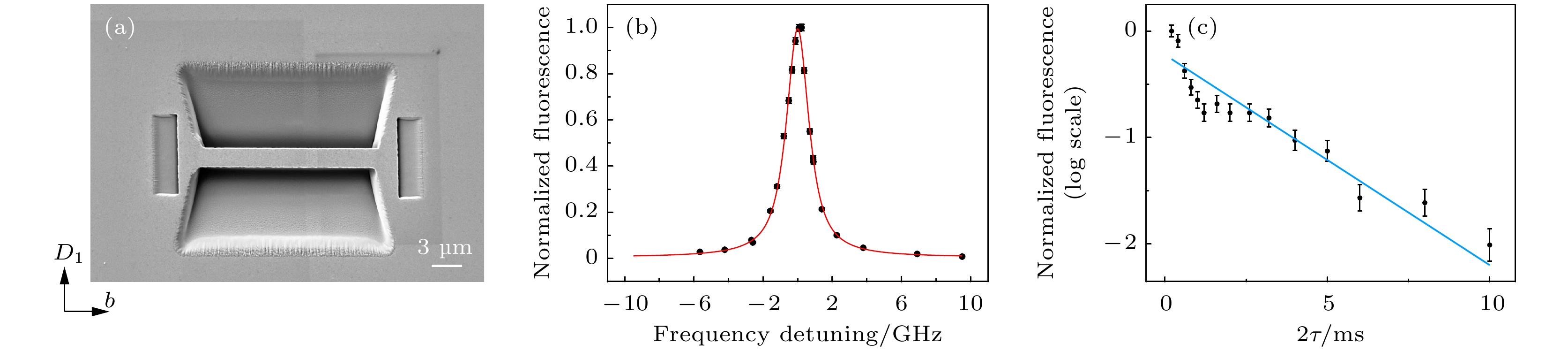
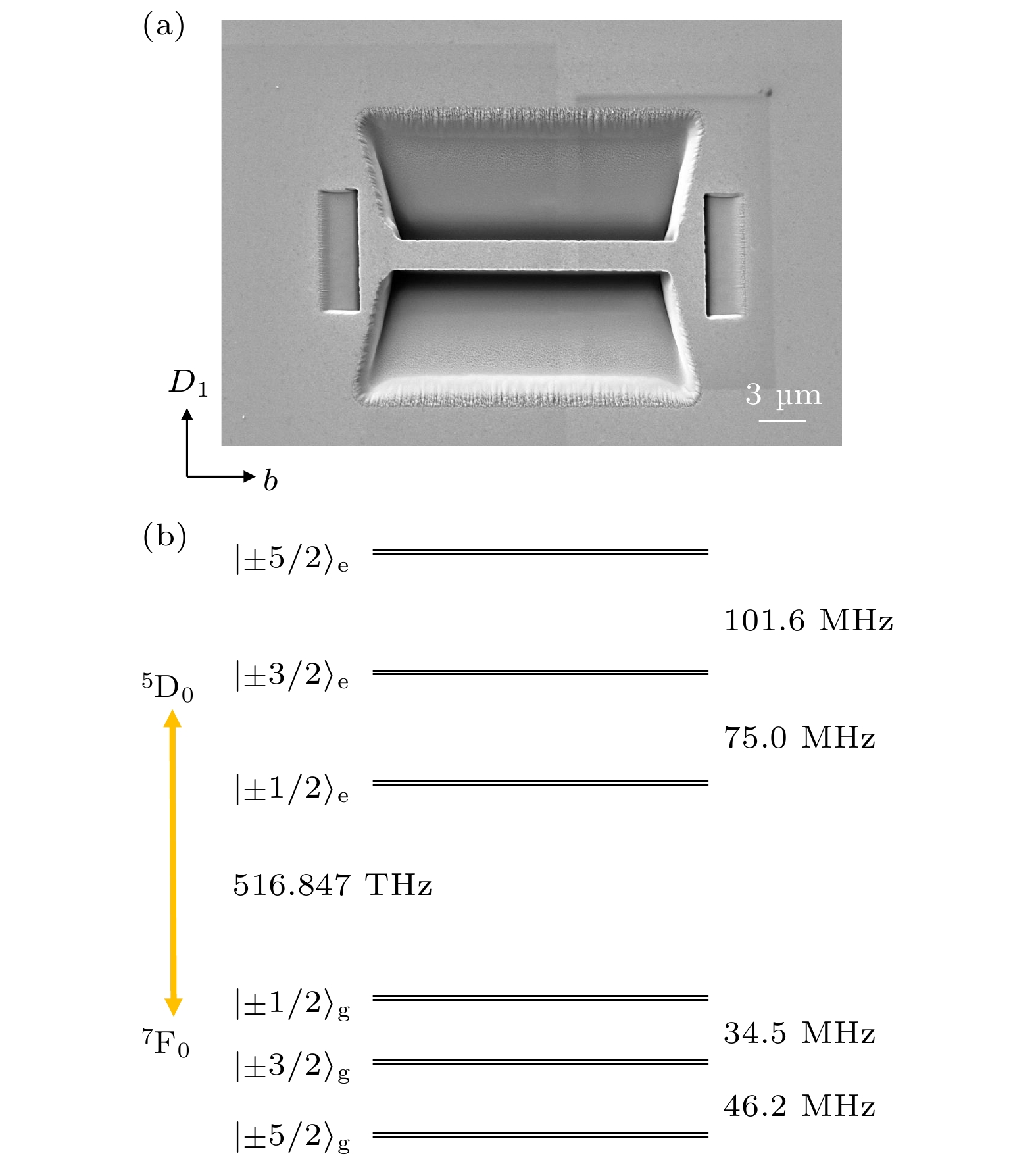
图1(a)展示了通过聚焦离子束(Crossbeam 550 FIB-SEM)刻蚀后的151Eu3+:Y2SiO5晶体的电子束成像照片. 该晶体中151Eu3+的掺杂浓度为0.07%, 尺寸沿晶体D1, D2, b轴方向分别为
$5\;{\mathrm{ mm }}\times 1\;{\mathrm{mm}}\times 4\;{\mathrm{mm}} $ . 151Eu3+的能级结构如图1(b)所示. 在晶体的$5\;{\mathrm{mm}} \times4\;{\mathrm{mm}} $ 抛光面上刻蚀出悬梁臂波导, 悬梁臂的长度(沿b轴)为20 µm, 宽度(沿D1轴)为2 µm. 悬梁臂的输入输出端加工了一对45°斜面, 使激光在斜面上全反射耦合进悬梁臂中, 再从另一端斜面出射. 加工过程中离子束电流从10 pA到3 nA变化, 便于快速地刻蚀出光滑且平整的表面. 在聚焦离子束加工过程中, 样品表面会积累电荷, 导致加工时发生漂移现象[35]. 为了抑制此现象, 利用电子束蒸镀技术使晶体表面均匀地覆盖一层厚度为50 nm的铜金属薄膜, 从而提升晶体表面的导电性能. 在聚焦离子束加工完成后, 通过氧化剂去掉金属镀层以便于光学探测. 为了修复加工过程中引入的缺陷并提高悬梁臂波导的耦合效率, 对加工样品进行了退火. 退火过程是经过6 h升到800 ℃, 再维持此温度6 h, 最后经历6 h降至室温, 此退火过程重复了两次. -
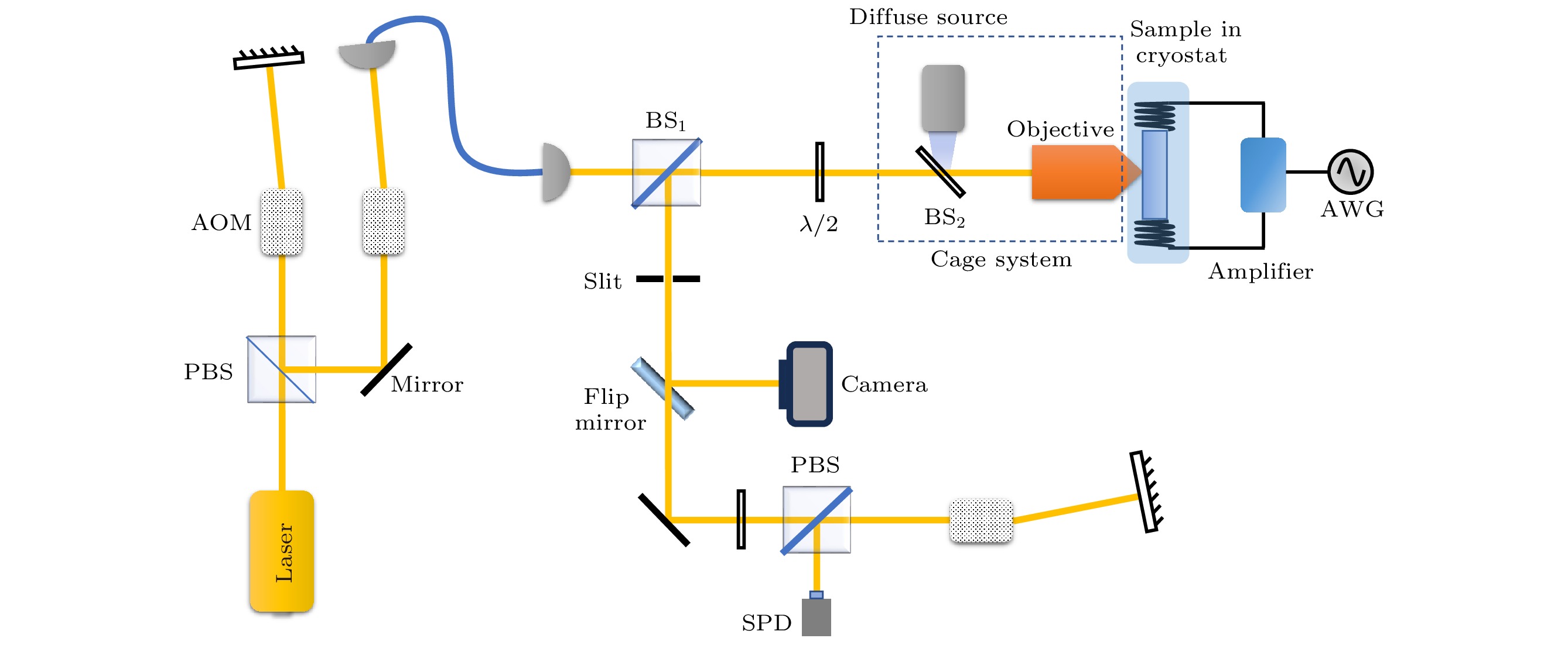
图2 是测量样品光学与超精细跃迁性质的实验装置图. 本文使用的激光器是倍频半导体激光器(Toptica, TA-SHG), 通过超稳F-P腔锁定后的激光线宽低于1 kHz. 首先, 双次通过的声光调制器对激光的频率和幅度进行调制. 然后, 单次通过的声光调制器作为快速光开关进一步提高脉冲的关断比. 单模光纤将光传输到图中右侧的波导耦合光路, 在分束器(BS1)后通过半波片控制入射光的偏振方向使波导的耦合效率达到最大. 该偏振方向同时对准了晶体的D1轴使得151Eu3+吸收达到最大. 本文搭建了一套共聚焦的笼式系统用于将激光耦合到悬梁臂波导中, 同时收集悬梁臂波导另一端输出的激光. 所使用的物镜是Mitutoyo的LCD Plan Apo NIR HR 50x, 它具有0.65的数值孔径和9.6 mm的工作距离. 此物镜能够校正0.7 mm玻璃厚度的低温腔窗片所产生的像差. BS1的反射端是信号输出端. 通过相机观察晶体加工的表面成像以及光斑的位置, 借此辅助完成耦合的粗调过程. 最后的探测装置包括双次通过的声光调制器构成的快速光开关, 用于保护单光子探测器. 悬梁臂波导的输入-输出耦合效率为22%, 波导出射光的单模收集效率为60%.
晶体样品放置于3 K工作温度的低温恒温器中, 搭配上三轴低温位移台便于耦合激光与悬梁臂波导. 除特别声明外, 实验中样品的工作温度都设置在3 K. 亥姆霍兹线圈安装在晶体两侧(两侧的线圈匝数分别为4匝), 用于发射射频信号以实现对151Eu3+离子的自旋操控. 该射频信号由任意波形发生器产生, 并经过250 W的脉冲式射频放大器放大.
-
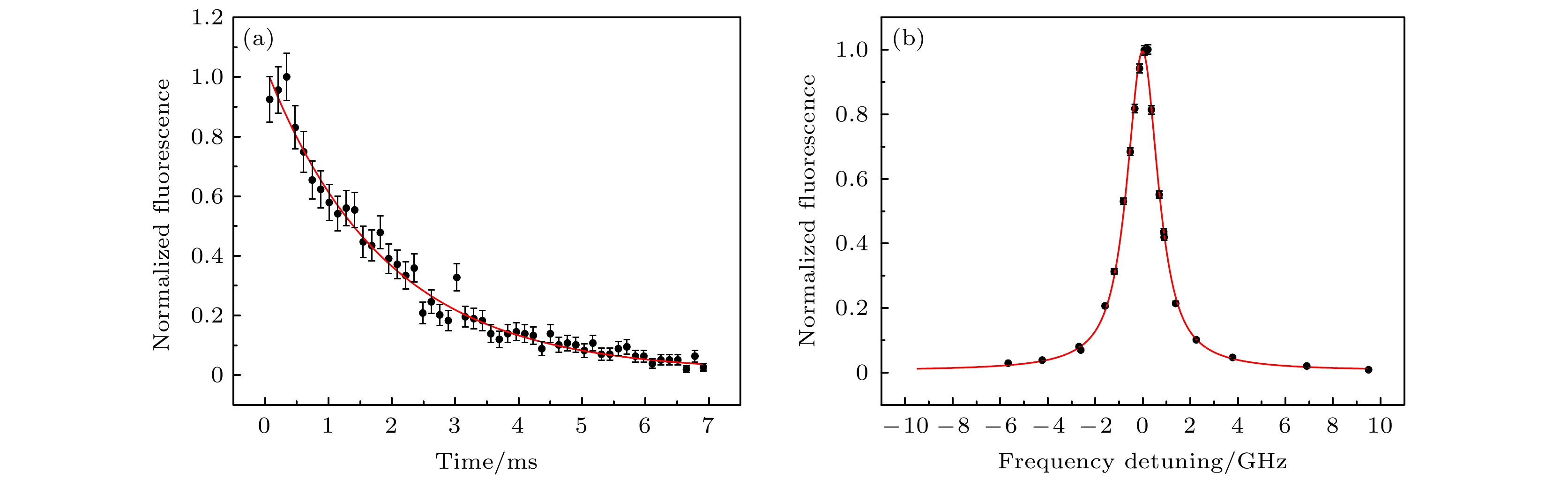
和典型的激光直写波导(20 µm直径, 12 mm长度)相比[31], 悬梁臂波导内的151Eu3+离子数量下降了约6个量级. 这导致悬梁臂波导的151Eu3+离子吸收光谱难以直接测试, 故本文利用光致激发荧光测量的实验手段[44]. 如图3(a)所示, 利用光学泵浦对布居数进行初始化后, 观察光致激发荧光随时间的衰减曲线, 可以得到光学上能级布居数寿命T1为(1.9±0.1) ms, 与块状晶体的光学T1一致[45]. 为了进一步调控上能级布居数寿命, 可以加工高Q值的光子晶体腔, 通过Purcell效应来提高151Eu3+离子激发态的自发辐射速率, 从而提高光学泵浦以及自旋极化的效率[42].
光学跃迁和超精细跃迁的非均匀展宽反映的是每个离子局域环境的差别, 直接体现了微纳加工过程的破坏性. 从存储器的角度看, 光学非均匀展宽加宽会导致有效吸收降低, 从而导致存储效率下降[39]. 为此, 本文首先测试了波导内151Eu3+离子的光学非均匀展宽.
为了确保每个测试周期中151Eu3+离子的布居数能恢复到热平衡态, 避免光谱烧孔效应[45], 测试中样品温度控制在18 K, 实验的循环周期设置为200 ms. 激发光脉冲是时间宽度1 ms和扫描带宽3.8 MHz的啁啾脉冲. 通过改变激发光脉冲的中心频率, 并测量激发脉冲10 µs后2 ms探测窗口的荧光计数来分析光学跃迁展宽.
实验结果如图3(b)黑点所示. 151Eu3+离子的光学非均匀展宽线型采用pseudo-Voigt函数拟合[44,46,47]:
其中,
$ L(\omega) $ 和$ G(\omega) $ 分别代表洛伦兹线型和高斯线型, μ为洛伦兹线型在混合线型中的权重系数,$ V_0 $ 为本底, A为曲线面积. 曲线的半高全宽为非均匀展宽. 拟合后的光学非均匀展宽为(1.58±0.05) GHz, 其中μ为0.93±0.06, 表明当前的光学非均匀展宽由洛伦兹线型所主导[46]. 相比于块状晶体的光学非均匀展宽[44,45], 波导内151Eu3+离子的展宽增大了约0.26 GHz. 展宽提高的原因可能是晶体在安装过程中受到的应力不均匀导致的加宽[48], 以及晶体在µm量级的表面品质有所下降. 相比激光直写加工过程[30], 聚焦离子束技术的实际加工展宽更小, 破坏性更低. 加工过程采用的退火技术可能修复了晶体缺陷, 从而减弱加工过程中光学非均匀展宽的加宽. 这一结果启发我们对于激光直写波导, 也可以采用退火等修复手段进一步降低加工展宽.151Eu3+离子的光跃迁及超精细跃迁的相干性都会受到周围磁噪声的干扰. 而聚焦离子束会从结构表面注入镓离子, 这可能对151Eu3+离子的光学和超精细跃迁都引入额外的退相干过程, 因此对151Eu3+离子的相干性测试对于评价这一加工手段的可行性至关重要. 光学均匀线宽[38,49]直接反映了光学相干寿命的上限, 体现了光学跃迁的相干性, 并实际制约了光谱烧孔等操作的分辨率[45,50]. 在加工过程中, 我们采用金属薄膜和极低的离子束电流, 用于减少注入的镓离子数目, 以保护151Eu3+离子的相干性. 本文使用瞬态光谱烧孔[51,52]来测量光学均匀线宽. 在样品的非均匀展宽之内, 输入三束频率间隔相等且光强一致的激光. 当三束光的频率间隔大于均匀线宽时, 每束激光会独立激发样品, 它们产生的荧光信号约等于一束光的3倍. 当三束光的频率间隔小于均匀线宽时, 荧光信号的总量约为一束光的
$ \sqrt{3} $ 倍. 因此荧光信号会随着三束光频率间隔的增大而增大, 变化过程呈洛伦兹线型:其中Δ为频率间隔,
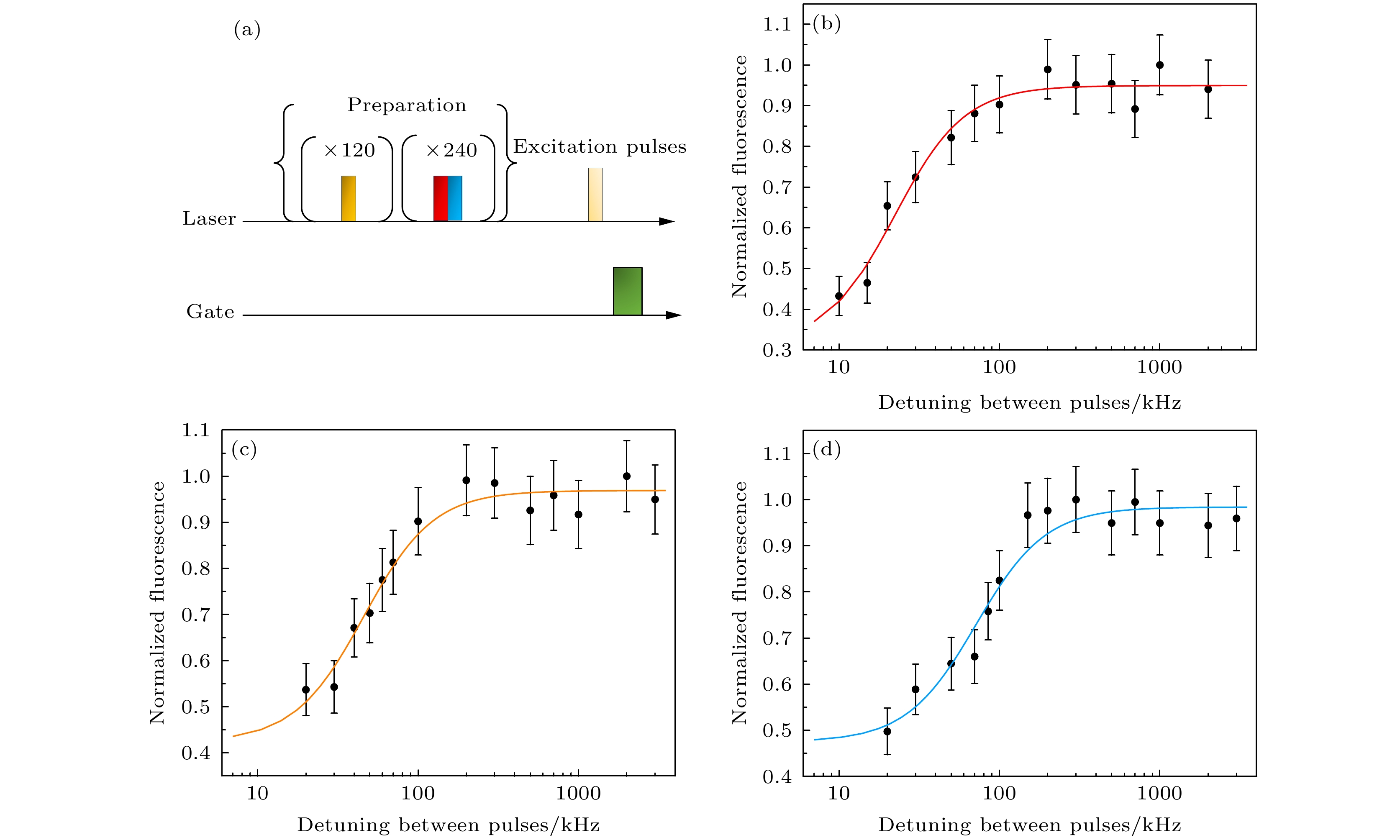
$ L_0 $ 为本底,$ A_{\mathrm{L}} $ 为曲线面积,$ w_{\mathrm{L}} $ 为曲线的半高全宽. 光学均匀线宽的上限是半高全宽的一半[49].为了增强荧光信号, 参考文献[31]设计泵浦脉冲来初始化样品布居数. 此过程首先是在f0中心频率处制备一个带宽9.6 MHz的烧孔, 然后在(f0±27.9) MHz的两个中心频率处分别制备带宽46.2 MHz的烧孔. 这样即可在中心频率f0处获得带宽9.6 MHz的增强吸收带. 每个烧孔脉冲的时间宽度为1 ms, 且两步初始化过程的时间间隔为1 ms. 两步初始化过程的脉冲重复次数分别为120次和240次. 激发光采用三束强度一致的单频脉冲, 时间宽度为0.15 ms, 频率分别为f0, f0 ± Δf. 测量这三束光产生的荧光随Δf的变化. 完整的脉冲时序图如图4(a)所示. 在单频激发脉冲功率分别为220, 440和660 nW下, 所测得的荧光变化曲线如图4(b)—(d)所示. 三者拟合出的均匀线宽分别为(22±3) kHz (图4(b)), (46±6) kHz (图4(c)), (71±10) kHz (图4(d)). 由于图4(b)的荧光信号较弱, 故设定实验重复次数为1500次, 剩余两组实验的重复次数设定为1000次. 可以看到均匀线宽随激光功率增强而变大, 这符合瞬时光谱扩散(ISD)效应的预期. 拟合数据得到的瞬时光谱扩散系数
$ S_{\rm ISD} $ 为(0.96±0.01)×10–12 Hz·cm3. 该结果与此前块状晶体的实验也在相同的量级上[45]. 本文采用的激发光功率密度偏大, 导致了较强的瞬时光谱扩散效应, 进一步降低激发功率有望测到显著降低的光学均匀线宽. 然而受制于当前实验的信噪比, 激发光功率已难以进一步降低. 预期未来可以通过提升器件效率以及制造腔结构等手段, 来获取更弱激发功率条件下的光学均匀线宽数据. 保持长寿命的光学相干性是实现傅里叶极限的单光子发射的必要条件, 这对于量子网络中独立量子节点间的全同性光子干涉也具有重要意义[53]. -
为了实现基于151Eu3+自旋波的应用, 接下来进一步表征悬梁臂波导中151Eu3+离子的超精细跃迁特性. 7F0基态的
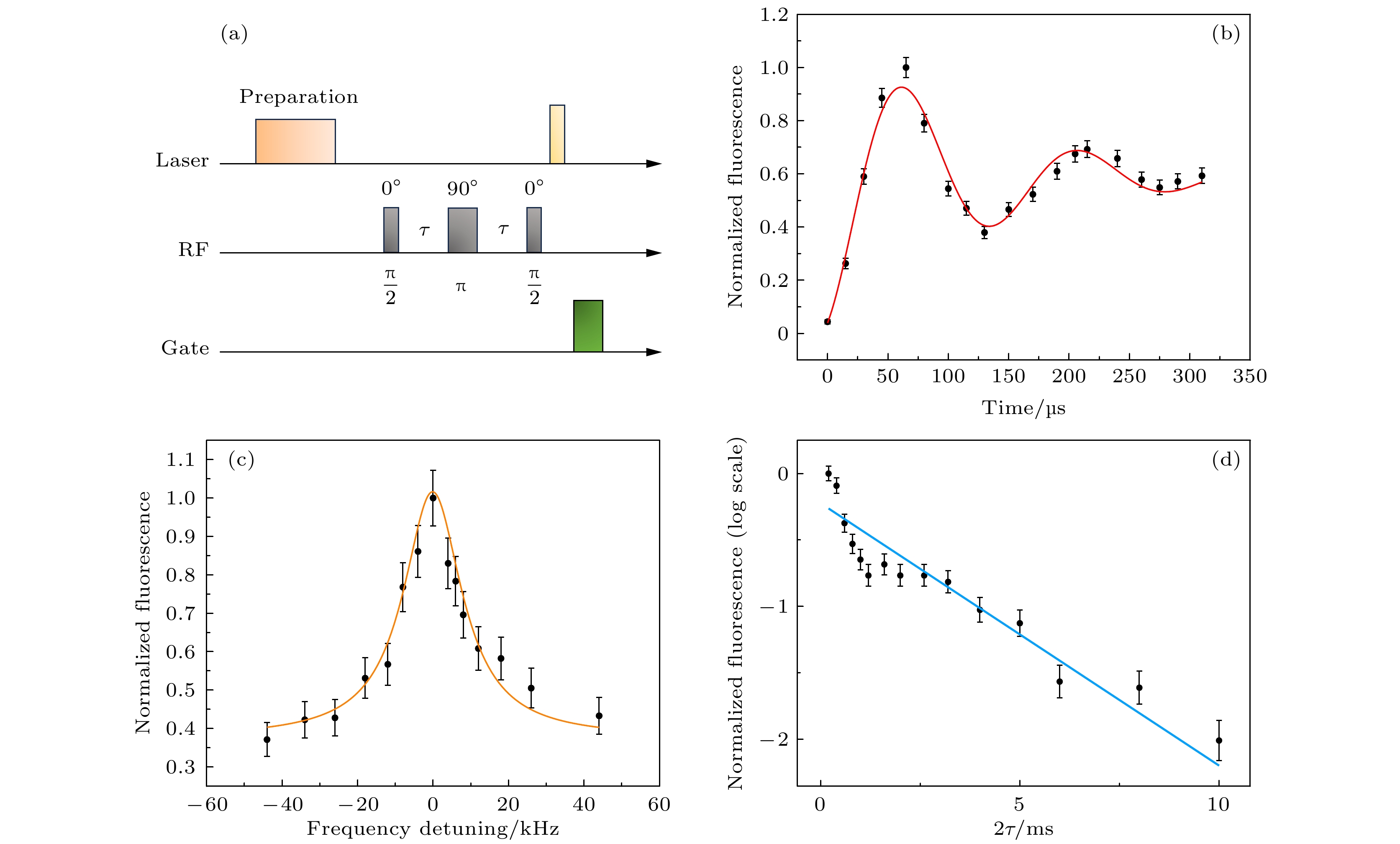
$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ 超精细跃迁的分析是基于光学探测磁共振(ODMR)技术[44]. 图5(a)展示了利用荧光测试自旋相干寿命的脉冲序列. 所施加的射频(RF)序列是自旋回波(spin echo)序列[54]. 布居数被初始在$ |{\pm3/2}\rangle_{\mathrm{g}} $ 上, 在t = 0的时刻, 利用晶体旁的亥姆霍兹线圈产生π/2射频脉冲使151Eu3+离子进入$ |{\pm1/2}\rangle_{\mathrm{g}} $ 与$ |{\pm3/2}\rangle_{\mathrm{g}} $ 的叠加态. 经过一段自由演化时间τ, 再次施加一个π射频脉冲, 其相位需要与第一个脉冲相差90°, 使得自旋态演化方向翻转180°. 经过同样的演化时间τ后, 151Eu3+离子系综会重新会聚产生自旋回波. 在此刻施加一个π/2射频脉冲, 其相位与第一个脉冲一致, 可以将布居数转移到$ |{\pm1/2}\rangle_{\mathrm{g}} $ 上以便基于光学荧光手段的探测. 在射频脉冲序列结束后, 施加与$ |{\pm1/2}\rangle_{\mathrm{g}} $ 共振的激发光脉冲产生荧光信号. 这一荧光信号会随着演化时间的延长而衰减, 从而获得$ |{\pm1/2}\rangle_{\mathrm{g}} $ 与$ |{\pm3/2}\rangle_{\mathrm{g}} $ 超精细跃迁的相干寿命.实验中使用的π射频脉冲是通过自旋章动(spin nutation)测得的[55], 如图5(b)所示. π脉冲的宽度为65 µs, 而
$ \pi/2 $ 脉冲的脉宽为π脉冲的一半. 从图5(b)可以得到Rabi频率为$ \varOmega_{\mathrm{R}}/2\pi $ = (7.6± 0.2) kHz, 振荡的衰减常数为$ \tau_{\mathrm{R}} $ = (120±10) µs. 因为自发辐射和退相干过程, Rabi振荡会随时间衰减. 根据公式$ 1/\tau_{\mathrm{R}} = 3/(4 T^{\rm spin}_1)+ 1/(2 T_2^{*\rm spin}) $ [56], 其中T$ ^{\rm spin}_1 $ 为自旋布居数寿命, T$ _2^{*\rm spin} $ 为超精细跃迁的纯退相干时间(pure dephasing time). Eu3+离子的自旋布居数寿命长达23天, 计算时可忽略[45], 推算出超精细跃迁的纯退相干时间为(60±5) µs, 对应的自旋非均匀展宽为(17±1) kHz.自旋非均匀展宽会导致每个离子的零一阶塞曼(ZEFOZ)磁场点有细微差别, 直接限制系综自旋相干寿命的上限[57]. 另外, 超精细跃迁的非均匀展宽加宽会导致动力学解耦所需求的π脉冲的保真度降低. 综合而言, 跃迁展宽会导致存储器存储寿命和存储效率的下降. 进一步利用ODMR直接测量自旋跃迁的非均匀展宽, 即通过扫描射频脉冲频率测量光脉冲激发的荧光强度来获得跃迁谱, 具体测量序列与前期工作[44]一致. 如图5(c)所示, 得到
$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ 超精细跃迁的自旋非均匀展宽为(19±3) kHz. 此结果相较于同浓度的块状晶体增加了3.6 kHz[44], 并且提高的比例与光学非均匀展宽相近. 这一对比说明导致自旋非均匀展宽增加的机制与光学非均匀展宽增加的机制应类似, 且退火技术可能同样修复了加工过程中超精细跃迁的非均匀展宽.保持长的自旋相干寿命, 是实现长寿命量子存储的必要条件, 对于实用化量子中继及可移动量子存储器的实现具有重要意义[19]. 图5(d)展示悬梁臂波导中151Eu3+离子的
$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ 跃迁的退相干过程. 在短时间内, 实验数据出现振荡过程, 这是由于地磁场引起的超精细能级的微小劈裂导致的调制效果[58,59]. 按照单指数$ \exp{(-2\tau/T_2)} $ 拟合实验数据[58,59], 得到的自旋相干寿命T2为(5.1$ \pm $ 0.6) ms. 这一结果也与我们在相同条件下的块状晶体中测得的自旋相干寿命一致, 表明聚焦离子束刻蚀对于151Eu3+:Y2SiO5在地磁场下的自旋相干寿命没有可观测的影响. 本工作为在纳米尺度实现151Eu3+离子的长寿命自旋波量子存储奠定了基础. -
本文首次利用聚焦离子束刻蚀工艺在151Eu3+:Y2SiO5晶体的表面刻出三角形悬梁臂波导, 研究了悬梁臂波导中的151Eu3+离子的光学和超精细跃迁特性. 表征了悬梁臂波导中151Eu3+离子的光学上能级布居数寿命、光学与自旋非均匀展宽等性质, 并测试了光学均匀线宽与自旋相干寿命. 这些结果均与块状晶体中的对应参数基本保持一致, 表明聚焦离子束刻蚀对151Eu3+:Y2SiO5晶体的损伤程度很低, 展现该材料在利用聚焦离子束技术实现集成化量子存储器方面的应用潜力. 本文基于聚焦离子束刻蚀的悬梁臂波导的截面宽度为2 µm, 相比在151Eu3+:Y2SiO5晶体上加工的激光直写波导[31], 当前波导截面宽度下降了一个量级, 而151Eu3+离子的光学及自旋非均匀展宽的增加并不显著, 对晶体的损伤程度更低, 这对于151Eu3+离子在超长寿命量子存储中的应用具有重要意义[44,57], 体现了聚焦离子束刻蚀相比飞秒激光刻蚀的潜在优势. 聚焦离子束加工的波导具有更小的尺寸, 相比于激光直写波导, 可以进一步提高单一器件上的量子存储通道的数量, 利用非球透镜阵列可以实现对量子存储器的阵列耦合.
后续工作可以在悬梁臂波导上进一步刻蚀周期性矩形凹槽, 实现光子晶体腔的加工[33-35,40]. 此加工过程的主要挑战在于凹槽的周期控制精度需达到1 nm量级, 并保持凹槽的侧面垂直于波导上表面[35], 这些加工误差将直接影响光子晶体腔的Q值. 相比本文中的波导加工, 尽管凹槽结构的引入增大了刻蚀面积, 但由于刻蚀过程中采用更低电流的离子束, 预计镓离子的注入量将保持在较低水平, 预期Y2SiO5晶体内部的磁环境噪声不会发生显著变化. 高Q值的光子晶体腔可以有效增强151Eu3+离子与光场的相互作用, 基于Purcell效应降低151Eu3+离子的光学上能级布居数寿命, 从而提升其发光速率. 由于光学跃迁相干寿命受限于光学跃迁布居数寿命, 故腔内151Eu3+离子的光学相干寿命会相应地缩减, 而腔内151Eu3+离子的自旋相干寿命则不受影响. 最终, 有望实现基于单个151Eu3+离子的量子光源以及长寿命量子存储.
聚焦离子束加工的硅酸钇波导中铕离子的光学与超精细跃迁
Optical and hyperfine spectroscopic investigations on europium ions doped in yttrium orthosilicate waveguides fabricated by focused ion beam milling
-
摘要: 量子存储是大尺度量子网络的重要组成部分, 基于波导等微纳结构的可集成量子存储可以提供更好的可扩展性并实现更低的光电能耗. 在众多量子存储候选介质中, 151Eu3+:Y2SiO5晶体具有长达6 h的自旋相干寿命和1 h的相干光存储时间, 成为长寿命存储的优异候选材料. 本文通过聚焦离子束在151Eu3+:Y2SiO5晶体表面加工出三角形悬梁臂波导, 波导截面的边长为2 µm, 长度为20 µm, 并对三角形悬梁臂波导中的151Eu3+离子的7F0—5D0光学跃迁以及7F0基态的超精细跃迁开展了研究. 结果显示, 在2 µm尺度的悬梁臂波导中151Eu3+离子基本保持了和块状晶体中151Eu3+离子一致的跃迁展宽及相干寿命, 可以支持量子存储任务的实现. 该工作为实现纳米尺度的151Eu3+离子可集成量子存储器以及单个151Eu3+离子的探测打下基础.Abstract: Quantum memory is a crucial element in large-scale quantum networks. Integrated quantum memories based on micro-/-nano structures, such as waveguides, can significantly enhance the scalability and reduce the consumption of optical and electrical power. 151Eu3+:Y2SiO5 stands out as an exceptional candidate material for quantum memory, because it possesses a spin coherence lifetime of 6 h and an optical storage lifetime of 1 h. Here we employ focused ion beam technology to fabricate a triangular nanobeam on the surface of a Y2SiO5 crystal. The width and length of the nanobeam are 2 μm and 20 μm, respectively. The optical lifetime and inhomogeneous broadening of 151Eu3+ in the triangular nanobeam are measured by fluorescence spectroscopy. The optical lifetime is (1.9±0.1) ms and the optical inhomogeneous broadening is (1.58±0.05) GHz at a doping level of 0.07% for 151Eu3+. The hyperfine transition spectra are measured by using optically detected magnetic resonance and spin inhomogeneous broadening of (19±3) kHz is obtained. Furthermore, we analyze the coherence properties of optical and hyperfine transitions, respectively, via transient spectral hole burning and spin echo measurement. We obtain an optical homogeneous linewidth down to (22±3) kHz, which is still limited by the instantaneous spectral diffusion. The spin coherence lifetime under the geomagnetic field is (5.1±0.6) ms. The results demonstrate that 151Eu3+ ions embedded within the 2 μm triangular nanobeam essentially retain the same optical and hyperfine transition properties as those observed in bulk crystals. Consequently, this research lays a foundation for studying the integrated quantum memories based on 151Eu3+ ensembles and the detection of the single 151Eu3+ ion based on the focused ion beam technique.
-
Key words:
- rare-earth-doped crystal /
- quantum memory /
- focused ion beam /
- quantum information .
-

-
图 1 (a)浓度为0.07%的151Eu3+:Y2SiO5晶体经过聚焦离子束加工后的扫描电子显微镜图像, 在晶体D1×b面的俯视图中, 三角形悬梁臂波导的宽度沿D1轴为2 µm, 长度沿b轴为20 µm, 悬梁臂的输入输出端面为45°斜面. (b) Y2SiO5晶体中的site-1 151Eu3+离子在地磁场环境下的基态7F0和激发态5D0的超精细能级结构图
Figure 1. (a) Scanning electron microscope (SEM) image of 151Eu3+:Y2SiO5 crystal (doping level: 0.07%) fabricated by focused ion beam milling. In the top view of the D1×b plane, the width (D1 axis) and length (b axis) of the triangular nanobeam structure are 2 µm and 20 µm, respectively. Two slopes at 45° relative to the surface of the crystal are milled at both ends of the triangular nanobeam. (b) Energy-level diagram for the ground state 7F0 and the excited state 5D0 of site-1 151Eu3+ ions in Y2SiO5 crystal at the geomagnetic field.
图 2 实验装置图. 黄色直线代表580 nm激光的路径, 蓝色曲线代表单模光纤, PBS是偏振分束器, BS是非偏振分束器, AOM是声光调制器, AWG是任意波形发生器, SPD是单光子探测器,
$ \lambda/2 $ 是半波片. 激光通过调制光路再由单模光纤传输到耦合光路, 虚线方框以内的部分为笼式系统, 其中发散的白光源(diffuse source)经过BS2照射到晶体表面. 蓝色阴影区代表低温恒温器, 内部装有待测样品与亥姆霍兹线圈. 样品出射的信号光再一次经过笼式系统, 在BS1另一端通过狭缝(slit). 可以通过可翻转的反射镜(flip mirror)反射光场在相机上观察成像, 也可以通过AOM光开关后由SPD进行探测Figure 2. Experimental setup. The yellow line represents the transmission path for 580-nm laser and the blue curve represents a single-mode fiber. PBS, polarization beam splitter; BS, beam splitter; AOM, acousto-optic modulator; AWG, arbitrary waveform generator; SPD, single photon detector;
$ \lambda/2 $ represents a half-wave plate. The 580-nm laser is modulated by AOMs and collected with a single-mode fiber. The cage system within the dotted box includes a diffuse source which is a white-light source to illuminate the crystal surface through BS2. The blue shadowed area indicates a cryostat with the sample and Helmholtz coils inside. The signal light emitted from the sample is transmitted through the cage system again and spatially filtered by a slit at the another side of BS1. If the flip mirror is turned on then the sample can be imaged on the camera, otherwise, the signal is detected by a SPD after being gated by a double-passed AOM.图 3 (a) Y2SiO5悬梁臂波导中151Eu3+的7F0
$ \rightarrow $ 5D0跃迁荧光寿命图. 黑色圆点为数据点, 红色曲线是拟合的指数衰减曲线, 误差条表示为一个标准差, 本文中误差条均代表同一含义. (b) Y2SiO5悬梁臂波导中151Eu3+的7F0$ \rightarrow $ 5D0跃迁荧光激发谱. 黑色圆点为数据点, 红色曲线是由(1)式拟合的pseudo-Voigt型曲线, 中心频率点代表516.8478 THzFigure 3. (a) Fluorescence decay for the 7F0
$ \rightarrow $ 5D0 transition of 151Eu3+ in the Y2SiO5 nanobeam. The black dots are the fluorescence data and the red curve is fitted by a single exponential decay. Error bars indicate one standard deviation with the same meaning in whole paper. (b) Fluorescence excitation spectrum for the 7F0$ \rightarrow $ 5D0 transition of 151Eu3+ in the Y2SiO5 nanobeam. The black dots are fluorescence data, and the red curve is fitted by pseudo-Voigt function according to Eq.(1). The center frequency is 516.8478 THz.图 4 (a)测试Y2SiO5悬梁臂波导中151Eu3+光学均匀线宽的脉冲时序图. 首先是准备阶段, 其目的是为了初始化布居数. 在准备阶段结束40 ms后, 同时输入三束功率和频率间隔一致且时间宽度0.15 ms的高斯单频激发光. 在10 µs后, 光开关打开一个2 ms的窗口用于测量荧光信号. (b)—(d) 220 nW (b), 440 nW (c)和660 nW (d)的激发光下, 荧光信号随激发光的频率间隔的变化曲线图. 不同颜色的曲线是拟合的洛伦兹曲线
Figure 4. (a) Pulse sequence for measuring the optical homogeneous linewidth of 151Eu3+ in the Y2SiO5 nanobeam. Preparation process initializes the atomic population for each repeat of measurements. 40 ms after the preparation process, we apply the excitation pulses which are three Gaussian pulses with a duration of 0.15 ms with equal frequency spacing. 10 µs after the excitation, the detection gate opens for 2 ms to detect the fluorescence signal. (b)–(d) Fluorescence signal depending on the frequency spacing of excitation pulses, with excitation powers of 220 nW (b), 440 nW (c) and 660 nW (d). Solid lines are fitted in accordance with Lorentzian lineshape.
图 5 (a)测试Y2SiO5悬梁臂波导中151Eu3+离子的自旋相干寿命的序列图. 在准备阶段后, 通过线圈施加
$ \pi/2-\pi-\pi/2 $ 的自旋回波(spin echo)脉冲序列, 每个射频脉冲的时间间隔τ相等, 射频脉冲的相位依次为$ 0^\circ-90^\circ-0^\circ $ . 射频脉冲结束后, 施加一个啁啾带宽3 MHz和时间宽度500 µs的啁啾型光脉冲, 并随后探测2 ms的荧光信号; (b) Y2SiO5悬梁臂波导中151Eu3+离子$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ 的spin nutation测试. 红色曲线是拟合的阻尼正弦函数曲线; (c) Y2SiO5悬梁臂波导中151Eu3+离子$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ 的超精细跃迁谱, 橙色曲线是拟合的pseudo-Voigt型曲线; (d)荧光信号随自旋回波序列的总时间的变化图Figure 5. (a) Pulse sequence for measuring spin coherence lifetime of 151Eu3+ in the Y2SiO5 nanobeam. The spin-echo sequence (RF pulses
$ \pi/2-\pi-\pi/2 $ ) are applied by the Helmholtz coils after the preparation process. The phases of the RF pulses are$ 0^\circ-90^\circ-0^\circ $ . After the RF pulses, the sample is excited by a chirp pulse with a duration of 500 µs and a bandwidth of 3 MHz, and then fluorescence signal is detected with a 2-ms window. (b) Spin nutation measurement on the$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ transition of 151Eu3+ in the Y2SiO5 nanobeam. The red curve is fitted by damped sine lineshape. (c) Fluorescence-detected spectrum for$ |{\pm1/2}\rangle_{\mathrm{g}} $ $ \leftrightarrow $ $ |{\pm3/2}\rangle_{\mathrm{g}} $ transition. The orange curve is fitted by pseudo-Voigt lineshape. (d) Fluorescence signal as a function of the total time of the spin-echo sequence. -
[1] Lukin M D 2003 Rev. Mod. Phys. 75 457 doi: 10.1103/RevModPhys.75.457 [2] Zhou Z, Liu C, Li C, Guo G, Oblak D, Lei M, Faraon A, Mazzera M, De Riedmatten H 2023 Laser Photonics Rev. 17 2300257 doi: 10.1002/lpor.202300257 [3] Lei Y, Kimiaee Asadi F, Zhong T, Kuzmich A, Simon C, Hosseini M 2023 Optica 10 1511 doi: 10.1364/OPTICA.493732 [4] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932 doi: 10.1103/PhysRevLett.81.5932 [5] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33 doi: 10.1103/RevModPhys.83.33 [6] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221 doi: 10.1103/PhysRevLett.78.3221 [7] Kimble H J 2008 Nature 453 1023 doi: 10.1038/nature07127 [8] Lvovsky A I, Sanders B C, Tittel W 2009 Nat. Photonics 3 706 doi: 10.1038/nphoton.2009.231 [9] Hong C K, Mandel L 1986 Phys. Rev. Lett. 56 58 doi: 10.1103/PhysRevLett.56.58 [10] Nunn J, Reim K, Lee K C, Lorenz V O, Sussman B J, Walmsley I A, Jaksch D 2008 Phys. Rev. Lett. 101 260502 doi: 10.1103/PhysRevLett.101.260502 [11] Davidson O, Yogev O, Poem E, Firstenberg O 2023 Phys. Rev. Lett. 131 033601 doi: 10.1103/PhysRevLett.131.033601 [12] Imamoḡlu A 2002 Phys. Rev. Lett. 89 163602 doi: 10.1103/PhysRevLett.89.163602 [13] Clausen C, Sangouard N, Drewsen M 2013 New J. Phys. 15 025021 doi: 10.1088/1367-2630/15/2/025021 [14] Liu X, Hu X M, Zhu T X, Zhang C, Xiao Y X, Miao J L, Ou Z W, Li P Y, Liu B H, Zhou Z Q, Li C F, Guo G C 2024 Nat. Commun. 15 8529 doi: 10.1038/s41467-024-52912-3 [15] Thiel C, Böttger T, Cone R 2011 J. Lumin. 131 353 doi: 10.1016/j.jlumin.2010.12.015 [16] De Riedmatten H, Afzelius M, Staudt M U, Simon C, Gisin N 2008 Nature 456 773 doi: 10.1038/nature07607 [17] Longdell J J, Alexander A L, Sellars M J 2006 Phys. Rev. B 74 195101 doi: 10.1103/PhysRevB.74.195101 [18] Fraval E, Sellars M J, Longdell J J 2004 Phys. Rev. Lett. 92 077601 doi: 10.1103/PhysRevLett.92.077601 [19] Zhong M, Hedges M P, Ahlefeldt R L, Bartholomew J G, Beavan S E, Wittig S M, Longdell J J, Sellars M J 2015 Nature 517 177 doi: 10.1038/nature14025 [20] Rančić M, Hedges M P, Ahlefeldt R L, Sellars M J 2018 Nature Phys. 14 50 doi: 10.1038/nphys4254 [21] Ortu A, Holzäpfel A, Etesse J, Afzelius M 2022 npj Quantum Inf. 8 29 doi: 10.1038/s41534-022-00541-3 [22] Ma Y, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2021 Nat. Commun. 12 2381 doi: 10.1038/s41467-021-22706-y [23] Saglamyurek E, Sinclair N, Jin J, Slater J A, Oblak D, Bussières F, George M, Ricken R, Sohler W, Tittel W 2011 Nature 469 512 doi: 10.1038/nature09719 [24] Usmani I, Afzelius M, De Riedmatten H, Gisin N 2010 Nat. Commun. 1 12 doi: 10.1038/ncomms1010 [25] Businger M, Nicolas L, Mejia T S, Ferrier A, Goldner P, Afzelius M 2022 Nat. Commun. 13 6438 doi: 10.1038/s41467-022-33929-y [26] Yang T S, Zhou Z Q, Hua Y L, Liu X, Li Z F, Li P Y, Ma Y, Liu C, Liang P J, Li X, Xiao Y X, Hu J, Li C F, Guo G C 2018 Nat. Commun. 9 3407 doi: 10.1038/s41467-018-05669-5 [27] Seri A, Lago-Rivera D, Lenhard A, Corrielli G, Osellame R, Mazzera M, de Riedmatten H 2019 Phys. Rev. Lett. 123 080502 doi: 10.1103/PhysRevLett.123.080502 [28] Chen F, De Aldana J R V 2014 Laser Photonics Rev. 8 251 doi: 10.1002/lpor.201300025 [29] Liu C, Zhu T X, Su M X, Ma Y Z, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 260504 doi: 10.1103/PhysRevLett.125.260504 [30] Zhu T X, Liu C, Zheng L, Zhou Z Q, Li C F, Guo G C 2020 Phys. Rev. Appl. 14 054071 doi: 10.1103/PhysRevApplied.14.054071 [31] Zhu T X, Liu C, Jin M, Su M X, Liu Y P, Li W J, Ye Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 128 180501 doi: 10.1103/PhysRevLett.128.180501 [32] Liu D C, Li P Y, Zhu T X, Zheng L, Huang J Y, Zhou Z Q, Li C F, Guo G C 2022 Phys. Rev. Lett. 129 210501 doi: 10.1103/PhysRevLett.129.210501 [33] Zhong T, Kindem J M, Miyazono E, Faraon A 2015 Nat. Commun. 6 8206 doi: 10.1038/ncomms9206 [34] Miyazono E, Zhong T, Craiciu I, Kindem J M, Faraon A 2016 Appl. Phys. Lett. 108 011111 doi: 10.1063/1.4939651 [35] Zhong T, Rochman J, Kindem J M, Miyazono E, Faraon A 2016 Opt. Express 24 536 doi: 10.1364/OE.24.000536 [36] Kindem J M, Ruskuc A, Bartholomew J G, Rochman J, Huan Y Q, Faraon A 2020 Nature 580 201 doi: 10.1038/s41586-020-2160-9 [37] Dibos A M, Raha M, Phenicie C M, Thompson J D 2018 Phys. Rev. Lett. 120 243601 doi: 10.1103/PhysRevLett.120.243601 [38] Weiss L, Gritsch A, Merkel B, Reiserer A 2021 Optica 8 40 doi: 10.1364/OPTICA.413330 [39] Zhu T X, Su M X, Liu C, Liu Y P, Wang C F, Liu P X, Han Y J, Zhou Z Q, Li C F, Guo G C 2024 National Sci. Rev. 161 doi: 10.1093/nsr/nwae161 [40] Bayn I, Meyler B, Salzman J, Kalish R 2011 New J. Phys. 13 025018 doi: 10.1088/1367-2630/13/2/025018 [41] Zhong T, Kindem J M, Bartholomew J G, Rochman J, Craiciu I, Verma V, Nam S W, Marsili F, Shaw M D, Beyer A D, Faraon A 2018 Phys. Rev. Lett. 121 183603 doi: 10.1103/PhysRevLett.121.183603 [42] Zhong T, Kindem J M, Bartholomew J G, Rochman J, Craiciu I, Miyazono E, Bettinelli M, Cavalli E, Verma V, Nam S W, Marsili F, Shaw M D, Beyer A D, Faraon A 2017 Science 357 1392 doi: 10.1126/science.aan5959 [43] Craiciu I, Lei M, Rochman J, Kindem J M, Bartholomew J G, Miyazono E, Zhong T, Sinclair N, Faraon A 2019 Phys. Rev. Appl. 12 024062 doi: 10.1103/PhysRevApplied.12.024062 [44] 梁澎军, 朱天翔, 肖懿鑫, 王奕洋, 韩永建, 周宗权, 李传锋 2024 物理学报 73 100301 doi: 10.7498/aps.73.20240116 Liang P J, Zhu T X, Xiao Y X, Wang Y Y, Han Y J, Zhou Z Q, Li C F 2024 Acta Phys. Sin. 73 100301 doi: 10.7498/aps.73.20240116 [45] Könz F, Sun Y, Thiel C W, Cone R L, Equall R W, Hutcheson R L, Macfarlane R M 2003 Phys. Rev. B 68 085109 doi: 10.1103/PhysRevB.68.085109 [46] Stoneham A M 1969 Rev. Mod. Phys. 41 82 doi: 10.1103/RevModPhys.41.82 [47] Lafitte-Houssat E, Ferrier A, Welinski S, Morvan L, Afzelius M, Berger P, Goldner P 2022 Opt. Mater.: X 14 100153 doi: 10.1016/j.omx.2022.100153 [48] Louchet-Chauvet A, Ahlefeldt R, Chanelière T 2019 Rev. Sci. Instrum. 90 034901 doi: 10.1063/1.5080086 [49] Gritsch A, Weiss L, Früh J, Rinner S, Reiserer A 2022 Phys. Rev. X 12 041009 doi: 10.1103/PhysRevX.12.041009 [50] Bartholomew J G, de Oliveira Lima K, Ferrier A, Goldner P 2017 Nano Lett. 17 778 doi: 10.1021/acs.nanolett.6b03949 [51] Szabo A 1975 Phys. Rev. B 11 4512 doi: 10.1103/PhysRevB.11.4512 [52] Völker S 1989 Annu. Rev. Phys. Chem. 40 499 doi: 10.1146/annurev.pc.40.100189.002435 [53] Reiserer A 2022 Rev. Mod. Phys. 94 041003 doi: 10.1103/RevModPhys.94.041003 [54] Meiboom S, Gill D 1958 Rev. Sci. Instrum. 29 688 doi: 10.1063/1.1716296 [55] Arcangeli A, Lovrić M, Tumino B, Ferrier A, Goldner P 2014 Phys. Rev. B 89 184305 doi: 10.1103/PhysRevB.89.184305 [56] Robledo L, Bernien H, van Weperen I, Hanson R 2010 Phys. Rev. Lett. 105 177403 doi: 10.1103/PhysRevLett.105.177403 [57] Ma Y Z, Lü Y C, Yang T S, Ma Y, Zhou Z Q, Li C F, Guo G C 2023 Phys. Rev. B 107 014310 doi: 10.1103/PhysRevB.107.014310 [58] Alexander A L, Longdell J J, Sellars M J 2007 J. Opt. Soc. Am. B: Opt. Phys. 24 2479 doi: 10.1364/JOSAB.24.002479 [59] Hahn E L 1950 Phys. Rev. 80 580 doi: 10.1103/PhysRev.80.580 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: