首页
登录
注册
-
离子溅射是指载能离子轰击固体表面, 打出离子和中性原子的现象[1]. 离子溅射是离子与固体相互作用过程中的重要物理过程之一, 在聚变反应堆的壁效应[2]、高能离子推进器、磁控溅射镀膜[3,4]、溅射离子泵、表面分析、高能离子的收集沉积[5,6]等领域均具有较高的应用价值. 在高能离子收集沉积过程, 常用的离子加速结构包含金属丝状结构, 其性能及使用寿命是影响试验运行稳定性的重要因素, 离子的溅射过程会造成金属丝的表面损失, 是影响服役性能及使用寿命的主要因素; 因此, 对离子溅射过程进行模拟, 研究不同合金靶材条件下的离子溅射产额, 并基于离子溅射过程对金属丝寿命进行分析, 延长金属丝结构使用寿命具有重要意义.
目前模拟离子溅射过程中主要有蒙特卡罗方法(Monte Carlo, MC)以及分子动力学方法(molecular dynamics, MD). 常用的基于蒙特卡罗方法进行离子溅射过程模拟的程序为SRIM (the stopping and rang of ions in matter)程序[7], 该程序基于1969年Sigmund建立的线性级联碰撞理论[8], 程序中同时包含了大量的实验修正数据, 对于离子入射单质靶材工况适用性强[9,10], 由于SRIM在程序计算过程中认为固体靶为非晶靶, 入射离子与靶材中原子的相互作用视为二体碰撞过程, 未考虑合金晶体结构和多体相互作用问题, SRIM程序的计算结果可能存在较大偏差.
分子动力学方法是按照该体系内部的动力学规律来确定位置和速度随时间演化的一种模拟方法, 通过跟踪系统中每个粒子的个体运动, 给出微观量(粒子坐标、速度)与宏观可观测量(温度、压力、比热、弹性模量等)的关系[11–15], 在计算过程中可以充分考虑合金基底中原子相互作用势, 和离子与合金表面多体相互作用[16], 更适用于高能离子入射合金靶材的离子溅射过程的计算.
本文基于分子动力学方法, 利用LAMMPS (large-scale atomic/molecular massively parallel simulator)程序[17,18]对基底材料进行原子晶体尺度建模, 建立重离子入射合金靶材初始状态及持续后入射靶材表面混乱状态下的离子溅射参数计算模型; 在此基础上研究不同合金不同离子入射角条件下的溅射产额及金属丝寿命与试验结果进行了对比, 并基于理论模型找到了一种有利于金属丝服役寿命提升的材料.
-
当载能离子入射合金靶材时, 会不断与合金靶材中原子发生碰撞并损失能量, 同时靶材中的原子在碰撞中获得的能量超过其位移能后脱离原来的晶格位置, 并与其他原子发生碰撞形成一系列反冲级联碰撞, 当靶材表面的原子获得的能量超过靶材表面的束缚能后脱离靶材表面形成溅射出射原子. 在离子溅射过程中, 离子溅射产额定义为每个入射离子引起靶材表面溅射出射原子的数量, 溅射产额与入射离子的种类、能量、靶材种类等多种因素相关.
-
在载能离子轰击合金靶材的LAMMPS建模模拟过程中, 选择具有周期性边界、表面取向为(111)的单个晶胞作为计算体系[19], 基体温度选择为900 K, 在计算过程中模型域大小的控制、原子间相互作用势的选取是影响模型复杂度及模型计算准确性的重要因素.
-
由于离子溅射过程能量作用区域大, 入射离子在靶材内发生级联碰撞的过程中, 入射离子能量由晶格间金属键进行高效传递, 由碰撞引起的能量传递距离较远, 而实际上影响碰撞溅射的较高能量传递范围很小. 对于溅射中心区域外部的原子层, 同时具备吸收能量与反射能量的能力, 为了充分反应靶材溅射发展过程的同时降低单原子计算时间, 提高计算效率, 选取较小的靶材表面高能碰撞区域(24×24×18(lattice))作为中心碰撞区域内层原子进行模拟. 同时利用Langevin控温法[20]在碰撞区域外包裹一层额外的能量吸收反射原子层, 以此替代大尺度模型中高能碰撞区域外的原子的方法. 图1为Langevin控温法模型域划分示意图.
在分子动力学模拟过程中, 原子和分子的轨迹是通过数值求解粒子相互作用系统的牛顿运动方程来确定, 其中粒子之间的力Fc及势能通常是通过原子间势或分子力学力场进行计算, 在内层高能原子碰撞区, 常用的描述原子间相互作用势有LJ (Lennard-Jones)势[21]、EAM (Embedded Atom Method)势[22]、ZBL (Ziegler Biersack Littmark)势[23]等, 其中LJ势通常用于描述二体原子之间的相互作用, EAM势用于描述金属原子之间的相互作用, ZBL势更适用于金属原子的近距离相互作用[23,24], 选择ZBL势做为原子间相互作用势函数.
根据Langevin控温模型公式, 在外层Langvein控温层, 在原有原子间作用力Fc基础上额外增加两项阻尼力Ff与Fr, 以此模拟无限大原子模型对控温层内部区域的应力吸收与反射:
式中, F为控温区原子所受合力, eV/Å; Fc为原子之间基于力场作用的保守力, eV/Å; Ff为与粒子速度成正比的摩擦阻力, eV/Å; Fr为温度T下原子与其他粒子随机碰撞所产生的力, eV/Å; m为原子质量, g; v为原子速度, Å/ps; α为阻尼系数, ps; kB为玻尔兹曼常数, 1.380649×10–23 J/K; T为原子温度, K; dt为计算时间步长, ps.
同时建立近似等价于无穷大基底(40×40×24 (lattice))的模型及确定的主要碰撞区域的原子模型, 分别选取不同阻尼系数, 对其进行相同入射位置、相同入射能量和相同入射角度的溅射模拟, 监控在原子入射过程中的平均原子能量变化, 当计算模型中碰撞原子能量变化与无穷大基板中碰撞原子能量变化相同或相近时, 即认为此时计算模型与无穷大基板等价, 当选取的阻尼系数使得内外层碰撞区域的原子能量波动, 与近似无穷大基底条件下的原子能量波动在各时间步长内的偏差均≤10%时, 此时的阻尼系数α值为所求.
-
由于离子引出过程持续时间较长, 持续入射一段时间后, 靶材表层含有大量的入射离子元素, 为提高靶材由初始入射状态至稳定初始入射状态的计算效率, 对持续入射状态靶材计算模型进行简化, 借助蒙特卡罗方法, 首先利用SRIM程序计算入射离子元素溅射产额为1时稳态条件下, 靶材内部入射元素含量和分布随深度变化的概率密度函数.
同时, 靶材经过离子入射后, 表层原子的晶格结构被破坏, 在经历足够多次的溅射后, 模拟区域的原子结构逐渐变得混乱, 最终达到稳定的混乱状态, 此时即为持续入射状态下靶材不掺杂离子的原子结构, 以此原子结构分布作为基础, 按照入射元素随深度变化的概率密度分布函数将不同深度原有原子替换为入射元素原子并进行充分弛豫, 即可得到近似稳态溅射的靶材原子模型, 基于此模型进行稳态条件下的溅射参数计算.
-
在高能重离子进行加速、收集的过程中, 常见用于离子加速的一种阴极结构为圆形丝状结构, 建立金属丝服役寿命计算模型, 对金属丝使用寿命进行评估.
在一定的离子入射强度及入射方向下, 对于圆形金属丝, 各处的入射仰角(离子入射方向与入射平面法线夹角)均不相同, 将圆形金属丝简化为不同等分区域内入射仰角相同的多边形计算. 金属丝的质量及表面损失为离子溅射损失, 单位时间各等分区域内截面变化如下:
式中,
$ \varPhi $ 为入射离子通量(s–1·cm–2);$ {M_{\text{i}}} $ 为入射原子相对摩尔质量;$ {Y_{\text{a}}} $ 为靶材所含元素的溅射产额,$ {M_{\text{a}}} $ 为靶材所含元素的相对摩尔质量,$ {\rho _{\text{t}}} $ 为靶材密度.通过计算不同离子入射总量下, 各等分区域截面变化情况, 得到金属丝截面随离子入射总量的变化情况, 进而获得金属丝寿命.
-
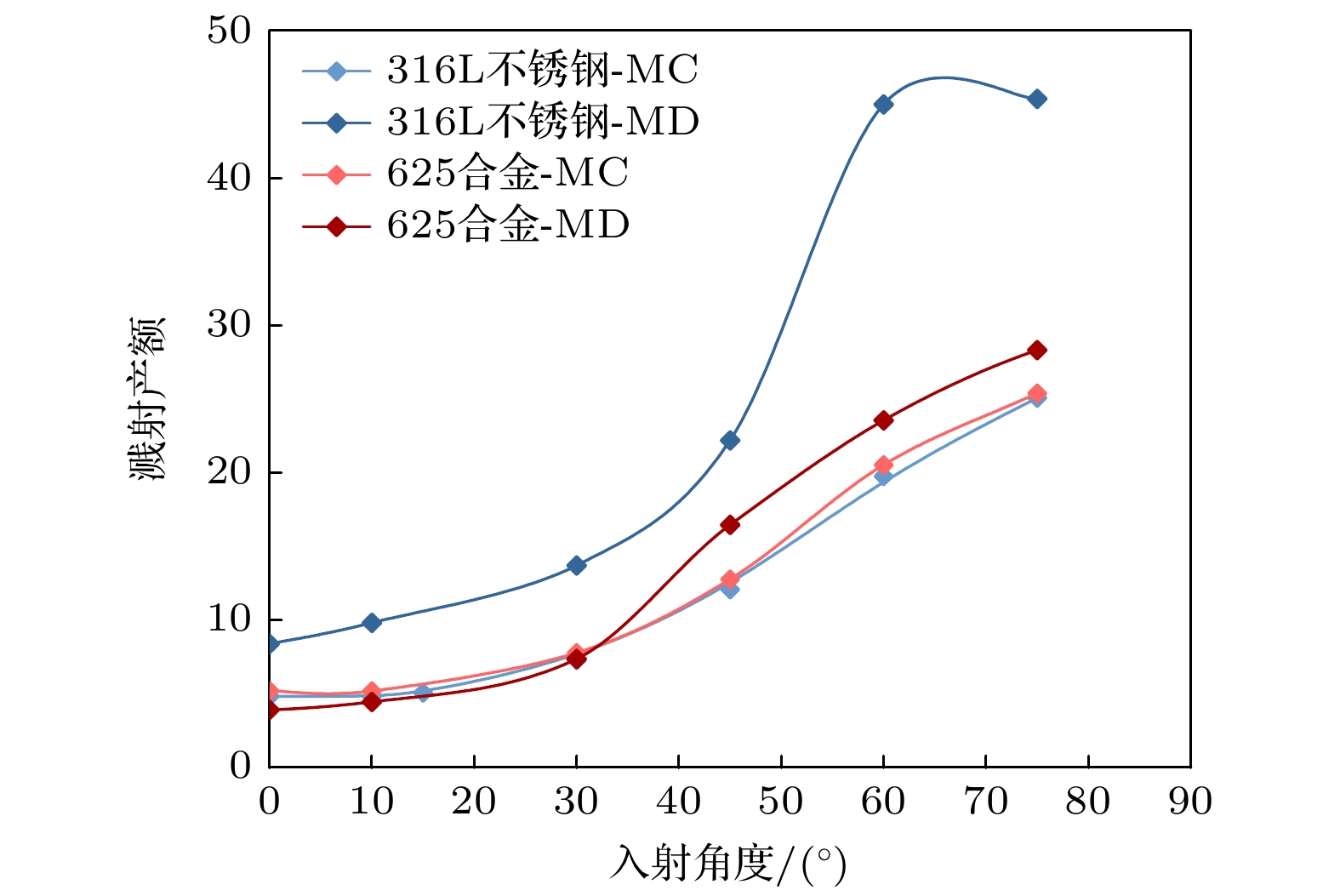
以铯元素为例, 计算了入射离子在能量为9 keV入射, 不同入射角, 316L不锈钢、625合金作为基底材料的条件下的溅射产额曲线及与SRIM计算结果的对比, 结果如图2所示.
由图2结果可知, 当基底材料为316L不锈钢时, 分子动力学计算的溅射产额结果约为SRIM计算的2倍; 当基底材料为625合金时, 分子动力学计算的溅射产额结果与SRIM结果相近. 对比结果表明, SRIM软件未在计算中考虑晶格结构对溅射过程的影响, 而该影响在溅射产额计算中不可忽略, 同时分子动力学计算结果与试验得到的金属丝材质为316L不锈钢时的寿命低于625合金结果相一致, 因此后续寿命计算均需要以分子动力学计算结果为基准, SRIM计算结果作为参考.
-
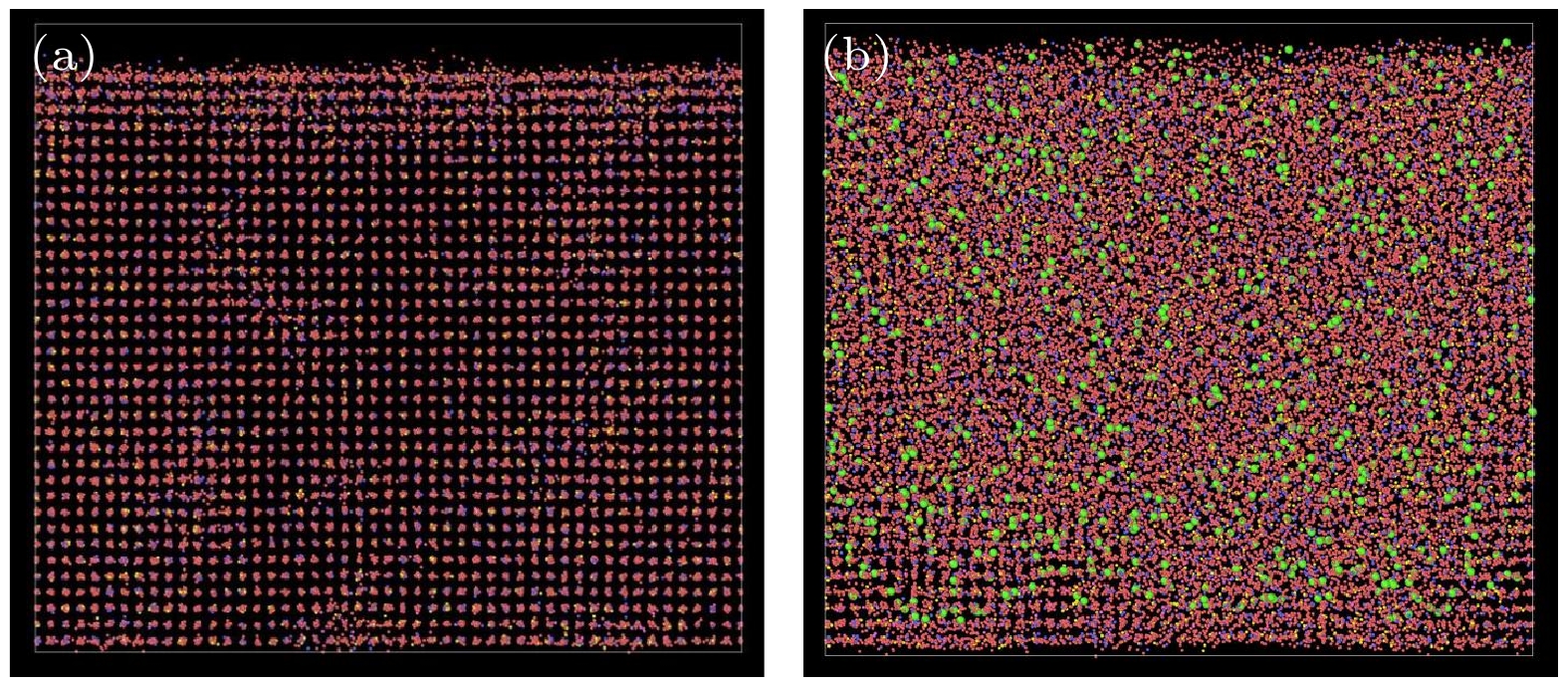
根据持续入射条件下的原子模型, 以铯元素在在能量为9 keV入射316L不锈钢为例, 得到持续入射条件下的不锈钢内部结构(图3(b)).
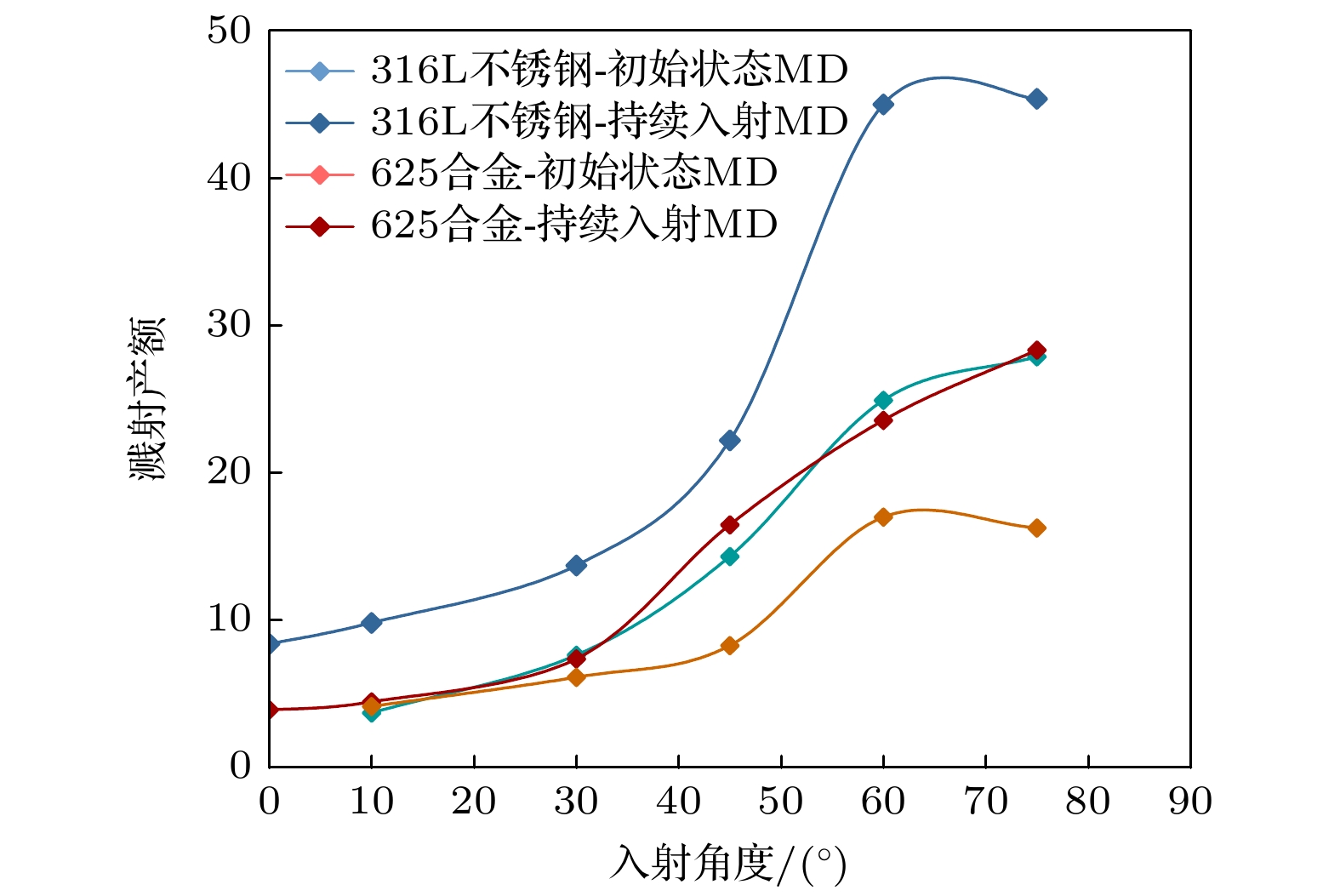
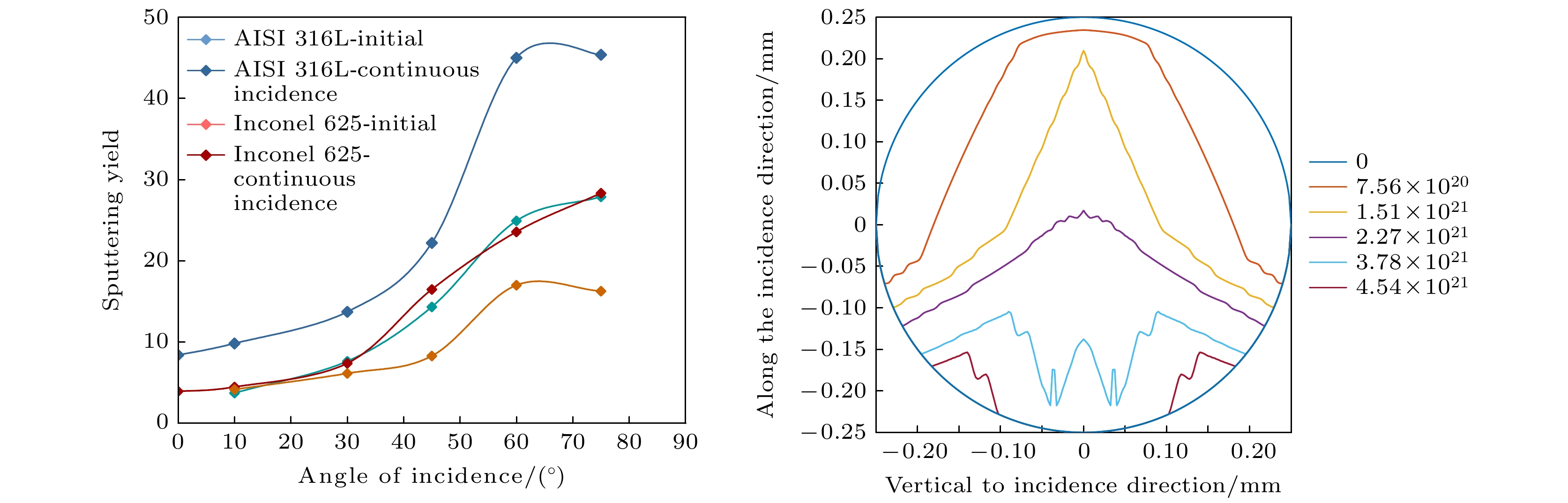
将持续入射后的原子模型及原子间相互作用势函数代入LAMMPS的计算中得到, 不同入射仰角, 316L不锈钢、625合金作为基底材料持续入射的条件下的溅射产额曲线, 结果如图4所示.
图4结果表明, 在初始状态下合金靶材具有完整的晶格结构, 相邻晶格原子间在溅射条件下能量传递指向性更高, 有更大的能量传递至靶材表面, 因此相比SRIM计算结果, 初始状态靶材分子动力学计算所得溅射产额更大. 由于经历长时间入射后, 合金金属表层晶格被破坏, 表层原子排列趋于混乱, 因此持续入射后混乱状态下的溅射产额小于初始状态溅射产额. 由于在625合金中含有8%—10%的钼元素, 部分钼元素在合金基体中以固溶的形式存在, 在强化了合金的同时, 给625合金带来了一部分的晶格畸变, 导致部分晶格不完整, 使得入射离子的能量在传递的过程中更为分散, 原子间的约束能力较弱, 因此入射能量在合金中的耗散较快, 传递至表面原子的能量较小, 使得溅射产额较小, 明显低于316L不锈钢的溅射产额.
-
为确定长时间入射后的金属丝表面形貌变化对离子溅射参数的影响, 对一块离子长时间持续入射后的金属平板表面进行了扫描电子显微镜(scanning electron microscope, SEM)表面形貌测试, 根据电镜对其表面的观测结果可知(图5), 宏观上平整的平板表面并非光滑平面, 经过离子入射, 表面呈现大小不一的“陨石坑”状结构. 该结构增加了部分粒子的入射角度, 提高了实际溅射产额, 因此需要评估“陨石坑”结构对实际溅射产额的影响.
根据图像可知, “陨石坑”结构半径范围在10 μm级别, 而溅射影响区域在100 Å (1 Å = 10–10 m), 因此“陨石坑”结构对于金属丝的溅射行为可视为宏观几何结构, 陨石坑壁按照斜平面进行计算. 建立“陨石坑”形貌模型, 近似高斯分布:
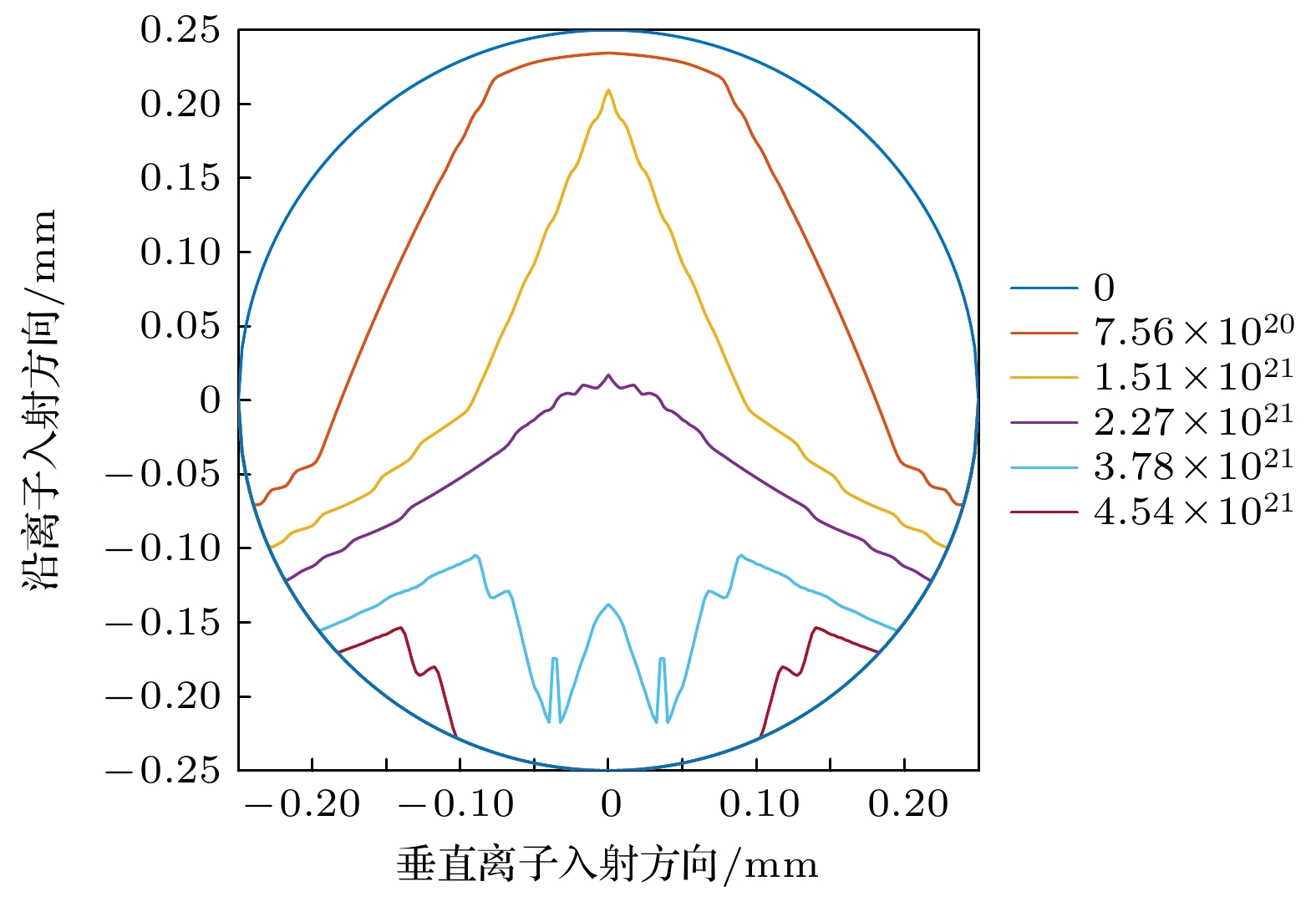
耦合“陨石坑”结构形貌模型, 集合离子溅射参数计算模型, 依据2.3节中所述金属丝截面随时间变化计算模型, 以铯元素入射为例, 计算得到表1所述入射条件下, 金属丝截面随离子入射时间变化的结果, 如图6所示.
根据图6结果, 金属丝在入射离子总量达到约3.70×1021时, 厚度方向上沿离子入射方向最薄处已降低至0.05 mm以下, 此时材料由于离子轰击所承受的拉力已超过材料能承受的拉力极限, 因此认为材料已失效; 为验证理论计算结果的准确性, 对在相同入射条件下, 离子入射总量约为2.27×1021时的金属丝截面进行扫描电子显微镜表面形貌测试, 试验测得金属丝截面形貌及尺寸如图7所示.
根据图7中结果, 将理论计算结果与实际实验测量相比, 宽度方向上误差为1.84%, 厚度方向上误差约为1.75%, 与理论值相比误差均<10%, 由此验证了离子溅射为影响金属丝寿命的主要因素, 同时验证了理论计算模型的准确性及适用性, 因此后续采用分子动力学方法进行不同材料的离子溅射过程的模拟, 寻找耐溅射材料, 优化金属丝服役寿命.
-
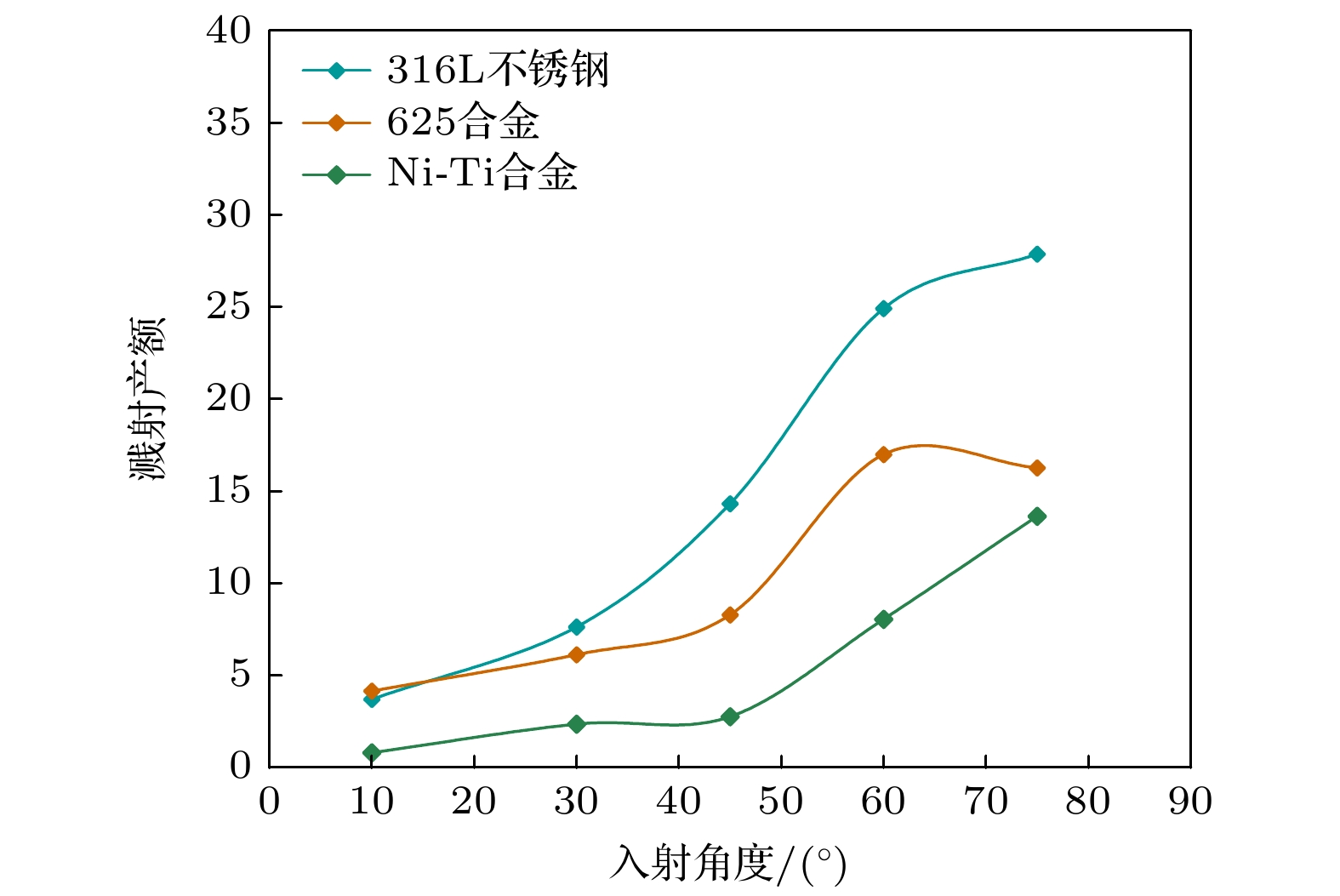
根据3.2节中分析, 验证了离子溅射为影响金属靶材寿命的主要因素, 在不改变金属丝初始直径条件下, 提升金属靶材寿命的主要方式为金属丝材料优化, 选取溅射产额较小、晶体结构松散、密度较高的材料, 可提升金属丝寿命. 经过多种元素计算, 评估Ni-Ti合金为面心立方晶体, 整体晶体结构较为松散, 晶格常数小于625合金, 吸收离子动能能力较强, 不同入射角条件下在离子持续入射后Ni-Ti合金与625合金相比的溅射产额如图8所示.
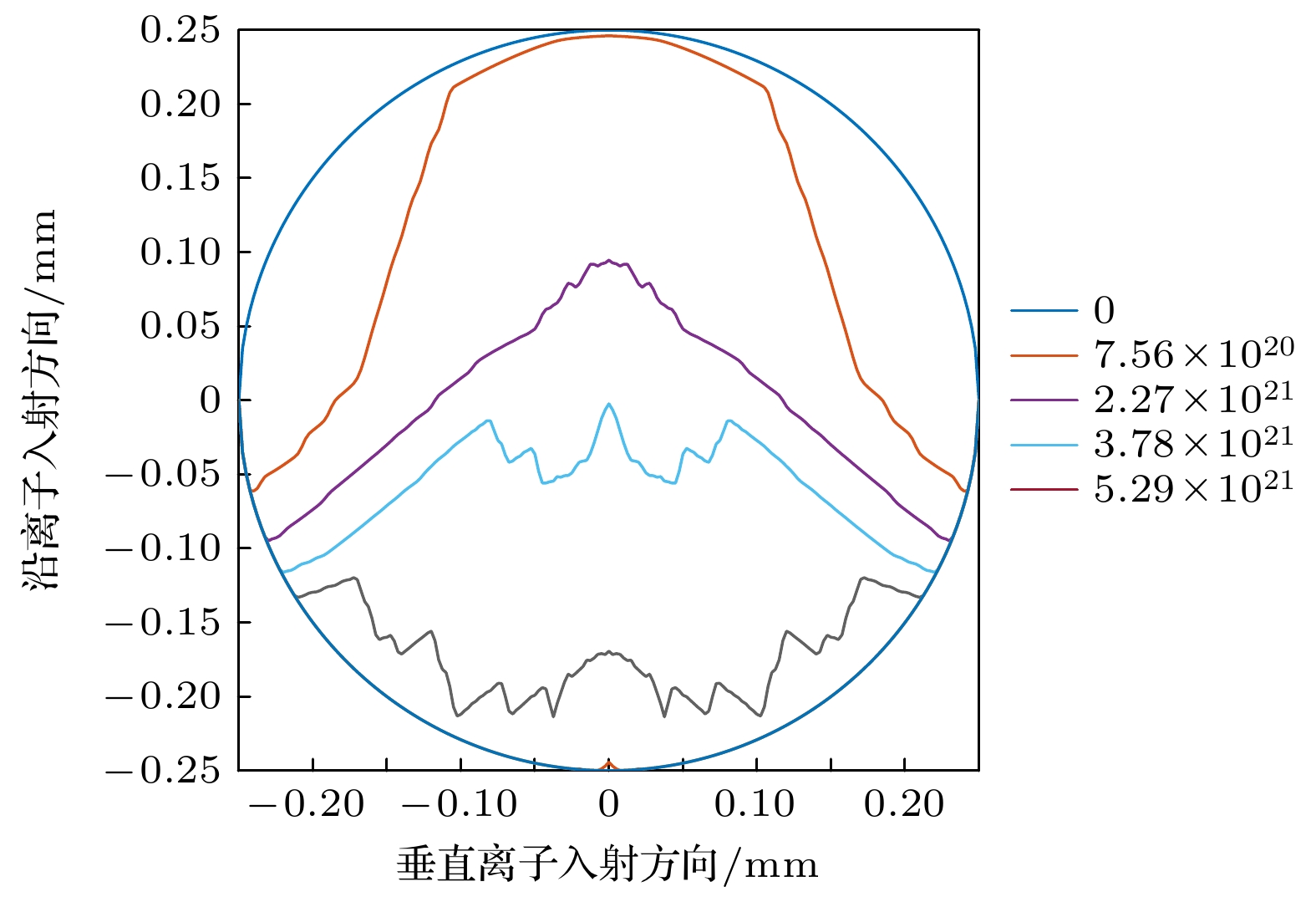
根据图8所示的结果, 相对625合金及316L不锈钢, 不同入射角度下Ni-Ti合金的溅射产额均更小. 在Ni-Ti合金材质下, 计算得到与3.2节中相同入射条件下, 金属丝截面随时间的变化曲线如图9所示.
根据图中结果, 金属丝材质为Ni-Ti合金时, 金属丝失效的入射离子总量可由3.70×1021提升至5.14×1021, 在离子束流密度不变的情况下金属丝寿命可提升约39%, 根据计算结果, 在后续选材过程中可选取Ni-Ti合金材料, 以此降低材料溅射产额, 延长金属丝使用寿命.
-
本文基于载能离子长时间收集沉积过程中, 离子溅射过程影响阴极金属丝服役性能及使用寿命的问题, 建立了基于分子动力学及Langevin控温模型的离子溅射参数计算模型及金属丝寿命计算模型, 并基于模型提出了金属丝寿命优化方式, 主要结论如下.
1)基于分子动力学模型及Langevin控温模型, 利用LAMMPS程序进行了靶材初始条件及离子持续高通量入射条件下下的靶材原子尺度建模, 建立了载能重金属离子入射复杂混合物合金靶材的离子溅射参数计算模型.
2)基于本文建立了溅射产额计算模型计算发现, 区别于SRIM软件计算得到的相同入射条件下, 625合金与316L不锈钢溅射产额相近结果, 分子动力学方法计算得到的625合金的溅射产额明显低于316L不锈钢, 这是由于625合金原子间约束能力较弱, 入射能量在合金中耗散较快, 传递至表面原子的能量较小, 使得同一入射角度下, 625合金, 溅射产额较小, 显著小于不锈钢的溅射产额.
3)计算得到了在给定入射条件下金属丝截面随试验时间变化的曲线, 预测了金属丝失效时间, 并进行了相同入射条件下金属丝截面与试验结果的对比, 金属丝宽度及厚度方向上计算结果与试验结果偏差均小于10%, 验证了理论计算模型的准确性和适用性, 对预测不同入射条件下金属丝使用寿命并进行优化改进具有重要意义.
4)基于本文建立的理论模型, 对金属丝寿命优化提升进行计算, 计算结果表明将金属丝材质由625合金优化为Ni-Ti合金, 金属丝寿命可实现显著提升, 提升比例约39%.
离子溅射对合金靶材寿命的影响
Influence of energetic heavy ion sputtering on lifetime of alloy target
-
摘要: 载能离子入射带负电的离子收集沉积结构过程中会发生离子溅射, 一种常用于离子加速过程的结构为圆形金属丝, 持续大量离子入射会引起金属丝的表面损失, 影响金属丝的服役性能及使用寿命. 目前, 由于常用于计算溅射产额的SRIM软件无法考虑合金晶体结构中包含的多体相互作用问题, 在高能离子入射合金靶材的溅射产额计算上具有较大误差, 因此本文基于分子动力学方法结合Langevin控温模型建立了高能金属离子入射合金靶材的离子溅射参数计算模型, 该模型具备持续入射过程中合金表面不同状态下的离子溅射参数计算功能, 利用该模型计算得到了用于离子加速的阴极金属丝的典型服役寿命, 试验值与理论值偏差<10%, 验证了理论模型的准确性和适用性, 基于此模型进行了金属丝服役寿命提升的理论优化, 并提出了使用Ni-Ti合金提升金属丝寿命的方法.Abstract: When energetic heavy ions are incident on negatively charged structure that collects and deposits ions, ion sputtering will occur. Metal wire is a structure commonly used for accelerating ions, the incidence of continuous high-throughput ions can cause surface loss of metal wire, affecting the service performance and lifespan of the metal wire. The SRIM software commonly used for calculating sputtering yield cannot consider the multi-body interaction problem contained in the alloy crystal structure. So, there is a significant error in calculating the sputtering yield of high-energy ions incident on alloy target. Based on the molecular dynamics method and Langevin temperature control model, the calculation model of ion sputtering parameters of energetic metal ions incident on alloy target is established in this work. The model is used to calculate the sputtering yield under the conditions of intact surface lattice of the target material and long-term incident surface lattice damage. The damages to the cathode metal wire under different incident ion fluences are further calculated, and the cross-sectional characterization of the metal wire is carried under typical working condition. The results show that the discrepancy between the experimental value and the theoretical value is less than 10%, which verifies the accuracy and applicability of the theoretical model. Based on this model, the search direction for sputtering resistant materials is proposed, meanwhile, a theoretical optimization is carried out to improve the service life of metal wire, and a method of using Ni-Ti alloy to improve the service life of metal wires is proposed, which is of great significance for predicting the service life of the metal wire under different conditions.
-
Key words:
- ion sputtering /
- molecular dynamics /
- alloy target /
- service life .
-
-
图 1 Langevin控温法模型域划分示意图
Figure 1. Schematic diagram of Langevin method model division.
图 2 不同入射角条件下的溅射产额曲线
Figure 2. Sputtering yield curves under different incident angles.
图 3 初始状态(a)以及持续入射(b)后的316L不锈钢结构
Figure 3. Initial state (a) and continuous incidence (b) of 316L stainless steel structure.
图 4 不同入射条件下316L不锈钢、625合金的溅射产额
Figure 4. Sputtering yield of 316L stainless steel and 625 alloy under different incident conditions.
图 6 金属丝截面随入射离子总量变化曲线
Figure 6. Cross sections of metal wires with different total incident ions.
图 8 Ni-Ti合金与625合金、316L不锈钢溅射产额对比
Figure 8. Sputtering yield of Ni-Ti alloy, 625 alloy, and 316L stainless steel.
图 9 Ni-Ti合金金属丝截面随入射离子总量变化
Figure 9. Cross sections of Ni-Ti alloy wires with different total incident ions.
表 1 金属丝寿命计算入射条件
Table 1. Calculation conditions for the life of metal wires.
入射条件 初始值 入射元素 铯 入射能量/keV 9 入射方向与金属丝平面夹角/(°) 10 入射离子通量/(s–1·cm–2) 2.1×1015 靶材 625合金 金属丝初始直径/mm 0.5 
下载: 导出CSV
-
[1] 田民波, 崔福斋 1987 物理 17 177 doi: CNKI:SUN:WLZZ.0.1987-03-017 Tian M B, Cui F Z 1987 Physics 17 177 doi: CNKI:SUN:WLZZ.0.1987-03-017 [2] 张莱, 张竹林 2006 安徽理工大学学报 26 69 doi: 10.3969/j.issn.1672-1098.2006.02.018 Zhang L, Zhang Z L 2006 Journal of Anhui Univ. of Sci. and Tech. 26 69 doi: 10.3969/j.issn.1672-1098.2006.02.018 [3] 李体军, 崔岁寒, 刘亮亮 李晓渊, 吴忠灿, 马正永, 傅劲裕, 田修波, 朱剑豪, 吴忠振 2021 物理学报 70 045202 doi: 10.7498/aps.70.20201540 Li T J, Cui S H, Liu L L, Li X Y, Wu Z X, Ma Z Y, Fu J Y, Tian X B, Zhu J H, Wu Z Z 2021 Acta Phys. Sin. 70 045202 doi: 10.7498/aps.70.20201540 [4] 陈畅子, 马东林, 李延涛, 冷永祥 2021 物理学报 70 180701 doi: 10.7498/aps.70.20202050 Chen C Z, Ma D L, Li Y T, Leng Y X 2021 Acta Phys. Sin. 70 180701 doi: 10.7498/aps.70.20202050 [5] 朱红莲, 王德武 2022 物理学报 51 1338 doi: 10.3321/j.issn:1000-3290.2002.06.036 Zhu H L, Wang D W 2022 Acta Phys. Sin. 51 1338 doi: 10.3321/j.issn:1000-3290.2002.06.036 [6] 谢国锋 2008 物理学报 57 1784 doi: 10.7498/aps.57.1784 Xie G F 2008 Acta Phys. Sin. 57 1784 doi: 10.7498/aps.57.1784 [7] Ziegler J F, Ziegler M D, Biersack J P 2008 Nucl Instrum. Meth. B 268 1818 doi: 10.1016/j.nimb.2010.02.091 [8] Sigmund P 1969 Phys. Rev. 184 383 doi: 10.1103/PhysRev.184.383 [9] 邵其鋆, 霍裕昆, 陈建新, 吴士明, 潘正瑛 1991 物理学报 40 659 doi: 10.7498/aps.40.659 Shao Q Y, Huo Y K, Chen J X, Wu S M, Pan Z Y 1991 Acta Phys. Sin. 40 659 doi: 10.7498/aps.40.659 [10] Mahne N, Cekada M, Panjan M 2022 Coatings 12 1541 doi: 10.3390/coatings12101541 [11] 樊康旗, 贾建援 2005 微纳电子技术 42 133 doi: 10.3969/j.issn.1671-4776.2005.03.009 Fan K Q, Jia J Y 2005 Micronanoelectr. Tech. 42 133 doi: 10.3969/j.issn.1671-4776.2005.03.009 [12] Lu H F, Zhang C, Zhang Q Y 2003 Nucl. Instrum. Meth. B 206 22 doi: 10.1016/S0168-583X(03)00705-5 [13] Pastewka L, Salzer R, Graff A 2009 Nucl. Instrum. Meth. B 267 3072 doi: 10.1016/j.nimb.2009.06.094 [14] Jr M F R, Maazouz M, Giannuzzi L A 2008 Appl. Surf. Sci. 255 828 doi: 10.1016/j.apsusc.2008.05.083 [15] Feil H, Zwol J, Zwart S T, Dieleman J 1991 Phys. Rev. B 43 13695 doi: 10.1103/PhysRevB.43.13695 [16] Lopez-Cazalilla A, Cupak C, Fellinger M 2022 Phys. Rev. Mate. 6 075402 doi: 10.1103/physrevmaterials.6.075402 [17] Plimpton S 1995 J. Comput. Phys. 117 1 doi: 10.1006/jcph.1995.1039 [18] Tran H, Chew H B 2023 Carbon 205 180 doi: 10.1016/j.carbon.2023.01.015 [19] 颜超, 段军红, 何兴道 2011 物理学报 60 088301 doi: 10.7498/aps.60.088301 Yan C, Duan J H, He X D 2011 Acta Phys. Sin. 60 088301 doi: 10.7498/aps.60.088301 [20] Nosé S 1984 J. Chem. Phys. 81 511 doi: 10.1063/1.447334 [21] Slavinskaya N A 1998 Matem. Mod. 34 3 doi: 10.1063/1.1701092 [22] Daw M S, Foiles S M, Baskes M I 1993 Mater. Sci. Rep. 9 251 doi: 10.1016/0920-2307(93)90001-U [23] Ziegler J F 1988 Ion Implantation Technology (Berlin, Heidelberg: Springer) pp122–156 [24] 颜超, 黄莉莉, 何兴道 2014 物理学报 63 126801 doi: 10.7498/aps.63.126801 Yan C, Huang L L, He X D 2014 Acta Phys. Sin. 63 126801 doi: 10.7498/aps.63.126801 -
计量
- 文章访问数: 577
- HTML全文浏览数: 577
- PDF下载数: 4
- 施引文献: 0