现实世界中的许多复杂系统对外部环境及扰动具有自适应性, 如生态系统、气候系统和神经系统等. 然而, 许多复杂系统都存在临界点, 越过临界点的系统将转变到一个完全不同的状态, 这种突然的转变称为临界转迁^[1]. 临界转迁往往发生在内部或外部条件微小变化的过程中, 这个过程很难预料, 通常会导致灾难性的结果^[2]. 特别是在神经系统中, 临界转迁往往伴随着疾病的发生^[3]. 因此, 对临界转迁进行早期预警具有十分重要的研究意义.

早期预警信号(early warning signals, EWS)是一套可以用来预测临界点的统计指标^[4]. 传统EWS(如方差、自相关系数等)大多是基于临界慢化现象(critical slowing down, CSD)得到的. CSD几乎是动力系统所有分岔类型所具有的共同特性^[2], 主要表现为系统对小扰动的恢复力下降, 体现为方差和自相关系数的增加^[5,6]. 在神经系统中, CSD与一些脑疾病的发作息息相关, 例如Maturana等^[3]发现在癫痫发作之前, 患者的大脑信号会出现CSD现象, 从中得到的EWS可用于预测癫痫等脑疾病的发作. 目前, 许多学者已经对临界转迁的EWS进行了广泛的研究^[4,7-10]. 其中, Dakos等^[4]提出了一个将基于度量的指标和基于模型的指标相结合的框架分析时间序列数据, 以成功识别即将到来的临界转迁; Carpenter等^[10]构建了非参数漂移-扩散-跳跃模型, 用以增加EWS的精度. 尽管传统EWS已经被广泛地应用于生态系统^[11,12]、气候系统^[13-15]和神经系统^[16]等复杂系统中. 但Dakos等^[17]发现, 在实际应用过程中, 传统EWS对外部噪声的稳健性较差, 并且动力系统的分岔有多种类型, 每种类型都有其独特的动力学特性^[18], 但传统EWS无法对分岔的类型进行区分. 2020年, Bury等^[19]提出了将功率谱作为EWS, 在准确预测即将到来的分岔同时, 能够对分岔类型进行区分. 之后, Chen等^[20]将基于功率谱的EWS应用于气候系统中. 在神经系统中, 不同的脑疾病可能是由不同类型的神经元异常放电引起的, 从动力学角度, 对应于动力系统的不同类型的分岔, 而目前对神经元分岔前EWS的相关研究较少, 因此, 对神经元的临界转迁前的EWS进行考察十分有必要.

本文将基于功率谱的EWS应用于模型神经元系统中, 分别对Morris-Lecar (ML)神经元和Hindmarsh-Rose (HR)神经元放电所对应的4种余维一分岔前的临界现象进行考察, 同时计算了时滞$\tau = 1$自相关系数和方差两种传统EWS, 详细分析了基于功率谱的EWS在预测模型神经元分岔的过程中相对于传统EWS的优势, 并且对神经元的I型兴奋和II型兴奋, 即鞍结分岔和Hopf分岔进行区分.

本节首先推导了自相关系数、方差和功率谱在折叠分岔和Hopf分岔中的近似解析解, 得到了随着动力系统接近分岔点, 以上3种EWS的变化趋势. 此后分别介绍了针对数值计算得到的随机模拟响应, 计算传统EWS, 即自相关系数和方差以及基于功率谱的EWS的方法.

Bury等^[19]提出了将功率谱作为EWS, 应用于复杂动力系统临界转迁的预测, 并对自相关系数、方差和功率谱3种EWS的近似解析解进行了以下推导.

考虑折叠分岔的拓扑范式:

其中$x$表示相对于平衡点的距离, $\lambda $是控制系统稳定性的特征值($\lambda \lt 0$). 假设系统受到较小的加性高斯白噪声的影响, 服从:

其中$ \xi \left( t \right) $为高斯白噪声过程, $\sigma $为噪声强度. 该过程是一个OU (Ornstein-Uhlenbeck)过程^[21], 对(2)式积分可以得到:

其中$x\left( 0 \right)$是过程的初始位置. 我们主要考察平稳过程的的统计数据, 因此可以去掉瞬态项, 得到:

在$\lambda \to 0$的情况下, 得到:

随机过程$x\left( t \right)$的自协方差函数定义为

其中$\tau $是滞后时间, $ \left\langle \cdots \right\rangle $表示随机变量的期望, 将(5)式代入(6)式可以得到:

假设高斯白噪声满足:

其中$\delta $是狄拉克函数, 之后对(7)式进行简化和积分可以得到:

由于$\lambda \lt 0$, 因此在稳态($t \to \infty $)时, 有

由此可以导出OU过程的方差和自相关系数的近似解, 分别如(11)式和(12)式所示:

其中$\tau $是滞后时间. 在接近折叠分岔时, $\lambda $从负方向接近0, 会导致方差和自相关分别单调增至无穷大和1. 该过程的功率谱可以使用Wiener-Khinchin定理计算, 该定理指出, 对于平稳随机过程, 功率谱是自协方差函数(10)式的傅里叶变换^[22]:

给定随机过程$\phi \left( \tau \right) = \phi \left( { - \tau } \right)$, (13)式可以化为

将(10)式代入, 得到:

积分得到:

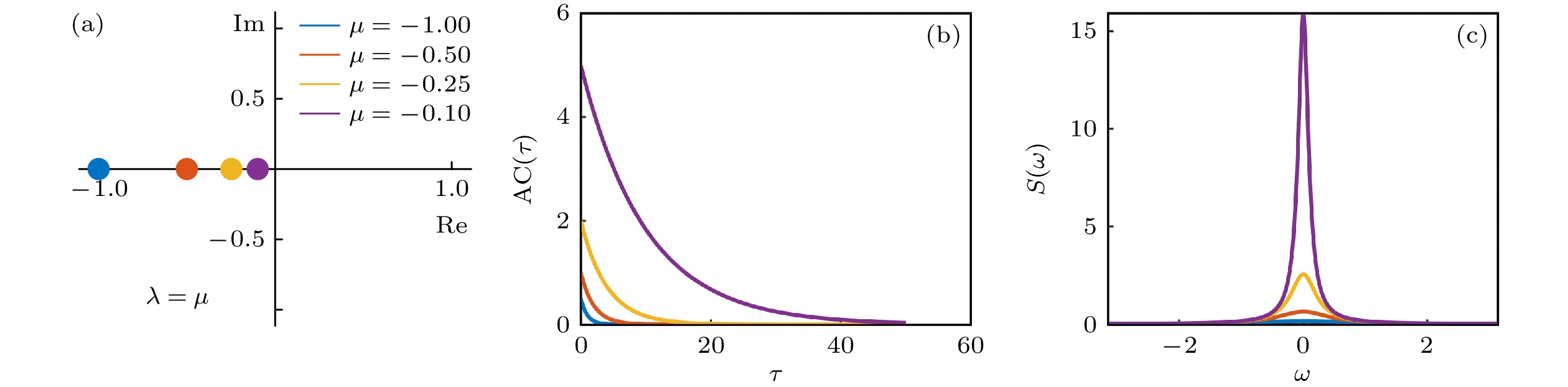
在图1中, 取$\sigma = 1$, 展示了距离分岔点不同距离处($ \mu = - 1, {\text{ }}\, - 0.5, \, {\text{ }} - 0.25, {\text{ }}\, - 0.1 $)自相关以及功率谱的变化, 其中$ \lambda = \mu $为主导特征值中的实部. 从图1(b)可以看出, 随着系统逐渐接近分岔点, 不同时滞$\tau $的自相关逐渐增大. 从图1(c)可以看出, 在折叠分岔的情况下, 功率谱的频率$\omega $应由零频率主导, 且功率谱零频率的幅值随着系统接近分岔点而增大, 因此从理论上来说功率谱可以作为折叠分岔的EWS.

考虑Hopf分岔的拓扑范式:

系统稳定性的特征值由$\lambda = \mu \pm {\text{i}}{\omega _0}$给出. 分别在$x$和$y$方向上加入高斯白噪声, 得到系统:

其中, ${\boldsymbol{ x}} $为状态向量${\left( {{x_1}, {\text{ }}{x_2}} \right)^{\text{T}}}$, ${\boldsymbol{ \xi}} \left( t \right) $是高斯白噪声过程$ {\left( {{\xi _1}, {\text{ }}{\xi _2}} \right)^{\text{T}}} $, $ {\boldsymbol{B}} $是噪声强度$ {\mathrm{diag}}\left( {{\sigma _1}, {\text{ }}{\sigma _2}} \right) $的矩阵, $ {\boldsymbol{J}} $为雅可比矩阵:

对(18)式积分可以得到:

稳态下的动力学表达式为

多维过程的协方差矩阵定义为

将(21)式代入, 得到:

在推导过程中, 假定白噪声相互独立, 即$ \left\langle {{\boldsymbol{\xi}} \left( t \right){{\boldsymbol{\xi }}^{\text{T}}}\left( {t'} \right)} \right\rangle = {\boldsymbol{I}}\delta \left( {t - t'} \right) $. 由于随机过程是平稳的:

对(23)式求导可以得到:

(25)式成为连续Lyapunov方程, 在二维情况下, 封闭解是已知的, 由(26)式给出:

可以通过(26)式衡量Hopf分岔前系统的方差, 假设噪声强度$ {\sigma _1} $和$ {\sigma _2} $相差很小, 即$ {\sigma _2} = {\sigma _1} + \varepsilon $, $ \varepsilon $很小, 在忽略高阶项的情况下, 可以得到方差的表达式如下:

通过(18)式和白噪声的统计特性可以得到:

求解(28)式得到:

其中${\boldsymbol{\varSigma}} = \phi \left( 0 \right)$, 所以可以直接从协方差矩阵$ {\boldsymbol{\varSigma }}$计算自协方差矩阵$\phi $, 得到:

因此自相关系数的表达式为

功率谱密度可以通过傅里叶变换得到:

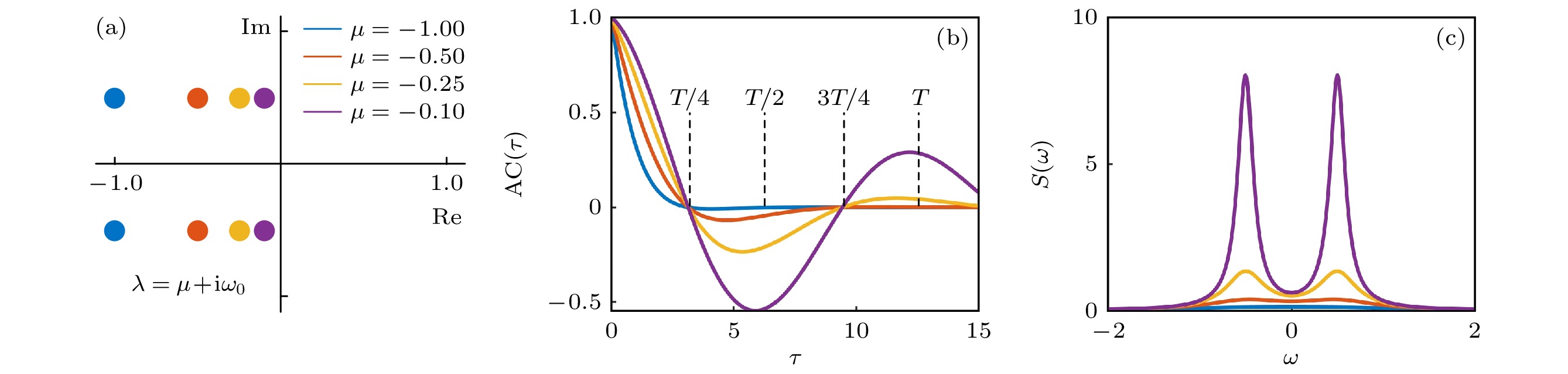
在图2中, 取$\sigma = 1$, ${\omega _0} = 0.5$, 画出了距离分岔点不同距离处($ \mu = - 1, \, {\text{ }} - 0.5, \, {\text{ }} - 0.25, \, {\text{ }} - 0.1 $)自相关以及功率谱的变化. 从图2(b)可以看出, 随着系统接近分岔点, 自相关系数的变化趋势取决于时滞$\tau $和基本振荡周期$T$之间的关系. 当时滞$\tau $较小时($\tau \lt {T {/ } 4}$), 自相关系数随着系统接近分岔点而增大; 而当时滞$\tau $接近基本振荡周期的一半时(${T {/ } 4} \lt \tau \lt {{3 T} {/ } 4}$), 自相关系数随着系统接近分岔点而减小. 从图2(c)可以看出, 在Hopf分岔的情况下, 功率谱的频率$\omega $应由特征值虚部${\omega _0}$, 即非零频率主导, 且功率谱的幅值随着系统接近分岔点而增加, 因此从理论上来说功率谱可以作为Hopf分岔的EWS.

综上所述, 随着系统接近分岔点, 自相关系数和功率谱峰值${S_{\max }}$均能产生有效的趋势, 以对即将到来的分岔进行预测; 但功率谱的主导频率不同, 因此能够对不同类型的分岔进行区分.

为了与基于功率谱的EWS进行对比, 本节引入了两种已经被广泛研究过的传统EWS, 即自相关系数和方差. 采用Dakos等^[4]提出的EWS工具箱中的标准方法计算传统EWS, 主要计算了自相关系数和方差两种传统EWS进行对比分析. 首先, 通过Lowess函数对数据进行去趋势处理, 随后, 在选定大小的滑动窗口上计算EWS指标, 以确保窗口内的序列可被视为近似静止.

方差是描述样本数据对均值$\bar x$偏差程度的特征量, 记为${s^2}$. 对于窗口$ \left\{ {{x_i}} \right\}_{i = 1}^n $中的数据点, 方差$ {s^2} $的计算公式为

自相关系数是描述同一变量在不同时刻相关性的统计量, 滞后长度为$\tau $的自相关系数记为$ \mathit{\mathit{\mathrm{AC}}}\left(\tau\right) $, 自相关系数的计算公式为

其中$ {s^2} $由(11)式计算得出.

计算基于功率谱的EWS, 首先要通过Welch方法^[23]获取功率谱的近似值, 该方法在滚动窗口中, 取许多重叠的Hamming窗上计算周期图, 将功率谱近似为周期图的平均值. Hamming窗$\left\{ {{x_j}} \right\}_{j = 1}^m$内的数据由以下函数进行加权:

加权后得到转换后的数据$\left\{ {{y_j}} \right\}_{j = 1}^m$, 周期图可由(36)式计算得到:

(37)式是$\left\{ {{y_j}} \right\}_{j = 1}^m$的离散傅里叶变换, 该方法相较计算滚动窗口全长上的周期图相比, 可以得到更加一致且无偏的功率谱估计.

功率谱的峰值${S_{\max }}$由功率谱$\left\{ {S\left( k \right)} \right\}_{k = 1}^n$计算得出:

本节分别在ML和HR模型神经元上考察神经元峰放电所对应的余维一分岔点附近的临界现象, 采用Euler-Maruyama方法对添加高斯白噪声的ML神经元和HR神经元进行数值计算, 时间步长$ \Delta t = 0.01 $, 模拟10⁴个步长. 计算了时滞$\tau = 1$自相关系数、方差和功率谱3种EWS, 对模型神经元仿真计算, 得到EWS进行对比分析.

参考Prescott等^[24]考虑的一种ML神经元模型, 并在膜电位项上添加加性高斯白噪声, 模型的描述如下:

其中, $V$代表神经元膜电位, $\omega $代表钾离子通道的激活变量, $I$代表外加电流刺激. $ \sigma \xi \left( t \right) $为随机高斯白噪声, $\sigma $为噪声强度, $ \xi \left( t \right) $表示独立的高斯白噪声.

系统参数$ {E_{{\text{Na}}}} $, $ {E_{\text{K}}} $和$ {E_{{\text{leak}}}} $分别代表Na⁺, K⁺和泄漏电流的平衡电位; $ {g_{{\text{fast}}}} $, $ {g_{{\text{slow}}}} $和$ {g_{{\text{leak}}}} $分别表示相应的快速、慢速和泄漏电流的最大电导. 稳态激活函数和时间常数由(40)式给出:

以下参数参考Prescott等^[24]的取值: $ {E_{{\text{Na}}}} = 50 {\text{ mV}} $, $ {E_{\text{K}}} = - 100 {\text{ mV}} $, $ {E_{{\text{leak}}}} = - 70 {\text{ mV}} $, $ {g_{{\text{fast}}}} = 20 {\text{ ms/c}}{{\text{m}}^2} $, $ {g_{{\text{slow}}}} = 20 {\text{ ms/c}}{{\text{m}}^2} $, $ {g_{{\text{leak}}}} = 2 {\text{ ms/c}}{{\text{m}}^2} $, $ {\phi _{\text{ω}}} = 0.15 $, $C = 2 {\text{ μF/c}}{{\text{m}}^2}$, $ {\gamma _{\text{m}}} = 18 {\text{ mV}} $. 噪声强度$\sigma = 0.02$, 选择参数$I$作为系统的分岔参数. Liu等^[25]研究表明, 该ML模型神经元在不同的参数下会产生不同的分岔行为, 因此其余参数$ {\beta _{\text{m}}} $, $ {\beta _{\text{ω }}} $和$ {\gamma _{\text{ω }}} $根据不同的分岔类型而确定.

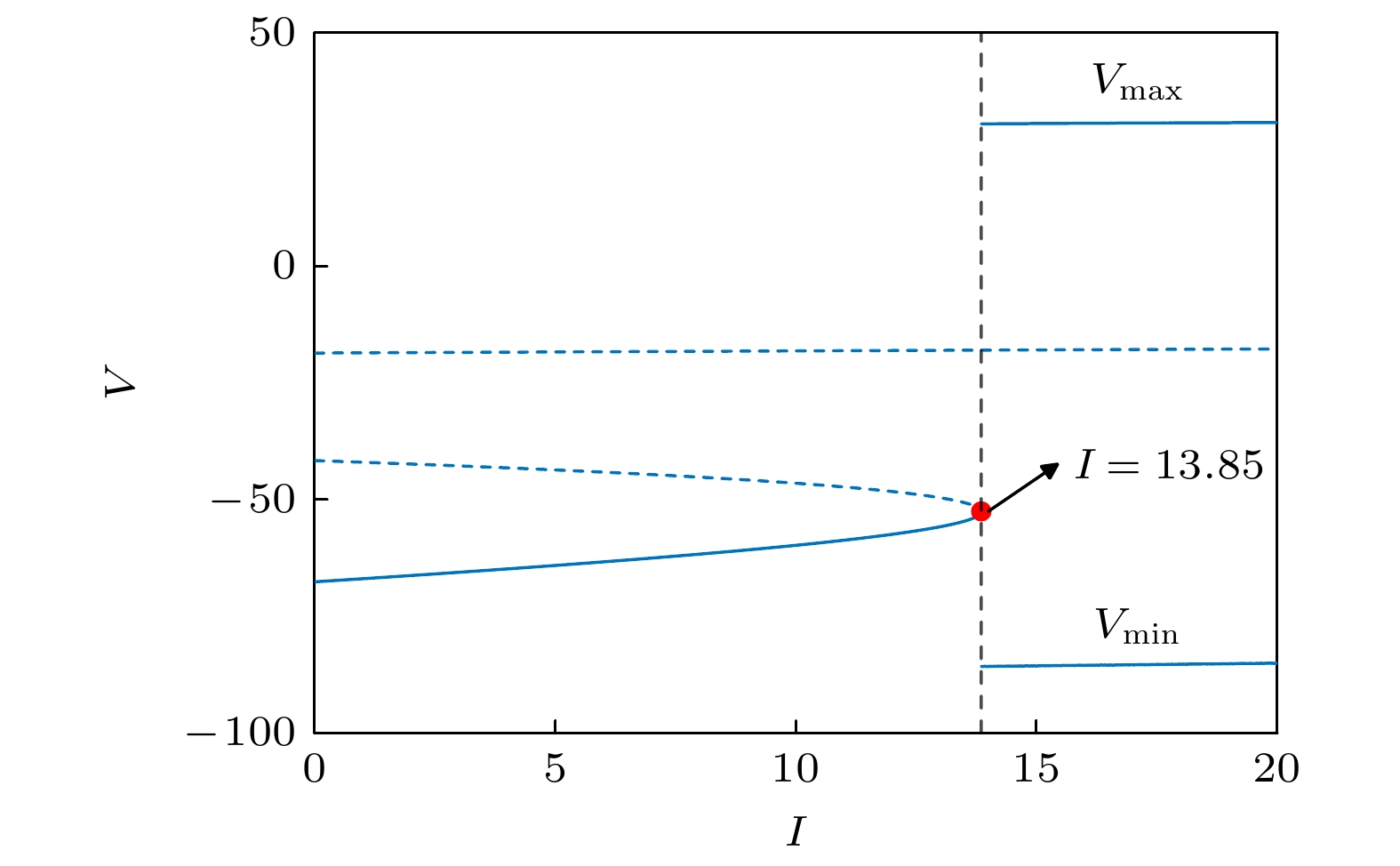
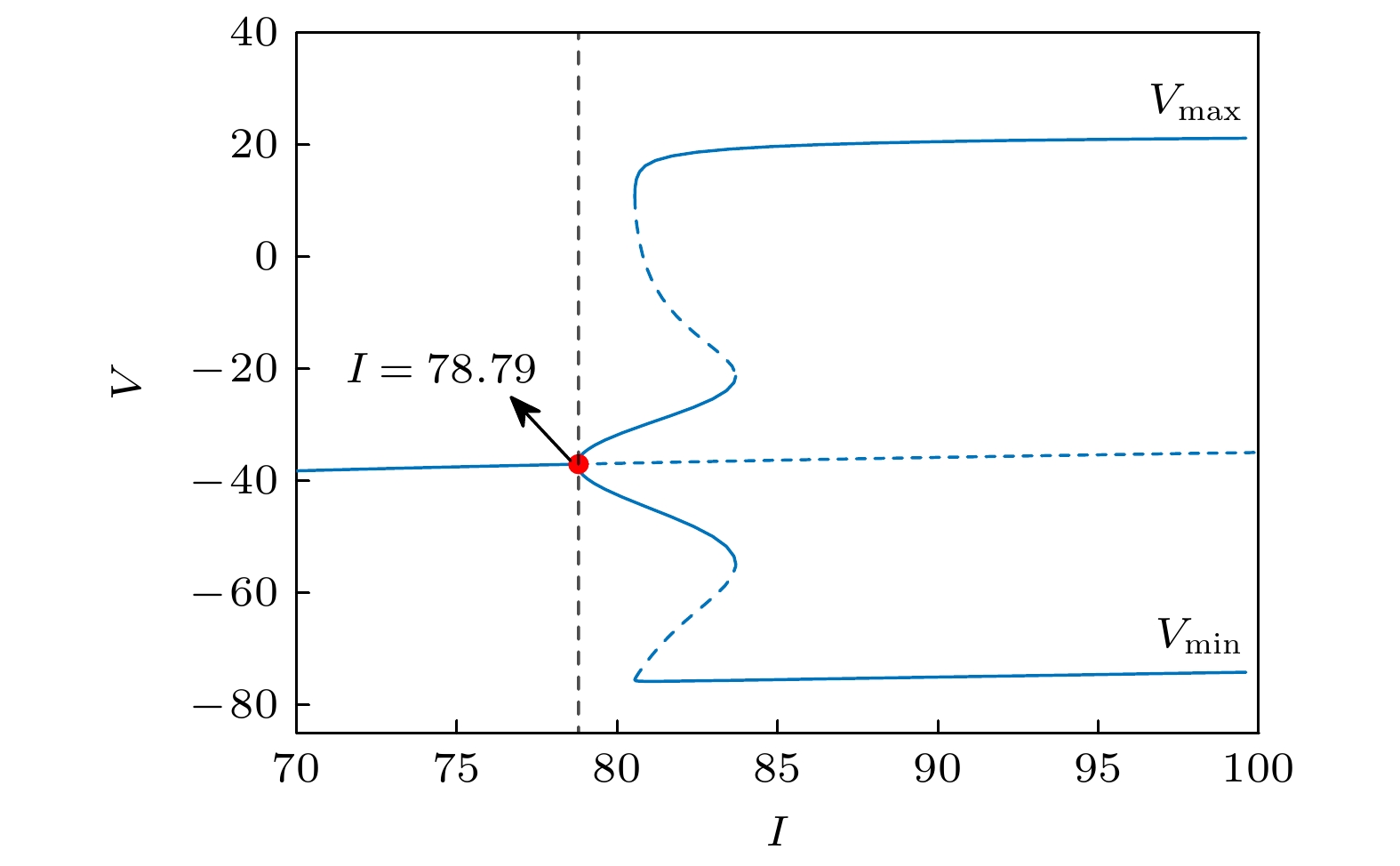
根据Liu等^[25]的研究, 当$ {\beta _{\text{m}}} = - 12 {\text{ mV}} $, $ {\beta _{\text{ω }}} = - 10 {\text{ mV}} $, $ {\gamma _{\text{ω }}} = 13 {\text{ mV}} $时, 该ML模型在$I = 13.85$时发生不变圆上的鞍结分岔(saddle-node bifurcation on invariant circle, SNIC)分岔, 分岔图如图3所示.

图3显示了随着分岔参数$I$从0增大到20, ML模型的膜电位对外加电流的分岔图. 随着分岔参数$I$的逐渐增大, 稳定平衡点与不稳定平衡点逐渐接近, 并在$I = 13.85$时的鞍结分岔点上碰撞并消失, 由不变圆上的鞍结点分岔成为一个稳定的极限环. 由于研究的目标是在分岔点前进行早期预警, 因此我们重点研究分岔点前的时间序列, 对应于分岔图上蓝色粗实线部分.

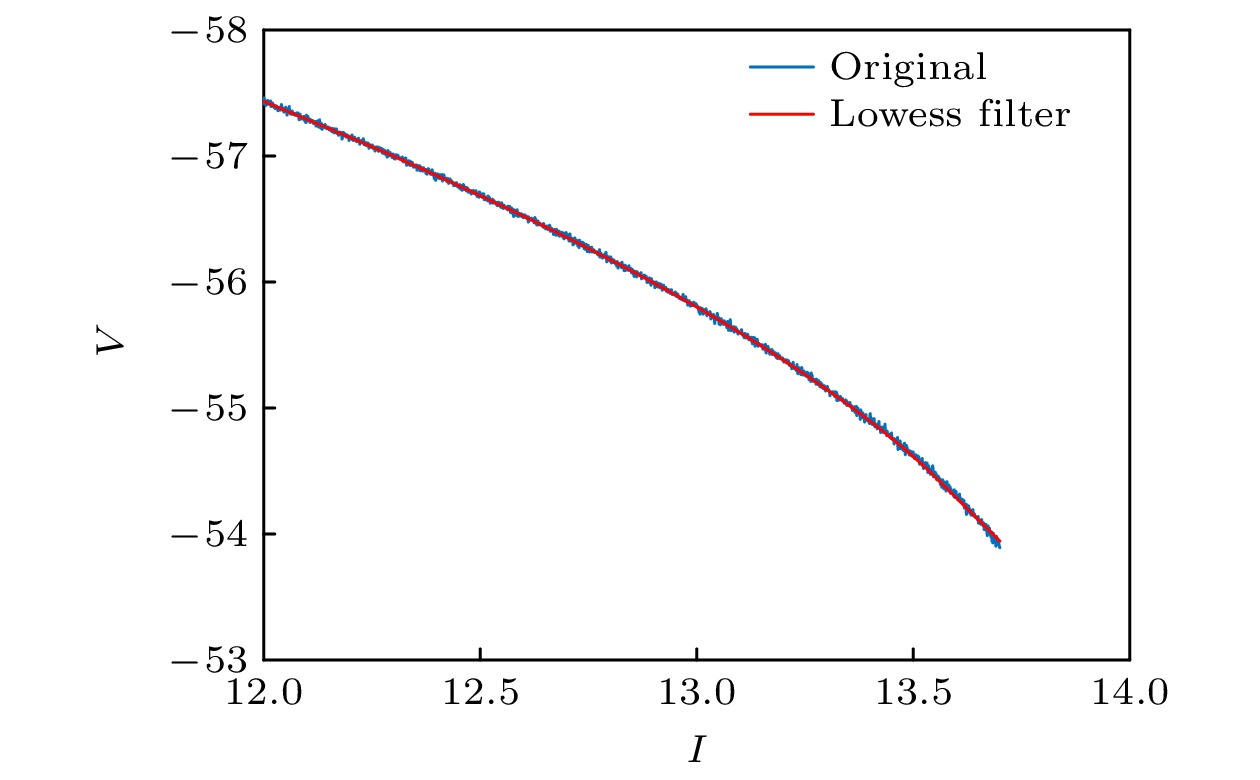
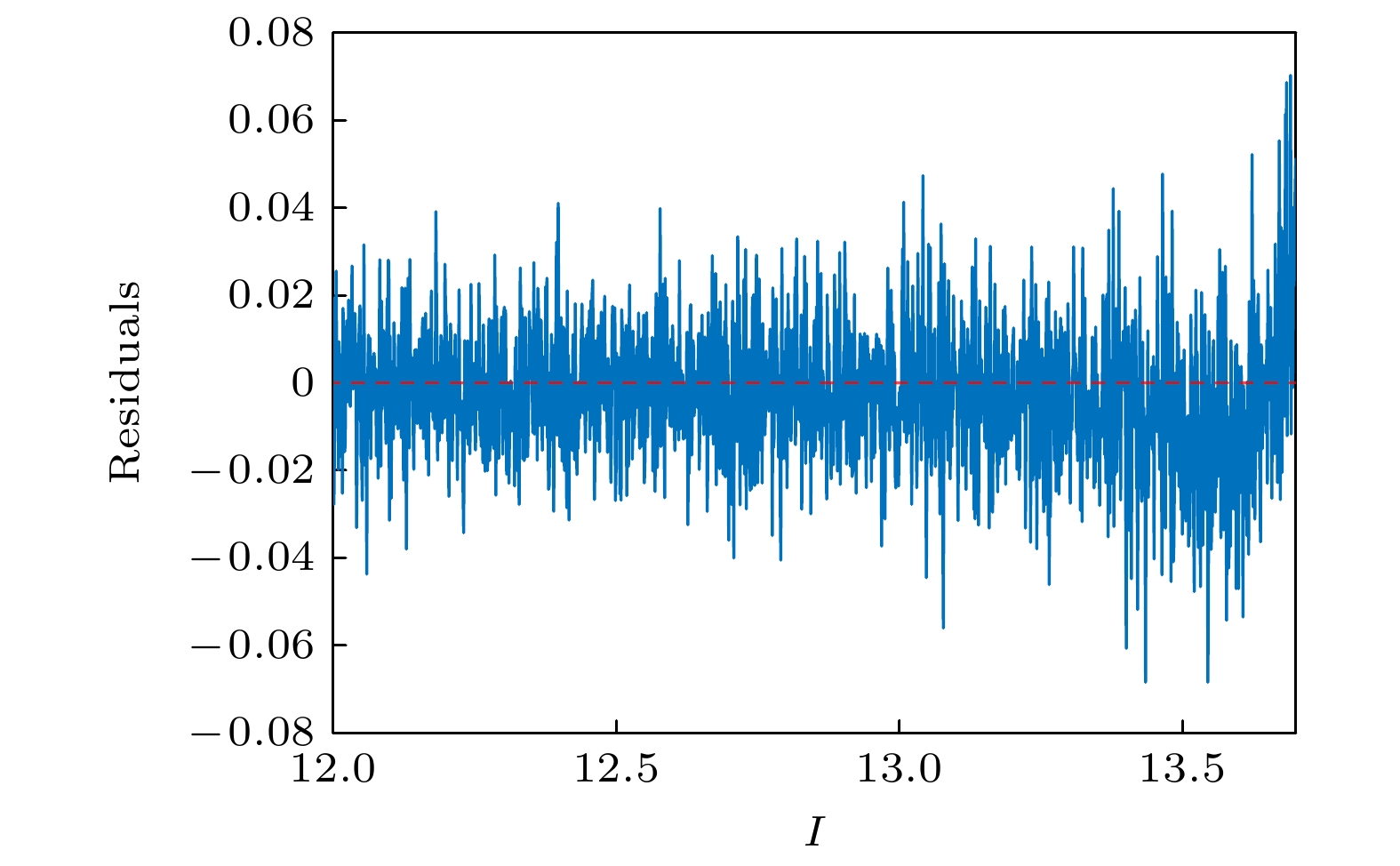
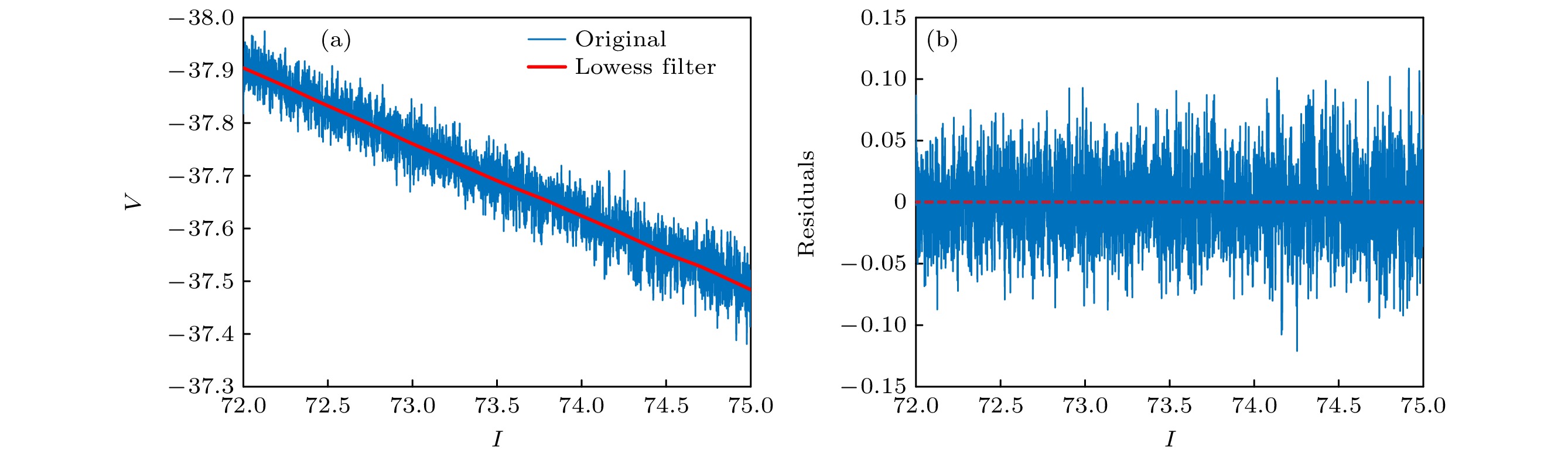
针对该ML模型, 对于分岔点前的稳定分支, 取$I \in \left[ {12, {\text{ }}13.7} \right]$进行分析, 使分岔参数$I$以$\varDelta = 0.001$从12逐渐增至13.7, 对每个分岔参数进行随机模拟, 得到SNIC分岔前膜电位对增大的电流刺激$I$的模拟响应如图4所示.

在对响应序列分析前, 要对序列进行去趋势处理, 避免趋势项(直流分量)对功率谱的频率产生影响. 采用Lowess滤波器对时间序列进行平滑, 得到的趋势项如图4红色实线所示. 从原始数据中减去趋势项, 得到残差数据, 如图5所示.

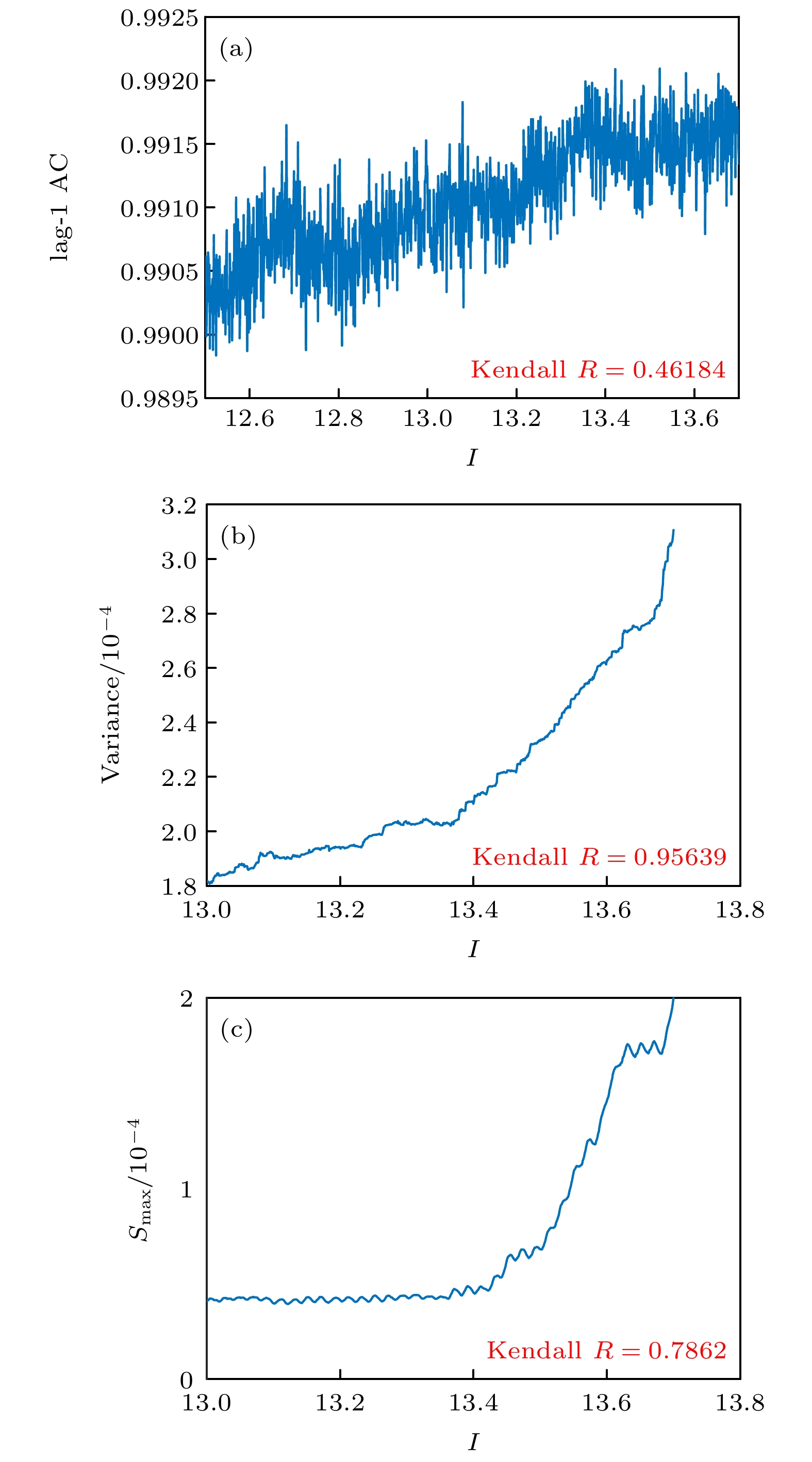
对上述模型进行200次重复随机模拟, 每次模拟计算原始时间序列的时滞$\tau = 1$自相关系数和方差以及残差时间序列的功率谱, 取平均值得到EWS, 如图6所示.

由于EWS主要通过其在分岔点前所产生的趋势来进行预警, 因此本文采用Kendall系数$R$^[26]来衡量EWS所产生趋势的程度. Kendall系数$R$的取值范围为–1—1, 相关系数小于0表示两变量负相关, 大于0表示正相关, 等于0表示两变量相互独立. 相关系数的绝对值越大, 表示两变量间的相关程度越密切; 相关系数越接近于0, 表示相关越不密切.

时滞$\tau = 1$自相关系数、方差和${S_{\max }}$均随着系统逐渐接近分岔点而增大. 其中方差的Kendall系数$R = 0.95639$, 预测效果最佳; ${S_{\max }}$的Kendall系数$R = 0.7862$, 能够在分岔点前进行有效的预测; 时滞$\tau = 1$自相关系数的Kendall系数$R = 0.46184$, 预测效果差, 从图中也能看出其随着控制参数的变化时波动较大, 无法在分岔前形成明显的趋势对分岔点进行预测.

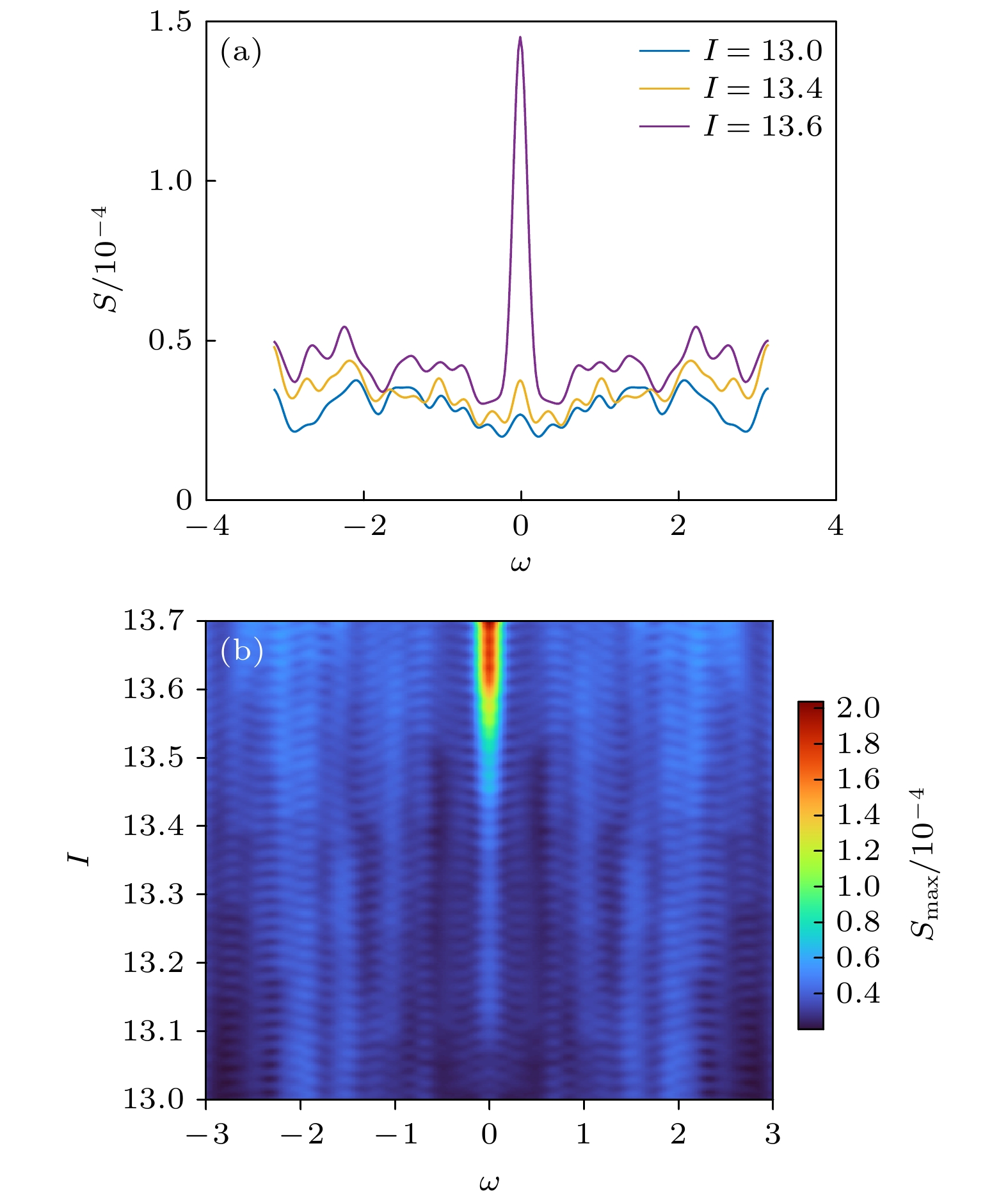
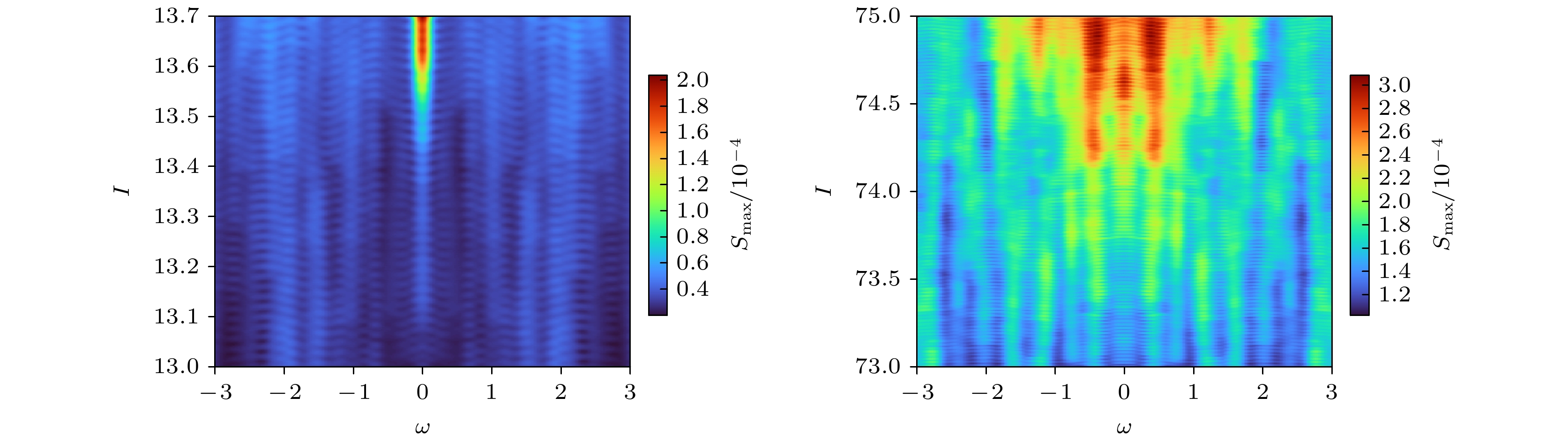
对于功率谱密度进行分析, 绘制$I = 13.0, \; 13.4, 13.6$的功率谱密度如图7(a)所示. 可以看出, 随着分岔参数$I$接近分岔点, 功率谱密度的幅值整体呈上升趋势, 且对于SNIC分岔, 功率谱的最大幅值由零频率主导, 非零频率幅值处于较低状态, 这种结果的出现也与前文的理论推导相符合. 如图7(b)所示, 绘制功率谱的等高线图, 可以看出随着分岔参数$I$逐渐接近分岔点, 零频率主导的功率谱幅值呈现出明显的上升趋势, 因此基于功率谱的EWS能够对SNIC分岔做出准确的预测.

根据Liu等^[25]的研究, 当$ {\beta _{\text{m}}} = - 1.2 {\text{ mV}} $, $ {\beta _{\text{ω }}} = - 20.5 {\text{ mV}} $, $ {\gamma _{\text{ω }}} = 10 {\text{ mV}} $时, 该ML模型在$I = 78.79$时发生超临界Hopf分岔, 分岔图如图8所示.

图8显示了随着分岔参数$I$从70增至100, ML模型的单参数分岔图. 当分岔参数$I$较小时, 系统存在一个稳定的平衡点, 随着分岔参数$I$逐渐增大, 在$I = 78.79$时, 稳定平衡点经过Hopf分岔点, 变为不稳定平衡点, 同时产生一个稳定的极限环. 如上文所述, 重点研究分岔点前的时间序列, 对应于分岔图上蓝色粗实线部分.

针对该ML模型, 对于分岔点前的稳定分支, 取$I \in \left[ {72, 75} \right]$进行分析, 使分岔参数$I$以$\varDelta = 0.001$从72逐渐增至75, 对每个分岔参数, 进行随机模拟, 得到超临界Hopf分岔前膜电位对增大的电流刺激$I$的模拟响应如图9(a)所示. 通过Lowess滤波器进行去趋势处理, 得到的残差序列如图9(b)所示.

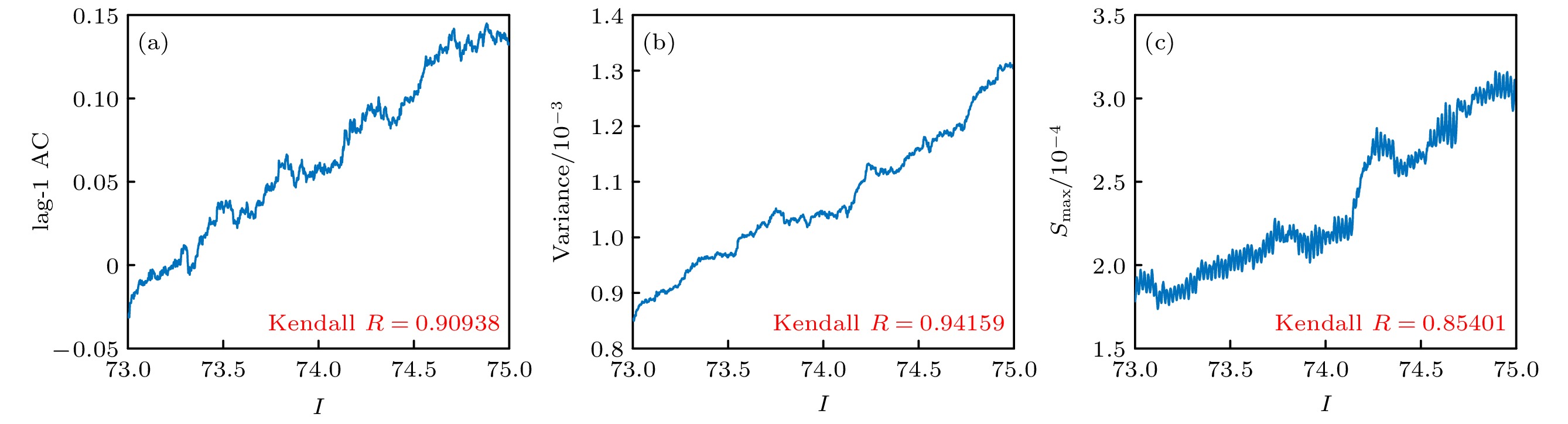
对上述模型进行200次重复随机模拟, 每次模拟计算原始时间序列的时滞$\tau = 1$自相关系数和方差以及残差时间序列的功率谱, 取平均值得到EWS如图10所示.

时滞$\tau = 1$自相关系数、方差和${S_{\max }}$均随着系统逐渐接近分岔点而增大. 在ML模型的超临界Hopf分岔前, 3种EWS均产生了较为明显的上升趋势, 且Kendall系数$R$均接近于1, 因此3种EWS都能够较为准确地预测该ML模型的超临界Hopf分岔.

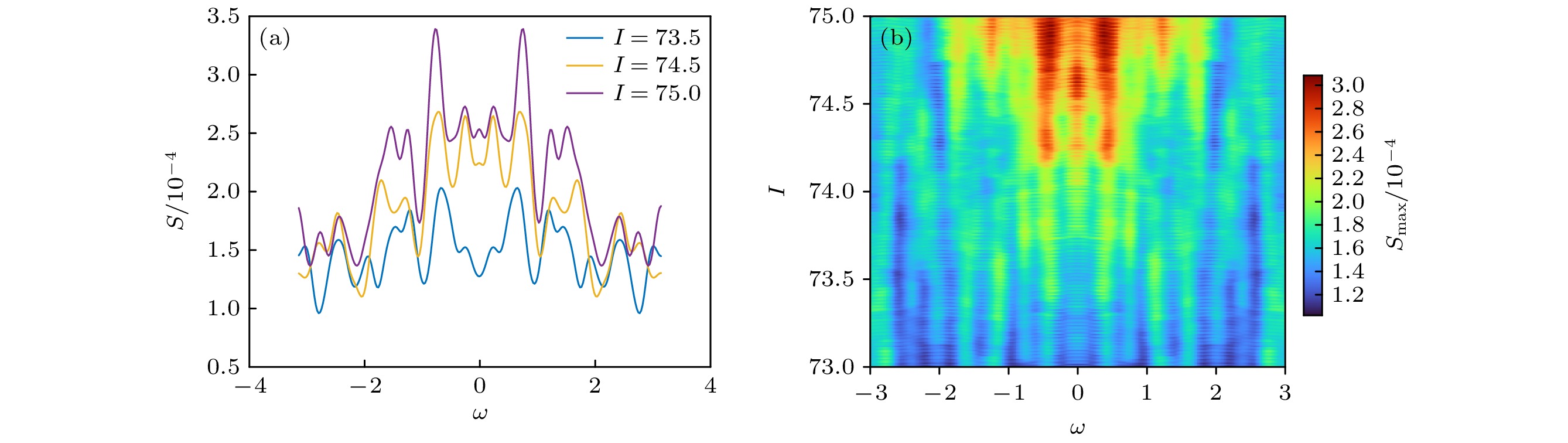
对于功率谱密度进行分析, 绘制$I = 73.5, {\text{ }}74.5, 75.0$的功率谱密度如图11(a)所示. 可以看出, 随着分岔参数$I$接近分岔点, 功率谱密度的幅值整体呈上升趋势, 且对于超临界Hopf分岔, 功率谱的最大幅值由非零频率主导, 这种结果也与前文的理论推导相符合. 如图11(b)所示, 绘制功率谱的等高线图, 可以看出随着分岔参数$I$逐渐接近分岔点, 非零频率主导的功率谱幅值呈现出明显的上升趋势, 因此基于功率谱的EWS能够对超临界Hopf分岔做出准确的预测, 同时针对功率谱主导频率的不同, 可以对SNIC分岔和超临界Hopf分岔进行区分.

参考Lü等^[27]提出的一种考虑了电磁感应的HR神经元模型, 并在膜电位项上添加加性高斯白噪声, 模型描述如下:

其中, 状态变量$x$, $y$, $z$, $\varphi $分别表示神经元的膜电位、恢复变量的慢电流、自适应电流和穿过细胞膜的磁通量; $ \sigma \xi \left( t \right) $为随机高斯白噪声, $\sigma $为噪声强度, $ \xi \left( t \right) $表示独立的高斯白噪声; ${k_0}$, ${k_1}$, ${k_2}$为磁通反馈增益; $I$表示外加电流刺激. $a$, $b$, $c$, $d$, $s$, $r$, ${\chi _0}$均为系统参数. 磁控忆阻器的忆导$ W\left( \varphi \right) $表达式为

其中参数$\alpha $和$\beta $为确定的常数.

以下参数参考Lü等^[27]的取值: $a = 1.0$, $b = 3.0$, $c = 1.0$, $s = 4.0$, $r = 0.006$, ${\chi _0} = - 1.61$, ${k_1} = 0.9$, ${k_2} = 0.5$, $\alpha = 0.2$, $\beta = 0.03$, $\sigma = 0.01$. 选择参数$I$作为系统的分岔参数. Lü等^[27]研究表明, 该HR模型神经元在不同的参数下会产生不同的分岔行为, 因此其余参数$d$与${k_0}$根据具体的分岔类型而确定.

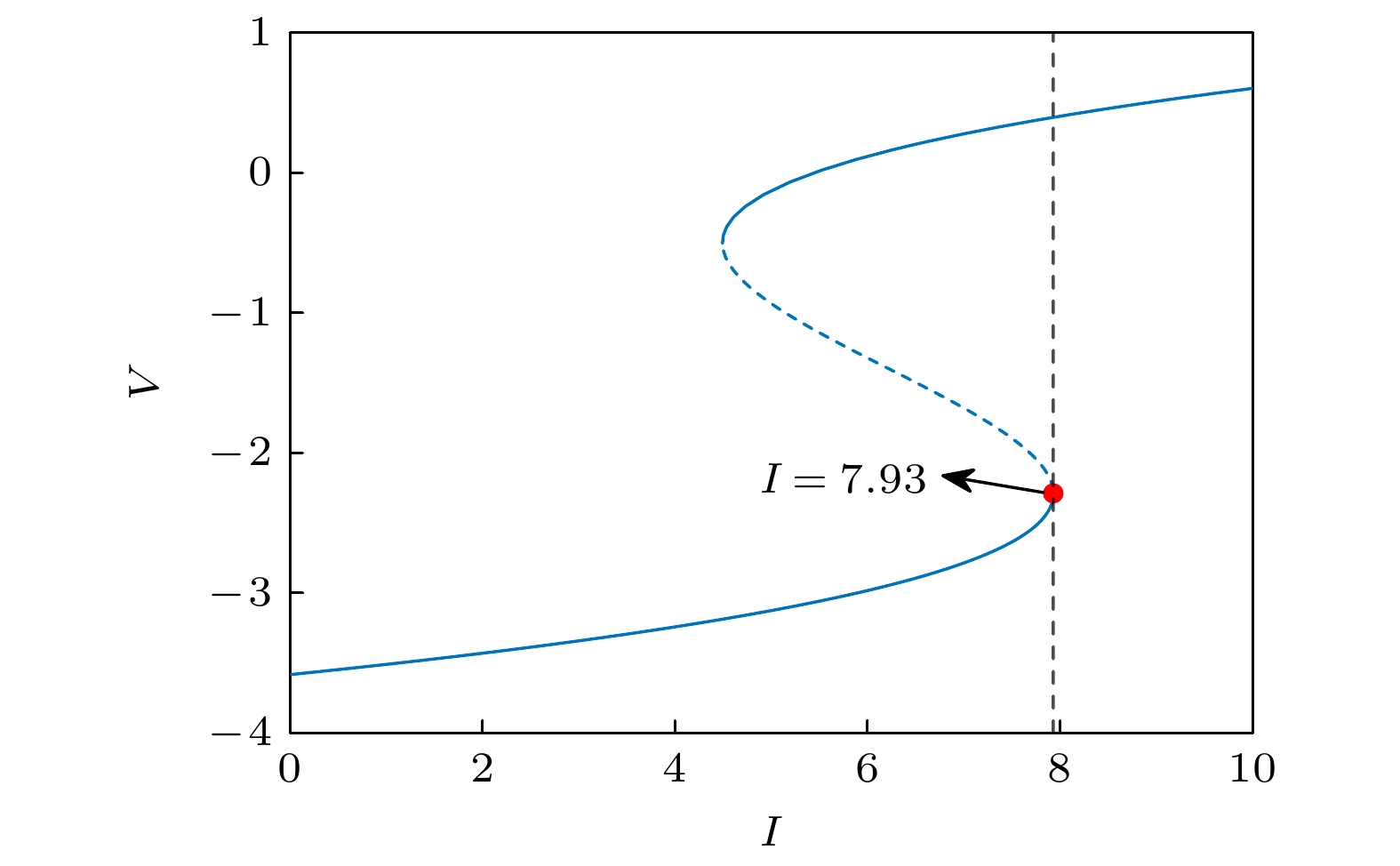
根据Lü等^[27]的研究, 当$d = 8.0$, ${k_0} = 1.0$时, 该HR模型在$I = 7.93$时发生鞍结分岔. 随着分岔参数$I$从0增至10, HR模型膜电位对外加电流的分岔图如图12所示. 当分岔参数$I$较小时, 系统存在一个稳定的平衡点, 随着分岔参数$I$逐渐增大, 稳定平衡点与不稳定平衡点逐渐接近, 并在$I = 7.93$时的鞍结分岔点上碰撞并消失, 发生鞍结分岔. 重点研究分岔点前的时间序列, 对应于图12蓝色粗实线部分.

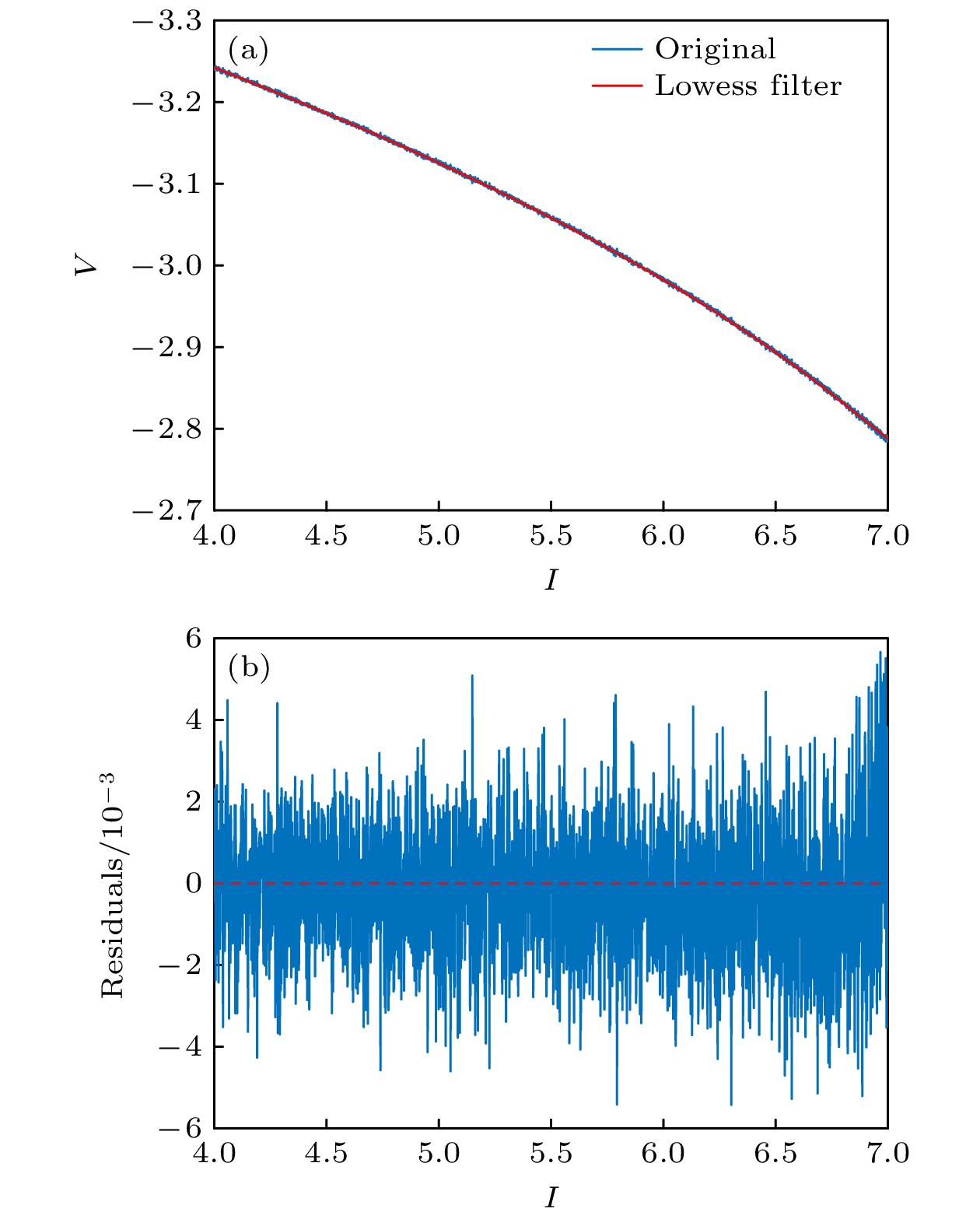
针对该HR模型, 对于分岔点前的稳定分支, 取$I \in \left[ {5, {\text{ }}7} \right]$进行分析. 使分岔参数$I$以$\varDelta = 0.001$从5逐渐增至7, 对每个分岔参数, 进行随机模拟, 得到鞍结分岔前膜电位对增大的电流刺激$I$的模拟响应, 如图13(a)所示. 通过Lowess滤波器进行去趋势处理, 得到的残差序列如图13(b)所示.

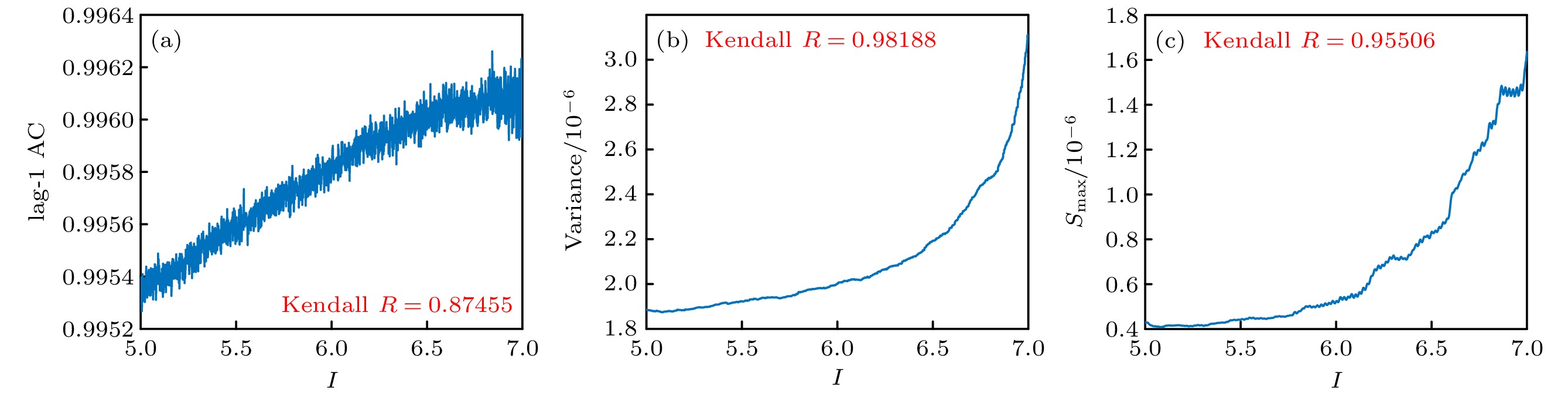
对上述模型进行200次重复随机模拟, 每次模拟计算原始时间序列的时滞$\tau = 1$自相关系数和方差以及残差时间序列的功率谱, 取平均值得到EWS如图14所示. 时滞$\tau = 1$自相关系数、方差和${S_{\max }}$均随着系统逐渐接近分岔点而增大. 其中方差的Kendall系数$R = 0.98188$, ${S_{\max }}$的Kendall系数$R = 0.95506$, 这两种EWS的预测效果很好, 能够在分岔点前进行有效的预测; 时滞$\tau = 1$自相关系数的Kendall系数$R = 0.87455$, 预测效果较好, 但从图中可以看出其随着控制参数的变化时波动较大, 受到噪声的影响较为明显.

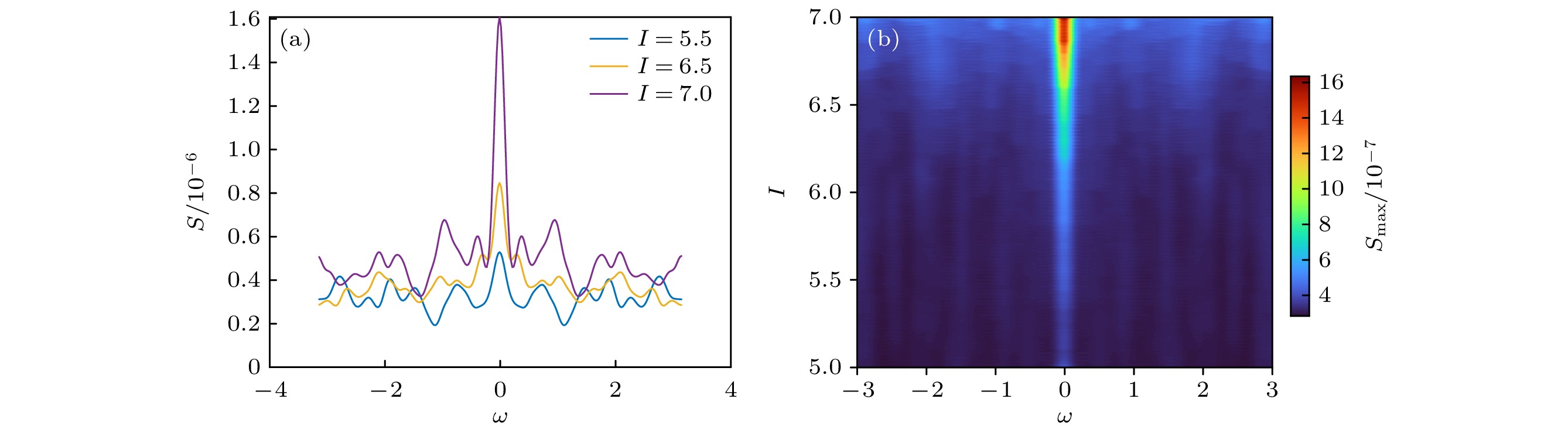
对于功率谱密度进行分析, 绘制$I = 5.5, {\text{ }}6.5, 7.0$的功率谱密度如图15(a)所示. 可以看出, 随着分岔参数$I$接近分岔点, 功率谱密度的幅值整体呈上升趋势, 且对于鞍结分岔, 功率谱的最大幅值由零频率主导, 非零频率幅值处于较低状态. 如图15(b)所示, 绘制功率谱的等高线图, 可以看出随着分岔参数$I$逐渐接近分岔点, 零频率主导的功率谱幅值呈现出明显的上升趋势, 因此基于功率谱的EWS能够对鞍结分岔做出准确的预测.

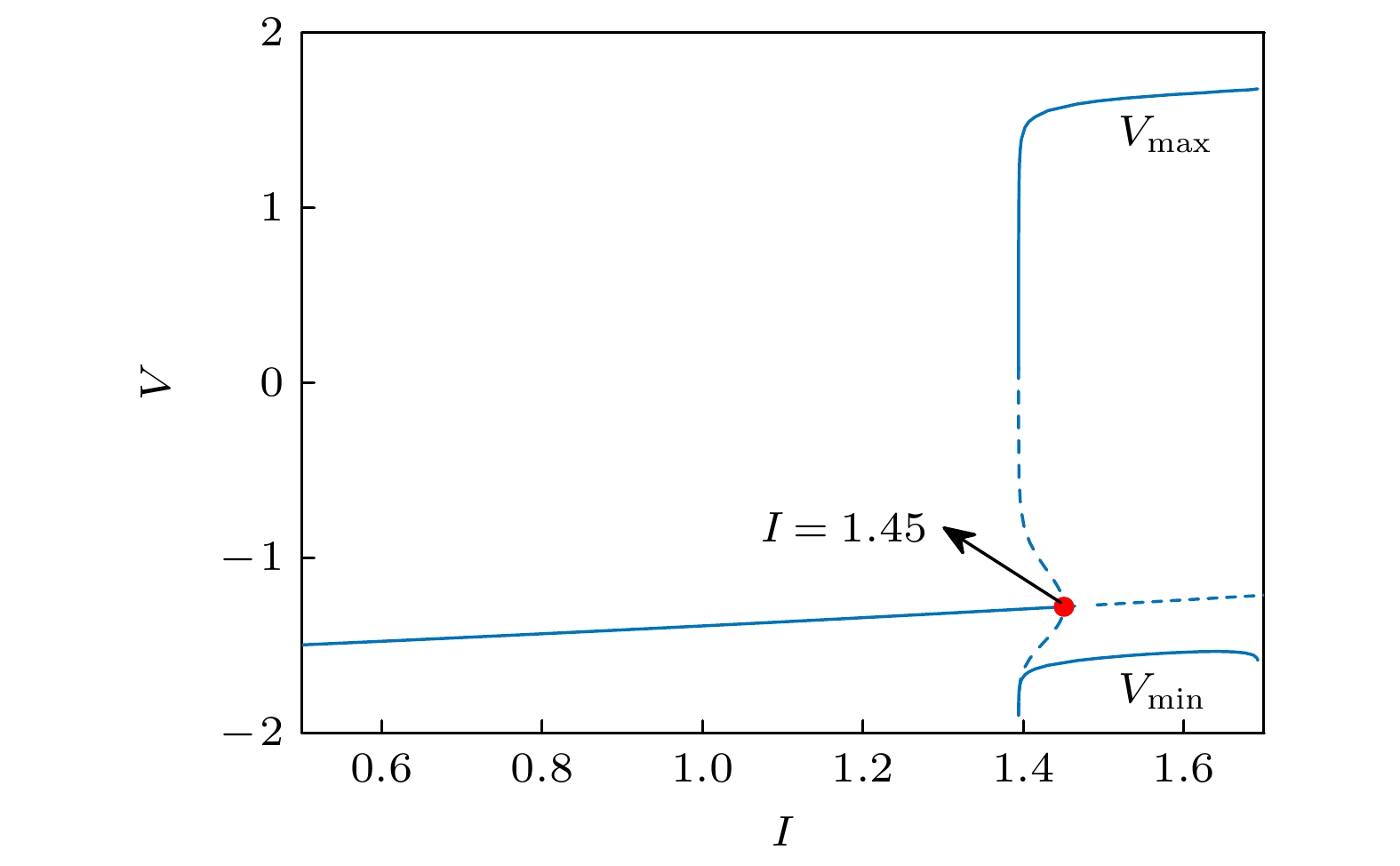
根据Lü等^[27]的研究, 当$d = 5.0$, ${k_0} = 0.1$时, 该HR模型在$I = 1.45$时发生亚临界Hopf分岔. 图16为随着分岔参数$I$从0.5增至1.7, HR模型的膜电位对外加电流的分岔图. 当分岔参数$I$较小时, 系统存在一个稳定的平衡点, 随着分岔参数$I$逐渐增大, 在$I = 1.45$时, 稳定平衡点经过Hopf分岔点, 变为不稳定平衡点, 同时产生一个逆向的不稳定极限环分支, 在经过分岔点后, 系统突然从稳定的平衡状态跳跃到远离平衡点的振荡状态. 同样重点研究分岔点前的时间序列, 对应于图16蓝色粗实线部分.

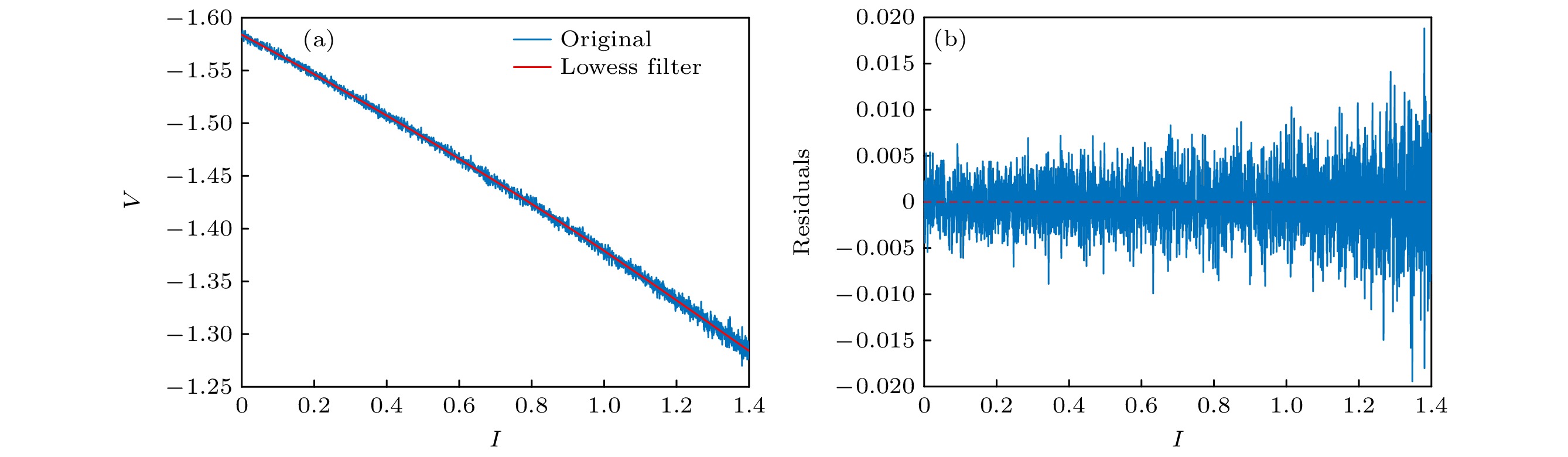
针对该HR模型, 对于分岔点前的稳定分支, 取$I \in \left[ {0, {\text{ }}1.4} \right]$进行分析, 使分岔参数$I$以$\varDelta = 0.001$从0逐渐增至1.4, 对每个分岔参数, 进行随机模拟, 得到亚临界Hopf分岔前膜电位对增大的电流刺激$I$的模拟响应如图17(a)所示. 通过Lowess滤波器进行去趋势处理, 得到的残差序列如图17(b)所示.

对上述模型进行200次重复随机模拟, 每次模拟计算原始时间序列的时滞$\tau = 1$自相关系数和方差以及残差时间序列的功率谱, 取平均值得到EWS如图18所示.

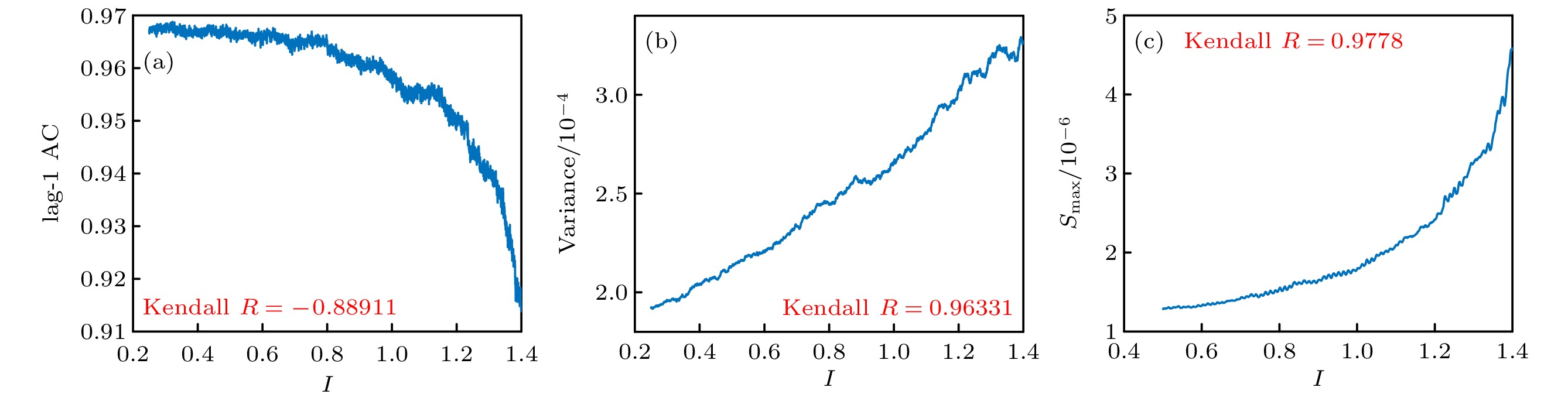
时滞$\tau = 1$自相关系数随着系统逐渐接近分岔点而减小, 说明其${\omega _0}$约为基本振荡周期的一半. 方差和${S_{\max }}$均随着系统逐渐接近分岔点而增大, 其中${S_{\max }}$的Kendall系数$R = 0.9778$最大, 说明其趋势最为明显, 预测效果最好, 因此对于该HR模型的亚临界Hopf分岔, ${S_{\max }}$为最佳的EWS.

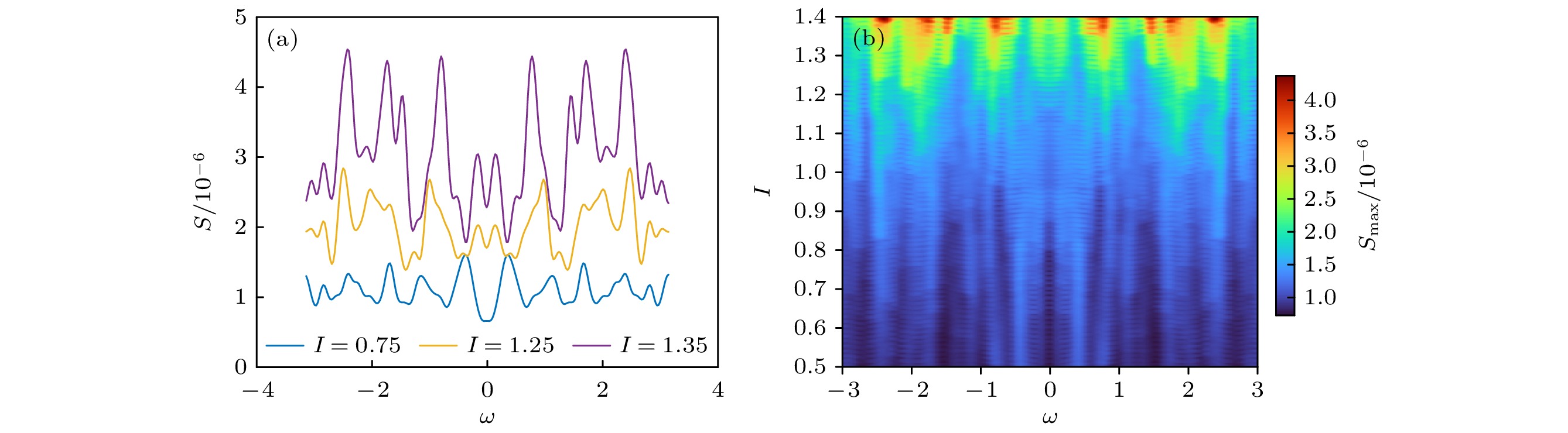
对于功率谱密度进行分析, 绘制$I = 0.75, {\text{ }}1.25, 1.35$的功率谱密度如图19(a)所示. 可以看出, 随着分岔参数$I$接近分岔点, 功率谱密度的幅值整体呈上升趋势, 且对于亚临界Hopf分岔, 功率谱的最大幅值由非零频率主导. 如图19(b)所示, 绘制功率谱的等高线图, 可以看出分岔参数$I$逐渐接近分岔点, 非零频率主导的功率谱幅值呈现出明显的上升趋势, 因此基于功率谱的EWS能够对亚临界Hopf分岔做出准确的预测, 同时针对功率谱主导频率的不同, 可以对鞍结分岔和亚临界Hopf分岔进行区分.

综上所述, 基于功率谱的EWS能够准确地通过明显的趋势预测即将到来的分岔点. 同时, 相较于传统的EWS, 如自相关系数和方差等指标, 根据功率谱的主导峰值频率不同, 可以对鞍结分岔和Hopf分岔进行较为准确的区分: 当主导峰值频率为零频率时, 分岔类型为鞍结分岔或SNIC分岔, 对应神经元的I型兴奋; 当主导峰值频率为非零频率时, 分岔类型为超临界Hopf分岔或亚临界Hopf分岔, 对应神经元的II型兴奋. 该指标在保证预测稳健性的同时, 对基本的分岔类型做出了准确区分.

目前, 对复杂动力系统发生临界转迁的EWS研究大多集中于气候系统和生态系统中, 对神经元系统临界转迁前的EWS研究较少, 因此, 本文重点考察模型神经元分岔前的EWS. 由于传统的EWS存在在噪声影响下鲁棒性较差、无法识别不同类型的分岔等问题, 人们提出了基于功率谱的EWS, 该方法的噪声鲁棒性较好, 且能够对鞍结分岔和Hopf分岔进行区分. 本文选取了一种ML模型神经元和一种考虑了电磁感应的HR模型神经元分别进行了分析. 对ML模型神经元, 考察了其SNIC分岔和超临界Hopf分岔前的临界行为, 分别计算了时滞$\tau = 1$自相关系数、方差和功率谱3种EWS, 结果表明, 基于功率谱的EWS在预报分岔的性能方面与方差相当, 优于时滞$\tau = 1$自相关系数, 同时根据功率谱主导频率的不同, 其可以对上述两种分岔类型进行区分. 对HR模型神经元, 考察了其鞍结分岔和亚临界Hopf分岔前的临界行为, 同样计算了上述3种EWS, 结果表明, 基于功率谱的EWS预报分岔的性能最佳, 且可以对上述两种分岔类型进行区分. 本文将功率谱方法应用于神经元系统放电的预测上, 结果表明该方法在准确预测神经元放电的基础上, 还能够对神经元的I型兴奋(鞍结分岔)和神经元的II型兴奋(Hopf分岔)进行区分. 但研究过程中也发现, 基于功率谱的EWS无法对相同神经元兴奋型所涉及的分岔作出进一步的区分, 如鞍结分岔和SNIC分岔, Hopf分岔中的超临界与亚临界情形, 后续我们将力求寻找一种新的指标, 能够对相同神经元兴奋型的具体分岔类型作出区分. 另外, 目前关于除高斯白噪声外的噪声类型对EWS性能影响的研究较少, 后续我们也将对其他类型的噪声的影响作必要的研究和讨论.