-
光学涡旋是一种具有螺旋型波前结构和确定光子轨道角动量(orbital angular momentum, OAM)的特殊光场[1–5]. 20世纪70年代科学家就提出了光学涡旋的概念, 并对涡旋光场的环形光强分布特征和光轴处存在的相位奇异性进行了大量研究[6,7]. 然而直到1992年, Allen等[8]才从理论上阐明了携带轨道角动量涡旋光场的物理图像, 即具有螺旋相位波前且涡旋中心光强为零的光束. 涡旋光束携带exp(i
$ \ell \theta $ )的相位因子, 其中每个光子都携带$ \ell \hbar $ 轨道角动量, θ为空间方位角, ℓ为拓扑荷数(topological charges, TC), 因此涡旋光束也被称为轨道角动量光束[9]. 与自旋角动量不同, 轨道角动量可以取任意数, 因此利用光子的轨道角动量可以构建高维希尔伯特空间. 这种特性使得它可以成为高维经典信息和量子信息的理想载体[10]. 当轨道角动量取分数时, 光束成为分数阶涡旋光束, 具有分数轨道角动量(fractional orbital angular momentum, FOAM). FOAM具有独特的物理性质, 如任意的径向缺口、丰富的相位结构和更高的调制维度[11]. 这些物理性质使得分数阶涡旋光具有更多的调控参数, 从而可以承载更多的信息, 具有更强的编码能力和参数控制能力. 因此, 分数阶涡旋光已被广泛应用于光学微粒操作[12]、光信息传输[13,14]、光学成像[15]等领域. 在分数阶涡旋光束的应用中, 对其OAM阶次进行识别是一项核心的任务. 传统的识别方法包括Mach-Zehnder干涉法[16,17]、模式互转换法[18,19] 和机器学习法[20–24]等. 其中, 机器学习法具有独特的优势, 可以在学习过程中将各种外部因素考虑在内, 并自动进行模式识别, 这对于一些复杂物理现象的研究非常有帮助[25,26]. 但是, 上述研究主要处理的是普通分数阶涡旋光的识别, 并未涉及衍射的影响. 实际上, 衍射对涡旋光束的传播影响十分明显, 特别是对于分数阶涡旋光束, 螺旋相位的不连续性使其在实际应用中更容易在长距离传输、存在大气湍流等条件下发生强衍射, 进而影响OAM阶次识别的准确度[23,27]. 如何实现有衍射条件下的分数阶涡旋机器学习识别, 目前仍是一个亟需解决但少见诸报道的问题.本文针对含衍射分数阶涡旋光, 从分数阶拓扑荷数ℓ和传播距离z这两个自由度来识别OAM模式. 在大气湍流(atmospheric turbulence, AT)环境下, 采用基于残差网络(residual network, ResNet)的101层结构(包括100个卷积层和一个全连接层)对失真分数阶OAM模式进行检测. 实验结果表明, 该方法可以准确识别传播距离为100 cm, 间隔为5 cm, 模式间隔为0.1的FOAM模式, 准确率达到99.69%. 此外, 该方法还具备良好的泛化能力, 在复杂传输环境下仍能有效抵抗干扰, 为FOAM光束在多维编码和传感测量中的应用提供了新的思路.
-
本节首先介绍涡旋光产生的理论, 然后介绍产生涡旋光的实验.
-
把一束高斯光
$ \exp \left( { - {{{r^2}}}/{{\omega _0^2}}} \right) $ 打在空间光调制器(spatial light modulator, SLM)上, 并在SLM上加载相位掩模$ \exp(-{\mathrm{i}}\ell\theta) $ , 则光束在SLM平面上的光场可表示为[28]其中拓扑荷数ℓ是一个分数值,
$ \omega_{0} $ 为高斯束腰, r和θ分别为径向坐标和方位角坐标. 对于(1)式表示的分数阶高斯涡旋光束, 我们通常将分数阶涡旋相位项分解为整数阶涡旋相位项的基:在傍轴近似的框架下, 利用Collins积分方程可以计算
$ E_{1}(r, \theta) $ 在传播后的场分布[29]:其中
$ r_{1} $ 和$ \theta_{1} $ 是输出平面的径向坐标和方位角坐标, z为传播距离,$ k = 2\pi/\lambda $ 为波数, λ为波长. 光在距离z的自由空间中传播的ABCD传递矩阵为方程(5)表示超几何高斯模式,
$ {}_{1}F_1(\alpha, \beta, z) $ 是一个合流超几何函数,$ \Gamma (n) $ 是Gamma函数,$ b_{1} $ 和$ \varepsilon_{1} $ 定义为基于上述计算, 可以得到在传播不同距离z后, 不同ℓ值的涡旋光束的横向强度分布.
在实际通信中, 由于大气湍流的存在, 涡旋光束的螺旋相位结构容易受到扭曲, 从而导致模式分散和强度分布的畸变. 因此, 本实验利用带有von Karman湍流谱的Kolmogorov模型来模拟空间光调制器中受大气湍流影响的情况, 从而实现了一种具有失真特性的通信模式[30,31], 其失真程度可以通过Fried参数进行量化. 在SLM上添加的湍流相位掩模的表达式为[32,33]
其中
$ \phi_{NN} (\kappa) = 0.023 r_0^{ - 5/3} (\kappa^2 + \kappa_0^2 )^{ - 11/6} {\mathrm{e}}^{ - \kappa^2 /\kappa_m^2 } $ 和Fried参数$ r_0 = (0.423 k^2 C_n^2 z)^{- 3/5} $ .$ {\mathbb{R}} $ 表示复数域的实部,$ {\cal{F}}^{-1} $ 表示傅里叶逆变换运算. 另外, κ,$ \kappa_0 $ 和$ {\mathbb{M}}_{N N} $ 分别表示空间频率、中心空间频率和编码随机矩阵.$ C_n^2 $ 是大气折射率结构常数, 其数值大小用来表示湍流强度.在SLM上同时添加分数阶涡旋相位和湍流相位掩模后, 光束在SLM平面上的振幅变为
通过将(8) 式代入(5)式, 可以得到经湍流畸变后的光场分布
$ E_{2}^{\prime}(r_1, \theta_1, z) $ .根据(8)式, 可以对涡旋光束进行模拟, 得到不同ℓ值和z值条件下的涡旋光分布. 图2展示了无湍流和有湍流条件下的涡旋光束空间分布.
-
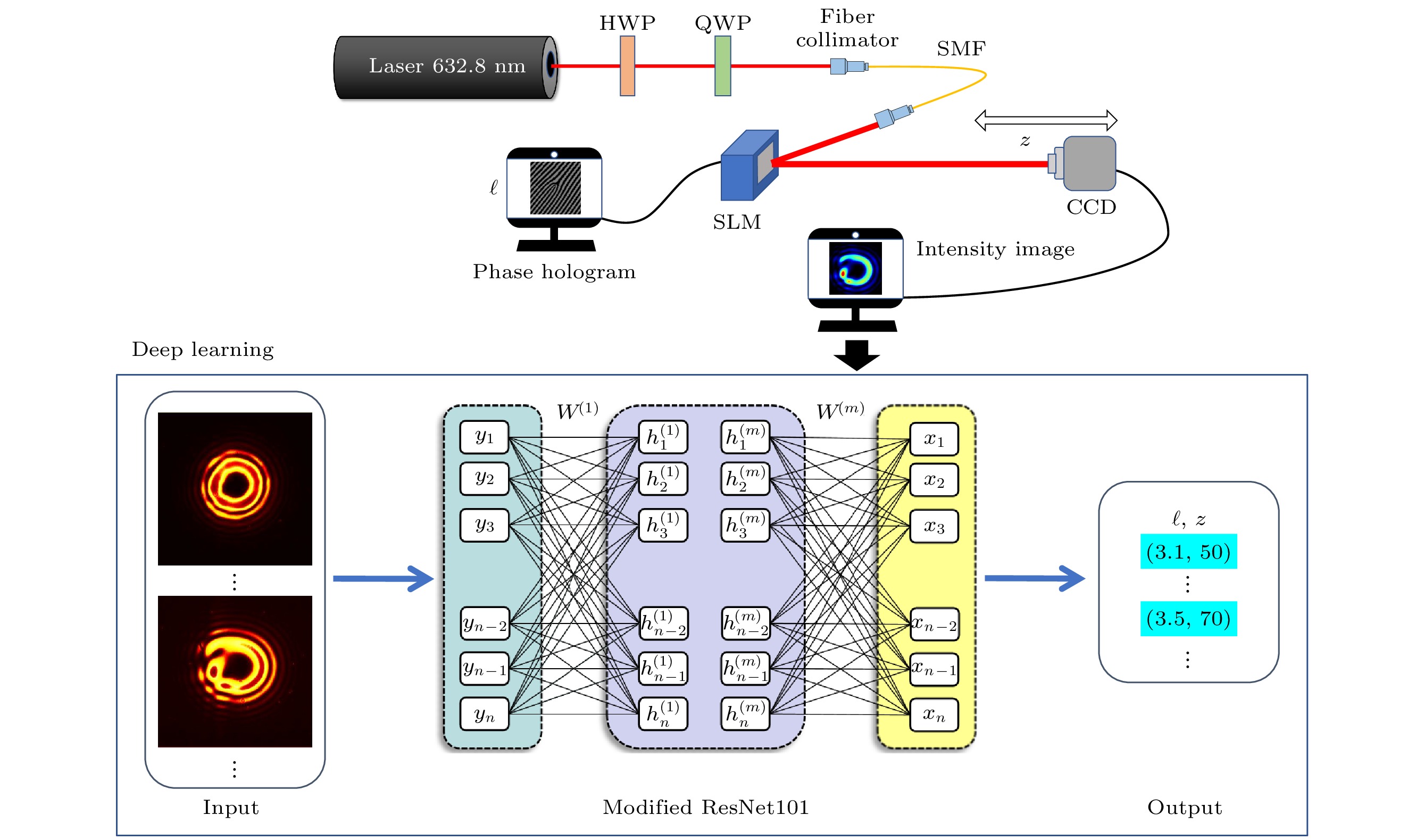
制备衍射条件下分数阶涡旋光的实验装置见图1. 首先, 将波长为632.8 nm的He-Ne激光束通过半波片(HWP)和四分之一波片(QWP)调节偏振, 然后, 将其耦合到单模光纤中, 使其空间模式变为纯净的高斯分布. 接着, 使用放大率为10×、有效焦距为17 mm的物镜来实现光束准直, 准直后的束腰约为2 mm. 把准直后的高斯光束打在SLM上, 转换为涡旋光束. 其中, SLM上加载了计算机生成的相位全息图, 为了模拟大气传输过程中的湍流, 可以在全息图中增加一个湍流相位. 最后, 利用CCD相机采集涡旋光束的强度图像并发送到计算机进行训练. 移动CCD的位置来控制传播距离. 其中 ℓ 的取值范围为1.0—9.9,
$ \Delta \ell = 0.1 $ , 传播距离z的范围为50—100 cm, 步长为5 cm, 湍流强度系数$ C_n^2 $ 为$ 5\times10^{-10} \;{\rm{mm}}^{-2/3} $ .分数阶涡旋光不仅在相位上呈现出奇异性, 而且在径向方向发生了错位. 该错位现象将导致衍射图案的中心对称性遭到破坏, 从而产生一系列影响. 不同拓扑荷数ℓ和不同传播距离z的情况下的空间分布如图2所示, 其中图2(a)为无湍流的无畸变模态的空间分布, 图2(b)为受大气湍流影响下畸变模态的空间分布. 第一行和第三行是实验获得的图像, 第二行和第四行是理论模拟的图像. 通过对比实验结果和理论模拟, 发现它们之间的空间轮廓十分相似, 从而验证了我们的理论模型的正确性. 从图2可以看到, 中心孔径和衍射孔径的大小均随涡旋光束拓扑荷数和传播距离的增大而增大. 当拓扑荷数接近半整数时, 径向间隙更明显, 径向间隙两侧的光强明显大于其他位置.
-
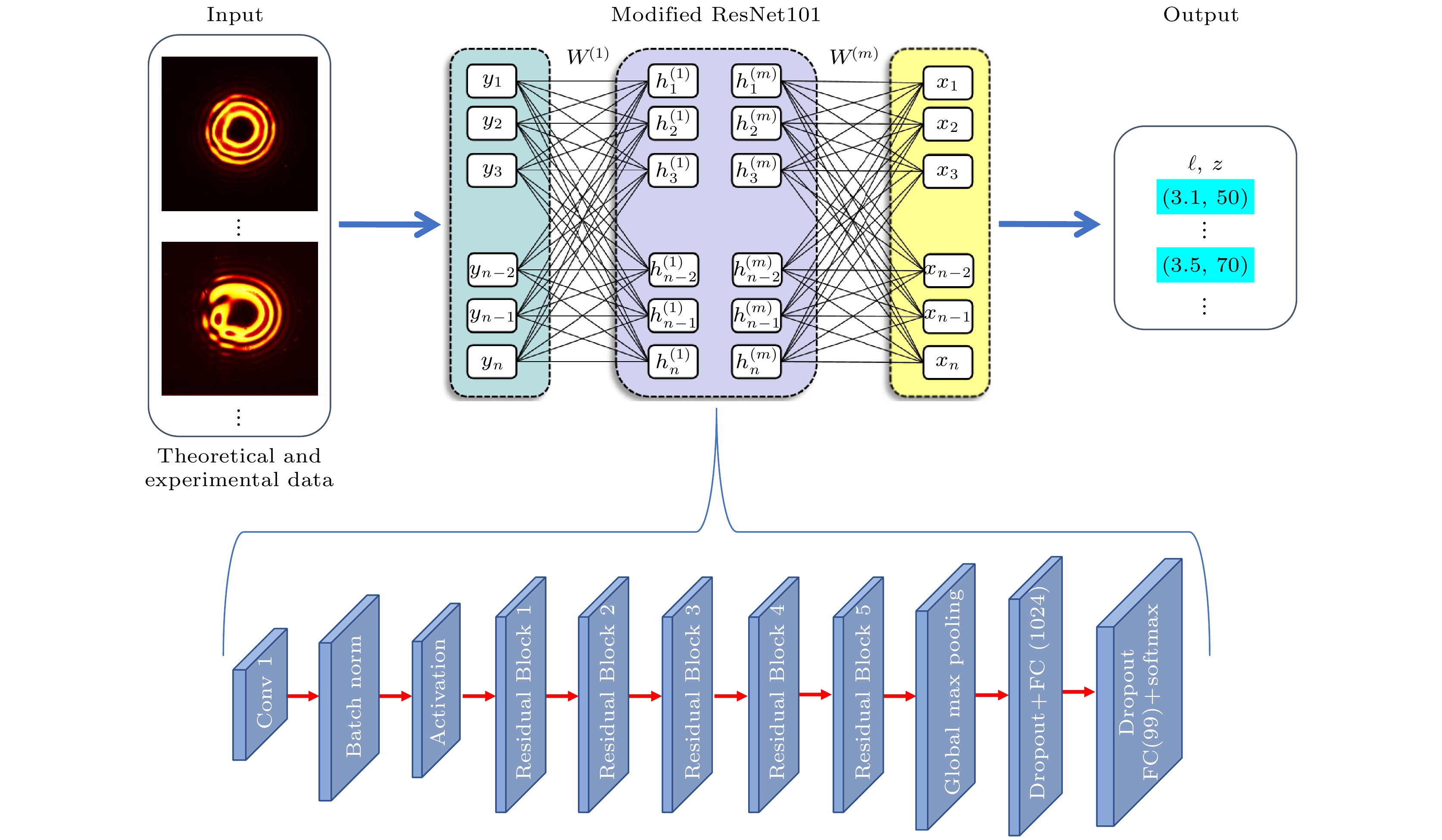
本文采用ResNet迁移学习方法, 网络结构如图3所示. 首先利用之前的网络模型参数作为涡旋光图像训练网络模型的初始化值. ResNet-101以一个普通的卷积层开始, 该层负责对输入图像进行特征提取, 通常使用3×3的卷积核. 在卷积层后面, 每个卷积操作结果都会经过批量归一化(batch normalization, BN)层实现在每个小批量(mini-batch)数据上进行归一化处理. 随后针对分数阶涡旋光图像识别的特点, 采用线性整流函数(rectified linear unit, ReLU)作为激活函数, 引入非线性变换, 增加模型的表达能力, 加快网络的训练和收敛速度, 抑制过拟合并提高模型的鲁棒性. ReLU函数具有计算简单、无梯度饱和的优点, 且具有单边抑制的特点, 能更好地提取图像特征. 该模型通过5个残差模块实现更深层的训练, 提取更高层次的特征. 每个残差块由多个卷积层、批量归一化层和激活函数层组成, 使用跳跃连接(skip connection)和残差学习, 残差块能够解决深度网络中的梯度消失和梯度爆炸问题, 从而使得网络更易于训练和优化. 在最后一个残差块之后, 本模型增加全局最大池化层, 将特征图压缩为一个向量, 减少参数, 提高计算速度. 在此之后, 加入一个全连接网络, 该网络由两个全连接层组成, 在每个全连接层之前加入一个随机丢弃(dropout)层, 随机删除一些参数以最小化过拟合, 并将预训练网络的最后一层完全连接. 最后将该层的输出设定为本文分数阶涡旋光图像数据集的分类数99, 并通过对训练集进行识别, 得到训练精度. 在整个算法中使用了迁移学习技术(transfer learning toolkit, TLT)[34], 它利用预训练的模型, 使得我们可以仅通过少量的数据集即可实现准确的识别结果, 效率非常高[22,35].
针对迁移学习中多类别分类的目标任务特点, 选择分类交叉熵损失函数[36]来评估每个轮次(epoch)的训练结果:
其中n为样本数, m为分类数,
$ \hat{y}_{i m} $ 表示真标签(值为0或1),$ y_{im} $ 为神经网络给出的第m类的预测值. 在训练过程中, 采用自适应矩估计(adaptive moment estimation, Adam)优化器[37]更新权重和偏差参数, 使损失函数最小化. 分类交叉熵损失函数能够充分利用标签信息, 对每个类别的预测概率进行建模, 最大化正确类别的预测概率, 并对于错误分类的样本会给予较大的惩罚, 从而促使模型更加关注难以分类的样本. 交叉熵损失函数具有很强的泛化能力, 即使在未知数据集上, 也能够很好地预测. 此外, 它还有良好的凸优化性, 即当模型预测的概率值接近真实标签值时, 损失函数的值会越来越小, 而当模型预测的概率值远离真实标签值时, 损失函数的值会越来越大, 从而有助于模型训练的收敛. -
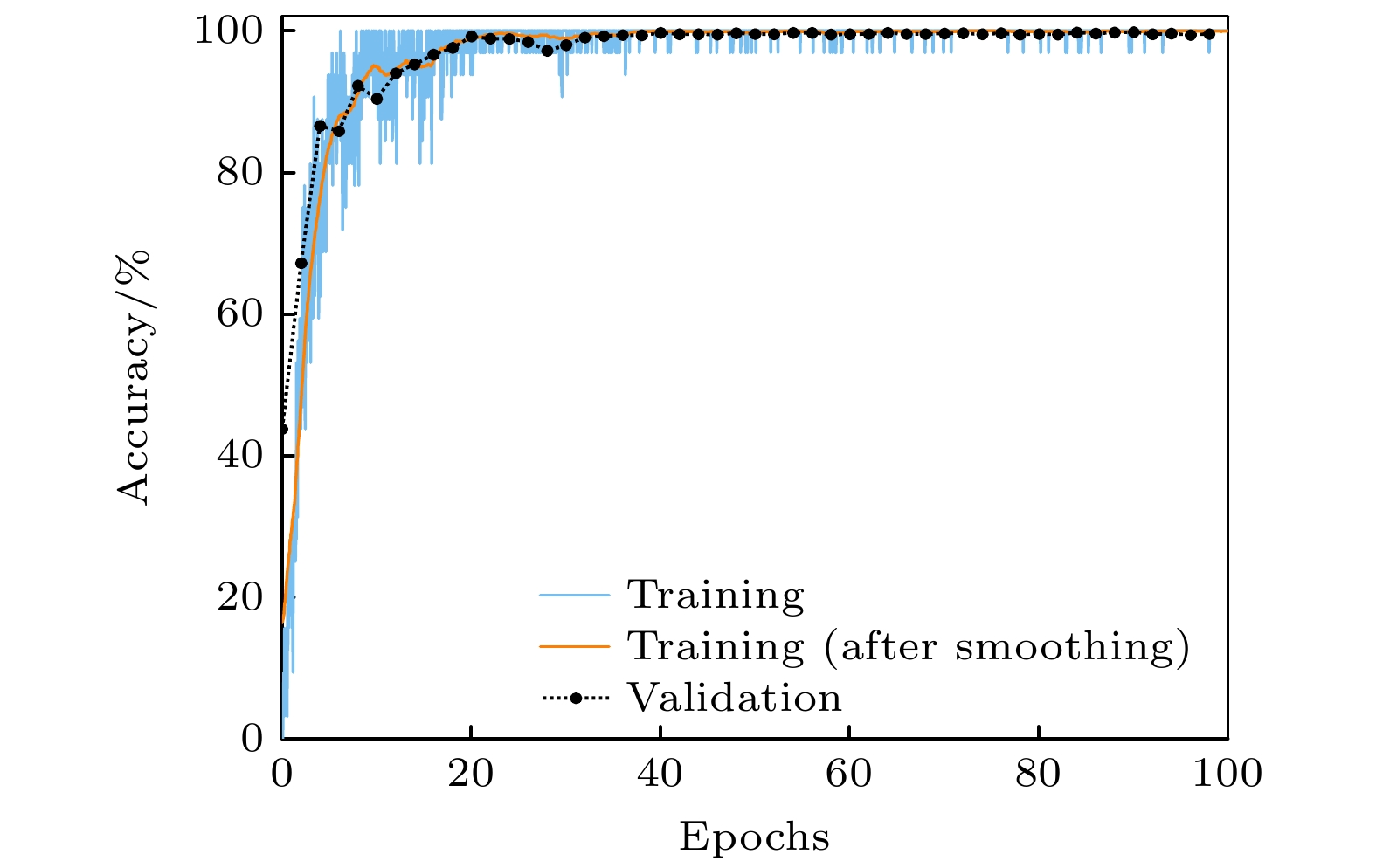
在构建了机器学习模型之后, 下面把2.2节中得到的实验光强分布图和理论模拟光强分布图进行训练, 其中实验光强分布图和理论模拟光强分布图按7∶3构成整个数据集, 训练集样本数量为7920, 验证集数量为1980, 测试集样本数量为990, 每张图像的分辨率为480像素 × 360像素. 本次实验的硬件平台为一台配备Intel(R) Core (TM) i5-7300 HQ @2.5 GHz处理器和一块Nvidia GeForce GTX 1050 Ti GPU (显存4 GB)的计算机, 编译环境为Python 3.9, 深度学习平台为TensorFlow 1. 初始学习率(learning rate)设置为0.001, 权重参数(weight)使用Adam优化器, 批量大小(batch size)为16, epoch数为100. 在迭代训练和验证过程中的准确度结果如图4所示, 其中淡蓝色实细线、橙色实粗线和黑色点虚线分别表示训练集的准确率、平滑处理后的训练集准确率和验证集准确率. 从图4可以看到, 在大约10个epoch的时间内, 有一个快速上升的趋势, 准确度值明显增加. 经过40个epoch后, 准确度曲线趋于稳定, 100个epoch之后, 在识别具有不同ℓ值和不同z值的涡旋光束时, 准确率高达99.69%. 结果表明该模型具有较强的预测性能. 由于训练过程中湍流相位更新的变化, 图中的准确率曲线呈现出非光滑性.
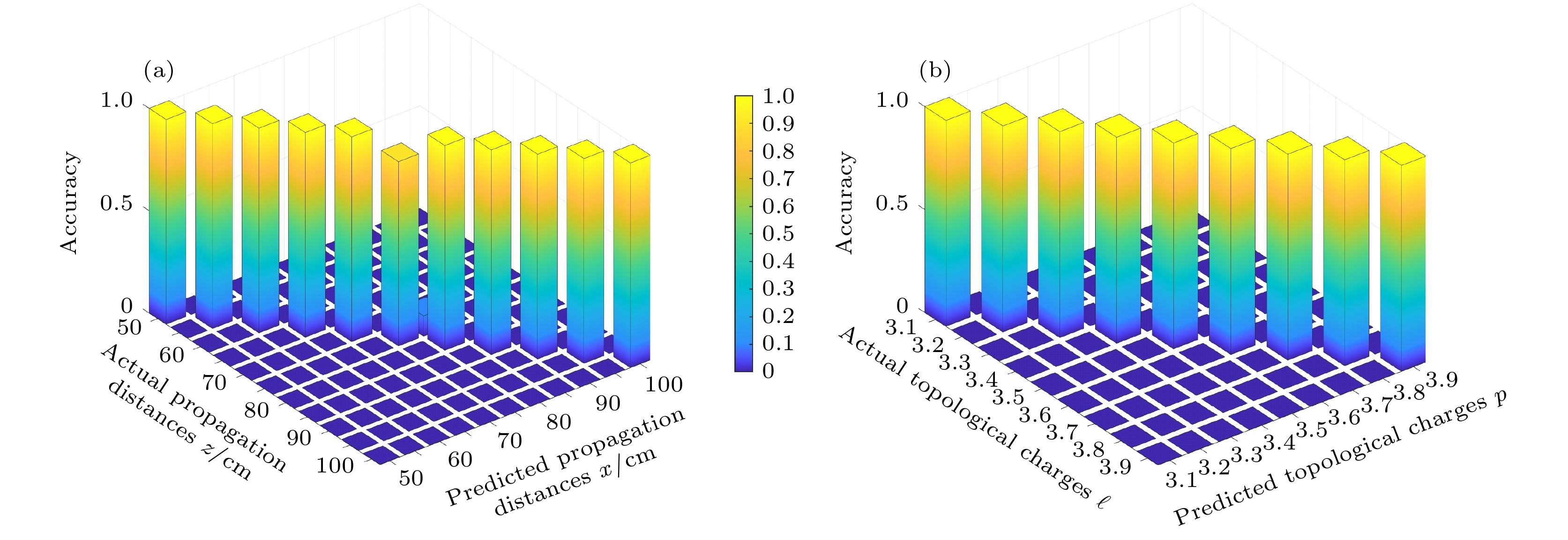
使用训练好的模型对测试集中的图片进行识别, 得到的混淆矩阵如图5所示. 纵坐标表示输入的角动量拓扑荷数和距离, 横坐标表示机器学习识别的角动量拓扑荷数和距离. 当识别出的轨道角动量拓扑荷数和距离等于光强分布图的真实轨道角动量拓扑荷数和距离时, 该值将落在对角线上的相应位置上. 若除对角线外, 矩阵元素中出现大于0的值, 则表示对这些图像的轨道角动量拓扑荷数识别存在偏差. 图5(a)为
$ \ell = 3.5 $ 时预测传播距离与真实传播距离之间的归一化混淆矩阵. 图5(b)显示了$ z = 75 $ cm时ℓ预测值与ℓ真实值之间的归一化混淆矩阵. 可以看到, 几乎所有测试的OAM模式都被正确识别, 只有一个错误的预测位于相邻的OAM状态, 这表明在本实验中也可以清楚地识别出微小的差异. 并且该方法具有良好的泛化能力和鲁棒性. -
本工作只是对湍流环境中不同传播距离下FOAM模式识别的初步探索. 模拟的湍流属于弱湍流范围, 在强湍流中准确识别FOAM模态与传输距离还需进一步探索. 可以考虑通过湍流补偿或图像重构等方法改善湍流的影响.
本文距离测量范围是50—100 cm, 距离比较短, 这个距离下大气湍流效应对光束传播影响有限, 和实际通信情况差异较大, 但是本文的实验结果证明了我们方法的可行性. 在后续的工作中我们会深入研究远距离情况下分数阶涡旋光衍射过程的机器学习识别问题.
面向未来, 本工作有望在多种场景中获得应用. 首先, 在测距方面, 分数阶涡旋光束的衍射特征可用于测量光束的传输距离. 通过分析涡旋光拓扑荷数和衍射距离, 可以精准地实现物体位置的测量. 其次, 在空间光通信方面, 分数阶涡旋光的拓扑荷数可以实现更高的模式复用, 提高通信容量; 在通信接收端做衍射的检测则有助于提高通信系统的稳定性. 最后, 在光镊应用方面, 分数阶涡旋光镊能够操纵粒子的空间位置, 通过考虑衍射效应, 可以更加准确地实现涡旋光对粒子的控制.
-
本文提出并设计了一个基于ResNet的深度学习方法. 通过训练ResNet模型学习FOAM模式与衍射强度剖面之间的映射关系, 从而实现对不同传播距离下FOAM模式的准确识别. 该方法考虑了空间传输过程中大气湍流等因素的影响, 因此该识别方案在特殊环境下也能实现高精度识别, 具有传统方法无法实现的超细FOAM模式和传播距离的区分能力. 该模型为高精度识别具有较强抗扰性的FOAM模式提供了一种可行的方法, 同时能够实现对传播距离的识别, 其识别传播距离间隔为5 cm, 模式间隔为0.1的FOAM模式, 准确率达到99.69%. 这将有助于推动FOAM模式在测距、光通信、微粒子操作等领域的实际应用.
感谢美国路易斯安那州立大学由成龙博士的讨论.
分数阶涡旋光衍射过程的机器学习识别
Machine learning identification of fractional-order vortex beam diffraction process
-
摘要: 分数阶涡旋光束具有分数轨道角动量(fractional orbital angular momentum, FOAM)模式, 理论上可以无限增加传输容量, 因此在光通信领域具有巨大的应用前景. 然而, 分数阶涡旋光束在自由空间传播时, 螺旋相位的不连续性使其在实际应用中容易受到衍射的影响, 进而影响FOAM阶次识别的准确度, 严重制约基于FOAM的实际应用. 如何实现有衍射条件下的分数阶涡旋光的机器学习识别, 目前仍是一个亟需解决且少见诸报道的问题. 本文提出一种基于残差网络(residual network, ResNet)的深度学习(deep learning, DL)方法, 用于精确识别分数阶涡旋光衍射过程的传播距离和拓扑荷值. 实验结果表明, 该方法可以在湍流条件下识别传播距离为100 cm, 间隔为5 cm, 模式间隔为0.1的FOAM模式, 准确率为99.69%. 该技术有助于推动FOAM模式在测距、光通信、微粒子操作等领域的实际应用.Abstract: Fractional-order vortex beams possess fractional orbital angular momentum (FOAM) modes, which theoretically have the potential to increase transmission capacity infinitely. Therefore, they have significant application prospects in the fields of measurement, optical communication and microparticle manipulation. However, when fractional-order vortex beams propagate in free space, the discontinuity of the helical phase makes them susceptible to diffraction in practical applications, thereby affecting the accuracy of OAM mode recognition and severely limiting the use of FOAM-based optical communication. Achieving machine learning recognition of fractional-order vortex beams under diffraction conditions is currently an urgent and unreported issue. Based on ResNetA, a deep learning (DL) method of accurately recognizing the propagation distance and topological charge of fractional-order vortex beam diffraction process is proposed in this work. Utilizing both experimentally measured and numerically simulated intensity distributions, a dataset of vortex beam diffraction intensity patterns in atmospheric turbulence environments is created. An improved 101-layer ResNet structure based on transfer learning is employed to achieve accurate and efficient recognition of the FOAM model at different propagation distances. Experimental results show that the proposed method can accurately recognize FOAM modes with a propagation distance of 100 cm, a spacing of 5 cm, and a mode spacing of 0.1 under turbulent conditions, with an accuracy of 99.69%. This method considers the effect of atmospheric turbulence during spatial transmission, allowing the recognition scheme to achieve high accuracy even in special environments. It has the ability to distinguish ultra-fine FOAM modes and propagation distances, which cannot be achieved by traditional methods. This technology can be applied to multidimensional encoding and sensing measurements based on FOAM beam.
-
Key words:
- fractional vortex beams /
- machine learning /
- atmosphere turbulence /
- residual network .
-

-
图 2 不同拓扑荷数
$\ell $ 和不同传播距离z的涡旋光束空间分布 (a)无湍流影响的无畸变模态的空间分布; (b)大气湍流影响的畸变模态的空间分布. 第一行和第三行是实验获得的图像, 第二行和第四行是理论模拟的图像Figure 2. Spatial profiles of vortex beams with different topological charges
$\ell $ and different propagation distances z: (a) Spatial distribution of distortionless modes without turbulence; (b) the spatial distribution of distortion modes affected by atmospheric turbulence. The first and third rows are the images acquired from the experiment, and the second and fourth rows represent the theoretically simulate.图 5 训练后的深度学习算法的混淆矩阵 (a)
$ \ell=3.5$ 时, 预测传播距离与真实传播距离之间的归一化混淆矩阵; (b)$ z=75$ cm时$\ell $ 的预测值和$\ell $ 的真实值之间的归一化混淆矩阵Figure 5. The confusion matrix of our trained deep learning algorithm: (a) The normalized confusion matrix between the predicted propagation distance and the true propagation distance for
$ \ell=3.5$ ; (b) normalized confusion matrix between predicted$\ell $ values and true$\ell $ values for z = 75 cm. -
[1] Shen Y, Wang X, Xie Z, Min C, Fu X, Liu Q, Gong M, Yuan X 2019 Light Sci. Appl. 8 90 doi: 10.1038/s41377-019-0194-2 [2] Bai Y, Lü H, Fu X, Yang Y 2022 Chin. Opt. Lett. 20 012601 doi: 10.3788/COL202220.012601 [3] Zhang H, Zeng J, Lu X, Wang Z, Zhao C, Cai Y 2022 Nanophotonics 11 241 doi: 10.1515/nanoph-2021-0616 [4] Chen X, Wang S, You C, Magaña-Loaiza O S, Jin R B 2022 Phys. Rev. A 106 033521 doi: 10.1103/PhysRevA.106.033521 [5] Guo Z, Chang Z, Meng J, An M, Jia J, Zhao Z, Wang X, Zhang P 2022 Appl. Opt. 61 5269 doi: 10.1364/AO.461251 [6] Nye J F, Berry M V 1974 Proc. R. Soc. London, Ser. A 336 165 [7] Brygndahl O 1973 J. Opt. Soc. Am. 63 1098 doi: 10.1364/JOSA.63.001098 [8] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185 doi: 10.1103/PhysRevA.45.8185 [9] Senthilkumaran P, Sato S, Masajada J 2012 Int. J. Opt. 2012 1 doi: doi:10.1155/2012/741693 [10] Wang J, Yang J Y, Fazal I M, et al. 2012 Nat. Photonics 6 488 doi: 10.1038/nphoton.2012.138 [11] Kotlyar V V, Kovalev A A, Nalimov A G, Porfirev A P 2020 Phys. Rev. A 102 023516 doi: 10.1103/PhysRevA.102.023516 [12] Zhu L, Tang M, Li H, Tai Y, Li X 2021 Nanophotonics 10 2487 doi: 10.1515/nanoph-2021-0139 [13] Nicolas A, Veissier L, Giner L, Giacobino E, Maxein D, Laurat J 2014 Nat. Photonics 8 234 doi: 10.1038/nphoton.2013.355 [14] Otte E, Rosales-Guzmán C, Ndagano B, Denz C, Forbes A 2018 Light Sci. Appl. 7 18009 doi: 10.1038/lsa.2018.9 [15] Bu X, Zhang Z, Chen L, Liang X, Tang H, Wang X 2018 IEEE Antennas Wirel. Propag. Lett. 17 764 doi: 10.1109/LAWP.2018.2814980 [16] Li X, Tai Y, Lü F, Nie Z 2015 Opt. Commun. 334 235 doi: 10.1016/j.optcom.2014.08.020 [17] Leach J, Courtial J, Skeldon K, Barnett S M, Franke-Arnold S, Padgett M J 2004 Phys. Rev. Lett. 92 013601 doi: 10.1103/PhysRevLett.92.013601 [18] Beijersbergen M W, Allen L, Van der Veen H, Woerdman J 1993 Opt. Commun. 96 123 doi: 10.1016/0030-4018(93)90535-D [19] Zhou J, Zhang W, Chen L 2016 Appl. Phys. Lett. 108 111108 doi: 10.1063/1.4944463 [20] Krenn M, Fickler R, Fink M, Handsteiner J, Malik M, Scheidl T, Ursin R, Zeilinger A 2014 New J. Phys. 16 113028 doi: 10.1088/1367-2630/16/11/113028 [21] Doster T, Watnik A T 2017 Appl. Opt. 56 3386 doi: 10.1364/AO.56.003386 [22] Liu Z, Yan S, Liu H, Chen X 2019 Phys. Rev. Lett. 123 183902 doi: 10.1103/PhysRevLett.123.183902 [23] Jing G, Chen L, Wang P, Xiong W, Huang Z, Liu J, Chen Y, Li Y, Fan D, Chen S 2021 Results Phys. 28 104619 doi: 10.1016/j.rinp.2021.104619 [24] Guo H, Qiu X, Chen L 2022 Phys. Rev. Appl. 17 054019 doi: 10.1103/PhysRevApplied.17.054019 [25] Gao H, Zhang Z, Yang Y 2023 Appl. Opt. 62 5707 doi: 10.1364/AO.486664 [26] Wu Y, Wang A, Zhu L 2023 Opt. Express 31 36078 doi: 10.1364/OE.501510 [27] Zhao Y, Zhong X, Ren G, He S, Wu Z 2017 Opt. Commun. 387 432 doi: 10.1016/j.optcom.2016.10.069 [28] Zhou Z Y, Zhu Z H, Shi B S 2023 Quantum Eng. 2023 4589181 [29] Collins S A 1970 J. Opt. Soc. Am. 60 1168 doi: 10.1364/JOSA.60.001168 [30] Bos J P, Roggemann M C, Gudimetla V S R 2015 Appl. Opt. 54 2039 doi: 10.1364/AO.54.002039 [31] Glindemann A, Lane R, Dainty J 1993 J. Mod. Opt. 40 2381 doi: 10.1080/09500349314552401 [32] Bhusal N, Lohani S, You C, Hong M, Fabre J, Zhao P, Knutson E M, Glasser R T, Magaña-Loaiza O S 2021 Adv. Quantum Technol. 4 2000103 doi: 10.1002/qute.202000103 [33] Lü H, Guo Y, Yang Z X, Ding C, Cai W H, You C, Jin R B 2022 Front. Phys. 10 843932 [34] Fernando B, Habrard A, Sebban M, Tuytelaars T 2014 arXiv: 1409.5241 [cs.CV] [35] Krizhevsky A, Sutskever I, Hinton G E 2017 Commun. ACM 60 84 doi: 10.1145/3065386 [36] Zhang Z, Sabuncu M 2018 Advances in Neural Information Processing Systems 31 8778 [37] Kingma D P, Ba J 2014 arXiv: 1412.6980 [cs.LG] -


 首页
首页 登录
登录 注册
注册




 下载:
下载: