首页
登录
注册
-
静电MEMS扬声器因其尺寸小、集成度高、功耗低、音频质量佳等优点被广泛应用于医疗器械、便携式电子设备、汽车电子等领域[1-2]。随着数字信号处理技术和微型扬声器的发展，全数字式扬声器集成化系统对高性能扬声器的需求不断增加[3]。
静电MEMS扬声器通常由两个平行板构成，利用两个板之间的电容变化实现电声转换，但是由于静电力的限制，两个板之间的间隙较小，导致振膜只能进行小偏转，且输出的声压级较低[4-5]。如何在保持高声压级的同时降低工作电压是一个关键问题。目前解决方法如下：一、使用新型材料，比如石墨烯[6]、聚合物[7-8]、氮化物/氧化物[9]等材料制作MEMS扬声器，然而新材料可能存在强度不足、可靠性差、成本较高和工艺复杂等问题，导致批量生产应用困难；二、通过引入新结构减少阻尼损失和提高功率来增加声压级。2020年Meera Vikas Garud等[10]引入了外围电极配置，在电极间隙1 μm，驱动电压主不超过100 V的情况下，可以实现与传统设计相当的声压级(40至60 dB)，且效率提高了至少两个数量级。2022年丁琦[11]通过设计不同的空腔结构和改变振膜结构提高了器件性能。2022年Antoine Verreault等[12]提出一种膜片悬浮结构，模拟结果表明，该扬声器能够在1 mm处产生85 dB的声压级，同时能很好的跟踪输入信号。2023年Sebastian Anzinger等[13]采用双背板结构，将工作电压限制在8 V以内，高频共振下测得该设备在10 cm处声压级最大为71.3 dB；三、构建扬声器阵列，利用数字声音重建(Digital Sound Reconstruction，DSR)技术[14]，通过系统集成和算法处理降低功耗的同时提高声压级[15-16]。2011年马登永等[17]研发了基于1bit和3bit编码模式的64元全数字式扬声器阵列系统，谐波失真小于1%。2013年徐宁[18]通过阵列天线理论的道尔夫—切比雪夫综合法和相控阵聚焦的方法，提高了微型扬声器阵列的指向性。2018年金瑞[19]采用SDM技术和平板换能器技术,提出了一种新型的数字直驱扬声器设计并进行了实际测试。此方法对算法、器件以及系统设计有较高的要求，目前技术尚未成熟。
基于上述分析，本文提出一种具有双背板、悬臂梁和缓冲锥的复合式振膜结构静电MEMS扬声器，在提高工作效率的同时实现快速声学响应和高线性声学输出。通过双背板结构补偿振膜的介质恢复力，增加扬声器的稳定性；同时，悬臂梁和缓冲锥的复合式振膜结构可以降低工作电压和振膜下拉无法恢复的可能性，增加扬声器的可靠性。利用Comsol Multiphysics软件建立有限元模型，对上述结构进行仿真优化。结果表明，本文提出的静电MEMS扬声器性能得到了显著提升。通过对性能仿真结果分析，验证该扬声器的响应时间小于23 μs，且声学输出满足线性相加的需求，具有良好的声学响应特性。此扬声器可用于DSR技术，有望解决当前扬声器对DSR技术再现声音动态范围和质量的限制问题。
-
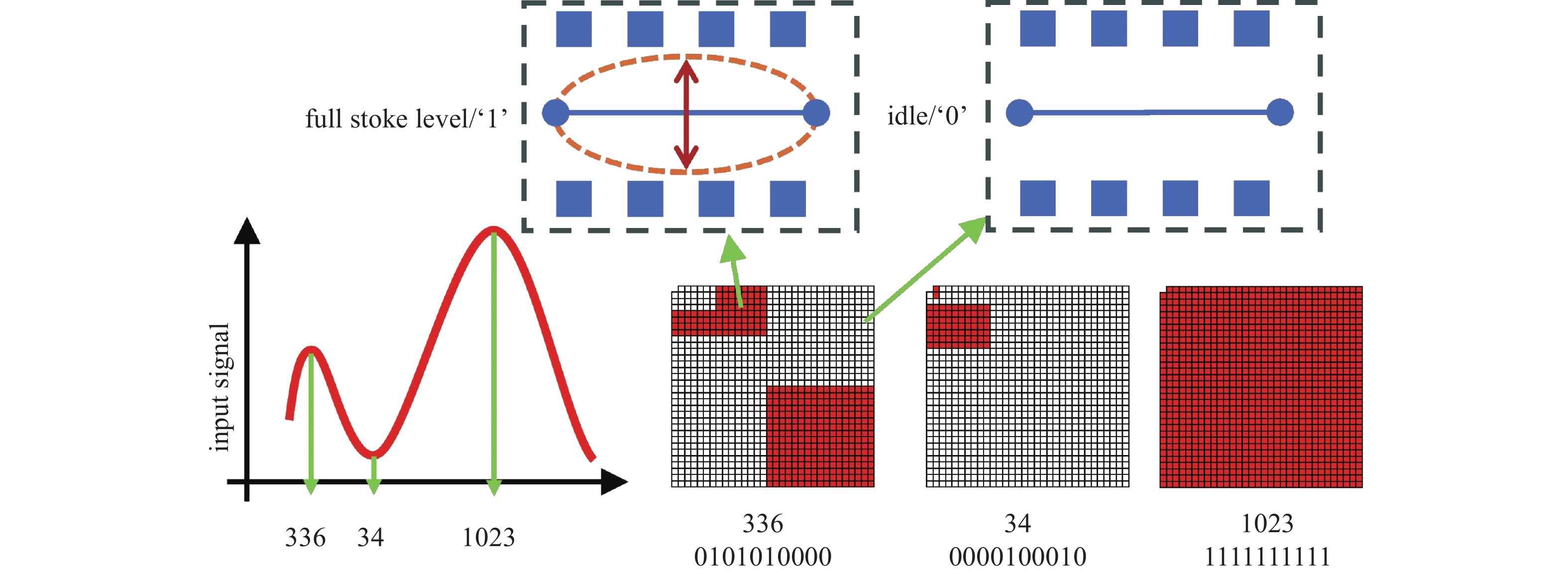
DSR技术与传统的模拟声音重建不同，与MP3或光盘中使用的数字音频信号无关。DSR技术基于振膜激励，振膜的冲程水平以全振幅驱动，同时振动面积对应着输入信号的变化。因此，数字声音重建需要大量的扬声器微元。
在数字声音重建中，每个扬声器只存在两个状态，全振幅(数字真/一)或无振幅(数字假/零)，音频信号在输入的过程中被数字化，其幅值在量化后分配给相应的扬声器比特组。十位扬声器的工作原理如图1所示。
数字扬声器产生声音的响度取决于振膜的振幅，而声音的频率则与振膜振幅的时变性有关[14-16]。因此，基于数字扬声器阵列进行音频数字化重建需要满足以下几个条件：
（1）单个微型扬声器的声学响应速度会限制将数字信号转换为模拟信号的采样率，而模拟−数字音频转换的采样通常以44.1 kHz进行[20]，这对应于23 μs的采样周期，所以单个微型扬声器的响应时间应该在23 μs的数量级上；
（2）扬声器微元在使用过程中声学响应保持需要保持良好的可重复性和一致性，提高输出音频质量；
（3）声压取决于扬声器的数量，为了有效预测声压级，简化数字化音频重建过程，扬声器微元之间的声学输出应满足线性相加。
-
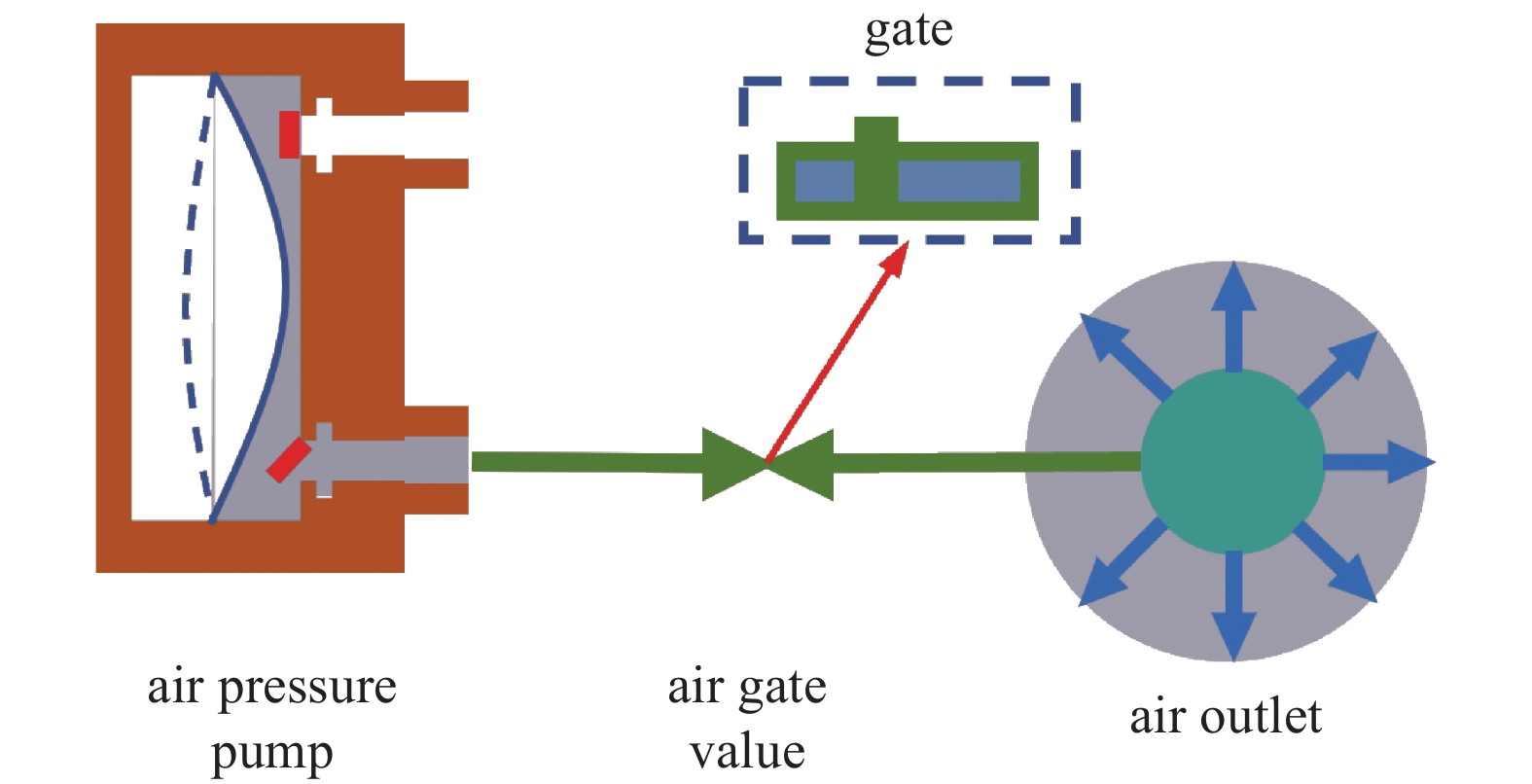
扬声器可以看作一个整流源，空气从恒压泵通过空气阀流到空气出口，如图2所示。
整流源通过空气阀中的闸门振动，而闸门的振动可以视为质量−弹簧−阻尼系统，系统的振动方程为[5]：
其中，
$w(t)$ 为气阀中闸门的位移，$\xi $ 为阻尼系数，$ \omega_{\mathrm{n}} $ 为角固有频率，M为系统模型中的等效质量，$ f\mathrm{_e}(t) $ 为施加在闸门上离散的机械脉冲力，可以用单位阶跃函数$u(t)$ 表示为：$ F[u(t)-u(t-W\mathrm{_p})] $ 。对于理想整流源的声压，只考虑空气通过阀门从出口流出的速度，因此，根据伯努利定理，出口处的气流速度随着阀门中闸门的位移而线性变化，空气流速可以表示为[16]：
其中，
$ \sigma_{\mathrm{d}}=\omega_{\mathrm{n}}\xi $ ，$ \omega_{\mathrm{d}}=\omega_{\mathrm{n}}\sqrt{\xi^2-1} $ ，$ W_{\mathrm{p}} $ 为脉冲宽度，a为空气通过闸门间隙的横截面积，$ C\mathrm{_{pipe}} $ 为管道中的空气流速。$W$ 可以表示为：式(2)表示
$\dot w$ 与位移无关，而是由气流速度决定，因此$\dot w$ 可以改写为：$\dot W$ 可以表示为：假设闸门的振动频率在超声波范围内较高，且
${(kr)^2} > > 1$ ，$k$ 为波束，因此，声波与速度的变化同相，此时整流源的辐射的声压可表示为：其中，
$r$ 、$R$ 和${R_0}$ 分别是声源的半径，与声源的距离和声源的位置，整流源的波动方程可以写为：
其中，
因此，将式(4)代入式(8)可得：
该方程表示，声压与理想声辐射(
${(kr)^2} > > 1$ )的振动速度成正比。 -
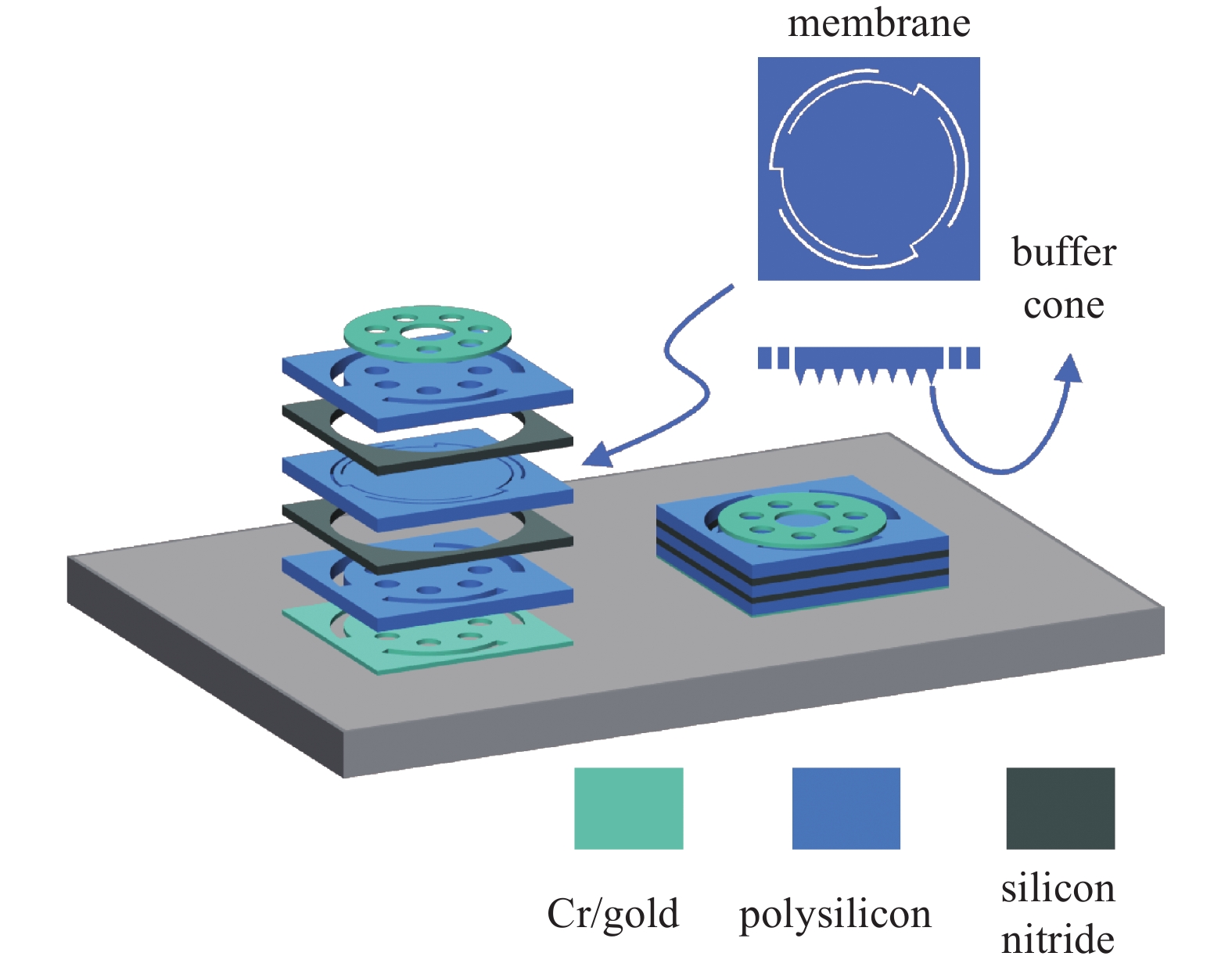
本文提出的扬声器采用双背板结构，可以补偿振膜的介质恢复力，增加扬声器的稳定性；在背板和电极上刻有声孔，用于调节振膜与背极板之间的声学阻抗；振膜边缘的悬臂梁结构来可以降噪和降低工作电压；通过缓冲锥结构可以降低振膜下拉无法恢复的可能性，增加扬声器的可靠性。背板和振膜均由多晶硅掺杂制成，电极由铬/金构成，空腔周围的支撑层由氮化硅构成。扬声器结构示意图如图3所示。
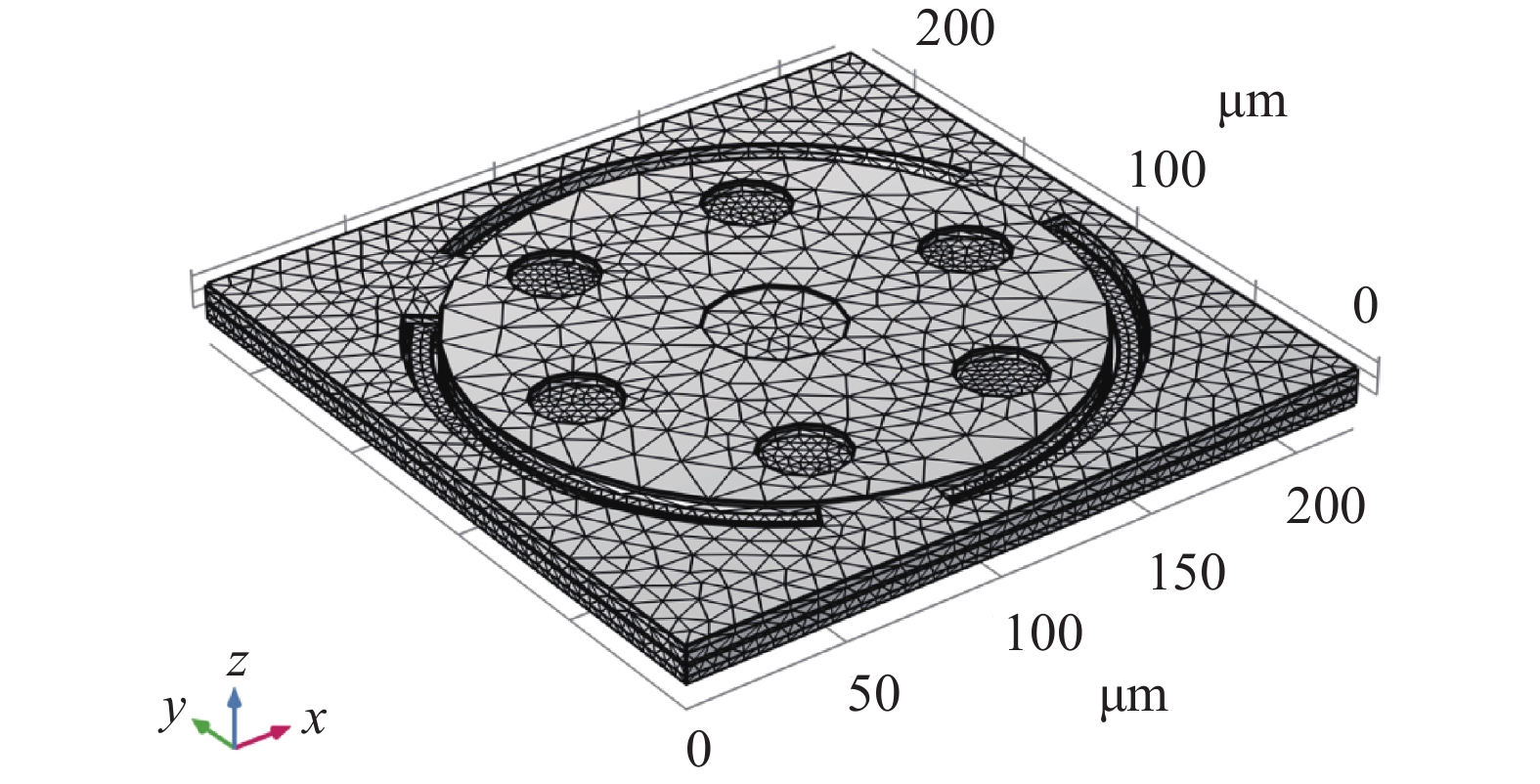
为了研究尺寸、固有频率等因素对扬声器振膜位移的影响以及扬声器微元对单位阶跃脉冲的响应，在Comsol Multiphysics中对其进行了建模。扬声器微元有限元模型如图4所示。
-
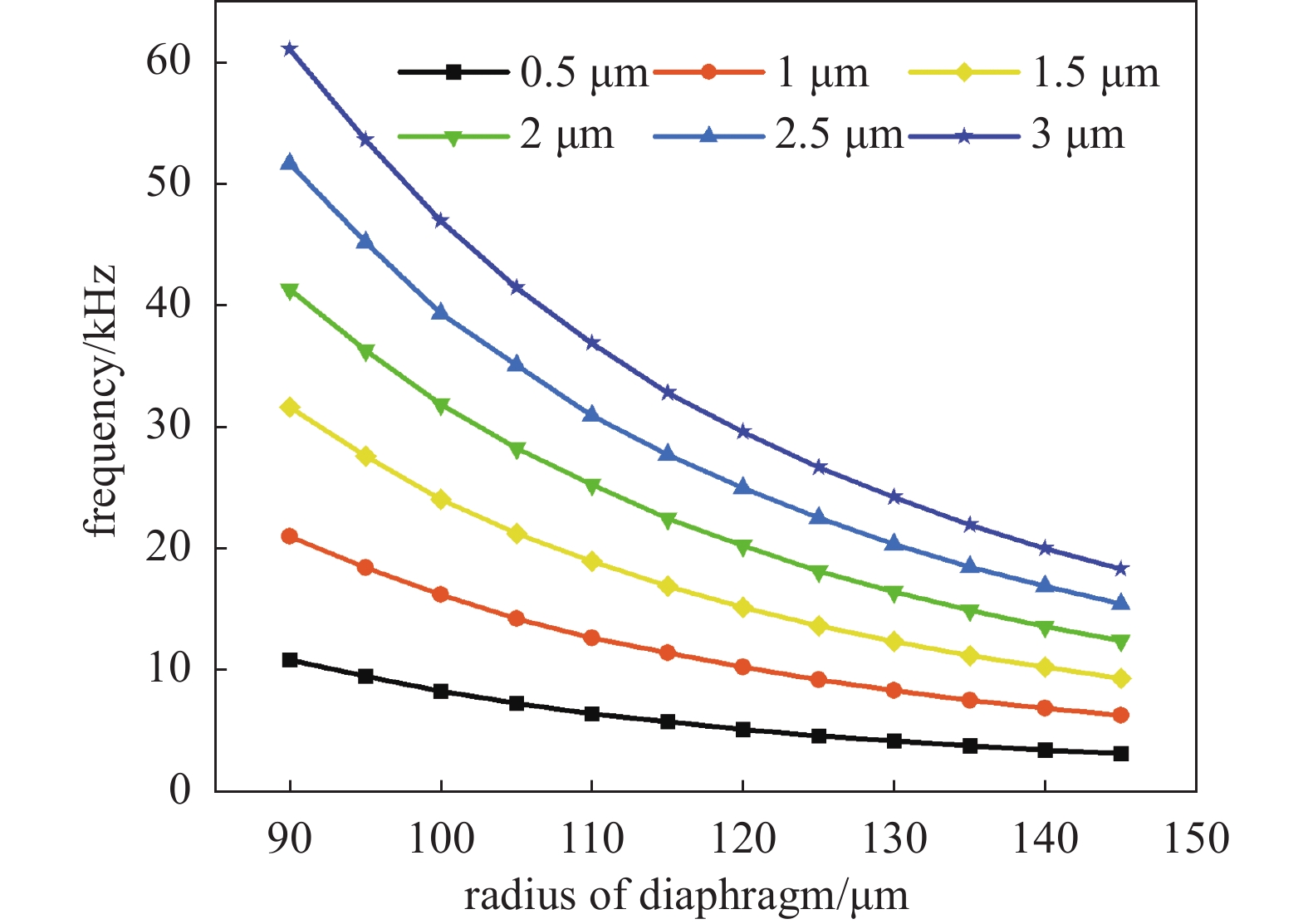
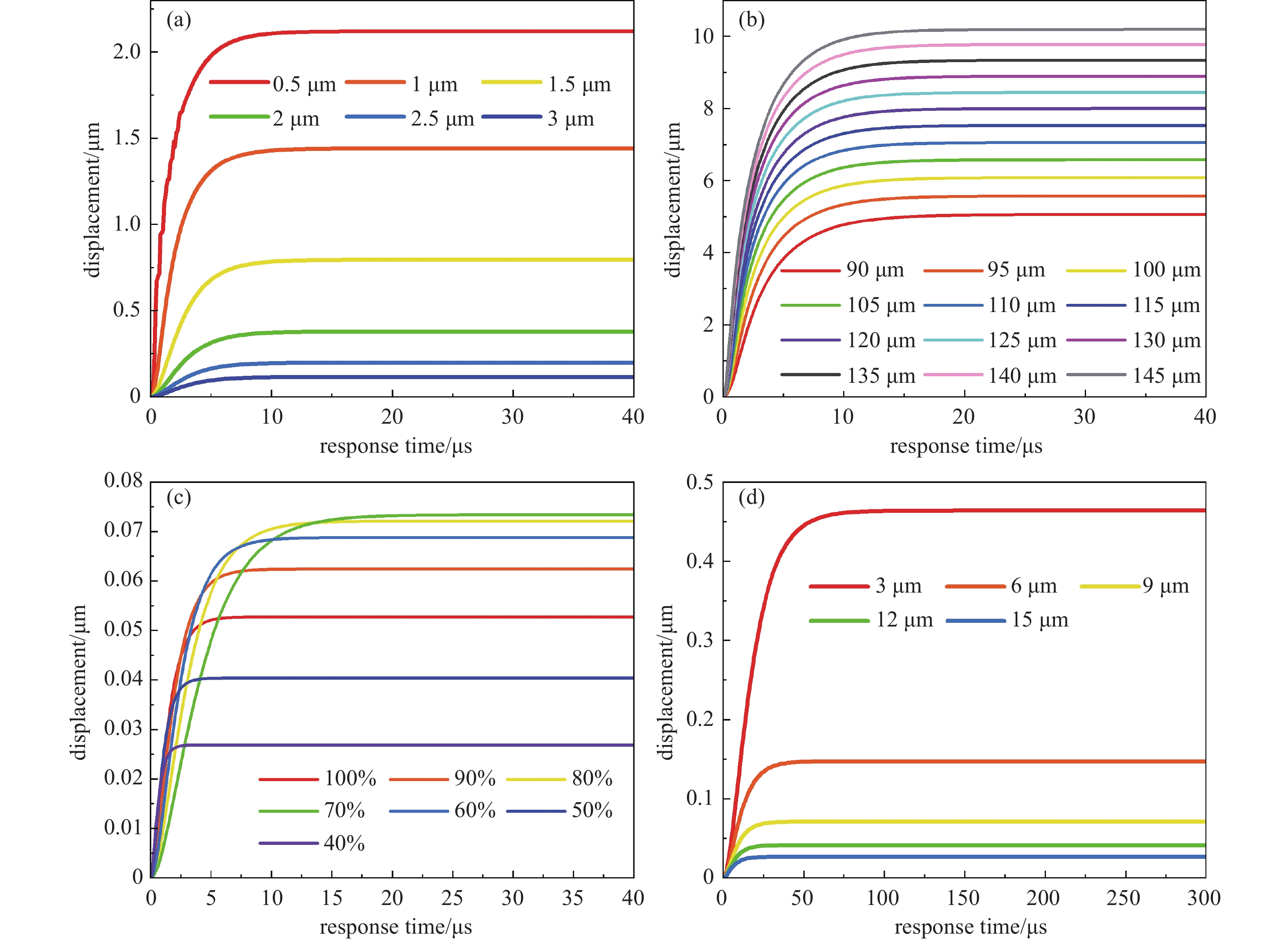
研究表明谐振频率是扬声器的固有属性，只与振膜材料性质和几何参数有关，选择扬声器的振膜半径从90 μm开始，以5 μm为间隔增加至145 μm，选择扬声器的振膜厚度从0.5 μm开始，以0.5 μm为间隔增加至3 μm，结果如图5所示。图中的各条曲线代表不同厚度的振膜，可以看出谐振频率随振膜半径的减小或厚度的增加而增加，其关系如方程(12)所示。
其中，
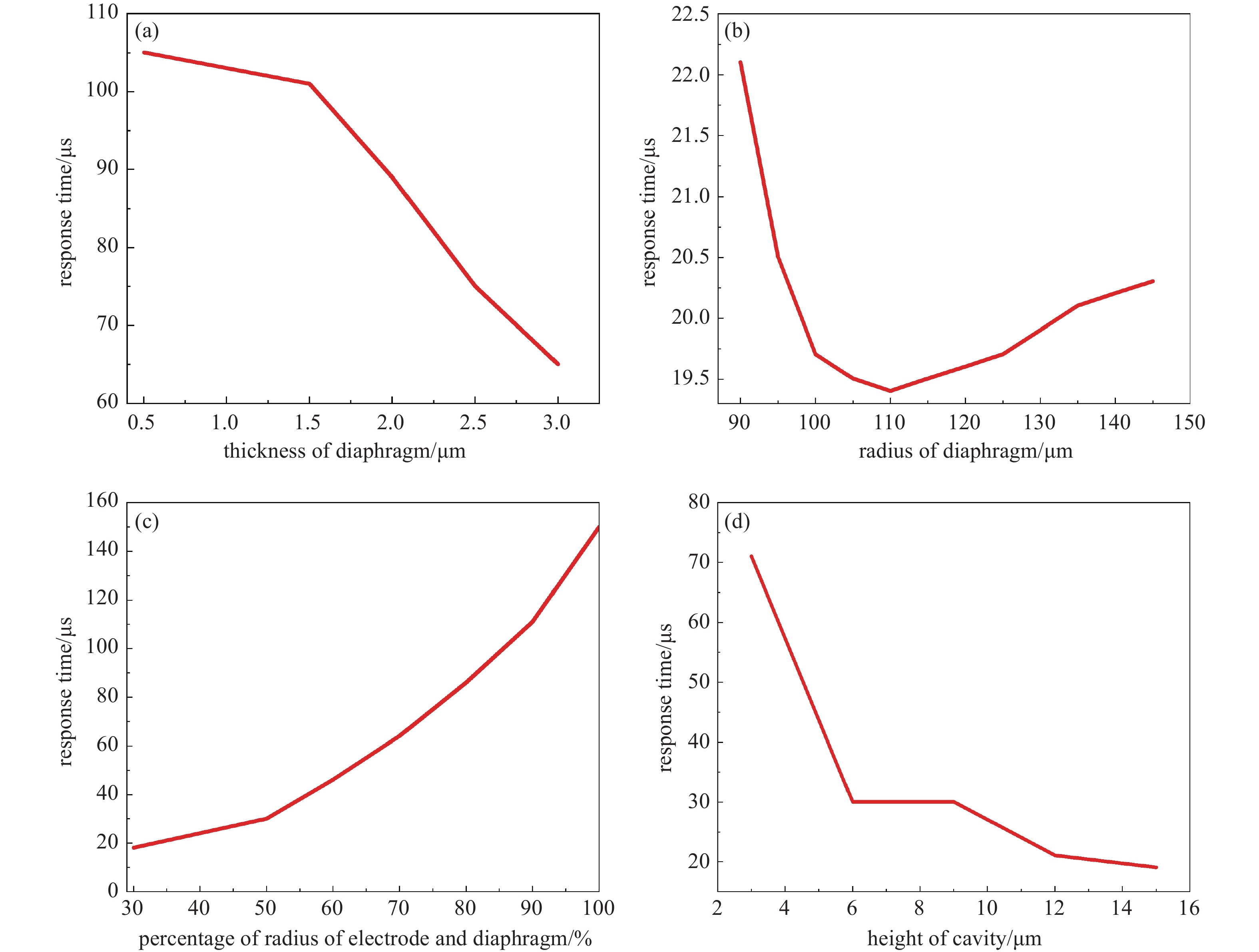
$h$ 为振膜厚度，$D$ 为振膜直径，$ f\mathrm{_r} $ 为谐振频率，$Y$ 为杨氏模量，$\rho $ 为振膜材料密度，$\sigma $ 为泊松比。在数字音频重建中，响应时间应该足够短，以便能够迅速对输入的数字脉冲做出反应，同时在两个采样点之间完成声波的生成和衰减；而振膜的最大位移决定声压级输出大小。综上，分别对振膜厚度、振膜半径、电极/振膜半径比、空腔高度进行控制变量，分析上述参数对振膜最大位移和响应时间的影响，以此确定扬声器的几何参数。
选择振膜厚度从0.5 μm开始，以0.5 μm为间隔增加至3 μm，结果如图6(a)、图7(a)所示。可以看出振膜最大位移随着振膜厚度的增加而减小，其响应时间随着振膜厚度的增加而减少，说明振膜厚度的增加会增加膜片的刚度，降低膜片的应变，使膜片更快到达最大位移，综合考虑选择膜片厚度为1 μm。
选择振膜半径从90 μm开始，以5 μm为间隔增加至145 μm，结果如图6(b)、图7(b)所示。可以看出振膜最大位移随着振膜半径的增加面增加，其响应时间与振膜半径并非正比关系，在受到相同静电力的情况下，当振膜半径增大，其应变增大，当振膜半径增大到一定程度时，达到最大位移所需应变时间变长，而响应时间在110 μm时最小，因此振膜半径选择110 μm。
选择电极/振膜半径比从40%开始，以10%为间隔增加至100%，结果如图6(c)、图7(c)所示。可以看出振膜最大位移与电极/振膜半径比非正比关系，响应时间随电极/振膜半径比的增加而增加，当电极/振膜半径比减小时振膜中心受到的静电力增大，到达最大位移的时间减少，但由于电极边缘会产生弯曲力矩，其位移峰值约为振膜峰值半径的70%，因此电极/振膜半径比选择40%。
选择空腔总高度从3 μm开始，以3 μm为间隔增加至15 μm，结果如图6(d)、图7(d)所示。可以看出振膜最大位移随空腔高度增加而减少，其响应时间随空腔高度的增加而减少，空腔高度增加会使振膜受到的静电力减小，降低应变，使振膜更快到达最大位移，当形变相同时，静电力的减小会使响应时间增加，但静电力对响应时间的影响并非主要因素，所以图7(d)中响应时间出现平台现象后继续减少。振膜最大位移受空腔高度限制，从而影响声压级的输出，但空腔高度的增加会使工作电压过大，因此综合考虑选择空腔总高度为6 μm。
通过有限元分析进行结构优化并结合当前工艺，静电MEMS扬声器结构参数如表1所示。
-
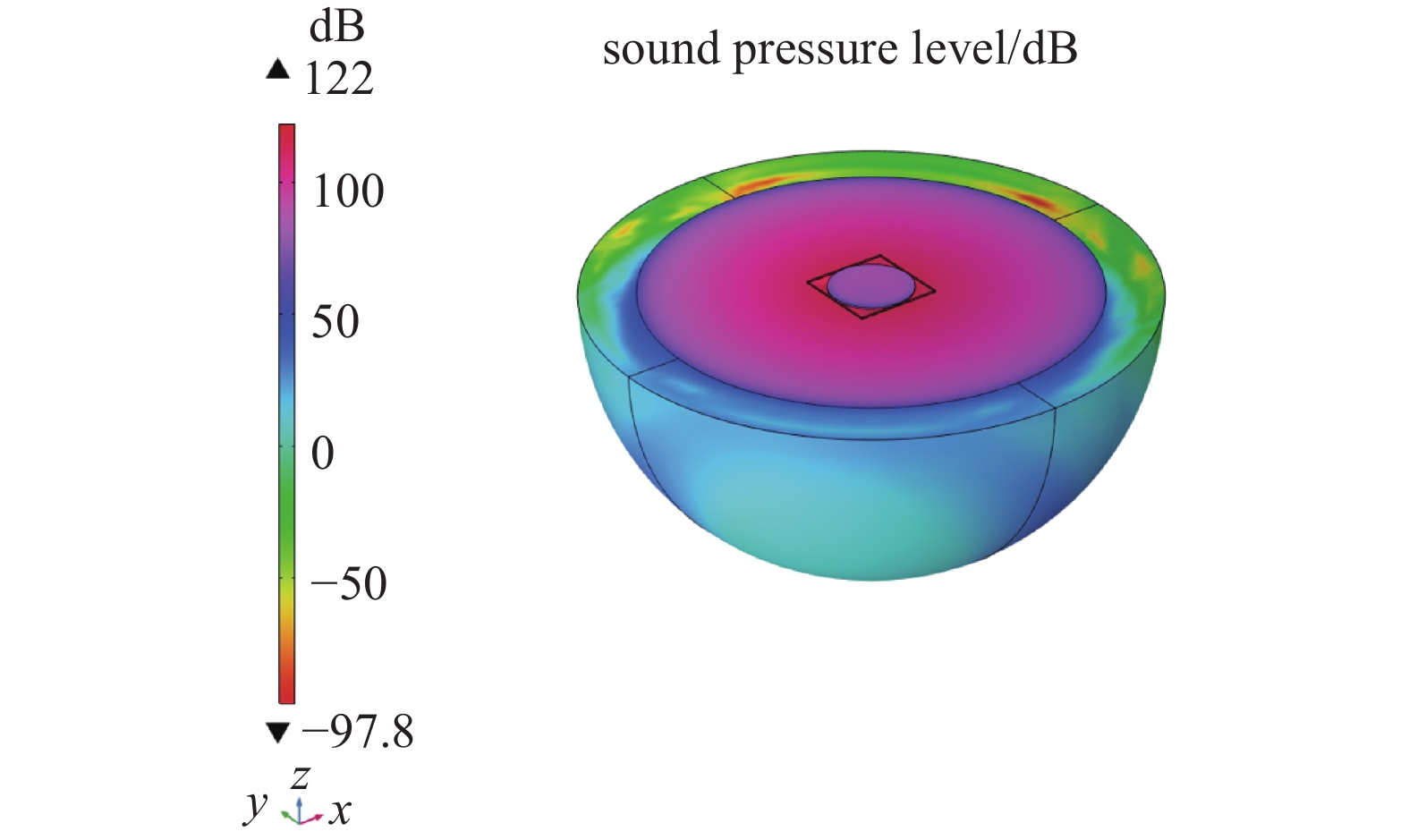
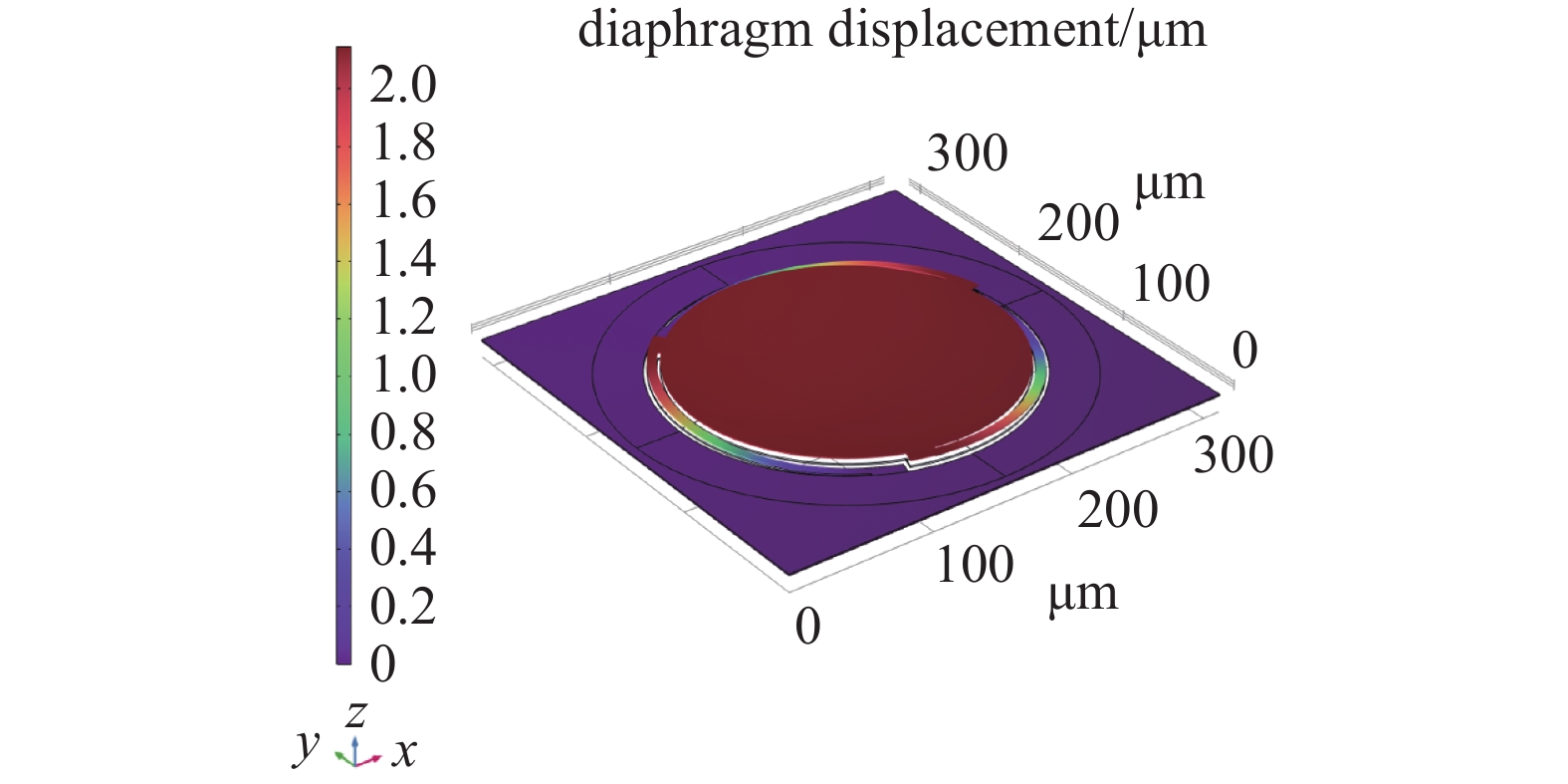
在固体力学、静电、压力声学物理场中对扬声器进行三维建模，扬声器的振膜位移及声场仿真结果如图8、图9所示。
本文提出的静电MEMS扬声器在12 V直流电压，12 V交流电压40 kHz、1 mm处的条件下测试，可以产生46.035 dB的声压级，在24 V恒定电位输入下，振膜可以在23 μs内达到2.14 μm最大位移。相较文献[7]中提出的扬声器，在90 V电压测试下，声音输出水平为35 dB，在150 V恒定电位输入下，振膜大约需要125 μs才能达到1.5 μm的最大位移，性能有所提高。
-
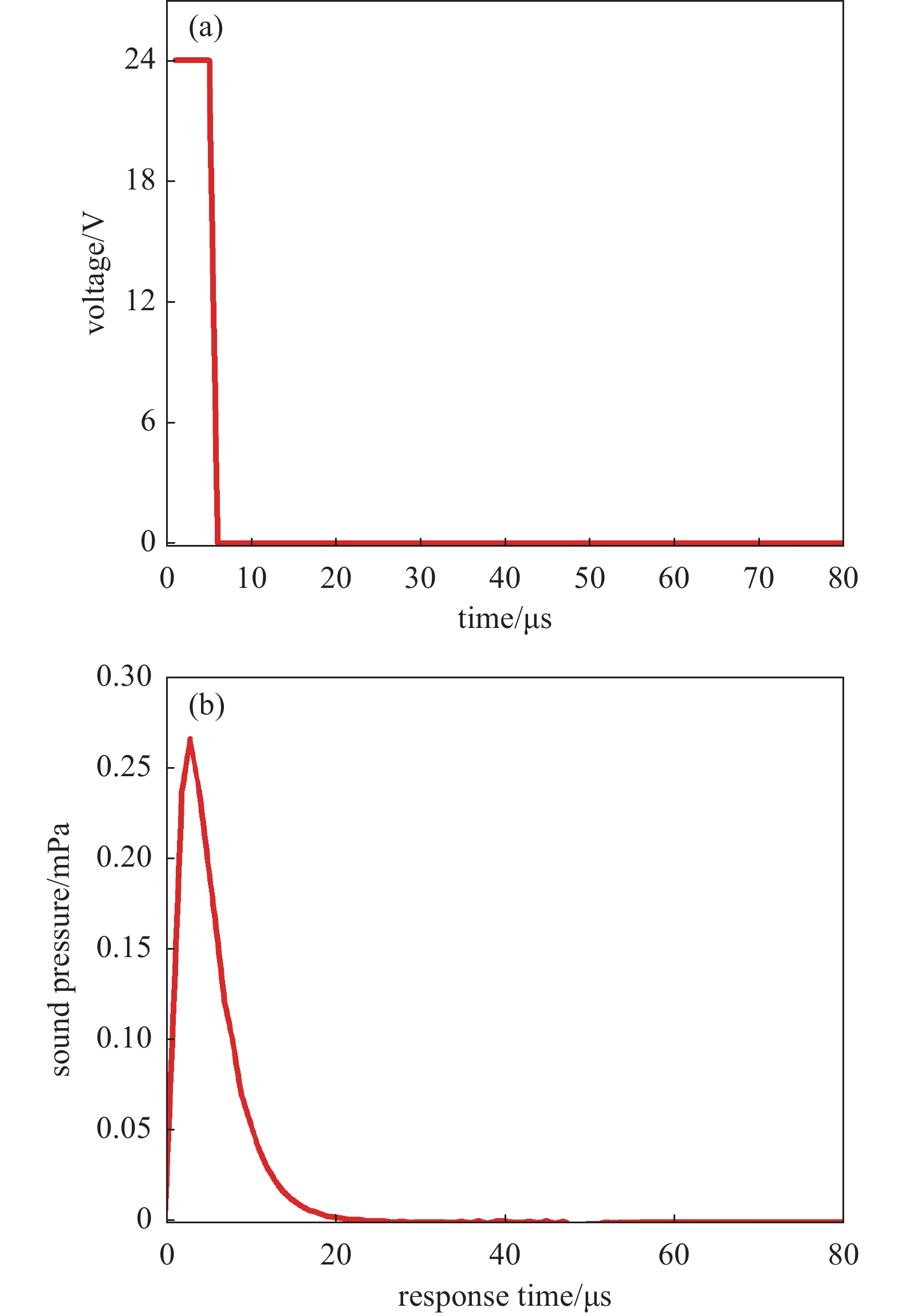
由于数字扬声器是通过振膜的激励和数字信号的处理发声，扬声器的振膜有两种启动方式，重置模式和无复位模式。重置模式指在每个数字位后将膜设置回初始位置，会产生周期性的负声波和正声波；无复位模式将膜保持在全振幅的状态，直到设置下一位，通过无复位模式可以抵消负声波或将模的势能传递到下一比特。本文利用COMSOL有限元软件，采用无复位模式，设置两个扬声器微元，通过时延的方式来抵消第一个扬声器产生的负声压。通过仿真实验对扬声器的声学响应进行分析，结果如图10所示。由图可见，在高度为24 V，宽度5 μs的矩形脉冲激励下，扬声器的声学输出在1 mm处为2.66×10−4 Pa且在不到23 μs的时间内降至0(或可忽略不计)，因此，当使用宽度小于5 μs矩形脉冲对振膜进行激励时，扬声器响应时间均小于23 μs，这意味着本设计中的扬声器可以满足第1部分中提到的第一个要求，以44.1 kHz的采样率对声音进行数字重建。
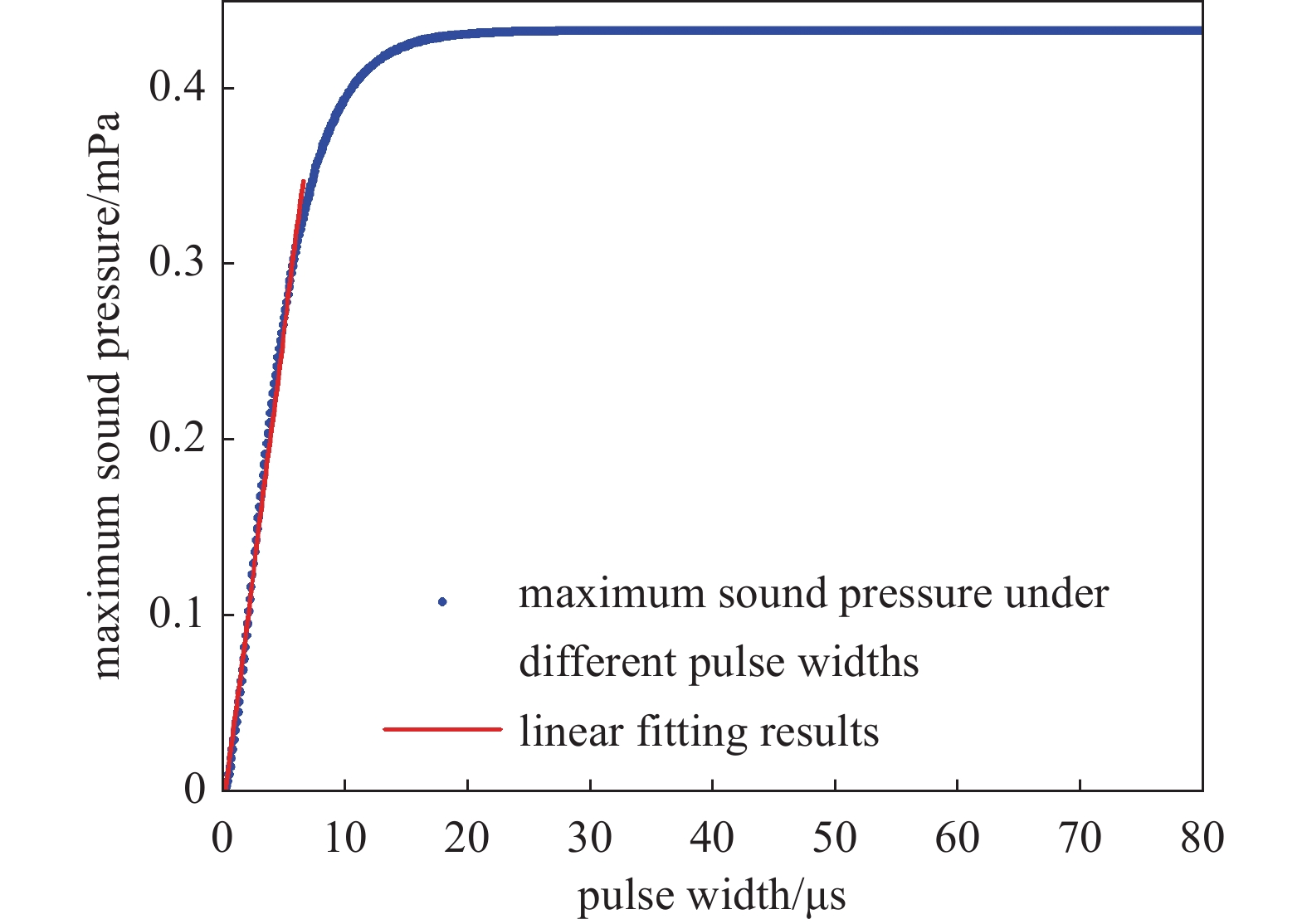
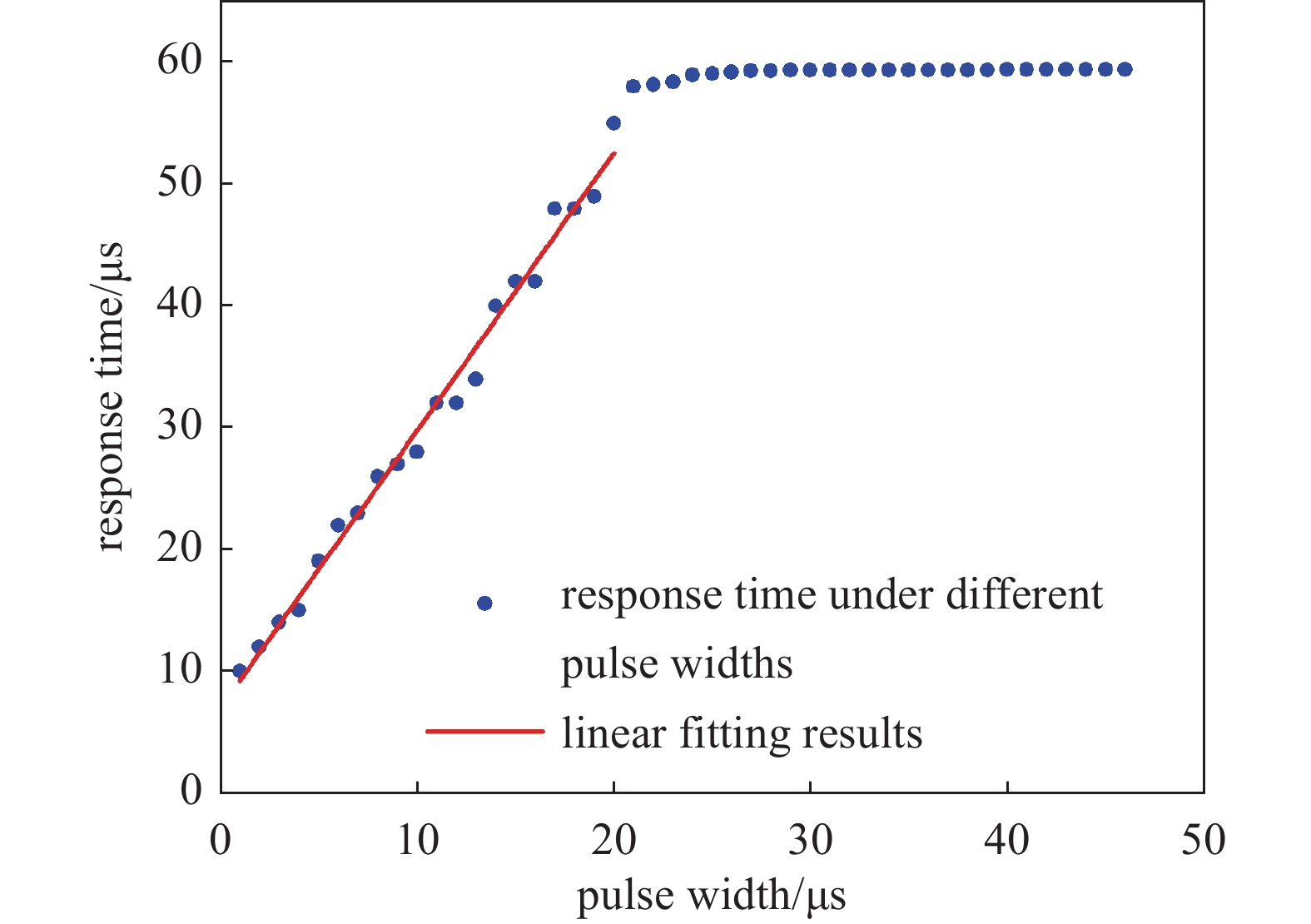
如图11所示，扬声器产生的最大压力与脉冲宽度之间的关系是非线性的，但是在0到20 μs呈线性关系。而响应时间则是在0到6 μs内呈线性关系，如图12所示。因此当激励脉冲宽度小于5 μs时，扬声器声学输出的最大压力及响应时间呈线性关系。
$ {R}^{2} $ 系数为分别为0.99302和0.98936，线性回归方程如表2所示。由于系数大于0.95，这说明本设计的扬声器可以满足数字重建的第三个要求，声学输出满足线性相加。 -
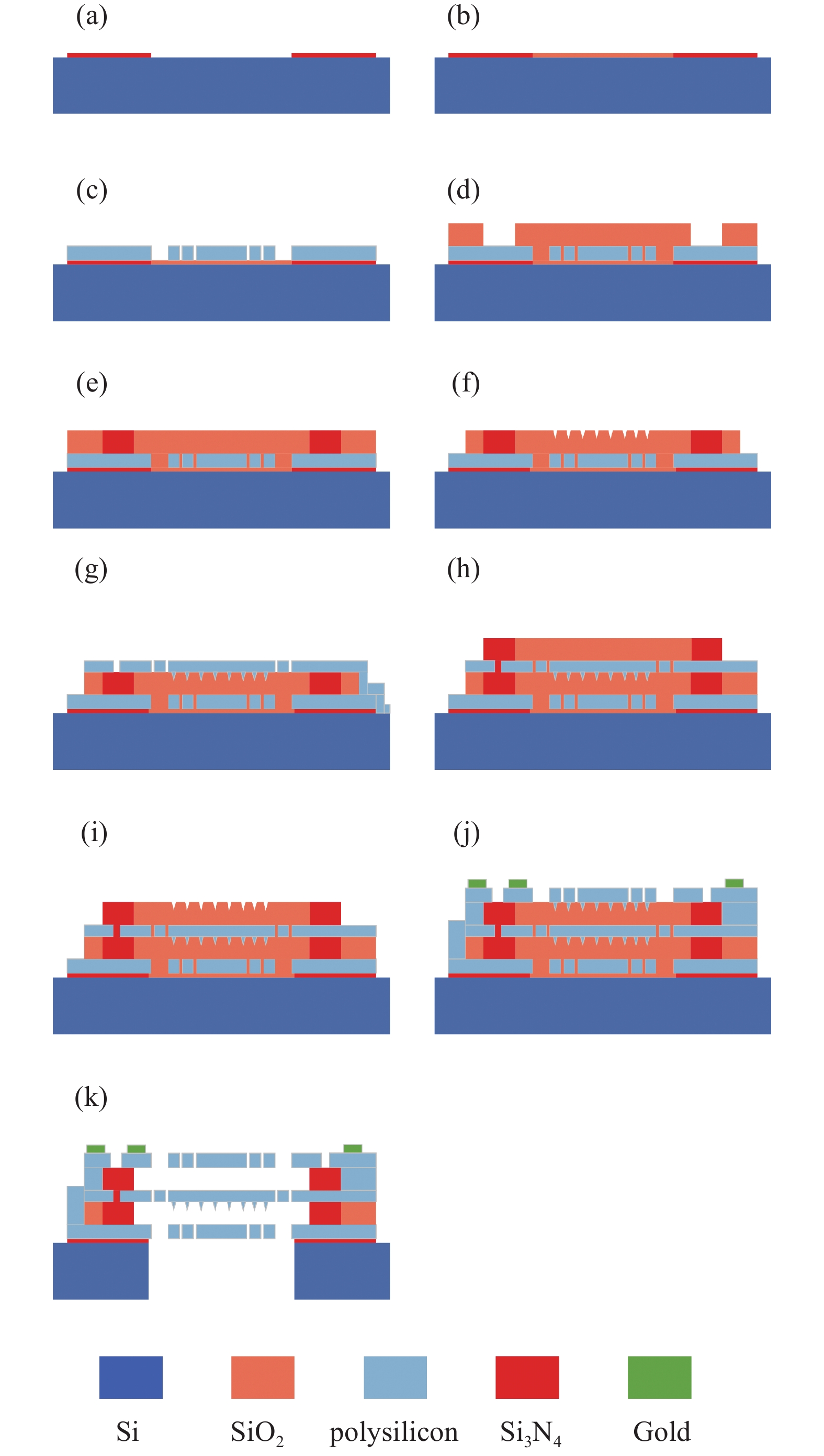
本文提出的扬声器工艺流程如图13所示。
（1）首先在单晶硅上形成前端结构两侧介质层，由氮化硅组成，如图13(a)所示。
（2）前端结构两侧介质层中淀积光刻形成中间介质层，由二氧化硅组成，用作刻蚀停止层，如图13(b)所示。
（3）在前端结构上通过淀积多晶硅、掺杂和光刻形成下背板结构，如图13(c)所示。
（4）在下背板上淀积一层二氧化硅用作牺牲层，然后在氧化层两侧刻蚀形成沟槽，如图13(d)所示。
（5）在两侧沟槽中形成氮化硅并进行平坦化工艺，如图13(e)所示。
（6）通过刻蚀在下牺牲层形成凹陷用作形成缓冲锥，如图13(f)所示。
（7）在下牺牲层上淀积多晶硅、掺杂和光刻形成振膜结构和形状，如图13(g)所示。
（8）在振膜上淀积二氧化硅光刻后在两侧淀积氮化硅，之后进行平坦化工艺，如图13(h)所示。
（9）在上牺牲层刻蚀凹陷，如图13(i)所示。
（10）在上牺牲层通过淀积多晶硅、掺杂和光刻形成上背板结构，然后通过金属剥离技术形成电极，如图13(j)所示。
（11）通过深反应离子刻蚀出背腔，释放牺牲层，如图13(k)所示。
-
本文针对当前基于DSR技术的扬声器再现声音动态范围窄、失真严重的问题，提出了一种可用于DSR技术的静电MEMS扬声器，具有良好的响应速度和线性输出。扬声器采用双背板结构以及悬臂梁和缓冲锥的复合式振膜结构。通过Comsol Multiphysics有限元仿真对扬声器进行结构优化，研究了振膜厚度、振膜半径、电极/振膜半径比、空腔高度对扬声器在恒定电压激励下声学响应的影响，并综合考虑确定几何结构参数。基于上述几何结构参数进行对扬声器性能进行仿真。结果表明，本文提出的静电MEMS扬声器在12 V直流电压，40 kHz、12 V交流电压、1 mm处的条件下测试，可以产生46.035 dB的声压级，在24 V恒定电位输入下，振膜可以在23 μs内达到2.14 μm最大位移。之后对扬声器性能进行分析，验证扬声器在宽度小于5 μs的矩形脉冲激励下响应时间小于23 μs，声学输出的最大压力及响应时间与激励脉冲呈线性关系，满足数字化音频重建条件，可用DSR技术，为实现高质量的音频体验和精确的声音再现提供技术支持。
基于数字声音重建的静电MEMS扬声器设计
Design of Electrostatic MEMS Speaker Based on Digital Sound Reconstruction
-
摘要: 针对目前基于数字声音重建技术的扬声器再现声音动态范围窄、失真严重的问题，设计了一种响应速度快、声学输出可线性相加的静电MEMS扬声器。该扬声器采用了包括双背板、悬臂梁和缓冲锥的复合式振膜结构，显著降低了扬声器的振膜刚度和提高了振动自由度，从而优化了扬声器的工作效率并减少了响应时间。利用Comsol Multiphysics软件对扬声器进行几何结构参数优化和性能仿真，确定当扬声器的振膜厚度为1 μm，振膜半径为110 μm，电极/振膜比为40%，空腔高度为6 μm时综合性能最优，结果证明该扬声器的声学响应时间低于23 μs且声学输出满足线性相加，这表明该扬声器具有良好的声学响应，为实现数字声音重建提供良好技术支持。最后，基于MEMS加工工艺设计了静电MEMS扬声器的工艺流程。Abstract: Aiming at tackling the current challenges of limited dynamic range and significant distortion in digital audio reconstruction with speakers, we have developed an electrostatic MEMS (Micro-Electro-Mechanical Systems) speaker with rapid response and linearly summable acoustic output. The speaker incorporates a composite diaphragm structure featuring a dual backplate, cantilever beam, and buffering cone, which significantly reduces the diaphragm's stiffness and enhances its vibrational freedom. Consequently, this design optimizes the operational efficiency and reduces response time. Utilizing Comsol Multiphysics software, we conducted geometrical optimization and performance simulation of the speaker and the optimum combination of structural parameters is determined as follows: the film thickness of the loudspeaker is 1 μm, the film radius is 110 μm, the electrode/film ratio is 40%, and the cavity height is 6 μm. The results confirmed that the acoustic response time of the speaker is under 23 μs, and the acoustic output adheres to the principles of linear superposition, indicating a high-quality acoustic response. These findings suggest that the speaker provides robust technical support for the implementation of digital audio reconstruction. Finally, we have designed a fabrication process for the electrostatic MEMS speaker based on MEMS manufacturing techniques, ensuring the device's precision and performance in real-world applications.
-
-
图 1 扬声器启动数量与量化后的输入信号关系
Figure 1. The relationship between the number of speaker activations and the quantized input signal
图 5 谐振频率随振膜半径及厚度的变化结果
Figure 5. The variation of resonant frequency with the radius and thickness of the diaphragm
图 6 不同参数对位移的影响。（a）振膜厚度，（b）振膜高度，（c）电极/振膜半径比，（d）空腔高度
Figure 6. Effect of different parameters on displacement. (a) Film thickness, (b) film height, (c) electrode/film radius ratio, (d) cavity height
图 7 不同参数对响应时间的影响。（a）振膜厚度，（b）振膜半径，（c）电极/振膜半径比，（d）空腔高度
Figure 7. Effect of different parameters on response time. (a) Film thickness, (b) film radius, (c) electrode/film radius ratio, (d) cavity height
图 10 矩形机械脉冲及声学响应。（a）矩形脉冲，（b）声学响应
Figure 10. Rectangular mechanical pulses and acoustic response. (a) Rectangular pulse, (b) acoustic response
图 11 最大声压与脉冲宽度的关系
Figure 11. Relationship between maximum sound pressure and pulse width
图 13 扬声器工艺流程。（a）前端结构，（b）填充介质层，（c）背板结构，（d）牺牲层和沟道，（e）填充沟道，（f）刻蚀凹槽，（g）振膜结构，（h）牺牲层，（i）刻蚀凹槽，（j）第二个背板结构和电极，（k）牺牲释放
Figure 13. Process flow of speaker. (a) Front structure, (b) filled dielectric layer, (c) backplate structure, (d) sacrificial layer and Channel, (e) filling channels, (f) etching depression, (g) diaphragm structure, (h) sacrificial layer, (i) etching depression, (j) second backplate structure and electrodes, (k) sacrifice and release
表 1 静电MEMS扬声器有限元模型参数
Table 1. FEM parameters of electrostatic MEMS speaker
结构层 材料 半径/μm 厚度(高度)/μm 电极(上/下) 铬、金 30/110 0.2 振膜 多晶硅 110 1 背板(上/下) 多晶硅 110 3 空腔(上/下) / 110 3 
下载: 导出CSV
表 2 线性回归结果
Table 2. Linear regression results
关系 ${R^2}$ 线性方程 最大声压和脉冲宽度 0.99302 $ M_{\mathrm{p}}=550.835W_{\mathrm{p}}-1.6525\times10^{-4} $ 响应时间和脉冲宽度 0.98936 $ R\mathrm{_T}=2.2812W_{\mathrm{p}}+6.9473\times10^{-6} $
下载: 导出CSV
-
[1] Wang H, Ma Y, Zheng Q, et al. Review of recent development of MEMS speakers[J]. Micromachines,2021,12(10):1257 doi: 10.3390/mi12101257 [2] Zawawi S A, Hamzah A A, Majlis B Y, et al. A review of MEMS capacitive microphones[J]. Micromachines,2020,11(5):484 doi: 10.3390/mi11050484 [3] Gemelli A, Tambussi M, Fusetto S, et al. Recent trends in structures and interfaces of MEMS transducers for audio applications: A review[J]. Micromachines,2023,14(4):847 doi: 10.3390/mi14040847 [4] Hall N A, Okandan M, Littrell R, et al. Simulation of thin-film damping and thermal mechanical noise spectra for advanced micromachined microphone structures[J]. Journal of microelectronmechanical systems,2008,17(3):688−697 doi: 10.1109/JMEMS.2008.918384 [5] 高铁成, 远桂民, 王昊. 电容式微机械超声换能器的设计与仿真[J]. 天津工业大学学报,2021(4):84−88 (in Chinese) Gao T C, Yuan G M, Wang H. Design and simulation of air-coupled CMUT[J]. Journal of Tiangong University,2021(4):84−88 [6] 程先哲, 杨鹏, 张勇等. 基于石墨烯薄膜的静电扬声器理论建模与仿真分析[J]. 电子测量与仪器学报,2017,31(12):1896−1901 (in Chinese) Cheng X A, Yang P, Zhang Y, et al. Theoretical modeling and simulation analysis of electrostatic loudspeaker based on graphene membrane[J]. Journal of Electronic Measurement and Instrumentation,2017,31(12):1896−1901 [7] Arevalo A, Castro D, Conchouso D, et al. Digital electrostatic acoustic transducer array[C]. In2016 IEEE 11th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS) 2016 Apr 17: 225−228 [8] Arevalo A, Byas E, Conchouso D, et al. A versatile multi-user polyimide surface micromachinning process for MEMS applications[C]. In10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems 2015 Apr 7: 561−565 [9] Zheng Z, Yao Y, Liu J A, et al. Highly sensitive CMUT-based humidity sensors built with nitride-to-oxide wafer bonding technology[J]. Sensors and Actuators B: Chemical,2019,294:123−131 doi: 10.1016/j.snb.2019.05.003 [10] Garud M V, Pratap R. A novel MEMS speaker with peripheral electrostatic actuation[J]. Journal of Microelectromechanical Systems,2020,29(4):592−599 doi: 10.1109/JMEMS.2020.3003463 [11] 丁琦. 基于电容式微机械超声换能器的微压传感器研究[D]. 中北大学, 2022 (in Chinese) Ding Q. Research of micro pressure sensor based on capacitive micromachined ultrasonic transducer[D]. 2022, North University of China [12] Verreault A, Cicek P V, Robichaud A. A surface-micromachined levitating MEMS speaker[C]. In2022 20th IEEE Interregional NEWCAS Conference (NEWCAS), 2022, 134−138 [13] Anzinger S, Bretthauer C, Wasisto H S, et al. Dual-backplate CMUTs with wide bandwidth and low driving voltage for airborne applic-ations[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,2023,70(10):1286−1294 doi: 10.1109/TUFFC.2023.3309997 [14] Diamond B M, Neumann J J, Gabriel K J. Digital sound reconstruction using arrays of CMOS-MEMS microspeakers[C]. InTRANSDUCE-RS'03. 12th International Conference on Solid-State Sensors, Actuators and Microsystems. Digest of Technical Papers (Cat. No. 03TH8664), 2003, 238−241 [15] Busbridge S C, Fryer P A, Huang Y. Digital loudspeaker technology: current state and future developments[C]. InAudio Engineering Society Convention 112 2002 Apr 1, 2002, 205−209 [16] Tumpold D. Modeling and optimization methods of an electrostatically driven MEMS speaker[D]. Shaker, 2014 [17] 马登永, 蔡野锋, 沐永生, 等. 全数字式扬声器阵列系统的设计与实现[J]. 电声技术,2011,35(011):25−29 (in Chinese) Ma D Y, Cai Y F, Mu Y S, et al. Design and implementation of all-digital loudspeaker array system[J]. Loudspeaker and Microphone,2011,35(011):25−29 [18] 徐宁. 微型声频定向扬声器相控阵聚焦研究[D]. 杭州: 电子科技大学, 2013 (in Chinese) Xu N. Micro audio directional system phase array research[D]. Hangzhou: University of Electronic Science and Technology of China, 2013 [19] 金瑞. 基于SDM和平板换能器技术的数字直驱扬声器创新设计[J]. 昆明冶金高等专科学校学报,2018,34(1):28−35 (in Chinese) Jin R. Innovative design of digital direct-drive loudspeaker based on SDM and plate transducer technology[J]. Journal of Kunming Metallurgy College,2018,34(1):28−35 [20] Kontomichos F, Mourjopoulos J, Tatlas N A. Alternative encoding techniques for digital loudspeaker arrays[C]. InAudio Engineering Society Convention 122, 2007, 2 , 881−889 -
计量
- 文章访问数: 192
- HTML全文浏览数: 192
- PDF下载数: 4
- 施引文献: 0